首页
登录
注册
-
铁电钙钛矿氧化物凭借其独特的自发极化特性及在外场(电场、力场)下的动态响应能力, 已成为现代电子器件的核心功能材料[1,2]. 这类材料不仅表现出优异的铁电性、压电性和介电性, 还因其高居里温度、高极化稳定性及低损耗特性, 在非易失性存储器[3,4]、高精度压电传感器[5-7]、高频滤波 器[8]等关键器件中得到了广泛应用, 同时也在医疗超声成像、精密机电系统及微机械执行器等[9-11]领域展现出卓越的应用潜力.
随着柔性电子技术的快速发展, 例如可穿戴健康监测设备、人工电子皮肤、仿生软体机器人等, 对兼具高电子性能与力学柔韧性的铁电材料提出了新的挑战[12-15]. 然而, 传统无机铁电氧化物由于其强离子键或共价键主导的晶体结构, 使得材料表现出较高的本征脆性. 此外, 刚性基底的力学夹持效应进一步抑制了铁电畴的自由演化, 降低了材料的极化翻转效率和电滞回线对外场的动态响应能力[16,17]. 这些因素严重制约了传统铁电材料在柔性电子领域的应用. 因此, 如何在保持优异铁电性能的同时提高材料的力学柔韧性, 成为柔性铁电器件发展的关键科学问题. 近年来, 薄膜新制备技术的快速发展, 给具有优异力学弹性和电学性能的高质量自支撑铁电薄膜的突破提供了新思路. 例如, 通过脉冲激光沉积(PLD)技术结合牺牲层刻蚀技术(如Sr3Al2O6水溶层)等新制备方法, 研究者成功制备了自支撑单晶铁电薄膜[18-23](如BaTiO3, BiFeO3). 这些薄膜在180°折叠过程中不产生断裂, 并且在移除弯曲负载后能够恢复至初始形态, 从而克服了刚性基底的约束. 更重要的是, 得益于应变工程和应变梯度工程的调控, 这些自支撑铁电薄膜在极化分布和拓扑畴结构方面展现出更丰富的可调控性. 在此背景上, (PbTiO3)n/(SrTiO3)n超晶格体系因其原子级异质界面设计成为近年来铁电材料研究的热点. 该体系中的界面应变、静电耦合与梯度能量协同作用, 使得其能够稳定多种非平凡铁电畴结构, 包括通量闭合畴[24]、极性涡旋[25-27]、斯格明 子[28]等拓扑畴态. 例如, Yadav等[25]通过扫描透射电子显微镜在(SrTiO3)10/(PbTiO3)10超晶格中观察到周期性涡旋-反涡旋阵列, 其中极化矢量沿闭合路径连续旋转. 而这些拓扑畴的形成源于多能量竞争的动态平衡: 晶格不匹配导致的弹性能、PbTiO3到SrTiO3层的极化不连续性带来的静电能以及改变极化方向或大小所需的梯度能, 而周期性极化旋转的出现有效地降低了系统的总自由能.
在铁电薄膜研究中, 应变工程已被广泛用于调控晶格畸变, 从而影响畴结构的稳定性和极化翻转动力学. 经典的热力学理论指出, 面内压缩应变可抑制PbTiO3中的面内a畴的产生, 促使面外c畴占主导, 从而提升剩余极化强度. 然而, 在柔性器件的实际工作环境中, 薄膜往往处于非均匀应变状态, 导致材料内部出现显著的应变梯度, 进而引发挠曲电效应[29]. 与均匀应变不同, 应变梯度不仅会改变局部极化方向, 还可能影响畴壁的演化动力学. 尽管已有研究初步探讨了单层铁电薄膜中应变梯度对铁电性能的影响[30-32], 但在多层异质结构(如(PbTiO3)n/(SrTiO3)n)中, 应变梯度与界面耦合的协同作用机制仍未完全厘清, 这一问题的解决对于优化柔性铁电异质结器件的电学与力学性能至关重要.
因此, 选择(SrTiO3)10/(PbTiO3)10/(SrTiO3)10 (STO/PTO/STO, 其中下标数字表示单位晶胞的数量)柔性异质三层膜模型作为研究对象, 本文系统性地探讨了该体系在不同弯曲应变梯度作用下的畴结构演化行为. 通过逐步调控弯曲曲率半径, 研究了U型弯曲与N型弯曲两种应变模式下铁电畴的演化规律, 并结合相场模拟计算了宏观电滞回线的变化趋势. 本文的研究结果揭示了弯曲应变梯度对多层铁电薄膜畴结构及极化翻转行为的影响机理, 进一步拓展了柔性力学调控策略在异质铁电结构中的应用潜力. 本研究不仅有助于理解多层铁电薄膜中力电耦合机制, 也为未来柔性铁电器件的铁电性能优化提供了理论基础.
-
本研究通过相场模拟方法, 研究了柔性铁电三层薄膜在弯曲变形(N型弯曲和U型弯曲)下的极化翻转行为. 模拟参数如表1所列[33,34]. 在相场方法中, 序参量是描述系统微观结构演化的核心变量. 它通常是一个随空间和时间变化的连续函数, 用于表征相变过程中材料不同相态的演化行为[35-37]. 在铁电相场模型中, 序参量P通常表示材料的自发极化, 其本质是一个三维矢量场: P = (Px, Py, Pz), 其中Px, Py, Pz分别表示沿x, y, z方向的极化分量(x, y, z三轴分别表示[100], [010]和[001]晶向). 极化P的空间分布决定了铁电材料的畴结构, 而不同畴的相互作用和演化受外部应力、电场、温度等因素调控. 特别地, 在柔性铁电薄膜系统中, 外加弯曲等力学变形会显著影响极化的空间分布, 从而导致畴结构的翻转. 极化矢量的动态演化由时间依赖性相场方程控制, 其形式为
其中r表示体系的空间坐标, t表示时间, L是与畴壁迁移率相关的动力学系数. 该演化方程描述了铁电极化随时间的弛豫过程, 最终达到稳定的热力学平衡态. F则表示由朗道自由能、梯度能、弹性能、静电能以及挠曲电耦合能共同组成的总自由能:
在无应力边界条件下, 薄膜体系的朗道自由能密度fLand可通过极化矢量的分量展开为多项式形式, 如下所示:
其中α1, α11, α12, α111, α112和α123为朗道自由能展开的材料系数, 其中, α1是与温度T有关的.
梯度能密度fgrad与极化的梯度相关, 描述了畴壁对总自由能的贡献部分. 可表示为
其中G11, G12, G44和
$ G_{44}' $ 为梯度能系数. 我们采用爱因斯坦记号表示张量, 下标中的逗号表示空间微分, 如$ {P_{i, j}} = \partial {P_i}/\partial {x_j} $ .系统的弹性能密度felas表示为
其中C11, C12和C44是弹性系数, eij表示弹性应变. 在多数钙钛矿体系中, 弹性应变
${e_{ij}} = {\varepsilon _{ij}} - \varepsilon _{ij}^0$ . 而本征应变$\varepsilon _{ij}^0$ 与材料的自发极化相关, 其关系为其中Q11, Q12和Q44是材料的电致伸缩系数.
静电能密度fele的表达式为
其中Ex, Ey和Ez是电场分量; ε0是真空介电常数; κb是材料的相对介电常数. 根据静电学理论, 内建电场可由
$ {E_i} = - {\varphi _{, i}} $ 表示, 其中φ是电势. 电势的分布通过静电平衡方程求解:此外, 如果考虑非均匀应变引入的应变梯度效应的话, 要引入体系的挠曲电耦合能fflexo, 其可以看作应变梯度与极化之间的耦合作用, 可以表达为
其中fijkl是挠曲电耦合系数, 对于立方晶体, 挠曲电耦合系数通常具有三个独立分量: 纵向耦合系数f11(= f1111)、横向耦合系数f12(= f1122)和剪切耦合系数f44(= f1212).
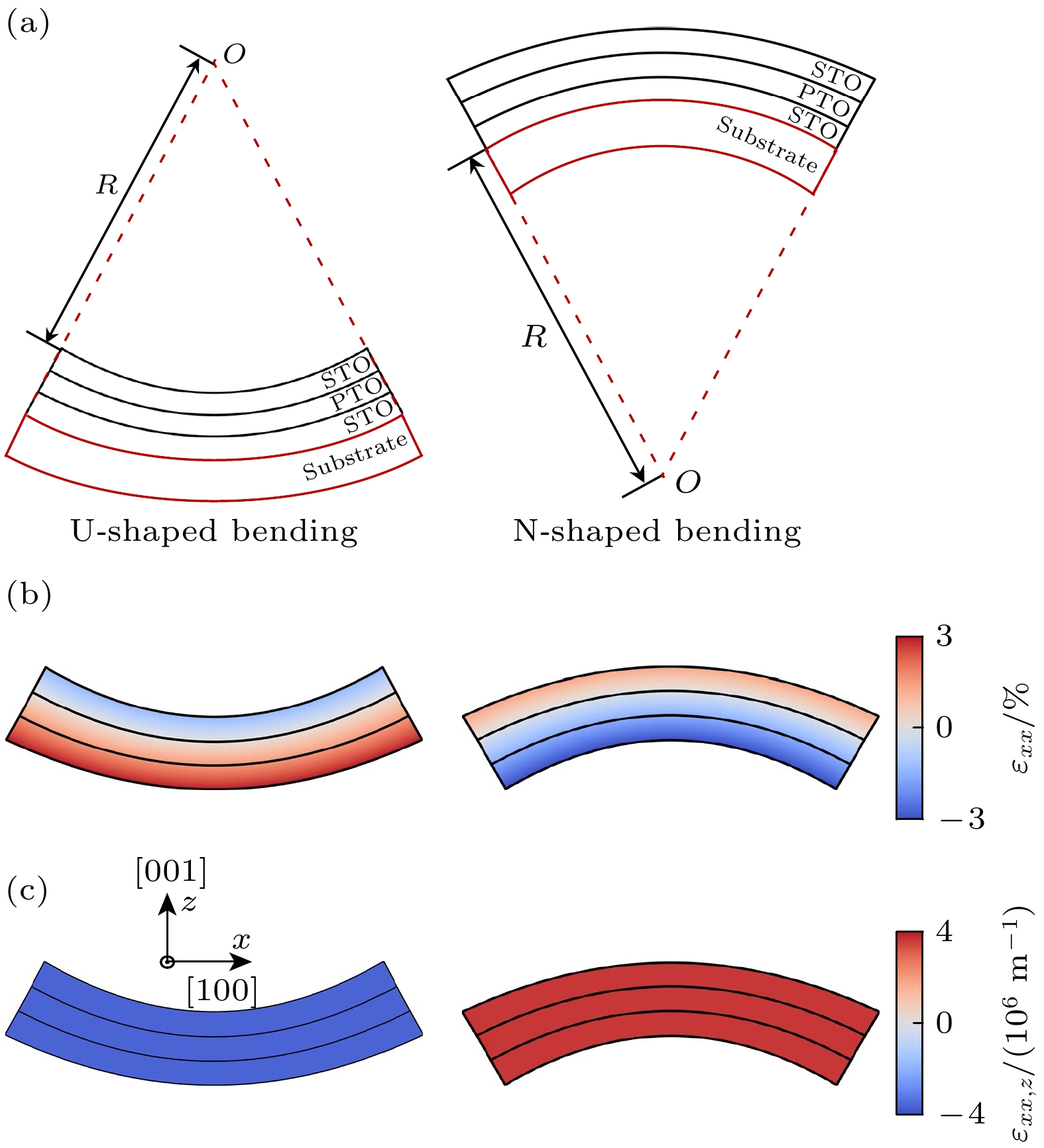
图1展示了柔性STO/PTO/STO三层铁电薄膜在U型(向上凹)和N型(向下凹)两种弯曲形变状态下的相场计算模型. 模拟尺寸为150Δx×150Δx×30Δx, 其中Δx = 0.4 nm. PTO和STO层的厚度均为10Δx. 模拟过程中, 薄膜顶部设定为自由应力边界, 而底部则与柔性衬底相连接, 以更真实地反映实验条件下的力学约束效应. 此外, 为了确保极化分布与应变场的空间连续性, 计算域在面内方向采用周期性边界条件, 避免由于边界效应导致的人工截断误差, 从而更准确地捕捉薄膜内部畴结构的演化特征. 其中, 在计算STO/PTO/STO三层铁电薄膜弯曲状态下的畴结构时采取的是开路电学边界条件 (
$ {{{D}}_i}{{{n}}_i} = 0 $ , Di是电位移矢量, ni指求解表面上法线的单位矢量n的分量); 而在计算电滞回线时为了与实验上电极状态一致, 因此采取短路边界条件(顶部和底部的电势设定为0 V或特定的外加电势). 薄膜顶部和底部的极化边界条件为自由边界条件. 图1(a)分别展示了U型和N型弯曲状态下的三层膜结构及其相应的弯曲半径R. 其中, R代表弯曲曲率半径, 其大小决定了整个体系的应变分布. 当R逐渐减小(即弯曲程度增大), 薄膜内部的应力状态及极化响应均会发生显著变化, 从而影响铁电畴结构的稳定性及翻转动力学. 值得注意的是, 尽管两种弯曲方式均能在铁电薄膜中引入应变梯度, 但其具体的应力分布模式却存在显著差异. 图1(b)进一步展示了U型和N型弯曲状态下铁电异质薄膜的应变分布. 计算结果表明, 在U型弯曲条件下, 三层膜的中性层以下区域承受面内拉应变, 而以上区域则处于面内压应变; 相反, 在N型弯曲条件下, 中性层以上区域受拉伸, 而以下区域则受压缩. 这种非均匀应变分布的形成机制主要归因于弯曲变形的作用. 换而言之, 这种应变梯度的方向取决于弯曲方式, 并且在不同区域呈现镜像对称关系. 在弯曲过程中, 铁电异质薄膜的上层与下层经历不同程度的拉伸或压缩, 从而在晶格尺度上诱导显著的应变梯度. 由于柔性衬底直接承受外加载荷, 且其与铁电薄膜之间的界面处变形量最大, 因此该区域的应变量级最为明显. 值得注意的是, 该计算方法及实验设计与大多数实际研究中采用的弯曲变形方式保持一致, 即通过柔性衬底的弯曲驱动铁电异质薄膜发生形变[19,20,38], 从而在宏观尺度上调控应变场的分布及其对极化结构的影响. -
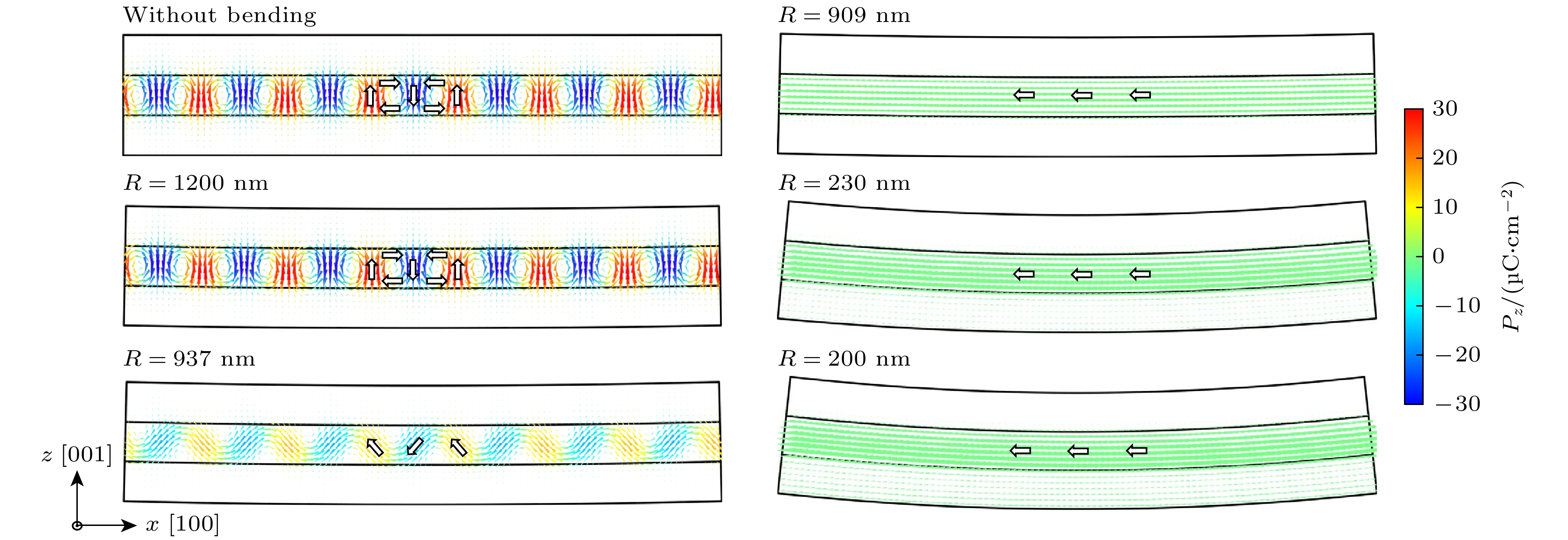
图2展示了U型弯曲变形下, STO/PTO/STO三层铁电薄膜内部的畴结构演化行为. 在该体系中, 由于PTO和STO具有不同的晶格参数(分别为3.955 Å和3.905 Å), 导致异质层之间存在失配应变. 具体而言, PTO层受到面内压缩应变, 而STO层则处于面内拉伸应变状态. 这种层间应变的不匹配对体系的极化分布、畴结构稳定性以及外场调控行为产生重要影响.
在无弯曲形变的初始状态下(R→∞), PTO层内部的铁电畴结构表现为极性涡旋对, 这与体系的弹性交互作用、静电能以及极化梯度能之间的竞争平衡密切相关. 每个涡旋核心的极化矢量沿闭合路径旋转, 其核心直径在4—5 nm, 与Yadav等[25]观察的极性涡旋结构一致. 涡旋态的形成本质上是体系通过局部极化旋转来降低总能量的一种策略, 其中, 介电层-铁电层之间的界面静电屏蔽效应在稳定拓扑结构方面起到了关键作用. 随着弯曲曲率半径R的减小(即弯曲程度增加), PTO层的应变状态逐渐发生变化, 进而影响畴结构的稳定性和拓扑形态. 当R > 937 nm时, 体系仍然维持原始的极性涡旋对特征, 表明在该应变条件下, 界面应变能的积累尚不足以驱动畴结构的拓扑相变. 然而, 当R下降至937 nm时, PTO层内部的极化构型发生突变, 原本的极性涡旋对演化为首尾相接的涡流态, 并在空间分布上呈现锯齿形排列. 这种结构重构可归因于弯曲变形引入的应变状态, 其不仅调控了局部极化旋转方向, 还显著改变了体系的能量分布, 使得原有的涡旋对结构不再稳定. 当R进一步减小(R = 200 nm), STO/PTO/STO三层膜的上表面主要承受压缩应变(εxx ≈ –1.35%), 而下表面主要承受拉伸应变(εxx ≈ 3%). 此时体系的面内拉伸应变占据主导地位, 最终导致PTO层内部的极化构型彻底转变为面内a畴.
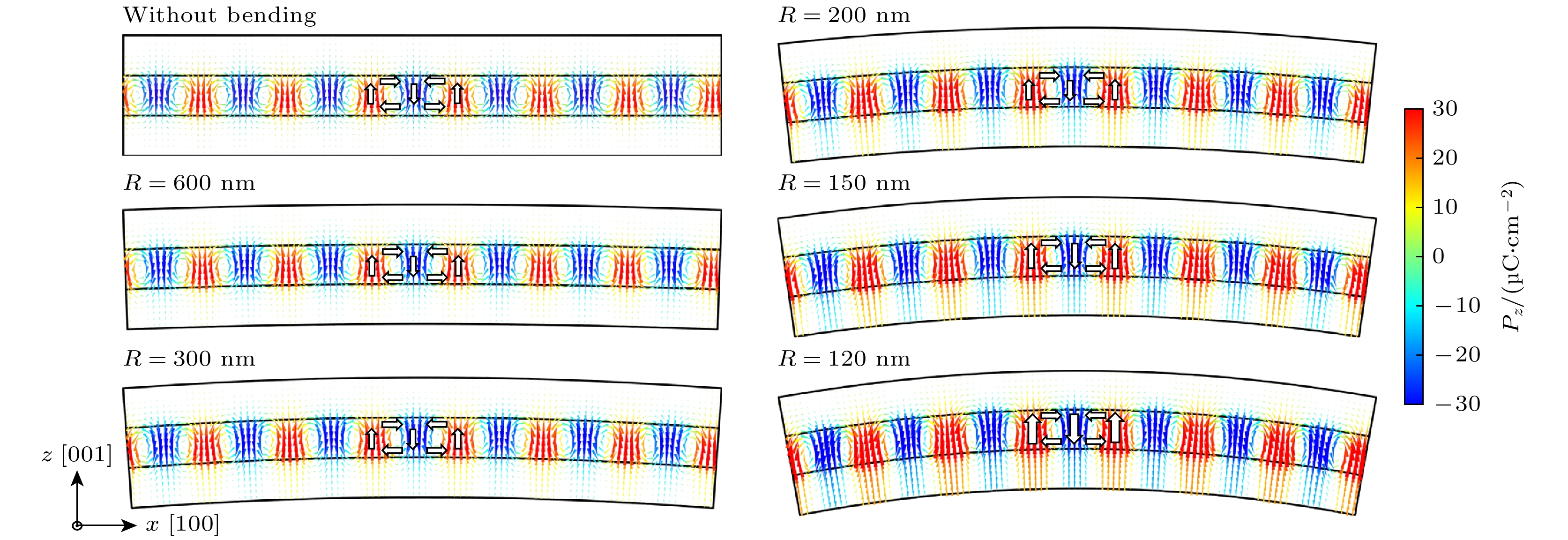
图3展示了N型弯曲变形作用下STO/PTO/STO三层铁电薄膜内部的畴结构演化行为. 相较于U型弯曲, N型弯曲的主要特征在于底层(柔性衬底)施加变形边界条件. 这导致体系下半部分的压缩应变占主导, 从而对局部极化构型产生重要影响, 并可能诱导新的畴结构演化路径.
在较大弯曲曲率半径(即弯曲程度较小时), PTO层内部的极性涡旋对(polar vortex pairs)仍然稳定存在, 这表明在该条件下, 体系的应变梯度尚不足以破坏原始涡旋态的能量平衡. 然而, 随着N型弯曲曲率半径R的进一步减小(即弯曲程度增加). 如当R = 120 nm时, N型弯曲变形导致的上表面拉伸应变(εxx ≈2.27%)与下表面压缩应变(εxx≈–5%), 体系的面内压缩应变进一步增强, 导致极性涡旋对的尺度逐渐缩小. 这一现象表明, 弯曲诱导的应变调控效应能够有效地抑制涡旋核心的空间扩展性, 并促使局部极化矢量逐步朝着面外方向排列. 当弯曲程度进一步增大时, 体系的极化构型发生明显转变: 极性涡旋对逐渐演化为具有180度畴壁的面外c畴, 即极化方向沿着薄膜法向方向排列. 这一畴转变行为可归因于两方面因素: 一是弯曲变形引入的非均匀压缩应变抑制了极化旋转自由度, 使得面内极化成分减少, 而面外极化占据主导; 二是STO层的介电调控作用增强, 在较强的N型弯曲应变作用下, STO层内的铁电极化现象逐渐显现, 进一步促进了PTO层内部180°畴壁的形成和稳定. 此外, 随着弯曲程度的进一步增加, STO层本身的极化特征也变得显著, 最终形成具有180°畴壁的面外c畴. 在N型弯曲条件下, 应变 梯度方向的变化不仅影响极性涡旋对的稳定性, 还对铁电畴结构的空间分布起到了显著的调控作用.
相关弯曲应变调控畴结构演化行为表明, U型或N型的弯曲方向不仅能够驱动铁电畴的拓扑相变, 同时也可以通过调控应变梯度方向来选择性地稳定特定的极化结构.
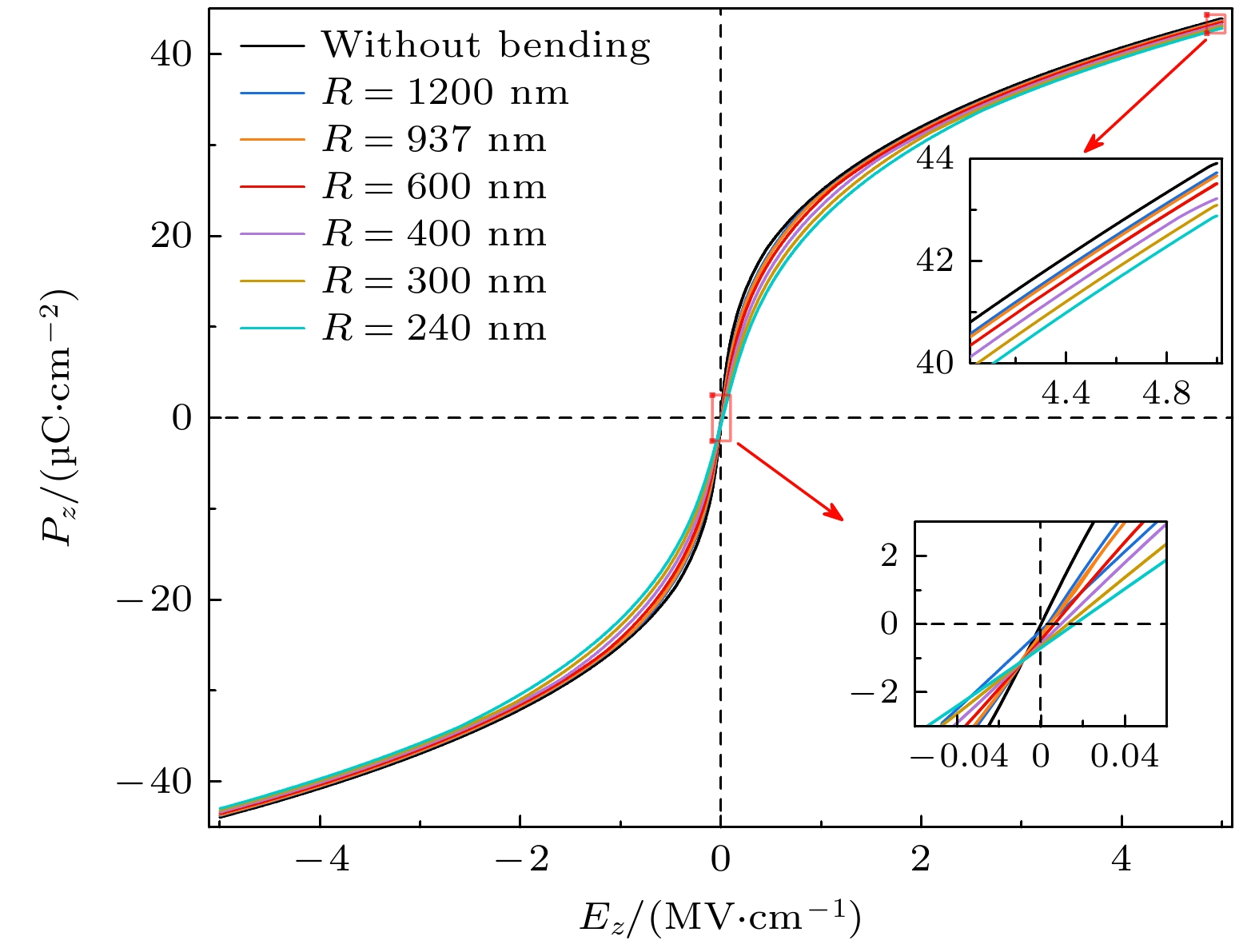
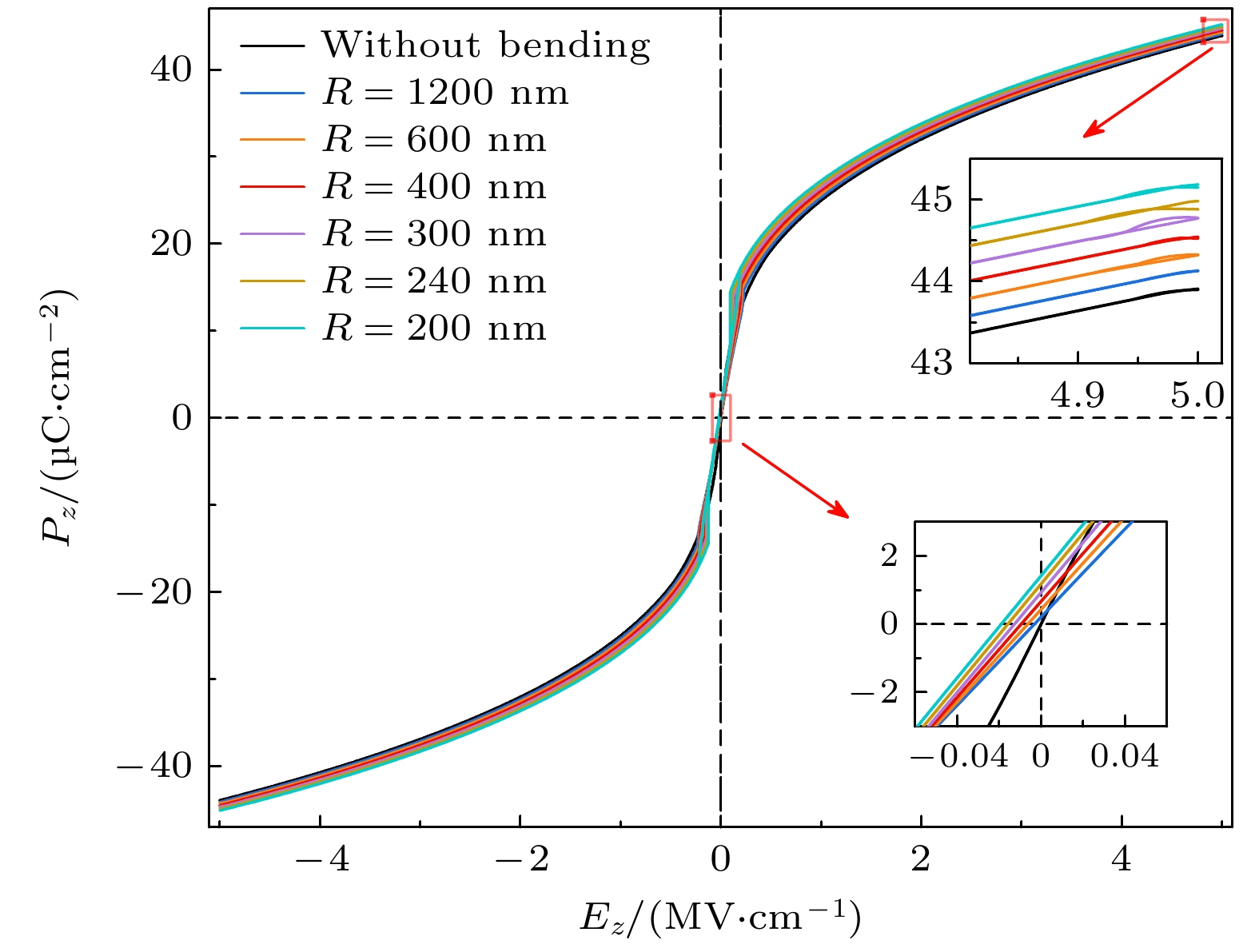
在研究了弯曲变形对STO/PTO/STO三层膜内部畴结构演化的影响之后, 进一步探讨弯曲变形对三层膜宏观电滞回线的调控机制. 如图4所示, U型弯曲条件下STO/PTO/STO三层膜的电滞回线出现显著的整体偏移现象. 值得指出的是, 虽然U型与N型弯曲在PTO层中均可能引入一定程度的应变作用, 但更关键的是其在厚度方向上形成了不同方向的应变梯度, 体系内部的应变梯度εxx,z会引发横向挠曲电场
${{E}}_z^{{\mathrm{flexo}}} = {{f}_{12}}{\varepsilon _{xx, z}}$ 的产生. 一般情况下, 钙钛矿材料的挠曲电耦合系数f12为正, 这意味着不同的弯曲形态(U型或N型)会导致方向相反的挠曲电场. 在U型弯曲(R = 240 nm)下, STO/PTO/STO三层膜的上表面主要承受压缩应变(εxx ≈ –1.13%), 下表面主要承受拉伸应变(εxx ≈ 2.5%), 从而在厚度方向形成负向应变梯度(εxx, z ≈ –3.03×106 m–1), 引发面外方向的负向挠曲电场. 该挠曲电场有效地调控了极化翻转过程, 使得电滞回线整体向右下方偏移(如图4中心区域的放大图所示).进一步分析发现, 随着U型弯曲程度的增大(即弯曲曲率半径R变小), 这一偏移效应逐渐增强, 进而引起矫顽电场(Ec)、最大极化强度(Pmax)和剩余极化强度(Pr)的变化, 如表2所列. 在未弯曲状态下, 由于STO/PTO/STO三层膜内部主要为极性涡旋对结构, 且在施加循环电场后, 零电场状态下形成面内单畴, 因此矫顽电场和剩余极化强度均接近零. 相比之下, 当三层膜处于U型弯曲且曲率半径 R = 240 nm时, 矫顽电场由0 kV/cm增大至16.67 kV/cm, 而剩余极化强度变为负向的–0.69 μC/cm2. 而由于U型弯曲引入的面内拉应变, 导致电偶极子倾向于面内方向排布, 从而导致整体的最大极化强度随之减小. 最大极化强度从未弯曲状态下的43.90 μC/cm2降低至42.86 μC/cm2. 这种电滞回线的整体偏移与畴结构演化密切相关, 表明弯曲变形不仅能够通过应变调控畴结构, 还会通过挠曲电效应显著改变体系的宏观铁电响应.
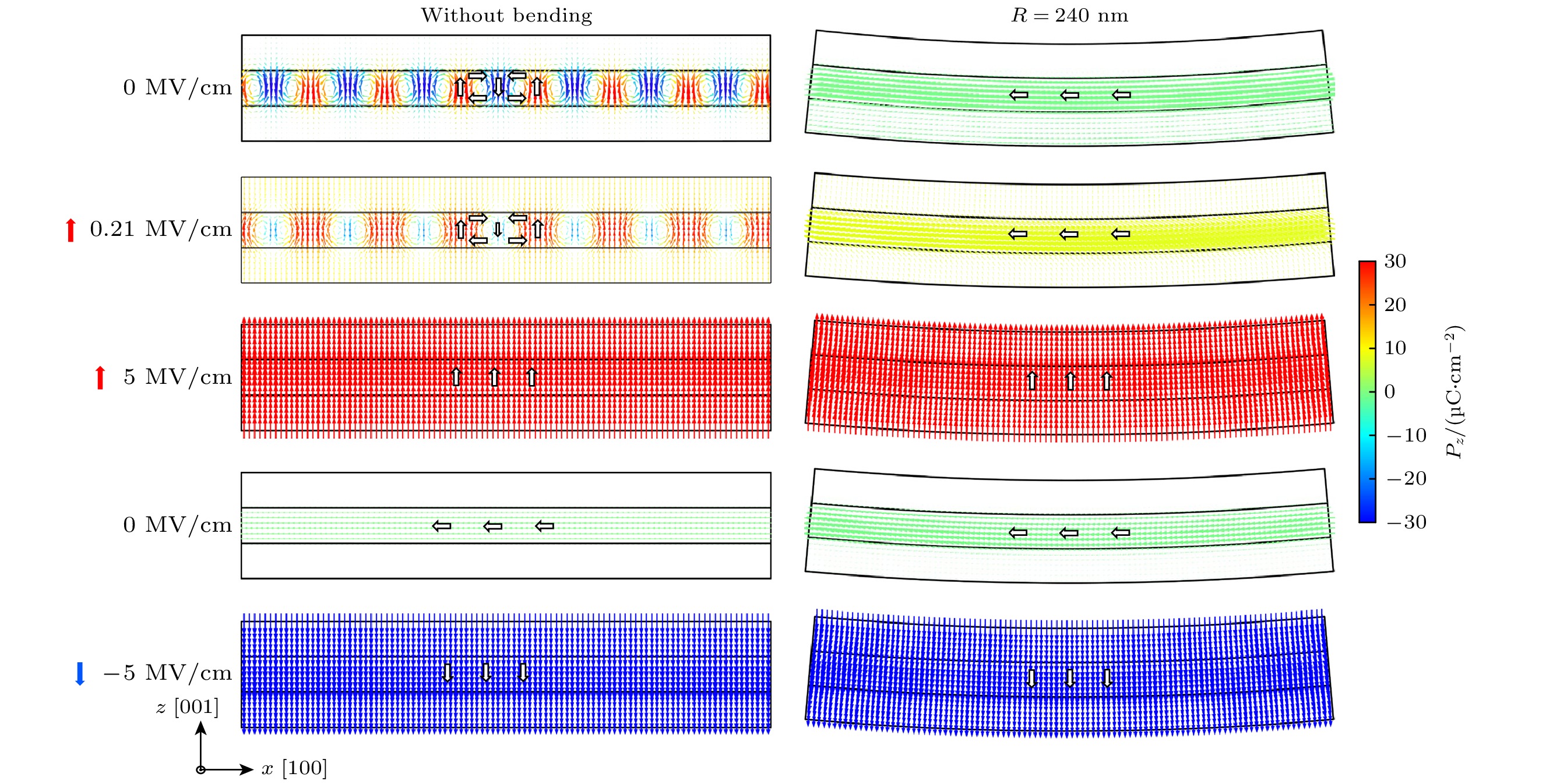
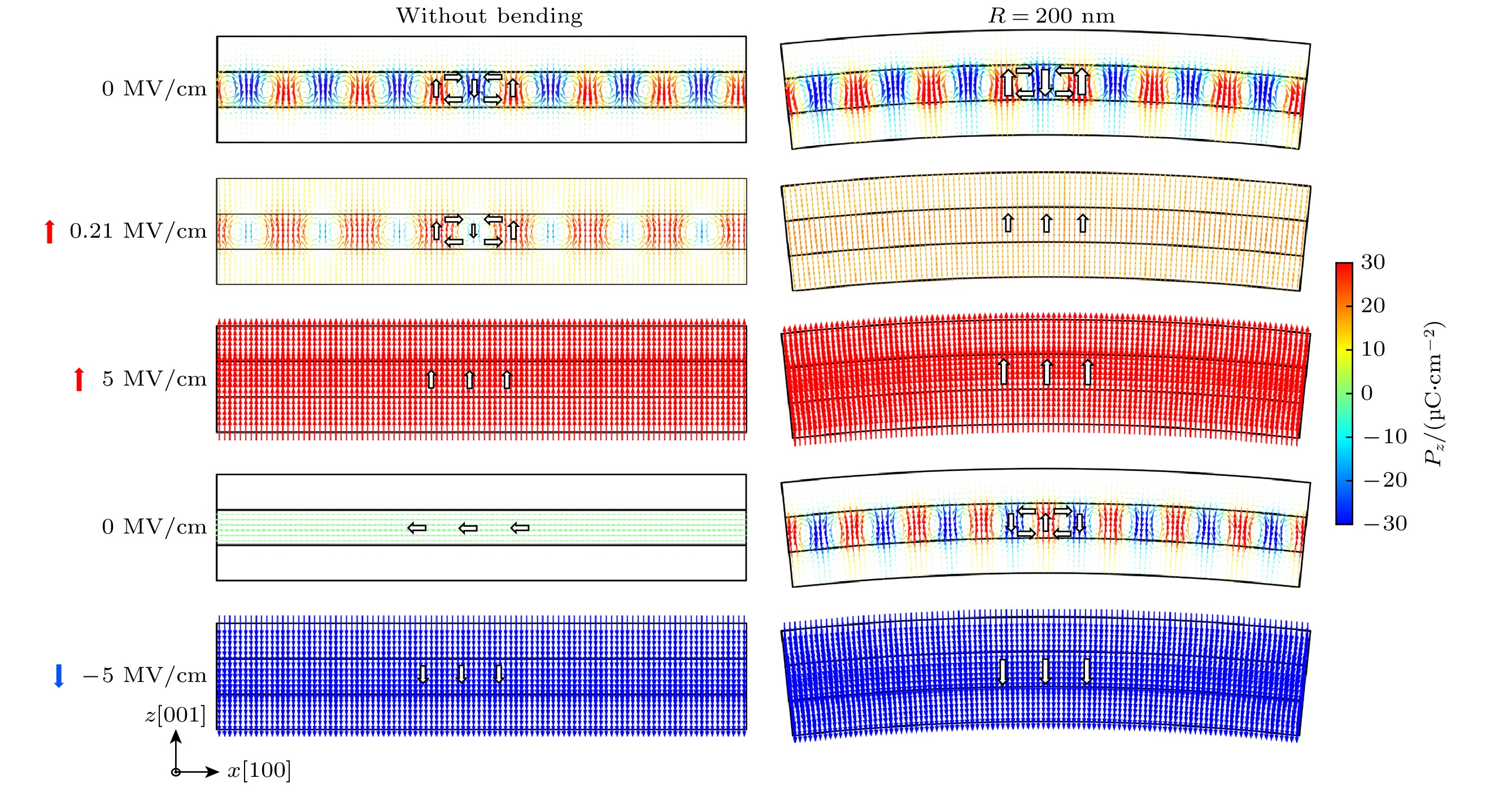
图5展示了U型弯曲变形下STO/PTO/STO三层膜的极化分布在外加电场作用下的演化过程. 在未弯曲状态下且未施加外加电场(0 MV/cm)时, PTO层内部的电偶极子自发形成周期性顺时针-逆时针极性涡旋对阵列. 当施加正向电场时, 极化分布发生显著重构. 比如当电场增至0.21 MV/cm时, 涡旋核心逐渐湮灭, 部分面外极化分量沿着外加电场方向发生偏转, 逐渐转向面外向上. 从而最终演化为如电场为5 MV/cm下的面外单畴结构, 此时PTO层内所有电偶极子方向与外加电场方向一致. 值得注意的是, 当电场从面外向上降至0后, 体系不再恢复至原始涡旋态, 而是变为面内单畴, 这表明体系具有一定的滞后效应. 当三层膜处于U型弯曲(曲率半径R = 240 nm)时, PTO层受到占主导的面内拉应变. 由于拉应变的引入, 面外极化分量(c畴)稳定性降低, 极化矢量更倾向于沿面内方向排列, 从而形成面内单畴结构. 当电场增至5 kV/cm时, 极化分布趋于均匀化系统进入面内单畴态.
接下来, 我们研究在N型弯曲变形下柔性三层膜表现出的宏观电滞回线行为, 如图6所示. 在N型弯曲条件下, STO/PTO/STO三层膜在面外方向产生正向挠曲电场, 从而导致电滞回线整体发生左上方向偏移(如图6中心区域的放大图所示), 并且随着N型弯曲程度的增大(即曲率半径R逐 渐减小), 偏移程度逐步增强, 表明挠曲电场的调 控效应随弯曲变形增强而显著提升. 从而导致三 层膜的矫顽电场、最大极化强度和剩余极化强度 均发生变化, 具体数值变化见表3. 矫顽电场方面, 在未弯曲状态下, 体系的矫顽电场接近0, 因为PTO层主要由涡旋对构成; 当曲率半径R = 200 nm时, 矫顽电场变至–19.44 kV/cm. 剩余极化强度方面, 未弯曲状态下Pr近似为0, 这是由于体系零场时主要呈现涡旋态, 极化无明显自发取 向; 当R = 200 nm时, Pr增加至1.42 μC/cm², 表明N型弯曲诱导的正向挠曲电场促进了面外极化分量的形成, 使得零场下体系更容易保持剩余极化. 最大极化强度方面, 由于N型弯曲引入面内压缩应变, 该应变增强了电偶极子向面外方向排列的倾向, 从而提升了体系的饱和极化值; 未弯曲状态下Pmax为43.90 μC/cm², 而当R = 200 nm时, Pmax增大至45.15 μC/cm², 表明N型弯曲有助于增强铁电响应. 这一现象的物理机制主要归因于弯曲诱导的应变梯度调控, N型弯曲产生的正向挠曲电场促进面外极化方向的排列, 使得零场下剩余极化增强, 导致电滞回线向左上偏移; 同时, 面内压缩应变效应进一步增强面外极化的稳定性, 使得最大极化强度增加, 并增强了极化翻转所需的临界电场, 导致矫顽电场显著增加. 综上所述, 剩余弯曲通过应变调控与挠曲电场效应, 不仅影响了电滞回线的整体偏移, 还改变了体系的极化翻转特性, 为柔性铁电薄膜的力-电耦合机制研究提供了重要的物理见解.
图7展示了N型弯曲变形下STO/PTO/STO三层膜的极化分布随电场演化的动态过程. 当N型弯曲曲率半径R为200 nm且未施加电场(0 MV/cm)时, 弯曲变形导致的上表面拉伸应变(εxx≈1.5%)与下表面压缩应变(εxx≈–3%), 诱导产生面外正向应变梯度场(εxx,z ≈3.61×106 m–1). 由于压缩应变在整个体系中占主导作用, 使得PTO层内的极化构型主要表现为周期性涡旋-反涡旋阵列. 然而, 与U型弯曲相比, N型弯曲引入的面内压缩应变使得晶格沿面外方向收缩, 从而进一步稳定面外c畴, 并显著抑制面内a畴的成核过程. 当外加面外电场增至0.21 MV/cm时, 体系的畴结构已完全转变为面外c畴, 表明N型弯曲下的挠曲电场调控已足以驱动极化矢量朝向面外方向排列. 随着电场继续增大至正向饱和值(E = 5 MV/cm)时, 体系进入稳定的面外单畴态, 其最大极化强度(Pmax=45.15 μC/cm²)相比未弯曲状态(43.90 μC/cm²)提升了2.9%. 这一极化增强效应源于N型弯曲产生的应变梯度与外加电场之间的协同作用, 即挠曲电场的方向与外加电场方向一致, 两者叠加后共同驱动极化矢量沿面外方向排列, 提升体系的极化响应能力. 在移除外加电场后, 体系的剩余极化强度仍保持正向, 且与图6中的电滞回线左上方偏移相对应, 进一步验证了应变梯度符号对极化翻转路径的非对称调控作用. 图7所揭示的极化演化动态过程不仅深化了对柔性铁电薄膜中力学-电学协同效应的理解, 同时也为柔性铁电器件的性能优化(如多态存储、手性传感)提供了新的理论依据.
-
本文通过相场模拟系统探究了弯曲应变梯度对STO/PTO/STO三层铁电薄膜畴结构及宏观电滞回线的调控机制. 结果表明, U型和N型弯曲变形方式通过引入不同的应变梯度方向, 显著地影响了薄膜内部的极化分布和拓扑畴演化. U型弯曲诱导的负向挠曲电场导致电滞回线向右下方偏移, U型弯曲曲率半径为240 nm时, 矫顽电场增大至16.67 kV/cm, 剩余极化强度变为负值(–0.69 μC/cm²), 且最大极化强度降低至42.86 μC/cm², 表明占主导的拉应变抑制了面外极化分量的稳定性. 相反, N型弯曲产生的正向挠曲电场促使电滞回线向左上方偏移, N型弯曲曲率半径为200 nm时, 矫顽电场改变至–19.44 kV/cm, 剩余极化强度提升至1.42 μC/cm², 最大极化强度增至45.15 μC/cm², 反映了占主导的面内压缩应变对面外极化的增强作用. 此外, 弯曲应变梯度驱动了极性涡旋对向面内或面外单畴的拓扑相变, 揭示了应变梯度与界面静电耦合的协同效应. 这些发现不仅阐明了弯曲变形对铁电畴结构及电响应的调控机制, 还为柔性铁电器件的设计提供了理论依据.
感谢北京理工大学力学系李永恒博士的讨论.
弯曲应变梯度作用下铁电三层膜畴翻转的相场模拟研究
Phase-field simulation of domain switching in ferroelectric trilayer films under bending-induced strain gradient
-
摘要: 柔性铁电材料在可穿戴电子领域具有重要应用前景, 然而其动态弯曲过程中应变梯度与极化翻转的力-电耦合物理机制仍缺乏系统性的研究. 本研究基于相场模拟, 系统地探讨了(SrTiO3)10/(PbTiO3)10/(SrTiO3)10三层异质膜在U型和N型弯曲下的畴结构演化及其宏观电学响应. 研究表明, 通过改变弯曲变形方向可以产生方向相反的挠曲电场, 导致电滞回线发生相应方向的偏移. 此外, 弯曲应变和应变梯度可驱动极性涡旋态与单畴态之间的拓扑相变, 其中界面静电能、弹性约束及梯度能的协同作用对拓扑结构的稳定性起关键作用. 本研究揭示了弯曲变形通过力-电耦合效应实现畴构型与电响应的定向调控机制, 为高密度柔性存储器和能量收集器件的跨尺度设计奠定了理论基础, 并进一步拓展了拓扑态工程在柔性电子领域的应用前景.Abstract: Flexible ferroelectric materials possess considerable potentials for wearable electronics and bio-inspired devices, yet their mechano-electric coupling mechanisms under dynamic bending conditions remain incompletely understood. In his work, the effects of bending deformation on domain structures and macroscopic ferroelectric responses in (SrTiO3)10/(PbTiO3)10/(SrTiO3)10 flexible ferroelectric trilayer films are systematically investigated using phase-field simulations. By constructing computational models for upward-concave (U-shaped) and downward-concave (N-shaped) bending configurations, the strain distribution and its regulation mechanism on polarization patterns under different curvature radii are analyzed. The results reveal distinct strain gradients across bending modes: U-shaped bending induces compressive strain in the upper layer and tensile strain in the lower layer, generating a negative out-of-plane strain gradient. Conversely, N-shaped bending reverses this strain distribution. Such inhomogeneous strains drive significant polarization reconfiguration within the PTO layer. At a moderate curvature (large R), the system retains stable vortex-antivortex pairs. Reducing bending radius (smaller R) promotes divergent topological transitions—U-shaped bending facilitates vortex pair transformation into zigzag-like domains, while N-shaped bending drives vortex-to-out-of-plane c-domain evolution. Notably, bending-induced strain gradients impose transverse flexoelectric fields that markedly change trilayer hysteresis loops. U-shaped bending introduces a negative flexoelectric field, shifting loops rightward with maximum polarization (Pmax) decreasing. In contrast, N-shaped bending generates a positive field, enhancing Pmax via leftward loop shifting. The polarization switching analysis under electric field further demonstrates bending-mediated control of domain evolution pathway and reversal dynamics. These findings not only elucidate profound bending effects on flexible ferroelectrics’ domain architectures and functional properties but also provide theoretical guidance for designing strain-programmable ferroelectric memories, adaptive sensors, and neuromorphic electronics.
-
Key words:
- phase-field simulation /
- bending /
- strain gradient /
- ferroelectric vortex .
-
-
图 1 (a) 铁电三层膜的两种弯曲示意图, 这里R是弯曲曲率的半径; (b) 铁电三层膜在U型弯曲和N型弯曲下的面内应变εxx分布; (c) 铁电三层膜在U型弯曲和N型弯曲下的应变梯度εxx,z分布
Figure 1. (a) Schematic diagrams of the two bending configurations of the ferroelectric trilayer film, where R is the radius of curvature; (b) in-plane strain εxx of the ferroelectric trilayer film under U-shaped and N-shaped bending; (c) strain gradient εxx,z of the ferroelectric trilayer film under U-shaped and N-shaped bending.
图 2 STO/PTO/STO三层膜在不同U型弯曲半径下畴结构演化行为
Figure 2. Domain evolution behavior in STO/PTO/STO trilayer films under different U-shaped bending radii.
图 3 STO/PTO/STO三层膜在不同N型弯曲半径下畴结构演化行为
Figure 3. Domain evolution behavior in STO/PTO/STO trilayer films under different N-shaped bending radii.
图 4 STO/PTO/STO三层膜在不同U型弯曲半径下的电滞回线
Figure 4. Hysteresis loops of STO/PTO/STO trilayer films under different U-shaped bending radii.
图 5 STO/PTO/STO异质膜在U型弯曲变形下的电场调控极化分布特性
Figure 5. Electric field-modulated polarization distribution in STO/PTO/STO trilayers under U-shaped bending deformation.
图 6 STO/PTO/STO三层膜在不同N型弯曲半径下的电滞回线
Figure 6. Hysteresis loops of STO/PTO/STO trilayer films under different N-shaped bending radii.
图 7 STO/PTO/STO异质膜在N型弯曲变形下的电场调控极化分布特性
Figure 7. Electric field-modulated polarization distribution in STO/PTO/STO trilayers under N-shaped bending deformation.
表 1 相场模拟所用的材料参数取值[33,34] (SI单位制, 温度为300 K)
Table 1. Material parameter values in the phase-field simulations (SI unit, T=300 K).
变量 数值 变量 数值 PTO $ {\alpha _1}/({10^8}{\text{ }}{\mathrm{J}} {\cdot} m {\cdot} {{\mathrm{C}}^{ - 2}}) $ $ - 1.706 $ $ {{{Q}}_{11}}/({{\mathrm{m}}^4} {\cdot} {{\mathrm{C}}^{ - 2}}) $ 0.089 $ {\alpha _{11}}/({10^7}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^5} {\cdot} {{\mathrm{C}}^{ - 4}}) $ $ - 7.3 $ $ {{{Q}}_{12}}/({{\mathrm{m}}^4} {\cdot} {{\mathrm{C}}^{ - 2}}) $ –0.026 $ {\alpha _{12}}/({10^8}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^5} {\cdot} {{\mathrm{C}}^{ - 4}}) $ $ 7.5 $ $ {{{Q}}_{44}}/({{\mathrm{m}}^4} {\cdot} {{\mathrm{C}}^{ - 2}}) $ 0.0675 $ {\alpha _{111}}/({10^8}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^9} {\cdot} {{\mathrm{C}}^{ - 6}}) $ $ 2.6 $ $ {{{G}}_{11}}/({10^{ - 10}}{\text{ }}{\mathrm{N}} {\cdot} {{\mathrm{m}}^4} {\cdot} {{\mathrm{C}}^{ - 2}}) $ $ 1.44 $ $ {\alpha _{112}}/({10^8}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^9} {\cdot} {{\mathrm{C}}^{ - 6}}) $ $ 6.1 $ $ {{{G}}_{12}}/({\mathrm{N}} {\cdot} {{\mathrm{m}}^4} {\cdot} {{\mathrm{C}}^{ - 2}}) $ 0 $ {\alpha _{123}}/({10^8}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^9} {\cdot} {{\mathrm{C}}^{ - 6}}) $ $ - 3.7 $ $ G_{44},G_{44}'/(10^{-11}\text{ }\mathrm{N}{\cdot}\mathrm{m}^4{\cdot}\mathrm{C}^{-2}) $ $ 7.2 $ $ {{c}_{11}}/({10^{11}}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^{ - 3}}) $ $ 2.3 $ $ {{f}_{11}}/{\mathrm{V}} $ 1.6 $ {{c}_{12}}/({10^{11}}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^{ - 3}}) $ $ 1 $ $ {{f}_{12}}/{\mathrm{V}} $ –0.8 $ {{c}_{44}}/({10^{10}}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^{ - 3}}) $ $ 7 $ $ {{f}_{44}}/{\mathrm{V}} $ 0.15 STO $ {\alpha _1}/({10^8}{\text{ }}{\mathrm{J}} {\cdot} {\mathrm{m}} {\cdot} {{\mathrm{C}}^{ - 2}}) $ $ 2.017 $ $ {{{Q}}_{44}}/({{\mathrm{m}}^4} {\cdot} {{\mathrm{C}}^{ - 2}}) $ 0.00957 $ {\alpha _{11}}/({10^9}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^5} {\cdot} {{\mathrm{C}}^{ - 4}}) $ $ 1.7 $ $ {{{G}}_{11}}/({10^{ - 10}}{\text{ }}{\mathrm{N}} {\cdot} {{\mathrm{m}}^4} {\cdot} {{\mathrm{C}}^{ - 2}}) $ $ 1.44 $ $ {\alpha _{12}}/({10^9}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^5} {\cdot} {{\mathrm{C}}^{ - 4}}) $ $ 4.45 $ $ {{{G}}_{12}}/({\mathrm{N}} {\cdot} {{\mathrm{m}}^4} {\cdot} {{\mathrm{C}}^{ - 2}}) $ 0 $ {{c}_{11}}/({10^{11}}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^{ - 3}}) $ $ 3.3 $ $ {{{G}}_{44}}, {{G}}_{44}'/({10^{ - 11}}{\text{ }}{\mathrm{N}} {\cdot} {{\mathrm{m}}^4} {\cdot} {{\mathrm{C}}^{ - 2}}) $ $ 7.2 $ $ {{c}_{12}}/({10^{11}}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^{ - 3}}) $ $ 1 $ $ {{f}_{11}}/{\mathrm{V}} $ –3.21 $ {{c}_{44}}/({10^{11}}{\text{ }}{\mathrm{J}} {\cdot} {{\mathrm{m}}^{ - 3}}) $ $ 1.25 $ $ {{f}_{12}}/{\mathrm{V}} $ 1.47 $ {{{Q}}_{11}}/({{\mathrm{m}}^4} {\cdot} {{\mathrm{C}}^{ - 2}}) $ 0.0457 $ {{f}_{44}}/{\mathrm{V}} $ 1.07 $ {{{Q}}_{12}}/({{\mathrm{m}}^4} {\cdot} {{\mathrm{C}}^{ - 2}}) $ –0.0135 εr (PTO/STO) 20 
下载: 导出CSV
表 2 STO/PTO/STO三层膜在U型弯曲变形下电滞回线的矫顽电场、最大极化强度和剩余极化强度
Table 2. Coercive electric field, maximum polarization, and remnant polarization of the ferroelectric hysteresis loop in STO/PTO/STO trilayer films under U-shaped bending deformation.
U型弯曲-
R/nmεxx,z/
(106 m–1)Ec/
(kV·cm–1)Pmax/
(μC·cm–2)Pr/
(μC·cm–2)未弯曲 0 0 43.90 0 1200 –0.61 2.78 43.72 –0.29 937 –0.77 2.78 43.64 –0.31 600 –1.14 5.56 43.52 –0.46 400 –1.82 11.11 43.30 –0.57 300 –2.42 13.89 43.05 –0.64 240 –3.03 16.67 42.86 –0.69
下载: 导出CSV
表 3 STO/PTO/STO三层膜在N型弯曲变形下电滞回线的矫顽电场、最大极化强度和剩余极化强度
Table 3. Coercive electric field, maximum polarization, and remnant polarization of the ferroelectric hysteresis loop in STO/PTO/STO trilayer films under N-shaped bending deformation.
N型弯曲-
R/nmεxx,z/
(106 m–1)Ec/
(kV·cm–1)Pmax/
(μC·cm–2)Pr/
(μC·cm–2)未弯曲 0 0 43.90 0 1200 0.61 –2.78 44.13 0.21 600 1.14 –5.56 44.33 0.43 400 1.82 –8.33 44.53 0.67 300 2.42 –13.89 44.78 0.93 240 3.03 –16.67 44.88 1.18 200 3.61 –19.44 45.15 1.42
下载: 导出CSV
-
[1] Setter N, Damjanovic D, Eng L, Fox G, Gevorgian S, Hong S, Kingon A, Kohlstedt H, Park N Y, Stephenson G B, Stolitchnov I, Taganstev A K, Taylor D V, Yamada T, Streiffer S 2006 J. Appl. Phys. 100 051606 doi: 10.1063/1.2336999 [2] Martin L W, Rappe A M 2017 Nat. Rev. Mater. 2 16087 doi: 10.1038/natrevmats.2016.87 [3] Scott J F, Paz de Araujo C A 1989 Science 246 1400 doi: 10.1126/science.246.4936.1400 [4] Ramesh R, Aggarwal S, Auciello O 2001 Mater. Sci. Eng., R 32 191 doi: 10.1016/S0927-796X(00)00032-2 [5] R. Bowen C, A. Kim H M, Weaver P, Dunn S 2014 Energy Environ. Sci. 7 25 doi: 10.1039/C3EE42454E [6] Silva J P B, Silva J M B, Oliveira M J S, Weingärtner T, Sekhar K C, Pereira M, Gomes M J M 2019 Adv. Funct. Mater. 29 1807196 doi: 10.1002/adfm.201807196 [7] Singh A, Monga S, Sharma N, Sreenivas K, Katiyar R S 2022 J. Asian Ceram. Soc. 10 275 doi: 10.1080/21870764.2022.2075618 [8] Lancaster M J, Powell J, Porch A 1998 Supercond. Sci. Technol. 11 1323 doi: 10.1088/0953-2048/11/11/021 [9] Wang W, Li J, Liu H, Ge S 2021 Adv. Sci. 8 2003074 doi: 10.1002/advs.202003074 [10] Han X, Ji Y, Yang Y 2022 Adv. Funct. Mater. 32 2109625 doi: 10.1002/adfm.202109625 [11] Park J S, Jung S Y, Kim D H, Park J H, Jang H W, Kim T G, Baek S H, Lee B C 2023 Microsyst. Nanoeng. 9 1 doi: 10.1038/s41378-022-00443-6 [12] Yu H, Chung C C, Shewmon N, Ho S, Carpenter J H, Larrabee R, Sun T, Jones J L, Ade H, O’Connor B T, So F 2017 Adv. Funct. Mater. 27 1700461 doi: 10.1002/adfm.201700461 [13] Yao M, Cheng Y, Zhou Z, Liu M 2020 J. Mater. Chem. C 8 14 doi: 10.1039/C9TC04706A [14] Gao W, Zhu Y, Wang Y, Yuan G, Liu J M 2020 J. Materiomics 6 1 doi: 10.1016/j.jmat.2019.11.001 [15] Jia X, Guo R, Tay B K, Yan X 2022 Adv. Funct. Mater. 32 2205933 doi: 10.1002/adfm.202205933 [16] Ryu J, Priya S, Park C S, Kim K Y, Choi J J, Hahn B D, Yoon W H, Lee B K, Park D S, Park C 2009 J. Appl. Phys. 106 024108 doi: 10.1063/1.3181058 [17] Shi Q, Parsonnet E, Cheng X, Fedorova N, Peng R C, Fernandez A, Qualls A, Huang X, Chang X, Zhang H, Pesquera D, Das S, Nikonov D, Young I, Chen L Q, Martin L W, Huang Y L, Íñiguez J, Ramesh R 2022 Nat. Commun. 13 1110 doi: 10.1038/s41467-022-28622-z [18] Ji D, Cai S, Paudel T R, Sun H, Zhang C, Han L, Wei Y, Zang Y, Gu M, Zhang Y, Gao W, Huyan H, Guo W, Wu D, Gu Z, Tsymbal E Y, Wang P, Nie Y, Pan X 2019 Nature 570 87 doi: 10.1038/s41586-019-1255-7 [19] Dong G, Li S, Yao M, Zhou Z, Zhang Y Q, Han X, Luo Z, Yao J, Peng B, Hu Z, Huang H, Jia T, Li J, Ren W, Ye Z G, Ding X, Sun J, Nan C W, Chen L Q, Li J, Liu M 2019 Science 366 475 doi: 10.1126/science.aay7221 [20] Peng B, Peng R C, Zhang Y Q, Dong G, Zhou Z, Zhou Y, Li T, Liu Z, Luo Z, Wang S, Xia Y, Qiu R, Cheng X, Xue F, Hu Z, Ren W, Ye Z G, Chen L Q, Shan Z, Min T, Liu M 2020 Sci. Adv. 6 eaba5847 doi: 10.1126/sciadv.aba5847 [21] Zhou Y, Guo C, Dong G, Liu H, Zhou Z, Niu B, Wu D, Li T, Huang H, Liu M, Min T 2022 Nano Lett. 22 2859 doi: 10.1021/acs.nanolett.1c05028 [22] Cai S, Lun Y, Ji D, Lv P, Han L, Guo C, Zang Y, Gao S, Wei Y, Gu M, Zhang C, Gu Z, Wang X, Addiego C, Fang D, Nie Y, Hong J, Wang P, Pan X 2022 Nat. Commun. 13 5116 doi: 10.1038/s41467-022-32519-2 [23] Wang J, Liu Z, Wang Q, Nie F, Chen Y, Tian G, Fang H, He B, Guo J, Zheng L, Li C, Lü W, Yan S 2024 Adv. Sci. 11 2401657 doi: 10.1002/advs.202401657 [24] Tanwani M, Gupta P, Powar S, Das S 2025 Small 21 2405688 doi: 10.1002/smll.202405688 [25] Yadav A K, Nelson C T, Hsu S L, et al. 2016 Nature 530 198 doi: 10.1038/nature16463 [26] Hsu S L, McCarter M R, Dai C, Hong Z, Chen L Q, Nelson C T, Martin L W, Ramesh R 2019 Adv. Mater. 31 1901014 doi: 10.1002/adma.201901014 [27] Hong Z, Damodaran A R, Xue F, Hsu S L, Britson J, Yadav A K, Nelson C T, Wang J J, Scott J F, Martin L W, Ramesh R, Chen L Q 2017 Nano Lett. 17 2246 doi: 10.1021/acs.nanolett.6b04875 [28] Das S, Tang Y L, Hong Z, et al. 2019 Nature 568 368 doi: 10.1038/s41586-019-1092-8 [29] Lun Y, Wang X, Kang J, Ren Q, Wang T, Han W, Gao Z, Huang H, Chen Y, Chen L Q, Fang D, Hong J 2023 Adv. Mater. 35 2302320 doi: 10.1002/adma.202302320 [30] Guo C, Yang H, Dong S, Tang S, Wang J, Wang X, Huang H 2024 Adv. Electron. Mater. 10 2400001 doi: 10.1002/aelm.202400001 [31] Guo C, Wang J, Huang H 2024 Appl. Phys. Lett. 125 062903 doi: 10.1063/5.0225448 [32] Zhou M J, Peng K, Tan Y Z, Yang T N, Chen L Q, Nan C W 2025 Acta Mater. 288 120805 doi: 10.1016/j.actamat.2025.120805 [33] Li Q, Nelson C T, Hsu S L, et al. 2017 Nat. Commun. 8 1468 doi: 10.1038/s41467-017-01733-8 [34] Xu T, Wu C, Zheng S, Wang Y, Wang J, Hirakata H, Kitamura T, Shimada T 2024 Phys. Rev. Lett. 132 086801 doi: 10.1103/PhysRevLett.132.086801 [35] 刘迪, 王静, 王俊升, 黄厚兵 2020 物理学报 69 127801 doi: 10.7498/aps.69.20200310 Liu D, Wang J, Wang J S, Huang H B 2020 Acta Phys. Sin. 69 127801 doi: 10.7498/aps.69.20200310 [36] 高荣贞, 王静, 王俊升, 黄厚兵 2020 物理学报 69 217801 doi: 10.7498/aps.69.20201195 Gao R Z, Wang J, Wang J S, Huang H B 2020 Acta Phys. Sin. 69 217801 doi: 10.7498/aps.69.20201195 [37] 梁德山, 黄厚兵, 赵亚楠, 柳祝红, 王浩宇, 马星桥 2021 物理学报 70 044202 doi: 10.7498/aps.70.20201623 Liang D S, Huang H B, Zhao Y N, Liu Z H, Wang H Y, Ma X Q 2021 Acta Phys. Sin. 70 044202 doi: 10.7498/aps.70.20201623 [38] Li Y, Zatterin E, Conroy M, et al. 2022 Adv. Mater. 34 2106826 doi: 10.1002/adma.202106826 -
图( 7) 表( 3)
计量
- 文章访问数: 32
- HTML全文浏览数: 32
- PDF下载数: 1
- 施引文献: 0