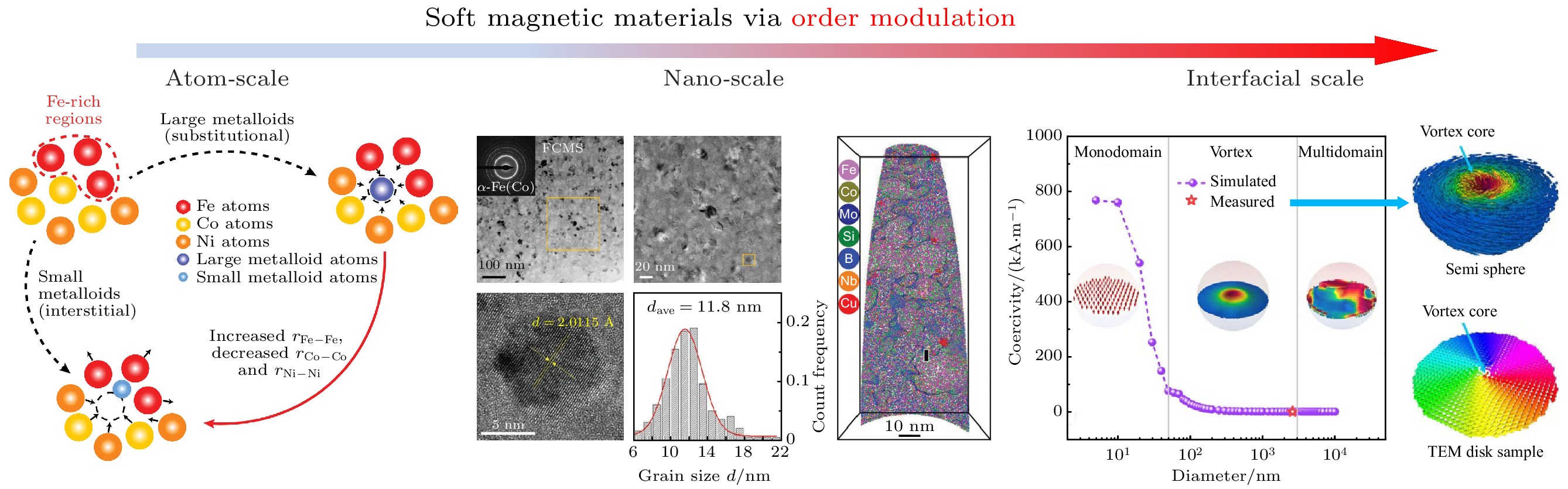
-
软磁材料是一类低矫顽力(小于1000 A/m)、高磁导率及剩磁小的特殊铁磁/亚铁磁材料, 在外加磁场作用下易于磁化与退磁, 广泛应用于变压器、电感、电机等电能变换设备, 是电子电力设备的关键材料[1]. 近年来, 伴随着半导体制造技术取得重大突破以及材料成本的逐步降低, 氮化镓、碳化硅等第3代半导体材料在新能源汽车、5G通信、人工智能(artificial intelligence, AI)等现代高科技产业领域开始规模化应用. 这些第3代半导体凭借宽禁带、耐高压、高击穿电场等优异特性[2], 推动现代电子器件向高频化、高效化、小型化方向发展. 在此趋势下, 能够与第3代半导体相匹配的高频(>1 MHz)用软磁材料已成为制约产业进一步发展的关键瓶颈. 同时, 高速电机在运行过程中所产生的离心载荷与振动情况, 对软磁材料的机械强度和韧性提出了更高要求[1,3].
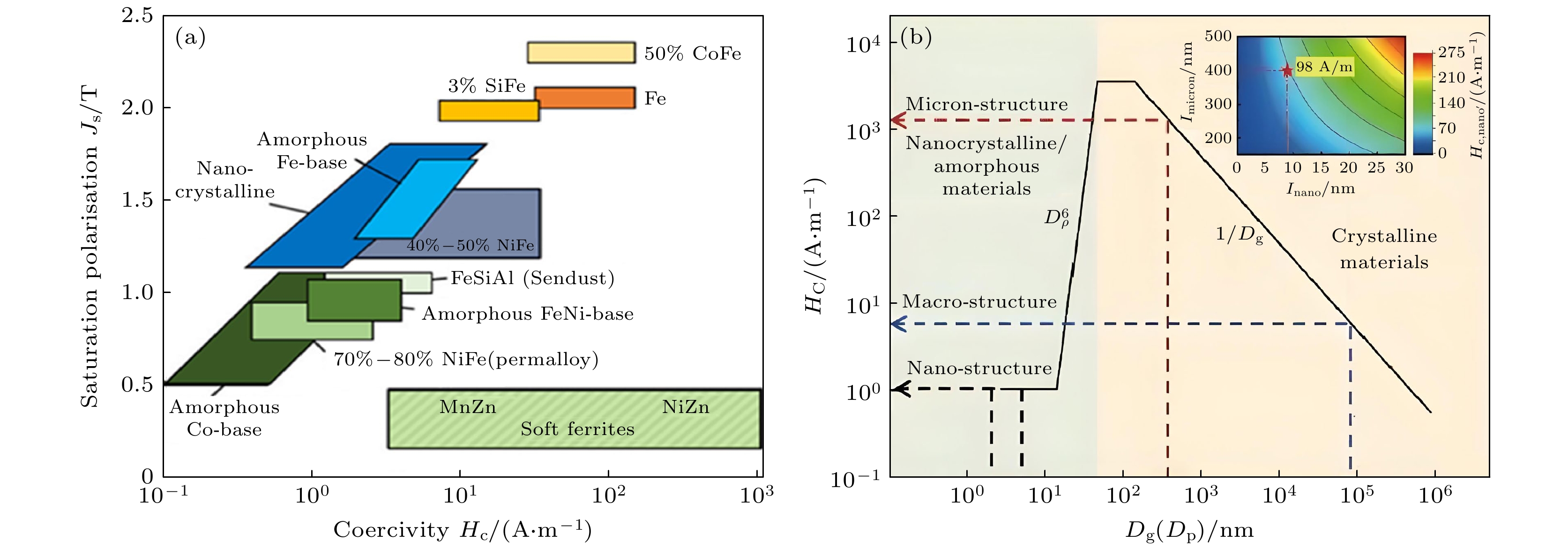
纵观软磁材料的研发历程, 其始终与电力电子关联产业的前行步伐紧密交织, 是电气产业升级的关键驱动力. 在19世纪末—20世纪初, 铁是唯一的软磁材料, 凭借较高的饱和磁化强度以及磁导率, 为早期诸如简易发电机、变压器等电磁设备筑牢根基, 助力人类初步达成电能与机械能之间的相互转换, 由此拉开电气化时代的大幕. 1900年前后, 人们尝试往铁里添加硅元素, 这一举措有效提升了材料的电阻率, 进而降低了涡流损耗情况, 而且还能维持相对较高的磁导率[1,4]. 这一改进使得硅钢在大型变压器和电机等设备中得到广泛应用, 极大地提高了电力传输和转换的效率. 以铁和硅钢为代表的早期软磁材料, 为电力工业的基础建设供应了关键的功能材料. 然而, 它们在高频环境下存在磁导率迅速下滑、电磁损耗偏高状况, 致使设备发热严重且能效降低, 这在很大程度上限制了其在高频工况场景下的应用. 在此背景下, 软磁铁氧体应运而生, 其磁导率在150 kHz以下保持基本不变, 且具有很高的电阻率, 能够有效抑制涡流损耗, 在高频应用中表现出色[5]. 软磁铁氧体的问世, 使得电感器、变压器这类磁性元器件能够在更高频率工况下有效运转, 为通信、广播电视、计算机等电子产业的崛起以及后续电气化发展供应了关键材料. 近年来, 随着宽禁带(wide-bandgap, WBG)半导体器件的面世, 电力电子设备的工作频率获得大幅提升. 非晶态以及纳米晶软磁材料, 凭借其高磁导率、高频损耗低的优势, 契合了 WBG 器件对于软磁材料的相关要求. 第3代宽禁带半导体器件崭露头角促使电子器件的工作频率进一步攀升至 MHz 乃至于 GHz 范围[6]. 同时, 高功率密度的车载充电系统和大型算力数据中心的电压调节系统, 要求软磁材料具有高饱和磁感应强度以及优异的扛饱和能力. 在此背景下, 金属软磁粉末绝缘包覆后通过粉末冶金工艺制备而成的软磁复合材料(磁粉芯), 由于兼具金属软磁的高饱和磁感应强度和铁氧体的低损耗特性[7], 为高频、高功率电子设备和电机的发展提供了新的材料选择.
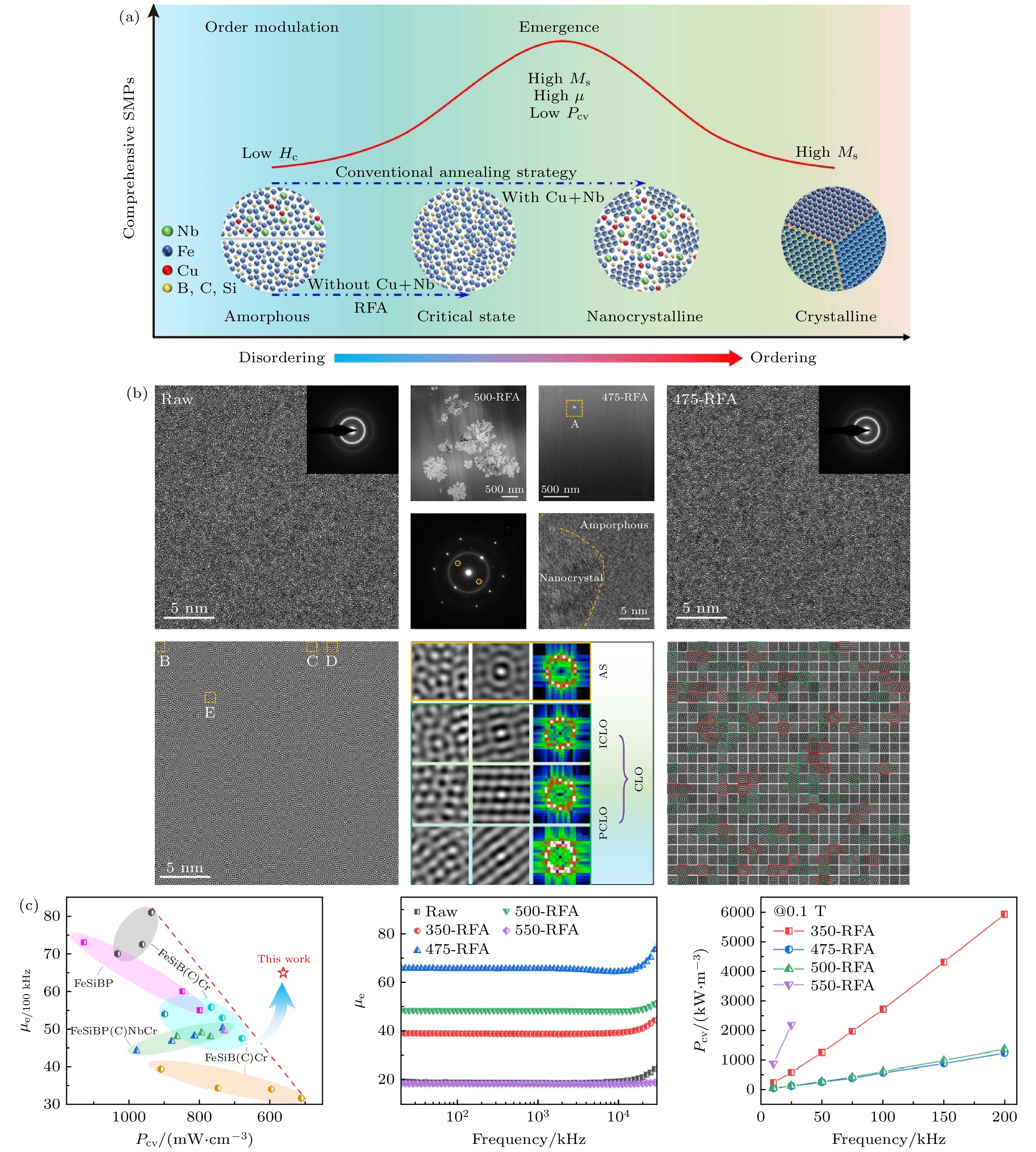
当前, 非晶基软磁材料的基本性能正逐渐逼近物理极限, 以饱和磁感应强度为例, α-Fe基合金的理论极限约为2.2 T(基于Slater-Pauling曲线), 而目前实验室制备的非晶已达到1.94 T[8], 矫顽力也降低至0.5 A/m[9], 在兼顾玻璃形成能力的前提下, 实际优化空间较小. 此外, 各种磁性能之间的互斥关系更加凸显, 以软磁合金为例, 其饱和磁感应强度主要由平均原子磁矩浓度及其交换耦合作用强度所决定[10], 这就要求合金成分中需包含较高比例铁磁性元素, 并且要具有合适的配比, 以便产生更多排列紧密且一致的磁矩. 然而, 铁磁性元素含量的增大会导致非晶形成能力快速降低, 进而使得纳米晶形核与长大过程难以控制[8], 在后续的热处理环节中很难获取低矫顽力, 由此形成了饱和磁感应强度与矫顽力之间的相互制约关系. 在高性能非晶基软磁材料的研发进程中, 非晶形成能力、磁强度以及磁 “软度” 之间的权衡问题成为关键挑战. 这种材料基本性能之间的复杂权衡关系, 使得材料的设计与制备必须同时应对多重矛盾, 已然成为当前材料学科发展中亟待攻克的关键科学难题. 如何借助变革性策略开发出具备极限性能组合的高性能软磁材料, 现已成为该领域的研究热点. 自然界中广泛存在的复杂、多尺度分级结构, 即微结构的有序化, 造就了许多兼具多功能特性的材料[11,12], 诸如兼具高强度与韧性的贝壳、竹子等. 这种仿照自然界生物结构的材料设计理念, 通过构建多尺度有序结构(序调控), 为解决材料性能冲突难题提供了全新思路. 非晶合金内部蕴含着丰富的序结构, 对其力学、磁学、催化等多种性能产生着重要影响[13]. 序调控理念为高性能软磁材料的研发开辟了新的路径. 本文着重介绍了序调控的科学理论基础, 总结了当前发现的与宏观磁学性能紧密相关的序结构、序构形式, 综述了基于序调控的非晶基软磁材料开发以及序参量调控研究的最新成果, 旨在深化对基本软磁性能权衡的物理本质、多种磁序态的竞争与调控等科学问题的理解.
-
序调控理念的起源可追溯至20世纪30年代所提出的朗道理论[14]. 该理论以序参量为核心概念, 构建起一个描述连续相变过程的统一框架. 它通过阐述系统由无序状态向有序状态的转变历程, 解析了相变过程中物质性能所发生的显著变化. 序参量(order parameter)是用于表征系统有序化程度以及对称性特征的物理量[15]. 在一级相变过程中, 序参量的数值会产生不连续的变化, 这一过程通常伴随着潜热的释放, 例如液-气相变以及某些固-液相变便属于一级相变[16]. 而在二级相变中, 序参量则从零开始连续地变化至非零值, 对称性也逐渐降低[16]. 在磁性材料中, 朗道理论的核心思想体现为磁化强度(磁矩)作为序参量, 定量刻画了磁性材料中磁有序态的涌现机制. 例如, 在铁磁性材料中, 当温度高于居里温度时, 材料内部的“小磁体”方向呈现出随机且均匀对称的状态, 在宏观层面不展现出磁性; 然而, 当温度降低至居里温度以下, 磁化强度自发增大, 标志着系统进入有序铁磁态.
朗道理论为磁相变提供了统一理论框架, 提出了序参量这一概念; 协同学理论重点指出了序参量关联的子系统耦合作用带来的集体效应. 协同学理论的创立者赫尔曼·哈肯提出, 序参量就如同木偶戏中的牵线人, 其操控着木偶们起舞, 而木偶们反过来也会对其产生影响、对其加以制约[17]. 协同学是一门致力于研究系统中的众多子系统如何借助协同作用形成有序结构的跨学科理论[18]. 该理论重点关注系统在临界条件下, 如何通过内部协同作用产生集体行为, 进而促成宏观有序结构的形成. 协同学理论认为序参量是少数几个主导系统宏观行为的关键变量, 当系统逼近不稳定点或临界点时, 它们决定了系统整体的动力学行为、有序状态以及新结构的产生. 序参量能够驱使大量的微观变量, 促使系统中的各个部分协同作用, 从而生成有序结构. 复杂开放系统中, 大量子系统相互作用所产生的集体效应, 是系统有序结构形成的内在驱动力[19]. 当复杂系统受到外部能量的作用, 或者物质聚集达到某种临界值时, 子系统之间便会产生协同作用, 促使系统从无序状态转变为有序状态, 并从混沌中催生出某种稳定的结构. 在磁性体系中, 协同学理论揭示了微观磁矩通过交换相互作用形成的协同效应. 当温度接近居里点时, 局域磁矩的涨落通过交换作用耦合, 形成集体有序行为. 此时, 磁化强度作为主导序参量, 驱动系统从无序顺磁态向有序铁磁态转变. 在Fe基非晶合金中, 短程有序团簇的磁矩通过交换耦合在中程序尺度上协同排列, 显著降低矫顽力并增强饱和磁化强度[20].
在前两种理论的基础上, 突变理论描绘了集体效应最大化产生的反常特性涌现现象. 当系统的某些参数缓慢变化并抵达临界点时, 系统可能会突然发生突变, 迅速跃迁至新的状态[21]. 在工程学领域, 突变理论能够助力理解诸如突然断裂、材料屈服、机械失效等现象[22]. 在材料科学范畴, 大量基础粒子集合所表现出的行为, 无法用少量粒子的行为来解释, 在粒子逐渐聚集的过程中, 一些特殊结构的出现会引发量变到质变的过程, 表现为宏观性能的突变. 在序调控过程中, 材料内部有序-无序结构重新排列, 复杂性逐渐增加, 当增加到一定程度时, 便会诱导材料极限性能组合的出现. 临界现象是指当系统或物质处于或接近临界点时, 所展现出的一些独特、异常的性质, 是物理学中处于边缘却充满惊喜的现象. 这种临界现象及其带来的反常特性在非晶合金的制备、塑性变形、磁性等领域也无处不在[23]. 对于材料序参量关联诱导性能突变背后的规律、机制的研究, 构成了基于序调控研发高性能非晶基软磁材料的理论根基.
-
从凝聚态物理的视角来看, 物质磁性是时间反演对称性破缺的产物, 对称性破缺意味着序参量不为零的磁有序相的出现[24]. 在铁磁材料中, 磁化强度(磁矩)作为序参量, 在居里温度附近发生显著变化, 描述了从顺磁态(无序态)到铁磁态(有序态)的相变[25]. 当温度高于居里温度时, 材料内部的小磁体方向呈现出随机且均匀对称的状态, 故而在宏观层面不展现出磁性; 唯有当对称性遭受破坏, 内部结构趋于有序, 材料才会显现出整体的磁矩. 在居里温度这一临界点上, 磁体内部会涌现尺寸各异的团簇, 团簇内部联系紧密, 形成大小不一的磁矩[26]. 团簇的形成打破了原有的对称性, 其产生的磁矩促使周围的小磁体与其同向排列, 一旦跨越临界点, 材料便会产生整体磁性. 此过程的关键推动力源自系统内部无序的小个体之间逐渐产生的关联作用. 从数学层面而言, 这种关联作用被定义为平均值的乘积不等于乘积的平均值, 二者之间的差值则被称为关联函数 G(r)[25,26]. 关联函数(长度)越大, 表明关联作用越强, 有序程度也就越高. 在关联作用的约束之下, 个体之间的涨落相互影响, 影响力随着小系统的成长而逐渐增强, 只要涨落中产生的新相超过一定长度, 它便能够稳定存在并不断生长, 直至扩展至整个系统, 此时相变便会发生.
从微观层面看, 物质由原子构成, 原子由原子核与核外电子组成. 电子在原子中因绕核运动产生轨道磁矩, 因自旋产生自旋磁矩. 原子核磁矩约为电子磁矩的 1/1836.5[27], 故原子磁矩主要源于电子的轨道磁矩和自旋磁矩, 这是物质磁性的根本来源. 在固体(包括晶态和非晶态)中, 原子受邻近原子核电场和电子静电场影响, 部分电子成为相邻原子的共享电子, 电子结构改变, 部分轨道磁矩被冻结, 导致固体中原子磁矩偏离理论值[26]. 实际材料中, 磁各向异性、缺陷、应力、磁场、温度等因素使磁矩无法自由排列. 为实现能量最小化并受多种磁矩相互作用机制驱动, 材料内部形成各类形状各异的磁畴、畴壁等微观结构.
磁性是原子磁矩排列方式的宏观表现. 从原子磁矩到物质宏观磁性, 学界提出了诸多理论以阐释原子磁矩的排列方式与相互作用机制, 涵盖早期分子场理论[28]、量子力学交换作用理论[29], 以及巡游电子模型[30]和RKKY (Ruderman-Kittel-Kasuya-Yosida interaction)互作用[31]等. 1907 年, Weiss 提出分子场唯象理论以解读铁磁性. Weiss 假设铁磁物质内部存在一强大分子磁场, 使其能克服热扰动的不利影响, 将磁矩整齐排列, 进而引发自发磁化[28]. 该理论成功阐释了铁磁体的能量特性, 并对诸多实验结果进行定量描述, 但未能阐明分子场的起源. 1928年, 海森伯构建了基于局域磁矩的交换相互作用理论, 指出铁磁性分子场源于电子间的交换作用, 揭示了Weiss分子场的本质[29]. 局域电子模型可解释磁性绝缘体化合物的磁化行为, 但对于具有3d电子公有化运动特性的磁性金属, 原子磁矩概念适用性有限. 1934年, Stoner[30]提出基于能带理论的巡游电子模型, 将过渡金属的铁磁性归因于巡游电子间的相互作用, 凸显非局域电子对铁磁性的重要作用, 并给出判断铁磁自发磁化的Stoner判据. 巡游电子模型成功解释了过渡金属诸多重要实验现象, 如单原子平均磁矩非玻尔磁子整数倍、合金磁矩遵循Slater-Pauling曲线等. 此后, 氧离子耦合交换作用理论[32]与 RKKY 互作用理论[31]相继问世, 揭示了以氧离子、电子气为媒介传递的交换作用机制, 解释了过渡金属氧化物、稀土合金等多类材料的铁磁、反铁磁、亚铁磁行为.
电子之间的强相互作用导致磁矩的有序排列, 导致材料性能偏离独立粒子模型, 产生了铁磁序、反铁磁序等多种宏观磁性物质. 电子间的强关联效应是磁性材料中序的形成的重要条件. 因此, 序结构的排列有序化应能够增强单一或多个尺度上有序单元之间的耦合作用, 对磁矩特性及其进动行为产生显著影响. 序参量理论与磁学理论的结合为序调控提供了全面框架. 两者均通过研究微观单元(如原子磁矩)的相互作用, 阐释宏观磁有序态的形成. 磁学理论从唯象和量子层面揭示了微观单元间相互作用的本质, 并阐明了反映磁性本质的物理参数, 为序参量理论奠定重要科学基础. 序参量理论则基于统计物理与热力学, 阐述了在更广泛体系中新特性产生的规律及其涌现特征, 为理解复杂磁性材料的构效关系提供了关键视角.
-
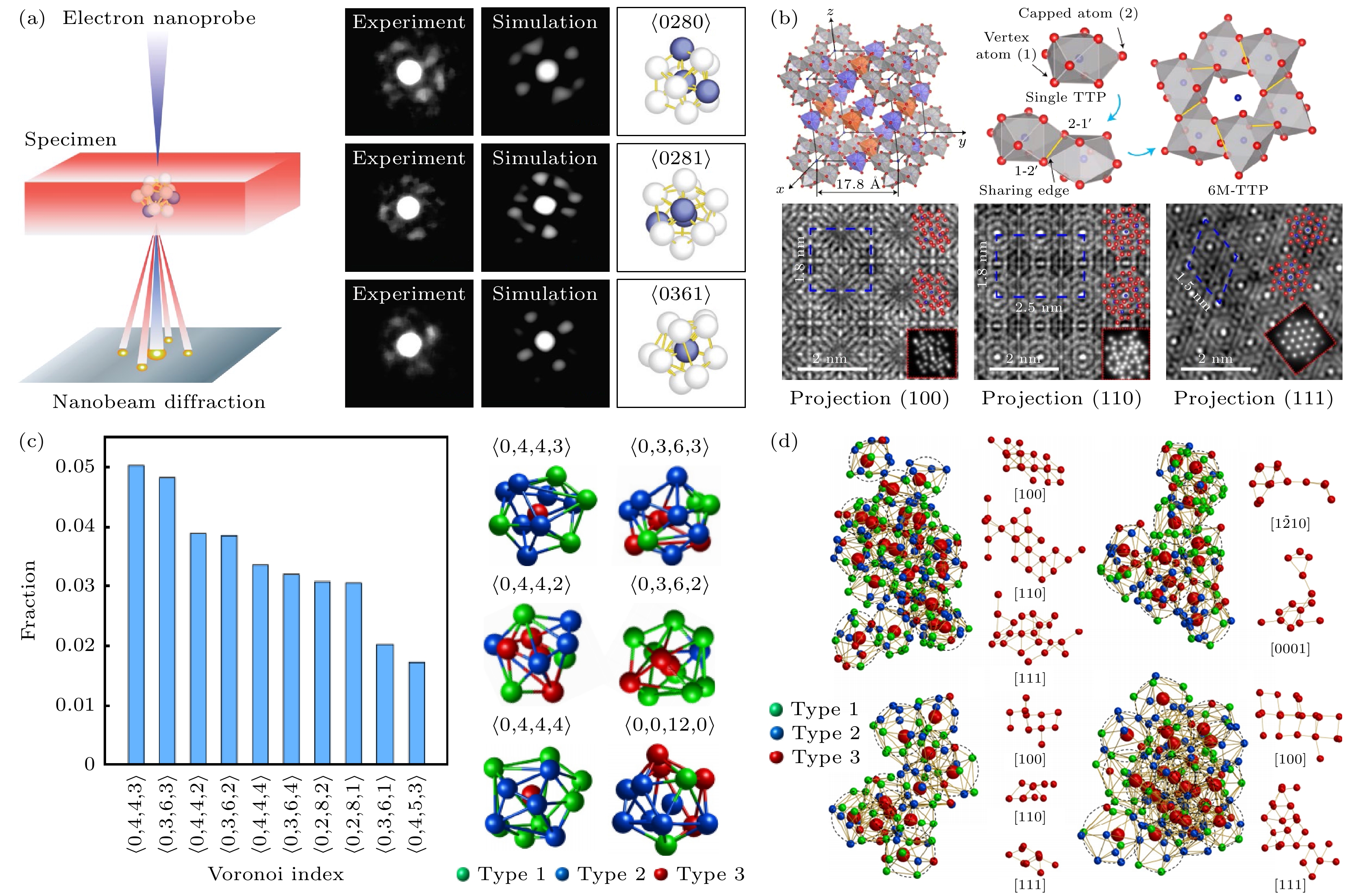
自1959年非晶合金问世, 其内部结构探究便备受关注. 基于长程无序的基本认识, 学者提出诸多结构模型, 如硬球密堆[33]、无规密堆网络模型[34]等. 后续实验与模拟研究发现非晶合金存在多样“序”结构, 像短程序[35]、中程序[36], 甚至高压下的长程拓扑序[37]. Elliott对这些序结构分类[38]: 短程序尺寸<0.5 nm, 结构类似相应晶体相, 源于原子间化学相互作用; 中程序尺寸0.5—2 nm, 由短程有序团簇特定方式连接形成. 基于“序”的多种非晶结构模型被提出, 如团簇堆积[39]、准团簇密堆[40]、分形团簇堆积[41]和渗透团簇模型[42]等. 非晶合金内部不同尺度序结构可通过球差电镜与电子断层扫描(atomic electron tomography, AET)等高分辨手段探测解析. Hirata等[43]借助纳米束电子衍射观察到单个原子团簇及其扩展结构的不同衍射模式, 为短、中程序的存在提供了直接证据(图1(a)). Lan等[36]在Pd-Ni-P非晶合金中发现关联非晶结构与立方晶化相的手性中程序结构-六元三帽三棱柱(6M-TTP)(图1(b)), 该结构在铸态样品中由短程序团簇独特手性方式长程无序堆积, 一定温度下可转变为有序亚稳立方相. Yang等[44]利用 AET 技术精确测定了非晶合金中18000多个原子三维位置, 确定了4种类晶状中程序结构(图1(c), (d)).
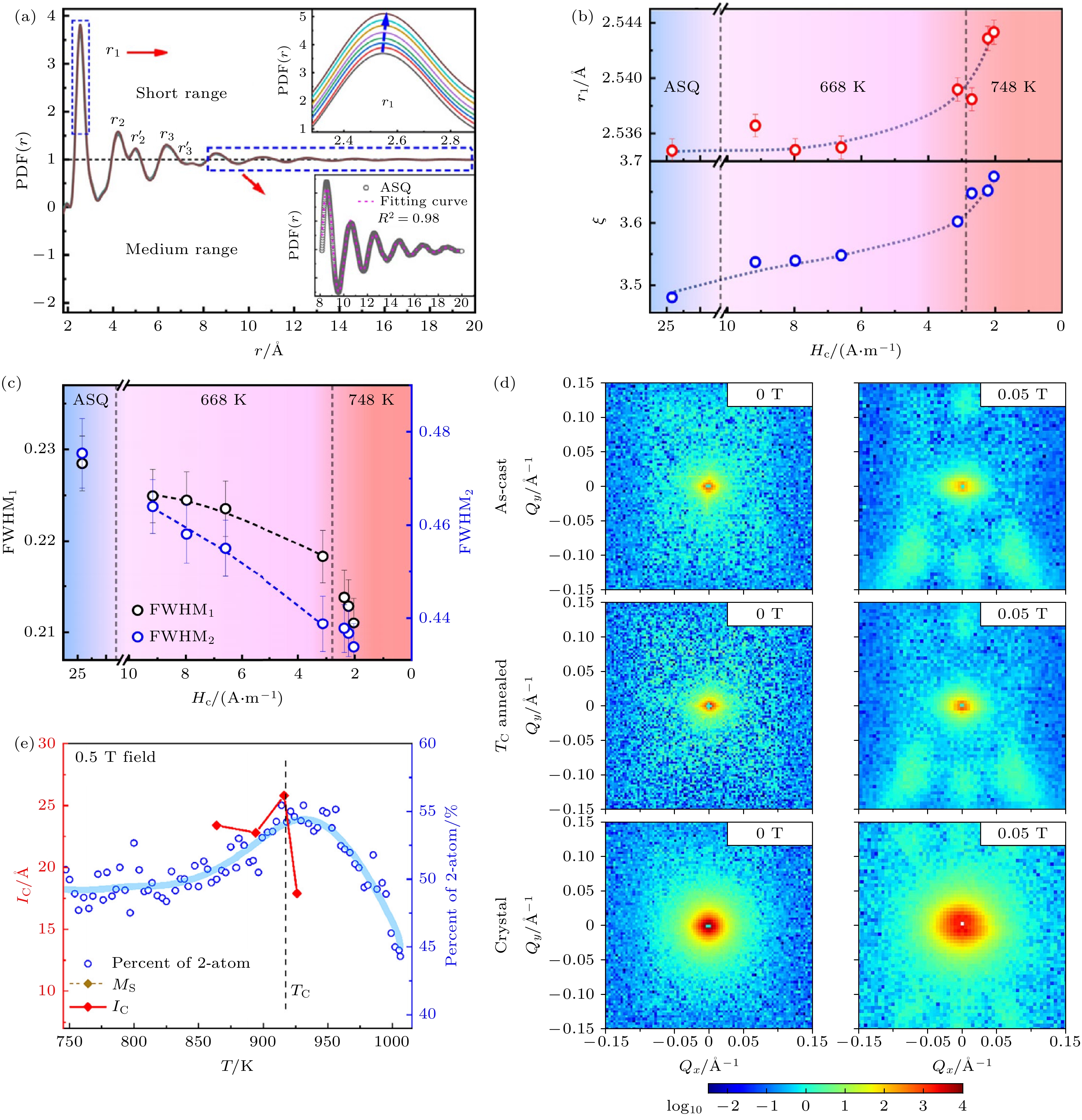
非晶合金的结构序、磁序与磁学性能的内在关联, 是基于序调控开发高性能非晶基软磁材料的重要基础. 结构序由元素化学相互作用、构型熵等多因素决定, 显著影响电子分布与交换作用, 进而改变磁矩大小和磁稳定性. 例如, BCC结构α-Fe相结构稳定性高于FCC结构γ-Fe相[45], 电子态密度在费米能级处强度更高, 较大原子间距利于电子自旋平行排列, 故磁矩和磁稳定性更高, 而γ-Fe通常呈反铁磁性. 非晶合金纳米尺度及原子尺度的微小磁结构变化很难被磁光克尔、磁力显微镜等方式捕捉. Tong等[20]通过同步辐射研究发现退火诱导致密Fe-M短程有序团簇的形成(图2(a)—(c)), 增强了局域铁磁交换相互作用, 而在中程序尺度下, 磁非均匀性降低利于降低矫顽力. Ge等[46]利用原位磁场同步辐射与小角中子散射技术, 在Fe-Dy-B-Nb体系中发现具类似六角形拓扑序构的纳米磁畴(图2(d)), 其磁相关长度与团簇边共享模式演变呈一致规律性(图2(e)). 类似地, Bai等[47]发现随退火温度升高, Fe78Si9B13非晶条带三原子共享模式增加, 单原子共享模式减少, 中程序结构有序化使饱和磁化强度增大. 一般而言, 非晶序结构原子间距、键长减小及更大 Fe 原子比例将促进磁交换作用, 提高磁强度.
-
与硅钢、铁氧体等传统软磁材料相比, 非晶基软磁材料具高饱和磁感应强度、高电阻率与低矫顽力等特性, 在高频、高效、低损耗等苛刻服役环境下优势显著. 非晶基软磁材料主要有丝材、条带、粉体及由粉末冶金工艺制备的块体软磁复合材料(磁粉芯). 鉴于非晶合金多尺度序结构对磁学性能的重要影响, 本节将从原子尺度、纳米尺度、界面相尺度介绍相关研究进展.
-
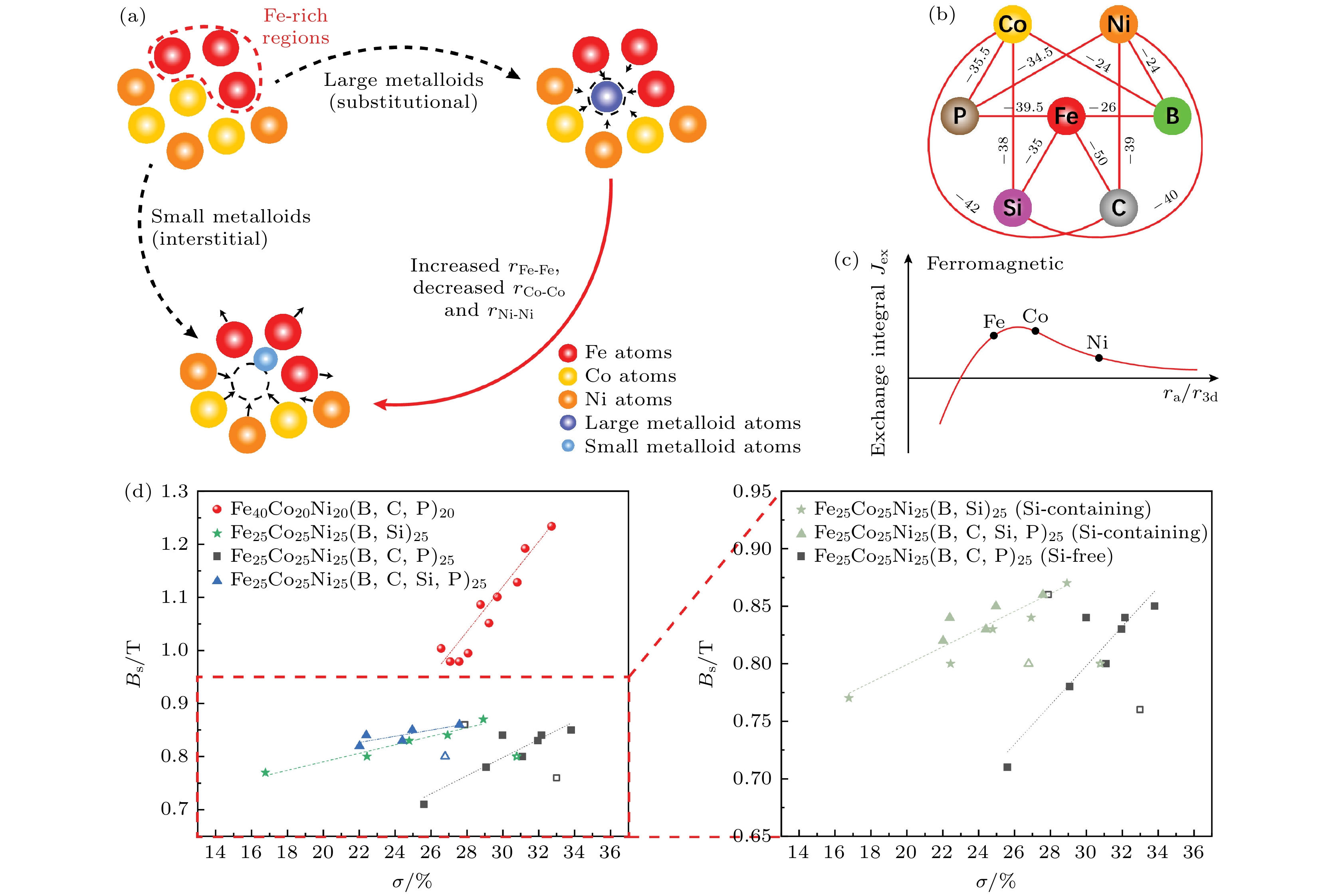
非晶软磁合金磁学性能与原子尺度短程、中程有序结构直接相关. 原子团簇的形成受化学成分、制备工艺与后续处理条件影响, 本质是元素间相互作用、热力学与动力学条件的权衡. 元素种类、比例与混合焓对团簇结构及稳定性影响显著. 改变Fe局域团簇结构, 将更多反铁磁团簇转化为铁磁团簇, 可在不增大Fe含量的前提下提高磁强度. 如在Fe-B合金中, B原子周围团簇与Fe2B相原子团簇结构相似, 形成 B-B2Fe8团簇[48]. 添加Si后, Si原子替代团簇中心B原子, 形成Si-B2Fe8团簇结构[49]. Si原子加入改变了团簇尺寸和形状, 合适原子比例(如近共晶点)可促进特定团簇形成, 获得最大程度团簇内原子相互作用, 提升合金热稳定性. 混合焓描述了合金中不同元素混合时的能量变化, 较强负混合焓意味着非晶结构中原子间关联作用强. Fe基非晶合金体系微合金化主要包含Co, Mo, Ni等磁性金属元素B, P, C等非金属元素. Shi等[50]提出基于Bethe-Slater曲线的 “framework + fluctuation” 模型[50](图3(a), (b)), 模型通过引入“波动参数”σ, 量化了不同非金属元素对铁磁性金属原子分布的影响(图3(c), (d)). 当铁磁金属含量固定时, 饱和磁感应强度由Fe40Co20Ni20B5C5P10的0.97 T提高至Fe40Co20Ni20B9C7P4的1.25 T, 提高幅度达29%, 而对应的矫顽力则由0.5 A/m提高至13.0 A/mm, 变化幅度达25倍. 在铁磁性元素含量与比例一定情况下, 不同非金属原子与铁磁性金属元素混合焓不同, 改变了铁磁元素的原子尺度分布, 例如, 小原子半径的非金属元素(如B和C)倾向于占据铁磁性金属原子间的间隙位置, 增大 Fe-Fe 间距; 大原子半径的非金属元素(如P)倾向于替代铁磁性金属原子, 减小 Co-Co, Ni-Ni 间距. 这些结构变化通过Bethe-Slater曲线影响交换积分, 进而影响非晶合金居里温度、饱和磁感应强度等磁学性能.
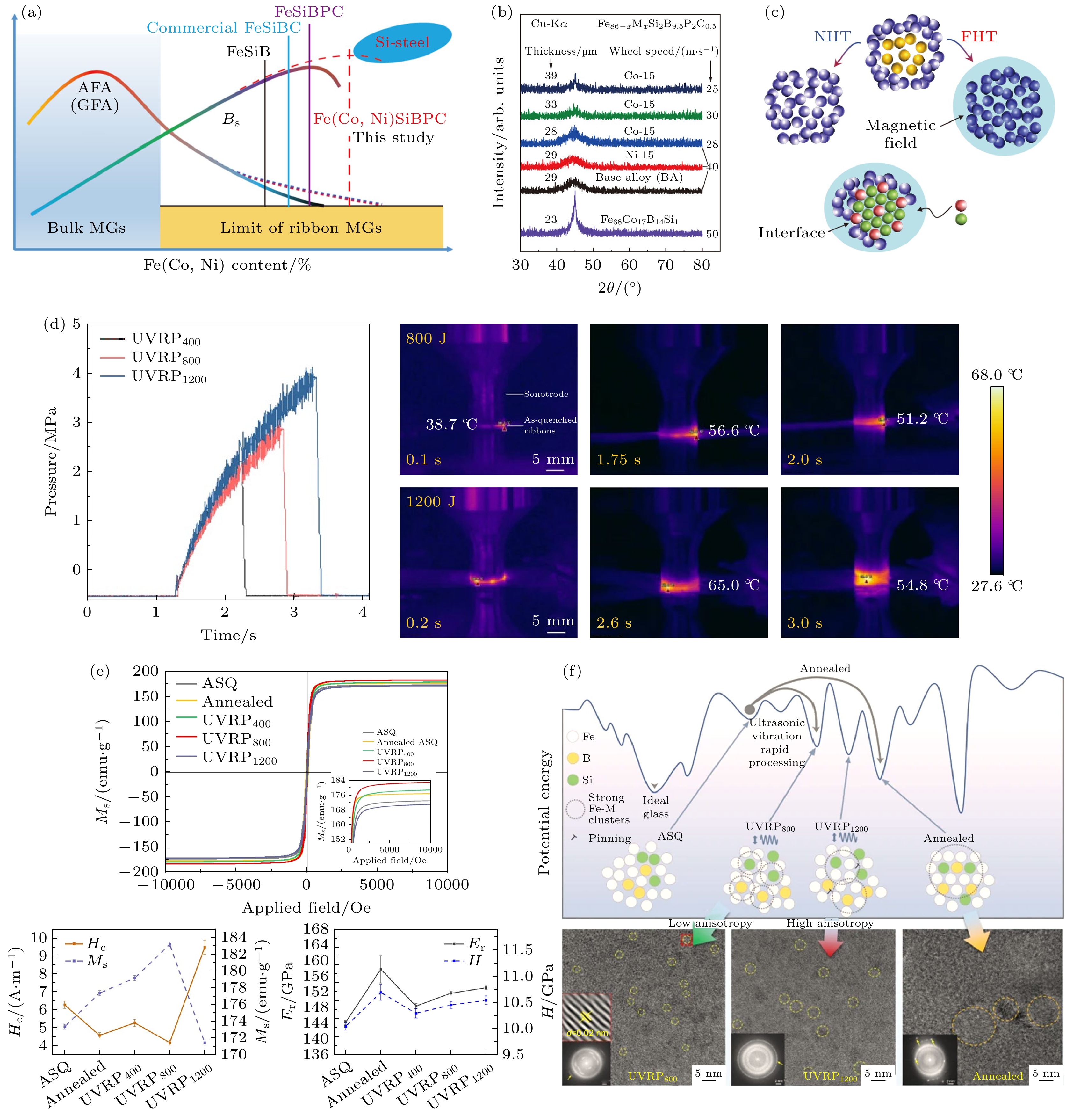
对于特定成分的合金体系, 通过热、磁场和超声场等特种能场可以实现原子尺度序调控, 从而获得高性能非晶基软磁材料. 高饱和磁感应强度往往需要高的铁磁性元素含量, 但这同时也降低了合金的非晶形成能力[8]. 基于饱和磁感应强度与非晶形成能力之间的权衡, Zhao等[51]提出在临界非晶形成能力条件下获得高密度团簇, 并结合磁场热处理调控磁结构不均匀性的理念(图4(a), (b)), 利用调控甩带与热处理参数获得的高密度团簇促进铁磁交换作用, 获得了高达1.86 T的高饱和磁感应强度、同时保持低矫顽力(2 A/m)和高磁导率(24000)的Fe71(Co, Ni)15B9.5Si2P2C0.5非晶软磁合金. 高温退火可能诱导晶化, 难以获得均匀分布的铁磁团簇以实现理想软磁特性. 为此, Li等[52]通过超声振动对Fe基非晶条带进行快速后处理, 获得了具有高饱和磁化强度(183.2 emu/g)和低矫顽力(4.2 A/m)的性能组合(图4(d), (e)). 超声振动可促进非晶内部原子级应力松弛的快速激活, 使结构发生自发调节. 适当的超声能量输入可以精确地将非晶合金的势能驱动到稳定的低能盆地(图4(f)). 这一过程可形成大小为2—3 nm的高密度、强磁性Fe-M(Si, B)团簇, 减弱磁各向异性, 从而产生优异软磁特性[52].
在磁场辅助热处理中, 静磁能可无接触传输到材料内部, 改变原子排列、自组装与迁移扩散等行为. Zhang等[53]研究磁场热处理对 Fe80Si9B11非晶合金结构与性能影响, 发现在653 K下进行1 T磁场退火时, 样品最大磁通密度、弹性模量与硬度分别提高 13.7%, 36.6%, 9.4%, 矫顽力与磁滞损耗分别降低71.5%和68.2%, 并认为性能变化源于磁场诱导生成大量球对称二十面体团簇与少量平移对称团簇.
非晶软磁粉芯的高频损耗改善常伴随饱和磁化强度、磁导率降低[54]. 为突破饱和磁化强度/磁导率与磁芯损耗倒置关系, Shao等[55]提出在居里温度到晶化温度范围内通过旋转磁场热处理进行原子尺度序调控, 构筑非晶向纳米晶转变临界态结构(图5(a)), 成功在商用 FeSiBCCr 非晶粉中引入体积分数约21%的1 nm左右类α-Fe中程序(图5(b)). 其饱和磁化强度为 170 emu/g, 有效磁导率为65且稳定到10 MHz, 磁芯损耗(0.01 T, 1 MHz)为70 mW/cm3 (图5(c)). 分子动力学模拟结果表明, 相比普通热处理, 旋转磁场热处理可缩短晶化孕育期50%, 有利于非晶基体析出局域有序结构[55]. 临界态结构磁粉芯具规则板条状磁畴结构, 磁畴变宽, 畴壁运动驱动力更小, 因此具有优异软磁性能.
-
在Fe基非晶软磁合金体系中, 还存在一种特殊晶化相, 即体心立方结构的α-Fe相, 其部分原子可能被合金成分包含的Si, Co等原子取代, 热稳定性进一步提高[56]. α-Fe相一般通过在第一晶化峰温度对铸态非晶合金进行退火晶化获得. α-Fe相具有较高的磁矩, 同时纳米晶粒之间通过非晶基体发生铁磁交换作用, 这种交换作用可以将纳米晶的磁矩与非晶基体的磁矩耦合起来形成均匀的磁化状态, 降低磁化过程中的能量损耗, 从而显著提高饱和磁感应强度和磁导率, 同时降低矫顽力[4](图6(a)). 作为影响磁学性能的重要功能基元, α-Fe(Si, Co)相构成的非晶-纳米晶双相序构调控成为重要研究内容, 其中α-Fe相的晶粒尺寸、分布和晶界特性是关键序参量. 纳米晶之间的铁磁交换作用长度L0与磁晶各向异性的平均涨落(平均各向异性)成反比[57]. 当晶粒尺寸D远小于L0时, 磁导率和矫顽力分别与D–6和D6成正比. 晶粒细化, 矫顽力将显著降低、磁导率增大[57](图6(b)). 当晶粒尺寸远小于畴壁宽度时, 磁晶各向异性在纳米尺度上随机波动. 这种随机波动通过铁磁交换作用被平均化, 从而显著降低有效磁各向异性[4]. 在Fe基纳米晶合金中, 晶粒尺寸为10—15 nm时, 局部磁晶各向异性常数K1可以降低到105 J/m3量级[4], 从而实现优异的软磁性能.
学者们探索了多种方式以细化晶粒, 如成分设计、磁致晶化等. 成分设计是通过添加促进晶粒形核、抑制晶粒长大元素实现晶粒细化, 常见的促进晶粒形核元素为Cu[59,60], Co[9], Au[61]等(通常与Fe具有正混合焓, 且其在结构中形成的前躯体与α-Fe具有较低的错配度), 抑制晶粒长大元素为Nb[62], Mo[9]等(扩散缓慢). 但这些大多为非磁性元素, 添加后不可避免地降低了饱和磁感应强度, 因此研究人员将研究重心转向具有预存纳米晶结构的高Fe含量非晶纳米晶合金的晶粒细化. Li等[59]提出预存α-Fe晶粒间的强竞争生长与Nb元素的协同效应可有效抑制α-Fe纳米晶过度长大的策略, 在高Fe含量Fe-Si-B-Cu合金带材的非晶基体中分散着高密度的预存Cu团簇和α-Fe纳米晶粒(以毗邻和包围Cu团簇的两种形态形成), 该类前驱体在低速升温热处理条件下即可获得微细纳米晶组织. Han等[61]通过Au-P[61]、Cu-P[60]前驱体团簇的分解在预存纳米晶Fe-P基非晶纳米晶薄带中获得了细小且均匀分布的α-Fe纳米晶结构. 调控前驱体团簇结构虽然能够实现晶粒细化, 但依旧难以摆脱对非磁性元素的依赖.
为了获得均匀、细密的非晶-纳米晶双相序构, Li等[63]反常规地去除传统纳米晶合金成分中促进形核和抑制扩散元素, 通过质量分数为4.6%的常见类金属元素(B, Si, P和C)的组合添加, 稳定非晶相和纳米晶间基体相以调和饱和磁感应强度与非晶形成能力的矛盾, 设计了Fe85.5B10Si2P2C0.5合金, 并在临界冷却速率下快冷预制高密度的形核点, 诱导类金属瞬态富集界面以细化晶粒. 这种独特的成分、工艺设计思路相当于将同等铁含量的硅钢纳米晶化, 去除晶界的同时保留了α-Fe相的超高饱和磁感应强度, 从而获得了接近硅钢的饱和磁感应强度(1.87 T)和优异的软磁性能.
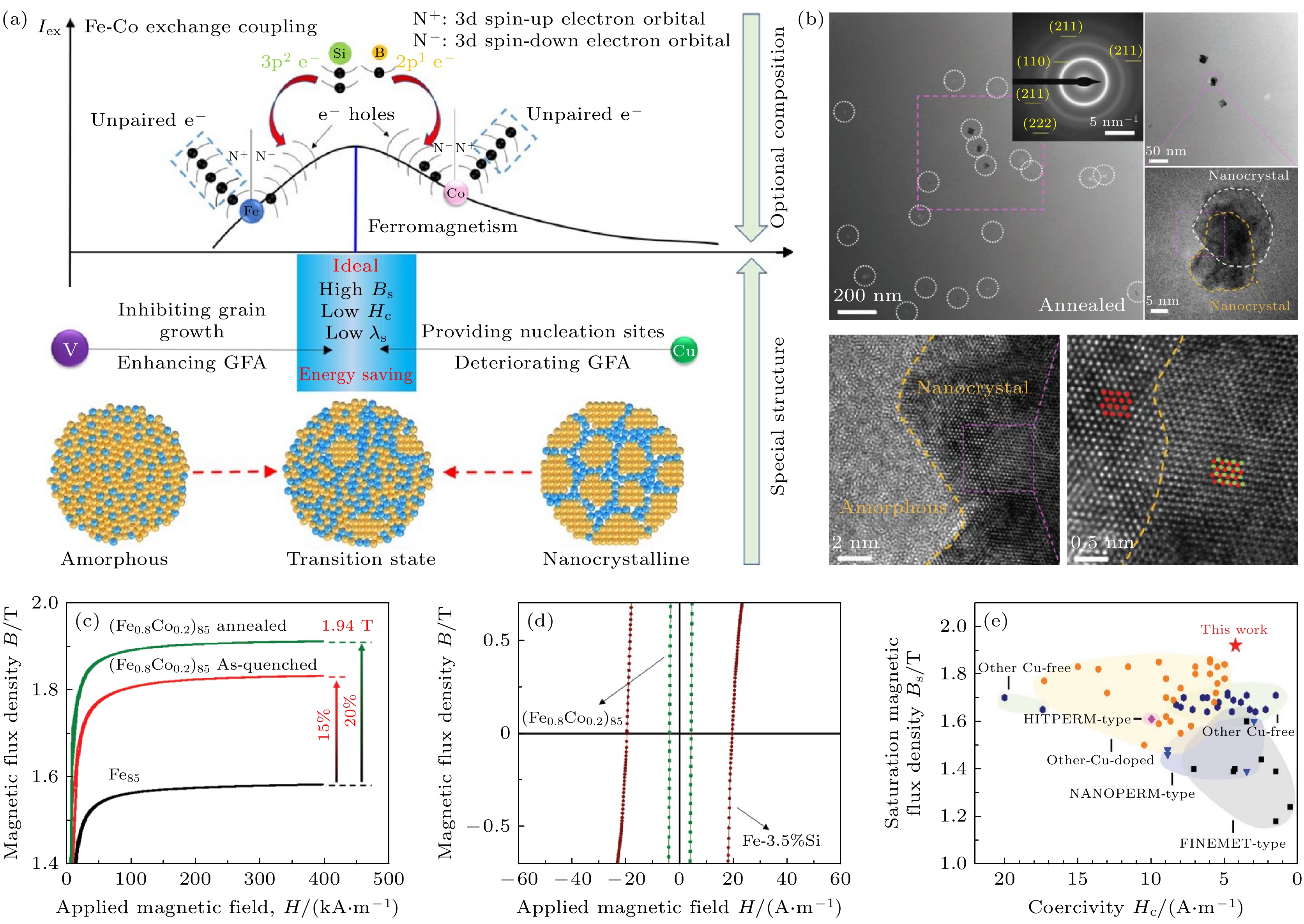
不同于以往通过提高铁磁性元素含量的成分设计思路, Li等[8]通过添加适量Co以提高其交换耦合作用, 并微合金化Cu, V等元素以平衡非晶形成能力、软磁性能和形核长大之间的相互关系(图7(a)), 设计了(Fe0.8Co0.2)85B12Si2V0.5Cu0.5新型合金. 该合金由体积分数为0.5%的纳米晶、非晶基体内小于5 nm的类晶体团簇的过渡态序构组合而成(图7(b)). 该合金具有迄今为止纳米晶合金材料中的最高Bs值(1.94 T)和最低极限的Hc(4.3 A/m) (图7(c)—(e)). 过渡态序构增强了局域磁矩交换作用, 同时具有超低的磁各向异性和畴壁钉扎效应[8].
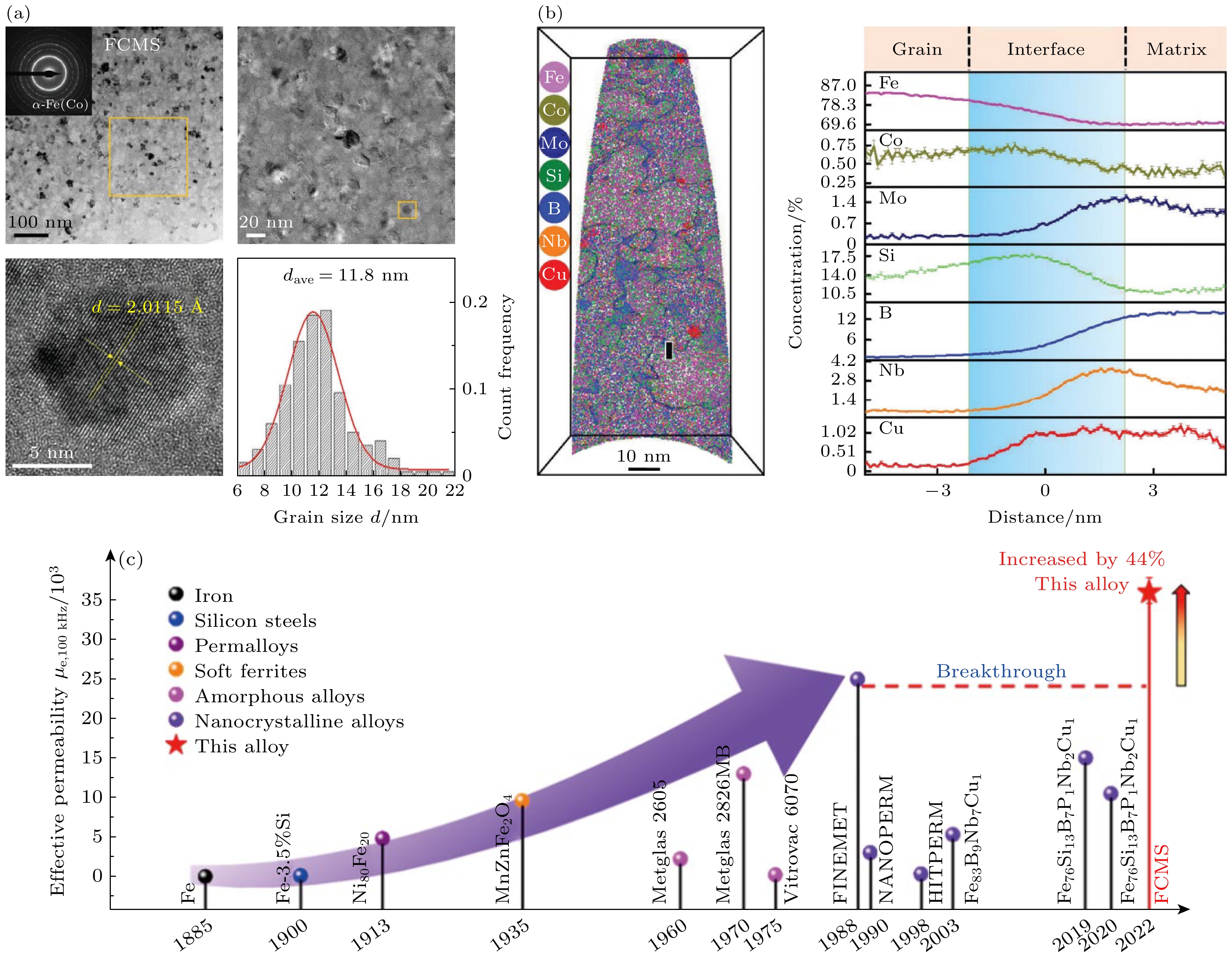
磁致晶化通常是将磁场引入热处理过程中, 将静磁能无接触地传输到材料内部, 改变原子排列、自组装和迁移扩散等行为而实现晶粒细化. Duan等[64,65]对FeSiB等合金进行磁场辅助热处理研究中发现, 强磁场对于铁磁性析出相具有磁化能(12 T磁场作用下, 磁化能可达数百J/mol), 该磁化能可以降低形核势垒、降低形核半径, 从而显著提高α-Fe的形核率. 此外, 强磁场作用下Si元素在α-Fe中具有更高的固溶度, 可以驱动非晶基体内的Si元素向α-Fe相迁移, 提高α-Fe相中的Si含量或富集在其周围, 从而抑制晶粒长大[64]. 强磁场的引入具有与Cu和Nb等元素掺杂类似的作用, 同时显著提高合金饱和磁感应强度. 为了提高纳米晶软磁合金的高频磁导率, Zhou等[9]通过在传统FeSiBCuNb纳米晶合金体系中微量添加Co和Mo元素, 在外加磁场诱导下, 利用Fe-Co磁性原子团簇作为纳米晶的成核位点, 并通过Mo和Nb元素的协同作用抑制纳米晶生长, 形成平均晶粒尺寸11.8 nm的非晶-纳米晶双相结构(图8(a), (b)). 这种由磁不均匀性驱动的新型纳米晶化机制获得的纳米晶合金在高频下表现出超高磁导率, 100 kHz下比同厚度的Finemet合金高出44%, 1 MHz下高出65%, 同时还具有极低的损耗(120 kW/cm3@0.2 T, 100 kHz)[9] (图8(a), (b)). 其高频磁性能起源于超细非晶-纳米晶双相序构产生的极低磁晶各向异性、磁弹性各向异性以及特殊磁畴运动机制. 随着磁场强度增大, 畴壁几乎不随着外加磁场变化而移动, 在达到临界强度时, 所有磁矩从平面外反折到同一方向, 畴壁瞬间消失[9]. 这种独特的磁畴运动机制使该合金在高频下更容易被磁化, 从而大幅提高了高频磁导率、降低其高频损耗.
-
非晶软磁复合材料, 也称磁粉芯, 是由非晶粉末经过绝缘包覆、压制、热处理等粉末冶金工艺制备而成的[54], 其继承了非晶软磁合金的高饱和磁感应强度、低矫顽力特性, 同时兼具高电阻率、极低的高频损耗等优异性能, 在中高频领域具有巨大应用潜力. 然而, 其广泛应用也面临着脆性大、高密度成型困难、热稳定性差以及磁导率偏低等挑战[54]. 为了应对上述挑战, 提升非晶软磁复合材料的性能, 界面序调控成为关键手段. 通过优化界面材料与结构设计、制备工艺调控磁粉芯内部的铁磁序构、应力状态以及涡流分布, 实现磁学性能提升.
由绝缘包覆形成的核壳结构是磁粉芯的基本结构单元, 芯部粉末与界面之间的铁磁序构形式对磁相互作用、磁畴运动具有显著影响, 是提高磁导率、降低高频损耗的重要研究思路. 经过大量研究, 界面设计由早期的单一绝缘界面向绝缘与导磁兼顾、多材料与多尺度结构结合的复合多功能界面转变[54]. 传统的界面设计主要关注静态绝缘性能, 通过在颗粒表面形成一层绝缘层来减少涡流损耗. 例如, 有机树脂[66](环氧树脂、硅树脂等)、无机氧化物[67,68](SiO2, TiO2等)等被广泛作为粉末包覆层, 这些非磁性材料与非晶粉末形成铁磁芯-非磁壳的铁磁序构形式, 虽然能提高电阻率、降低高频涡流损耗, 但同时也因“磁绝缘”而显著降低了磁导率. 随后, Ni-Zn铁氧体[69]、Fe3O4[70]等磁性界面与非晶粉末形成的铁磁芯-铁磁壳序构被证实能够增强磁相互作用、缓解磁稀释效应而显著提升磁粉芯的磁导率.
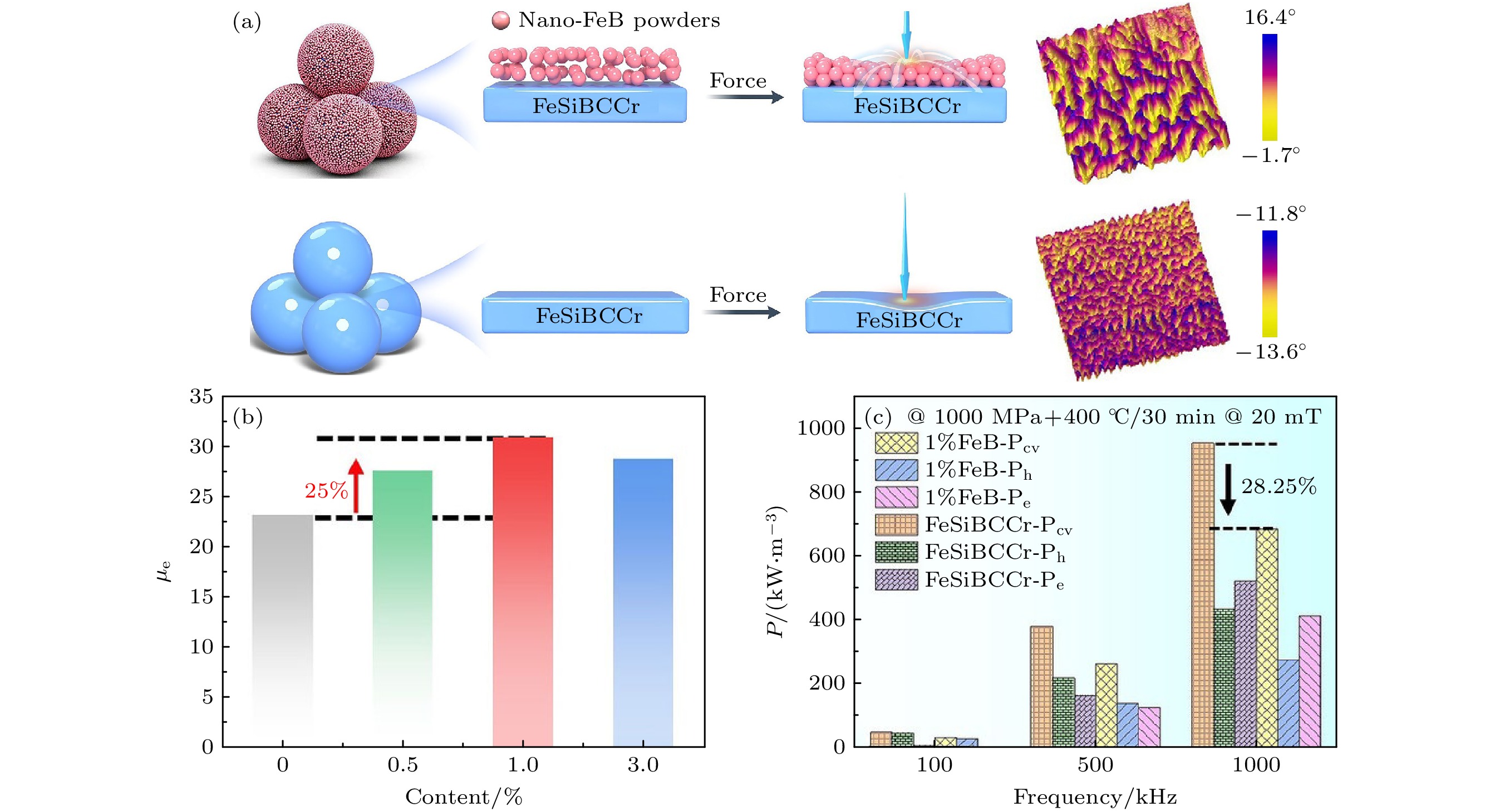
在此基础上, 通过结合多种材料的优点优化界面性能, 如使用有机-无机复合界面[71](如TiO2/环氧树脂)和磁性-绝缘复合界面[72](如Fe3O4/环氧树脂), 不仅提高了电阻率, 同时增强界面结合强度、磁响应而改善磁粉芯的力、磁综合性能. 放电等离子烧结(spark plasma sintering, SPS)通过高能脉冲直流电流直接加热粉末颗粒, 在颗粒间产生等离子体放电效应, 促进原子扩散和粉末结合, 能够在短时间内实现致密化成型[73–75]. Lu等[69]通过SPS技术制备了由MgO/NiZn Fe2O4铁氧体复合界面包覆的Fe6.5Si磁粉芯, 在芯部粉末和铁氧体界面之间引入MgO界面层能够在提高电阻率、降低高频损耗的同时通过应力屏蔽效应降低矫顽力和磁滞损耗. 非晶粉末硬度高, 磁粉芯的冷压成型压力高达1.8 GPa, 内部残余应力成为磁畴钉扎点而恶化软磁性能. 因此, Bai等[76]提出了一种在非晶软磁粉末与绝缘层之间构建由非晶纳米颗粒组成的应力缓冲层的策略(图9(a)), 通过化学还原法在FeSiBCCr粉末表面原位合成了非晶FeB纳米颗粒, 制备了不同纳米颗粒掺杂比例的核壳结构FeSiBCCr@FeB/有机树脂复合磁粉芯. 纳米颗粒作为相对柔软的缓冲层起到分散应力的作用, 结合FeB纳米颗粒自身的强磁性, 可以在不牺牲磁导率和磁化强度的前提下, 显著降低高频磁芯损耗[76] (图9(b), (c)).
-
序调控技术在非晶基软磁材料领域取得了显著进展, 通过精确调控材料内部的序结构, 在很大程度上突破了现有软磁材料基本磁学性能间的倒置关系. 这些研究成果和认识为开发新一代高性能非晶基软磁材料提供了新的设计思路和方法. 然而, 从实验室研究到大规模产业化应用仍面临诸多挑战. 首先, 高频高性能软磁合金粉末的批量化可控制造存在瓶颈. 快速凝固技术(如气雾化)需精确调控粉末粒径(微米级), 而工业化生产中批次一致性、形貌均匀性及残余应力控制难度较高, 直接影响高频损耗与磁导率稳定性. 其次, 大尺寸超薄非晶带材(厚度<15 μm)的量产工艺尚未成熟, 高速冷却(>106 K/s)与带材表面平整度、卷绕脆性大之间的矛盾突出. 此外, 复杂序调控工艺(如磁场退火、纳米界面设计)的高成本与规模化设备投入, 进一步制约了产业化进程. 未来需开发低成本体系、智能化工艺监控技术及标准化评价体系, 推动序调控软磁材料从实验室向市场的高效转化.
在新能源汽车、5G通信和人工智能等新兴领域的推动下, 软磁材料的应用将继续向高频化、多功能化、绿色化发展. 在极限工况下, 材料性能的开发将更加接近于物理极限而陷入瓶颈, 突破这种性能瓶颈需要创新材料研发范式、发现新的物理机制和开发先进表征技术. 软磁材料作为典型的电子强关联体系, 序调控理念在解决这种材料性能权衡难题中将发挥更大的潜力.
-
还原论认为复杂事物、系统与现象可理解为更简单、基础部分组合. 还原论指导下传统材料学研究范式基于“元素组成-组织结构-宏观性能”三角关系, 推动材料强度理论、凝聚态物理、量子力学等领域发展. 但这种依赖元素种类、个人经验与试错的传统研发方式效率低. 为突破复杂权衡关系, “功能基元-序构-极限性能”新型材料研发范式应运而生. 通过引入特定功能基元改变材料电子、原子结构, 进而影响宏观性能, 再调控功能基元间序构, 改变电子、原子结构周期性, 材料性能有望大幅提升或展现新奇特性[11]. 从功能基元及序构角度研究软磁材料, 能更直接理解、调控性能, 提高开发效率.
在新型材料研究范式的框架下, 软磁材料的开发需要借助计算材料学、高通量技术与人工智能大模型等先进研究手段的深度融合. 当前, 非晶基软磁材料的序调控研究仍处于初步探索阶段, 发现了一些特殊的功能基元及有趣的序构形式, 但相关研究并不深入. 功能基元的本征特性对宏观性能的影响规律及调控机理、序构引发的功能基元间协同、耦合增强效应以及建立面向特定性能组合的功能基元与序构逆向生成准则、框架等问题亟待解决. 例如, 非晶基软磁材料中功能基元及其序构形式的高通量发现是面临的首要挑战, 需要借助高通量计算与人工智能技术建立起针对目标属性的预测、逆向设计模型. 具体而言, 可结合机器学习算法构建序参量(如短程序团簇密度、中程序拓扑构型、界面相分布)与磁性能(如饱和磁化强度、矫顽力、高频损耗)之间的非线性映射关系. 通过高通量实验与模拟生成的结构-性能数据库, 训练模型识别关键序构特征及其协同效应, 实现从“序构指纹”到目标性能的精准预测. 此外, 强化学习与生成对抗网络算法可进一步用于探索非晶合金成分-工艺-序构-性能的复杂相空间, 逆向生成满足特定磁学性能需求的序构设计方案.
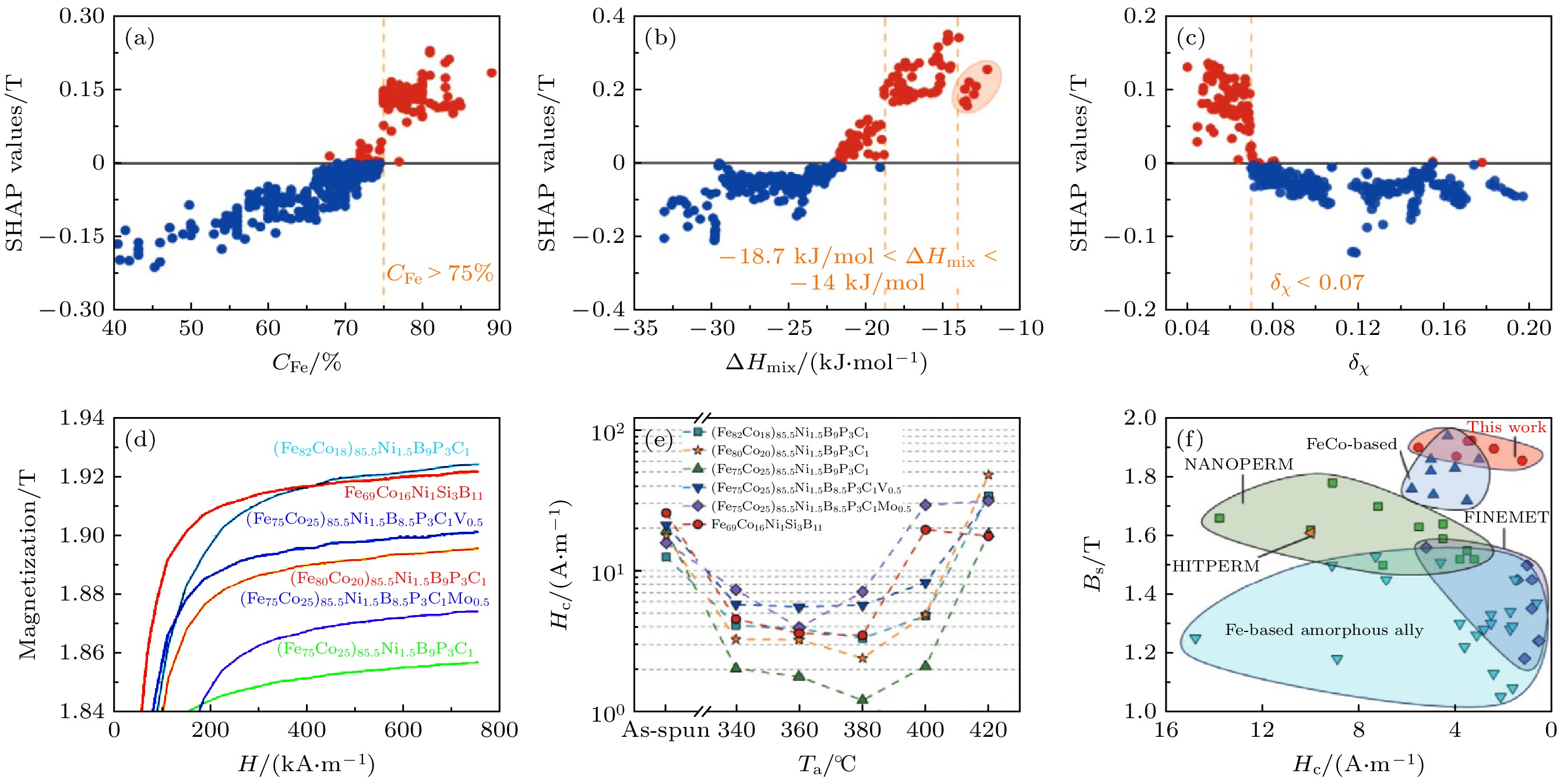
近期, Yang等[77]建立了3种不同的机器学习模型(XGBoost、随机森林和支持向量机)来准确预测Fe基非晶合金的饱和磁感应强度, 通过特征分析发现Fe含量、混合焓和电负性差是影响饱和磁感应强度的关键因素. 为了平衡非晶形成能力和饱和磁感应强度, 铁原子含量需超过75%, 混合焓应介于–18.7— –14 kJ/mol之间, 而电负性差异应小于0.07 (图10(a)—(c)). 基于上述准则, 该团队设计了饱和磁感应强度达1.92 T 的(Fe82Co18)85.5Ni1.5B9P3C1和Fe69Co16Ni1Si3B11非晶软磁合金, 磁场退火后矫顽力可降至1.2 A/m (图10(d)—(f)). 该工作进一步揭示了机器学习在序参量提取中的潜力: 通过特征重要性分析, 可识别出影响磁性能的主导序构参量, 为实验设计提供物理指导. 未来, 结合多尺度建模生成跨尺度序构数据, 并融合物理约束(如朗道理论、交换作用方程)构建可解释的混合机器学习模型, 将实现序调控机制与性能优化的双向解析.
-
在超越摩尔时代的集成电路封装技术中, 如嵌入式电感等, 急需在高达100 MHz以上频率工作的软磁材料, 要求其具有稳定的磁导率. 在高频交变磁场作用下, 传统Fe基软磁合金中的磁畴壁会发生共振[78], 导致磁畴壁的运动和翻转跟不上磁场的变化, 进而使磁导率降低. 粉末尺寸效应导致的能量与磁序状态变化, 不仅能够通过引入丰富界面而降低涡流损耗, 同时诱导特殊的磁性拓扑序构而调控磁学性能. 纳米非晶粉末比表面积大、极易氧化, 表面往往会自发生成厚度2—20 nm左右的氧化膜, 不仅避免了绝缘包覆导致的磁稀释效应, 同时有效抑制了涡流的产生而显著降低高频损耗[79]. 因此, 非晶纳米磁粉芯通常具有高饱和磁感应强度和极低的高频损耗[79], 同时有望将截止频率提高至GHz, 满足超高频应用领域的需求.
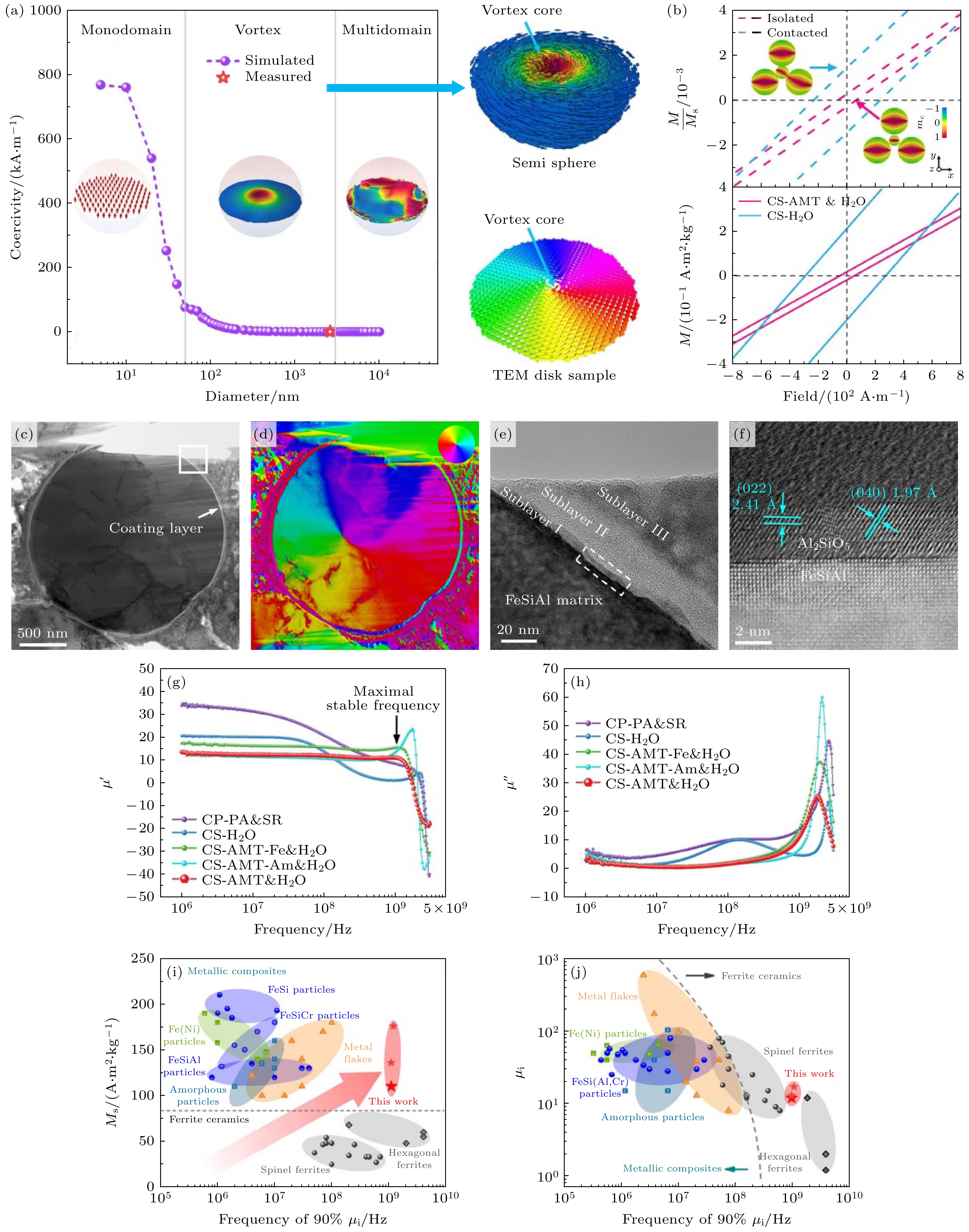
当磁性粉末的尺寸减小时, 材料内部的磁序状态会发生显著变化. 在较大的磁性颗粒中, 磁化通常以多畴结构存在, 即材料内部存在多个磁畴, 每个磁畴的磁化方向不同, 这些磁畴之间通过畴壁相互分隔. 然而, 当颗粒尺寸减小到微米甚至纳米级别时, 多畴结构变得不稳定, 较小的尺寸增强磁化矢量之间的交换作用、形状各向异性对磁化方向的约束作用减弱, 从而促使磁化矢量在颗粒内部形成一种有序的涡旋状排列, 形成磁涡旋结构. 在磁涡旋结构中, 磁化矢量的涡旋状排列使得感应电流难以在材料内部形成闭合回路, 从而减少了涡流的产生. 传统软磁复合材料大多使用具有多畴结构的软磁粉, 高频下多畴结构中的磁畴壁运动会导致磁导率下降. 为此, Bai等[80]通过冷烧结技术制备了一种基于磁涡旋结构的软磁复合材料(图11(a)), 由超细FeSiAl颗粒构成, 这些颗粒通过Al2SiO5/SiO2/Fe2(MoO4)3多层异质结构隔离并共价键合(图11(c)—(f)). FeSiAl颗粒展现出磁涡旋结构, 与传统软磁材料的多畴结构截然不同. 这种结构的形成归因于FeSiAl颗粒的零磁晶各向异性和零磁致伸缩常数, 满足了磁涡旋形成的内在要求. “磁涡旋”拓扑序构与“磁绝缘”的组合使得磁化旋转过程更加接近Snoek极限, 实现了在高达1 GHz的频率下展现出稳定的磁导率, 初始磁导率为13 (图11(g)—(j)). 此外, 由于颗粒间外延生长的界面, 复合材料的极限抗压强度也增加到了337.1 MPa[80]. 通过冷烧结技术制备的基于磁涡旋结构的软磁复合材料, 为高频磁性器件的发展提供了新的可能性.
-
磁粉芯作为未来高频应用的理想材料, 但其成型成为制约其广泛应用的重要瓶颈. 现有工艺主要为冷压成型, 而Fe基非晶粉末的变形能力差, 冷压成型需要施加高达1800 MPa的机械压力. 这种高压会使非晶粉末表面发生局部塌陷和变形, 从而在粉芯内部引入大量的残余应力. 这些内部应力会干扰磁粉颗粒的正常磁化过程, 导致磁畴壁移动受阻, 增加磁化所需的能量. 同时, 高成型压力也不可避免地损坏绝缘涂层的完整性, 降低软磁复合材料的电阻率. 高成型压力带来的残余应力和绝缘层破坏, 使粉芯的磁导率和直流偏置性能下降、损耗增大, 限制了其在高频、大电流等条件下的应用. 开发新型低应力的成型和结构调控工艺未来成为研究重点.
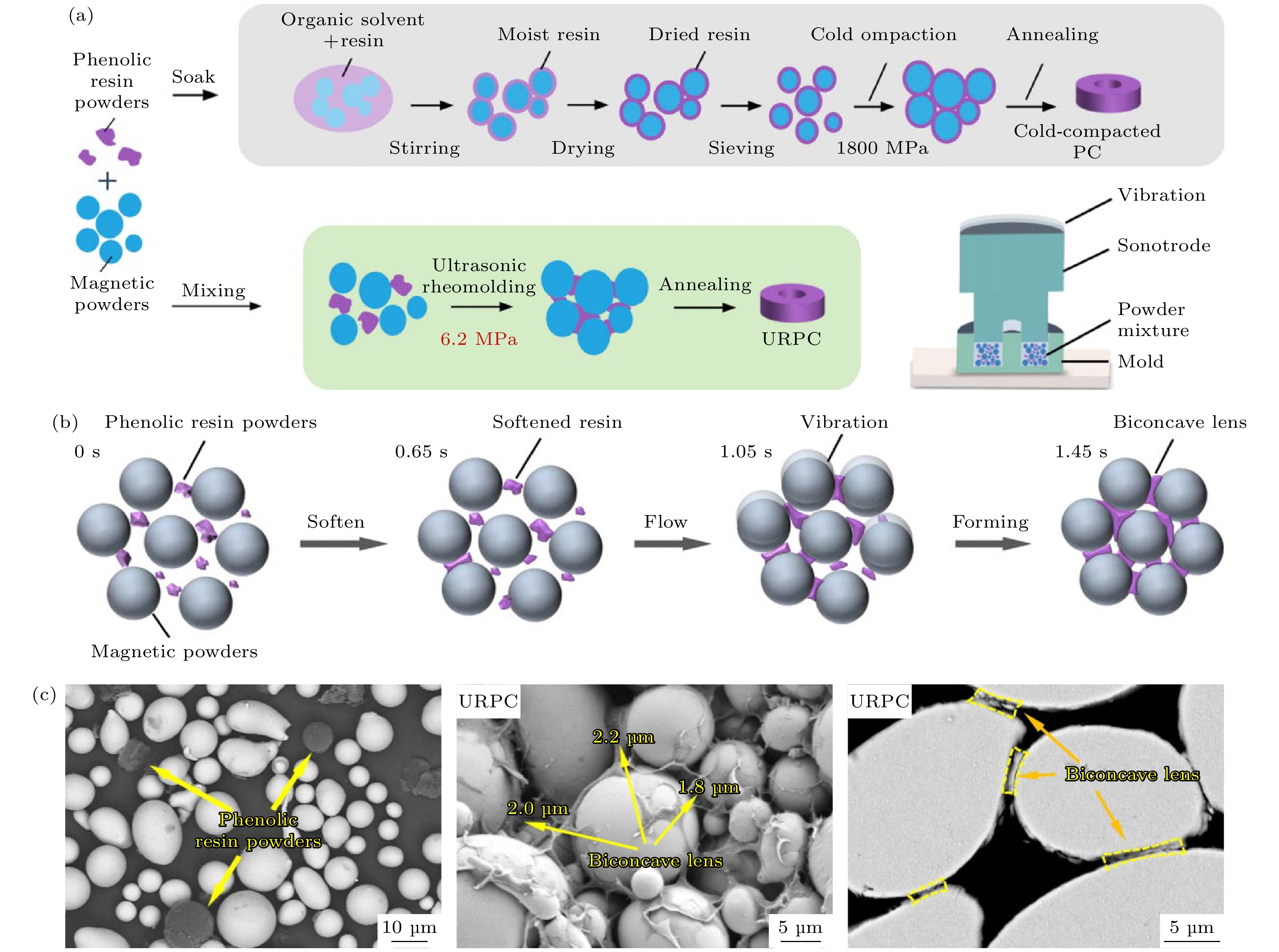
为此, Li等[81]提出了一种超声流变成型(UR)工艺来制造非晶磁粉芯(图12), 成型压力可降低至6.2 MPa, 仅为冷压成压力(1800 MPa)的1/300, 且在超声成型过程中产生的最高温度仅为183 ℃, 有效解决了传统冷压成型的残余应力大、且难以消除的问题. 通过超声振动使树脂粉末软化并流动到磁粉颗粒之间, 形成局部自适应的双凹透镜状绝缘结构. 这种结构能有效缓冲高机械应力对磁粉颗粒磁化的影响, 在低内部应力和低孔隙率的协同作用下, 保持更好的磁化效率, 从而改善磁耦合问题并打破磁导率和直流偏置性能之间的权衡关系.
-
当前, 非晶基软磁材料磁结构表征及其在近使役条件下动态演变机制尚不清晰. 非晶基软磁材料原子排列缺乏长程有序性, 导致其磁畴结构与传统晶体材料差异显著, 同时无序性使磁畴形成与演变机制更复杂, 难用传统晶体磁畴理论解释. 此外, 非晶基软磁材料中磁畴尺寸通常较小且分布不均, 实验中捕捉与表征这些微小磁畴结构和动态行为困难. 传统磁畴表征技术, 如磁光克尔显微镜与洛伦兹电镜, 分辨率有限, 难以清晰分辨纳米尺度磁畴结构. 实际应用中, 非晶基软磁材料常处于动态变化外部条件(如高频磁场、机械载荷等)下工作, 但目前缺乏近使役条件下原位观测技术手段. 非晶固体中磁畴形成、演化与湮灭过程可能涉及畴壁运动、磁矩旋转与磁畴间相互作用等多种物理机制, 这些动态行为复杂性使高分辨率实验数据获取、分析与理论建模面临巨大挑战.
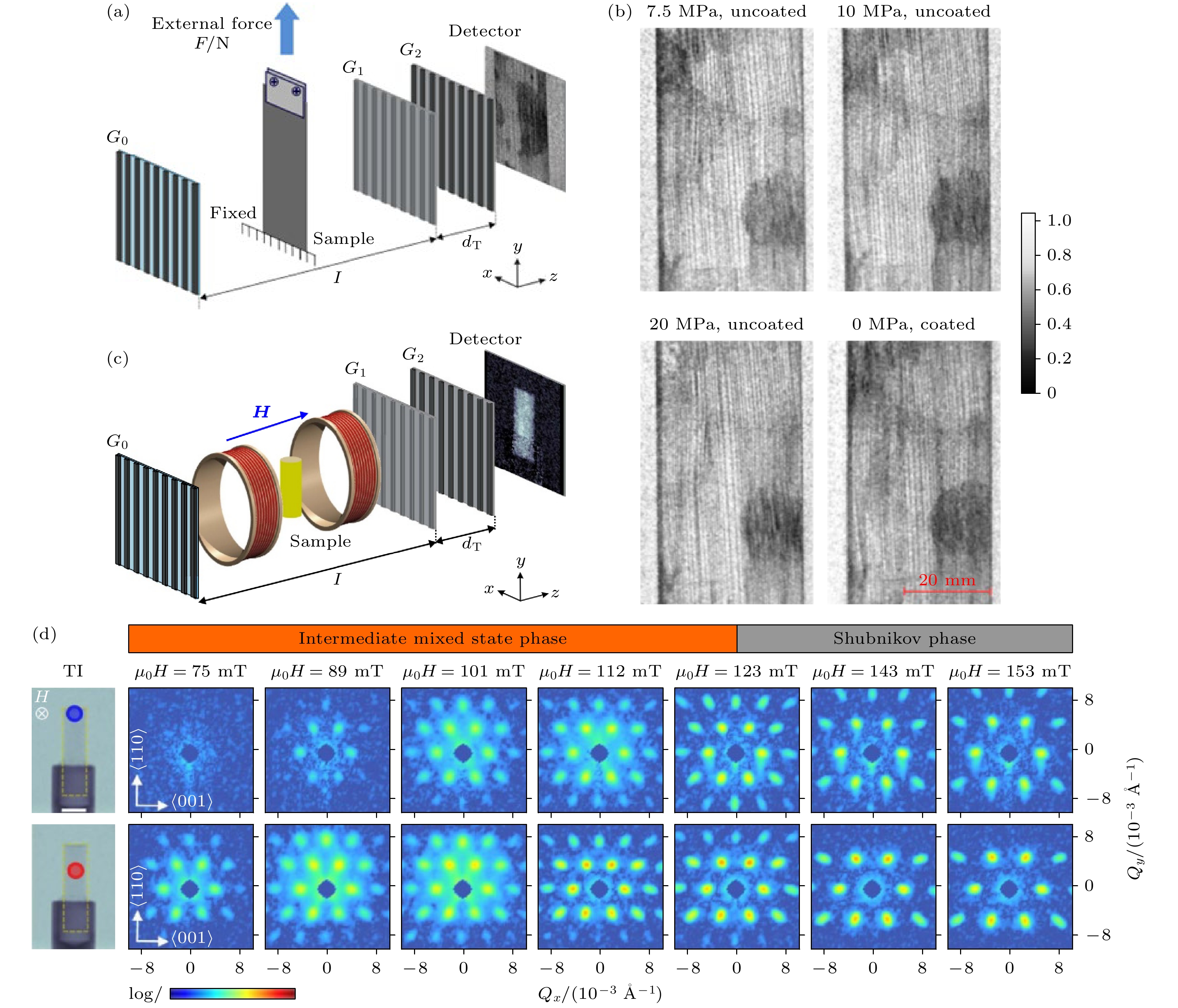
中子具有磁矩, 可与材料中原子磁矩直接相互作用产生特有的磁散射信号, 且中子对大多数材料穿透深度大(厘米量级), 可开展原子尺度到宏观尺度的磁结构研究, 为理解非晶基软磁材料复杂行为提供关键信息. 近年来, 中子光栅成像系统结合相应的分离算法可以同时获得样品的吸收、折射和散射3种图像, 充分揭示了样品的结构信息[82,83]. 其中, 散射图像作为光栅相衬成像方法的第3种成像模态, 尤其适用于磁畴结构的可视化, 可以提供系统分辨率以下的物体微结构信息[84]. 瑞士保罗谢尔研究所(PSI)基于Talbot-Lau光栅干涉仪散射成像, 观测到传统吸收成像中无法观测的磁畴结构[85], 并在之后的研究中结合原位环境初步实现了磁化频率、应力大小对高磁导率钢的磁畴动态行为的影响的观测[86] (图13(a), (b)). Reimann等[87]通过中子散射成像技术系统研究了超导体Nb在中间混合态(IMS)的畴结构和成核行为(图13(c), (d)), 发现在非椭球形、无钉扎的Nb样品中, IMS相优先在样品中心成核并向边缘扩展, 最终在边缘演变为Shubnikov相, 且顶部和底部的相变延迟了14 mT, 揭示了IMS畴分布的强烈不均匀性及样品形状对磁畴结构的显著影响. 中子散射成像技术的引入, 对建立非晶基软磁材料局域磁畴静态分布规律、长程关联作用与动态演变机制有重要推动作用.
-
非晶软磁是一片广阔天地, 序调控大有可为. 序调控策略不仅在非晶基软磁材料中取得显著进展, 也为其他功能材料设计与开发提供了有效借鉴. 未来, 随着对序调控机制深入理解与新技术不断涌现, 基于序调控的高性能非晶基软磁复合材料将在更多领域展现广阔应用前景. 同时, 序调控策略也为材料科学领域带来新研究方向与挑战, 如多尺度序结构设计、制造方法等. 这些研究不仅有助推动材料性能进一步提升, 也将为材料科学发展注入新活力. 期待基于序调控的高性能非晶基软磁复合材料在更多领域得到应用, 推动现代产业前沿发展.
序调控工程创制高频非晶基软磁材料研究进展
Research progress of ordered regulation engineering for developing high-frequency amorphous-based soft magnetic materials
-
摘要: 在现代电子通信、人工智能产业快速变革的浪潮中, 第3代半导体的规模化应用推动着高性能高频软磁材料需求的日益增长. 然而, 传统软磁材料的基本性能之间存在着复杂的权衡关系, 例如饱和磁化强度与矫顽力、磁导率与损耗、机械强度与矫顽力往往不能同时兼得. 非晶基软磁材料以内部不同尺度序结构作为关键功能基元, 催生了极其丰富的物理特性. 序调控是一种通过优化序结构本征特性、序构形式来提升性能的理念, 为突破软磁性能的矛盾关系开拓了新的设计维度. 本文首先介绍了软磁材料的发展历程, 然后阐述了序调控的科学理论基础, 综述了基于序调控工程创制高性能非晶基软磁材料的最新进展, 重点介绍短程序、中程序、非晶-纳米晶双相等影响宏观物性的关键序构形式对软磁性能的影响及其作用机制, 最后指出了面向未来高精尖产业前沿的新一代高频软磁材料发展方向.Abstract:
The rapid advancement of modern electronics, telecommunications, and artificial intelligence has driven an urgent demand for high-performance soft magnetic materials, particularly those compatible with third-generation semiconductors. These semiconductors, characterized by wide bandgaps, high breakdown fields, and superior thermal conductivity, enable power devices to operate at higher frequencies (> 1 MHz) and power densities. However, traditional soft magnetic materials, such as silicon steels and ferrites, face inherent trade-offs between critical properties: saturation magnetization (Bs) versus coercivity (Hc), permeability versus core loss, and mechanical strength versus magnetic “softness”. These limitations hinder their applications in emerging high-frequency high-efficiency scenarios. Amorphous soft magnetic materials, with their unique hierarchical ordered structures ranging from atomic scale to nano scale, offer a revolutionary platform to overcome these trade-offs. These materials exhibit rich physical properties governed by short-range order (SRO, < 0.5 nm), medium-range order (MRO, 0.5–2.0 nm), and amorphous-nanocrystalline dual-phase architectures. The concept of order modulation strategically tailoring the intrinsic characteristics (e.g., cluster density, topological configuration) and spatial arrangements of these ordered structures has emerged as a transformative approach to decoupling conflicting material properties. This review systematically examines the following key aspects: 1) Historical evolution of soft magnetic materials The development of soft magnetic materials has kept pace with advances in power electronics technology, from early silicon steels and ferrites to modern amorphous and nanocrystalline alloys. The advent of Fe-based amorphous alloys and finemet-type nanocrystalline alloys marks milestones in achieving high Bs (>1.6 T), ultra-low Hc (< 1 A/m), and reduces core losses at high frequencies. However, performance bottlenecks still exist near theoretical limits, and require innovative strategies. 2) Theoretical foundations of order modulation Order parameter theory: Landau’s phase transition theory and synergetics elucidate how magnetic order parameters govern macroscopic properties. In amorphous alloys, magnetic interactions are dominated by SRO clusters and their MRO arrangements. Magnetism-structure relationships: advanced techniques, such as atomic electron tomography (AET) and synchrotron pair distribution function (PDF) analysis, reveal that SRO/MRO structures directly influence exchange coupling, magnetic anisotropy, and domain wall dynamics. For instance, Fe-M (M = Si, B) clusters with dense packing enhance Bs, while MRO homogenization reduces Hc. 3) Advances in order-modulated amorphous soft magnetic materials Atomic-scale modulation: elemental doping (e.g., Co, Mo, Cu) and energy-field treatments (e.g., magnetic annealing and ultrasonic vibration) optimize local atomic configurations. For example, ultrasonic processing of Fe78Si9B13 ribbons induces stress relaxation, forming 2–3 nm Fe-M clusters that increase Bs to 183.2 emu/g while maintaining Hc at 4.2 A/m. Nanoscale dual-phase design: controlled crystallization of α-Fe(Si) nanocrystals (<15 nm) within an amorphous matrix creates exchange-coupled nanocomposites. Co-Mo co-doping in FeSiBCuNb alloys refines grain size to 11.8 nm, achieving a permeability of 65000 H/m at 100 kHz–44% higher than traditional finemet alloys. Interface engineering in soft magnetic composites (SMCs): core-shell architectures (e.g., FeSiB@FeB nanoparticles) with stress-buffering interfaces reduce eddy current losses while preserving permeability. Cold sintering of vortex-domain FeSiAl powders enables GHz-range operation with stable permeability (μi = 13 at 1 GHz). 4) Future directions and challenges Machine learning-driven design: integrating high-throughput simulations with AI models (e.g., XGBoost, random forests) accelerates the discovery of optimal compositions and order parameters. Recent work predicts Bs by using Fe content, mixing enthalpy, and electronegativity differences, guiding the synthesis of (Fe82Co18)85.5Ni1.5B9P3C1 alloys with Bs = 1.92 T. The new magnetic topology structure: the magnetic vortex structures and skyrmion-like configurations in ultrafine powders show the prospect of ultra-high-frequency applications (>100 MHz). Low-stress manufacturing: innovations such as ultrasonic rheoforming reduce compaction pressures by 99% (to 6.2 MPa), alleviating residual stress and improving SMC performance. In situ characterization: neutron scattering and grating-based imaging techniques enable real-time observation of domain dynamics under operational conditions (e.g., stress, magnetic fields). In conclusion, ordered modulation represents a paradigm shift in the design of soft magnetic material, linking atomic-scale interactions with macroscopic performance. By using multi-scale ordered structures and advanced manufacturing technologies, the next-generation amorphous-based materials are expected to revolutionize high-frequency power electronics, electric vehicles, and AI-driven systems. However, challenges in scalable production, cost-effective processing, and standardized evaluation must be addressed to accelerate industrial adoption. -
Key words:
- soft magnetic materials /
- amorphous alloy /
- order modulation /
- functional block .
-

-
图 1 非晶合金的多尺度“序”结构 (a)利用纳米束电子衍射与从头算分子动力学模拟相结合的方法确定Zr66.7Ni33.3非晶合金的短程序结构[43]; (b) Pd41.25Ni41.25P17.5非晶合金的六元三顶三角棱柱簇(6M-TTP)手性中程序结构[36]; (c)由AET确定的非晶纳米颗粒的代表性短程序结构[44]; (d)由AET确定的非晶纳米颗粒的4种类晶状中程序结构[44]
Figure 1. Multi-scale ordered structures in amorphous alloys: (a) Short-range order (SRO) in Zr66.7Ni33.3 determined via combined nanobeam electron diffraction and ab initio molecular dynamics simulations[43]; (b) chiral medium-range order (MRO) featuring 6M-TTP clusters in Pd41.25Ni41.25P17.5[36]; (c) representative SRO in amorphous nanoparticles revealed by atomic electron tomography (AET)[44]; (d) four crystal-like MRO configurations identified by AET[44].
图 2 非晶合金的短/中程序结构与磁学性能的内在关联 (a)不同退火参数下非晶合金的同步辐射PDF曲线[20]; (b)矫顽力与PDF第一峰位置r1和峰强衰减指数ξ的关联[20]; (c)矫顽力与结构因子曲线第1峰和第2峰半高宽FWHM的关联[20]; (d)铸态、退火态和晶态样品在有无磁场下的小角中子散射图[46]; (e) (Fe0.71Dy0.05B0.24)96Nb4非晶合金的边共享中程序比例、饱和磁化强度、磁相关长度随温度的变化[46]
Figure 2. Short/medium-range order-magnetic property relationships in amorphous alloys: (a) Synchrotron-derived pair distribution functions (PDF) for various annealing states[20]; (b) correlations between coercive and PDF characteristics (first peak position r1, decay coefficientξ)[20]; (c) dependence of coercivity on structural disorder (FWHM of first two structure factor maxima)[20]; (d) magnetic field response of nanostructures revealed by SANS in different structural states[46]; (e) temperature-dependent medium-range ordering and magnetic characteristics (saturation magnetization, correlation lengths) in Fe-Dy-B-Nb metallic glass[46].
图 3 基于元素掺杂的原子尺度序调控[50] (a) “framework + fluctuation”模型示意图, 展示了不同类型非金属原子引起的结构“波动”; (b) FeCoNiBCSiP 高熵金属玻璃体系的混合焓; (c) Bethe-Slater曲线; (d)饱和磁化强度与“波动参数”σ的内在关联
Figure 3. Atomic-scale order modulation via elemental doping[50]: (a) Schematic of the “framework + fluctuation” model, illustrating structural fluctuations induced by diverse non-metal atoms; (b) mixing enthalpy of the FeCoNiBCSiP high-entropy metallic glass; (c) Bethe-Slater curve; (d) correlation between saturation magnetization and the fluctuation parameter (σ).
图 4 基于外加能场的原子尺度序调控 (a)不同合金系统中非晶形成能力和饱和磁感应强度对铁磁元素(Fe, Co, Ni))含量的依赖关系示意图[51]; (b)结合成分设计和磁场热处理制备的非晶合金XRD图谱[51]; (c)磁场热处理过程中, 松散区域的磁性原子在团簇界面的扩散[51]; (d)超声处理过程中, 与输入能量相关的压力和温度变化[52]; (e)超声处理对Fe78Si9B13条带的磁学、力学性能的影响[52]; (f)超声处理对非晶合金内部原子尺度结构的调控[52]
Figure 4. Atomic-scale ordering modulation via external energy fields: (a) Composition dependence of glass-forming ability and saturation magnetization in Fe/Co/Ni-based alloy systems[51]; (b) XRD patterns of compositionally optimized amorphous alloys after magnetic annealing[51]; (c) field-enhanced diffusion of magnetic atoms at cluster interfaces during magnetic annealing[51]; (d) ultrasonic-induced pressure/temperature evolution as a function of input energy[52]; (e) ultrasonic effects on magnetic/mechanical properties of Fe78Si9B13 ribbons[52]; (f) ultrasonic modulation of atomic-scale structure in amorphous alloys[52].
图 5 临界态序构设计突破磁导率与高频损耗的互斥关系[55] (a)序调控策略示意图; (b)磁场热处理诱导类α-Fe中程序结构的产生; (c)临界态序构软磁复合材料的性能
Figure 5. Breakthrough in permeability-loss trade-off through critical-state ordered structure design[55]: (a) Schematic of ordering modulation strategy; (b) formation of in α-Fe-like medium-ordered structure via magnetic-field annealing; (c) performance of critical-state ordered soft magnetic composites.
图 7 过渡态序构突破饱和磁化强度和矫顽力的互斥关系[8] (a)过渡态软磁合金设计策略; (b)少量嵌套纳米晶和类晶区分布在非晶基体内的过渡态序构; (c) B-H曲线; (d)过渡态(Fe0.8Co0.2)85合金和Fe-3.5%Si合金的放大B-H曲线; (e)性能对比
Figure 7. Transitional-state ordered structure overcoming the trade-off between saturation magnetization and coercivity[8]: (a) Design strategy for transitional-state soft magnetic alloys; (b) coherently dispersed nanocrystal/crystal-like region hybrid architecture within the amorphous matrix; (c) B-H curves; (d) comparative view of locally amplified B-H curves between transitional-state (Fe0.8Co0.2)85 alloy and conventional Fe-3.5%Si alloy; (e) performance comparison.
图 8 基于磁不均匀性驱动纳米晶化的新型高频高磁导率软磁材料[9] (a) Co和Mo共掺杂实现晶粒尺寸细化至11.8 nm; (b)成分分布; (c)不同年份开发的各种软磁材料在100 kHz下的磁导率
Figure 8. Magnetic inhomogeneity-driven nanocrystallization for developing high-performance soft magnetic materials with high-frequency permeability[9]: (a) Grain refinement to 11.8 nm achieved by Co-Mo co-doping; (b) composition distribution; (c) permeability at 100 kHz for various soft magnetic materials across development years.
图 9 利用无序纳米颗粒作为应力缓冲界面开发综合性能优异的磁粉芯[76] (a)表面纳米工程对应力和磁畴的调控示意图; (b)磁导率; (c)高频损耗
Figure 9. Engineering high-performance magnetic powder cores through disordered nanoparticle stress-buffering interfaces[76]: (a) Schematic illustration of stress and magnetic domain regulation via surface nanoengineering; (b) permeability; (c) high-frequency loss.
图 10 通过人工智能技术加速高性能非晶基软磁材料的研发[77] (a) Fe含量、(b)混合焓和(c)电负性差对饱和磁感应强度的影响; (d) B-H曲线; (e)矫顽力随退火温度的变化; (f)性能对比
Figure 10. AI-accelerated development of high-performance amorphous soft magnetic alloys[77]: (a) Effects of Fe content, (b) mixing enthalpy, and (c) electronegativity difference on the saturation magnetization; (d) B-H curves; (e) annealing temperature dependence of coercivity; (f) performance comparison.
图 12 超声低应力流变成型工艺[81] (a)工艺流程示意图; (b)超声成型过程中局域自适应绝缘结构的形成; (c)软磁复合材料内部组织形貌
Figure 12. Ultrasonic-assisted low-stress rheoforming process[81]: (a) Schematic of the processing steps; (b) formation mechanism of localized adaptive insulating structures during ultrasonic forming; (c) microstructural evolution of the soft magnetic composite.
图 11 粉末尺寸效应驱动的新型磁性拓扑序构软磁复合材料[80] (a)不同直径FeSiAl颗粒的畴结构和矫顽力模拟; (b)磁绝缘结构的磁性能模拟; (c)—(f)磁涡旋结构的微观结构和畴结构; (g)—(i)磁涡旋结构的性能
Figure 11. Powder-size-engineered novel magnetic topological ordering in soft magnetic composites[80]: (a) Simulated domain structures and coercivity of FeSiAl particles with varying diameters; (b) calculated magnetic properties of the magnetic insulated architecture; (c)–(f) microstructural characteristics and domain configurations of magnetic vortex arrays; (g)–(i) properties of magnetic vortex structure.
图 13 中子散射技术在磁结构研究的应用 (a)原位应力中子散射装置示意图[86]; (b)应力作用下的高磁导率钢内部磁畴演变[86]; (c)原位磁场中子散射装置示意图[87]; (d)磁场作用下的超导体Nb内部磁畴演变[87]
Figure 13. Applications of neutron scattering in magnetic structure investigations: (a) Schematic of an in-situ stress neutron scattering setup[86]; (b) stress-induced magnetic domain evolution in high-permeability steel[86]; (c) schematic of an in-situ magnetic field neutron scattering setup[87]; (d) magnetic-field-driven magnetic domain evolution in superconducting Nb[87].
-
[1] Silveyra J M, Ferrara E, Huber D L, Monson T C 2018 Science 362 eaao0195 doi: 10.1126/science.aao0195 [2] Yu Q 2024 HSET 81 484 doi: 10.54097/2q3qyj85 [3] Wang H, Lamichhane T N, Paranthaman M P 2022 Mat. Today Phys. 24 100675 doi: 10.1016/j.mtphys.2022.100675 [4] Herzer G 2013 Acta Mater. 61 718 doi: 10.1016/j.actamat.2012.10.040 [5] Talaat A, Suraj M V, Byerly K, Wang A, Wang Y, Lee J K, Ohodnicki Jr P R 2021 J. Alloys Compd. 870 159500 doi: 10.1016/j.jallcom.2021.159500 [6] Rafin S S H, Ahmed R, Haque M A, Hossain M K, Haque M A, Mohammed O A 2023 Micromachines 14 2045 doi: 10.3390/mi14112045 [7] Perigo E A, Weidenfeller B, Kollár P, Füzer J 2018 Appl. Phys. Rev. 5 031301 doi: 10.1063/1.5027045 [8] Li X S, Zhou J, Shen L Q, Sun B A, Bai H Y, Wang W H 2023 Adv. Mater. 35 2205863 doi: 10.1002/adma.202205863 [9] Zhou J, Li X S, Hou X B, Ke H B, Fan X D, Luan J H, Peng H L, Zeng Q S, Lou H B, Wang J G, Liu C T, Shen B L, Sun B A, Wang W H, Bai H Y 2023 Adv. Mater. 35 2304490 doi: 10.1002/adma.202304490 [10] Oumsalem A, Bourezig Y, Nabi Z, Bouabdallah B 2018 Turk. J. Electr. Eng. Compu. Sci. 26 1249 doi: 10.3906/elk-1711-106 [11] Zhang H T, Zhang T, Zhang X 2023 Adv. Sci. 10 2300193 doi: 10.1002/advs.202300193 [12] Shao L L, Luo Q, Zhang M J, Xue L, Cui J X, Yang Q Z, Ke H B, Zhang Y, Shen B L, Wang W H 2024 Nat. Commun. 15 4159 doi: 10.1038/s41467-024-48531-7 [13] 柯海波, 周靖, 童星, 汪卫华 2024 科技导报 42 1 Ke H B, Zhou J, Tong X, Wang W H 2024 Sci. Techn. Rev. 42 1 [14] Cowley R 1980 Adv. Phys. 29 1 doi: 10.1080/00018738000101346 [15] Natarajan A R, Thomas J C, Puchala B, Van der Ven A 2017 Phys. Rev. B 96 134204 doi: 10.1103/PhysRevB.96.134204 [16] Jiang Q, Wen Z, Jiang Q, Wen Z 2011 Thermodynamics of Materials (Springer) pp157–206 doi: 10.1007/978-3-642-14718-0 [17] Zhang H 2022 Models and Methods for Management Science (Springer) pp301–361 doi: 10.1007/978-981-19-1614-4 [18] Haken H 1975 Rev. Mod. Phys. 47 67 doi: 10.1103/RevModPhys.47.67 [19] Haken H 1989 Rep. Prog. Phys. 52 515 doi: 10.1088/0034-4885/52/5/001 [20] Tong X, Zhang Y, Wang Y C, Liang X Y, Zhang K, Zhang F, Cai Y F, Ke H B, Wang G, Shen J Makino A, Wang W H 2022 J. Mater. Sci. Technol. 96 233 doi: 10.1016/j.jmst.2021.01.098 [21] Zeeman E C 1976 Sci. Am. 234 65 doi: 10.1038/scientificamerican0476-65 [22] Zhang E H, Zhou B K, Yang L, Li C F, Li P 2023 Trans. Soc. Min. Metall. Explor. 40 1865 doi: 10.1007/s42461-022-00713-x [23] 任景莉, 于利萍, 张李盈 2017 物理学报 66 176402 doi: 10.7498/aps.66.176402 Ren J L, Yu L P, Zhang L Y 2017 Acta Phys. Sin. 66 176402 doi: 10.7498/aps.66.176402 [24] Machida Y, Nakatsuji S, Onoda S, Tayama T, Sakakibara T 2010 Nature 463 210 doi: 10.1038/nature08680 [25] Laughlin D E 2019 Metall. Mater. Trans. A 50 2555 doi: 10.1007/s11661-019-05214-z [26] Alonso J 2000 Chem. Rev. 100 637 doi: 10.1021/cr980391o [27] Filbet F, Xiong T, Sonnendrücker E 2018 SIAM J. Appl. Math. 78 1030 doi: 10.1137/17M1112030 [28] Anderson P 1950 Phys. Rev. 79 705 doi: 10.1103/PhysRev.79.705 [29] Stepanov E, Brener S, Krien F, Harland M, Lichtenstein A, Katsnelson M 2018 Phys. Rev. Lett. 121 037204 doi: 10.1103/PhysRevLett.121.037204 [30] Stöhr J, Siegmann H C 2006 Magnetism: From Fundamentals to Nanoscale Dynamics (Springer) pp479–520 doi: 10.1007/978-3-540-30283-4 [31] Hosseini M V, Askari M 2015 Phys. Rev. B 92 224435 doi: 10.1103/PhysRevB.92.224435 [32] Kosarim A, Smirnov B 2005 J. Exp. Theor. Phys. 101 611 doi: 10.1134/1.2131929 [33] Bernal J 1960 Nature 185 68 doi: 10.1038/185068a0 [34] Bernal J D 1959 Nature 183 141 doi: 10.1038/183141a0 [35] Luo W K, Sheng H W, Alamgir F M, Bai J M, He J H, Ma E 2004 Phys. Rev. Lett. 92 145502 doi: 10.1103/PhysRevLett.92.145502 [36] Lan S, Zhu L, Wu Z D, Gu L, Zhang Q H, Kong H H, Liu J Z, Song R Y, Liu S N, Sha G, Wang Y G, Liu Q, Liu W, Wang P Y, Liu C T, Ren Y, Wang X L 2021 Nat. Mater. 20 1347 doi: 10.1038/s41563-021-01011-5 [37] Zeng Q S, Sheng H W, Ding Y, Wang L, Yang W G, Jiang J Z, Mao W L, Mao H K 2011 Science 332 1404 doi: 10.1126/science.1200324 [38] Ye J C, Lu J, Liu C T, Wang Q, Yang Y 2010 Nat. Mater. 9 619 doi: 10.1038/nmat2802 [39] Miracle D B 2004 Nat. Mater. 3 697 doi: 10.1038/nmat1219 [40] Sheng H, Luo W, Alamgir F, Bai J, Ma E 2006 Nature 439 419 doi: 10.1038/nature04421 [41] Ma D, Stoica A D, Wang X L 2009 Nat. Mater. 8 30 doi: 10.1038/nmat2340 [42] Chen D Z, Shi C Y, An Q, Zeng Q, Mao W L, Goddard III W A, Greer J R 2015 Science 349 1306 doi: 10.1126/science.aab1233 [43] Hirata A, Guan P, Fujita T, Hirotsu Y, Inoue A, Yavari A R, Sakurai T, Chen M W 2011 Nat. Mater. 10 28 doi: 10.1038/nmat2897 [44] Yang Y, Zhou J H, Zhu F, Yuan Y K, Chang D J, Kim D S, Pham M, Rana A, Tian X Z, Yao Y G, Osher S J, Schmid A K, Hu L B, Ercius P, Miao J W 2021 Nature 592 60 doi: 10.1038/s41586-021-03354-0 [45] Tang J, Xiang H P, Xu L, Qu S J, Feng A H, Li N, Ping D H 2025 Metals 15 98 doi: 10.3390/met15020098 [46] Ge J C, Gu Y, Yao Z Z, Liu S N, Ying H Q, Lu C Y, Wu Z D, Ren Y, Suzuki J, Xie Z H, Ke Y B, Zeng J R, Zhu H, Tang S, Wang X L, Lan S 2024 J. Mater. Sci. Technol. 176 224 doi: 10.1016/j.jmst.2023.07.066 [47] Bai Y W, Li J C, Zhang J, Dong B S, Li X X, Zhao X L, Cui Z H, Li T, Hu L N 2024 J. Non-Cryst. Solids 624 122705 doi: 10.1016/j.jnoncrysol.2023.122705 [48] Tian H, Zhang C, Zhao J J, Dong C, Wen B, Wang Q 2012 Physica B 407 250 doi: 10.1016/j.physb.2011.10.042 [49] 耿遥祥, 王英敏 2020 金属学报 56 1558 doi: 10.11900/0412.1961.2020.00112 Geng Y X, Wang Y M 2020 Acta Metall. Sinica 56 1558 doi: 10.11900/0412.1961.2020.00112 [50] Shi L X, Shao Y, Fan Z Y, Wang R B, Lu C Y, Yao K F 2023 Acta Mater. 254 118983 doi: 10.1016/j.actamat.2023.118983 [51] Zhao C L, Wang A D, He A N, Chang C T, Liu C T 2021 Sci. China Mater. 64 1813 doi: 10.1007/s40843-020-1593-0 [52] Li H Z, Sohrabi S, Li X, Li L Y, Ma J, Peng H L, Yang C 2025 Rare Met. 44 2853 doi: 10.1007/s12598-024-03101-0 [53] Wang C X, Wu Z Y, Feng X M, Li Z, Gu Y, Zhang Y, Tan X H, Xu H 2020 Intermetallics 118 106689 doi: 10.1016/j.intermet.2019.106689 [54] Lu S H, Wang M G, Zhao Z K 2023 J. Non-Cryst. Solids 616 122440 doi: 10.1016/j.jnoncrysol.2023.122440 [55] Shao L L, Bai R S, Wu Y X, Zhou J, Tong X, Peng H L, Liang T, Li Z Z, Zeng Q S, Zhang B, Ke H B, Wang W H 2024 Mater. Futures 3 025301 doi: 10.1088/2752-5724/ad2ae8 [56] 胡玉平, 平凯斌, 闫志杰, 杨雯, 宫长伟 2011 物理学报 60 107504 doi: 10.7498/aps.60.107504 Hu Y P, Ping K B, Yan Z J, Yang W, Gong C W 2011 Acta Phys. Sin. 60 107504 doi: 10.7498/aps.60.107504 [57] Wohlfarth E P 1986 Handbook of Magnetic Materials (Vol. 2) (Elsevier doi: 10.1016/S1574-9304(05)80064-1 [58] Brück E H 2017 Handbook of Magnetic Materials (Vol. 26) (Elsevier doi: 10.1016/bs.hmm.2017.09.002 [59] Li Y H, Jia X J, Zhang W, Zhang Y, Xie G Q, Qiu Z Y, Luan J H, Jiao Z B 2021 J. Mater. Sci. Technol. 65 171 doi: 10.1016/j.jmst.2020.05.049 [60] Xi G G, Sun C, Han M H, Li H G, Cui J L, Zhang T 2024 J. Non-Cryst. Solids 633 122951 doi: 10.1016/j.jnoncrysol.2024.122951 [61] Han M H, Sun C, Xi G G, Meng Y, Luo Q, Yu X Q, Zhang W F, Liu H, Xu H J, Zhang T 2024 Rare Met. 43 5242 doi: 10.1007/s12598-024-02707-8 [62] Yoshizawa Y a, Oguma S, Yamauchi K 1988 J. Appl. Phys. 64 6044 doi: 10.1063/1.342149 [63] Li H, Wang A D, Liu T, Chen P B, He A N, Li Q, Luan J H, Liu C T 2021 Mater. Today 42 49 doi: 10.1016/j.mattod.2020.09.030 [64] Duan L P, Wang K, Wang E G, Jia P 2021 Acta Metall. Sin. (English Letters) 34 1163 doi: 10.1007/s40195-021-01206-4 [65] Jia P, Wang E G, Han K 2016 Materials 9 899 doi: 10.3390/ma9110899 [66] Chen S F, Chen C Y, Cheng C S 2015 J. Alloys Compd. 644 17 doi: 10.1016/j.jallcom.2015.04.125 [67] Zhou B, Dong Y Q, Chi Q, Zhang Y Q, Chang L, Gong M J, Huang J J, Pan Y, Wang X M 2020 Ceram. Int. 46 13449 doi: 10.1016/j.ceramint.2020.02.128 [68] Zhou B, Dong Y Q, Liu L, Chang L, Bi F Q, Wang X M 2019 J. Magn. Magn. Mater. 474 1 doi: 10.1016/j.jmmm.2018.11.014 [69] Lu S H, Liu T, Wang M G, Zhao Z K 2025 J. Alloys Compd. 1016 178874 doi: 10.1016/j.jallcom.2025.178874 [70] Ma R, Chang L, Ye S L, Xie H Z, Xiao Q, Zhang L, Si J J, Yu P 2023 Powder Technol. 426 118639 doi: 10.1016/j.powtec.2023.118639 [71] Zhou B, Chi Q, Dong Y Q, Liu L, Zhang Y Q, Chang L, Pan Y, He A N, Li J W, Wang X M 2020 J. Magn. Magn. Mater. 494 165827 doi: 10.1016/j.jmmm.2019.165827 [72] Chi Q, Chang L, Dong Y Q, Zhang Y Q, Zhou B, Zhang C Z, Pan Y, Li Q, Li J W, He A N, Wang X M 2021 Adv. Powder Technol. 32 1602 doi: 10.1016/j.apt.2021.03.017 [73] Ding H P, Gong P, Chen W, Peng Z, Bu H T, Zhang M, Tang X F, Jin J S, Deng L, Xie G Q 2023 Int. J. Plast. 169 103711 doi: 10.1016/j.ijplas.2023.103711 [74] Ding H P, Bao X Q, Jamili-Shirvan Z, Jin J S, Deng L, Yao K F, Gong P, Wang X Y 2021 Mater. Des. 210 110108 doi: 10.1016/j.matdes.2021.110108 [75] Ding H P, Bao X Q, Zhang M, Jin J S, Deng L, Yao K F, Solouk A, Gong P, Wang X Y 2023 Adv. Powder Mater. 2 100109 doi: 10.1016/j.apmate.2023.100109 [76] Bai R S, Shao L L, Ding H P, Li X S, Zhou J, Xue Z Y, Ke H B, Wang W H 2025 J. Mater. Sci. Technol. 211 82 doi: 10.1016/j.jmst.2024.04.081 [77] Yang S Y, Zang B W, Xiang M L, Shen F Y, Song L J, Gao M, Zhang Y, Huo J T, Wang J Q 2025 Adv. Funct. Mater. 2425588 doi: 10.1002/adfm.202425588 [78] Yan M, Yi S B, Fan X Y, Zhang Z H, Jin J Y, Bai G H 2021 J. Mater. Sci. Technol. 79 165 doi: 10.1016/j.jmst.2020.12.009 [79] Li W C, Han X F, Li Q, Wu J K, Li W J, Zhan H C, Ying Y, Yu J, Zheng J W, Qiao L, Li J, Che S L 2023 J. Alloys Compd. 936 168164 doi: 10.1016/j.jallcom.2022.168164 [80] Bai G H, Sun J Y, Zhang Z H, Liu X L, Bandaru S, Liu W W, Li Z, Li H X, Wang N N, Zhang X F 2024 Nat. Commun. 15 2238 doi: 10.1038/s41467-024-46650-9 [81] Li H Z, Yan Y Q, Cai W S, Li L Y, Yan A, Liu L H, Ma J, Ke H B, Li Q, Sun B A, Wang W H, Yang C 2024 Nat. Commun. 15 9510 doi: 10.1038/s41467-024-53592-9 [82] Strobl M, Betz B, Harti R, Hilger A, Kardjilov N, Manke I, Gruenzweig C 2016 J. Appl. Crystallogr. 49 569 doi: 10.1107/S1600576716002922 [83] Weiss H A, Steentjes S, Tröber P, Leuning N, Neuwirth T, Schulz M, Hameyer K, Golle R, Volk W 2019 J. Magn. Magn. Mater. 474 643 doi: 10.1016/j.jmmm.2018.10.098 [84] Strobl M 2014 Sci. Rep. 4 7243 doi: 10.1038/srep07243 [85] Grünzweig C, David C, Bunk O, Dierolf M, Frei G, Kühne G, Schäfer R, Pofahl S, Rønnow H, Pfeiffer F 2008 Appl. Phys. Lett. 93 112504 doi: 10.1063/1.2975848 [86] Betz B, Rauscher P, Harti R, Schäfer R, Van Swygenhoven H, Kaestner A, Hovind J, Lehmann E, Grünzweig C 2016 Appl. Phys. Lett. 108 012405 doi: 10.1063/1.4939196 [87] Reimann T, Mühlbauer S, Schulz M, Betz B, Kaestner A, Pipich V, Böni P, Grünzweig C 2015 Nat. Commun. 6 8813 doi: 10.1038/ncomms9813 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: