在核物理与核技术应用的广袤领域中, 核反应数据构成了理论探索与实际应用的基石. 其中, 中子辐射俘获反应(n, γ)数据在恒星核合成、反应堆工程、中子活化分析以及国防安全等关键领域发挥着不可或缺的作用.

在恒星核合成的复杂进程中, 各类原子核的俘获截面是构建精确核天体物理模型的核心要素. 这些截面数据对于深入洞悉恒星从诞生到演化的全过程, 以及比铁更重元素在极端天体物理环境下的形成机制, 具有不可估量的价值. 缺中子核素的合成作为恒星核合成研究的关键环节, 高度依赖于p-过程. 然而, 目前 p-过程模型仍存在诸多不确定性, 这凸显了精确测量相关核反应数据的紧迫性和重要性. ⁸⁵Sr作为p-过程关键起始核素⁸⁴Sr的邻近核, 其丰度与⁸⁴Sr丰度以及 p-过程密切相关, 使其成为深入研究p-过程的关键突破口. 同时, 精确的⁸⁵Sr(n, γ)截面可修正s过程路径中分支点⁸⁵Sr→ ⁸⁶Sr的流量分配. 在渐近巨星分支 (asymptotic giant branch, AGB) 恒星s过程核合成中, 中子幻数(如 n = 82)附近的核素(如¹⁴²Nd)对中子俘获截面高度敏感. 实验表明^[1], 这些核素的截面精度若优于5%—8%, 可显著降低模型预测与太阳丰度分布的差异.

精确测定⁸⁵Sr(n, γ)截面, 对于构建高精度的丰度模型具有决定性意义, 不仅能够更准确地模拟和预测恒星核合成过程中元素的产生、演化与分布, 减少模型对中子密度、温度等参数的依赖不确定性. 还有助于完善我们对宇宙演化进程的认知, 与观测对比, 改善对富锶恒星(如钡星)光谱的拟合, 检验恒星演化理论. 为天体物理学研究提供更为坚实的理论基础^[2–5].

目前, 通过大量的实验工作, 众多稳定核素的俘获截面已被成功测量并积累了丰富的数据. 然而, 在现代核科学的众多研究领域和实际应用场景中, 短寿命(半衰期在数年及以内)放射性核素的俘获截面数据同样不可或缺. 令人遗憾的是, 针对这类短寿命放射性核素俘获截面数据的实验研究极为匮乏. 深入剖析其原因, 主要体现在以下几个方面: 首先, 放射性核素材料的获取与制靶面临着严峻的技术挑战, 同时伴随着高昂的成本投入; 其次, 高比活度靶材的使用不仅给辐射防护工作带来了巨大的困难, 还会对探测器造成不可逆的辐射损伤; 再者, 在强衰变本底的干扰下, 获取高质量的信号非常困难; 此外, 靶核自身衰变会引入复杂的本底干扰, 严重影响测量的准确性. 这些因素相互影响, 使得直接测量短寿命放射性核素的俘获截面成为一项极具挑战性的任务. 借助放射性束流设施, 结合弱束缚核氘的中子转移反应与逆运动学实验方法, 为短寿命核素俘获截面测量提供了可行途径, 但限制明显^[6]. 实验中放射性束流强度低, 低截面测量困难, 强关联多体系统里旁观者质子引入的系统误差难以消除, 且该方法本质是替代法, 并非理想测量方式. 逆运动学方法对束流强度要求高, 放射性核束流的产生复杂、束流强度难以满足统计量要求, 成本高、技术复杂; 反应机制复杂, 数据分析难, 探测器效率和分辨率受影响, 理论模型不确定. 其他常用研究方法如Oslo方法, 依赖准确核能级结构信息, 否则易导致系统性偏差; 需大量数据保证精度, 对低产额反应数据获取难、统计误差大; 基于简化假设, 在非平衡态或量子效应显著反应中受限, 数据分析复杂、不确定性高.

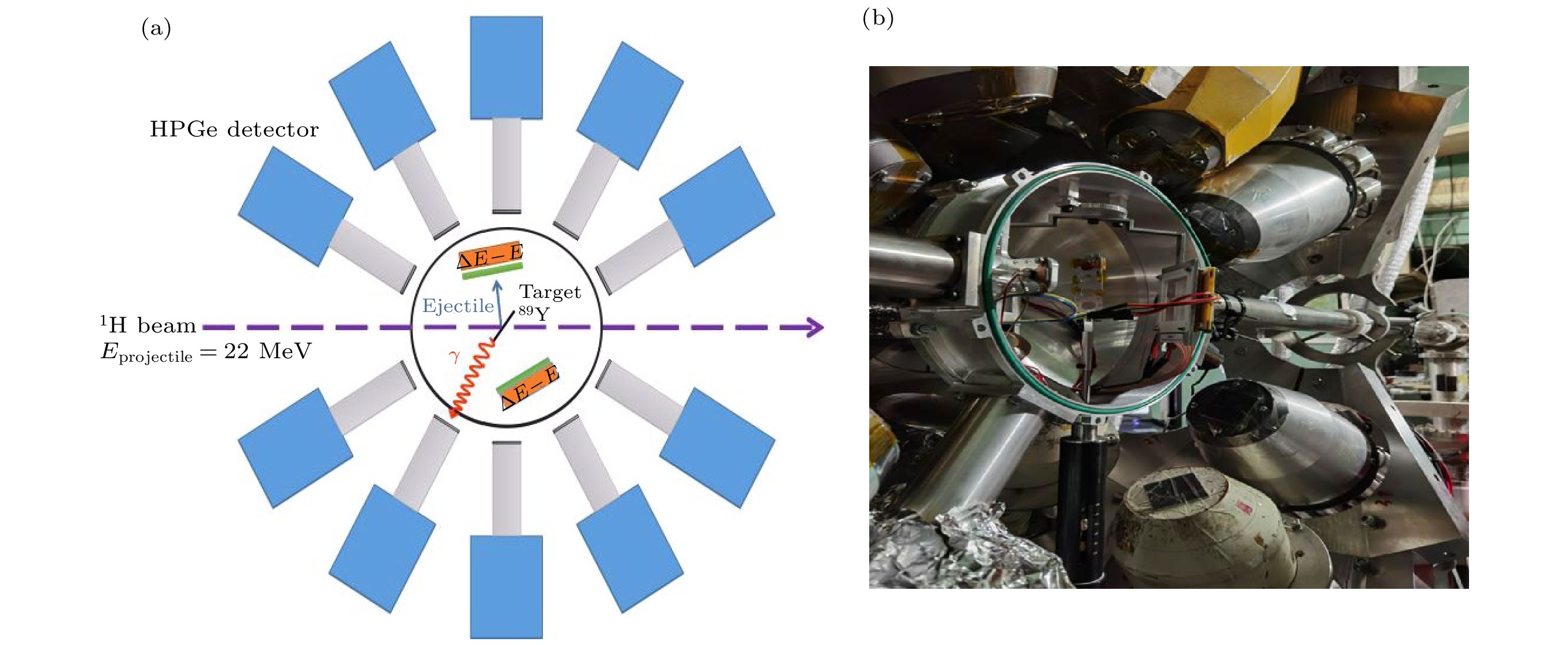
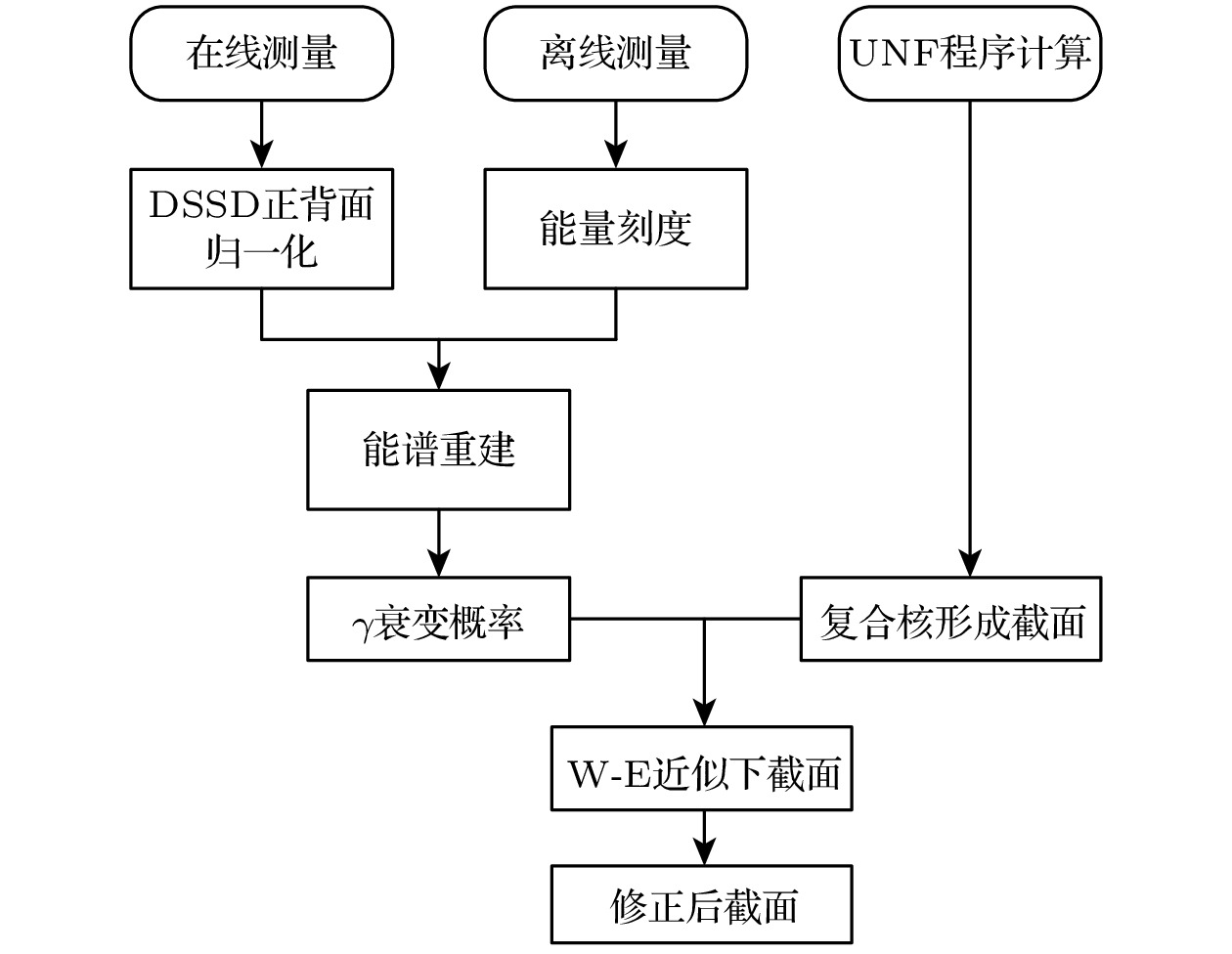
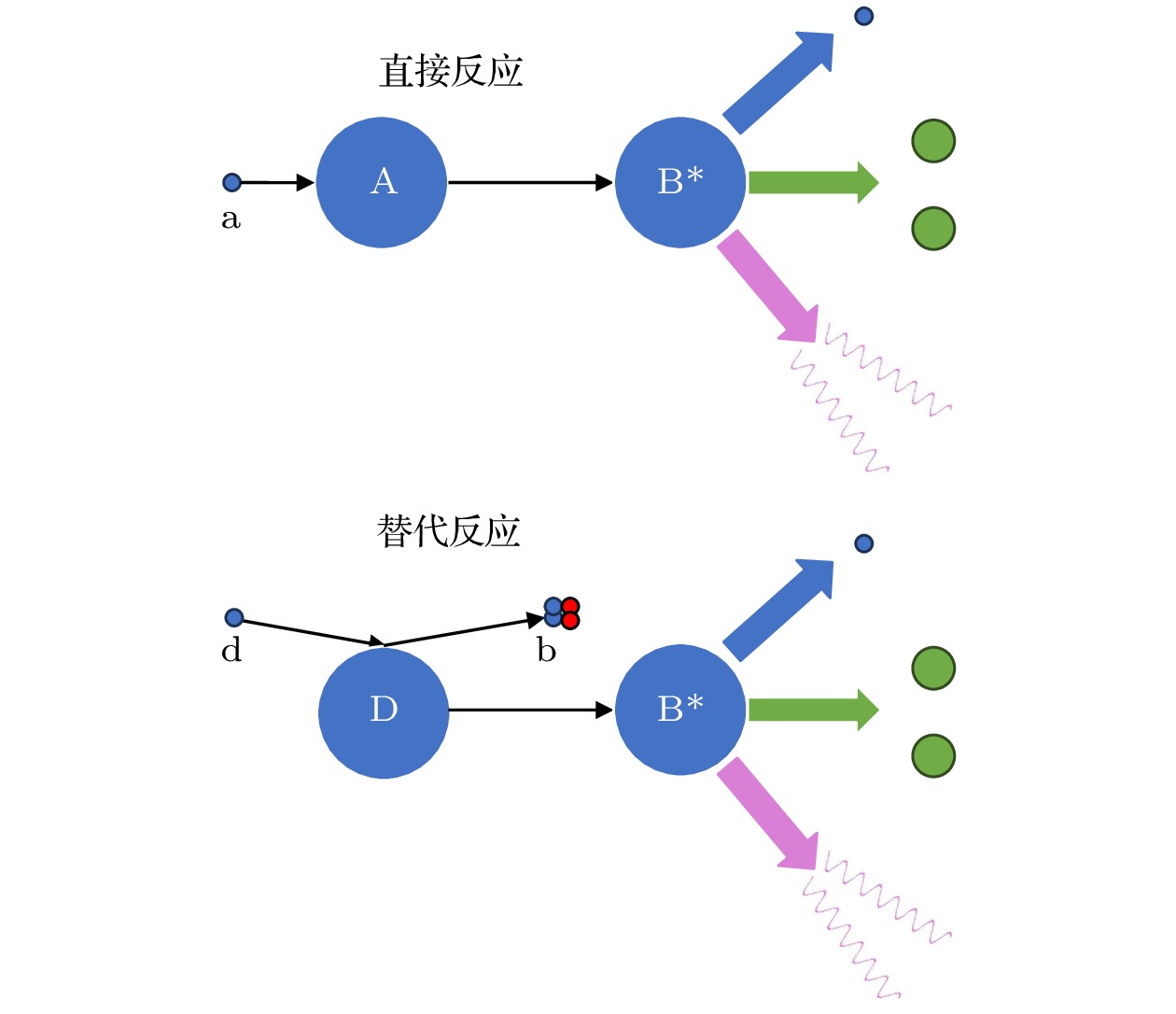
在各类间接测量方法中, 替代反应法(surrogate reaction method)以其独特的优势脱颖而出, 成为目前测量短寿命核素俘获截面的一种极具潜力的方法^[7]. 该方法由Cramer和Britt^[8,9]于20世纪70年代首次提出, 其基本原理基于复合核理论. 即某些稳定核素发生的核反应能够与所求不稳定核素发生的核反应形成相同的复合核, 并且在复合核形成与衰变相互独立的假设前提下, 通过相同的衰变道进行衰变, 如图1所示. 基于这一原理, 可以利用稳定核素靶来研究不稳定核素的复合核反应截面, 从而绕过直接测量短寿命放射性核素的诸多困难.

2006年, Boyer等^[10]运用替代反应法, 通过²³²Th(³He, pγ)²³⁴Pa反应对²³³Pa(n, γ)截面展开了测量. 2009年, Allmond等^[11]的实验利用21 MeV的氘核在²³⁵U靶上的质子剥除反应来产生²³⁶U复合核, 用来得到²³⁵U(n, γ)截面. 2017年, 马南茹等^[12]提出轻带电粒子的俘获反应作为替代反应的替代俘获法, 通过²³⁶U(α, f)和²³⁶U(α, 2n)的测量, 分别得到了²³⁹Pu(α, f)和²³⁹Pu(n, 2n)反应截面. 2016年, 颜胜权等^[13–15]使用替代比率法, 利用⁹²Zr(¹⁸O, ¹⁶O) ⁹⁴Zr以及⁹⁰Zr(¹⁸O, ¹⁶O) ⁹⁰Zr 反应, 以⁹¹Zr(n, γ) ⁹²Zr截面作为参考, 得到了⁹³Zr(n, γ) ⁹⁴Zr在中子能量E_n = 0—8 MeV 时的截面, 结果显示在E_n > 3 MeV处与评价库的吻合度良好. 随后, 他们运用同样的方法, 又得到了⁹⁵Zr(n, γ) ⁹⁶Zr以及⁵⁹Fe(n, γ) ⁶⁰Fe的截面数据. 在 2018—2020年期间, 替代反应法在理论计算领域实现了重大突破, 成功从理论层面计算出了替代反应的Jπ分布. Escher等^[16]运用⁸⁹Y(p, d)反应来确定⁸⁷Y(n, γ)截面. 为了验证该方法的可靠性, 他们还采用⁹²Zr(d, p)反应获得⁹⁰Zr(n, γ)截面, 以对方法进行检验.

本文聚焦于短寿命的⁸⁵Sr核(T_1/2 = 64.849 d)的中子俘获反应. 目前, 该反应尚无直接测量数据, 现有的基于唯象模型评价数据在本实验研究的能区(0.02 —1.22 MeV)相对误差可达到70%, 这为相关研究带来了一定挑战. 在⁸⁵Sr(n, γ)反应中, 入射中子与⁸⁵Sr靶相互作用, 形成激发态的复合核⁸⁶Sr*, 随后复合核通过γ射线发射进行退激衰变. 本研究通过p + ⁸⁹Y→α + ⁸⁶Sr*反应形成相同的复合核, 将对短寿命核素的研究转化为对稳定核素反应的研究. 通过实验测量, 结合理论计算方法, 深入探究⁸⁵Sr(n, γ)反应截面. 本工作不仅旨在为核物理、天体物理等相关领域的研究提供关键的数据支持, 填补该领域在⁸⁵Sr核中子俘获截面数据方面的空白, 还有助于进一步推动该方法在短寿命核素中子俘获截面测量中的广泛应用与发展, 为解决更多类似的核反应数据测量困难提供新的思路与方法.

替代反应法基于Bohr的复合核理论假设, 即复合核出射道独立于入射道, 按照描述复合核出射道截面的Hauser-Feshbach公式^[17], 其截面为

式中${{\alpha}}$代表入射反应道, ${{\chi}}$代表出射反应道, ${E_{{\text{ex}}}}$为形成复合核的激发能, $ \sigma _{{\alpha}}^{{\text{CN}}}\left( {{E_{{\text{ex}}}}{, } J{, } {\pi}} \right) $为激发能${E_{{\text{ex}}}}$, 自旋宇称为$ J{, } {\pi} $的复合核的形成截面, $G_{{\chi}}^{{\text{CN}}} \left( {{E_{{\text{ex}}}}{, } J, {\pi}} \right)$为复合核衰变(退激发)到${{\chi}}$道的分支比. 入射粒子a的动能${E_{\text{a}}}$与复合核的激发能${E_{{\text{ex}}}}$相关, 可表示为

其中, $ {A_{\text{A}}} $和$ {A_{\text{a}}} $分别代表靶核粒子和入射粒子的核子数, $ {S_{\text{a}}} $代表入射粒子a的从形成的复合核分离的能量, 即复合核分离能, 对于中子即为中子分离能$ {S_{\text{n}}} $.

在替代反应中, 复合核B^*可通过直接反应 d + D → b + B^* 形成, 即p + ⁸⁹Y → α + ⁸⁶Sr^* 并通过出射粒子α来确定的复合核的种类以及激发能. 在替代反应中形成复合核B^*的布居概率为$ F_{\text{δ }}^{{\text{CN}}}\left( {{E_{{\text{ex}}}}{, } J{, } {\pi}} \right) $, 其中$ {\text{δ }} $代表产生反应 d + D → b + B^*, 且B^*处于激发能${E_{{\text{ex}}}}$, 自旋宇称为$ J{, } {\pi} $. 由此, 可用复合核衰变概率$ {P_{{\text{δ}}\chi}}\left( {{E_{{\text{ex}}}}} \right) $来代表替代反应形成激发能为${E_{{\text{ex}}}}$的复合核B^*以衰变道$\chi $衰变概率, 根据(1)式, 可表示为

而在实验中, 该复合核衰变概率也可通过实验测定:

其中, $ {\varepsilon _{{\chi}}} $表示衰变道${{\chi}}$的探测效率, $ {N_{\text{δ }}} $为直接反应后的出射粒子计数, 对应复合核形成事件, $ {N_{{\text{δ}}\chi}} $为探测到的复合核衰变事件数. 由此可以通过实验结合已有较好的光学势计算结果的复合核形成截面, 从而得到难以直接测量的短寿命核反应截面.

如果能够通过理论准确计算$ F_{\text{δ }}^{{\text{CN}}}\left( {{E_{{\text{ex}}}}{, } J{, } {\pi}} \right) $, 结合通过实验去测得$ P_{{\text{δ}}\chi}^{{\text{exp}}} $, 就可根据(3)式抽取$G_{{\chi}}^{{\text{CN}}}\left( {{E_{{\text{ex}}}}{, } J, {\pi}} \right)$, 然后利用(1)式得到准确的待测反应截面. 但是, $ F_{\text{δ }}^{{\text{CN}}} $往往很难通过理论方法进行准确计算, 使得不能根据实验准确抽取$ G_{{\chi}}^{{\text{CN}}} $.

为解决这一问题, 引入Weisskopf-Ewing (W-E)近似^[18], 其认为$G_{{\chi}}^{{\text{CN}}}\left( {{E_{{\text{ex}}}}{, } J, {\pi}} \right)$是独立于$ J, {\pi} $的, 即

此时, 复合核衰变概率$ P_{{\text{δ}}\chi}^{} $为

显然, $ \displaystyle\sum\nolimits_{J, {\pi}} {F_{\text{δ }}^{{\text{CN}}}\left( {{E_{{\text{ex}}}}, J, {\pi}} \right)} \equiv 1 $, 因此分支比$ g_{{\chi}}^{{\text{CN}}}\left( {{E_{{\text{ex}}}}} \right) $可直接由复合核的衰变概率得到:

即实验测得的$ P_{{\text{δ}}\chi}^{{\text{exp}}}\left( {{E_{{\text{ex}}}}} \right) $就是$ g_{{\chi}}^{{\text{CN}}}\left( {{E_{{\text{ex}}}}} \right) $, 则反应截面为

其中,

在这一假设下, 不需计算$ F_{\text{δ }}^{{\text{CN}}}\left( {{E_{{\text{ex}}}}{, } J{, } {\pi}} \right) $, 而复合核形成截面$ \sigma _{{\alpha}}^{{\text{CN}}} $容易计算, 从而结合实验测量的$ P_{{\text{δ}}\chi}^{{\text{exp}}}\left( {{E_{{\text{ex}}}}} \right) $能够直接得到截面.

为了更充分地运用 W-E 近似, Plettner等^[19]引入了替代比率法(surrogare ratio method, SRM). 在此方法中, $ R(E) $表示两个不同反应截面的比率, 具体形式为

其中, 下标1和2分别对应两个替代反应: a₁ + A₁ → $\rm B_1^* $ → c₁ + C₁ 以及 a₂ + A₂ → $\rm B_2^* $ → c₂ + C₂ . 这意味着为了获取相关数据, 需要进行两次实验测量. 通过这种方式, 就能够借助一个较为可靠的参考截面, 推算出待测截面.

基于 W-E 近似理论, R(E)可进一步写作:

如前文所述, 复合核的形成截面$ \sigma _{}^{{\text{CN}}} $能够通过计算得出. 而其中$ {{G_{{{{\chi}}_{1}}}^{{\text{CN1}}}(E)} {/ } {G_{{{{\chi}}_{2}}}^{{\text{CN2}}}(E)}} $需通过实验测定:

在实际情况中, 对于出射粒子的探测工作而言, $ {{{\varepsilon _{{{{\chi}}_{2}}}}(E)} {/ } {{\varepsilon _{{{{\chi}}_{1}}}}(E)}} $这一参数可以单独确定, 并且通常可以认为二者相等.

另外, $ {{{N_{{{\text{δ}}_{1}}}}(E)} {/ } {{N_{{{\text{δ}}_{2}}}}(E)}} $这一数值由两个实验的束流强度、靶厚以及测量事件共同决定, 其值为常数. 为了简化表达过程, 将其设定为 1. 通过实验测定得到的$ {R^{^{\exp }}}(E) $表达式为

由此可见, 在实验过程中, 并不需要测量直接反应后的出射粒子计数$ {N_{\text{δ }}} $, 如此一来, 便有效避免了因底衬等杂质引发的本底问题.

然而W-E近似也存在一定的局限性^[20–22], 离散态的自旋宇称布居受复合核反应机制的显著影响, 反应机制决定了角动量传递与耦合方式、宇称组合分配, 还影响复合核激发能与态密度分布以及衰变模式, 进而塑造了离散态自旋宇称的布居特征. 故替代反应和待测反应$ J, {\pi} $布居往往并不一致, 此时$ G_{{\chi}}^{{\text{CN}}} $与$ J, {\pi} $的关联将导致系统误差, 对此的修正将在后文中讨论.

本次实验在中国原子能科学研究院HI-13串列加速器L40束线上的在束γ实验终端进行, 利用加速器产生的质子束流轰击⁸⁹Y靶, 质子能量为22 MeV, 束流强度约为1 nA, ⁸⁹Y靶为自支撑金属靶, 厚度为330 μg/cm².

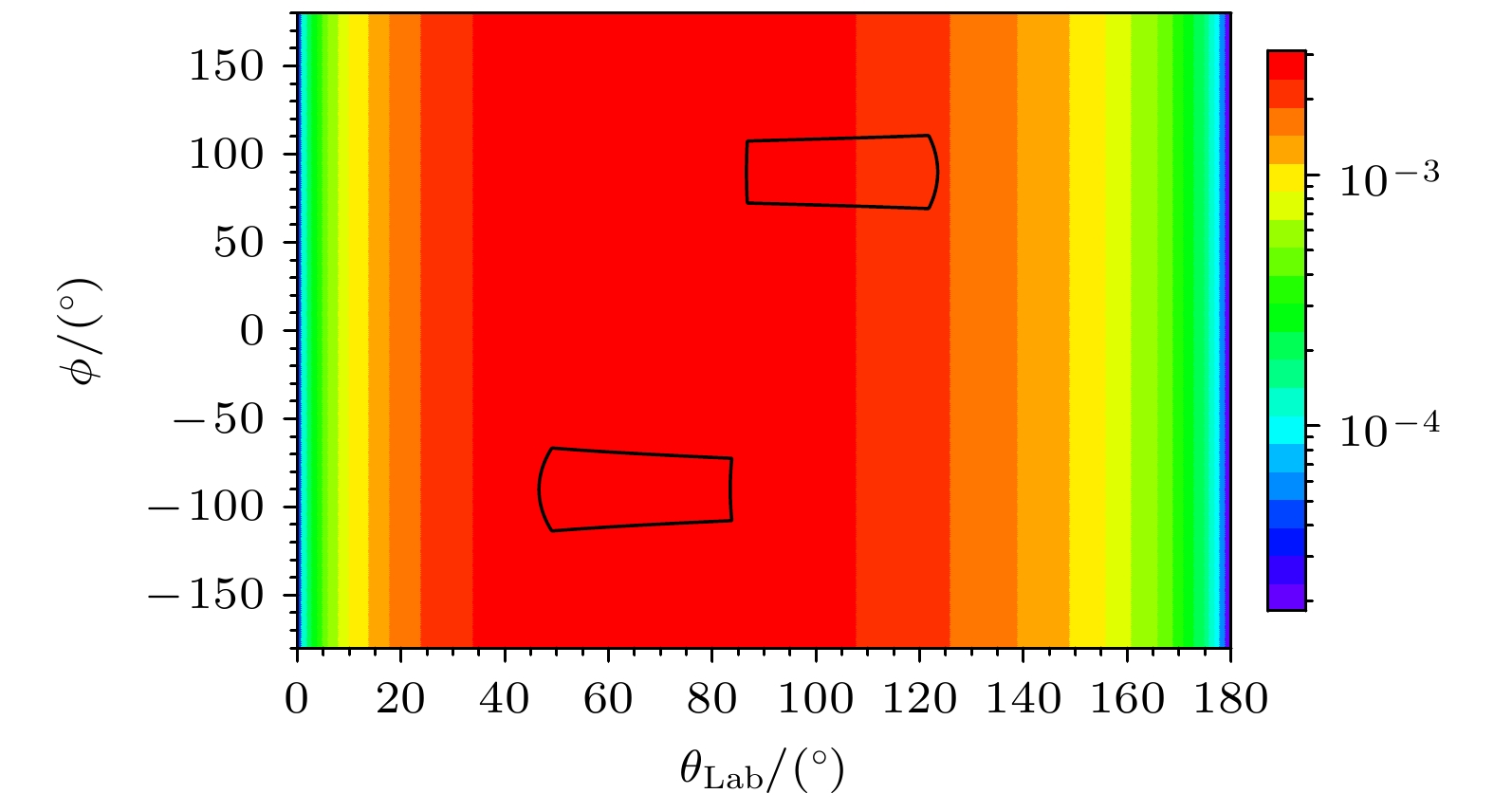
带电粒子探测使用两组硅探测器阵列组成的ΔE–E望远镜^[23], 每组由一个有效面积50 mm×50 mm, 厚度为80 μm或100 μm, 双面各16条的双面硅条探测器(double-sided silicon strip detector, DSSD)作为ΔE探测器, 其后放置两个厚度为1500 μm的四分硅探测器(quad silicon detector, QSD)测量带电粒子穿过双面硅条探测器后的剩余能量. 两组探测器围绕靶中心布置, 置于相对束流65°和–100°的方位, 其覆盖角度分别从65°—84°以及从–82°到–119°. 计算⁸⁹Y(p, α)反应的出射α粒子θ-ϕ分布, 如图2所示, 计算得到在放置位置处, 两组望远镜的探测效率分别为3.62%和2.71%. 由此可实现出射带电粒子的粒子鉴别与能量探测, 反推出复合核⁸⁶Sr*的激发能, 以此作为触发信号, 对瞬发γ射线进行符合测量.

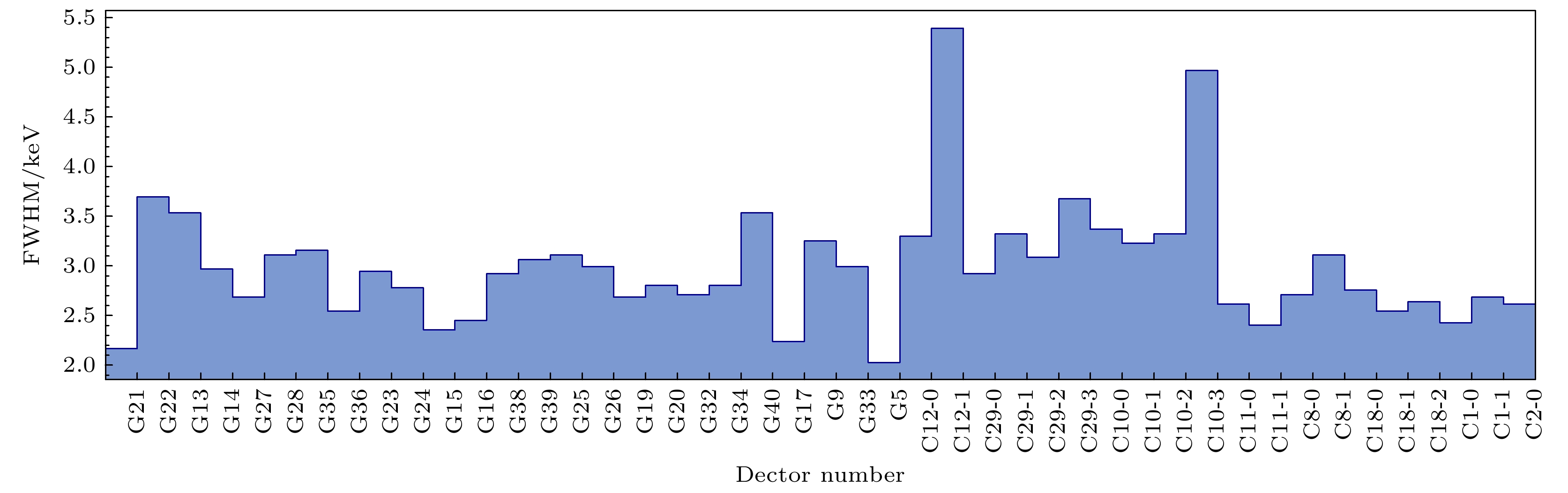
γ探测器采用中国联合Gamma探测器阵列^[24], 最多可放置40个HPGe探测器. 其分别分布于31°, 61°, 90°, 119°, 149°. 本次实验使用了25个HPGe同轴探测器以及8个Clover探测器. HPGe探测器的能量分辨一般以⁶⁰Co的1332.5 keV特征峰的FWHM表征, 本次实验使用的探测器能量分辨率见图3, 除去两个分辨率较差的Clover探测器模块. 平均分辨率约为2.99 keV, 探测器总体分辨水平较高. 利用HPGe探测器阵列高的探测效率和能量分辨, 得到了与出射α事件符合的特征γ射线能谱, 在后续数据处理中筛选出有效的符合事件. 实验设备布局如图4所示.

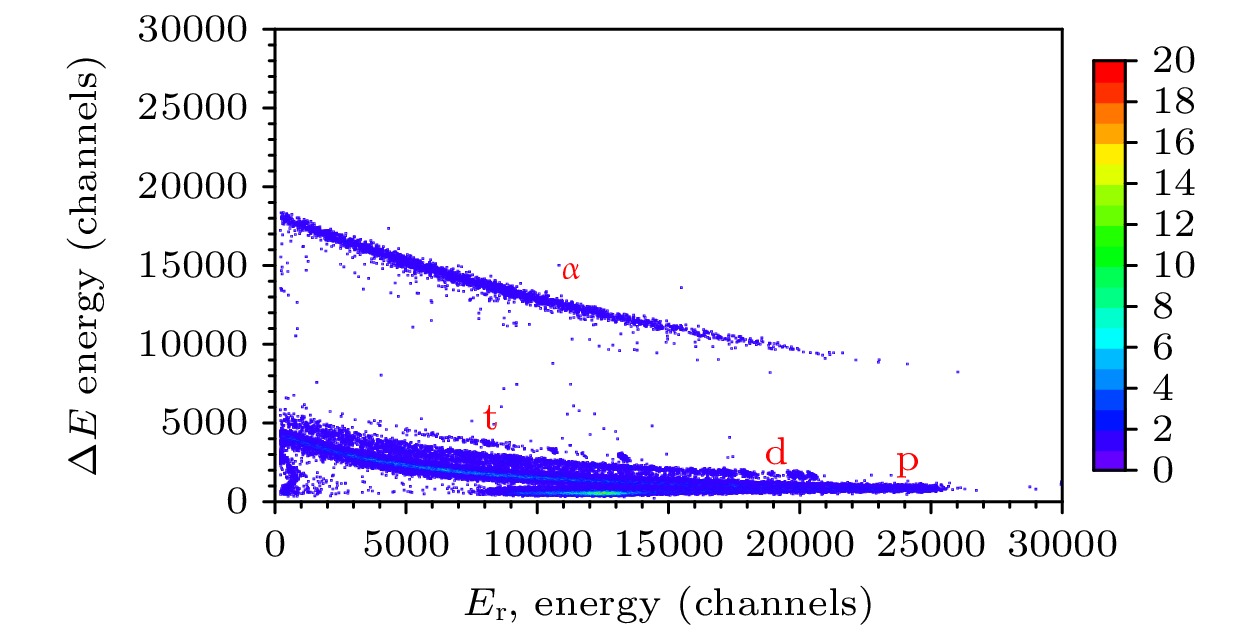
质子轰击⁸⁹Y靶会产生多种剩余核, 并伴随有(p, p'), (p, d), (p, t)以及(p, α)等反应. 出射带电粒子通过望远镜探测器中的能量损失与剩余能量的关联谱进行识别. 如图5所示, 为通过望远镜探测器前两层实现的粒子鉴别, 自上而下的条带分别为α, t, d, p. 其中, α主要源于融合蒸发, 而t, d, p的高能出射部分, 主要源于直接反应(弹散、非弹、转移), 而低能部分主要源于融合蒸发. 从图5可以看到, α, t, d的动能可完全沉积在前两层探测器中, 而质子因能量高质量小而穿透能力强, 在第2层25000道处存在拐点, 拐点左下方事件质子并未完全沉积于前两层探测器中. 本次实验主要关注的是⁸⁹Y(p, α)⁸⁶Sr*, 作为⁸⁵Sr(n, γ)的替代反应. 实验技术路线如图6所示.

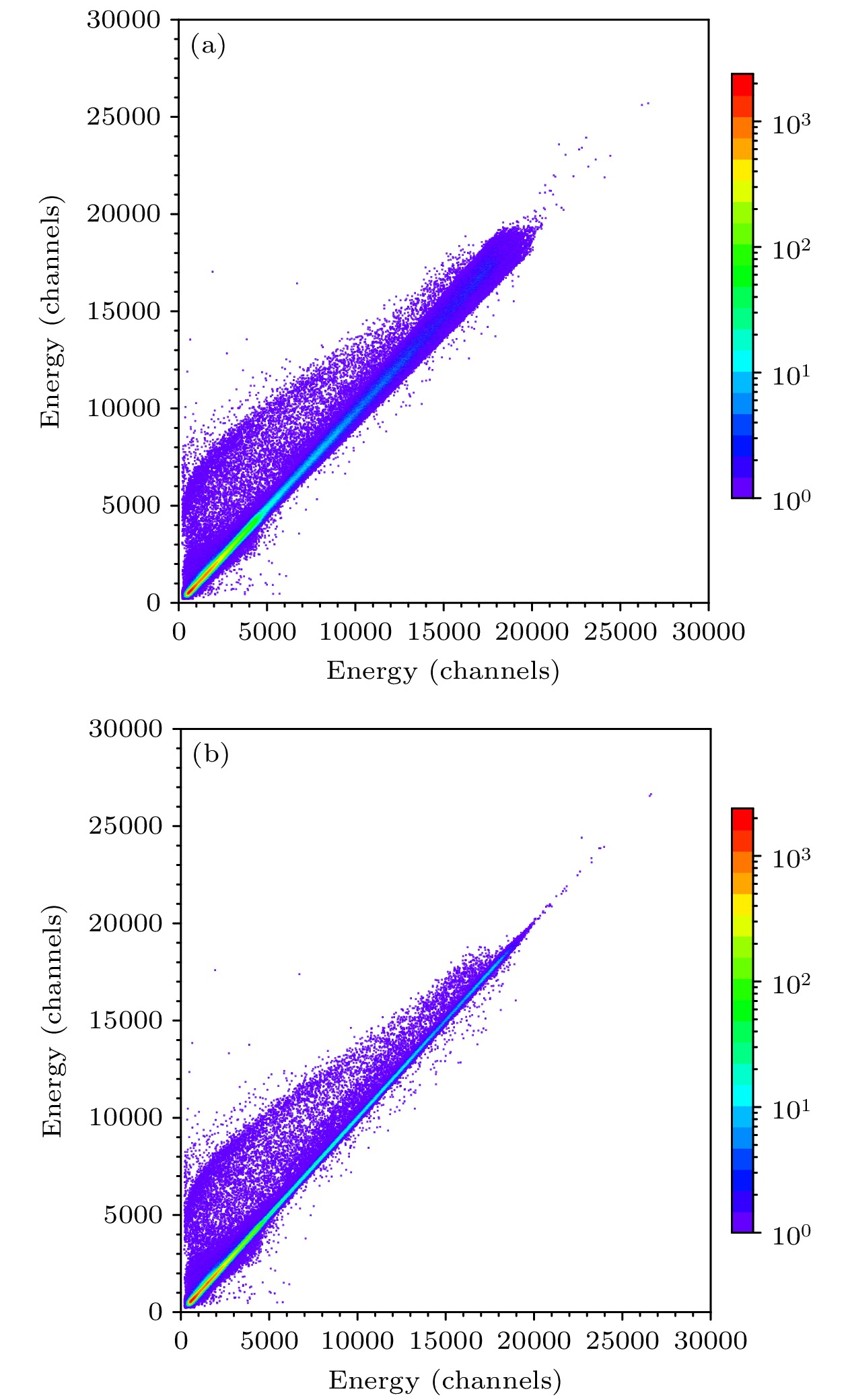
每一片DSSD的正反面共32路信号. 信号分别经过前置放大器后进入数字化获取插件, 由于电子器件性能的细微差别, 每一路信号的能量响应特性不同. 如果采用传统的能量刻度方法对DSSD的每一条进行刻度, 则每一片DSSD需要重复32次处理, 工作量巨大. 此外, 对于一些事件数较少的信号路, 难以积累足够的统计量来单独进行能量刻度. 同时, 人为操作也会因主观性而造成一定的误差. 为了克服上述问题, 采用自归一化方法对探测器信号进行预处理^[25]. 这种自归一化方法与粒子类型无关, 涵盖能量范围广, 可以直接利用实验数据快速处理, 有利于实验过程中数据的在线分析. 如图7所示, 展示了自归一前后的DSSD正背面能量关联谱, 可见正背面能量响应归一化后, 能量关联谱为一条标准的y = x直线.

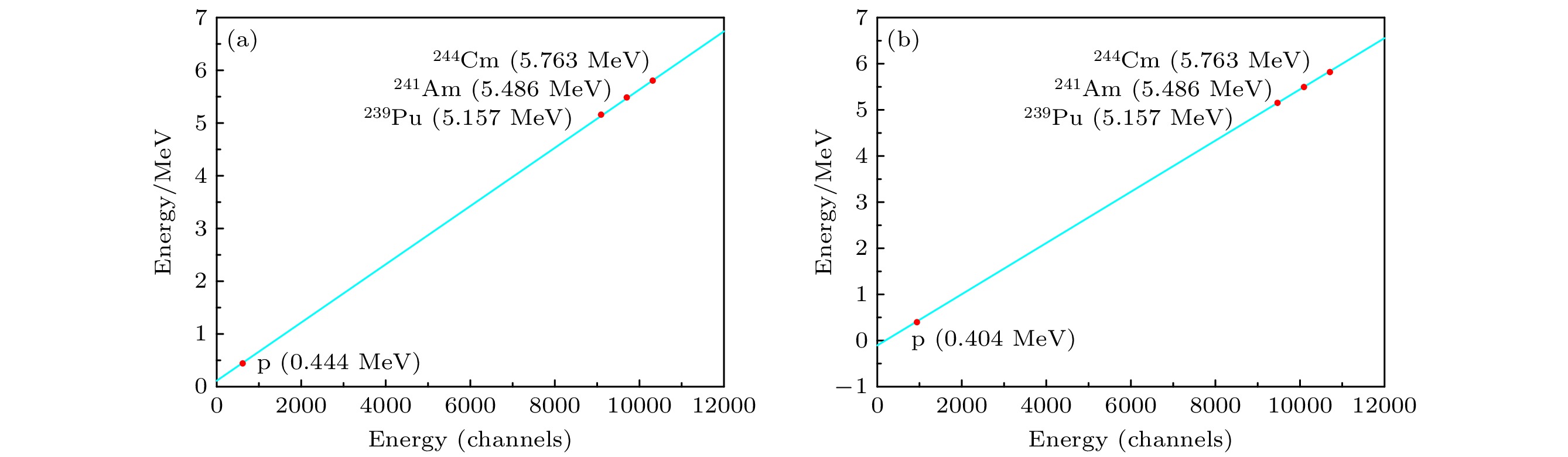
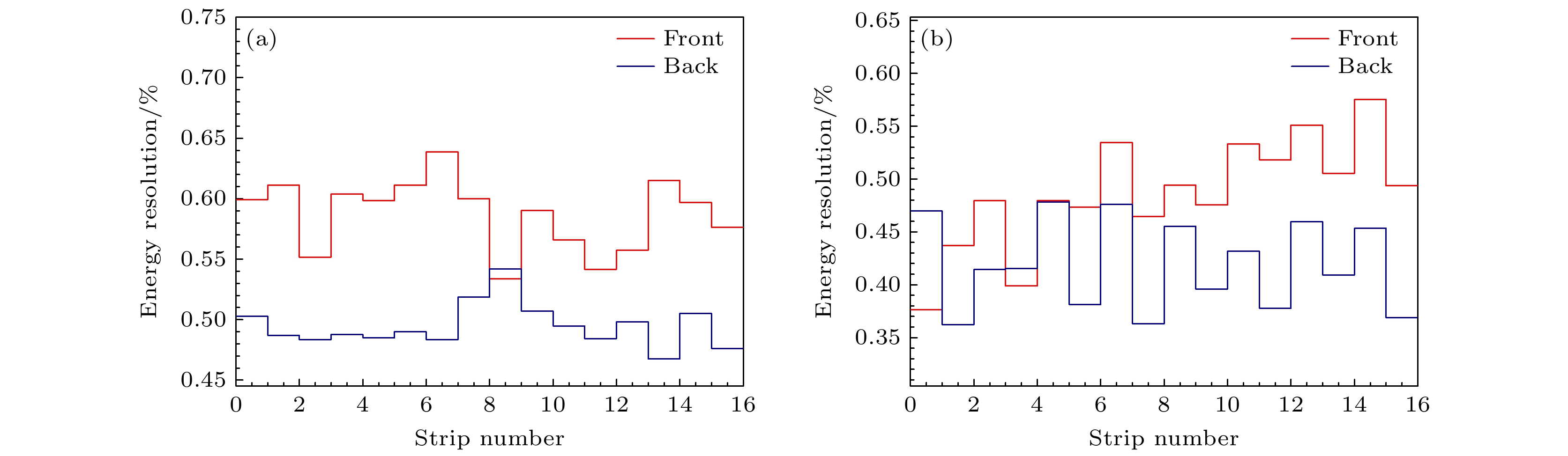
对硅探测器进行能量刻度通常采用3α放射源刻度, 以已知能量的α放射源作为标准. 本次实验中硅探测器能量沉积最大为13 MeV, 若仅使用3α源进行刻度, 将会在高能区带来较大误差, 故需增加高能区的能点进行刻度, 利用在线实验的出射带电粒子进行刻度. 在这里主要选用质子轰击⁸⁹Y核过程中, 出射的弹散质子所对应的能点. 利用LISE++ ^[26]计算此类粒子在探测器中的能量沉积, 结合3α源的3个能点, 即可得到刻度曲线, 如图8所示. 同时, 利用3α源中²⁴⁴Cm的α峰作标准, 给出了DSSD 探测器正背面的能量分辨率, 如图9所示. 可以看出DSSD探测器探测器正背面能量分辨率有一定差别, 但总体分辨率都在0.35%—0.65%, 能够实现轻粒子的粒子鉴别.

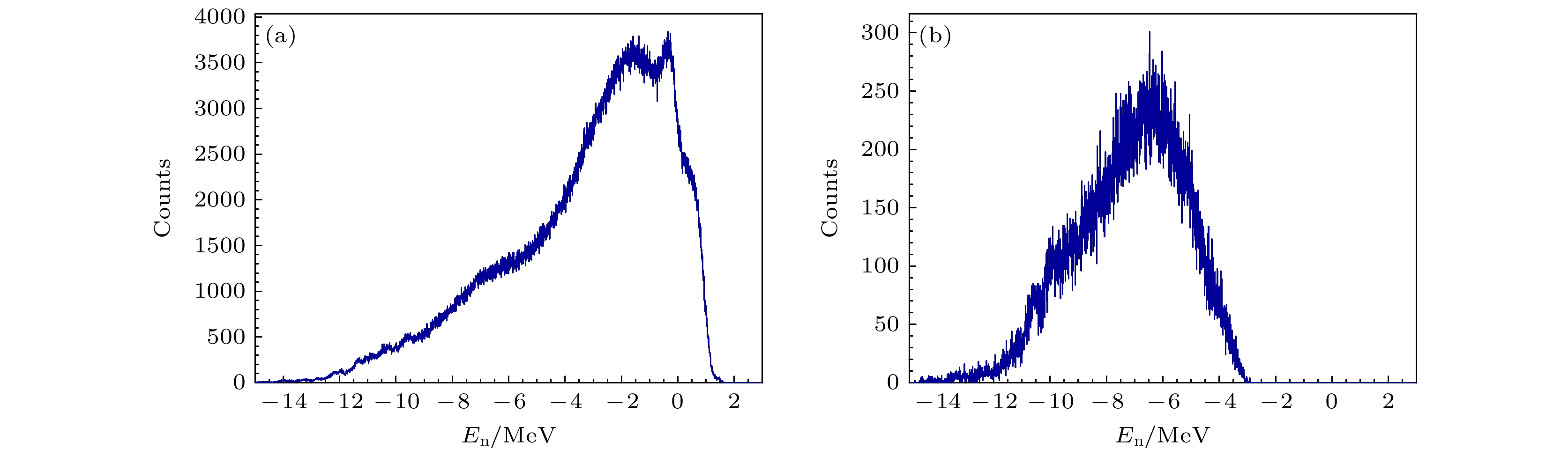
刻度完成后, 可获得由绝对能量损失构成的PID谱, 本文主要关注α粒子. ⁸⁹Y(p, α)⁸⁶Sr^*是两体反应, (14)式为实验室系下的出射粒子能量与剩余核激发能关系, 结合(2)式, 即可反推出等效中子能量, 如图10所示. 由于出射粒子运动学问题, 导致后角处(–100°)望远镜探测器无法探测到质心系中能量较低的α粒子, 从而其激发能对应的等效中子能量小于0, 不符合本文研究内容, 故以下只关注前角处(65°)望远镜探测器探测到的α粒子. 而后对望远镜探测器与高纯锗γ探测器的事件进行时间关联, 得到有效符合事件. 符合事件筛选以两探测器的时间差为标准, 筛选时间窗设为–600—200 ns.

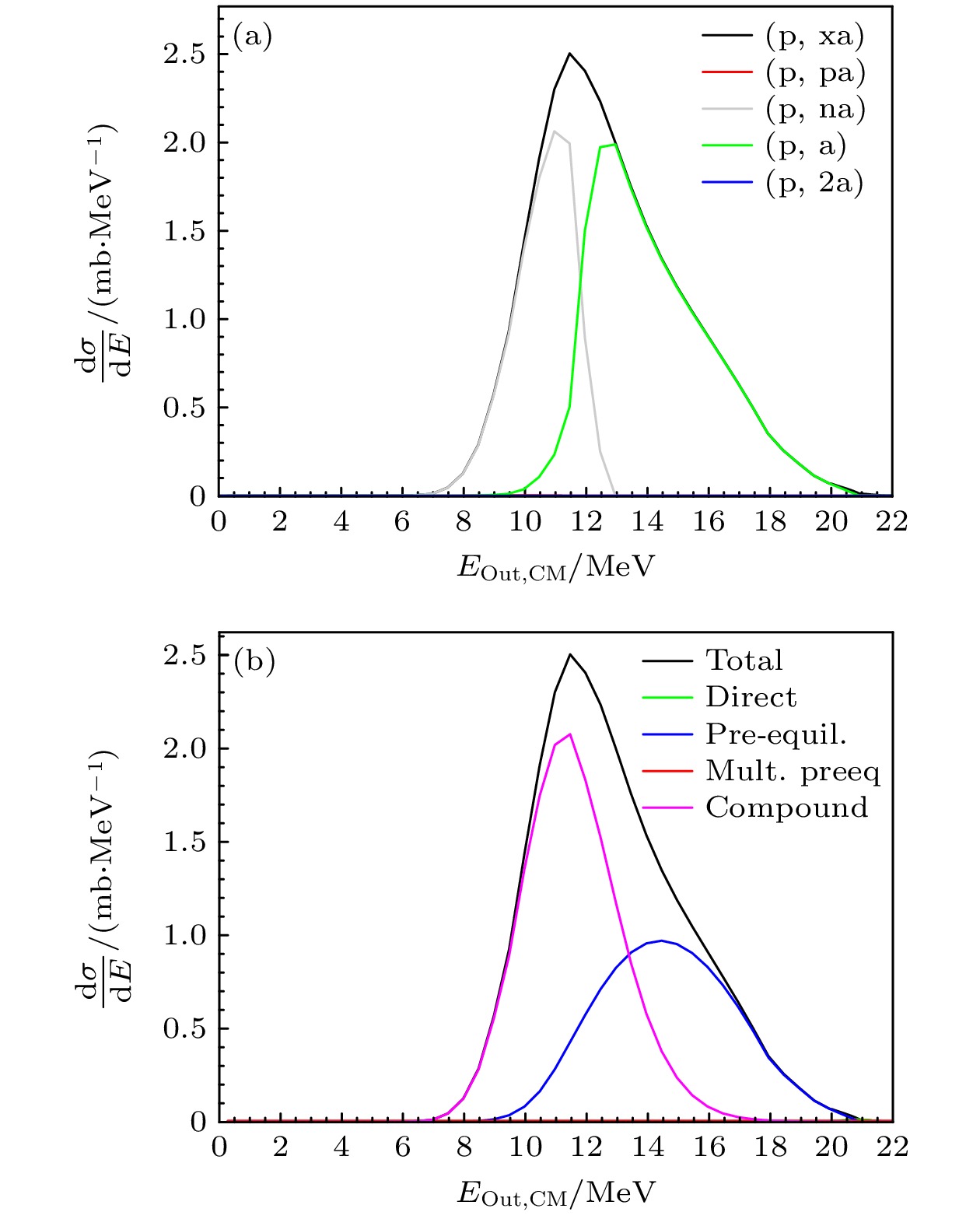
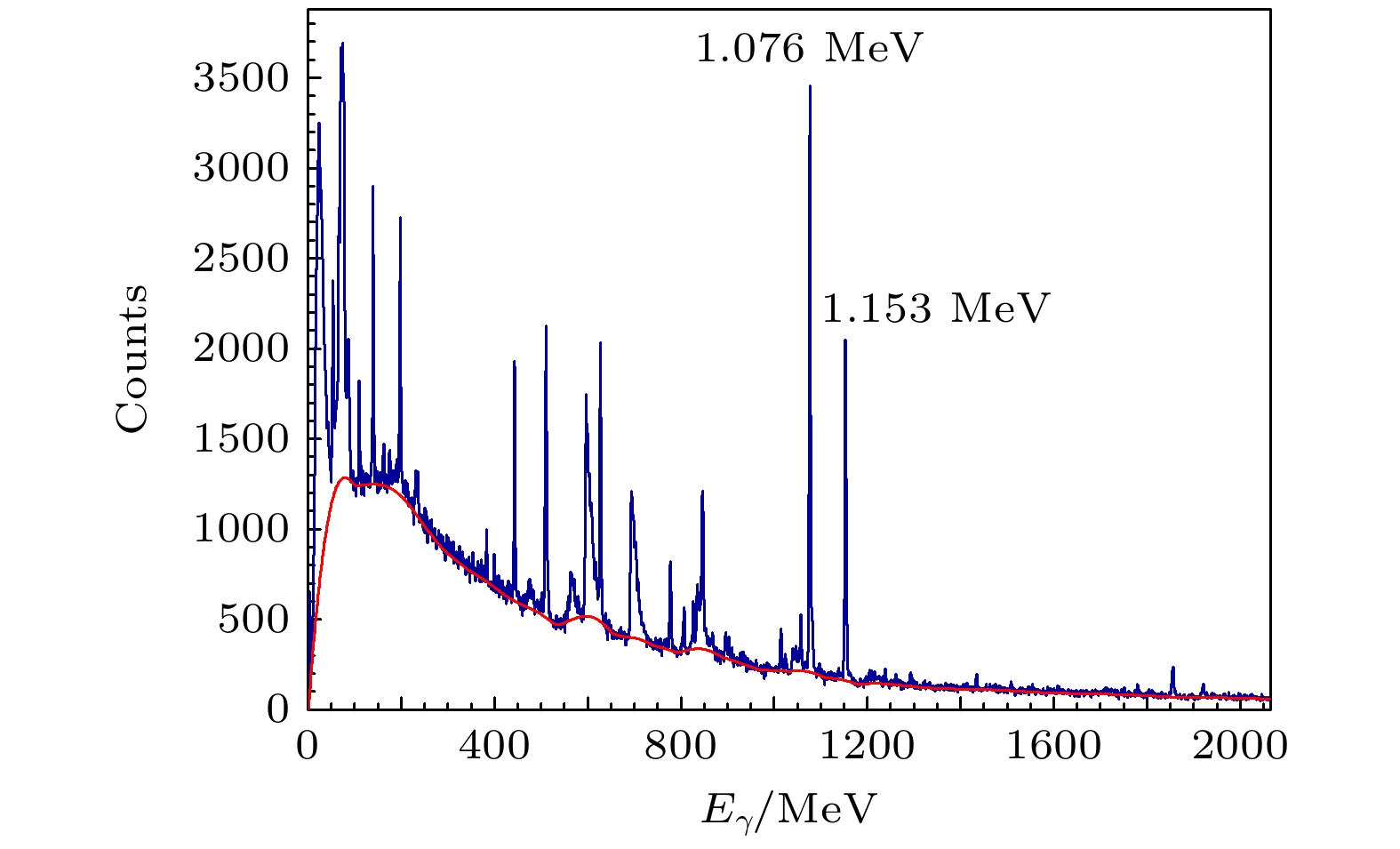
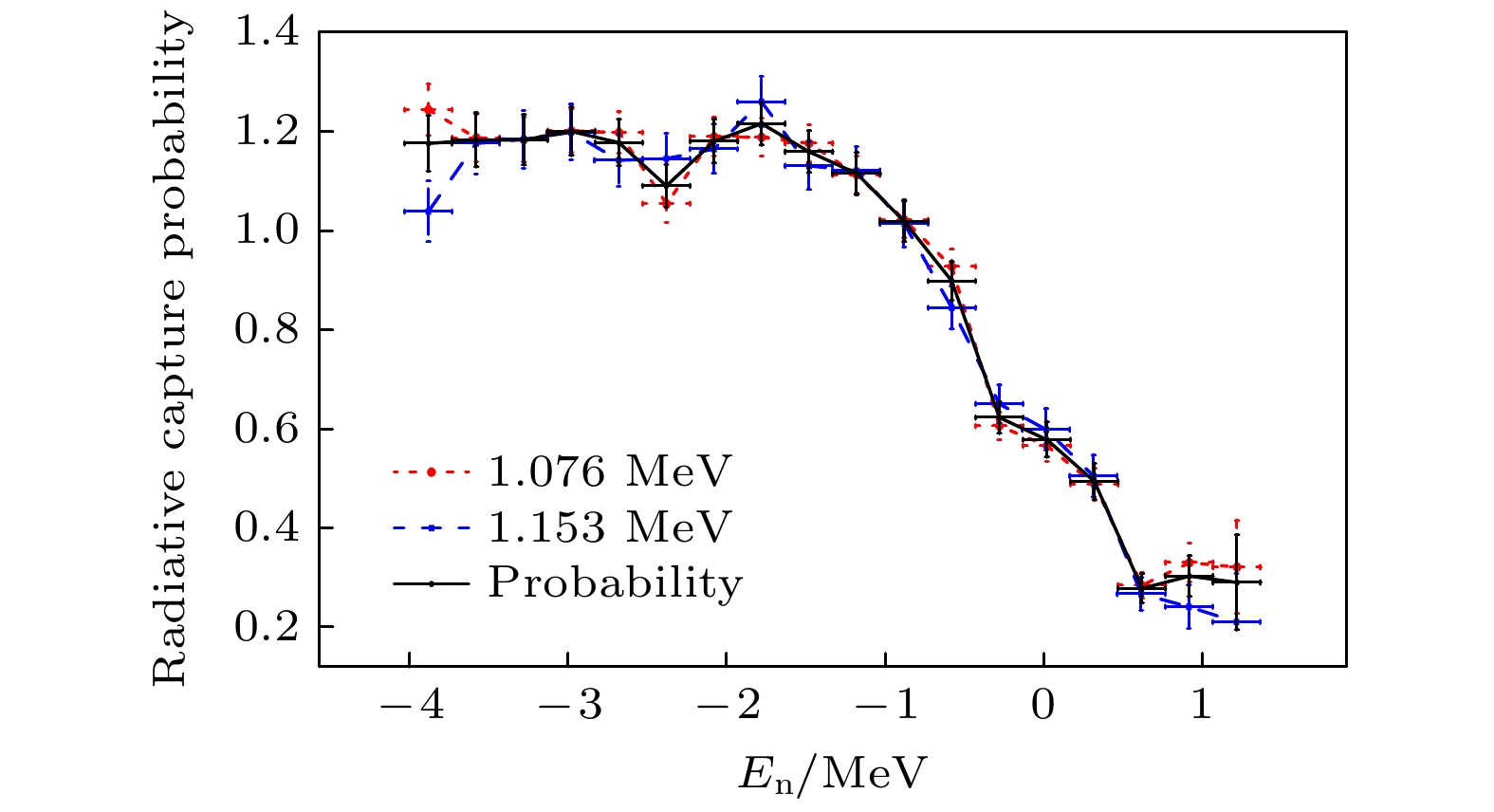
利用Talys^[27]软件对22 MeV能量下质子入射⁸⁹Y反应出射α能谱进行模拟, 如图11所示, 出射α主要由两个反应道产生, 包括低能部分的(p, nα), 以及高能部分的(p, α). 在对应E_n > 0时, 即$ {E}_{{\mathrm{e}}{\mathrm{x}}} $> S_n时, 形成的复合核将有足够的激发能蒸发中子, 此时其将和发射γ的反应道相互竞争, 在E_n > 1 MeV后, γ衰变概率$P_{\text{γ }}^{{\text{exp}}}$→0^[28], 故选取等效中子能量区间为–4—2 MeV.

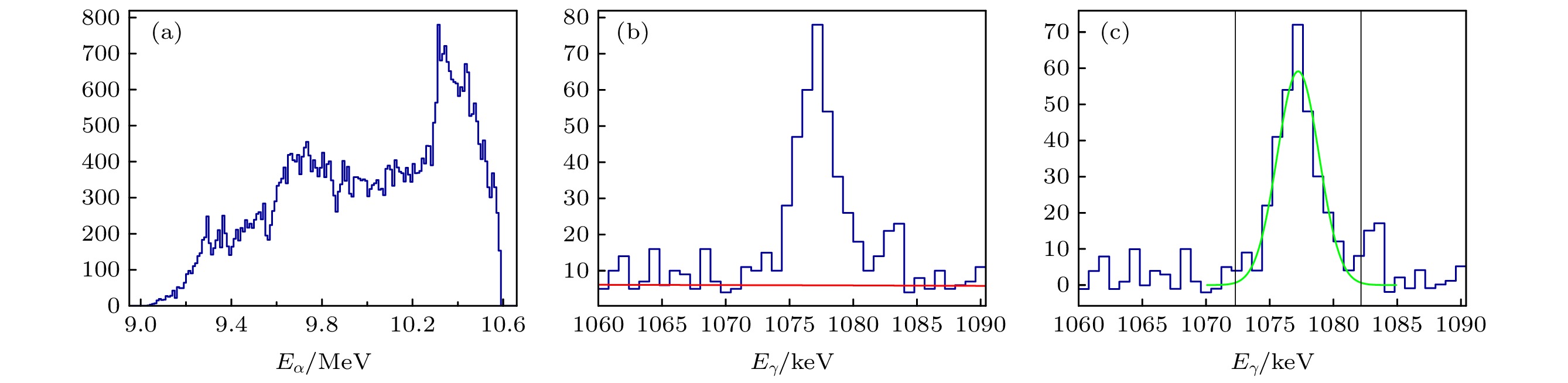
图12为实验所得符合γ谱. 结合统计因素, 共选取两条特征γ进行替代反应的计算, 分别为1.076 Mev和1.153 MeV. 图13(a)为选取的一个等效中子能点${E_{\text{n}}}$= (0.62±0.15) MeV时对应的α粒子计数, 对应(4)式中的$ {N_{\text{δ }}}{\varepsilon _{{\chi}}} $, 图13(b)为对应中子能量范围的符合γ能谱中1.076 MeV γ峰, 红线为使用ROOT程序^[29]得到的本底, 图13(c)为扣除本底后的1.076 MeV γ峰, 绿线为对其进行高斯拟合, 以$3\sigma $范围作为特征峰计数, 即为图中竖线包含部分.

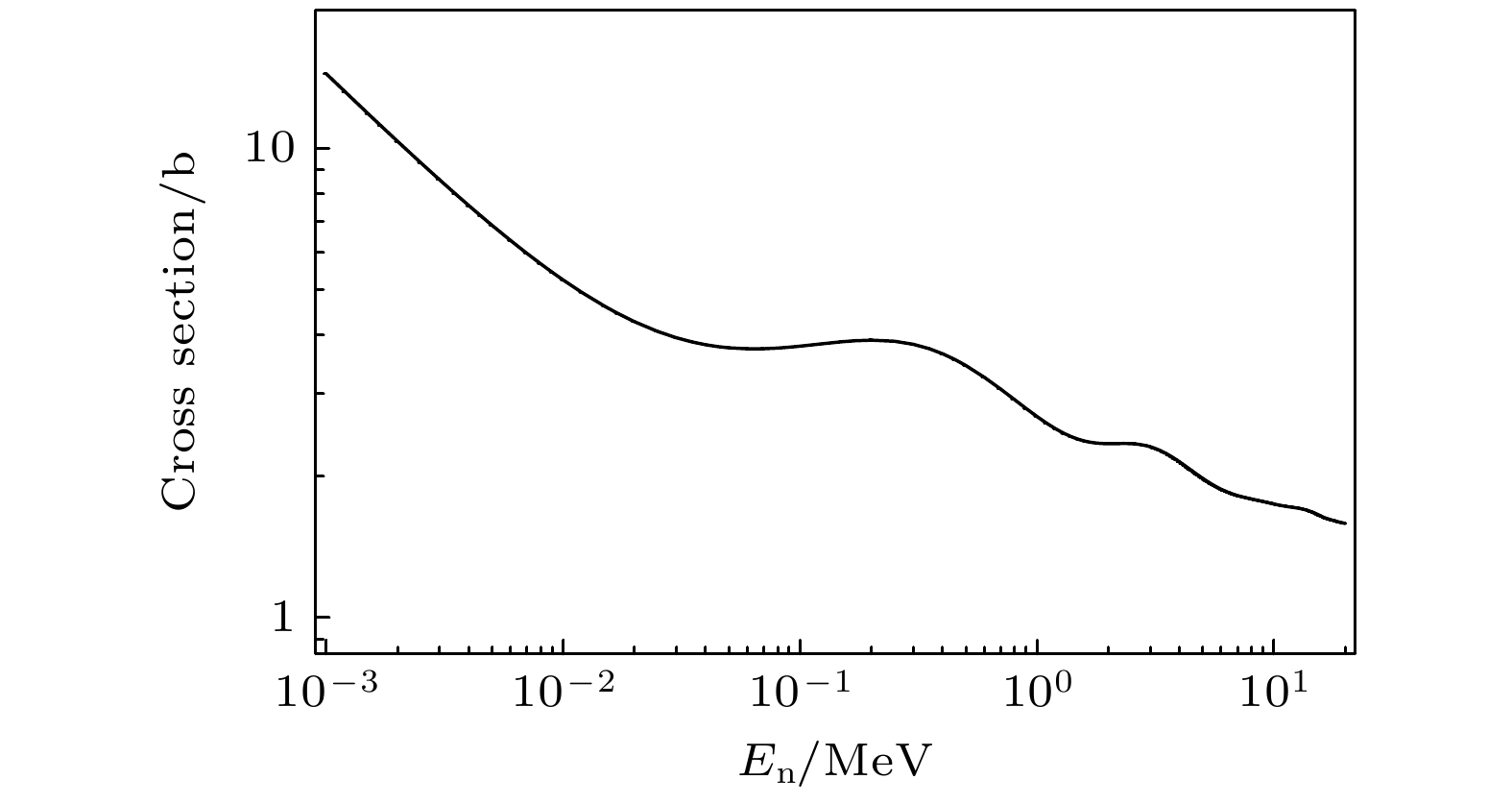
由此可以得到bin宽为0.3 MeV不同等效中子能量下的特征γ峰计数, 对应(4)式中的$ {N_{{\text{δ}}\chi}} $, 即可得到多个能点的$ {{{N_{{\text{δ}}\chi}}} {/ } {{N_{\text{δ }}}{\varepsilon _{{\chi}}}}} $. 从图11得到, 在${E_{{\text{out}}}}$ < 9 MeV时, 无法出射中子, 认为复合核的衰变道仅存在出射γ, 故在这一范围内γ衰变概率可看作1, 即$P_{\text{γ }}^{{\text{exp}}} = 1$, 此时${E_{\text{n}}}$ < –1 MeV. 将这一范围内的点按统计进行加权平均, 再将所有点以该平均值作归一化, 即可获得不同特征γ的$P_{\text{γ }}^{{\text{exp}}}$随中子能量的变化曲线. 根据不同特征γ的统计进行加权, 获得$P_{\text{γ }}^{{\text{exp}}}$, 如图14所示.

利用基于唯象光学模型的UNF程序^[30]可以计算复合核形成截面. 在UNF程序中, 涉及中子、变化粒子和γ射线引起的反应. 在整个反应过程中考虑了角动量守恒和宇称守恒. 复合核形成截面与中子能量的关系如图15所示.

实验误差主要来源于以下几方面: UNF 程序计算复合核形成截面的误差主要源于统计模型近似与输入参数不确定性. 误差约在10%; 对于直接反应((p, α)), TALYS 的 DWBA(扭曲波玻恩近似)近似可描述前冲角分布特征, 与实验数据的前向峰值位置一致性较好(误差< 10°), 但微分截面绝对值因光学势参数的适用性存在约20%不确定度; ROOT程序中扣除本底误差的主要来源本底模型的适用性和拟合参数的统计不确定性, 计算得到约为3%.

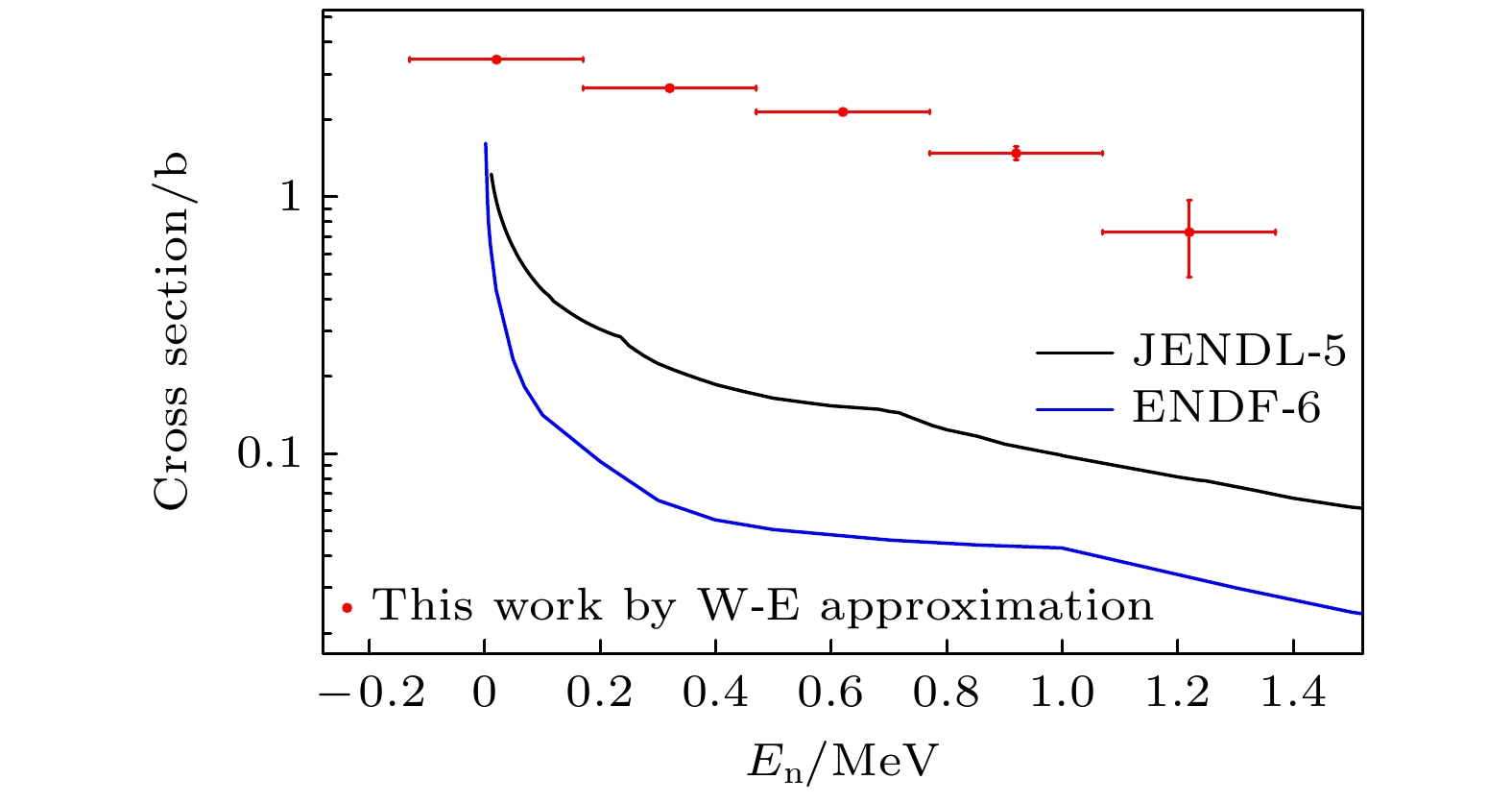
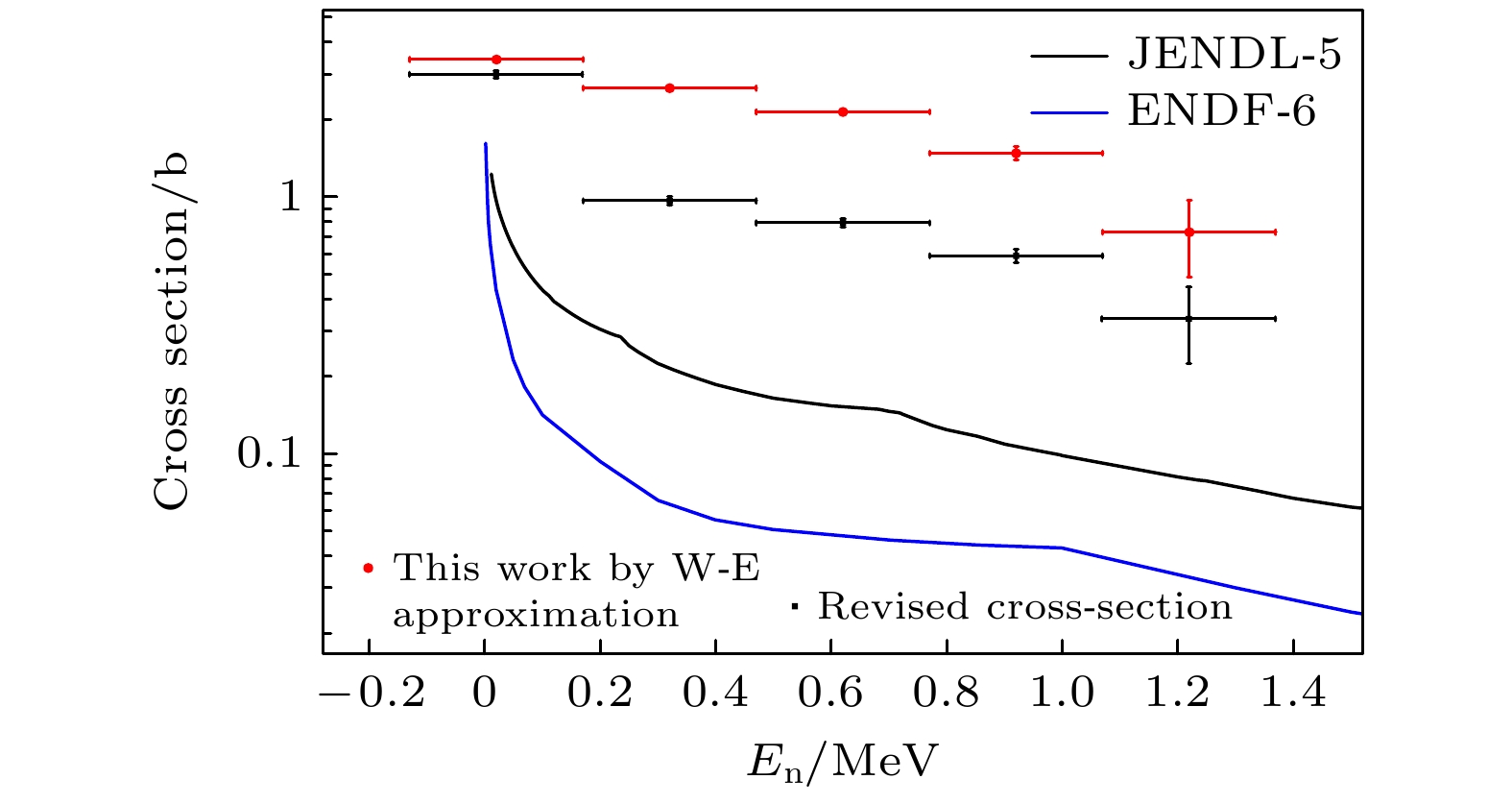
由此, 通过实验与理论计算分别得到了复合核衰变概率$P_{\text{γ }}^{{\text{exp}}}$与复合核形成截面$ \sigma _{{\alpha}}^{{\text{CN}}} $, 根据(8)式即可计算得到⁸⁵Sr(n, γ)反应截面, 如图16所示. 与现有评价数据库JENDL-5和ENDF-6的数据进行对比, 发现约有一个数量级的差别.

Weisskopf-Ewing近似假设复合核的衰变概率与角动量和宇称无关, 即分支比$ G_{{\chi}}^{{\text{CN}}} $不依赖于Jπ. 这在高能区成立, 因为此时复合核的能级密度足够高, 各种角动量和宇称的态都有贡献, 导致分支比趋于平均. 但在低能区, Forssén等^[31]利用替代反应确定⁹¹Zr(n, γ)截面时发现, 对于低能中子俘获反应(如⁹¹Zr(n, γ))中, 中子携带的角动量极少(主要为s波和p波), 而替代反应(如⁹²Zr(α, α′))产生的复合核角动量分布更宽. 此时, γ衰变分支比$ G_{{\chi}}^{{\text{CN}}} $对Jπ的依赖性极强, 而 W-E近似假设$ G_{{\chi}}^{{\text{CN}}} $与Jπ无关, 导致结果不够可靠. 此外, 低能区复合核仅能通过少数通道衰变(如中子发射或γ衰变). 中子传输系数(如s/p波共振)与γ传输系数的竞争使分支比高度依赖具体量子态. 例如, ⁹²Zr中某些Jπ态的γ衰变概率接近1, 而其他态低至10^–3, 与近似假设矛盾. 侧面说明W-E近似在低能区失效.

由于⁸⁶Sr*的γ衰变概率对Jπ敏感, 需要使用模拟计算将得到的(n, γ)截面进行修正^[32]:

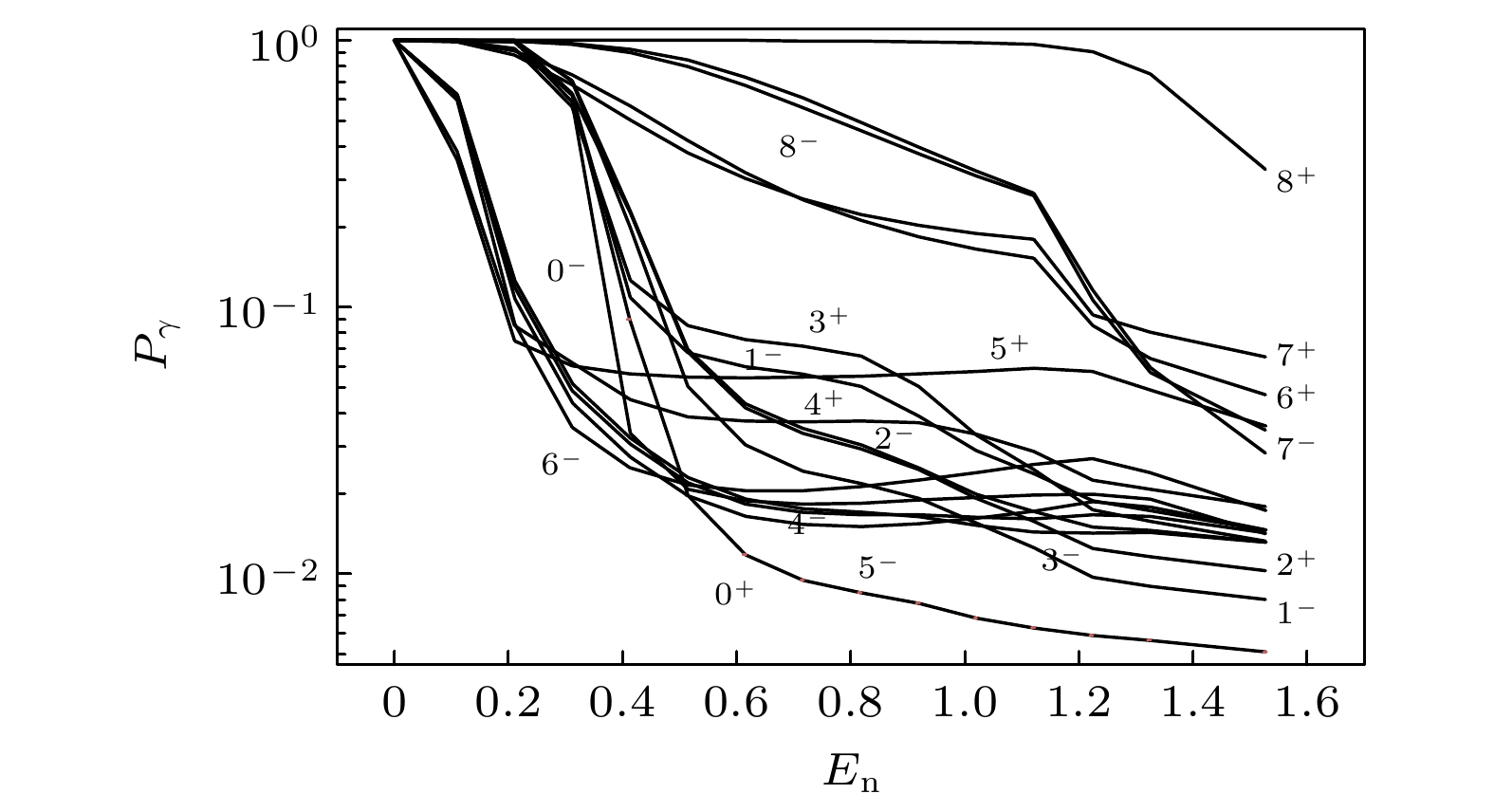
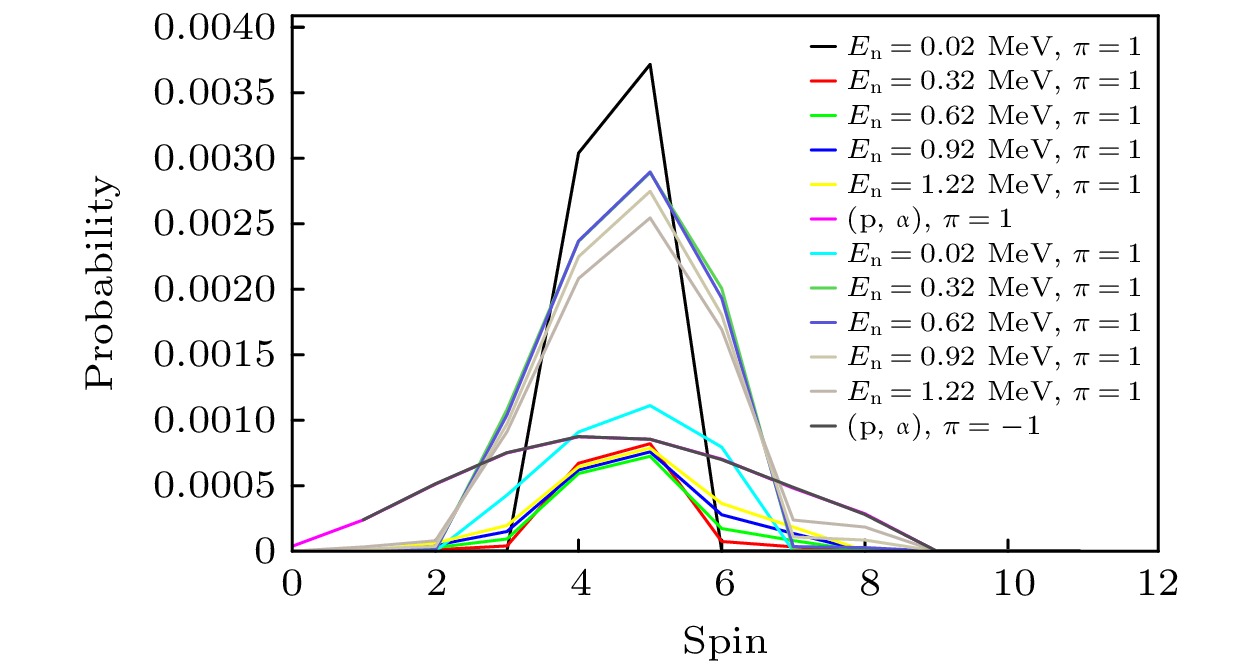
图17为通过 TALYS 计算得到⁸⁶Sr*各自旋/宇称态的γ道衰变概率随等效中子能量的变化关系. 图中明显体现了γ道衰变概率对复合核Jπ量子数的依赖性. γ衰变概率在E_n = 0 MeV以上出现的明显下降, 是由于与发射中子道的竞争所致, 仅在自旋值较低时才被观察到. 图18为直接反应与替代反应形成复合核的Jπ布居差异, 其中⁸⁶Sr*在直接反应中的Jπ布居情况主要由4^–, 5^–, 6^– 和 4⁺, 5⁺态主导, 而替代反应的自旋分布的宽度约为直接反应自旋分布宽度的两倍, 从而存在较多的布居于J = 0, 1或J > 6的态的核, 对于此类复合核, 与J = 4—6的复合核不同, 它们通过γ衰变的概率随等效中子能量下降要慢, 特别是高自旋复合核的下降速度要慢得多. 这显示在此复合核体系中W-E近似失效, 部分原因可归因于高自旋复合核内的离心势垒以及低自旋复合核角动量与发射中子轨道角动量的不匹配.

$ P_{\left( {{\text{n}}, \gamma } \right)}^{{\text{cal}}} $的计算通过将单个的$P_{\text{γ }}^{}\left( {J, {\pi}} \right)$以图18中所示的Jπ布居概率进行加权并求和而得到. 因此, 可通过单个的$P_{\text{γ }}^{}$分布, 以了解影响该区域中$ P_{\left( {{\text{n}}, \gamma } \right)}^{{\text{cal}}} $的因素. 由(15)式可得到修正后⁸⁵Sr(n, γ)反应的截面, 如图19所示. 修正的截面结果表明, 在E_n = 0.02—1.22 MeV范围内, 加入Jπ布居修正对⁸⁵Sr中子俘获的影响最大可达36%. 大部分实验点统计误差为3%—5%, 由于γ的统计随等效中子能量升高而变差, 在E_n = 1.22 MeV处, 误差为30%.

对于短寿命核的中子俘获反应截面测量, 替代反应法巧妙绕开难点, 借替代反应降低实验难度, 虽然其精度受理论假设影响, 但对制靶要求及辐射防护难度较低. 直接测量法虽理想条件下精度高、可直取关键参数, 却因短寿命核靶的制备和辐射防护存在困难; 理论计算方法基于物理模型推导、无需实操, 却因系统复杂、模型简化易致偏差且需调参; Oslo方法靠精准测粒子能谱与角分布、结合理论模型获取信息, 对设备精度要求很高, 多用于中低能核反应研究, 需专门理论框架与算法分析数据. 经与这些方法对比, 体现了替代反应法的独特优势.

本文通过实验研究了替代反应法测量⁸⁵Sr (n, γ)中子俘获反应截面, 解决了直接测量的困难. 得到的俘获截面与JENDL-5与ENDF-6无实验数据的编评结果具有相同的趋势, 体现了替代法结果的合理性. 由于γ衰变概率对复合核的自旋和宇称有较强的依赖性以及W-E近似在本实验核反应体系内的局限性^[33–36], 实验结果存在替代反应与直接反应的复合核Jπ布居的不匹配, 需要对此种不匹配进行补偿, 进而对结果进行修正. 为了获得相对可靠的结果, 使用了TALYS计算的Jπ布居对实验数据(n, γ)截面进行修正.

为了更加细致准确地解决角动量宇称错配的问题, 需要通过理论建模方法进行进一步的修正, 特别是考虑自旋、宇称和激发能对替代反应复合核的形成和衰变过程的依赖^[16], 以及标准Hauser-Feshbach理论^[37]中潜在的宽度波动. 这一领域的进展将有助于更全面地了解核反应机制, 并建立一种可靠的间接方法来获得难以直接测量的截面.