随着空间激光通信、空间对地遥感和空间天文观测等类太空活动的日益频繁, 航天器对指向精度和稳定度的要求越来越高^[1]. 微振动是航天器指向精度和稳定度的重要制约因素之一, 其具有频带宽、幅值小、难控制的特点^[2]. 尤其是对于遥感卫星、空间望远镜、激光通信等需要高指向精度和稳定度的航天器, 微振动会对其指向性能产生较大的影响. 例如, 遥感卫星的微振动是由运动部件(制冷机、飞轮、控制力矩陀螺等)引起的, 它能激发卫星复合材料板、蜂窝板等结构的振动, 并传递至遥感器安装部位, 进而影响遥感器的成像质量. 遥感卫星的摄像机在无微振动干扰时的聚焦精度为5 μm, 而在受到微振动干扰后, 其聚焦精度超过14.97 μm, 从而导致拍摄的图像变得模糊^[3–5].

为了降低微振动对航天器的影响, 目前常用的方法^[6]包括主动振动控制、被动隔振、主被动混合控制等. 其中, 主动控制和主被动混合控制因结构复杂、需要外部能量输入以及对结构可靠性和控制算法要求高等原因, 导致其工程应用时的成本较高^[7]. 被动隔振因具有结构简单、无能耗、稳定性高的特点, 是航天器低频隔振的重要方法之一, 尤其是近年来发展迅速的准零刚度隔振技术. Molyneux^[8]提出的三弹簧结构是一种经典的准零刚度隔振结构, 它由一个垂直弹簧和两个斜弹簧组成. 其中, 垂直方向的弹簧主要用于承载, 提供较高的静态 刚度; 两个斜弹簧的作用主要是在一定范围内提供负刚度, 抵消垂向弹簧的正刚度, 使得系统的动刚度为零, 从而大幅降低系统的隔振频率^[9]. 张月英^[10]通过传递率实验对比研究了三弹簧准零刚度结构与经典线性结构的隔振性能. 结果表明, 线性结构的隔振起始频率为4.2 Hz, 三弹簧准零刚度结构的隔振起始频率仅为0.5 Hz. 由于三弹簧结构的准零刚度范围十分有限, 因此其在较强的激励条件下, 隔振起始频率会迅速提升^[11]. Zhou等^[12]提出一种具有凸轮-滚子-弹簧机制的准零刚度隔振器, 实验结果表明该准零刚度隔振系统的起始隔振频率为3 Hz, 而其对应的线性隔振系统的起始隔振频率则为5.53 Hz, 这表明准零刚度系统能够有效降低隔振频率, 具有良好的低频隔振性能.

为了进一步拓宽准零刚度范围, 降低起始隔振频率, 研究者们提出了一系列拓宽准零刚度范围的方法. Kovacic等^[11]将结构非线性和预压缩引入三弹簧准零刚度系统的斜弹簧中, 理论研究结果表明这种方法能够大幅拓宽准零刚度范围. Zhao等^[13]将三弹簧准零刚度系统的斜弹簧数量由两个增至四个, 理论研究表明当系统等效刚度小于竖直弹簧刚度的1/2时, 其准零刚度范围约为经典双斜弹簧系统的两倍. Deng等^[14]提出了多层三弹簧准零刚度结构, 理论分析表明, 当系统总的等效刚度低于10 N/m时, 12层三弹簧结构的准零刚度范围约为单层三弹簧结构的2.5倍. Liu等^[15]发现通过在负刚度弹簧与质量块之间增加可调非线性惯性元件, 可以有效抑制准零刚度的硬化现象, 从而提高强激励条件下的隔振性能. 郝志峰^[16]在准零刚度结构中引入分段阻尼, 该方法不仅能够降低起始隔振频率, 同时也提高了高频隔振性能. 阮子悦^[17]提出了基于移动凸轮机构的连续变阻尼准零刚度隔振系统, 能够同时提高高频与低频的隔振性能. Yan等^[18]在准零刚度隔振器中引入了杠杆结构和涡流阻尼器, 实验结果表明调整杠杆结构和涡流阻尼器参数能降低起始隔振频率.

在斜弹簧准零刚度系统的基础上, 学者们也提出了不同构型的准零刚度结构. 例如, Liu等^[19]使用屈曲梁代替原有的斜弹簧, 避免了弹簧受压发生轴向屈曲的问题. Wang等^[20]采用两个三弹簧结构代替原有的负刚度元件进一步降低了隔振的起始频率, 结果显示在激励较小时, 传统准零刚度隔振系统的起始隔振频率为线性系统的20.56%, 而双准零刚度隔振结构起始隔振频率仅为线性系统的9.88%. Wu等^[21]采用磁铁替换了经典三弹簧准零刚度系统中的斜弹簧, 通过调节相斥磁铁之间的距离, 也可以实现准零刚度. 安隽翰^[22]则使用4组气缸构造了准零刚度隔振系统, 可以通过调节气缸的等效刚度, 实现不同负载条件下的准零刚度隔振, 是一种可调的准零刚度隔振系统.

近年来, 许多研究者提出了多种仿生准零刚 度结构, 也具有很好的低频隔振性能^[23]. 例如, Wu 等^[24]模仿鸟类脚部骨架的形状结构, 提出了一种仿鸟类肢体的X形低频隔振结构. 实验结果表明, 该结构的共振频率仅为1.32 Hz, 相较于传统线性隔振器降低了4.39 Hz. Yan等^[25]受到猫身骨架的启发, 提出了一种具有多边形骨架的准零刚度结构, 实验表明该仿生结构的隔振起始频率为3 Hz. Shi等^[26]从山羊的后肢得到灵感设计了一种仿生的准零刚度结构, 实验表明该结构能够有效抑制3.2 Hz以上的振动. Zeng等^[27]受青蛙肢体构型启发提出带扭簧的多连杆机构, 相较于线性隔振器和传统的三弹簧结构, 该结构具有更低的起始隔振频率和更快的振动衰减速度. Yan等^[28]提出了一种仿动物脚趾的准零刚度结构, 其在6 mm的大位移激励下依然能够对3 Hz以上的振动进行有效隔离. Jin等^[29]提出了一种仿人类脊柱的准零隔振器, 结果表明, 通过增加准零刚度单元的层数可以显著降低整个系统的隔振起始频率. 除了鸟类、猫、青蛙等动物具有良好的稳定性之外, 许多节肢动物在大幅低频载荷下也具有良好的稳定性. 例如, Ling等^[30]提出了一种仿甲虫准零刚度结构, 实验发现该仿生结构的共振频率仅为1.7 Hz, 具有优异的低频隔振性能. 除此之外, 当蛛网在风载作用下出现大幅低频晃动时, 蜘蛛身体却不会出现大幅的晃动; 螳螂在摇晃的树叶上能够保持身体相对静止, 从而提升捕食成功率. Long等^[31]研究发现蜘蛛在一段时间内被振动刺激后仍然可以准确跟踪和食用猎物. 观察发现, 螳螂、蜘蛛等节肢动物的腿部形状较为类似, 都呈现出一种M形结构.

受此启发, 本文提出了一种仿节肢动物腿部的M形仿生结构, 并对其动力学机理开展了研究. 具体研究内容包括: 第2节给出M形结构的设 计方法及其动力学模型; 第3节对其等效刚度、准零刚度范围等静态特性开展对比分析; 第4节运用谐波平衡法进行近似求解, 并通过数值仿真进行有效性验证, 并且研究该非线性系统的动力学响 应特性. 将其与经典三弹簧准零刚度结构进行对比, 研究其传递率特性以及激励幅值的影响规律; 第5节分析几何形状对M形仿生结构隔振性能的影响规律.

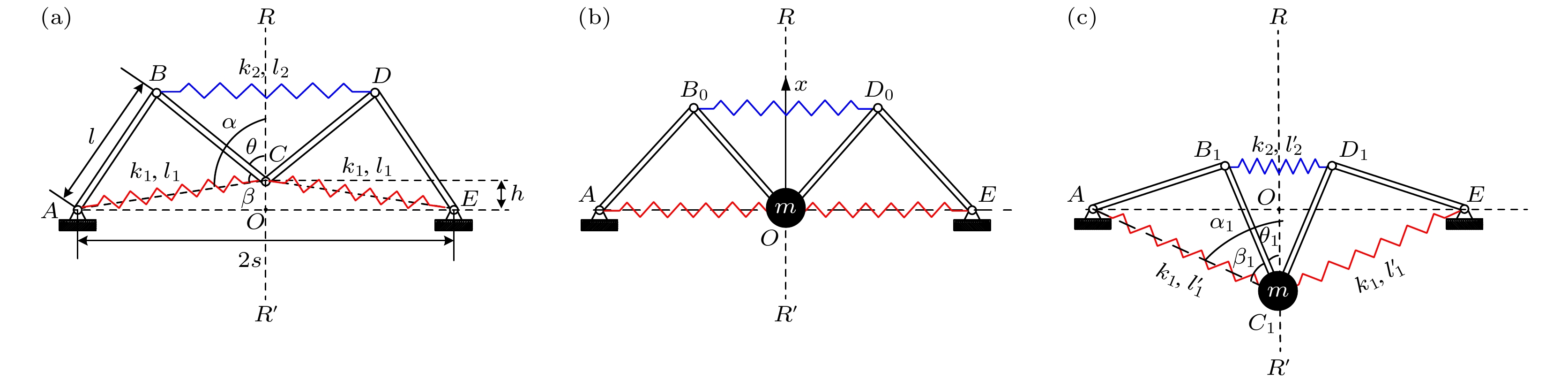
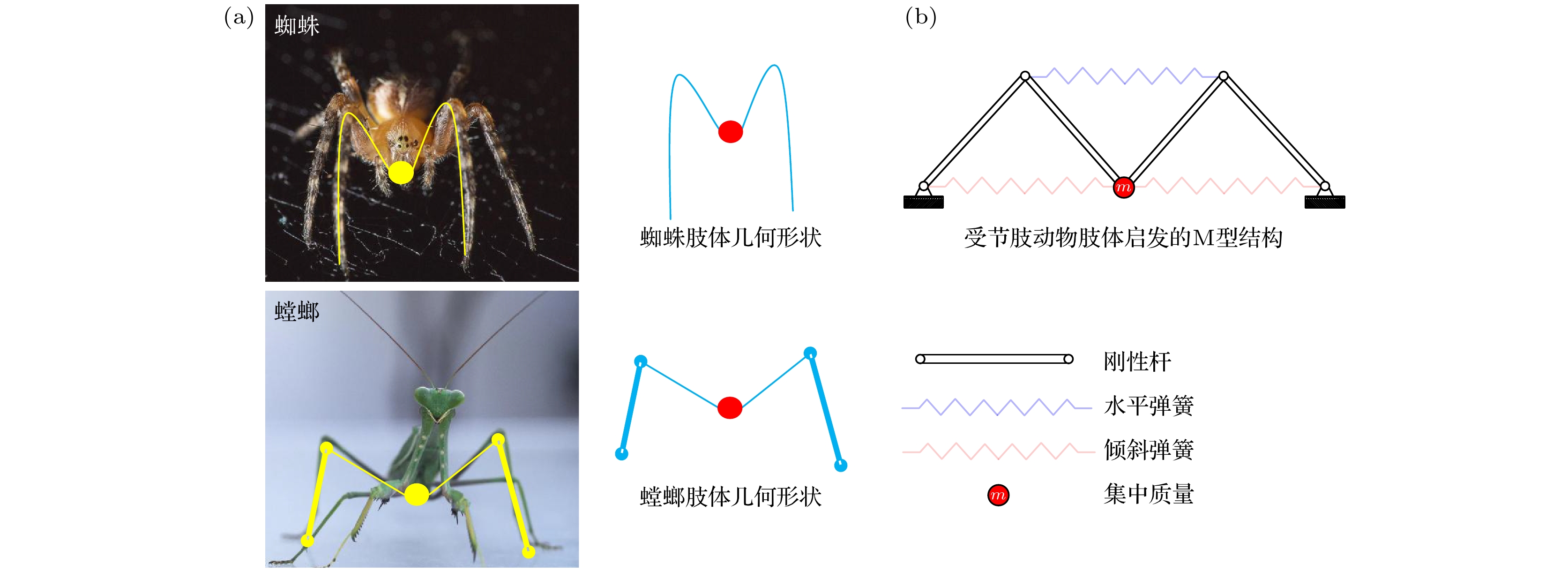
节肢动物通常是由多组节肢共同支撑着身体, 并使其保持稳定. 图1(a)所示为蜘蛛和螳螂等自然界中常见的节肢动物. 观察发现, 它们肢体的形状都类似于字母“M”. 由于这种特殊的构造, 才能使得它们在复杂多变的环境载荷下仍然能够保持身体的稳定. 受蜘蛛和螳螂等节肢动物腿部构造的启发, 本文提出了一种仿生M形结构, 如图1(b)所示. 该结构由3种元件共同组成, 分别是细长的刚性杆、等效集中质量和弹簧. 其中, 细长的刚性杆模拟的是蜘蛛的腿部结构, 其两端与基础铰接, 中间与集中质量m相连, 形成了M形结构. 为了便于分析, 这里将蜘蛛的身体近似为等效集中质量m, 不考虑其尺寸影响. 3个弹簧中, 位于上面的水平弹簧模拟的是蜘蛛的背部肌肉, 位于下面的弹簧(与基础相连)模拟的是腿部肌肉. 值得注意的是, 真实的蜘蛛肌肉远比图1(b)中的等效弹簧要复杂得多. 整个系统受到来自基础的垂向激励, 模拟的是蜘蛛在蛛网上受到的基础载荷. 在实际应用中, 被隔振的物体位于集中质量m处, 低频振动来源于基础.

为了研究所提出的仿生M形结构的动力学特性, 首先需要建立其动力学模型. 图2(a)为M形结构的几何模型, 它关于对称轴RR'左右对称, 并由4根刚杆, 两个倾斜弹簧AC, EC, 一个水平弹簧BD共同组成. 其中, 4根杆为刚体, 3个弹簧为线性弹簧. A和E为结构与基础的铰接点, O为AE的中点, OA与OE的长度为s. 4根杆的材料相同, 横截面积相同, 长度均为l, 杆之间连接方式为铰接, 铰接点分别为B, C, D. 杆与基础的连接方式也为铰接, 铰接点为A, E. 两倾斜弹簧原长均为l₁, 倾斜弹簧一端连接基础另一端连接BC, DC两杆的铰接点C. 水平弹簧两端连接B, D两点, 长度为l₂. 集中质量为m. α为倾斜弹簧AC与对称轴RR' 之间的夹角, β为杆BC与倾斜弹簧AC之间的夹角, θ为杆BC与对称轴RR' 之间的夹角. 图2(a)是没有集中质量时, M形结构的初始状态, 对应的弹簧长度也是弹簧的原长; 图2(b)是增大集中质量m之后, 整个M形结构静止时的平衡状态, 此时两个斜弹簧恰好处于水平状态; 图2(c)是在基础激励作用下, 整个系统某一时刻的运动状态. 从图中不难发现, 位于下方的两个斜弹簧与经典的三弹簧准零刚度系统中的两个斜弹簧是一样的, 在一定位移范围内均具有负刚度特性. 因此, 该仿生M形结构是否具有低频隔振能力, 主要取决于M形结构的几何特征和水平斜弹簧刚度.

定义坐标y为质量块在竖直方向的位移, 坐标z为基础在竖直方向的位移, 正方向均为向上, 集中质量相对于基础的位移可以表示为 x = y – z.

当质量块出现相对位移x时, 倾斜弹簧和水平弹簧的长度分别变为$ l_1' $和$ l_2' $, 如图2(c)所示. 根据几何关系, 可得

其中, 水平弹簧变形后的长度$ l_2' $可以表示为

根据积化和差公式可知:

根据M形结构的几何关系, 满足:

将(4)式代入(3)式, 可得

将(5)式代入(2)式, 可得

由此, 得到斜弹簧的变形量Δ₁和水平弹簧的变形量Δ₂:

此外, 弹簧的原长满足几何关系:

式中, 可以采用拉格朗日方程建立系统的动力学方程. 系统的拉格朗日方程为

其中, T, U和D分别是系统的动能、势能和阻尼耗散力做功.

不考虑细杆的质量与转动惯量, 系统的动能只包含集中质量的动能, 即

其中, z是基础位移, 上标“·”是关于时间t的导数.

系统的势能包括两个斜弹簧和一个水平弹簧的弹性势能, 以及集中质量块的重力势能, 即

将(7)式代入(11)式, 可得

系统阻尼耗散能D可表示为

其中, c为黏滞阻尼系数.

将(10)式、(12)式、(13)式代入(9)式, 可得

其中,

式中, m是隔振对象的质量, x是隔振对象对基础的相对位移, z是基础位移. 考虑简谐激励$\ddot z = A\sin \left( {\omega t} \right)$, 其中A是激励的加速度幅值, ω是激励频率, t为时间.

将系统势能对x求偏导, 可得系统的恢复力:

其中, f_Mo是斜弹簧产生的恢复力, f_Mh是水平弹簧产生的恢复力, f_g是重力.

由于系统静止时的平衡位置在零点, 因此当x = 0时, f_M = 0. 由此可得

这里, m_load是M形结构承载的集中质量, 与水平弹簧的刚度k₂和杆长l成正比.

根据(16)式, 恢复力对位移求导可得系统的等效刚度为

根据准零刚度条件, 当x = 0时, 系统的等效刚度K_M = 0. 由此, (18)式可以简化为

其中, α是准零刚度条件下斜弹簧与水平弹簧的刚度比. 由(19)式可知, α与杆长l成正比, 与h成反比. 因此, M形结构的杆长l越长, 或者M形结构中心的初始高度h越小, 均会导致α增大, 这意味着为了达到准零刚度, 斜弹簧与水平弹簧的刚度差也越来越大. 至于参数s, 其与弹簧刚度比α之间的关系则更为复杂, 并且也直接影响M形结构的形状.

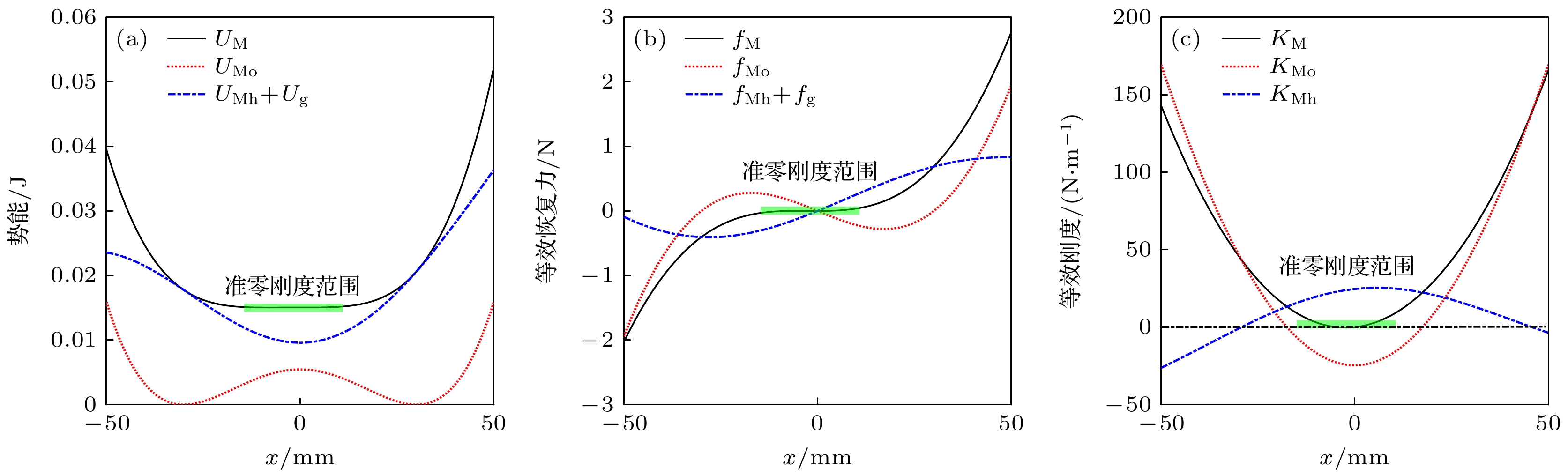
假设M形结构的参数如表1所示, 图3(a)—(c)分别给出了两种结构的势能、恢复力和等效刚度. 首先, M形结构的势能由斜弹簧的弹性势能(U_Mo)、水平弹簧的弹性势能(U_Mh)和重力势能(U_g)共同组成. 其中斜弹簧的势能是一个典型的双稳态势能, 其在x = 0 附近存在一个势能垒; 而剩余的势能则在x = 0附近形成了一个势能阱. 当势能垒的高度与势能阱的深度满足一定条件时, 系统的总势能就会在x = 0附近形成一个斜率接近于零的势能阱, 从而形成准零刚度系统. 从恢复力与等效刚度特性(图3(b), (c))上看, 在x = 0附近, 斜弹簧提供的是等效负刚度, 而M形结构的水平弹簧则提供的是等效正刚度. 将两者结合后, 系统在x = 0附近的总刚度就接近于零, 从而构成M形准零刚度结构(M-shape quasi-zero-stiffness, MQZS). 这种通过正负刚度模块达到准零刚度的方法是准零刚度结构设计的常用方法之一.

对于MQZS结构, 其主要参数包括: 负载质量m、倾斜弹簧的刚度k₁和长度l₁、水平弹簧的 刚度k₂和长度l₂、水平距离s、垂直高度h. 其结构参数确定的基本步骤如下: 首先, 根据安装环境的尺寸选择杆长l、水平距离s和垂直高度h, 其中s与l之间须满足l < 2s < 2l; 其次, 根据负载质量m和(17)式确定水平弹簧的刚度k₂; 最后, 根据(19)式确定倾斜弹簧的刚度k₁.

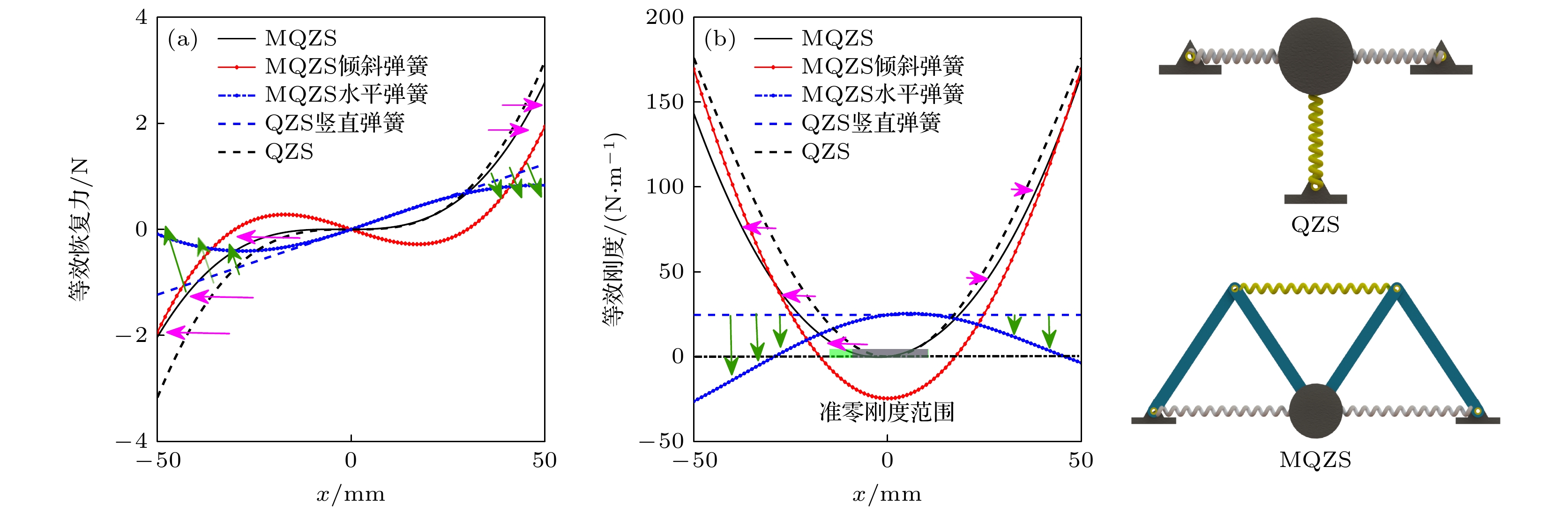
为了便于分析M形准零刚度结构的特点, 现将其与经典的三弹簧准零刚度(quasi-zero-stiffness, QZS)结构进行对比. 从结构上看, MQZS结构与经典三弹簧QZS结构均采用一对斜弹簧作为负刚度单元, 其主要区别在于三弹簧结构的正刚度是由一个垂直线性弹簧提供的线性正刚度, 而MQZS结构的正刚度则是由MQZS结构中的水平线性弹簧提供的非线性正刚度. 因此, 需要重点分析MQZS结构非线性正刚度对系统准零刚度特性的影响. 在对比分析中, 两种结构的斜弹簧是相同的, 而提供正刚度的结构则是根据相应的准零刚度条件确定参数.

图4对比了两种准零刚度结构的恢复力与等效刚度特性. 首先, 斜弹簧结构产生的负刚度, 其幅值在x = 0 mm处最大; 并且随着x距离零点越远, 负刚度幅值会迅速减小, 直至变为正刚度. 由于传统的三弹簧结构采用的正刚度弹簧是线性的, 因此整个系统虽然能够在x = 0 mm处达到零刚度, 但是随着位移幅值的增大, 系统总刚度会迅速上升, 导致其准零刚度范围是十分有限的. 从图4(b)可知, 与三弹簧系统的线性正刚度相比, MQZS结构的正刚度是非线性的, 并且随着位移的增加, 正刚度也会迅速减小. 因此, 当斜弹簧的负刚度幅值随着位移迅速增加时, MQZS结构水平弹簧产生的等效正刚度则会快速降低, 从而降低整个系统总刚度的增加速度, 达到拓宽准零刚度范围的目的. 为便于对比, 令系统等效刚度低于某一刚度阈值k_c时, 其位移范围就是系统的准零刚度范围^[11], 对应的位移宽度就是准零刚度宽度D_c. 这里, 选取刚度阈值k_c为斜弹簧刚度的1/50, 即8 N/m. 那么, 三弹簧系统的准零刚度范围是[–9.69, 9.68] mm, 准零刚度宽度为19.37 mm; 而MQZS结构的准零刚度范围是[–14.23, 9.684] mm, 准零刚度宽度为23.914 mm, 增大了23.45%. 因此, MQZS准零刚度结构具有更宽的准零刚度范围, 对降低隔振起始频率具有重要意义.

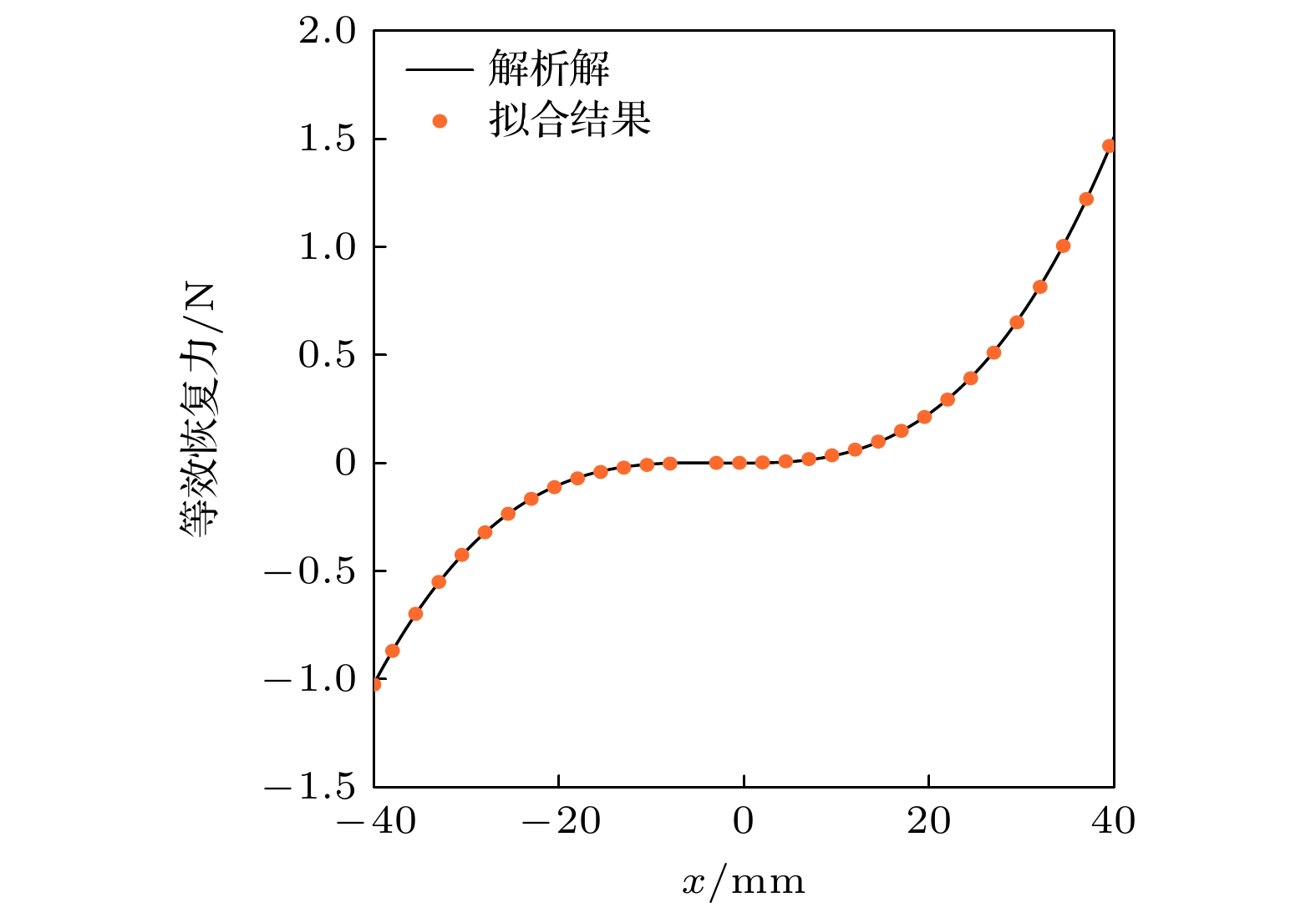
为了分析MQZS准零刚度结构的动力学特性, 本节采用谐波平衡法对其进行了近似求解. 在进行谐波平衡分析之前, 首先运用多项式拟合方法将系统运动方程中的非线性恢复力与非线性阻尼进行等效表示. 系统的恢复力可以表示为

其中, A₁, A₂, A₃均为多项式拟合系数.

将(20)式代入运动方程(14)后, 可得

图5对比了拟合结果与精确解(结构参数见表1). 从图5可知, 选取三阶多项式进行拟合就可以取得较好的结果. 此时, 非线性刚度拟合系数分别是: A₁ = 0.4066, A₂ = 153.9943, A₃ = 19633, 其中, 二次项系数与三次项系数均为正. 这意味着, 一方面系统在大激励条件下将呈现出硬弹簧特性; 另一方面, 在采用谐波平衡法进行近似求解时, 需要同时考虑一次谐波和二次谐波的影响.

假设系统的响应满足:

其中, a₁(t), b₁(t), a₂(t), b₂(t)为响应系数, 为了便于开展解的稳定性分析, 这里假设其是关于时间t的一次函数.

基础位移满足:

其中, Z₀是基础位移激励的幅值.

将(22)式对时间分别求一次和两次导数, 就可以得到系统的速度与加速度, 将其与(23)式一并代入(21)式后, 进行谐波平衡, 并忽略三次及以上谐波的影响, 可得

其中,

在稳定状态, 系统响应系数q = [a₁, b₁, a₂, b₂]^T为常数, 其关于时间的导数为零. 因此, (24)式可以简化为

(26)式是一个非线性方程组, 含有4个未知数和4个方程. 通过求解, 可以得到响应系数 q = [a₁, b₁, a₂, b₂]^T的解. 将其代入(22)式可得系统的相对位移响应x.

系统的绝对位移响应为

绝对幅值为

系统传递率为系统绝对位移响应与基础位移响应之比, 即

为了对解的稳定性进行分析, 将(24)式写成矩阵的形式:

其中矩阵G与F(q)的具体结果在附录A中.

(30)式可以转换成状态方程的形式:

其中, $\boldsymbol P = \boldsymbol G^{-1} \boldsymbol F(\boldsymbol q) $. 解的稳定性取决于P(q)的雅可比矩阵. 将(26)式计算得到的解代入P(q)的雅可比矩阵, 如其行列式小于零, 则是稳定解; 如行列式大于零, 则是不稳定解.

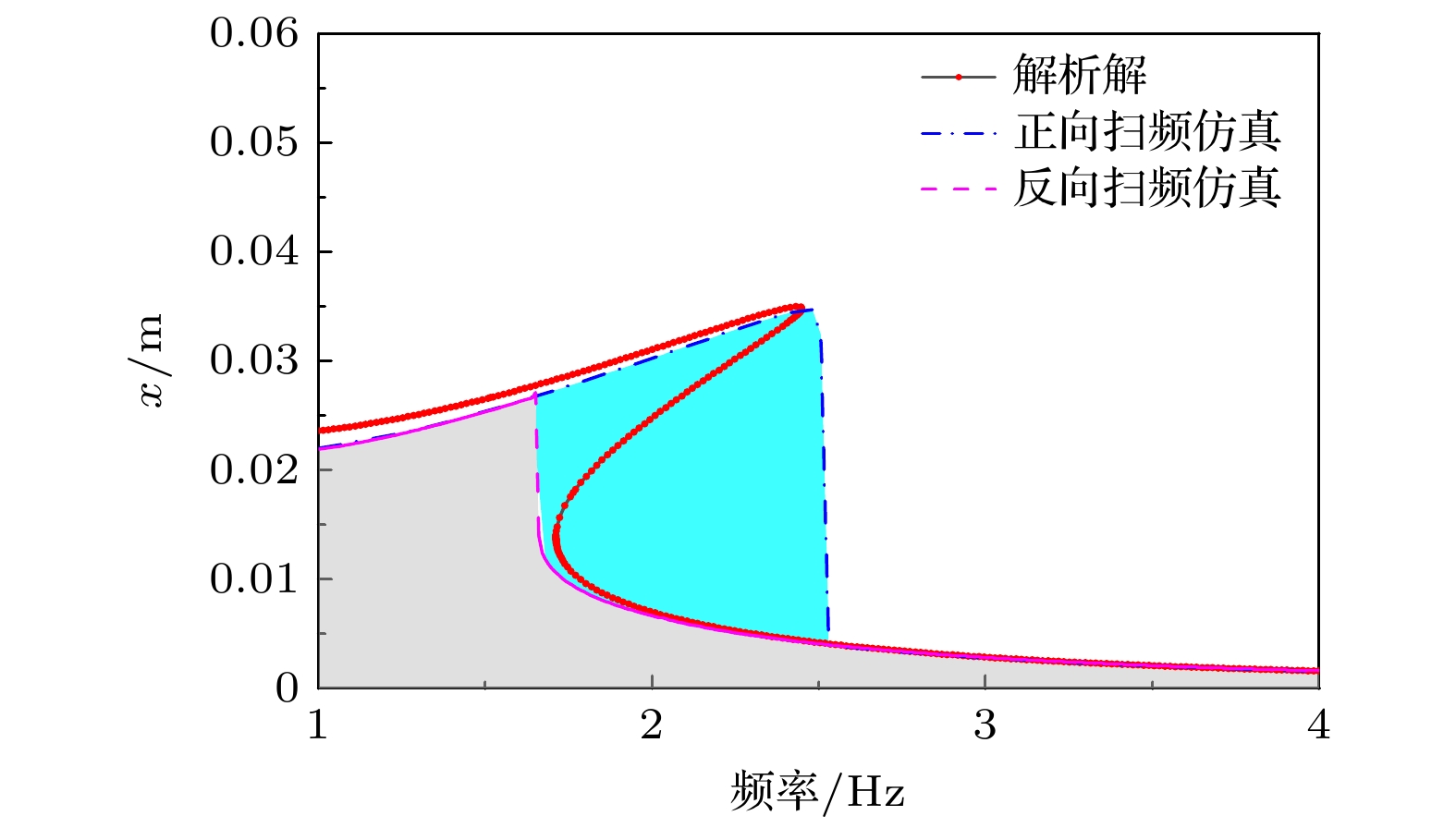
为了验证近似解的精确性, 现通过数值仿真对其进行验证. 选择四阶龙格库塔法对系统运动方程进行数值求解, 开展正向扫频和反向扫频仿真. 其中, 基础激励A = 1.0 m/s², 扫频方式为线性, 扫频频带为1—4 Hz, 扫频速度均为0.005 Hz/s, 系统结构参数如表1所示. 图6对比了近似解析解与数值仿真结果. 从频率幅值曲线上看, 近似解与仿真结果也是符合的, 具有较好的预测精度, 因此可以用于开展后续的分析.

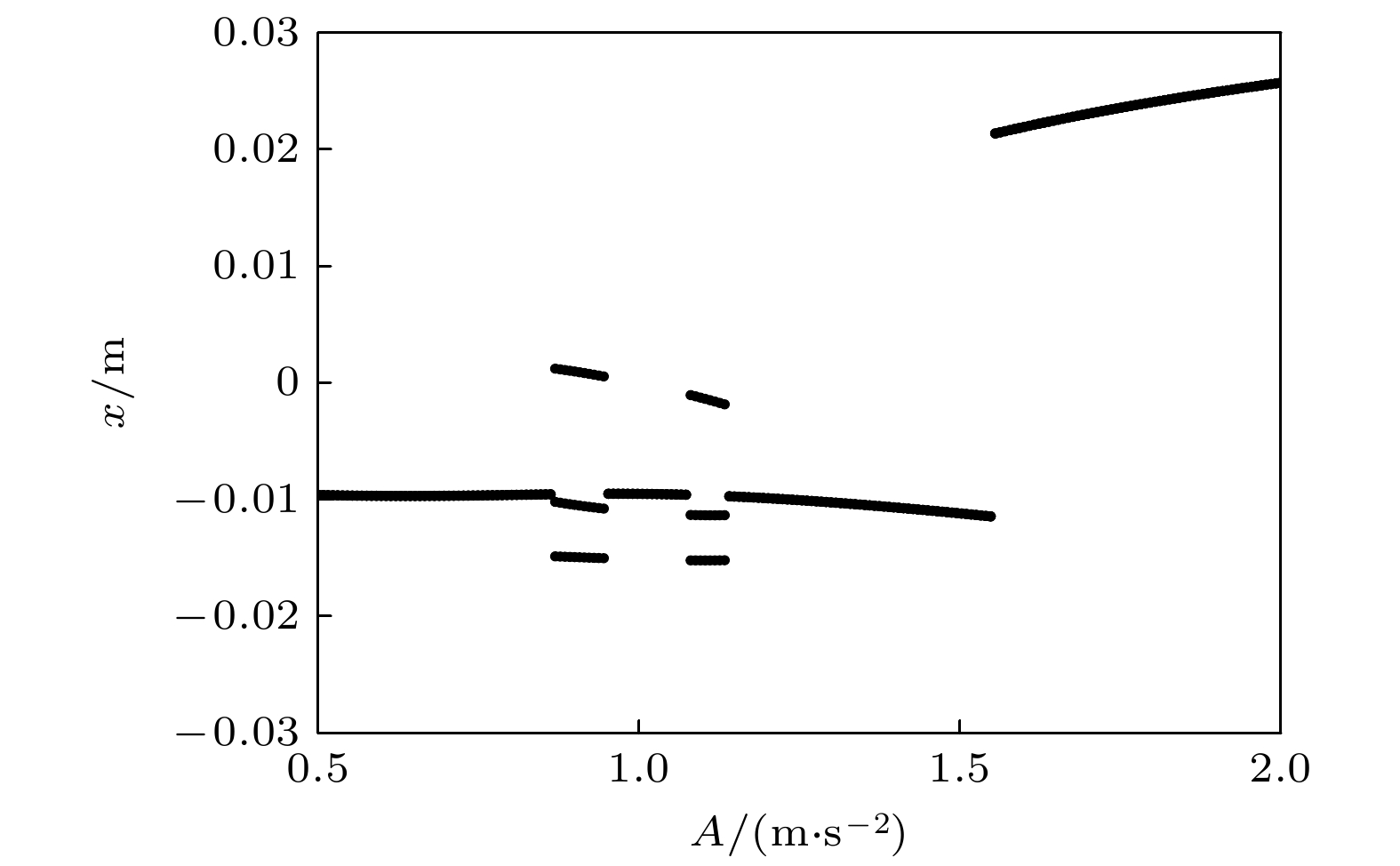
为了研究M形仿生结构的动态响应特性, 现对其参数分叉特性进行研究. 从图6可知, 当激励频率为2.2 Hz时, 系统存在多个稳定解, 系统的响应特性十分丰富. 为此, 选择激励频率2.2 Hz, 将激励幅值从A = 0.5 m/s²逐渐增至A = 2.0 m/s², 得到系统的激励幅值分岔图(图7).

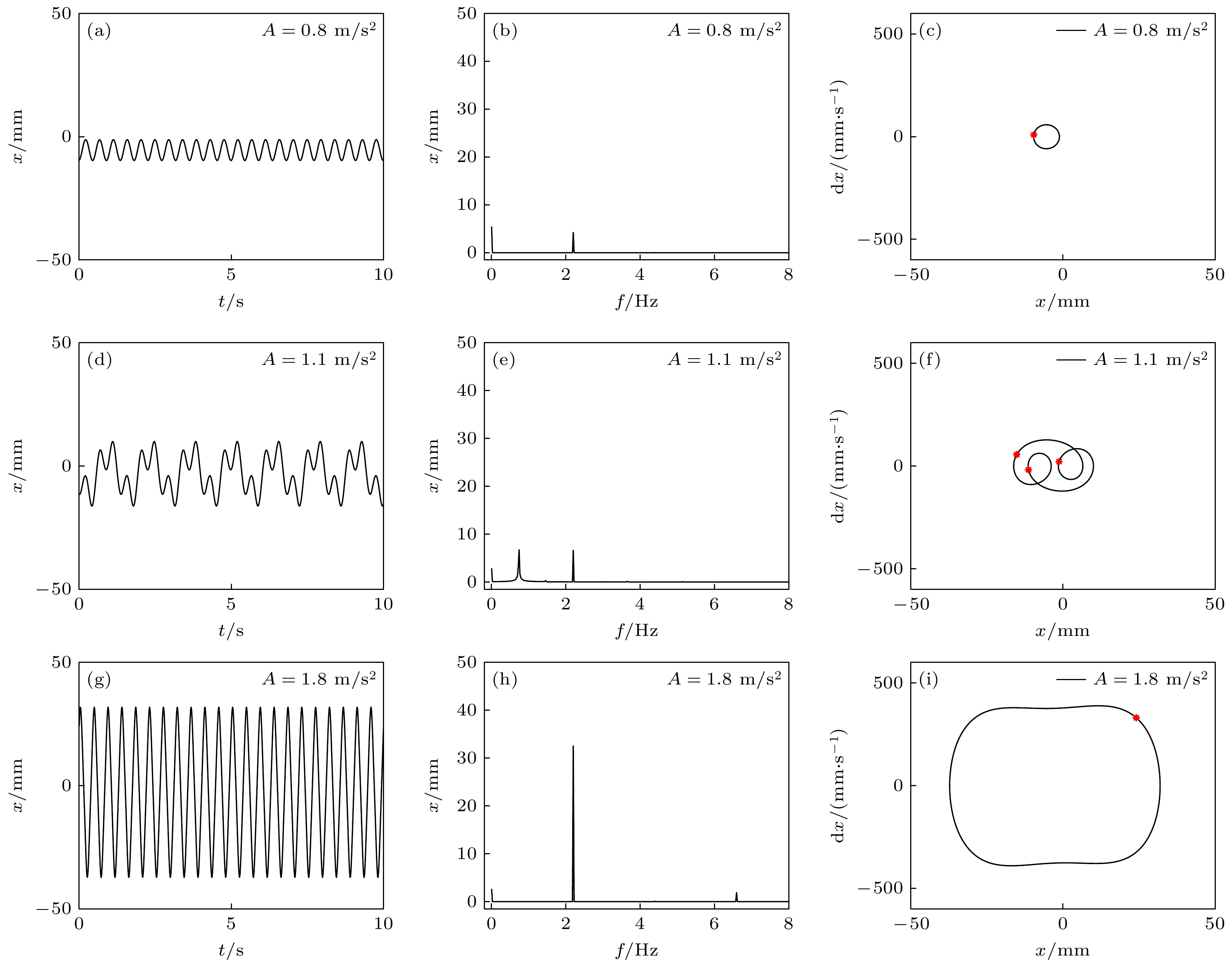
为了研究不同运动的响应特性, 选择了3个不同的激励幅值(A = 0.8 m/s², 1.1 m/s²以及1.8 m/s²)进行数值仿真. 图8为3种激励条件下的时域图、频域图、相图及庞加莱截面等. 当激励幅值A = 0.8 m/s²时, 系统处于小振幅周期一运动, 其响应主要频率分量为2.2 Hz, 此时系统结构非线性的影响很小; 当激励幅值增至A = 1.1 m/s²时, 系统从周期一运动演变成了周期三运动, 其响应幅值明显增大, 并且主要频率分量为2.2 Hz和0.733 Hz (1/3倍频), 此时结构非线性的影响十分明显; 最后, 当激励幅值增至A = 1.8 m/s²时, 系统的响应又重新回到周期一运动, 但是此时系统的响应幅值较高, 并且主要频率分量为2.2 Hz和6.6 Hz. 由此可知, 在激励幅值由A = 0.8 m/s²增至A = 1.1 m/s²时, 系统从周期一运动变为周期三运动, 发生了周期倍化分岔; 随着激励幅值的继续增大又恢复了周期一运动.

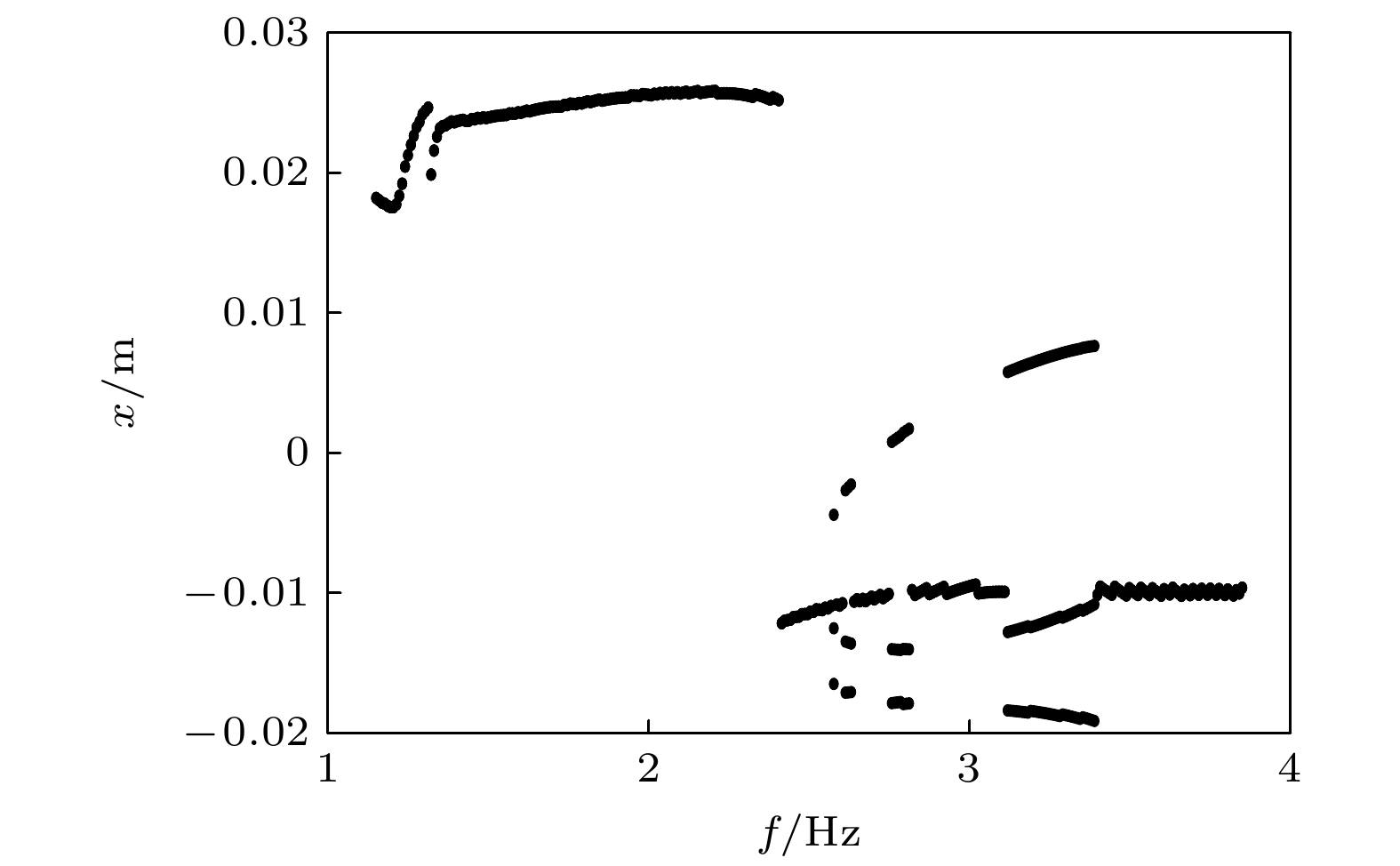
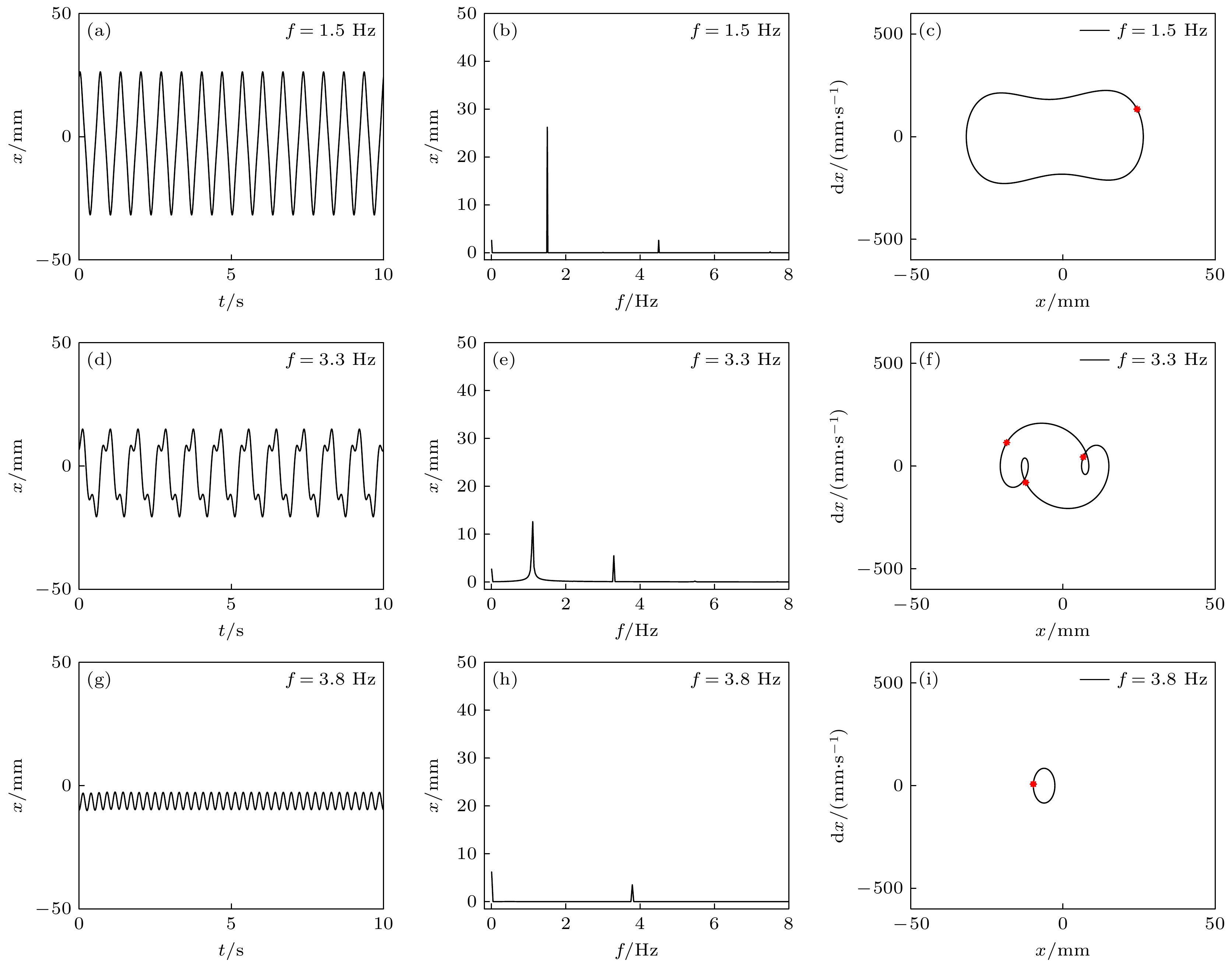
激励频率也会改变系统的动力学响应特性. 图9为频率分岔图, 其中激励幅值为A = 2 m/s², 激励频率取1.0—4.0 Hz. 从图9可知, 随着频率的增大, 系统也会出现周期一和周期三运动. 分别选择了3个频率(f = 1.5 Hz, f = 3.3 Hz, f = 3.8 Hz)进行动态响应仿真分析, 其时域、频域以及相图如图10所示. 当激励频率f = 1.5 Hz时, 系统处于大振幅周期一运动, 其响应的主要频率分量为1.5 Hz和4.5 Hz(三倍频); 而当激励频率变为f = 3.3 Hz后, 系统处于周期三运动, 此时振动幅值减小, 响应的主要频率分量为3.3 Hz和1.1 Hz (1/3倍频); 最后当激励频率为f = 3.8 Hz时, 系统处于小振幅周期一运动, 振动幅值很小, 并且响应频率主要分量为3.8 Hz. 综上可见, 随着激励频率从1.0 Hz开始增大后, 系统由单周期响应向三周期响应转变, 发生了周期倍化分岔; 而当激励频率远离系统共振区间后, 系统将以小振幅周期一运动.

为了分析仿生M形准零刚度结构的隔振性能, 现将其与经典的三弹簧准零刚度系统进行对比. 图11为基础激励A = 1.0 m/s²时, 两种结构的传递率曲线. 首先, 从零传递率点观察, 三弹簧QZS结构零传递率点对应的频率为1.82 Hz, 仿生MQZS结构零传递率对应的频率为1.72 Hz, 比前者降低了5.49%; 从峰值频率观察, 三弹簧QZS结构的响应峰值位于3.14 Hz, 仿生MQZS结构的响应峰值位于2.86 Hz, 比前者降低了8.92%; 从传递率峰值观察, 三弹簧QZS结构的最大传递率为54.07 dB, MQZS的最大传递率达到了51.66 dB, 比前者低了2.41 dB. 最后, 对比隔振频带内的振动隔离效果, MQZS结构的传递率与三弹簧QZS结构十分接近. 以f = 3 Hz为例, 三弹簧QZS结构的传递率为–49.90 dB, MQZS准零刚度的传递率为–49.94 dB. 主要原因是在低能轨道上, 系统的响应幅值很小, 受到结构非线性的影响也很小. 由此可知, MQZS相较于经典的三弹簧QZS, 其优势在于降低峰值频率和幅值、以及降低隔振起始频率; 对于在高频区域, 两者的隔振性能是接近的.

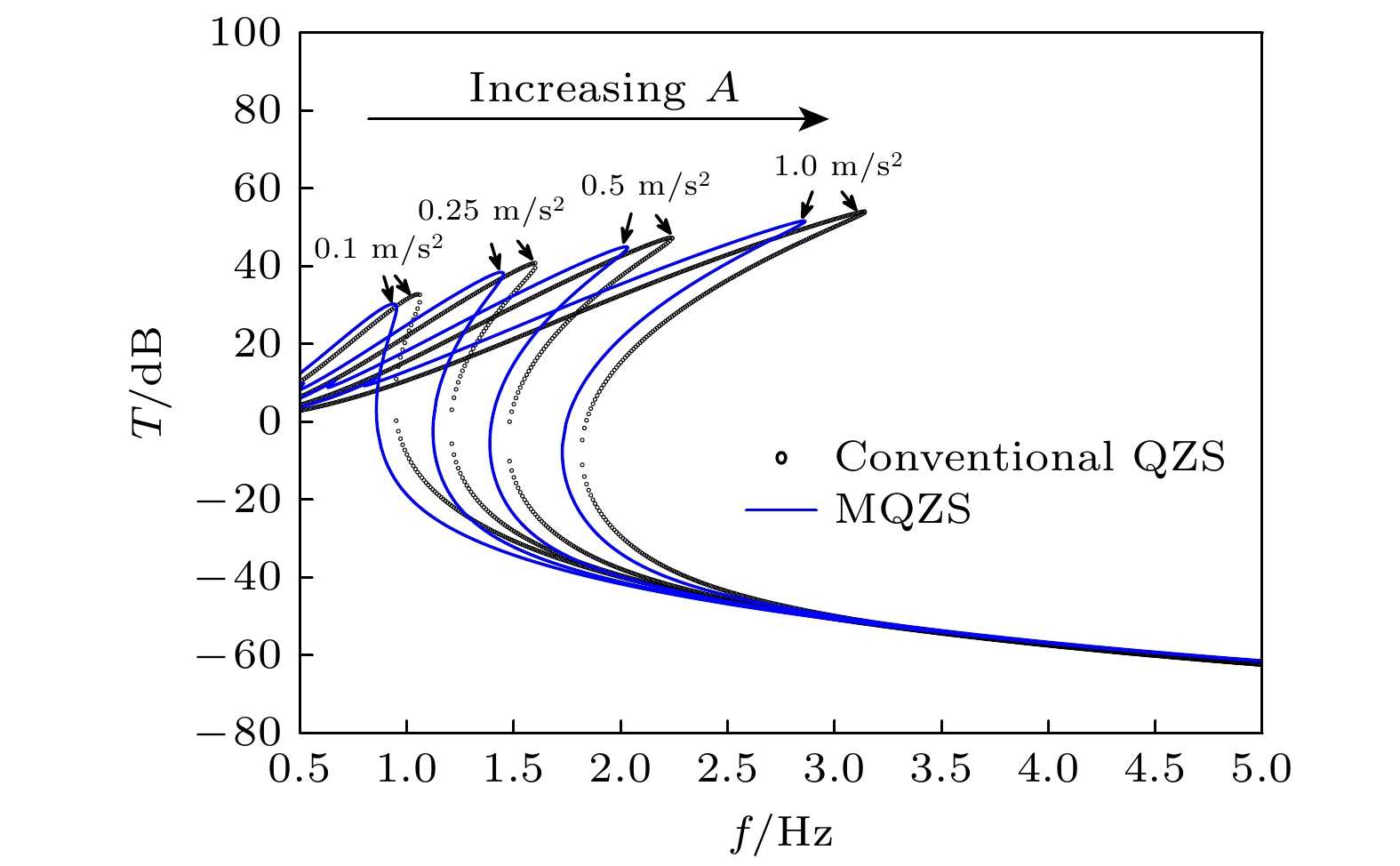
非线性低频隔振结构的隔振性能往往与激励幅值和结构阻尼密切相关. 因此, 图12对比了4种加速度激励条件(A = 0.1 m/s², A = 0.25 m/s², A = 0.5 m/s², A = 1 m/s²)下, MQZS结构和三弹簧QZS结构的传递率特性. 从整体上看, 在这4种激励条件下, 仿生MQZS结构的隔振起始频率、峰值频率和峰值响应幅值均低于三弹簧QZS结构. 具体地, 在基础加速度激励为0.1 m/s², 0.25 m/s², 0.5 m/s²和1 m/s²时, MQZS结构的零传递率频率分别为0.86, 1.12, 1.39, 1.73 Hz; 三弹簧QZS结构的零传递率频率分别为: 0.95, 1.21, 1.48, 1.82 Hz.

在传递率峰值方面, MQZS结构的峰值频率和传递率分别是: 0.96 Hz和30.32 dB、1.43 Hz和38.45 dB、2.03 Hz和45.02 dB、2.86 Hz和51.66 dB; 三弹簧QZS结构的峰值频率和传递率分别是1.05 Hz和32.78 dB、1.60 Hz和40.81 dB、2.23 Hz和47.32 dB、3.14 Hz和54.07 dB. 由上可知, MQZS结构在不同加速度激励幅值下均能够降低隔振起始频率和峰值频率与传递率, 并且随着加速度激励幅值的增大, 其峰值频率降低效果也越显著.

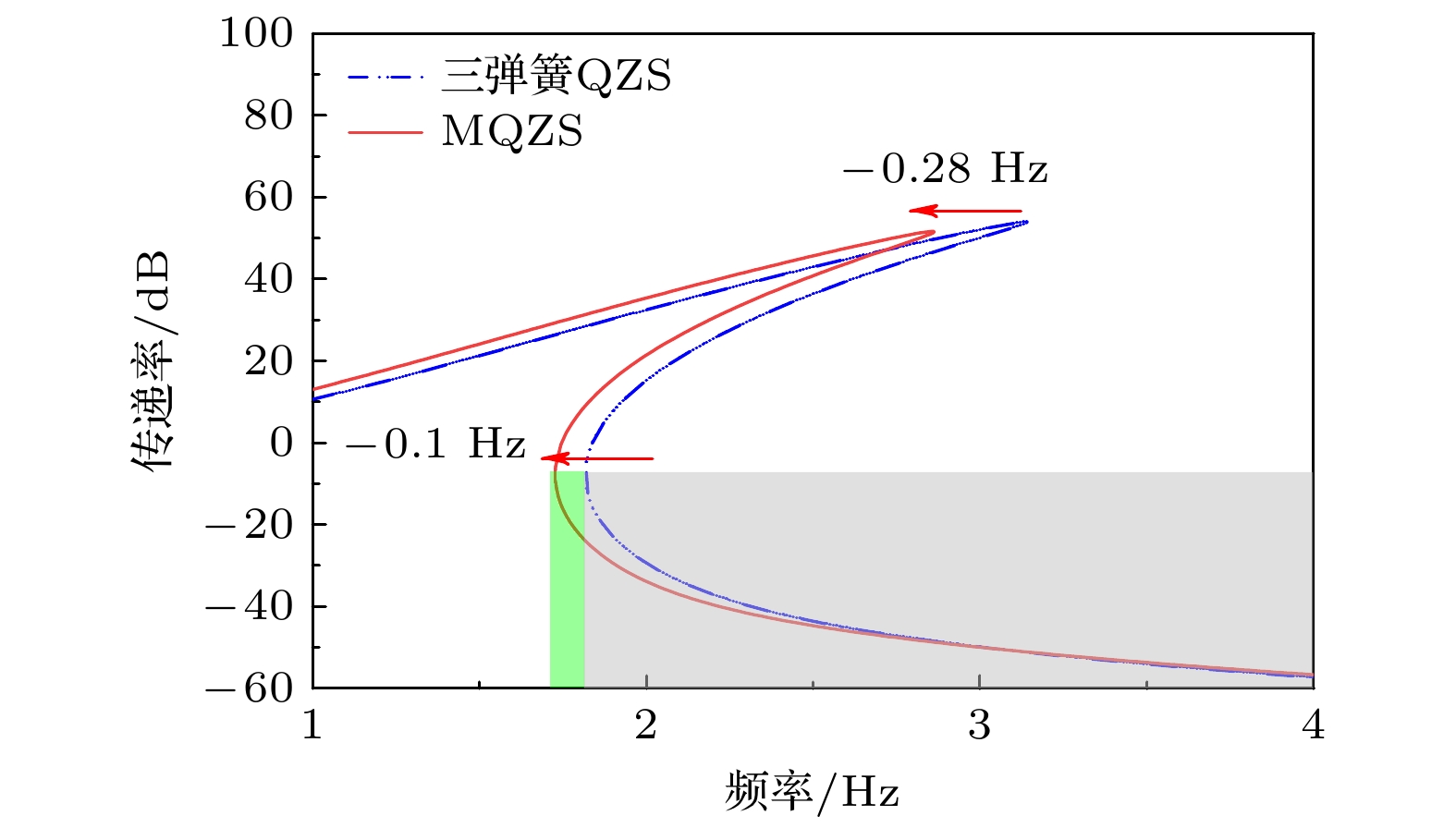
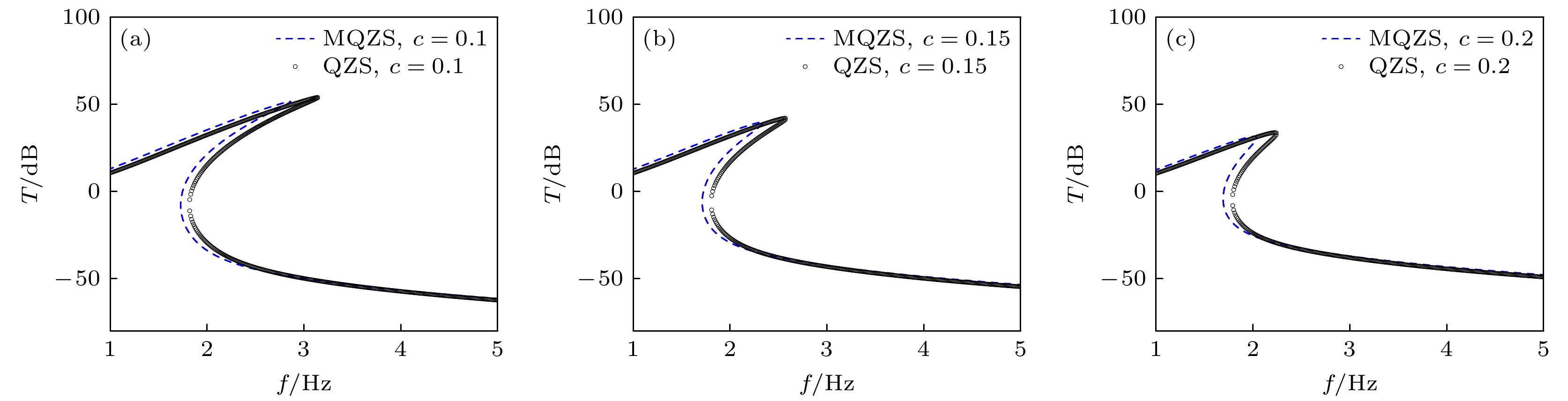
图13进一步对比了不同阻尼条件下两种QZS结构传递率 (A = 1.0 m/s²). 整体上看, 随着阻尼的增大, 两种结构的传递率峰值频率和幅值均会大幅减小, 并且MQZS结构的传递率频率、峰值以及起始隔振频率均低于三弹簧QZS结构. 当阻尼c = 0.1 N·s/m时, MQZS结构比三弹簧QZS的峰值频率、峰值传递率以及起始隔振频率分别降低了0.28 Hz, 2.4 dB和0.09 Hz; 当阻尼c = 0.15 N·s/m时, MQZS结构比三弹簧QZS的峰值频率、峰值传递率以及起始隔振频率分别降低了0.248 Hz, 2.32 dB和0.098 Hz; 当阻尼增至c = 0.2 N·s/m时, MQZS结构比三弹簧QZS的峰值频率、峰值传递率以及起始隔振频率分别降低了0.22 Hz, 2.2 dB和0.099 Hz. 由此可知, MQZS结构的主要优势集中在响应峰值处, 并且随着阻尼的增大, 这种优势反而会降低. 主要原因是随着阻尼的增大, 系统的响应幅值会大幅降低, 这会降低结构非线性的影响, 导致MQZS结构相对三弹簧QZS结构的优势降低.

综上所述, 与三弹簧QZS结构相比, MQZS结构在不同加速度和阻尼条件下均展现出了更好的低频隔振性能, 并且这种性能增强效果在响应增大时更为显著.

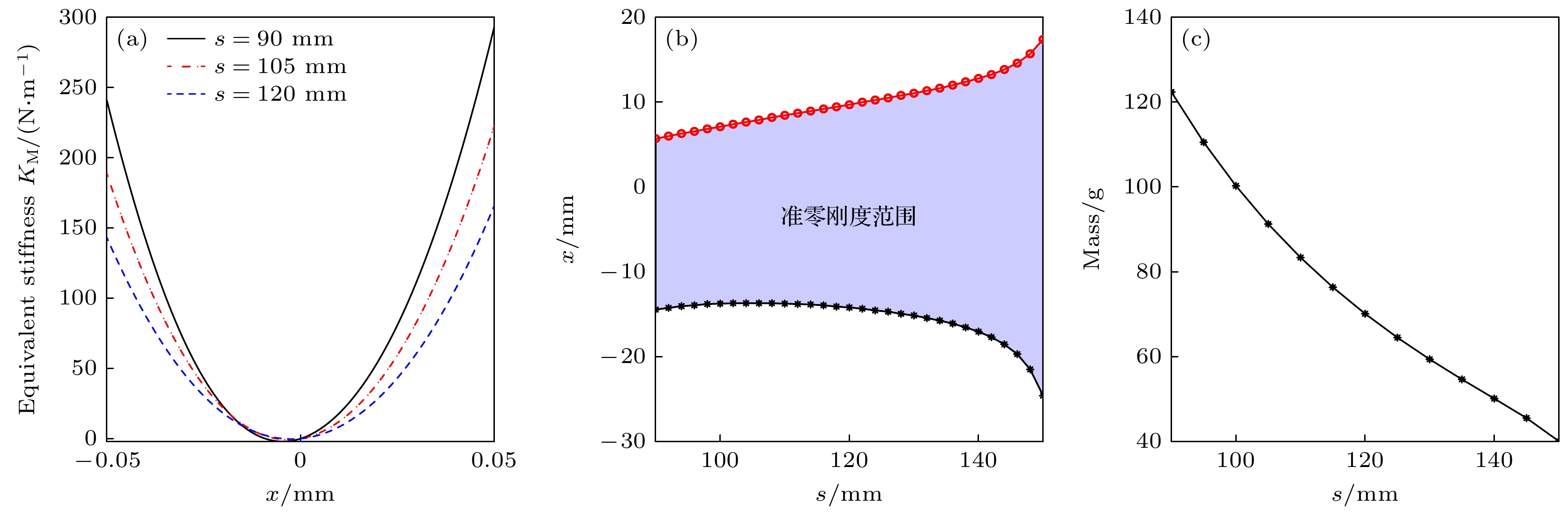
自然界中, 不同的节肢动物, 其M形腿部结构的形状也会有所不同. 为此, 有必要研究不同形状对MQZS结构准零刚度隔振特性的影响规律. M形结构的形状主要与杆长、支座在水平方向上的距离有关. 对于同一个节肢动物, 其腿的长度通常是确定的. 因此当身体负载发生变化时, 通常只能通过改变两脚之间的跨度调节其形状, 即调节参数s的大小改变M形结构的形状. 为此, 需要重点研究参数s的影响规律. 图13(a)首先给出了不同s时, 整个系统的等效刚度. 从图中可知, 当s增大时, 等效刚度曲线呈现出向两侧扩散的趋势, 导致准零刚度范围的增加. 图13(b)进一步给出了s对准零刚度位移范围的影响规律, 即随着s的增大, 系统的准零刚度范围会逐渐增大. 例如当s = 90 mm时, 系统准零刚度宽度为20.15 mm; 当s增至150 mm时, 准零刚度宽度为42 mm, 增大了108.4%. 最后, 从图14(c)可知, 随着参数s的增大, MQZS结构的有效负载质量也会逐渐减小. 这意味着, 增大参数s虽然能够大幅拓宽准零刚度范围, 但是其负载质量却越来越小. 因此在设计MQZS结构的M形几何形状时需要综合考虑负载质量的因素.

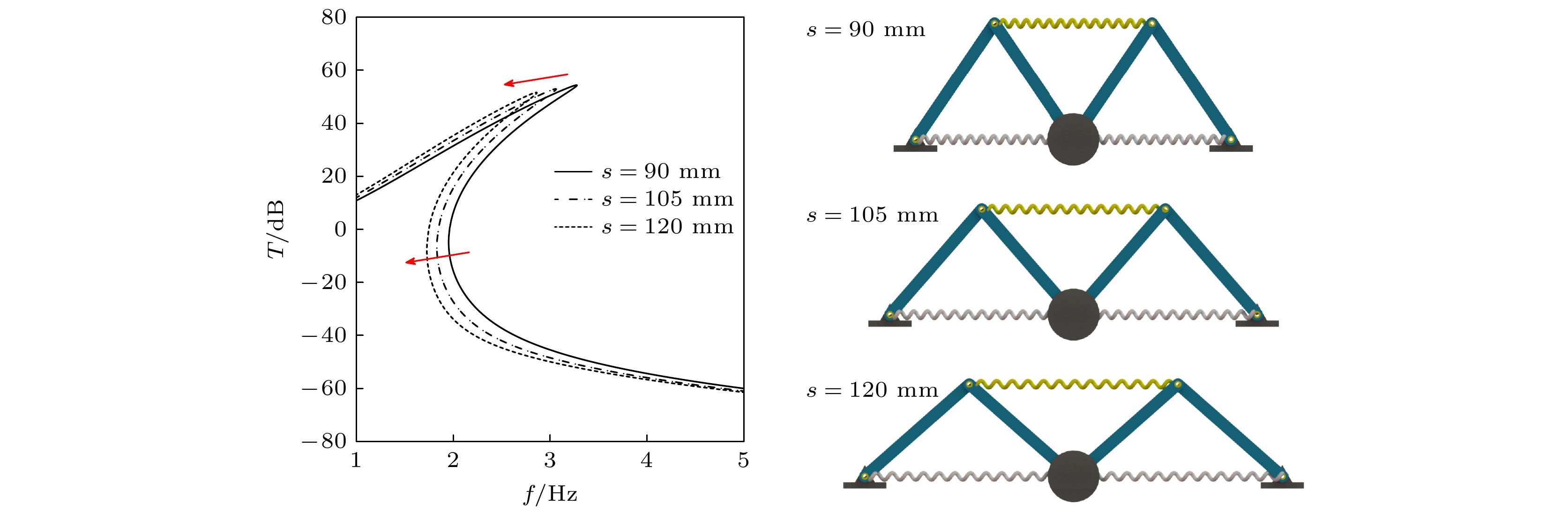
为了分析几何形状对M形准零刚度结构低频隔振性能的影响, 选取了3个不同的几何参数s (分别是90 mm, 105 mm, 120 mm), 并对比分析了其在A = 0.1 m/s²加速度激励下的传递率特性, 如图15所示, 随着s的增大, 传递率峰值频率会快速向低频移动, 并且峰值传递率也会降低. 其中, 峰值频率从3.72 Hz逐渐降低至2.86 Hz, 峰值传递率从54.44 dB降低至51.66 dB. 同时, 起始隔振频率也随着s的增大, 由1.95 Hz降低至1.74 Hz. 进一步给出了不同s条件下M形结构的几何形状. 从图15可知, 类似蜘蛛腿部的扁平状M形结构(s更大)具有更低的隔振频率, 更好的低频隔振效果. 而在实际设计中, 需要综合考虑负载质量与隔振性能的要求, 可以采用多组扁平状的M形结构, 既能够有效分摊负载质量, 也可以兼顾低频隔振性能. 这与节肢动物腿部特征是基本一致的, 常见的节肢动物通常拥有几组甚至几十组类M形肢体, 用以分摊身体的重量负载; 同时, 得益于M形几何结构, 节肢动物依然能够保持较好的低频隔振能力, 从而保持身体的平衡与稳定.

本文受到节肢动物腿部几何特征的启发, 提出了一种基于仿生M形低频隔振结构, 并对其动力学特性与低频隔振机理进行研究. 根据仿生M形结构的设计方案, 建立其动力学模型; 通过开展静态特性分析, 研究其准零刚度特性; 运用谐波平衡法推导得到其近似解析解, 并研究其动力学特性. 接着, 将其与经典的三弹簧准零刚度结构进行了隔振性能对比分析. 最后, 研究基础激励幅值、阻尼以及M形几何形状对系统低频隔振特性的影响规律.

1) 仿生MQZS结构的M形几何特征能够使得水平线性弹簧产生垂向的非线性正刚度, 并且能够在更宽的范围内补偿非线性负刚度, 从而有效拓宽准零刚度范围.

2) 与经典三弹簧QZS结构相比, MQZS结构能够有效降低隔振起始频率、峰值频率以及峰值传递率; 并且随着激励幅值的增大或者阻尼的减小, 系统隔振性能也会明显提升.

3) 当M形几何构型趋向于扁平状态时, MQZS结构的峰值频率、峰值频率以及隔振起始频率以及负载质量均会逐渐降低. 因此, 在实际应用中, 需要综合考虑负载质量和低频隔振性能选择MQZS结构的几何构型.

(23)式是采用谐波平衡法得到的方程组, 其可以写成矩阵的形式:

矩阵G满足:

F(q)表示为

其中,