腔光力系统使得光与机械振子之间的相互作用成为可能, 为宏观量子系统的基础物理研究^[1,2]以及量子信息处理^[3]和精密传感^[4–6]的实际应用提供了一个平台. 系统中机械振子的运动与光学模式相互作用, 使得光学响应可灵敏感知到机械振子在外界干扰下的变化, 从而能对包括位移^[7,8]、质量^[4,9,10]、力^[11–13]、应变^[14]和温度^[15]等多种物理量进行灵敏感知. 光力系统构造简单, 机械振子种类多样, 能灵活适用于多种物理场景, 且具有高的灵敏度, 因此基于光力系统的质量传感器在超灵敏检测领域扮演了重要角色^[4,9,10]. 光力系统的质量传感器在生物分子或病毒的质量检测^[9,16], 以及纳米尺度物质或颗粒的检测^[9,17,18]中存在巨大潜力.

腔光力系统中质量传感的基本原理是通过光学响应中透射峰频率偏移量, 可以检测由于吸附物引起的机械振子频率偏移δf. 通常, 由于吸附物的质量δm与振子频率偏移δf之间存在线性关系, 满足δf = Rδm ^[4,9], 因此通过测量得到的振子频率偏移δf可实现对吸附物质量δm的测量. 而灵敏度和分辨率(最小可检测质量δm_min)是腔光力系统质量传感器中的两个重要指标. 系统分辨率的提高, 关键依赖于最小可测量的频率偏移量δf_min和系统的灵敏度. 灵敏度的提高可通过减小振子有效质量实现, 以及利用光力系统中异常点(exceptional points, EPs)^[19,20]. 但是实现EPs需要腔光力系统为非厄米系统, 需要满足宇称-时间对称性或者反宇称-时间对称性, 因此在实验上实现相对复杂一些. 而最小可测量的频率偏移量δf_min的提高, 可通过提高腔的品质因子Q和利用光力系统中线性或非线性的光学效应减小输出光谱中响应峰的线宽.

腔光力系统中腔模和机械模之间通过辐射压力耦合, 能够产生许多独特的光学现象, 如光力诱导透明(optomechanically induced transparency, OMIT)^[21–24]、光力诱导的四波混频^[25–27]和高阶边带光谱^[28,29]等. 基于这些线性或非线性的光学效应, 可减小输出光谱的线宽, 提高基于光力系统的质量传感器的分辨率, 如基于四波混频^[30–32]、光力诱导透明^[25,33]和光力诱导吸收^[34]的质量传感方案. 对于利用光力诱导透明效应的质量传感方案, 由于其透射峰对应光力系统的本征值, 因此透射峰的频率偏移量与振子频移的对应关系实质为系统本征值实部与振子频移的关系, 而本征值的虚部改变则对应与透射峰线宽的变化. 然而振子的频移对光力系统本征值的实部和虚部的影响仍缺少研究.

此外, 连续域束缚态(bound states in the continuum, BIC)^[35]是一类特殊的奇点, 在该点有一个完全受限的模式, 线宽近似为零, 对应该模式的光波或者声波无法辐射出去. 其形成可以由辐射模式之间的破坏性干涉引起^[36–38], 也可以由结构对称性的失配引起^[37,38]. BIC不仅能减小能量损耗, 而且能实现很小的线宽, 并能提高光与物质的相互作用^[39]. 这些特性使其对周围折射率或环境的微小变化都产生剧烈响应, 因此BIC传感器在折射率传感^[40,41]、生物传感^[38,42]和环境监测^[39,43]等领域具重要的应用价值. 例如, 双C形金属超表面结构的太赫兹准BIC生物传感器^[44], 双矩形硅柱超表面结构的相位询问型BIC折射率传感器^[45]以及成对硅半圆柱超表面结构的准BIC双参数(折射率和温度)传感器^[46], 这些利用超表面结构的BIC传感器实现了对生物分子、折射率和环境温度的灵敏检测. 而在光力学系统中利用BIC实现的质量传感仍鲜有研究, 如果将BIC技术应用于光力学质量传感方案, 使光力学系统响应光谱线宽变得极小, 则有望实现超高的质量分辨率.

本文通过双腔光力系统在蓝失谐条件下实现了BIC, 并利用该光力系统中的BIC奇点特性, 提出一个具有超高分辨率的质量传感方案. 基于输入输出关系给出系统的光学响应和透射光谱, 证明系统在蓝失谐下能形成类似于红失谐情况下的双光力诱导透明(double-OMIT, DOMIT)现象^[47]. 不同于DOMIT的是, 系统的中间窄峰是一个增益峰. 而系统中出现的3个峰对应着3个本征值, 通过研究中间增益峰对应的本征值虚部和实部, 揭示BIC点的形成条件, 从而得到基于BIC点实现超高分辨率质量传感的条件. 在BIC形成的条件下, 通过透射光谱证明系统可实现超高分辨率的质量传感, 进一步地通过本征值虚部和实部及其灵敏度增加因子随振子频移的变化证明了该BIC质量传感方案在振子频移影响下具有较好的稳定性, 能保持超高的分辨率以及精确的质量测量.

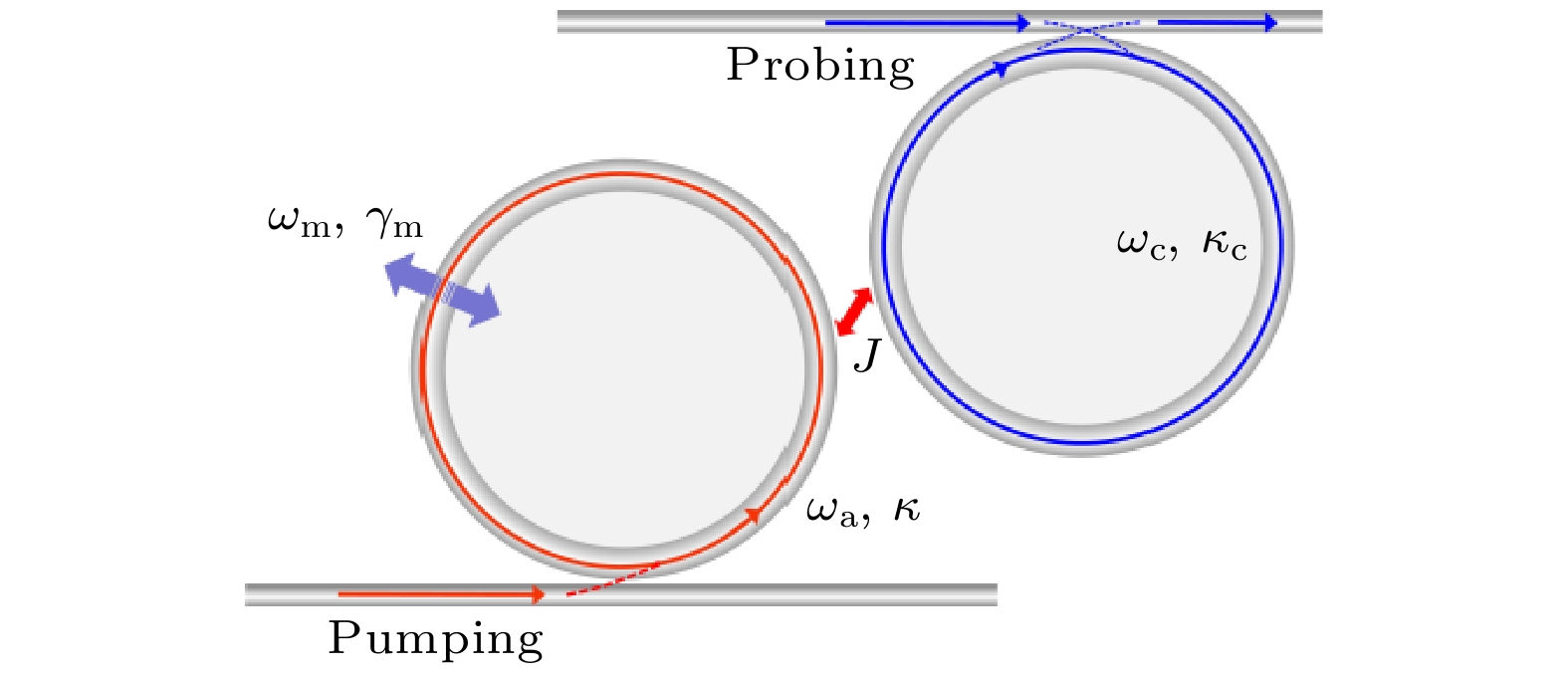
如图1所示, 考虑一个由两个光腔组合的双腔光力系统, 其中一个光腔和机械振子耦合, 形成光力腔. 这样的双腔光力系统在实验上可以通过两个耦合的回音壁模式(whispering-gallery-mode, WGM)腔实现^[48,49]. 该双腔光力系统中机械振子的本征频率为$ {\omega _{\text{m}}} $, 并通过辐射压力与腔场相互作用, 而腔场的本征频率为$ {\omega _{\text{a}}} $, 受到一个振幅和频率分别为${\varepsilon _{\text{l}}}$和${\omega _{\text{l}}}$的泵浦场驱动. 另外一个辅助光腔中输入弱探测光, 其频率和振幅分为${\omega _{\text{p}}}$和${\varepsilon _{\text{p}}}$. 因此可以给出系统总的哈密顿量为

其中, 等号右侧第1项、第2项和第3项分别表示腔场、机械振子和辅助腔的无相互作用的哈密顿量. 第4项和第5项表示腔模与机械模和辅助腔的相互作用, 相应的耦合强度分别为${g_{\text{m}}}$和$ J $. $a$和$b$分别是腔模和机械模的湮灭算符, 满足对易关系$[n\, , \, {n^\dagger }] = 1$, 其中$n = a, \, b$. 在$U = \exp [ {\text{i}}{\omega _{\text{l}}}({a^\dagger }a + c_{}^\dagger {c_{}})t ]$下, 利用变换$\tilde H = \;UH{U^\dagger } - {\text{i}}\hbar U{{\partial {U^\dagger }} {/ } {\partial t}}$^[50], 可以得到在旋转坐标下的哈密顿量:

其中$\varDelta = {\omega _{\text{a}}} - {\omega _{\text{l}}}$, ${\varDelta _{\text{c}}} = {\omega _{\text{c}}} - {\omega _{\text{l}}}$ 和 ${\varDelta _{\text{p}}} = {\omega _{\text{p}}} - {\omega _{\text{l}}}$. 利用(2)式的哈密顿量, 可得到海森伯-朗之万方程为

式中, ${\gamma _{\text{m}}}$, $\kappa $, ${\kappa _{\text{c}}}$分别代表机械振子, 光力腔a和辅助腔c的衰减率. 而${b_{{\text{in}}}}$, ${c_{{\text{in}}}}$和${a_{{\text{in}}}}$分别表示相应的噪声算符, 其对应的平均值为零. 当量子涨落关联远小于平均值乘积时, 即$\left\langle A \right\rangle \left\langle B \right\rangle \gg \left\langle {(\delta A)(\delta B)} \right\rangle $, 可以采用平均场近似^[51,52]. 在平均场近似($\left\langle {AB} \right\rangle = \left\langle A \right\rangle \left\langle B \right\rangle $)下^[51–54], 可以得到这些算符满足的运动方程组:

上述方程在$ {\varepsilon _{\text{l}}} \gg {\varepsilon _{\text{p}}} $情况下, 可对海森伯-朗之万方程进行线性化处理, (4)式中的算符改写为其涨落和平均值的和^[55], 即$\left\langle a \right\rangle = \alpha + \delta a$, $\left\langle b \right\rangle = \beta + \delta b$和$\left\langle c \right\rangle = C + \delta c$. 计算得到的平均值为

由此, 就可以得到线性化的海森伯-朗之万方程:

其中$ G_{\mathrm{m}}=g\mathrm{_m}\left|\alpha\right| $. 采用拟解形式进行求解, 即代入

在Stokes边带情况下, 采用旋波近似, 可以忽略(6)式中的非旋波项$ \text{i}G_{\mathrm{m}}\delta b $和$ \text{i}G_{\mathrm{m}}\delta a $^[55], 可得

依据输入输出关系, 透射光满足:

透射率可以由(9)式给出:

其中, ${\varepsilon _{\text{T}}}$表示腔场对探测场的光学响应, 其表达式为

其中,

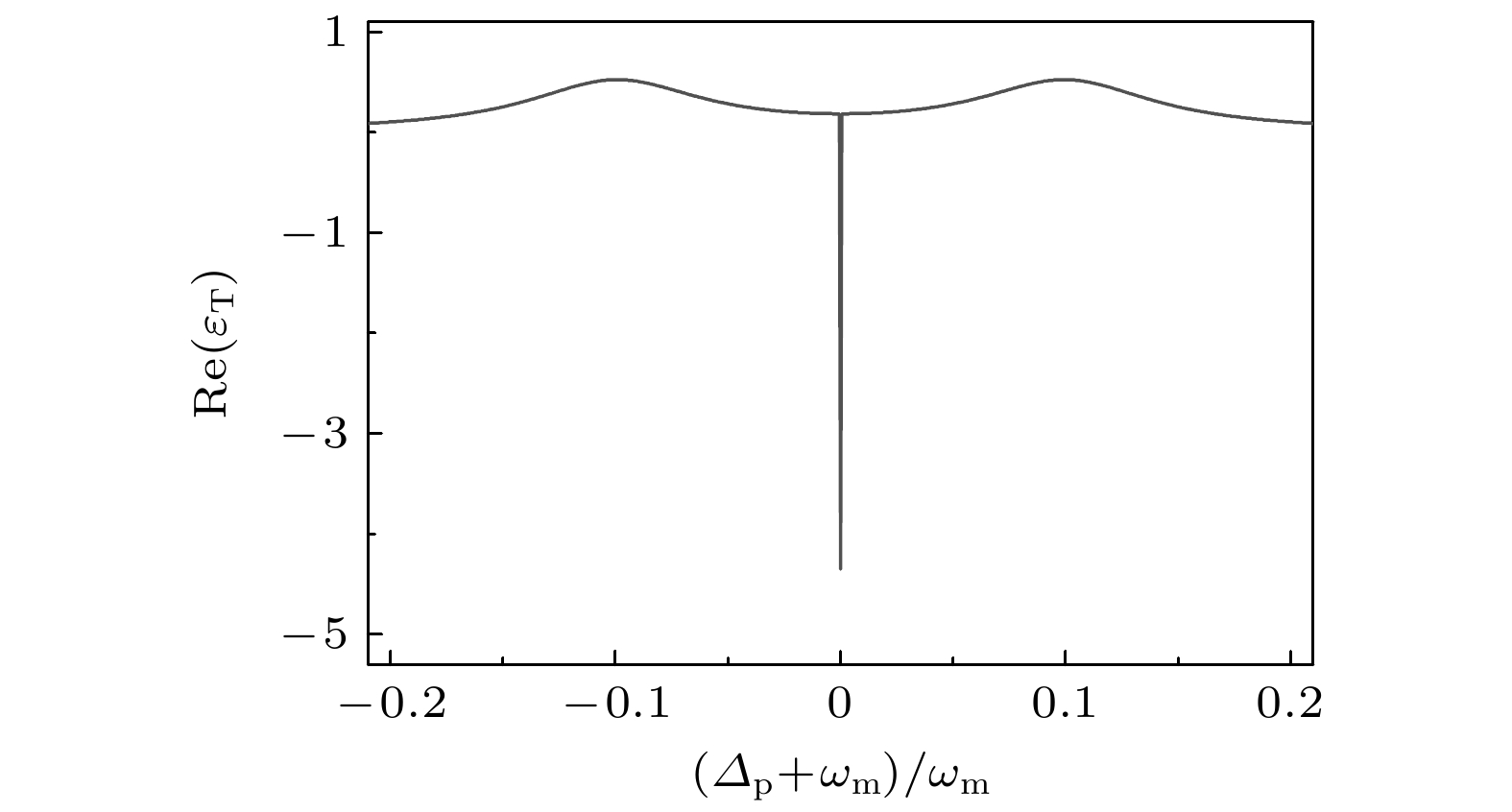
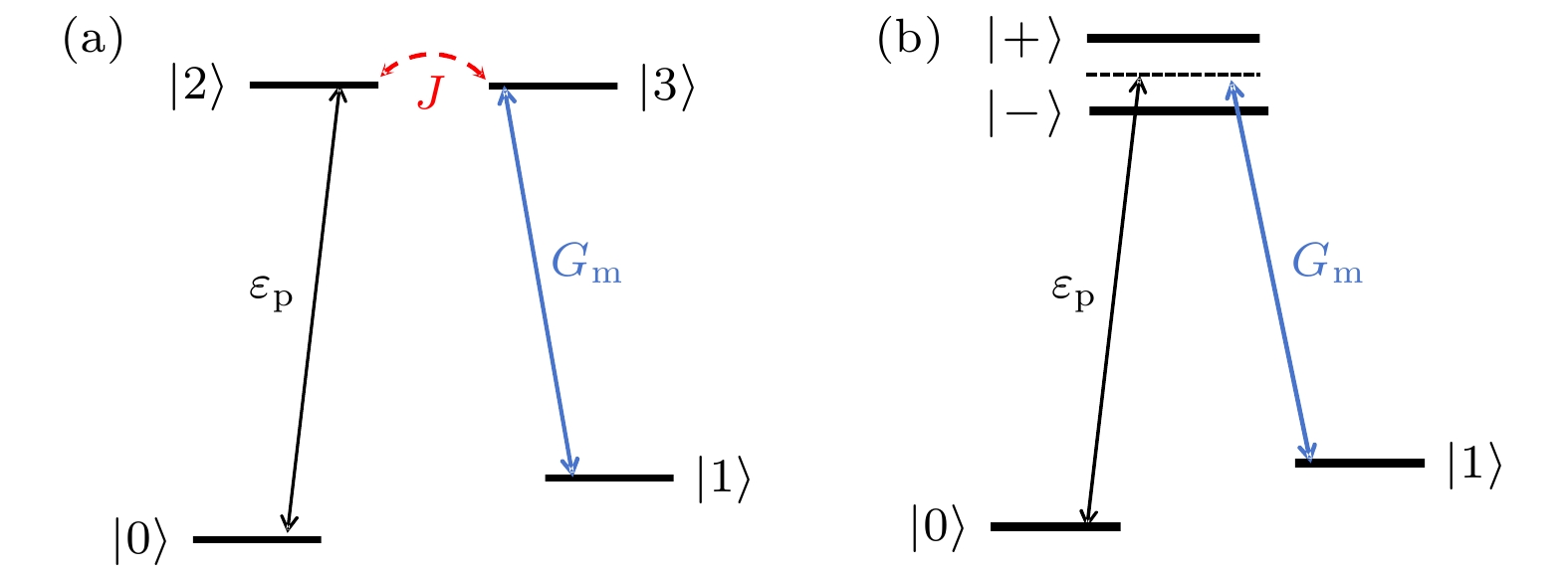
${\varepsilon _{\text{T}}}$的虚部${{\mathrm{Im}}} ({\varepsilon _{\text{T}}})$表示色散, 实部${{\mathrm{Re}}} ({\varepsilon _{\text{T}}})$表示吸收, 图2给出了${{\mathrm{Re}}} ({\varepsilon _{\text{T}}})$随探测场失谐量的变化. 显然, 在吸收光谱中存在3个峰值, 其中在$ {\varDelta _{\text{p}}} + {\omega _{\text{m}}} \approx \pm 0.1{\omega _{\text{m}}} $处出现两个宽的吸收峰, 在两宽峰中间$ {\varDelta _{\text{p}}} + {\omega _{\text{m}}} = 0 $出现一个窄的增益峰. 中间窄峰对应系统的双光子共振情况, 即$ \varDelta = {\varDelta _{\text{c}}} = {\varDelta _{\text{p}}} $, 这时多个量子跃迁通道之间的量子干涉引起中间窄峰的形成, 与多能级原子系统中的双电磁诱导透明形成中间窄峰一致^[56,57]. 为了进一步分析其中的量子干涉效应, 图3(a)给出了双腔光力学系统的能级结构, 探测光场与腔模c耦合能引起能级$ \left| 0 \right\rangle $与$ \left| 2 \right\rangle $之间的跃迁. 在蓝失谐情况下, 光机械耦合引起能级$ \left| 1 \right\rangle $和$ \left| 3 \right\rangle $的相互作用. 而两个光腔在耦合强度J下的相互作用对应能级$ \left| 2 \right\rangle $和$ \left| 3 \right\rangle $之间的相互作用. 依据缀饰态理论, 能级$ \left| 2 \right\rangle $和$ \left| 3 \right\rangle $可以形成缀饰态$ \left| \pm \right\rangle = {{(\left| 2 \right\rangle \pm \left| 3 \right\rangle )} {/ } {\sqrt 2 }} $^[58]. 这时系统会形成两个不同的Λ型子系统, 分别对应两条量子跃迁通道$\left| 0 \right\rangle \leftrightarrow $ $ \left| + \right\rangle \leftrightarrow \left| 1 \right\rangle $和|$ \left| 0 \right\rangle \leftrightarrow \left| - \right\rangle \leftrightarrow \left| 1 \right\rangle $, 如图3(b)所示. 依据四能级冷原子系统的研究报道^[59,60], 这两条量子跃迁通道形成双暗态共振的量子干涉效应, 引起中间窄峰的产生, 形成准BIC.

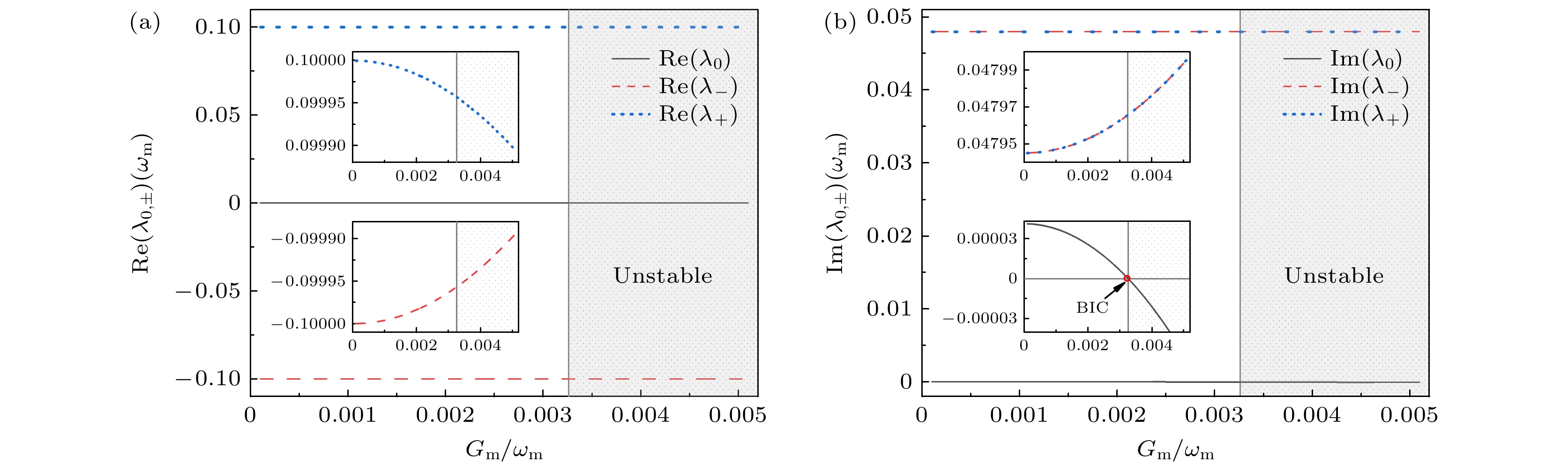
图2吸收光谱中的3个峰对应着系统3个本征值${\lambda _{{\text{0, }}\, \pm }}$, 本征值满足以下方程:

图4为本征值${\lambda _{{\text{0, }}\, \pm }}$的实部和虚部随光力耦合强度${G_{\text{m}}}$的变化. 可以看到${\lambda _ \pm }$的实部$ {{\mathrm{Re}}} ({\lambda _ \pm }) $近似在$ \pm 0.1{\omega _{\text{m}}} $, 并且随光力耦合作用${G_{\text{m}}}$变化很小, 说明这两个吸收峰由两腔耦合作用所决定(当$ J \gg {G_{\text{m}}} $时), 并且两个腔场在耦合作用J下形成的模式分裂, 对应的分裂峰位于$ {{\mathrm{Re}}} ({\lambda _ \pm }) \approx \pm J $. 中间窄峰对应双光子共振条件, 其本征值的实部$ {{\mathrm{Re}}} ({\lambda _0}) $值为0, 如图4(a)所示. 并且从图4(b)可以看到, $ {\lambda _0} $的虚部$ {{\mathrm{Im}}} ({\lambda _0}) $可达到$ {10^{ - 5}}{\omega _{\text{m}}} $量级比机械振子的衰减率小, 意味着其对应形成的峰线宽很小, 正如图2所示. 并且随着光力耦合强度${G_{\text{m}}}$增大$ {\lambda _0} $的虚部$ {{\mathrm{Im}}} ({\lambda _0}) $进一步减小, 当$ d = 0 $时, 即$ G_{\text{m}}^{} = \sqrt {{{(4 J_{}^2{\gamma _{\text{m}}} - \kappa {\kappa _{\text{c}}}{\gamma _{\text{m}}})} {/ } {4{\kappa _{\text{c}}}}}} $, 其虚部为零, 形成连续域束缚态(BIC)奇异点^[35], 中间峰的线宽变为0. 在这时候, 光力协同性$ {C_{\text{m}}} = {{4 G_{\text{m}}^{2}} {/ } {\kappa {\gamma _{\text{m}}}}} $与双光腔协同性$ {C_1} = {{4 J_{}^2} {/ } {\left( {\kappa {\kappa _{\text{c}}}} \right)}} $满足$ {C_{\text{m}}} = {C_1} + 1 $, 这种条件下中间窄峰线宽变为零形成BIC奇点.

当$ {\varDelta _{\text{p}}} = - {\omega _{\text{m}}} $时, 光谱上出现中间窄峰, 可从中间峰的频率位置读取出机械振子的频率. 因此可通过透射谱中峰的频率偏移量, 读取出由于外界影响因素导致的振子频移$\delta {\omega _{\text{m}}}$. 同时, 由于在BIC点附近对应线宽非常小, 有望能实现超高的分辨率. 机械振子可以近似考虑为一个简谐振子, 其有效质量为$ m $, 弹性常数为$ k $, 相应本征频率${\omega _{\text{m}}} = \sqrt {{k {/ } m}} $^[4,9]. 显然当机械振子有效质量增加$ \delta m $时, 机械振子的频率会减少变为${\omega _{\text{m}}} - \delta {\omega _{\text{m}}}$, 相反, 当机械振子有效质量减少$ \delta m $时, 机械振子的频率会增加变为${\omega _{\text{m}}} + \delta {\omega _{\text{m}}}$. 因此, $ \delta {\omega _{\text{m}}} $和$ \delta m $的关系为^[4,9]

其中, $ R = \left| {{R_1}} \right| $, $ {R_1} = {\left( {{{\partial {\omega _{\text{m}}}} {/ } {\partial m}}} \right)^{ - 1}} = - {{{\omega _{\text{m}}}} {/ } {2 m}} $为质量响应度^[62].

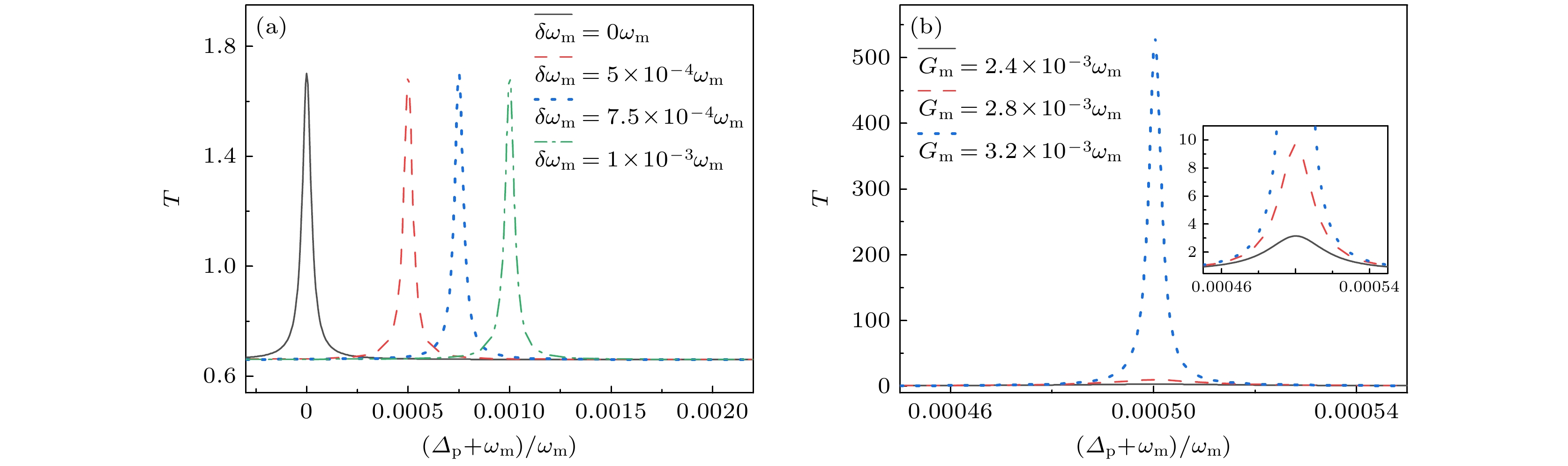
铬原子具有较高的吸附能, 容易吸附到物品表面上^[9], 以铬原子作为样品, 考虑测量吸附的铬原子总质量分别为10 pg, 15 pg和20 pg. 同时依据参考的实际实验数据, 在系统中机械振子的有效质量为$m \approx 10\, {\text{ng}}$^[49,61]. 根据(12)式计算得到吸附 的铬原子引起的频移$\delta {\omega _{\text{m}}}$分别为$5 \times {10^{ - 4}}{\omega _m}$, $7.5 \times {10^{ - 5}}{\omega _{\text{m}}}$和$1 \times {10^{ - 3}}{\omega _{\text{m}}}$. 取${g_1} = 0.1{\omega _{\text{m}}}$, $ G_{\mathit{\mathit{\mathrm{m}}}}=0.001\omega_{\text{m}} $和$ {\varDelta _{\text{c}}} = \varDelta ' = - {\omega _{\text{m}}} $, 在图5(a)作频移$\delta {\omega _{\text{m}}}$分别为0, $5 \times {10^{ - 4}}{\omega _m}$, $7.5 \times {10^{ - 5}}{\omega _{\text{m}}}$和$1 \times {10^{ - 3}}{\omega _{\text{m}}}$时的透射光谱. 当没有振子频移时, 从透射光谱可以看到, 对应图2吸收光谱的中间窄峰的位置处形成一个透射峰, 并且随着频移$\delta {\omega _{\text{m}}}$增大透射峰向频率增大的方向移动, 并且透射峰的频率偏移量与频移$\delta {\omega _{\text{m}}}$一致, 说明该系统能通过透射光谱实现对机械振子频移的读取, 这时振子频移与探测光场的失谐量满足$ \delta {\omega _{\text{m}}} = - ({\varDelta _{\text{p}}} + {\omega _{\text{m}}}) $. 此外, 可以看到其透射光谱对应的透射峰大于等于1, 说明输入的探测光经过光腔后没有变弱, 保证了输出信号的强度. 进一步考虑光力耦合强度对透射峰的影响, 在图5(b)中作不同光力耦合强度下系统的透射光谱图, 显然随着光力耦合强度变大, 透射峰峰值增大, 相应的线宽减小, 与图4(b)中本征值${\lambda _0}$的虚部随$ {G_{\text{m}}} $减小趋势一致. 并且$ {G_{\text{m}}} $增大不会导致透射峰的偏移, 保证了频率读取的精度. 考虑最小可分辨频移$ \delta {\omega _{{\text{m-min}}}} $为透射峰对应的半峰全宽(full width at half maximum, FWHM)^[18,63], 即有$\delta {\omega _{{\text{m - min}}}} = {\rm Im} ({\lambda _0})$. 在${\omega _{\text{m}}} \gg \delta {\omega _{\text{m}}}$时, 可以认为机械振子对应的有效品质因子${Q_{{\text{eff}}}}$满足${Q_{{\text{eff}}}} \approx {{{{\mathrm{Im}}} ({\lambda _0})} {/ } {{\omega _{\text{m}}}}}$, 即有${Q_{{\text{eff}}}} \approx {{\delta {\omega _{{\text{m-min}}}}} {/ } {{\omega _{\text{m}}}}}$, 依据频移与质量变化的关系(12)式, 可以给出最小质量分辨率为

可知随着线宽减小, 系统可分辨的最小质量也随之越小. 因此, 基于BIC奇异点的质量传感方案能实现超高的分辨率.

对于理想情况下, 系统中间峰对应的本征值保持不变, 即${\lambda _0} = 0$, 这时总能保持$ {\varDelta _{\text{p}}} = - ({\omega _{\text{m}}} - \delta {\omega _{\text{m}}}) $, 测量的振子频移没有任何偏差, 然而振子频移的引入会使(11)式出现额外的项从而改变本征值, 影响透射峰的本征值. 为了探究系统在测量吸附物质量时的稳定性和可靠性, 考虑频移$\delta {\omega _{\text{m}}}$对本征值${\lambda _0}$的影响. 机械振子在吸附物影响下其振动频率从${\omega _m}$变为${\omega _m} - \delta {\omega _m}$, 这时本征值变化量为${\lambda _{0, \, \pm }}$满足的方程为

其中,

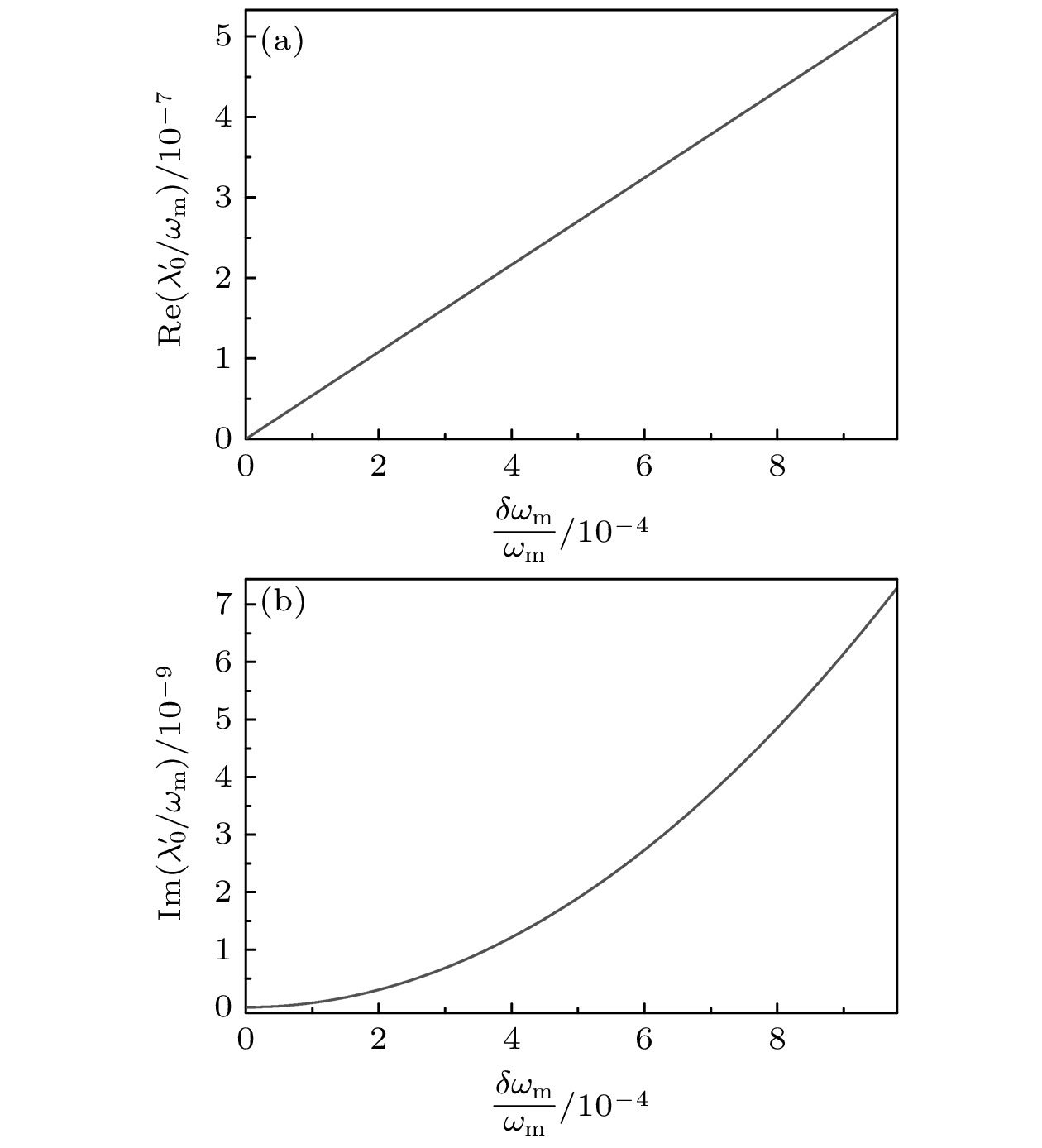
通过(14)式, 可以求出本征值${\lambda '_0}$, 图6(a), (b)分别给出了本征值${\lambda '_0}$的实部${\rm Re} ({\lambda '_0})$和虚部${\rm Im} ({\lambda '_0})$随频移的变化. 显然本征值的实部${\rm Re} ({\lambda '_0})$随频移$\delta {\omega _{\text{m}}}$呈线性变化, 此时透射峰的位置为${\varDelta _{\text{p}}} = - ({\omega _{\text{m}}} - \delta {\omega _{\text{m}}}) + {\rm Re} ({\lambda '_0})$. 而虚部${\rm Im} ({\lambda '_0})$虽然会随着频移$\delta \omega _{\text{m}}^{2}$的增大而增大, 但是仍保持很小的值, 这也意味着中间透射峰的线宽仍然很小在${10^{ - 9}}\delta {\omega _{\text{m}}}$量级. 例如, 在频移$\delta {\omega _{\text{m}}}$=$0.001{\omega _{\text{m}}}$时, 对应透射峰的线宽为$2{\pi} \times 0.078 \, {\text{Hz}}$, 约为机械振子衰减率的$9 \times {10^{ - 5}}$倍, 最小质量分辨率$\delta {m_{\min }}$达到0.15 fg. 在频移$\delta {\omega _{\text{m}}}$=$0.0001{\omega _{\text{m}}}$时, 对应透射峰的线宽为$2{\pi} \times 7.8 \times {10^{ - 4}}\, {\text{Hz}}$, 最小质量分辨率$\delta {m_{\min }}$达到1.5 ag.

此外, 我们将基于BIC的光力学质量测量方案与一些经典的光力学质量测量方案进行对比, 这些经典的光力学质量测量方案包括四波混频^[30–32]、光学分子^[62]和等离子激元^{[63, 64]}. 采用双腔结构的四波混频^[32]以及光学分子^[62]的质量测量方案都可以使机械振子的有效衰减率分别从$2{\pi} \times 140\, {\text{Hz}}$和$2{\pi} \times 41\, {\text{kHz}}$降为$1.8\, {\text{Hz}}$和$2{\pi} \times 4.1\, {\text{kHz}}$. 而基于BIC的光力学质量测量方案则可使机械振子的有效衰减率从$ 2{\pi} \times 0.83 \, {\text{kHz}} $降到0.49 Hz, 能更大地提高机械振子的有效品质因子. 因此, BIC的光力学质量测量方案能实现比双腔结构的四波混频^[32]和光学分子^[62]方案(fg量级)更低的质量分辨率, 达到ag量级. 而等离子激元方案^{[63, 64]}, 其振子质量很小为zg量级且具有较大的本征频率为GHz量级, 因此其质量分辨率能达到yg量级. 但是其最小可分辨质量与振子有效质量的比值${{\delta {m_{\min }}} {/ } m}$约为${10^{ - 3}}$, 而BIC光力学质量测量方案中该比值更小为${10^{ - 6}}$, 从而降低了对振子质量的要求, 能够以更大的振子质量实现对质量更小的吸附物的测量.

为了进一步考虑本征值实部和虚部随频移的变化, 引入灵敏度增加因子^[19,20]:

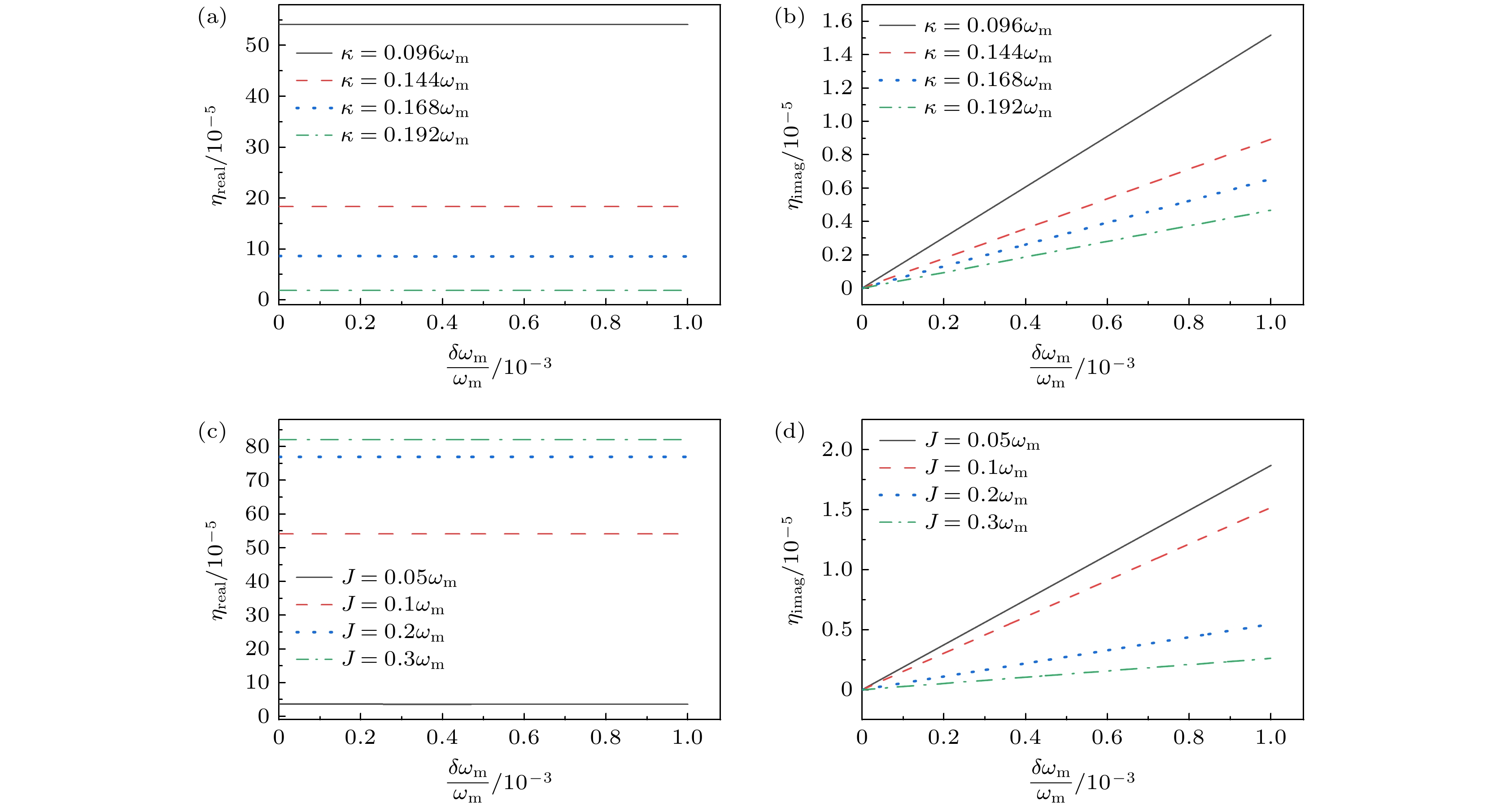
其中$\delta {\lambda _0} = {\lambda '_0} - {\lambda _0}$. 图7给出了在不同的腔耗散率和腔耦合强度下灵敏度增加因子${\eta _{{\text{real}}}}$和${\eta _{{\text{imag}}}}$随频移$\delta {\omega _{\text{m}}}$的变化曲线. 从图7(a), (b)可以看出, ${\eta _{{\text{real}}}}$和${\eta _{{\text{imag}}}}$随腔耗散率$\kappa $的增大而减小, 而${\eta _{{\text{real}}}}$随腔耦合强度$J$的增大而增大, 相反${\eta _{{\text{imag}}}}$随腔耦合强度$J$的增大而减少, 如图7(c), (d)所示. 因此, 通过腔的衰减率$\kappa $和光力耦合强度$ {G_{\text{m}}} $能够调控系统的灵敏度增加因子${\eta _{{\text{real}}}}$和${\eta _{{\text{imag}}}}$, 并且当腔耗散较大时能使灵敏度增加因子${\eta _{{\text{real}}}}$和${\eta _{{\text{imag}}}}$更小. 此外, 灵敏度增加因子${\eta _{{\text{real}}}}$基本不随$ \delta\omega\mathrm{_m} $变化, 表明本征值的实部的偏移量与$ \delta\omega\mathrm{_m} $呈线性关系, 而灵敏度增加因子${\eta _{{\text{imag}}}}$随$ \delta\omega\mathrm{_m} $呈线性变化, 表明本征值虚部的变化量与$ \delta\omega_{\mathrm{m}}^2 $呈线性关系, 如图7所示. 但是灵敏度增加因子${\eta _{{\text{real}}}}$和${\eta _{{\text{imag}}}}$非常小, 在${10^{ - 5}}$量级, 说明本征值实部和虚部的偏移量随$ \delta\omega\mathrm{_m} $变化很小. 因此在频移$\delta {\omega _{\text{m}}}$的影响下, 系统本征值${\lambda _0}$的实部保持与频移$\delta {\omega _{\text{m}}}$呈线性关系, 保证透射峰频率偏移量与频移$\delta {\omega _{\text{m}}}$的线性关系, 并且即使频移为$0.001{\omega _{\text{m}}}$, 从图6(b)可知, 其线宽仍能保持${10^{ - 9}}\delta {\omega _{\text{m}}}$, 说明系统仍保持超高的分辨率. 综上所述, 我们认为该质量传感方案在振子频移下仍能保持超高的分辨率以及精确的质量测量.

本文在理论上提出了一个基于BIC奇点的具有超高分辨率的质量传感方案. 通过求解线性化海森伯-朗之万方程, 给出双腔光力系统的光学响应系数和透射光谱, 证明了在蓝失谐情况下在系统满足双光子共振条件时能形成一个狭窄的增益峰, 并给出了增益峰对应的本征值. 基于增益峰本征值的虚部随光力耦合强度的变化, 给出了系统形成BIC奇异点的条件为$ G_{\text{m}}^{} = \sqrt {{{(4 J_{}^2{\gamma _{\text{m}}} - \kappa {\kappa _{\text{c}}}{\gamma _{\text{m}}})} {/ } {4{\kappa _{\text{c}}}}}} $, 对应光力协同性$ {C_{\text{m}}} $等于双光腔协同性$ {C_1} $+1. 由于BIC点处对应线宽为零, 并且透射峰位于探测场失谐量与机械振子本征频率之和为零处, 因此透射光谱中峰的频率偏移量等于机械振子频移量从而能实现超高分辨率的质量传感. 最后, 研究了机械振子吸附物导致的振子频移对增益峰的本征值及相应的灵敏度增加因子的影响, 证明了在$ G_{\text{m}}^{} = \sqrt {{{(4 J_{}^2{\gamma _{\text{m}}} - \kappa {\kappa _{\text{c}}}{\gamma _{\text{m}}})} {/ } {4{\kappa _{\text{c}}}}}} $条件下, 本征值在机械振子频移影响下变化很小. 透射峰频谱位置保持与机械振子频移的一一对应关系, 线宽同样能保持较小的值可小于1 Hz, 说明在振子平移影响下基于BIC的质量传感方案能保持超高的分辨率以及精确的质量测量. 在较大机械振子频移下($\delta {\omega _{\text{m}}} = 0.001{\omega _{\text{m}}}$), 系统的最小质量分辨率仍可达到0.15 fg, 小的机械振子频移下($\delta {\omega _{\text{m}}} = 0.0001{\omega _{\text{m}}}$), 最小质量分辨率达到1.5 ag. 本工作方案为光力系统实现BIC提供了一种路径, 为提高腔光力系统质量传感器的分辨率提供了新方法.