超强激光与物质相互作用能产生大量能量在百 keV量级的超热电子^[1]. 超热电子在靶材料中传输时, 将靶原子的K壳层电子电离而产生Kα特征线辐射. 由于这种Kα射线源具有高亮度、短脉宽等特点, 其可应用于背光照相、相衬成像和谱诊断等领域^[2–6]. 然而, 超热电子在靶材料中传输时也会产生宽能量范围的轫致辐射连续谱. Kα线谱与其附近轫致辐射连续谱的强度比, 即Kα辐射的对比度, 一般为几至几十^[2,7–10]. Kα辐射的对比度是重要参数, 提高Kα辐射的对比度对于Kα辐射的一些应用, 如相衬成像^[3]、生物差分成像^[11]、波带板成像^[12]、谱诊断^[6]等具有很大的好处.

实验上可以在Kα源与被照射样品之间插入晶体、滤片等元件分光或滤波来提高Kα辐射的对比度^[13–15], 但晶体反射、滤片吸收等会减小Kα光子通量. 直接提高Kα源辐射对比度的研究较少. 超热电子产生的Kα辐射是近似各向同性的^[9,16], 而轫致辐射与产生辐射的电子运动方向有关, 辐射谱密度是其辐射方向与电子运动方向夹角的函数^[17]. 越靠近电子运动方向, 轫致辐射强度越大, 即轫致辐射具有各向异性. 入射电子的能量越高, 轫致辐射的各向异性越显著^[18,19]. 因此Kα辐射的对比度与超热电子的传输有关, 已被实验观察证实^[7]. 本研究组之前的模拟表明, 超热电子产生的轫致辐射方向性越好, Kα辐射的对比度越高. 然而, 超热电子在靶中传输时被靶物质散射导致超热电子束横向扩散, 轫致辐射的方向性变差, 会降低Kα辐射的对比度^[19]. 如果能够对靶中运动的超热电子束进行准直, 降低电子束的发散程度, 则有望获得更高对比度的Kα辐射.

激光与等离子体作用可以产生强度达10²—10⁴ T的磁场^[20]. 已有研究指出, 在靶中引入几十至数百T的磁场可以实现对超热电子的准直, 例如利用激光辐照电容线圈靶产生沿激光传播方向的外加轴向磁场准直电子^[21], 或者采用两束激光辐照固体靶, 在靶中产生自生横向环形磁场准直电子^[22,23]等. 尽管这些外加磁场或自生磁场能够准直电子束, 但是能否提高Kα辐射的对比度尚未有研究. 本文旨在研究利用类似对超热电子有准直作用的磁场直接提高Kα辐射对比度的可能性.

超热电子产生X射线是个复杂的过程, 涉及超热电子被靶原子散射偏转、电离靶原子和相应Kα辐射产生、轫致辐射产生等多种物理过程. 一种有效的研究方法是蒙特卡罗数值模拟^[24]. 本文采用蒙特卡罗方法, 模拟了铜靶中存在轴向匀强磁场或高斯分布环形磁场时超热电子在靶中的传输和X射线产生, 研究了不同的入射电子能量、靶厚度等条件下, 磁场对Kα辐射对比度的影响. 选择铜作为靶材料是因为铜的Kα辐射能量为8.05 keV, 被广泛研究^[8,9,25]且在许多方面有应用, 如相衬成像和谱诊断等^[3,26]. 本文第2节介绍在蒙特卡罗模拟中电磁场对电子传输作用的模型, 第3节是模拟结果与分析, 第4节给出结论.

本文研究使用电子在铜靶中传输和产生X射线的蒙特卡罗程序. 在无电磁场条件下有关电子散射偏转、能损、Kα特征线辐射和轫致辐射产生的蒙特卡罗模型和程序已在文献[19]中介绍. 为了模拟靶中存在电磁场时超热电子的输运, 本文在该程序中加入了电磁场对电子传输的影响, 并假设在超热电子传输过程中电磁场不随时间变化. 设在不包含电磁场作用的蒙特卡罗模型中, 电子与靶原子发生某种相互作用过程后自由飞行s的距离^[19]. 若靶内存在电场或磁场, 电子与靶原子发生相互作用时忽略电磁场影响, 发生相互作用后仍飞行s的距离, 但是位置和速度的方向由电磁力的一阶近似给出^[27], 分别为

其中$ {{\boldsymbol{r}}_0} $和$ {\boldsymbol{r}}(s) $分别是本次和下次作用前电子的位置, $ {{\boldsymbol{v}}_0} $和$ {\boldsymbol{v}}(s) $分别是本次和下次作用前电子的速度, $ {{\boldsymbol{\hat v}}_0} $是$ {{\boldsymbol{v}}_0} $的归一化矢量, $ {\boldsymbol{E}} $和$ {\boldsymbol{B}} $分别是电场强度和磁感应强度, e和$ {m_{\text{e}}} $分别是电子的电荷量和质量, c是真空中光速, $ \beta = {v_0}/c $, $ \gamma = {\left( {1 - {\beta ^2}} \right)^{ - 1/2}} $. 在数值计算中为了减小上述一阶近似导致的误差, (2)式仅用来给出电子运动速度的方向, 电子速度的大小由电子的能量$ {E_{\text{k}}} $计算得到. 电子与靶原子发生下次相互作用前的能量$ {E_{\text{k}}} $由两个位置的电势差计算得到:

其中$ {E_{{\text{k0}}}} $和$ {E_{\text{k}}}(s) $分别是本次和下次作用前电子的能量, $ \varphi $是电势. 本文探究靶中磁场对Kα辐射对比度的影响, (1)式和(2)式中的电场$ {\boldsymbol{E}} $为0, 磁场不会改变电子的能量, 电子在靶中的能量损失仅由阻止本领计算得到.

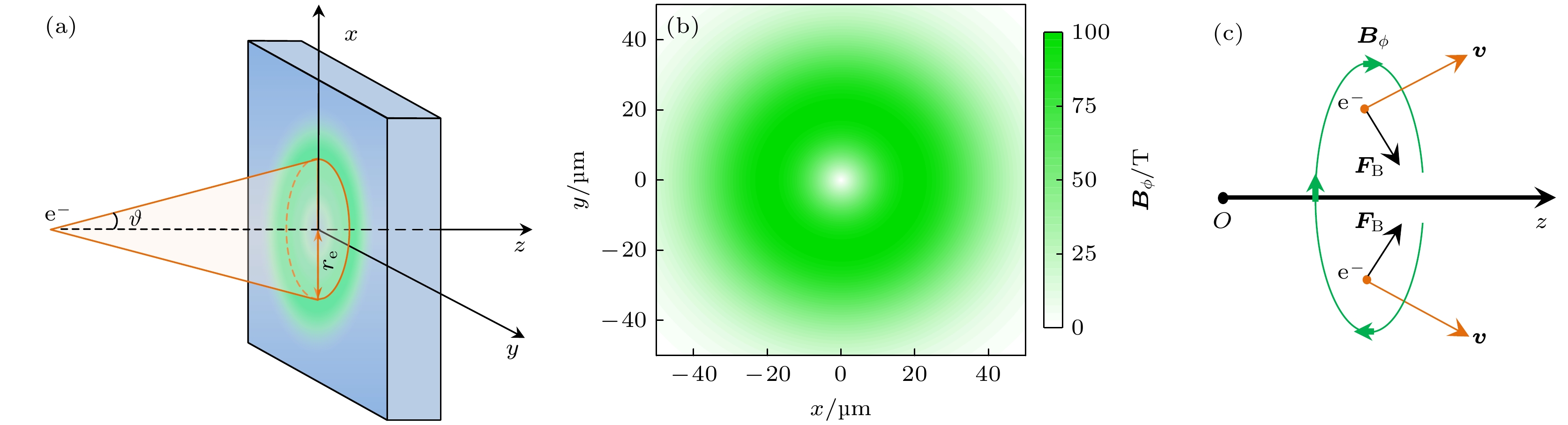
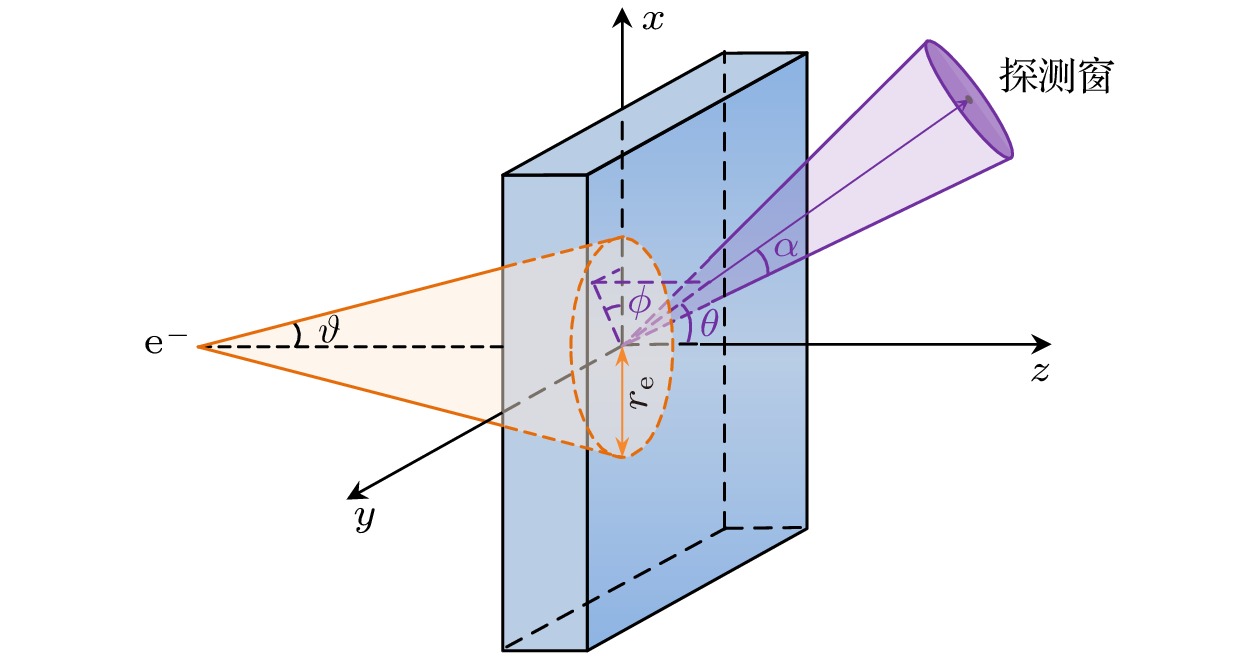
本文对电子束轰击铜靶时, 靶中分别存在轴向匀强磁场或高斯分布环形磁场对Kα辐射对比度的影响进行了模拟和分析. 激光辐照固体靶时在靶的前表面激光焦斑区域附近产生超热电子, 超热电子有一定的发散角^[28,29]. 为此, 如图1所示, 设模拟的电子束初始位于z轴负方向上一点, 沿z轴方向传播, 半发散角为$ \vartheta = {30^ \circ } $, 单位立体角内电子通量密度均匀分布. 在到达靶的前表面($ z = 0 $)时电子束圆斑的中心也就是铜平面靶的前表面的中心, 位于坐标原点, 电子束圆斑的半径为$ {r_{\text{e}}} = 20{\text{ μm}} $. 每次模拟的电子束包含$ 2 \times {10^8} $个电子. 铜靶的z方向厚度为$ \Delta z = 30{\text{ μm}} $, 在x和y方向上的宽度为$ \Delta x = \Delta y = 120{\text{ μm}} $. 图1中$ \theta $和$ \phi $分别代表探测窗的中心相对于坐标原点的极角和方位角. 探测窗距离坐标原点1 m, 半径为$ 8.75 \times {10^{ - 2}}{\text{ m}} $, 对应的半锥角$ {\text{α}}= {5^ \circ } $, 可以接收到足够数量的X射线光子以降低X射线谱的数据抖动.

通常情况下激光与物质作用产生的超热电子能谱类似玻尔兹曼分布^[30], 在模拟中入射电子能谱取$ f({E_{\text{k}}}) = {T_{\text{h}}}^{{{ - 1}}}\exp ( - {E_{\text{k}}}/{T_{\text{h}}}) $, 其中$ {T_{\text{h}}} $是超热电子温度, 电子能量范围从0—$ 10{T_{\text{h}}} $. 在某些情况下超热电子能谱呈现准单能谱^[31], 那么入射电子能谱取截掉低能部分的玻尔兹曼分布, 即入射电子能量从$ {E_{\text{c}}} $到$ 10{T_{\text{h}}} $. 此外, 为了分析不同能量电子的影响, 在部分模拟中取入射电子能谱为单一能量$ {E_{\text{k}}} $.

下面通过数值模拟探究轴向(即z方向)匀强磁场提高Kα辐射对比度的可能性, 分别模拟了靶中无磁场(WOB)或存在匀强磁场$ {{{{\boldsymbol{B}}}}_{\boldsymbol{z}}} = B_z \hat {\boldsymbol{z}} $时, $ \hat{\boldsymbol{ z}} $是z方向单位矢量, 温度为$ {T_{\text{h}}} = 600{\text{ keV}} $的玻尔兹曼能量分布的电子束或能量为$ {E_{\text{k}}} = 600{\text{ keV}} $的单能电子束入射$ 30{\text{ μm}} $厚的铜平面靶产生的Kα辐射和轫致辐射.

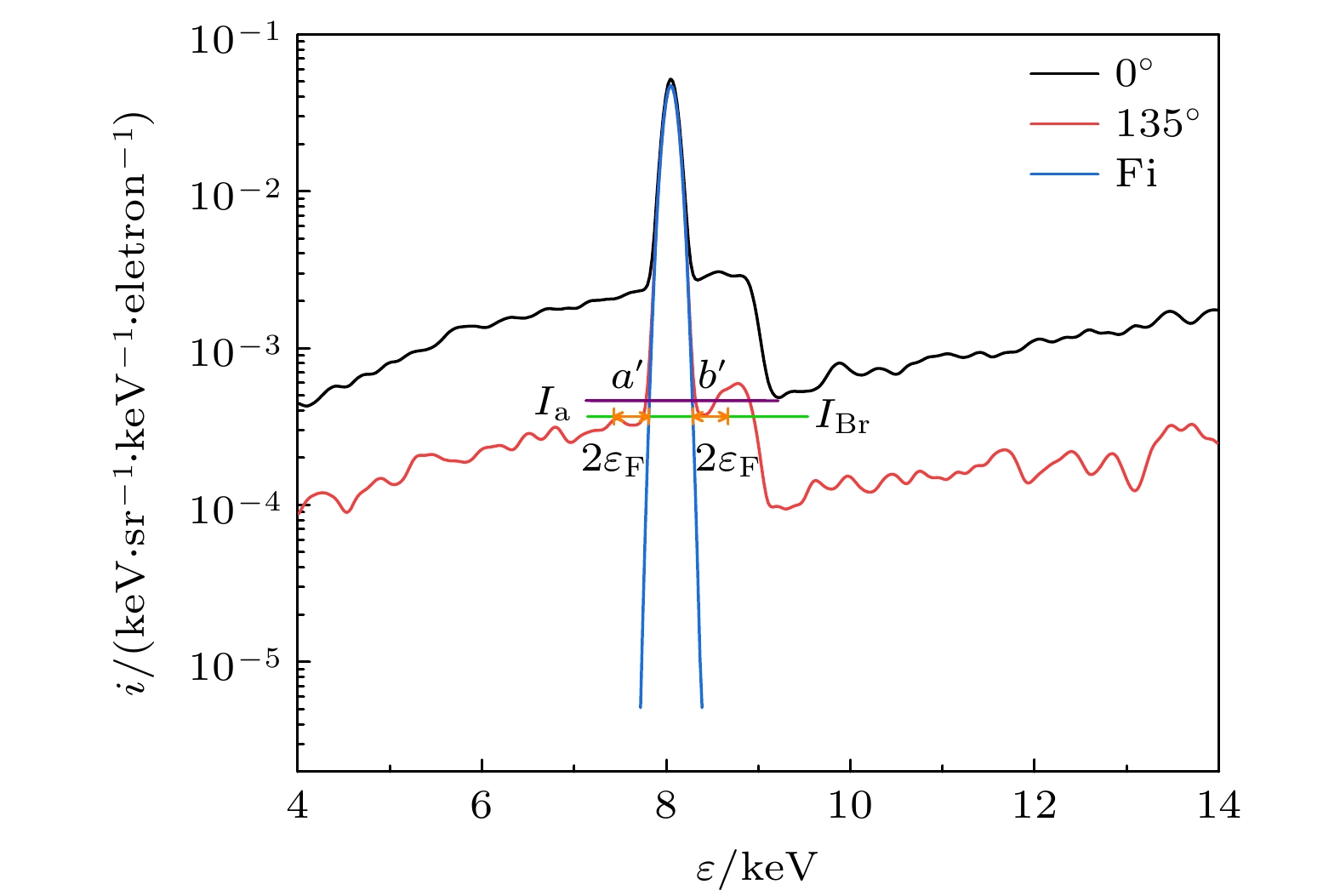
Kα辐射的对比度是从模拟结果合成的X射线谱得到的. 参考以往实验和模拟得到的Kα线谱的半高全宽^[8,32], 即谱密度峰值的一半对应的宽度, 对模拟中产生的 Kα辐射和轫致辐射都进行高斯展宽处理, 高斯展宽的半高全宽设为$ {\varepsilon _{\text{F}}} = 0.18{\text{ keV}} $. 图2是用这样方法给出的$ {T_{\text{h}}} = 600{\text{ keV}} $的电子束入射无磁场的铜靶时, 在$ \theta = {0^ \circ } $和$ {135^ \circ } $两个方向分别得到的X射线谱(探测窗放置在y-z平面内, $ \phi = {90^ \circ } $). 模拟给出轫致辐射最大光子能量可达入射电子能量, 图中只给出了4—14 keV范围的光谱.

Kα辐射对比度的计算方法与本研究组之前研究^[19]中方法相同. 以图2中$ \theta = {135^ \circ } $的X射线谱为例, 首先对Kα线谱的峰值的一半以上的部分进行高斯拟合得到曲线$ {F_{\text{i}}} $ (蓝色线), 取距离Kα线谱最近的小峰的峰值为$ {I_{{\text{Br}}}} $, 然后画一条水平线$ i(\varepsilon ) = {I_{{\text{Br}}}} $(绿色线), 其中$ i $表示X射线谱密度, $ \varepsilon $为光子能量, 该水平线与$ {F_{\text{i}}} $的两个交点对应的光子能量分别记为$ a $和$ b $($ a < b $). 通过将$ (a - 2{\varepsilon _{\text{F}}}, a) $和$ (b, b + 2{\varepsilon _{\text{F}}}) $范围内的谱密度求均值得到轫致辐射连续谱的平均强度:

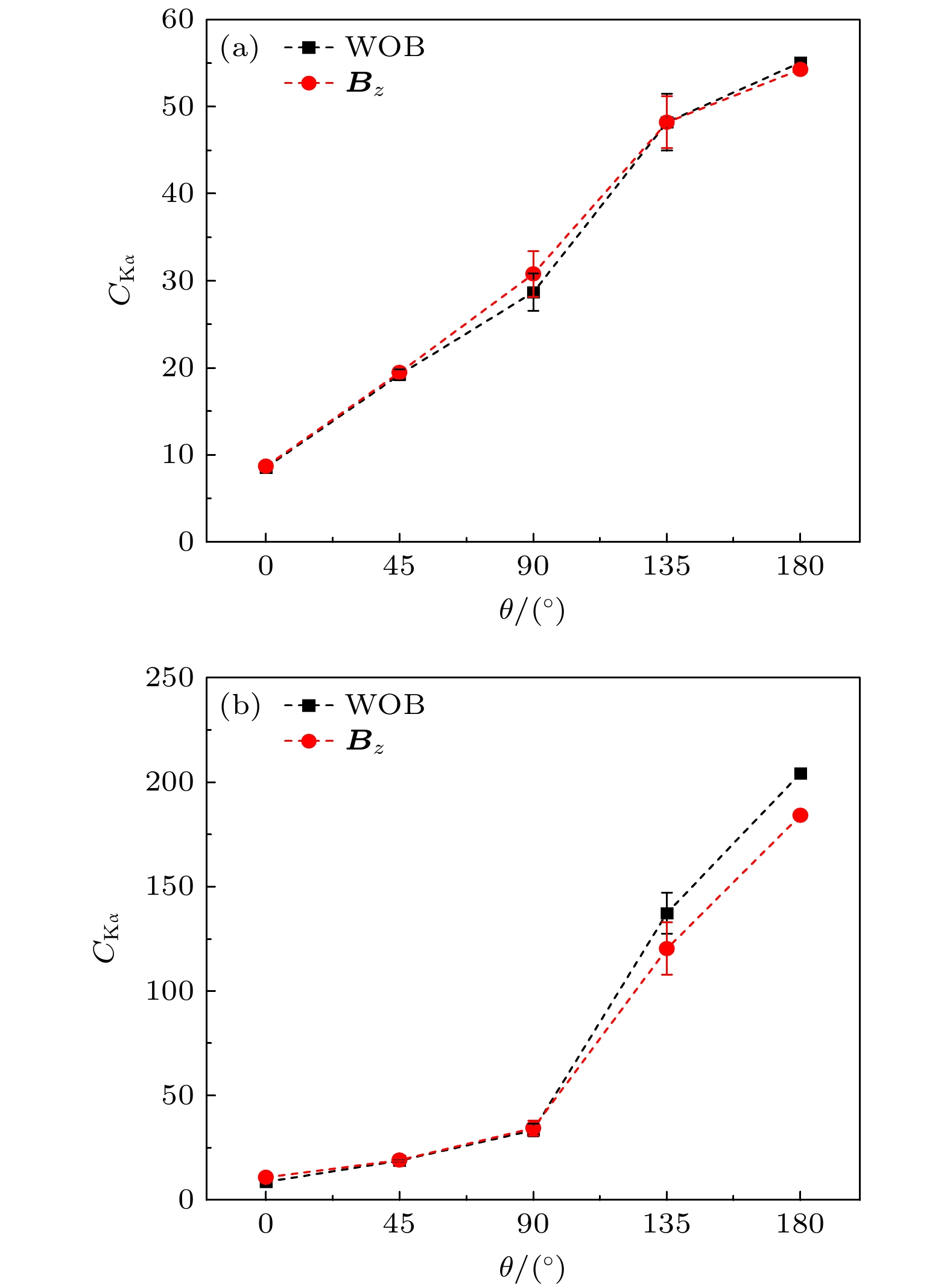
将新的水平线$ i(\varepsilon ) = {I_{\text{a}}} $ (紫色线)与$ {F_{\text{i}}} $的两个交点对应的光子能量记为$ a' $和$ b' $($ a' < b' $). Kα辐射的对比度$ {C_{{{{\mathrm{K}}{\text{α}}}}}} $定义为

$ {T_{\text{h}}} = 600{\text{ keV}} $的玻尔兹曼能量分布电子束入射时, 靶中无磁场与存在z方向匀强磁场$ {{{B}}_z} = 100{\text{ T}} $时不同$ \theta $方向的Kα辐射对比度如图3(a)所示. 探测窗分别设置在$ \theta = {0^ \circ }, {\text{ }}{45^ \circ }, {\text{ }}{90^ \circ }, {\text{ }}{135^ \circ } $和$ {180^ \circ } $这5个角度方向. 考虑到几何对称性和减小数值涨落, 对于每个$ \theta $, 探测窗的$ \phi $取$ {0^ \circ } $—$ {360^ \circ } $, 间隔$ {10^ \circ } $, 共36个值. 图3中数据点对应$ \theta $取不同值时从36个探测窗得到的Kα辐射对比度计算的平均值, 误差棒是这36个对比度的标准差. 其中$ \theta = {0^ \circ } $和$ {180^ \circ } $时标准差为0, 这是因为在这两个方向取不同的$ \phi $时得到的探测窗相同, 对比度只有一个值. 结果显示, $ \theta = {0^ \circ } $的 Kα辐射对比度较小, $ \theta = {180^ \circ } $的对比度较大. 原因是轫致辐射在$ \theta = {0^ \circ } $较强, 在$ \theta = {180^ \circ } $方向较弱^[17,19]. 而且, 靶中无磁场与存在z方向匀强磁场时Kα辐射对比度差别很小. 本文还模拟了改变磁场强度和电子温度的情况, 结论不变, 外加z方向匀强磁场对提高Kα辐射对比度基本没有影响.

类似图3(a), 图3(b)为$ {E_{\text{k}}} = 600{\text{ keV}} $的单能电子束入射时靶中无磁场与存在z方向匀强磁场$ {{{B}}_z} = 100{\text{ T}} $时不同$ \theta $方向的Kα辐射对比度. 结果显示, 与图3(a)玻尔兹曼能量分布电子束入射相比, 单能电子束入射时Kα辐射对比度的各向异性更强, 原因是单能电子产生轫致辐射的各向异性更强^[19]. 尽管如此, $ {E_{\text{k}}} = 600{\text{ keV}} $的单能电子束入射时, 靶中无磁场与存在z方向匀强磁场时Kα辐射对比度也差别不大. 以上结果表明, 不管玻尔兹曼能量分布的电子束入射(图3(a))还是单能电子束入射(图3(b)), 靶中无磁场与存在z方向匀强磁场时Kα辐射的对比度都很接近, z方向匀强磁场并不能有效提高Kα辐射的对比度.

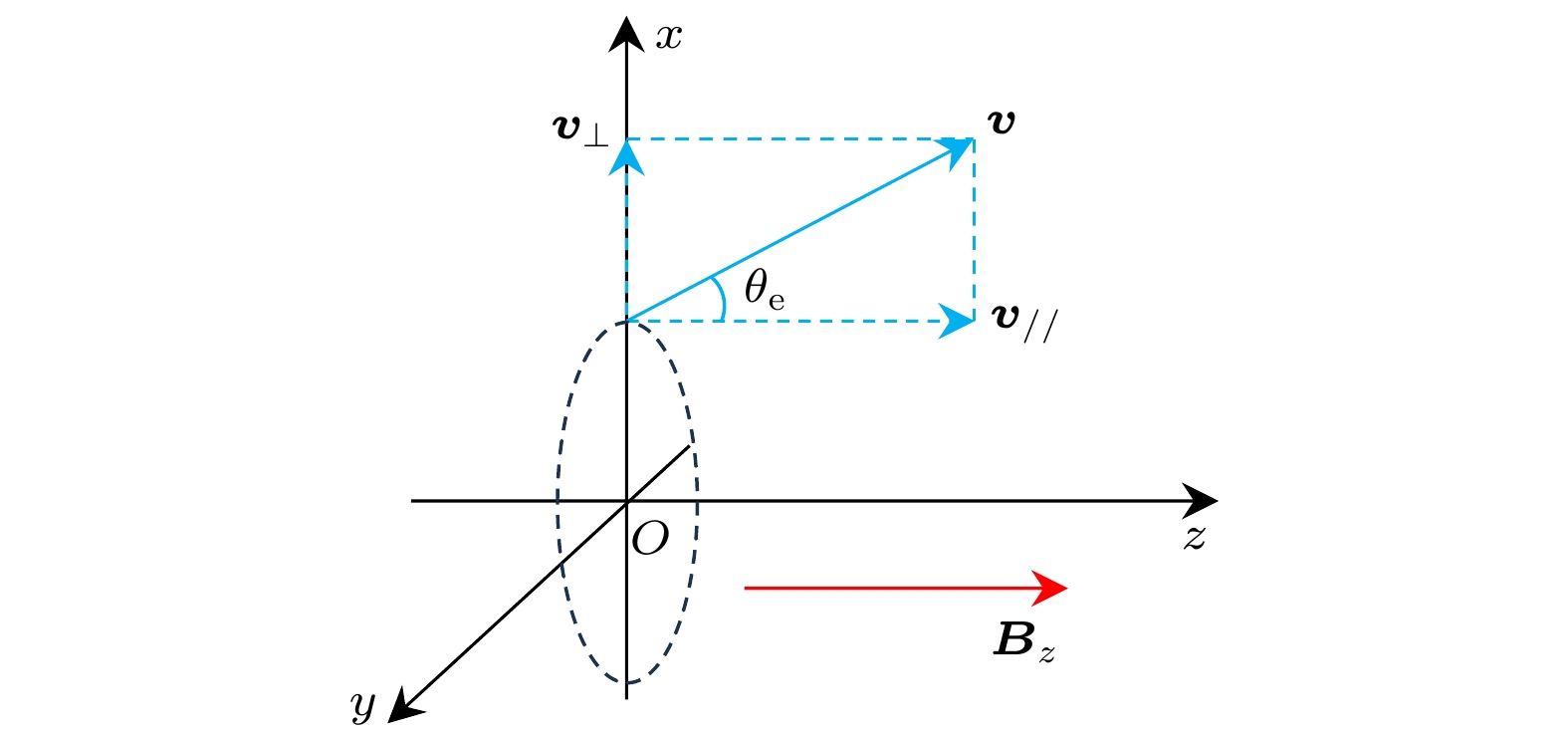
下文分析z方向匀强磁场不能有效提高Kα辐射对比度的原因. 考虑空间中有一电子, 初始位于x轴上, 其速度$ {\boldsymbol{v}} $在x-z平面内, 与z轴的夹角为$ {\theta _{\text{e}}} $, 如图4所示. 电子的速度$ {\boldsymbol{v}} $可分解为垂直z轴的速度分量$ {{\boldsymbol{v}}_ \bot } $和平行于z轴的速度分量$ {{\boldsymbol{v}}_{//}} $. 若没有磁场, 由于电子有x方向的恒定速度分量, 其在运动过程中位置会逐渐远离z轴. 若空间中存在沿z方向的匀强磁场$ {{\boldsymbol{B}}_z} $, 电子受到洛伦兹力$ {{\boldsymbol{F}}_{\text{B}}} = - e{\boldsymbol{v}} \times {{\boldsymbol{B}}_z} $, 磁场$ {{\boldsymbol{B}}_z} $对$ {{\boldsymbol{v}}_{//}} $没有影响, 会改变$ {{\boldsymbol{v}}_ \bot } $的方向, 但不会改变其大小.$ {{\boldsymbol{v}}_ \bot } $保持在x-y平面内且大小不变. 电子在空间中做螺旋运动, 其运动轨迹在x-y平面内的投影是一个半径不变的圆. 电子运动方向与z轴夹角的余弦值为$ \cos {\theta _{\text{e}}} = {v_{{\text{//}}}}/v $, 在螺旋运动过程中保持不变. 因此, z方向匀强磁场对电子的准直是将电子的位置约束在一定范围内, 不会改变电子运动方向与z轴的夹角$ {\theta _{\text{e}}} $. 而轫致辐射强度是其辐射方向与电子运动方向夹角的函数^[17], 相对于电子运动方向具有柱对称分布. 因此, 采用本文沿z方向的均匀分布发散束入射, 与无磁场情况相比, z方向匀强磁场无法增强轫致辐射的方向性. 以上分析没有考虑电子被靶物质散射的影响. 即使考虑了散射的影响, 参见图3, 模拟结果也证实, 无磁场和存在z方向匀强磁场两种情况下, 统计得到的电子运动方向与z轴的平均夹角几乎不变, 因此这两种情况下Kα辐射的对比度很接近, z方向匀强磁场不能有效提高Kα辐射的对比度.

下文探究环形磁场对Kα辐射对比度的影响. 参考以往对超热电子准直研究中的磁场^[22,23], 本文研究中设靶区域内存在高斯分布的环形磁场, 如图5(a)中绿色区域所示, 磁场在x-y平面内的分布可以表示为

其中$ {B_0} $是磁场的峰值, $ {r_{\text{a}}} = \sqrt {{x^2} + {y^2}} $, $ {\sigma _{\text{f}}} $表征磁场峰值与z轴的距离, $ \hat {\boldsymbol{x}} $和$ \hat {\boldsymbol{y}} $分别是x和y方向的单位矢量. 图5(b)展示了$ {B_0} = 100{\text{ T}} $, $ {\sigma _{\text{f}}} = 20{\text{ μm}} $的磁场在x-y平面内的分布.

环形磁场对电子的偏转作用与磁场的方向有关, 如图5(c)所示, 空间中的磁力线是中心位于z轴上的圆, 沿着z轴正向看, 磁力线为逆时针方向. 在z轴一侧的电子受到的洛伦兹力$ {{\boldsymbol{F}}_{\text{B}}} $驱使其向z轴的另一侧偏转, 使得电子运动方向与z轴的夹角减小, 从而准直电子束. 后文如无特别说明, 使用的环形磁场与此处介绍的相同, 且$ {B_0} = 100{\text{ T}} $.

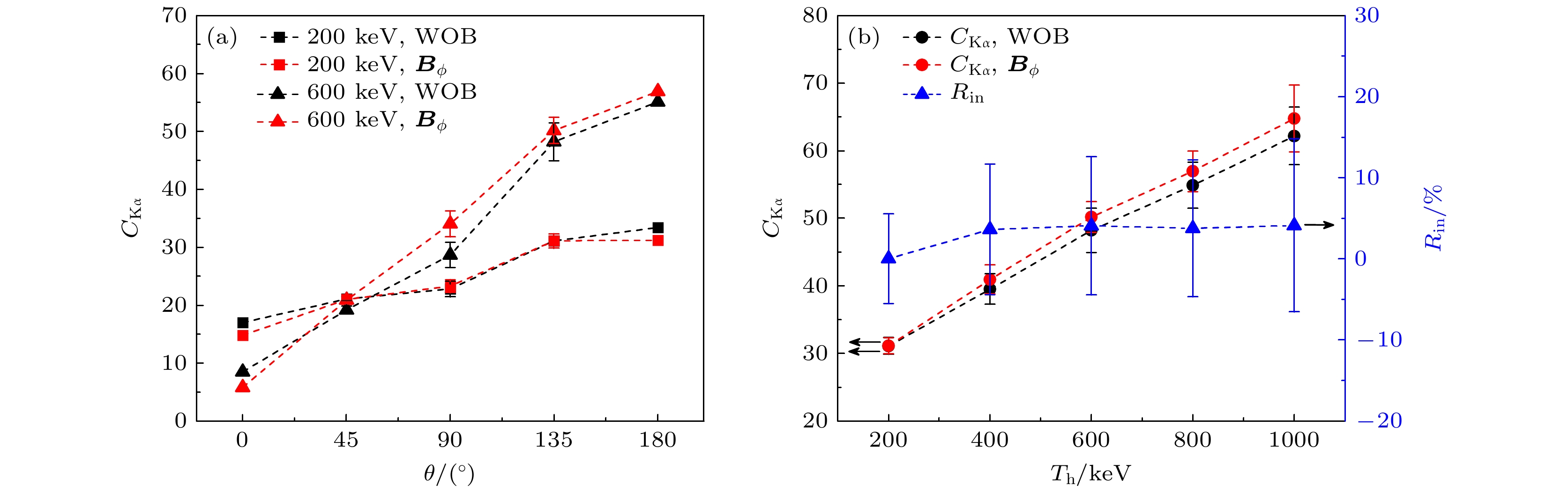
首先, 探究玻尔兹曼能量分布电子束入射的情况. 图6为靶中无磁场(WOB)和存在高斯分布的环形磁场($ {{\boldsymbol{B}}_\phi } $)时, 温度为200—1000 keV的玻尔兹曼能量分布的电子束入射$ 30{\text{ μm}} $厚的铜平面靶的模拟结果.

图6(a)是$ {T_{\text{h}}} = 200{\text{ keV}} $或600 keV电子束入射时Kα辐射沿不同$ \theta $值方向的对比度, 可以看出, $ {T_{\text{h}}} = 600{\text{ keV}} $的Kα辐射的对比度的各向异性比$ {T_{\text{h}}} = 200{\text{ keV}} $的各向异性更强, 这是因为能量更高的电子产生的轫致辐射的方向性更强. 在平面靶的电子束入射一侧($ \theta > {90^ \circ } $)得到的Kα辐射对比度更高. 对比无磁场(WOB)和存在磁场($ {{\boldsymbol{B}}_\phi } $)的结果可见, 存在环形磁场$ {{\boldsymbol{B}}_\phi } $时Kα辐射的对比度提升不大. 以$ \theta = {135^ \circ } $为例, $ {T_{\text{h}}} = 200{\text{ keV}} $的无磁场和存在磁场时Kα辐射对比度皆为31.1. $ {T_{\text{h}}} = 600{\text{ keV}} $的对比度均值也仅由无磁场时的48.2提高到存在磁场$ {{\boldsymbol{B}}_\phi } $时的50.2.

图6(b)展示了$ \theta = {135^ \circ } $的Kα辐射的对比度均值与入射电子温度$ {T_{\text{h}}} $的关系. 可以看出, 无论是否存在磁场, 随着电子温度的升高, $ \theta = {135^ \circ } $的对比度逐渐增大, 这是因为更高能电子的轫致辐射的方向性更好. 但是, 加磁场$ {{\boldsymbol{B}}_\phi } $对Kα辐射对比度的提高并不显著. 相较于无磁场的情况, 定义存在磁场时Kα辐射对比度的增幅为$ {{R_{{\text{in}}}} = {C_{{{{\mathrm{K}}{\text{α}}}}}}({{\boldsymbol{B}}_\phi })} {/ } {{C_{{{{\mathrm{K}}{\text{α}}}}}}({\text{WOB}})} - 1 $, 其中$ {C_{{{{\mathrm{K}}{\text{α}}}}}}({\text{WOB}}) $和$ {C_{{{{\mathrm{K}}{\text{α}}}}}}({{\boldsymbol{B}}_\phi }) $分别是靶中无磁场和存在磁场$ {{\boldsymbol{B}}_\phi } $时的Kα辐射对比度. $ {T_{\text{h}}} = 200{\text{ keV}} $时, $ {C_{{{{\mathrm{K}}{\text{α}}}}}}({\text{WOB}}) $和$ {C_{{{{\mathrm{K}}{\text{α}}}}}}({{\boldsymbol{B}}_\phi }) $均为31.1, 对比度增幅$ {R_{{\text{in}}}} $为0. $ {T_{\text{h}}} = 1000{\text{ keV}} $时加磁场$ {{\boldsymbol{B}}_\phi } $使对比度由62.2提高到64.7, 对比度增幅$ {R_{{\text{in}}}} $也仅为4.1%. 可见, 玻尔兹曼能量分布电子束入射时, 加磁场$ {{\boldsymbol{B}}_\phi } $对Kα辐射对比度的提高并不显著.

对于玻尔兹曼能量分布的电子束, 其中相当大部分电子的能量较低, 例如$ {T_{\text{h}}} = 600{\text{ keV}} $时, 0—200 keV的电子占入射总电子数的28.4%. 低能电子在靶中传输时散射角较大, 在磁场中回旋半径较小, 电子在靶中运动轨迹杂乱, 磁场$ {{\boldsymbol{B}}_\phi } $难以减小电子运动方向与z轴的夹角; 另一方面, 这些低能电子产生的轫致辐射的方向性较差, 加磁场$ {{\boldsymbol{B}}_\phi } $难以大幅增强轫致辐射的方向性. 下文进一步分析不同能量单能电子入射时情况.

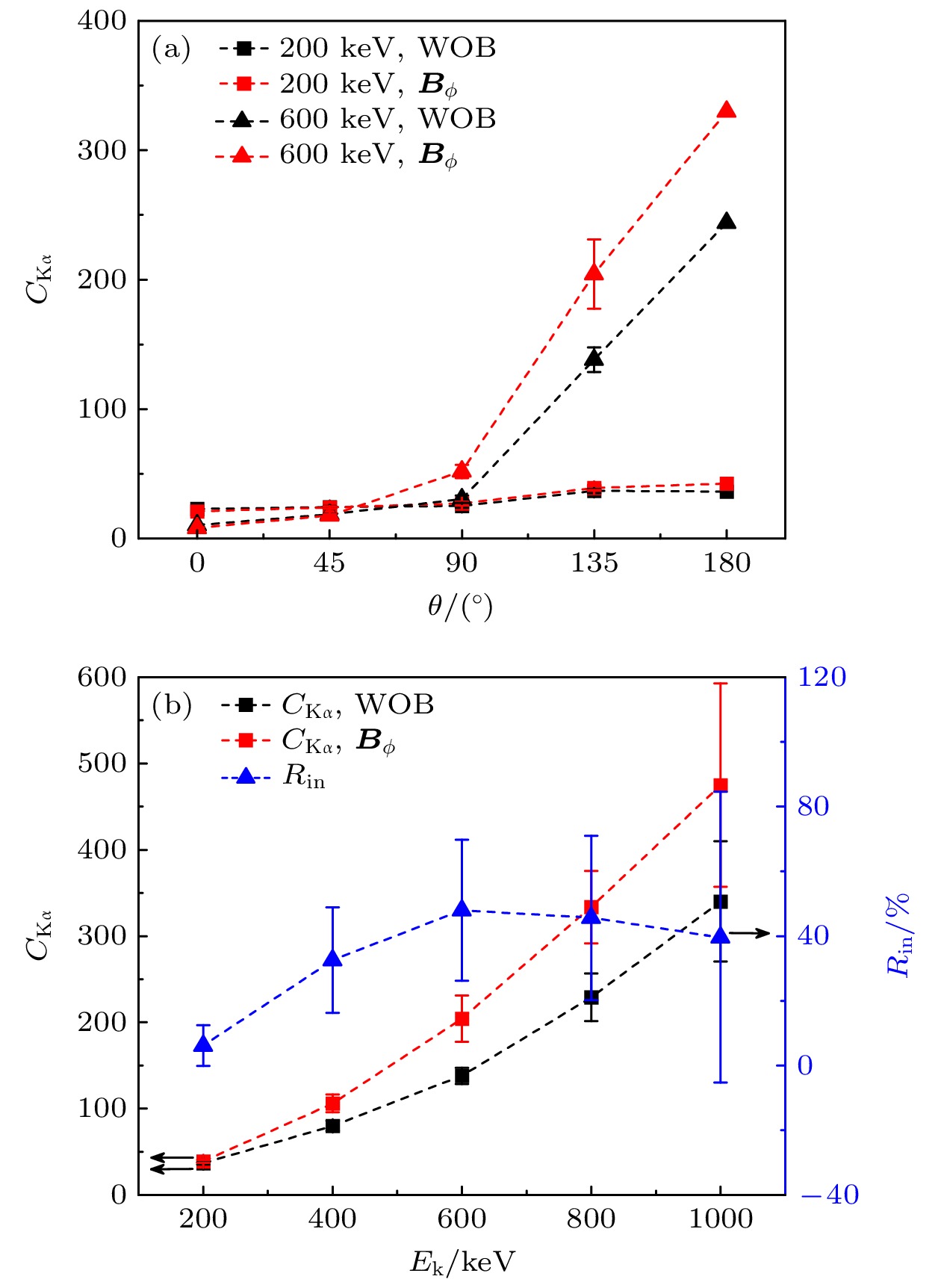
本文模拟了能量在200—1000 keV范围的单能电子束入射$ 30{\text{ μm}} $厚的铜平面靶的情况, 除了入射电子的能量是单能外, 其他模拟参数与图6相同. 能量$ {E_k} $分别为200 keV和600 keV的电子束入射时各探测角度的Kα辐射的对比度如图7(a)所示.$ {E_k} = 200{\text{ keV}} $时, 无磁场和存在磁场$ {{\boldsymbol{B}}_\phi } $时$ \theta = {135^ \circ } $的对比度分别为36.7和39.0, 增幅不大; $ {E_k} = 600{\text{ keV}} $时, 无磁场和存在磁场$ {{\boldsymbol{B}}_\phi } $时$ \theta = {135^ \circ } $的对比度分别为138.1和204.4, 增幅明显. 图7(b)给出了不同能量的单能电子束入射时无磁场与存在磁场$ {{\boldsymbol{B}}_\phi } $时$ \theta = {135^ \circ } $的Kα辐射对比度. 与图6相比, 单能电子束入射时Kα辐射的对比度更高, 得益于单能电子入射时轫致辐射的方向性更好. 其次, 单能电子束入射时, 加磁场$ {{\boldsymbol{B}}_\phi } $能带来更显著的对比度提升. 从图7(b)还可得到, 200, 600和1000 keV的对比度增幅$ {R_{{\text{in}}}} $分别为6.2%, 48.0%和39.7%, 表明入射电子能量较大时, 加磁场$ {{\boldsymbol{B}}_\phi } $才能有效提高Kα辐射的对比度.

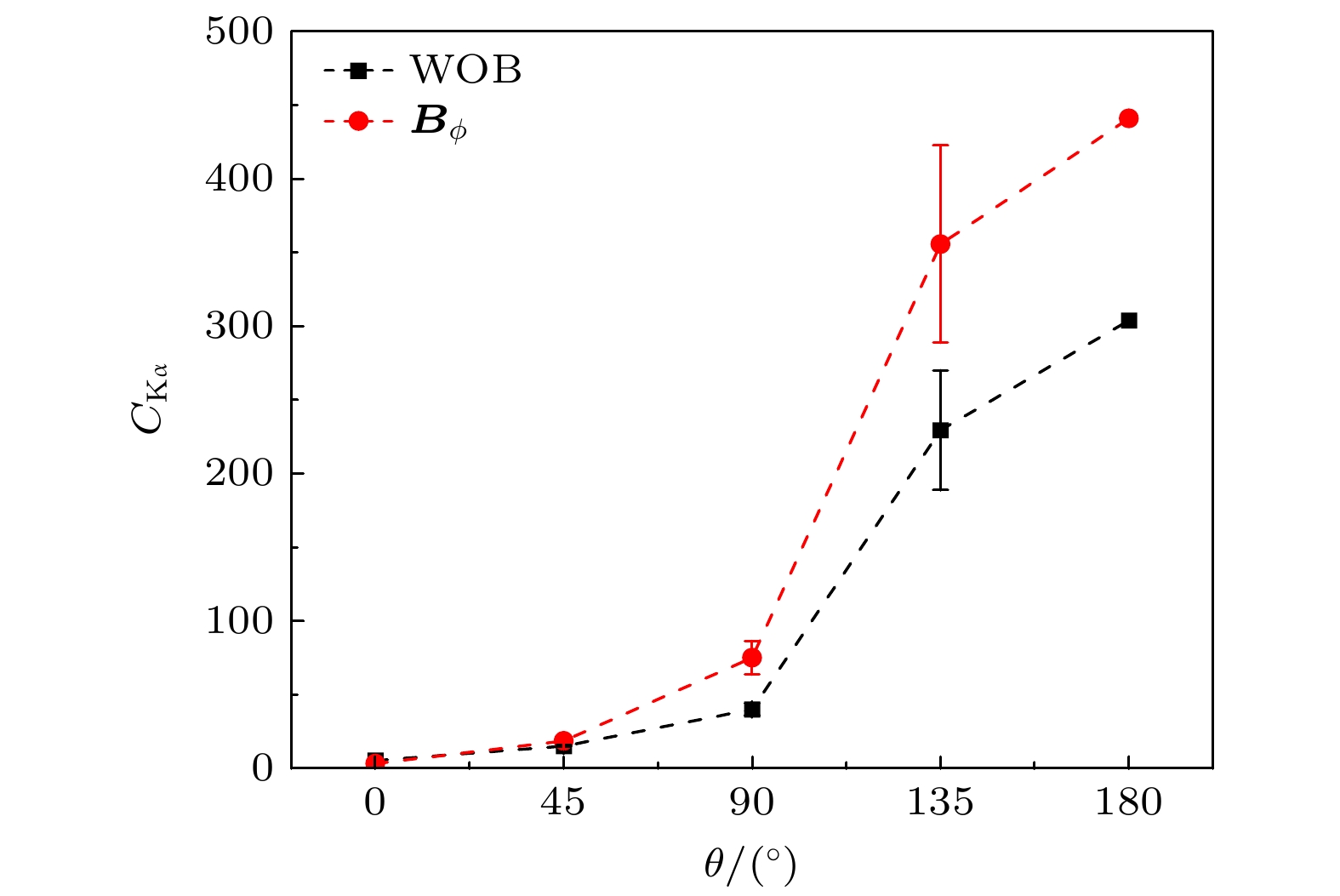
本文还模拟了截掉能量小于500 keV的$ {T_{\text{h}}} = 600{\text{ keV}} $的玻尔兹曼分布电子束入射$ 30{\text{ μm}} $厚铜平面靶的情况. 除了入射电子的能谱分布, 其他参数与图6(a)中$ {T_{\text{h}}} = 600{\text{ keV}} $的算例相同, 模拟结果如图8所示. 无磁场与存在环形磁场$ {{\boldsymbol{B}}_\phi } $时$ \theta = {135^ \circ } $的Kα辐射对比度分别为229.4和355.7, 对比度增幅$ {R_{{\text{in}}}} $达55.0%, 已经超过图7(b)中600 keV单能电子入射时的对比度增幅($ {R_{{\text{in}}}} = 48.0\% $). 以上对单能电子束入射和截掉低能部分的玻尔兹曼能量分布电子束入射的模拟结果, 确认了3.2.1节中玻尔兹曼能量分布电子束入射时Kα辐射的对比度增幅不大的原因是其中含有相当大部分低能电子.

实验方面已有方法减少超热电子能谱中的低能电子成分. 例如, Toncian等^[31]使用高强度短脉冲激光辐照纳米厚度的超薄靶, 通过激光直接加速机制在激光传播方向产生能量达MeV的准单能谱电子束. Braenzel等^[33]使用高对比度激光脉冲辐照间隔适当距离的两个超薄靶, 第1个靶用于加速电子, 而第2个靶增大能谱中高能电子的比例. 参考这些方法设计实验, 将有助于本文研究结果应用到实验中产生更高对比度的Kα辐射.

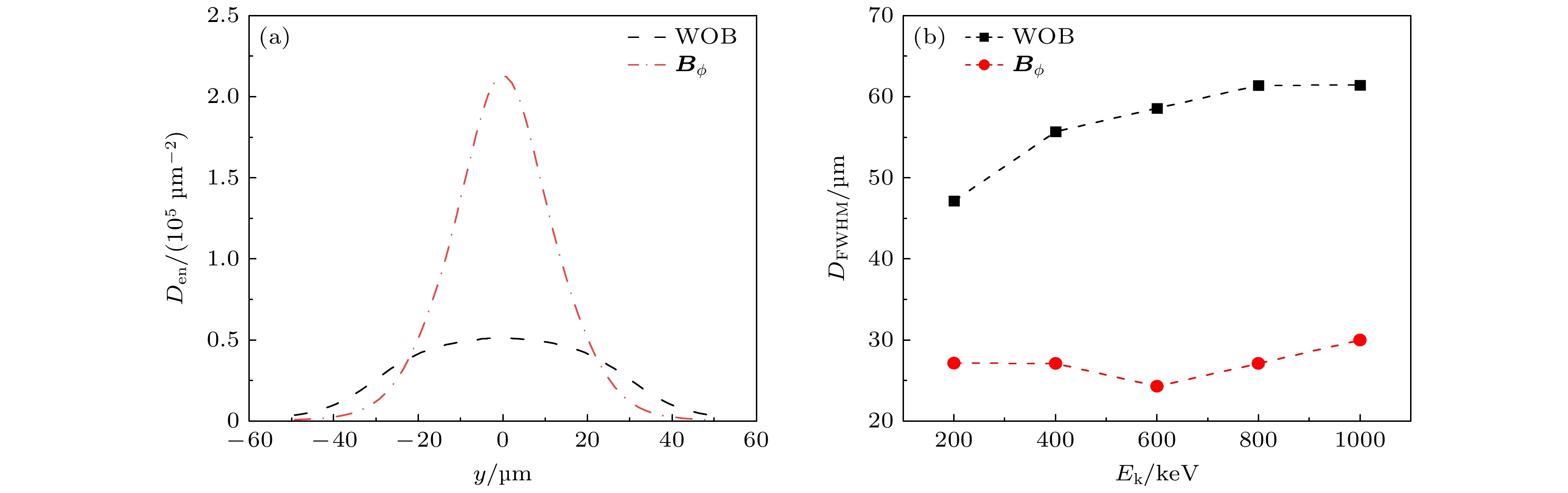
图9(a)给出了无磁场与存在环形磁场$ {{\boldsymbol{B}}_\phi } $条件下, $ {E_{\text{k}}} = 600{\text{ keV}} $的单能电子束入射, 传输到靶后表面的电子束斑过其中心沿y方向的电子数密度分布$ {D_{{\text{en}}}} $, 单位为单位面积的电子数. 设$ {D_{{\text{en}}}} $分布的半高全宽为$ {D_{{\text{FWHM}}}} $, 无磁场与存在磁场$ {{\boldsymbol{B}}_\phi } $时$ {D_{{\text{FWHM}}}} $分别为58.6 μm和24.3 μm, 体现了磁场$ {{\boldsymbol{B}}_\phi } $对电子束的准直作用. 图9(b)给出了不同能量的单能电子束入射时无磁场和存在磁场$ {{\boldsymbol{B}}_\phi } $时靶后表面的$ {D_{{\text{FWHM}}}} $. 对于能量在200—1000 keV范围的电子束, 存在磁场$ {{\boldsymbol{B}}_\phi } $时的$ {D_{{\text{FWHM}}}} $都明显小于无磁场的$ {D_{{\text{FWHM}}}} $, 表明磁场$ {{\boldsymbol{B}}_\phi } $对电子束有明显的准直作用. 以上结果表明, 环形磁场不仅能准直电子束, 也能有效提高Kα辐射的对比度.

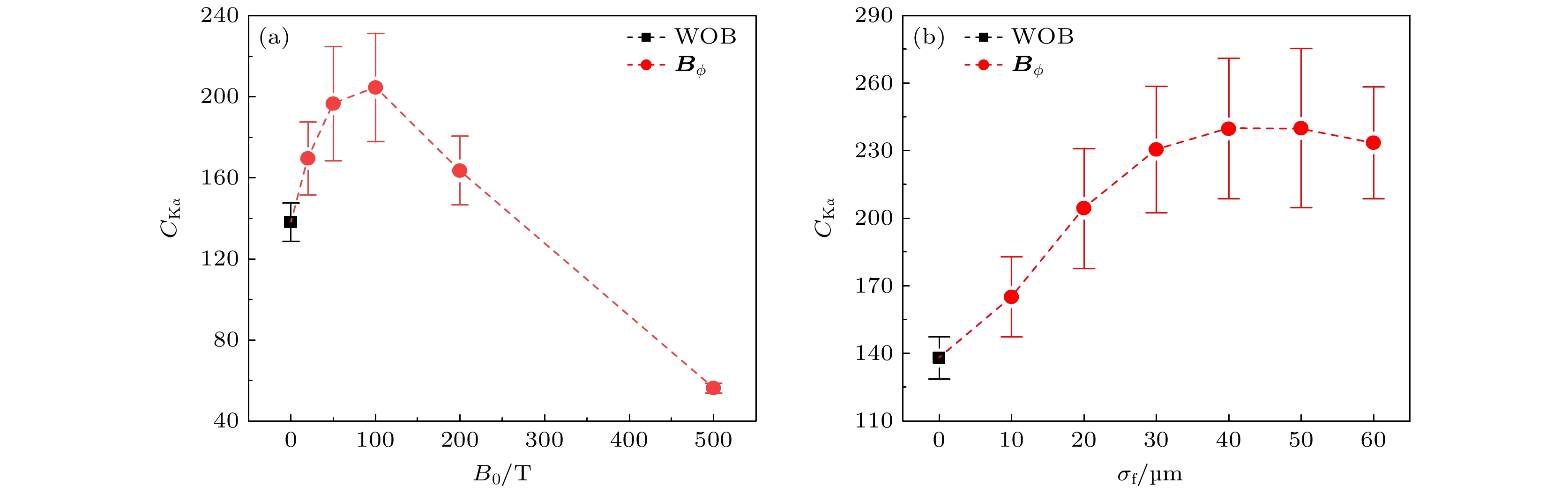
以上的模拟中环形磁场的峰值$ {B_0} $为100 T, 峰值半径$ {\sigma _{\text{f}}} $为20 μm. 考虑到实验中环形磁场的大小与空间分布会受到入射激光等因素的影响, 本节研究$ {B_0} $和$ {\sigma _{\text{f}}} $变化时对Kα辐射对比度的影响. 靶和入射电子束的参数与图7(a)中入射电子能量为600 keV的算例相同, 图10给出了存在不同$ {B_0} $和$ {\sigma _{\text{f}}} $的环形磁场$ {{\boldsymbol{B}}_\phi } $时单能600 keV电子束入射30 μm厚铜靶在$ \theta = {135^ \circ } $的Kα辐射对比度.

图10(a)给出了存在$ {\sigma _{\text{f}}} = 20{\text{ μm}} $, 不同$ {B_0} $的环形磁场$ {{\boldsymbol{B}}_\phi } $以及无磁场时$ \theta = {135^ \circ } $的Kα辐射对比度. 无磁场时, Kα辐射的对比度为138.1; 存在磁场$ {{\boldsymbol{B}}_\phi } $时, 随着$ {B_0} $从0增大到500 T, 对比度先增大后减小. Kα辐射的对比度在$ {B_0} = 100{\text{ T}} $附近达到最大, 为204.4.$ {B_0} = 500{\text{ T}} $时, Kα辐射的对比度为56.1, 比无磁场时的对比度还要小. 图10(b)给出了靶中存在$ {B_0} = 100{\text{ T}} $, 不同$ {\sigma _{\text{f}}} $的环形磁场以及无磁场时$ \theta = {135^ \circ } $的Kα辐射对比度. 可以看出, Kα辐射的对比度随着$ {\sigma _{\text{f}}} $的增大而逐渐增大, 在$ {\sigma _{\text{f}}} $达到约40 μm后趋于平缓.

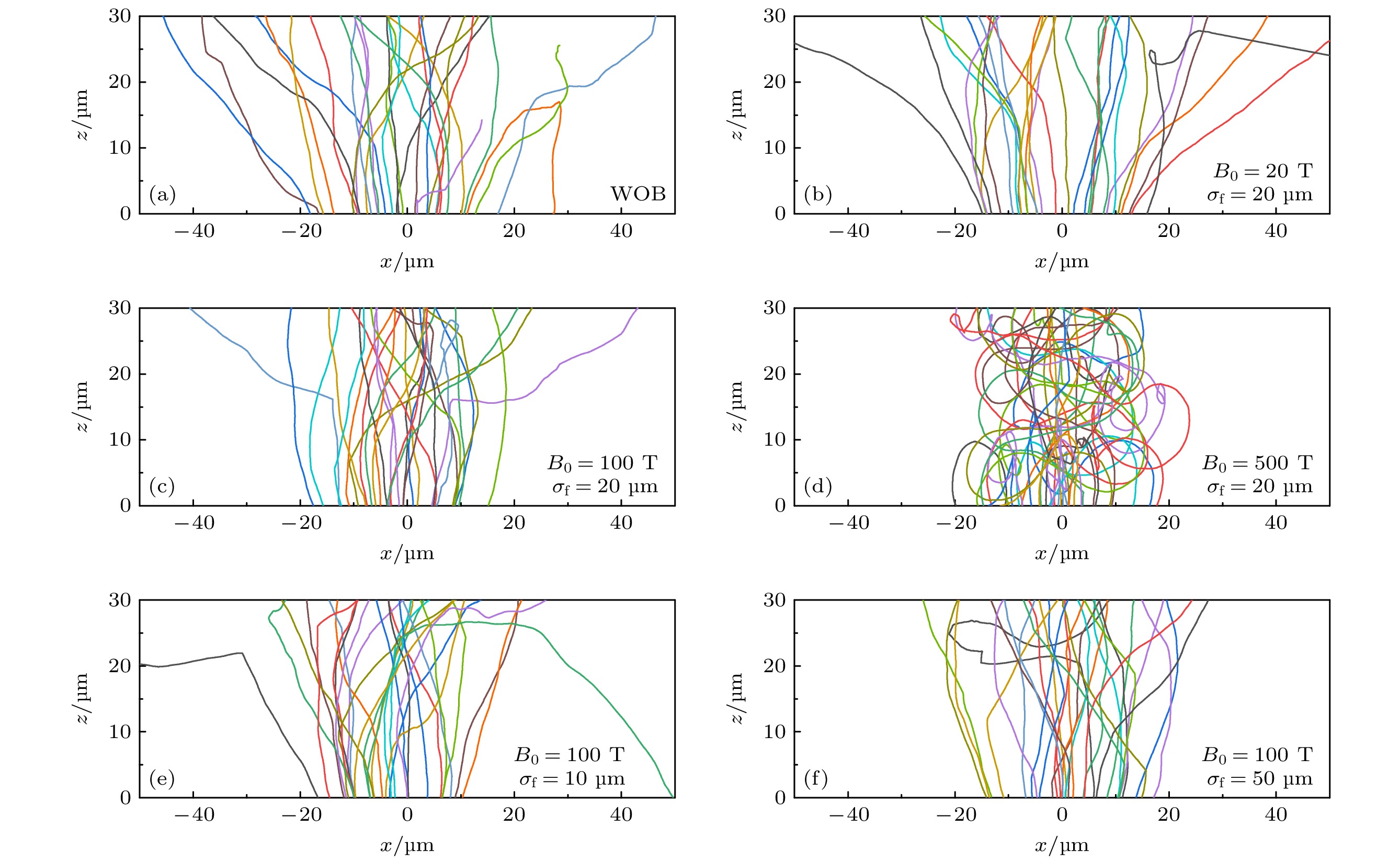
为了分析图10的结果, 图11给出了靶中存在不同$ {B_0} $和$ {\sigma _{\text{f}}} $的环形磁场时电子的运动轨迹. 为了清晰展示, 每个模拟中入射电子束仅包含30个单能600 keV的电子. 图11(a)—(d)分别为无磁场和存在$ {B}_{0}=20, \; {100}, \;500\; {\mathrm{T}} \;({\sigma }_{\text{f}}=20\text{ μm)} $的环形磁场时的电子轨迹. 从图11(a)—(c), 随着$ {B_0} $的增大, 磁场对电子的准直作用逐渐增强, 对应的$ {135^ \circ } $方向Kα辐射的对比度逐渐增大. 但当$ {B_0} $太大时, 以图11(d)为例, 电子在靶中的回旋半径较小, 在靶中会偏转更大的角度, 导致电子运动方向与z轴的夹角增大, 轫致辐射的方向性变差, 对应的$ \theta = {135^ \circ } $方向的Kα辐射对比度更小. 图11(e), (c), (f)分别为$ {B_0} = 100\;{\text{ T}} $, $ {\sigma _{\text{f}}} $= 10, 20和50 μm的环形磁场时的电子轨迹. $ {\sigma _{\text{f}}} $= 10 μm时(图11(e))磁场$ {{\boldsymbol{B}}_\phi } $对电子的准直效果不如$ {\sigma _{\text{f}}} = 20 $, 50 μm的情况(图11(c), (f)), 这是因为磁场的峰值半径$ {\sigma _{\text{f}}} $越大, 可以准直更多的电子. 因此, 图10(b)中$ \theta = {135^ \circ } $的对比度随着$ {\sigma _{\text{f}}} $的增大而增大. 由于靶前表面电子束斑半径$ {r_{\text{e}}} = 20{\text{ μm}} $, $ {\sigma _{\text{f}}} $达到40 μm及更大时环形磁场已能约束绝大部分电子, 再增大$ {\sigma _{\text{f}}} $已不能进一步提高Kα辐射对比度.

对200, 1000 keV等其他能量的电子束入射的研究表明, 对应Kα辐射对比度增幅最大的磁场峰值仍在$ {B_0} = 100{\text{ T}} $附近. 这是因为入射电子束是发散束, 使得环形磁场对电子束的准直效果对入射电子的能量不敏感.

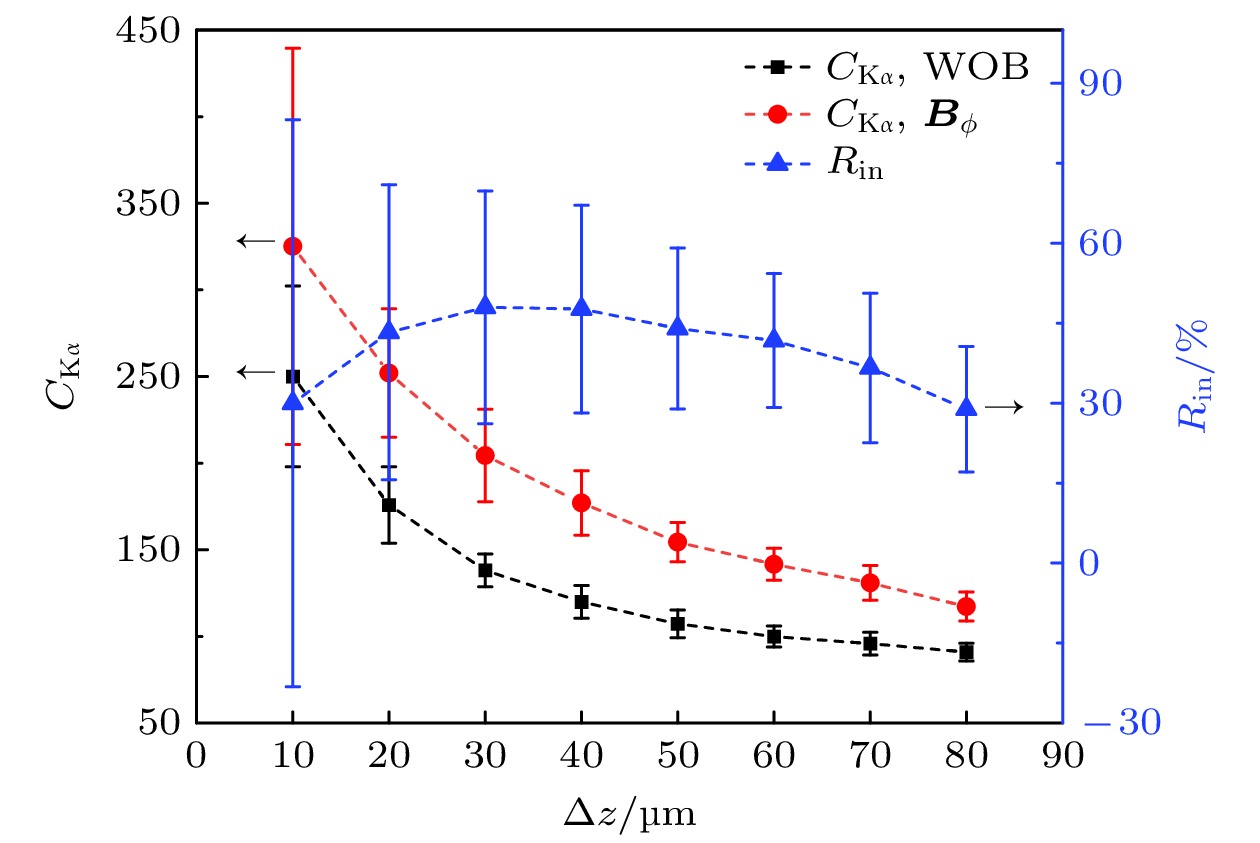
考虑到实验中薄膜靶的厚度可能变化, 本文模拟了无磁场和存在磁场$ {{\boldsymbol{B}}_\phi } $时单能600 keV的电子束入射厚度为$ \Delta z = 10—80{\text{ μm}} $的铜平面靶的情况. 靶在x和y方向的厚度$ \Delta x = \Delta y = 120{\text{ μm}} $, 保持不变, 其余参数与图7(a)中入射电子能量为600 keV的算例相同.

图12给出600 keV的单能电子束入射不同厚度的铜平面靶时$ \theta = {135^ \circ } $的Kα辐射对比度. 随着靶厚度的增大, $ \theta = {135^ \circ } $的Kα辐射对比度逐渐减小, 这是因为随着靶厚度的增大, 电子在靶内散射次数更多, 轫致辐射的方向性变差^[19]. 不过从Kα辐射对比度的增幅$ {R_{{\text{in}}}} $来看, 对于10—80 μm厚的铜靶, $ {B_0} = 100{\text{ T}} $的环形磁场对$ \theta = {135^ \circ } $的Kα辐射对比度的增幅均在28%以上, 表明对比度增幅对靶厚度的变化不敏感.

针对超热电子产生的Kα辐射, 本文采用蒙特卡罗数值模拟, 研究了对超热电子束传输有准直 作用的轴向匀强磁场和高斯分布的环形磁场提高Kα辐射对比度的可能性. 模拟和分析表明, 轴向匀强磁场无法增强轫致辐射的方向性, 不能有效 地提高Kα辐射的对比度. 若靶中存在高斯分布的环形磁场, 入射电子能谱具有玻尔兹曼能量分布时, 由于含有相当大部分低能电子且它们的轫致辐射方向性较差, Kα辐射对比度的增幅很小; 当截掉低能部分的玻尔兹曼能谱电子束或能量较高 的单能电子束入射时, 沿入射电子束后向的Kα辐射对比度有明显提高. 能量为600 keV的单能电子束入射时, $ {135^ \circ } $方向的Kα辐射对比度可提高48.0%. 在200—1000 keV电子能量范围, 对比度增幅最大的磁场峰值在100 T左右. Kα辐射的对比度增幅对靶厚度的变化不敏感. 本文结果可为磁场提高Kα辐射对比度提供参考. 轴向磁场和环形磁场对Kα辐射对比度的影响不同或可应用于区分磁场分布.

感谢本研究组张宇和李亮亮在程序建立之初的讨论和贡献, 感谢中国科学技术大学超级计算中心对本文数值计算的支持和帮助.