高级搜索

超低频/射频联合驱动容性耦合等离子体中二次电子效应的模拟

,  ,  , 

downloadPDF

上一篇

下一篇

史寒旭, 李欣阳, 张钰如, 王友年. 超低频/射频联合驱动容性耦合等离子体中二次电子效应的模拟[J]. 物理学报, 2025, 74(13): 135203-1. doi: 10.7498/aps.74.20250341
引用本文: 史寒旭, 李欣阳, 张钰如, 王友年. 超低频/射频联合驱动容性耦合等离子体中二次电子效应的模拟[J]. 物理学报, 2025, 74(13): 135203-1. doi: 10.7498/aps.74.20250341
shu
Hanxu SHI, Xinyang LI, Yuru ZHANG, Younian WANG. Numerical investigation of the secondary electron effect in capacitively coupled plasmas driven by ultra-low frequency/radio frequency sources[J]. Acta Physica Sinica, 2025, 74(13): 135203-1. doi: 10.7498/aps.74.20250341
Citation: Hanxu SHI, Xinyang LI, Yuru ZHANG, Younian WANG. Numerical investigation of the secondary electron effect in capacitively coupled plasmas driven by ultra-low frequency/radio frequency sources[J]. Acta Physica Sinica, 2025, 74(13): 135203-1. doi: 10.7498/aps.74.20250341
shu

超低频/射频联合驱动容性耦合等离子体中二次电子效应的模拟

  • 大连理工大学物理学院, 三束材料改性教育部重点实验室, 大连　116024

    • 作者简介: 史寒旭. E-mail: 1697165527@qq.com .
    通讯作者: E-mail: yrzhang@dlut.edu.cn.; 

  • 中图分类号: 52.50.Qt, 52.65.-y

Numerical investigation of the secondary electron effect in capacitively coupled plasmas driven by ultra-low frequency/radio frequency sources

  • Key Laboratory of Materials Modification by Laser, Ion, and Electron Beams, Ministry of Education, School of Physics, Dalian University of Technology, Dalian 116024, China

    • Corresponding author: E-mail: yrzhang@dlut.edu.cn.; 

  • MSC: 52.50.Qt, 52.65.-y

  • 摘要: 采用二维流体模型, 研究了不同的超低频电压、二次电子发射系数和极板间隙下, 二次电子对双频容性耦合等离子体特性的影响, 其中超低频源频率为400 kHz. 首先, 采用依赖离子能量的二次电子发射系数, 发现电子密度随超低频电压呈现出先降低后增高的趋势. 这是由于一方面, 较高的超低频电压会压缩有效放电体积; 另一方面, 极板发射的二次电子可以获得更多的能量, 进而增强电离过程. 通过与固定的二次电子发射系数的结果相比, 发现在较低的超低频电压下, 采用依赖能量的二次电子发射系数的结果接近于固定值为0.1的情况; 随着超低频电压的增加, 当采用依赖能量的发射系数时, 密度涨幅超过固定值为0.2的结果, 说明超低频电压对二次电子效应的增强效果并不是线性的. 最后, 对比了不同极板间隙下的等离子体特性, 发现随着极板间隙从2 cm增加到4 cm, 电离率的峰值有所下降, 但电子密度显著地增加, 等离子体的径向均匀性有所改善. 此外, 随着超低频电压的升高, 极板间隙对密度的影响越显著. 本文的研究结果有助于深入地理解超低频电源参数对于二次电子效应的影响, 并为等离子体工艺的优化提供一定的指导.
    Abstract: In recent years, capacitively coupled plasmas driven by ultra-low frequency source have received increasing attention, because they are beneficial to generating ions with high energy and small scattering angle, which aligns well with the current trend in high aspect ratio etching. Since the sheath becomes thicker when an ultra-low frequency source is applied, the secondary electron emission becomes significant. Indeed, these energetic secondary electrons can enhance the ionization process and even affect the discharge mode. In this work, a two-dimensional fluid model is employed to study the influence of secondary electrons on the dual-frequency capacitively coupled plasma under different ultra-low frequency voltages, secondary electron emission coefficients and inter-electrode gaps. The high frequency is fixed at 13.6 MHz, and the ultra-low frequency is fixed at 400 kHz. First, by using the ion energy dependent secondary electron emission coefficient, it is shown that the electron density first decreases and then increases with ultra-low frequency voltage rising. This is because, on the one hand, the higher ultra-low frequency voltage leads to thicker sheath, and therefore, the effective discharge volume is compressed. On the other hand, secondary electrons emitted from electrodes can obtain more energy, thus enhancing the ionization process. By comparing with the results obtained with a fixed secondary electron emission coefficient, it is found that in the low voltage range, the evolution of the electron density is similar to that with a fixed coefficient of 0.1. While, in the high voltage range, the growth of the electron density is even more pronounced than that with a fixed coefficient of 0.2, indicating that the enhancement of the secondary electron effect by ultra-low frequency voltage is non-linear. Finally, the influence of discharge gap on the plasma properties is also discussed. It is shown that with the inter-electrode gap increasing from 2 to 4 cm, the maximum ionization rate becomes lower, but the electron density rises significantly, and the plasma radial uniformity is improved. When inter-electrode gap is large, secondary electrons can completely collide with neutral species, so their influence on the electron density at high ultra-low frequency voltage is more significant. The results obtained in this study contribute to understanding the influence of ultra-low frequency source on the secondary electron effect, and provide some guidance for optimizing plasma processing.
  • 加载中

  • 图 1  二维腔室结构示意图

    Figure 1.  Schematic diagram of two-dimensional chamber structure.

    下载: 全尺寸图片 幻灯片

    图 2  采用经验公式计算的二次电子发射系数下, 电子密度的(a)轴向分布和(b)径向分布随超低频电压的变化

    Figure 2.  Variation of (a) axial distribution and (b) radial distribution of electron density with ultra-low frequency voltage under secondary electron emission coefficient calculated by empirical formula.

    下载: 全尺寸图片 幻灯片

    图 3  超低频电压不同时, 采用经验公式计算二次电子发射系数下, 腔室中心r = 0 cm处电离率的时空分布　(a) 100 V; (b) 400 V; (c) 700 V; (d) 1000 V

    Figure 3.  Using empirical formula to calculate the temporal and spatial distribution of ionization rate at r = 0 cm in the center of the chamber under the secondary electron emission coefficient, ultra-low frequency: (a) 100 V; (b) 400 V; (c) 700 V; (d) 1000 V.

    下载: 全尺寸图片 幻灯片

    图 4  采用经验公式计算二次电子发射系数下, 超低频电压1000 V时, 腔室中心r = 0 cm处的(a)轴向电场和(b)电子温度的时空分布

    Figure 4.  Using empirical formula to calculate the temporal and spatial distribution of (a) axial electric field and (b) electron temperature at the center of the chamber r = 0 cm at ultra-low frequency voltage of 1000 V under the secondary electron emission coefficient.

    下载: 全尺寸图片 幻灯片

    图 5  不同的二次电子发射系数下, 体平均电子密度随超低频电压的变化

    Figure 5.  Variation of volume average electron density with ultra-low frequency voltage under different secondary electron emission coefficients.

    下载: 全尺寸图片 幻灯片

    图 6  超低频电压为200 V时, 不同二次电子发射系数下, 电离率的时空分布　(a) $ {\gamma _{\text{i}}} $ = 0; (b) $ {\gamma _{\text{i}}} $ = 0.1; (c) $ {\gamma _{\text{i}}} $ = 0.2; (d)采用经验公式计算$ {\gamma _{\text{i}}} $

    Figure 6.  Time and space distribution of ionization rate under different secondary electron emission coefficients at ultra-low frequency voltage of 200 V: (a) $ {\gamma _{\text{i}}} $ = 0; (b) $ {\gamma _{\text{i}}} $ = 0.1; (c) $ {\gamma _{\text{i}}} $ = 0.2; (d) ${\gamma _{\mathrm{i}}} $ calculated by empirical formula.

    下载: 全尺寸图片 幻灯片

    图 7  超低频电压为1000 V时, 不同二次电子发射系数下, 电离率的时空分布　(a) $ {\gamma _{\text{i}}} $ = 0; (b) $ {\gamma _{\text{i}}} $ = 0.1; (c) $ {\gamma _{\text{i}}} $ = 0.2; (d)采用经验公式计算$ {\gamma _{\mathrm{i}}} $

    Figure 7.  Time and space distribution of ionization rate under different secondary electron emission coefficients at ultra-low frequency voltage of 1000 V: (a) $ {\gamma _{\text{i}}} $ = 0; (b) $ {\gamma _{\text{i}}} $ = 0.1; (c) $ {\gamma _{\text{i}}} $ = 0.2; (d) $ {\gamma _{\mathrm{i}}}$ calculated by empirical formula.

    下载: 全尺寸图片 幻灯片

    图 8  不同放电间隙下, 体平均电子密度随超低频电压的变化

    Figure 8.  Variation of volume average electron density with ultra-low frequency voltage under different discharge gaps.

    下载: 全尺寸图片 幻灯片

    图 9  不同放电间隙下, 超低频电压为600 V时, 电子密度的分布　(a) 2 cm; (b) 3 cm; (c) 4 cm

    Figure 9.  Distribution of electron density under different discharge gaps and ultra-low frequency voltage of 600 V: (a) 2 cm; (b) 3 cm; (c) 4 cm.

    下载: 全尺寸图片 幻灯片

    图 10  不同放电间隙下, 超低频电压为100 V时, 电离率的时空分布　(a) 2 cm; (b) 3 cm; (c) 4 cm

    Figure 10.  Temporal and spatial distribution of ionization rate under different discharge gaps and ultra-low frequency voltage of 100 V: (a) 2 cm; (b) 3 cm; (c) 4 cm.

    下载: 全尺寸图片 幻灯片

    图 11  不同放电间隙下, 超低频电压为600 V时电离率的时空分布　(a) 2 cm; (b) 3 cm; (c) 4 cm

    Figure 11.  Temporal and spatial distribution of ionization rate under different discharge gaps and ultra-low frequency voltage of 600 V: (a) 2 cm; (b) 3 cm; (c) 4 cm.

    下载: 全尺寸图片 幻灯片

    表 1  Ar等离子体中的电子碰撞反应

    Table 1.  Electron collision reactions in Ar plasma.

    表达式 阈值/eV 参考文献
    Ar+e→Ar+e 0.0 [23,24]
    Ar+e→Arm+e 11.6 [25]
    Ar+e→Arr+e 11.7 [25]
    Ar+e→Ar++2e 15.8 [26]
    Arm+e→Ar++2e 4.2 [26]
    Arr+e→Ar++2e 4.1 [27]
    下载: 导出CSV
  • [1] 戴忠玲, 毛明, 王友年 2006 物理 35 693 doi: 10.3321/j.issn:0379-4148.2006.08.014 Dai Z L, Mao M, Wang Y N 2006 Physics 35 693 doi: 10.3321/j.issn:0379-4148.2006.08.014
    [2] Kim S S, Hamaguchi S, Yoon N S, Chang C S, Lee Y D, Ku S H 2001 Phys. Plasmas 8 1384 doi: 10.1063/1.1350671
    [3] 谭毅成, 伍尚华, 朱佐祥, 向其军, 朱祖云, 田卓 2018 人工晶体学报 47 1272 Tan Y C, Wu S H, Zhu Z X, Xiang Q J, Zhu Z Y, Tian Z 2018 J. Synth. Cryst. 47 1272
    [4] Lieberman M A, Lichtenberg A J 2008 Principles of Plasma Discharges & Materials Processing 11 800 doi: 10.1002/0471724254
    [5] Chabert P, Braithwaite N 2011 Physics of Radio-Frequency Plasmas (Cambridge: Cambridge University Press
    [6] Lee J K, Manuilenko O V, Babaeva N Y, Kim H C, Shon J W 2005 Plasma Sources Sci. Technol. 14 89 doi: 10.1088/0963-0252/14/1/012
    [7] Han L, Kenney J, Rauf S, Korolov I, Schulze J 2023 Plasma Sources Sci. Technol. 32 115018 doi: 10.1088/1361-6595/ad0d06
    [8] Kim H H, Shin J H, Lee H J 2023 J. Vac. Sci. Technol. , A 41 023004 doi: 10.1116/6.0002242
    [9] Zhou Y, Zhao K, Ma F F, Liu Y X, Gao F, Julian Schulze, Wang Y N 2024 Appl. Phys. Lett. 124 064102 doi: 10.1063/5.0190803
    [10] Zhou Y, Zhao K, Ma F F, Sun J Y, Liu Y X, Gao F, Zhang Y R, Wang Y N 2025 Plasma Sources Sci. Technol. 34 035016 doi: 10.1088/1361-6595/adc331
    [11] Wang J C, Tian P, Kenney J, Rauf S, Korolov I, Schulze J 2021 Plasma Sources Sci. Technol. 30 075031 doi: 10.1088/1361-6595/ac0da4
    [12] Liu J, Zhang Q Z, Liu Y X, Gao F, Wang Y N 2013 J. Phys. D: Appl. Phys. 46 235202 doi: 10.1088/0022-3727/46/23/235202
    [13] Hartmann P, Korolov I, Escandon L J, Gennip W V, Buskes K, Schulze J 2022 Plasma Sources Sci. Technol. 31 055017 doi: 10.1088/1361-6595/ac6e05
    [14] Hartmann P, Wang L, Nosges K, Berger B, Wilczek S, Brinkmann R P, Mussenbrock T, Juhasz Z, Donko Z, Derzsi A, Lee E, Schulze J 2020 Plasma Sources Sci. Technol. 29 075014 doi: 10.1088/1361-6595/ab9374
    [15] Liu G H, Wang X Y, Liu Y X, Sun J Y, Wang Y N 2018 Plasma Sources Sci. Technol. 27 064004 doi: 10.1088/1361-6595/aaca8c
    [16] Schulze J, Donko Z, Luggenholscher D, Czarnetzki U 2009 Plasma Sources Sci. Technol. 18 034011 doi: 10.1088/0963-0252/18/3/034011
    [17] Takagi S, Chikata T, Sekine M 2021 Jpn. J. Appl. Phys. 60 SAAB07
    [18] Donko Z, Schulze J, Hartmann P, Korolov I, Czarnetzki U, Schungel E 2010 Appl. Phys. Lett. 97 081501 doi: 10.1063/1.3481427
    [19] Schulze J, Donko Z, Schuengel E, Czarnetzki U 2011 Plasma Sources Sci. Technol. 20 045007 doi: 10.1088/0963-0252/20/4/045007
    [20] Saikia P, Bhuyan H, Yap S L, Escalona M, Favre M, Wyndham E, Schulze J 2019 Phys. Plasmas 26 083505 doi: 10.1063/1.5094603
    [21] 张钰如, 高飞, 王友年 2021 物理学报 70 095206 doi: 10.7498/aps.70.20202247 Zhang Y R, Gao F, Wang Y N 2021 Acta Phys. Sin. 70 095206 doi: 10.7498/aps.70.20202247
    [22] Zhang Y R, Xiang X, Zhao S X, Bogaerts A, Wang Y N 2010 Phys. Plasma 17 113512 doi: 10.1063/1.3519515
    [23] Kurokawa M, Kitajima M, Toyoshima K, Kishino T 2011 Phys. Rev. A 84 062717 doi: 10.1103/PhysRevA.84.062717
    [24] De Heer F J, Jansen R H J, Van Der Kaay W 1979 J. Phys. B: Atom. Mol. Phys. 12 979 doi: 10.1088/0022-3700/12/6/016
    [25] Tachibana K 1986 Phys. Rev. A 34 1007 doi: 10.1103/PhysRevA.34.1007
    [26] Rejoub R, Lindsay B G, Stebbings R F 2002 Phys. Rev. A 65 042713 doi: 10.1103/PhysRevA.65.042713
    [27] Ali M A, Stone P M 2008 Int. J. Mass Spectrom. 271 51 doi: 10.1016/j.ijms.2007.10.006
    [28] Phelps A V, Pitchford L C, Pedoussat C, Donko Z 1999 Plasma Sources Sci. Technol. 8 B1 doi: 10.1088/0963-0252/8/4/401
    [29] Brinkmann R P 2007 J. Appl. Phys. 102 093303 doi: 10.1063/1.2772499
    [30] Horvath B, Daksha M, Korolov I, Derzsi A, Schulze J 2017 Plasma Sources Sci. Technol. 26 124001 doi: 10.1088/1361-6595/aa963d
    [31] Campanell M D, Khrabrov A V, Kaganovich I D 2012 Phys. Rev. Lett. 108 255001 doi: 10.1103/PhysRevLett.108.255001
    [32] Campanell M D 2013 Phys. Rev. E 88 033103 doi: 10.1103/PhysRevE.88.033103
  • 加载中
图( 11) 表( 1)
计量
  • 文章访问数:  28
  • HTML全文浏览数:  28
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-15
  • 刊出日期:  2025-07-05

超低频/射频联合驱动容性耦合等离子体中二次电子效应的模拟

    通讯作者: E-mail: yrzhang@dlut.edu.cn.; 
    作者简介: 史寒旭. E-mail: 1697165527@qq.com
  • 大连理工大学物理学院, 三束材料改性教育部重点实验室, 大连　116024
  • 收稿日期:  2025-03-15

摘要: 采用二维流体模型, 研究了不同的超低频电压、二次电子发射系数和极板间隙下, 二次电子对双频容性耦合等离子体特性的影响, 其中超低频源频率为400 kHz. 首先, 采用依赖离子能量的二次电子发射系数, 发现电子密度随超低频电压呈现出先降低后增高的趋势. 这是由于一方面, 较高的超低频电压会压缩有效放电体积; 另一方面, 极板发射的二次电子可以获得更多的能量, 进而增强电离过程. 通过与固定的二次电子发射系数的结果相比, 发现在较低的超低频电压下, 采用依赖能量的二次电子发射系数的结果接近于固定值为0.1的情况; 随着超低频电压的增加, 当采用依赖能量的发射系数时, 密度涨幅超过固定值为0.2的结果, 说明超低频电压对二次电子效应的增强效果并不是线性的. 最后, 对比了不同极板间隙下的等离子体特性, 发现随着极板间隙从2 cm增加到4 cm, 电离率的峰值有所下降, 但电子密度显著地增加, 等离子体的径向均匀性有所改善. 此外, 随着超低频电压的升高, 极板间隙对密度的影响越显著. 本文的研究结果有助于深入地理解超低频电源参数对于二次电子效应的影响, 并为等离子体工艺的优化提供一定的指导.

English Abstract

    全文HTML

    1.   引　言

    • 随着社会对高性能、小尺寸和便携式设备的需求日益增长, 高集成度、高算力芯片的研发也越来越受到关注. 容性耦合等离子体(capacitively coupled plasma, CCP)源具有结构简单且能够产生大面积均匀等离子体等优点, 被广泛应用于芯片制造中[1–3]. 近年来, 人们提出可以采用双频容性耦合等离子体源, 来更加精准地调控离子能量与离子通量. 其中, 高频电源主要控制离子密度, 低频电源主要控制离子能量[4,5]. 采用双频电源驱动可以降低高能粒子轰击引起的材料表面损伤[6], 同时有助于提高处理效率, 这对于工业上的大规模生产至关重要. 目前, 工业上常用的双频频率为13.56 MHz+2 MHz, 27.12 MHz+2 MHz等组合.

      随着晶圆集成度的提升, 刻蚀槽的深宽比不断增加, 刻蚀工艺也面临着许多新挑战, 如刻蚀速率降低等. 为了进一步提高离子能量, 人们尝试将双频CCP中的低频频率降低至kHz范围内. 近年来, 人们对含有超低频电源的双频CCP中的离子能量和离子通量进行了深入研究. Han等[7]采用一维PIC模型, 发现在氧气放电中, 离子能量分布函数(IEDF)的低能峰由鞘层塌缩时的最小鞘层电压决定. Lee等[8]则指出IEDF的能峰宽度和离子通量同样受到高频电压的控制. Zhou等[9,10]证实了在较低的超低频频率下, 能够获得具有较窄散射角和较高能量的离子. Wang等[11]和Liu等[12]分别在Ar及Ar/O2混合放电中发现, 随着超低频功率或电压的增加, IEDF的高能峰向高能区移动. Hartmann等[13]也指出调整驱动电压波形, 能够有效地控制离子的能峰峰值与位置.

      需要注意的是, 在超低频/射频联合驱动的双频CCP中, 高能离子的轰击会在电极表面诱导出二次电子发射. 这些二次电子经由鞘层电场加速后会获得大量的能量, 进而显著增强电离过程, 甚至改变放电模式[14]. 然而目前关于二次电子效应的研究, 大多集中在由MHz双频源驱动的放电中. Liu等[15]在双频CCP中观察到随着低频电压的增加, 放电从α模式向γ模式转变. 其中, α模式表示电离过程主要发生在鞘层扩张相位, 而由二次电子主导的放电则称为γ模式[16]. Takagi等[17]在双频CCP的模型中考虑了二次电子的影响, 大幅降低了实验与模拟结果的差异. Donkó等[18]采用PIC/MCC模拟发现, 二次电子效应会显著影响双频CCP中离子通量与离子能量随低频电压的变化趋势. Schulze等[19]指出考虑二次电子发射后, 电非对称效应对离子通量与离子能量的独立控制效果更好. Partha等[20]分别测量了双频CCP中的电子密度与离子电流, 发现二次电子的影响随着气压的升高而变得显著. 由于电源频率对等离子体特性的影响是非线性的, 因此MHz双频CCP中的二次电子效应可能与超低频/射频联合驱动放电有所不同. 尤其是不同的二次电子发射系数及极板间隙下, 二次电子对放电模式的影响还有待进一步研究.

      本文将采用二维流体模型研究超低频/射频联合驱动的容性耦合等离子体中的二次电子效应, 重点关注二次电子发射系数和极板间隙对于电子密度及电离率的影响. 本文的模拟结果有助于深入地理解超低频/射频联合驱动的双频容性耦合等离子体特性, 并对高深宽刻蚀工艺的优化具有一定的指导意义.

    2.   模　型

      2.1.   模型框架

    • 本文采用二维流体模型[21]研究了超低频/射频联合驱动CCP中的二次电子效应. 通过对玻尔兹曼方程的各阶矩进行积分, 可以得到流体力学模型中的连续性方程、动量方程与能量方程. 通过与泊松方程进行耦合, 可以模拟出腔室内等离子体的产生与输运过程, 进而得到宏观特性的时空分布.

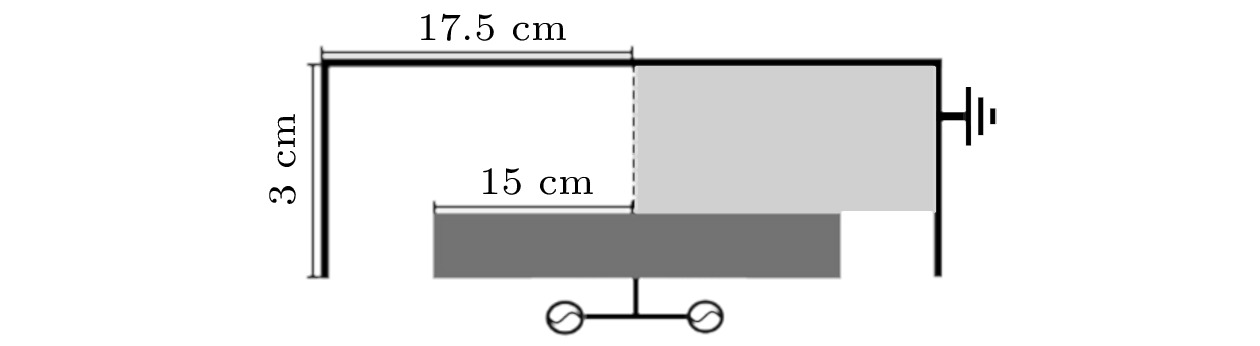
      图1为二维腔室结构示意图, 其具有轴对称结构, 图中灰色区域为计算区域. 腔室由上下极板与侧壁组成, 其中上极板半径为17.5 cm, 下极板半径为15 cm, 高度为3 cm. 下极板接双频电源, 频率分别为13.6 MHz与400 kHz, 上极板和侧壁接地. 下面将详细介绍所采用的流体模型.

      • 2.2.   流体模型

    • 本文采用的流体力学模型, 与Zhang等[22]报道的类似. 其中, 各种粒子的密度分布主要通过求解连续性方程获得:

      其中${n_{\text{e}}}$, ${n_{\text{i}}}$, ${n_{\text{n}}}$分别是电子、离子与中性粒子的密度; ${{\boldsymbol{\varGamma}} _{\text{e}}}$, $ {{\boldsymbol{\varGamma}} _{\text{i}}} $, ${{\boldsymbol{\varGamma }}_{\text{n}}}$则是电子、离子与中性粒子的通量; ${S_{\text{e}}}$, ${S_{\text{i}}}$, ${S_{\text{n}}}$分别是电子、离子与中性粒子的碰撞反应源项. 本研究中, 考虑的碰撞过程包括弹性碰撞、电离和激发, 具体的反应及系数如表1所列. 此外, 中性粒子温度设置为373 K.

      在电子的动量方程中, 由于电子的质量很小, 惯性项和对流项可以忽略不计, 故而采用漂移扩散近似来描述:

      其中, ${m_{\text{e}}}$为电子质量, ${T_{\text{e}}}$为电子温度, ${k_{\text{B}}}$为玻尔兹曼常数, $e$为元电荷, ${\boldsymbol{E}} $为泊松方程计算的静电场. ${v_{\text{e}}}$为电子动量转移系数, 其表达式为

      其中$ {\sigma _{{\text{en}}}} $为相应的碰撞截面; $ {\overline \upsilon _{\text{e}}} $为电子运动的平均速度. 中性粒子通量则采用菲克第一定律来求解:

      其中, ${D_{\text{n}}}$为中性粒子的扩散系数.

      离子速度$ {{\boldsymbol{u}}_{\mathrm{i}}} $由全动量方程来描述:

      其中$ {m_{\text{i}}} $是离子的质量; $ {T_{\text{i}}} $是离子的温度, 本文中设为373.16 K. $ {Z_{\text{i}}} $为离子所带的电荷数, $ {m_{\text{g}}} $为背景气体质量, $ {v_{\text{i}}} $为离子的碰撞频率:

      其中${\sigma _{{\text{ig}}}}$代表离子与背景气体的碰撞截面; ${n_{\text{g}}}$为背景气体的密度, 根号表达式部分则代表离子运动的平均速度.

      电子温度则采用电子能量方程来求解:

      其中${{{W}}_{\text{e}}}$为电子碰撞反应导致的能量损耗, ${{\boldsymbol{q}}_{\text{e}}}$为电子能流密度, 其表达式为

      在流体模型中, 静电场${\boldsymbol{E}} $与电势$\varphi $通过求解泊松方程来得到:

      其中${\varepsilon _{\text{r}}}$为介质区域的相对介电常数, ${\varepsilon _0}$为真空介电常数.

      • 2.3.   边界条件

    • 在模拟中, 还需要合理的边界条件以保证模型的完整性. 在下极板处, 电势的边界条件为

      其中, 上极板和侧壁处:

      在器壁表面, 电子密度的边界条件为

      其中, $ {n_{{\text{e, bou}}}}{|_{{\text{in}}}} $表示与器壁相邻处的电子密度, $ \Delta \varphi $表示相邻网格的电势差.

      在腔室的对称轴处, 一般认为电子的径向通量与能流密度为零. 在器壁表面, 电子通量为

      其中$ {u_{{\text{e, th}}}} = \sqrt {{8}{k_{\text{B}}}{T_{\text{e}}}/{m_{\text{e}}}\pi } $为电子的热速度; $\varTheta = {0}{.25}$为电子反射系数; $ {\gamma _{\text{i}}} $为二次电子发射系数, 本文采用的经验公式[28]来自氩气放电实验数据的拟合结果:

      其中$\varepsilon $为离子能量. 此外, 电子能流密度的边界条件为

    3.   结果与讨论

      3.1.   二次电子效应

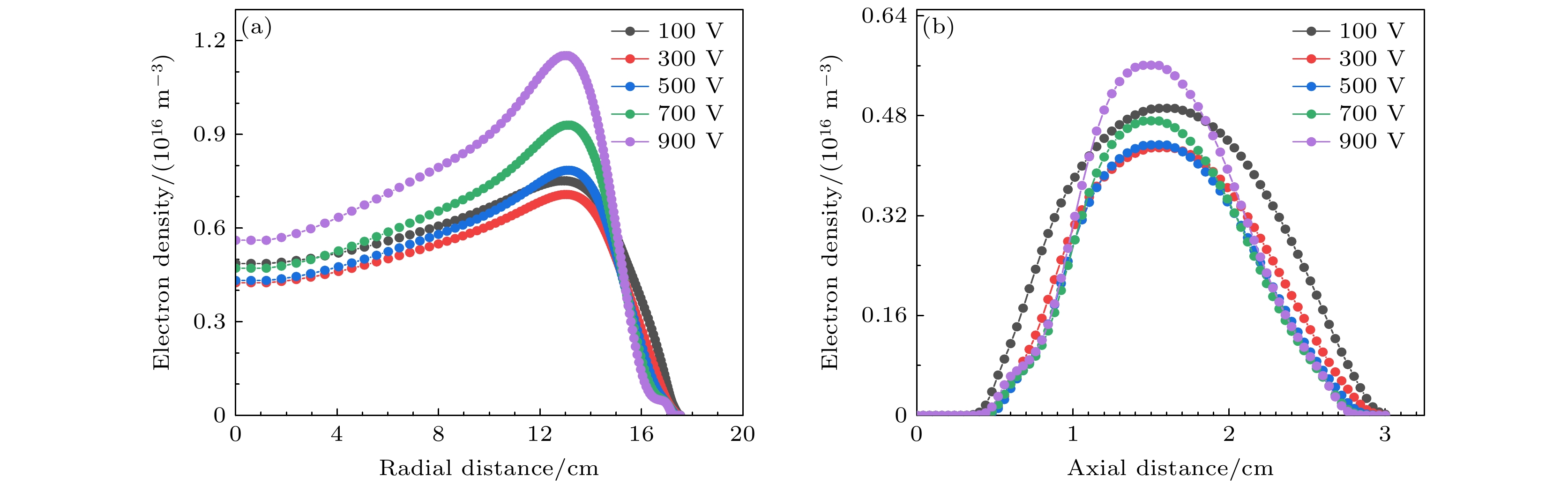
    • 图2给出了采用经验公式计算二次电子发射系数时, 轴向与径向的电子密度分布随超低频电压的变化, 其中高频电压固定为150 V, 气压为40 Pa. 在双频CCP中, 超低频电压的增加会使得正离子获得更高的能量, 进而提高二次电子发射系数; 另一方面, 极板发射的二次电子可以经由鞘层电势降加速获得更多能量, 进而增强电离碰撞过程. 从图2(a)中可以发现随着超低频电压从100 V增加至300 V, 电子密度略微下降, 但径向分布几乎不变. 随着超低频电压进一步增加, 电子密度有所增加, 尤其是径向边缘处的密度峰值增加显著, 等离子体的径向均匀性变差. 图2(b)展示了r = 0 cm处电子密度的轴向分布. 类似地, 电子密度的轴向峰值也随着超低频电压的增加而呈现先减小后增加的趋势, 密度极小值对应的超低频电压为300 V. 这是由于随着电压从100 V增加至300 V, 鞘层最大厚度由0.68 cm增加到0.72 cm (鞘层边界采用Brinkman标准[29]来确定), 这使得有效放电体积被压缩, 电子密度有所下降. 随着超低频电压进一步增加, 极板发射的二次电子可以从超低频源中获得更多能量, 进而等离子体产生过程得到显著增强.

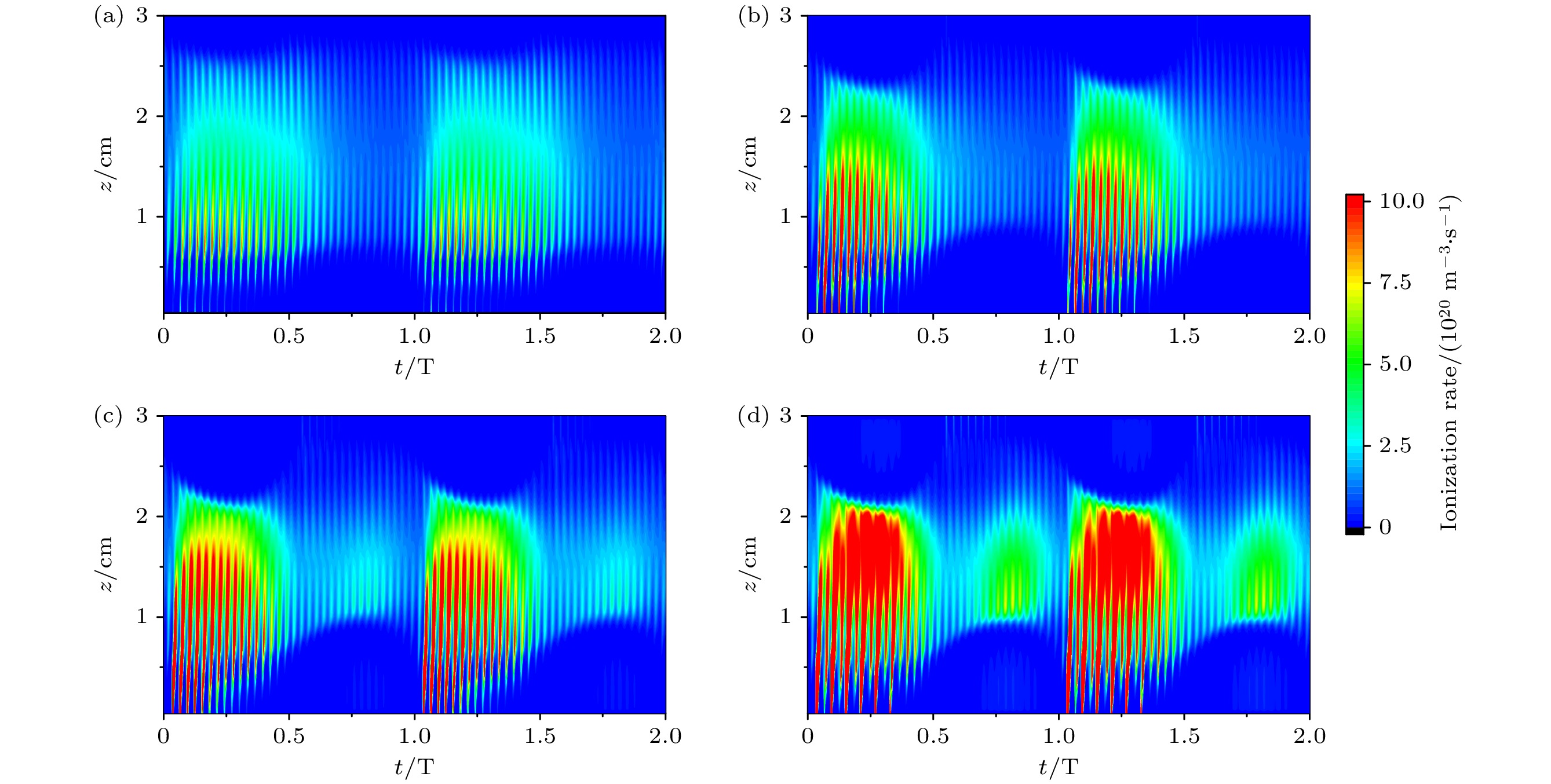
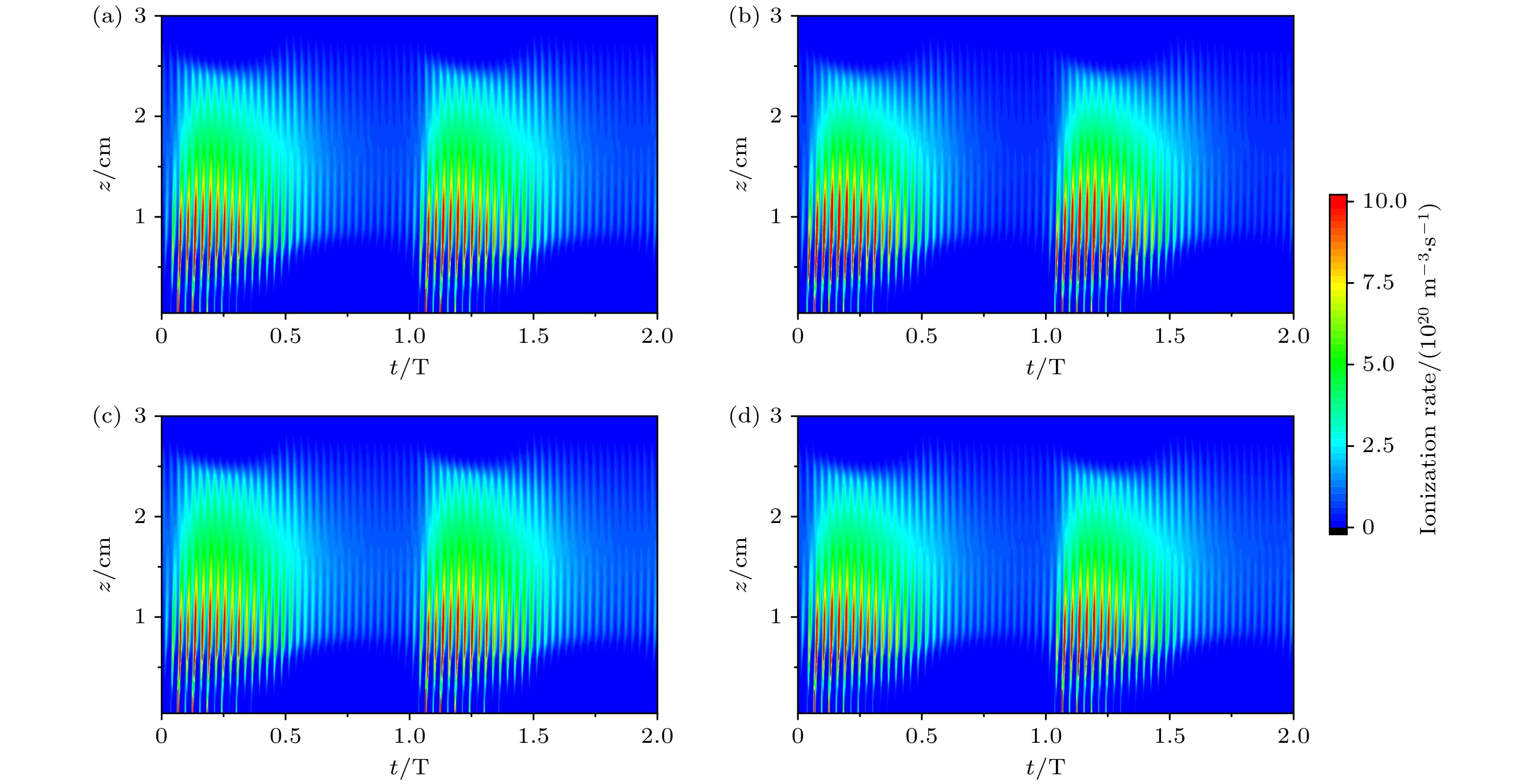
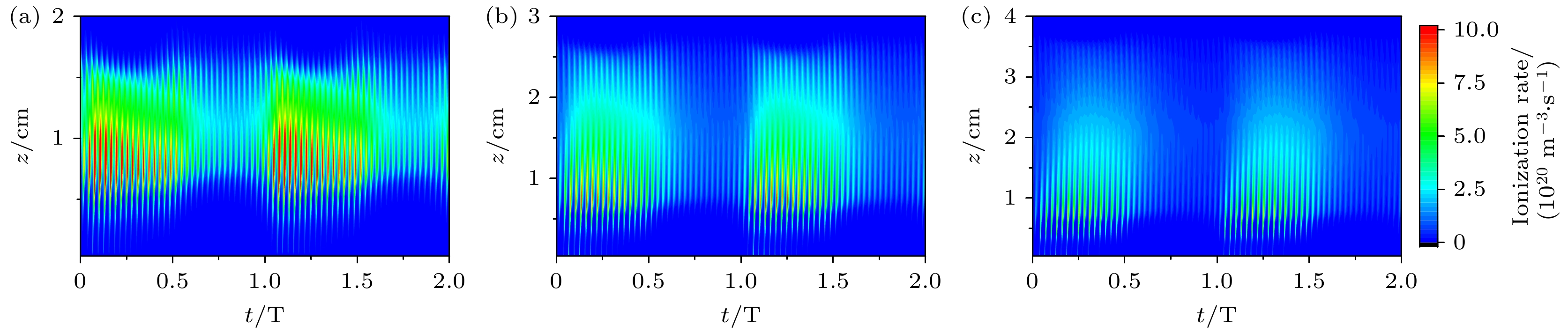
      为了进一步解释电子密度随超低频电压的非单调变化趋势, 图3显示了超低频电压分别为100, 400, 700和1000 V时, 径向中心处电离率的时空分布. 从图3中可以发现, 电离率随时间呈现出明显的振荡行为, 这主要源自高低频鞘层的扩张与塌缩. 当超低频电压为100 V时, 电离过程主要发生在超低频鞘层的扩张相位, 即放电处于α模式, 如图3(a)所示. 随着超低频电压提高到400 V, 鞘层变厚(最大厚度由100 V时的0.72 cm增加到0.92 cm), 超低频鞘层扩张相位的电离峰越来越明显. 当超低频电压为700 V时, 极板产生的二次电子经由鞘层加速后获得大量能量, 其与背景气体发生电离碰撞, 并在超低频鞘层的完全扩张相位引起一个电离次峰, 如图3(c)所示. 随着超低频电压提高到1000 V, 超低频鞘层完全扩张相位处的电离次峰变得更为显著, 放电逐步由α模式向α-γ混合模式转变, 如图3(d)所示.

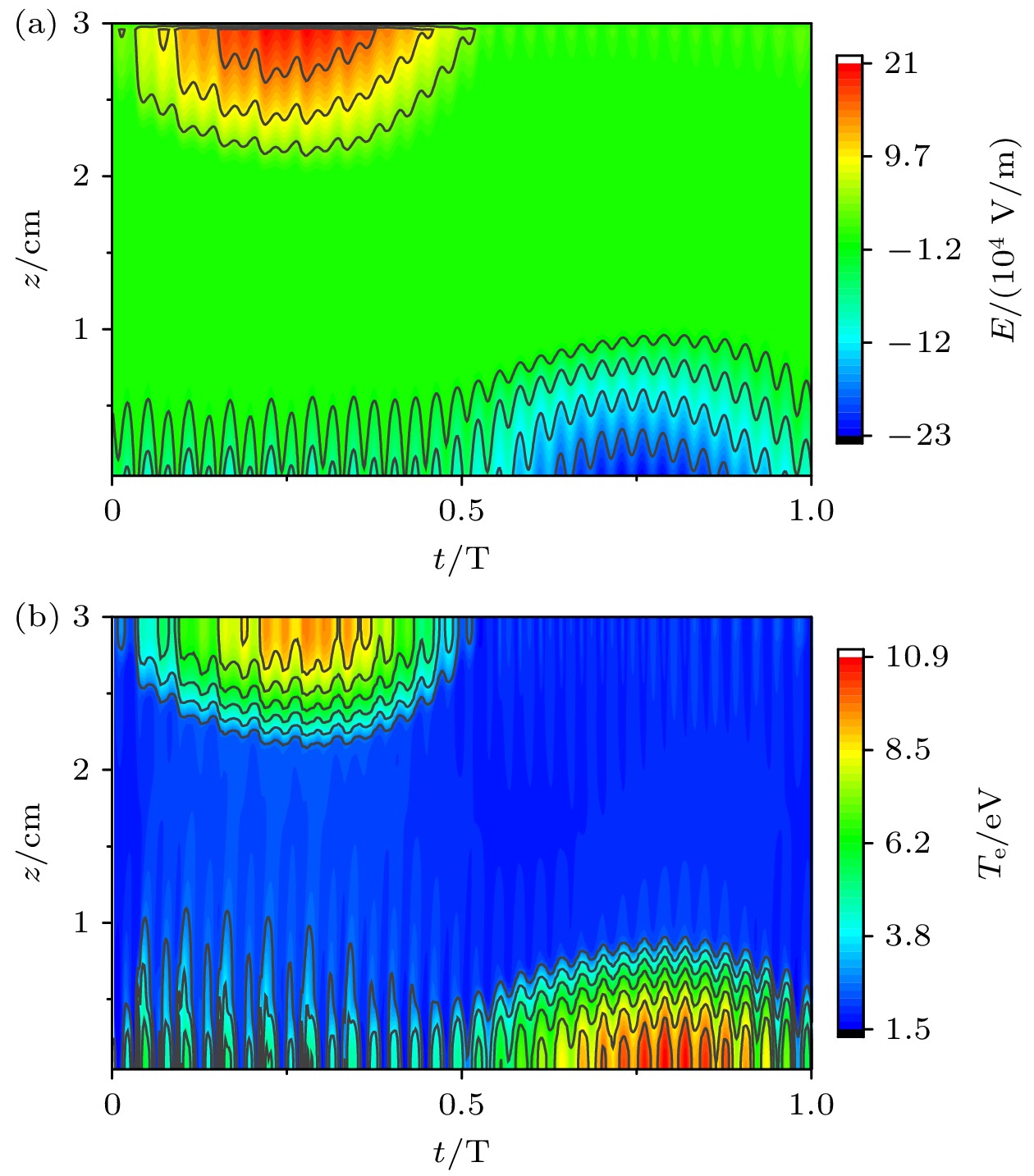
      此外, 随着超低频电压的提高, 超低频鞘层塌缩相位处极板表面的电离率也有所增强, 如图3(d)所示, 这是由反转电场[14,30–32]引起的. 图4展示了超低频电压为1000 V时, 腔室中心处轴向电场和电子温度的时空分布图. 通过对轴向电场的分析, 可以发现当下极板表面的电离率出现极大值时, 此处的电场幅值为正, 即电场发生反转. 这是由于二次电子的存在导致流向极板的电子通量减小, 而反转电场的存在能够使得更多的电子在鞘层塌缩相位流向极板, 从而使极板上的正负电荷能够在一个周期内保持平衡. 在反转电场的作用下, 部分体区内的电子被加速打向极板并获得更多能量. 因此, 此处的电子温度显著上升(图4(b)), 进而增强了电离过程(图3(d)).

      • 3.2.   二次电子发射系数的影响

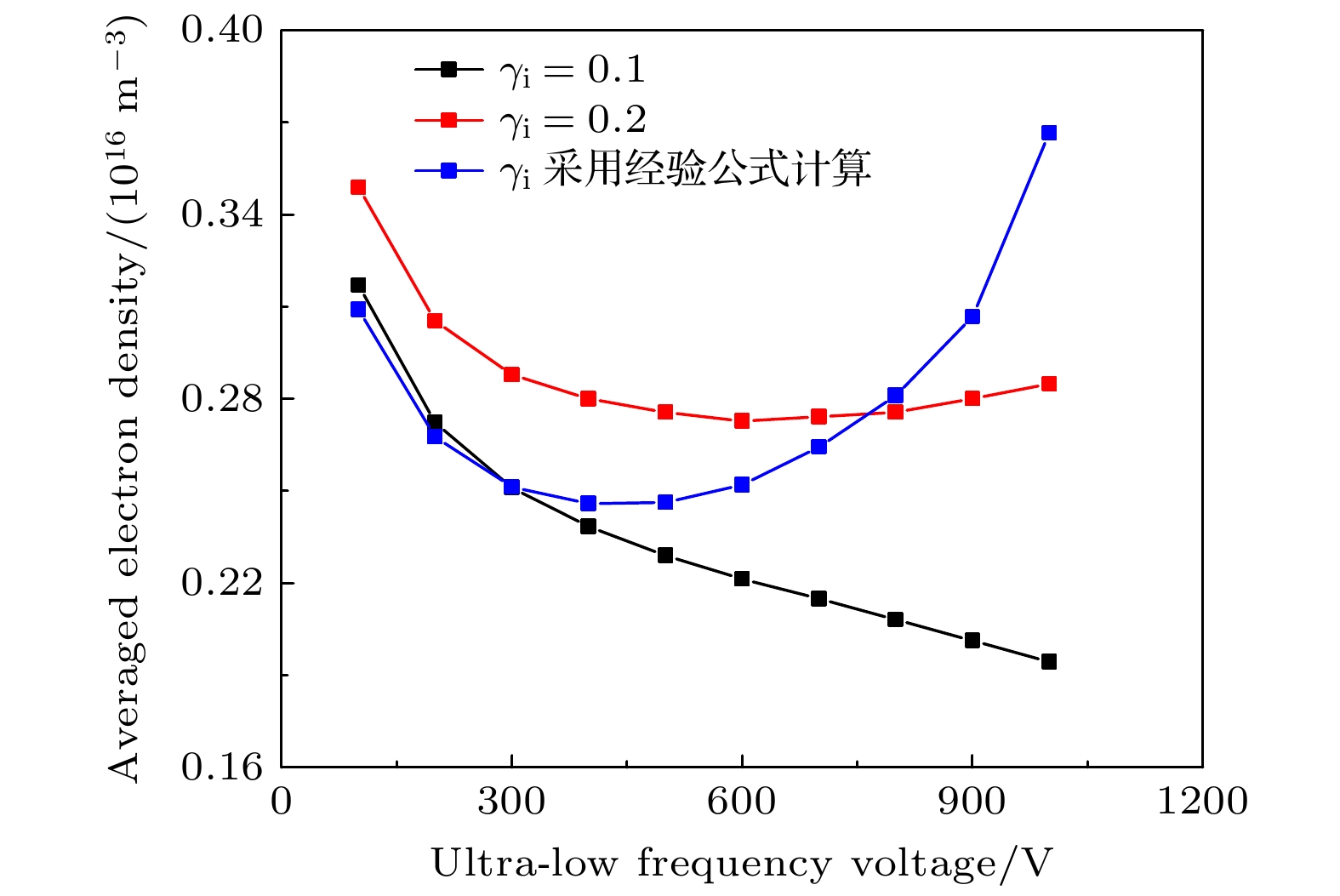
    • 图5给出了不同的二次电子发射系数下, 体平均电子密度随超低频电压的变化趋势. 当二次电子发射系数$ {\gamma _{\text{i}}} $固定为0.1时, 体平均电子密度随着超低频电压的增加而逐渐降低. 这是由于一方面, 较低的$ {\gamma _{\mathrm{i}}} $导致发射的二次电子数量有限, 无法显著增强电离过程; 另一方面, 超低频电压的增加使鞘层变厚(最大鞘层厚度由100 V时的0.72 cm增加到1000 V时的1.15 cm), 有效放电体积被压缩, 因此电子密度有所降低.

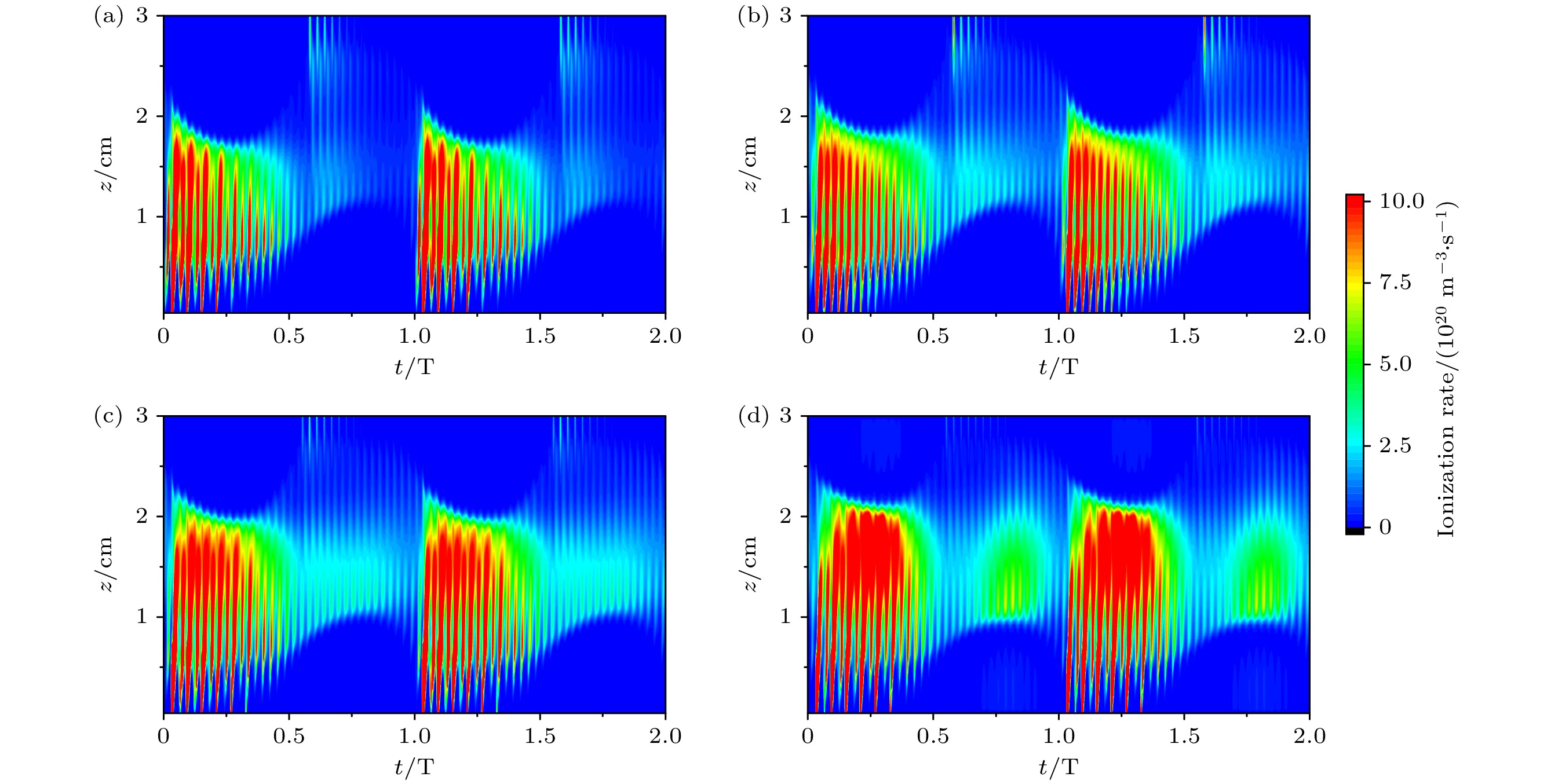
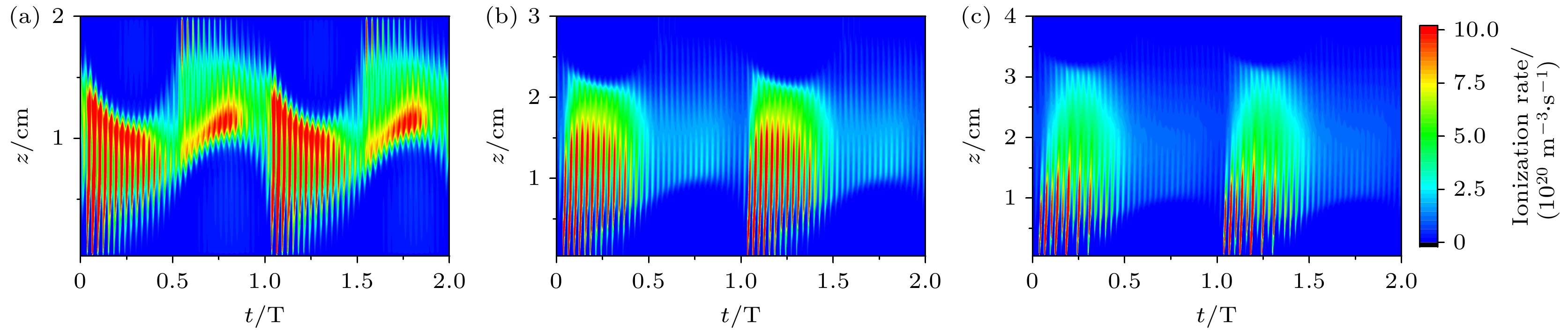
      当$ {\gamma _{\text{i}}} $固定为0.2或采用经验公式计算时, 体平均电子密度随超低频电压都呈现先减小后增加的趋势, 电子密度的拐点分别出现在700和400 V左右. 这是由于随着超低频电压的增加, 一方面体区被压缩, 另一方面二次电子可以获得更多能量进而增强电离过程, 二者之间的竞争机制导致电子密度呈现非单调的变化趋势. 此外, 当采用经验公式计算$ {\gamma _{\text{i}}} $时, 可以发现当超低频电压低于400 V时, 电子密度的变化趋势与$ {\gamma _{\text{i}}} $固定为0.1时类似, 说明此时由于入射离子能量较低, 自洽计算得到的二次电子发射系数近似为0.1. 随着超低频电压的增加, 离子穿越鞘层获得的能量有所提高, 这使得经验公式计算得到的二次电子发射系数显著增加. 此时, 体平均电子密度随超低频电压的涨幅超过$ {\gamma _{\text{i}}} $固定为0.2的情况.

      为了进一步解释二次电子发射系数对于电子密度的影响, 图6与图7分别给出了超低频电压为200与1000 V时, 不同的二次电子发射系数下电离率的时空分布. 通过对比可以发现, 当超低频电压为200 V时, 不同二次电子发射系数下, 电离率的时空分布几乎一致. 这说明在较低的超低频电压下, 二次电子的影响十分微弱. 这是由于此时二次电子获得的能量十分有限, 无法对电离过程产生显著影响. 当超低频电压为1000 V时, 二次电子发射系数的影响变得显著. 如当$ {\gamma _{\text{i}}} $ = 0时, 电离率的时空分布受到双频鞘层振荡的调制, 其峰值出现在超低频鞘层的扩张相位, 如图7(a)所示. 随着$ {\gamma _{\text{i}}} $增加至0.1和0.2, 超低频鞘层扩张至最大相位处的电离率逐渐提高. 尤其是当采用经验公式计算二次电子发射系数时, 二次电子引起的电离峰值约是体区峰值的1/2. 这是因为一方面, 较高的超低频电压提高了入射离子的能量, 进而增强了离子诱导二次电子发射过程; 另一方面, 二次电子也从较大的鞘层电势降中获得更高的能量, 进而显著地增强了电离过程.

      • 3.3.   极板间隙对等离子体的影响

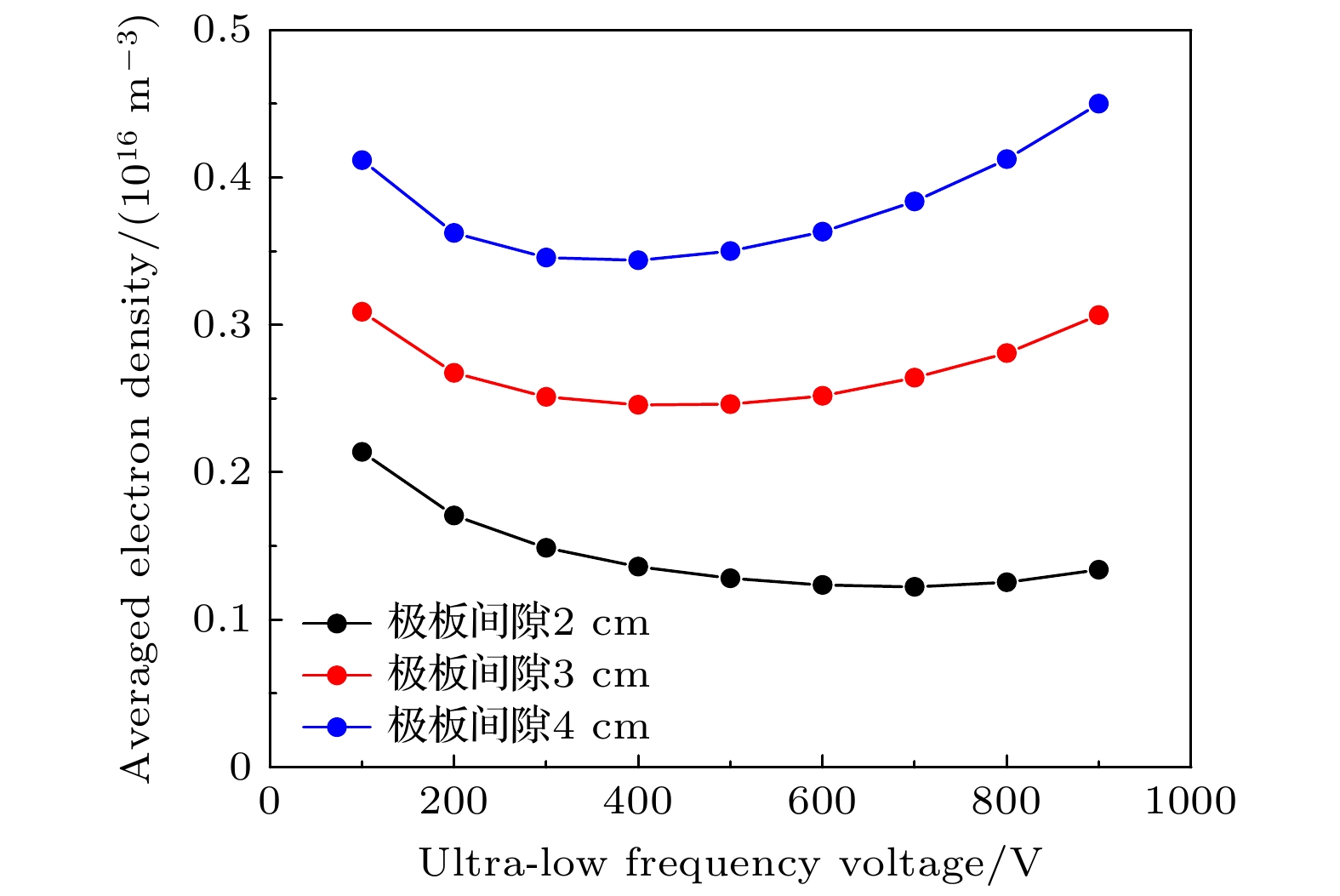
    • 图8展示了放电间隙为2, 3, 4 cm三种情况下, 体平均电子密度随超低频电压的变化趋势, 其中二次电子发射系数均采用经验公式计算. 从图8中可以发现, 在三种间隙下, 电子密度均随超低频电压出现先下降后增加的趋势, 且随着间隙的增加, 密度拐点出现在更低的电压下. 这是因为当放电间隙为4 cm时, 即使最大鞘层厚度随超低频电压由100 V时的0.7 cm增加到600 V时的0.9 cm左右, 但由于放电间隙较大, 鞘层厚度变化对有效放电体积的影响十分有限; 另一方面, 极板发射的高能二次电子可以在体区经历充分的碰撞, 并更有效地增强电离过程. 此外, 在相同的超低频电压下, 电子密度随极板间隙的增加而增加, 且差异随着超低频电压的增加而变得明显. 这同样是由于极板间隙越大, 高能二次电子进入体区后碰撞越充分, 其对电子密度的提升效应越显著.

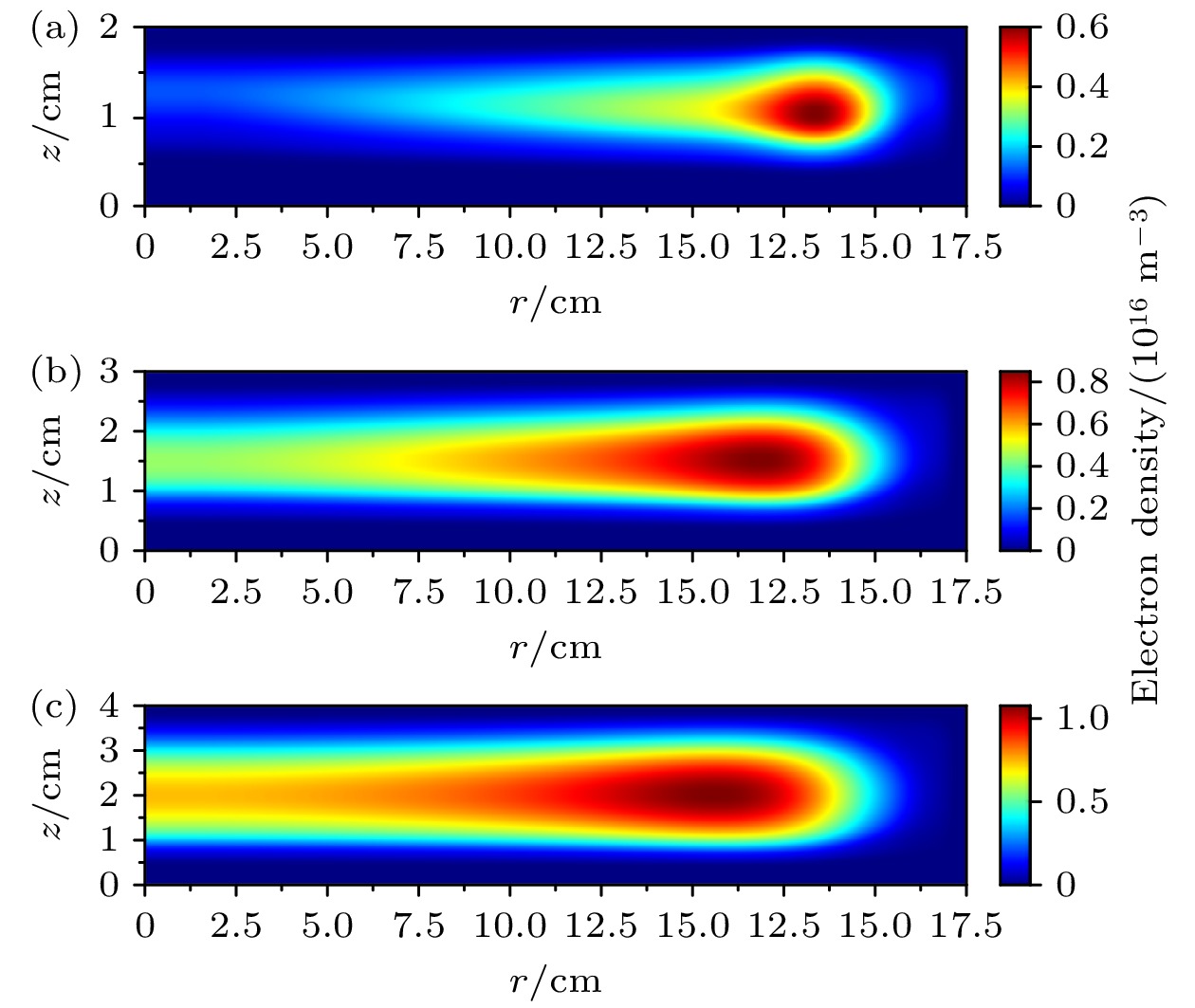
      极板间隙除了影响等离子体密度的幅值外, 还会对其空间分布产生调制. 图9展示了不同的极板间隙下, 超低频电压为600 V时, 电子密度的空间分布. 由图9可以看到, 在较小的极板间隙下, 电子密度集中于径向边缘处. 随着极板间隙的增加, 腔室内部的电子密度整体有所提升, 径向均匀性不断提高. 在其他超低频电压下, 电子密度空间分布随极板间隙的变化规律与600 V时类似.

      为了进一步解释极板间隙对于二次电子效应及等离子体特性的影响, 分别对超低频电压为100和600 V的情况下, 腔室中心处电离率的时空分布进行了研究. 当超低频电压为100 V时, 二次电子效应较弱. 随着极板间隙的增加, 电离率的幅值逐渐下降, 如图10所示. 这是因为随着极板间隙的增加, 电子可以经历更加充分的碰撞, 导致其不断损失能量, 进而影响电离率的峰值. 在4 cm间隙下, 尽管电离率峰值较低, 但由于有效电离体积远大于2 cm的情况, 因此电子密度仍随着极板间隙的增加而升高.

      当超低频电压固定为600 V时, 电离率的时空分布显著区别于100 V的结果, 如图11所示. 当极板间隙为2 cm时, 电离率的峰值出现在超低频鞘层的扩张相位及鞘层最厚处. 随着极板间隙由2 cm增加到4 cm, 电离率的峰值逐渐降低, 鞘层扩张最大相位处的电离峰逐渐消失. 这是因为随着极板间隙的不断增加, 电子能够进行充分的碰撞而损耗能量, 因此电离率幅值有所下降. 此外, 与100 V的结果对比, 在相同的放电间隙下, 600 V的电离峰值更高. 但由于此时的鞘层较厚(4 cm间隙下, 100 V时的最大鞘层厚度为0.7 cm, 而600 V时为0.9 cm), 有效放电体积较小, 因此体平均密度低于100 V的结果.

    4.   结　论

    • 本文采用流体模型, 研究了二次电子对于双频容性耦合Ar等离子体特性的影响, 其中高频频率为13.6 MHz, 超低频频率为400 kHz, 气压为40 Pa. 研究表明, 二次电子会对等离子体特性产生影响. 当采用经验公式计算二次电子发射系数时, 随着超低频电压的增加, 电子密度首先出现下降趋势, 这是由于鞘层变厚使得有效放电体积被压缩. 随着超低频电压进一步增加, 二次电子获得更高的能量并显著增强电离过程, 这使得轴向和径向的电子密度增加, 同时放电模式逐渐由α模式向α-γ混合模式转变. 此外, 在较高的超低频电压下, 超低频鞘层塌缩相位的电离率也有所提高, 这是由于反转电场对电子的加热增强了此处的电离.

      随后, 本文研究了二次电子发射系数对于等离子体特性的影响. 发现当二次电子发射系数较低如0.1时, 体平均电子密度随着超低频电压的升高逐渐降低. 这是由于在较低的二次电子发射系数下, 极板上产生的二次电子数量较少, 即使其在较高的超低频电压下能够获得足够的能量, 但对于电离过程的增强也十分有限. 而当二次电子发射系数固定为0.2时, 二次电子数量增加, 在较高的超低频电压下, 大量的二次电子显著增强电离过程, 使得电子密度有所提高. 当采用经验公式计算二次电子发射系数时, 在较低的超低频电压下, 其结果与固定值0.1的情况类似, 说明此时由于入射离子的能量较低, 发射的二次电子数量有限. 随着超低频电压的增加, 二次电子效应逐渐变得明显, 密度的增长趋势甚至超过固定值0.2的情况, 说明较高的离子轰击能量增强了二次电子效应. 此外, 当超低频电压为1000 V时, 相较于二次电子发射系数固定为0.1和0.2的情况, 采用经验公式计算二次电子发射系数的情况下, 超低频鞘层完全扩张相位处的电离峰最为明显.

      最后, 还研究了极板间隙对于等离子体特性的影响. 随着极板间隙的增加, 有效碰撞体积增加, 虽然电离率的幅值有所下降, 但电子密度显著上升, 同时等离子体的径向均匀性也会提高. 此外, 当超低频电压较高时, 在2 cm的极板间隙下, 鞘层完全扩张相位处由二次电子引发的电离增强现象更为明显. 综上, 本文重点关注了在含有超低频源的放电中, 不同的超低频电压和放电间隙下, 二次电子对等离子体特性的影响, 相关结果为探寻合适的腔室结构与驱动电压来改善充电效应、优化等离子体工艺过程, 提供了一定的指导.

    参考文献 (32)

目录

/

返回文章
返回