-
在光伏和平板显示等领域, 通常采用大面积容性耦合腔室来进行硅基薄膜等离子体增强化学气相沉积(plasma enhanced chemical vapor deposition, PECVD)[1-3]. 随着市场竞争愈发激烈, 提升生产效率成为行业发展的关键驱动力. 为实现这一目标, 腔室尺寸不断增大, 驱动频率也从传统的13.56 MHz提高至27.12 MHz, 甚至更高. 然而, 这也导致沉积薄膜不均匀的问题日益突出[4-9]. 如何在保证生产效率的同时实现大面积薄膜的均匀沉积, 已成为困扰光伏和平板显示等领域的主要难题之一.
在大面积容性耦合腔室放电中, 沉积薄膜的均匀性受到多种因素影响. 除了腔室结构以及气流和温度分布不均匀外[10-13], 电磁效应, 尤其是驻波效应的影响不容忽视. 考虑到放电时等离子体的存在使电极之间传播的电磁波波长相比于真空波长明显变短, 当电磁波的波长缩短至与电极尺寸相当时, 驻波效应就可能成为影响均匀性的主要因素[4,14,15]. Schmidt等[4,14,15]采用二极管探头、静电探头和光纤探头分别测量了大面积平板电极在不同驱动频率下真空时电极间轴向电场强度、放电时电极表面离子通量以及等离子体发光强度的径向分布、薄膜厚度的空间分布. 其实验结果表明, 随着驱动频率从13.56 MHz升高至100 MHz, 真空情况下驻波效应越发显著, 电极间轴向电场强度呈现中心高边缘低分布. 放电情况下, 平板电极间距不变, 轴向电场强度更大的区域电势幅值更高, 此时电极不再能够被视为等势体. 电势幅值更高的区域等离子体密度更高, 此时发光强度、离子和中性基团通量也均更高, 从而导致沉积的薄膜变厚.
此后, 研究人员针对甚高频驱动放电中的驻波效应进行了大量研究. Lieberman等[16-23]通过理论解析、数值模拟和实验诊断, 详细分析了二维容性耦合放电腔室内电磁波的传播机制, 发现驻波效应的产生主要是传播方向平行于电极的表面波波长变短导致的. 此时, 电极间的轴向电场振幅会呈现中心高、边缘低的径向非均匀分布. 在足够高的频率下, 轴向电场振幅和等离子体密度甚至可能出现多个交替的峰值和谷值. 这些理论还在Liu等[24]和Han等[25,26]的实验中得到了验证. 以上关于驻波效应的研究大多集中于适用于半导体领域的较小尺寸腔室的放电, 因此普遍认为驱动频率达到甚高频以上的放电中才会出现驻波效应. 然而, 在适用于光伏和平板显示领域的较大尺寸腔室中, 即使驱动频率尚未达到甚高频(13.56—40 MHz)也可能出现驻波效应. Sansonnens等[27]在边长为1 m的腔室中, 观察到在27和40 MHz的驱动频率下, 沉积的薄膜呈现出径向中心处较厚、径向边缘处较薄的现象, 证实了驱动频率低于甚高频的大尺寸腔室放电中驻波效应对薄膜均匀性的影响. Chen等[28]在边长3 m、驱动频率13.56和27.12 MHz的容性放电模拟研究中, 同样发现了明显的驻波效应和其导致的等离子体密度径向不均匀. 上述研究表明, 在大面积容性腔室中, 即使驱动频率没有达到甚高频, 电极间的表面波波长也可能与电极尺寸相当, 从而引发驻波效应. 这时, 驱动电极不再能被视为等势体, 其表面电势幅值和电极间的轴向电场沿径向呈非均匀分布, 进而导致等离子体密度沿径向非均匀分布, 最终影响沉积薄膜的径向均匀性.
此外, 大量前期研究表明, 沉积薄膜质量与入射粒子通量参数密切相关, 其中离子通量和能量/角度分布函数(ion energy distribution function, IEDF; ion angle distribution function, IADF)以及中性基团通量等关键参数对薄膜厚度都具有决定性影响[29-35]. 然而, 当放电中存在驻波效应时, 上述物理量将呈现显著的空间非均匀分布, 从而引发薄膜沉积的不均匀. 要同时分析这些物理量的时空演化会导致两个难题: 第一是实验中难以实现多参数(离子能量、角度分布及中性粒子通量等)同时的空间分辨诊断; 第二是模拟中需要耦合求解电磁场方程、等离子体输运方程与表面反应过程, 计算复杂度随腔室尺寸、放电气体种类、气压等参数变化呈指数级增长. 因此针对工业级PECVD设备对工艺参数优化需求, 测量参数和模拟复杂程度的合理简化是必然的.
基于以上研究, 发现驱动电极电势幅值的分布与薄膜厚度的分布存在极强的相关性, 因此可以通过计算驱动电极的电势幅值分布来间接确定沉积薄膜的厚度分布, 而不必同时耦合求解电磁场方程、等离子体输运方程与表面反应过程. 在容性耦合放电腔室中, 由于电极间距与真空波长相比很小, 在两个电极之间传播的电磁波在真空中是纯横电磁波(transverse electromagnetic wave, TEM)模式, 也被称为表面波[16,36], 在等离子体存在时变为准TEM模式. 对于表面波主导的模式, 电场基本上是与电磁波传播方向垂直的. 如果电磁波在等离子体中的趋肤深度足够大, 趋肤效应忽略不计, 麦克斯韦方程组可以简化为电极表面的电压波动方程, 即传输线方程. 在传输线模型中, 可以将等离子体近似为电介质, 从而计算得到放电时电极间传播的电磁波的波数和驱动电极电势幅值的分布.
然而, 在之前的研究中, 对等离子体的近似计算大多忽略了电子与中性粒子弹性碰撞, 这导致无法考虑表面波沿径向衰减的影响. 电正性气体放电中, 表面波的径向衰减在较高气压下比较显著, 此时电子密度较高, 电磁波沿轴向传入体区的趋肤深度较小. 当趋肤深度小于体区宽度一半时, 表面波会受屏蔽[16], 驻波效应会减弱而趋肤效应等其他电磁效应会增强. 因此在电正性气体放电中, 气压较高时, 驻波效应一定程度上会被抑制. 而在电负性气体放电过程中, 负离子的生成会造成电子损耗, 与电正性气体放电相比, 其电子密度更低, 趋肤深度也更大. 因此, 电负性气体放电中可能会存在气压较高, 驻波效应仍然主导放电的情况, 此时不能忽略表面波径向衰减的作用. 此外, 为了改善驻波效应导致的不均匀问题, 研究人员探索了如电源采用对称多点馈入[15]和使用曲面电极[14,27,37]等多种策略, 在一定程度上减轻了驻波效应引起的不均匀问题, 然而这些改善措施需要首先确定腔室中驻波的波长或驱动电极的电势幅值分布.
鉴于此, 本文以光伏生产中PECVD常用的硅烷(SiH4)、氢气(H2)混合气体为研究对象, 利用流体模型计算给定参数下的等离子体状态, 如电子密度、鞘层厚度、电子-中性粒子弹性碰撞频率和趋肤深度等. 再将计算结果与传输线模型进行耦合, 计算出腔室中传播的表面波的波数, 从而更准确地反映放电参数变化对驱动电极电势幅值分布的影响. 此外, 本文还研究了电源馈入位置和分布以及曲面电极对驻波效应的抑制和改善效果, 期望能为解决工业上面临的驻波效应引起的不均匀问题提供有价值的参考.
-
假设电磁波在等离子体中的趋肤深度
$ \delta $ ($ \delta = c/{\omega }_{{\mathrm{p}}{\mathrm{e}}} $ , c是真空光速,$ { \omega }_{{\mathrm{p}}{\mathrm{e}}}=\sqrt{{{\mathrm{e}}}^{2}{n}_{{\mathrm{e}}}/{\varepsilon }_{0}{m}_{{\mathrm{e}}}} $ 是等离子体频率)足够大, 可以忽略趋肤效应. 当电极曲率较小时, 电磁波的横向分量可以忽略不计, 可以近似为传播方向与轴向电场$ {E}_{z} $ 垂直的表面波. 此时磁场只有一个横向分量Ht, 麦克斯韦方程组可以简化为[4]其中,
$ {\nabla }_{{\mathrm{t}}}=\left(\dfrac{\partial }{\partial x}\right)\hat{x}+\left(\dfrac{\partial }{\partial y}\right)\hat{y} $ ,$ {\varepsilon }_{0} $ 和$ {\mu }_{0} $ 分别是真空介电常数和磁导率,$ {\varepsilon }_{{\mathrm{r}}} $ 是电极间介质的相对介电常数,$ {J}_{z} $ 是电流源,$ \omega $ 是电源的角频率.沿
$ z $ 方向从0到$ d $ 积分方程(1)和方程(2)并代入电极间的电压:以及电极表面的电流
可以得到:
其中,
$ d $ 是电极间距,$ \boldsymbol{n} $ 是指向电极表面的单位法向量. 方程(5)是表面电流连续性方程, 其中$ Y= {{\mathrm{j}}\omega {\varepsilon }_{0}}\bigg/{\displaystyle\int_{0}^{d}\left(1/\varepsilon \left(z\right)\right){\mathrm{d}}z} $ 表示电极间单位面积的并联导纳. 方程(6)是电极表面电流变化引起的电压变化,$ Z={\mathrm{j}}\omega {\mu }_{0}d $ 表示电极单位面积的串联阻抗, 只要趋肤深度足够大, 它就与等离子体状态变化无关.真空情况下
$ Y = {{\mathrm{j}}\omega {\varepsilon }_{0}}/{\ d} $ ; 而当存在等离子体时,$ Y = {{\mathrm{j}}\omega {\varepsilon }_{0}}\Big/ \displaystyle\int_{0}^{d} \Big( \dfrac1{\varepsilon_{\rm eff}} \Big) {{\mathrm{d}} z} $ ,$ {\varepsilon }_{{\mathrm{eff}}} = \dfrac1d \bigg[ \displaystyle\int_{0}^{d} {\mathrm{d}}z {\varepsilon (z)} \bigg]^{-1} $ 是电极间有效相对介电常数. 对于鞘层区, 电子密度极低, 可以将鞘层区的介电常数近似为真空介电常数, 即$ \varepsilon \left(z\right)=1 $ . 在等离子体体区, 相对介电常数$ \varepsilon \left(z\right)={\varepsilon }_{{\mathrm{p}}{\mathrm{l}}}=1-{[\omega }_{{\mathrm{p}}{\mathrm{e}}}/\omega (\omega -{\mathrm{j}}{\nu }_{{\mathrm{e}}{\mathrm{n}}})] $ , 其中$ {\nu }_{{\mathrm{e}}{\mathrm{n}}} $ 是电子-中性粒子弹性碰撞频率.当电源馈入位置位于电极的上表面时需要求解的方程为:
其中,
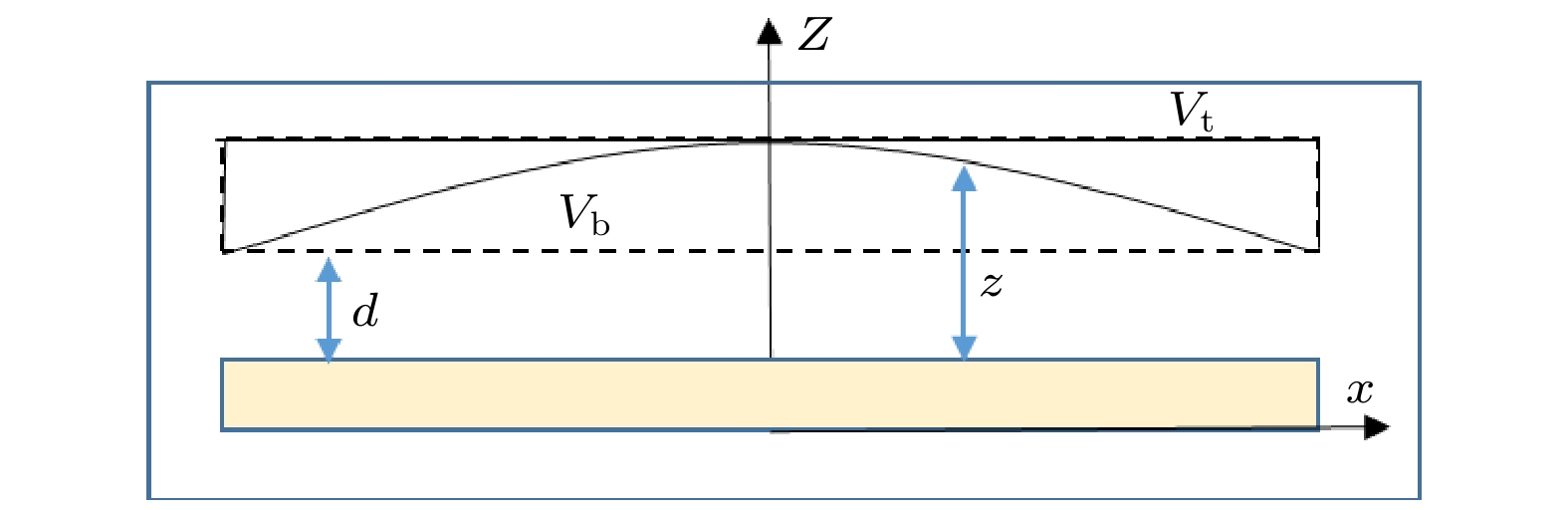
$ {k}_{0} = {\omega }/{c} $ 是真空波数,$ {V}_{{\mathrm{t}}} $ 是驱动电极上表面与金属屏蔽罩之间的电势差,$ {V}_{{\mathrm{b}}} $ 是驱动电极下表面与接地电极之间的电势差,$ {k}_{{\mathrm{p}}}={k}_{0}\sqrt{{\varepsilon }_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}}} $ 是电极间传播的表面波波数,$ f(x, y) $ 在电源馈入位置为1, 其他区域为0. 腔室结构如图1所示, 电极为平面的情况下, 电极形状如图中虚线所示, 此时$ z=d $ , 方程(8b)左侧的第2项为零; 电极为曲面的情况下, 电极形状$ z $ 通过$ \dfrac{{V}_{{\mathrm{b}}}(x, y)}{z(x, y)}=\dfrac{{V}_{{\mathrm{b}}}({x}_{0}, {y}_{0})}{z({x}_{0}, {y}_{0})}=\text{const} $ 迭代计算获得, 如图中实线所示. 此时在图中虚线处施加绝缘介质防止绝缘介质与曲面电极之间产生放电, 保持放电区域间距仍为$ d $ . 这里不考虑绝缘介质和电极厚度的影响, 假设上电极边界处电压和电流连续, 边界条件为$ {V}_{{\mathrm{t}}}={V}_{{\mathrm{b}}} $ 和$ {d}_{{\mathrm{e}}}\dfrac{\partial {V}_{{\mathrm{b}}}}{\partial \boldsymbol{n}}=-d\dfrac{\partial {V}_{{\mathrm{t}}}}{\partial \boldsymbol{n}} $ , 其中$ {d}_{{\mathrm{e}}} $ 是驱动电极上表面与金属屏蔽罩之间的间隙, 设置为5 mm. 这里假设电极与屏蔽罩之间没有放电, 为真空环境, 因此该参数变化在本文中几乎没有影响. 下电极和屏蔽罩均设为接地, 即电势为0. 通过二维有限元方法求解方程(8a)和(8b), 即可得到电极间传播的表面波波数和驱动电极电势幅值二维分布. 空间离散采用非均匀网格剖分, 网格从径向边缘向电源馈入点位置处线性加密. 以单个电源馈入点位于电极中心时为例, 最小网格面积为0.15 cm2, 最大网格面积为19.82 cm2, 网格数为1694.等离子体状态变化对表面波传播的影响体现在电极间有效相对介电常数
$ {\varepsilon }_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ 中. 考虑表面波的径向衰减时,$ {\varepsilon }_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}}=\dfrac{d{\varepsilon }_{{\mathrm{p}}{\mathrm{l}}}}{2 d{\varepsilon }_{{\mathrm{p}}{\mathrm{l}}}+(d-2{d}_{{\mathrm{s}}{\mathrm{h}}})} $ , 而忽略表面波的径向衰减时认为$ {\varepsilon }_{{\mathrm{p}}{\mathrm{l}}} $ 远大于1,$ {\varepsilon }_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}}=d/\left(2{d}_{{\mathrm{s}}{\mathrm{h}}}\right) $ . 需要指出的是, 在之前Schmidt等[14]和Sansonnens[37]的研究中不仅忽略了表面波的径向衰减, 而且鞘层厚度$ {d}_{{\mathrm{s}}{\mathrm{h}}} $ 通常采用人为预设值, 而非基于实验测量或数值模拟获得的结果. 这导致放电参数(包括气压、气体比例和功率等)与鞘层厚度的变化之间未能建立定量关联. 为解决这一局限性, 本研究通过流体模型, 在给定放电条件下自洽计算等离子体状态参数, 从而更好地体现放电参数变化对电极间表面波波数及驱动电极电势幅值分布的影响. -
在二维流体模型中, 采用有限体积法将连续性方程(离子和电子)、漂移-扩散近似方程(离子和电子)以及电子能量方程与泊松方程耦合求解. 对于中性粒子, 则耦合求解连续性和扩散方程, 具体的方程形式和边界条件在之前的工作中已有详细介绍[38,39]. 另外, 计算中考虑了与硅烷和氢气相关的11个粒子和24个反应, 反应及其系数列表见表1. 表中cal表示根据麦克斯韦分布的电子能量分布函数从相应的碰撞截面计算得到的碰撞反应速率系数, 碰撞截面参考 Bleecker[40]的工作. 同时, 不考虑等离子体空间分布的影响, 流体模型的计算结果取时间周期和空间平均, 平均后的电子密度、鞘层厚度和电子-中性粒子弹性碰撞频率用于计算等离子体频率、趋肤深度和等离子体有效相对介电常数, 并代入传输线模型中计算波长和电势幅值分布. 其中, 鞘层厚度根据Brinkmann鞘层判据[41]计算得到.
-
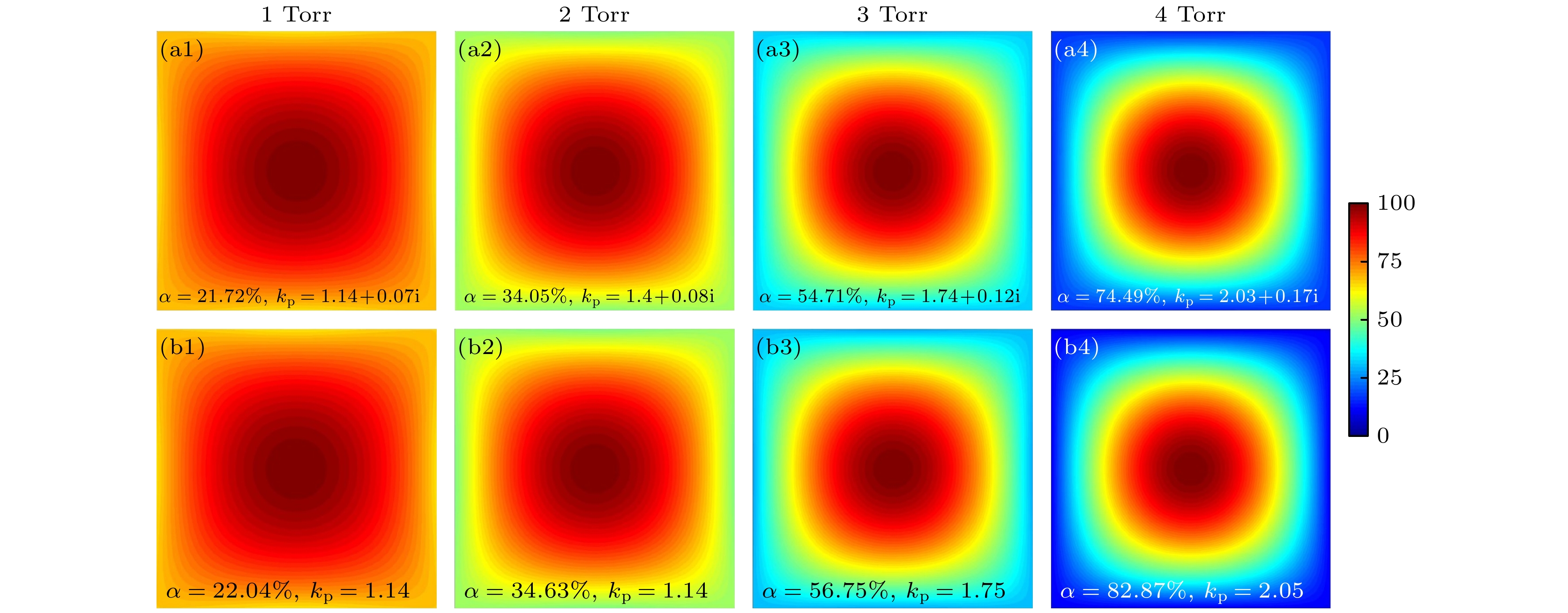
在本研究中, 放电驱动频率为 27.12 MHz, 放电气体为SiH4/H2混合气体, 电极大小为2 m×2 m的正方形. 表2 展示了电压幅值100 V, 间距1.6 cm, 气压1—4 Torr, 气体比例SiH4/SiH4+H2 = 1%, 功率大致8—12 kW放电条件下周期和空间平均的电子密度、鞘层厚度、趋肤深度、电子-中性粒子弹性碰撞频率和电极间有效相对介电常数. 根据表2中的等离子体状态计算出的驱动电极电势幅值的二维分布(以下简称电势分布)如图2所示, 电源馈入点位于电极上表面中心处.
$ \alpha =\dfrac{({V}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}}-{V}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}})}{({V}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}}+{V}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}})} $ 是不均匀度, 用于衡量电势分布的均匀性, 其数值越小意味着电势分布均匀性越好, 其中$ {V}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}}{\mathrm{和}}{V}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}} $ 分别代表电势的最大值与最小值. 图2(a1)—(a4)的结果考虑了表面波径向衰减的作用, 因此表面波波数$ {k}_{{\mathrm{p}}} $ 是复数,$ {k}_{{\mathrm{p}}} $ 的实部越大表示表面波波长越短, 而虚部越大表示表面波在电极下表面从径向边缘向径向中心传播的过程中衰减越显著[36], 此时电势分布给出的是方程(8b)复电势取模的计算结果; 图2(b1)—(b4)是忽略表面波径向衰减作用的结果, 因此波数只有实部.从图2可以看出, 随着气压升高, 电势分布中心高边缘低的趋势越发明显, 电势分布的均匀性变差, 不均匀度从21.72%升高至74.49%. 由于背景气体分子数随着气压升高而增多, 碰撞愈发剧烈, 电子密度逐渐升高, 鞘层变薄, 这导致表面波波数的实部增大, 表面波波长变短, 驻波效应逐渐显著. 同时, 对比图2(a1)—(a4)与图2(b1)—(b4)的结果可以发现, 较低气压情况下, 电势分布及其均匀性几乎没有差别(小于1%). 此时表面波波数的虚部远小于实部, 表面波径向衰减对电势分布的影响并不明显. 而较高气压下(尤其是4 Torr), 如果不考虑表面波径向衰减, 电极边缘处电势略小, 与图2(a1)—(a4)相比略有变化, 电势分布的不均匀度差别小于10%. 在这种硅烷含量较少等离子体功率密度较高的情况下, 随气压升高, 电子密度迅速升高(大约10倍), 而弹性碰撞频率升高4倍左右, 此时电势分布均匀性变化主要来自于表面波波长缩短, 而表面波径向衰减作用不显著. 如果气压进一步升高, 弹性碰撞频率升高的同时趋肤深度减小, 表面波将逐渐被屏蔽, 驻波效应削弱, 趋肤效应等其他电磁效应作用开始显现. 所以, 在硅烷含量较少而功率较高的情况下, 表面波径向衰减作用可以忽略.
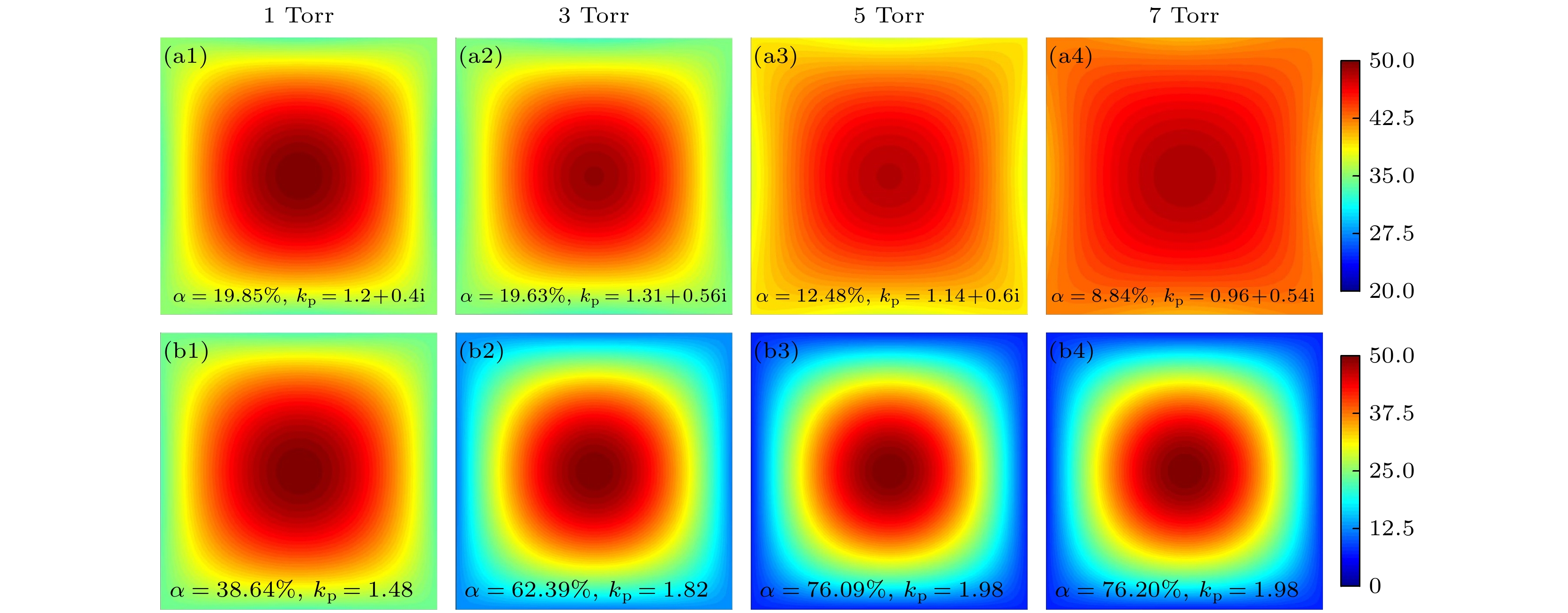
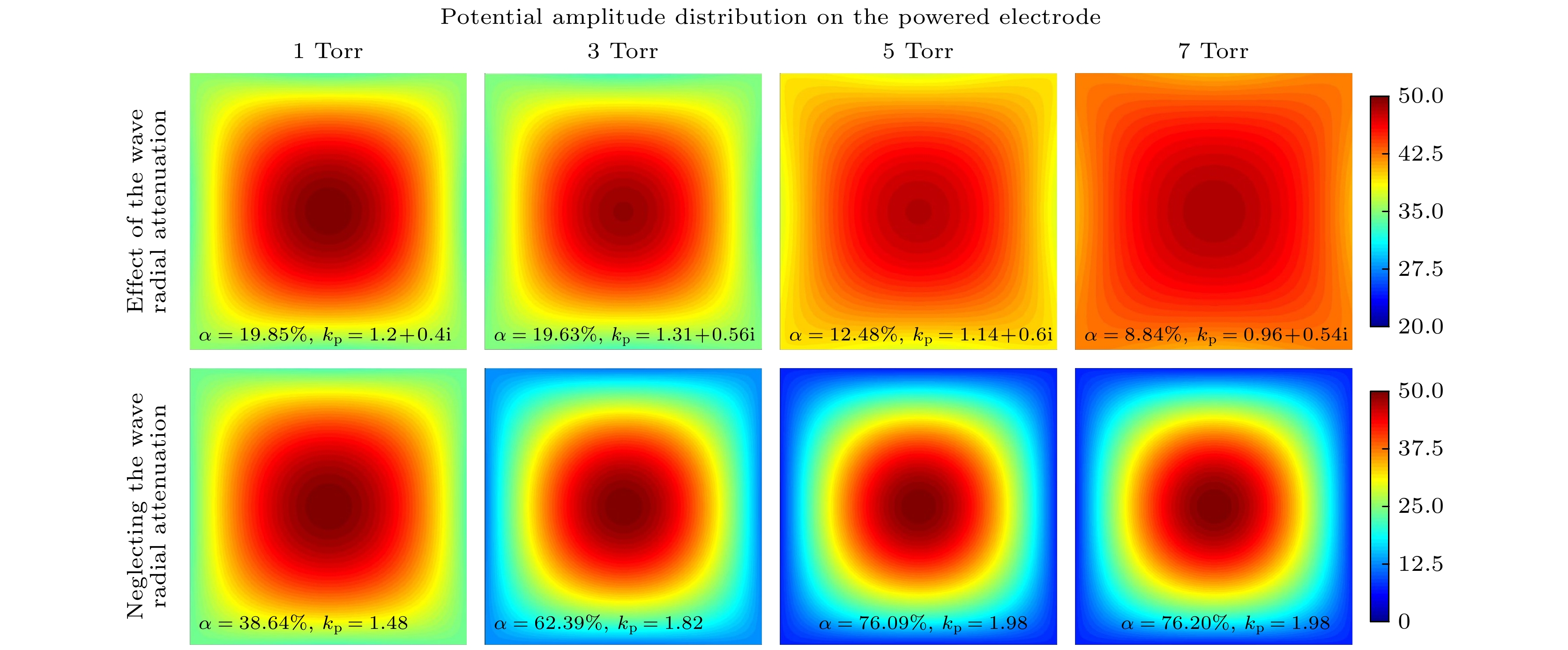
由于硅烷碰撞截面较大, 随着硅烷含量的升高, 电子-中性粒子弹性碰撞频率会升高. 同时, 损失电子生成负离子的附着反应电子能量阈值较低, 会消耗大量低能电子, 电子密度下降, 放电呈电负性. 所以硅烷含量较高等离子体功率密度较低时, 有效相对介电常数的虚数部分不能忽略, 表面波的径向衰减作用将会变得重要. 表3给出了硅烷占比为90%时周期和空间平均的电子密度、鞘层厚度、趋肤深度、电子-中性粒子弹性碰撞频率和等离子体有效介电常数, 此时放电条件为: 电压幅值 50 V, 电极间距 2 cm, 功率 2—5 kW.
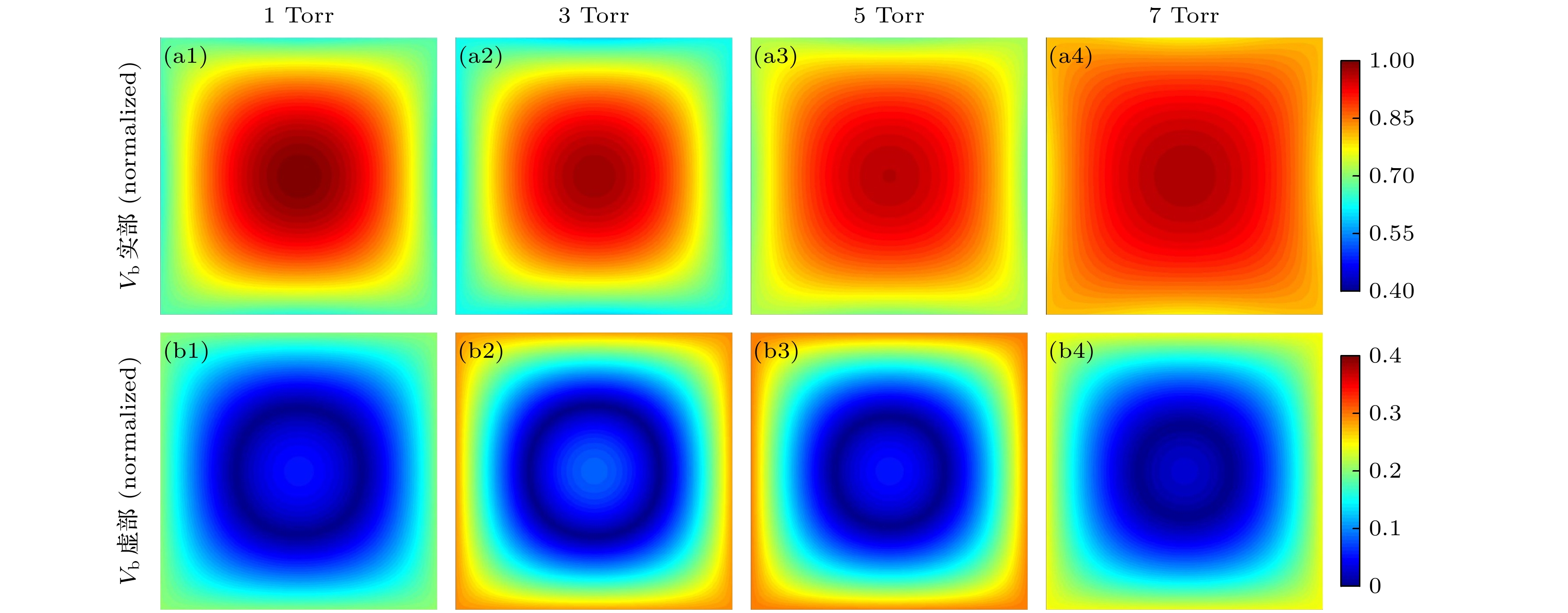
从表3可以看出, 硅烷含量较高功率较低的情况下, 电子密度随气压升高先升高后降低, 这是由于更加剧烈的碰撞导致平均电子温度下降, 附着反应的发生概率相对增大, 放电的电负性变强. 并且由于较低功率情况下, 电子密度较低, 趋肤深度较大, 驻波效应将在更广的气压范围内起主导作用. 图3分别给出了考虑和忽略表面波径向衰减时的电势分布. 考虑表面波径向衰减时(图3(a1)—(a4)), 随气压升高, 表面波波数实部从1.2降低至0.96, 腔室中传播的表面波波长变长. 电势分布的均匀性随气压升高逐渐变好, 不均匀度从19.85%下降至8.84%. 而忽略表面波径向衰减时, 随气压升高, 表面波波数从1.48提升至1.98, 腔室中传播的表面波波长缩短, 电势分布的均匀性随气压升高变差, 不均匀度从38.64%提升至76.2%, 驻波效应持续增强, 结论正好相反. 这是因为忽略表面波径向衰减时仅考虑了鞘层区, 忽略了放电中体区所导致的波数变化, 导致简化的计算模型得出的表面波波长偏短. 图4给出了考虑表面波径向衰减时不同气压下电势实部和电势虚部的归一化分布. 电势的实部表示与电源同相位的电势幅值, 虚部则反映由相位差所导致的电势正交分量, 相位角
$ \theta = {\mathrm{a}}{\mathrm{r}}{\mathrm{c}}{\mathrm{t}}{\mathrm{a}}{\mathrm{n}}\left[{\mathrm{I}}{\mathrm{m}}\left({V}_{{\mathrm{b}}}\right)/{\mathrm{R}}{\mathrm{e}}\left({V}_{{\mathrm{b}}}\right)\right] $ . 结果表明, 电势虚部的峰值出现在电极径向边缘区域, 随着表面波径向衰减的增强, 电势虚部及其对应相位角的增大. 这表明如果忽略表面波径向衰减, 简化的计算模型将显著低估电极径向边缘区域的电势, 驻波效应的作用被放大. 考虑表面波径向衰减时, 复电势的模均匀性更好, 体现了逐渐升高的电子与中性粒子弹性碰撞频率对驻波效应的抑制作用, 与Lieberman等[16,18]的理论推导结果相同.在光伏PECVD薄膜生产中, 为确保后续工艺不受影响并使光伏电池光电转化效率达标, 通常要求薄膜不均匀度控制在10%以内, 甚至需严格控制在3%以内. 研究结果表明, 采用平面电极时, 电势分布不均匀度显著超过10%, 极端情况下可达80%以上, 显然无法满足工业生产的要求. 正如前文中提到的, 研究腔室中驻波的波长变化和分布是进行后续的诸如电源多点对称馈入、曲面电极等均匀性改善措施的前提, 因此本研究在考虑了表面波的径向衰减的情况下对这些均匀性改善手段也进行了重新评估. 以电势分布均匀性相对较差的表2和图2的相关结果为例, 首先研究改变电源馈入位置对电势分布均匀性的改善效果.
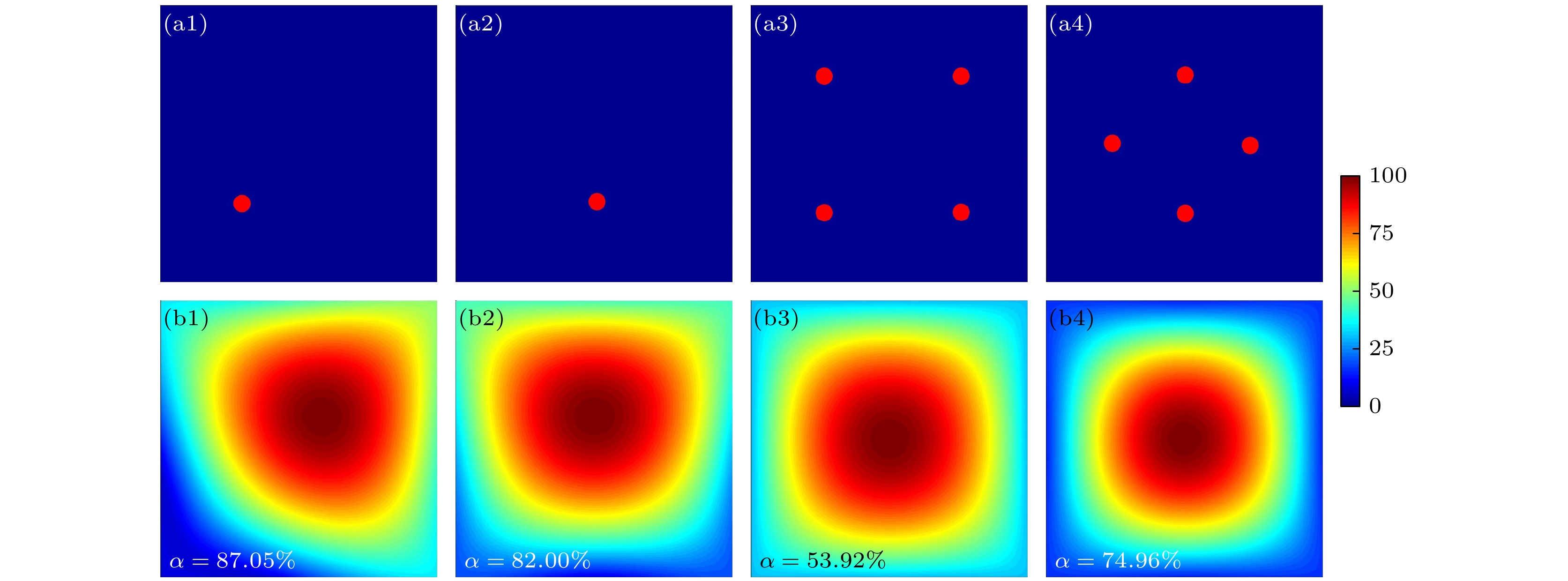
图5(a1)—(a4)展示了电源在电极上表面的馈入位置和分布的4组案例, 图5(b1)—(b4)是气压为3 Torr的情况下, 4组案例对应的电势分布. 第1组案例单个电源馈入点位于电极上表面对角线上距离左下端点1/4连线长度处; 第2组案例单个电源馈入点位于电极上表面边长中点连线上距离下边中点1/4连线长度处; 第3组和第4组案例采用4个电源馈入点, 其中第3组案例中馈入点分别位于电极上表面对角线的1/4连线长度处, 第4组案例中馈入点分别位于电极上表面边长中点连线的1/4连线长度处.
从结果可以发现, 第1组案例中电源位于左下区域, 电势分布的峰值出现在电极间偏右上方区域. 由于射频以上频率的电磁波在金属材料中的趋肤深度极小, 电磁波无法穿透金属, 其传播方向是首先沿着电极上表面馈入点处至电极边缘处, 然后经过电极边缘到达电极之间的径向边缘处, 最终在电极之间沿径向边缘向径向中心方向传播, 因此电源馈入位置会影响表面波的传播路径. 第1组案例中电源馈入点位于电极上表面左下区域, 使得表面波在电极上表面需经历更长的路径才能抵达右上区域. 表面波在电极上表面传播时路径长度的差异导致叠加后形成电势分布的峰值位于远离电源馈入位置的右上方区域. 同样的原因, 第2组案例中电势分布的峰值出现在远离馈入点的偏上方位置. 根据这一原理, 采用多点电源馈入就可以使多个馈入源形成的驻波互相叠加, 达到改善均匀性的目的. 从结果可以看出, 第3组案例中电势分布不均匀度为53.92%, 相比于电源中心单点馈入时的54.71%(图2(a3))来说有所改善, 然而效果并不十分显著; 而第4组案例中电势分布不均匀度为74.96%, 相比于电源中心单点馈入时的均匀性更差. 调整电源馈入点有利于驻波的波峰和波节相互叠加, 从而优化电势分布均匀性. 针对本文采用的方形电极结构, 将电源馈入位置向电极端点移动时, 波峰会沿对角线方向向对侧端点方向发生偏移. 参数扫描结果显示, 当馈入点位于端点至中心点距离的 1/2 位置时, 电压峰值偏离中心的距离达到最大的同时不会出现第2个波峰, 此时采用4个对称分布的馈入点可实现最大程度的波峰与波节的叠加. 然而, 受限于电极尺寸与表面波波长的关系, 波峰偏移幅度较小, 导致叠加过程中仍存在一定程度的波峰重合, 均匀性改善效果因此受限. 理论上, 若电极间波长与电极尺寸匹配, 使电极区域恰好形成一个波峰与一个波节, 通过对称馈入点的波峰波节抵消机制, 可实现最优的均匀性改善效果.
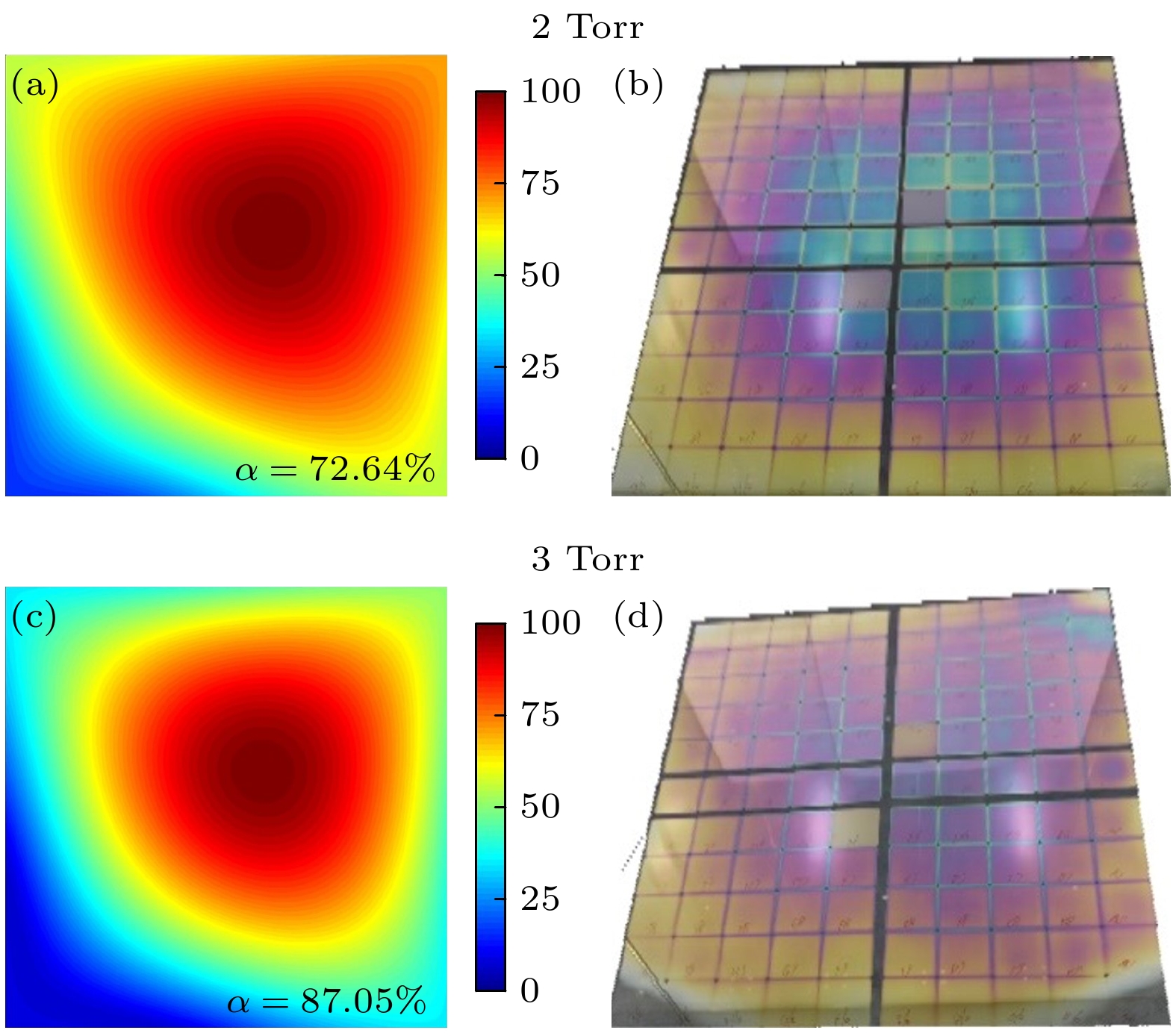
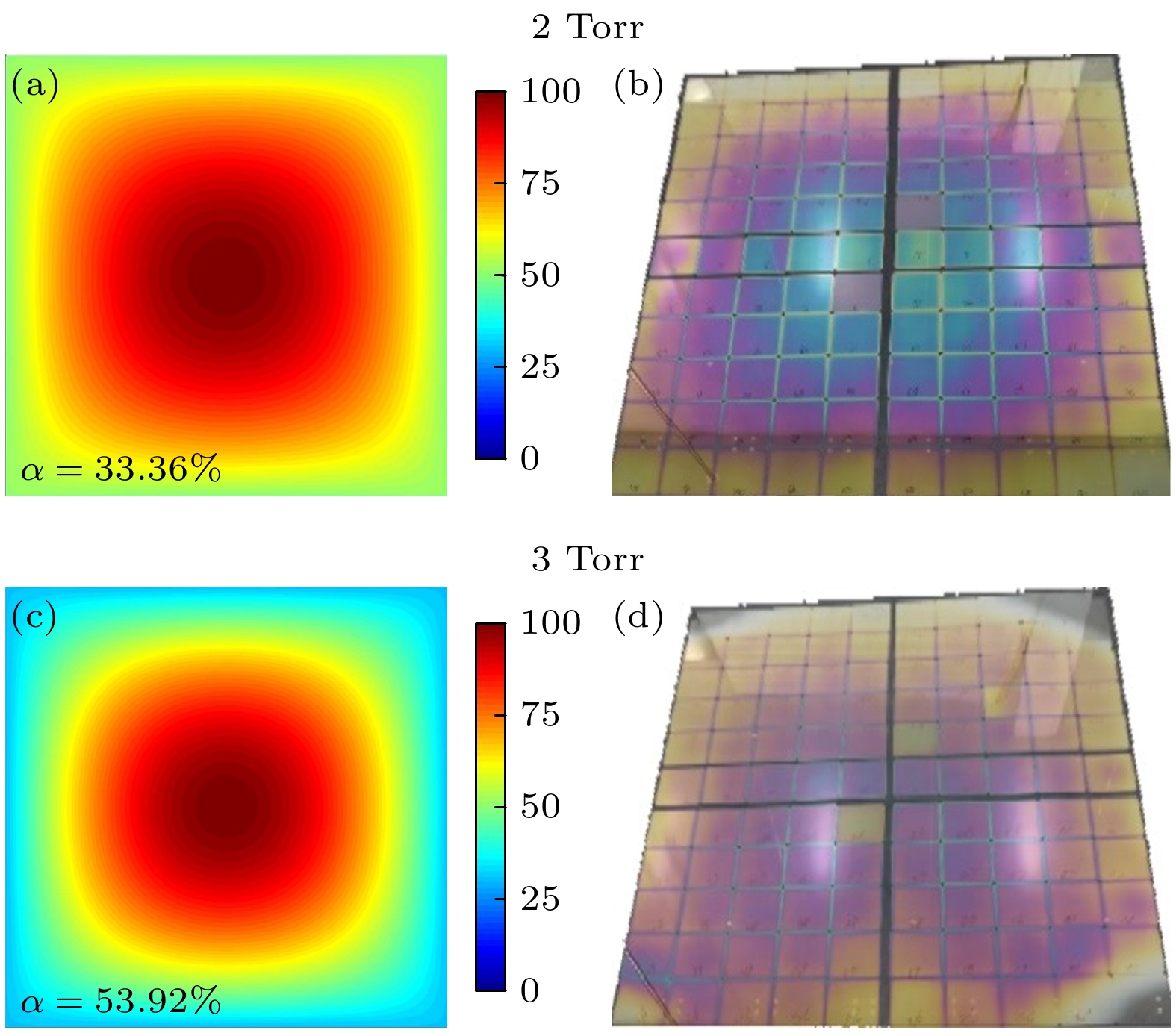
本研究模拟结果和光伏硅基薄膜PECVD工艺腔室中实验结果进行了验证. 图6给出了与案例一电源馈入方式相同时, 2 Torr和3 Torr气压下模拟计算的电势分布和实验观测的薄膜沉积结果. 实验结果中蓝绿色区域沉积薄膜的厚度最厚, 紫色区域略薄, 黄白色区域最薄, 银色区域为基片颜色, 意味着几乎没有薄膜沉积. 通过实验与模拟结果的对比可以清晰地发现, 当馈入源位于左下时, 电势分布和沉积薄膜厚度的峰值均出现在偏右上区域, 而左下区域的电势幅值较低, 沉积的薄膜也较薄. 在 3 Torr气压下, 由于波长变短, 这种效应表现得更为明显, 左下区域电势幅值极小, 靠近边缘区域几乎为零. 从图6(d)的实验结果中也可以看出, 左下区域沉积的薄膜也极薄, 在最边缘区域无薄膜沉积. 图7展示了与案例三电源馈入方式相同时, 2 Torr和3 Torr气压下模拟计算的电势分布和实验观测的薄膜沉积结果. 其中, 模拟结果显示, 相较于中心单点馈入, 2 Torr和3 Torr情况下采用4个对称电源馈入点均能够使电势分布均匀性 得到一定程度的改善. 然而, 随着气压升高, 表面波波长变短仍然是导致均匀性变差的主要因素. 实验结果同样表明, 2 Torr气压下沉积薄膜厚度分布呈现出中心高边缘低的特征, 且峰值位于中心区 域; 3 Torr气压下沉积薄膜厚度均匀性明显更差, 四角区域沉积薄膜变薄, 甚至几乎无薄膜沉积, 实验与模拟结果呈现出相互对应的变化趋势. 实际上, 由于工艺腔室结构较为复杂, 难以保证完全对称, 这就导致沉积薄膜厚度分布不可避免地存在一定程度的不对称. 在工业生产中, 可以通过调节电源馈入位置来抵消部分腔室几何结构的不对称, 从而有效提升沉积薄膜的均匀性. 但在本研究选取的参数条件下, 表面波波长较长, 通过多个电源馈入点形成驻波叠加实现的均匀性提升效果相对有限.
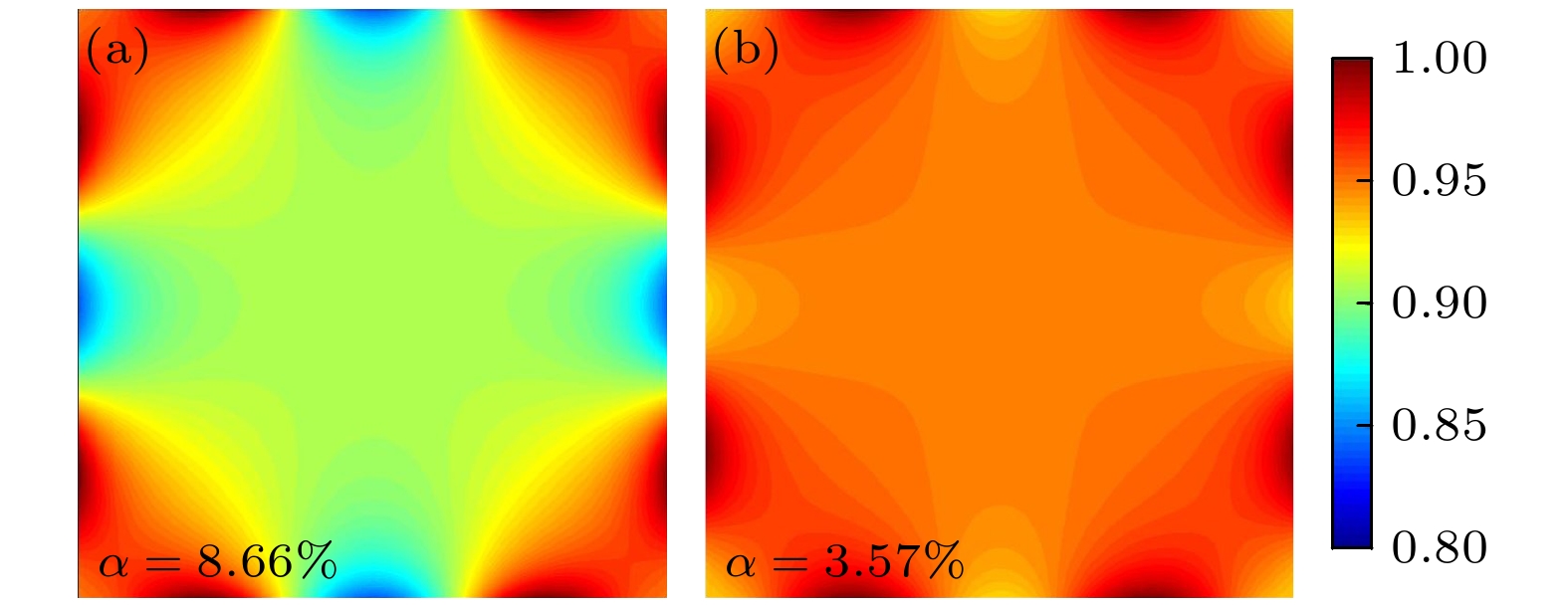
另一种改善均匀性的方式是采用曲面电极. 其作用原理在于, 如图1所示, 曲面电极与绝缘介质间真空区域在电极间串联阻抗中起分压作用, 使放电区域的分压相应减小. 这一变化会导致径向中心区域电场强度减弱、带电粒子密度降低, 进而使中心区域的沉积速率下降至与边缘区域相近, 最终实现均匀性提升的目标. 值得注意的是, 相较于传统平面电极, 曲面电极的结构特性会使得电源的一部分功率沉积在曲面电极的真空区域. 图8给出了采用曲面电极时, 在4 Torr气压下分别采用方案一和方案三的电源馈入方式的归一化电势分布. 采用曲面电极时需要在电极曲面的最低平面处施加一层绝缘介质来保证放电区域间距相等, 因此这里给出的是归一化电势分布. 结果显示: 在采用方案一的电源馈入方式时, 曲面电极的加入使不均匀性从74.49%大幅降至8.66%, 均匀性得到有效改善; 在采用方案三的电源馈入方式时, 曲面电极的使用使得均匀性得到进一步改善至3.57%, 表明曲面电极对均匀性的优化效果十分显著, 可以使大面积高气压下的镀膜均匀性满足光伏工艺的生产要求, 这一点也在之前的工作中得到了验证[1]. 需要注意的是, 由于当前曲面电极加工后形状固定, 仅适用于特定表面波分布, 若波长和分布改变, 优化效果会显著下降, 而表面波波长对电源馈入位置、放电功率、气压、气体比例等参数变化较为敏感. 因此, 在上述参数波动较小的工艺条件下, 采用曲面电极优化均匀性具有适用性; 而当参数变化幅度较大时, 则需考虑采用多腔室匹配不同曲面电极形状, 或结合其他均匀性优化手段.
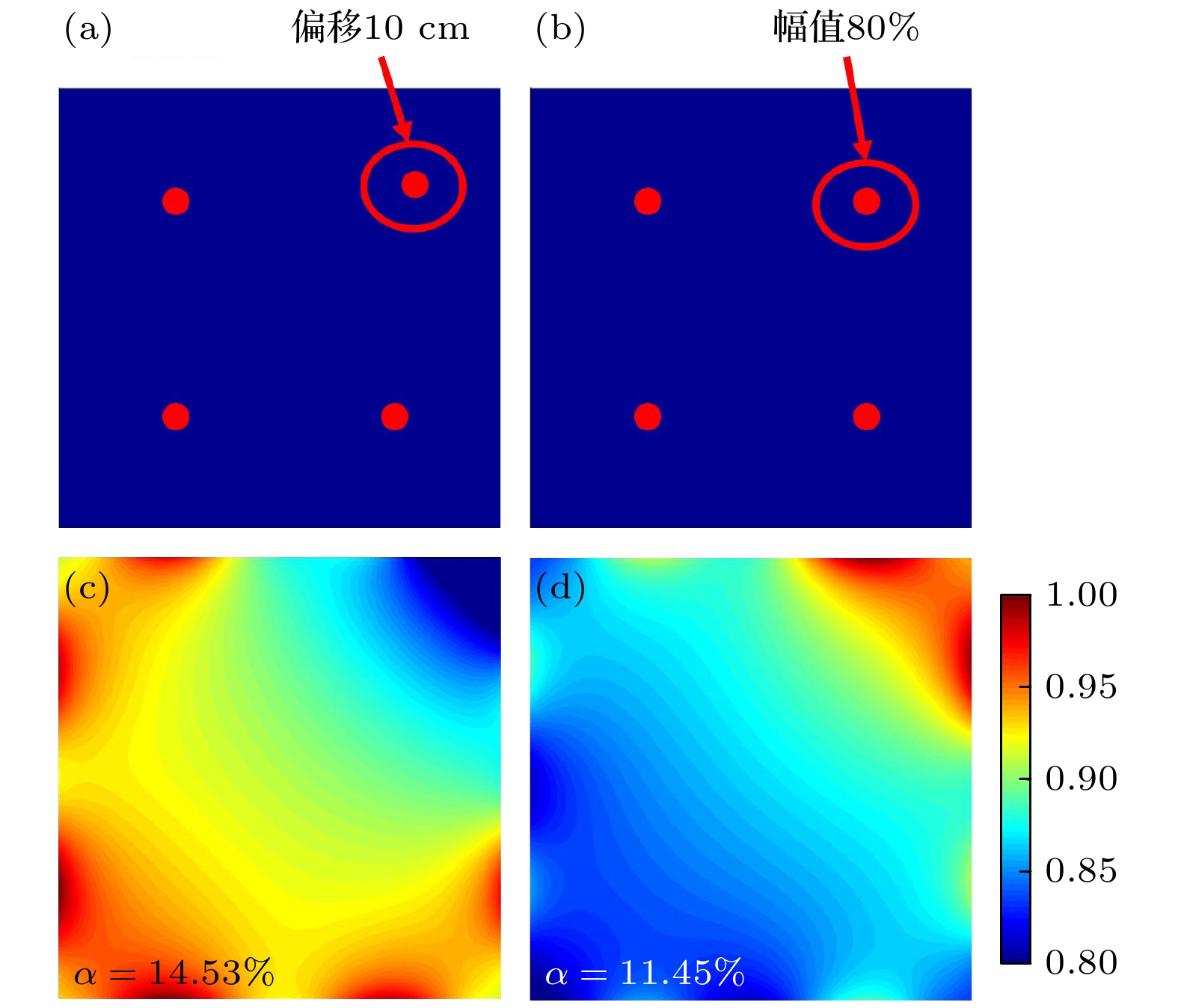
此外, 采用曲面电极对加工和安装的精度也提出了更高的要求, 如图9所示. 采用曲面电极和方案三的电源馈入方式时, 如果右上角馈入点偏离理想位置10 cm, 电势分布均匀性就会明显变差, 从3.57 %变为14.53 %. 同样情况下, 如果右上角电源馈入点的电流幅值只有理想情况下的80%, 也会导致电势分布均匀性明显恶化, 从3.57%变为11.45%, 不均匀度均超过了10%, 优化效果不理想, 可能导致镀膜均匀性无法满足生产要求. 这清晰地表明, 在工业生产中, 首先需要精准地找出影响沉积薄膜均匀性的主要因素, 然后根据产品的具体要求灵活地选择优化方式, 才能达到最适宜的生产效果.
-
本研究聚焦于光伏和平板显示等领域中大面积容性耦合放电驻波效应致使沉积薄膜不均匀的关键问题, 通过将流体模型与传输线模型耦合, 考虑电子-中性粒子弹性碰撞对表面波的径向衰减, 以硅基薄膜沉积常用的硅烷氢气混合气体为研究对象, 分析了气压、气体比例和功率等放电参数对驱动电极电势幅值分布的影响, 并且探索了几种用于提升均匀性的方法, 以及它们的有效范围和效果.
研究发现, 功率较高硅烷占比较低时(电负性较弱), 表面波的径向衰减并不显著, 表面波波长的变化是影响驱动电极电势幅值分布的主导因素. 而功率较低硅烷占比较高时(电负性较强), 趋肤深度较大, 在较高气压下放电仍然由驻波效应主导. 这种情况下电子-中性粒子弹性碰撞频率较高, 表面波径向衰减对表面波波数和驱动电极电势幅值分布的影响不可忽略.
为提升均匀性, 本研究还探索了改变电极形状和电源馈入分布的策略, 并且在实验中验证了驱动电极电势幅值分布与沉积薄膜厚度分布的对应关系. 采用多点馈入电源驱动并调整电源馈入位置能够优化驱动电极电势幅值分布的均匀性. 在本文放电条件下, 采用4个对称的电源馈入点并使其位于电极端点至中心点距离的1/2位置时, 可实现最大程度的波峰与波节叠加, 从而改善驱动电极电势幅值分布的均匀性. 但受表面波波长限制, 叠加过程中仍存在一定程度的波峰重合, 效果有限. 而采用曲面电极会使得电源的一部分功率沉积在曲面电极的真空区域, 使中心区域的沉积速率下降至与边缘区域相近, 最终实现均匀性提升的目标. 同时采用对称四点馈入电源和曲面电极能显著提升驱动电极电势幅值分布的均匀性, 但对参数设定和加工精度要求极高, 稍有偏差就会导致优化效果显著下降.
总之, 本研究通过分析气压、气体比例和功率等对等离子体参数和表面波传输的影响, 给出了驱动电极电势幅值分布的变化规律, 为工业生产提供了关键参数的调控依据. 在未来的工作中, 还需要进一步在复杂工况下(例如腔室结构、气体流动、温度分布等)分析驻波效应对等离子体中电子、离子、中性粒子分布的影响, 以及驻波效应对沉积薄膜质量的影响, 从而更全面准确地研究驻波效应, 为解决工业实际问题提供有力支持和切实可行的实践指导.
大面积容性耦合放电驻波效应对驱动电势分布均匀性的影响
Influence of standing wave effect on uniformity of potential distribution between electrodes in large-area capacitively coupled discharges
-
摘要: 在光伏和平板显示等领域, 通常采用大面积容性耦合腔室进行等离子体增强化学气相沉积. 随着腔室尺寸增大和驱动频率提高, 受驻波效应影响, 驱动电极电势幅值分布不均匀, 从而导致沉积薄膜不均匀的问题日益凸显. 针对此问题, 本文通过流体模型与传输线模型耦合, 以光伏硅基薄膜沉积中常用的硅烷氢气混合气体为研究对象, 考虑电子-中性粒子弹性碰撞, 研究了气压、气体比例和功率等参数对表面波传播以及驱动电极电势幅值分布的影响. 模拟结果与实际工艺腔室中薄膜沉积实验结果进行了对照, 验证了驱动电极电势幅值分布与薄膜厚度分布之间的对应关系. 研究表明, 在功率较低硅烷含量较高时, 表面波的径向衰减十分显著, 从而成为影响驱动电势幅值分布不均匀的主导因素. 本文还研究了调整电源馈入位置和采用多个电源馈入点来优化电势幅值分布均匀性的方法, 受表面波波长限制, 这两种方法效果有限. 而采用曲面电极能显著提升电势幅值分布的均匀性, 然而对参数设定和加工精度要求较高. 本研究不仅深化了对驻波效应作用机制的理解, 还为工业生产中解决驻波效应对薄膜均匀性的影响提供理论支撑与指导, 有望推动相关产业技术革新.
-
关键词:
- 容性耦合放电 /
- 等离子体增强化学气相沉积 /
- 驻波效应
Abstract:Large-area capacitively coupled discharges are widely used in plasma enhanced chemical vapor deposition (PECVD) processes for solar cell and display manufacturing. With the increase of the chamber size and driving frequency for improving production efficiency, the non-uniformity of deposited film induced by standing wave effects becomes more serious, which deserves more attention and in-depth research. Based on a fluid model coupled with a transmission line model, the potential amplitude distribution on the powered 2 m2 electrode and the plasma characteristics in a capacitive plasma sustained in a silane/hydrogen discharge driven at 27.12 MHz are investigated. This work identifies three key control parameters: pressure, silane content, and input power, with particular emphasis on radial wave attenuation caused by electron-neutral elastic collisions. The simulation results are validated by industrial experimental results, confirming the relationship between the distributions of potential amplitude on the powered electrode and the film thickness. Two different mechanisms emerge from the analysis. Under the conditions of low silane content and high power, the surface wave radial attenuation is not significant and the surface wave wavelength variations dominate the potential amplitude distribution on the powered electrode. Conversely, in the case of high silane content and low power, significant radial attenuation of the surface wave leads to the noticeable weakening of the standing wave effect due to higher electron-neutral collision frequency. Neglecting the radial attenuation of the surface wave will result in significant deviations in the potential amplitude distribution on the powered electrode as shown in the following figure. Strategies such as adjusting power input positions or using multiple power input are studied to improve uniformity, but the improvements are still limited. Although it requires strict parameter control and machining precision, the shaped electrode demonstrates remarkable uniformity improvement of the potential distribution. In the future work, it is necessary to further analyze the influence of the standing wave effects on the radial distributions of electron, ions, and neutral radicals under complex conditions, such as different chamber structures, gas flows, and temperature distributions, as well as the influence on the quality of deposited films. This will enable a more comprehensive and accurate study of standing wave effects, providing support and guidance for solving real industrial problems. -

-
图 2 不同气压下的考虑(a1)—(a4)和忽略(b1)—(b4)表面波径向衰减情况下的驱动电极电势幅值的二维分布(以下简称电势分布)以及每种情况下的电势分布不均匀度
$ \alpha $ 和表面波波数$ {k}_{{\mathrm{p}}} $ , 电极尺寸为2 m × 2 m, 其他放电条件与表2相同Figure 2. Two-dimensional distributions of the potential amplitude on the powered electrode with (a1)–(a4) or without (b1)–(b4) the consideration of the surface wave radial attenuation under different pressures, with the potential nonuniformity factor
$ \alpha $ and surface wave number$ {k}_{{\mathrm{p}}} $ for each case. Electrode size: 2 m × 2 m; other discharge conditions are the same as in Table 2.图 3 不同气压下的考虑(a1)—(a4)和忽略(b1)—(b4)表面波径向衰减情况下的电势分布以及每种情况下的电势分布不均匀度
$ \alpha $ 和表面波波数$ {k}_{{\mathrm{p}}} $ . 电极尺寸为2 m × 2 m; 其他放电条件与表3相同Figure 3. Distributions of the potential with (a1)–(a4) or without (b1)–(b4) the consideration of the surface wave radial attenuation under different pressures, with the potential nonuniformity factor
$ \alpha $ and surface wave number$ {k}_{{\mathrm{p}}} $ for each case. Electrode size is 2 m × 2 m; other discharge conditions are the same as in Table 3.图 4 不同气压下考虑表面波径向衰减时归一化的电势分布的实部(a1)—(a4)和虚部(b1)—(b4). 电极尺寸为2 m × 2 m; 其他放电条件与表3相同
Figure 4. Distributions of the real part (a1)–(a4) and imaginary part (b1)–(b4) of the normalized potential with the consideration of the surface wave radial attenuation. Electrode size is 2 m × 2 m; other discharge conditions are the same as in Table 3.
图 5 不同案例下电源馈入位置示意图(a1)—(a4)和对应的电势分布(b1)—(b4)以及电势分布不均匀度
$ \alpha $ . 电极尺寸为2 m × 2 m; 放电气压为3 Torr; 其他放电条件与表2相同Figure 5. Distributions of power input positions (a1)–(a4) under different cases, and the potential (b1)–(b4), as well as the potential nonuniformity factor α. Electrode size is 2 m × 2 m; pressure is 3 Torr; other discharge conditions are the same as in Table 2.
图 6 不同气压下采用图5(a1)馈入方式模拟计算的电势分布(a), (c)和相同条件下实验观测的沉积薄膜厚度分布(b), (d). 模拟与实验放电参数相同, 电极尺寸为2 m × 2 m; 其他放电条件与表2相同
Figure 6. Distributions of the potential from simulation (a), (c) and the deposited film thickness from experiment (b), (d) under different pressures with the case of power input in Fig. 5(a1). Discharge parameters of simulation and experiment are consistent, electrode size is 2 m × 2 m; other discharge conditions are the same as in Table 2.
图 7 不同气压下采用图5(a3)馈入方式模拟计算的电势分布(a), (c)和相同条件下实验观测的沉积薄膜厚度分布(b), (d). 模拟与实验放电参数相同, 电极尺寸为2 m × 2 m; 其他放电条件与表2相同
Figure 7. Distributions of the potential from simulation (a), (c) and the deposited film thickness from experiment (b), (d) under different pressures with the case of power input in Fig. 5(a1). Discharge parameters of simulation and experiment are consistent, electrode size is 2 m × 2 m; other discharge conditions are the same as in Table 2.
图 8 采用曲面电极和图5(a3)馈入方式情况下放电区域归一化的电势分布. 电极尺寸为2 m × 2 m; 放电气压为 4 Torr; 其他放电条件与表2相同
Figure 8. Distributions of the normalized potential with the shaped electrode and the case of power input in Fig. 5(a3). Electrode size is 2 m × 2 m; pressure is 4 Torr; other discharge conditions are the same as in Table 2.
图 9 采用曲面电极和图5(a3)馈入方式情况下, 当右上角电源偏离理想位置(a)和电源电流幅值偏离理想值(b)时归一化的电势分布(c), (d). 电极尺寸为2 m × 2 m; 放电气压为 4 Torr; 其他放电条件与表2相同
Figure 9. Distributions of the normalized potential (c), (d) when the power input position deviates from the ideal position (a) or the current amplitude deviates from the ideal value (b) with the shaped electrode and the case of power input in Fig. 5(a3). Electrode size is 2 m × 2 m; pressure is 4 Torr; other discharge conditions are the same as in Table 2.
表 1 流体模型中计算硅烷氢气放电的反应及其系数
Table 1. Reactions and corresponding coefficients in fluid models for silane/hydrogen discharges.
序号 反应 阈值能/eV 系数[38,39]
/(cm3·s–1)R1 SiH4+e→SiH4+e — cal R2 SiH4+e→ $ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{3}^{+} $ +H+2e11.9 cal R3 SiH4+e→ $ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{3}^{-} $ +H5.7 cal R4 SiH4+e→ $ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{2}^{-} $ +2H5.7 cal R5 SiH4+e→SiH3+H+e 8.3 cal R6 SiH4+e→SiH2+2H+e 8.3 cal R7 H2+e→H2+e — cal R8 H2+e→2H+e 8.9 cal R9 H2+e→ $ {{\mathrm{H}}}_{2}^{+} $ +2e15.4 cal R10 Si2H6+e→Si2 $ {{\mathrm{H}}}_{4}^{+} $ +2H+2e10.2 cal R11 Si2H6+e→SiH3+SiH2+H+e 7.0 cal R12 $ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{3}^{+} $ +$ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{3}^{-} $ →2SiH3— 1.0×10–8 R13 $ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{3}^{+} $ +$ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{2}^{-} $ →SiH3+SiH2— 1.0×10–8 R14 $ {{\mathrm{H}}}_{2}^{+} $ +$ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{3}^{-} $ →SiH3+H2— 1.0×10–8 R15 $ {{\mathrm{H}}}_{2}^{+} $ +$ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{2}^{-} $ →SiH2+H2— 1.0×10–8 R16 Si2 $ {{\mathrm{H}}}_{4}^{+} $ +$ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{3}^{-} $ →SiH3+H2— 1.0×10–8 R17 Si2 $ {{\mathrm{H}}}_{4}^{+} $ +$ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{2}^{-} $ →3SiH2— 1.0×10–8 R18 SiH4+ $ {{\mathrm{H}}}_{2}^{+} $ →$ {{\mathrm{S}}{\mathrm{i}}{\mathrm{H}}}_{3}^{+} $ +H2+H— 1.0×10–8 R19 SiH4+H→SiH3+H2 — 1.2×10–12 R20 Si2H6+H→H2+Si2H5 — 7.0×10–12 R21 Si2H6+H→SiH3+SiH4 — 3.5×10–12 R22 SiH3+SiH3→SiH4+SiH2 — 1.5×10–10 R23 SiH2+H2→SiH4 — 2.7×10–14 R24 SiH2+SiH4→Si2H6 — 2.3×10–11 表 2 不同气压下周期和空间平均的电子密度(
$ {n}_{{\mathrm{e}}} $ )、鞘层厚度($ {d}_{{\mathrm{s}}{\mathrm{h}}} $ )、趋肤深度($ \delta $ )、电子-中性粒子弹性碰撞频率($ {\upsilon }_{{\mathrm{e}}{\mathrm{n}}} $ )和电极间有效相对介电常数($ {\varepsilon }_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ ); 放电条件为电压幅值100 V, 间距1.6 cm, 功率范围8—12 kW, SiH4/SiH4+H2 = 1%Table 2. Periodically and spatially averaged electron density (
$ {n}_{{\mathrm{e}}} $ ), sheath thickness ($ {d}_{{\mathrm{s}}{\mathrm{h}}} $ ), skin depth ($ \delta $ ), electron-neutral elastic collision frequency ($ {\upsilon }_{{\mathrm{e}}{\mathrm{n}}} $ ), and effective relative permittivity ($ {\varepsilon }_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ ) under different pressures; discharge conditions: voltage 100 V, gap 1.6 cm, power range 8–12 kW, SiH4/SiH4+H2 = 1%.p/Torr $ {n}_{{\mathrm{e}}} $ /(1015 m–3)$ {d}_{{\mathrm{s}}{\mathrm{h}}} $ /cm$ \boldsymbol{\delta } $ /cm$ {\upsilon }_{{\mathrm{e}}{\mathrm{n}}} $ /(1010Hz)$ {\varepsilon }_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ 1 5.98 0.20 6.88 0.36 4.02+0.46i 2 19.56 0.13 3.80 0.72 6.08+0.68i 3 37.57 0.08 2.74 1.08 9.30+1.29i 4 55.81 0.06 2.25 1.44 12.65+2.20i 表 3 不同气压下周期和空间平均的电子密度(
$ {n}_{{\mathrm{e}}} $ )、鞘层厚度($ {d}_{{\mathrm{s}}{\mathrm{h}}} $ )、趋肤深度($ \delta $ )、电子-中性粒子弹性碰撞频率($ {\upsilon }_{{\mathrm{e}}{\mathrm{n}}} $ )和电极间相对介电常数($ {\varepsilon }_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ ), 放电条件为电压幅值50 V, 间距2 cm, 功率大致2—5 kW, SiH4/SiH4+H2 = 90%Table 3. Periodically and spatially electron density (
$ {n}_{{\mathrm{e}}} $ ), sheath thickness ($ {d}_{{\mathrm{s}}{\mathrm{h}}} $ ), skin depth ($ \delta $ ), electron-neutral elastic collision frequency ($ {\upsilon }_{{\mathrm{e}}{\mathrm{n}}} $ ), and effective relative permittivity ($ {\varepsilon }_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ ) under different pressures, discharge conditions: voltage 50 V, gap 2 cm, power range 2–5 kW, SiH4/SiH4+H2 = 90%.p/Torr $ {n}_{{\mathrm{e}}} $ /(1015 m–3)$ {d}_{{\mathrm{s}}{\mathrm{h}}} $ /cm${\delta } $ /cm$ {\upsilon }_{{\mathrm{e}}{\mathrm{n}}} $ /(1010 Hz)$ {\varepsilon }_{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ 1 2.40 0.15 10.86 0.59 3.99+3.02i 3 7.72 0.10 6.06 1.77 4.33+4.53i 5 9.12 0.08 5.57 2.94 2.88+4.25i 7 8.70 0.08 5.70 4.12 1.94+3.18i -
[1] Yu C, Gao K, Peng C W, He C R, Wang S B, Shi W, Allen V, Zhang J T, Wang D Z, Tian G Y, Zhang Y F, Jia W Z, Song Y H, Hu Y Z, Colwell J, Xing C F, Ma Q, Wu H T, Guo L Y, Dong G Q, Jiang H, Wu H H, Wang X Y, Xu D C, Li K, Peng J, Liu W Z, Chen D, Lennon A, Cao X M, De Wolf S, Zhou J, Yang X B, Zhang X H 2023 Nat. Energy 8 1375 doi: 10.1038/s41560-023-01388-4 [2] Crose M, Kwon J S I, Tran A, Christofides P D 2017 Renewable Energy 100 129 doi: 10.1016/j.renene.2016.06.065 [3] Crose M, Sang Il Kwon J, Nayhouse M, Ni D, Christofides P D 2015 Chem. Eng. Sci. 136 50 doi: 10.1016/j.ces.2015.02.027 [4] Schmidt H 2006 Ph. D Dissertation (Lausanne: EPFL [5] Schmitt J P M 1989 Thin Solid Films 174 193 doi: 10.1016/0040-6090(89)90889-4 [6] Meyyappan M, Colgan M J 1996 J. Vac. Sci. Technol. A 14 2790 doi: 10.1116/1.580201 [7] Surendra M, Graves D B 1991 Appl. Phys. Lett 59 2091 doi: 10.1063/1.106112 [8] Curtins H, Wyrsch N, Favre M, Shah A V 1987 Plasma Chem Plasma P 7 267 doi: 10.1007/BF01016517 [9] Liu Y X, Zhang Q Z, Zhao K, Zhang Y R, Gao F, Song Y H, Wang Y N 2022 Chin. Phys. B 31 085202 doi: 10.1088/1674-1056/ac7551 [10] Kim H J, Lee H J 2017 J. Phys. D: Appl. Phys. 122 053301 doi: 10.1063/1.4996998 [11] Kim H J, Lee H J 2017 Plasma Sources Sci. Technol. 26 085003 doi: 10.1088/1361-6595/aa78b4 [12] Kim H J 2021 Vacuum 187 110104 doi: 10.1016/j.vacuum.2021.110104 [13] Kim H J, Lee H J 2016 Plasma Sources Sci. Technol. 25 065006 doi: 10.1088/0963-0252/25/6/065006 [14] Schmidt H, Sansonnens L, Howling A A, Hollenstein Ch, Elyaakoubi M, Schmitt J P M 2004 J. Appl. Phys. 95 4559 doi: 10.1063/1.1690096 [15] Sansonnens L, Pletzer A, Magni D, Howling A A, Hollenstein C, Schmitt J P M 1997 Plasma Sources Sci. Technol. 6 170 doi: 10.1088/0963-0252/6/2/010 [16] Lieberman M A, Booth J P, Chabert P, Rax J M, Turner M M 2002 Plasma Sources Sci. Technol. 11 283 doi: 10.1088/0963-0252/11/3/310 [17] Chabert P, Raimbault J L, Rax J M, Lieberman M A 2004 Phys. Plasmas 11 1775 doi: 10.1063/1.1688334 [18] Lee I, Graves D B, Lieberman M A 2008 Plasma Sources Sci. Technol. 17 015018 doi: 10.1088/0963-0252/17/1/015018 [19] Lieberman M A, Lichtenberg A J, Kawamura E, Marakhtanov A M 2015 Plasma Sources Sci. Technol. 24 055011 doi: 10.1088/0963-0252/24/5/055011 [20] Wen D Q, Kawamura E, Lieberman M A, Lichtenberg A J, Wang Y N 2017 J. Phys. D: Appl. Phys. 50 495201 doi: 10.1088/1361-6463/aa9627 [21] Zhao K, Liu Y X, Kawamura E, Wen D Q, Lieberman M A, Wang Y N 2018 Plasma Sources Sci. Technol. 27 055017 doi: 10.1088/1361-6595/aac242 [22] Lieberman M A, Kawamura E, Chabert P 2022 Plasma Sources Sci. Technol. 31 114007 doi: 10.1088/1361-6595/aca11f [23] Liu J K, Zhang Y R, Zhao K, Wen D Q, Wang Y N 2021 Plasma Sci. Technol. 23 035401 doi: 10.1088/2058-6272/abe18f [24] Liu Y X, Gao F, Liu J, Wang Y N 2014 J. Appl. Phys. 116 043303 doi: 10.1063/1.4891504 [25] Han D M, Liu Y X, Gao F, Wang X Y, Li A, Xu J, Jing Z G, Wang Y N 2018 J. Appl. Phys. 123 223304 doi: 10.1063/1.5024835 [26] Han D M, Su Z X, Zhao K, Liu Y X, Gao F, Wang Y N 2021 Plasma Sci. Technol. 23 055402 doi: 10.1088/2058-6272/abf72a [27] Sansonnens L, Schmidt H, Howling A A, Hollenstein Ch, Ellert Ch, Buechel A 2006 J. Vac. Sci. Technol. A 24 1425 doi: 10.1116/1.2189266 [28] Chen Z, Rauf S, Collins K 2010 J. Appl. Phys. 108 073301 doi: 10.1063/1.3489950 [29] Faraz T, Arts K, Karwal S, Knoops H C M, Kessels W M M 2019 Plasma Sources Sci. Technol. 28 024002 doi: 10.1088/1361-6595/aaf2c7 [30] Kuboi N 2023 J. Micro/Nanopattern. Mats. Metro. 22 041502 doi: 10.1117/1.JMM.22.4.041502 [31] Oehrlein G S, Brandstadter S M, Bruce R L, et al. 2024 J. Vac. Sci. Technol. B 42 041501 doi: 10.1116/6.0003579 [32] Chang J, Chang J P 2017 J. Phys. D: Appl. Phys. 50 253001 doi: 10.1088/1361-6463/aa71c7 [33] 邱华檀, 王友年, 马腾才 2002 物理学报 51 1332 doi: 10.7498/aps.51.1332 Qiu H T, Wang Y N, Ma T C 2002 Acta Phys. Sin. 51 1332 doi: 10.7498/aps.51.1332 [34] Tinck S, Bogaerts A 2012 Plasma Processes & Polym. 9 522 doi: 10.1002/ppap.201100093 [35] Kessels W M M, Hoefnagels J P M, Boogaarts M G H, Schram D C, Van De Sanden M C M 2001 J. Appl. Phys. 89 2065 doi: 10.1063/1.1344911 [36] 刘建凯 2022 博士学位论文(大连: 大连理工大学) Liu J K 2022 Ph. D Dissertation (Dalian: Dalian University of Technology [37] Sansonnens L 2005 J. Appl. Phys. 97 063304 doi: 10.1063/1.1862770 [38] Jia W Z, Wang X F, Song Y H, Wang Y N 2017 J. Phys. D: Appl. Phys. 50 165206 doi: 10.1088/1361-6463/aa6299 [39] Jia W Z, Liu R Q, Wang X F, Liu X M, Song Y H, Wang Y N 2018 Phys. Plasmas 25 093501 doi: 10.1063/1.5008586 [40] Bleecker K D, Bogaerts A, Gijbels R, Goedheer W 2004 Phys. Rev. E 69 056409 doi: 10.1103/PhysRevE.69.056409 [41] Brinkmann R P 2007 J. Appl. Phys. 102 093303 doi: 10.1063/1.2772499 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: