-
近年来, 过渡金属硫族化合物(TMDCs)单分子层因其独特的晶体结构和物理化学性质在纳米科技和能源应用领域得到广泛研究和探索[1–4]. 随着材料科学的进步, 特别是在原子层沉积和化学气相沉积等合成技术的帮助下, 多种Janus TMDCs单分子层被发现并成功合成[5–10]. 这些Janus TMDCs单分子层通过改变上下层硫族元素的种类来打破材料的结构对称性, 在热电、光电、传感器以及量子设备等领域具有很大的应用潜力[11–15].
已有的工作对Janus TMDCs在电子结构[14,16]、声子输运[16–20]和热电性能[18,21–23]等方面都进行了广泛的研究. Patel等[23]报道WSTe单分子层在1200 K下具有2.56的热电优值, 提出Janus TMDCs单分子层是有潜力的热电材料. Han等[24]发现WSSe单分子层纳米带在近室温下的热电优值高达4.13, 远高于WS2和WSe2单分子层纳米带的热电性能. 应变在材料实际应用中普遍存在, 并且对热输运性能和热电性能具有显著影响[4,25]. 由于独特的晶体结构, 二维TMDCs通常展现出较高的拉伸应变极限. 在模拟研究方面, Zhang等[15]利用分子动力学模拟研究了MoSSe单分子层的力学性能, 发现在1—800 K的温度范围内, MoSSe单分子层沿扶手椅型和锯齿形方向的极限应变均高于10%. 在实验研究方面, 采用具有圆形微孔的SiO2基底结合原子力显微镜技术, Zhang等[26]发现二维WSe2能承受至少7.3%的拉伸应变而不破裂; Bertolazzi等[27]报道MoS2单分子层的拉伸极限应变高达11%. 关于热输运性能, Pan等[28]基于第一性原理的晶格动力学计算研究了拉伸应变对PtSTe单分子层晶格热导率的影响, 发现晶格热导率在8%的拉伸应变下由25.71 W·m–1·K–1降低到3.21 W·m–1·K–1. 关于电输运性能, Cui等[13]发现双轴应变可以有效调控PtSSe, PtSTe和PtTeSe的能带结构, 从而影响其带隙; Ahmad等[29,30]基于第一性原理计算发现应变对ZrSSe, HfSSe, PtSSe及其异质双分子层能带结构和带隙具有显著影响. 在热电性能方面, Wang等[31]采用第一性原理研究了应变对MoSSe-WSeTe异质结的影响, 发现适量的应变可以显著提高异质结的热电性能; Rajneesh等[32]发现拉伸应变可以降低WSSe单分子层的晶格热导率, 提高其热电性能. 尽管Janus TMDCs单分子层的性能已有一定程度的研究, 但应变对Janus TMDCs单分子层热输运性能、内在声子行为和热电性能的影响尚未完全明晰, 亟需揭示应变作用下的Janus TMDCs单分子层的微纳尺度热电输运机理.
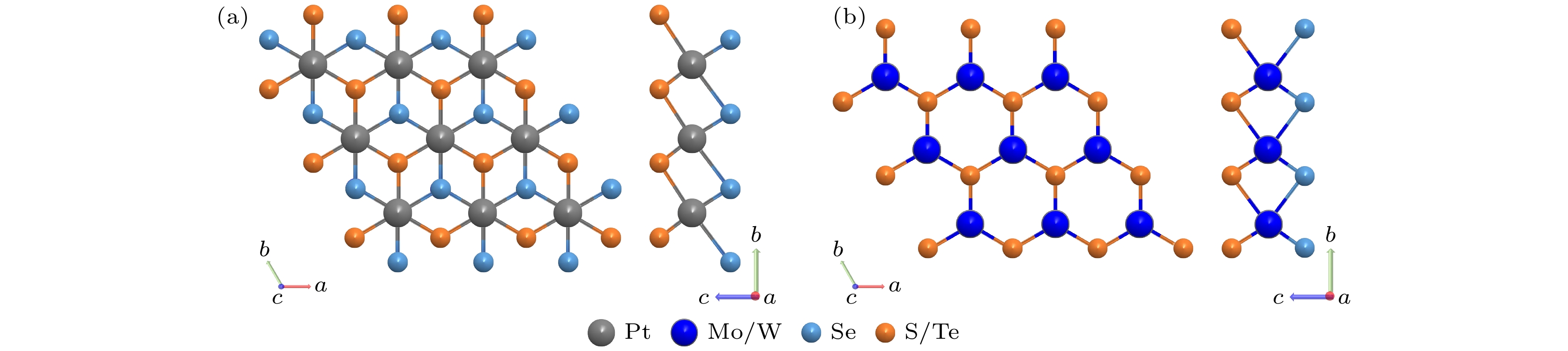
本文以Janus TMDCs单分子层为研究对象, 其晶体结构如图1所示, 包含具有1 T相晶体结构的PtSSe和PtTeSe, 以及具有1 H相晶体结构的MoSSe, MoTeSe, WSSe和WTeSe. 采用基于第一性原理的晶格动力学计算, 研究了拉伸应变对声子输运行为的影响; 采用形变势理论, 研究了拉伸应变对热电性能的影响, 为应变调控Janus TMDCs单分子层的热输运和热电性能提供了理论依据.
-
材料的热电转换效率由热电优值(ZT)表征:
其中S为塞贝克系数, σ为电导率, T表示温度, κl表示晶格热导率, κe为电子热导率.
声子输运性质和晶格热导率由基于第一性原理的晶格动力学和Boltzmann方程迭代求解获得. 密度泛函理论(DFT)和密度泛函微扰理论(DFPT)计算由开源软件Quantum Espresso[33]完成. 采用模守恒赝势, 交换关联泛函采用广义梯度近似下的Perdew-Burke-Ernzerhof (PBE)方法[34]. 在z方向设置2 nm的真空层以消除周期性导致的模拟误差. 动力学矩阵由DFPT计算获得, 采用14×14×1的电子波矢网格及6×6×1的声子波矢网格, 平面波截断能为160 Ry, 电荷密度截断能设置为640 Ry, 自洽计算收敛阈为10–18 Ry. 非简谐力常数由有限差分方法获得, 构建超胞大小为4×4×1, 考虑到第8近邻原子, 电子波矢网格为1×1×1, 自洽计算收敛阈为10–12 Ry. 晶格热导率通过ShengBTE软件[35]迭代求解Boltzmann输运方程获得, 声子波矢网格为120×120×1. 通过计算Born有效电荷和介电张量, 对动力学矩阵进行长程修正. 所有计算参数均进行了收敛性测试. α方向的晶格热导率(κlα)可以表示为
式中, CV为声子体积比热容, vg为声子群速度, τ为声子寿命, λ表示不同的声子模式.
电输运性能在BoltzTraP2软件[36]中采用基于弛豫时间近似的Boltzmann输运方程计算. 电子弛豫时间(τe)基于有效质量近似的形变势理论获得
其中μ为载流子迁移率; m*为输运方向的有效质量. 载流子迁移率计算公式如下:
式中, md为平均有效质量, C为弹性常数, E1为形变势常数, 详细计算方法见Zhao等[4]报道的研究. σ和S的具体计算参见Li等[37]报道的研究. 电子热导率根据Wiedemann-Franz定律[38]计算:
式中, L为洛伦兹常数.
-
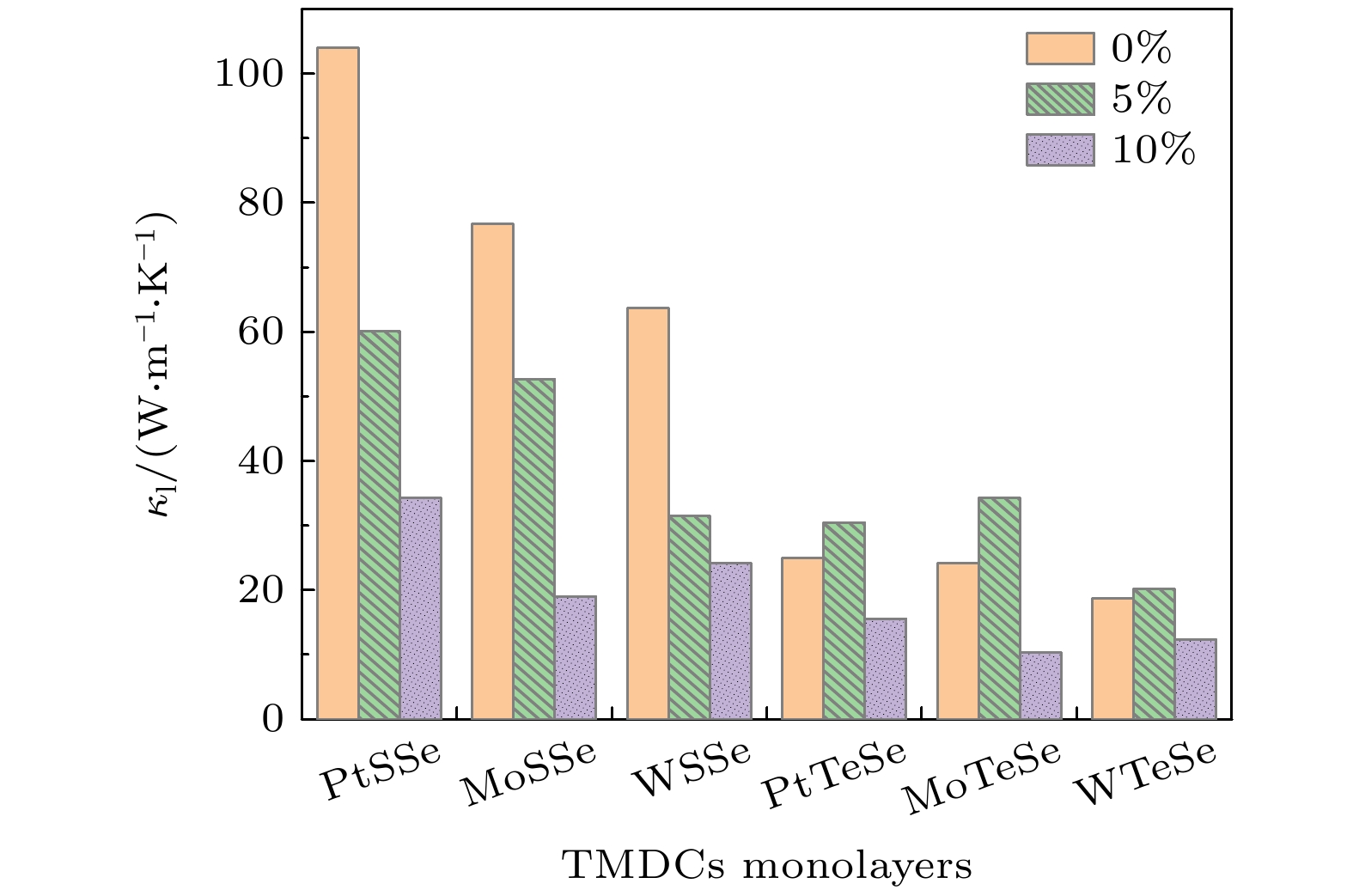
图2为室温下Janus TMDCs 单分子层在未施加应变、施加5%拉伸应变以及施加10%拉伸应变下的晶格热导率. 由图2可以看出, MSSe (M = Mo, W 和Pt)单分子层的晶格热导率普遍高于MTeSe单分子层. 在未施加应变时, PtSSe的晶格热导率最高, 为104 W·m–1·K–1, 与Liu等[17]报道的计算结果接近; WTeSe的晶格热导率最低, 为18.71 W·m–1·K–1. 在0—10%的应变范围内, MSSe单分子层的热导率单调递减, 在10%拉伸应变下, PtSSe, MoSSe和WSSe热导率分别下降了67%, 75%和63%. 在0—10%拉伸应变作用下, MTeSe单分子层的热导率先增大后减小, 在10%拉伸应变作用下, MoTeSe的晶格热导率仅为10.39 W·m–1·K–1. 应变对Janus TMDCs单分子层的热导率影响显著, 研究应变对其热导率影响的内部机理可以进一步提高Janus TMDCs单分子层的应用潜力.
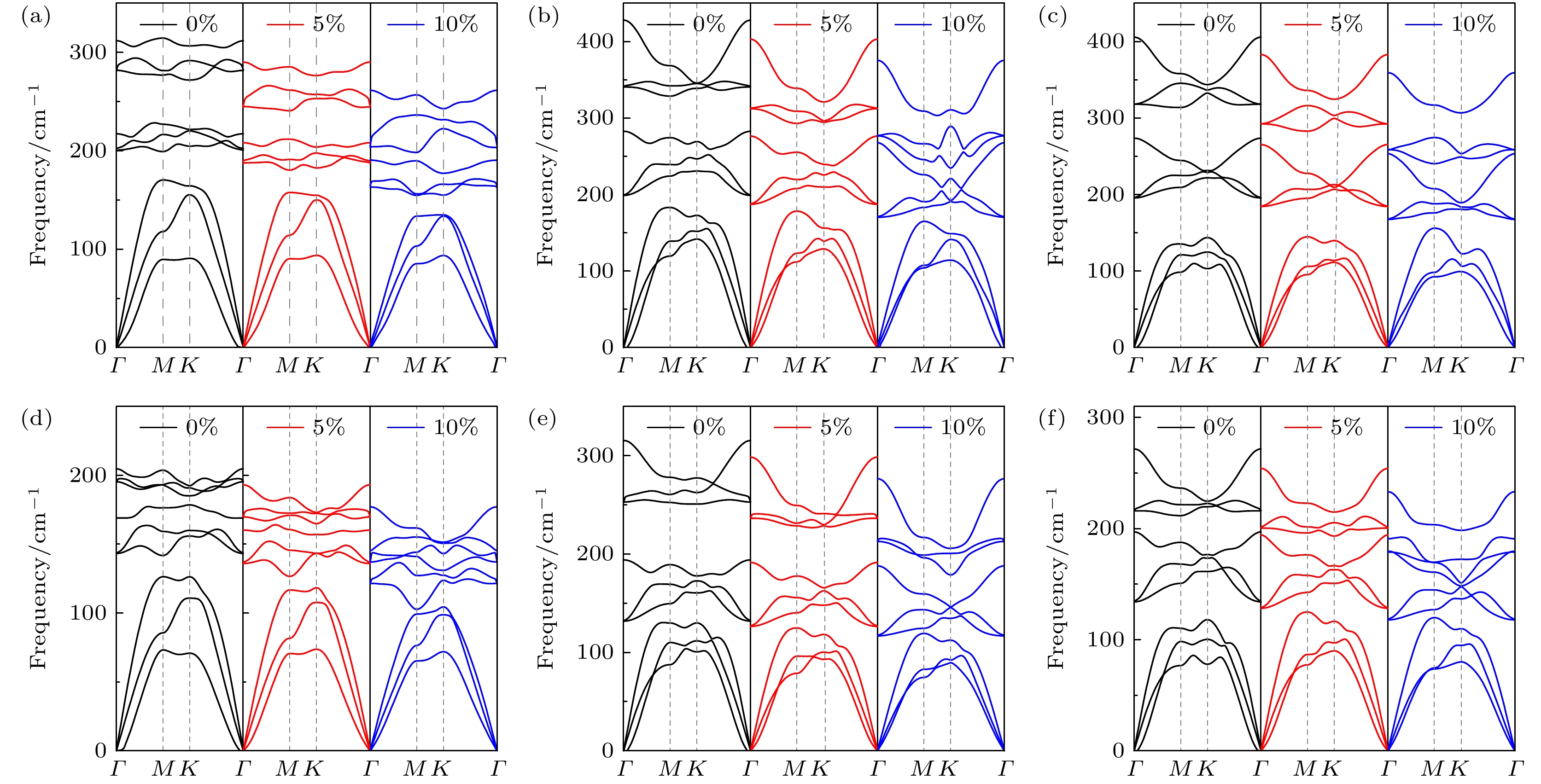
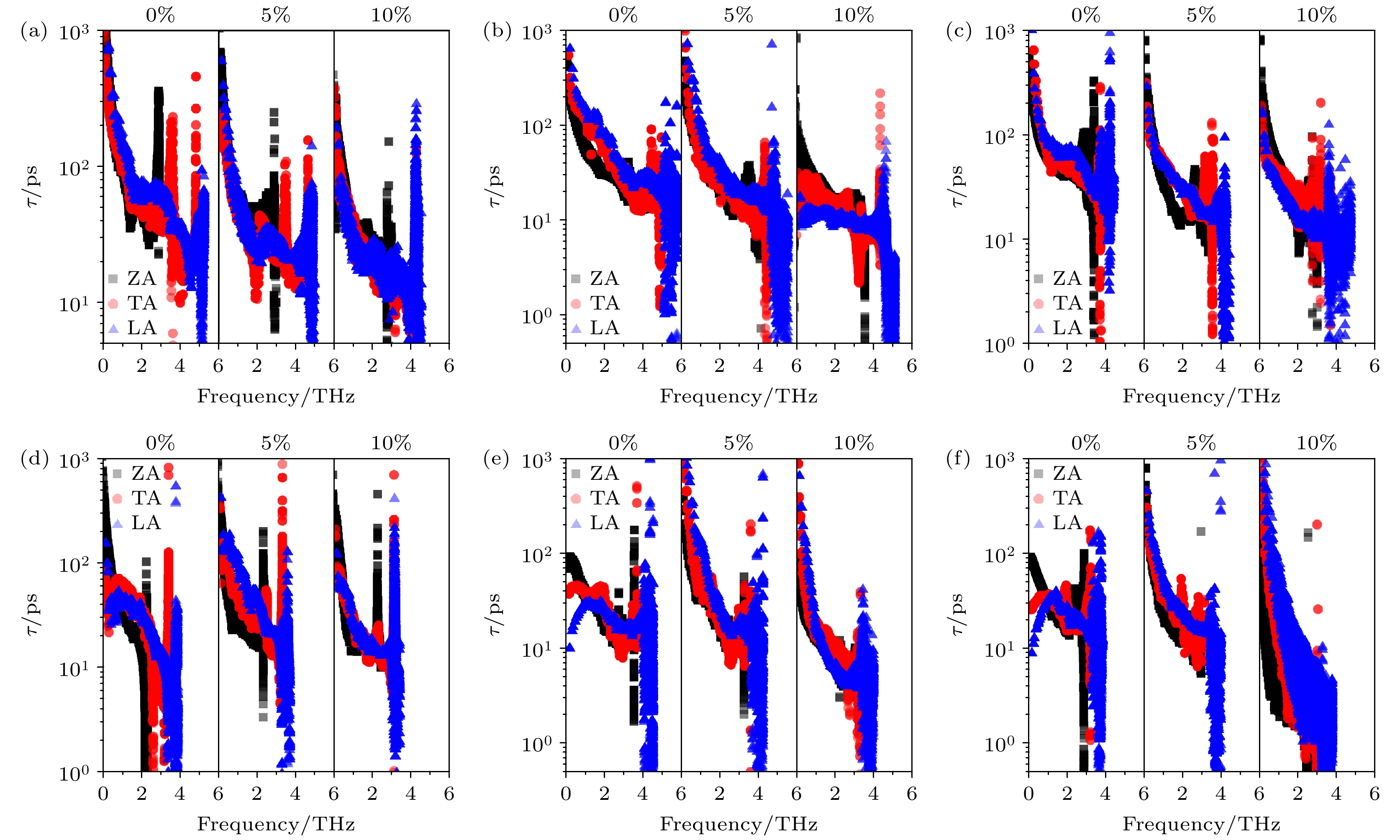
Janus TMDCs单分子层在不同应变作用下的声子色散关系如图3所示. 声子色散不存在虚频, 说明体系结构稳定. 每个单分子层的原胞包含三个原子, 因而其色散关系有九条分支, 频率较低的三条分支为声学分支, 频率较高的六条分支为光学分支. 声子色散曲线的斜率表示声子群速度, 声学分支比较陡峭, 具有较大的声子群速度, 光学分支比较平坦, 声子群速度较小. 在拉伸应变的作用下, 所有单分子层的光学分支明显软化, 声学分支变化不显著. 本文研究的6种单分子层的晶格热导率均主要由声学分支贡献(声子分支贡献超过95%), 因此需要进一步研究声子模层面的输运性质, 以明晰应变对晶格热导率影响的内部机理.
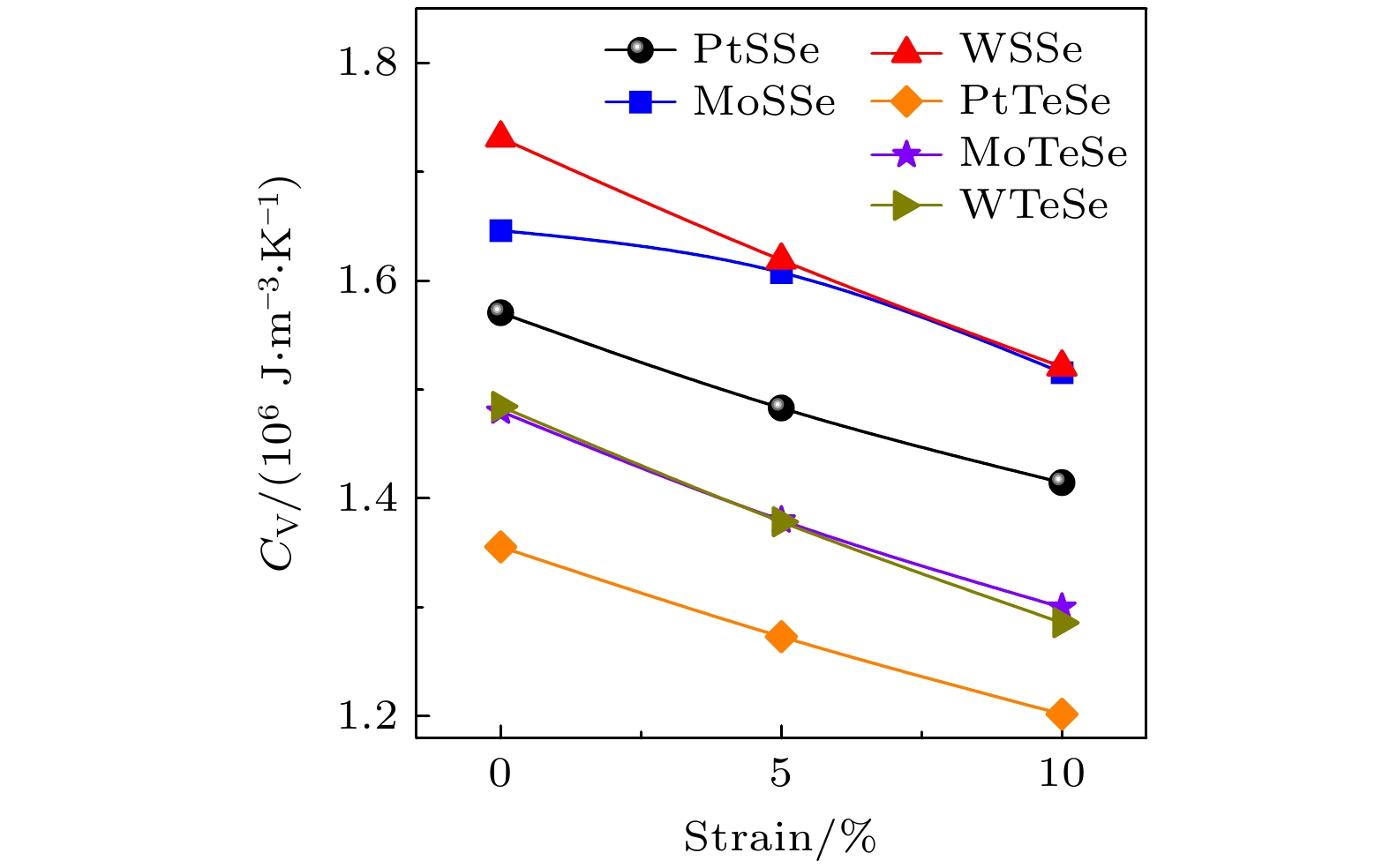
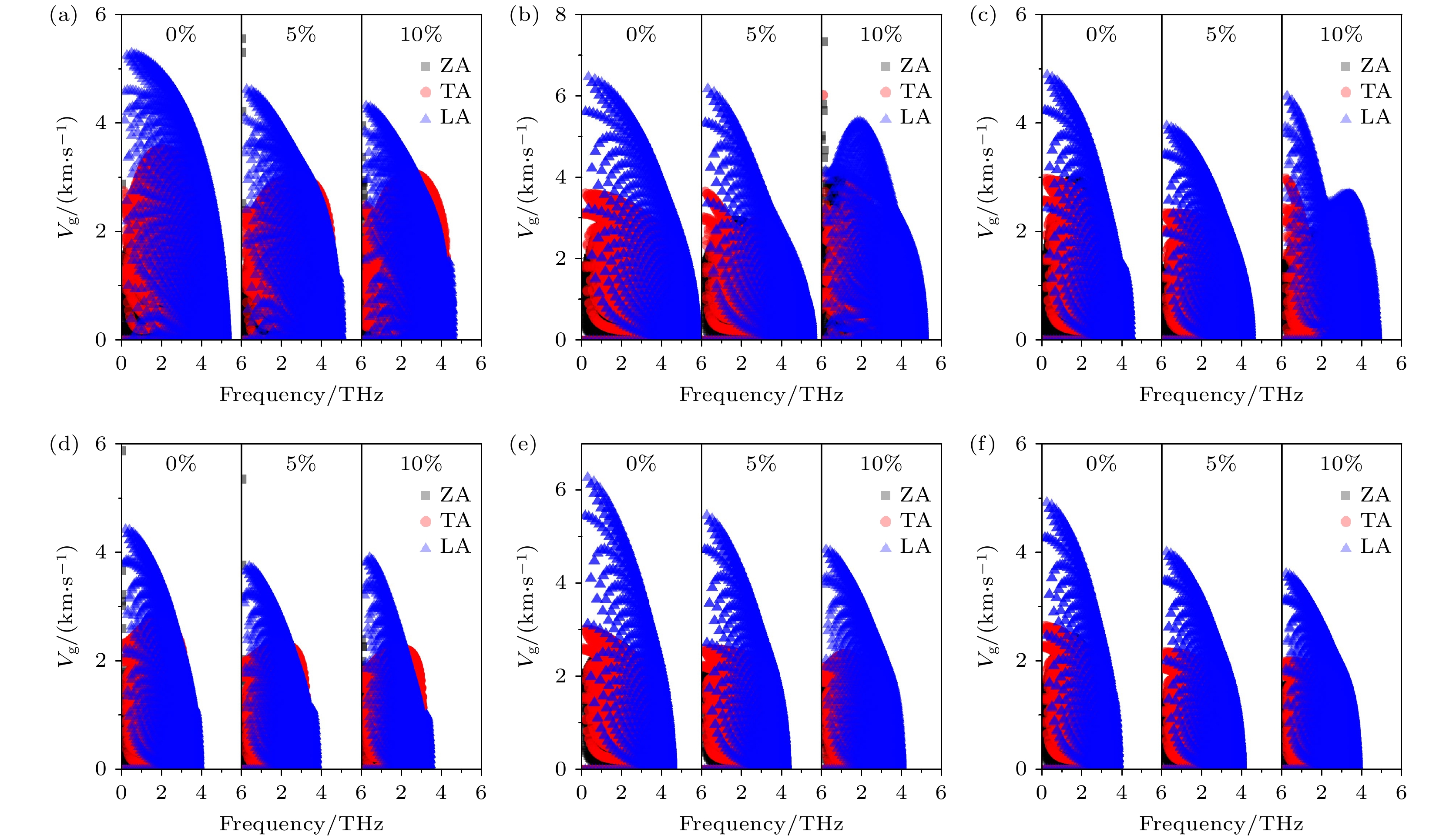
根据声子动理论, 晶格热导率与声子体积比热容、声子群速度和声子寿命有关. 图4展示了不同应变作用下的体积比热容. 在拉伸应变作用下, 所有单分子层的体积比热容均单调减小. 不同应变作用下的声子群速度如图5所示. 在拉伸应变作用下, 声子群速度呈现降低趋势. 图6为不同应变作用下的声子寿命. 随着拉伸应变的作用, MSSe的声子寿命单调降低; MTeSe的声子寿命在5%拉伸应变的作用下增大, 当拉伸应变增加到10%后, 声子寿命又轻微降低. 声子寿命的变化趋势与晶格热导率的变化趋势类似, 因此声子寿命可能是影响晶格热导率的主导因素. 为了验证这一猜想, 后续对比热容、声子群速度和声子寿命对晶格热导率的影响进行了定量评估. 此外, 声子群速度和非简谐散射率是影响晶格热导率的主要因素[39,40]. 由声子模层面的分析, 可以明晰MSSe单分子层的晶格热导率普遍高于MTeSe单分子层的内在机理. 由声子色散关系和声子群速度可知, Te原子替换S原子后, 体系的声子群速度明显降低, 这是由于重原子降低了声子色散曲线的斜率及原子的振动频率. 此外, 由声子寿命可知, Te原子替换S原子后, 体系的非简谐散射率, 尤其是声学声子的非简谐散射率显著增强. 与MSSe单分子层相比, MTeSe单分子层具有更低的声子群速度和更高的非简谐散射率, 因此MTeSe具有更低的晶格热导率.
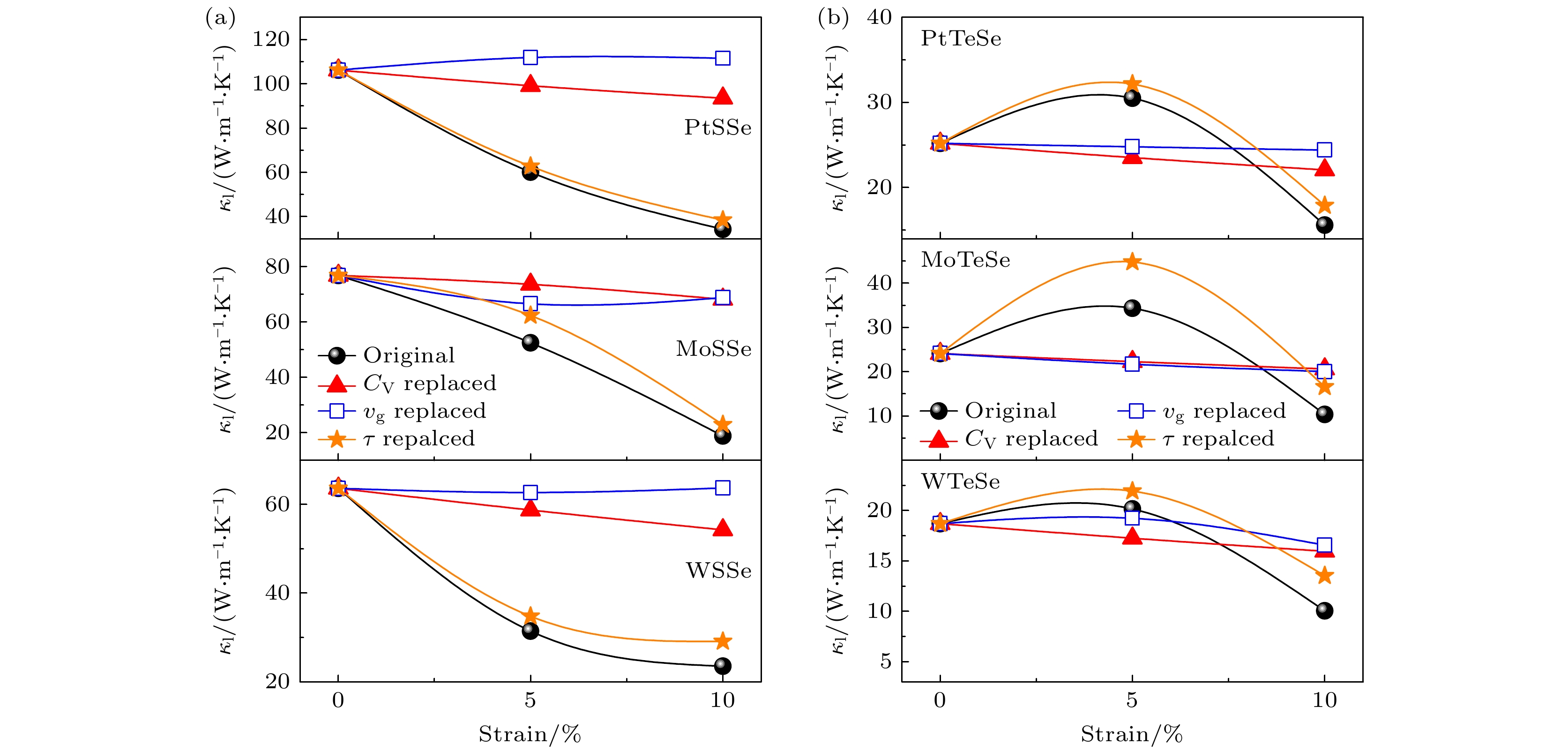
为了定量评估体积比热容、声子群速度和声子寿命的变化对晶格热导率的影响, 本文在(2)式中采用不同应变作用下的值替换未施加应变状态下的值进行交叉计算[41]. 例如, 研究体积比热容的变化对晶格热导率的影响时, 热导率的计算采用不同应变作用下的体积比热容和未施加应变状态下的声子群速度和声子寿命. 图7展示了交叉计算的热导率结果. 黄色曲线表示采用不同应变作用下的声子寿命交叉计算的热导率, 黑色曲线表示实际热导率. 采用不同应变下的声子寿命交叉计算获得的热导率与实际热导率的变化趋势一致且数值大小接近. 因此, 声子寿命是Janus TMDCs单分子层晶格热导率随拉伸应变变化的主导因素. 热导率在应变作用下的非单调变化在多种材料体系中已被广泛报道[41–45], 为了进一步探究应变作用下MTeSe单分子层的声子寿命非单调变化的内在机理, 本工作对应变作用下三声子散射相空间(散射概率)和格林爱森参数(散射强度)的变化进行了分析, 发现MSSe单分子层在拉伸应变作用下散射强度和散射概率均单调增加, 因此其热导率单调降低; MTeSe单分子层在拉伸应变作用下散射概率单调增加, 但散射强度先减小后增加, 所以MTeSe单分子层热导率的非单调变化来源于声子散射强度和散射概率的竞争机制.
-
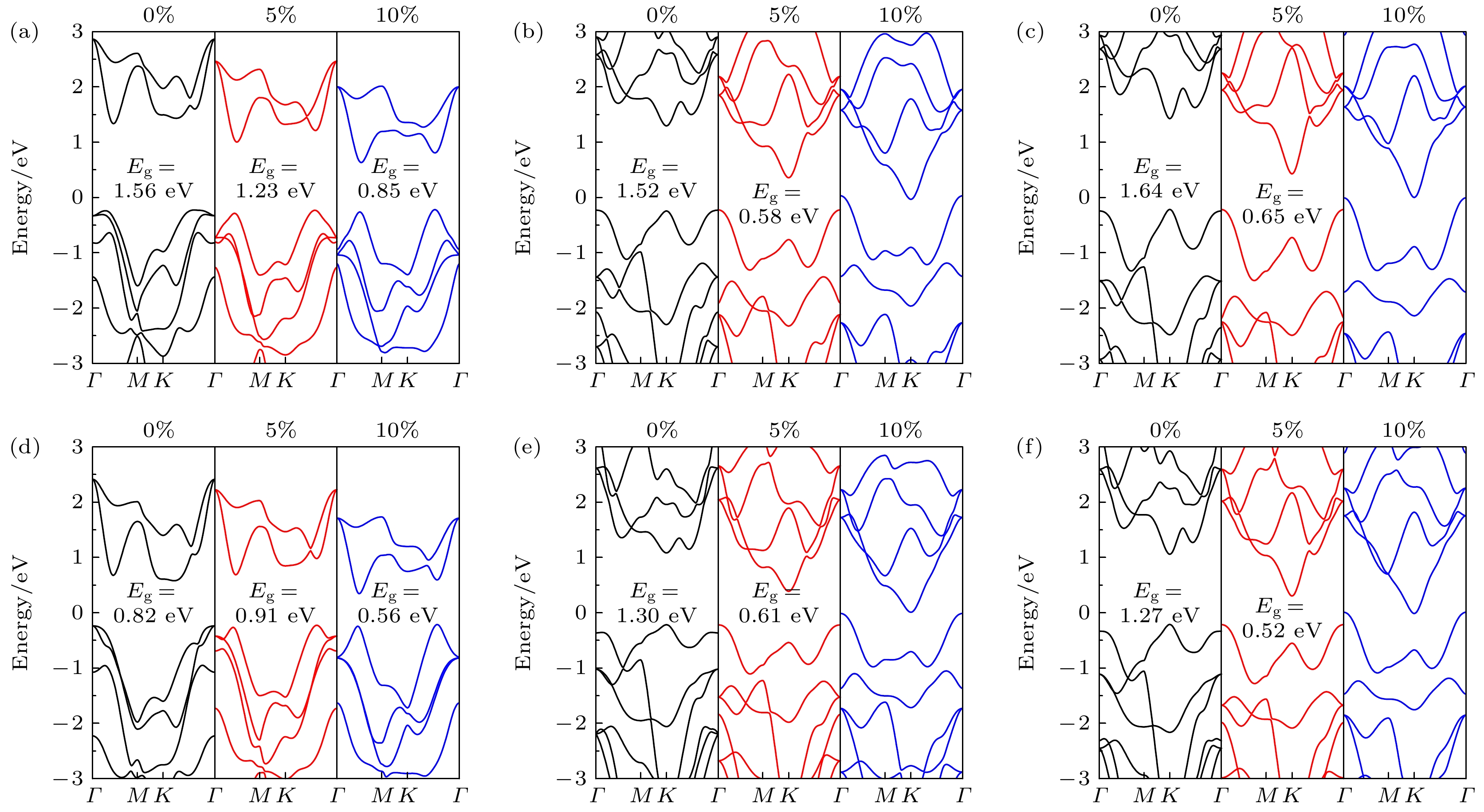
不同应变作用下Janus TMDCs单分子层的能带结构如图8所示. 未施加应变时, 6种单分子层均为半导体, 随着拉伸应变的增加, 带隙逐渐减小. 在10%拉伸应变下, PtSSe和PtTeSe单分子层仍为半导体, 其带隙分别为0.85 eV和0.56 eV; 而MoSSe, WSSe, MoTeSe和WTeSe单分子层的带隙闭合, 表现为金属性. 优异的热电性能需适宜的带隙, 因此后续电输运性能和热电性能的研究主要针对半导体型Janus单分子层.
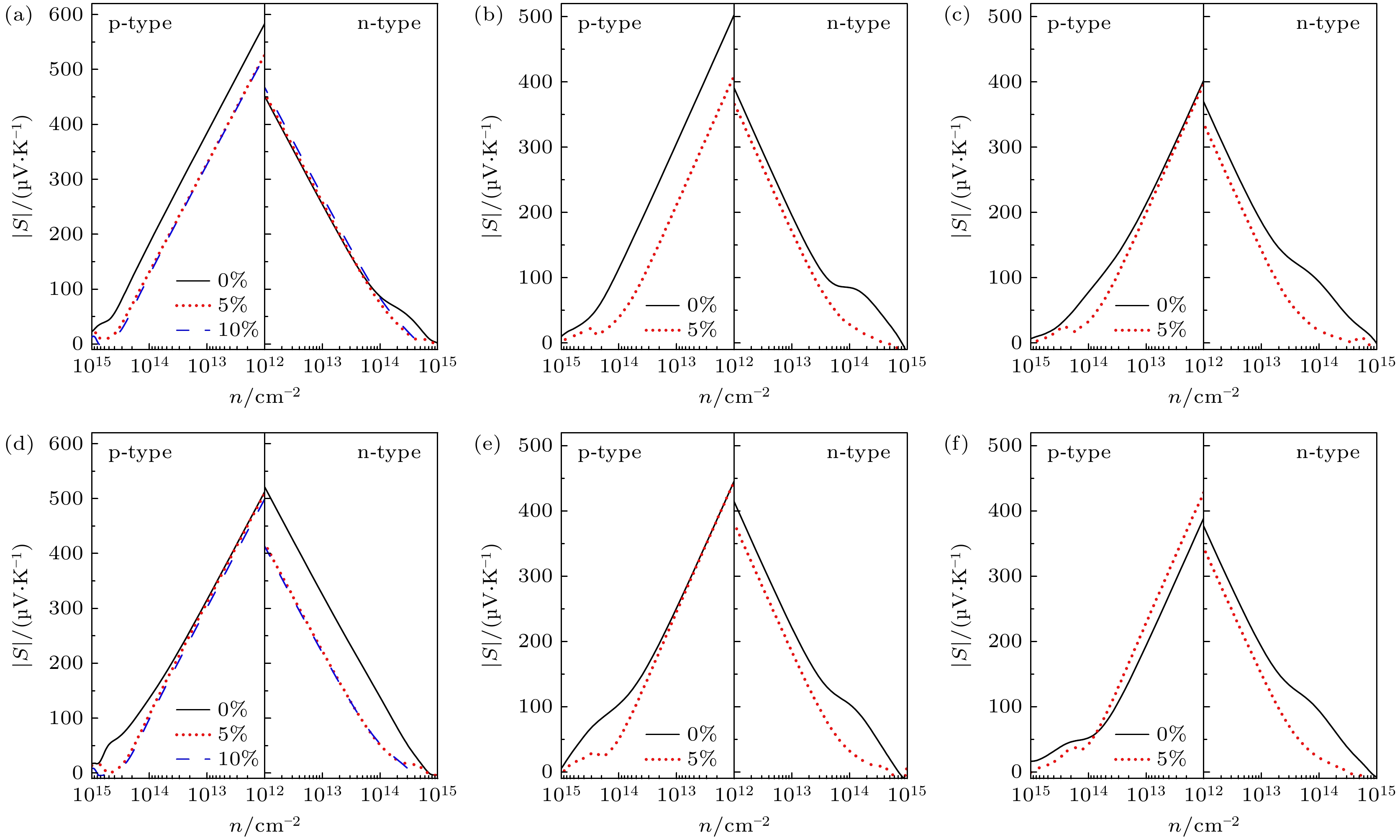
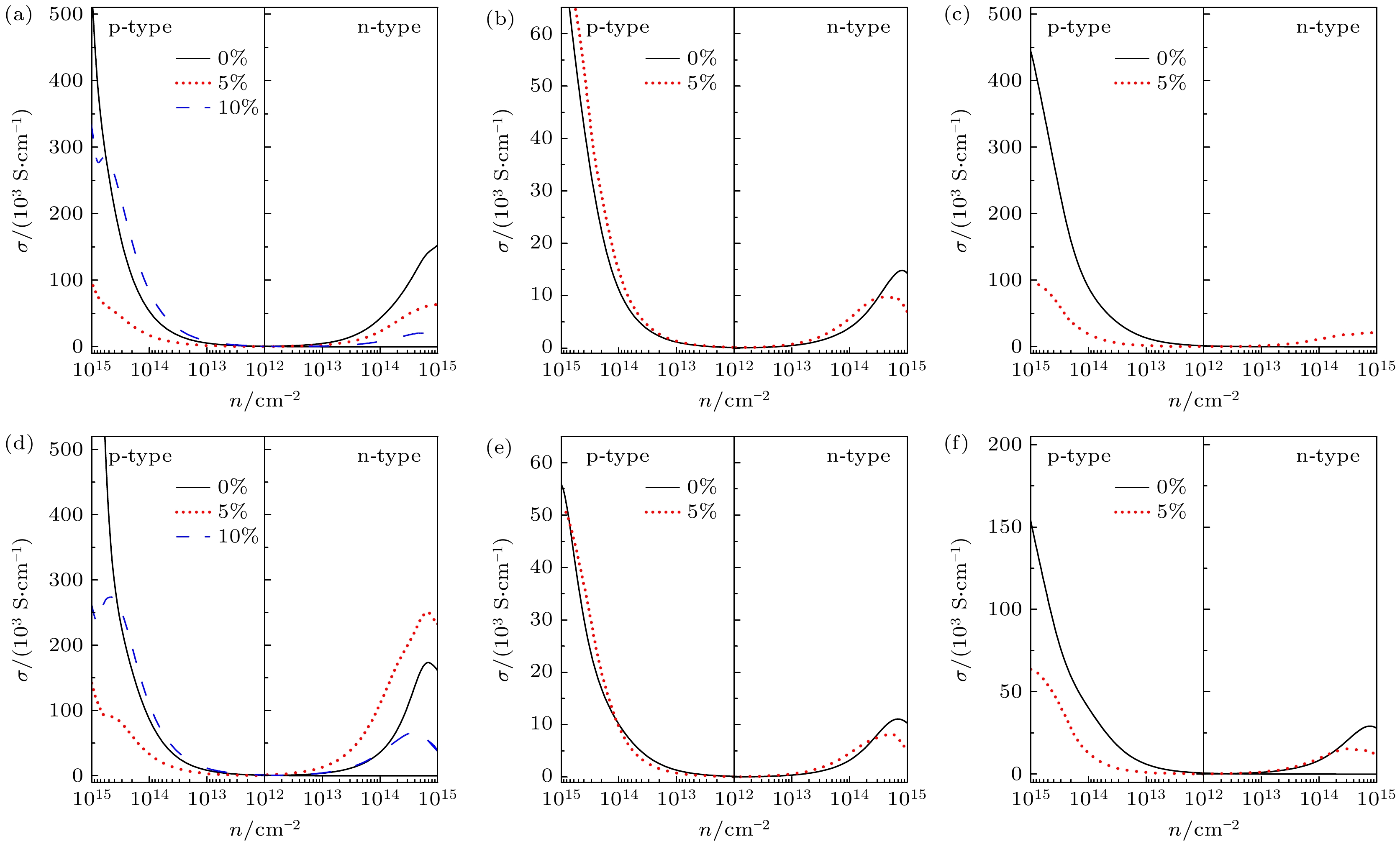
不同应变作用下Janus TMDCs单分子层的室温塞贝克系数和电导率分别如图9和图10所示. 随着载流子浓度增加, 电导率增大, 塞贝克系数减小. 大部分Janus单分子层的塞贝克系数随拉伸应变而减小, 这源于价带顶(VBM)和导带底(CBM)的移动和变形. VBM对应p型热电材料性能, CBM对应n型热电材料性能. 在拉伸应变作用下, VBM和CBM变得更加陡峭, 导致载流子有效质量减小, 塞贝克系数降低. 在低载流子浓度下, p型PtTeSe的塞贝克系数受拉伸应变影响较小, 应变使其VBM从Γ点转移至Γ-M和Γ-K, 提升能带兼并度(增强塞贝克系数)的同时VBM陡峭化(降低载流子有效质量, 削弱塞贝克系数), 两者共同作用使塞贝克系数基本保持不变. p型WTeSe的塞贝克系数随拉伸应变增大, 这源于5%应变下VBM从K点至Γ点的转移使得载流子有效质量增加. 电导率也与载流子有效质量相关, 有效质量越小, 迁移率越高, 电导率越大. 在10%应变下PtTeSe电导率略增, 这源于陡峭的VBM降低有效质量, 提升载流子迁移率.
-
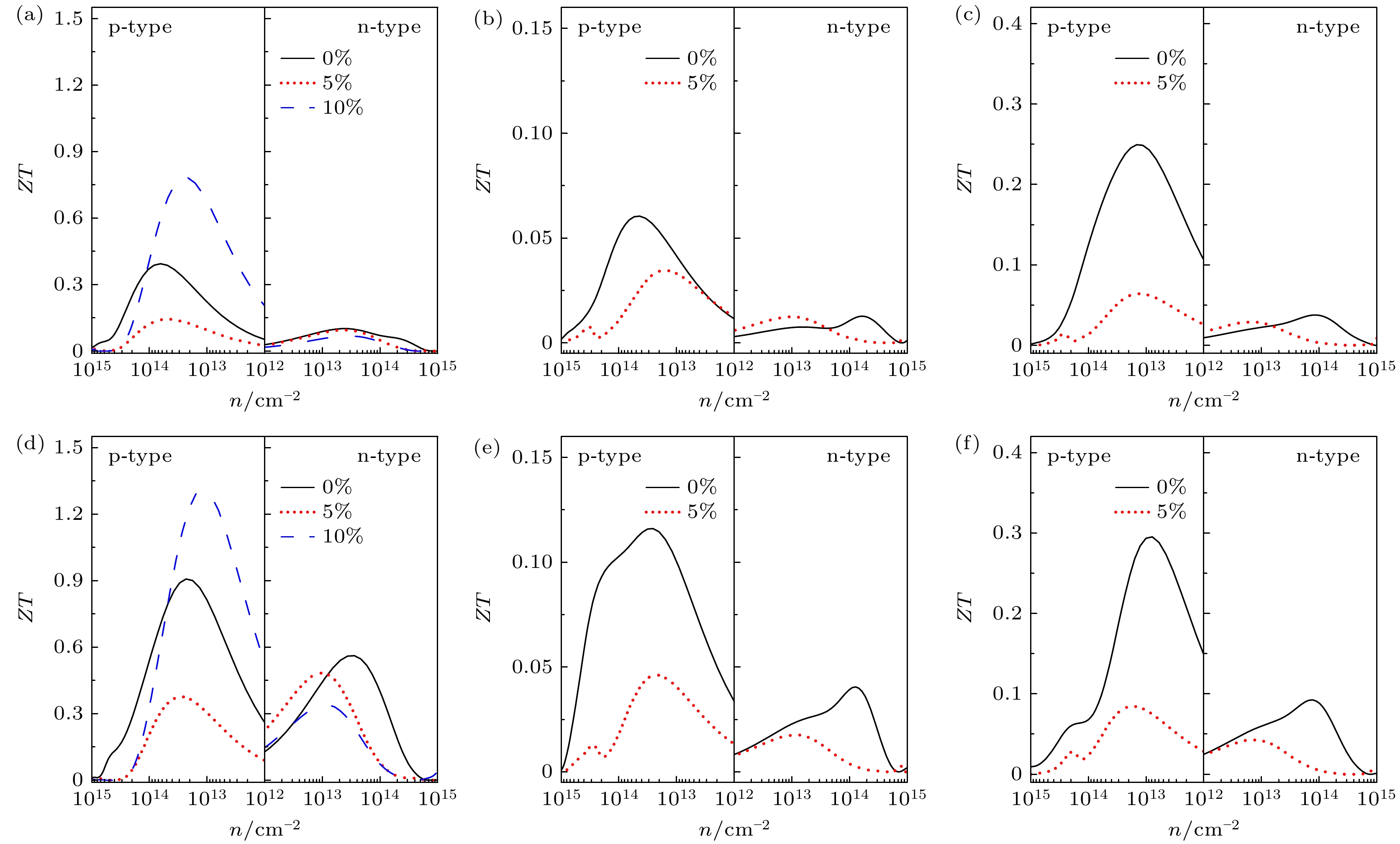
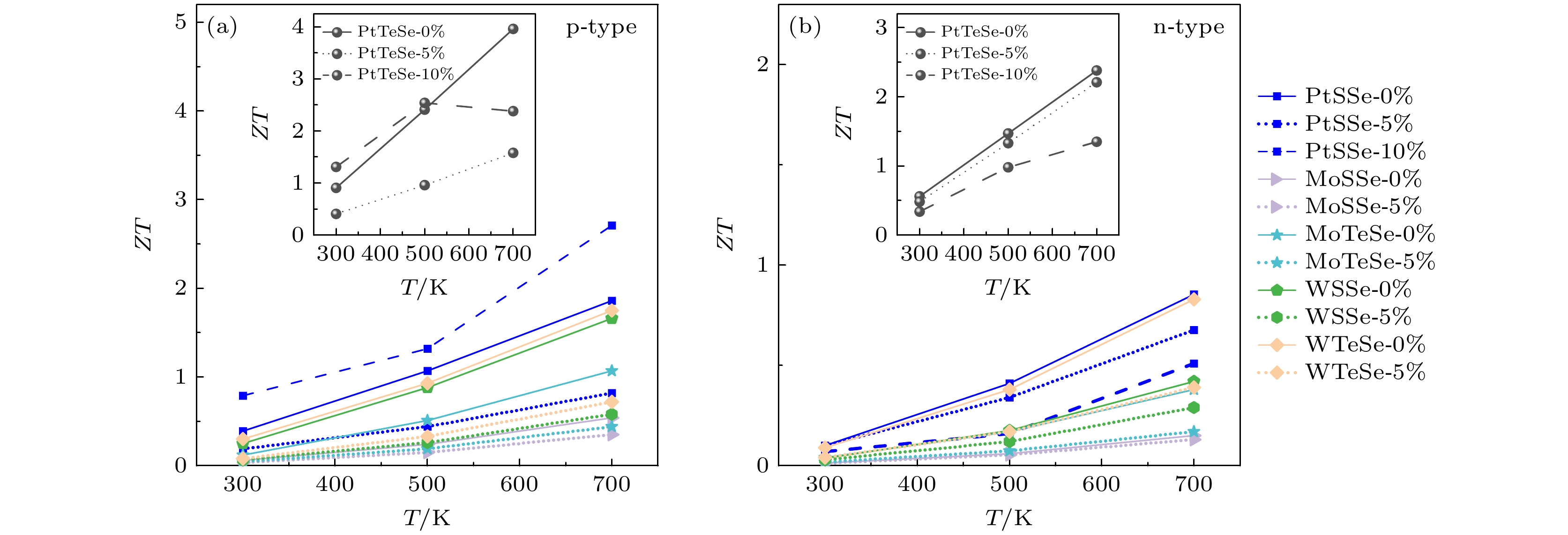
综合热输运性能和电输运性能的计算结果, 应变作用下Janus TMDCs单分子层的室温热电性能如图11所示. 结果显示, 这6种单分子层的p型热电性能普遍优于n型. MoSSe, WSSe, MoTeSe和WTeSe的ZT值较低, 而PtSSe和PtTeSe的ZT值较高. 在最佳载流子浓度下, PtSSe和PtTeSe的室温ZT值分别为0.39和0.91. PtSSe和PtTeSe的热电性能在5%拉伸应变下降低, 在10%拉伸应变下升高. 在拉伸应变影响下, PtSSe和PtTeSe的塞贝克系数轻微降低, 且在5%与10%应变下接近; 电导率在5%拉伸下降低, 而在10%拉伸下由于VBM的变化, 导致载流子迁移率显著提升, 电导率略有增加. 同时, PtSSe和PtTeSe的晶格热导率在5%拉伸应变下增加, 在10%拉伸应变下减小. 因此, 电子能带结构和声子输运性能的协同作用导致PtSSe和PtTeSe在拉伸应变下ZT值的非单调变化. 在10%拉伸应变下, PtTeSe单分子层室温ZT值高达1.31, 在TMDCs热电材料中极具竞争力. 不同温度下的热电性能如图12所示. 除10%拉伸应变下的p型PtSeTe单分子层外, 所有体系的热电优值均随温度升高而单调增加, 高温下应变对ZT值的影响和室温下的规律相同. 10%拉伸应变下的p型PtTeSe比较特殊, 在300 K和500 K下, 10%拉伸应变可以提高PtTeSe的热电性能, 并且ZT随温度升高而增大, 700 K时, p型PtTeSe的ZT值在10%拉伸应变的作用下降低, 且700 K的ZT值低于500 K的ZT值. 对于10%拉伸应变的p型PtTeSe, 当温度由500 K升高到700 K时, 电导率几乎不变的同时塞贝克系数显著降低, 这可能与高温下10%拉伸应变作用下PtTeSe单分子层的能带结构变化有关. 700 K下, 未施加应变p型PtTeSe的ZT值高达3.96, n型PtTeSe的ZT值高达2.38.
最后, 对本工作中使用的模型和近似方法的有效性进行讨论. 本文采用形变势理论对Janus TMDCs单分子层的电输运性能进行预测, 需要注意的是形变势理论仅考虑了长声学波声子与载流子之间的相互作用, 没有考虑其他声子与载流子之间的散射, 这不可避免地导致载流子弛豫时间和ZT值的高估. 但是通过对Janus TMDCs单分子层的性质进行分析, 形变势理论的计算结果仍然具有重要的参考价值. 首先, 形变势理论在二维热电材料的研究中广泛应用并且具有可接受的准确性[46,47]. 尤其是在中等载流子浓度和中低温度范围内, 声学声子散射通常是电声输运的主要限制因素[48]. 其次, 已有研究表明在Janus TMDCs单分子层中, 声学声子散射是主要的电子散射机制之一, 符合形变势理论的适用范围. Liu等[17]通过电声耦合计算发现在PtSSe单分子层中, 由于结构对称性的打破, 三种声学声子模式都表现出较高的电声散射率. 因此, 在Janus TMDCs单分子层中采用形变势理论近似电子-声子散射不会颠覆性地偏离材料的实际输运行为. 第三, 本工作侧重于Janus TMDCs在应变工程下热电性能的比较, 而非绝对值的精确预测. 本文中所有的体系均在统一理论框架下进行计算, 虽然形变势理论可能整体上高估ZT的绝对值, 但对ZT的变化趋势及不同材料之间ZT的相对高低并无影响. 因此, 尽管形变势方法相对于电声耦合计算存在近似, 但是在本工作中, 形变势方法仍然具有有效性, 其结论仍然具有参考价值.
-
本文基于第一性原理研究了应变对6种Janus TMDCs单分子层声子热输运性能和热电性能的影响. 声子热输运性能方面, PtSSe具有最高的晶格热导率, 为104 W·m–1·K–1. PtSSe, MoSSe和WSSe单分子层的热导率普遍高于PtTeSe, MoTeSe和WTeSe. 在0—10%的应变范围内, PtSSe, MoSSe和WSSe单分子层的热导率单调下降, 而PtTeSe, MoTeSe和WTeSe单分子层的热导率先升高后降低. 声子模层面的分析与热导率的交叉计算表明声子寿命是Janus TMDCs单分子层晶格热导率随拉伸应变变化的主导因素. 热电性能方面, 室温下, 未施加应变时PtTeSe的热电优值为0.91, 而在10%拉伸应变下可提升至1.31; 700 K下, p型PtTeSe单分子层的热电优值高达3.96, n型PtTeSe单分子层的热电优值高达2.38, 显示其作为热电材料的高潜力. 应变作用下PtTeSe热电性能的提升来源于晶格热导率的降低及能带结构的调整. 本研究为Janus TMDCs单分子层热输运性能和热电性能的调控提供了理论基础.
双轴应变对单层Janus过渡金属硫族化合物热输运和热电性能的影响
Influence of biaxial strain effects on thermal transport and thermoelectric performance of Janus transition metal dichalcogenide monolayers
-
摘要: Janus过渡金属硫族化物单分子层具有独特的晶体结构和物理化学性质, 在微纳尺度电子器件及热电转换领域具有巨大的应用潜力. 深入探索其热输运和热电性能对于实际应用至关重要. 本文采用基于密度泛函理论的第一性原理计算, 研究了拉伸应变对Janus过渡金属硫族化合物单分子层(PtSSe, PtTeSe, MoSSe, MoTeSe, WSSe和WTeSe)声子热输运性能和热电性能的影响. 对于热输运性能, 在0—10%的拉伸应变范围内, PtSSe, MoSSe和WSSe单分子层的晶格热导率单调减小; PtTeSe, MoTeSe和WTeSe单分子层的晶格热导率先增大后减小. 通过对声子模层面的深入分析, 发现声子寿命是影响晶格热导率在拉伸应变下变化的主导因素. 对于热电性能, 本研究发现PtTeSe单分子层表现出极佳的热电性能, 室温下其热电优值为0.91, 在10%的拉伸应变下, 热电优值达1.31. 700 K下, p型PtTeSe单分子层的热电优值高达3.96, n型PtTeSe单分子层的热电优值高达2.38. 本研究表明PtTeSe单分子层是具有潜力的热电材料, 应变工程是调控Janus过渡金属硫族化物单分子层热输运和热电性能的有效策略.
-
关键词:
- Janus过渡金属硫族化合物 /
- 热电性能 /
- 应变 /
- 第一性原理
Abstract: Janus transition metal dichalcogenide monolayers, characterized by antisymmetric crystal structures and unique physical properties, show great potential applications in micro/nano-electronic devices and thermoelectrics. In this work, the strain-tuned phonon thermal transport and thermoelectric performance of six Janus transition metal dichalcogenide monolayers are systematically investigated by first-principles calculations. This study focuses on monolayers of PtSSe and PtTeSe with a 1T-phase crystal structure, as well as monolayers of MoSSe, MoTeSe, WSSe, and WTeSe with a 1H-phase crystal structure. For all these monolayers, first-principles calculations are performed using the open-source software Quantum ESPRESSO. The lattice thermal conductivity is obtained based on lattice dynamics and iterative solutions of the Boltzmann transport equation. The thermal conductivities of PtSSe, MoSSe, and WSSe monolayers are generally higher than those of PtTeSe, MoTeSe, and WTeSe. Acoustic phonons are responsible for the majority of thermal transport, contributing over 95%. Under unstrained conditions, monolayer PtSSe demonstrates a superior thermal conductivity of 104 W·m–1·K–1, making it advantageous for thermal management applications in electronic devices. Under tensile strain, the thermal conductivities of PtSSe, MoSSe, and WSSe monolayers exhibit a monotonic decrease trend; however, for PtTeSe, MoTeSe, and WTeSe monolayers, their thermal conductivities initially show an increase trend, followed by a subsequent decrease trend. Under a 10% tensile strain, the thermal conductivities of these six Janus monolayers all demonstrate a reduction exceeding 60%. Furthermore, this work provides a comprehensive analysis of the influences of strain on specific heat capacity, phonon group velocity, and phonon lifetime. The phonon mode-level analysis and cross-calculated thermal conductivity (with specific heat capacity, phonon group velocity, and phonon lifetime replaced by values under different strain conditions) reveal that phonon lifetime is the dominant factor governing thermal conductivity under strain. For electrical transport properties, calculations are performed using the Boltzmann transport equation based on deformation potential theory. At room temperature, the thermoelectric figure of merit (ZT) for PtTeSe is 0.91 without strain, which can be improved to 1.31 under 10% tensile strain. The ZT value reaches as high as 3.96 for p-type PtTeSe and 2.38 for n-type PtTeSe at 700 K, indicating that the PtTeSe monolayer is a highly promising thermoelectric material. Strain-induced enhancement in the thermoelectric performance of PtTeSe is facilitated by reducing lattice thermal conductivity and reconfigurating the band structure. This work demonstrates that strain engineering is an effective strategy for adjusting the thermal transport and thermoelectric properties of Janus transition metal dichalcogenide monolayers.-
Key words:
- Janus transition metal dichalcogenides /
- thermoelectric /
- strain /
- first-principles .
-

-
图 7 采用不同应变作用下的比热容、声子群速度和声子寿命交叉计算的Janus TMDCs单分子层热导率 (a) PtSSe, MoSSe和WSSe; (b) PtTeSe, MoTeSe和WTeSe
Figure 7. Cross-calculated thermal conductivity with heat capacity, phonon group velocity, and phonon lifetime replaced by values under different strains for Janus TMDCs monolayers: (a) PtSSe, MoSSe, and WSSe; (b) PtTeSe, MoTeSe, and WTeSe.
-
[1] Zhang Y, Lü Q, Wang H, Zhao S, Xiong Q, Lü R, Zhang X 2022 Science 378 169 doi: 10.1126/science.abq0883 [2] 武鹏, 谈论, 李炜, 曹立伟, 赵俊博, 曲尧, 李昂 2023 物理学报 72 118101 doi: 10.7498/aps.72.20230273 Wu P, Tan L, Li W, Cao L W, Zhao J B, Qu Y, Li A 2023 Acta Phys. Sin. 72 118101 doi: 10.7498/aps.72.20230273 [3] Manzeli S, Ovchinnikov D, Pasquier D, Yazyev O V, Kis A 2017 Nat. Rev. Mater. 2 17033 doi: 10.1038/natrevmats.2017.33 [4] 赵欣, 唐桂华, 李一斐, 张敏 2021 工程热物理学报 42 2455 Zhao X, Tang G H, Li Y F, Zhang M 2021 Journal of Engineering Thermophysics 42 2455 [5] Zhang J, Jia S, Kholmanov I, Dong L, Er D, Chen W, Guo H, Jin Z, Shenoy V B, Shi L, Lou J 2017 ACS Nano 11 8192 doi: 10.1021/acsnano.7b03186 [6] Lu A Y, Zhu H, Xiao J, Chuu C P, Han Y, Chiu M H, Cheng C C, Yang C W, Wei K H, Yang Y, Wang Y, Sokaras D, Nordlund D, Yang P, Muller D A, Chou M Y, Zhang X, Li L J 2017 Nat. Nanotechnol. 12 744 doi: 10.1038/nnano.2017.100 [7] Lin Y C, Liu C, Yu Y, Zarkadoula E, Yoon M, Puretzky A A, Liang L, Kong X, Gu Y, Strasser A, Meyer H M, III, Lorenz M, Chisholm M F, Ivanov I N, Rouleau C M, Duscher G, Xiao K, Geohegan D B 2020 ACS Nano 14 3896 doi: 10.1021/acsnano.9b10196 [8] Trivedi D B, Turgut G, Qin Y, Sayyad M Y, Hajra D, Howell M, Liu L, Yang S, Patoary N H, Li H, Petrić M M, Meyer M, Kremser M, Barbone M, Soavi G, Stier A V, Müller K, Yang S, Esqueda I S, Zhuang H, Finley J J, Tongay S 2020 Adv. Mater. 32 2006320 doi: 10.1002/adma.202006320 [9] Sant R, Gay M, Marty A, Lisi S, Harrabi R, Vergnaud C, Dau M T, Weng X, Coraux J, Gauthier N, Renault O, Renaud G, Jamet M 2020 npj 2D Mater. Appl. 4 41 doi: 10.1038/s41699-020-00175-z [10] Qin Y, Sayyad M, Montblanch A R P, Feuer M S G, Dey D, Blei M, Sailus R, Kara D M, Shen Y, Yang S, Botana A S, Atature M, Tongay S 2022 Adv. Mater. 34 2106222 doi: 10.1002/adma.202106222 [11] Huang S J, Zhang T, Zeng Z Y, Geng H Y, Chen X R 2024 Vacuum 224 113143 doi: 10.1016/j.vacuum.2024.113143 [12] Liu J, Shen T, Wang L, Ren J C, Liu W, Li S 2024 Adv. Funct. Mater. 34 2401737 doi: 10.1002/adfm.202401737 [13] Cui H, Yang T, Peng X, Zhang G 2022 J. Mater. Res. Technol. 18 1218 doi: 10.1016/j.jmrt.2022.03.027 [14] 张德贺, 周文哲, 李奥林, 欧阳方平 2021 物理学报 70 096301 doi: 10.7498/aps.70.20201888 Zhang D H, Zhou W Z, Li A L, Ouyang F P 2021 Acta Phys. Sin. 70 096301 doi: 10.7498/aps.70.20201888 [15] 张宇航, 李孝宝, 詹春晓, 王美芹, 浦玉学 2023 物理学报 72 046201 doi: 10.7498/aps.72.20221815 Zhang Y H, Li X B, Zhan C X, Wang M Q, Pu Y X 2023 Acta Phys. Sin. 72 046201 doi: 10.7498/aps.72.20221815 [16] Tao W L, Yi M, E. H C, Yan C, Ji G F 2019 Philos. Mag. 99 1025 doi: 10.1080/14786435.2019.1572927 [17] Liu C, Yao M, Yang J, Xi J, Ke X 2020 Mater. Today Phys. 15 100277 doi: 10.1016/j.mtphys.2020.100277 [18] Bera J, Betal A, Sahu S 2021 J. Alloys Compd. 872 159704 doi: 10.1016/j.jallcom.2021.159704 [19] Guo S D 2018 Phys. Chem. Chem. Phys. 20 7236 doi: 10.1039/C8CP00350E [20] Han D, Qin H, Tu H, Chen Y, Sun H, Xue Y, Zeng X 2025 J. Electron. Mater. 54 2180 doi: 10.1007/s11664-024-11721-6 [21] Tao W L, Lan J Q, Hu C E, Cheng Y, Zhu J, Geng H Y 2020 J. Appl. Phys. 127 035101 doi: 10.1063/1.5130741 [22] Guo S D, Li Y F, Guo X S 2019 Comput. Mater. Sci. 161 16 doi: 10.1016/j.commatsci.2019.01.035 [23] Patel A, Singh D, Sonvane Y, Thakor P B, Ahuja R 2020 ACS Appl. Mater. Interfaces 12 46212 doi: 10.1021/acsami.0c13960 [24] Han D, Wang M, Yang X, Du M, Cheng L, Wang X 2022 J. Alloys Compd. 903 163850 doi: 10.1016/j.jallcom.2022.163850 [25] Zhang M, Tang G H, Li Y F, Fu B, Wang X Y 2020 Int. J. Thermophys. 41 57 doi: 10.1007/s10765-020-02627-6 [26] Zhang R, Koutsos V, Cheung R 2016 Appl. Phys. Lett. 108 042104 doi: 10.1063/1.4940982 [27] Bertolazzi S, Brivio J, Kis A 2011 ACS Nano 5 9703 doi: 10.1021/nn203879f [28] Pan L, Carrete J, Wang Z 2022 J. Phys. Condens. Mater. 34 015303 doi: 10.1088/1361-648X/ac2a7a [29] Ahmad S, Idrees M, Khan F, Nguyen C V, Ahmad I, Amin B 2021 Chem. Phys. Lett. 776 138689 doi: 10.1016/j.cplett.2021.138689 [30] Ahmad S, Khan F, Amin B, Ahmad I 2021 J. Solid State Chem. 299 122189 doi: 10.1016/j.jssc.2021.122189 [31] Wang C, Chen Y-X, Gao G, Xu K, Shao H 2022 Appl. Surf. Sci. 593 153402 doi: 10.1016/j.apsusc.2022.153402 [32] Chaurasiya R, Tyagi S, Singh N, Auluck S, Dixit A 2021 J. Alloys Compd. 855 157304 doi: 10.1016/j.jallcom.2020.157304 [33] Giannozzi P, Baroni S, Bonini N, Calandra M, Car R, Cavazzoni C, Ceresoli D, Chiarotti G L, Cococcioni M, Dabo I, Dal Corso A, de Gironcoli S, Fabris S, Fratesi G, Gebauer R, Gerstmann U, Gougoussis C, Kokalj A, Lazzeri M, Martin-Samos L, Marzari N, Mauri F, Mazzarello R, Paolini S, Pasquarello A, Paulatto L, Sbraccia C, Scandolo S, Sclauzero G, Seitsonen A P, Smogunov A, Umari P, Wentzcovitch R M 2009 J. Phys. Condens. Mater. 21 395502 doi: 10.1088/0953-8984/21/39/395502 [34] Hamann D R 2013 Phys. Rev. B 88 085117 doi: 10.1103/PhysRevB.88.085117 [35] Li W, Carrete J, A. Katcho N, Mingo N 2014 Comput. Phys. Commun. 185 1747 doi: 10.1016/j.cpc.2014.02.015 [36] Madsen G K H, Carrete J, Verstraete M J 2018 Comput. Phys. Commun. 231 140 doi: 10.1016/j.cpc.2018.05.010 [37] 李一斐, 唐桂华, 张敏, 赵欣 2022 工程热物理学报 43 479 Li Y F, Tang G H, Zhang M, Zhao X 2022 Journal of Engineering Thermophysics 43 479 [38] Han D, Yang X, Du M, Xin G, Zhang J, Wang X, Cheng L 2021 Nanoscale 13 7176 doi: 10.1039/D0NR09169C [39] Tang Z, Wang X, Li J, He C, Chen M, Tang C, Ouyang T 2023 Phys. Rev. B 108 214304 doi: 10.1103/PhysRevB.108.214304 [40] Bhojani A K, Kagdada H L, Singh D K 2025 Phys. Rev. B 111 085419 doi: 10.1103/PhysRevB.111.085419 [41] Yuan K, Zhang X, Tang D, Hu M 2018 Phys. Rev. B 98 144303 doi: 10.1103/PhysRevB.98.144303 [42] Tang Z Y, Wang X X, Li J, He C Y, Tang C, Wang H M, Chen M X, Ouyang T 2023 Appl. Phys. Lett. 122 172203 doi: 10.1063/5.0149288 [43] Tang Z, Wang X, He C, Li J, Chen M, Tang C, Ouyang T 2024 Phys. Rev. B 110 134320 doi: 10.1103/PhysRevB.110.134320 [44] Lindsay L, Broido D A, Carrete J, Mingo N, Reinecke T L 2015 Phys. Rev. B 91 121202 doi: 10.1103/PhysRevB.91.121202 [45] Zhang M, Tang G, Li Y 2021 ACS Omega 6 3980 doi: 10.1021/acsomega.0c05907 [46] 王艳, 陈南迪, 杨陈, 曾召益, 胡翠娥, 陈向荣 2021 物理学报 70 116301 doi: 10.7498/aps.70.20201939 Wang Y, Chen N D, Yang C, Zeng Z Y, Hu C E, Chen X R 2021 Acta Phys. Sin. 70 116301 doi: 10.7498/aps.70.20201939 [47] Li Y F, Tang G H, Fu B, Zhang M, Zhao X 2020 ACS Appl. Energy Mater. 3 9234 doi: 10.1021/acsaem.0c01591 [48] Wang N, Li M, Xiao H, Gao Z, Liu Z, Zu X, Li S, Qiao L 2021 npj Comput. Mater. 7 18 doi: 10.1038/s41524-020-00476-3 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: