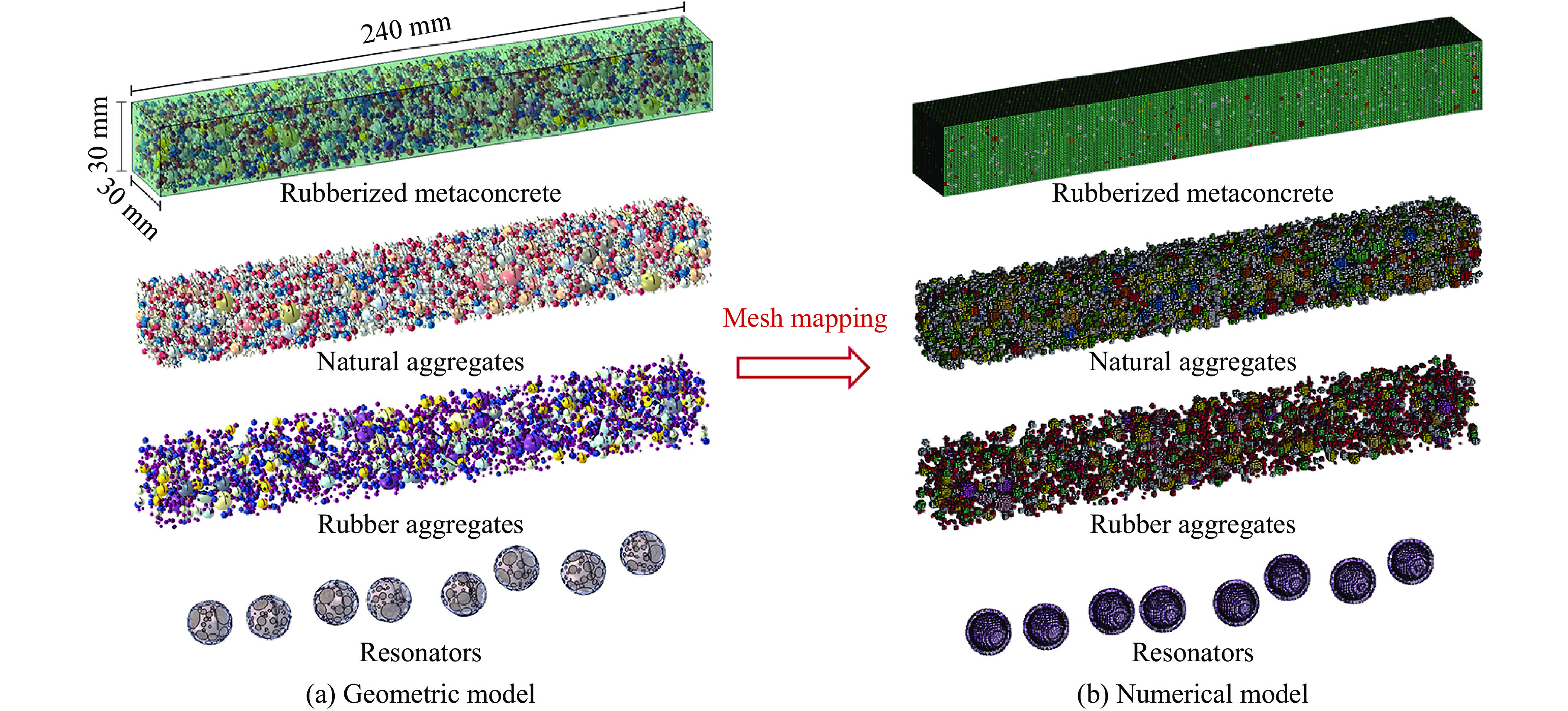
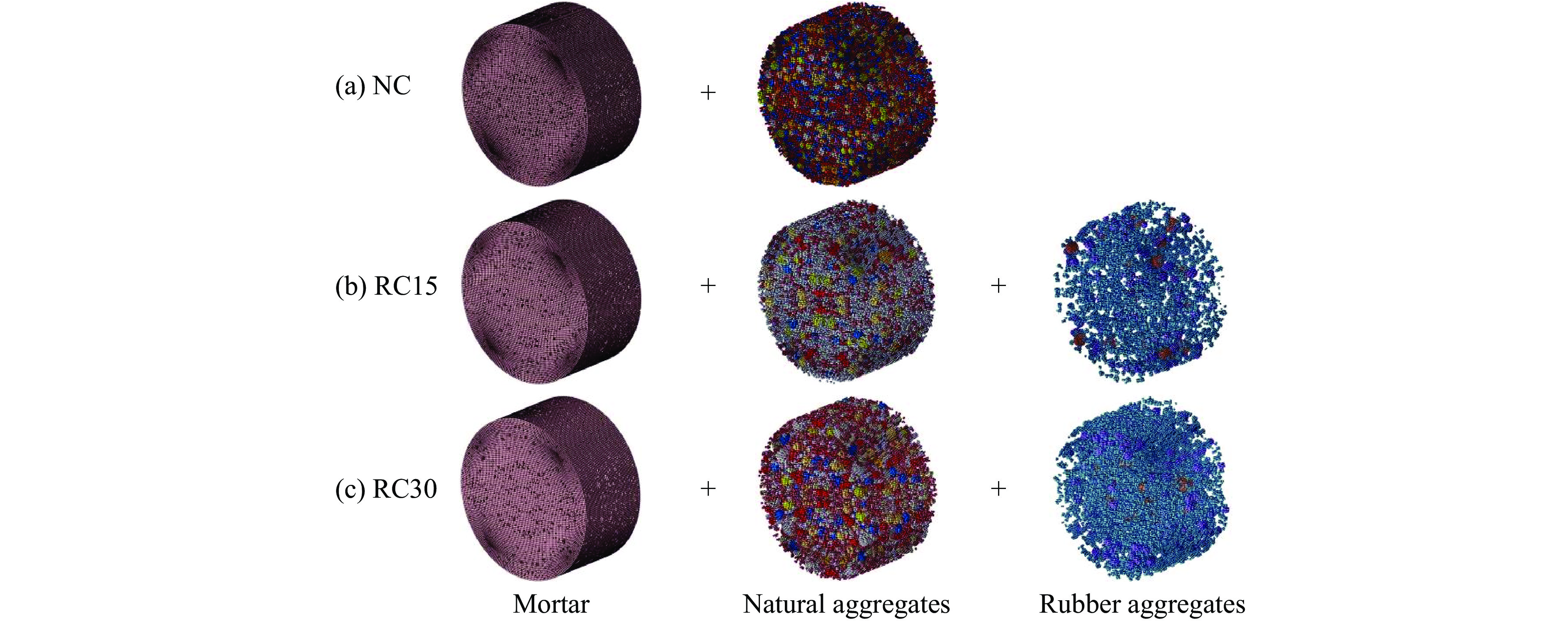
橡胶超材料混凝土的细观结构由均质砂浆、天然骨料、橡胶骨料和谐振器4部分组成。各部分之间的接触区域被称为界面过渡区（interfacial transition zone，ITZ）。在混凝土细观结构中，通常认为ITZ的实际厚度在10～50 μm之间^[20–21]。若在数值模型中采用此网格尺寸，将会产生极其庞大的单元数量，当前计算机的求解能力难以应对该挑战。因此，将各部分间的ITZ简化为共节点连接，以确保模型连续，并统一规定骨料为球形，该简化方式及骨料形状的选取在众多混凝土细观数值模拟中被广泛采用，取得了相对可靠的结果^[22–23]。

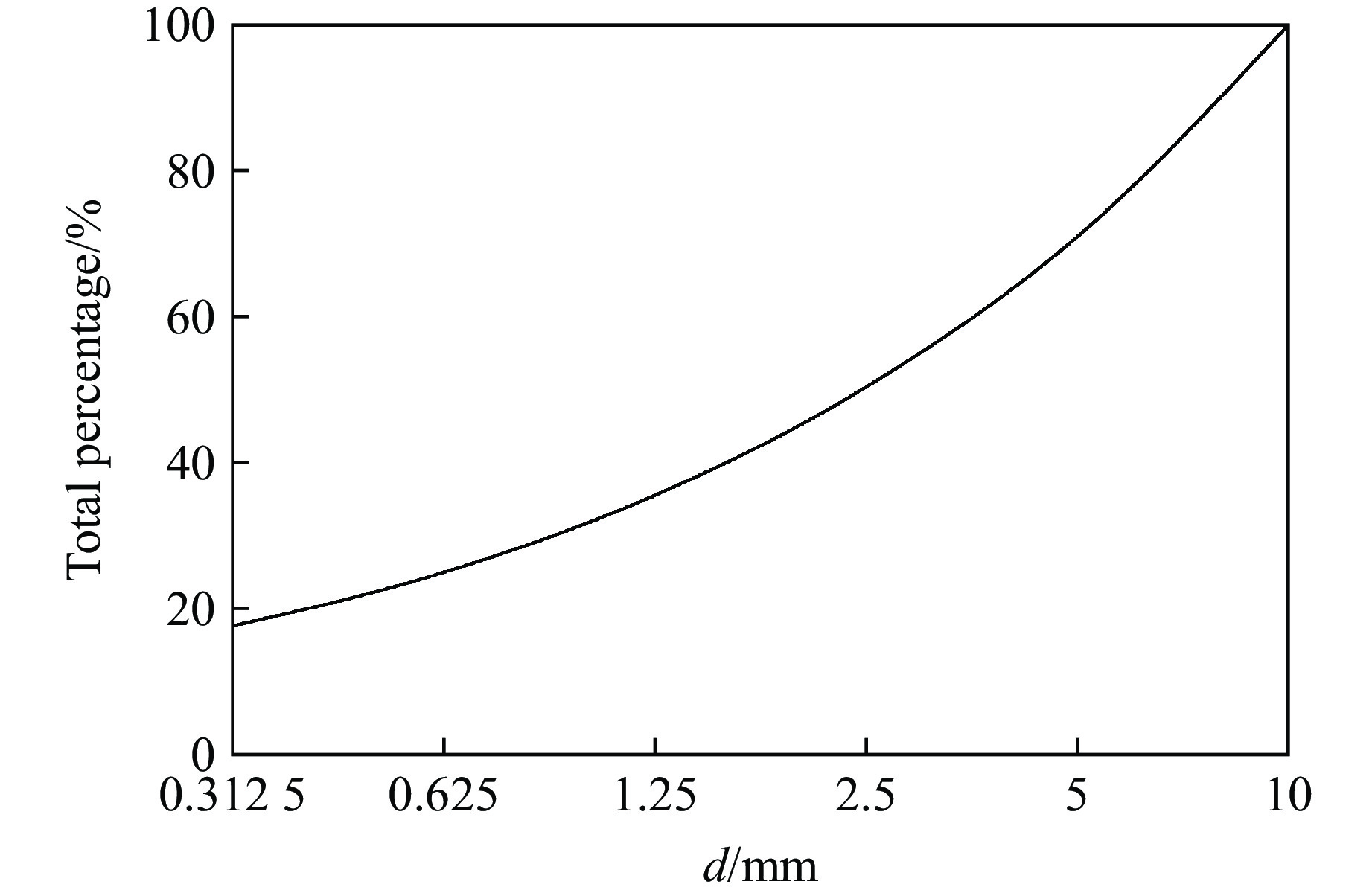
此外，为消除混凝土中骨料总量对数值结果的影响，设置骨料体积占试件总体积的45%，粒径遵循富勒级配，在1～10 mm区间分布^[24]，以确保混凝土内骨料级配的理想密度和整体强度。富勒级配表示为

式中：d为骨料粒径；d_max为骨料的最大粒径；P_d为骨料粒径为d的过筛率；n为方程指数，0.45≤n≤0.70，本研究取0.50^[25]。富勒级配曲线见图1。

除规范骨料含量之外，其分布需满足随机性。参考Pan等^[26]对混凝土内天然骨料分布的研究，骨料生成及投放程序遵循以下步骤：

(1) 确定粒径范围、投放区域及体积含量；

(2) 在投放区域内随机生成不同粒径的骨料；

(3) 若骨料满足在规定区域内且不重叠，则放置骨料，否则返回上一步，重新随机生成；

(4) 重复上述步骤，直至满足体积含量要求。

以橡胶骨料体积占骨料总体积30%的橡胶超材料混凝土（MRC30）为例，其几何模型如图2(a)所示，以网格映射法为媒介实现几何模型向数值模型的转化，如图2(b)所示。需要说明的是，图2(a)中的谐振器是以手动切割试件内部区域的方式投放，旨在提升骨料生成程序的运行效率，同时消除“谐振器位置分布”这一变量对后续研究的影响。

近几十年，国内外学者对混凝土的力学响应进行了广泛研究，并提出了多种符合水泥基体动态性能的材料本构模型，包括CSCM（continuous surface cap model）、CDPM2（concrete damage plastic model 2）、K&C（Karagozian and Case）模型等。K&C模型是由Malvar等^[27]在伪张量模型的基础上开发的，能够精确描述混凝土的体积压缩行为，可对爆炸冲击荷载下混凝土的力学响应和损伤状态进行高精度预测^[28–29]，因此，在动态加载数值模拟中被推荐为首选材料模型^[30–32]。基于上述考虑，本研究中砂浆和天然骨料采用K&C模型，该模型在LS-DYNA中集成为MAT_72R3号材料，通过输入基本材料参数即可实现对K&C模型全部参数的自动标定，具体材料参数见表1^{[26, 33]}。

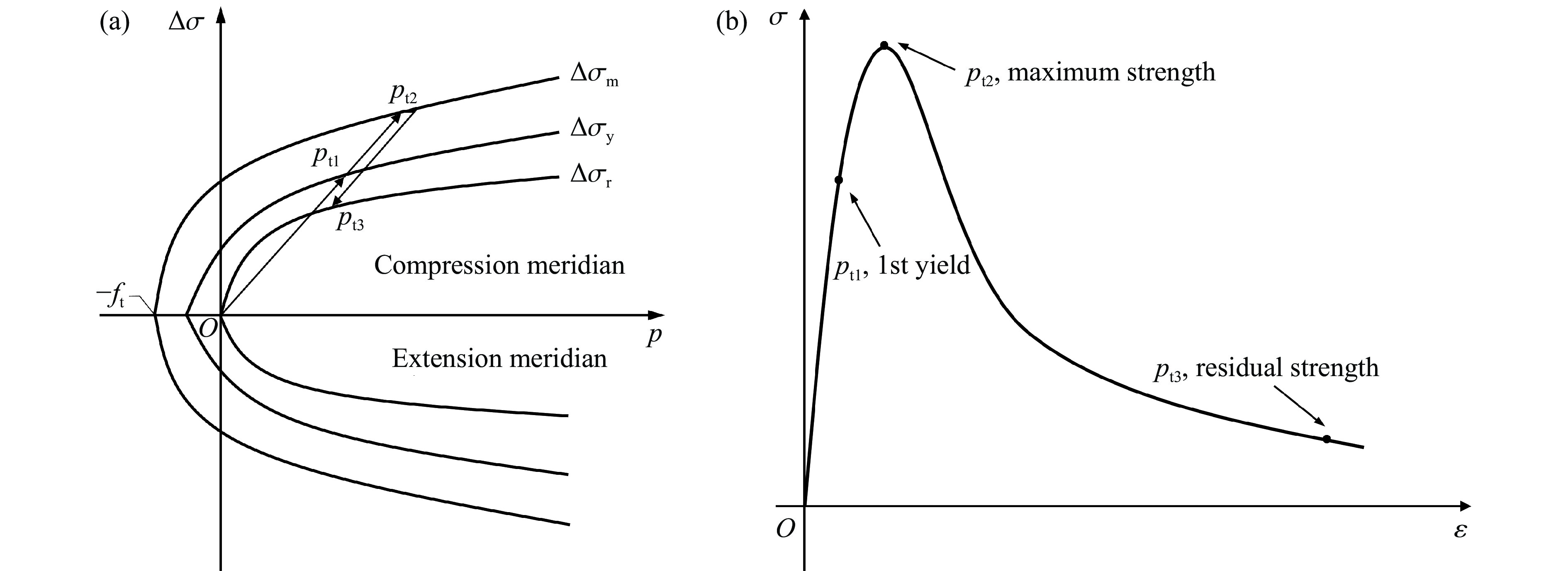
K&C模型是以最大强度面（$ \Delta \sigma_{\mathrm{m}} $）、屈服强度面（$ \Delta \sigma_{\mathrm{y}} $）和残余强度面（$ \Delta \sigma_{\mathrm{r}} $）描述材料在不同加载阶段的损伤特征，其强度面函数^[34]为

式中：p为静水压力；a_i、a_iy、a_jf（i=0, 1, 2；j=1, 2）为强度面参数，通过对混凝土试件在不同静水压力（p=−(σ_xx+σ_yy+σ_zz)/3）下进行三轴和单轴拉压测试获得。

结合图3（f_t为抗拉强度）可知，压力上升使混凝土先从弹性阶段转化为屈服阶段，达到屈服强度面后在硬化阶段抵达最大强度面，最后在软化阶段回退至残余强度面。强度面函数用于描述混凝土从开始受压到损伤破坏时的应力变化过程，将受力情况与损伤行为相联系，以此定义混凝土的力学特征。

橡胶材料具有高度的非线性力学响应和极大的失效应变，通常采用应变-能量密度函数表征其超弹性应力-应变关系。Mooney^[35]于1940年提出关于大弹性形变的应变能理论，之后Rivlin等^[36]对应变-能量密度函数进行修正，最终形成了Mooney-Rivlin模型。该模型被广泛应用于橡胶材料的数值模拟，被证实在动态荷载下可对其力学行为进行准确描述^[26]。本研究采用Mooney-Rivlin模型对橡胶骨料进行模拟，其应变-能量密度函数为

式中：W为单位体积材料在变形过程中储存的应变能；C₁₀、C₀₁、d₀和l为材料参数，由试验标定；I₁、I₂和J为柯西-格林应变张量的不变量，J=1表示不可压缩橡胶。该模型在LS-DYNA中集成为MAT_27号材料，仅需输入C₁₀和C₀₁即可完成对橡胶模型的基本定义，具体材料参数见表1。

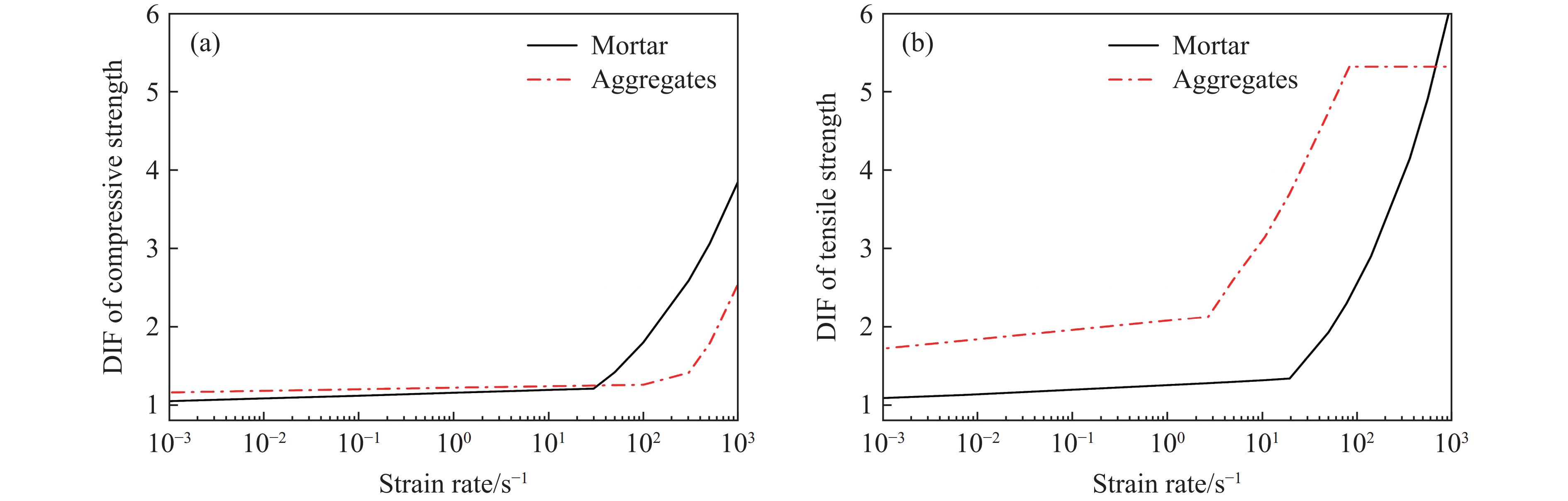
混凝土动态和准静态力学性能差异显著，主要表现为率相关的强度增强效应，也称应变率效应^[37–40]。在LS-DYNA中，应变率效应通过定义应变率-动态增长因子（dynamic increase factor，DIF）函数实现。为确保混凝土基质动态强度的可靠性，本研究采用CEB推荐的压缩强度的DIF（φ_c）和拉伸强度的DIF（φ_t）函数^[41]，该函数由大量水泥砂浆和混凝土试验数据拟合而成，具体表述如下

式中：f_cd为动态压缩强度；f_cs为准静态压缩强度； $ {\dot \varepsilon _{\mathrm{d}}} $为当前应变率； $ {\dot \varepsilon _{{\mathrm{cs}}}} $为准静态压缩时的参考应变率，取3×10⁻⁵ s⁻¹。

式中：f_td为动态拉伸强度；f_ts为准静态拉伸强度； $ {\dot \varepsilon _{{\mathrm{ts}}}} $为准静态拉伸时的参考应变率，取1×10⁻⁶ s⁻¹。

此外，由于水泥砂浆与天然骨料的质量密度存在差异，导致其侧向惯性约束效应不同^[42]，且均质水泥与岩石材料的损伤机制不同，因此，在动态荷载下，天然骨料的DIF应被重新定义，其压缩DIF和拉伸DIF采用如下表达式^[42–43]

为避免高估天然骨料的动态拉伸强度，当应变率大于50 s⁻¹时，天然骨料的拉伸DIF取定值^[26]。根据上述DIF拟合函数，绘制混凝土砂浆和天然骨料的DIF曲线，如图4所示。

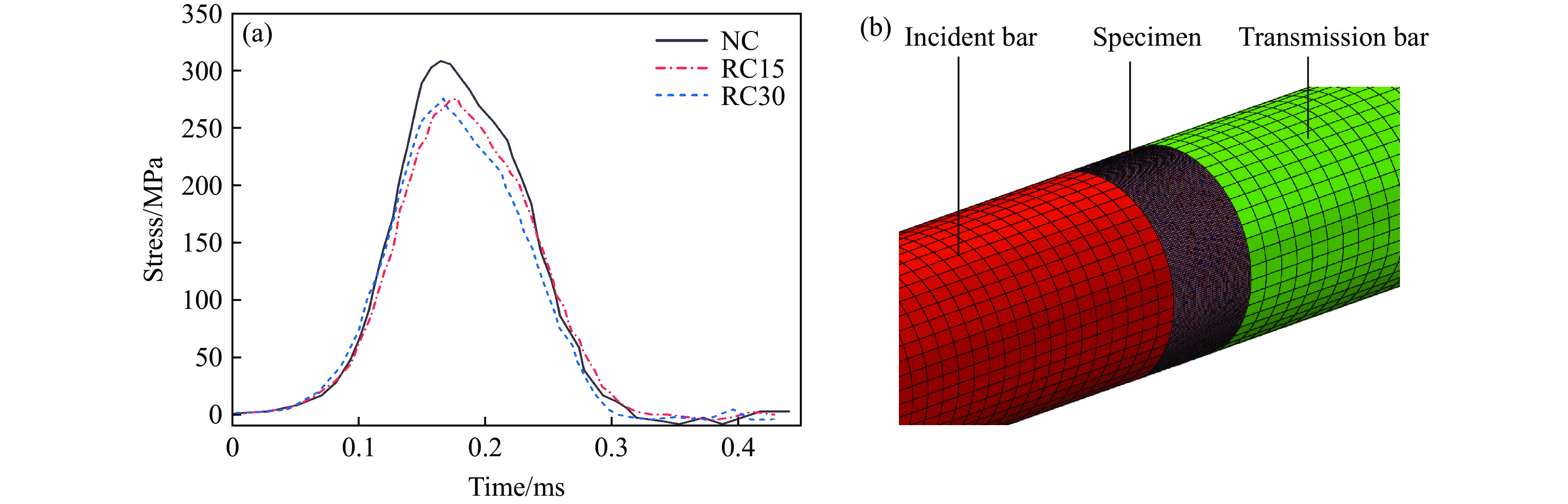
Pham等^[24]对不同橡胶含量的混凝土试件进行分离式霍普金森压杆（split Hopkinson pressure bar，SHPB）试验，试件尺寸为$\varnothing $100 mm×50 mm，浇筑24 h后采用浸水养护法养护至测试龄期（28 d），以达到设计强度，其配合料按照AS 1012.2标准^[44]配置。参照该试验，采用1.2节中的细观混凝土模型及参数，在LS-DYNA内对不同橡胶含量的混凝土试件进行SHPB冲击模拟，验证细观模型和材料模型的可靠性。

如图5所示，SHPB装置由撞击杆、入射杆、试件和透射杆4部分组成。撞击杆、入射杆和透射杆由复合钢材制成，其屈服强度、密度、弹性模量和泊松比分别为1141 MPa、7800 kg/m³、240 GPa和0.3，长度分别为5500和3000 mm，杆直径与试件保持一致。撞击杆对入射杆高速冲击，在入射杆内形成入射波，部分应力波在入射杆末端被反射形成反射波，其余应力波则经过试件传递至透射杆，形成透射波。根据一维应力波传播理论，通过测量不同时刻入射杆和透射杆内的反射应变ε_R和透射应变ε_T，可获得试件应力σ(t)、应变率$ \dot{\varepsilon} $(t) 和应变ε(t)，分别表示为

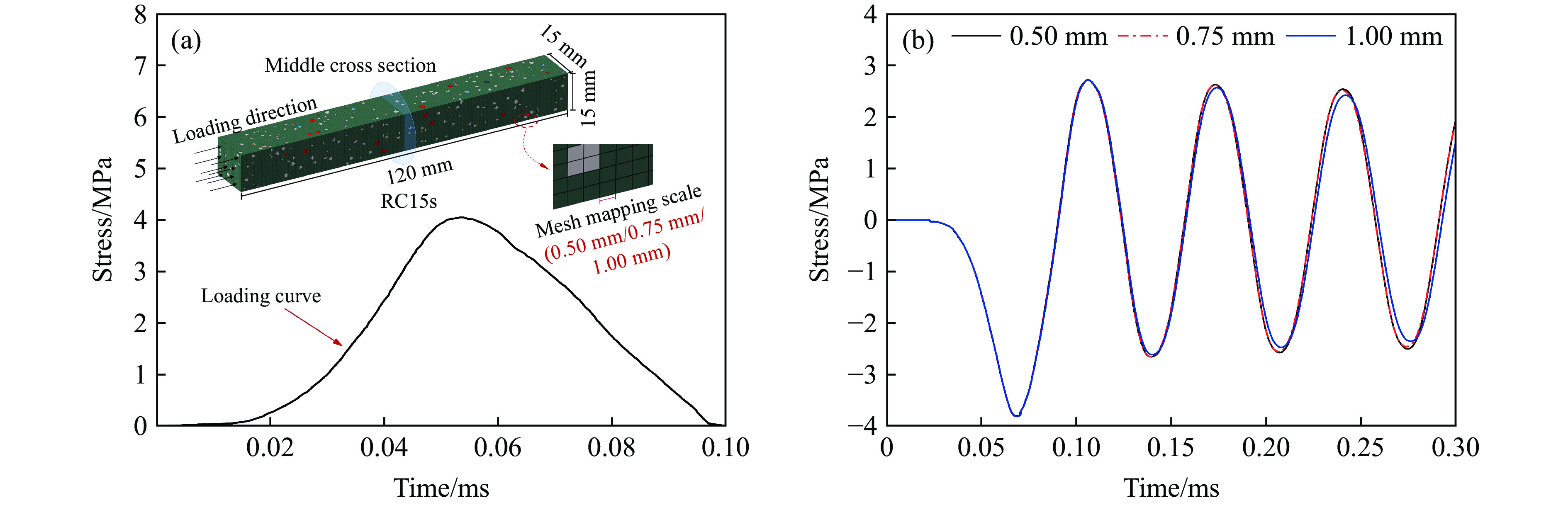
式中：A_s和L分别为试件的横截面积和长度；E、A和C₀分别为杆的弹性模量、横截面积和应力波传播速度，$ C_{0}=\sqrt{E / \rho} $，ρ为杆的密度。

采用网格映射法搭建几何模型与数值模型之间的桥梁。映射尺寸在计算精度与计算效率的权衡中起决定作用。在进行SHPB试验的数值模拟之前，需进行网格收敛性分析，以确定网格映射尺寸。

如图6(a)中的插图所示，建立尺寸为15 mm×15 mm×120 mm的橡胶混凝土试件（命名为RC15s），分别以0.50、0.75和1.00 mm的尺寸对试件进行网格映射，对不同网格尺寸的RC15s施加如图6(a)所示荷载，输出各试件中部横截面平均应力时程曲线，见图6(b)。经对比，当网格尺寸为0.50和0.75 mm时，两者的应力时程曲线无明显差异；当网格尺寸为1.00 mm时，曲线出现偏移，说明此时收敛性较差。综合考虑模拟精度和计算效率，网格尺寸选取0.75 mm，以获得真实且理想的数值模拟效果。

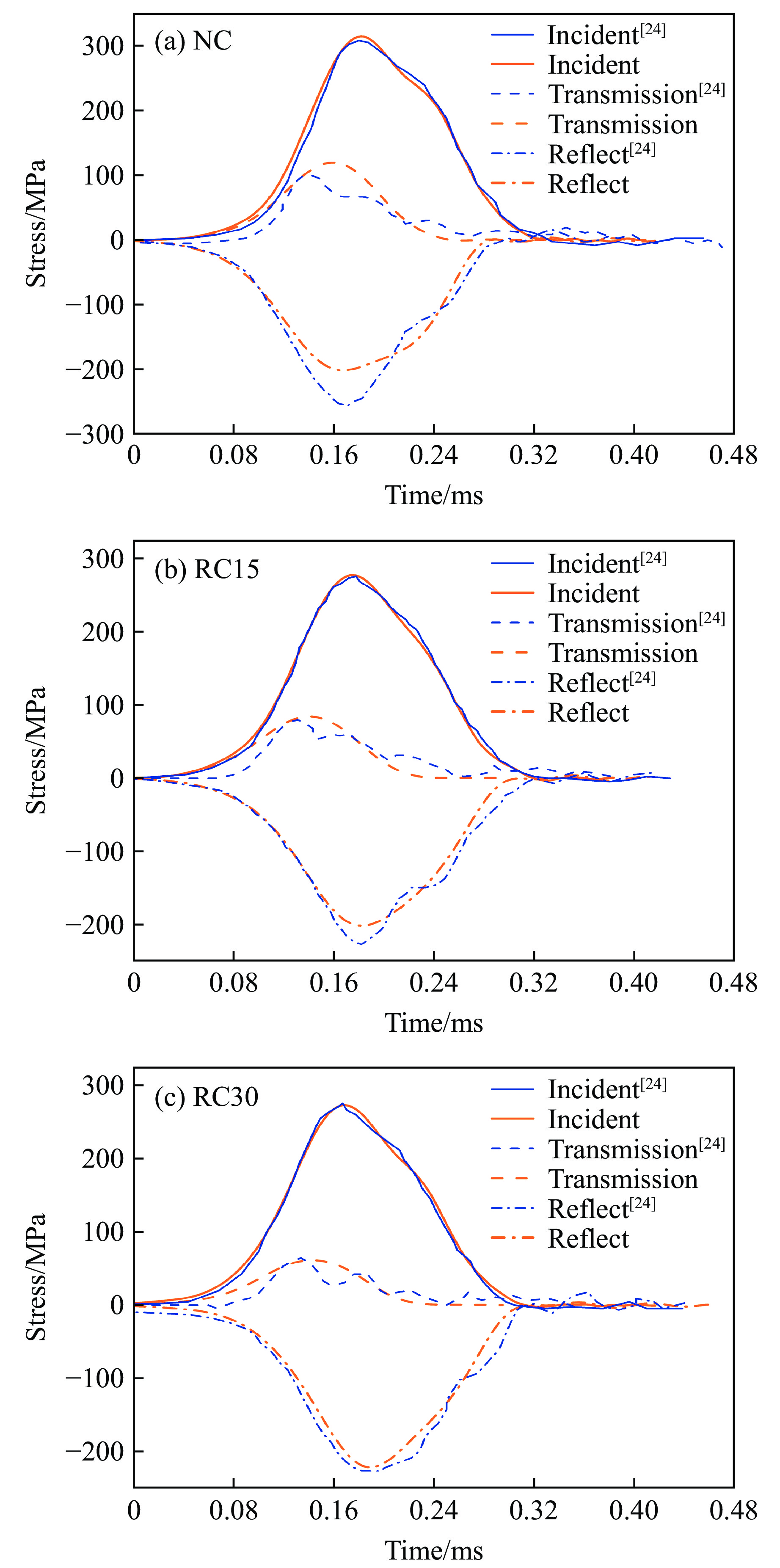
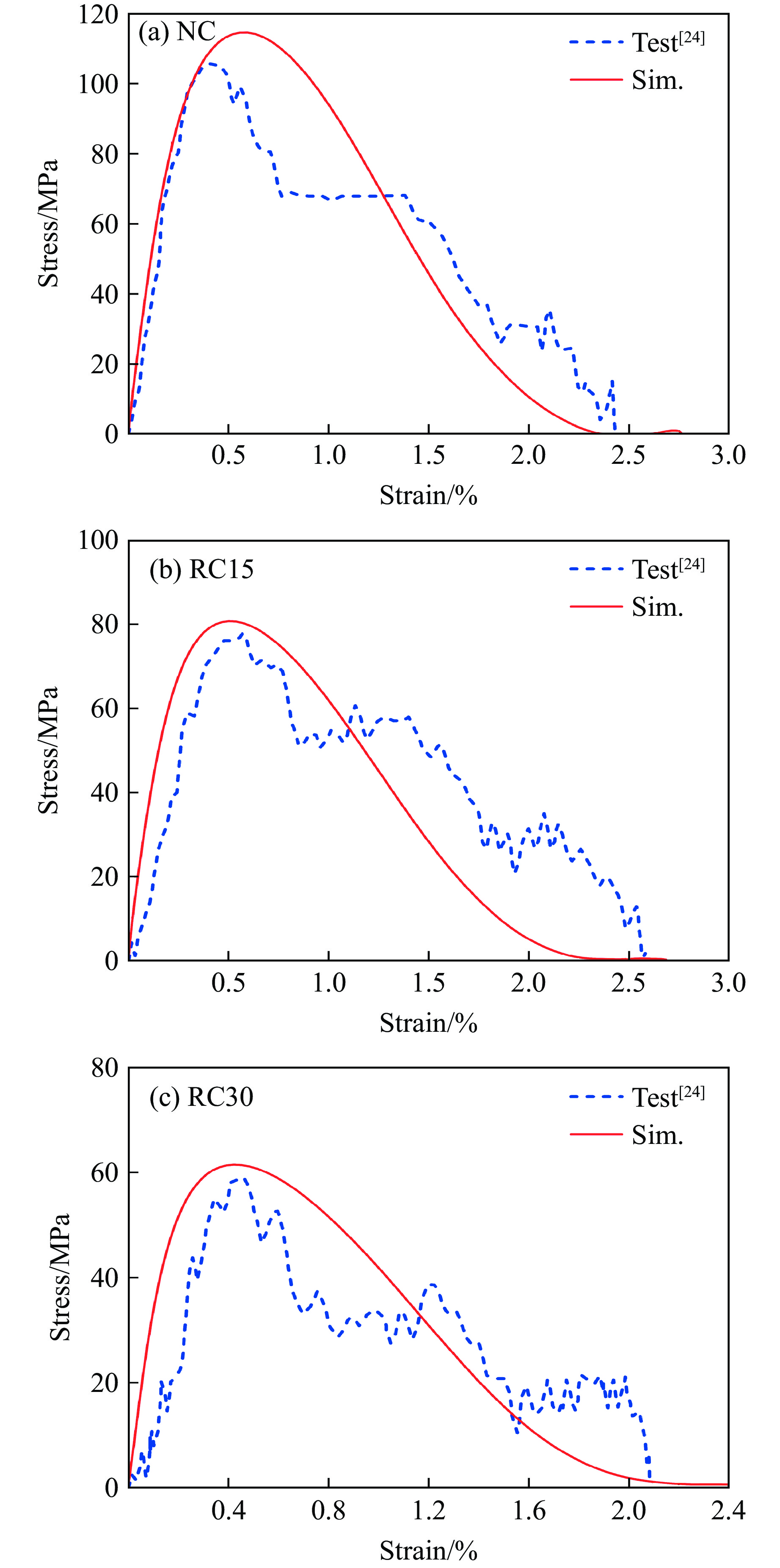
如图7所示，建立与Pham等^[24]试验一致的细观混凝土数值模型，根据橡胶骨料在总骨料中的体积分数，将试件分为普通混凝土（normal concrete）试件NC（0%）、橡胶混凝土试件RC15（15%）和RC30（30%）。提取试验中入射杆的应力时程曲线作为数值模拟中入射杆端面的加载条件，如图8(a)所示，以模拟试验中撞击杆冲击入射杆端面产生入射波的过程。SHPB数值模型见图8(b)，网格映射后，试件共计1132568个单元。各部件之间采用*AUTOMATIC_SURFACE_TO_SURFACE接触算法，入射杆和透射杆均采用线弹性本构模型模拟。通过比较试验与数值计算中入射杆和透射杆中部的应力时程曲线来验证数值模型的有效性，结果如图9所示。由图9可知，各试件的SHPB数值模拟结果与试验结果吻合较好，显示出细观混凝土内骨料含量及分布的合理性，同时验证了综合运用K&C模型和Mooney-Rivlin材料模型开展细观混凝土数值模拟的可行性。

为进一步验证数值模型的动态力学响应，提取入射杆及透射杆中部应变时程曲线，以一维应力波传播理论为基础，通过式(8)、式(9)和式(10)得到不同试件的动态压缩应力-应变曲线，并与试验结果进行比较。如图10所示，总体上看，数值模拟曲线与试验结果吻合，证明了细观模型和材料模型的可靠性，可为后续研究类混凝土的动态力学性能提供数据支撑。

谐振器受迫振动是超材料混凝土激发其动态优势的关键，因此，可将超材料混凝土的带隙等效为谐振器内核的振动频率范围，该范围虽受谐振器自身几何因素和物理因素的影响，但是为带隙的主观调控提供可能。

冲击荷载下，应力波按一定频率在试件内传递，使波能在特殊频率范围内聚集，该频率范围称为波能集中频带。快速傅里叶变换（fast Fourier transform，FFT）可将时程曲线在频域内形成新的幅值分布，为波能集中频带可视化提供方法。能量在波能集中频带内聚集是试件破坏隐患，而超材料混凝土在带隙内拥有良好的吸能表现，因此，将谐振器内核振动频率调控至波能集中频带内，实现带隙与波能集中频带同频，可最大限度地发挥超材料混凝土的动态性能优势。

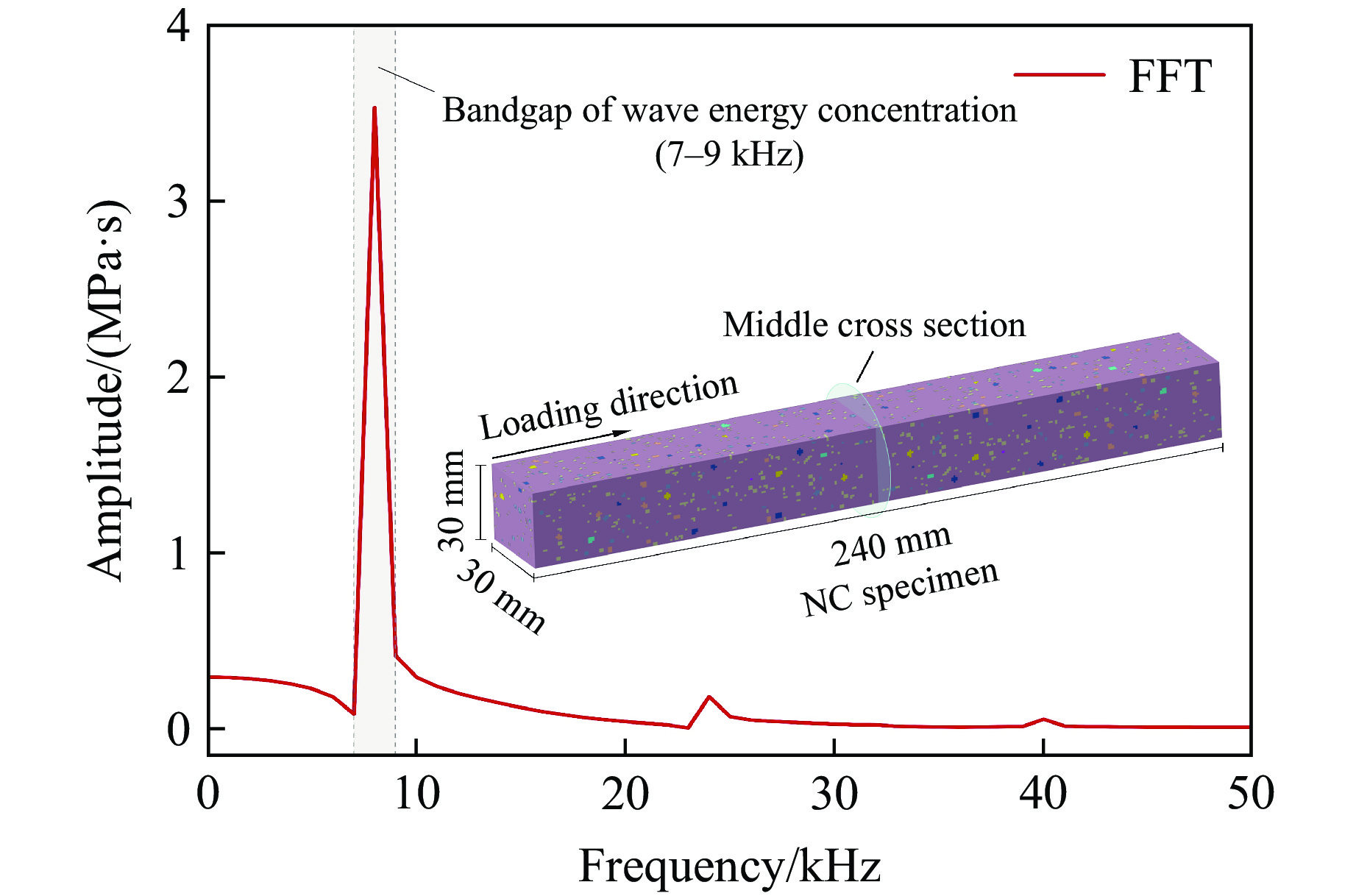
如图11所示，建立尺寸为30 mm×30 mm×240 mm的普通混凝土试件，在其左侧施加冲击荷载，如图6(a)所示，提取试件中部横截面平均应力时程曲线，经FFT转换后，波能集中频带为7～9 kHz，该范围为谐振器的主观设计提供依据。

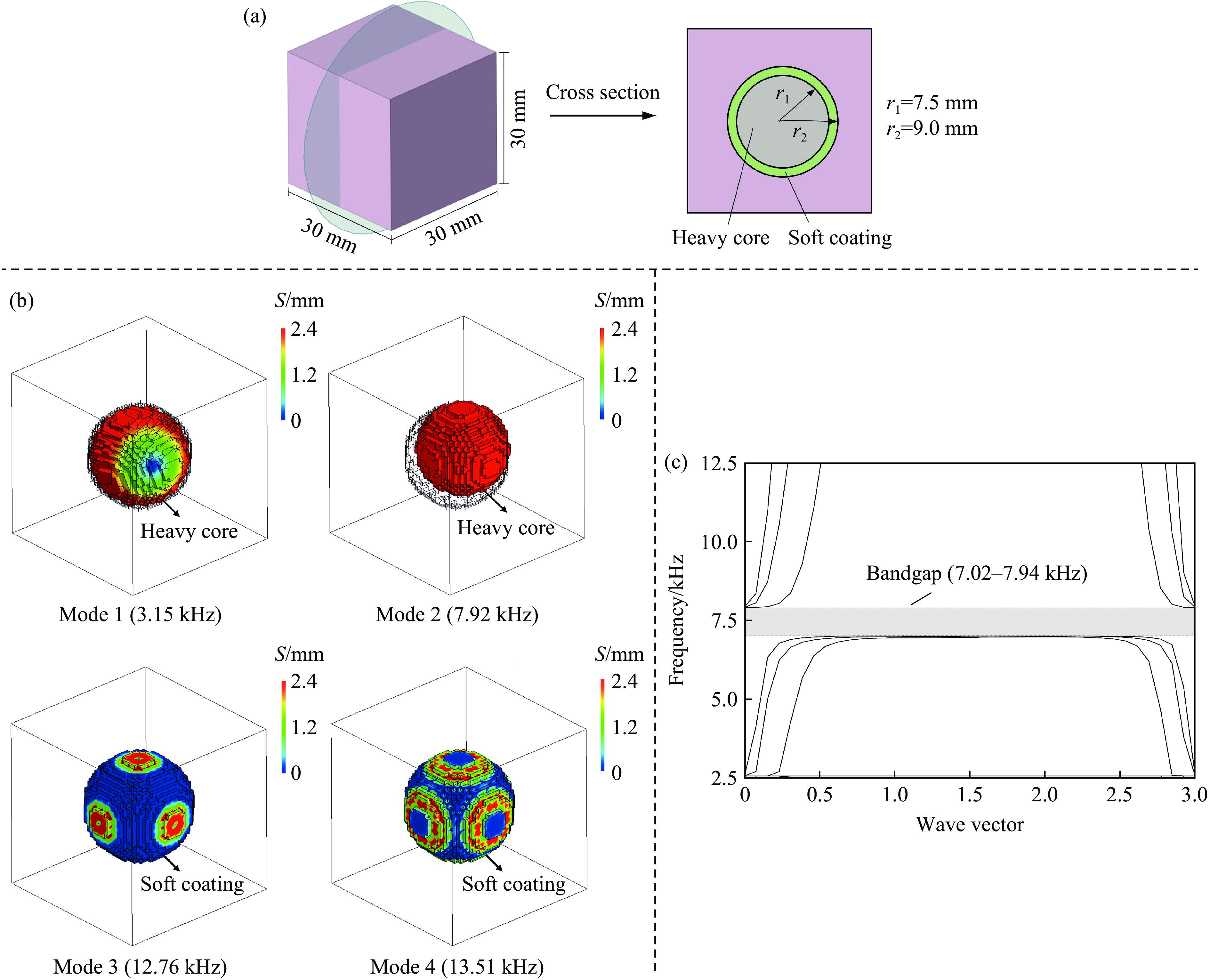
如图12(a)所示，建立尺寸为30 mm×30 mm×30 mm的超材料混凝土单胞模型（r₁和r₂分别为内核半径和单胞半径），经网格映射后，单元总数为6.4×10⁴，单胞中各组分间均为共节点连接，对基体外表面完全固定，采用K&C模型模拟。调整谐振器尺寸及材料属性，对单胞进行多次模态分析，使其振动频率移至7～9 kHz。经分析，确定谐振器内软涂层厚度和内核直径分别为1.5和15 mm，两者均采用线弹性材料，具体参数如表2所示。

提取单胞前四阶模态所对应的固有频率及位移（S）云图，以确定其运动形式。如图12(b)所示，一阶和二阶模态分别表现为谐振器内核的转动和振动，三阶和四阶模态则表现为软涂层振动、转动和弯曲的综合状态，其中振动模态所对应的固有频率为7.92 kHz，落在波能集中频带内。此外，基于图12(a)的单胞结构，在COMSOL Multiphysics中分析布里渊区^[45]内频率与波矢之间的关系，如图12(c)所示，单胞的能带结构绘制于第一布里渊区内^[45]，禁止波传播的频率范围为7.02～7.94 kHz，形成带隙。

需要说明的是，虽然网格映射所产生的尺寸差异使图12(b)中的振动频率落于图12(c)所示的带隙边缘，但差异的存在同样使内核振动频率更贴近波能集中频带中心，对带隙与波能集中频带的同频具有促进作用，使超材料混凝土的动态性能得以充分地释放。

如图13所示，建立普通混凝土（NC）、橡胶混凝土（RC30）、超材料混凝土（MNC）和橡胶超材料混凝土（MRC30）的数值模型，试件尺寸同图11，研究不同试件在冲击荷载下的力学响应和动态性能。

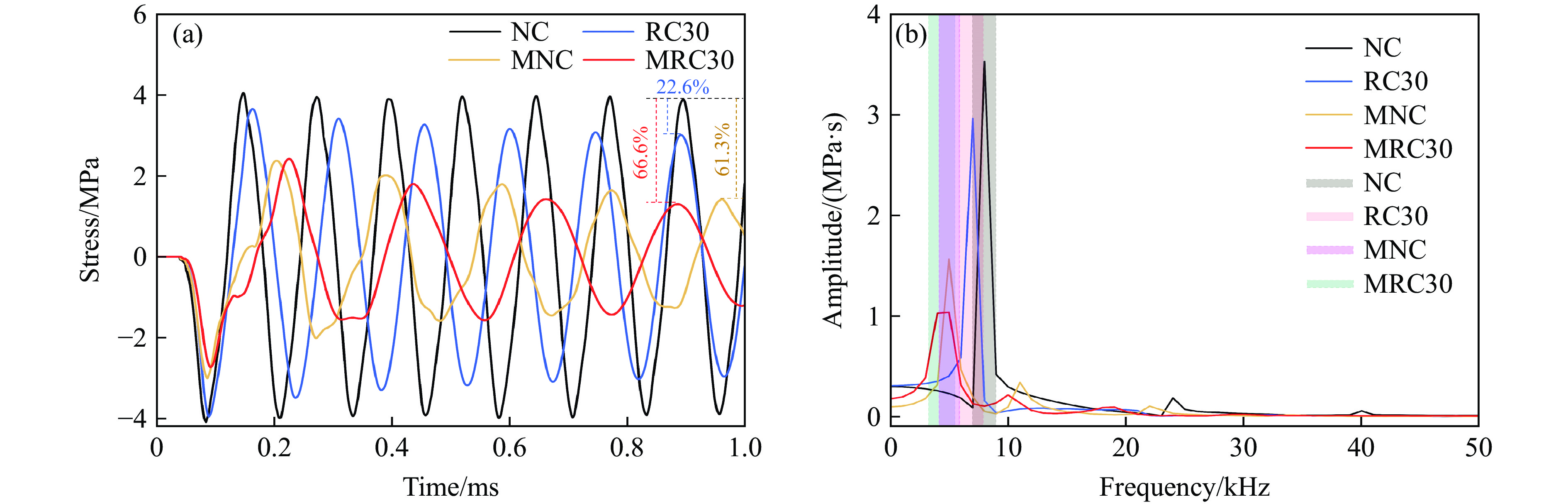
橡胶超材料混凝土作为一种新型抗冲击材料，在低幅值荷载下对冲击波的衰减及能量耗散表现直接影响其在基础防护结构中应用的可靠性和安全性。因此，以SHPB剥落试验为基础，简化加载过程，直接对各试件端面施加低幅值（4 MPa）冲击荷载，同图6(a)，提取试件中部横截面的平均应力时程曲线并进行FFT转换，以研究各试件内部应力波的传递及波能集中情况，结果如图14所示。

与图14(a)中NC在0.8～1.0 ms时间段内的峰值拉应力相比，RC30、MNC和MRC30在相同时间段内的峰值拉应力分别下降22.6%、61.3%和66.6%，其中MRC30表现出最显著的衰波优势。这表明，在谐振器和橡胶骨料均能有效衰减荷载应力波的基础上，将橡胶混凝土与超材料混凝土相结合，所形成的新型抗冲击材料对应力波的衰减效果得到进一步提升，体现其动态性能优势。

式中：${P_{(n)}}$为能量占比（$0 \leqslant {P_{(n)}} \leqslant 1$），E_t为整个试件的动能与内能之和，E_c为试件内某一组分的动能与内能之和。

需要特别指出，尽管橡胶骨料会导致应力波的传递出现一定的“延后效应”，致使试件内波频发生变化，如RC30的波能集中频带随之“前移”（见图14(b)），但是得益于谐振器的主观调控作用，能量在MNC和MRC30的波能集中区域均被有效吸收和转移，尤其在MRC30中，能量仅允许以更低密度的形式聚集，进一步证明了MRC30的动态性能优势。

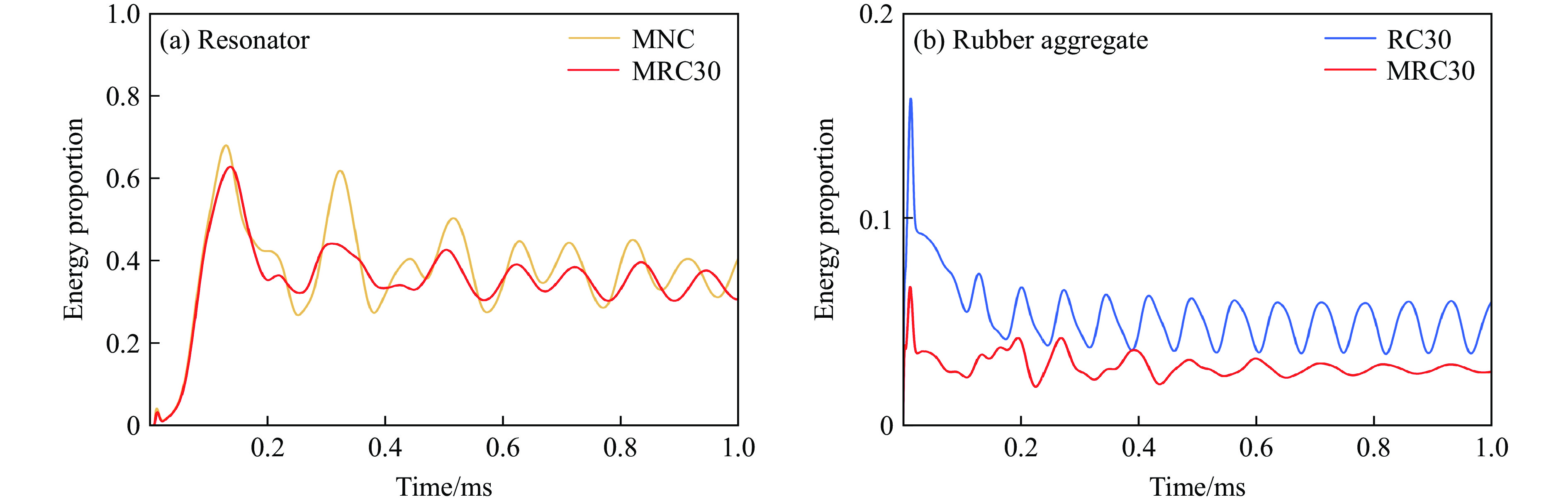
此外，各试件在0.8～1.0 ms时间段内的峰值拉应力下降率存在差异。与NC相比，RC30的峰值拉应力下降22.6%，而MRC30与MNC之间的差异仅为8.3%，表明橡胶骨料对普通混凝土的衰波效果优于超材料混凝土。如图15所示，对不同试件内谐振器和橡胶骨料含能进行归一化处理（见式(11)），结果表明，橡胶骨料对谐振器吸能效率的影响较小（图15(a)），但谐振器的加入使橡胶骨料的含能占比明显降低（图15(b)），说明MRC30中谐振器与橡胶骨料的衰波效果并非线性叠加，两者的共存对橡胶骨料的衰波能力产生消极影响。综合分析表明，橡胶骨料在MRC30内的衰波效果不可忽视，在材料动态力学性能提升中发挥重要作用。

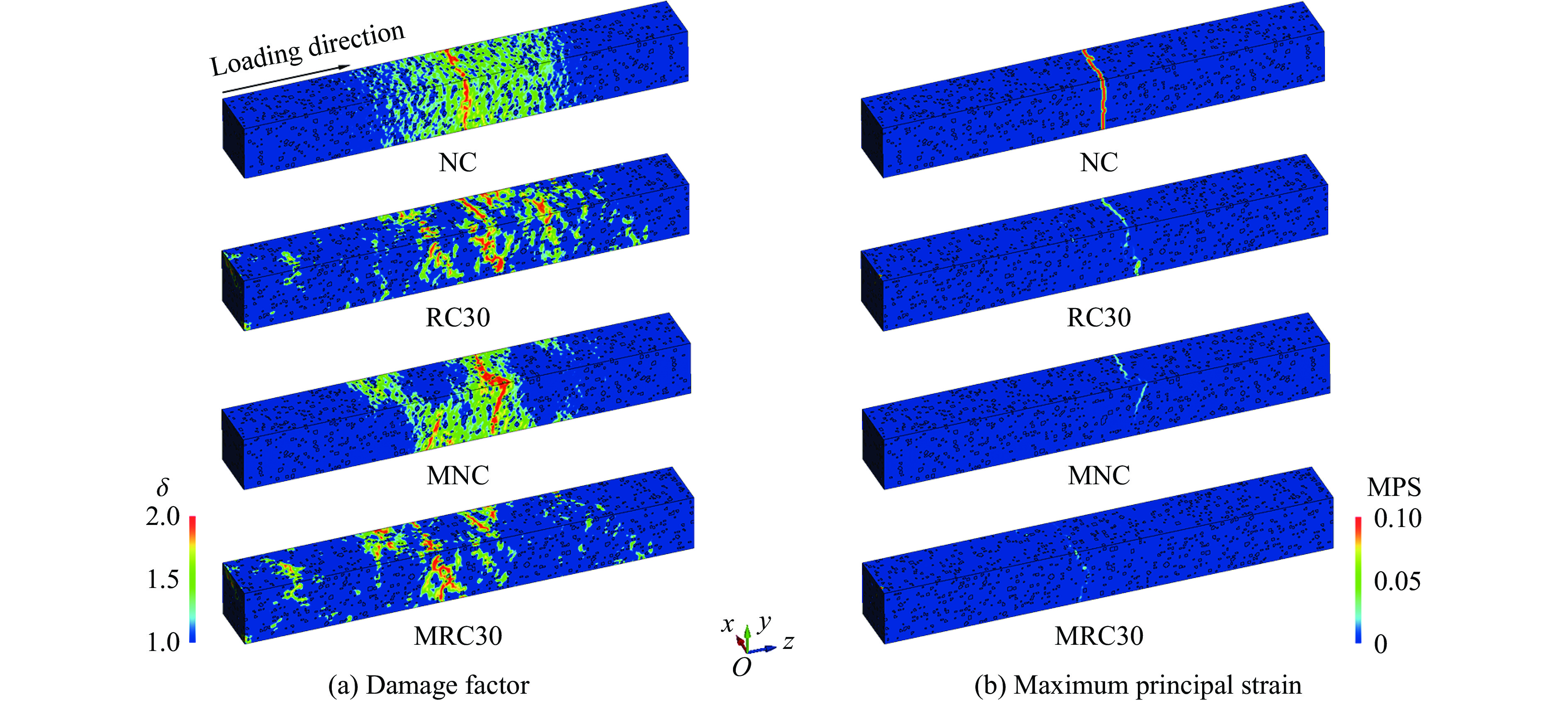
MRC30在低幅值冲击荷载下已初步展现其动态性能优势，但在军用爆炸等领域，尤其是面对战略武器爆炸时产生的高幅值冲击波，防护结构将遭受重大威胁。为研究MRC30在高幅值冲击荷载下的力学响应，以图6(a)中的荷载为参照，在保持其持续时间不变的前提下，将峰值应力提升至20 MPa，输出各试件在1.0 ms时的损伤因子（δ）和最大主应变（maximum principal strain，MPS）云图，分别表征其损伤区域和损伤程度。损伤因子δ=2λ/(λ+λ_m)^[27]，其中：λ和λ_m分别为累积应变和最大承受应变，如图16所示。

从图16(a)可以看出，RC30的损伤形式不同于NC的脆性损伤，其损伤区域较为“分散”，表明能量在试件内部耗散，使损伤区域呈现出明显的扩展趋势。如图16(b)所示，RC30的损伤区域虽因能量分耗而扩展，但其损伤程度远低于NC，体现橡胶骨料在抑制裂纹持续扩展方面的积极作用。MRC30的损伤区域不仅拥有RC30的损伤特征，还保留了MNC的低损伤程度特性，继承了橡胶混凝土和超材料混凝土的动态性能优势，实现了抗冲击性能的进一步提升。

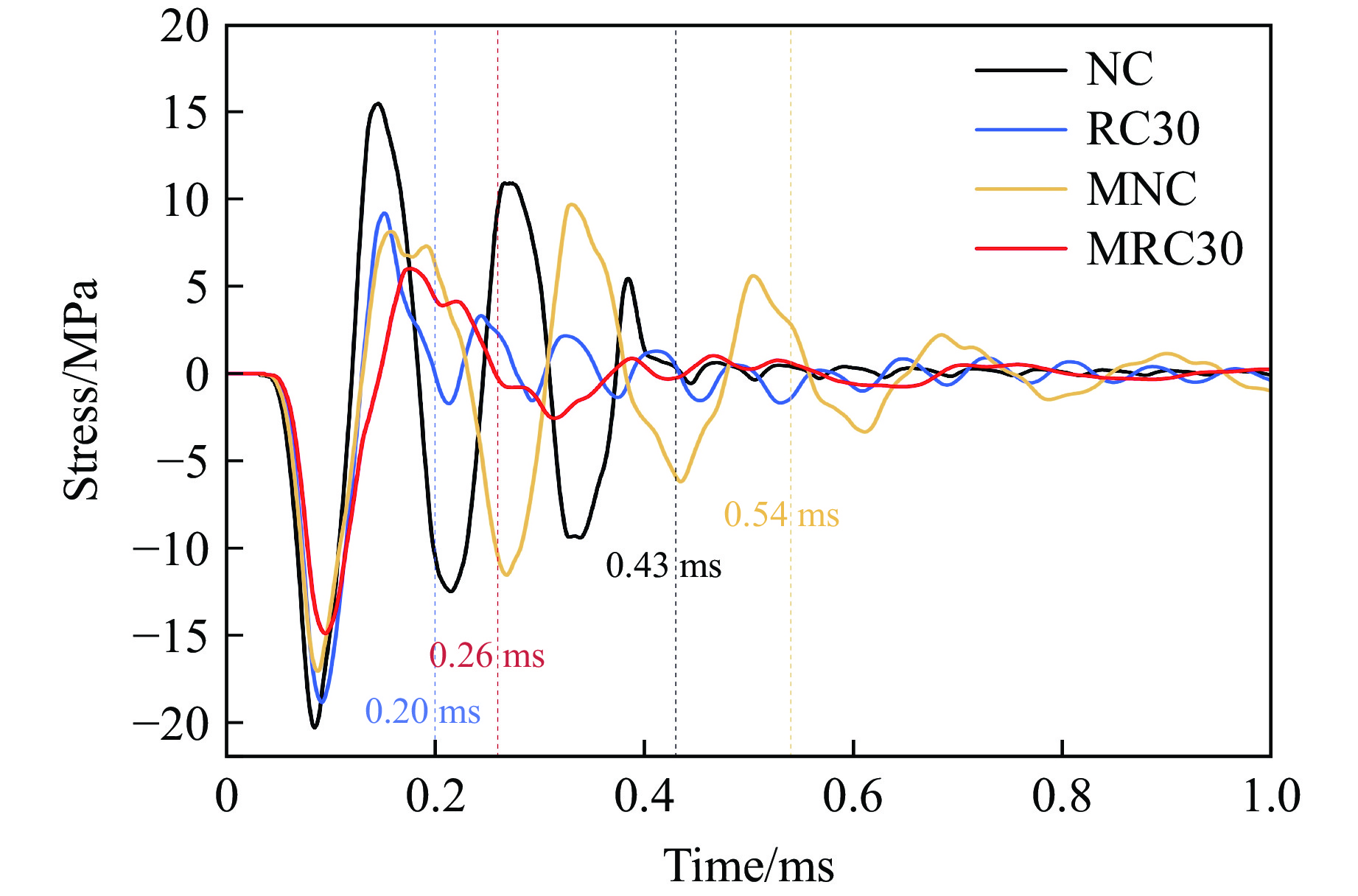
冲击荷载作用下，不同试件的中截面平均应力时程曲线如图17所示。与图14(a)对比，应力传播呈现明显的非周期性特征，这是由于试件内部损伤导致波能被消耗，应力传播路径受阻，进而使应力曲线出现幅值下降、周期缩短、振荡频繁等现象。根据试件损伤因子云图以及图17中应力幅值的变化情况，NC、RC30、MNC和MRC30的破坏时刻以虚线标出，分别为0.43、0.20、0.54和0.26 ms，其中，由于橡胶含量与试件强度呈负相关，RC30和MRC30的破坏时刻相对靠前。通常而言，试件破坏时刻的提前意味着损伤程度的加剧，但是结合图16(b)中各试件的损伤程度可以看出，RC30和MRC30并不遵循这一规律。

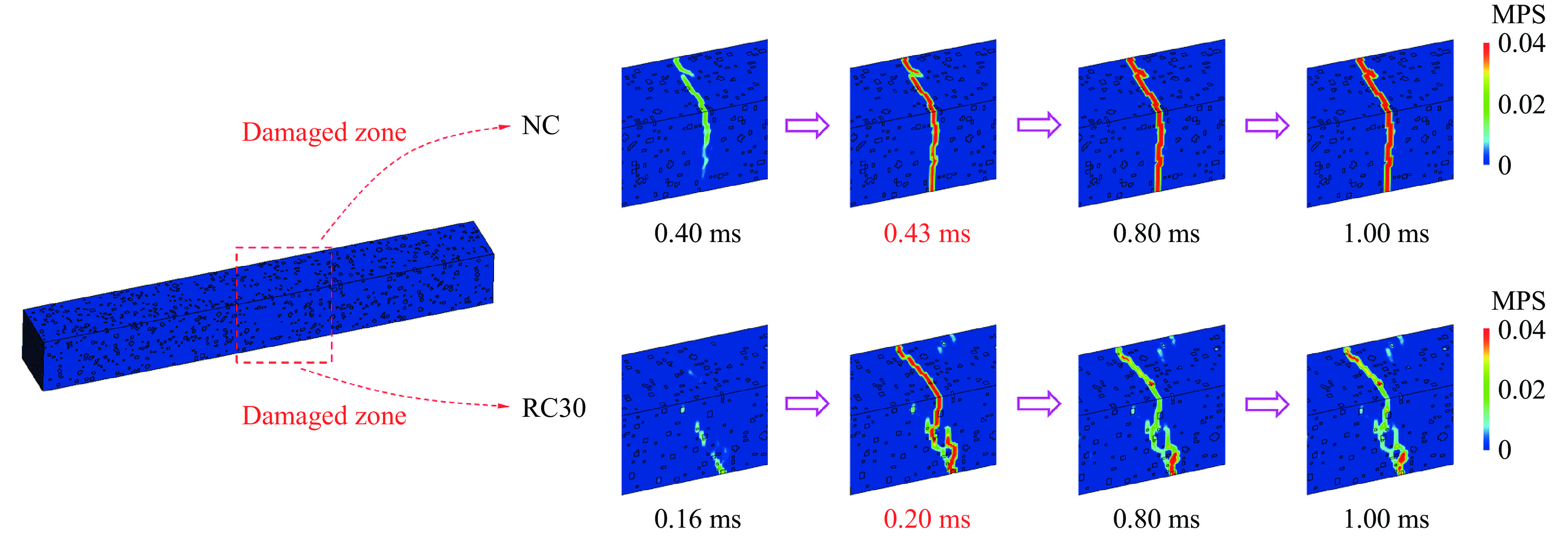
不同时刻NC和RC30损伤区域的最大主应变云图如图18所示，其中，NC的形变过程保持脆性特征，自0.43 ms形成横断破坏后，其损伤程度随时间的推移而逐渐加剧。与此不同，RC30在0.20 ms发生横断破坏后，损伤程度随时间的推移而逐渐降低，这是由于裂纹在脆性基质内扩展时，橡胶骨料虽然在试件开裂过程中产生极大形变，但是超弹性特征使其难以产生塑性损伤，具有恢复形变的能力，橡胶骨料抑制裂纹的持续扩张，致使试件的损伤程度降低。

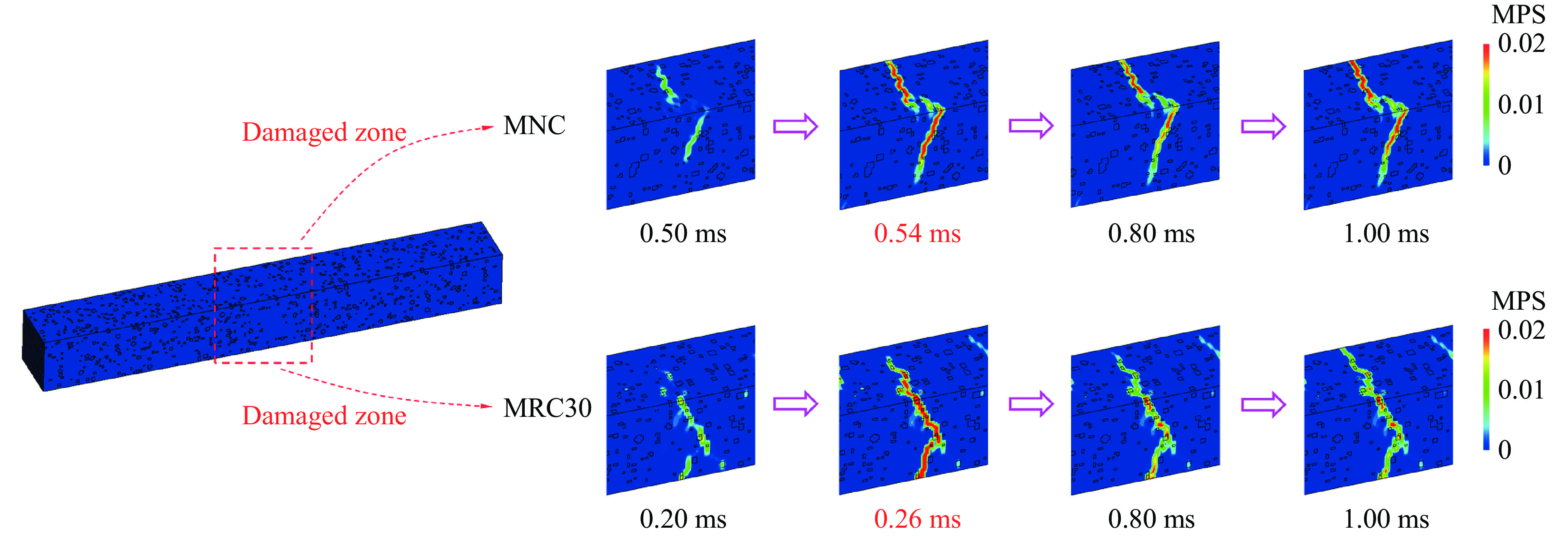
图19显示，MRC30在0.26 ms发生破坏后同样出现损伤程度降低的现象，说明橡胶骨料对超材料混凝土的韧性提升也起到积极作用。此外，由于谐振器采用线弹性材料，使MNC在一定程度上抑制损伤程度的加剧，并且抑制效果可在MRC30中与橡胶骨料的作用相叠加，从而进一步改善MRC30的韧性和功能完整性，提升其抗爆炸冲击能力。

橡胶骨料对类混凝土的动态性能提升具有积极作用，本研究将对橡胶骨料的几何参数和物理参数进行分析，以揭示橡胶骨料的含量和粒径对橡胶超材料混凝土动态性能的影响，为确定橡胶骨料在橡胶超材料混凝土中的最佳含量和最优粒径提供依据。

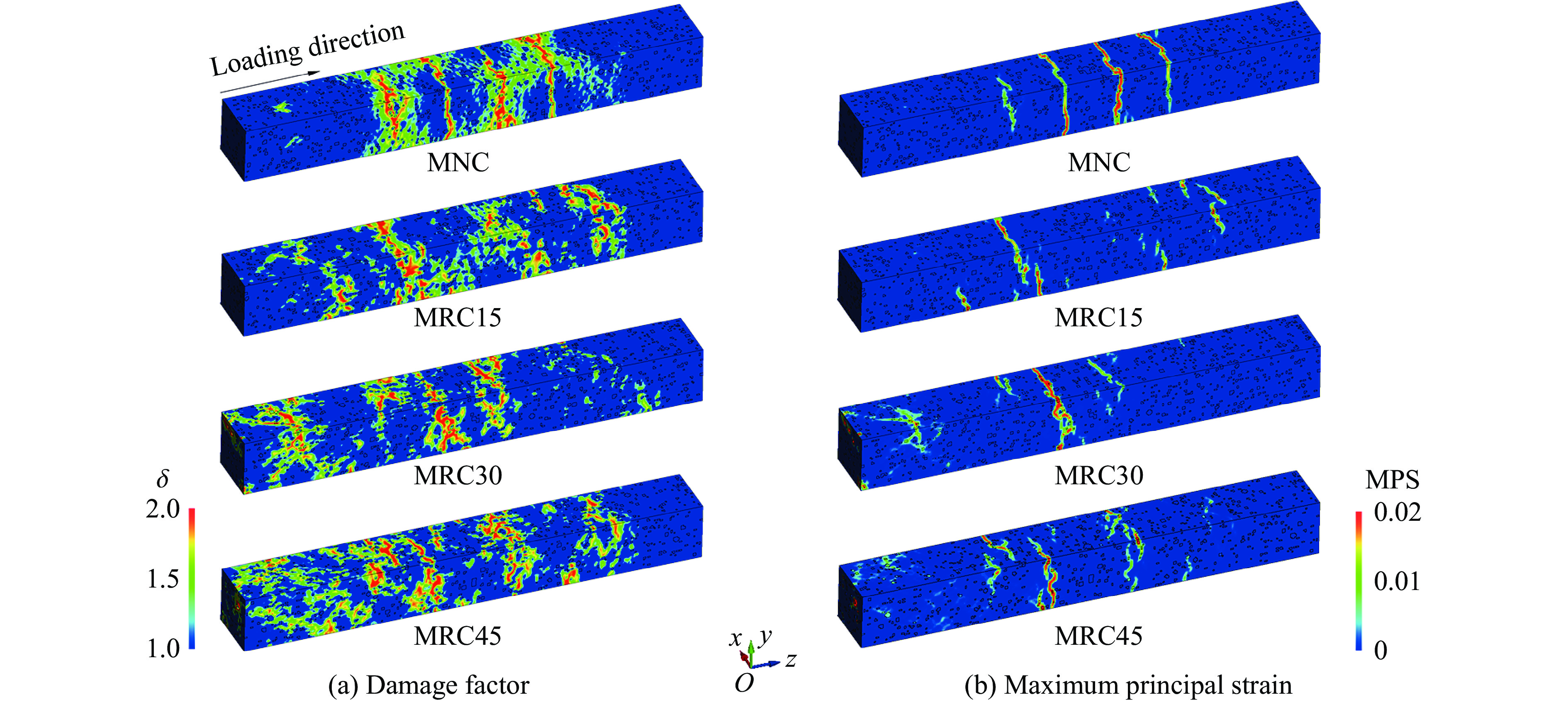
为研究橡胶骨料含量对橡胶超材料混凝土动态性能的影响，新增MRC15和MRC45试件，其天然骨料替换率分别为15%和45%。参考前述方法，将冲击荷载的峰值应力提升至30 MPa，输出不同试件的损伤因子和最大主应变云图，如图20所示。

如图20(a)所示，橡胶骨料有效地使谐振器周围区域形成“分散”损伤效应，且损伤区域的“分散性”与橡胶含量呈正相关。从图20(b)可以看出，尽管MRC15、MRC30和MRC45的损伤程度均低于MNC，但橡胶超材料混凝土的损伤程度与橡胶含量之间并无明显规律，说明橡胶含量与试件强度之间的负相关性在一定程度上对试件的损伤程度造成影响，形成“韧性上升”与“强度下降”之间的冲突。

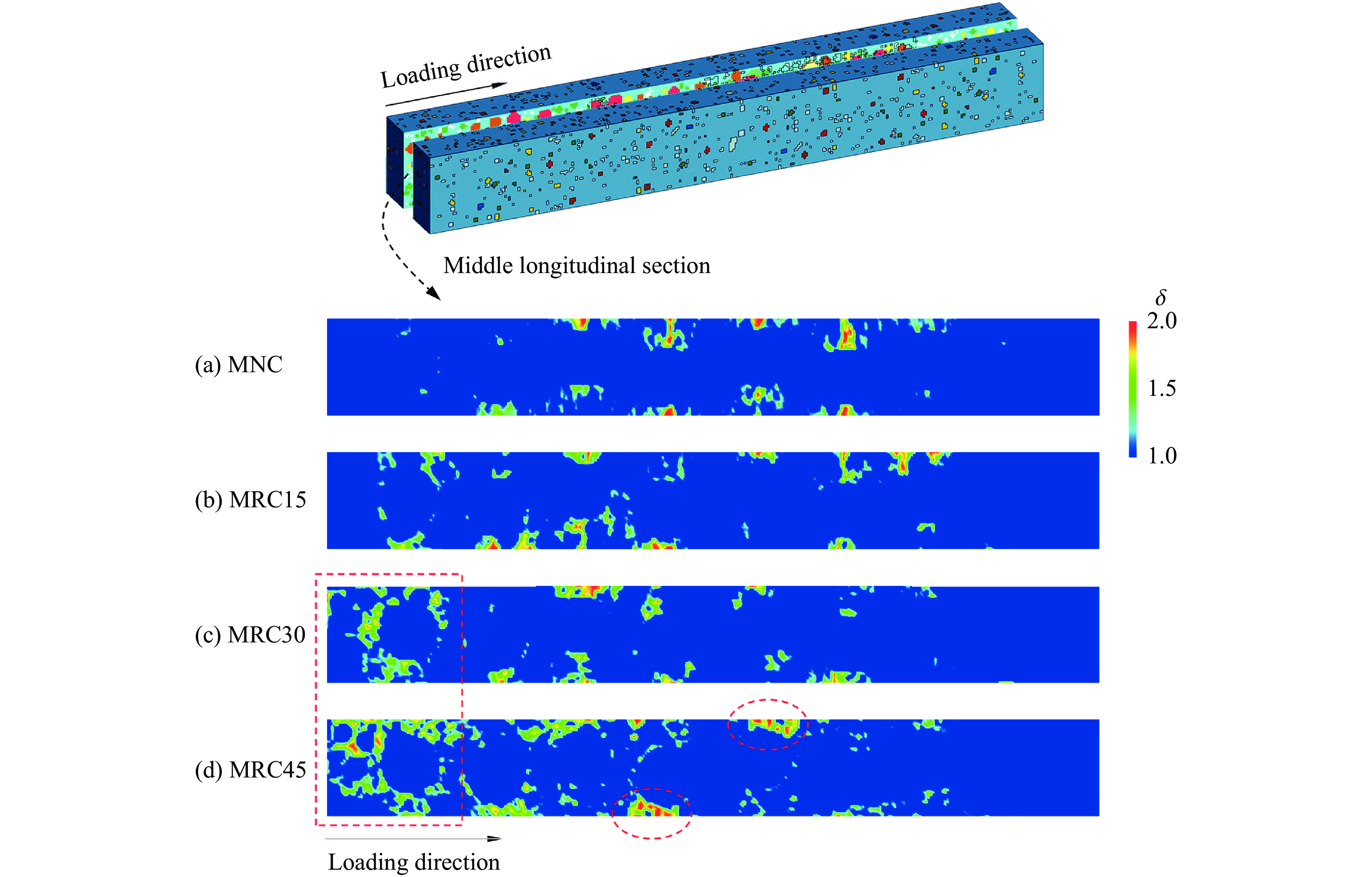
不同试件的纵截面损伤因子云图如图21所示。随着强度的下降，MRC30和MRC45内部加载端出现不同程度的损伤，其中MRC45的中部区域甚至出现局部破坏，如图21中红色虚线框选区域所示，说明“强度”在试件整体损伤中占主导地位。相较之下，MRC15在保持较低损伤程度的同时，损伤区域并未明显扩展，在韧性与强度之间达到平衡。因此，建议将超材料混凝土中天然骨料总体积的15%～30%替换为橡胶骨料，以优化其动态力学性能，提升抗冲击能力。

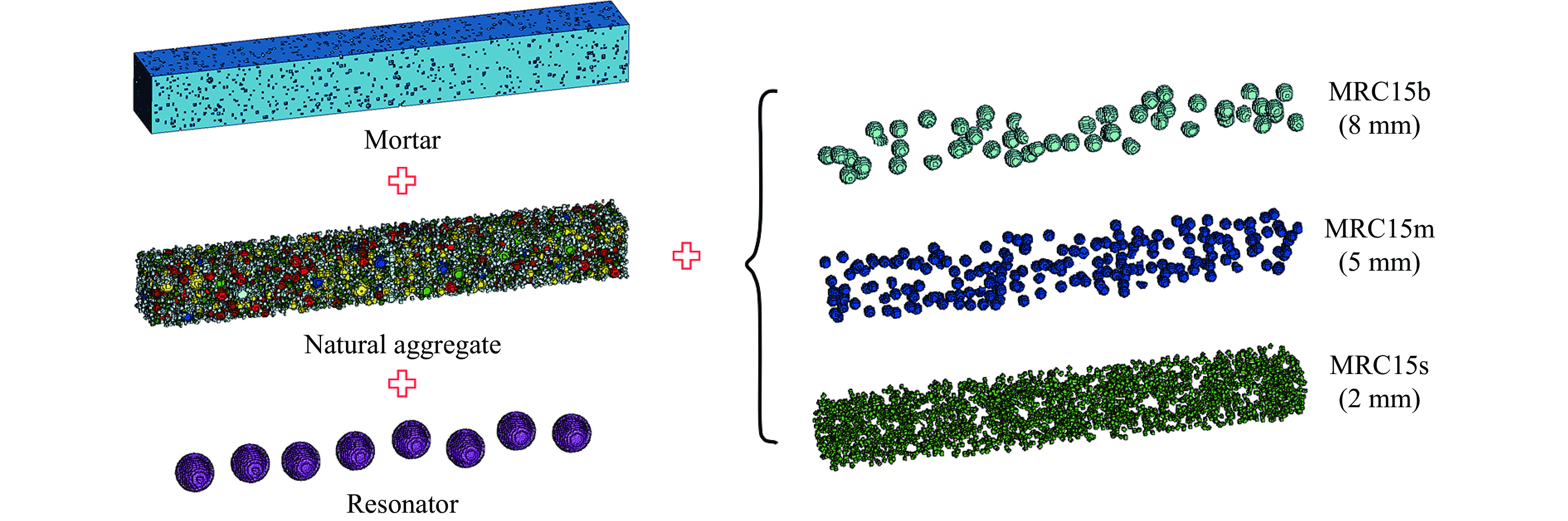
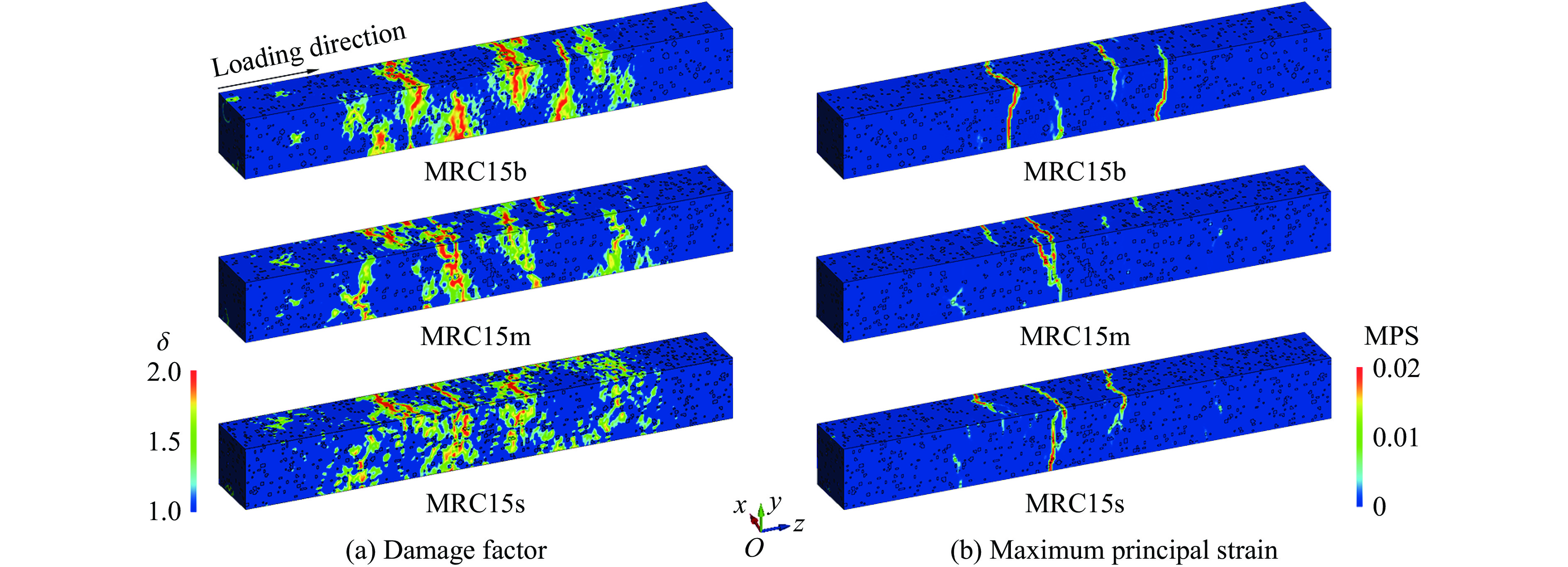
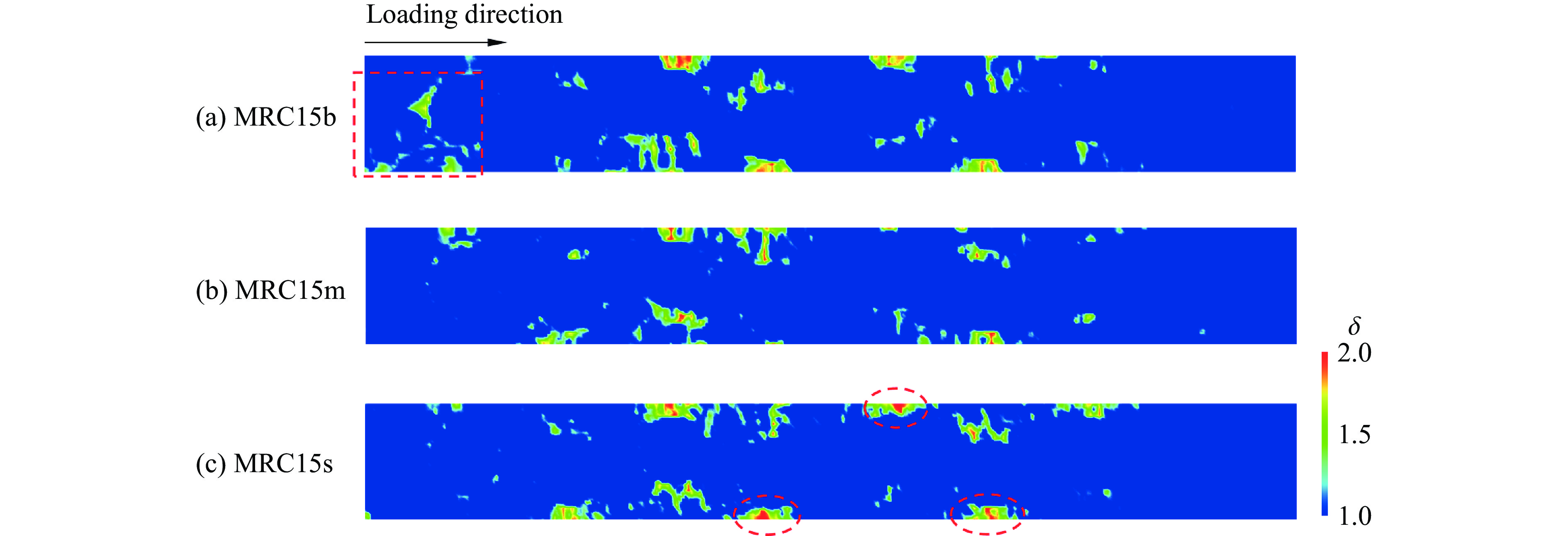
为研究橡胶骨料粒径对橡胶超材料混凝土动态性能的影响，选取3.1节中动态性能较优异的MRC15作为研究对象。如图22所示，在橡胶骨料体积分数不变的前提下，将其粒径分别控制为8、5和2 mm，并依次命名为MRC15b、MRC15m和MRC15s。对含不同橡胶粒径的试件施加与3.1节相同的冲击荷载，输出其损伤因子和最大主应变云图，如图23所示。

损伤区域的“分散性”作为类橡胶混凝土的损伤特征，对试件的损伤程度具有抑制作用。如图23(a)所示，在相同体积含量下，MRC15s内橡胶骨料的数量优势使其表面损伤区域明显“分散”，表明橡胶骨料的密集分布有助于抑制损伤扩展，但数量差异造成的骨料分布不均同样导致试件的局部强度发生变化。如图23(b)所示，MRC15b的骨料密集度较低，导致损伤区域的韧性下降，损伤程度加剧；MRC15s的骨料密集分布，但局部强度较低，损伤程度较大；而MRC15m则通过适中的橡胶粒径实现了骨料密集度与局部强度之间的相对平衡，使损伤程度降至三者中最低。

MRC15b和MRC15s中由于橡胶粒径相差较大，导致其内部骨料分布的疏密程度存在一定差异，出现不同程度的塑性损伤，如图24中红色虚线框所示。因此，对于橡胶含量已确定的橡胶超材料混凝土，动态调控橡胶粒径，使橡胶超材料混凝土在局部强度与韧性之间达到平衡，是提升其抗冲击性能的关键所在。

通过在超材料混凝土基质中加入橡胶骨料，探索了一种新型抗冲击复合材料—橡胶超材料混凝土，利用有限元软件建立其细观数值模型，研究了冲击荷载下其动态性能优势，得到如下主要结论。

(1) 橡胶骨料的加入有效地增强了超材料混凝土的衰波能力，对其动态性能的提升有积极作用。

(2) 橡胶材料的超弹性使类橡胶混凝土的损伤区域呈现“分散”特征，既降低了损伤程度，又提升了韧性和功能完整性。

(3) 橡胶含量与试件强度的负相关性导致试件的损伤程度与橡胶含量之间呈现非线性关系，建议将骨料总体积的15%～30%替换为橡胶骨料，以提升试件的抗冲击性能。

(4) 在橡胶体积含量确定的情况下，其粒径变化造成“局部强度”与“韧性”的对立，需要从宏观上调控橡胶骨料粒径对试件整体动态性能的影响，平衡骨料分布与损伤程度之间的关系，以确定橡胶骨料的最终应用粒径。