-
剪切增稠液(shear thickening fluid,STF)是一种非牛顿流体,当剪切速率在一定范围内增大时,STF的黏度迅速增大,逐渐由液态转变为固态。将STF通过浸渍方式与凯夫拉(Kevlar)织物复合,可制成一种新型复合材料。该复合材料兼具防护性和轻便性,可以应用于个人防护、减振缓冲等领域,具有广阔的应用前景。
在实验方面,已有诸多学者开展了不同速度下STF浸渍Kevlar织物的冲击实验,发现经STF浸渍后Kevlar织物的抗冲击性能和抗穿刺性能均得到了大幅的提升,在冲击过程中能够消耗更多的能量[1–3]。基于低速冲击实验,Mawkhlieng等[4]认为,剪切增稠液的流变特性对Kevlar织物抗冲击性能的增强起到了十分重要的作用。通过纱线拔出实验,Majumdar等[5]认为,纱线间摩擦作用的增加导致STF浸渍Kevlar织物表现出更好的力学性能,其后的相关实验结果[6–7]也表明,经STF浸渍后Kevlar织物的纱线拔出力明显提高。Liu等[8]认为,剪切增稠液的流变特性和纱线间的摩擦对增强STF浸渍Kevlar织物的抗冲击性能起到了十分重要的作用。
在数值模拟方面,目前STF浸渍Kevlar织物的有限元模型大致可分为细观模型、流固耦合模型和宏观模型。细观模型将STF浸渍的强化作用表现为纱线间摩擦力的增加[9–10],流固耦合模型在构建模型时结合了STF的流变特性[11–12],宏观模型则主要考虑Kevlar织物材料模型参数的改变[13]。以上建模方法在模拟STF浸渍Kevlar织物受冲击载荷后的残余速度、破坏形貌、能量吸收等方面均取得了较好的成果。近期,Liao等[14]建立了一种STF浸渍Kevlar织物的连续介质损伤力学(continuum damage mechanics, CDM)本构模型,通过引入动态增强因子(dynamic increase factor, DIF)探究STF流变特性的影响,数值模拟结果与弹道冲击和低速撞击实验数据吻合较好。
综上所述,STF的流变特性和纱线间的摩擦是造成STF浸渍Kevlar织物具有更好抗冲击性能的主要因素。本研究在Liao等[14]工作的基础上,通过引入残余强度因子(residual strength factor, RSF),结合STF的流变特性与纱线拔出实验结果,综合考虑上述2种增强机理,进一步发展STF浸渍Kevlar织物的CDM动态本构模型。通过对STF浸渍Kevlar织物在不同速度下的冲击实验进行数值模拟,将模拟结果与已有的实验数据进行对比,验证本构模型的有效性与准确性。
-
STF浸渍Kevlar织物为正交材料,在建模过程中忽略细观结构,认为织物是均匀连续的,在此基础上建立材料的宏观本构模型。假定材料的应力-应变行为在损伤前保持线弹性,其损伤行为由模量的衰减来表征。通过引入动态增强因子(应变率效应)和残余强度因子,并结合STF的流变特性与纱线拔出实验结果,发展一种连续介质损伤力学本构模型。该本构模型包括损伤准则、损伤软化、应变率效应3个方面。
-
对于STF浸渍Kevlar织物,考虑以下7种损伤模式[14–15]。
(1) 纵向(X/Y方向)拉伸/剪切损伤,考虑织物受到冲击作用时经纱和纬纱方向的单轴拉伸与横向剪切损伤
式中:E为弹性模量;G为剪切模量;
$\varepsilon $ 为应变;$\gamma $ 为剪切应变;下标1和2表示纵向(X/Y方向),即织物经纱与纬纱方向;下标3表示横向(Z方向),即织物厚度方向;$ {X_{\rm{t}}} $ 、$ {Y_{\rm{t}}} $ 为纵向拉伸强度;$ {S_{ 12}} $ 、$ {S_{ 23}} $ 、$ {S_{ 31}} $ 为不同方向的剪切强度。运算符号“$\left\langle {} \right\rangle $ ”定义为(2) 面内方向(X/Y方向)压缩损伤,考虑织物受到冲击作用时经纱与纬纱方向基于最大应变准则的平面内压缩损伤
式中:
$ {X_{\rm{c}}} $ 、$ {Y_{\rm{c}}} $ 为纵向压缩强度。(3) 厚度方向压缩损伤,织物受到冲击作用时冲击区域会出现较高的压缩应力,造成挤压损伤
式中:
${Z_{\rm{c}}}$ 为织物横向压缩强度。(4) 面内剪切损伤,考虑到平面剪切应力会破坏织物结构,而不会发生纤维断裂
(5) 厚度方向拉伸/剪切损伤,考虑织物受到冲击作用时厚度方向的拉伸与剪切损伤
式中:
${Z_{\rm{t}}}$ 为织物横向拉伸强度。在上述7种损伤模式中,
${f_j}$ (j=1,2,···,7)表示损伤因子。当${f_j} \geqslant 1$ 时,认为对应模式的损伤开始发生,并进入损伤演化阶段。 -
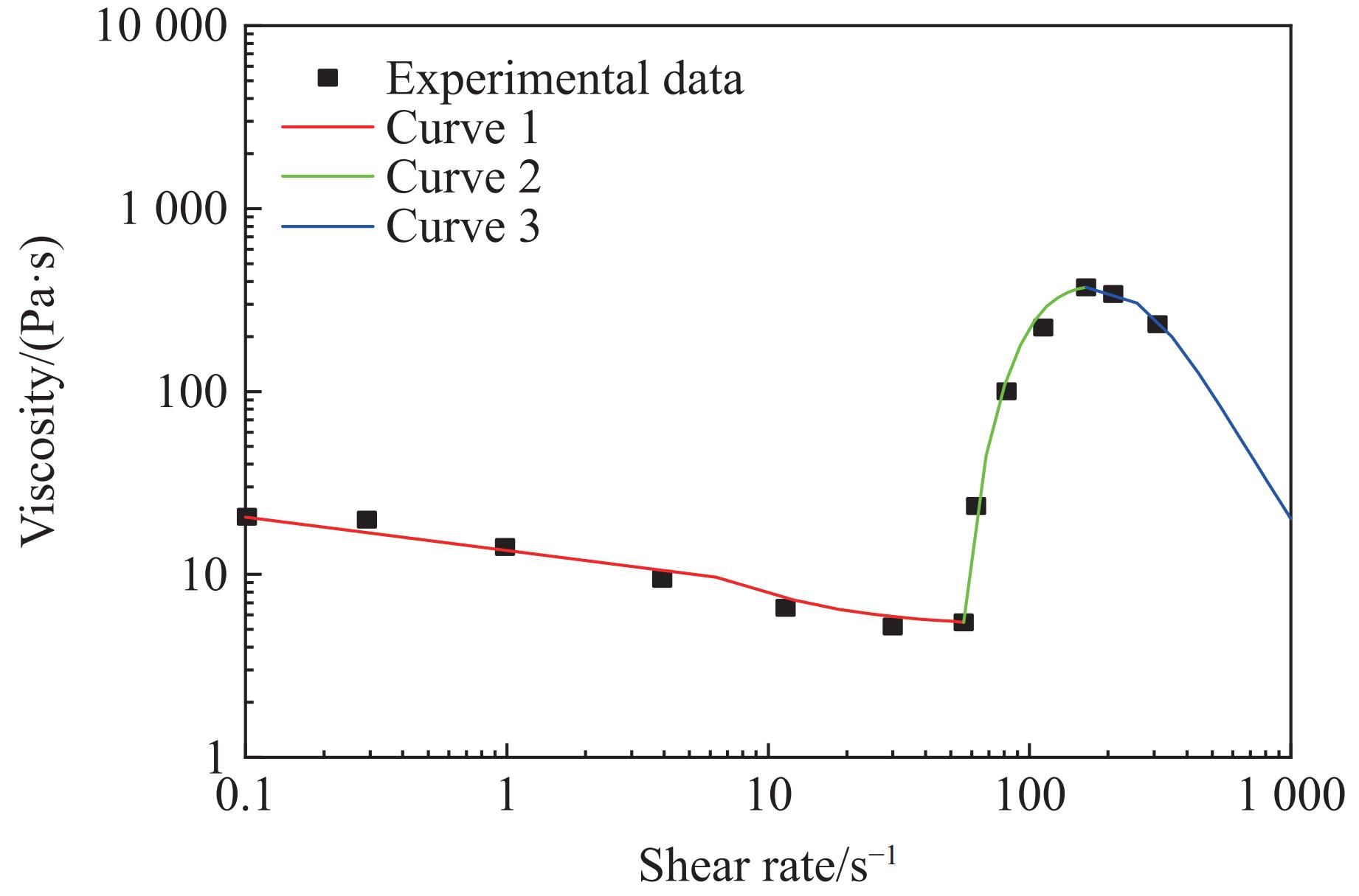
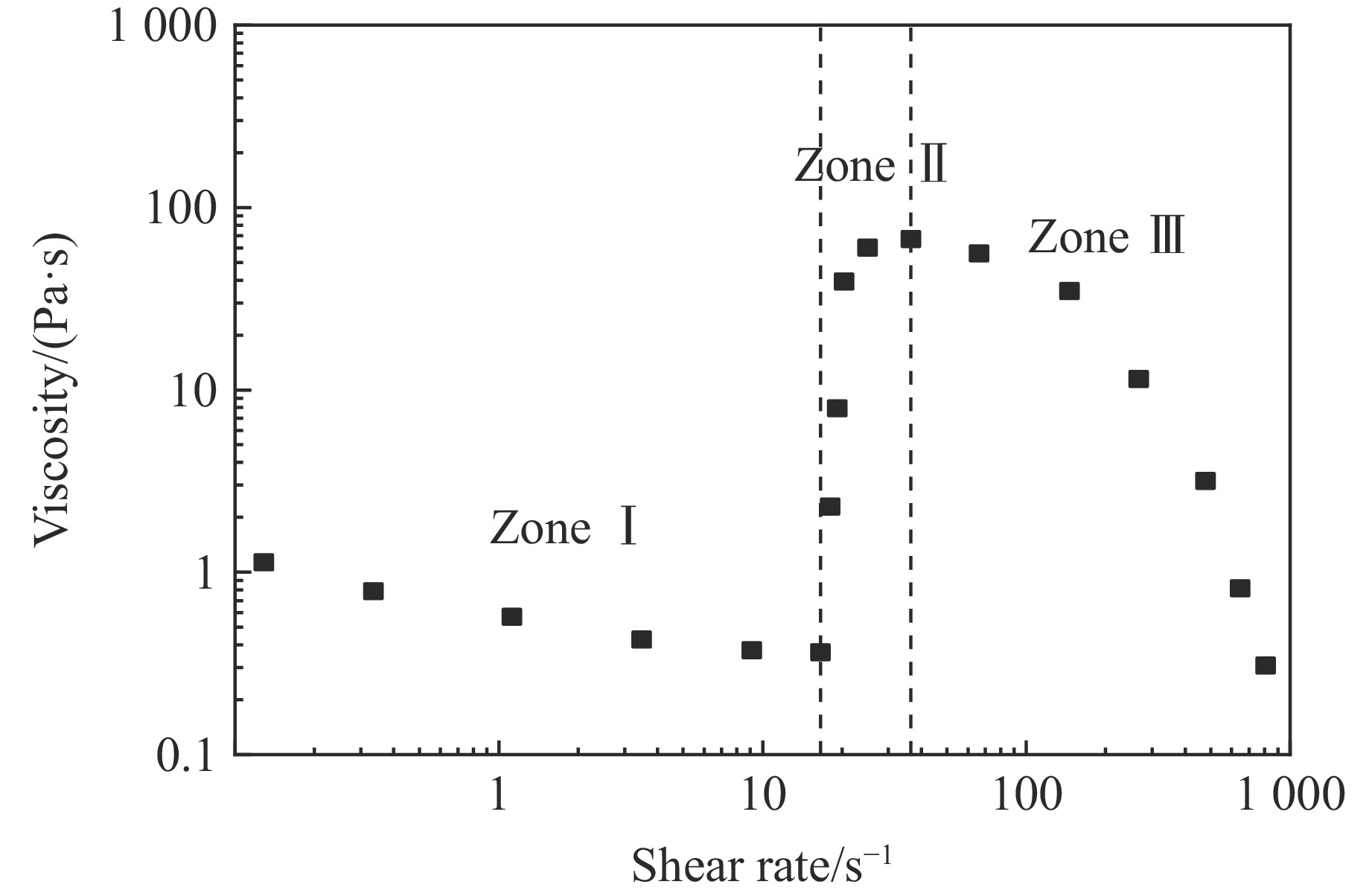
典型的STF流变特性可以分为3个区域:剪切变稀区域(Zone Ⅰ)、剪切增稠区域(Zone Ⅱ)、剪切再变稀区域(Zone Ⅲ),如图1所示。
采用分段函数对STF的流变特性进行拟合[16],该分段函数结合了STF流变特性3个区域的特点:在低剪切速率下出现轻微的剪切变稀(Zone Ⅰ),在临界剪切速率以上黏度急剧增加(Zone Ⅱ),在高剪切速率下出现明显的剪切变稀区域(Zone Ⅲ)。所提出的函数具有连续的导数,使其适用于数值模拟,并且与实际测量的STF流变特性吻合良好。具体表达式为
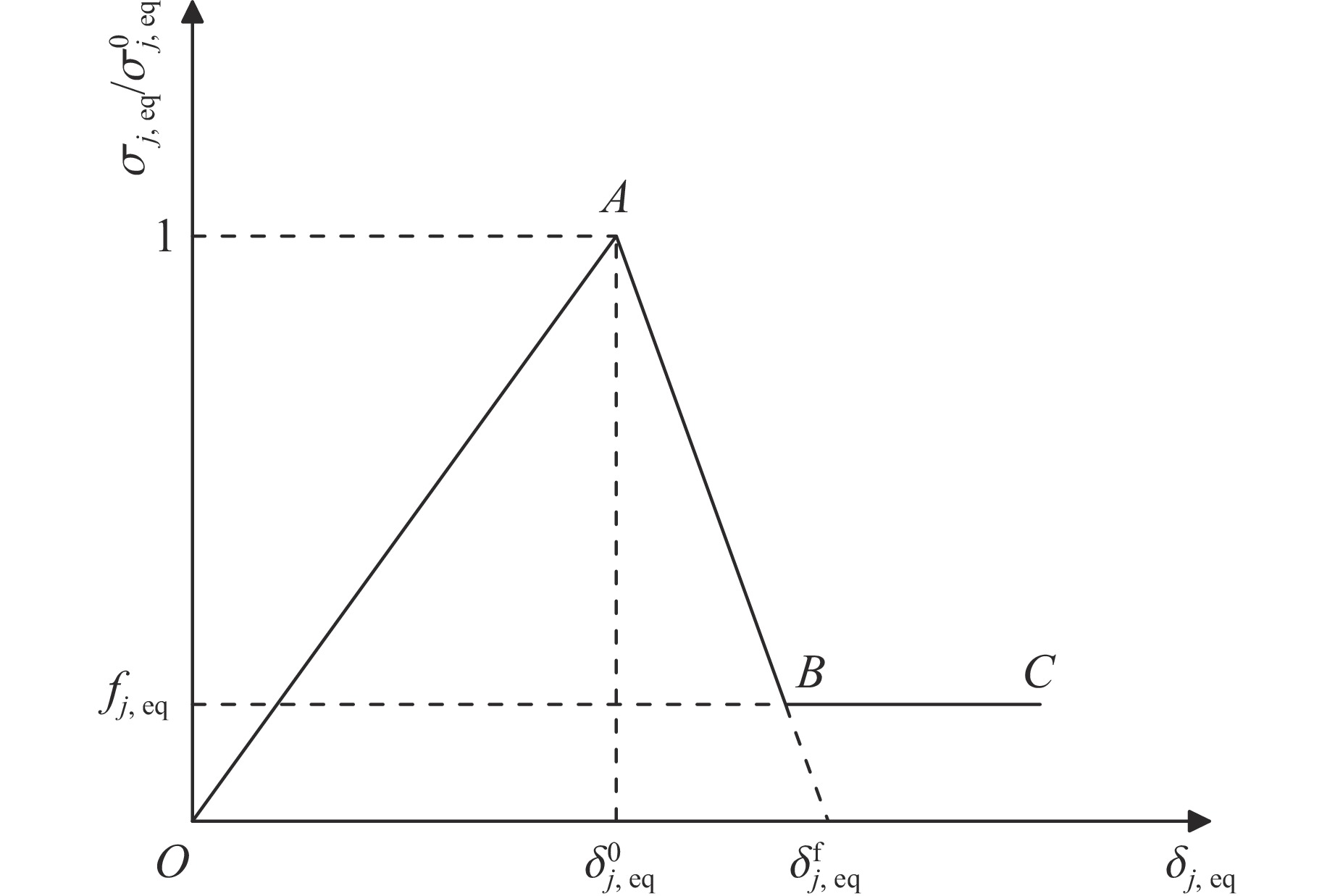
式中:
$ \eta (\dot \gamma ) $ 和$ {\eta _i}(\dot \gamma ) $ (i=Ⅰ,Ⅱ,Ⅲ)为黏度,${\eta _0}$ 、${\eta _{\rm{c}}}$ 和${\eta _{\max }}$ 分别为初始黏度、临界黏度和峰值黏度,${\dot \gamma _{\rm{c}}}$ 为临界剪切速率,${\dot \gamma _{\max }}$ 为峰值黏度对应的剪切速率,$ {K_i}$ (i=Ⅰ,Ⅱ,Ⅲ)、$ {n_i} $ (i=Ⅰ,Ⅱ,Ⅲ)均为拟合常数。当进入损伤演化阶段时,材料的损伤随着加载而不断积累,表现为材料模量的软化。在有限元计算中,Xin等[15]采用应力-位移关系并结合断裂能来描述材料的损伤演化过程,在一定程度上减少了单元敏感性。本研究中,损伤演化过程也采用应力-位移关系,如图2所示。
该损伤演化过程结合了先前渐进损伤模型的研究[14–15, 17–18],在线性损伤软化的基础上,引入残余强度因子(residual strength factor,
$ {f_{\rm{rs}}} $ )描述在加载过程中织物纤维的断裂拔出、摩擦吸能等现象。经STF浸渍后,织物纱线间摩擦有所增加,纱线拔出实验可以表征这一现象[19–20]。研究表明,纱线拔出峰值力的增加与STF的剪切增稠特性有关[21–22],结合这一现象,$ {f_{\rm{rs}}} $ 的表达式为式中:
$ {f_{\rm{rs0}}} $ 为纯Kevlar织物的残余强度因子,其值通过试算得到;$ \eta $ 为当前黏度,可以通过流变特性得到。$ k $ 的表达式为式中:Fs与Fn分别为纱线拔出实验中STF浸渍Kevlar织物与纯Kevlar织物的峰值力。
引入状态变量
${\phi _j}$ 表示单一损伤模式下的损伤程度,考虑到STF具有可逆性,对损伤程度设置损伤极限值$ \xi $ 。结合之前提出的残余强度因子$ {f_{\rm{rs}}} $ ,${\phi _j}$ 的表达式为式中:
$\delta _{j,{\rm{eq}}}^{\rm{f}}$ 为等效失效位移,$\delta _{j,{\rm{eq}}}^0$ 为初始等效位移。$\delta _{j,{\rm{eq}}}^{\rm{f}}$ 可以通过以下表达式得到式中:
${G_{{j}}}$ 为断裂能参数,$\sigma _{j,{\rm{eq}}}^0$ 为初始等效应力。$\delta _{j,{\rm{eq}}}^0$ 和$\sigma _{j,{\rm{eq}}}^0$ 的具体表达式为式中:
$ {\delta _{j,{\rm{eq}}}} $ 和$ {\sigma _{j,{\rm{eq}}}} $ 分别为等效位移和等效应力。不同损伤模式下具体的计算方法如表1所示,其中${L_{\rm{c}}}$ 表示单元特征尺寸。$ \xi $ 的表达式为式中:
$ {m_{\rm{t}}} $ 和$ {m_{\rm{n}}} $ 分别为STF浸渍Kevlar织物的总质量和其中Kevlar织物的质量。材料的损伤过程被认为是不可逆的,因此,状态变量
${\phi _j}$ 应为时间的单调递增函数,即满足以下关系式式中:t为时间,
$\Delta t $ 为时间的改变量。考虑到不同的损伤模式之间存在损伤耦合现象,引入损伤变量$ {\omega _i} $ 表示这一现象,具体表达式为其中,
${q_{ij}}$ 定义为计算得到材料在不同方向上的
$ {\omega _i} $ 后,可以通过下式计算得到含有损伤变量的柔度矩阵$ {\boldsymbol{S}} $ 式中:
$ {\nu _{12}} $ 、$ {\nu _{23}} $ 、$ {\nu _{31}} $ 、$ {\nu _{13}} $ 、$ {\nu _{21}} $ 、$ {\nu _{32}} $ 为不同方向的泊松比。将柔度矩阵$ {\boldsymbol{S}} $ 求逆即可得到刚度矩阵$ {\boldsymbol{C}} $ ,即更新后的应力
$ \boldsymbol{ \sigma } $ 可由刚度矩阵$ {\boldsymbol{C}}$ 与更新后的应变$ \boldsymbol \varepsilon $ 通过下式得到其中
$ \boldsymbol{ \sigma} $ 与$ \boldsymbol {\varepsilon } $ 具体为 -
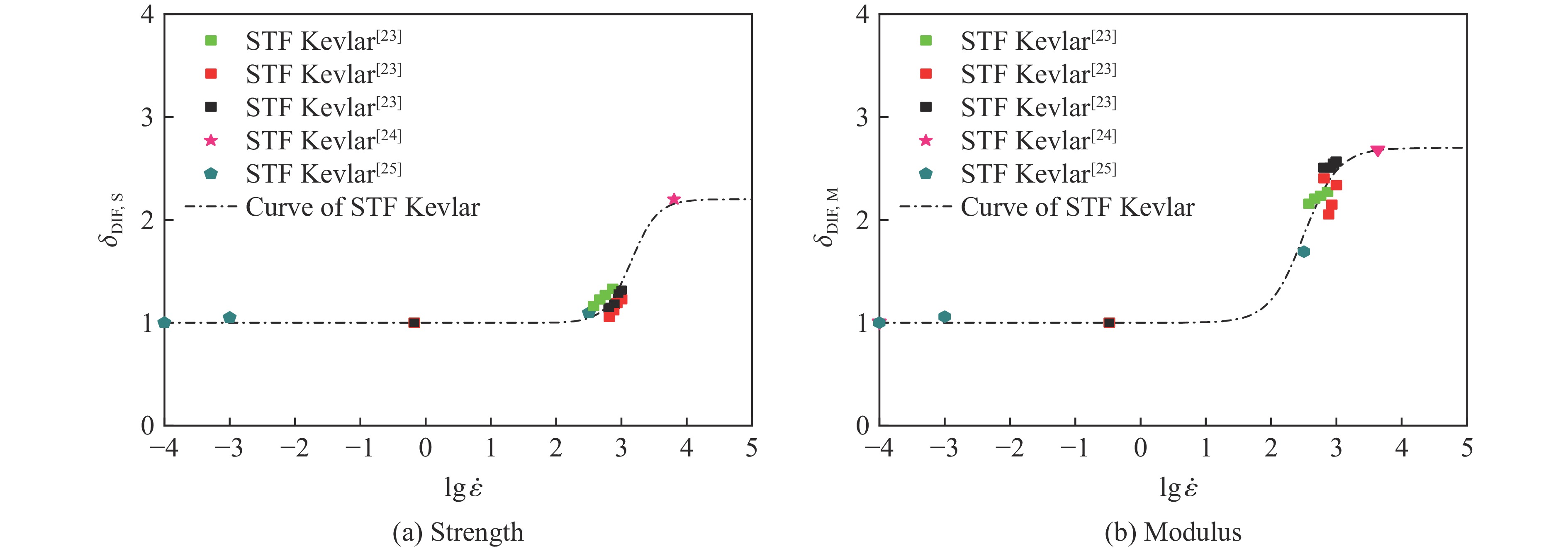
大量实验[23–25]证明,STF浸渍Kevlar织物存着明显的应变率效应。在此,引入动态增强因子(dynamic increase factor, DIF)在统一框架内描述STF浸渍Kevlar织物材料的应变率效应[14–15],动态增强因子(
$\delta_{\rm{DIF}} $ )的具体表达式为式中:A、B、C均为拟合参数;
${\dot \varepsilon _0}$ 为参考应变率,${\dot \varepsilon _0} = 1\,{{\rm{s}}^{ - 1}}$ 。STF浸渍Kevlar织物的强度与模量的DIF曲线如图3所示,可以看到,式(24)的拟合效果良好,其中:AS=3.15,BS=2.5,CS=2.2;AM=2.5,BM=1.9,CM=2.7(下标S表示强度,M表示模量)。
考虑应变率效应后材料的强度和模量分别表示为
式中:SRT、ERT分别为强度、模量的动态值,[S0]、[E0]分别为强度、模量的静态值,
$\delta_{\rm{DIF,\;S}} $ 和$ \delta_{\rm{DIF,\; M}}$ 分别为强度和模量的动态增强因子。[S0]、[E0]具体的分量为式中:
$ {E_{11}} $ 、$ {E_{22}} $ 、$ {E_{33}} $ 为不同方向的弹性模量,$ {G_{12}} $ 、$ {G_{23}} $ 、$ {G_{31}} $ 为不同方向的剪切模量,$ {X_{\rm{t}}} $ 、$ {Y_{\rm{t}}} $ 、$ {Z_{\rm{t}}} $ 为不同方向的拉伸强度;$ {X_{\rm{c}}} $ 、$ {Y_{\rm{c}}} $ 、$ {Z_{\rm{c}}} $ 为不同方向的压缩强度;$ {S_{12}} $ 、$ {S_{23}} $ 、$ {S_{31}} $ 为不同方向的剪切强度。上述动态本构模型可以通过用户材料子程序(VUMAT)编程实现,将其嵌入有限元软件 ABAQUS/Explicit中,具体的数值算法如图4所示。首先,通过ABAQUS/Explicit主程序计算应变增量(
$\Delta\varepsilon $ );然后,将应变增量传递给用户子程序,子程序读取输入文件的材料参数,并根据流程图更新应变和应力;最后,将应变和应力返回主程序中,完成当前时间步长的计算。 -
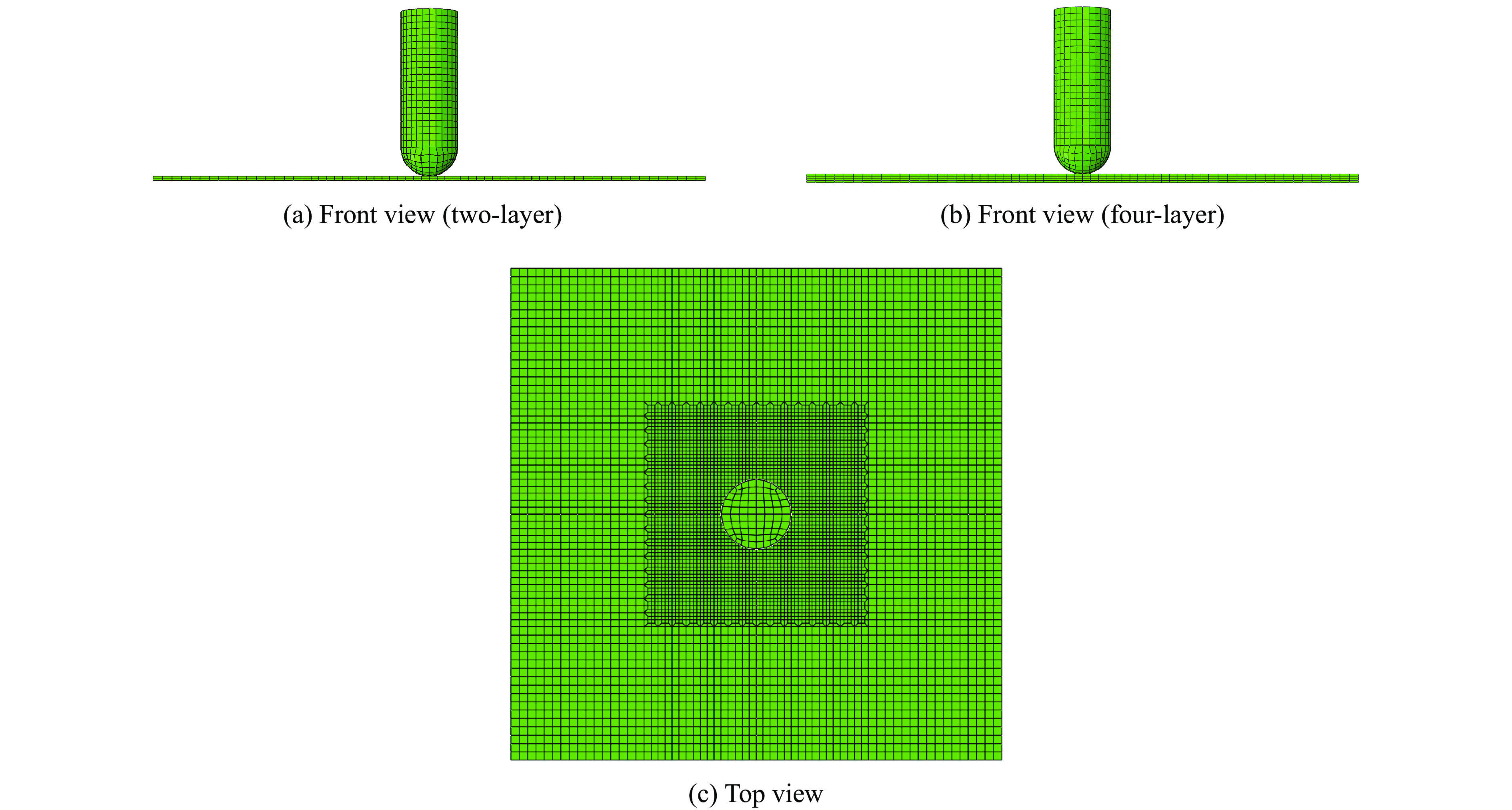
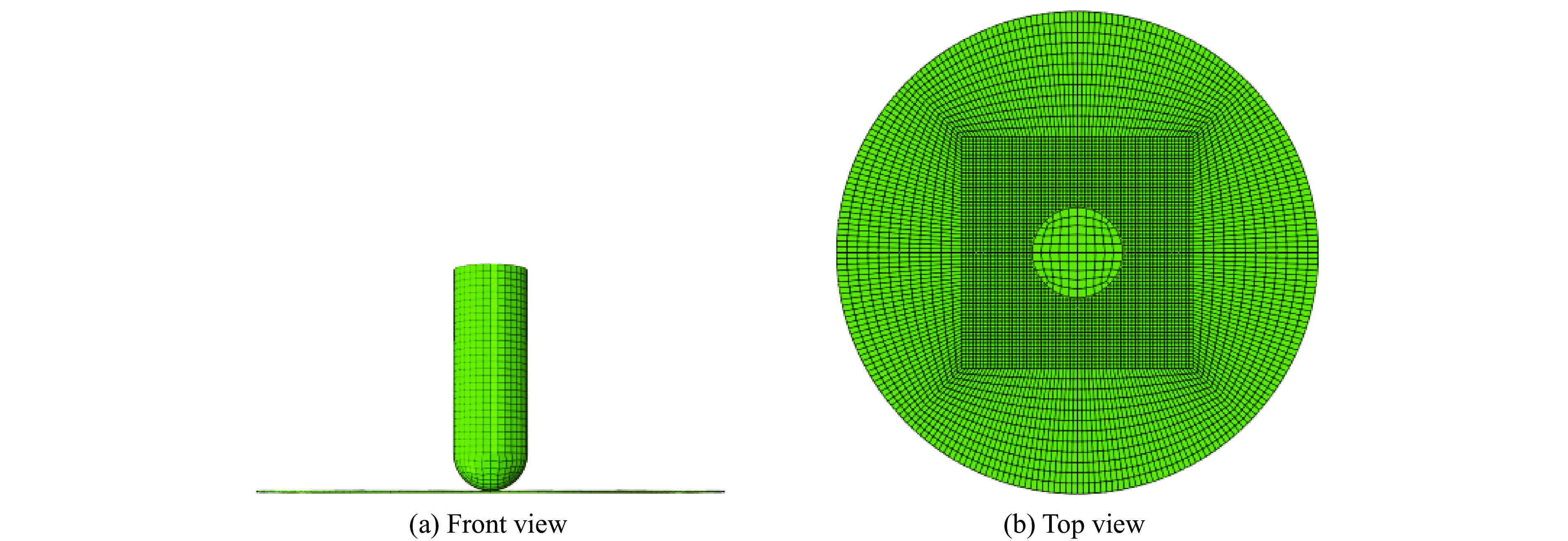
Khodadadi等[26]对STF浸渍Kevlar织物进行了弹道冲击实验,根据实验描述建立有限元模型,如图5所示。半球头型弹的直径为8.74 mm,质量m=11.18 g,简化为刚体。织物在建模中视为连续均匀的薄板,尺寸为70 mm×70 mm。为节省计算时间,对织物中部30 mm×30 mm的冲击区域进行网格加密,单元尺寸为0.5 mm×0.5 mm,其余区域的单元尺寸为1.0 mm×1.0 mm,每层织物厚度方向划分为一层单元,尺寸为0.28 mm。织物四周施加固支(ENCASTRE)约束,弹体在运动过程中不允许转动,弹体与织物、织物与织物之间均采用通用接触(general contact),摩擦因数为0.25。
通过实验[23, 25, 27]证明,STF浸渍Kevlar织物与纯Kevlar织物的静态材料力学性能无明显差异,因此,在数值模拟中,STF浸渍Kevlar织物的材料参数可由纯Kevlar织物的材料参数代替,如表2所示。
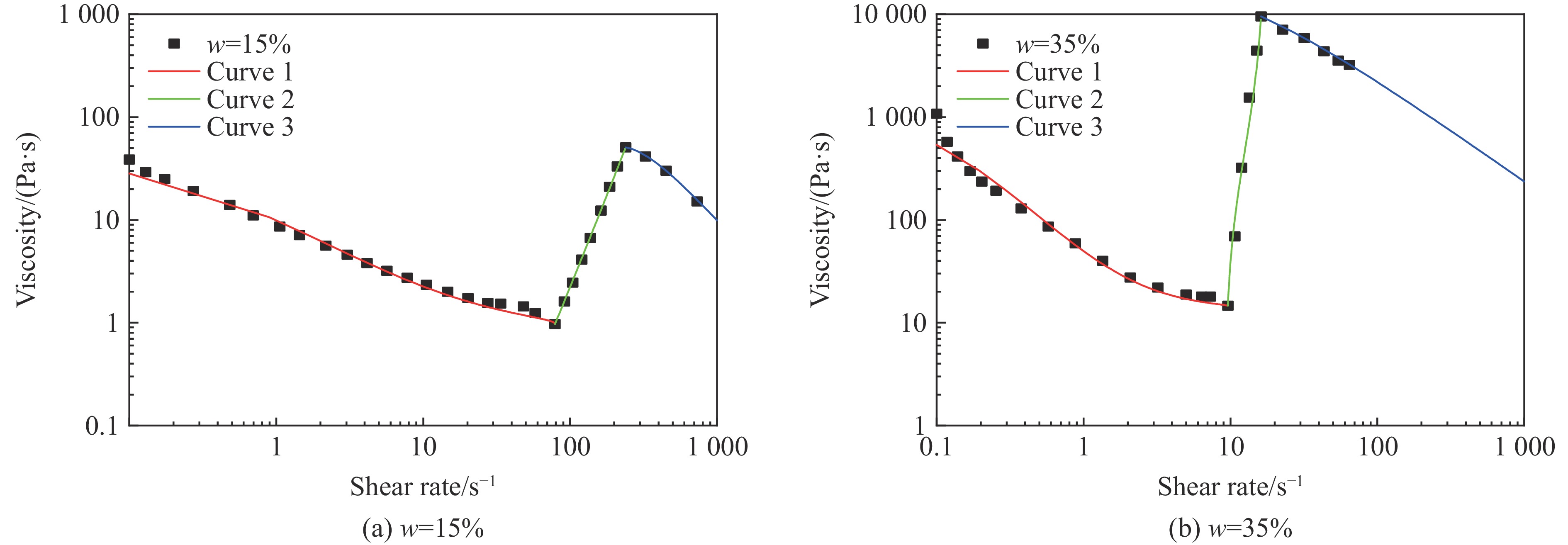
使用式(9)拟合得到STF流变特性的各参数,如表3所示,其中:w为STF中SiO2的质量分数。拟合曲线与流变实验结果的对比如图6所示,可以看到,两者具有很好的一致性。
不同STF浸渍Kevlar织物的密度存在差异,在数值模拟中设置为对应的密度,计算公式为
式中:
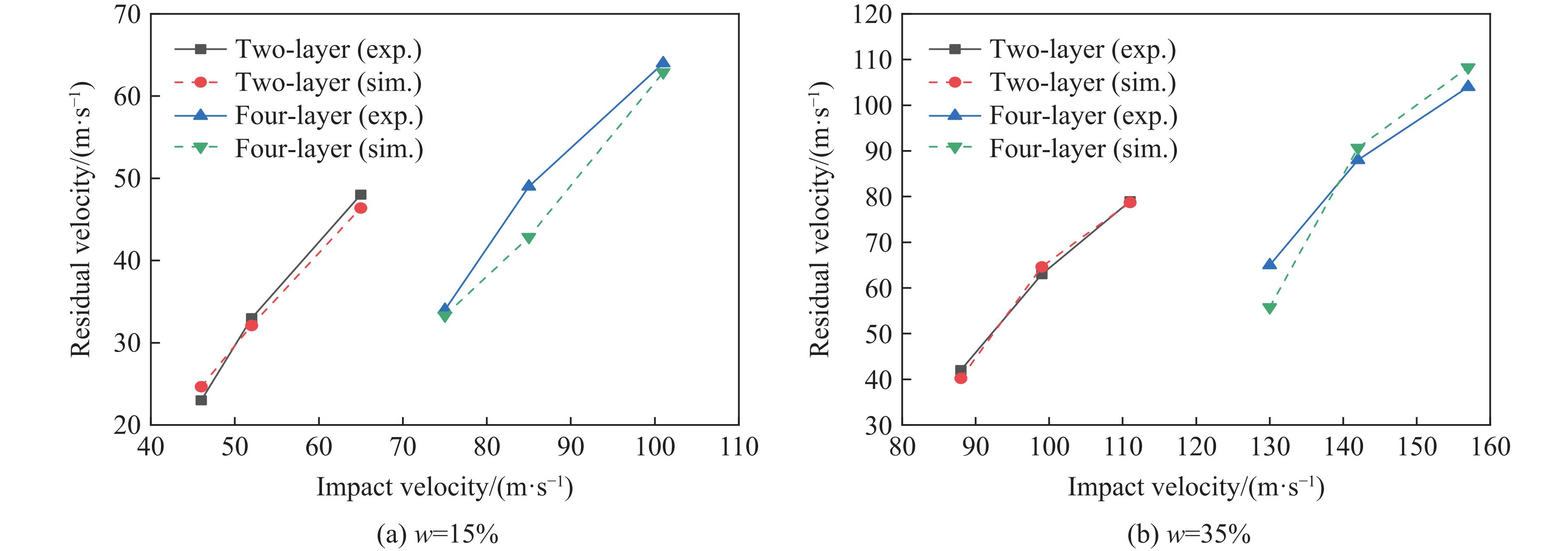
$\rho $ 为织物密度;${\rho _{\rm{areal}}}$ 为织物面密度;$ T $ 为织物厚度,1层织物的厚度为0.28 mm。本例模拟过程中使用的各材料参数如表4所示。数值模拟得到的残余速度与实验结果的对比如图7所示,可以看到两者吻合较好。破坏形貌的对比如图8所示,可以看到,数值模拟得到的破坏形貌、整体变形程度与实验结果相似。
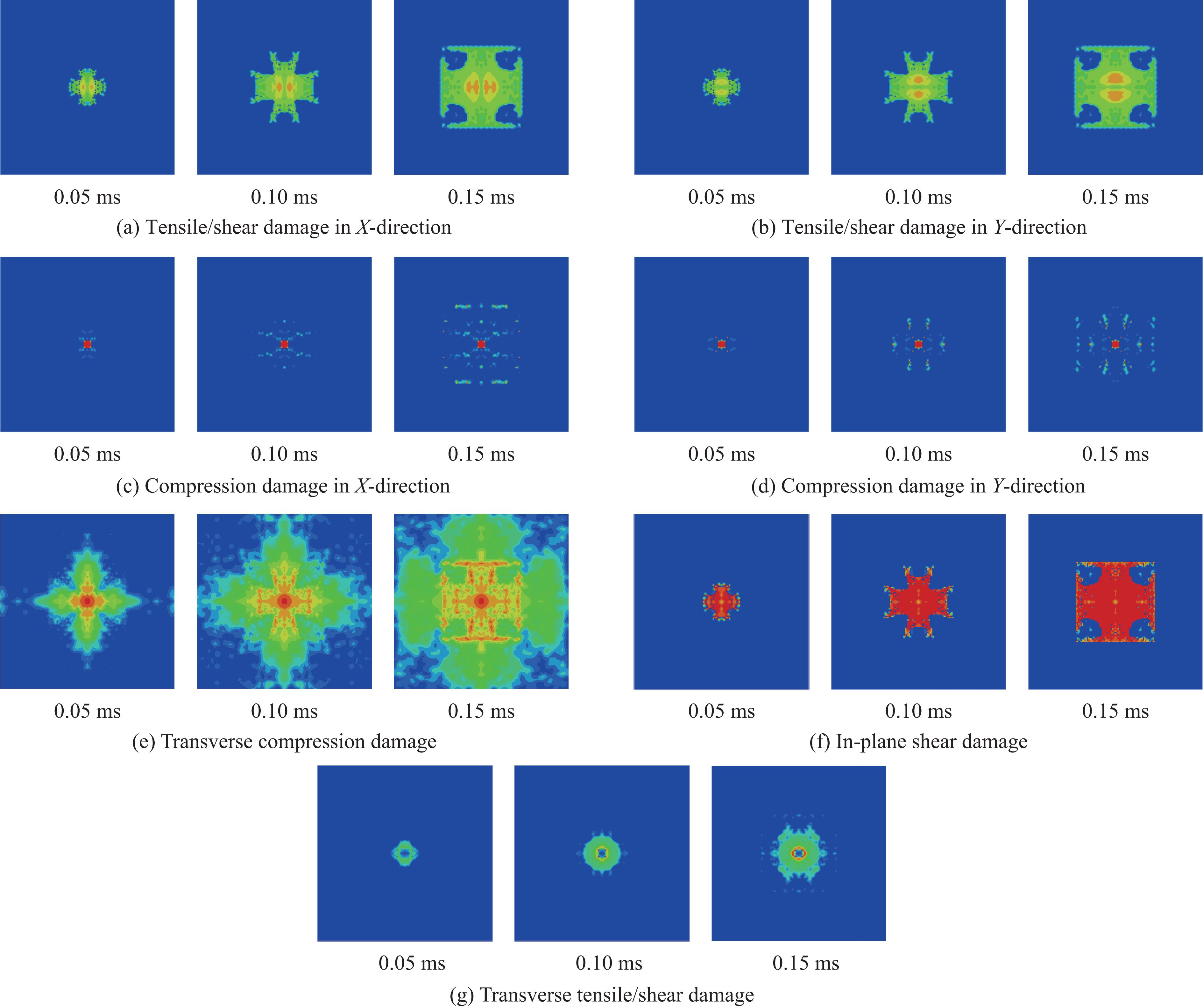
以w=15%的STF浸渍Kevlar织物受到75 m/s的冲击速度为例,不同损伤模式的损伤云图如图9所示,其中标尺统一,因为设置了损伤极限为0.444,所以从蓝色到红色代表损伤范围为0~0.444,为对比损伤区域的大小,不显示变形。从图9可以看到,不同损伤模式的损伤面积均随着冲击时间的增加而增大,拉伸/剪切损伤模式的损伤面积始终大于压缩损伤模式的损伤面积。该结果与Liao等[14]的结果具有相似之处,表明STF浸渍Kevlar织物在受到冲击载荷时以拉伸/剪切损伤为主。
-
Xie等[35]开展了STF浸渍Kevlar织物的低速冲击实验,建立了如图10所示的有限元模型。其中落锤冲头是直径为16 mm、质量为2.5 kg的半球头型弹,在建模中简化为刚体。织物被直径为100 mm的圆形夹具固定。为节省计算时间,仅对部分织物进行建模,织物四周施加固支(ENCASTRE)约束以模拟实验条件,对织物中部48 mm×48 mm的冲击区域进行网格加密,单元尺寸为0.75 mm×0.75 mm,每层织物厚度方向划分为一层单元,尺寸为0.28 mm。设置弹体在运动过程中不转动,弹体与织物、织物与织物之间均采用通用接触,摩擦因数为0.25。
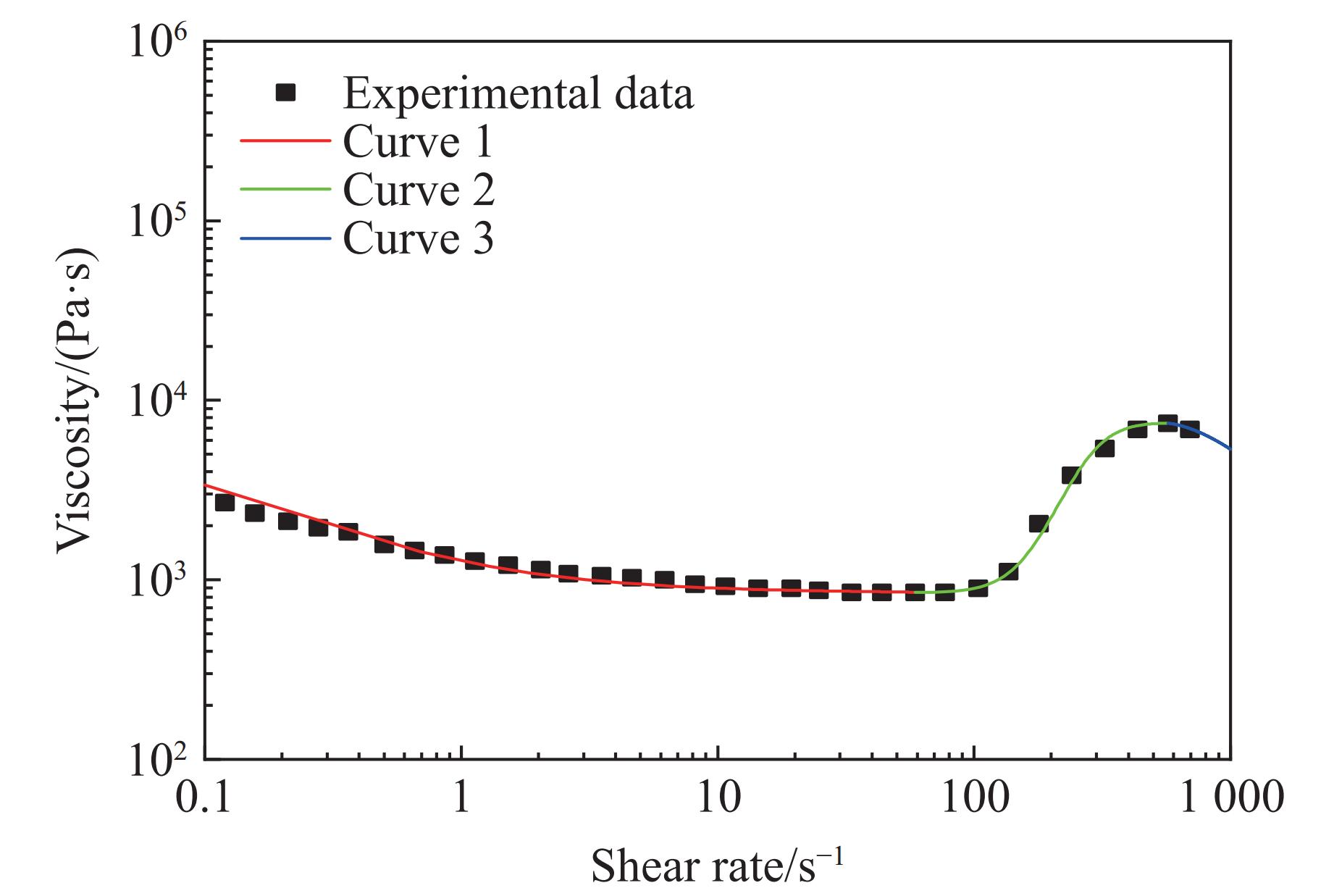
STF的流变特性使用式(9)进行拟合。各参数取值如表5[35]所示,拟合曲线与流变实验结果的对比如图11所示,可以看到,拟合结果与实验数据相符。
模拟中所用的材料参数如表6[35–36]所示,其中
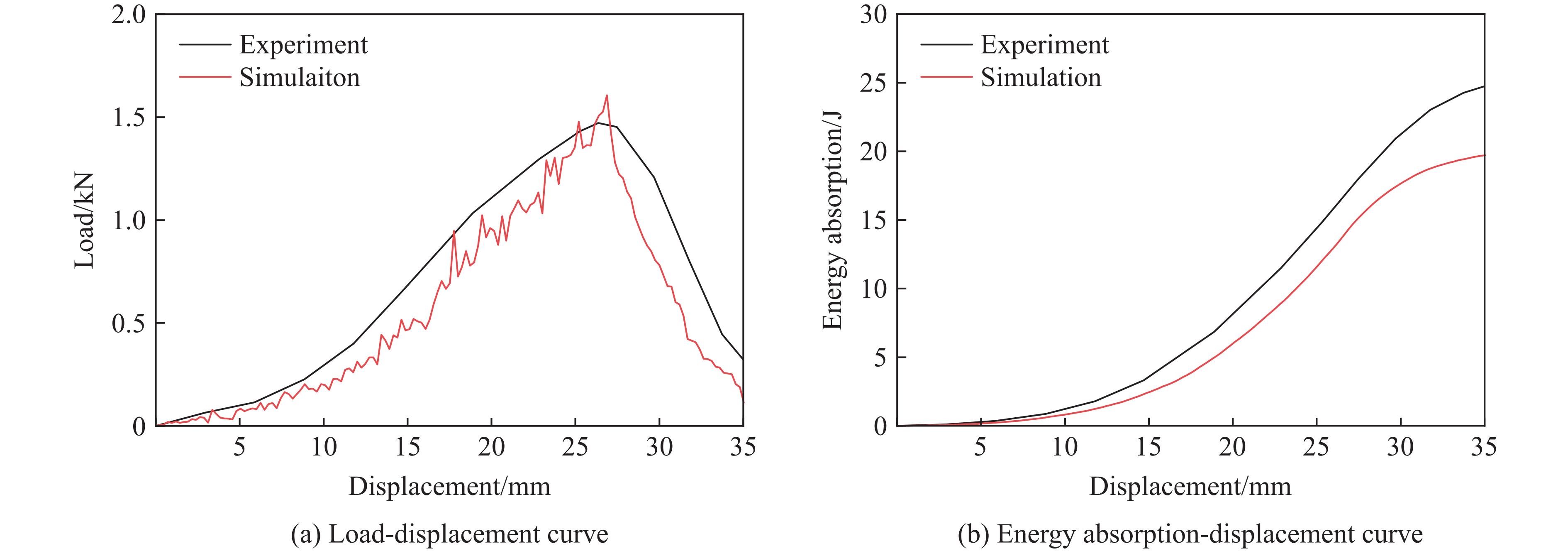
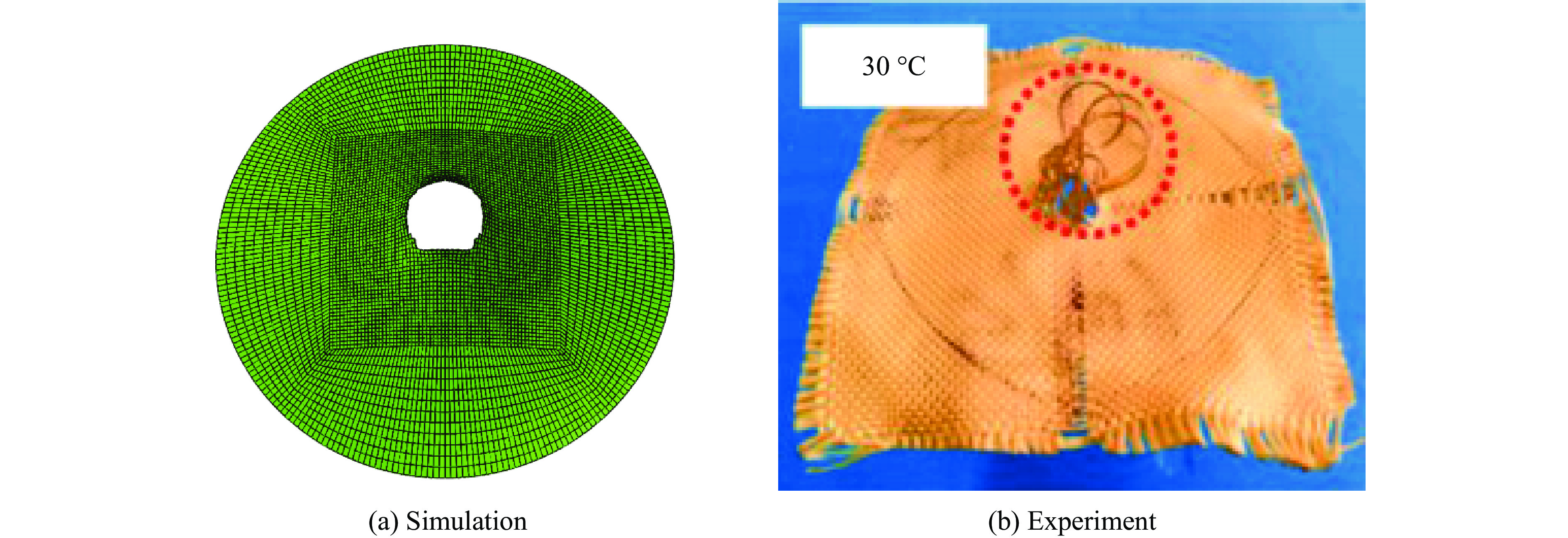
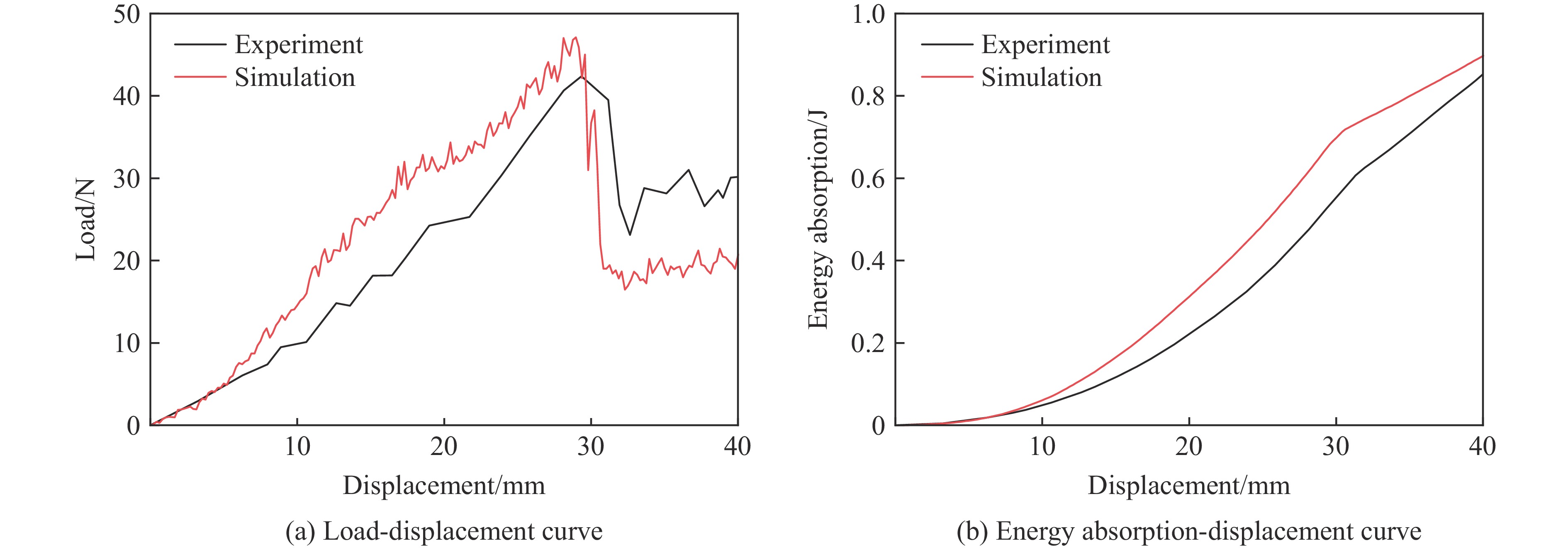
$ k $ 值可以通过Qin等[36]的实验得到。STF浸渍Kevlar织物的低速冲击数值模拟的载荷-位移曲线、能量吸收-位移曲线与实验结果的对比如图12所示。从图12可以看出,数值模拟的载荷-位移曲线与实验结果相符,整个冲击过程中能量吸收与实验结果的相对误差基本维持在20%左右。数值模拟得到的STF浸渍Kevlar织物受到低速冲击时的破坏形貌与实验结果的对比如图13所示,可以看到,两者均在织物的中心区域出现一个明显的圆形缺口,由于所建模型为宏观模型,纱线的一些行为无法得到很好的体现。
-
Qin等[36]针对STF浸渍Kevlar织物开展了准静态穿刺实验,根据实验表述建立有限元模型,如图14所示。其中,刀具全长为100 mm,宽度为20 mm,厚度为4 mm,在模拟过程中视为刚体。织物被直径为80 mm的圆形夹具固定。为节省计算时间,仅对该部分织物进行建模,织物四周施加固支(ENCASTRE)约束以模拟该实验条件,对织物中部30 mm×30 mm的冲击区域进行网格加密,单元尺寸为0.5 mm×0.5 mm,每层织物厚度方向划分为一层单元,尺寸为0.28 mm。设置刀具在运动过程中不转动,弹体与织物、织物与织物之间均采用通用接触,摩擦因数为0.25。
采用式(9)拟合STF的流变特性。各参数取值如表7[36]所示,拟合曲线与流变实验结果的对比如图15所示,可以看到,拟合结果与实验数据具有一致性。
STF浸渍Kevlar织物的准静态刺入数值模拟的载荷-位移曲线、能量吸收-位移曲线与实验结果的对比如图16所示。可以看到,数值模拟得到的载荷-位移曲线与实验结果相符,整个穿刺过程中的能量吸收与实验结果的相对误差基本维持在15%。
数值模拟得到的STF浸渍Kevlar织物破坏形貌与实验结果的对比如图17所示,可以看到,两者形成的织物缺口相似,都呈现椭圆形。
-
基于先前的研究,通过引入动态增强因子(应变率效应)和残余强度因子,结合 STF的流变特性与纱线拔出实验结果,发展了STF浸渍Kevlar织物的连续介质损伤力学动态本构模型。利用建立的本构模型开展了不同冲击速度下STF浸渍Kevlar织物侵彻的数值模拟,并与弹道冲击、低速冲击、准静态穿刺实验结果进行了对比,得到如下主要结论:
(1)所发展的动态本构模型能较好地预测STF浸渍Kevlar织物的冲击响应;
(2) STF浸渍后Kevlar织物抗冲击性能的增强效应主要通过本构模型中的动态增强因子和残余强度因子实现,这2个因子与STF的流变特性和纱线拔出力有关;
(3) 数值模拟结果与实验得到的残余速度、峰值载荷和能量吸收数据吻合较好,相对误差分别在10%、10%和20%以内。
剪切增稠液浸渍凯夫拉织物的动态本构模型
A Dynamic Constitutive Model for Shear Thickening Fluid Impregnated Kevlar Fabric
-
摘要: 剪切增稠液(shear thickening fluid, STF)浸渍凯夫拉(Kevlar)织物是一种新型复合材料,相比纯Kevlar织物,具有更好的抗冲击性能,研究其动态本构模型具有重要的理论意义和应用价值。首先,通过引入动态增强因子(应变率效应)和残余强度因子,结合STF的流变特性和纱线拔出实验结果,发展了STF浸渍Kevlar织物的连续介质损伤力学本构模型;然后,利用提出的本构模型,开展了不同冲击速度下STF浸渍Kevlar织物侵彻的数值模拟;最后,将模拟结果与文献中的相关实验结果进行对比分析。结果表明:所建立的本构模型能够预测STF浸渍Kevlar织物在冲击载荷作用下的力学响应和破坏形貌,并且能够描述STF浸渍后Kevlar织物抗冲击性能的增强效应。
-
关键词:
- 剪切增稠液 /
- Kevlar织物 /
- 连续介质损伤力学本构模型 /
- 流变特性 /
- 纱线间摩擦
Abstract: Shear thickening fluid (STF) impregnated Kevlar fabric is a new type of composite materials which has better impact resistance as compared with neat Kevlar fabric. On the basis of previous work, a dynamic constitutive model for STF impregnated Kevlar fabric is firstly developed by introducing dynamic increase factor (strain rate effect) and residual strength factor in combination with the rheological properties of STF and yarn pull out test results. Numerical simulations of STF impregnated Kevlar fabric at different impact velocities are then conducted using the proposed constitutive model. Finally, the numerical results are compared with the relevant experimental data. It is shown that the present constitutive model can predict well the impact response of STF impregnated Kevlar fabrics in terms of residual velocity, load-displacement curve and damage morphology, lending support to the accuracy and usefulness of the dynamic constitutive model for STF impregnated Kevlar fabric. -

-
Damage mode ${\delta _{j,{\rm{eq}}}}$ ${\sigma _{j,{\rm{eq}}}}$ Tensile/shear damage in X-direction ${L_{\rm{c}}}\sqrt {{{\left\langle {{\varepsilon _{11}}} \right\rangle }^2}+{{{{\gamma _{12}^2}} }}+{{ {{\gamma _{31}^2}} }}} $ ${L_{\rm{c}}}\left( {{E_{11}}{{\left\langle {{\varepsilon _{11}}} \right\rangle }^2}+{G_{12}}{{{{\gamma _{12}^2}} }}+{G_{31}}{{{{\gamma _{31}^2}} }}} \right)/{\delta _{\rm{1,eq}}}$ Tensile/shear damage in Y-direction ${L_{\rm{c}}}\sqrt {{{\left\langle {{\varepsilon _{22}}} \right\rangle }^2}+{{ {{\gamma _{12}^2}} }}+{{ {{\gamma _{23}^2}} }}} $ ${L_{\rm{c}}}\left( {{E_{22}}{{\left\langle {{\varepsilon _{22}}} \right\rangle }^2}+{G_{12}}{{ {{\gamma _{12}^2}} }}+{G_{23}}{{{{\gamma _{23}^2}}}}} \right)/{\delta _{\rm{2,eq}}}$ Compression damage in X-direction ${L_{\rm{c}}}\sqrt {{{\left\langle {{{\varepsilon }_{11}'}} \right\rangle }^2}} $ ${L_{\rm{c}}}\left( {{E_{11}}{{\left\langle {{{\varepsilon}_{11} '}} \right\rangle }^2}} \right)/{\delta _{\rm{3,eq}}}$ Compression damage in Y-direction ${L_{\rm{c}}}\sqrt {{{\left\langle {{{\varepsilon }_{22}'}} \right\rangle }^2}} $ ${L_{\rm{c}}}\left( {{E_{22}}{{\left\langle {{{\varepsilon }_{22}'}} \right\rangle }^2}} \right)/{\delta _{\rm{4,eq}}}$ Transverse compression damage ${L_{\rm{c}}}\sqrt {{{\left\langle {{{\varepsilon }_{33}'}} \right\rangle }^2}} $ ${L_{\rm{c}}}\left( {{E_{33}}{{\left\langle {{{\varepsilon }_{33}'}} \right\rangle }^2}} \right)/{\delta _{\rm{5,eq}}}$ In-plane shear damage ${L_{\rm{c}}}\sqrt {{{{{\gamma _{12}^2}} }}} $ ${L_{\rm{c}}}\left( {{G_{12}}{{ {{\gamma _{12}^2}} }}} \right)/{\delta _{\rm{6,eq}}}$ Transverse tensile/shear damage ${L_{\rm{c}}}\sqrt {{{\left\langle {{\varepsilon _{33}}} \right\rangle }^2}+{{{{\gamma _{23}^2}} }}+{{{{\gamma _{31}^2}} }}} $ ${L_{\rm{c}}}\left( {{E_{33}}{{\left\langle {{\varepsilon _{33}}} \right\rangle }^2}+{G_{23}}{{ {{\gamma _{23}^2}} }}+{G_{31}}{{ {{\gamma _{31}^2}} }}} \right)/{\delta _{\rm{7,eq}}}$ 表 2 数值模拟中STF浸渍Kevlar织物的材料参数[23, 28–34]
Table 2. Material parameters of STF impregnated Kevlar fabric in the numerical simulations[23, 28–34]
E11/GPa E22/GPa E33/GPa G12/GPa G23/GPa G31/GPa ${\nu _{12}}$ ${\nu _{23}}$ ${\nu _{31}}$ 70 70 7 16.4 1.8 1.8 0.33 0.40 0.40 Xt/MPa Yt/MPa Zt/MPa Xc/MPa Yc/MPa Zc/MPa S12/MPa S23/MPa S31/MPa 2 758 2 758 24 580 580 60 180 180 180 表 3 弹道冲击实验中STF流变特性的拟合参数[26]
Table 3. Parameters for fitting the rheological properties of STF used in ballistic impact experiments[26]
w/% ${\eta _0}/({\rm{Pa}} \cdot{\rm{ s}})$ ${\eta _{\rm{c}}}/({\rm{Pa}} \cdot{\rm{ s}})$ ${\eta _{\rm{max}}}/({\rm{Pa}} \cdot{\rm{ s}})$ ${\dot \gamma _{\rm{c}}}$ /s−1${\dot \gamma _{\rm{max}}}$ /s−1KⅠ KⅡ KⅢ nⅠ nⅡ nⅢ 15 38.775 0.972 50.624 78.952 238.946 −1 000 −0.001 7 0.003 6 0.46 1.0 1.4 35 1 078.201 14.663 9 540.340 9.603 16.151 −1 000 −0.006 5 0.040 0 0.71 1.1 1.0 表 4 弹道冲击实验中数值模拟的材料参数[26]
Table 4. Material parameters for the numerical simulations of ballistic impact experiments[26]
w/% $ {\rho _{\rm{areal}}} $ /(kg·m−2)$ {f_{\rm{rs0}}} $ $ k $ $ \xi $ 15 0.523 0.4 0.272 0.444 35 0.722 0.4 0.957 0.321 表 5 低速冲击实验中STF流变特性的拟合参数[35]
Table 5. Parameters for fitting the rheological properties of STF used in low velocity impact experiments[35]
${\eta _0}/({\rm{Pa}} \cdot{\rm{ s}})$ ${\eta _{\rm{c}}}/({\rm{Pa}} \cdot{\rm{ s}})$ ${\eta _{\rm{max}}}/({\rm{Pa}} \cdot{\rm{ s}})$ ${\dot \gamma _{\rm{c}}}$ /s−1${\dot \gamma _{\rm{max}}}$ /s−1KⅠ KⅡ KⅢ nⅠ nⅡ nⅢ 20.677 5.26 362 54.5 164.725 −5 −0.02 0.005 0.7 1.2 2.0 Table 6. Material parameters for the numerical simulations of low velocity impact experiments[35–36]
$ {\rho _{\rm{{areal}}}} $ /(kg·m−2)$ {f_{\rm{rs0}}} $ $ k $ $ \xi $ 0.3032 0.16 0.814 0.796 表 7 准静态穿刺实验中STF流变特性的拟合参数[36]
Table 7. Parameters for fitting the rheological properties of STF used in quasi-static puncture experiments[36]
${\eta _0}/({\rm{Pa}} \cdot {\rm{s}})$ ${\eta _{\rm{c}}}/({\rm{Pa}} \cdot{\rm{ s}})$ ${\eta _{\rm{max}}}/({\rm{Pa}} \cdot{\rm{ s}})$ ${\dot \gamma _{\rm{c}}}$ /s−1${\dot \gamma _{\rm{max}}}$ /s−1KⅠ KⅡ KⅢ nⅠ nⅡ nⅢ 2845 852 7449 58.808 570.207 − 20000 −0.006 0.0012 0.47 1.7 1.4 -
[1] LI T T, DAI W N, WU L W, et al. Effects of STF and fiber characteristics on quasi-static stab resistant properties of shear thickening fluid (STF)-impregnated UHMWPE/Kevlar composite fabrics [J]. Fibers and Polymers, 2019, 20(2): 328–336. doi: 10.1007/s12221-019-8446-6 [2] LIU L L, YANG Z Z, ZHAO Z H, et al. The influences of rheological property on the impact performance of Kevlar fabrics impregnated with SiO2/PEG shear thickening fluid [J]. Thin-Walled Structures, 2020, 151: 106717. doi: 10.1016/j.tws.2020.106717 [3] LIU B, LIU Q, PAN Y C, et al. An impact-resistant and flame-retardant CNTs/STF/Kevlar composite with conductive property for safe wearable design [J]. Composites Part A: Applied Science and Manufacturing, 2023, 168: 107489. doi: 10.1016/j.compositesa.2023.107489 [4] MAWKHLIENG U, MAJUMDAR A. Deconstructing the role of shear thickening fluid in enhancing the impact resistance of high-performance fabrics [J]. Composites Part B: Engineering, 2019, 175: 107167. doi: 10.1016/j.compositesb.2019.107167 [5] MAJUMDAR A, LAHA A. Effects of fabric construction and shear thickening fluid on yarn pull-out from high-performance fabrics [J]. Textile Research Journal, 2016, 86(19): 2056–2066. doi: 10.1177/0040517515619357 [6] LI D Y, WANG R, LIU X, et al. Shear-thickening fluid using oxygen-plasma-modified multi-walled carbon nanotubes to improve the quasi-static stab resistance of Kevlar fabrics [J]. Polymers, 2018, 10(12): 1356. doi: 10.3390/polym10121356 [7] QIN J B, GUO B R, ZHANG L, et al. Soft armor materials constructed with Kevlar fabric and a novel shear thickening fluid [J]. Composites Part B: Engineering, 2020, 183: 107686. doi: 10.1016/j.compositesb.2019.107686 [8] LIU M, ZHANG S S, LIU S, et al. CNT/STF/Kevlar-based wearable electronic textile with excellent anti-impact and sensing performance [J]. Composites Part A: Applied Science and Manufacturing, 2019, 126: 105612. doi: 10.1016/j.compositesa.2019.105612 [9] KORDANI N, VANINI A S, AMIRI H. Numerical solution of penetration into woven fabric target impregnated with shear thickening fluid [J]. Polymers and Polymer Composites, 2016, 24(4): 281–287. doi: 10.1177/096739111602400407 [10] KHODADADI A, LIAGHAT G H, SABET A R, et al. Experimental and numerical analysis of penetration into Kevlar fabric impregnated with shear thickening fluid [J]. Journal of Thermoplastic Composite Materials, 2018, 31(3): 392–407. doi: 10.1177/0892705717704485 [11] SEN S, BIN JAMAL M N, SHAW A, et al. Numerical investigation of ballistic performance of shear thickening fluid (STF)-Kevlar composite [J]. International Journal of Mechanical Sciences, 2019, 164: 105174. doi: 10.1016/j.ijmecsci.2019.105174 [12] XIE Z H, CHEN W, LIU Y Y, et al. Design of the ballistic performance of shear thickening fluid (STF) impregnated Kevlar fabric via numerical simulation [J]. Materials & Design, 2023, 226: 111599. doi: 10.1016/j.matdes.2023.111599 [13] LIU L L, CAI M, LUO G, et al. Macroscopic numerical simulation method of multi-phase STF-impregnated Kevlar fabrics. part 2: material model and numerical simulation [J]. Composite Structures, 2021, 262: 113662. doi: 10.1016/j.compstruct.2021.113662 [14] LIAO J B, WEN H M. A constitutive model for shear thickening fluid (STF) impregnated Kevlar fabric subjected to impact loading [J]. International Journal of Impact Engineering, 2024, 191: 104990. doi: 10.1016/j.ijimpeng.2024.104990 [15] XIN S H, WEN H M. A progressive damage model for fiber reinforced plastic composites subjected to impact loading [J]. International Journal of Impact Engineering, 2015, 75: 40–52. doi: 10.1016/j.ijimpeng.2014.07.014 [16] GALINDO-ROSALES F J, RUBIO-HERNÁNDEZ F J, SEVILLA A. An apparent viscosity function for shear thickening fluids [J]. Journal of Non-Newtonian Fluid Mechanics, 2011, 166(5/6): 321–325. doi: 10.1016/j.jnnfm.2011.01.001 [17] 王敏, 文鹤鸣. 碳纳米管/碳纤维增强复合材料层合板低速冲击响应和破坏的数值模拟 [J]. 爆炸与冲击, 2022, 42(3): 033102. doi: 10.11883/bzycj-2021-0050 WANG M, WEN H M. Numerical simulations of response and failure of carbon nanotube/carbon fibre reinforced plastic laminates under impact loading [J]. Explosion and Shock Waves, 2022, 42(3): 033102. doi: 10.11883/bzycj-2021-0050 [18] LIAO J B, WANG M, WEN H M. A dynamic constitutive model for carbon nanotubes (CNTs) modified unidirectional fibre reinforced plastic laminates [J]. International Journal of Impact Engineering, 2024, 183: 104793. doi: 10.1016/j.ijimpeng.2023.104793 [19] BAI R X, LI W K, LEI Z K, et al. Experimental study of yarn friction slip and fabric shear deformation in yarn pull-out test [J]. Composites Part A: Applied Science and Manufacturing, 2018, 107: 529–535. doi: 10.1016/j.compositesa.2018.02.001 [20] BAI R X, MA Y, LEI Z K, et al. Shear deformation and energy absorption analysis of flexible fabric in yarn pullout test [J]. Composites Part A: Applied Science and Manufacturing, 2020, 128: 105678. doi: 10.1016/j.compositesa.2019.105678 [21] LEE B W, KIM I J, KIM C G. The influence of the particle size of silica on the ballistic performance of fabrics impregnated with silica colloidal suspension [J]. Journal of Composite Materials, 2009, 43(23): 2679–2698. doi: 10.1177/0021998309345292 [22] PARK J L, YOON B I, PAIK J G, et al. Ballistic performance of p-aramid fabrics impregnated with shear thickening fluid; part I–effect of laminating sequence [J]. Textile Research Journal, 2012, 82(6): 527–541. doi: 10.1177/0040517511420753 [23] LIU L L, CAI M, LUO G, et al. Macroscopic numerical simulation method of multi-phases STF impregnated Kevlar fabrics. part 1: quasi-static and dynamic mechanical test [J]. Composite Structures, 2021, 266: 113780. doi: 10.1016/j.compstruct.2021.113780 [24] CAO S S, CHEN Q, WANG Y P, et al. High strain-rate dynamic mechanical properties of Kevlar fabrics impregnated with shear thickening fluid [J]. Composites Part A: Applied Science and Manufacturing, 2017, 100: 161–169. doi: 10.1016/j.compositesa.2017.04.015 [25] LIU L L, YANG Z Z, LIU X, et al. Yarn dynamic tensile behavior and meso-scale numerical simulation method for STF-Kevlar fabrics [J]. Thin-Walled Structures, 2021, 159: 107319. doi: 10.1016/j.tws.2020.107319 [26] KHODADADI A, LIAGHAT G, VAHID S, et al. Ballistic performance of Kevlar fabric impregnated with nanosilica/PEG shear thickening fluid [J]. Composites Part B: Engineering, 2019, 162: 643–652. doi: 10.1016/j.compositesb.2018.12.121 [27] MA Y, HONG X, LEI Z K, et al. Shear response behavior of STF/Kevlar composite fabric in picture frame test [J]. Polymer Testing, 2022, 113: 107652. doi: 10.1016/j.polymertesting.2022.107652 [28] NATH R B, FENNER D N, GALIOTIS C. Elasto-plastic finite element modelling of interfacial failure in model Kevlar 49 fibre-epoxy composites [J]. Composites Part A: Applied Science and Manufacturing, 1996, 27(9): 821–832. doi: 10.1016/1359-835X(96)00053-X [29] ZHENHUA Z, LULU L, WEI C, et al. Numerical simulation methodology of multi-layer Kevlar 49 woven fabrics in aircraft engine containment application [J]. International Journal of Crashworthiness, 2019, 24(1): 86–99. doi: 10.1080/13588265.2017.1422374 [30] DETERESA S J, ALLEN S R, FARRIS R J, et al. Compressive and torsional behaviour of Kevlar 49 fibre [J]. Journal of Materials Science, 1984, 19(1): 57–72. doi: 10.1007/BF02403111 [31] YEUNG K K H, RAO K P. Mechanical properties of Kevlar-49 fibre reinforced thermoplastic composites [J]. Polymers and Polymer Composites, 2012, 20(5): 411–424. doi: 10.1177/096739111202000501 [32] FISCHER M, SCHMID R. Matrix properties and composite failure [J]. Colloid and Polymer Science, 1986, 264(5): 387–398. doi: 10.1007/BF01419542 [33] LEAL A A, DEITZEL J M, GILLESPIE JR J W. Compressive strength analysis for high performance fibers with different modulus in tension and compression [J]. Journal of Composite Materials, 2009, 43(6): 661–674. doi: 10.1177/0021998308088589 [34] HUANG J Z, LI Q H, YANG Q, et al. Measurement and research of the transverse mechanical properties of high performance fibers [J]. Key Engineering Materials, 2011, 492: 384–387. doi: 10.4028/www.scientific.net/KEM.492.384 [35] XIE Z H, LIU Y Y, LIU L L, et al. Research on the adaptability of STF-Kevlar to ambient temperature under low-velocity impact conditions [J]. Polymer Testing, 2024, 133: 108416. doi: 10.1016/j.polymertesting.2024.108416 [36] QIN J B, WANG T W, YUN J, et al. Response and adaptability of composites composed of the STF-treated Kevlar fabric to temperature [J]. Composite Structures, 2021, 260: 113511. doi: 10.1016/j.compstruct.2020.113511 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: