楼梯作为建筑空间中连接垂直层级的核心通道, 其行人运动的高效性与安全性直接关系公共场所的疏散能力与运行秩序. 然而, 楼梯几何结构的非均匀性(如台阶高度、踏板深度)与行人步行运动的动态耦合, 使得该场景下的运动建模面临显著挑战. 尤其在高峰时段或紧急情况下, 行人间的物理接触与局部拥挤易引发跌倒、踩踏等风险. 因此, 构建高保真度的楼梯行人运动模型, 揭示其动态稳定性机制与群体交互规律, 对优化建筑布局^[1,2]、制定智能疏散策略^[3,4]具有重要理论与应用价值.

在行人运动建模领域, 国内外学者已提出多种经典框架. 宏观层面, 流体动力学模型通过类比人群流动与连续介质运动, 揭示了密度-速度的基本关系^[5,6]; 微观层面, 社会力模型^[7–9]、元胞自动机模型^[10–12]等成为人群仿真领域的里程碑成果. 然而, 上述模型多针对平面环境设计, 难以直接适用于楼梯场景的三维几何约束. 近年来, 元胞自动机^[13–17]与基于Agent的模型^[18–20]通过离散化空间与规则驱动行为, 在楼梯仿真中取得一定进展. 例如, 金辉和郭仁拥^[21]提出的元胞传输模型描述了楼梯区域行人路径选择, 但未考虑三维空间中的稳定性约束与步态异步性问题. Wang等^[22]考虑了楼梯配置描述行人运动, Huo等^[23]使用扩展晶格气体模型分析平面-楼梯的行人合并流, 但未对大规模群体中行人稳定性进一步分析. 这些不足制约了模型在安全评估与应急管理中的实际应用.

针对上述问题, 本文提出一种双层空间耦合的行人运动模型, 通过分层建模方法, 融合楼梯几何约束、个体运动学特性及群体力学交互机制. 主要创新点包括: 1)构建“双足一点”多节点系统, 分层处理质心运动与双足支撑的时空关系; 2)基于三维元胞离散化方法, 建立满足几何匹配约束的连续跨步运动模型; 3)设计准同步状态切换机制, 协调多智能体步态周期的动态同步; 4)结合投影分离轴检测与各向异性碰撞动力学模型, 量化接触力对行人稳定性的扰动效应. 通过仿真实验, 本文系统地揭示了楼梯行人运动的动态演化规律, 为复杂场景下的疏散路径规划与安全风险评估提供理论支撑.

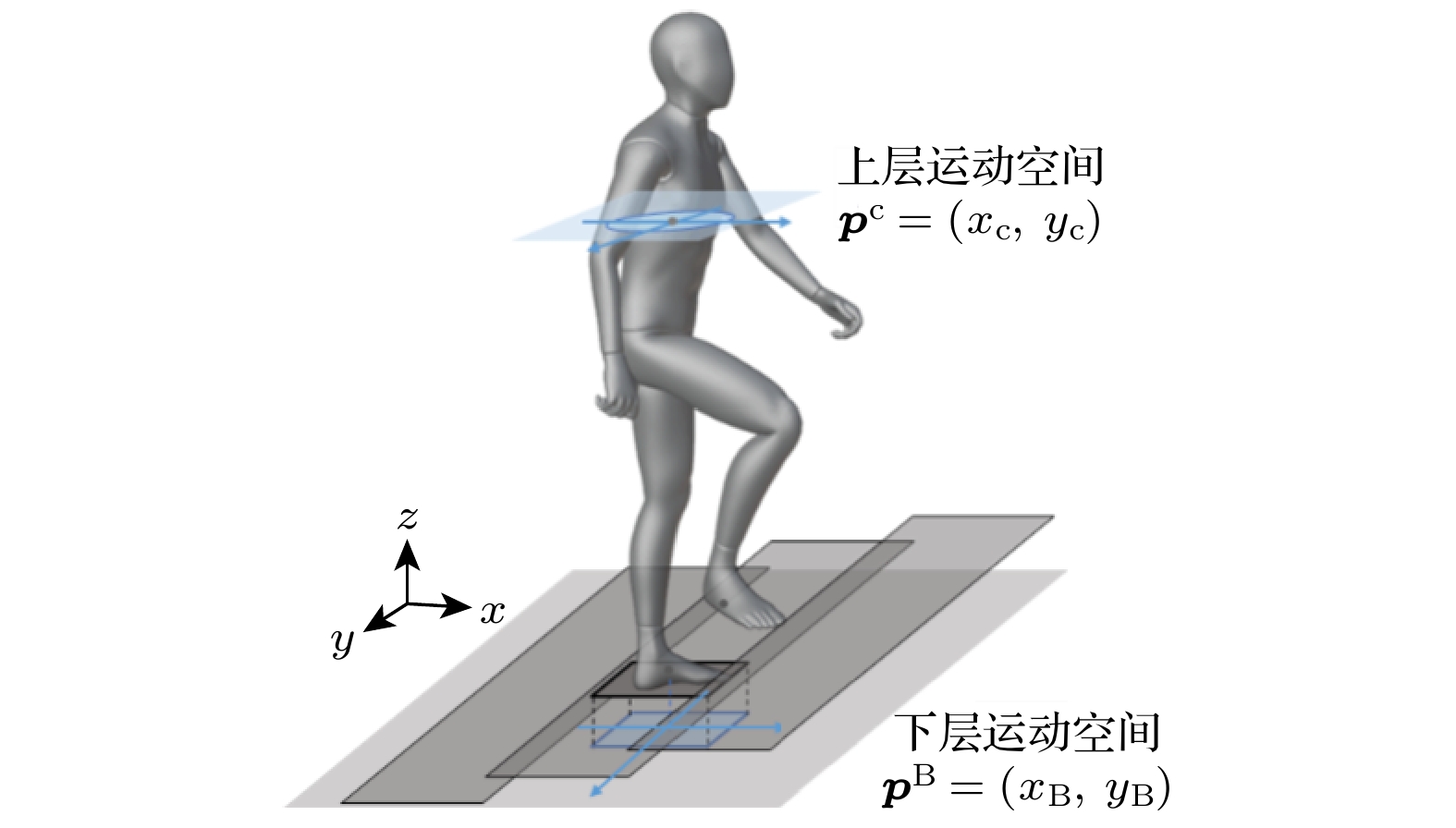
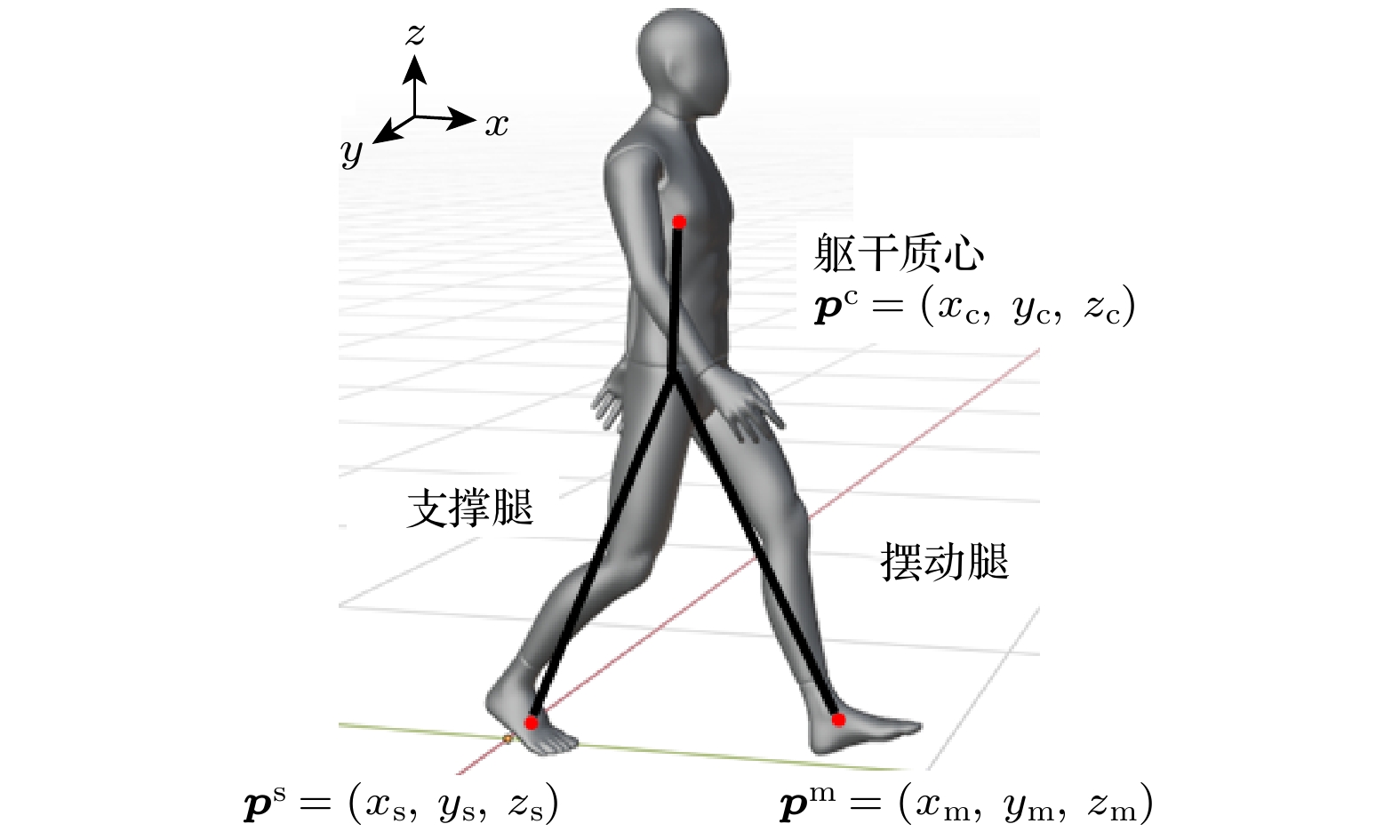
为了模拟楼梯环境中的行人运动, 本研究提出一种双层运动模型. 模型将行人抽象为“双足一点”的多节点系统(图1), 并构建双层运动空间(图2). “双足”指步进时的支撑足${{p}^{\text{s}}}$和移动足${{p}^{\text{m}}}$, “一点”为躯干质心${{p}^{\text{c}}}$, 其位置由三维空间全局坐标系描述. 上层由质心运动空间构成, 在检测行人接触冲突时, 忽略相邻个体的垂直位移差异, 将其投影至同一平面进行接触分析; 下层为下肢运动空间, 简化为由双足投影对角点构成的最小外接矩形区域.

模型将行人$ {\text{Ped}} \in {\text{crowd}} $(crowd为研究人群)定义为

其中${E_{{\text{upper}}}}\left\langle {{{p}^{\text{c}}}, {D_{\text{b}}}, {W_{\text{b}}}, \hat o} \right\rangle $表示上层空间椭圆状形态, 椭圆中心为质心${{p}^{\text{c}}}$在上层空间的位置, 其长、短轴分别由躯干肩宽${W_{\text{b}}}$和厚度${D_{\text{b}}}$定义, 椭圆方向与躯干朝向$\hat o$保持一致); ${R_{{\text{lower}}}}\left\langle {{{p}^{\text{m}}}, {{p}^{\text{s}}}, M} \right\rangle $表示下层空间的矩形区域, 受双足(支撑足${{p}^{\text{s}}}$和移动足${{p}^{\text{m}}}$)位置以及支撑状态$M$影响. $\theta $是行人躯干倾斜角度. $\zeta \left( \psi \right)$为行人所处运动状态$\psi $的持续时长($\psi \in \left\{ {S1, S2, S3} \right\}$): 状态切换时, 其持续时长重置, $\zeta = 0$; 否则, 按时间间隔累积叠加. $\left\{ {{T^n}, {T^{n + 1}}} \right\}$为行人的第n步单步运动时间序列. 本文关键符号及其简要说明列于表1.

模型将行人运动状态分为三类: 1)稳定运动状态(S1): 行人保持平衡, 自主控制运动; 2)动态失衡状态(S2): 外部扰动打破行人动态平衡, 失 衡状态下行人躯干绕支撑点倾斜; 3)失稳倒地状态(S3): 行人运动彻底失稳, 处于不可逆的倒地 状态.

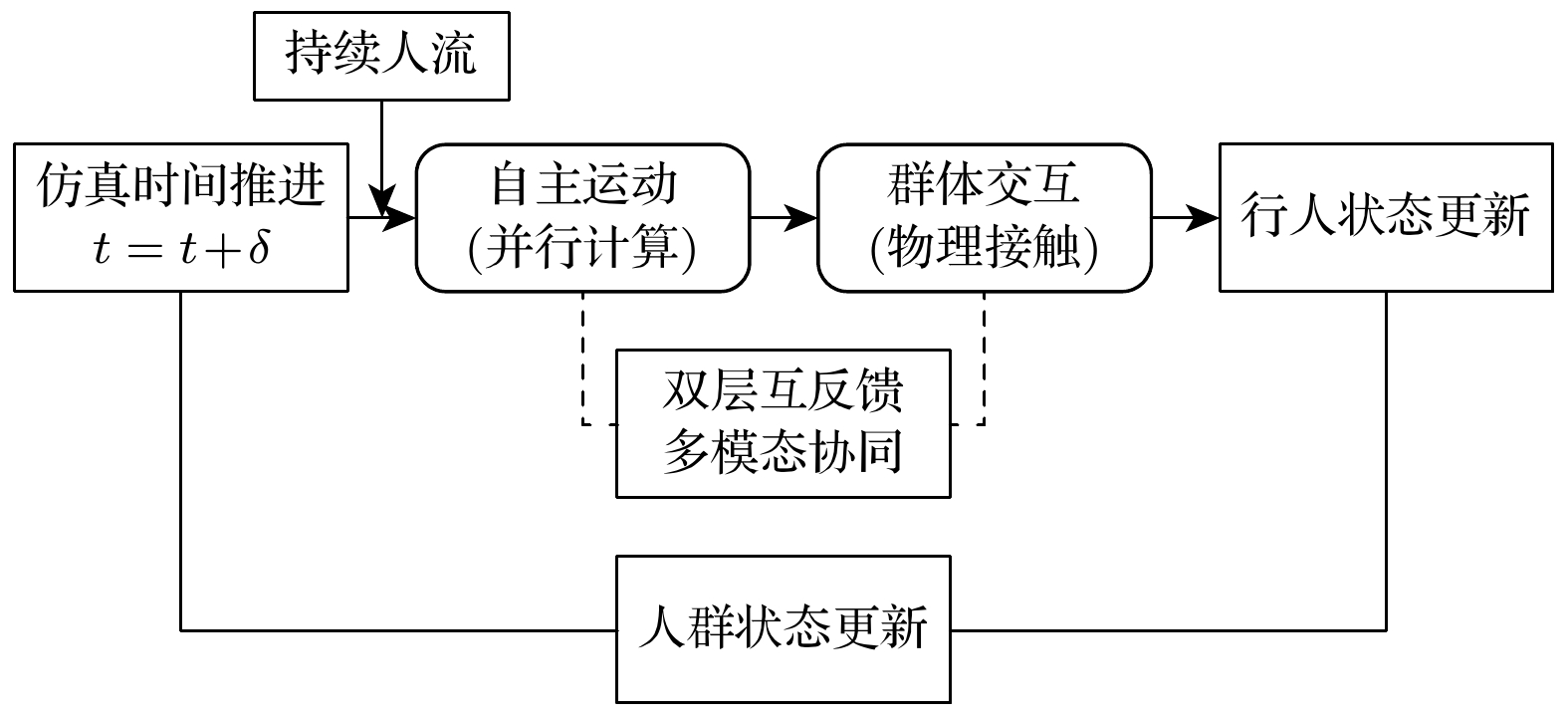
模型框架如图3所示, 主要包括行人运动与群体交互两部分. 行人运动状态的更新源自自主运动机制, 并受外界干扰(如群体内的接触碰撞)影响. 此外, 在指定区域按固定时间间隔添加新个体, 模拟动态人群流动; 移动至场景边界外或失去移动能力的个体被排除在研究人群(crowd)之外.

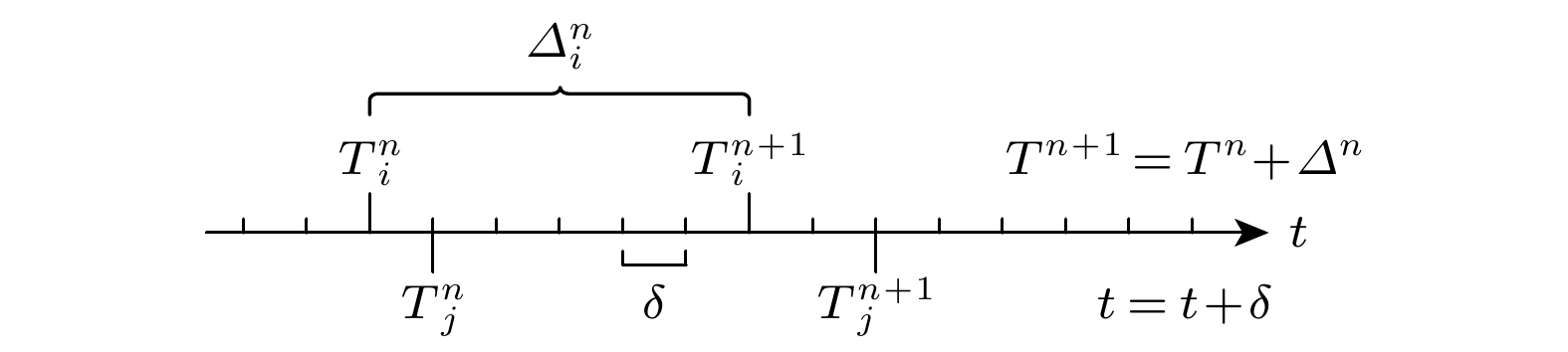
行人通过下肢交替摆动实现连续步态运动, 其周期特征(步频、单步时长等)因路径和速度差异而异. 在大规模群体仿真中, 模型以固定仿真步长$\delta $推进, 而每个个体独立规划运动时间序列$\left\{ T_i^n, T_i^{n + 1} \right\}$. 由于时间离散化引起的累积误差和步态异步性, 可能导致计算冗余或状态冲突. 为此, 本模型采用离散-连续混合时间框架^[24], 其时间结构如图4所示, 具体分为以下两层时序结构:

1)全局仿真时钟: 基于固定时间步长$ \delta $推进, $ t=t+\delta $, 确保多个体的时空状态同步更新;

2)个体步态时序: 每个行人保持独立的步态周期序列$\left\{ {{T^n}, {T^{n + 1}}} \right\}$, 其中${T^{n + 1}} = {T^n} + {\varDelta ^n}$, ${\varDelta ^n}$为第n个跨步运动的持续时长.

为解决步态异步问题, 提出准同步状态切换机制, 通过“接近即切换”规则将个体步态周期与全局时钟对齐, 确保多智能体时空一致性.

对行人i, 其第n步跨步结束时刻为$T_i^{n + 1}$. 在全局时钟迭代中, 若当前时间t满足$\left| {t - T_i^{n + 1}} \right| \leqslant \varepsilon $($\varepsilon = 0.5\delta $为同步容差阈值), 则触发强制相位迁移将该步的结束时刻截断或延长, 对齐至全局时钟节点. 行人状态更新流程(参见图5(c)蓝色框)包括以下步骤.

Step 1: 终止当前移动足运动, 将摆动足定位至目标落脚点${{p}^{\text{m}}} \leftarrow {C_{\text{t}}}$.

Step 2: 重分配双足支撑状态, 交换支撑足与移动足角色, 更新位置参数${{p}^{\text{m}}}(t) \leftrightarrow {{p}^{\text{s}}}(t)$.

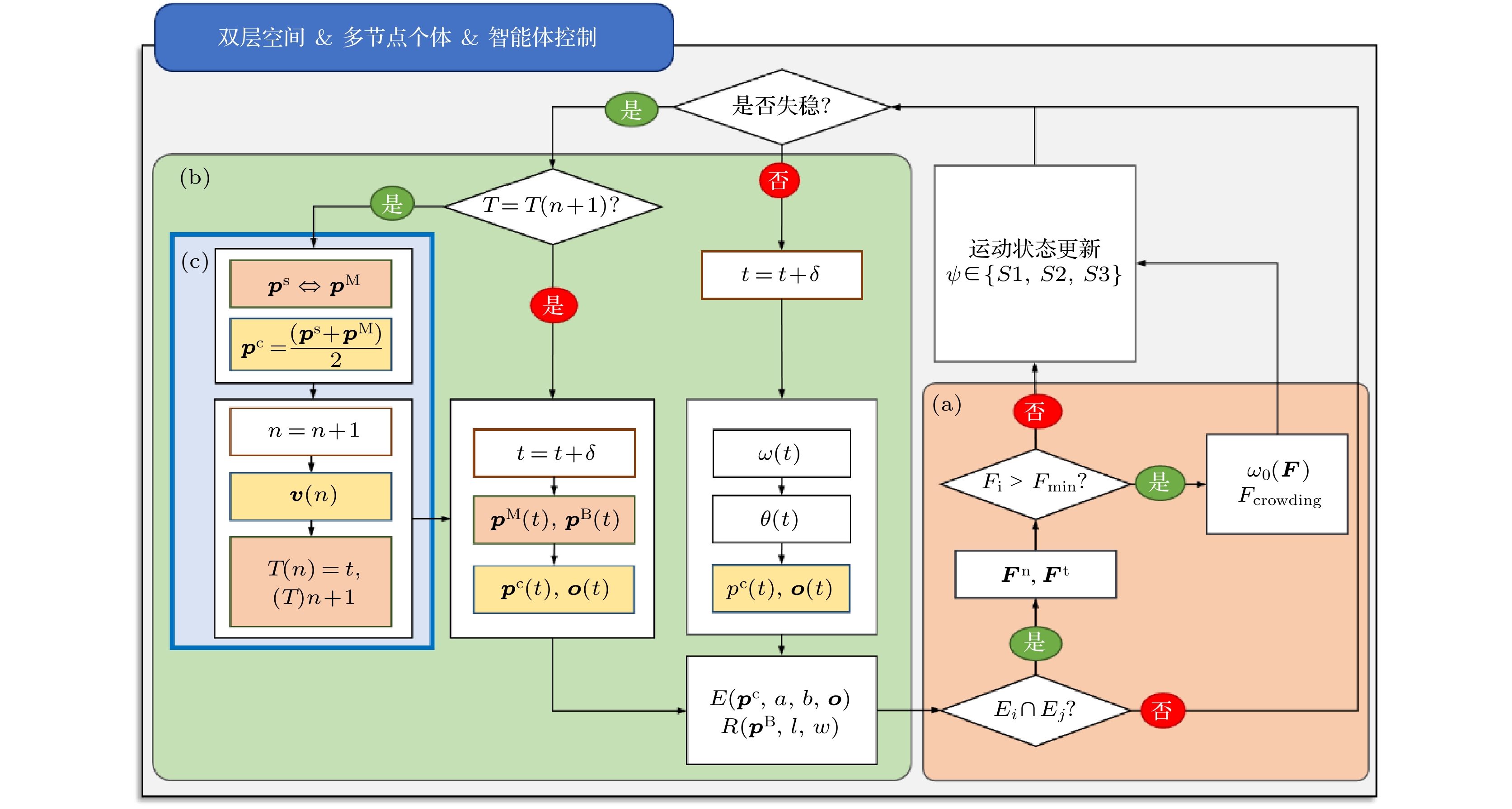
Step 3: 递增步态计数器$ n \leftarrow n + 1 $, 并重置个体步态时序${T^n} \leftarrow t$.

模型的运行逻辑如图5所示^[25]. 对于处于平稳步进状态(S1)的行人, 当仿真时间t接近第n步步态运动的结束时刻时, 双足支撑状态切换, 并规划下一步跨步运动. 移动足与质心按规划移动, 每个时间步长结束后更新节点位置, 并调整上下层空间形态. 对于失稳状态(S2)个体, 应用能量守恒原理计算躯干倾斜运动参数. 采用刚体力学和分离轴定义检测个体间碰撞, 量化物理接触对稳定性的影响. 更新行人运动状态$ \psi $. 模型采用并行计算架构, 所有行人状态同步更新.

模型通过双层交互机制实现动态耦合:

1)下层反馈: 根据当前步态更新行人位置, 输出双足支撑状态至上层;

2)上层反馈: 检测接触冲突并计算接触力, 若稳定性指标异常(如旋转角速度$ \omega $增大), 则调整下层步态参数(如由单支撑变为双支撑$M:1 \to 2$);

3)通过动态稳定性分析机制实时更新行人所处运动状态.

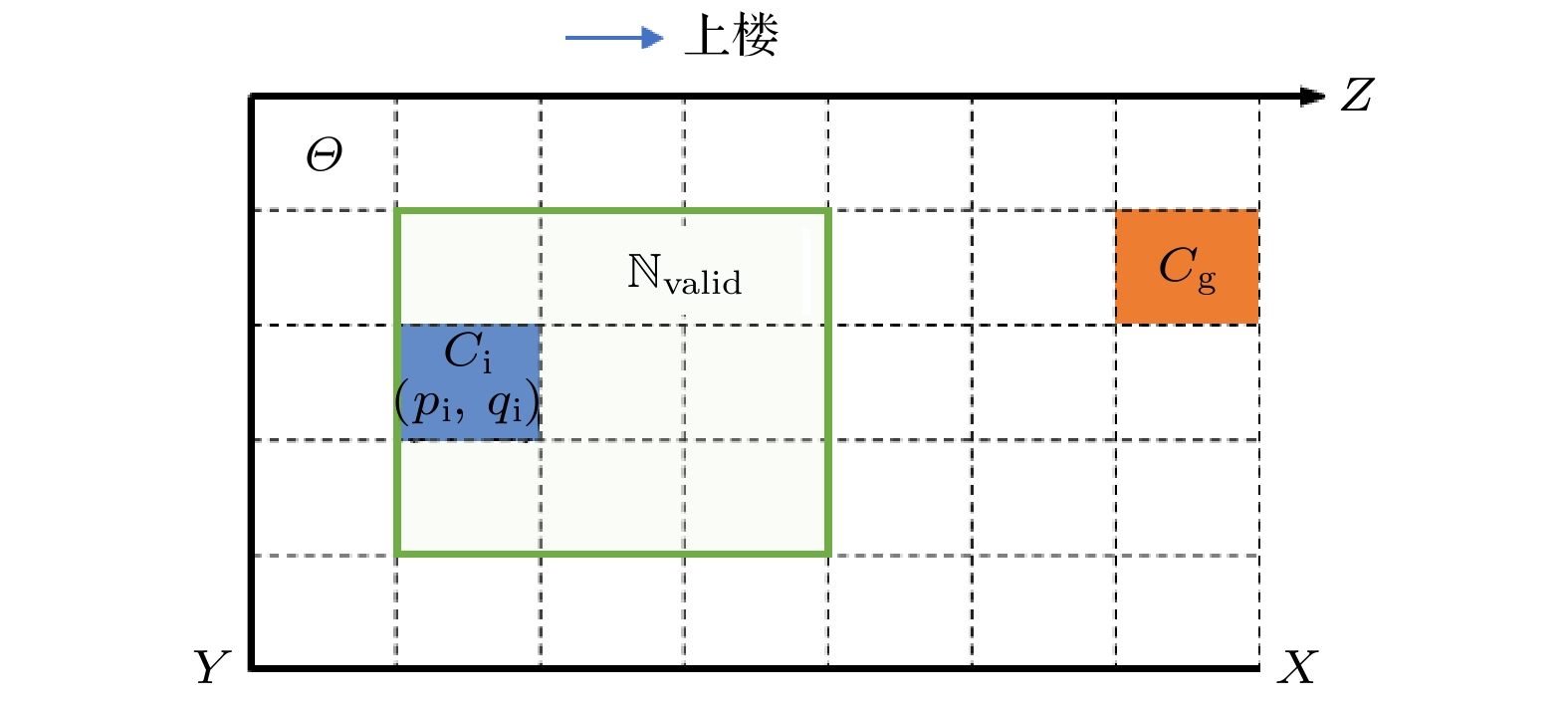
考虑楼梯几何特征对行人步态的影响, 本研究提出一种基于三维元胞的离散空间建模方法. 将楼梯环境抽象为由规则元胞构成的三维网格系统, 每个元胞对应物理空间中的台阶踏板上的矩形单元, 其尺寸($ {l_x} \times {l_y} $)由楼梯几何配置(台阶踏板深度$ {d_{{\text{stair}}}} $)和行人特征参数(足部宽度$ {W_{{\text{foot}}}} $)共同决定: ${l_x} = {d_{{\text{stair}}}}$, ${l_y} = 1.2{W_{{\text{foot}}}}$. 以楼梯底端第一层台阶的一侧为原点, 沿上行方向建立全局坐标系, 其中X轴为水平方向, Z轴为垂直方向. 元胞空间位置集合$\mathbb{C} = \left\{ {({x_p}, {y_q}, {z_q})|p \in {\mathbb{Z}^ + }, q \in {\mathbb{Z}^ + }} \right\}$($ {\mathbb{Z}^ + } $为正整数集合)中, 任意元胞${C_{p, q}}$中心坐标为

其中$p$为行号($1 \leqslant p \leqslant P\left( { = \left\lfloor {{w_{{\text{stair}}}}/{l_y}} \right\rfloor } \right)$, 不超过台阶踏板总宽$ {w_{{\text{stair}}}} $可划分网格的最大整数$P$), $q$为列号($1 \leqslant q \leqslant Q$, 不超过楼梯台阶总层数$Q$), $ {h_{{\text{stair}}}} $为单层台阶高度. 为记录元胞占用状态, 构建数值矩阵$\varTheta = \left\{ {0, 1, 2, \cdots} \right\}$, 其中, 0表示该元胞未被占用, 1表示被单个体占用, 2表示被双个体占用, 以此类推.

行人双足运动被建模为基于支撑足的元胞迁移过程(图6). 单个步态周期内, 支撑足占据元胞${C_i} = \mathbb{C}\left\{ {{p_i}, {q_i}} \right\}$, 模型根据上下楼方向构建移动邻域, 选择最优目标作为摆动足落脚点. 具体包括以下步骤.

1)基于支撑足${C_i} = \mathbb{C}\left\{ {{p_i}, {q_i}} \right\}$邻域构建候选落脚点集合, 根据目标方向(上下楼)定义移动邻域:

并确保有效邻域点满足网格边界约束:

2)考虑行人阻碍约束, 计算候选点${C_{\text{t}}} \in {\mathbb{N}_{{\text{valid}}}} (p,q)$及其上下左右邻域的占用数值之和(反映局部拥挤 程度):

密度越低(${D_{p, q}}$越小), 落脚优先级越高.

3)目标导向由候选点到最终目标点${C_{{\text{goal}}}} = \mathbb{C}\left\{ {{p_g}, {q_g}} \right\}$的曼哈顿距离定义:

距离越短(${S_{p, q}}$越小), 目标吸引力越强.

4)综合效用函数选择最优目标:

其中$ \mathrel\backepsilon $=1用于避免除零错误; $\alpha $和$\beta $为目标吸引和行人排斥作用程度的调节参数. 效用值越大表示该点越优, 选择综合效用值最大的点作为下一落脚点.

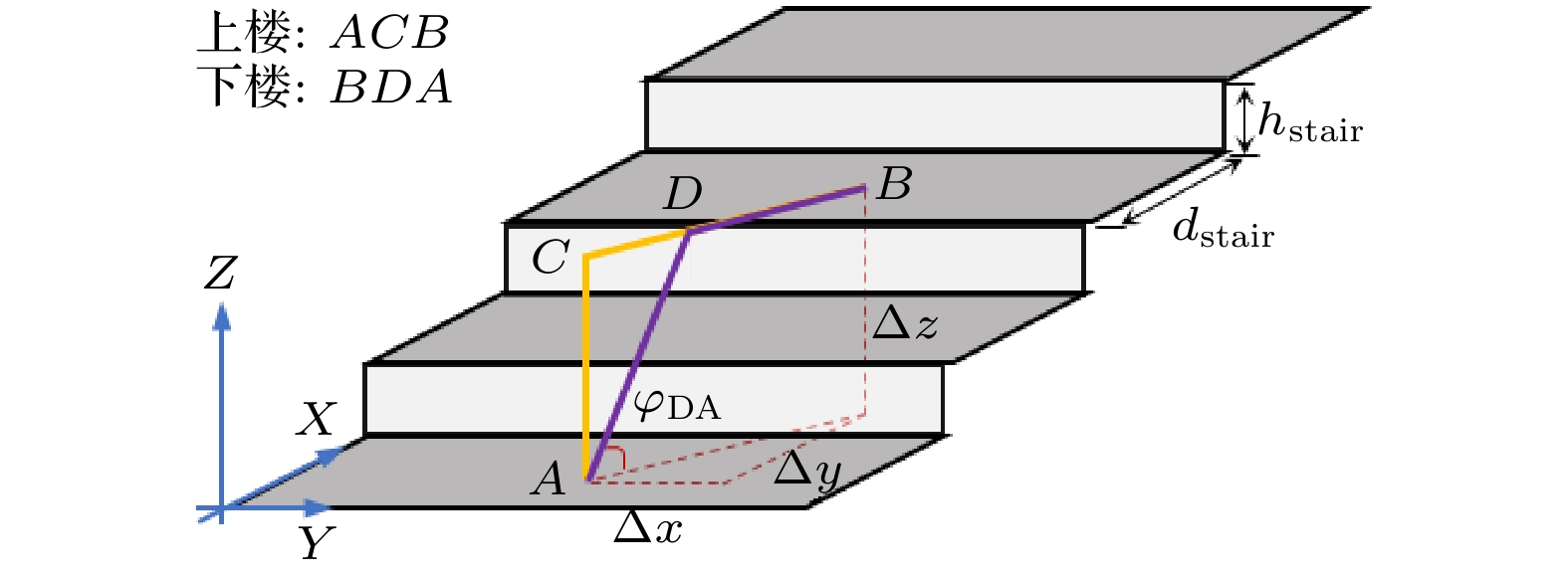
考虑行人运动方向对楼梯上行人的运动动态有影响, 基于三维元胞空间建模框架, 本研究提出差异化上下楼路径生成算法, 通过分段参数化路径满足几何约束. 模型将跨步动作分解为两类^[16]: 上行(垂直抬升-水平前移复合运动)与下行(水平前移-斜坡下降复合运动). 几何分析时, 假定行人i位于位置A(上楼)或位置B(下楼), 目标落脚点为位置B(上楼)或位置A(下楼).

1)上行路径生成

当移动足从点$ A(x_{A}, y_{A}, z_{A})$跨步至点$ B(x_{B}, y_{B}, z_{B}) $时, 摆动足移动路径如图7中A-C-B所示, 其上行路径总长度为

其中, 位移坐标差为$ \Delta x=\left|{x}_{A}-{x}_{B}\right|,\Delta y=\left|{y}_{A}- {y}_{B}\right|,\;\Delta z=\left|{z}_{A}-{z}_{B}\right| $.

单步步态周期时长${\varDelta _{\text{a}}}$由期望移动速度${u_{\text{a}}}$(预设为0.3 m/s^[26])决定:

其中$K({C_B})$为落脚点元胞的效用值大小.

路径方程建模为分段线性函数:

其中该步态周期内的时间变量${t_n} = t - {T^n}$($ {t_n} \in \left[ 0, {\varDelta _{\text{a}}} \right] $); 平面移动方向${d_{AB}} = \dfrac{{({x_A}, {y_A}) - ({x_B}, {y_B})}}{{\left\| {({x_A}, {y_A}) - ({x_B}, {y_B})} \right\|}}$.

2)下行路径生成

当下行移动足沿图7中B-D-A从点B迁移至点A时, 计算路径长度:

其中楼梯局部坡面斜角$ {\varphi _{DA}} = {\tan ^{ - 1}}\left( {{{2{h_{{\text{stair}}}}} {/ } {{d_{{\text{stair}}}}}}} \right) $.

此时, 单步步态周期时长${\varDelta _{\text{d}}}$由期望移动速度$ {u_{\text{d}}} $(预设为0.4 m/s^[26])主导:

其中$K({C_B})$为落脚点元胞的效用值大小.

分段路径方程为($ {t_n} \in \left[ {0, {\varDelta _{\text{d}}}} \right] $):

更新步态参数(期望移动速度${{\boldsymbol{v}}^{\text{e}}}$、跨步时长$\varDelta $、躯干朝向$\hat o$):

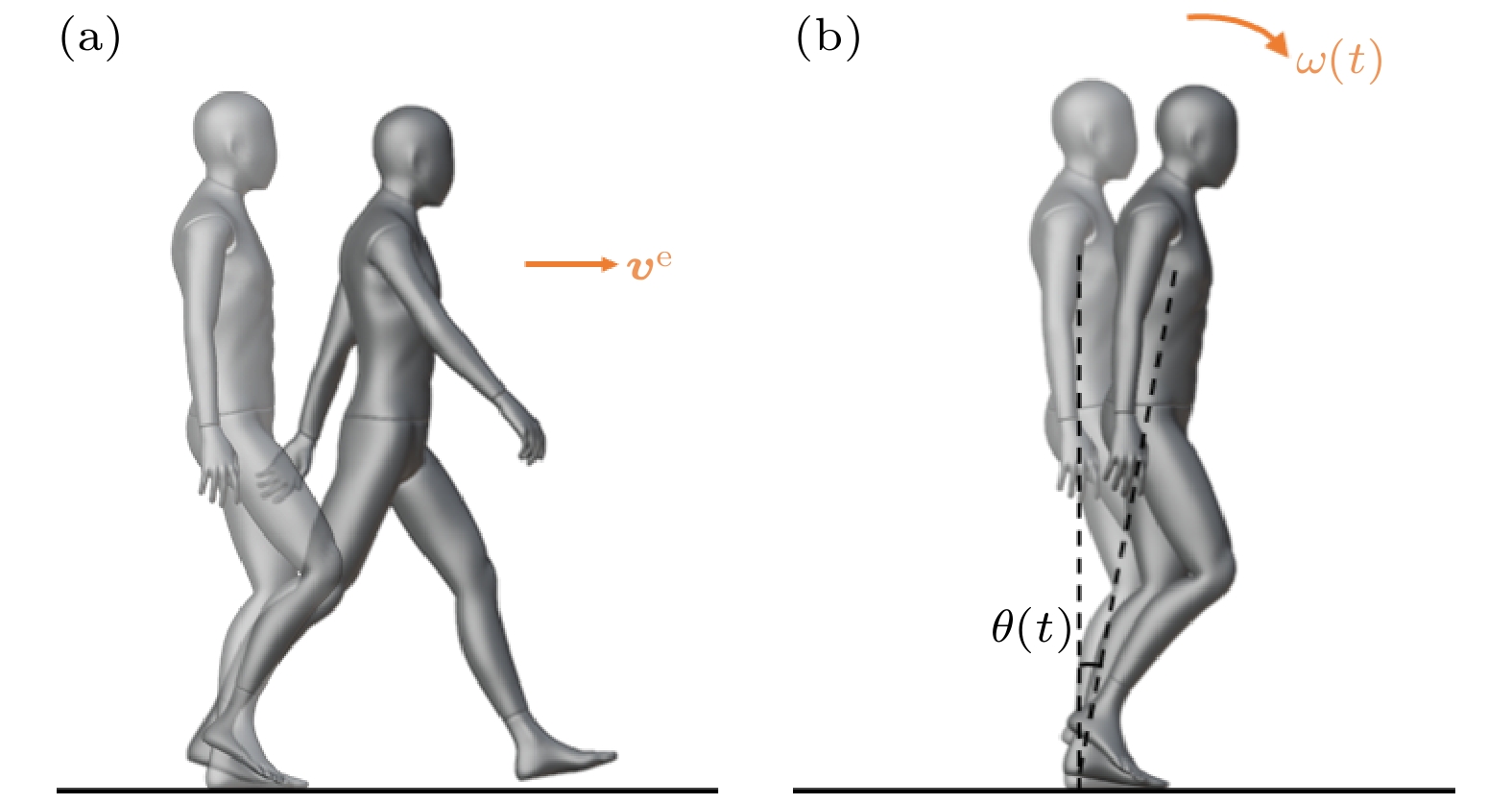
1)平稳运动状态(S1)

对于平稳步进的个体(图8(a)), 行人在双支撑阶段规划期望移动, 并基于准同步机制在单步运动结束时刻交替双足执行下一步运动. 随着全局仿真时间推进($ t = t + \delta $), 行人下肢摆动推动躯干前移:

2)失衡前倾状态(S2)

当个体运动平衡被打破, 上层躯干在重力作用下沿初始角速度绕支撑点旋转倾斜(图8(b)). 基于能量守恒定理, 计算随失稳时长变化的角速度和倾斜角度:

其中$m$为行人质量; $g$为重力加速度; ${H_{\text{c}}}$为行人质心高度; ${I_r}$为质心绕旋转点的转动惯量, ${I_{\text{r}}} = {I_{\text{c}}} + m{H_{\text{c}}}^2$, 其中${I_{\text{c}}}$为行人绕质心的转动惯量^[27].

将支撑足位置映射至元胞空间, 更新元胞占用矩阵$ \varTheta $.

上层空间中, 行人被抽象为以质心${{{\boldsymbol{p}}}^{\text{c}}}$为中心的椭圆区域, 其几何形态由肩宽${W_{\text{b}}}$、躯干厚度${D_{\text{b}}}$及移动方向(即躯干朝向$\hat o$)共同定义:

其中椭圆中心与质心在上层空间位置保持一致$({x_0}, {y_0}) = ({x_{\text{c}}}, {y_{\text{c}}})$, $\theta $为行人躯干倾角.

基于椭圆几何特性, 采用投影分离轴检测算法(projection-based separating axis test, PSAT): 对行人i和行人j的椭圆$ E_{i} $和$ E_{j} $, 计算所有分离轴(包括两椭圆长轴与短轴方向$A = \left\{ {{\hat o}_i}, \hat o_i^ \bot ,{{\hat o}_j}, \hat o_j^ \bot \right\}$)上的投影区间$\text{Proj}( \cdot )$. 若

即存在重叠的投影区间, 则判定接触; 否则无接触.

为量化人群接触影响, 将行人建模为质量集中于质点的刚体. 基于动量与角动量守恒定律, 建立碰撞动力学模型. 假设行人i和行人j在点$ {\boldsymbol{p}}_{ij} $处物理接触, 法向量$ \hat{{\boldsymbol{n}}} $由两椭圆梯度方向确定:

其中接触点$ {{\boldsymbol{p}}_{ij}} = {{\left( {{\boldsymbol{p}}_i^{\text{c}} + {\boldsymbol{p}}_j^{\text{c}}} \right)} {/ } 2} $为两椭圆中心连线的中点, $\nabla E$为行人椭圆方程的梯度, 表征接触点的几何法向. 将相对速度$ {{\boldsymbol{v}}}_{ij}({{\boldsymbol{v}}}_{ij}={{\boldsymbol{v}}}_{j}-{{\boldsymbol{v}}}_{i}) $沿法线方向分解:

应用动量和角动量守恒, 法向冲量$ {J_n} $和碰撞接触力$ {{\boldsymbol{F}}_{ij}} $计算如下:

式中, $e$为法向恢复系数; $\varepsilon $为松弛时间. ${m_i}$和${m_j}$分别为行人i和j的质量, ${{\boldsymbol{r}}_i}$和${{\boldsymbol{r}}_j}$分别为行人i和j到接触点的方向矢量; ${{\boldsymbol{r}}_{ij}}$是行人i和j之间的方向矢量. $ I_i^{\text{o}} $和$I_j^{\text{o}}$分别为行人i和j绕质心椭圆的转动惯量(${I_{\text{o}}} = \dfrac{1}{4}m\left( {{{(a/2)}^2} + {{(b/2)}^2}} \right)$, 其中$a$和$b$是椭圆形态的长轴和短轴大小).

对于多接触场景, 采用综合外力法:

$ {{\boldsymbol{F}}_{ij}} $为个体i和j之间的接触力, 同理$ {{\boldsymbol{F}}_{ik}} $, 其中i, j, ···, k 为不同行人编号.

行人在楼梯环境中的稳定性受步态规划、接触力扰动及几何约束共同影响. 稳定性控制理论表明, 当质心(center of mass, COM)的垂直投影位于支撑区域(the base of support, BOS)内时, 行人可保持动态平衡^[28,29]. 本模型通过耦合上层质心动力学与下层支撑区域约束, 量化接触力扰动下的失稳风险.

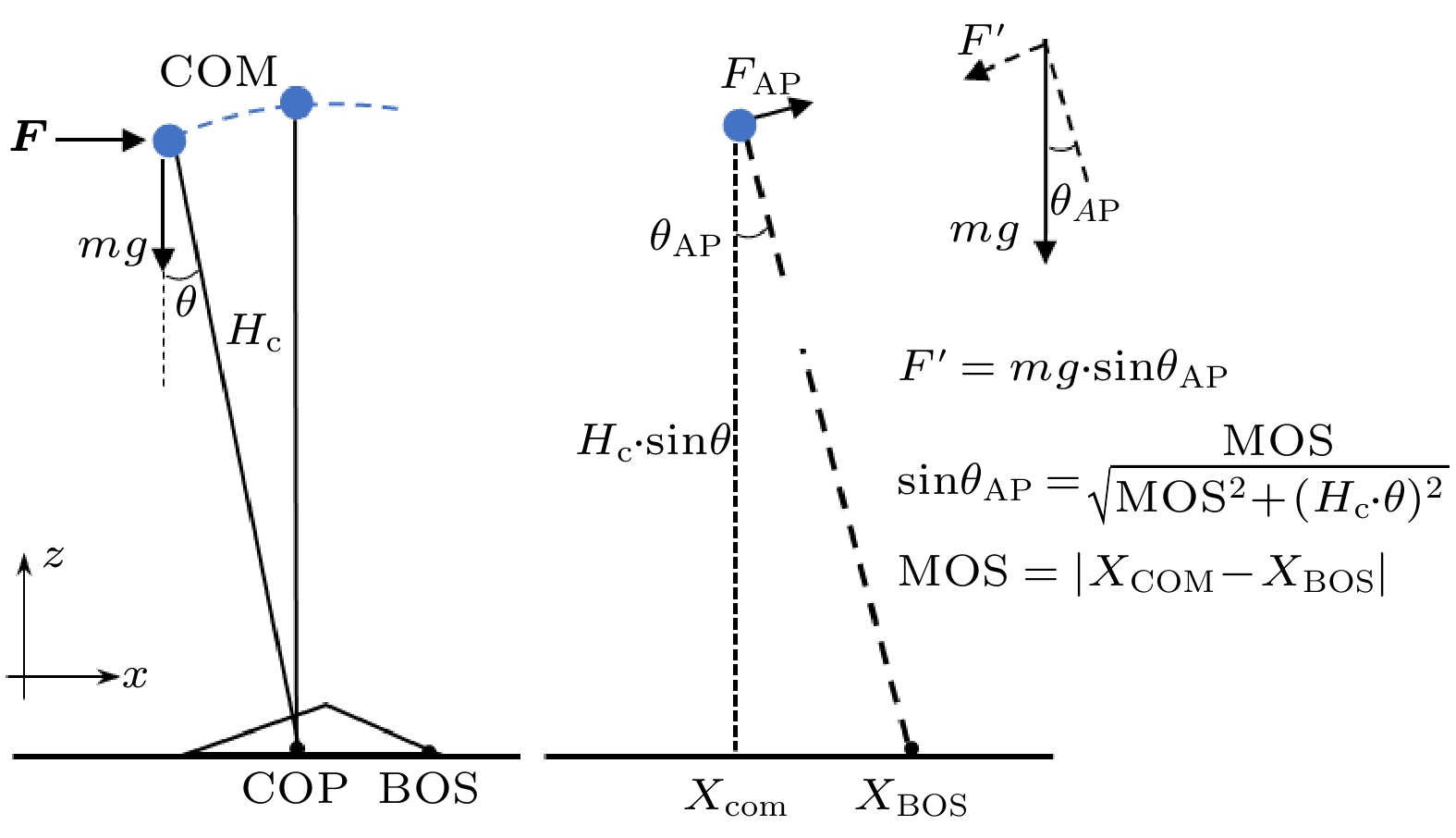
将行人简化为质点(上层空间)-支撑区域(下层空间)构成的倒立摆系统(图9). 下层空间的支撑区域(BOS)受双足运动状态影响. 单支撑阶段, BOS简化为支撑元胞所在矩形, 中心位置与 支撑足保持一致, $ {{{\boldsymbol{p}}}^B} = ({x_B}, {y_B}) = ({x_{\text{s}}}, {y_{\text{s}}}) $, 大小为元胞尺寸, ${L_{{\text{BOS}}}} = {l_x}$, ${W_{{\text{BOS}}}} = {l_y}$. 双支撑阶段, BOS扩展为双足投影对角区域, 其中心点位置 和大小由双足(支撑足${{{\boldsymbol{p}}}^{\text{s}}}$和移动足${{{\boldsymbol{p}}}^{\text{m}}}$)决定: ${{{\boldsymbol{p}}}^B} = \dfrac{{({x_{\text{m}}}, {y_{\text{m}}}) + ({x_{\text{s}}}, {y_{\text{s}}})}}{2}$, ${L_{{\text{BOS}}}} = \left( {({x_{\text{m}}}, {y_{\text{m}}}) - ({x_{\text{s}}}, {y_{\text{s}}})} \right) \cdot \hat o$, ${W_{{\text{BOS}}}} = \left( {({x_{\text{m}}}, {y_{\text{m}}}) - ({x_{\text{s}}}, {y_{\text{s}}})} \right) \cdot {\hat o^ \bot }$.

当个体受到初始扰动${\omega _0}$时, 其质心的外推运动轨迹为

为打破该动态平衡需施加的最小干扰力${F_{{\text{AP}}}}$为

即最大自主平衡控制力. 其中, $m$为行人的质量, $g$为行人的重力加速度, ${H_{\text{c}}}$为质心高度(即摆锤长度). MOS为摆动质心投影与支撑区域边界之间的距离(margin of stability), 受行人身高H影响: $ {\text{MO}}{{\text{S}}_{{\text{AP}}}} = 0.109 H $(前后侧)^[28].

基于生物力学调控能力与阈值约束, 动态评估行人运动稳定性.

Step 1: 当施加的外力超过自主平衡力, 即$ \left\| {\boldsymbol{F}} \right\| \cos \theta > {F_{{\text{AP}}}} $时, 触发初始失稳,

其中$\theta $为个体躯干倾角; ${H_{\text{c}}}$为质心高度; ${I_{\text{r}}}$为质心绕旋转点的转动惯量.

Step 2: 当躯干偏离Z轴的倾斜角大于阈值${\theta _{\text{T}}}$^[30]时, 即

个体摔倒失稳.

此外, 设置动态稳定性判别指标—稳定裕度$ \varPhi $, 定义为外推质心投影与支撑区域边界的归一化距离:

失稳判据分级响应: 若$ \varPhi $<0, 质心投影与支撑点之间的距离超过维持稳定的支撑边界, 共同完全失稳; 否则, 行人随机触发下层步态调整策略(如减速、跨步修正), 或是维持当前运动状态.

结合个体运动状态定义, 建立运动状态转换机制:

式中, $S1$表示平稳步进状态; $S2$表示失衡倾斜; $S3$表示失稳倒地状态.

本研究通过仿真实验验证双层模型在楼梯行人运动模拟中的有效性, 相关参数基于中国成年人人体尺寸^[31]、民用建筑设计规范^[32]以及实验观测数据^[30]或经验关系设置, 取值列于表2.

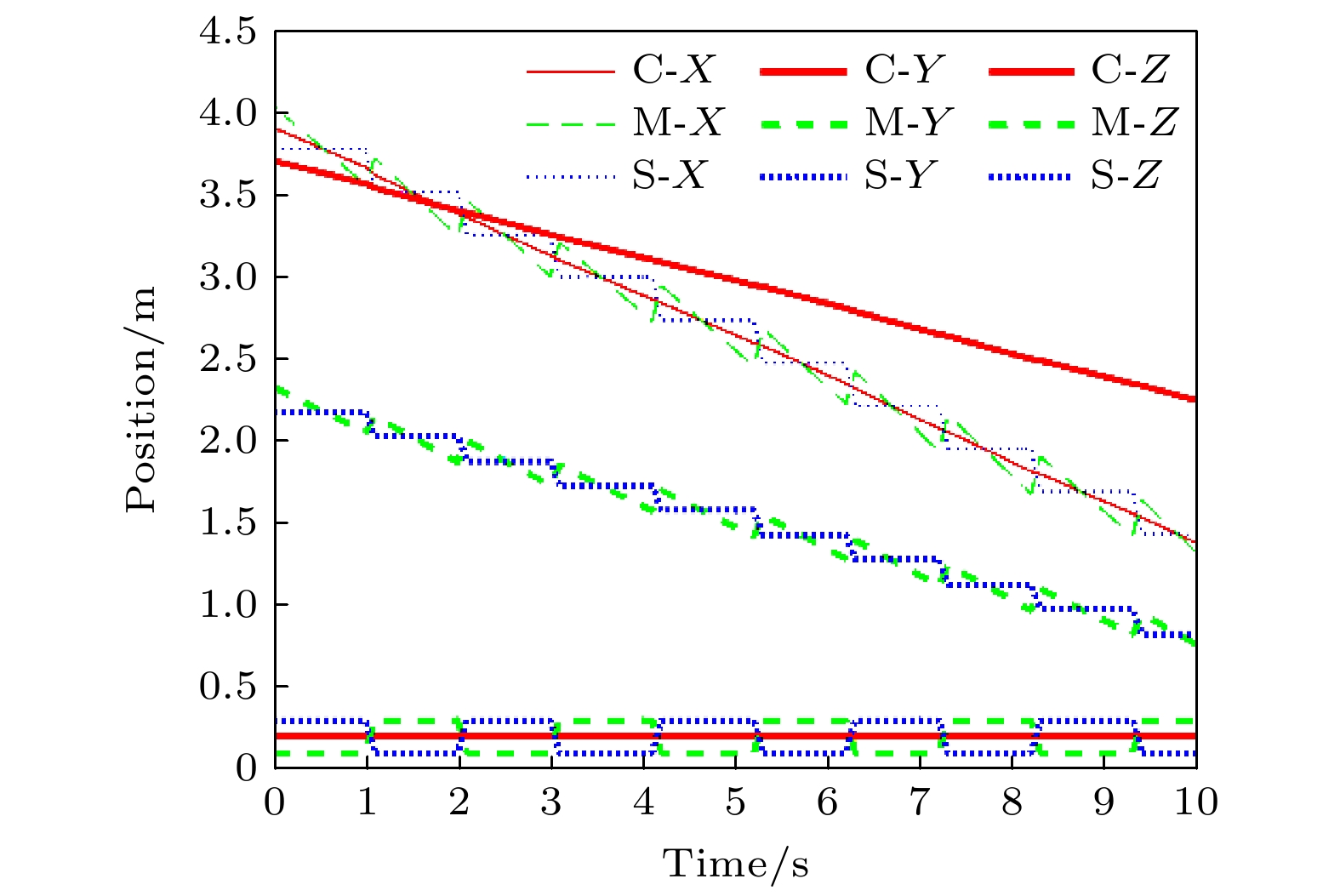
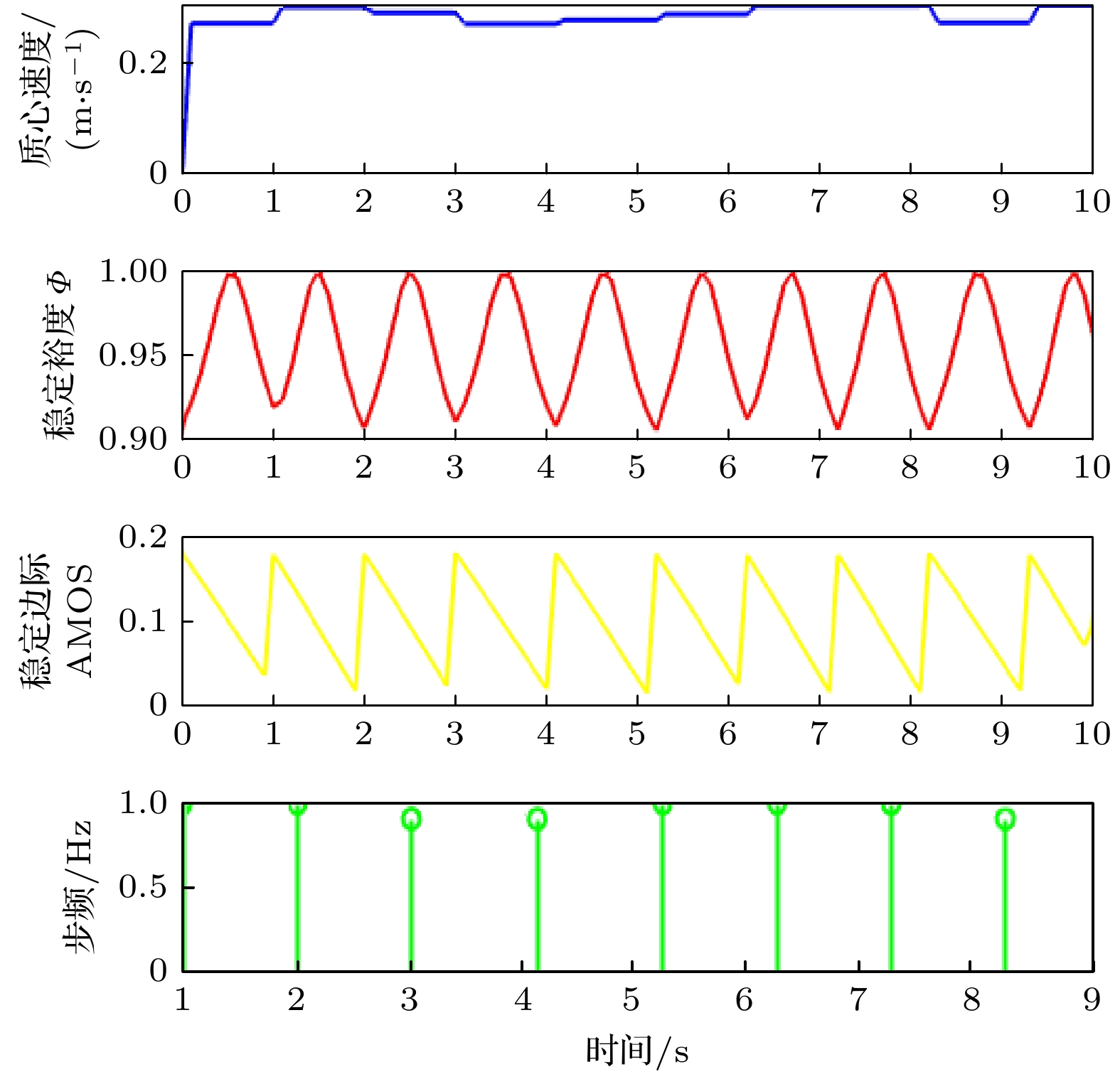
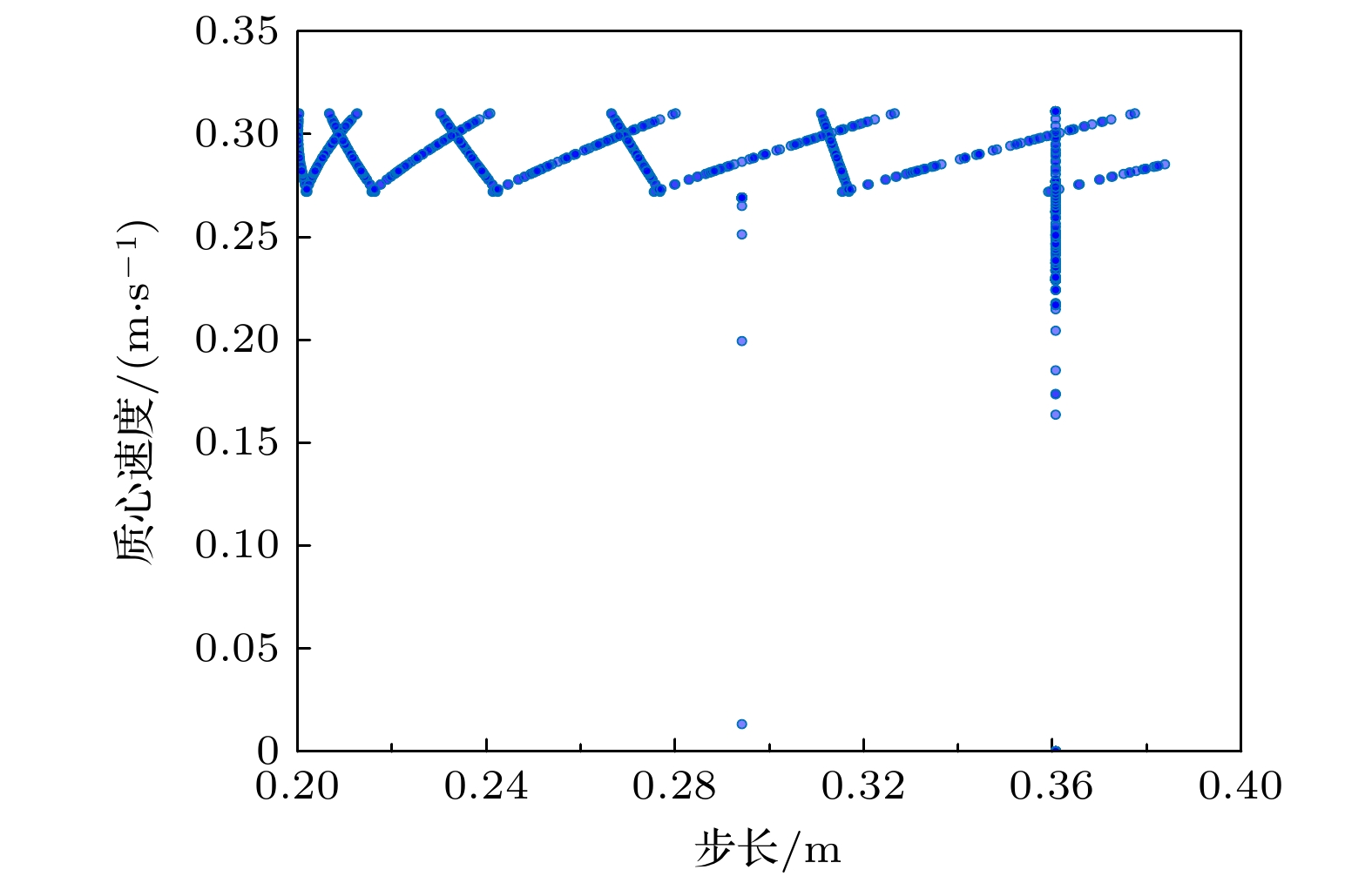
通过分析质心、支撑足与移动足的三维运动轨迹(图10), 验证了模型对楼梯几何约束的适应性. 质心在水平(X轴)与垂直(Z轴)方向的位移比($\Delta X/\Delta Z$≈0.57)与楼梯坡度理论值($\tan {\varphi _{{\text{stair}}}}$=0.5769)一致. 下肢运动特征方面, 支撑足的三维位置变化呈现分段式前进模式, 与步态周期中的支撑-摆动交替机制吻合. 在X-Y平面内, 支撑足与移动足的轨迹交错分布, 形成稳定的下层空间覆盖区域, 质心投影始终位于支撑足覆盖范围内, 体现了动态平衡的维持机制.

时序分析图(图11和图12)进一步揭示了步态动力学机制: 行人在无干扰上楼过程中, 移动速度稳定于0.3 m/s (标准差±0.03), 稳定裕度($\varPhi $)均值为0.96, 下肢摆动周期(步频1.2 Hz)与速度波动(振幅±0.05 m/s)同步, 而步长增大会显著加剧速度波动.

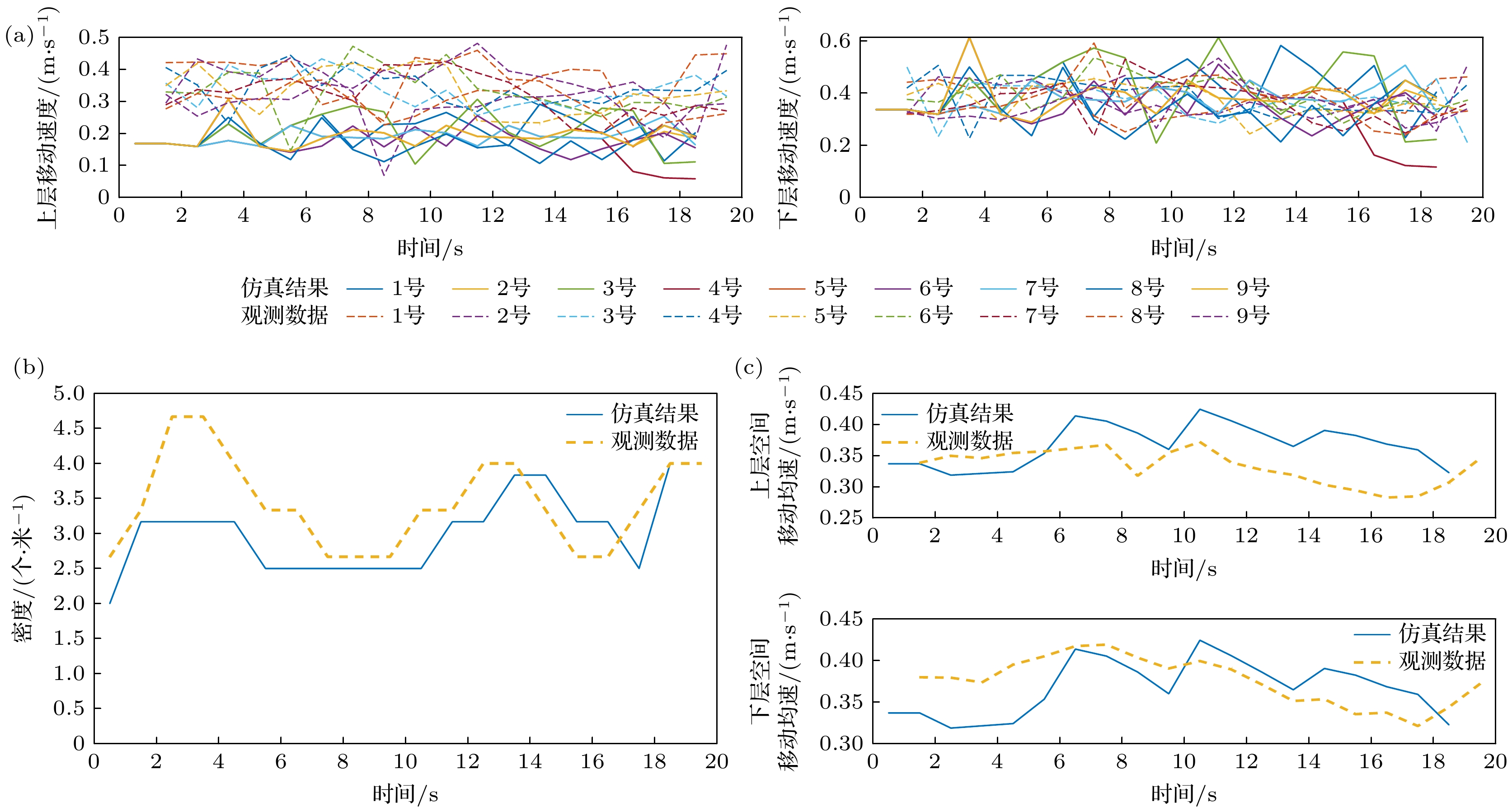
通过与Zhang等^[33]的观测数据对比验证模型的可靠性. 观测实验环境为含15个台阶的楼梯, 单个台阶高度为0.148 m, 踏板宽度为0.30 m, 研究采用相同配置进行仿真. 图13显示, 实验结果与观测数据在人群密度与速度变化趋势方面高度吻合, 模型能够准确刻画宏观运动动态. 上层空间移动均速仿真值为 (0.32 ± 0.03) m/s, 与观测数据(0.34 ± 0.05) m/s的置信高度吻合, 表明模型能够准确刻画宏观运动动态. 下层空间仿真结果(0.28 m/s)较观测值(0.31 m/s)偏低9.7%, 可能是由于模型简化策略: 准同步机制导致步态周期离散化误差, 以及短时段内匀速运动假设忽略了加速度波动.

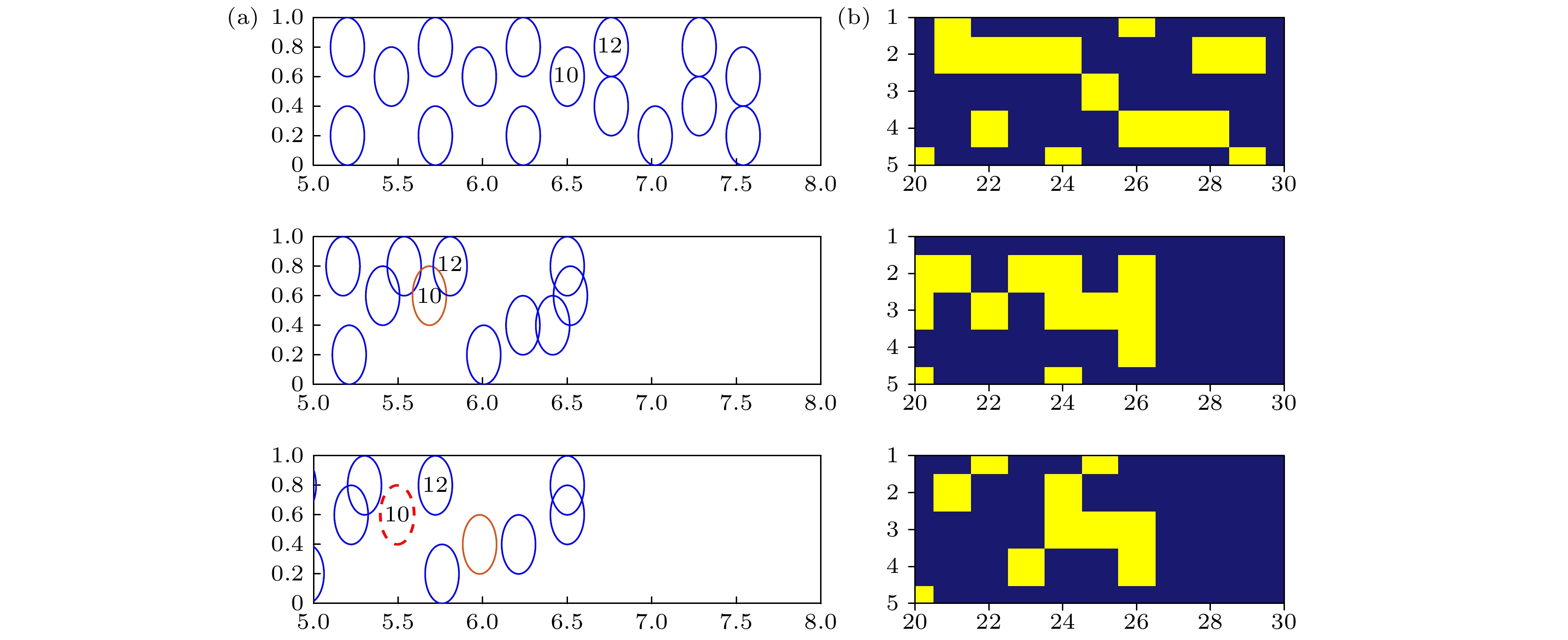
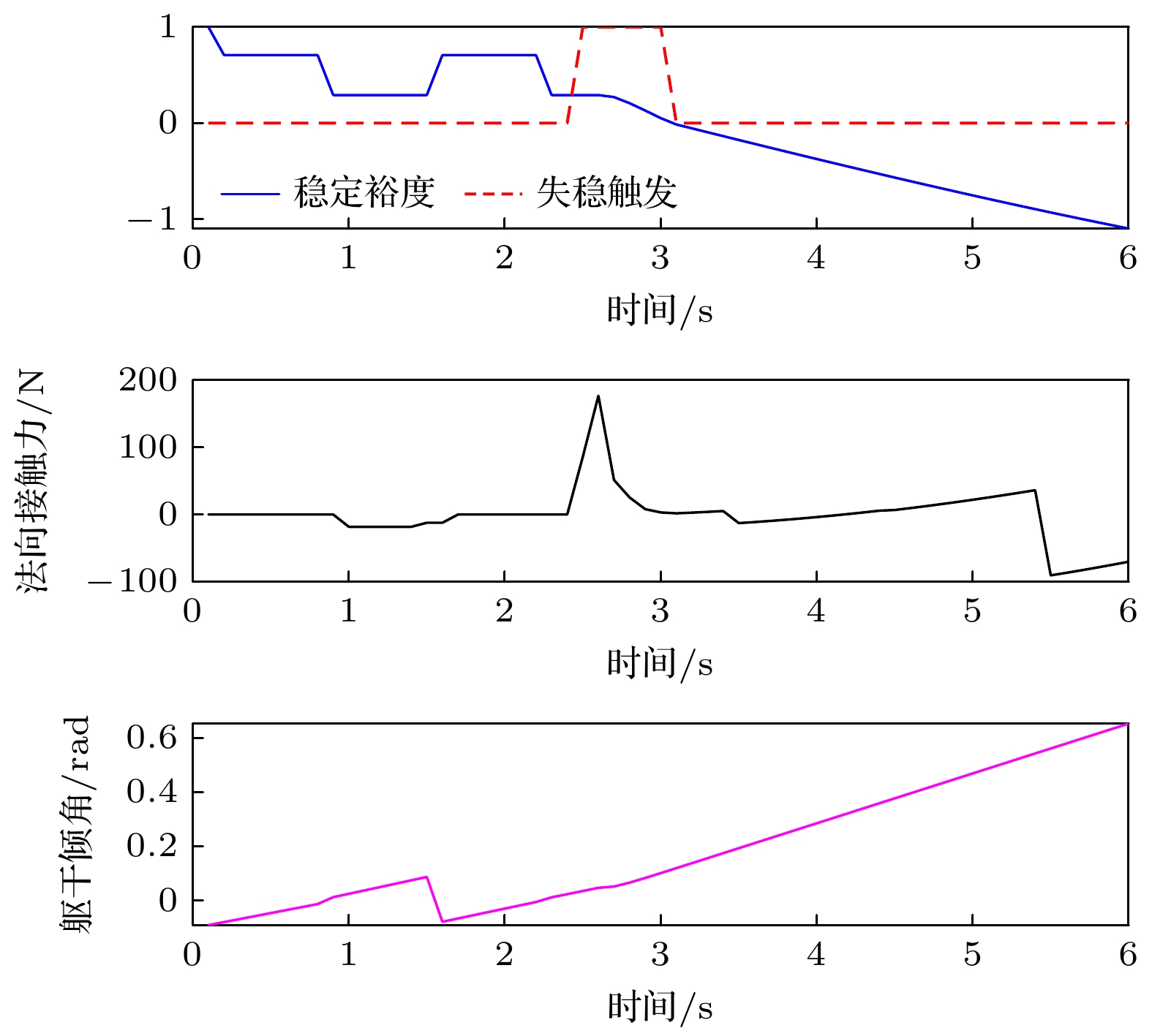
以10号个体为研究对象(质量为65.13 kg, 身高为1.69 cm), 其失稳过程可分为三个动力学阶段(图14和图15).

阶段一(接触冲突): 10号个体与12号个体发生法向接触(${E_{10}} \cap {E_{12}}$≠$\varnothing$), 接触力为$ F_{{\mathrm{n}}}= $185 N((23)式—(26)式), 超过行人自主平衡阈值(此时, ${F_{{\text{AP}}}}$=133 N), 触发初始扰动($\psi :S1 \to S2$).

阶段二(运动失衡): 接触力冲击导致动态平衡破坏, 质心外推速度增至0.38 m/s, 行人以初始角速度(${\omega _0}$ = 0.26 rad/s)绕支撑足旋转, 躯干倾角增大.

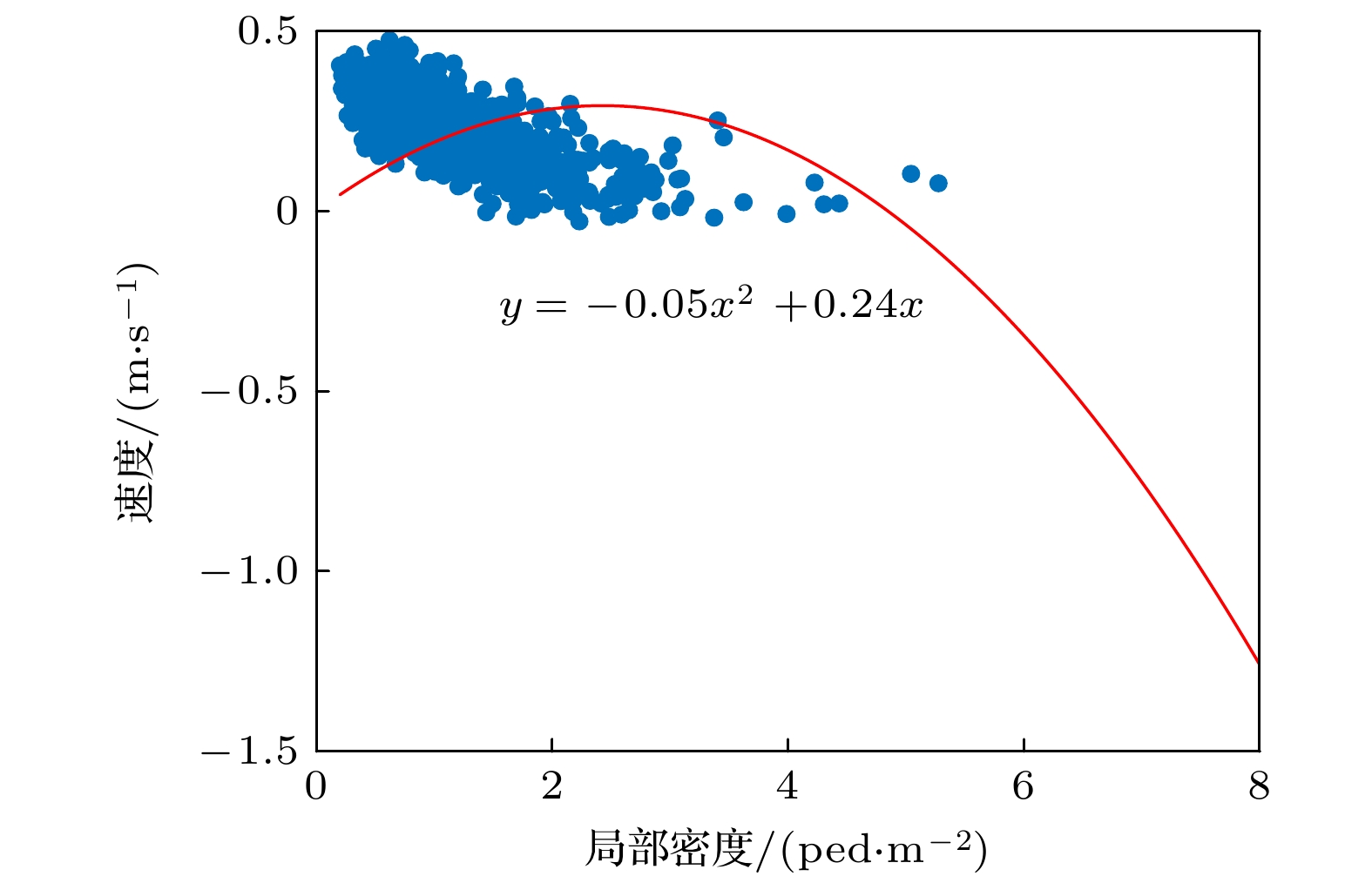
阶段三(持续倾倒): 质心垂直投影脱离支撑区域, 稳定裕度持续减小($ \varPhi $<0), 倾角增大至临界失稳角度($ \theta $>0.75 rad), 最终失稳倒地($\psi :S2 \to S3$).

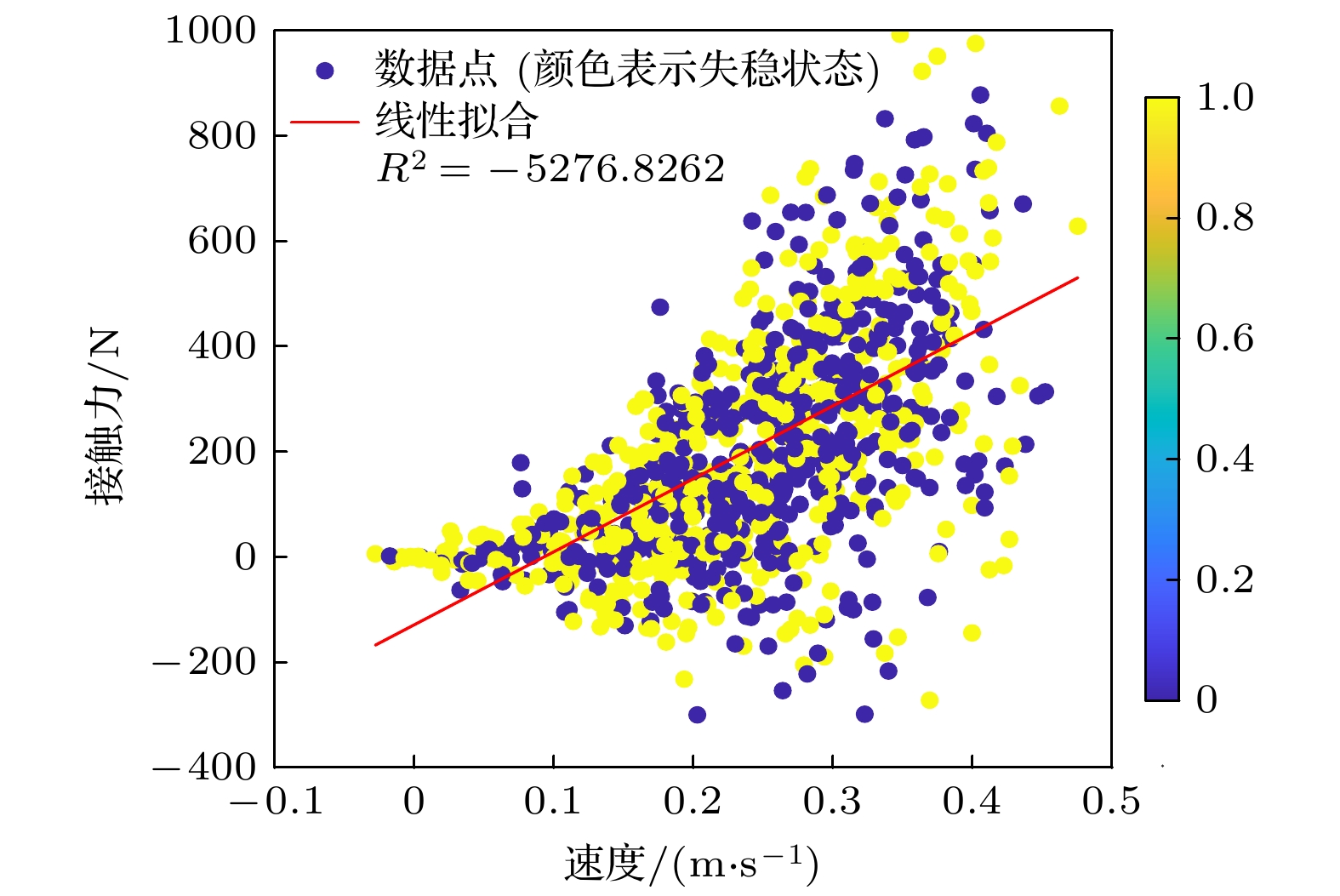
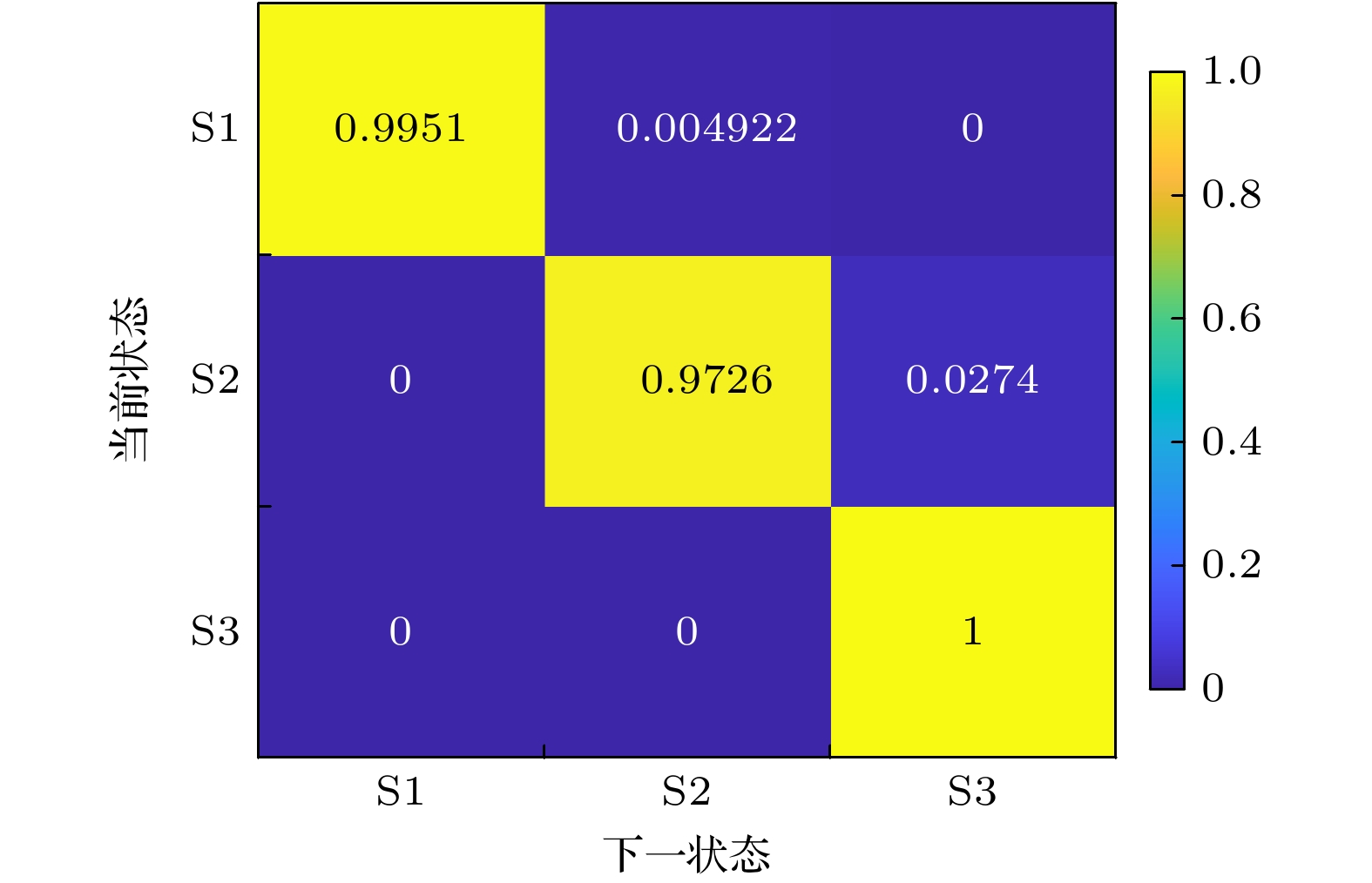
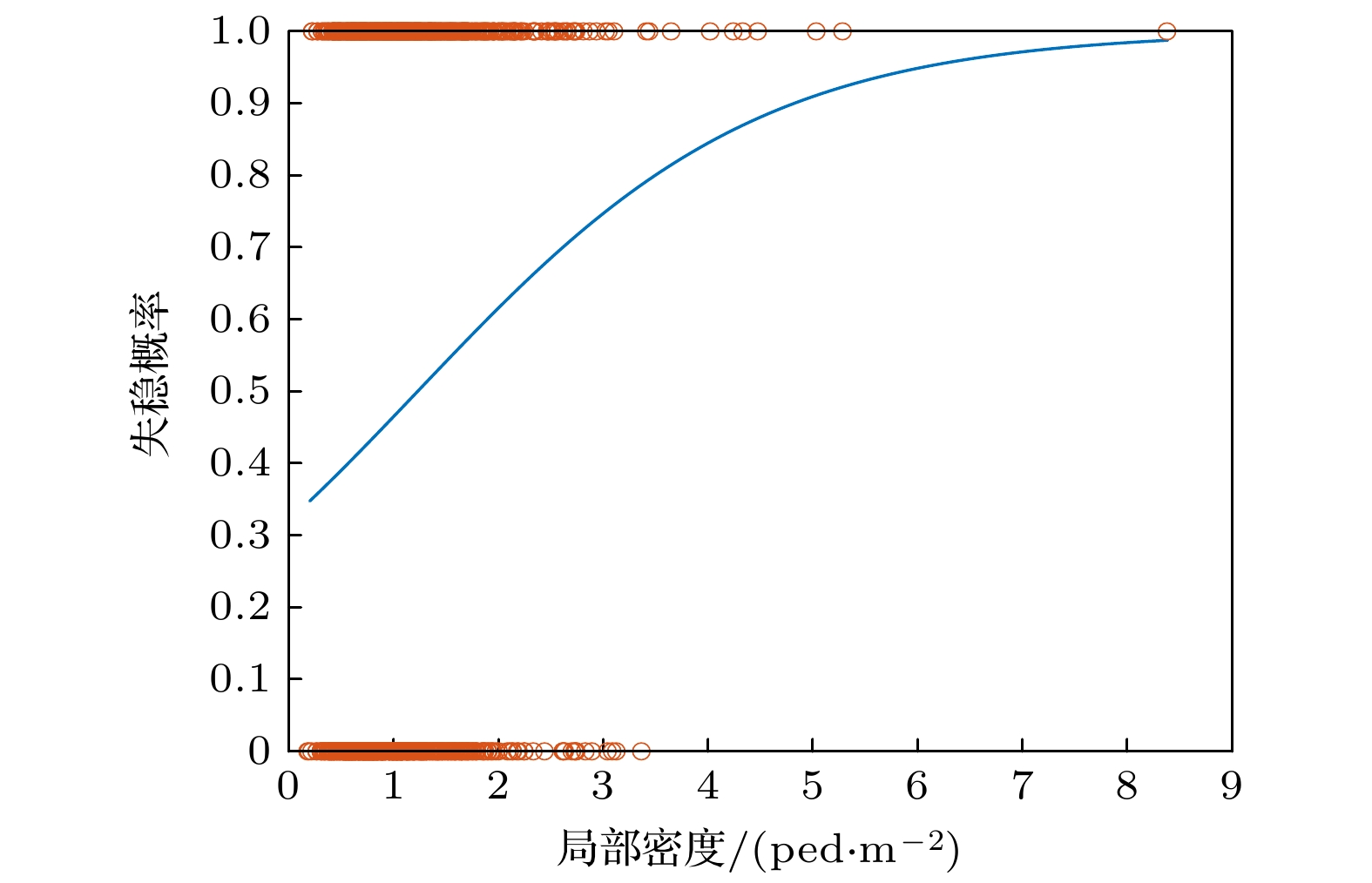
失稳事件中行人局部密度-速度关系(图16)呈现显著非线性特征: 中低密度(${\rho _{\text{l}}}$ < 3.0人/m²)时, 行人速度受密度影响较大; 高密度时, 个体移动空间被压缩, 速度趋近于群体均值(0.28 ± 0.04) m/s. 同时, 速度与交互接触力呈正相关(图17), 表明速度较快时会放大接触作用对稳定性的扰动, 加剧失稳风险.

基于状态转移概率矩阵(图18), 密度对失稳风险的驱动作用进一步验证: 个体从移动状态S1进入失稳状态S2的概率为0.49%, 尽管绝对概率较低, 但在高密度场景下, 频繁的物理接触与运动自由度受限会导致该概率持续累积, 使系统失稳风险呈指数增长. 一旦进入失稳状态S2, 个体以2.74%的概率向终止状态S3(倒地)转移, 极易引发群体失稳. 状态转移路径(S1→S2→S3)表明, 失稳是密度驱动下从局部失衡到全局崩溃的级联过程—局部密度升高通过限制运动自由度、加剧交互力, 逐步将个体推向不可逆的终止状态. 综合表明, 人群密度对失稳风险具有显著正向预测作用(图19).

基于双层行人模型中的移动规划算法(2.2节), 本研究分析了目标吸引权重(α)与行人排斥权重(β)对行人移动速度以及接触冲突的影响.

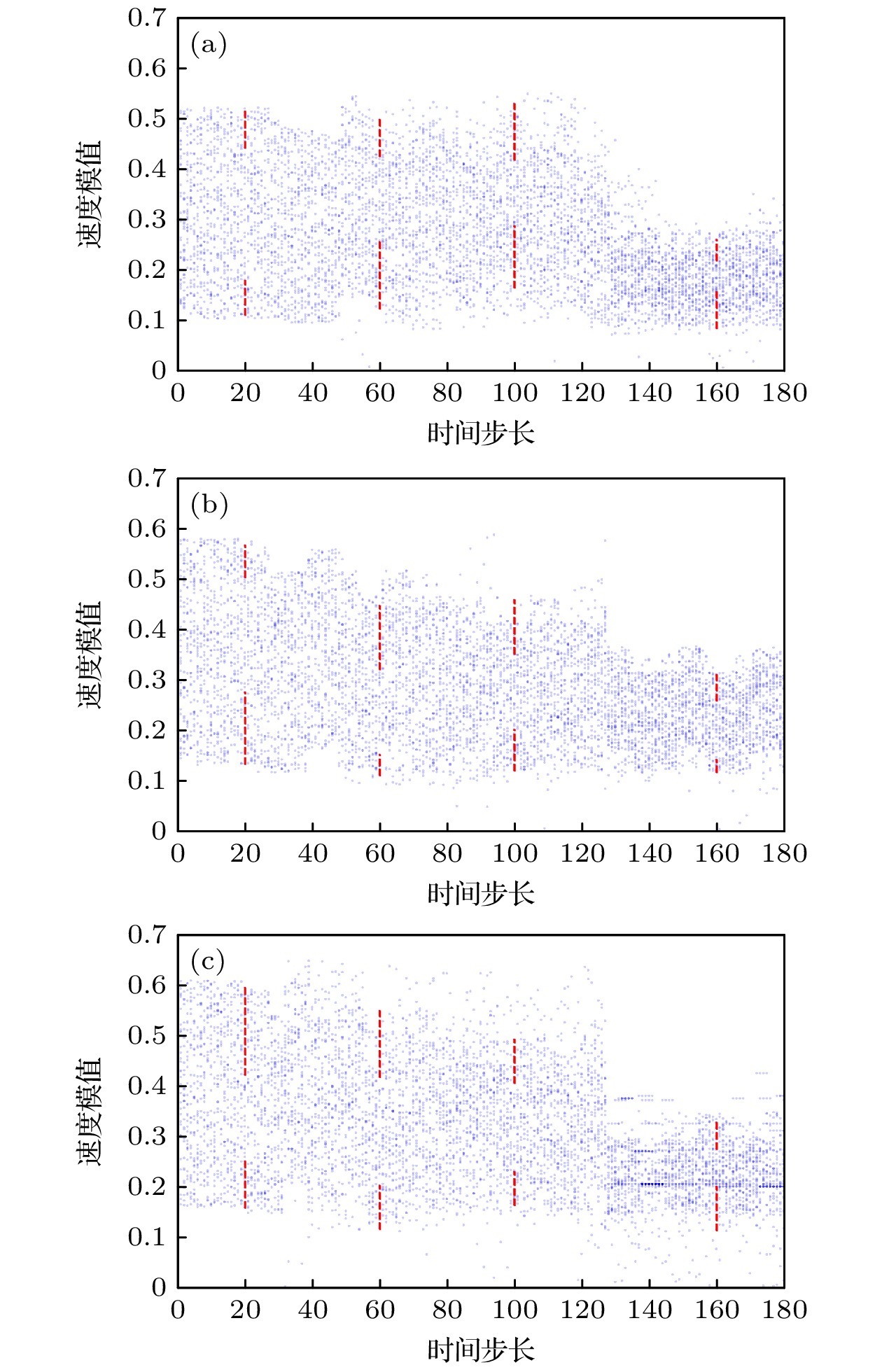
图20展示了个体速度在不同参数组合下的分布情况, 可见目标吸引权重(α)和局部拥挤排斥权重(β)的相对大小显著影响了个体速度分布的特性. 当β主导时, 个体的分散行为增强, 速度分布较为均匀; 当α和β平衡时, 群体行为趋于协调, 速度分布适中集中; 而当α主导时, 个体的趋同性增强, 速度分布高度集中.

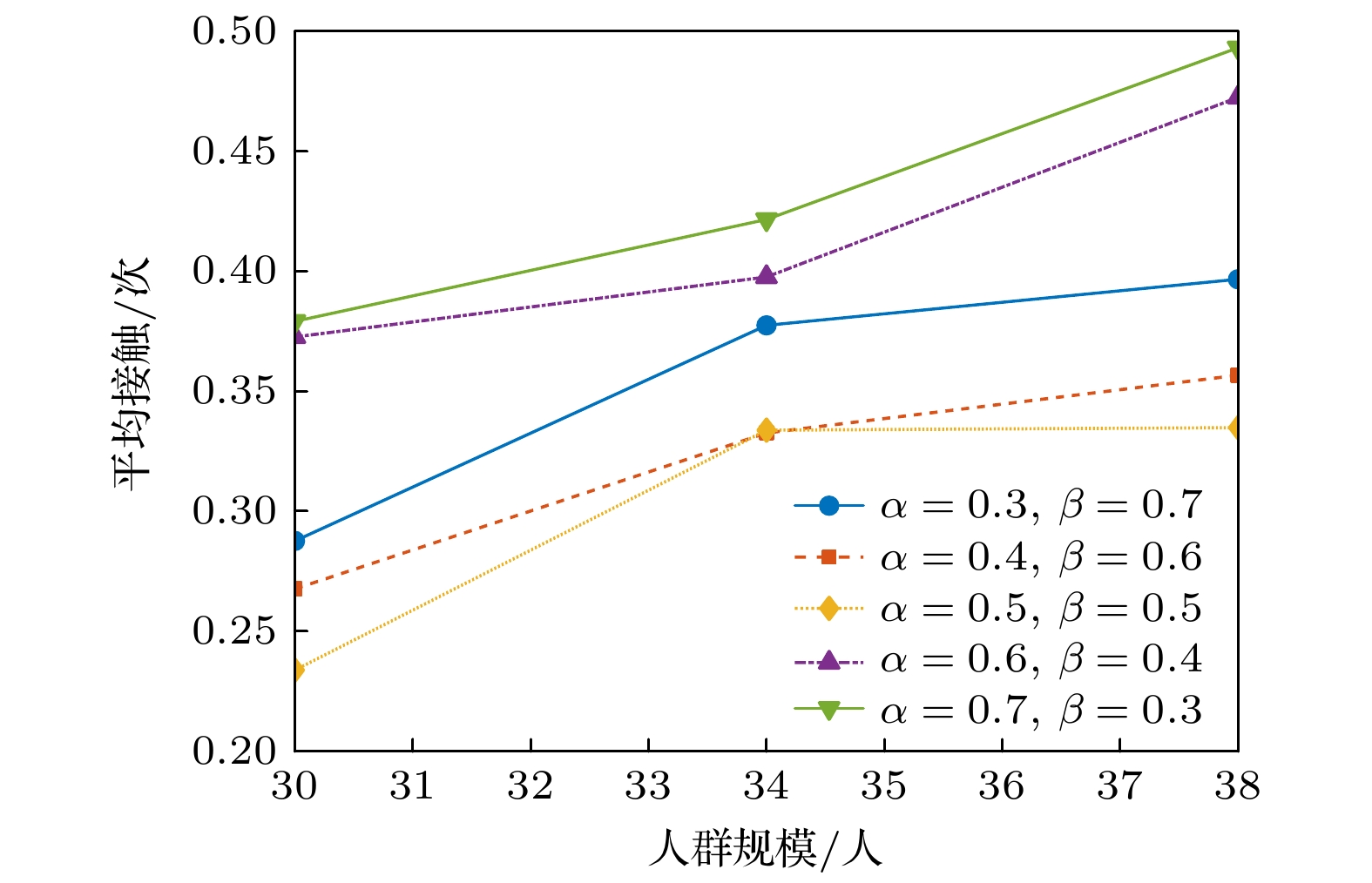
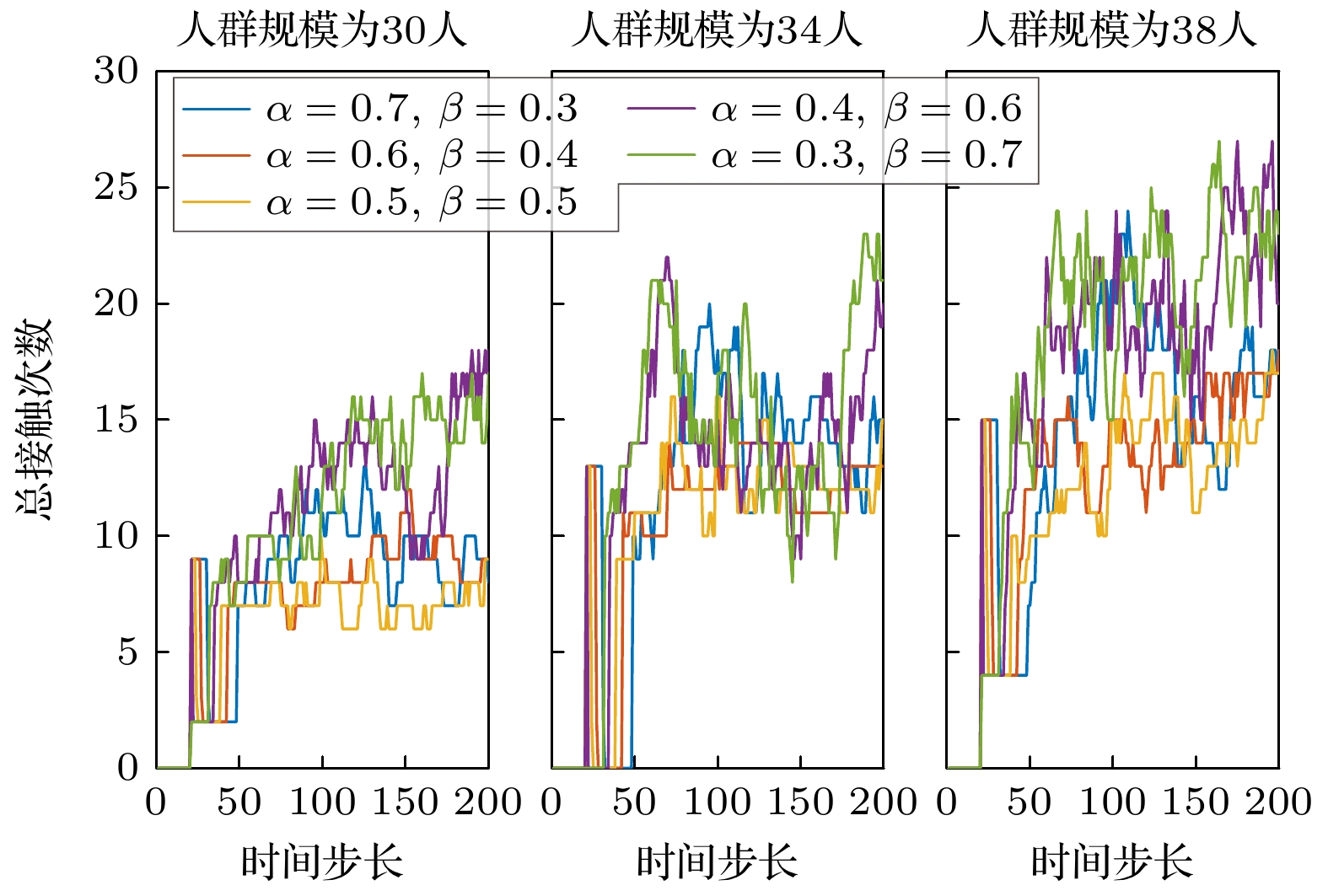
随着人群规模变化(从30人增加到38人), 平均接触冲突(同一时刻发生接触人数/人群数量)整体呈现上升趋势(图21), 每个时间步长内发生接触次数显著增加(图22). 不同参数组合(α和β)的表现亦存在差异: 当低目标权重(α<0.5)且高排斥权重(β>0.5)时, 平均冲突次数分布在较低值区域(<0.3次); 随着α权重增加、β权重减小, 接触次数峰值随移动时间推移显著上升, 38人规模下峰值达25人发生接触冲突, 表明增强目标吸引和减弱行人排斥权重对大规模人群接触冲突具有显著影响.

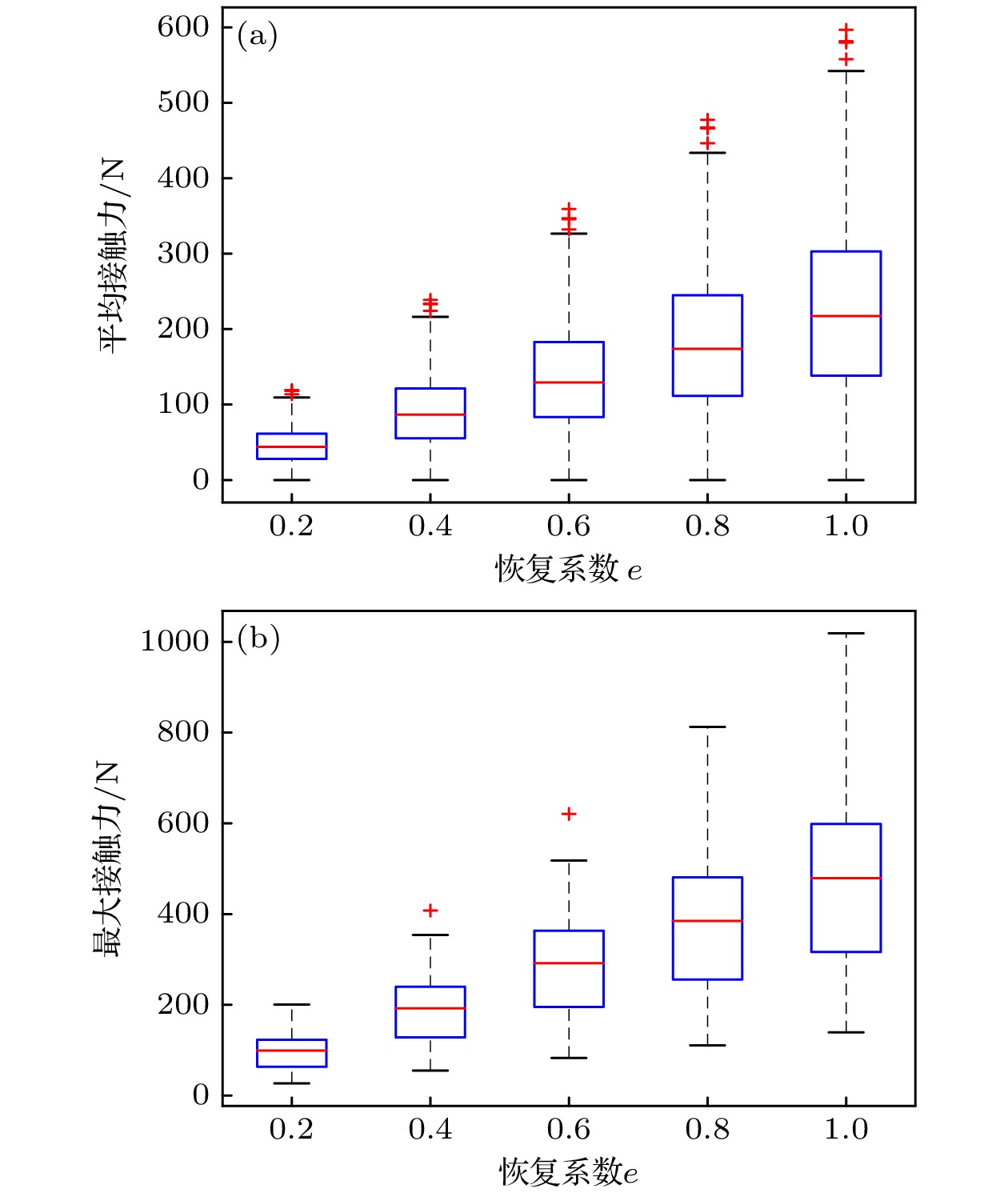
基于碰撞动力学模型(2.4节), 恢复系数(e)的增大显著影响接触力传递. 当e从0.2增至1.0时, 平均接触力均值从50 N升至200 N, 最大接触力上限从100 N增至450 N, 接触作用特征值分布范围扩大(图23). e = 1.0时, 接触力分布呈现显著离群值, 表明完全弹性碰撞可能导致接触力的剧烈波动.

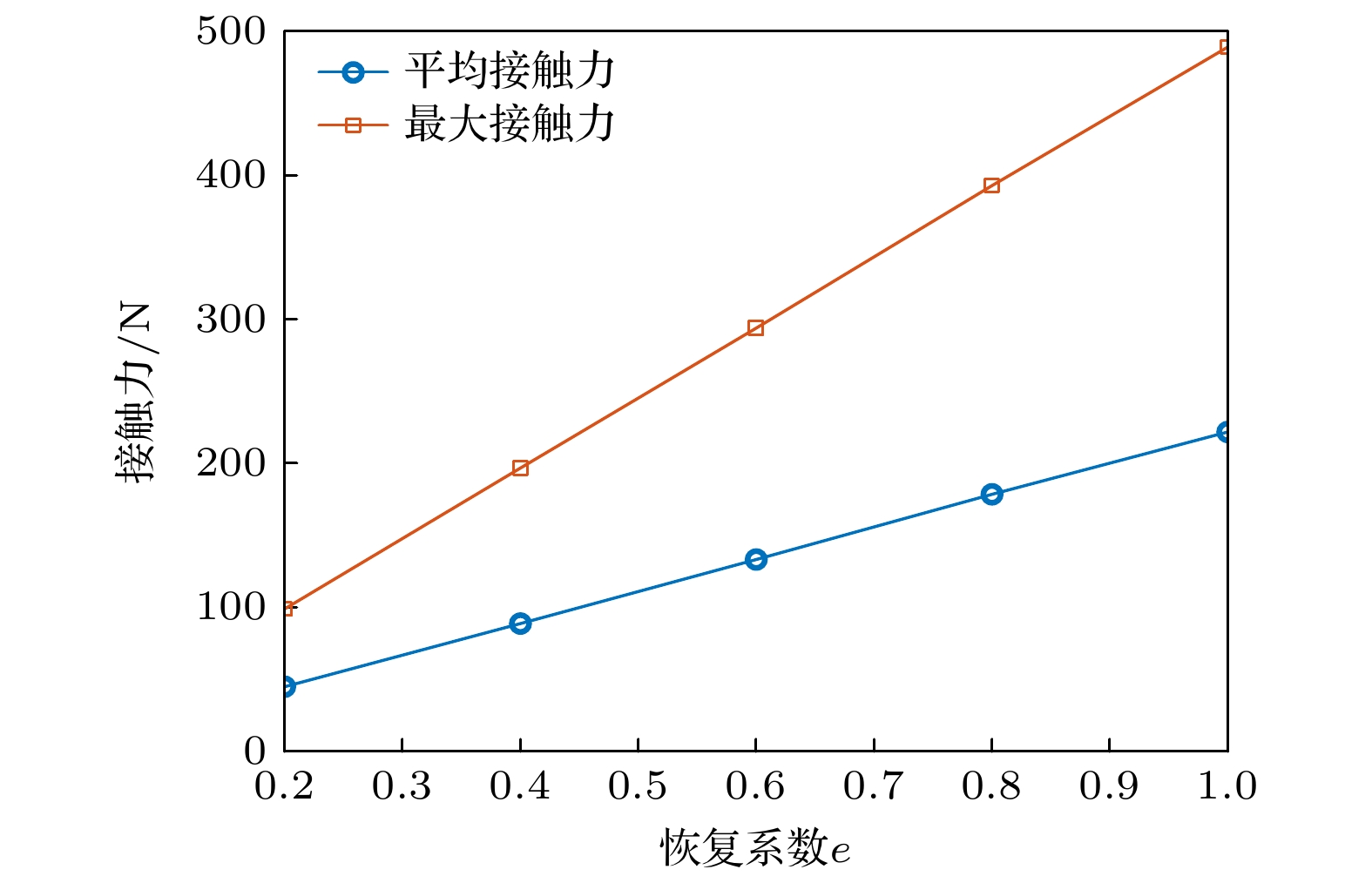
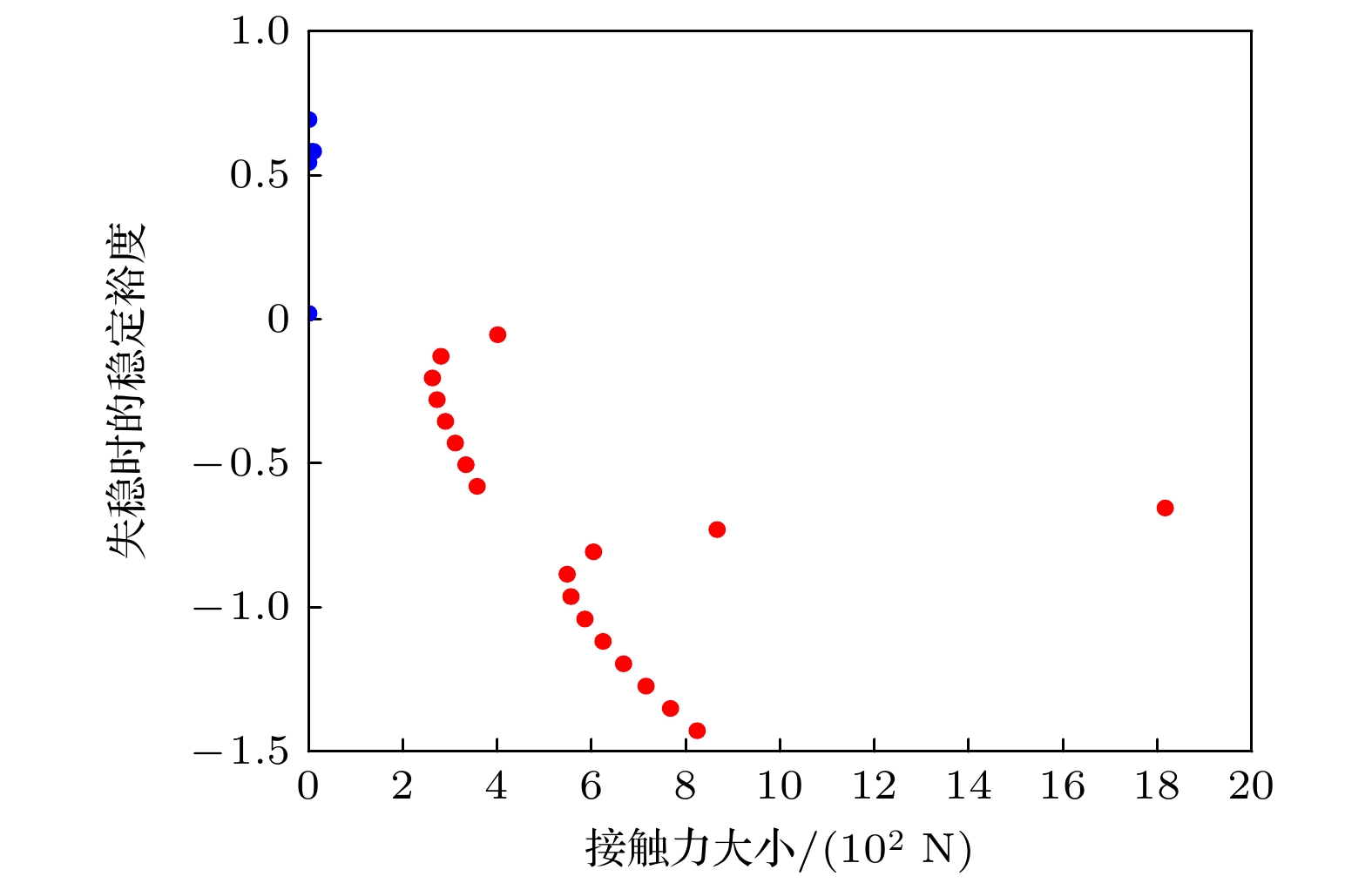
接触力均值与峰值均随恢复系数e的增加而增大(图24), 结合失稳事件分析(图25), 接触力与稳定裕度衰减速率呈正相关, 且当接触力超过400 N, 稳定裕度衰减速率显著加快.

针对楼梯场景高保真仿真难题, 本文提出了一种创新的双层运动模型, 通过分层建模方法融合楼梯几何约束、个体运动学特性及群体力学交互机制, 系统揭示了楼梯行人运动的动态演化规律. 模型采用分层设计实现行人运动学与动力学的动态耦合: 上层空间基于椭圆几何投影分离轴算法检测接触冲突, 下层空间基于元胞离散空间约束跨步路径, 实现步态连续迁移; 同时引入准同步状态切换机制协调大规模群体仿真的时空一致性, 降低计算冗余. 仿真实验表明, 模型能够准确复现行人运动的动态特征, 质心位移比与楼梯坡度理论值高度吻合, 群体速度与观测速度的小误差对比, 验证了模型在宏观与微观层面的可靠性.

动态稳定性分析表明, 当接触力扰动超过生物力学维持平衡阈值时, 质心投影脱离支撑区域的概率显著增加, 失稳事件呈现“局部失衡-持续崩溃”的演化规律. 高密度场景下, 接触力增大会加速稳定裕度衰减(至负值失稳). 此外, 模型参数的调整(如目标吸引权重与行人排斥权重的平衡、碰撞恢复系数的增大)会对群体行为和仿真效率产生影响.

当前模型未考虑行人心理行为异质性(如恐慌情绪)对运动决策的影响, 且匀速运动假设可能弱化加速度动态特性. 未来研究可进一步扩展至非规则楼梯或坡道等复杂环境, 结合实时数据驱动的动态参数校准, 提升仿真精度, 为智能疏散与建筑安全提供更全面的技术支撑.