-
2004年石墨烯被发现, 其色散关系是线性的, 电子的有效质量方程满足二维Dirac方程[1,2]. 硅烯、锗烯等更多具有线性色散关系的二维体系(Dirac材料)也被发现[3–5]. Dirac材料的电子具有相对论的量子特性, 为研究量子电动力学提供了平台, 半整数量子霍尔效应、Klein隧穿效应等现象都被证实[6,7]. 这些材料的高电子迁移率、长自由程等特性也备受青睐[8]. 如何求解不同电磁场下的Dirac方程成了研究者们关注的重要对象[9–14].
二维Dirac方程是一阶耦合微分方程组, 其求解比薛定谔方程更加困难[9]. 只有在均匀磁场、氢原子等极少数情况下该方程有解析解, 一般电磁场下不存在解析解[10]. 研究者们开发了Dirac方程的数值解法, 如对角化法、B样条函数法和差分法[11–14]. 它们在准确度或通用性上具有局限性, 在非缓变势下无法给出准确的物理图像[13,14]. 分区级数解法由于考虑不同区间解的性质, 最大程度地使用解析处理, 能够给出复杂电磁场下薛定谔方程的准确解, 在量子点(环)等电子态研究中发挥了重要作用[15]. 基于分区级数的原理, Zhu等[15]将Dirac方程通过去耦合转化为类似薛定谔方程的形式, 获得了库仑电势和均匀磁场下的解, 但由于去耦合导致附加奇点出现, 只能给出正能态. 本文将对耦合的Dirac方程直接进行级数展开, 从而避免附加奇点, 获得全面的能谱结构. 在推导过程中获得了Dirac电子形成束缚态的判据, 并通过计算相对论二维氢原子以及均匀磁场和线性电势下的Dirac电子态证实该方法的准确性和通用性.
-
石墨烯、硅烯等二维材料在Dirac锥附近的电子可看作相对论性的Dirac电子, 满足Dirac方程. 电子的哈密顿量形式如下[16]:
其中, vF是费米速度, Px和Py是动量算符, σx, σy和σz是Pauli矩阵, I是二维单位矩阵, A是磁矢势, M是质量场, Ve是外加电场,
$\tau = +1(-1) $ 代表K(K')谷. 在平面极坐标系下, 采用磁场规范A = Aθeθ, 并视电场和质量场为中心场, 其形式分别为Ve = Ve(r)和M = M(r). 设ψ是H对应的波函数, 满足Hψ = Eψ, 其是两分量的形式, 上下分量分别代表二维六边形蜂窝状晶格结构中AB两套子格子上的包迹波函数. 采用分离变量法, 将波函数记为$\psi = (R_{\rm A}{\mathrm{e}}^{{\mathrm{i}}l\theta}, {\mathrm{i}}R_{\rm B}{\mathrm{e}}^{{\mathrm{i}}(l + 1)\theta})/r^{0.5}$ , 其中i是虚数单位, l是角动量量子数. 将长度和能量单位分别设为$a_0=[\hbar / ({e}/B_0)]^{0.5} $ 和$E_0=\hbar v_\text{F}/a_0 $ . 令B0 = 1 T, 则a0 = 25.656 nm. 如果费米速度vF ≈ 106 m/s, E0 = 25.656 meV. 将(1)式中的哈密顿量代入Hψ = Eψ, 得到关于径向波函数的方程:(2)式中, j = l + 1/2是总角动量量子数. 根据级数理论, 将磁矢势Aθ展开为级数形式, 并将(2)式中的τj/r作为–1次幂项与Aθ合并为A. (2)式等号右端的能量E是未知的, 其与电势Ve地位相同, 把–E作为0次幂与Ve合并为V. 可将A, M和V写成:
式中, I1, I2和I3分别是磁矢势、质量场和电势级数展开的最高次幂. 质量一般为常数, 但在二维材料中质量也有随空间变化的情形, 此外相对论量子力学中的标量势S(r)与质量的地位相同[17]. 一般而言, A的最低次幂是–1, M的最低次幂是0, V的最低次幂是–1 (库仑电势
$\propto r^{-1} $ , 是最低次幂的电势). 简化(2)式可得 -
物理学家们运用级数解法获得了薛定谔方程下的氢原子、谐振子等问题的解析解, 推动了量子力学的发展. 对于复杂势场, 它们的径向方程无法在全区间以统一的级数形式展开或化为合流超几何方程从而得到解析解. 然而, 级数解法的思想仍然广泛应用[18]. 如图1所示, 通过分析薛定谔方程在正则奇点、常点和非正则奇点的性质, 将方程的解在正则区(正则奇点附近)、泰勒区(常点附近)和非正则区(非正则奇点至无穷远处)进行级数展开, 利用连接条件得到本征能量及对应的波函数[15]. 与薛定谔方程不同, Dirac方程(4)是耦合的微分方程组, 波函数具有二分量形式. 先把方程(4)去耦合, 得到两个独立、含有本征能量的二阶微分方程:
(5c)式中K1是方程(3)中I2和I3的最大值, 即K1 = max(I2, I3), (5d)式中K2 = K1 – 1, (5e)式中K3 = max(2I1, 2I2, 2I3)+ K1. 不同于薛定谔方程, 方程(5)各项前面的表达式更加复杂[14].
对于束缚态波函数而言, 方程(4)有正则奇点r = 0和非正则奇点r = ∞, 但去耦合可能会导致(5a)式和(5b)式产生附加奇点(它们是(5)式中W = 0的根). r = 0的邻域[0, r0]是正则区间, 其中r0的取值要保证该区间的收敛性. 如果波函数在某处接近于0且从该处到无穷远处波函数呈现出一直衰减到0的趋势, 可以将此位置记为r∞, [r∞, ∞]是实际计算的非正则区间. 如果对(5a) 式和(5b)式进行级数展开, 附加奇点会给方程 的级数展开带来更多的困难和不稳定性[19]. 但方 程(4)在[r0, r∞]之间不存在奇点, 因此在[0, r0]和 [r0, r∞]区间可以直接对(4)式的两个分量同时进行级数展开, 而不必考虑附加奇点的影响.
-
以r = 0为展开点, 在区间[0, r0]方程(4)的两分量有正则解, 其级数形式为
其中ρa, ρb是正则解上下分量的指标, H是待定常数, an, bn分别是上下分量级数展开中第n阶项前面的系数. 为找出ρa, ρb及an, bn之间的递推关系, 不妨让a0 = 1或b0 = 1. 将(6)式和方程(3)中A, M和V的多项式形式代入方程(4), 可得到
进行求导运算并将方程(7)等号左端形式相同的项写在一起, 可得
为找到ρa, ρb满足的指标方程, 需要找到方程(8)等号两端最低次幂的关系. 方程(8)等号左端最低次幂分别是
$ ({\rho _{\text{b}}} + {A_{ - 1}}){b_0}{r^{{\rho _{\text{b}}} - 1}} $ 和$ ({\rho _{\text{a}}} - {A_{ - 1}}) {a_0}{r^{{\rho _{\text{a}}} - 1}} $ , 等号右端最低次幂则取决于v–1是否为0 (电势中是否包含库仑势), 下文分两种情况讨论. -
第2种情况是v–1 = 0 (电势中不包含库仑势), 此时v0由于包含能量E, 该项一般不等于0. 方程(8)等号右端上下方程的最低次幂分别是
$ - ({m_0} + {v_0}){a_0}{r^{{\rho _{\text{a}}}}} $ 和$ - ({m_0} - {v_0}){b_0}{r^{{\rho _{\text{b}}}}} $ , 而方程(8)等号左端上下方程的最低次幂分别是$ ({\rho _{\text{b}}} + {A_{ - 1}}){b_0}{r^{{\rho _{\text{b}}} - 1}} $ 和$ ({\rho _{\text{a}}} - {A_{ - 1}}){a_0}{r^{{\rho _{\text{a}}} - 1}} $ . 如果使$ - ({m_0} + {v_0}){a_0}{r^{{\rho _{\text{a}}}}} $ 和$ ({\rho _{\text{b}}} + {A_{ - 1}}){b_0}{r^{{\rho _{\text{b}}} - 1}} $ 相等, 则$ {\rho _{\text{b}}} - 1 = {\rho _{\text{a}}} $ 且$ {\rho _{\text{a}}} = {A_{ - 1}} $ ; 如果使$ - ({m_0} - {v_0}){b_0}{r^{{\rho _{\text{b}}}}} $ 和$ ({\rho _{\text{a}}} - {A_{ - 1}}){a_0}{r^{{\rho _{\text{a}}} - 1}} $ 相等, 则$ {\rho _{\text{a}}} - 1 = {\rho _{\text{b}}} $ 且$ {\rho _{\text{b}}} = - {A_{ - 1}} $ . 指标$ {\rho _{\text{a}}} $ 和$ {\rho _{\text{b}}} $ 必须非负, 波函数才有意义, 再分两种情况讨论.1)当
$ {A_{ - 1}} \geqslant 0 $ 时,$ {\rho _{\text{a}}} = {A_{ - 1}} = \rho $ ,$ {\rho _{\text{b}}} ={\rho _{\text{a}}} + 1 $ . 如果令$ {a_0} = 1 $ , 则由$ - ({m_0} + {v_0}){a_0}{r^{{\rho _{\text{a}}}}} $ 与$ ({\rho _{\text{b}}} + {A_{ - 1}}){b_0}{r^{{\rho _{\text{b}}} - 1}} $ 相等, 可得到$ {b_0} $ , 并写成如下形式:对方程(8)进行指标变换, 与方程(12)和(13)的推导过程类似, 得到递推关系:
2)当
$ {A_{ - 1}} < 0 $ 时,$ {\rho _{\text{b}}} = - {A_{ - 1}} = \rho $ ,$ {\rho _{\text{a}}} ={\rho _{\text{b}}} + 1 $ . 如果令$ {b_0} = 1 $ , 由$ - ({m_0} - {v_0}){b_0}{r^{{\rho _{\text{b}}}}} $ 和$ ({\rho _{\text{a}}} - {A_{ - 1}}) {a_0}{r^{{\rho _{\text{a}}} - 1}} $ 相等, 可得到$ {a_0} $ , 并写成如下形式:对方程(8)进行指标变换, 与方程(12)和(13)的推导过程类似, 得到递推关系:
即得到了正则区波函数的级数形式, 但(6)式前面的待定常数H还需要通过波函数的连接条件确定. 接下来推导泰勒区[r0, r∞]波函数的级数形式.
第1种情况是v–1≠0 (电势中包含库仑势), 由方程(8)两端r的最低次幂前面的系数相等, 从而得到指标方程[20]:
方程(9)具有非平庸解, 可得到正则区间的指标为
如果令a0 = 1, 还可从(9)式得到b0. 为了便于推导, 写成矩阵形式:
为找到方程(8)中系数的递推关系, 对方程(8)指标进行变换, 可得到:
让方程(12)中每个等式两端的rn前面的系数相等, 可得到:
其中的min(x, y)表示x与y的最小值. 整理方程(13), 得到系数之间的递推关系为
-
为了级数在泰勒区[r0, r∞]能够快速收敛, 把该区间等分为N个小区间
$[r_{i-1}, r_i]~(i = 1, 2, \cdots , N) $ . 在第i个区间的中心$x = (r_{i-1} + r_i)/2 $ 将径向波函数展开为泰勒级数:由于Dirac方程在本质上是二阶微分方程, 其在常点邻域内应该有两个线性无关解[20], 将该区间的级数解写为两个线性无关的级数解, 如(19)式等号右边所示. 两解满足同样的递推关系, 其线性无关体现在前两项的系数不同, 所以只需将(19)式等号右边的第一解代入方程(4)进行推导, 可得到:
将方程(20)等号两端同时乘以r, 并把关于r的幂次展开为关于r – x的幂次, 得到:
其中
$ C_i^k = i!/k!/(i - k)! $ 是二项式系数. 将方程(21)中的指标进行变换(例如, 方程(21)中第1个等式等号左端第3项会出现$ {(r - x)^{n + k}} $ , 为了将$ {(r - x)^{n + k}} $ 变为与方程其他项相同的幂形式, 令$ n' = n + k $ 并变化求和符号顺序, 将$ n' $ 指标的求和符号放在最前面, 其取值范围为0—∞, 其次是$ k $ 指标的求和符号, 它的取值范围为0—$ \min (n, {I_1} + 1) $ , 最后是i指标的求和符号, 其取值范围是从$ \max (k - 1, - 1) $ 到$ {I_1} $ , 并把$ b_n^ * $ 中变为$ b_{n' - k}^ * $ , 最后再把$ n' $ 用$ n $ 取代), 可得到:令方程(22)等号两端(r – x)n前面的系数相等, 得到系数之间的递推关系:
根据(22)式中(r – x)0前面的系数相等, 得到如下关系:
(23)式和(24)式的递推关系也适用于(19)式第2解的系数[
$ {d_n}, d_n^* $ ]. 为了保证两解线性无关, 需要使它们的前两项系数不同, 令b0 = 1, b1 = 0以及d0 = 0, d1 = 1. -
在非正则区间[r∞, ∞], 束缚态的波函数呈现出指数衰减形式. 由于方程(4)中上下分量的衰减指数可能不同, 我们无法将上下分量同时进行级数展开. 非正则区间[r∞, ∞]不会出现因去耦合而产生的附加奇点, 可对去耦合的方程(5a)和(5b)分别进行级数展开, 如同求解薛定谔方程[15]. 方程(5a)和(5b)统一为
能量E包含在方程(5)中电势V的0次项级数中, 所以K1和K3的最小值是0. 根据方程(5c)和(5d)确定K2 = K1 – 1. 将方程(25)解的表达式写为e指数形式:
U(r)以幂级数形式出现. 将(26)式代入(25)式中, 得到关于G(r)的方程及其各项:
下面要找出U(r)中的K和各项系数. 为了保证(27)式有常规解, (27)式中P*(r)的幂次须高于Q*(r)的幂次[20]. 将U(r)代入P*(r)和Q*(r), 利用K2 = K1 – 1, 得到:
为使P*(r)的最高幂次高于Q*(r)的最高幂次, Q*(r)中幂次高于K1 + K – 2的级数项必须为0, 将Q*(r)写为幂次低于K1 + K – 1的项与幂次高于K1 + K – 2的项之和:
其中
Q*(r)的幂次必须低于K1 + K – 1, 所以T的各项必须均为0. 这就要求T中的K3 = K1 + 2K – 2, 即K = (K3 – K1 + 2)/2以及下式:
其中, K1 + K – 1 k K1 + 2K – 2. 将k = K3 = K1 + 2K – 2代入(33)式, 得到U(r)最高次幂的系数:
其中,
$ K = {{({K_3} - {K_1} + 2)} {/ } 2} $ .如果K>1, 从(33)式可以从高阶到低阶依次得到U(r)中K>k≥1阶级数前面的系数:
δ是Kronecker delta符号. 将U(r)代入(29)式和(30)式得P*(r)和Q*(r), 代入(27)式得
其中, C是待定常数, m是指标, c0 = 1. 将(37)式代入(36)式中, 得到:
对(38)式的指标进行变换后得到:
(39)式中r–n的系数都为0. (39)式的最高幂次是K1 + K – 2, 其系数为零确定指标m为
根据r–n的系数都为0, 可得到递推关系式:
式中, c的下标
$K_1 + K - 2 + n = 1, 2, 3, \cdots $ , 相应的$n = - (K_1 + K - 2) + 1, - (K_1 + K - 2) + 2, - (K_1 + K - 2) + 3, \cdots$ . 方程(37)中的待定常数C则需要根据非正则区与最邻近的泰勒区的连接条件确定. 下面推导各个区间的连接条件. -
在泰勒区[r0, r∞]第i个小区间[ri–1, ri], 令Δi = (ri – ri–1)/2, 其右边界和左边界为
其中:
根据波函数R的上下分量在第i–1区的右端与第i区的左端的连续性条件:
可得到第i – 1区与第i区的常数B和D之间的关系:
其中Ti–1, i是连接第i–1区与i区的常数[B, D]的传输矩阵. 第N区与第1区常数的关系:
为了连接正则区[0, r0]和泰勒区的第1区[r0, r1], 定义波函数的上下分量在r = r0的比例为K0. 为了连接非正则区[r∞, ∞]和泰勒区的第N个区间
$[r_{N-1}, r_N] $ (其中rN = r∞), 定义波函数的上下分量在r = r∞的比例为K∞. K0和K∞的定义是:将(42)式泰勒区第1区的左边与第N区的右边的上下分量代入(47)式, 得到:
根据(46)式的关系求出[BN, DN]的表达式并代入(48)式中, 得线性方程组:
其中:
方程(50)有非平庸解, 则其前面的矩阵M的行列式值为0. 由于M的元素中含有待定本征能量E, 它的行列式值det(M)包含E, 由此得到关于能量E的方程:
对于束缚态, 通过数值方法求解方程(51)可以获得一系列的本征能量E. 将E代入各个区间波函数的表达式, 归一化之后, 就获得了对应的径向波函数.
-
当电子处于束缚态时, 当r→∞时波函数应该衰减为0. 这意味着在非正则区间[r∞, ∞]方程(28)中的eU(r)必须是衰减的, 因此U(r)级数中展开的最高次幂项的系数必须是负实数. 根据(34)式, U(r)级数展开的最高次幂前面的系数是uK. 根据方程(3)和(5), 我们进一步得到uK的表达式
其中, I = max(I1, I2, I3). 当uK是负实数时, 波函数在r→∞时衰减至零, 此时形成的是束缚态. 当uK是虚数时, 波函数在r→∞时振荡, 此时形成的是扩展态. (52)式成为Dirac电子形成束缚态的判据. 根据(52)式, 磁场A和质量场M有助于uK形成负实数, 有助于Dirac电子束缚态的形成, 而电场V有助于uK形成虚数从而产生Klein效应. 具体而言, 如果A或M的最高幂次大于V的最高幂次(I1 > I3或I2 > I3), 此时uK没有电势项, 为负实数, Dirac电子存在束缚态且数目不受限制, 如石墨烯中均匀磁场和库仑电势下的情况[2,11]; 反之, 如果V的最高幂次大于A和M的最高幂次(I1 < I3且I2 < I3), 则Dirac电子会由于Klein效应而隧穿. 文献[21]通过将Dirac方程去耦合变换为(5a)式和(5b)式的形式, 分析了磁矢势与电势为幂指数的情形, 指出A的幂次大于V的幂次时才能存在束缚态, 属于判据(52)式的范畴. 如果A或M的最高幂次等于V的最高幂次(I1 = I3或I2 = I3), 此时需要比较它们最高次幂前面系数的大小才能确定Dirac电子束缚态的存在情况[14]. 总之, (52)式Dirac电子束缚态-非束缚态的判据适用于各种电场、磁场和质量场下的情形且给出了束缚态指数衰减的具体形式, 为调控Dirac电子量子状态提供了依据.
-
带电杂质会影响二维材料的输运性质和光谱性质, 其常见的电势是库仑电势. 此外, 研究二维材料中电子与电子之间的相互作用也需要考虑库仑电势, 因此Dirac电子在库仑电势下的量子态对于理解杂质态及电子相互作用具有重要意义[22]. 在库仑电势
$V_\text{e} = \alpha/r$ ($(\alpha = Z\text{e}^2/(4\pi\varepsilon\varepsilon_0/hbar v_\text{F}) $ 是精细结构常数)下, 对于无质量的Dirac电子, 由于A和M均为0, uK为虚数, 此时不存在束缚态[22]. 对于有质量的Dirac电子, M为常数, 能量E包含在电势的0阶幂次中. 根据方程(3c)和(52)式,$u_K = - (M^2 - E^2)^{0.5}$ , 此时存在束缚态且能量E<M. 相对论二维类氢原子的束缚态能级为[23]其中, n是径向量子数, j是总角动量量子数, (n, j)表示对应的量子态. 当库仑电势存在时, 根据方程(10), 其正则区的指标
$\rho = \rho_{\mathrm{a}} = \rho_{\mathrm{b}} = (j^2 -\alpha^2)^{0.5}$ 并非整数,$V_{\mathrm{e}} = \alpha/r $ 在r = 0处无穷大, 一般数值方法无法反映r = 0附近解的性质而不能准确拟 合此区域的波函数、获得较精确的解[11]. 本文方 法在获得正则解的基础上可以无限逼近波函数, 因此能够获得精确的解. 表1所示为α = –0.1, M = 500 meV时j = –1.5, –0.5, 0.5, –1.5最低4个能级的数值解和(53)式的解析解, 并比较了两者的相对误差, 相对误差低于10–8, 远低于文献[14]的10–3, 且随着j变大还会进一步降低. 图2所示为j = –0.5, 0.5最低的3个能级的波函数, 从中看到对于j<0, 同一量子态的下分量节点数比上分量节点数多1个, 对于j>0, 两者的节点数相同. 此外, 下分量比上分量小, 这是因为电子质量非零, 且当电子质量达到天然的质量512 MeV时, 下分量基本不存在, 上分量则变为薛定谔方程的波函数. 上述结果验证了分区级数解法在求解Dirac方程中具有非常高的准确性. -
均匀磁场下的二维Dirac电子具有朗道能级, 导致二维材料出现半整数量子霍尔效应. 横向电场会破坏朗道能级, 从而影响其输运和磁光谱性质, 因此探索Dirac电子在复杂电磁场下的行为有助于调控其输运和光谱性质[24]. 线性电势Ve = Fr是常见的电势模型[10], 根据(52)式的判据, 线性电势不能形成束缚态, 这与薛定谔方程完全不同. 如果在电子运动平面上施加垂直均匀磁场B, 其磁矢势Aθ = Br/2, 由(52)式,
$u_K = u_2 = -0.5(0.25B^2 - F^2)^{0.5} $ . 当F < 0.5B时, 存在束缚态; 当F > 0.5B时, 存在非束缚态. Dirac方程在Ve = Fr和Aθ = Br/2下不具有解析解. 如图3所示, 采用分区级数解法计算了磁场B = 10 T时j = –1/2, –3/2, 1/2, 3/2的前几个束缚态能级随着电场强度F的变化. 朗道能级的粒子-空穴对称性不再存在. 当F趋近于0时, 能级趋近于朗道能级, 呈现出高度的简并性. 电势解除了朗道能级的简并, 随着F的增大, 能级逐渐变大. 正能级间距变大且没有发生序列改变; 负能级间距变小则产生了序列变化. 当F = 0.5B时, 发生了有趣的现象: 如图3的竖直虚线所指, 正能束缚态仍然存在, 负能束缚态不能转化为正能的消失, 转化为正能的量子态仍然存在束缚态. 例如, 对j = –1/2, 在F = 0.5B时它原来的两个负能态(0, –1/2)和(1, –1/2)由于 转变为正能而继续以束缚态存在, 其波函数如图4(a), (b)所示. 根据公式(34), 在F = 0.5B时$u_K= u_{3/2} = -2(E_F)^{0.5}/3 $ , 只有能量E > 0时uK为实数, 才有束缚态存在. 图4(c), (d)中给出了原来正能态(0, –1/2)和(1, –1/2)在F = 0.5B时的波函数, 与图4(a), (b)比较, 其波函数更加集中于原点处, 有更强的局域性, 尽管其能量更高. 这是因为电势对于Dirac电子的正能态(电子态)和负能态(空穴态)具有相反的限制作用[2]. 以上结果表明, 线性电势会改变二维Dirac电子的朗道能级结构, 破坏了Dirac电子在磁场下的电子-空穴对称性, 导致态密度发生变化, 将影响二维材料的霍尔效应和磁光谱性质[24]. -
本文提出了求解相对论量子力学中二维Dirac方程的分区级数解法, 并用该方法计算了相对论氢原子的能级和波函数, 证实了该方法的准确性. 通过计算线性电势与均匀磁场组合下Dirac电子的能级和波函数, 该方法表现出具有求解复杂电磁场下Dirac方程的通用性. 在推导非正则区Dirac方程的解形式时, 得到了Dirac电子在电磁场下的束缚态的判别准则, 该准则把电场、磁场和质量场都包含在内, 为电磁场调控Dirac束缚态提供了依据. 该方法为进一步研究复杂电磁场下Dirac电子的能级结构、光谱性质等提供了计算工具.
此外, 在计算均匀磁场和线性电势下Dirac电子的能级和波函数时, 研究了Dirac电子能级随着线性电势强度的关系, 观察到负能态能级序列变化的现象. 对于均匀磁场和线性电势, 当F < 0.5B时, 由于磁场占主导作用束缚态存在, 反之则不存在束缚态. 在临界处F = 0.5B, 原来正能的束缚态仍然存在, 而只有某些原来的负能态由于接近于零能而转化为正能态, 其束缚态继续存在, 其余负能态的束缚态则消失. 这些结论丰富了我们对复杂电磁场下Dirac电子结构的认识, 为电磁场调控二维Dirac材料的电子结构提供了依据.
分区级数解法在二维Dirac方程中的应用
Solution of two-dimensional Dirac equation by sectioned series expansion method
-
摘要: 随着石墨烯等二维材料的发现, 相对论二维Dirac方程越来越受到研究者们的关注, 准确求解电磁场中的Dirac方程是研究和调控Dirac电子量子状态的基础. 通过将分区级数方法应用到Dirac方程中并对该方程在正则区、泰勒区和非正则区进行级数展开, Dirac电子束缚态的普适性判据被推导出来, 束缚态的能级和波函数被计算出来. 用该方法计算有质量Dirac电子在库仑电势下(相对论二维类氢原子)的能级和波函数并与解析解进行比较, 结果表明该方法具有非常高的准确性. 对均匀磁场和线性电势下Dirac电子态的计算结果表明, 该方法对于复杂电磁场中Dirac方程的求解具有普遍的适用性. 用该方法研究了均匀磁场B和线性电势V = Fr下Dirac电子束缚态随着电势强度的变化, 负能态的能级序列变化被观察到, 在临界处F = 0.5B, 正能态的束缚态仍然存在, 而只有能量超过0的少数负能态的束缚态才存在. 该方法提供了求解Dirac方程的有效工具并丰富了人们对相对论量子力学的认识.Abstract: With the discovery of two-dimensional materials like graphene, the relativistic two-dimensional Dirac equation has received increasing attention from researchers. Accurately solving the Dirac equation in electromagnetic fields is the foundation for studying and manipulating quantum states of Dirac electrons. Sectioned series expansion method is successful and accurate in solving Schrödinger equation under complex electromagnetic fields. Dirac equation is a system of coupled first-order differential equations with undermined eigenvalues, and it is more difficult to solve. By applying the sectioned series expansion principle to Dirac equation and conducting series expansions in regular, Taylor and irregular regions, we obtain an accurate method with wide applicability. With the method, a universal criterion for bound states of Dirac electrons in electromagnetic fields is derived and the energy levels and wave functions of bound states can be accurately calculated. The criterion given in the main text body shows that the magnetic field and mass field help to confine Dirac electrons while the electric field tends to deconfine them due to Klein tunneling. When the highest power of the electric potential is equal to that of the magnetic vector potential or the mass field, confined-deconfiend states depend on the comparison of their coefficients. We apply the method to two cases: one is massive Dirac electron in Coulomb electric potential (relativistic two-dimensional hydrogen-like atom) and the other is Dirac electron in uniform mangetic field (mangetic vector potenial is A = 1/2Br) and linear electric potential V = Fr. The energy levels of the hydrogen-like atom are calculated and compared with analytical solutions, demonstrating the exceptional accuracy of the method. By solving Dirac equation under uniform magnetic field and linear electric potential, the method proves to be broadly applicable to the solutions of Dirac equation under complex electromagnetic fields. Under uniform magnetic field B and V = Fr, as the F increases, level orders of negative energy states change and at the critical point F = 0.5B, the bound states of positive ones still exist while only certain negative ones can exist on condition that their energies exceed zero. The sectioned series expansion method provides an effective computational framework for Dirac equation and it deepens our understanding of relativistic quantum mechanics.
-

-
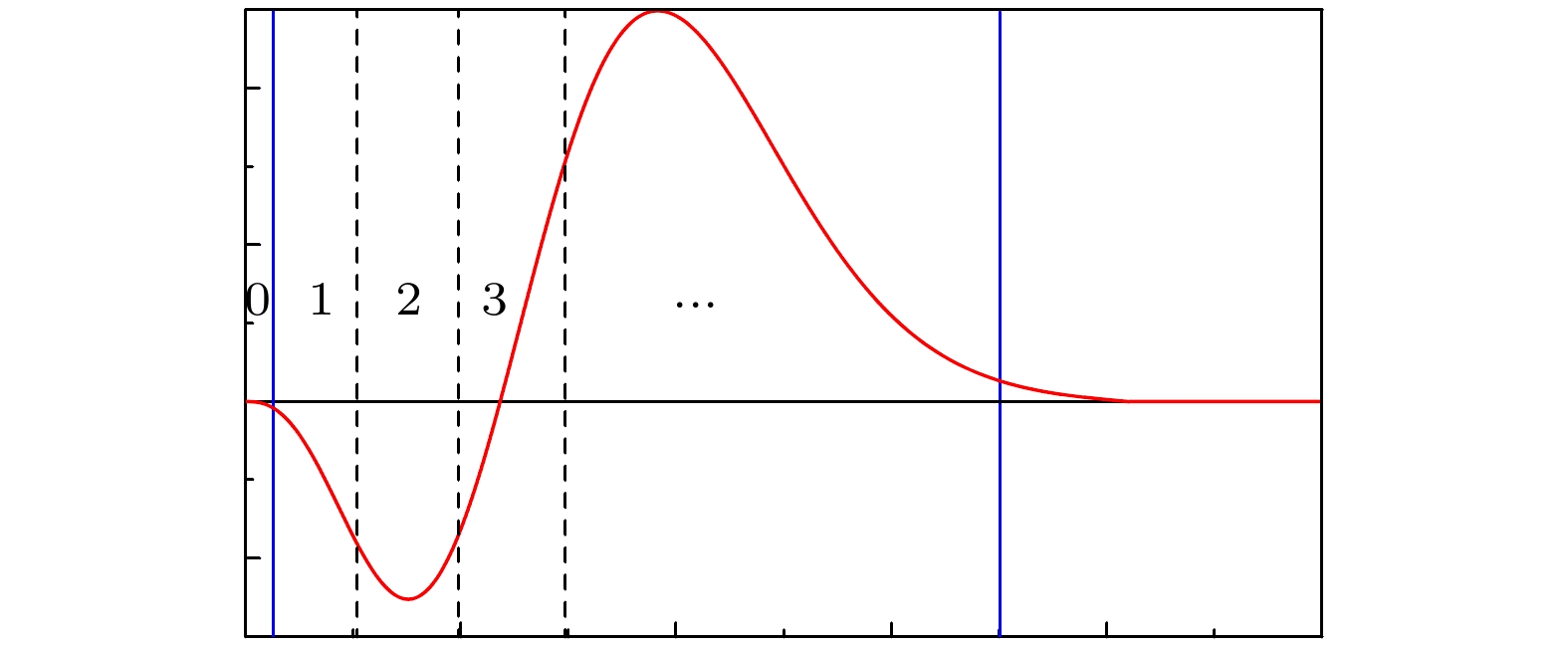
图 1 分区级数解法示意图, 径向波函数在不同区间分别用级数精确表示出来, 第0个区间是正则区(regular region), 最后是非正则区(irregular region), 中间都是泰勒区(Taylor region)
Figure 1. The sketch of the sectioned series expansion method, the radial wavefunction is exactly expressed by different series expansions in separate regions: The zeroth region is regular one, the last is irregular one and others between them are Taylor ones.
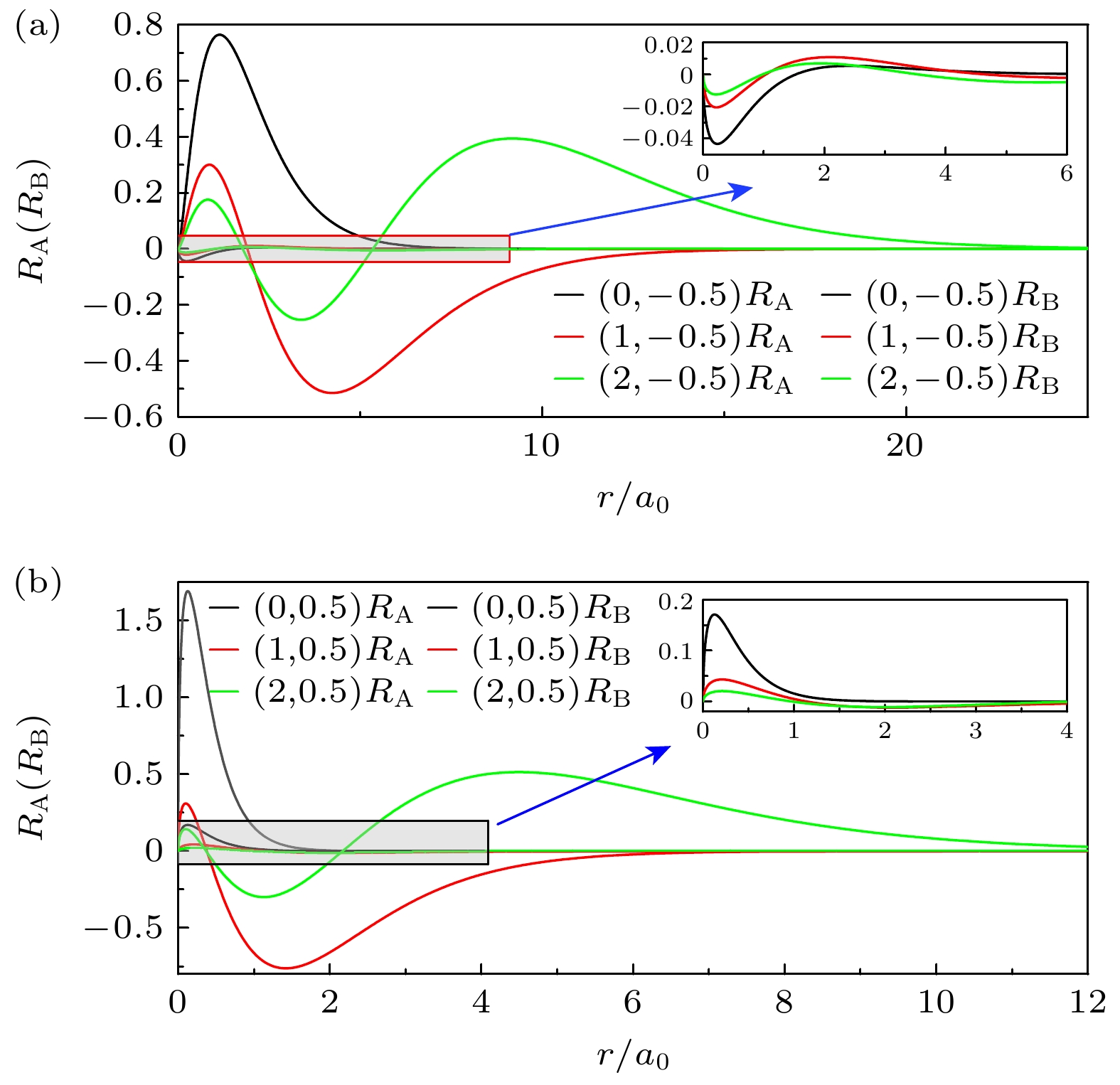
图 2 在库仑电势中的α = –0.1时用分区级数解法计算相对论氢原子能级的径向波函数上下分量(RA和RB), 在计算时取M = 500 meV, 粗线(细线)分别代表上下分量, 右上方的图是对局部波函数的放大, (a), (b)分别是j = –0.5和j = 0.5时最低的3个能级的波函数
Figure 2. The upper and lower components (RA和RB) of the radial wave function of the relativistic hydrogen atom calculated by sectioned series expansion method when α = –0.1 in the Coulomb electric potential and M = 500 meV, bold (thin) lines represent the upper (lower) components and the insets in the top right are the zooms of parts of the functions: (a), (b) The three lowest energy levels of j = –0.5 and j = 0.5, respectively.
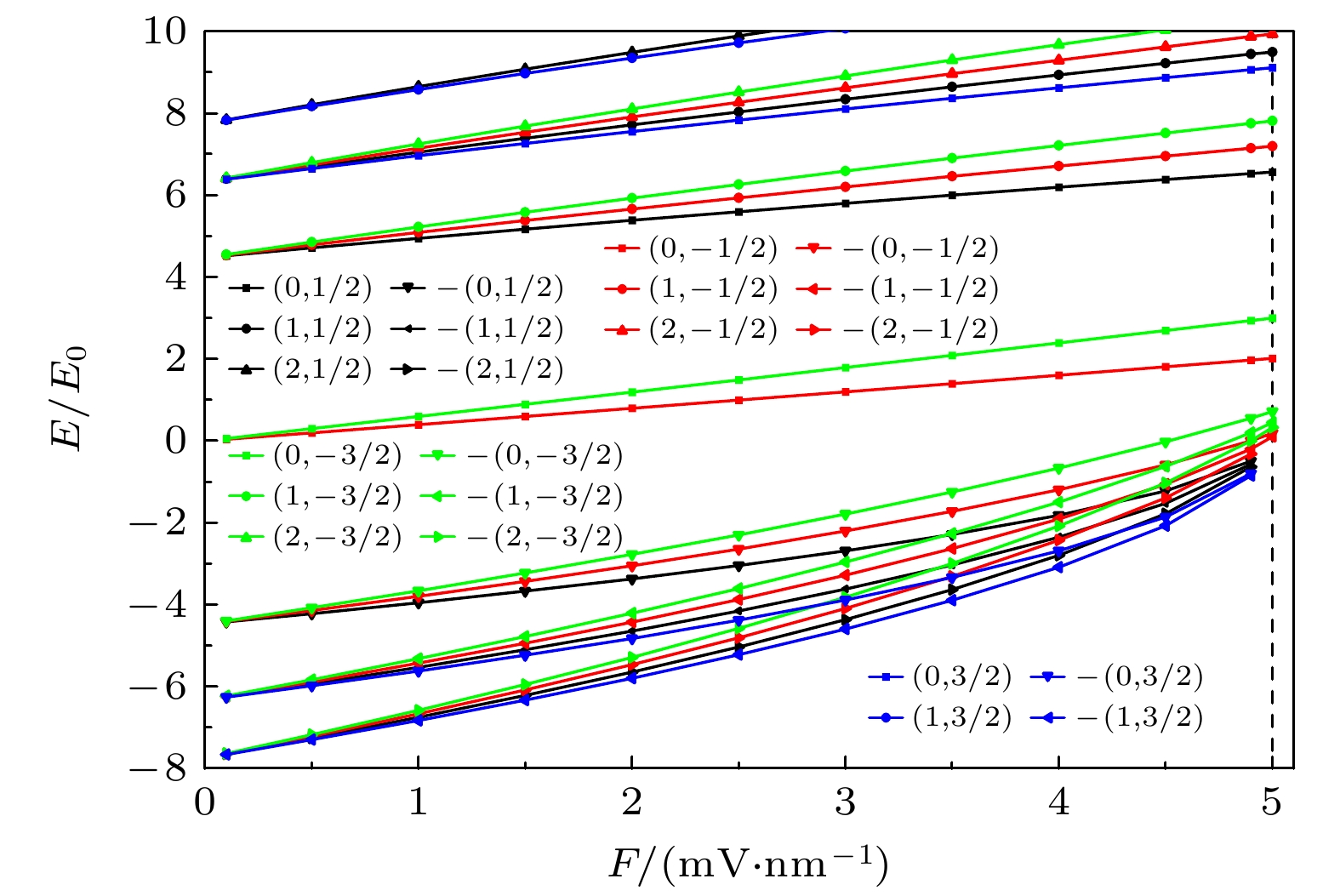
图 3 在均匀磁场B = 10 T时, 总角动量量子数j = –1/2, –3/2, 1/2, 3/2的能级随着线性电势V = Fr的变化, 其中(n, j)前面的负号表示负能态, F = 5时的垂直虚线是为了观察每个能级是否存在束缚态能级
Figure 3. The energy levels of the total angular momentum quantum number j = –1/2, –3/2, 1/2, 3/2 as a function of the linear electric potential, the minus signs in front of (n, j) indicates the negative energy states, and the vertical dashed line at F = 5 is to observe whether there is a bound state for every energy level.
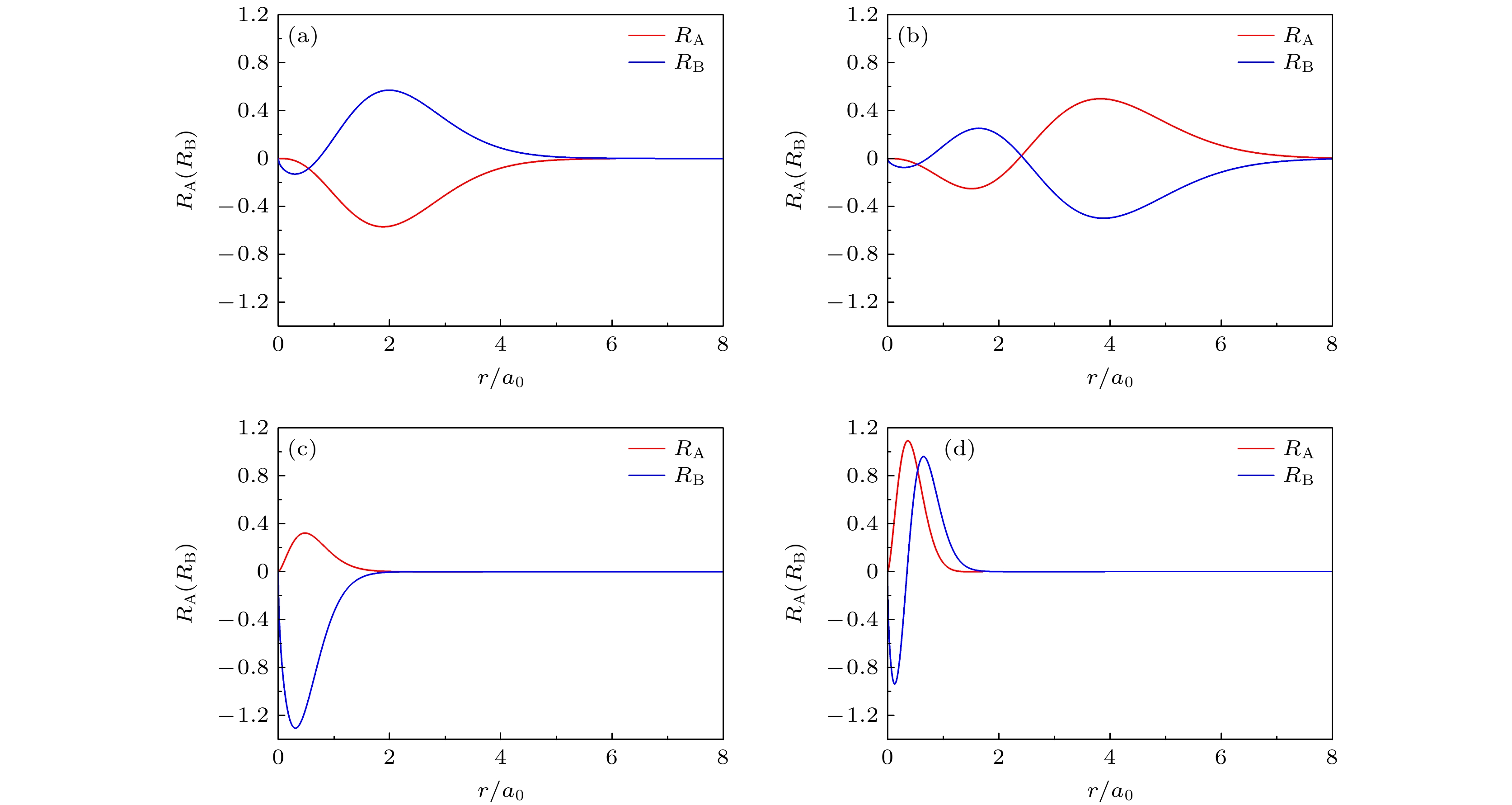
图 4 Dirac电子在F = 0.5B时均匀磁场和线性电势下j = –1/2的径向波函数的上下分量(RA和RB) (a), (b)分别是原来负能态(0, –1/2)和(1, –1/2)在F = 0.5B时转变为正能态的波函数; (c), (d) 分别是原来正能态(0, –1/2)和(1, –1/2)在F = 0.5B时的波函数
Figure 4. The upper and lower components (RA和RB) of the radial wave function of Dirac electron at F = 0.5B in homogenous magnetic field and linear electric potential when j = –1/2: (a), (b) The original negative energy levels (0, –1/2) and (1, –1/2); (c), (d) the original positive energy levels (0, –1/2) and (1, –1/2).
表 1 在库仑电势中的α = –0.1时用分区级数解法计算相对论氢原子能级的数值解与(53)式的解析解比较, 计算时取M = 500 meV, 能级均除以M
Table 1. Comparison between numerical energy levels by sectioned series expansion method and analytical energy levels by Eq. (53) when α = –0.1 in the Coulomb electric potential and M = 500 meV, with all energy levels divided by M.
(n, j) En, j 数值解 En, j 解析解 相对误差 (n, j) En, j 数值解 En, j 解析解 相对误差 0, –1.5 0.9991988238614 0.99919882386158 1.8×10–13 0, 0.5 0.9797958971133 0.97979589711327 2.9×10–14 1, –1.5 0.9995913079808 0.99959130798090 9.9×10–14 1, 0.5 0.9977551312156 0.99775512256234 8.7×10–9 2, –1.5 0.9997528114902 0.99975281149021 1.4×10–14 2, 0.5 0.9991944716637 0.99919446965227 2.0×10–9 3, –1.5 0.9998345510564 0.99983455105648 7.9×10–14 3, 0.5 0.9995897240939 0.99958972295987 1.1×10–9 0, –0.5 0.9977551536827 0.99775512256234 3.1×10–8 0, 1.5 0.99777530313970 0.99777530313972 1.8×10–14 1, –0.5 0.9991944768698 0.99919446965227 7.2×10–9 1, 1.5 0.99919882386160 0.99919882386158 2.2×10–14 2, –0.5 0.9995897256360 0.99958972295987 2.7×10–9 2, 1.5 0.99959130798070 0.99959130798090 2.0×10–13 3, –0.5 0.9997520675873 0.99975206631993 1.3×10–9 3, 1.5 0.99975281149010 0.99975281149021 1.1×10–13 0, 2.5 0.9991996881893 0.99919967974374 8.5×10–9 2, 2.5 0.99975295828120 0.99975295828121 9.3×10–15 1, 2.5 0.9995916199728 0.99959161997285 4.7×10–14 3, 2.5 0.99983463144880 0.99983463144884 4.0×10–14 -
[1] Semenoff G W 1984 Phys. Rev. Lett. 53 2449 doi: 10.1103/PhysRevLett.53.2449 [2] Sun S, Zhu J L 2014 Phys. Rev. B 89 155403 doi: 10.1103/PhysRevB.89.155403 [3] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666 doi: 10.1126/science.1102896 [4] Feng B, Ding Z, Meng S, Yao Y, He X, Cheng P, Chen L , Wu K 2012 Nano Lett 12 3507 doi: 10.1021/nl301047g [5] Gomes K K, Mar W, Ko W, Guinea F, Manoharan H C 2012 Nature 483 306 doi: 10.1038/nature10941 [6] Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V, Firsov A V 2005 Nature 438 197 doi: 10.1038/nature04233 [7] Elahi M M, Vakili H, Zeng Y, Dean C R, Ghosh A W 2024 Phys. Rev. Lett. 132 146302 doi: 10.1103/PhysRevLett.132.146302 [8] 陈晓娟, 徐康, 张秀, 刘海云, 熊启华 2023 物理学报 72 237201 doi: 10.7498/aps.72.20231786 Chen X J, Xu K, Zhang X, Liu H Y, Xiong Q H 2023 Acta Phys. Sin. 72 237201 doi: 10.7498/aps.72.20231786 [9] 冉扬强, 薛立徽, 胡嗣柱 2002 物理学报 51 2435 doi: 10.3321/j.issn:1000-3290.2002.11.006 RanY Q, Xue L H, Hu S Z 2002 Acta Phys. Sin. 51 2435 doi: 10.3321/j.issn:1000-3290.2002.11.006 [10] Silbar R R, Goldman T 2010 Eur. J. Phys. 32 217 [11] Kandemir B S, Mogulkoc A 2010 Eur. Phys. J. B 74 535 doi: 10.1140/epjb/e2010-00116-4 [12] Lee C M , Lee R C H, Ruan W Y, Chou M Y 2010 Appl. Phys. Lett. 96 212101 doi: 10.1063/1.3435478 [13] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y, Mitroy J 2012 Chin. Phys. Lett. 29 063101 doi: 10.1088/0256-307X/29/6/063101 [14] Giavaras G, Maksym P A, Roy M 2009 J. Phys. : Condens. Matter 21 102201 doi: 10.1088/0953-8984/21/10/102201 [15] Zhu J L, Xiong J J, Gu B L 1990 Phys. Rev. B 41 6001 doi: 10.1103/PhysRevB.41.6001 [16] Ezawa M 2012 New J. Phys. 14 33003 doi: 10.1088/1367-2630/14/3/033003 [17] Fishbane P M, Gasiorowicz S G, Johannsen D C, Kaus K 1983 Phys. Rev. D 27 2433 doi: 10.1103/PhysRevD.27.2433 [18] Batchelor M T, Henry R A, Lu X 2023 AAPPS Bulletin 33 29 doi: 10.1007/s43673-023-00105-3 [19] Zhu J L, Sun S 2012 Phys. Rev. B 85 035429 doi: 10.1103/PhysRevB.85.035429 [20] 王竹溪, 郭敦仁 2012 特殊函数概论(北京: 北京大学出版社) 第39—58页 Wang Z X, Guo D R 2012 Special Functions (Beijing: Peking University Press) pp39–58 [21] Giavaras G , Nori F 2010 Appl. Phys. Lett. 97 243106 [22] Pereira V M, Nilsson J, Neto A H C 2007 Phys. Rev. Lett. 99 166802 doi: 10.1103/PhysRevLett.99.166802 [23] Novikov D S 2007 Phys. Rev. B 76 245435 doi: 10.1103/PhysRevB.76.245435 [24] Lukose V, Shankar R, Baskaran G 2007 Phys. Rev. Lett 98 116802 doi: 10.1103/PhysRevLett.98.116802 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: