-
在核物理、粒子物理、宇宙学、天文学等领域的前沿方向中, 核物质与夸克物质的热力学性质(物态方程、有效质量、组分等)与致密星性质的研究是重点问题[1-4]. 科研工作者可以通过大型重离子对撞以及致密星体实验观测数据得到有限密 度、有限化学势的强相互作用物质热力学性质的线索. 致密星物质的物态方程决定着致密星体的质量和半径, 大质量致密星的观测结果要求其内部物 质的物态方程足够硬才能抵抗强大的引力. 近期的实验观测结果中, 大质量致密星尤其是两倍以上太阳质量的脉冲星的探测结果出现多次[5-10], 在引力波事件GW190814 中, 其主星的伴随天体的质量
$ m_2 $ 有可能高达$ 2.50M_{\odot} \text{—} 2.67 M_{\odot} $ [11]——如果选取夸克星作为这些大质量致密星的候选者, 对夸克 星物质的物态方程以及所选唯象模型的参数空 间都会有着很大的挑战. 依据目前的理论, 夸克星是由$ \beta $ 平衡的电中性夸克物质构成的, 实验上还不能排除其存在的可能性[12-23]. 近年来, 研究者进行了大量的奇异夸克星以及相应的唯象模型的探索[24-33], 大部分的研究热点集中在退禁闭的u, d, s三味夸克与轻子构成的奇异夸克物质和其所支持的大质量夸克星的性质. 构成夸克星的物质还有可能处于色味锁态: 此时u, d, s三味夸克的粒子数密度和化学势都相同, 处于最对称的基态, 星体物质中不再含有轻子[34-38]. 之前的工作表明, 色味锁夸克物质有可能比奇异夸克物质更稳定, 形成的色味锁夸克星的质量可能比奇异夸克物质构成的夸克星质量更大[39,40], 可以描述目前实验观测的大质量致密星.强磁场下致密星的性质一直是致密星物理的难点问题之一, 磁场对致密星物质的物态方程、磁制动问题、星体的加热与冷却过程的影响很大[41-49]. 部分致密星的表面磁场有可能达到
$ 10^{11}\;{\mathrm{G}} $ (1 G =10–4 T)以上, 内部磁场估算能够增加到$10^{18} $ —$ 10^{20}\;{\mathrm{G}} $ [50-60], 这类星体统称为磁星. 目前致密星内部磁场起源仍为未知问题, 人们在磁星内部可以将磁场强度进行密度依赖来唯象给出磁场强度分布[54]. 对于致密星中孕育的强磁场的来源, 目前仍处于探索阶段, 可以通过中子星演化的相关模型、“发电机”效应、致密星内部的化石假说等进行解释[61,62]. 本文着重讨论的是强磁场与有限温度情况下色味锁态夸克物质与相应的磁星的性质.本文首先推导同时考虑了磁场与温度的准粒子模型下色味锁态夸克物质的特性函数表达式. 之后计算色味锁夸克物质的物态方程、有效夸克质量、每核子熵、多方指数. 最后讨论不同等熵阶段下色味锁磁星的质量-半径关系与星体内部温度, 给出结论.
-
在研究色味锁夸克物质之前, 先介绍奇异夸克物质, 即由满足弱平衡条件(
$ \beta $ 稳定)的u, d, s夸克与电子和μ子形成的电中性夸克物质. 奇异夸克物质可能存在于致密星体内部, 也有可能形成自束缚的奇异夸克星. 目前存在理论支持奇异夸克物 质可作为核物质的基态候选者[63-65], 要求零温情况下该物质的每核子能量要低于56Fe的每核子 能量, 即E/A < 930 MeV. 由于没有发现正常核物质到纯u, d夸克物质(由u, d夸克和轻子通过$ \beta $ 平衡所形成)的自发相变, 故对于同模型的同套参数, 要求纯u, d夸克物质的每核子能量要高于930 MeV——此条件对唯象模型的参数空间有着较为严苛的要求[66-89], 有限温度与强磁场下的夸克星使用的模型参数组, 需要在零温情况下满足绝对能稳定条件. 在理论研究中, 夸克在高能高密情况下可通过色自由度与味耦合配对, 进而形成极为对称的色味锁态(color-flavor locked, CFL). 对于强磁场下的色味锁夸克物质(magnetized color-flavor locked, MCFL), 其带电粒子的热力学性质会发生朗道量子化, 进一步影响其热力学性质. 近年来, 对色味锁夸克物质的探索中, 人们利用了多种唯象模型得到零温下色味锁夸克物质甚至会处于更稳定的态, 可能形成自束缚的夸克星.本文采用准粒子模型, 该模型的主要特点是通过硬密环单圈近似得到化学势相关的夸克有效质量[25,38,66-69,90,91], 其具体表达式为
其中
$ m_{{\mathrm{q}}0} $ 对应着每一味夸克的裸质量, g是强相互作用耦合常数,$ \mu_{\mathrm{q }}$ 代表夸克的化学势.在强磁场与有限温度情况下, 可以利用有限温度场论与量子统计物理推导出每味夸克的粒子数密度, 其表达式为
这里
$ N_{\mathrm{c}} = 3 $ 表示色自由度,$ \mu = \left(\displaystyle\sum\nolimits_i\mu_i\right)/3 $ 表示色味锁夸克物质的平均化学势.$ \alpha_{\nu} = 2-\delta_{\nu, 0} $ 来自于强磁场下夸克物质的朗道能级求和,$ \nu $ 表示求和级数, 定义为$ \nu = n + \dfrac{1}{2}-\dfrac{q_i}{|q_i|}\dfrac{s}{2} $ (其中$ q_i $ 为夸克所带电荷, n表示主量子数, s为自旋量子数). (2)式的$ \varDelta $ 是色味锁夸克物质的能隙常数, 由于色味锁夸克物质具有对称性, 三味夸克的粒子数密度皆相等, 可以得到$ n_{\mathrm{B }}= 1/3(n_{\mathrm{u}} + n_{\mathrm{d }}+ n_{\mathrm{s)}} = n_{\mathrm{u}} = n_{\mathrm{d}} = n_{\mathrm{s}} $ . 能够发现能隙常数$ \varDelta $ 越大, 对于给定重子数的每味夸克的自由费米气体部分的贡献就越小. 色散关系的表达式为为得到色味锁夸克物质的物态方程, 需要先推导其热力学势密度, 表达式为
其中
$ B_{\mathrm{m}} $ 与袋常数类似, 能够提供真空负压模拟禁闭. 这里选取$ B_{\mathrm{m}} $ 写法的主要目的是为了与磁感应强度B做区分.$ {B^2}/{2} $ 来自磁场能量密度,$ B_i(\mu_i) = -\displaystyle\int\frac{\partial \varOmega_i}{\partial m_i}\frac{\partial m_i}{\partial \mu_i}\text d \mu_i $ 来自于有效质量的化学势相关项的推导.$ \varOmega_i $ 代表每味夸克的热力学势密度贡献, 具体表达式为色味锁夸克物质的自由能可以写作
能量密度可以通过
$ {\cal{E}} = {\cal{F}} + TS $ 得到,$ S = -\dfrac{\partial\varOmega}{\partial T } $ 为色味锁夸克物质的熵密度, 故在有限温度情况下, 能量密度与自由能密度会存在较大的温度相关的差值(零温情况下两者数值一致).磁星是致密星中特殊的存在, 拥有极高的磁场: 磁星的表面磁场为
$ 10^{11}\text{—}10^{15} $ G, 而内部磁场甚至能增加至1018 G 以上[54]. 目前对于磁星内部磁场成因的探究仍然是热点问题, 有理论指出磁星内部磁场可能是由核子、夸克等费米子的自旋极化产生[92]. 磁星内部强相互作用物质的旋转对称性会由于磁场的引入发生破缺, 进而会在星体物质中产生各向异性的压强: 人们定义纵向压强$ P_{/ /}$ 为与星体内部磁场方向平行的情况, 而与磁场方向垂直平面内存在的压强则定义为横向压强$ P_\perp $ [54,93-99], 相应的表达式为 -
在第2节推导结果的基础上, 本节展开计算结果的讨论. 本文选择的准粒子模型的参数组为g-2, 具体参数为g = 2,
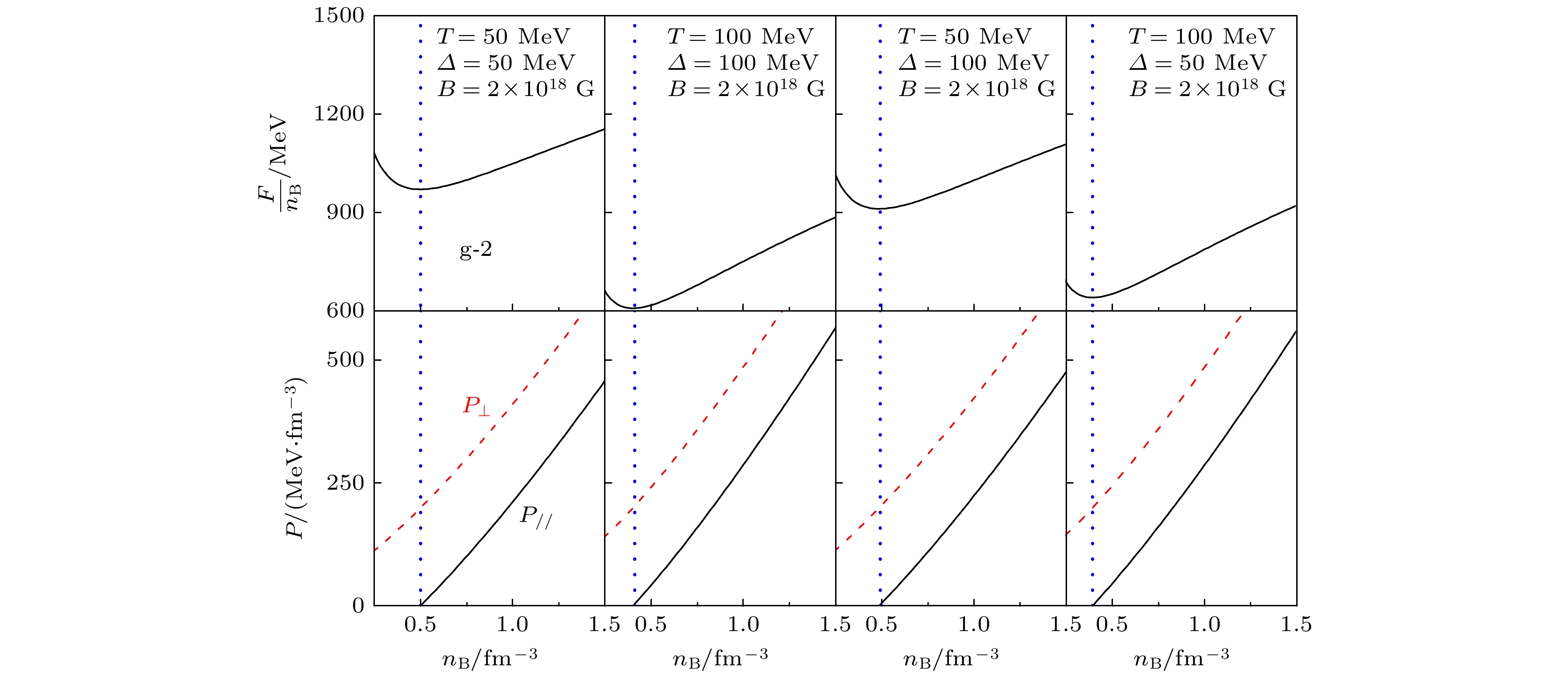
$ B_{\mathrm{m}}^{1/4} = 141\;{\mathrm{MeV}} $ . 在文献[69]中发现, 在满足绝对稳定条件的情况下利用这组参数可以描述质量为$ (2.01\pm0.04) M_{\odot} $ 的脉冲星PSR J0348 + 0432为奇异夸克星.图1计算了在不同温度与能隙常数下色味锁态夸克星物质的纵向压强、横向压强、每核子自由能随着色味锁态下重子数密度
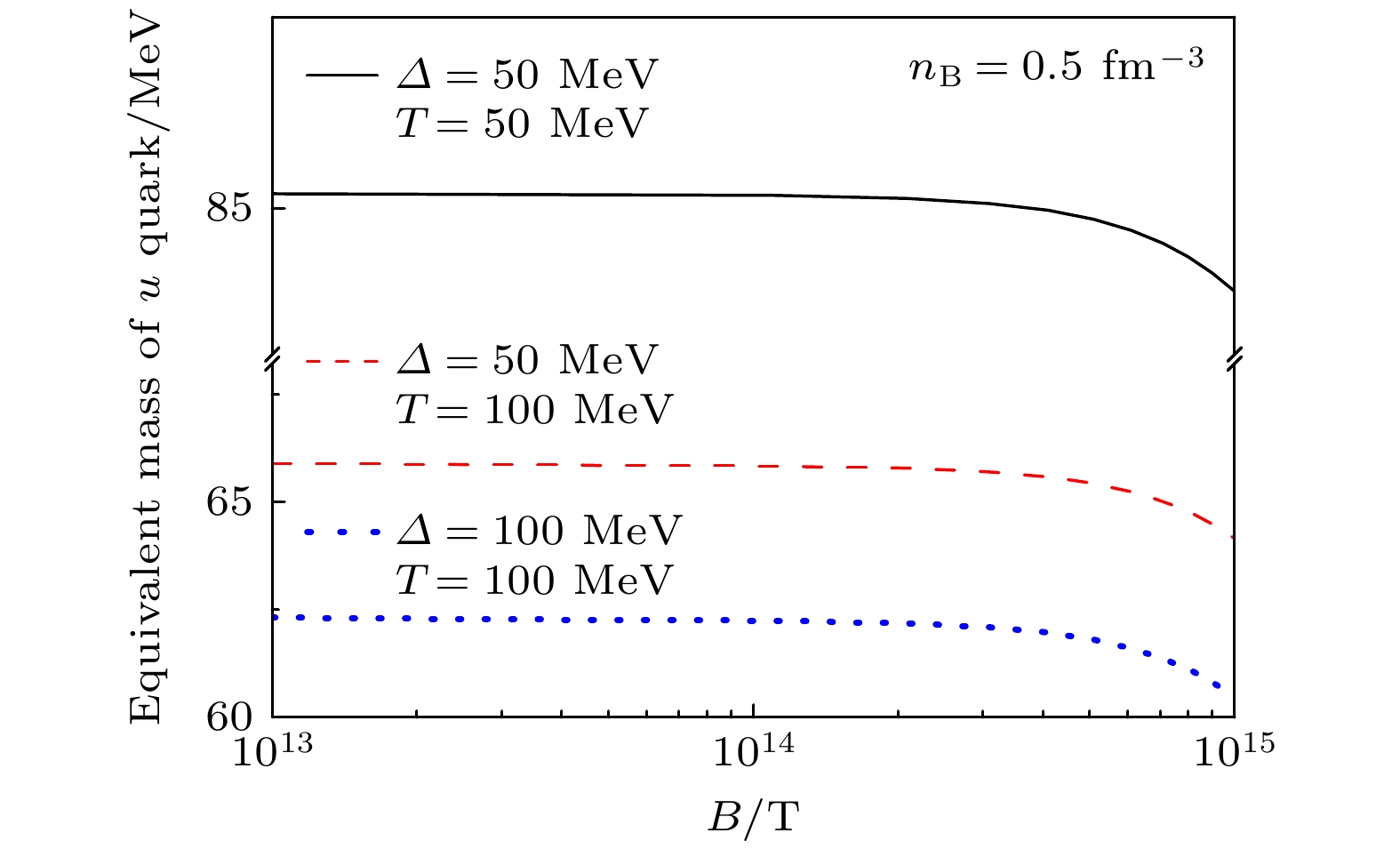
$ n_{\mathrm{B}} $ 的变化, 磁感应强度固定为$ B = 2\times10^{18} $ G. 从图中可见色味锁夸克物质在强磁场下的压强由于产生各向异性进而发生劈裂. 还可以从(6) 式与(8)式中直接看出每核子自由能与压强的劈裂也会随着磁场的增加而增大. 图1中能够看出每核子自由能会随着温度与$ \varDelta $ 的增加而减少, 增强了稳定性; 此外, 每核子自由能最低点所对应的重子数密度也会随着温度与$ \varDelta $ 的增加而减少. 需要指出, 在致密星体内部还可能存在更稳定的spin-one色超导态物质[100]. 从图1还可以发现, 每核子自由能最低点的重子数密度与纵向压强为零的重子数密度一致, 这体现了正确的推导结果给出的热力学自洽. 数值结果表明各向异性压强因温度的增加与$ \varDelta $ 的激发而显著增大, 从而物态方程变硬, 可以支持大质量的色味锁磁星. 从图1还能分析得到, 对于色味锁夸克物质, 其物态方程受温度的影响要大于$ \varDelta $ 的影响.图2进一步计算了不同温度与能隙常数下u夸克的有效质量随磁感应强度的变化. 能够发现在磁感应强度小于
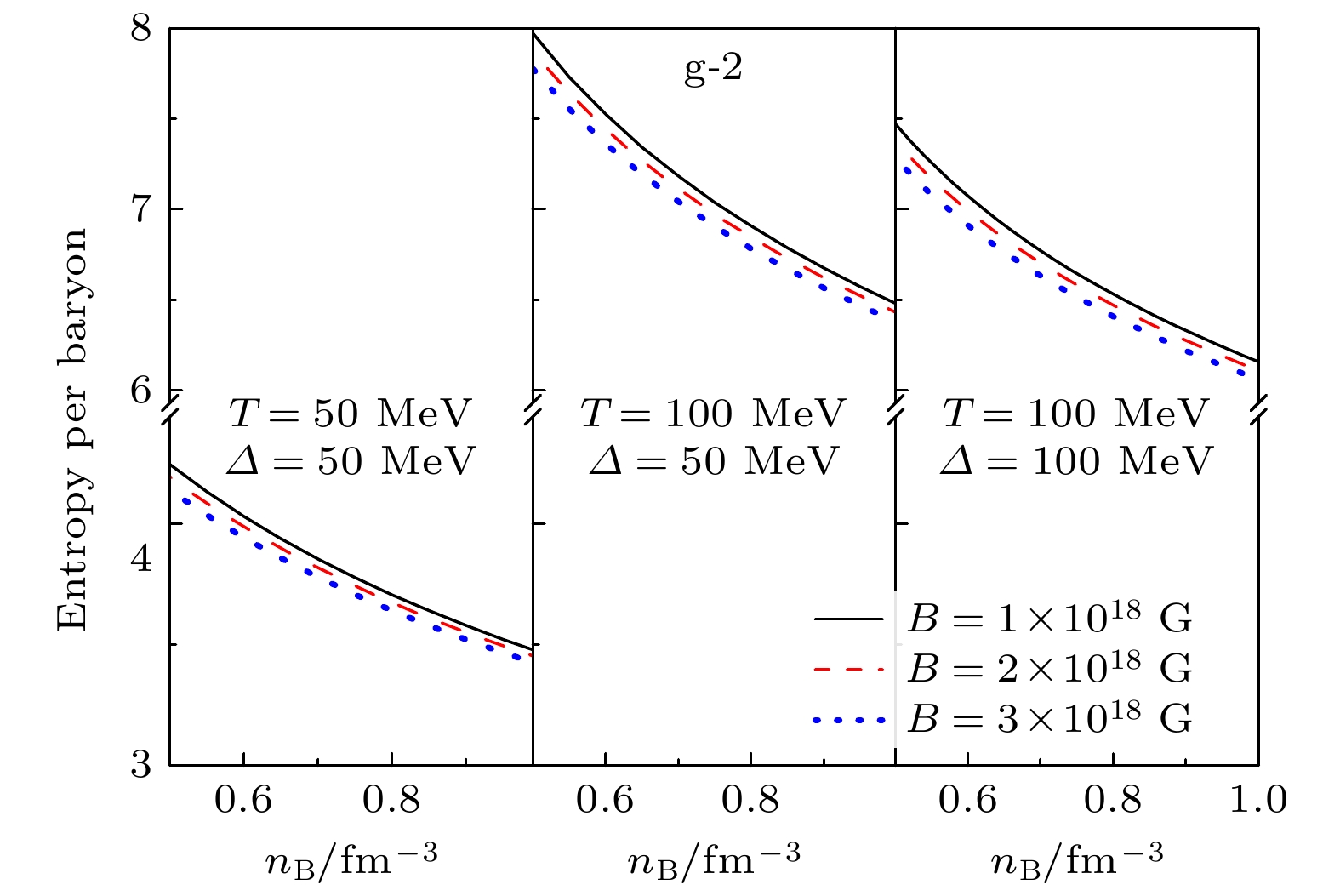
$ 1\times10^{14} $ T 时, 每种情况的有效夸克质量基本维持不变; 当磁感应强度继续增加时(大于$ 1\times10^{14} $ T), 有效质量会随着磁场的增加而开始明显降低, 体现出了基于准粒子模型的夸克有效质量的“反磁催化”效果. 图2结果还表明有效质量还会随着温度与$ \varDelta $ 的增加而降低, 这说明色味锁夸克物质里考虑强磁场、高温或高能隙常数情况会显著减少唯象模型中包含在有效质量项中的相互作用.图3计算了色味锁态下夸克星物质的每核子熵随着不同温度、磁场、能隙常数的变化. 可以发现, 每核子熵会随着磁感应强度的增加而降低; 随着温度的增加, 每核子熵会有显著增加; 随着
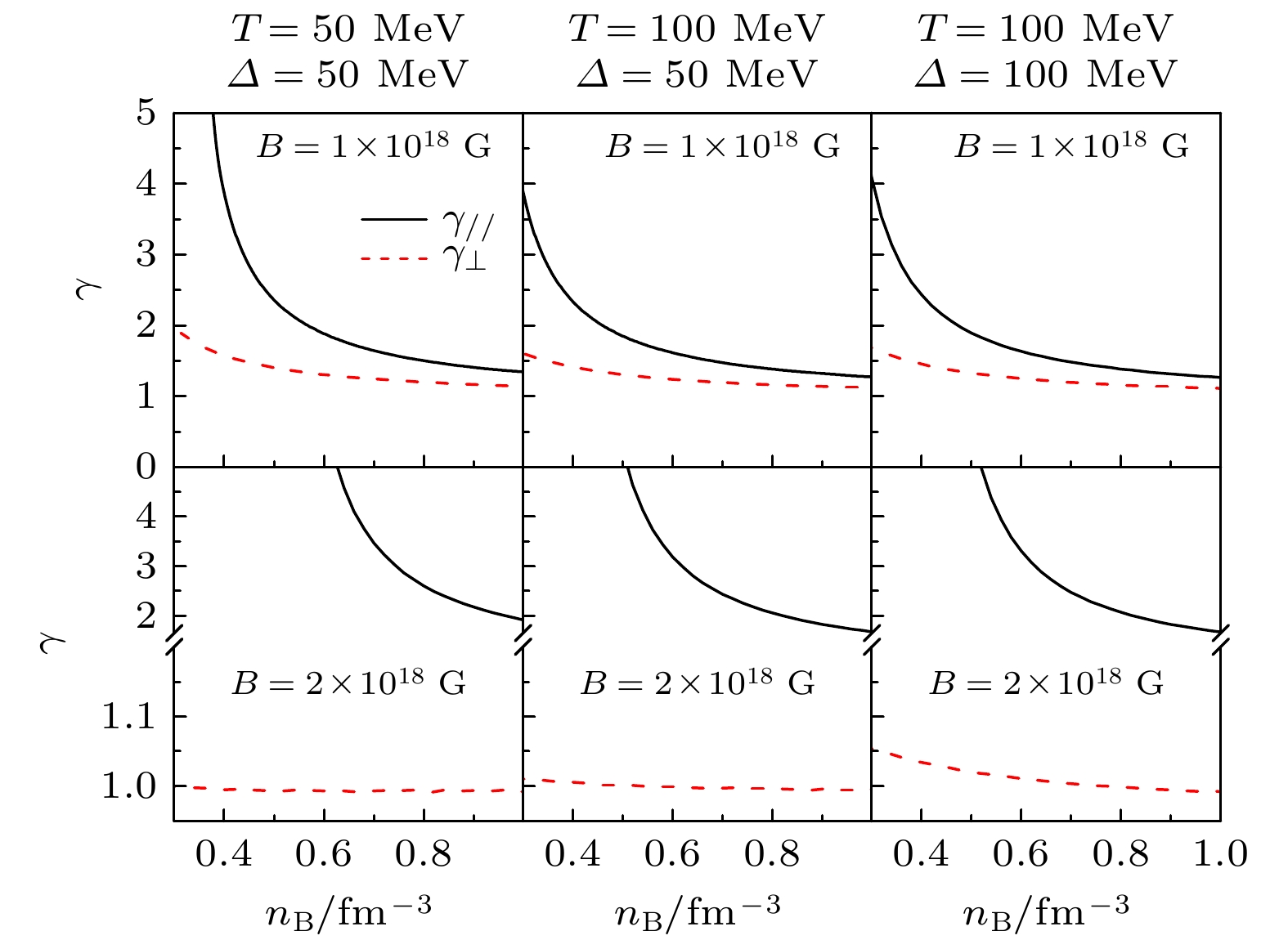
$ \varDelta $ 的增加, 每核子熵会降低. 故我们发现磁感应强度与$ \varDelta $ 的增加会减少系统的无序度, 反之提升温度会增加色味锁夸克物质的无序度.图4能够得到MCFL下夸克物质的多方指数随磁场、温度、能隙常数的变化规律. 多方指数的定义为
$ \gamma = \dfrac{\partial\ln P}{\partial\ln {\cal{E}}} $ , 由于强磁场下压强会发生各向异性, 故对应的多方指数也会呈现各向异性的特征. 在强磁场情况下分别用纵向压强$ P_{/ /} $ 与横向压强$ P_{\perp} $ 来计算, 可以得到纵向多方指数$ \gamma_{/ /}$ 与横向多方指数$ \gamma_{\perp} $ 的定义. 从图4能够发现多方指数在所有的情况下都会随着$ n_{\mathrm{B }}$ 的增大而显著减少. 在控制温度与$ \varDelta $ 不变的情况下, 纵向多方指数的大小皆大于横向多方指数; 当进一步增加磁场时, 多方指数之间的差值也会变大(横向多方指数会随着磁场的增加而减小, 纵向多方指数会随着磁场的增加而增加). 当磁场一定时, 多方指数会随着温度的增加而降低, 会随着$ \varDelta $ 的增大而增大. 多方指数体现压强相对于能量密度增加的幅度, 能直观体现出强相互作用物质的热力学性质的变化, 进而对致密星的性质产生影响. -
在致密星体研究中, 超强磁场下的致密星物质会产生自旋极化, 对简并压会有较大影响; 部分星体有可能向外释放大量的X 射线和软
$ {\text{γ}}$ 射线波段的闪耀, 进而瞬时爆发巨大能量, 可视为磁星候选者[101,102]. 可利用TOV (Tolman-Oppenheimer-Volkov)方程[103]来计算磁星的性质. 由于磁星内部磁场强度与方向的分布目前难以获悉, 故研究磁场下的夸克星性质一般采用密度相关磁场得到星体内部磁场强度分布[55,56,59,60]:其中,
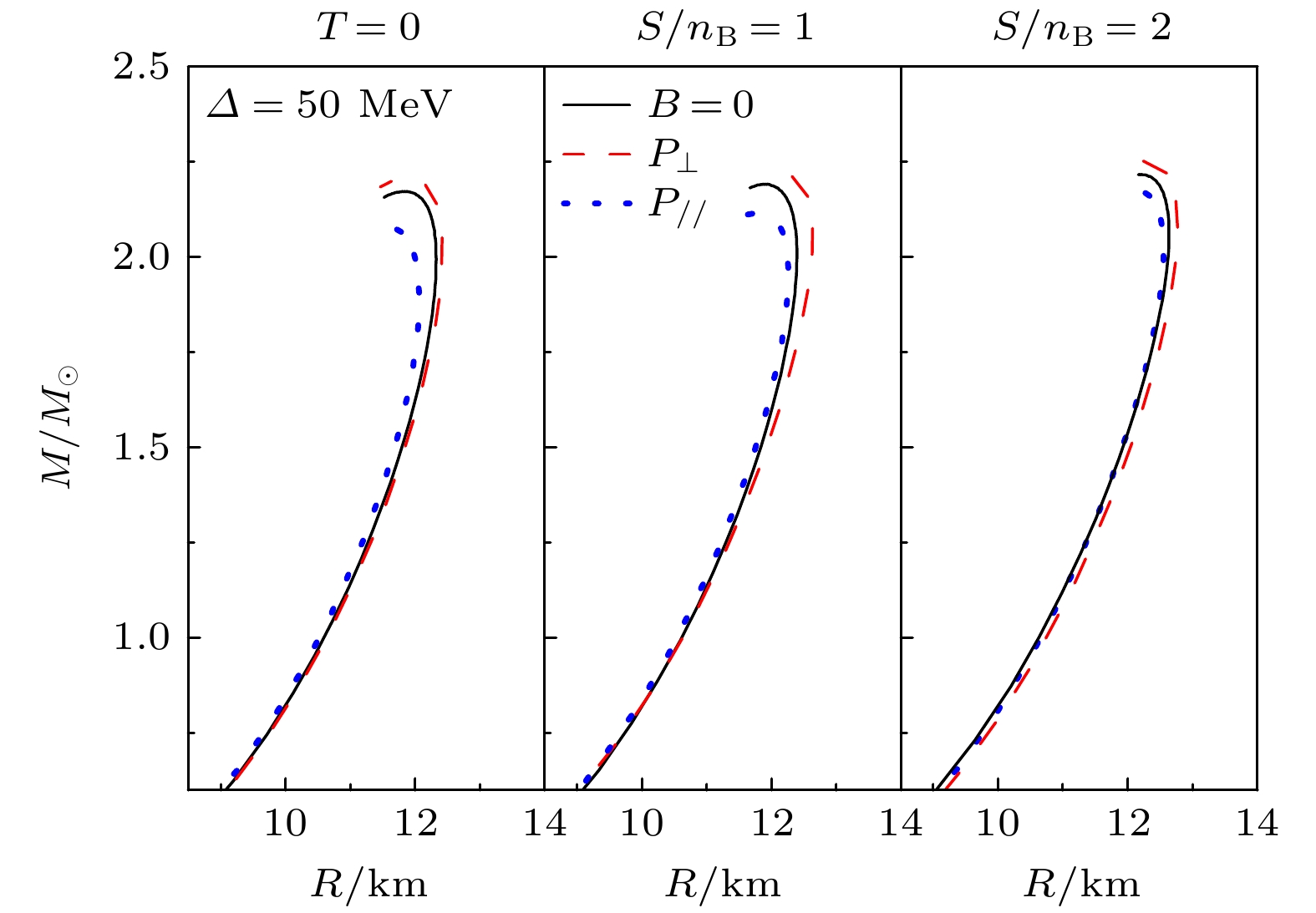
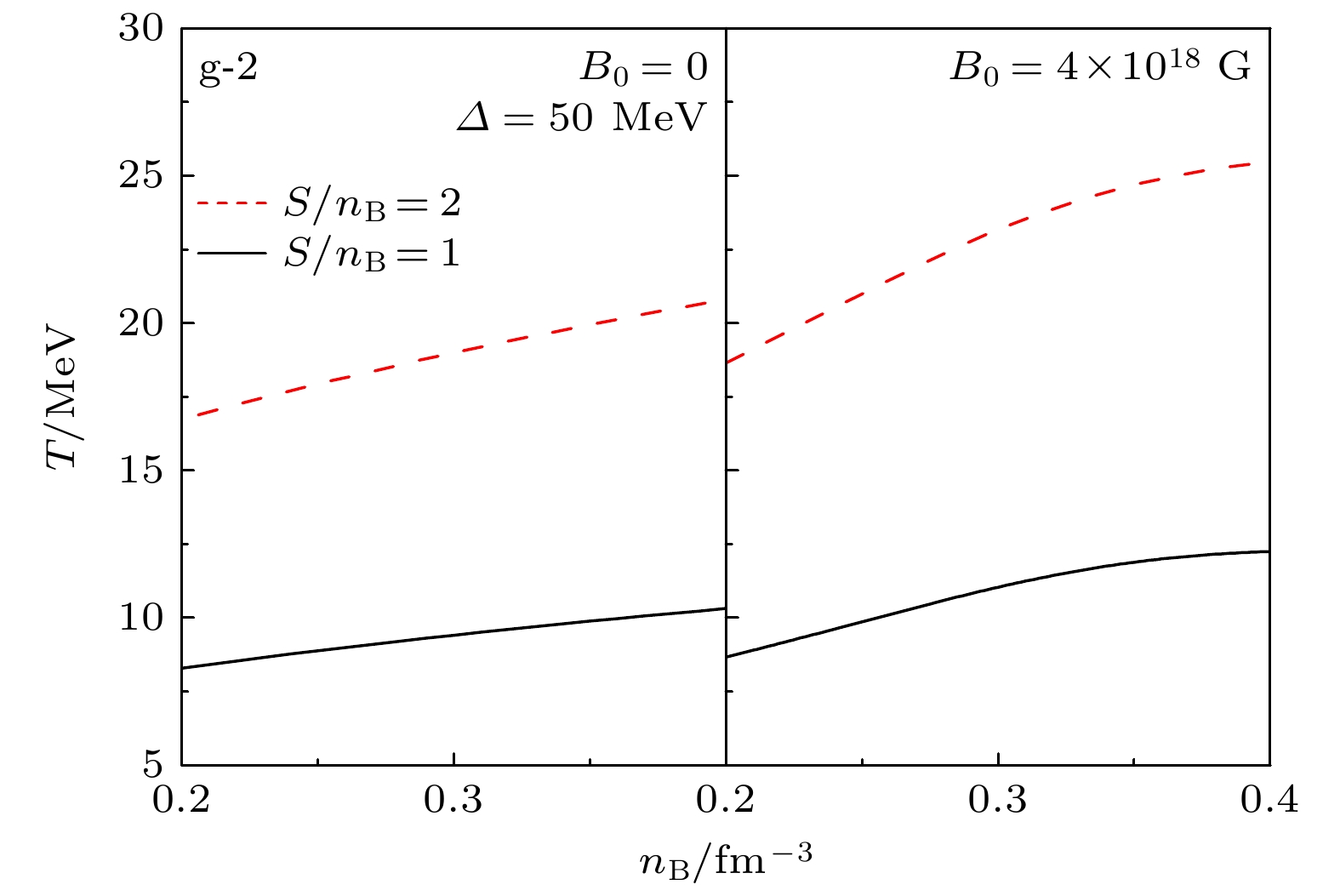
$ B_{\rm{surf}} = 1\times 10^{14}\; $ G代表磁星表面的磁场强度;$ n_0 = 0.16\; {\rm{fm}}^{-3} $ ;$ B_0 $ ,$ \beta_0 $ 和$ \gamma $ 可以模拟磁星中磁场的重子数密度依赖进而得到从中心到表面快速或者慢速下降的磁感应强度. 文献[104]利用$ \gamma = 3 $ ,$ \beta_0 = 0.001 $ 这套参数能够得到较合理的星体内部磁感应强度下降速率, 本文仍利用此套参数来计算磁星的质量与半径关系. 关于磁星内部的磁场方向的分布, 采取两种假定: 可以假设磁感线在夸克星内部沿着星体径向穿出再从另一端返回, 此为“径向磁场”情况; 另一种假设则是要求磁感线分布在垂直于径向的平面, 这种磁场极端分布定义为“横向磁场”. 对于径向磁场情况, 磁星的半径方向的抵消引力的压强为纵向压强$ P_{/ /} $ ; 对于横向磁场情况, 磁星的径向抵消引力的压强为横向压强$ P_{\perp} $ . 利用这两种磁星内部磁场的极端分布, 可以得到磁星质量取值的上下边界.图5计算了不同等熵阶段色味锁夸克星的质量半径关系,
$ \varDelta $ 选择为50 MeV, 对于磁星情况选取了$ B_0 = 4\times 10^{18}\;{\mathrm{G}} $ . 可以看到, 在图5中磁场为零时, 随着等熵阶段的每核子熵取值的增加, 星体最大质量会显著增大. 对于强磁场情况, 磁星的最大质量也会随着等熵阶段中的每核子熵的增加而增加. 当考虑磁星内部强磁场情况时, 能够看到径向磁场情况对应的磁星质量与磁星半径皆小于横向磁场情况的磁星质量与半径, 体现出磁场方向分布对磁星性质的显著影响. 从图4可以看出, 纵向多方指数的数值要大于横向多方指数; 结合图5 的结果, 能得到纵向压强对应的磁星的质量低于横向压强情况的磁星质量, 故能推断出纵向多方指数对应的磁星质量较小而横向多方指数对应的磁星质量较大, 体现出色味锁磁星最大质量会随着多方指数的增加而降低. 这个规律在我们之前基于不同唯象模型的夸克星工作中皆有发现[105-107].图6进一步计算了不同等熵阶段的色味锁磁星内部的温度随着重子数密度的变化. 可以看到, 随着每核子熵的增加, 星体内部温度变高, 而且星体内部的温度会随着星体中心密度的增加而增加, 在核心处会达到最高温度. 图6中还可以发现, 当考虑强磁场时, 色味锁夸克星物质内部的温度会增加, 色味锁磁星最大质量所对应的中心温度也会随着磁场的增加而增大. 结合图4—图6的结论发现, 每核子熵的增加会增加色味锁夸克星的内部温度, 进而会增加色味锁夸克星的质量; 随着温度的增加, 纵向多方指数与横向多方指数的取值都会明显降低. 由此我们推断, 对于基于准粒子模型的强磁场与有限温度下的色味锁夸克星, 其最大质量会随着星体物质的多方指数的增加而减少, 这很有可能是利用实验观测结果检验色味锁夸克星内部热力学性质的一个重要物理量. 我们进一步利用准粒子模型计算了零温、有限温度、强磁场下、有限温度与强磁场下奇异夸克星的最大质量与对应情况下的奇异夸克物质多方指数的关联规律, 发现基于准粒子模型的奇异夸克星的质量越大, 对应的夸克物质的多方指数就会越小, 与色味锁夸克星的结果相应. 下一步我们会讨论不同模型下的奇异夸克物质多方指数与夸克星最大质量的关联规律.
-
本文基于准粒子模型在磁场和有限温度下探究了色味锁态夸克物质与夸克星的性质, 结果表明色味锁夸克物质的每核子自由能、有效质量、每核子熵等物理量受磁场、温度、能隙常数的影响较大. 在强磁场中, 各向异性压强会随着温度与能隙常数的增加而增大. 结果还表明准粒子模型的有效夸克质量在色味锁态下会分别随着温度、能隙常数和磁场强度的增加而减少, 体现出了“反磁催化”的现象. 色味锁夸克物质的每核子熵会随着温度的增加而增加, 会随着磁场与能隙常数的增加而降低. 通过研究色味锁夸克物质的多方指数, 发现在强磁场下它也呈现出各向异性, 会随着温度与能隙常数的增加而降低. 在研究不同等熵阶段的色味锁磁星时, 发现最大星体质量在每核子熵更高的等熵阶段增加, 其内部温度也会随着更高的每核子熵的等熵阶段而增加. 对于基于准粒子模型的强磁场与有限温度下的色味锁夸克星, 发现星体物质的多方指数对色味锁磁星的质量影响很大, 会显著减少磁星质量.
强磁场与有限温度下色味锁夸克星的唯象模型
Phenomenological model of color-flavor-locked quark star under strong magnetic fields at finite temperatures
-
摘要: 基于准粒子模型对强磁场和有限温度下色味锁夸克物质与色味锁磁星的性质进行了讨论. 发现色味锁夸克物质的每核子自由能、有效质量、每核子熵等物理量受磁场、温度、能隙常数的影响较大, 并且强磁场、有限温度环境中色味锁夸克物质的压强会产生各向异性. 进一步研究了不同等熵阶段下的色味锁磁星的性质, 发现色味锁磁星的质量、半径等性质与磁星内部的磁场强度分布、磁场方向分布紧密相关, 磁星内部温度会随着每核子熵的增加而增大. 结论还表明色味锁夸克物质的多方指数会随着色味锁夸克星质量的增大而减少.Abstract: The properties of the color-flavor-locked (CFL) quark matter under strong magnetic fields at finite temperatures within a quasiparticle model are investigated in this work. Our results indicate that CFL quark matter pressure becomes anisotropic under strong magnetic fields, while its equation of state (EOS) and equivalent quark mass are both strongly affected by temperature, energy gap constant Δ, and strong magnetic field inside the CFL quark matter. The equivalent quark mass of CFL quark matter decreases with temperature and magnetic field strength increasing, which implies an inverse magnetic catalysis phenomenon. The results also indicate that the entropy per baryon of the CFL quark matter increases with temperature rising and decreases with Δ increasing. Furthermore, the properties of CFL magnetars in different isentropic stages are studied. The star mass and radius depend primarily on the strength and orientation of magnetic fieldinside the CFL magnestars. The maximum star mass increases with entropy per baryon increasing, while the star matter temperature rises at high isentropic stage. Moreover, the polytropic index of the CFL quark matter decreases with star mass increasing.
-
Key words:
- color-flavor-locked phase /
- quark star /
- magnetar .
-

-
-
[1] Glendenning N K 2000 Compact Stars (2nd Ed.) (New York: Spinger-Verlag, Inc. [2] Weber F 1999 Pulsars as Astrophyical Laboratories for Nuclear and Particle Physics (London: IOP Publishing Ltd [3] Lattimer J M, Prakash M 2004 Science 304 536 doi: 10.1126/science.1090720 [4] Steiner A W, Prakash M, Lattimer J M, Ellis P J 2005 Phys. Rep. 410 325 [5] Demorest P 2010 Nature 467 1081 doi: 10.1038/nature09466 [6] Antoniadis J 2013 Science 340 6131 [7] Shahbaz T, Casares J 2018 Astrophys. J. 859 54 doi: 10.3847/1538-4357/aabde6 [8] Thankful H, Cromartie 2020 Nature Astron. Lett. 4 72 [9] Fonseca E, Cromartie H T, Pennucci T T, et al. 2021 Astrophys. J. Lett. 915 L12 doi: 10.3847/2041-8213/ac03b8 [10] Miller M C, Lamb F K, Dittmann A J, et al. 2021 Astrophys. J. Lett. 918 L28 doi: 10.3847/2041-8213/ac089b [11] Abbott R 2020 Astrophys. J. Lett. 896 L44 doi: 10.3847/2041-8213/ab960f [12] Ivanenko D, Kurdgelaidze D F 1969 Lett. Nuovo Cimento 2 13 doi: 10.1007/BF02753988 [13] Itoh N 1970 Prog. Theor. Phys. 44 291 doi: 10.1143/PTP.44.291 [14] Bodmer A R 1971 Phys. Rev. D 4 1601 doi: 10.1103/PhysRevD.4.1601 [15] Witten E 1984 Phys. Rev. D 30 272 doi: 10.1103/PhysRevD.30.272 [16] Farhi E, Jaffe R L 1984 Phys. Rev. D 30 2379 doi: 10.1103/PhysRevD.30.2379 [17] Alcock C, Farh E, Olinto A 1986 Astrophys. J. 310 261 doi: 10.1086/164679 [18] Weber F 2005 Prog. Part. Nucl. Phys. 54 193 doi: 10.1016/j.ppnp.2004.07.001 [19] Bombaci I, Parenti I, Vidana I 2004 Astrophys. J. 614 314 doi: 10.1086/423658 [20] Staff J, Ouyed R, Bagchi M 2007 Astrophys. J. 667 340 doi: 10.1086/519545 [21] Herzog T M, Röpke F K 2011 Phys. Rev. D 84 083002 doi: 10.1103/PhysRevD.84.083002 [22] Stephanov M A, Rajagopal K, Shuryak E V 1998 Phys. Rev. Lett. 81 4816 doi: 10.1103/PhysRevLett.81.4816 [23] Terazawa H 1979 INS-Report (Tokyo: Univ. of Tokyo) p336 [24] Alford M, Reddy S 2003 Phys. Rev. D 67 074024 doi: 10.1103/PhysRevD.67.074024 [25] Alford M, Jotwani P, Kouvaris C, Kundu J, Rajagopal K 2005 Phys. Rev. D 71 114011 doi: 10.1103/PhysRevD.71.114011 [26] Baldo M 2003 Phys. Lett. B 562 153 doi: 10.1016/S0370-2693(03)00556-2 [27] Ippolito N D, Ruggieri M, Rischke D H, Sedrakian A, Weber F 2008 Phys. Rev. D 77 023004 doi: 10.1103/PhysRevD.77.023004 [28] Lai X Y, Xu R X 2011 Res. Astron. Astrophys. 11 687 doi: 10.1088/1674-4527/11/6/008 [29] Avellar M G B de, Horvath J E, Paulucci L 2011 Phys. Rev. D 84 043004 doi: 10.1103/PhysRevD.84.043004 [30] Bonanno L, Sedrakian A 2012 A&A 539 A16 [31] Chu P C, Wang B, Jia Y Y, Dong Y M, Wang S M, Li X H, Zhang L, Zhang X M, Ma H Y 2016 Phys. Rev. D 94 123014 doi: 10.1103/PhysRevD.94.123014 [32] Chu P C, Li X H, Wang B, Dong Y M, Jia Y Y, Wang S M, Ma H Y 2017 Eur. Phys. J. C 77 512 doi: 10.1140/epjc/s10052-017-5092-2 [33] Chu P C, Zhou Y, Chen C, Li X H, Ma H Y 2020 J. Phys. G: Nucl. Part. Phys. 47 085201 doi: 10.1088/1361-6471/ab9b06 [34] Bailin D, Love A 1984 Phys. Rep. 107 325 doi: 10.1016/0370-1573(84)90145-5 [35] Alford M G, Rajagopal K, Reddy S, Wilczek F 2001 Phys. Rev. D 64 074017 doi: 10.1103/PhysRevD.64.074017 [36] Shovkovy I A 2005 Found. Phys. 35 1309 doi: 10.1007/s10701-005-6440-x [37] Rajagopal K, Wilczek F 2001 Phys. Rev. L 86 3492 doi: 10.1103/PhysRevLett.86.3492 [38] Alford M G, Rajagopal K, Schaefer T, Schmitt A 2008 Rev. Mod. Phys. 80 1455 doi: 10.1103/RevModPhys.80.1455 [39] Lugones G, Horvath J E 2003 Astron. Astrophys. 403 173 doi: 10.1051/0004-6361:20030374 [40] Horvath J E, Lugones G 2004 Astron. Astrophys. 422 L1 doi: 10.1051/0004-6361:20040180 [41] Li X H, Gao Z F, Li X D, Xu Y, Wang P, WangN, Peng Q H 2016 Int. J. Mod. Phys. D 25 165000 [42] Gao Z F, Wang N, Shan H, L i, X D, Wang W 2017 Astrophys. J. 849 19 doi: 10.3847/1538-4357/aa8f49 [43] Deng Z L, Gao Z F, Li X D, Shao Y 2020 Astrophys. J. 892 4 doi: 10.3847/1538-4357/ab76c4 [44] Yan F Z, Gao Z F, Yang W S, Dong A J 2021 Astron. Nachr. 342 249 doi: 10.1002/asna.202113913 [45] Wang H, Gao Z F, Jia H Y, Wang N, Li X 2020 Universe 6 63 doi: 10.3390/universe6050063 [46] Li B P, Gao Z F 2023 Astron. Nachr. 344 e20220111 [47] Deng Z L, Li X D, Gao Z F, Shao Y 2021 Astrophys. J. 909 174 doi: 10.3847/1538-4357/abe0b2 [48] G ao, Z F, Omar N, Shi X C, Wang N 2019 Astron. Nachr. 340 1030 doi: 10.1002/asna.201913711 [49] Lander S K 2023 Astrophys.J. 947 L16 doi: 10.3847/2041-8213/acca1f [50] Woltjer L 1964 Astrophys. J. 140 1309 doi: 10.1086/148028 [51] Mihara T A 1990 Nature 346 250 doi: 10.1038/346250a0 [52] Chanmugam G 1992 Annu. Rev. Astron. Astrophys. 30 143 doi: 10.1146/annurev.aa.30.090192.001043 [53] Lai D, Shapiro S L 1991 Astrophys. J. 383 745 doi: 10.1086/170831 [54] Ferrer E J, Incera V, Keith J P, Portillo I, Springsteen P L 2010 Phys. Rev. C 82 065802 [55] Bandyopadhyay D, Chakrabarty S, Pal S 1997 Phys Rev. Lett. 79 2176 doi: 10.1103/PhysRevLett.79.2176 [56] Bandyopadhyay D, Pal S, Chakrabarty S 1998 J. Phys. G: Nucl. Part. Phys. 24 1647 doi: 10.1088/0954-3899/24/8/046 [57] Menezes D P, Pinto M, Benghi, Avancini S, Providência C 2009 Phys. Rev. C 79 035807 doi: 10.1103/PhysRevC.79.035807 [58] Menezes D P, Pinto M, Benghi, Avancini S, Providência C 2009 Phys. Rev. C 80 065805 doi: 10.1103/PhysRevC.80.065805 [59] Ryu C Y, Kim K S, Cheoun Myung-Ki 2010 Phys. Rev. C 82 025804 doi: 10.1103/PhysRevC.82.025804 [60] Ryu C Y, Cheoun Myung-Ki, Kajino T, Maruyama T, Mathews Grant J 2012 Astropart. Phys. 38 25 doi: 10.1016/j.astropartphys.2012.09.005 [61] Dong J M 2021 Mon. Not. R. Astron. Soc. 500 1505 [62] Fu G Z, Xing C C, Wang N 2020 Eur. Phys. J. C 80 582 doi: 10.1140/epjc/s10052-020-8140-2 [63] Aidala C, Akiba Y, Alfred M, et al. 2018 Phys. Rev. L 120 022001 doi: 10.1103/PhysRevLett.120.022001 [64] Zhang C, Mann R B 2021 Phys. Rev. D 103 063018 doi: 10.1103/PhysRevD.103.063018 [65] Yuan L W, Li A, Miao Z Q, Zuo B J, Bai Z 1984 Phys. Rev. D 105 123004 [66] Schertler K, Greiner C, Thoma M H, Schertler K, Greiner C, Thoma M H 1997 Nucl. Phys. A 616 659 doi: 10.1016/S0375-9474(97)00014-6 [67] Pisarski R D 1989 Nucl. Phys. A498 423 [68] Wen X J 2009 J. Phys. G: Nucl. Part. Phys. 36 025011 doi: 10.1088/0954-3899/36/2/025011 [69] Zhang Z, Chu P C, Li X H, Liu H, Zhang X M 2021 Phys. Rev. D 103 103021 doi: 10.1103/PhysRevD.103.103021 [70] Chu P C, Chen L W 2014 Astrophys. J. 780 135 [71] Chu P C 2018 Phys. Lett. B 778 447 doi: 10.1016/j.physletb.2018.01.064 [72] Chu P C, Chen L W 2017 Phys. Rev. D 96 103001 doi: 10.1103/PhysRevD.96.103001 [73] Chodos A, Jaffe R L, Ohnson K, Thorn C B, Weisskopf V F 1974 Phys. Rev. D 9 3471 doi: 10.1103/PhysRevD.9.3471 [74] Alford M, Braby M, Paris M, Reddy S 2005 Astrophys. J. 629 969 doi: 10.1086/430902 [75] Rehberg P, Klevansky S P, Hüfner J 1996 Phys. Rev. C 53 410 [76] Hanauske M, Satarov L M, Mishustin I N, Stocker H, Greiner W 2001 Phys. Rev. D 64 043005 doi: 10.1103/PhysRevD.64.043005 [77] Rüster S B, Rischke D H 2004 Phys. Rev. D 69 045011 doi: 10.1103/PhysRevD.69.045011 [78] Menezes D P, Providencia C, Melrose D B 2006 J. Phys. G 32 1081 doi: 10.1088/0954-3899/32/8/001 [79] Chao J Y, Chu P C, Huang M 2013 Phys. Rev. D 88 054009 doi: 10.1103/PhysRevD.88.054009 [80] Chu P C, Wang X, Chen L W, Huang M 2015 Phys. Rev. D 91 023003 doi: 10.1103/PhysRevD.91.023003 [81] Chu P C, Wang B, Ma H Y, Dong Y M, Chang S L, Zheng C H, Liu J T, Zhang X M 2016 Phys. Rev. D 93 094032 doi: 10.1103/PhysRevD.93.094032 [82] Chu P C, Chen L W 2017 Phys. Rev. D 96 083019 doi: 10.1103/PhysRevD.96.083019 [83] Roberts C D, Williams A G 1994 Prog. Part. Nucl. Phys. 33 477 doi: 10.1016/0146-6410(94)90049-3 [84] Zong H S, Chang L, Hou F Y, Sun W M, Liu Y X 2005 Phys. Rev. C 71 015205 doi: 10.1103/PhysRevC.71.015205 [85] Peng G X, Chiang H C, Yang J J, Li L, Liu B 1999 Phys. Rev. C 61 015201 doi: 10.1103/PhysRevC.61.015201 [86] Peng G X, Chiang H C, Zou B S, Ning P Z, Luo S J 2000 Phys. Rev. C 62 025801 [87] Peng G X, Li A, Lombardo U 2008 Phys. Rev. C 77 065807 doi: 10.1103/PhysRevC.77.065807 [88] Li A, Peng G X, Lu J F 2011 Res. Astron. Astrophys. 11 482 doi: 10.1088/1674-4527/11/4/010 [89] Schertler K, Greiner C, Sahu P K, Thoma M H 1998 Nucl. Phys. A 637 451 doi: 10.1016/S0375-9474(98)00330-3 [90] Alford M, Kouvaris C, Rajagopal K 2005 Phys. Rev. D 71 054009 doi: 10.1103/PhysRevD.71.054009 [91] Giannakis I, Hou D F, Ren H C, Rischke D H 2004 Phys. Rev. L 93 232301 doi: 10.1103/PhysRevLett.93.232301 [92] 董爱军, 高志福, 杨晓峰等 2023 物理学报 72 030502 doi: 10.7498/aps.72.20220092 Dong A J, Gao Z F, Yang X F, et al. 2023 Acta Phys. Sin. 72 030502 doi: 10.7498/aps.72.20220092 [93] Ferrer E J, Vivian de la Incera 2005 Phys. Rev. Lett. 95 152002 doi: 10.1103/PhysRevLett.95.152002 [94] Ferrer E J, Vivian de la Incera, Cristina M 2006 Nucl.Phys. B 747 88 doi: 10.1016/j.nuclphysb.2006.04.013 [95] Feng B, Ferrer E J, Vivian de la Incera 2011 Nucl.Phys. B 853 213 doi: 10.1016/j.nuclphysb.2011.07.016 [96] Paulucci L, Ferrer E J, Vivian de la Incera, Horvath J E 2011 Phys. Rev. D 83 043009 doi: 10.1103/PhysRevD.83.043009 [97] Isayev A A, Yang J 2011 Phys. Rev. C 84 065802 [98] Isayev A A, Yang J 2012 Phys. Lett. B 707 163 doi: 10.1016/j.physletb.2011.12.003 [99] Isayev A A, Yang J 2013 J. Phys. G: Nucl. Part. Phys. 40 035105 doi: 10.1088/0954-3899/40/3/035105 [100] Feng B, Hou D F, Ren H C, Wu P P 2010 Phys. Rev. L 105 042001 doi: 10.1103/PhysRevLett.105.042001 [101] Gao Z F, Li X D, Wang N, Yuan J P, Wang P, Peng Q H, Du Y J 2016 Mon. Not. R. Astron. Soc. 456 55 doi: 10.1093/mnras/stv2465 [102] Gao Z F, Wang N, Peng Q H, Li X D, Du Y J 2013 Mod. Phys. Lett. A 28 1350138 [103] Oppenheimer J R, Volkoff G M 1939 Phys. Rev. 33 374 [104] Chu P C, Chen L W, Wang X 2014 Phys. Rev. D 90 063013 doi: 10.1103/PhysRevD.90.063013 [105] Chu P C, Liu H, Liu H M, Ju M, Wu X H, Zhou Y, Li X H 2025 Eur. Phys. J. C 85 466 doi: 10.1140/epjc/s10052-025-14193-y [106] Chu P C, Liu H, Liu H M, Li X H, Ju M, Wu X H, Zhou Y 2024 Phys. Rev. D 110 123031 doi: 10.1103/PhysRevD.110.123031 [107] Chu P C, Liu H, Ju M, Wu X H, Liu H M, Zhou Y, Liu H, Lu S Y, Li X H 2024 Phys. Rev. D 110 043032 doi: 10.1103/PhysRevD.110.043032 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: