铁磁性材料在服役过程中产生的残余应力是影响其力学性能和结构完整性的关键因素, 磁记忆、磁声发射、磁巴克豪森、磁滞回线等方法能够实现对材料应力快速检测和表征^[1–4]. 磁声发射(magneto-acoustic emission, MAE)是最近兴起的一种无损检测方法, 该技术通过捕获材料磁化过程激发的应力波信号进行检测, 而这种应力波主要来源于内部磁畴旋转产生的磁致伸缩. 材料内部磁畴结构与应力状态密切相关, 使得磁声发射信号展现出对应力状态的高灵敏响应特性^[5]. Serbin等^[6]研究了铁磁材料在弹性变形和塑性变形阶段磁声发射信号的变化规律, 表明了在弹性变形阶段磁声发射信号逐渐增加, 而在塑性变形阶段磁声发射信号又逐渐减小. Stupakov等^[7]研究了不同频率下磁声发射信号的变化趋势, 并讨论其与磁化曲线和巴克豪森信号之间的联系. 当前, 很多学者认为磁声发射信号主要来源于内部90°磁畴的运动, 而180°磁畴的移动对MAE信号贡献极小. 而之前的一些研究工作对取向硅钢进行MAE信号机制研究, 发现在180°磁畴结构为主的有取向硅钢中, 即使是弱磁交变磁场下仅180°磁畴壁翻转也可以产生强烈的MAE信号. 综上, MAE信号的产生机制与应力场的多尺度调控作用尚未完全阐明, 特别是磁畴运动模式与磁声发射信号特征的内在关联仍存在争议. 亟需结合应力作用下的磁畴分析阐明MAE在应力载荷下的变化规律及其与磁畴运动特性之间的内在联系.

磁畴结构及其运动特性是决定宏观磁响应的关键性因素^[8–10]. 研究材料的磁畴结构, 特别是研究在各种服役环境下磁畴演变过程, 有助于厘清多场耦合作用下宏观磁响应的微观物理机理^[11,12]. 借助磁光克尔显微镜、电子显微镜、磁力显微镜、中子成像等先进磁畴观测技术^[13–16], 越来越多研究学者从磁无损检测表征、力磁耦合和磁滞建模等方面对磁畴开展了大量研究^[17]. Rudolf是磁畴研究领域的先驱, 基于磁光成像系统研究了拉应力、压应力、横向应力等对硅钢磁畴模式和畴壁动态行为的变化^[18]. Qiu等^[19,20]研究了晶界、应力和晶粒组织等对磁畴结构和畴壁运动的影响规律, 并初步提出可用磁畴动态特性进行材料表征. 为了模拟材料在各种工况下磁特性变化, 许多学者从磁化建模、磁特性预测等方面开展各类磁性材料磁畴动态行为的研究^[21–23]. 李永建等^[24]研究了拉应力作用下取向电工钢磁畴结构沿轧制方向的变化规律, 将拉应力与畴壁平移运动之间的关系量化处理, 由此采用基于畴壁平移运动的J-A 模型对材料的磁化特性进行描述. 磁畴运动受到多个因素的影响, 实际工况下, 畴壁的运动状态是受到多场耦合的共同影响^[25,26]. 同时, 还需要同步获取宏观电磁声响应信号, 研究磁响应信号和微观磁畴之间的内在关联.

针对上述挑战, 本文提出宏-微观协同的研究策略: 通过磁光克尔-磁声发射同步检测系统, 实现应力场作用下磁畴动态演变的原位观测与磁声发射信号的采集. 以典型铁磁材料取向硅钢为研究对象, 探究了单轴拉应力对附加磁畴形核和90°畴壁运动的抑制规律, 并建立基于磁畴体积变化的MAE信号衰减模型. 进一步结合晶粒内部和晶界区域的附加磁畴的变化, 阐明了多晶材料磁弹耦合效应与晶界钉扎效应的竞争机制. 研究成果为发展高精度磁声应力检测技术提供了理论支撑, 也为发展力-磁-声耦合模型、磁无损检测技术提供了理论基础.

Shibata和Ono^[27]通过对镍和铁的磁特性研究, 结合压电效应原理, 得出磁声发射信号源为90°磁畴壁的不可逆移动和磁矩的不可逆转动, 并提出磁声发射信号强度可表示为

式中, U为磁声发射信号强度; C为材料常数; V_i为第i个磁畴体积; ε为应变值; Δε为单位磁畴在磁化方向上应变值; Δt为第i个磁畴产生应变Δε所需要的时间. Σ为各个磁畴体积变化产生磁声发射累计贡献值.

针对铁磁性材料, 主要是由于磁畴体积变化引起磁化强度的变化, 而磁矩旋转对磁化贡献较小. 磁化强度与饱和磁化强度、磁畴体积应变之间的关系可表示为

其中θ为第i个磁畴的磁化矢量与指定参考方向的夹角; M_s为材料的饱和磁化强度; δV_i为第i个磁畴的体积变化. (2)式代表接近于外磁场方向的磁畴长大(使不接近于外磁场方向的磁畴缩小)对于总磁化的贡献, 即单位磁畴磁致伸缩产生的体积形变对于总磁化的影响, 这个过程是通过磁畴间界壁的位移来进行, 简称为畴壁位移过程.

磁化强度和磁场强度及应力的关系:

其中λ_s为材料的饱和磁致伸缩系数, 由材料自身性质所决定; σ为材料所受的应力. 因为

由(2)式可得

则有

所以可得

其中$K = \dfrac{{C \cdot M{}_{\text{s}}}}{{3{\lambda _{\text{s}}}\cos \theta }}$为一个常数, 它由材料本身的性质决定. (7)式给出了在磁声发射信号和应力之间的映射关系模型, 表明了磁声发射信号和应力倒数之间成线性关系. 后面将进一步通过实验验证磁声发射信号和应力之间的关系.

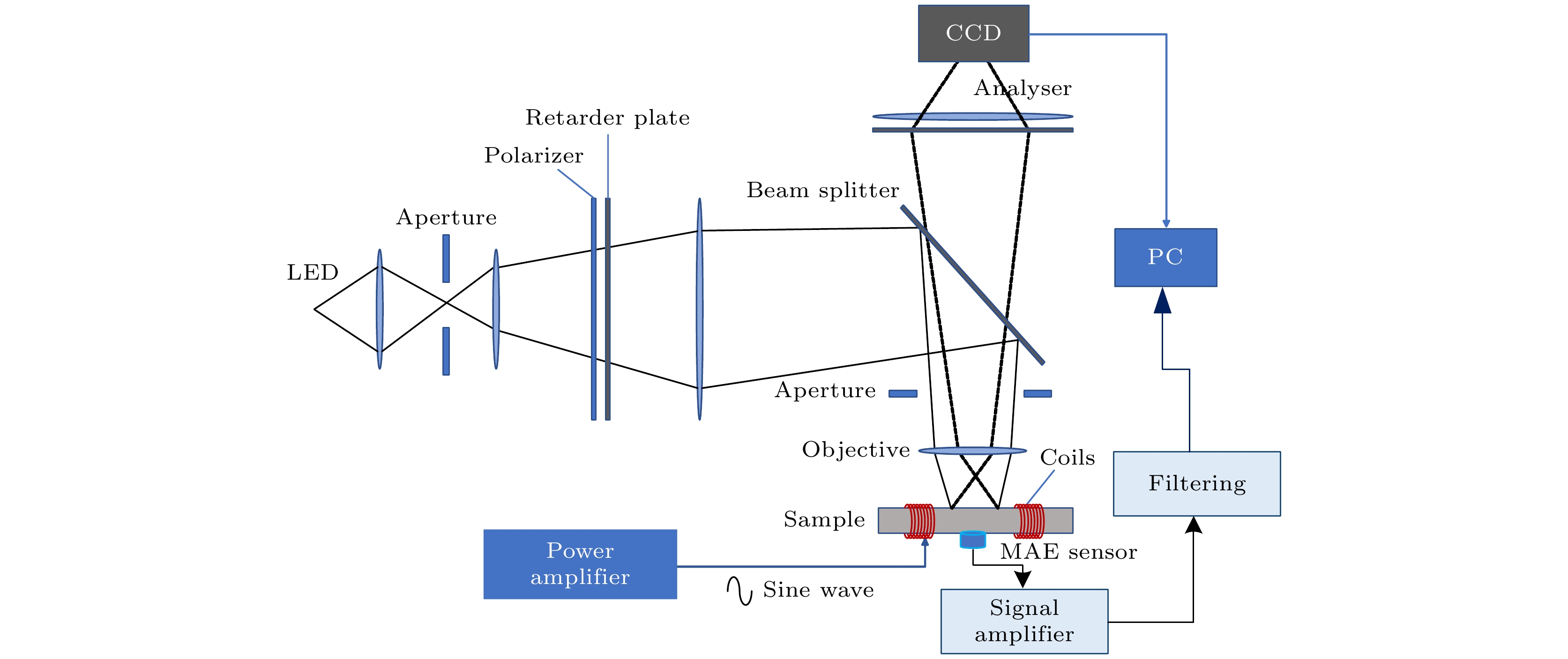
实验装置主要包括磁光成像系统、磁声发射检测系统和应力加载系统. 磁光成像系统主要包括: 光源、光路系统、CCD采集装置. 由LED发出一束自然光, 通过偏振片变为偏振光, 偏振光与磁畴之间产生磁光克尔效应, 使得偏振光的偏振方向发生变化^[13], 产生克尔转角. 通过检偏器可以检测出该克尔转角并通过CCD相机转换为数字图像, 磁光成像检测装置如图1所示.

磁声发射检测系统主要包括: 信号发生器、功率放大器、信号放大器、数据采集卡、亥姆霍兹线圈和MAE探头. 由信号发生器产生正弦激励信号通过功率放大器接入励磁线圈, 该线圈环绕在被测试样上, 用以产生均匀的交变磁场. 铁磁性材料内部磁畴在外加磁场下发生转动, 引起磁致伸缩并产生应力波, 即为磁声发射信号. 通过MAE探头将该磁声发射信号转化为电信号, 再经过信号放大器(60 dB)和带通滤波器即可获取MAE信号, 磁声发射检测装置如图1所示. 应力拉伸装置用于给材料施加一定应力, 模拟材料在实际工况下受到的残余应力, 应力大小可由应力显示仪读取, 应力装置介绍在文献[28]中有具体描述.

实验过程如下: 先将工件应力置零, 采用20 Hz正弦激励, 获取MAE信号. 然后, 采用交流降幅退磁, 获得退磁状态下的磁畴图像, 并施加不同大小的直流电可分别获取在不同磁场下的磁畴图像. 每次给材料增加11 MPa应力, 并重复上述步骤, 即可获得不同应力下MAE信号和磁畴图像信号.

实验中使用样品为取向硅钢, 该样品尺寸为300 mm× 30 mm× 0.3 mm, 样品经过腐蚀去除表面涂层, 然后打磨抛光至镜面, 用于磁畴观测.

分别测试了不同应力下MAE信号, 分析MAE信号随应力的演变规律. 接着, 观测不同应力下硅钢在不同位置磁畴随磁场的变化规律, 探究力和晶界对磁畴的影响, 并进一步讨论了在力耦合作用下磁畴和MAE之间内在联系.

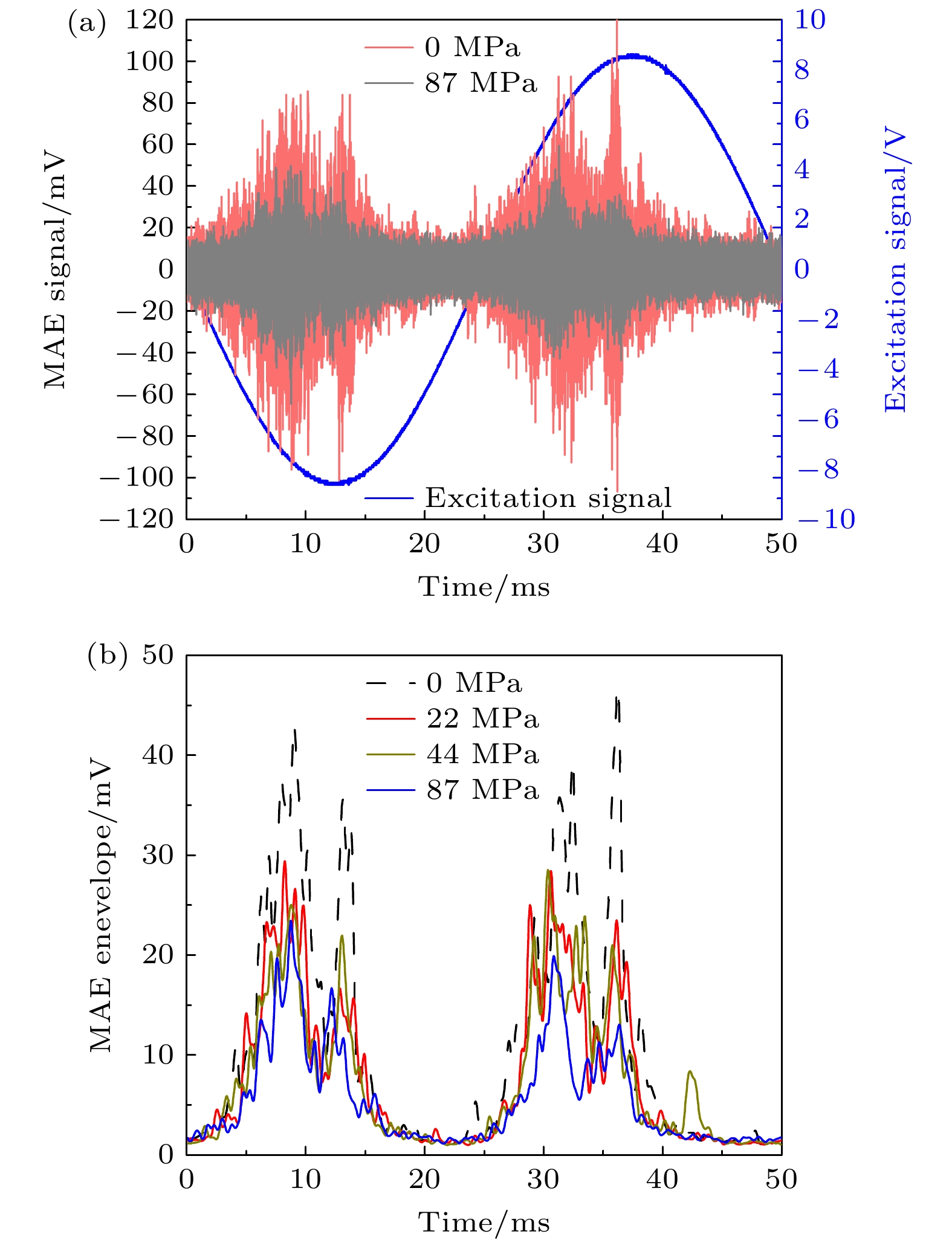
图2(a)为0和87 MPa下磁声发射原始信号. 激励信号从饱和状态降为0时, 反磁化磁畴开始形核, 内部磁畴开始发生旋转, 开始产生磁声信号, 磁声信号由于从样件传至探头需要一定时间, 因此磁声发射信号采集持续时间较长. 从不同应力下对比来看, 0 MPa时MAE信号相对较强, 当应力增加至87 MPa后, MAE信号明显减弱. 为了进一步探究MAE信号强度随应力变化规律, 通过计算得到了不同应力下MAE信号的包络线, 如图2(b)所示. 从图2(b)中可以看出, 在应力为0—44 MPa之间, 磁声发射信号降低较为明显, 而当应力值超过44 MPa后磁声发射信号降低较为缓慢.

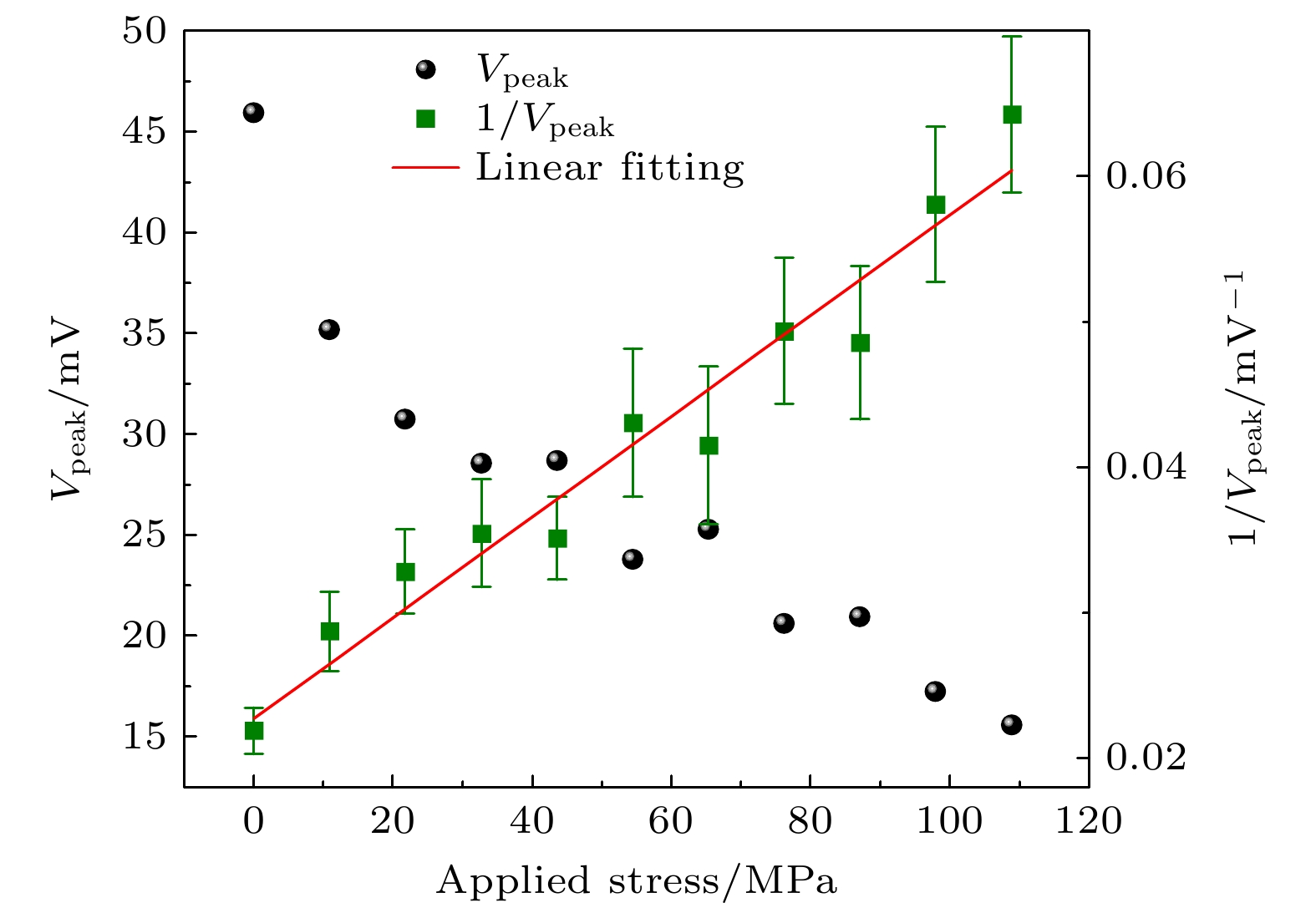
为了进一步获取MAE信号和应力之间的定量关系, 从反复磁化的8个周期中, 提取磁声发射包络线中峰值的平均值(V_peak), 得到了MAE峰值和应力之间的关系如图3左侧坐标所示. 显然MAE信号强度随应力先快速降低, 之后降低缓慢. 这种变化趋势, 通过求取其倒数, 可获得两者之间较好的线性模型. 图3右侧坐标描述了MAE信号峰值倒数(1/V_peak)随应力变化的趋势, 得到MAE信号倒数和应力之间呈现较好的线性关系, 其皮尔逊相关系数为0.98, 两者之间关系模型表示为${1 {/ } {{V_{{\text{peak}}}}}} = 3.46 \times {10^{ - 4}}\sigma + 0.023$. 这与2.1节中推导的力-磁-声模型一致, 验证了(7)式中模型的准确性.

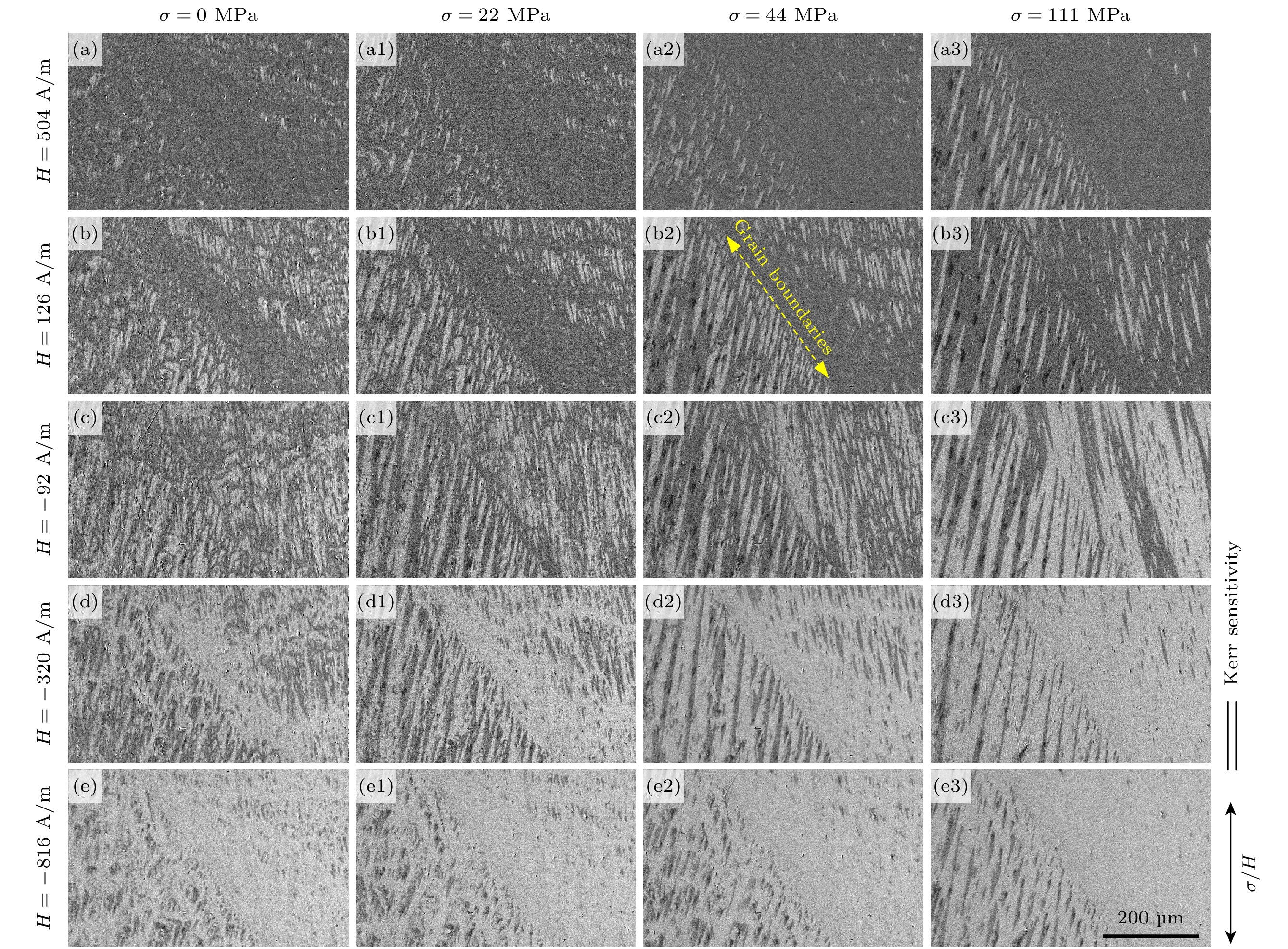
铁磁性材料磁畴的结构和大小、磁畴的运动状态都与应力有关. 为了探究应力对磁畴运动特性的影响, 首先在磁光成像系统观测下, 选取两个不同取向晶粒(晶粒1和晶粒2)进行磁畴模式与运动状态的观测和对比分析.

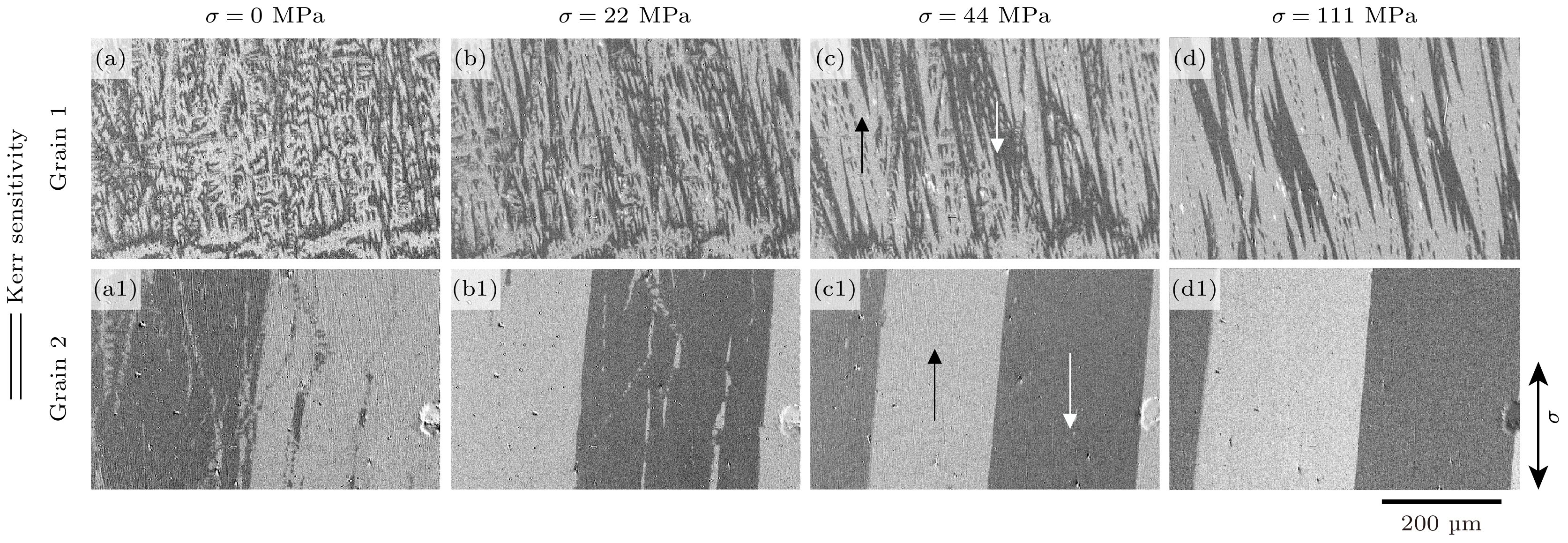
图4为晶粒1和晶粒2处分别施加了0, 22, 44和111 MPa拉应力的作用退磁状态下的磁畴模式, 图中亮暗区域表示了每个磁畴的自发磁化方向. 本次实验中磁光成像系统的克尔灵敏度与取向硅钢轧制方向一致, 即亮色区域为磁化方向朝上(180°磁畴), 暗色区域为磁化方向朝下(0°磁畴). 晶粒1处在应力为0 MPa时, 磁畴结构基本由附加磁畴组成, 并有较多的横向磁畴, 整体磁畴形态细小且分散. 当应力增加到22 MPa时, 出现了部分树枝状磁畴, 附加磁畴的数量减少, 横向磁畴消失. 当应力增加到44 MPa时, 附加磁畴大量减少, 转变为细长的树枝状磁畴, 但仍有附加畴位于主磁畴周围和内部; 当应力继续增加到111 MPa时, 图中磁畴结构基本为树枝状磁畴, 只有极少量的附加畴存在, 如图4(a)—(d)所示. 晶粒1晶体取向偏离[001]方向较大, 会在表面产生较大的漏磁场即退磁场, 需要形成附加磁畴形成闭合磁路, 降低退磁能. 当施加外加拉应力时, 由于磁弹耦合效应的影响, 使得附加磁畴数量减少, 而主磁畴逐渐变得清晰可见. 晶粒2处的晶粒取向与材料的轧制方向接近平行, 磁畴方向与易磁化方向平行, 为典型的0°和180°磁畴. 只有在0和22 MPa的应力下出现了少量的附加畴, 当增加到44 MPa时, 附加畴完全消失, 已完全转变为条状磁畴, 如图4(a1)—(d1)所示.

通过对比分析, 在不同晶粒内磁畴随应力增加的变化趋势大致相同, 附加畴会逐渐消失合并为主磁畴, 又由于晶粒取向差异、应力等因素的影响, 最后的磁畴结构会有所不同. 为进一步探究应力对磁畴运动特性的影响, 还需加入不同应力和不同磁场下的磁畴图像, 基于磁畴壁在外磁场的作用下会发生移动和翻转的特性, 分析不同应力下磁畴的动态行为规律.

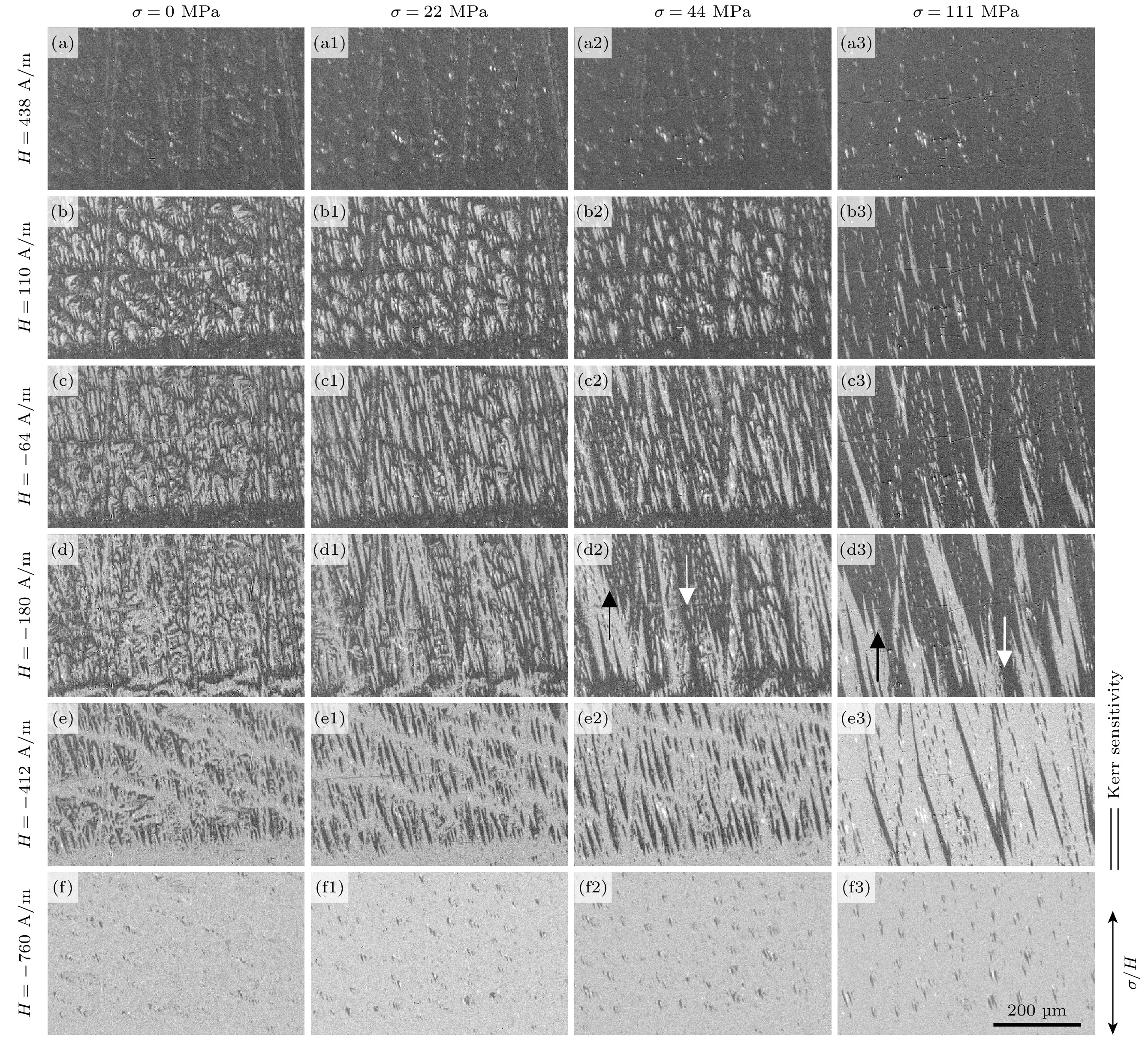
在外加磁场作用下, 磁畴壁发生移动和翻转, 并从一个平衡状态跳跃到另一个平衡状态, 磁畴也从正向饱和状态到负向饱和状态. 图5为样品的位置1处在0, 22, 44和111 MPa的拉应力和外加磁场共同作用下的磁畴模式图像. 磁场由饱和状态降低到438 A/m时, 有反向的点状附加磁畴开始出现, 如图5(a)所示. 在应力为111 MPa时, 磁畴最接近正向饱和状态, 反向附加磁畴的含量相对最少, 如图5(a3)所示. 当磁场强度反向增加到–64 A/m时, 在应力为0, 22和44 MPa下, 存在大量的反磁化畴, 并随着应力的增加, 附加磁畴由点状磁畴向针状磁畴转变, 如图5(c)、图5(c1)和图5(c2)所示. 而应力增加到111 MPa时, 反磁化畴的面积更少, 多为树枝状磁畴, 如图5(c3)所示. 当磁场继续反向增加至–412 A/m时, 随着应力的增加, 附加磁畴数量减少, 反向磁畴面积增加, 畴壁翻转的速度加快, 如图5(e)—(e3)所示. 当磁场为–760 A/m, 材料接近负向饱和状态时, 在不同应力下都存在附加磁畴, 并没有随着应力的增加而完全消失, 反而在应力111 MPa时附加磁畴数量更多, 如图5(f)和图5(f3)所示.

图6为晶粒2在0, 22, 44和111 MPa四个应力下沿着磁滞回线下降沿不同磁场下的磁畴模式. 在磁场强度为353 A/m时, 0和22 MPa应力下, 已经出现少量的反向磁畴, 而在44和111 MPa应力下仍然为正向饱和状态, 如图6(a)—(a3)所示. 当磁场降低到80 A/m时, 应力为0和22 MPa时, 出现楔形状和条状的反磁化畴, 而在应力为44和111 MPa时, 磁畴结构只有长条形的0°和180°磁畴, 如图6(c)—(c3)所示. 当磁场为–390 A/m时, 0 MPa应力下磁畴未到达饱和状态, 而111 MPa应力下已经到达饱和状态, 如图6(e)和图6(e3)所示. 应力的增加改变了磁畴模式, 并影响了畴壁移动和翻转的速度, 使得磁畴到达饱和状态所需的外加磁场更小.

综合上述分析, 在应力的作用下, 磁畴模式与主磁畴的形状发生改变, 表现在附加磁畴的数量随着应力的增加而减少, 从点状附加磁畴逐渐转变成树枝状或长条形磁畴, 并且使得磁畴壁移动和翻转更为容易, 磁畴达到饱和状态所需的外加磁场减小. 由于晶粒取向的影响, 导致不同晶粒的磁畴倾角不同, 当磁畴方向平行于易磁化轴时, 相同应力下磁畴达到饱和状态所需外加磁场更小; 磁畴方向偏离易磁化轴时, 表面会形成大量的附加磁畴磁通回路来降低退磁能, 并且不会随着应力的增加而完全消失.

3.3节讨论了在不同的晶粒内, 磁畴结构和运动特性受应力的显著影响, 同时也受晶粒取向的 影响. 在多晶磁性材料中, 晶界作为晶粒间的界面缺陷, 也会对磁畴结构和运动特性产生影响. 经过观测后选取两个位于晶界处的位置, 分别为位置1和位置2, 进行磁畴的观测和分析.

图7为位置1处在应力0, 22, 44和111 MPa下及不同磁场下的磁畴图像, 晶界两侧晶粒内的磁畴结构存在差异, 使得晶界的形状和轮廓较为清晰分辨出, 晶界标注如图7(b1)所示. 图7中晶界上半区比下半区存在更多的附加磁畴, 且磁化状态也存在明显差异, 表明了晶界两侧晶粒取向各异. 当磁场强度由饱和状态降为126 A/m, 晶界上半区已经出现了大量的反磁化畴, 而下半区仍然处于饱和状态, 如图7(b)—(b3)所示. 当磁场强度下降到–92 A/m时, 下半区出现了大量反向磁畴, 且多为条状磁畴, 如图7(c)—(c3)所示. 同时值得注意的是, 在晶界附近还出现大量细小的楔形磁畴, 在应力为111 MPa尤为明显, 如图7(c3)所示. 当磁场强度下降到–816 A/m, 晶界附近的磁畴仍未达到饱和状态, 如图7(e)所示. 由此可推断, 晶界对磁畴壁的运动存在阻碍作用, 磁畴达到饱和状态所需的外加磁场增加.

图8为位置2处在应力0, 22, 44和111 MPa下及不同磁场下的磁畴图像, 晶界已在图8(b2)中标注出. 当磁场强度为504 A/m时, 磁畴壁移动, 少量的反向磁畴开始出现, 晶界右上区域的反向磁畴开始出现的位置离晶界较远, 随着应力的增加, 右上区域反向磁畴面积减少, 左下区域反向磁畴形状转变成细长的针状, 且在晶界附近存在更细小的附加磁畴, 如图8(a)—(a3)所示. 当磁场强度下降到–92 A/m, 应力为0 MPa时, 晶界不清晰且附近的磁畴呈弯曲状; 应力增加到44 MPa时, 晶界清晰, 左下区域磁畴大部分转变为树枝状磁畴, 但晶界附近仍有大量附加磁畴; 应力增加到111 MPa时, 晶界附近的附加磁畴未完全消失, 如图8(c)—(c3)所示.

综合上述分析可得: 1)晶界作为晶粒间的界面, 原子排列不规则, 晶格畸变大, 晶界处能量高, 存在空位、位错等缺陷, 容易形成钉扎效应, 对磁畴壁的移动有阻碍作用. 磁畴壁在穿越晶界时需要克服额外的能量势垒, 使得磁畴达到饱和状态所需外加磁场强度增加; 2)晶界两侧的晶粒取向不同, 磁化矢量不一样, 使得晶界处产生磁极以形成退磁场, 导致晶界处始终存在附加磁畴; 3)应力增加, 晶粒内附加畴减少, 导致晶界处产生退磁场增加, 从而在应力较高时出现了新的反磁化畴.

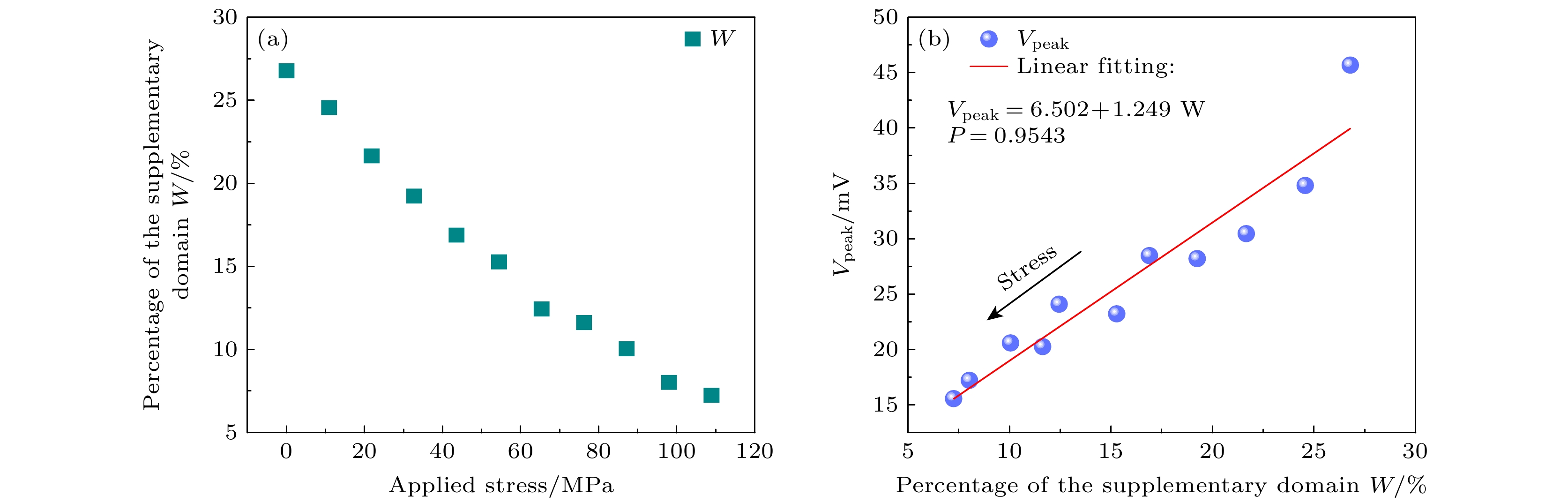
在探究应力对磁声发射信号影响实验中, 应力与磁声发射信号的峰值的倒数呈正相关, 再通过观测应力作用下磁畴模式的动态演变, 发现附加磁畴占比随应力增加呈递减趋势. 磁声发射信号的产生主要源于磁化过程中90°磁畴的运动和磁畴旋转 产生的磁致伸缩, 使得磁声发射信号和磁畴演变 之间一定存在内在联系. 进一步对样品多个位置进行分析, 并采用图像处理方式计算附加磁畴占比W(percentage of the supplementary domain), 并计算平均值, 代表整个样品附加磁畴占比. 图9(a)为附加磁畴占比随应力的变化趋势, 结合图3可以得出附加磁畴的占比随应力变化规律和磁声发 射信号变化规律相似. 为进一步求取两者之间相 关性, 将附加磁畴占比作为自变量, 而磁声发射信号峰值(V_peak)作为因变量, 得到了不同应力下附加磁畴占比和磁声发射信号峰值之间的关系, 如图9(b)所示. 显然, W和V_peak之间存在显著正相关关系. 线性拟合后两者之间相关系数P为0.95, 表明二者具有高度相关性, 线性拟合方程为${V_{{\text{peak}}}} = 6.502 + 1.249 W$.

通过分析可得, 附加磁畴占比与磁声发射信号的变化密切相关. 硅钢材料由许多取向不同的晶粒构成. 对于理想(110)平面内的晶粒而言, 内部磁畴应当为不存在任何柳叶刀等附加畴, 主要为0°和180°磁矩方向反向平行的主磁畴, 如图4(c1)所示, 在主磁畴两端, 会在晶界或者试样边沿处会形成90°磁畴, 降低退磁能. 除此之外, 实际上晶粒取向总会偏离(110)平面. 当晶粒取向和[001]轧制方向存在一定夹角时, 在平面外方向会存在较大磁矩分量, 并产生退磁场, 为了减少退磁能, 在偏离轧制方向晶粒内部会形成大量的附加畴, 并在材料内部会形成横向磁畴, 使得附加畴和主畴之间的磁通形成闭合回路, 进一步降低退磁能. 随着应力的增加, 由于磁弹耦合效应, 使得90°磁畴和附加磁畴数量减少, 如图4中晶粒1所示. 附加畴减少, 使得内部横向磁畴数量也随之减少, 导致退磁能和退磁场增加, 使得磁化过程主要以0°和180°畴壁移动为主, 90°磁畴旋转和横向磁畴运动过程减少, 导致(5)式中磁畴体积应变$ {d} \left( {\displaystyle \sum {\delta {V_i}} } \right) $幅值降低, 磁声发射信号强度降低, 如图3所示. 由于相邻两个晶粒内磁矩方向不平行, 使得磁通由一个晶粒流向相邻晶粒时会产生不连续性, 为了形成闭合回路, 减少退磁场, 晶界附近横截面积上会出现大量90°磁畴. 随着应力增加, 90°磁畴数量减少, 使得退磁能增加, 为了降低退磁场, 在晶界附近会形成大量楔形畴、迷宫畴和柳叶刀等附加畴, 如图7(c3)和图8(d2)所示. 随之, 在材料内部产生新的横向磁畴, 使得在应力较高时候, 磁声信号强度会降低但不会降至零. 综上, MAE信号受到横向磁畴和90°磁畴产生、湮灭和运动过程的影响, 而横向磁 畴变化与附加磁畴演变密切相关, 附加磁畴密度主要与主畴偏离(110)平面程度相关. 同时, 相邻两个晶粒取向差会导致在晶界附近产生附加畴. 总体而言, 应力作用下磁声发射信号的变化是应力-晶界–90°磁畴-附加磁畴相互调控和制约的过程.

(7)式的理论模型可对图3中磁声发射信号随应力演变规律的基本实验现象和规律给予合理解释, 也为发展磁声发射应力无损检测技术提供了一定的理论依据. 同时, 基于磁畴观测也初步揭示了磁声发射信号随应力变化的微观物理机理. 但是值得注意的是, 力-磁-声模型推导中磁畴对总磁化的贡献进行了简化, 忽略部分磁畴对磁化的贡献, 也忽略了部分磁畴模式对磁声发射的贡献. 本文观测的磁畴只是表面磁畴结构, 而内部的磁畴运动对磁声发射占据更为重要的作用, 而表面磁畴和内部磁畴之间存在一定差异. 同时, 实际构件磁畴模式非常多, 不同磁畴模式之间相互影响, 构件受到的应力也颇为复杂, 并非一维均匀应力分布. 实际材料中很难得到单一的磁畴模式, 使得磁声发射源于那种磁畴的运动仍然还需要进一步相关的实验论证. 当前的研究存在一些假设和简化, 限制了模型针对实际检测的应用能力. 作者希望在未来研究中, 从不同材料影响规律等方面进行模型完善和拓展, 以使其能够应用于实际检测中的复杂工况, 也需要借助相关磁畴观测技术进一步探讨磁畴与磁声发射之间的内在联系.

本文基于磁光成像和磁声发射原位同步观测系统, 从原理上推导磁声发射信号和应力之间数学-物理映射关系模型, 通过实验得到磁声发射信号强度和应力之间的量化关系, 并从磁畴演变角度阐述了应力-磁声发射-磁畴演变之间的内在联系.

1)推导了磁声发射信号强度和应力之间存在反比关系, 通过信号得到了应力和磁声发射信号峰值的倒数存在较好的线性关系.

2)从磁畴角度, 证明了晶粒内部附加磁畴随着应力增加而逐渐减少, 使得横向磁畴减少, 这是磁声发射信号随应力减弱的主要原因. 同时在晶界附近由于磁通的不连续性, 使得在应力施加到一定幅值后出现了新的反向磁畴.

3)验证了附加畴和磁声发射信号存在密切相关, 相关性达到了0.95, 并得到两者之间的关系方程为V_peak = 6.502+1.249W. 归纳总结得到应力和晶界对磁声发射信号和磁畴的调控作用, 并揭示了它们之间的内在联系.

本文研究结果对阐明磁声信号随应力的变化、发展力磁声耦合建模提供了微观理论解释, 也为磁声发射应力无损检测模型提供了理论支撑.