典型的二维过渡金属硫族化合物化学式可以表示为MX₂, 其中M代表过渡金属元素(Ti, V, Mo, W), X代表硫族元素(S, Se, Te)^[1]. 这类材料拥有着优异的电学^[2,3]、力学^[4]与光学特性^[5-7], 在低功耗、高性能及柔性光电器件领域具有巨大的应用潜力. 例如它们被广泛应用于隧穿晶体管^[8,9]、发光二极管^[10,11]、光电探测器^[10,12]和光伏电池^[13,14]等器件研发. 在这些应用中, 通过不同的二维过渡金属硫族化合物组合构建的平面异质结因其独特的界面相互作用和能带调控能力, 进一步拓展了材料的功能性. 目前这类材料的研究主要集中在WSe₂-MoS₂^[8,15], WSe₂-MoSe₂^[16,17], WSe₂-MoSe₂^[17], WS₂-MoSe₂^[11]等由W, Mo, S, Se四种元素组成的平面异质结体系中. 界面结构在很大程度上决定了异质结的性质, 因此精准解析界面原子结构至关重要. 然而, 实现原子分辨的界面成像仍然面临挑战, 尤其对于WS₂-MoSe₂平面异质结, W与S的原子序数相差大, 获得稳定清晰衬度的成像难度更大, 通常的透射电镜高角环形暗场(HAADF)成像技术难以满足要求. 近年, 积分差分相位衬度(iDPC)及其衍生成像方法为这个问题提供了一个可行的解决方案. 1974年, Rose^[18]提出了扫描透射电子显微镜(STEM)中的相位衬度. 同年, Dekkers和De Lang^[19]指出, 利用分区探头的相对信号差异来获取图像的技术可以应用于扫描透射电子显微镜(STEM), 也就是差分相位衬度(DPC)的早期想法. 1976年, Rose^[20]提出通过时间积分来重建相位. 2010年, Shibata等^[21]再次将DPC技术引入电子显微镜, 获得了第一批具有原子分辨率的实验结果, 并且在2012年用DPC技术获得了具有原子分辨率的内部电场的衬度图像^[22]. 2015年, $\text{Lazi}\acute{\text{c}} $等^[23]对Rose提出的积分理论进行了推广应用, 在薄样品上实现了低电子束低剂量的原子成像. 之后, 基于STEM的iDPC(iDPC-STEM)方法可对材料中轻重元素同时成像^[24], 在二维材料原子位置和缺陷表征^[25,26]的研究中发挥了重要作用. 因此, iDPC方法是实现原子序数差别大、电子束敏感的二维平面异质结界面结构精准表征最有前途的手段.

STEM成像过程可以理解为波函数的传递. 电子束被透镜聚焦的过程可以视为对其波函数进行了一次傅里叶变换. 记后焦面处的电子波函数为$ \varPsi (\boldsymbol{k}) $, 其中$ \boldsymbol{k}=\left({k}_{x}, {k}_{y}\right) $表示在后焦面上的位置, 则样品上表面的入射波函数可以表示为

理论上, 薄样品对电子束的影响是对其施加了一个传递函数$ {{\mathrm{e}}}^{{\mathrm{i}}\varphi \left(r\right)} $, 它仅仅影响入射波的相位. 对幅度的影响, 通常通过引入吸收势来考虑, 此处暂时不讨论吸收问题. 因此样品下表面的出射波表示为

其中$ \varphi \left(\boldsymbol{r}\right) $表示样品内的相位; $ {\boldsymbol{r}}_{{\mathrm{p}}} $表示扫描的过程. 同理我们在探测器平面中获得的波函数, 可以通过对出射波进行傅里叶变换得到:

运算符$ {\mathrm{*}} $表示卷积. 探测器平面的电子波强度分布为

$ {I}_{{\mathrm{D}}}(k, {r}_{{\mathrm{p}}}) $即为会聚束电子衍射(CBED)图样. 在没有样品、电子束直射探测器的情况下, $ {I}_{{\mathrm{D}}}(k, {r}_{{\mathrm{p}}}) ={\left|\varPsi \left(-k\right)\right|}^{2} $, 这是一个与光阑形状相同的盘状光斑, 被称为明场盘. 明场盘在探测器平面上的半径为$ {k}_{{\mathrm{B}}{\mathrm{F}}} $, 它与束流的汇聚半角$ \alpha $通过以下关系联系在一起: $ {k}_{{\mathrm{B}}{\mathrm{F}}}=\alpha /\lambda $, 其中$ \lambda $是STEM中电子束的波长.

在引入样品之前, 我们讨论最简单的情况, 即在样品平面上的一个恒定电场. 在这种情况下传递函数写为

其中$ \sigma $是比例常数. 将之代入(3)式可得

式中采用了相关性定理$ \mathcal{F}\left\{{{\mathrm{e}}}^{-{\mathrm{i}}\sigma E\cdot \left(\boldsymbol{r}+{\boldsymbol{r}}_{{\mathrm{p}}}\right)}\right\}\left({\boldsymbol{k}}\right)=\delta \big[k+ {\sigma E}/({2{\pi}})\big] $和(1)式. 则在作用样品平面的CBED图样的强度分布为

显然, 明场盘发生了整体性的位移, 大小为$ \sigma E/\left(2 \pi \right) $, 是电场的线性函数, 表明了CBED图样的线性性质.

在更一般情况下, $ \varphi \left({\boldsymbol{r}}\right) $由任意给定的样品决定, 样品内的电场可描述为$ E\left({\boldsymbol{r}}\right)=-\nabla \varphi \left({\boldsymbol{r}}\right) $情况也变得更加复杂, Müller等^[27]在模拟STEM成像的工作中发现, CBED图样的轮廓并不会随着材料局域电场变化有明显移动, 而只会改变其强度分布^[27]. 这一情况说明CBED相对样品内电场的线性性质很可能由其质心传递. 我们首先写出CBED图样质心的$ x $分量$ {I}^{{{\mathrm{C}}{\mathrm{O}}{\mathrm{M}}}_{x}} $:

其中$ k=({k}_{x}, {k}_{y}) $. 代入(3)式, 积分可写为

其中$ \overline{u} $(上划线)代表$ u $的复共轭.

根据傅里叶变换的微分关系$ {k}_{x}\cdot \mathcal{F}\left\{f\left(r\right)\right\}= \dfrac{1}{2{\mathrm{\pi }}{\mathrm{i}}}\mathcal{F} \left\{ \dfrac{\partial }{\partial x}f \left(r\right) \right\} $, 和复共轭关系$ \overline{\mathcal{F} \left\{ f \left(r\right) \right\}} = \mathcal{F} \{ \overline{f \left(-r\right)} \} $, (9)式可变为

应用卷积定理:

根据傅里叶逆变换有$ \displaystyle\iint_{-\infty}^{\infty}\mathcal{F} \{f(\boldsymbol{r})\} (k) {{\mathrm{d}}}^{2}k= f\left(0\right), $在(11)式的积分结果是有限值的情况下(对于大小有限的光斑, 这是显然的)可写为

将卷积展开并代入$ {r}{'}=0 $:

代入(2)式$ {\varPsi }_{{\mathrm{out}}}\left({\boldsymbol{r}}, {{\boldsymbol{r}}}_{{\mathrm{p}}}\right)={\varPsi }_{{\mathrm{in}}}\left(r\right){{\mathrm{e}}}^{{\mathrm{i}}\varphi \left(r+{r}_{{\mathrm{p}}}\right)} $, (13)式变为

可以看出, 其中第一项是与$ {\boldsymbol{r}}_{{\mathrm{p}}} $无关的常数, 第二项是$ {\left|{\varPsi }_{{\mathrm{i}}{\mathrm{n}}}\left(\boldsymbol{r}\right)\right|}^{2} $与$ \dfrac{\partial \varphi \left(\boldsymbol{r}\right)}{\partial x} $的互相关, 用计算符号$ \star $表示. 同样可以类比写出CBED图样质心的$ y $分量$ {I}^{{{\mathrm{C}}{\mathrm{O}}{\mathrm{M}}}_{y}} $, 则可以得到$ {I}^{{\mathrm{C}}{\mathrm{O}}{\mathrm{M}}}\left({\boldsymbol{r}}_{{\mathrm{p}}}\right) $的分解表达:

式中, $ {\hat{\boldsymbol{e}}}_{x} $和$ {\hat{\boldsymbol{e}}}_{y} $表示笛卡尔坐标系单位矢量. 将两项结合, 可以得到:

(16)式中的第一个积分与$ {\boldsymbol{r}}_{{\mathrm{p}}} $和样品无关, 它表示一个常数, 对应于在没有样品情况下获得的信号. 因此在这里可以直接忽略. 在实际应用中, 这个常数被设置为一个值, 以使得图像适合成像系统的灰度值范围. 在这里将其设置为零, 得到了质心的表达式:

由此可见, CBED的质心位置$ {\boldsymbol{I}}^{{\mathrm{C}}{\mathrm{O}}{\mathrm{M}}}\left({\boldsymbol{r}}_{{\mathrm{p}}}\right) $与偏移样品内势场的梯度$ \nabla \varphi \left(\boldsymbol{r}\right) $有着线性关系. 对于非磁性样品, 其内部仅存在一个静电势场$ \varphi \left(\boldsymbol{r}\right) $, 以及对应的样品内建电场$ \boldsymbol{E}\left(\boldsymbol{r}\right) $和电荷密度分布$ \rho \left(\boldsymbol{r}\right) $. 它们三者之间通过泊松方程和高斯定律相联系:

由(18)式可知, 为了获得直接依赖于$ \varphi \left(\boldsymbol{r}\right) $的图像, 需要对(17)式进行积分. 具体表达式为

$ {I}^{{\mathrm{i}}{\mathrm{C}}{\mathrm{O}}{\mathrm{M}}} $图像与$ {\boldsymbol{I}}^{{\mathrm{C}}{\mathrm{O}}{\mathrm{M}}} $满足梯度关系, 即$ {\boldsymbol{I}}^{{\mathrm{C}}{\mathrm{O}}{\mathrm{M}}}\left({\boldsymbol{r}}_{{\mathrm{p}}}\right)= \nabla \cdot {I}^{{\mathrm{i}}{\mathrm{C}}{\mathrm{O}}{\mathrm{M}}}\left({\boldsymbol{r}}_{{\mathrm{p}}}\right) $. 对于$ {\boldsymbol{k}}_{{\mathrm{p}}}\ne 0 $. 积分过的图像为一个任意常数, 将(17)式代入(19)式, 应用卷积定理得到:

将之变形可得

做逆傅里叶变换得到:

由此表明$ {I}^{{\mathrm{i}}{\mathrm{C}}{\mathrm{O}}{\mathrm{M}}} $图像对于样品带来的相位偏移$ \varphi \left(\boldsymbol{r}\right) $是线性的.

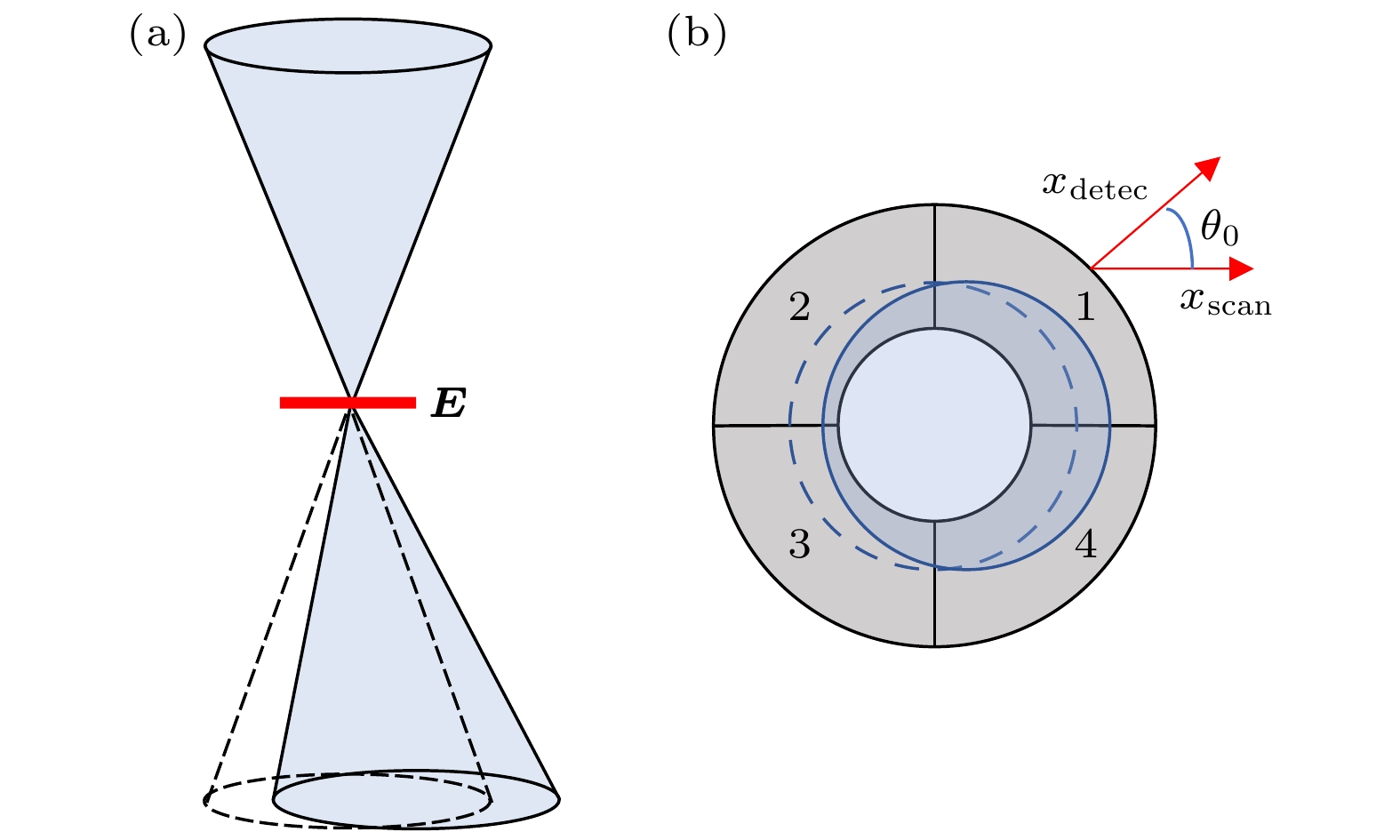
我们讨论最常用的四分区DPC探头的情形. 图1(a)展示了STEM表征过程中样品电场对电子束的偏转示意图, 红色矩形为样品, 电子束在样品的电场驱动下发生偏转, 虚线为真空时的居中状态. 图1(b)展示了分区探头的形貌和CBED在 探测器平面的偏转, 虚线和实心圆盘分别对应真 空情形和电子束受电场偏转的情形. 另外, 右上角标记了分区探头的$ x $方向(探头圆心到1号区域 中心的矢量方向)与扫描坐标系的$ x $方向. 它们往往存在夹角, 在使用DPC探头时, 需要注意探 头朝向与STEM扫描方向的夹角$ {\theta }_{0} $, 在计算DPC信号在扫描坐标系中的位置时, 需要将这个夹角考虑进去.

这里定义四分区探头数据的函数表达式:

其中$ \vartheta $表示k的方向角; $ {\theta }_{0} $决定相机与图像中坐标轴(即扫描方向)的夹角. 探头的内外半径分别表示为$ {k}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}} $和$ {k}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $. $ {k}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $通常大于明场盘的半径$ {k}_{{\mathrm{B}}{\mathrm{F}}} $, 对于中心无孔的探头, $ {k}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}=0 $. 则每个分区收到的信号强度表示如下:

将其展开:

其中$ {k}_{{\mathrm{B}}{\mathrm{F}}} $为明场盘的半径; $ ({\mu }_{x}, {\mu }_{y}) $为质心的偏移矢量, $ {\mu }_{x}, {\mu }_{y}\ll {k}_{{\mathrm{B}}{\mathrm{F}}} $. 由此可以解出明场盘在相对于扫描方向的坐标系的$ x $与$ y $轴上的偏移位移$ ({\mu }_{x}, {\mu }_{y}) $:

(26)式表明了DPC分区探头能直接表征CBED图样的质心偏移, 即直接表征样品中的电场. 同理, 可以用同样的办法求得DPC图像的积分iDPC来回溯样品中的势场$ \varphi \left(r\right) $:

$\text{Lazi}\acute{\text{c}} $等^[23]的模拟工作对比了iCOM与iDPC, 得到了两者非常相近的结论. 因此, 四象限的DPC探头结合对图像的后处理分析, 可以直接获得薄样品(非磁性)内部的势场$ \varphi \left(\boldsymbol{r}\right) $. 对于原子序数跨越大、电子束敏感的材料来说是一种非常理想的结构表征手段.

本研究对样品在球差矫正透射电镜STEM模式下使用8分区探头进行数据采集, 得到对应8个分区的扫描图像, 作为iDPC成像算法程序的输入数据. 图2展示了分区探头及iDPC成像示意图.

iDPC成像算法伪代码如下:

1) 导入8分区探头图像数据.

2) 用导入数据计算DPC的x, y分量图像. 公式如下:

其中$ {{\mathrm{c}}{\mathrm{h}}}_{1-8} $是每个分区的成像信号(图2(b)), 对应图2(a)中标记的探头分区, $ {\theta }_{0} $是八分区探头x方向与STEM扫描方向的夹角.

3) 根据DPC与iDPC的积分关系, 用傅里叶方法积分计算iDPC图像(图2(c)):

$ \mathcal{F} $与$ {\mathcal{F}}^{-1} $分别代表傅里叶变换与逆变换.

4) 对图像进行滤波, 降噪处理.

本研究以化学气相沉积生长的WS₂-MoSe₂单层平面异质结样品为研究对象, 样品的生长是在低压化学气相沉积(low-pressure chemical vapor deposition)系统中进行的. 该CVD系统装配了一个三温区管式炉(记为zone1-3). 我们首先在蓝宝石衬底上生长随机分布的三角形WS₂单层结构, 硫源(S)被放置在中心石英管内, 位于zone1区域. 氧化钨(WO₃)粉末分别装载在3个独立的石英管中, 放置在zone2区域. 蓝宝石衬底在生长前先在Ar/O₂气氛中于1000 ℃退火4 h, 随后被放置在zone3区域. 载气为Ar/H₂ (600/50 sccm), 生长过程中系统压力保持在1—5 Torr (1 Torr = 133 Pa)之间. 随后进行MoSe₂沉积, 其生长参数与WS₂类似, 仅将前驱体中的WO₃替换为MoO₃, 硫源替换为硒源(Se). 由于与已形成的WS₂相比, MoSe₂更易在蓝宝石衬底上直接生长, 经过充分的MoSe₂生长后, 实现了完全覆盖且连续的WS₂/MoSe₂平面异质结构薄膜.

样品的差分相位衬度(DPC)信号采集使用球差电镜在80 kV加速电压下获取, 电镜配备了八分区探头, 每个分区单独收集信号, 我们在STEM模式下使用的电子束电流低于23 pA. 图像采集时的相机长度为20 cm, 汇聚半角为22.4 mrad, 收集半角范围为0—27 mrad. 通过自行编写的算法程序, 由8个分区信号计算样品的iDPC图像. 8分区的外圈等价构成高角度环形暗场像(HAADF)探头, 在采集DPC数据的同时, 通过对外圈4个探头接收到的强度信号进行积分, 获得HAADF像, 并与该探头获得的其他信息一同分析.

图3展示了WS₂-MoSe₂平面异质结在不同成像模式下的结构信息. 我们选取图3(a)红框中的样品作为示例.

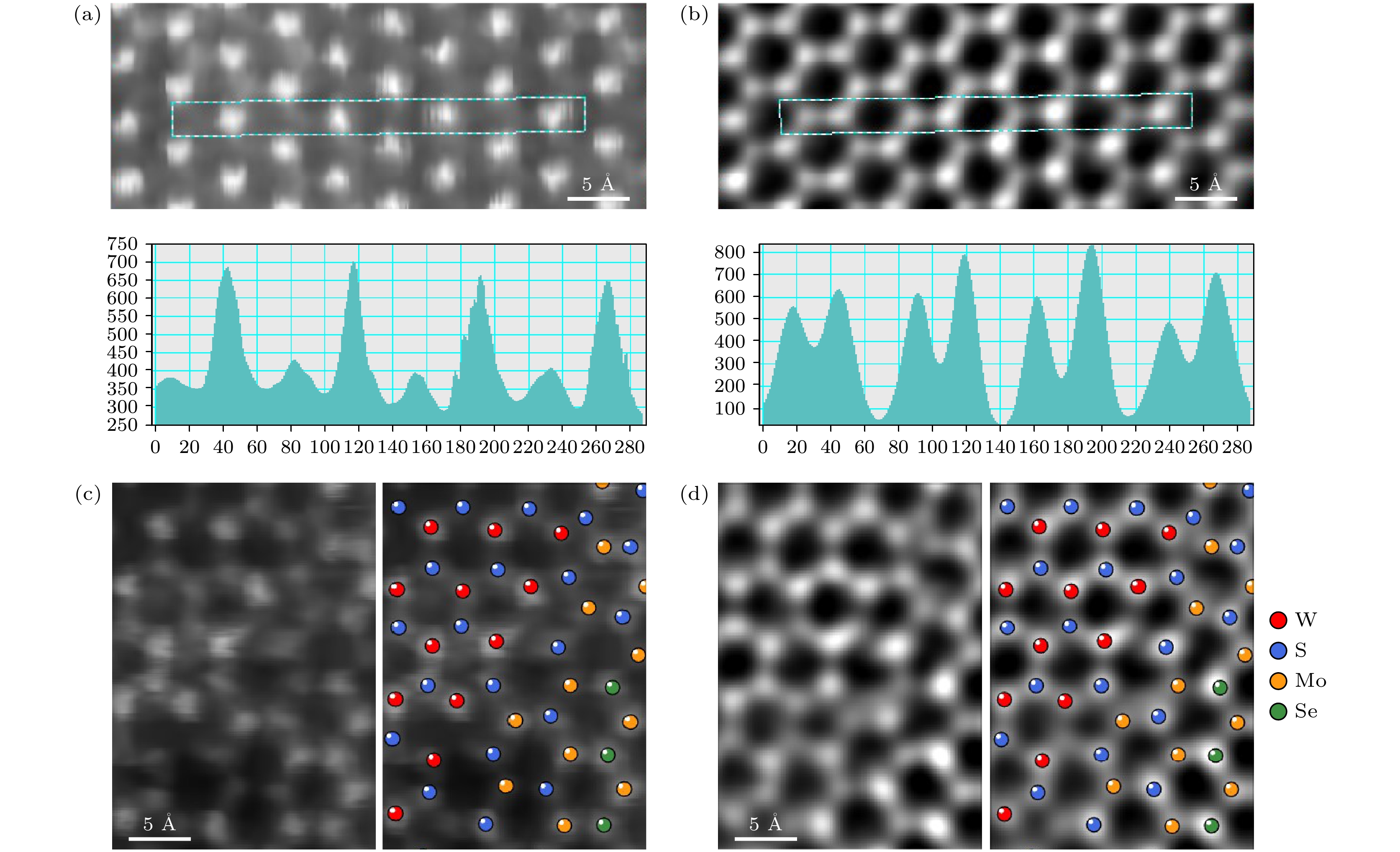
在高倍HAADF(图3(b), 图3(c))中, 可以观察到S原子的衬度几乎与背景噪声相当, 非常难以辨别. 在HAADF成像中, 衬度大约与原子序数Z的1.7次方成正比^[24]. 因此在实验中同时表征原子序数差距较大元素构成的材料时, 轻元素原子的衬度较小, 甚至不可见. 而在DPC图像和iDPC图像(图3(d), 图3(e)) 中, 能观察到DPC图像可以捕捉到S原子位置处的电场与电势信号. 图3(d)的插图色轮表示方向, 颜色的亮度表示电场的大小. 在iDPC图像中, S原子衬度清晰可见. 我们基于iDPC图像, 可以得到轻元素S的原子位置, 从而获得精确的原子结构. 与图3(e)对应的原子结构展示在图3(f)中.

为了进一步对比HAADF与iDPC两种成像方法对平面异质结的成像能力, 分别对这两种方法的图像中A, B位原子衬度做了线扫描强度分布(图4(a), 图4(b)). 在HAADF中, 扣除背底后, W原子和S原子在原子中心的位置衬度比大约在4倍左右, 再考虑到成像中W原子的直径相较于S原子更大, 考虑这个线扫描强度分布范围内包含了S原子周围空间的噪声, 实际的W, S原子衬度比值要更大. 这里定义图像信噪比SNR为WS₂ 区域S原子峰值强度与真空区域平均强度的比值, 对未经降噪处理的HAADF与iDPC图像进行计算, SNR_HAADF = 1.234, SNR_iDPC = 3.677, 由此可见, iDPC图像信噪比要显著优于HAADF. 另外, 从图4(a), 图4(c)中也可以看出, HAADF成像模式下S原子几乎没有衬度, 意味着无法对其进行精准定位, 也无从分析材料原子结构. 而在iDPC图像中(图4(c), 图4(d)), 由于图像衬度与材料内建电场有线性关系, 而与原子序数并无直接相关性, 可以见到S原子的衬度大大增强. 同时要注意到的是, 在图4(b)的线扫描强度分布中S原子和W原子在衬度上区别并不显著, 且在iDPC图像中的直径差别也甚微, 为了明确区分W原子晶格与S原子晶格, 同时获取HAADF和iDPC图像是十分必要的. 同理, 对于平面异质结的MoSe₂区域也是如此. 图4(c), 图4(d)展示了HAADF与iDPC图像在异质结界面处的原子成像对比, 红、蓝、黄、绿颜色分别表示W, S, Mo, Se原子, 图4(c), 图4(d)所用原子模型相同, 由iDPC图像分析得出. 可以发现在同一个实验过程中, 尤其是考虑到样品对电子束敏感的表征过程中, 连续采集带来的过高电子束剂量会破坏样品的本征结构, 甚至引发缺陷, 此时HAADF成像相较于iDPC, 在确定二维材料结构, 尤其是界面原子结构上, 要显著弱于iDPC成像. 这一方法拓展了我们对材料结构表征的边界.

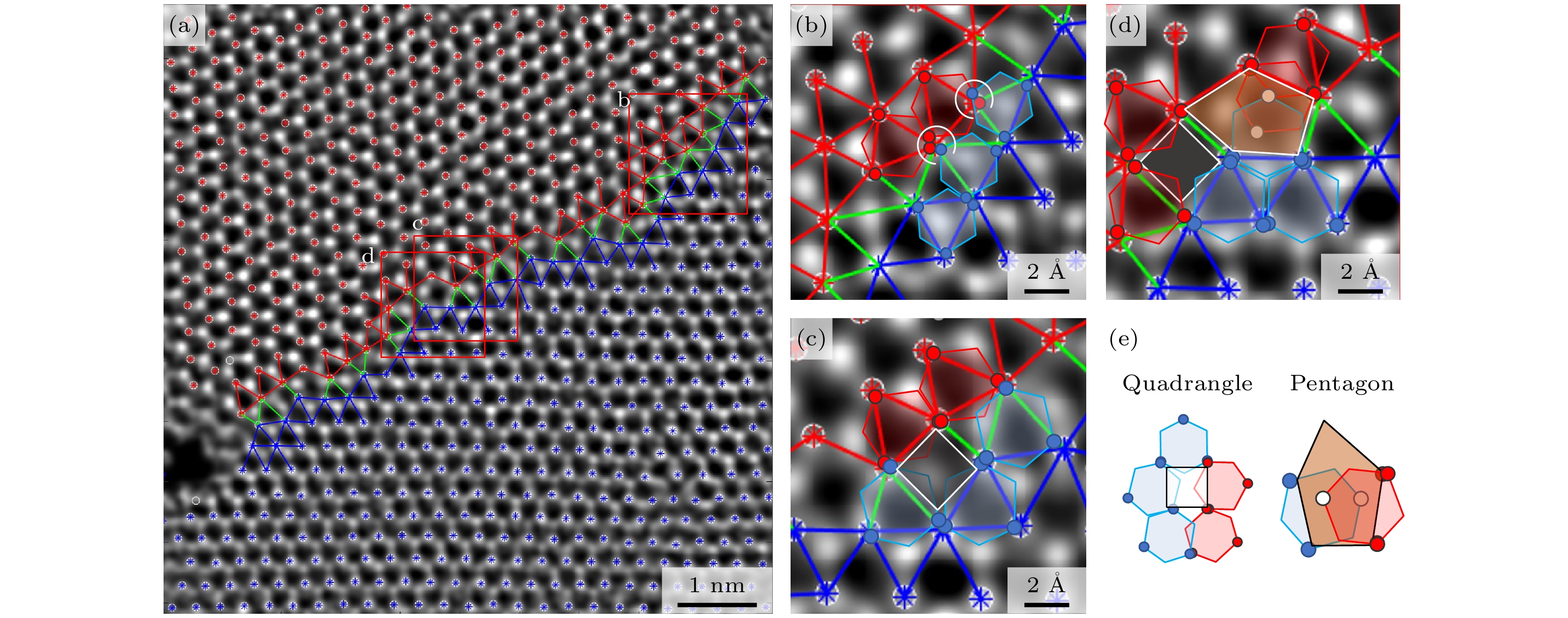
我们对8个界面区域构建原子结构, 进行了统计. WS₂-MoSe₂平面异质结两侧晶格的夹角分布在29°与35°之间. 在我们表征的平面异质结中, WS₂的平均晶格常数为3.18 Å, MoSe₂的平均晶格常数为3.16 Å, 两者之间相差6.3‰. 另外, 我们初步发现在边界附近, 晶格会在两个基矢方向分别发生约4‰与2％的应变, 显著畸变仅仅发生在边界直接接触的一个晶格周期内. 由此可推断, 相比角度因素来说, 界面两侧六角晶格的失配是由界面两侧晶格的夹角主导的, 界面晶格失配而累积的应力是特殊构型与空洞区域产生的主要原因. 经统计, 8个界面区域的原子结构主要有三种典型构型, 展示在图5中. 图中蓝色与红色连线表示界面同侧的A位晶格连接(W-W, Mo-Mo), 绿色表示界面间的A位原子晶格连接(W-Mo), 颜色区分可以帮助我们更清晰地观察界面构型. 在界面两侧晶格延伸位置差距并不大时, 两侧的晶格会共用同一个原子, 以变形但仍保持六角晶格的形式过渡融合, 此时的界面构型我们将之称为“融合型”(见图5(b)); 通常, 由于两种材料晶格相互之间存在角度差, 当界面从融合型过渡继续延伸时, 此时六角晶格B位原子的格点相对, A位原子会直接构成四边形以过渡完全不适配的晶格, 此处位于四边形内部的B位原子顶点只保留其中的一个, 与周围的四个A位原子共同成键, 经过一个四边形过渡后, 界面应力被释放, 同时又能以融合型相接 (见图5(c)); 最后一个非常典型的构型是“五边形”过渡构型, 当界面两侧晶格延伸位置差距较大时, 两个A位晶格融合会带来很大的应力, 此时两侧材料晶格会同时生成空位, 在过渡处形成五边形结构(见图5(d)).

在我们表征的8个界面中, 均观察到五边形结构与四边形结构相邻出现的情况, 图5(e)单独展示了四边形和五边形这两种构型.

我们通过解析球差校正电镜八分区探头实验数据, 并基于积分差分相位衬度(iDPC)成像技术原理, 自行编写算法程序, 对WS₂-MoSe₂单层异质结界面进行了精确表征. 结果表明, 与高角度环形暗场成像(HAADF)相比, iDPC在成像能力上显示出更高的信噪比, 能够清晰地获得轻元素原子的电场分布. 此外, iDPC技术能够同时精准定位W, Se, Mo和S等元素序数跨度较大的原子. 进一步, 我们利用iDPC技术表征了几种典型的界面原子结构, 演示了不同界面应力状况下的原子构型变化过程. 在原子分辨下揭示了二维材料界面原子结构特征, 为深入理解界面物性提供了重要依据. 本工作不仅拓展了二维材料界面结构精确表征方法, 也为相关光电与电子器件的设计和优化奠定了结构基础.