复杂网络作为一门新兴的交叉学科, 近年来受到广泛关注. 其涉及众多学科的知识和理论基础, 如系统科学、统计物理、数学、计算机与信息科学等^[1]. 在复杂网络的研究中, 关键节点的识别始终是一个核心问题, 这些节点对网络的连通性、功能性以及动力学行为具有至关重要的影响^[2], 例如, 在社交网络中, 关键节点往往是那些具有高度连接性和影响力的用户, 他们能够迅速传播信息或引导舆论方向^[3]; 在电力网络中, 关键节点可能是关键的变电站或输电线路, 其故障可能导致大范围的停电或网络瘫痪^[4]. 因此如何准确识别网络中的关键节点, 成为网络研究中的一个重要方向.

在讨论复杂网络时, 节点和连边是两个不可或缺的基本概念^[5], 目前, 已经有很多根据网络性质确定网络中节点排序的方法, 从仅考虑节点的连接数(节点度)^[6], 到聚集节点领域的重要性(特征向量中心性)^[7], 再到考虑节点在网络中的中心位置(介数中心性)^[8], 但这些方法大多基于网络的低维视角出发, 且从目标节点自身角度出发, 看邻居节点对自身的贡献. 值得注意的是, 近年来针对加权网络的关键节点识别研究取得了显著进展: 针对有向加权网络设计的“cw-壳分解算法”综合考虑节点的出度、入度及边权, 通过病毒传播仿真验证了其在节点分级中的有效性^[9]; Zhang等^[10]构建了多属性决策模型, 综合考虑节点强度、加权聚类系数和加权特征向量中心性. 此外, 多属性决策方法通过灰色关联和信息熵综合加权指标(如介数、紧密度和桥中心性), 在复杂网络中展现出更高的适用性^[11]. 然而, 这些方法仍主要局限于节点层面的局部特征分析, 对网络高阶拓扑结构的考量尚不充分.

随着互联网科技发展及网络科学研究的深入, 研究者们逐渐意识到网络的功能或各种动力学性质更多地与网络中的高阶拓扑结构、同质性子结构及网络的多个拓扑不变量等密切相关^[12–15]. 受到庞加莱数学理念的启发, Shi等^[16]借鉴代数拓扑和拓扑图论的基本思想和工具提出了认知网络的新视角——圈结构, 即关注网络中的高阶拓扑结构、同质性子结构及网络的多个拓扑不变量等. 圈不仅包含一般意义上的封闭环状连边结构, 也包括全连通结构, 构成封闭空间的洞结构.

近期的研究发现, 以圈结构为基础设计的网络具有最优的同步能力(全齐性网络)^[17]和控制鲁棒性^[18]; 而人脑神经中两种高阶圈结构——团(clique)和洞(cavity), 前者作为信息处理和记忆的单元, 后者作为跨脑区信息整合和分发的功能基础, 对于人脑的并行处理与高级认知活动至关重要^[19]. 此外, 圈结构也被用于刻画网络局部的节点聚集程度^[20-23]. 圈结构的研究不仅丰富了我们对复杂网络功能和结构的理解, 而且对于设计高效能的网络系统和理解生物网络的复杂性具有重要意义. 圈比(cycle raito, CR)作为一种衡量网络中圈结构丰度的新指标由Fan等^[24]提出, 已被证明能有效揭示网络的全局特性. 其通过量化网络中圈的数量和大小, 为理解网络的结构特性提供了新的视角, 且更换了一个新的思路, 即一个节点是否重要, 取决于其对邻居的结构和动力学过程的参与程度——节点的价值并非取决于以节点为中心看邻居们对节点的利用价值有几何, 而是看节点对邻居们的贡献. 如果节点对社会(圈上的邻居节点)的贡献越大, 承担的社会角色(包含节点的圈的数量)越多, 则节点越重要. 在无权网络中, 圈比的应用已显示出其在识别网络关键节点方面的潜力^[24].

然而, 现有研究存在两个重要局限: 首先, 当前加权网络关键节点识别方法多停留在传统中心性指标的加权扩展层面^[9–11], 缺乏对高阶拓扑结构的有效整合; 其次, 边权在网络分析中的独特价值尚未得到充分挖掘. 实际网络中, 边权不仅反映连接强度, 更蕴含着网络演化的动力学信息. 例如在动物社交网络中, 边权可表征互动频率, 影响群体行为模式^[25]; 平台在线社交网络中, 边权可以代表用户间的互动频率、信息交流的强度或信任程度^[26]; 在航空设施网络中, 边权可以代表航班的频率、航线的距离或乘客流量^[27]; 在电子邮箱网络中, 边权可能表示通信的频率或强度, 这有助于识别关键通信者和信息传播的模式^[28]; 在道路交通网络中, 边权可以代表道路的通行能力、距离或交通拥堵程 度^[29]. 这对于分析网络的鲁棒性、效率以及信息传播等方面至关重要^[30–33].

为弥补这些不足, 本文在加权网络中提出加权圈比(weighted cycle ratio, WCR)的概念, 旨在将边权信息纳入圈比的计算中, 以便更准确地反映网络的拓扑结构和节点间的实际联系. 加权圈比通过量化网络中圈结构的数量、大小以及边权的分布, 能够更全面地揭示网络的潜在特性, 为关键节点识别提供新的理论依据.

本文首先介绍了圈结构在网络拓扑分析的重要性, 接着详细介绍了圈矩阵和圈比的基本定义和在网络分析中的作用, 在此基础上提出加权圈矩阵和加权圈比的概念, 并进一步阐述加权圈比在网络分析中的优势, 为后续加权圈比的应用奠定理论基础.

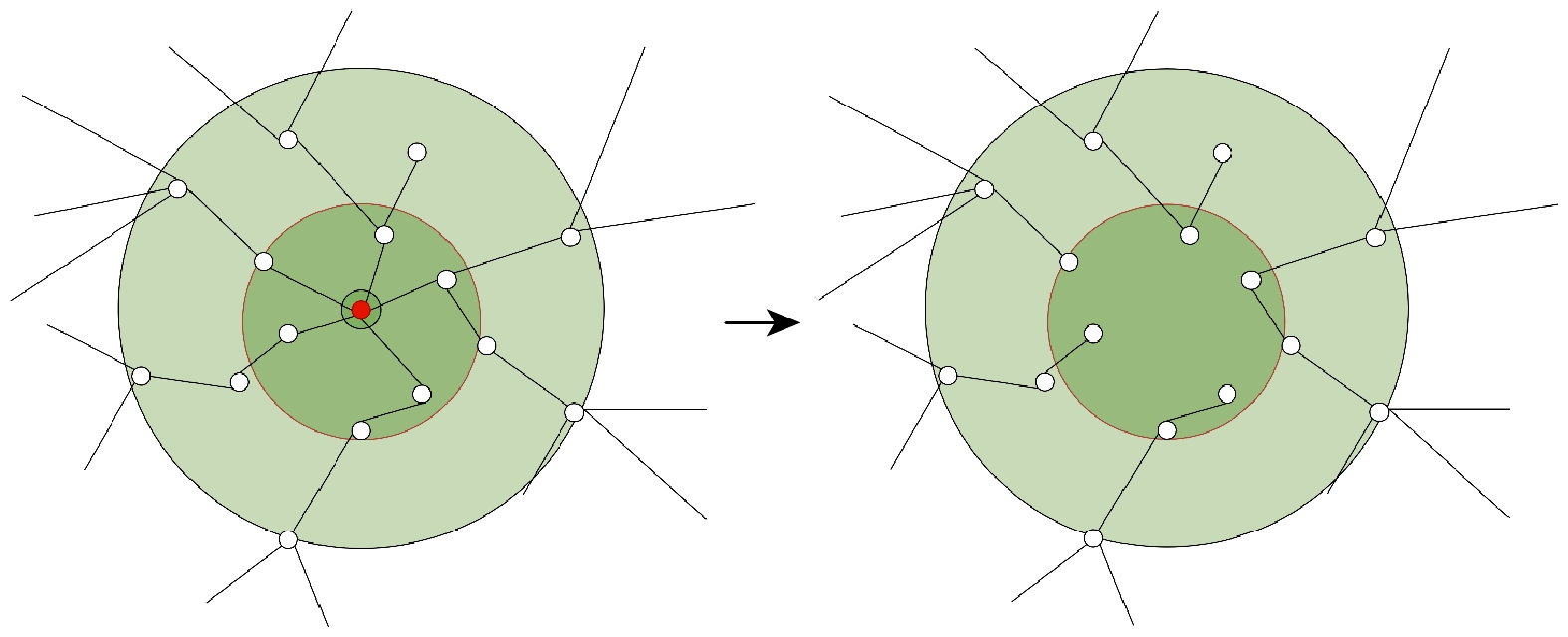
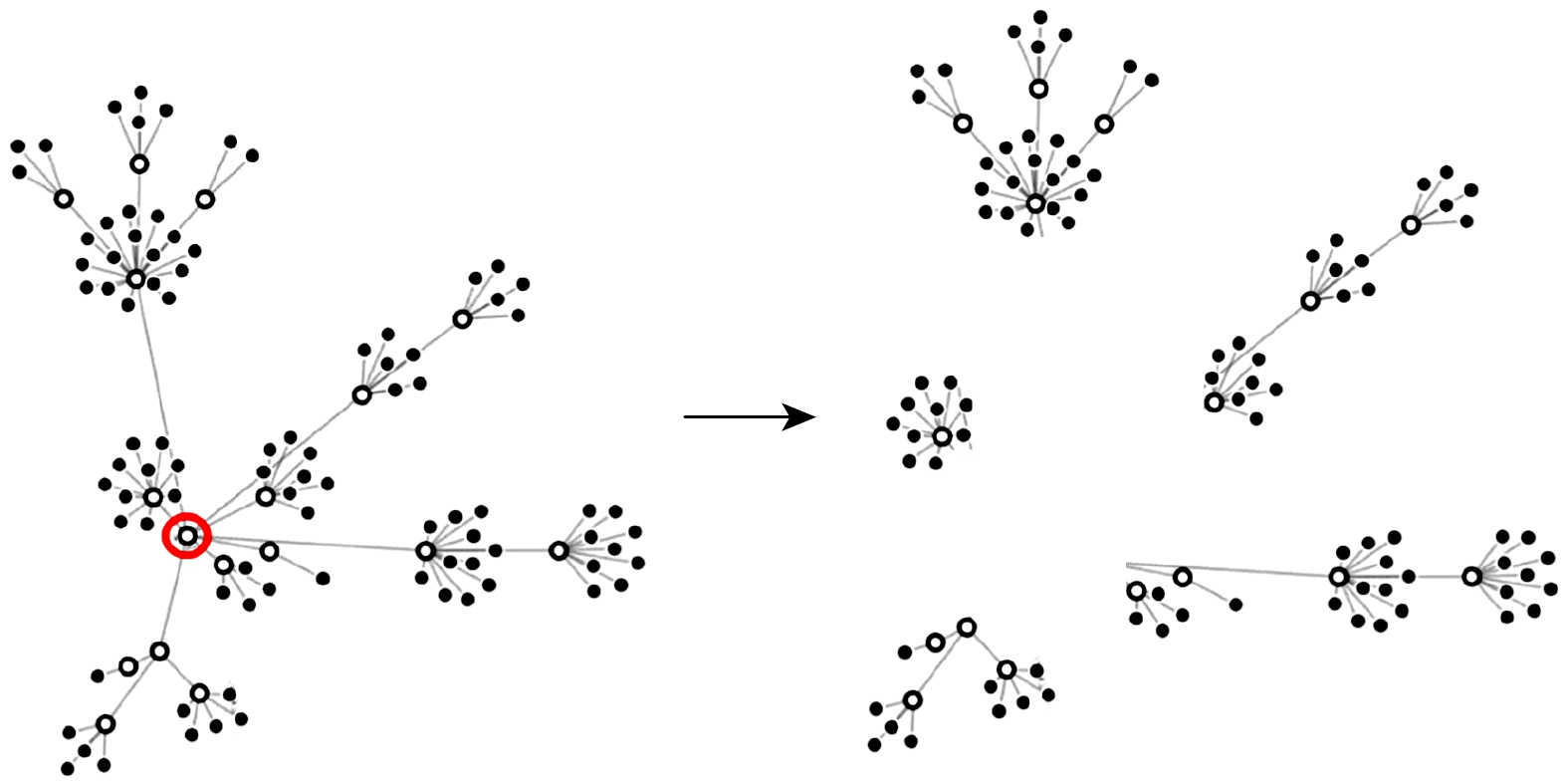
圈, 简而言之是由相同起点和终点构成的封闭的路径, 圈结构可以通过封闭路径来描述: 有一条长度为$ l $的圈可以表示为一个有序的节点序列${p_1}, {p_2}, \cdots , {p_l}$, ${p_1}$对任意的$ {{i}}\left(1\leqslant {{i}}\leqslant {{j}}\right) $, 节点${p_i}$和${p_{i + 1}}$之间存在一条连边, 三角形是最小的圈.

对于复杂网络而言, 如果没有圈结构, 这个网络会退化为树形网络, 如果移除任何一个节点或连边, 都会导致网络分裂成至少两个独立的子网络(如图1所示); 更进一步, 这种移除操作可能使网络彻底瓦解, 形成多个孤立的片段(如图2所示), 从而严重损害其功能. 相反, 在圈结构中的某个 节点或连边被移除, 圈中其他节点之间的连通性仍然得以保持. 圈结构为网络中的节点提供了额外的路径选择, 从而显著增强了网络的连通性, 赋予了网络更高的鲁棒性, 使其能够更好地抵御节点或连边的失效. 与链路和星形结构相比, 圈结构在网络中引入了冗余路径, 这对于维持网络的整体功能和稳定性至关重要.

定义一个无权无向网络$G\left( {V, E} \right)$, 有n个节点和m条边, 其中$V = \left\{ {{v_1}, {v_2}, \cdot \cdot \cdot , {v_n}} \right\}$为节点集, $E = \left\{ {{e_1}, {e_2}, \cdot \cdot \cdot , {e_m}} \right\}$为边集合. 圈矩阵式是一个用于描述网络中圈信息的矩阵, 包含节点i的最小尺寸的圈称为节点i的关联最短环(i的基本圈), 对应的圈的大小被称为节点i的周长. 定义$S = \bigcup\nolimits_{i \in V} {{S_i}} $, 表示G中所有基本圈的集合, 其中$ {{{S}}}_{{{i}}} $为节点i相关联的基本圈; 定义$C = {\left[ {{c_{ij}}} \right]_{n \times n}}$表示G的圈结构, 其中当$i \ne j$时, ${c_{ij}}$是S中同时通过节点i和j的基本圈的数量, 当$i = j$时, ${c_{ii}}$是S中包含节点i的基本圈的数量, 显然C是一个对称矩阵.

基于圈矩阵, 提出了用于衡量节点重要性的指数圈比, 计算公式如下:

根据上述定义, 当节点i不属于S中的任何圈时, 其圈比值为0.

上述关于圈比的定义考虑的是在无权网络中, 在许多加权网络中, 边权作为网络中节点关系强度或连接程度的度量, 具有至关重要的作用. 下面通过一个简易的网络, 描述圈比的计算过程.

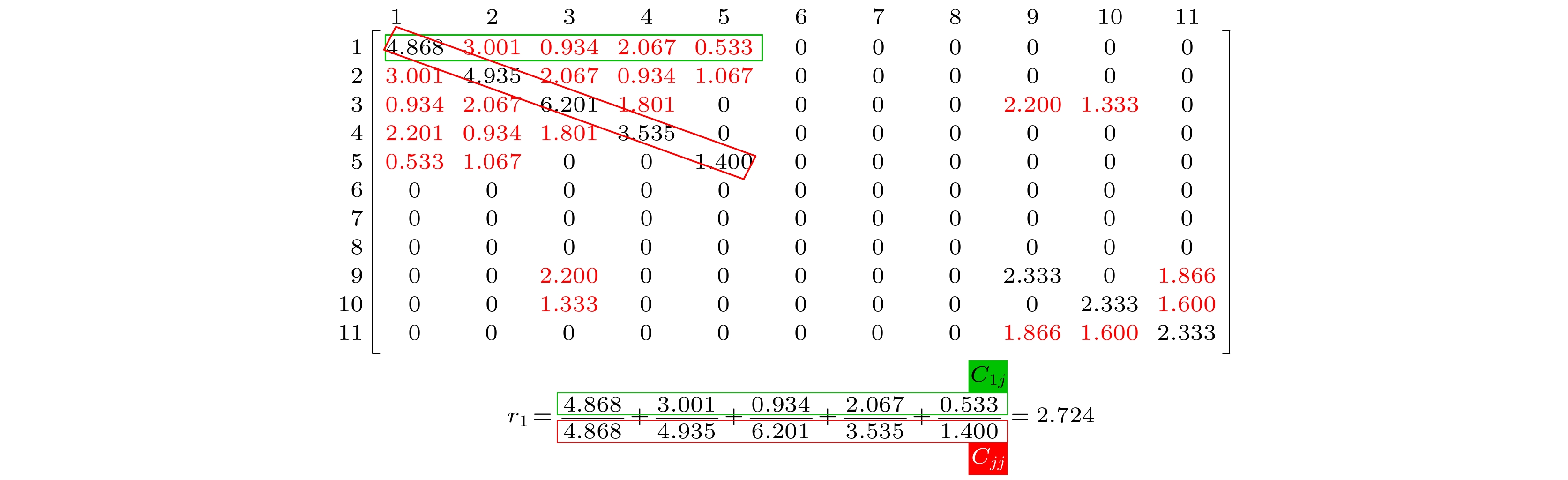
图3(a)所示为一个由11个节点和14条连边构成的网络. 节点的颜色鲜艳程度表示节点的度值大小, 颜色的饱和度和亮度越大, 节点的度值越大. 图3(b)展示了圈矩阵和计算节点1的圈比的过程. 每个分式代表了节点i与j共同参与的基本圈的圈权之和, 对于节点1而言, 矩阵绿色方格中的非零元素是与节点1有共同基本圈的邻居, ${c_{1 j}}$(j取1, 2, 3, 4, 5)代表这个圈的圈权之和, 红色方格中的元素是各个邻居的基本圈, ${c_{1 j}}$和${c_{jj}}$的比率之和就是节点1的圈比. 例如分式3/4, 3表示节点1和2共同组成的3个圈({1, 2, 5}, {1, 2, 3}, {1, 2, 4}), 4表示节点2组成的4个圈({2, 3, 1}, {2, 4, 1}, {2, 1, 5}, {2, 4, 3}).

定义一个加权的网络$ G'\left( {V, E, W} \right) $, 其中$V = \left\{ {{v_1}, {v_2}, \cdot \cdot \cdot , {v_n}} \right\}$为节点集, $E = \left\{ {{e_{ij}}|{v_{i, }}{v_j} \in V, i \ne j} \right\}$为边集合, ${e_{ij}}$表示节点i到节点j的连边, $W = \{ {w_{ij}}|{e_{ij}} \in E\} $表示${e_{ij}}$的权重. 定义$S = {U_{i \in V}}{S_i}$, 表示G中所有基本圈的集合, 定义$ {W}_{s}={U}_{{s}_{i}\in S}\text{ }{W}_{si} $, 表示基本圈的权重集合, 其中${W_{si}} = \displaystyle\sum\nolimits_{{e_{ij}} \in {S_i}} {{w_{ij}}} $; 定义$C' = {\left[ {{c_{ij}}} \right]_{n \times n}}$表示$ G' $的圈结构, 其中当$i \ne j$时, $ c_{ij}' $是S中同时通过节点i和j的所有基本圈的圈权之和, $ c_{ij}' = \displaystyle\sum\nolimits_{{e_{ij}} \in {S_i}} {{W_{si}}} $, 其中n表示同时通过节点i和j的基本圈的个数; 当$i = j$时, $ c_{ii}' $是S中包含节点i所有基本圈的边圈之和, $ c_{ii}' = \displaystyle\sum\nolimits_{{e_i} \in {S_i}} {{W_{si}}} $. $C'$显然也是对称矩阵. 基于加权圈矩阵, 提出相对应的加权圈比$wr$, 计算公式如下:

计算方式与圈比一致, 边权的信息在加权圈矩阵中体现. 在计算$c{'_{ij}}$时, 圈比矩阵是S中同时通过节点i和j的圈的数量, 加权圈比矩阵是S中同时通过节点i和j的圈的圈权之和, 下文通过一个简易的网络, 描述加权圈比的计算过程.

在图4(a)中, 依然选择与图3相同的网络拓扑结构, 分别赋予连边相应的权重, 边的长度代表节点之间关系的紧密程度, 边越短, 表示关系越紧密. 边权重的大小通过颜色的鲜艳程度来表示, 权重越大, 颜色的饱和度和亮度越大. 具体的权重值是通过对节点间的距离长度进行归一化处理后得到的. 归一化过程将距离转换到一个统一的尺度范围内, 并反向映射为权重值, 从而确保距离越短, 边权越大.

图4(b)展示了加权圈矩阵和计算节点1的加权圈比的过程. 每个分式代表了节点i与j共同参与的基本圈的圈权之和, 对于节点1而言, 矩阵绿色方格中的非零元素是与节点 1 有共同基本圈的邻居, $ c_{ij}' $ (j取1, 2, 3, 4, 5)代表这个圈的圈权之和, 红色方格中的元素是各个邻居的基本圈的圈权之和, $ c_{1 j}' $和$ c_{jj}' $ 的比率之和就是节点 1 的加权圈比. 例如分式3.601/4.935, 3.601表示节点1和2共同组成的圈({1, 2, 5}, {1, 2, 3}, {1, 2, 4})的圈权(1.4, 1.267, 0.934)之和, 4.935表示节点2组成的圈({2, 3, 1}, {2, 4, 1}, {2, 1, 5}, {2, 4, 3})的圈权(1.267, 0.934, 1.4, 1.334).

在对复杂网络中的节点进行加权圈比分析时, 在一些情况下, 边权信息无法体现节点之间的区别, 观察到节点9和节点10展现出相同的加权圈比值, 即2.376, 其计算如下:

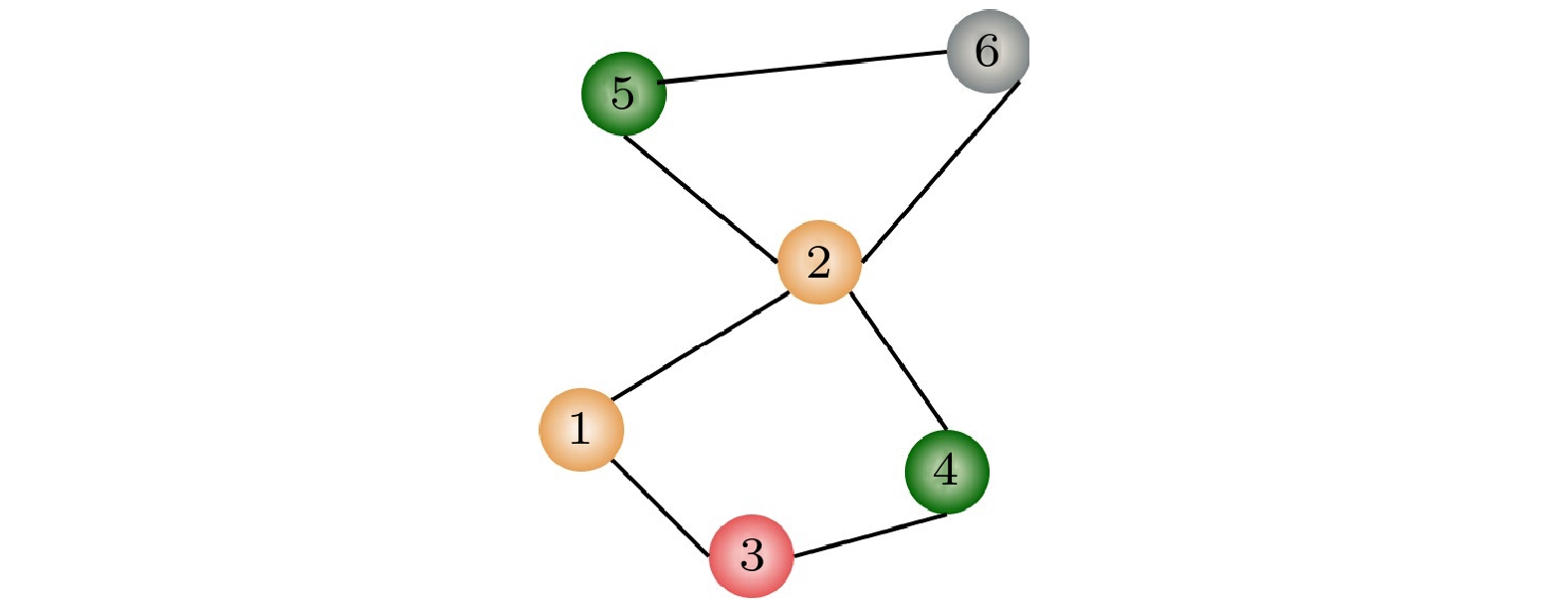
其中, $c_{3, 9}'$和$c_{3, 10}'$表示节点9和节点10与节点3之间的连接权重, 计算方式为

这一现象的成因可从它们的圈结构参与度进行解析. 具体来说, 节点9和节点10均参与了网络中的同一个基本圈{3, 9, 10, 11}, 并且它们与圈外节点的连接关系也相同, 即都与节点3和节点11相连. 因此, 在计算加权圈比时, 尽管边权信息被纳入考量, 但由于这两个节点在圈结构中的参与度和连接关系高度一致, 导致其加权圈比值相同. 类似地如图5所示, 节点5和节点6在由节点2, 5, 6构成的基本圈中, 仅与节点2形成了圈结构, 因此它们的加权圈比也相同. 同样, 在由节点1, 3, 4, 2构成的基本圈中, 节点1和节点4仅与节点2相连, 其加权圈比也相同. 在此种情况下, 连边不同的节点的加权圈比值却相同, 边权所包含的信息并未体现出, 为了解决此种情况, 修改$ c_{ij}' $的定义, 表示该节点i与节点j共同构成的基本圈的其他连边权重之和, 即

其中, n表示该节点与i和j节点的基本圈数.

在减去n倍的${w_{ij}}$后, $c_{ij}'$相较于原式变小, 且与边权${w_{ij}}$紧密相关. 通过这种方法, 我们更新了加权圈矩阵, 如图6所示, 红色标注的数字为相较于图4(b)发生改变的元素, 可以发现对角线元素$ {c}_{ii} $的值保持不变, 非对角线元素$c_{ij}'$的值整体有所减小. 特别是原先节点9, 10和11对应的c值现在明显不同, $c_{3, 9}'$= 2.333 – 0.133 = 2.200, $c_{3, 10}'$ = 2.333 –1 = 1.333, 相应的加权圈比也有所不同, $ {{{r}}}_{9} $ = 2.155 而 $ {{{r}}}_{10} $ = 1.901. 这一改进显著提升了区分度, 有效解决了原边权信息无法体现节点间差异的问题, 且更能体现圈比的内涵即一个节点参与到其他节点结构的程度.

如表1所列, 各节点所在基本圈, 两种加权 圈比的值(WCR¹为修改前的加权圈比), 以及几 个常见的加权网络节点指标: 点强、加权介数、加权接近中心性、加权特征向量中心性, 作为比较基准.

点强(degree centrality, NS)是衡量节点在网络中直接相连的边的权重总和的指标. 对于节点 i, 其点强${k_i}$可以计算如下:

其中, A 是加权邻接矩阵, $ {{{A}}}_{{\mathrm{i}}{\mathrm{j}}} $ 表示节点i 和 j 之间的边的权重.

加权介数(betweenness centrality, BC), 衡量了节点在网络中的中介性, 即该节点在所有最短路径中的重要性. 介数 $g\left( i \right)$ 可以通过以下公式计算:

其中, ${\sigma _{st}}$是从节点s和t之间的所有最短路径的边权之和, $ {\sigma _{st}}\left( i \right) $是其中通过节点i的路径数量.

加权接近中心性(closeness centrality, CC)接近中心性衡量了节点到网络中其他所有节点的平均距离. 对于加权网络, 接近中心性 $C\left( i \right)$可以计算如下:

其中, N是网络中的节点总数, ${d_{\text{w}}}\left( {j, i} \right)$ 是从节点j到节点i的最短路径的加权长度.

加权特征向量中心性(eigenvector centrality, EC)是一种基于节点邻居重要性的度量. 对于加权网络, 特征向量中心性 ${\text{E}}{{\text{C}}_i}$可以计算如下:

其中, ${w_{ij}}$表示节点j和i之间边的权重.

在表1中观察到在传统的圈比指标下, 节点1和节点2的圈比值相同, 同样地, 节点9, 10和11的圈比值也未能区分它们. 然而, 当我们采用改进后的加权圈比指标时, 这些原本数值相同的节点现在可以被成功区分. 在圈比和未改进的加权圈比排序中, 节点3均位居首位, 表明其在网络中占据着核心的地位. 拓扑结构相似的节点1和节点2紧随其后, 而节点9, 10和11也展现出相似的圈比值. 节点4和节点5在排序中位于末尾, 但在引入边权信息后的加权圈比中, 节点4的重要性显著提升, 超过了节点10, 这说明边权信息为其赋予了额外的重要性, 从而在拓扑结构的基础上提供了更深层次的洞察, 后续文中所提到的加权圈比皆为改进后的. 接下来将这一指标应用于现实世界的网络中, 以验证加权圈比在识别关键节点方面的性能和有效性.

在深入研究识别关键节点能力之前, 首先分析一下加权圈比与其他几个指标的相关性. 实验在6个不同领域的实际网络上进行: 欧洲道路交通网络(road), 电子邮箱网络(E-mail), 美国航空设施网络(USAair), 马尔科夫链转移矩阵(rw496), 海豚社交网络(dolphin)和平台在线社交网络(advogato). 它们的拓扑结构如表2所示.

采用肯德尔秩相关系数(Kendall's Tau)来衡量指标之间的相关性, 这是一种非参数统计方法, 用于衡量两个变量之间的单调相关性^[34]. 考虑两个与网络中所有N个节点相关的指数, $ X = ({x}_{1}, {x}_{2}, \cdots, {x}_{N}) $和$ Y = \left({y}_{1}, {y}_{2}, \cdots, {y}_{N}\right) $, 及由这些节点生成的N个两元组$\left( {{x_1}, {y_1}} \right), \left( {{x_2}, {y_2}} \right), \cdots, \left( {{x_N}, {y_N}} \right)$. 对于每个两元组$\left( {{x_i}, y} \right)$和$\left( {{x_j}, y} \right)$, 如果它们的排名一致, 即${x_i} > {x_j}$且$ y > {y}_{j} $或者${x_i} < {x_j}$且$ y < {y}_{j} $, 则认为它们是一致的. 如果它们的排名不一致, 即${x_i} > {x_j}$且$ y < {y}_{j} $或者${x_i} < {x_j}$且$y > {y_j}$, 则认为它们不一致. ${n^ + }$和${n^ - }$分别表示一致对和不一致对的数量. 此外, ${t_Y}$是所有${x_i} \ne x$且$ {y}_{i}= y $的两元组的数量. 需要注意的是, 如果${x_i} \ne x$且$ {y}_{i}= y $, 则该两元组不计入${t_X}$或${t_Y}$. 通过对所有$N\left( {N - 1} \right)/2$两元组进行比较, 肯德尔的$ \tau $系数被定义为

如果X和Y是独立的, $ {{\tau }} $应该接近零, 这意味着$\tau $的正值表示两个变量之间的正相关性, 而负值表示负相关性. 肯德尔秩相关系数$\tau $的值在–1和1之间, 其中1表示完全正相关, –1表示完全负相关, 0表示没有相关性.

考虑到的指标有未加权的圈比和加权网络中的点强、介数、接近中心性和特征向量中心性.

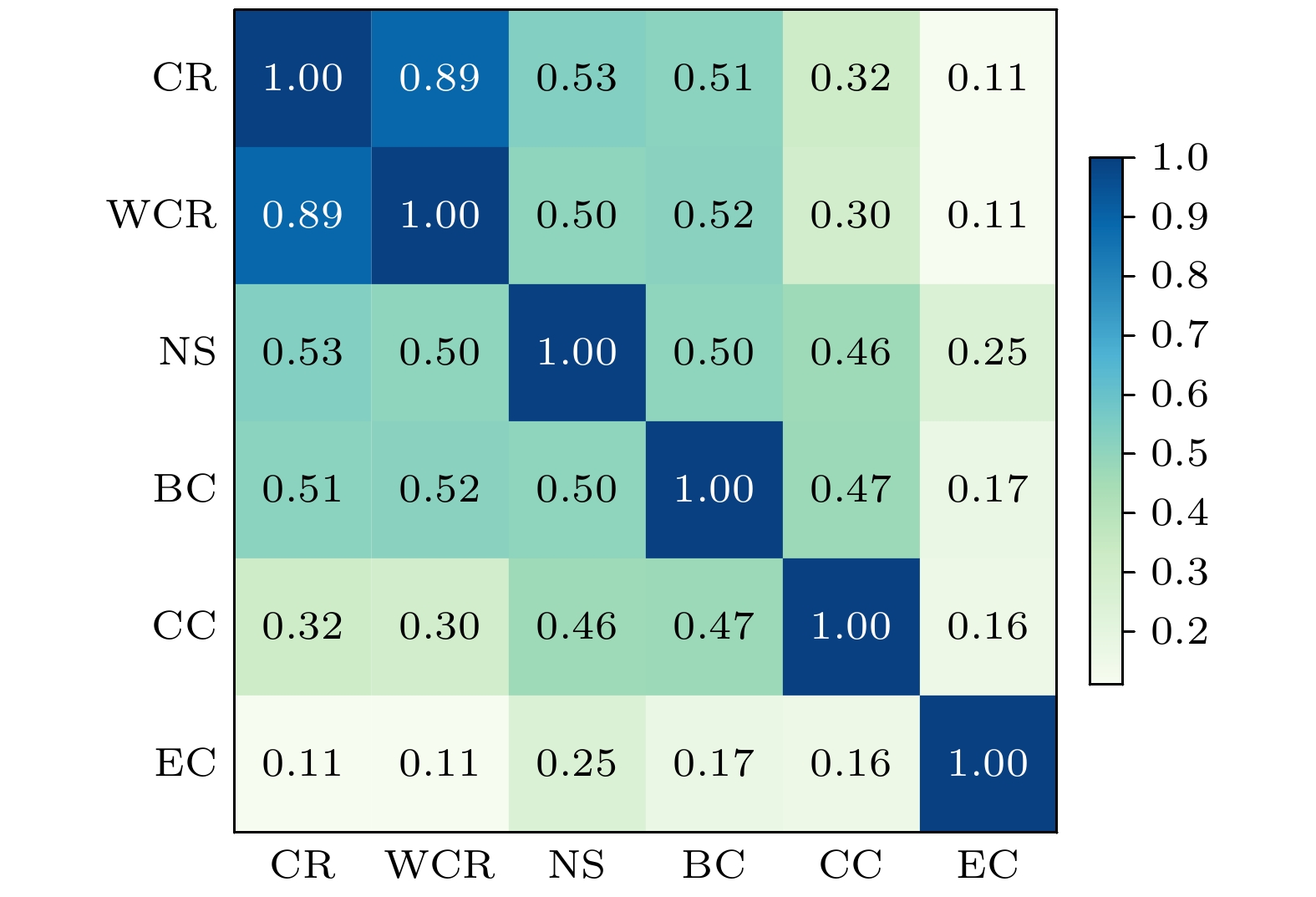
图7所示为6个网络中6个指标的平均相关系数矩阵, 颜色越深表示二者相关性系数越大. 可以发现圈比与加权圈比的肯德尔秩相关系数($\tau $)值为最大, 且与其他指标的$ {\mathrm{\tau }} $值相似, 即加权圈比与圈比有着较高的相似性, 两个指标所得到的节点排序在大体上相似, 部分节点因边权的价值重要性发生改变, 这与示例网络中得到的结果一致. 在示例网络中, 我们观察到加权圈比能够有效地区分那些在传统圈比中无法区分的节点, 这归功于边权信息的引入, 其为节点赋予了超越纯粹拓扑结构的重要性, 从而在某些情况下提升了原本圈比较低的节点的排序. 此外, 加权圈比与其他网络指标之间的相关性较低, 这一发现表明, 加权圈比所生成的节点排名不仅包含了其他排名所提供的信息, 还额外包含了独特的、丰富的信息层面.

接下来我们展示不同指标得到的节点排序. 然后测试加权圈比在识别关键节点方面的能力, 通过删除关键节点来观察网络的鲁棒性, 通过传染病模型测试网络的传播性.

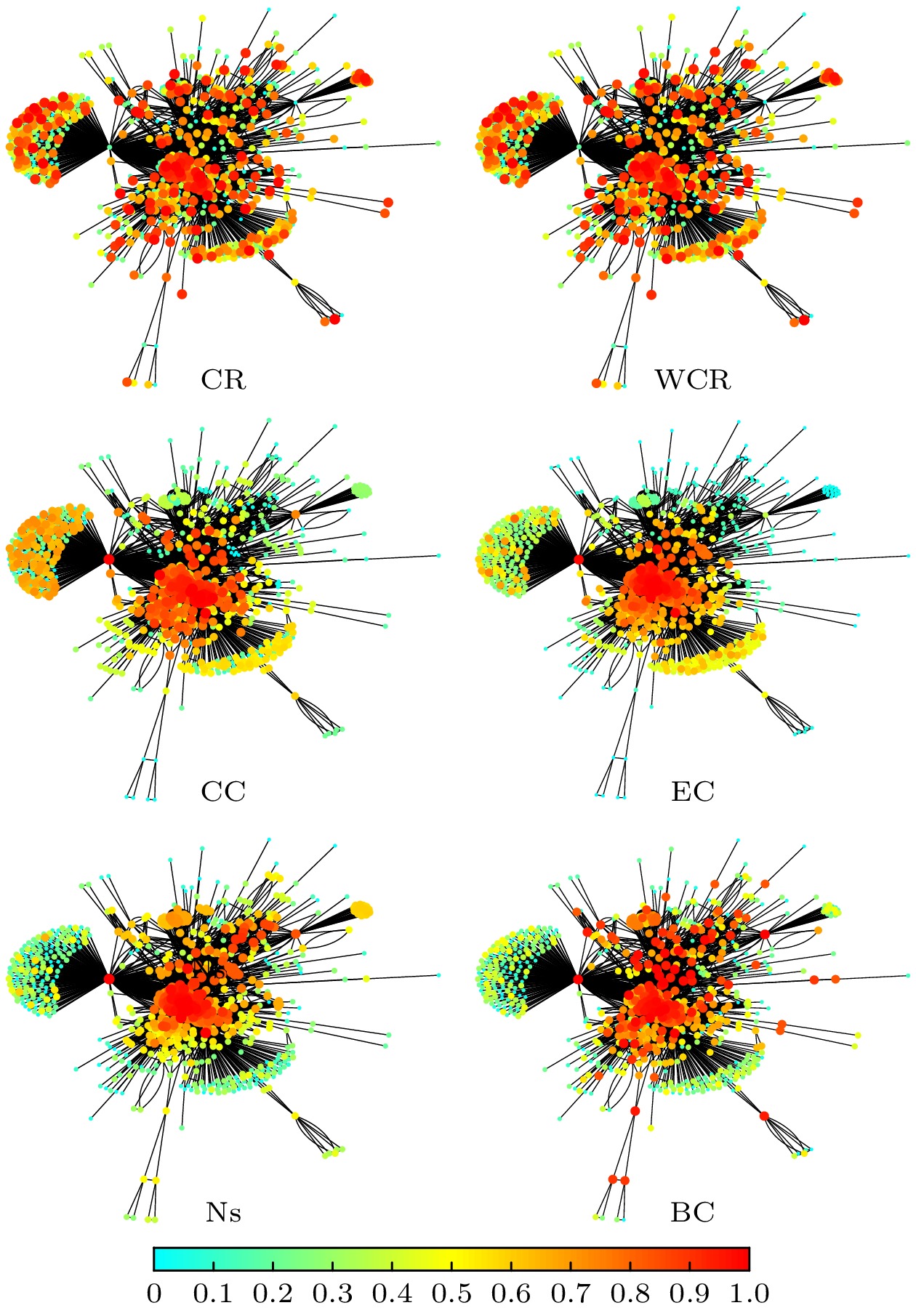
表3所示为基于6个指标得到的节点排序. 如图8所示, 为不同指标得到的节点排名的邮件网络可视化结果, 排名越靠前, 节点的大小越大, 颜色的饱和度和亮度越大. 从图8可以直观地看出, 度中心性、介数中心性和特征向量中心性所识别的关键节点彼此紧密相连, 并且倾向于聚集在网络的特定区域. 相比之下, 接近中心性所识别的关键节点则分布较为分散. 而圈比和加权圈比所选择的关键节点覆盖了整个网络的范围. 加权圈比和圈比在此网络中的分布整体相似, 究其原因可以发现, 该网络的节点数量多, 而圈比和加权圈比产生的排名, 往往只是部分节点排名的小范围变动, 在可视图中难以分辨.

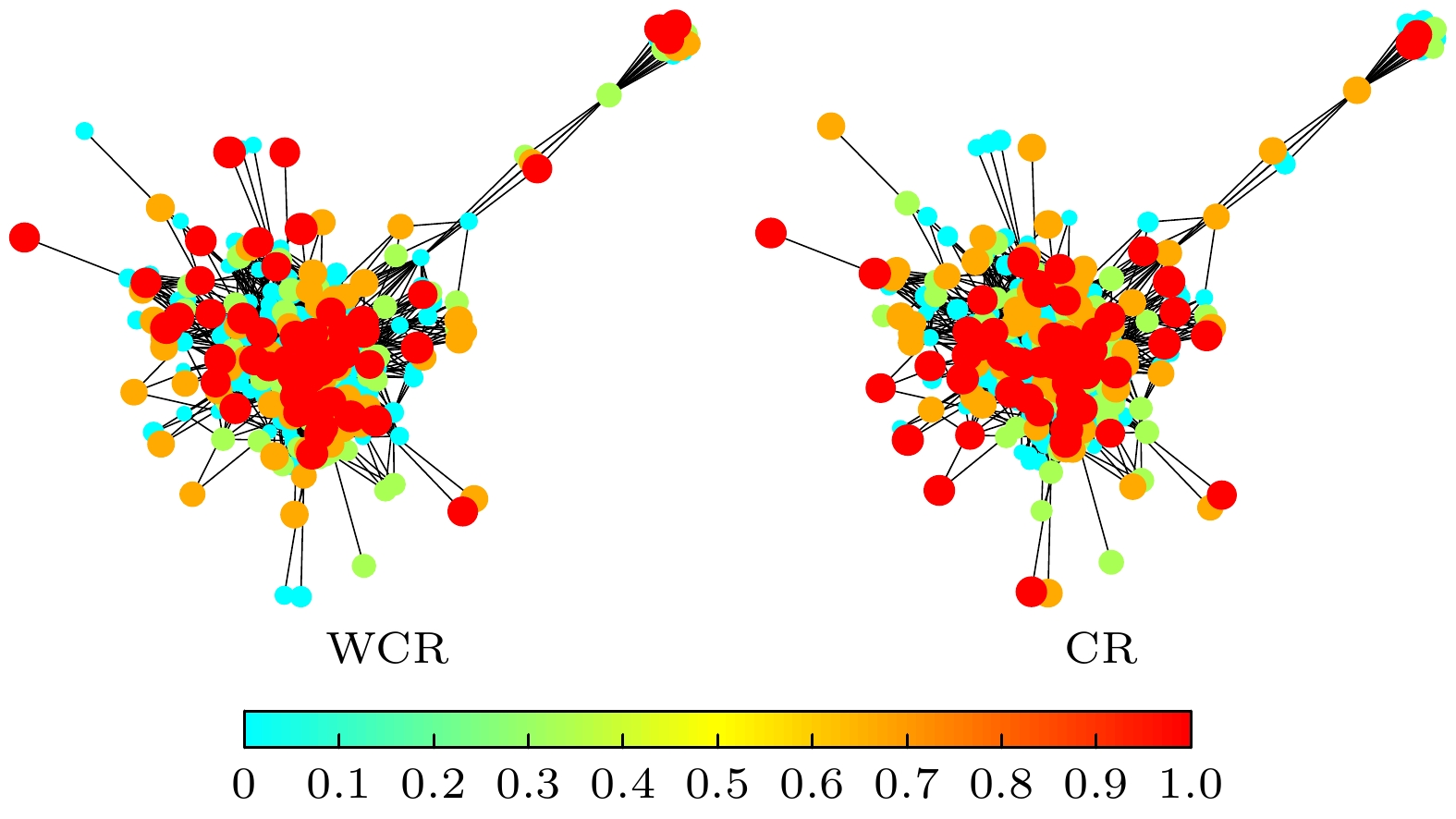
图9所示为节点数较少的海豚社交网络中圈比与加权圈比的可视化结果, 如表4所示, 为部分节点排序, 不难看出二者之间的区别, 一些节点在加入权重的影响后, 节点排名发生了变化, 这种情况下得到的关键节点更加体现了权重在网络中的重要性. 在选择一组关键节点时, 加权圈比显示出了其独特的优势. 如果所选的关键节点都集中在网络的一个区域内, 它们的影响力可能会高度重叠, 从而削弱对网络整体的影响力. 相反, 加权圈比能够识别出分布更广的关键节点, 这些节点能够更全面地影响网络的结构和功能, 因此在选择关键节点时, 加权圈比提供了一种更为有效和全面的方法. 这种全面性使得加权圈比在识别和选择对网络有战略意义的关键节点时, 成为一种宝贵的工具.

在探讨节点重要性领域, 连通性检验方法被广泛认为是评估节点排序质量的一个重要工具^[35,36]. 该方法通过系统地移除网络中的节点, 并监测网络性能的变化, 从而揭示节点排序的有效性. 在加权网络的背景下, 采用加权效率(weighted efficiency, EFF)^[37]作为衡量网络鲁棒性的关键指标. r的计算公式如下:

其中, n为网络中节点的数量, ${e_{ij}}$是节点i和j的权重.

为了直观地观察和比较网络结构在移除关键节点过程中的崩溃趋势, 采用以下方法: 每移除一个节点, 即记录一次网络性能指标r的值. 横坐标表示已删除节点占总节点数的比例, 而通过分析图像中线段的变化趋势, 可以比较不同节点排序策略下网络崩溃的速度. 此外, 计算在节点删除过程中r值的线段与x轴和y轴所围成的面积R, 即鲁棒性^[37]. 鲁棒性R越小, 表明所选指标在识别关键节点方面的性能越优越.

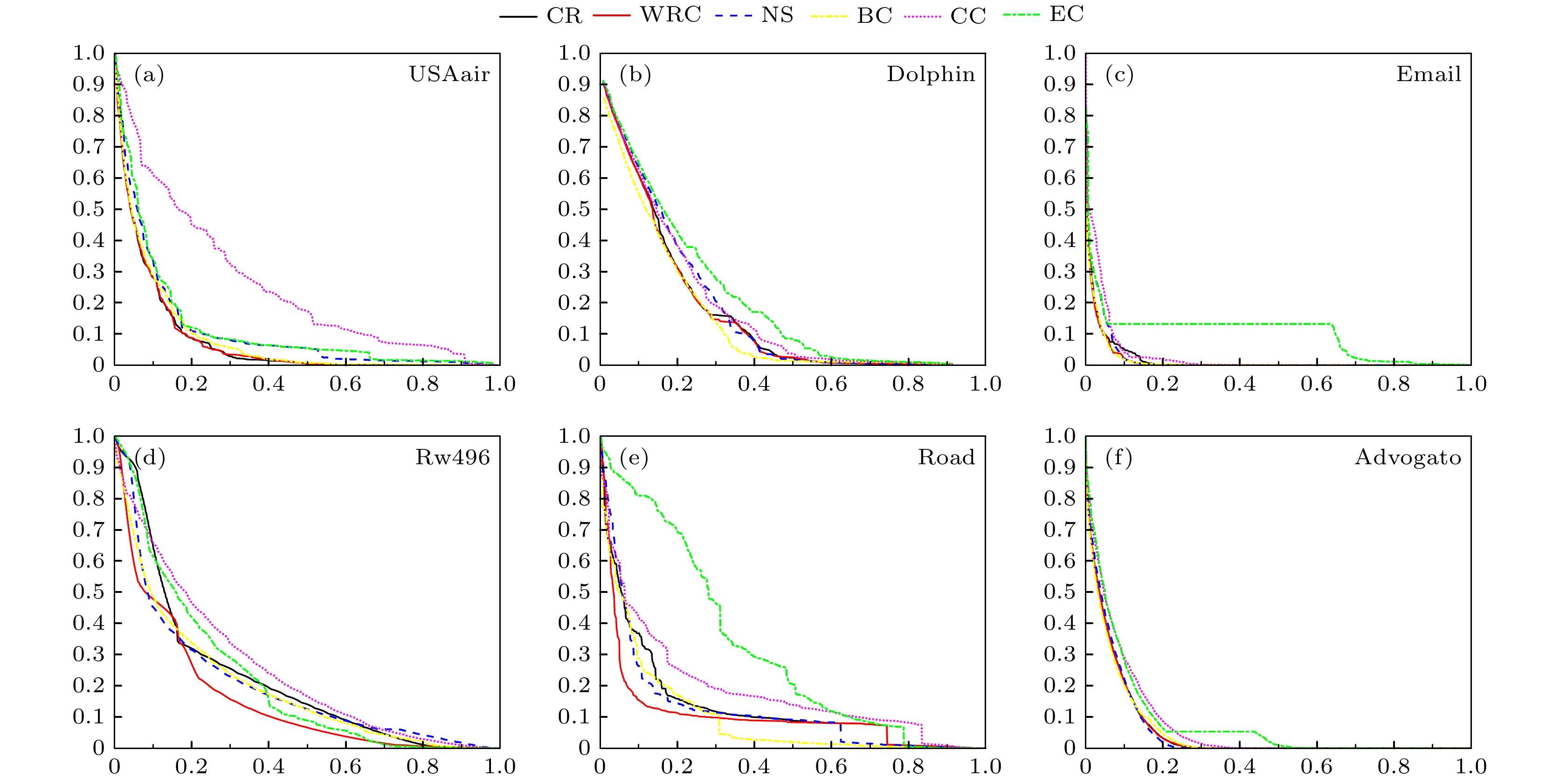
图10所示为6个实际网络中6个不同指标产生的网络崩溃过程, 黑色实线为圈比(CR), 红色实线为加权圈比(WCR), 蓝色虚线为点强(NS), 黄色实线为介数(BC), 紫色点线为接近中心性(CC), 绿色点划线为特征向量中心性(EC), 表5为不同指标下各网络的鲁棒性R的数值, 表6为各个指标的平均排名和平均R值.

图10(c), (f)中, 圈比和加权圈比的曲线几 乎重合, 在对应的两个实际网络中, 其加权圈比 和圈比指标得到的节点排序相似度较高, 多数节 点的排名在两个指标中仅仅相差几名(详见附录表A1), 边权对网络拓扑结构的影响力较小, 从鲁棒性指标R来看, 加权圈比略胜一筹. 介数的曲线重合度也较高, 从R值上看, 加权圈比效果都优于介数.

图10(e)中, 加权圈比的曲线下降速度明显快于圈比, 具有明显优势. 图10(b)中, 介数的网络崩溃效果明显优于加权圈比, 首个删除的节点就拉开差距, 究其原因, 发现Dolphin网络结构中基本圈最大仅为3, 网络中的圈结构较为单一, 但圈结构数量巨大, 同一节点与多个节点形成多个圈, 介数中心性更适合此种网络; E-mail网络结构与Dolphin相似, 但多了一部分基本圈为4的圈结构, 结构复杂了一些, R值略优于介数(详见附录图A1). 图10(e)中纵坐标值在0.1之前, 加权圈比的崩溃效果明显优于其他指标, 整体趋势先快后慢且在某一值时都有一个断崖式下降, 这是由于该节点的删除导致网络结构分裂为几个小的连通分量, 从R值上看, 尽管介数优于加权圈比, 但在曲线上, 加权圈比前期以极快的速度将r值减小了90%, 效果优于介数.

从表5和表6中不难观察到, 加权圈比和介数各占3个第一, 但是在6个网络中的平均排名和R的平均值来看, 加权圈比的综合数据排名第一, 略优于介数, 点强的效果中规中矩, 接近中心性和特征向量中心性的效果垫底, 整体来看加权圈比是识别维持网络流通性关键节点方面总体上最好的指数.

SIR模拟测试^[38,39]是从传播动力学角度检验节点重要性排序的, 其能够较好地模拟节点的传播能力, 进而以检验节点排序质量. 在实验中, 本文采用了标准的SIR传染病模型^[38,39], 节点被划分为三类, 分别是S类节点、I类节点和R类节点, 其中分别代表易感者、感染者和恢复者, 在每个时间步骤, S类节点有一定概率被感染者邻居所感染, 转化为I类节点, S类节点有一定概率会恢复. 选取节点排序中的前1/10作为感染者, 其他节点为易感染者, 并在特定时间步骤$ t $记录累积的感染者与恢复者节点数量, 以进行排名, 数量越多, 排名越高, 记录时间集中于在早期阶段其主导作用的影响节点^[40].

在实验参数设定中, 恢复概率$\gamma $设为0.01, 感染概率初值为${\beta _{\text{c}}}$, 其中计算公式为: ${\beta _{\text{c}}} = \langle k \rangle /( \langle {{k^2}} \rangle - \langle k \rangle )$, 其中$\left\langle k \right\rangle $和$\left\langle {{k^2}} \right\rangle $分别是平均度k的一阶矩和二阶矩考虑到边权的影响, 最终感染概率$\beta = {\beta _{\text{c}}} \times {e_{ij}}$, ${e_{ij}}$是节点$ {\mathrm{i}} $和j的边权. 这一设定反映了边的权重在传播中的重要作用, 因为边权可能表示节点之间的交互强度.

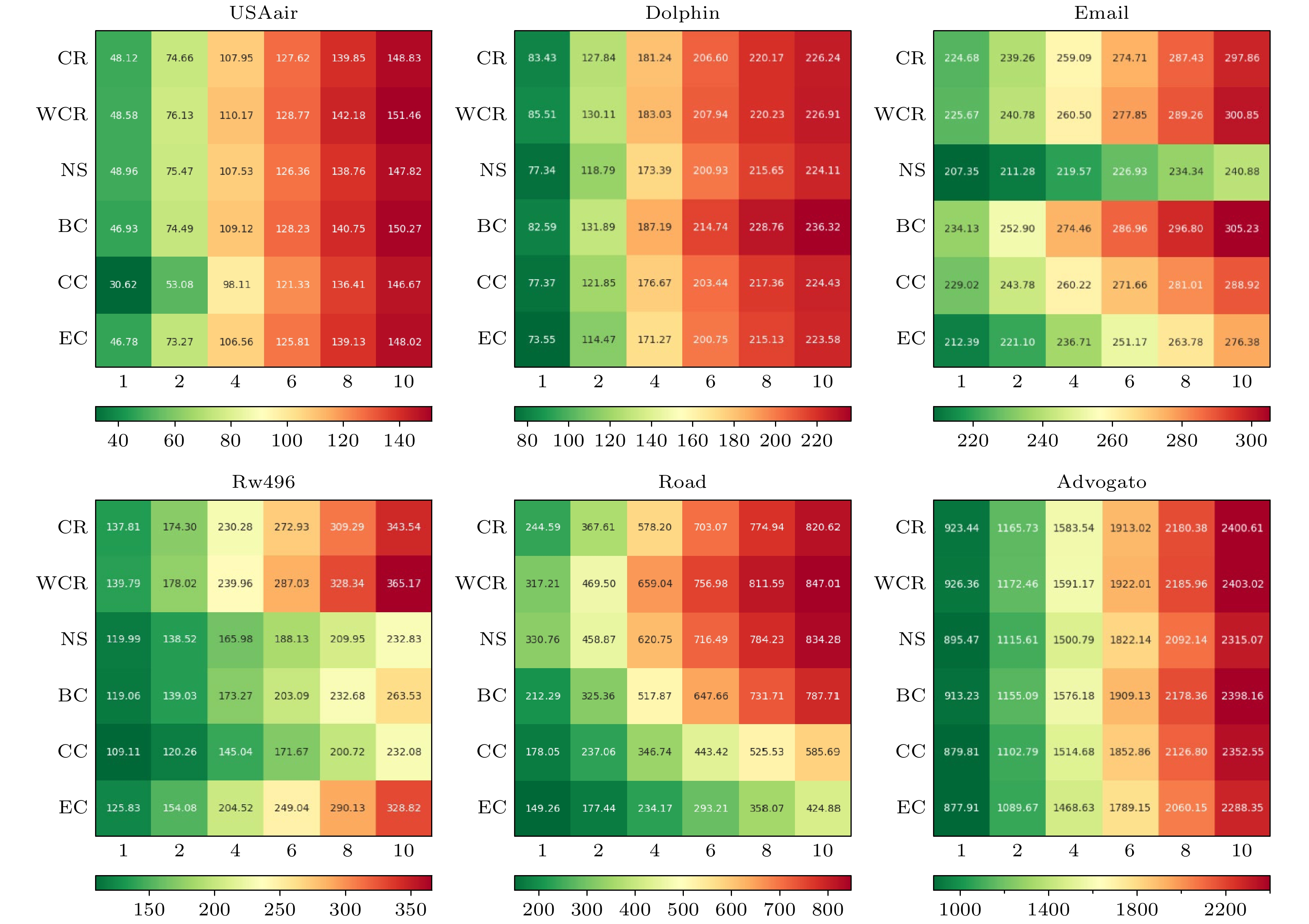
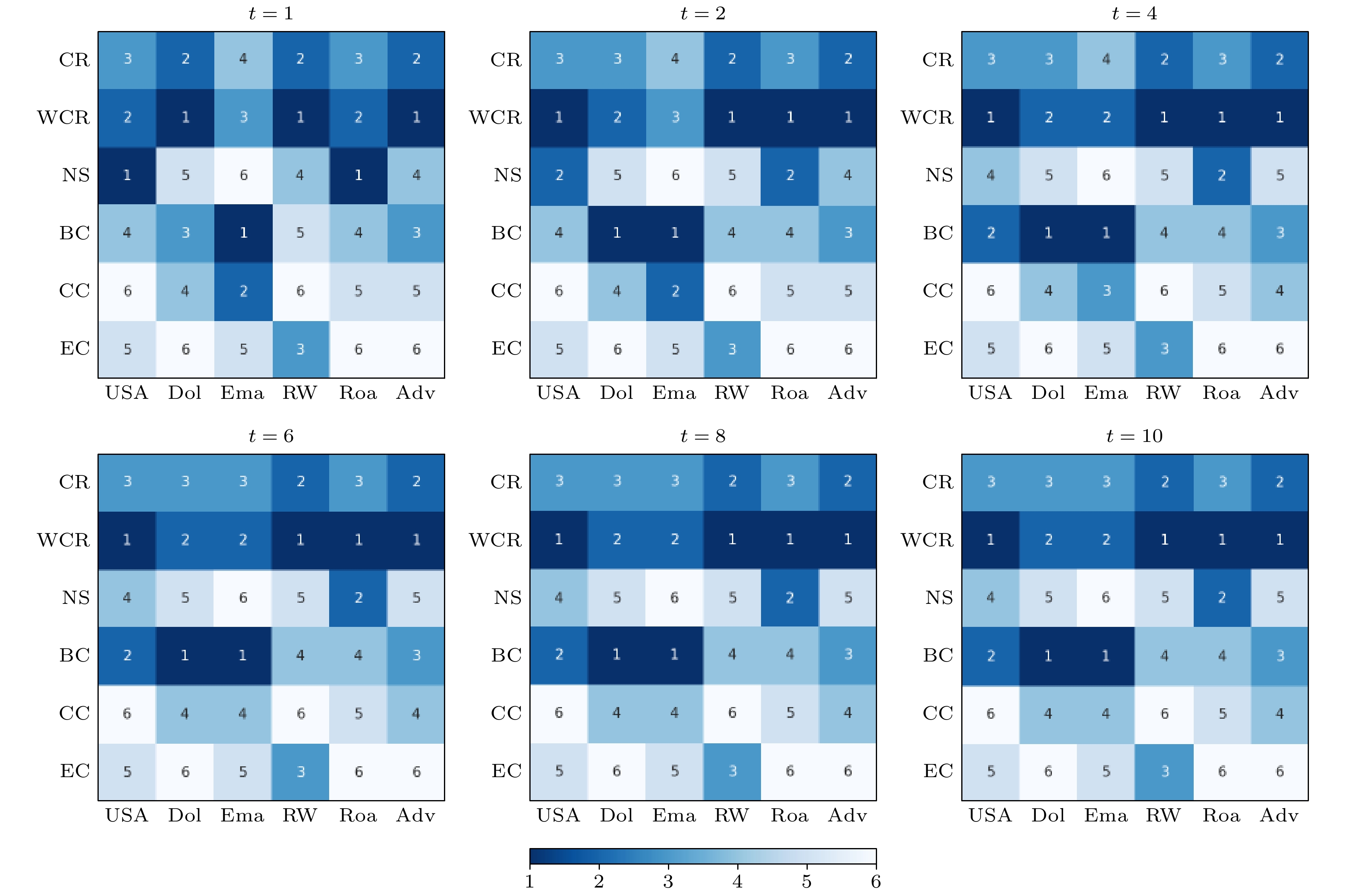
图11所示为时间步骤$ {{t}} $ = 1, 2, 4, 6, 8, 10时, 6个不同网络中各个指标累积的节点数量. 可以发现, 相对圈比和加权圈比的累积数量明显更多; 在USAair, Rw496, Advogato三个网络中, 加权圈比的累积数量均领先其他指标, 在Road网络中, 仅在$ {{t}}=1 $时刻少于点强, 其他时刻均领先其他指标, Dolphin和E-mail网络中加权圈比的累积数量略差于介数, 但仍比圈比效果好.

图12所示为不同时间段各个指标的排名, 表7是每个时段在不同网络中的排名以及所有时段的平均排名. 可以发现, 加权圈比在各个时间段的平均排名均为第一, 且最终平均排名也为第一. 综上所述, 加权圈比在评估节点在传染病模型中的传播能力方面表现出色, 尤其是在考虑边权对传播影响的情况下. 这一结果表明, 加权圈比是一个有效的指标, 能够准确反映节点在网络中的重要性.

本文基于圈比在加权网络中提出加权圈比的概念, 用于识别加权网络中的关键节点. 通过将边权信息融入圈比中, 克服了传统圈比在加权网络中的局限性, 提高了节点重要性评估的准确性. 通过对示例网络的分析, 验证了加权圈比的可行性; 在真实网络实验中, 相关性分析和节点排名网络结构可视化, 验证了加权圈比与圈比以及其他常用节点指标所包含信息的差异性, 通过删除关键节点过程中网络鲁棒性的变化和通过传染病模型观测关键节点的传播能力, 验证了加权圈比在关键节点识别效果上优于圈比以及其他加权网络中的节点基准指标. 实验数据表明, 介数识别关键节点的整体平均略差于加权圈比, 在有些网络中的效果较好, 在节点排名网络可视化结果中发现, 介数所识别的关键节点倾向于聚集在网络的特定区域, 这可能意味着, 介数更关注局部结构, 而加权圈比则能够识别出分布更广的关键节点. 未来研究可以进一步探讨加权圈比与其他指标, 如介数中心性, 在不同网络中关键节点识别方面的差异和优势.