首页
登录
注册
-
闪电与人类生活密切相关. 闪电电流的焦耳热使通道温度达到几万度[1,2], 往往引发森林火灾. 闪电的电流脉冲在空间产生的强烈电磁辐射也会威胁电力系统的安全运行, 并且闪电很难进行安全与定点观测[3]. 此外, 实验室高压放电的能量较小, 间隙较短, 与真实的自然闪电相差甚远[4]. 人工触发闪电(亦称为人工引雷)通过发射携带金属导线的火箭, 从而诱发大气形成长间隙的云地放电[5,6]. 这更接近于真实的自然闪电[5,7]. 因此, 研究触发闪电的电流和辐射电场有助于开展雷电防护[8].
触发闪电的电流研究有助于深入地理解闪电放电机制. Pokharel等[9]开展了闪电感应效应的研究. 杨静等[8]分析了山东触发闪电电流的统计分布. 先前我们研究了触发闪电的电流和通道半径、热导率与热扩散系数的相关物理性质[10].
触发闪电的辐射电场是闪电性质研究的重要组成部分. Rubenstein等[11]展示了在距离触发闪电500 m和30 m处测得的垂直电场波形. Schoene等[12]研究了近距离15 m和30 m处的电场性质, 发现电场与触发雷击将负电荷传输至地面的距离有关. 张其林等[5]研究了回击产生的电场变化呈现V形的脉冲, 得出电场随距离变化符合
$d^{-1.18} $ 的关系.触发闪电的磁场研究也是热点所在. Schoene等[12]测量了15 m和30 m处的磁场峰值. 蔡力等[7]指出18 m, 130 m和1.55 km处的先导磁场、回击磁场和磁场峰值与电流峰值呈线性关系. 杨静等[8]研究开发了一种由两个相互垂直的矩形线圈组成的磁场测量系统, 用于探测雷电放电产生的水平总磁场. 李晓等[13]利用低频磁传感器对闪电通道附近的地下磁场特性进行了观测, 发现了上行闪电先导辐射的微秒级磁场脉冲可在地下空间被检测到. 进一步地, 张其林等[5]也对触发闪电和自然闪电的光、电、磁信号进行了综合测量.
时域有限差分方法(FDTD)用中心差商代 替场量对时间和空间的一阶偏微商, 通过在时域 的递推模拟波的传播过程, 从而得出场分布[14]. 由于该方法可直接离散时域波动方程, 其差分格式中包含有介质的参量, 适合模拟各种复杂的结构, 因此在光学与电磁学领域得到了广泛的应用. 例如, 成林等[15]利用FDTD方法分析了AuNPs尺寸及颗粒间距对局部电场和消光特性的影响. Piltya等[16]探讨了时域有限差分法与有限元法的改进与优化. 另外, 时域有限差分方法也常常应用于电磁场模拟, 为有效研究与闪电的相关特性提供方便.
-
闪电通道等离子体基于两个基本假设: 1) 闪电通道在光学上是薄的; 2) 通道处于局部热力学平衡(LTE)[1,17]. 此时, 电子温度(Te)可以表示为[1,17]:
其中I, λ, g, A, k, E和C分别为谱线的相对强度、谱线波长、统计权重、跃迁率、玻尔兹曼常数、相应跃迁的最高激发能和拟合函数常数. 研究人员已经准确地计算出了N II和N I的A, λ和E等原子数据[18–24].
等离子体的电子密度(ne)可以用Saha公式给出[25]:
其中, 原子和离子下标分别表示同一元素的原子线和离子线. me, h, V, E和Te分别表示电子的质量、普朗克常数、电离能、高激发态的激发能和电子温度[26].
等离子体中的ne和Te与电导率(σ)密切相关[27], 表示为[28,29]
其中qmp取决于通道电子密度、粒子密度和碰撞积分.
内部电场(Eint)与通道电流(i)之间的关系为[30]
其中rc为核心通道半径, 取自实际的测量通道结果[9]. Eint取自大气击穿的电场数值, 通常为103 V/m左右[31,32].
-
时域有限差分法(FDTD)的麦克斯韦方程的形式如下[33]:
其中,
$ {\boldsymbol{E}},\;{\boldsymbol{D}},\;{\boldsymbol{H}},\;{\boldsymbol{B}},\;{\boldsymbol{J}} $ 和$ {{\boldsymbol{J}}_{\text{m}}} $ 分别代表电场强度、电通量密度、磁场强度、磁通量密度、电流密度和磁电流密度. 各向同性线性介质中的内在关系由以下公式给出:$ {\boldsymbol{D}} = \varepsilon {\boldsymbol{E}}, \;{\boldsymbol{B}} = \mu {\boldsymbol{H}}, \;{\boldsymbol{J}} = \sigma {\boldsymbol{E}} $ 和$ {{\boldsymbol{J}}_{\text{m}}} = {\sigma _{\text{m}}}{\boldsymbol{H}} $ , 其中$ \sigma $ 和$ {\sigma _{\text{m}}} $ 分别是电导率和磁导率.在圆柱坐标系中, 轴对称TM波的离散麦克斯韦方程的差分方案可以写成如下形式[33]:
磁场强度
$ {H}_{\varphi } $ 、电场的垂直分量Ez和径向分量${E_r}$ 进而可以通过数值模拟得到. -
闪电通道的基电流函数可以基于Heidler函数得出[33], 其表达式为
工程模型表示为[34]
其中
$u\left( {t - z/v} \right)$ 表示Heaviside函数. 当$t \geqslant z/{v_{\text{c}}}$ 时, 该函数等于1, 否则为0. P(z)是依赖于高度z的电流衰减因子. v是回击电流前缘速度, 其中${v_{\text{c}}}$ 表示回击电流传播速度, 在MTLL(modified transmission line with linear decay)模型中, 二者相等. 常见的工程模型主要包括Bruce和Golde模型(BG)[35], 传输线模型(TL) [36], 具有高度线性电流衰减的修改传输线模型(MTLL)[34], 具有高度指数电流衰减的修改传输线模型(MTLE)[34], 行波电流源(TCS) [37], 及Diendorfer和Uman模型(DU)[38]. 在之前的工作中, 我们对这些电流模型进行了对比, 结果表明: MTLL最适合闪电电流的模拟[39]. -
触发闪电在空间产生的电场主要由辐射电场(
$ {E}_{{\mathrm{r}}{\mathrm{a}}{\mathrm{d}}} $ )、静电场($ {E}_{{\mathrm{e}}{\mathrm{l}}{\mathrm{e}}} $ )和感应电场($ {E}_{{\mathrm{i}}{\mathrm{n}}{\mathrm{d}}} $ )构成[40]. 同时, 电场在柱坐标系下可分解为垂直分量${E_z}$ 和径向分量${E_r}$ [41]. 电磁波传播遵循$ {\boldsymbol{S}} = {\boldsymbol{E}} \times {\boldsymbol{H}} $ . 这表明电场与磁场均垂直于传播方向, 即径向分量${E_r}$ 为零[41]. 实际测量的电场即是垂直电场Ez[41].根据传输线(TL)模型, 辐射电场
$ {E}_{{\mathrm{r}}{\mathrm{a}}{\mathrm{d}}} $ 与峰值电流i之间的关系为其中
$ {\varepsilon }_{0} $ , c, D, v分别是真空介电常数、光速、水平观测距离、沿通道的回击速度. -
触发闪电的空间磁场包含感应磁场和辐射磁场[40]. 在近场区(<1 km), 感应磁场占主导地位; 辐射磁场源于电流的快速变化, 表现为横电磁波辐射, 在远场区占主导. 在柱坐标系中, 磁场的主要分量为方位角磁场
$H_\varphi $ , 即实验上的测量值[33].偶极子技术使用无穷小的时变偶极子作为电场和磁场的源, 是一种基于电流密度分布计算电磁场的方法[40]. 在距离闪电通道距离D处, 其磁场可以表示为
其中
$ i(t-R/c) $ 为TL模型,$ R=\sqrt{{z}^{2}+{D}^{2}} $ . -
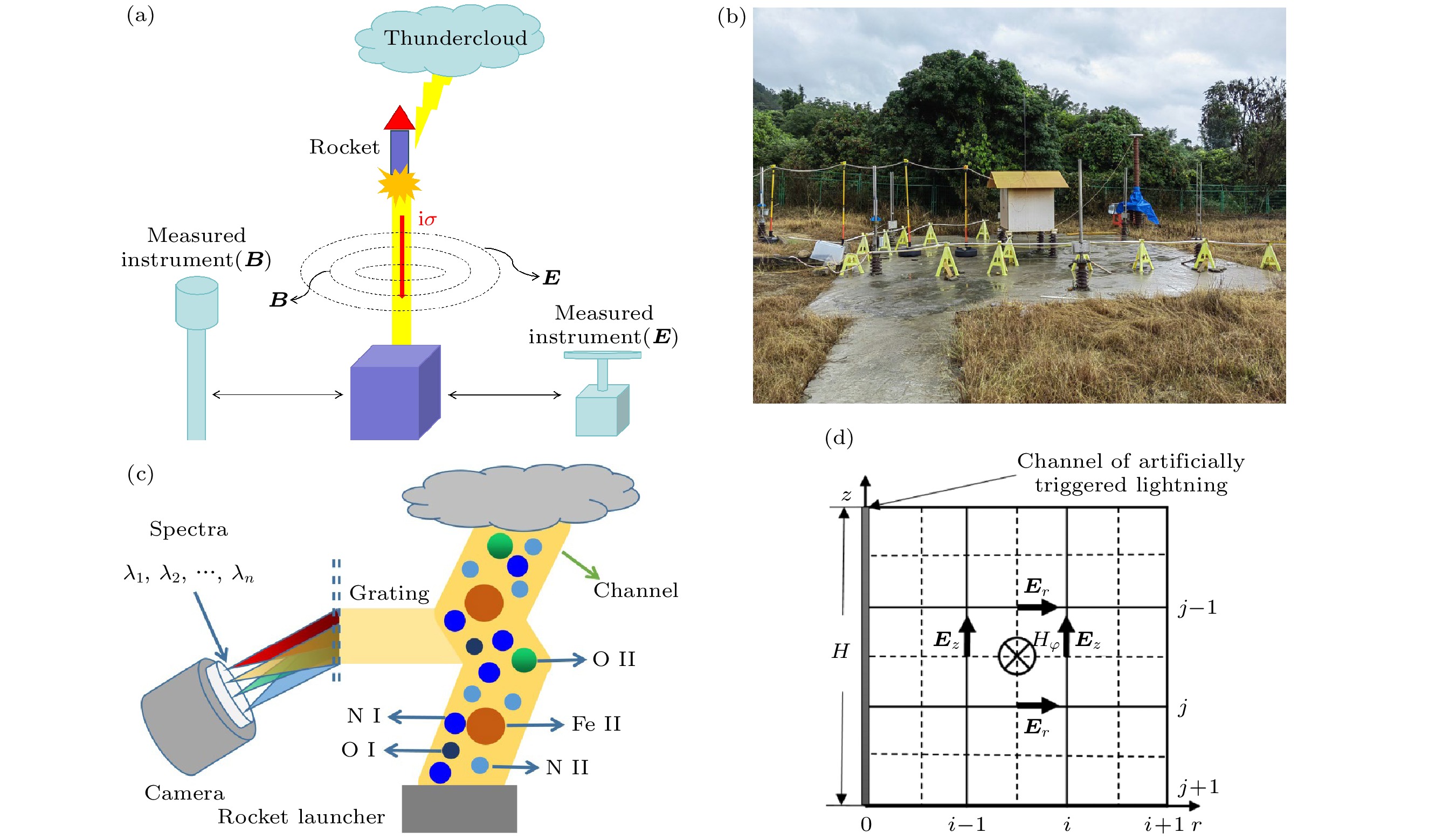
实验仪器涉及人工触发闪电的电场和磁场的测量. 当火箭发射并成功诱导大气放电, 闪电电流将激发形成一个电磁场, 安装在距离火箭发射点一定距离处的电磁场测量设备可以测量相关数据. 图1(a)为测量示意图; 图1(b)展示了广东触发闪电的实验仪器; 图1(c)展示了光谱仪和通道等离子体的示意图. 实验中通过火箭和导线实现人工触发闪电, 再由安装在放电通道底部的电流测量装置和安放在一定距离处的电磁场测量设备记录电流电场数据. 光谱的测量工作使用了带相机的光谱仪, 详细的实验仪器可以参考先前工作[39].
FDTD方法计算的闪电电场的网格空间如图1(d)所示. 最左边的是高度为5 km的闪电 通道. 在空间采样中, 电场分量和磁场分量在两个方向上总是相隔半个网格步长; 在时间采样中, 电场分量
${E_z}$ ,${E_r}$ 和磁场分量$ {H}_{\varphi } $ 相隔半个时间步长. 在计算过程中, 地球被视为一个完全导体. -
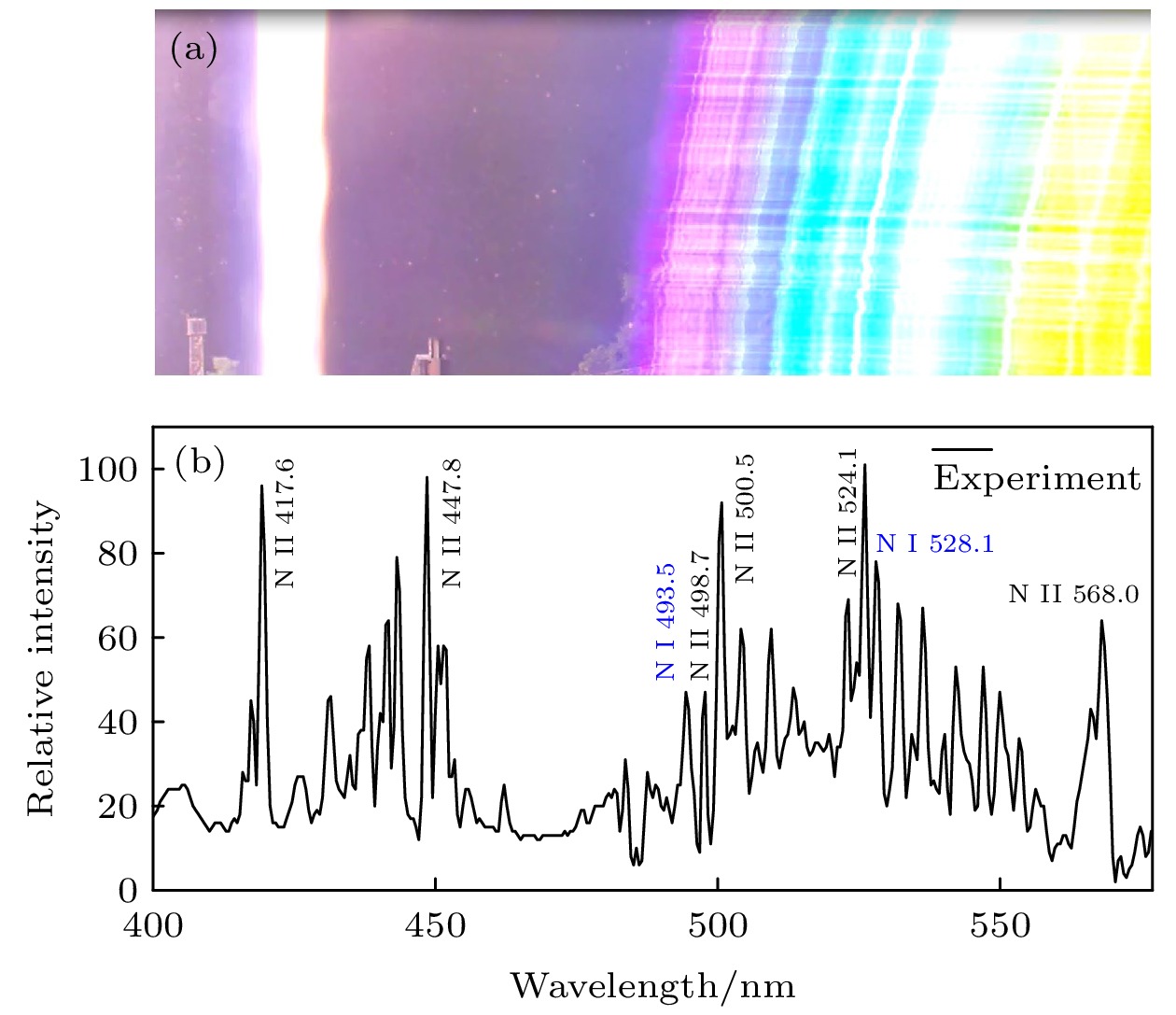
通过对中国广东2022年7月5日一次成功的人工触发闪电通道摄谱, 获得了该次触发闪电的通道光谱[42]. 图2给出了410—600 nm范围内的特征谱线. 可以看到, N I和N II光谱线为{N I: 493.5, 528.1; N II: 417.6, 447.8, 498.7, 524.1, 568.0 nm}. 表1展示了这些谱线的跃迁信息.
-
根据(1)式确定电子温度(
$ {T}_{{\mathrm{e}}} $ )为24537 K[1]. 然后, 基于方程(2)得出电子密度($ {n}_{{\mathrm{e}}} $ )约为8.71×$ {10}^{18} $ cm–3. 利用(3)式结合$ {T}_{{\mathrm{e}}} $ 和$ {n}_{{\mathrm{e}}} $ 的数值, 可以确定电导率($ \sigma $ )约为20372 S/m. -
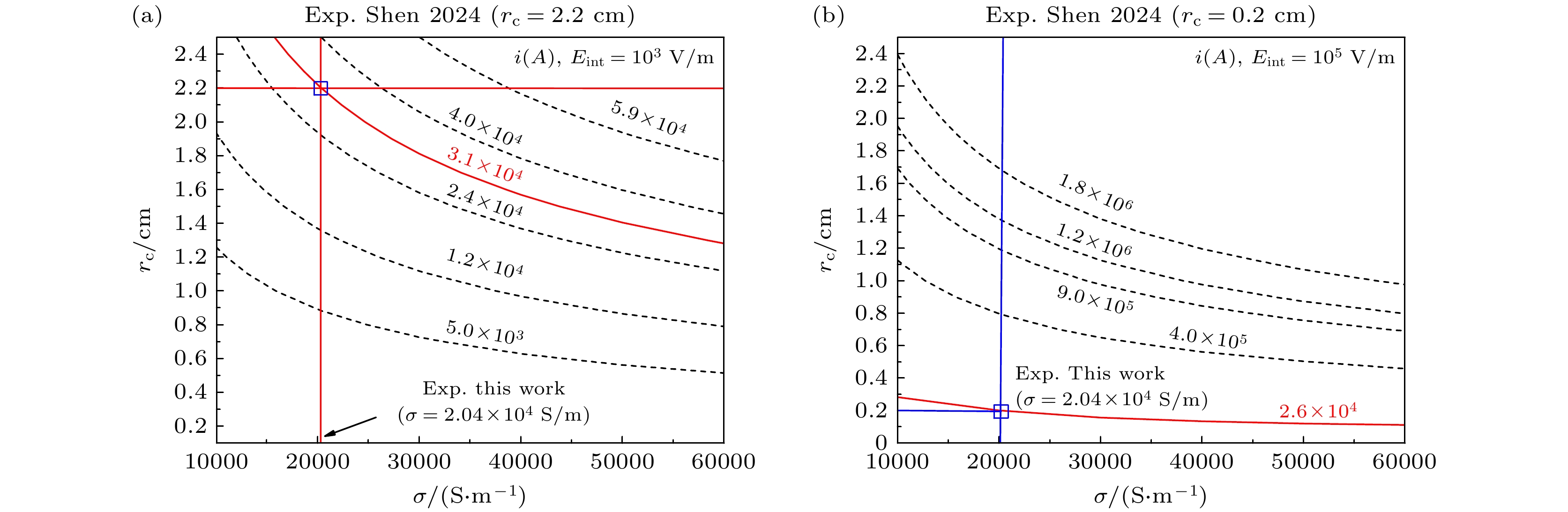
根据(4)式, 图3展示了闪电通道等离子体的内部电场(Eint)、半径(
$ {r}_{{\mathrm{c}}} $ )、通道电流(i)、电导率(σ)的依赖关系[9]. 在$ {E}_{{\mathrm{i}}{\mathrm{n}}{\mathrm{t}}} $ 和$ {r}_{{\mathrm{c}}} $ 的取值方面, 前者$ {E}_{{\mathrm{i}}{\mathrm{n}}{\mathrm{t}}} $ 采用击穿电场的两个极值($ {10}^{3} $ 和$ {10}^{5} $ V/m); 后者$ {r}_{{\mathrm{c}}} $ 取自先前的测量数值(0.2—2.2 cm[9]), 这与Rakov[34]得到闪电通道半径3 cm相近. 进而确定电流的最大值和最小值分别为30.9 kA和25.6 kA. -
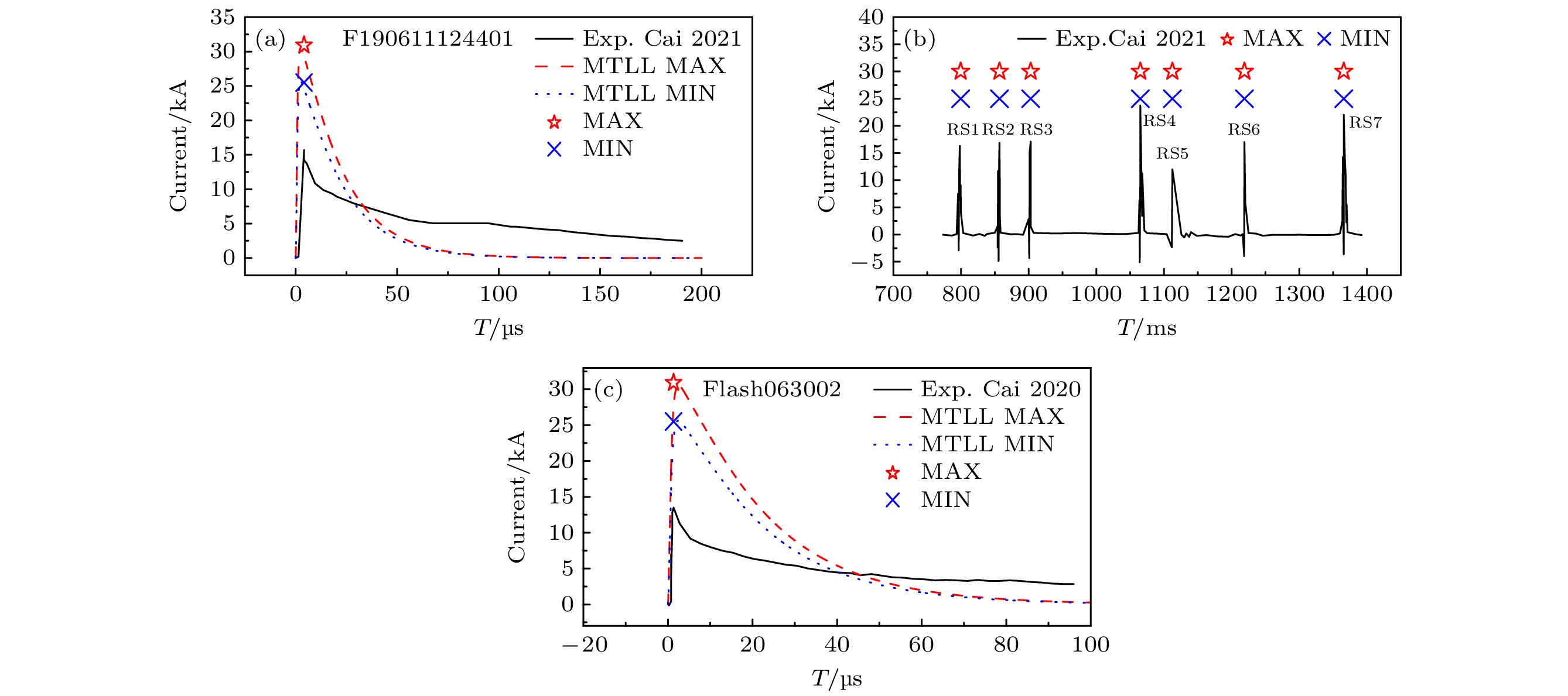
本文选择MTLL模型[39], 基于(7)式和(8)式, 对电流进行模拟, 其中
$P(z) = 1 - {z}/{H}, $ H为5 km. 图4为基于电流最大值和最小值开展的MTLL模拟. 结果表明: 目前测量结果比实验电流大1.5—2倍, 这可能源于光谱拍摄的是触发闪电通道的中部, 而实验电流测量的位置是触发闪电通道的最低端.此外, 当峰值电流衰减到100 μs后, MAX和MIN模拟电流趋于0 kA. 与此同时, 对比实验值得出[2,41]: 峰值电流差别为10 kA左右. 图4(b)为模拟其他几个放电回击的情况, RS4较为接近. 图4(c)也列出另一次实验电流的对比. 这用以3.4节的磁场分析.
-
基于(9)式和电流30.9, 25.6 kA, 表2给出了多个观测距离的电场结果. 结果表明: 回击速度和观测距离对辐射电场的影响较大.
-
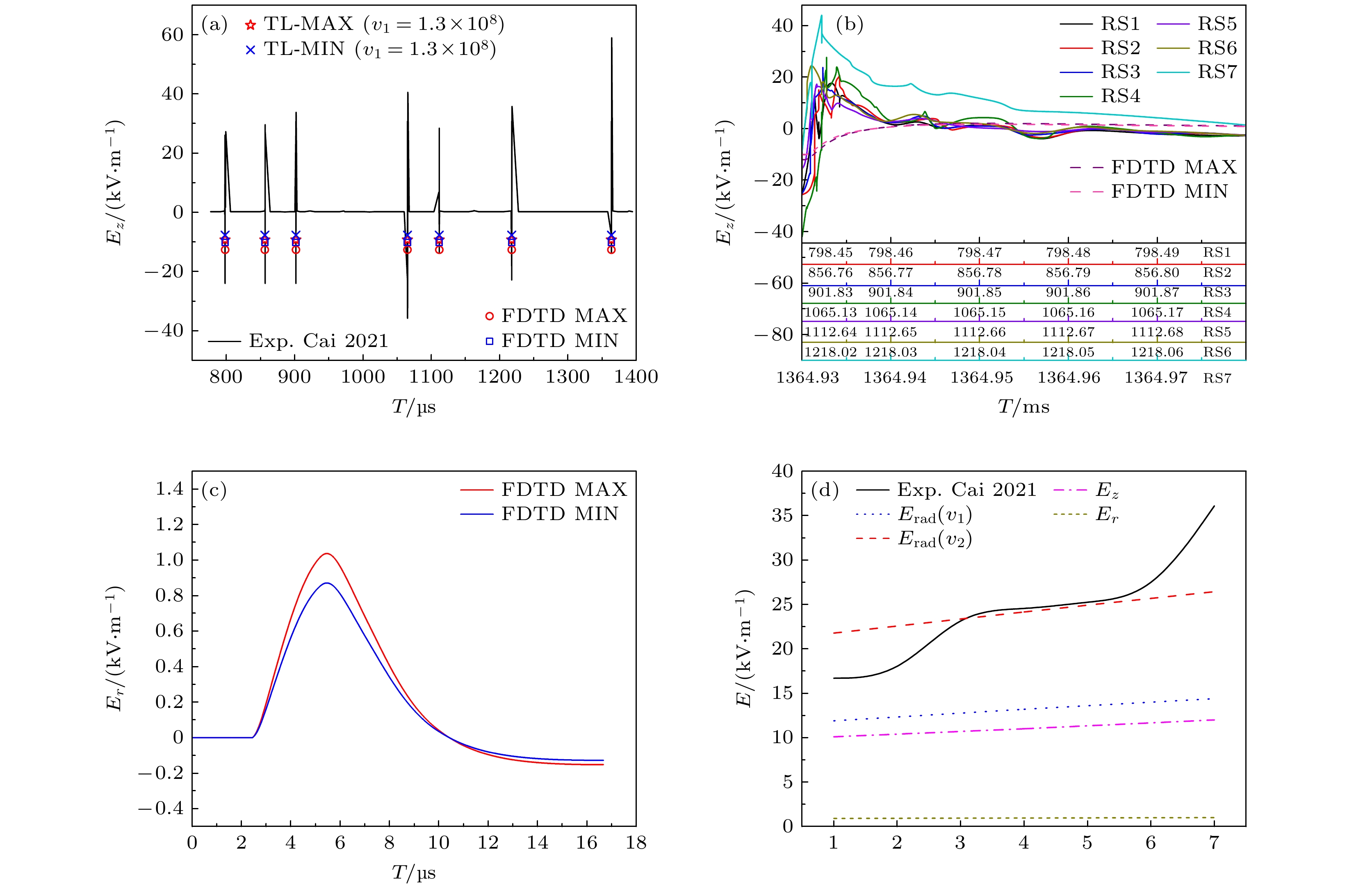
基于电流30.9和25.6 kA, 图5(a)和图5(b)给出了FDTD方法模拟的电场. 第四与第五次回击为最大值和最小值(14.4 kV/m, 11.9 kV/m). 此外, 图5(a)和图5(b)中的电场值偏差较大, 系过幅电场造成. 先前工作指出, 这可能是铁离子电流的影响造成的[39].
-
图5(c)为模拟的径向电场(
$ {E}_{{r}} $ )情况, 其中$ {E}_{r} $ 的波形峰值远小于$ {E}_{z} $ , 几乎为$ {E}_{z} $ 的$ {1}/{10} $ . 这侧面验证了: 实验上测量的是垂直分量的电场. -
通过分析表2和图5(d)中58 m处的各种电场数据, 结果表明: 1)当回击速度为
$v_2=2.5\times {10}^{8} $ m/s时, 辐射电场与实验电场接近; 2)当回击速度取$v_1=1.3\times {10}^{8} $ m/s时, 辐射电场与实验值相差较大, 却与FDTD模拟的$ {E}_{z} $ 接近; 3)$ {E}_{r} $ 最小, 约为$ {E}_{z} $ 的$ {1}/{10} $ . 另外, 实验电场测量中出现的过幅电场现象可能是由于火箭引线里铁元素的影响[39]. -
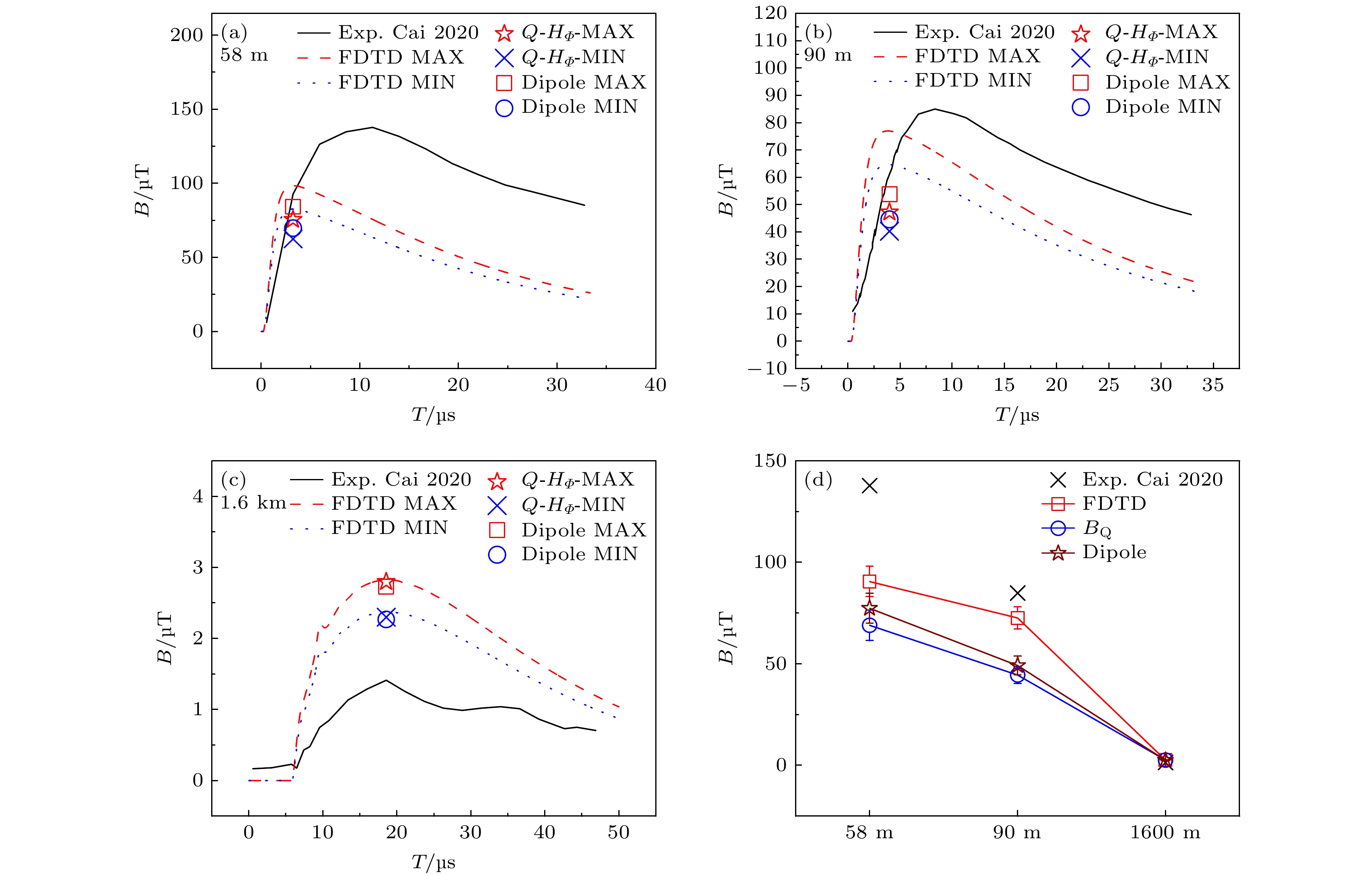
基于实验电流30.9和25.6 kA, 图6(a)为58 m处的FDTD模拟结果. 最大与最小值的模拟趋势相同. 同时, 与实验数据对比发现: FDTD模拟结果与实验有一定的偏差, 最大模拟值为98.5 μT, 而实验值为137.8 μT. 此外, 观察图6(b)发现: 在90 m处, FDTD模拟的磁场波形与实验结果符合较好. 例如, FDTD MAX数据为77 μT, 而实验结果为85 μT. 最后, 分析图6(c)得出: 在1.6 km处, FDTD最小模拟值2.3 μT与实验值1.4 μT的误差缩小到1 μT以内.
-
图6(a), (b), (c)展示了偶极子方法计算的磁场. 通过对比实验值可以得出结论: 偶极子计算方法计算的结果与FDTD方法和电荷-磁场极限估算的结果基本一致.
-
假设空间没有多余磁场(不考虑地球磁场, 周围物质引起的磁场等). 当一次闪电发生时, 云层到大地的中和电荷总量为Qtot. 假设闪电周围的磁场全部由Qtot引起, 称为电荷-磁场. Qtot可以通过两种极限途径实现中和: 1) Qtot以脉冲电流Ip的形式中和, 此时产出的磁场由辐射磁场引起; 2) Qtot以稳恒电流IQ的形式中和, 此时产出的磁场近似由静电场引起. 根据电荷守恒律得到,
此时, 两种方式的电流关系近似如下,
借助Biot-Savart方法, 磁场BQ与电流IQ之间的关系由以下公式给出:
其中μ0, B, D和I分别为真空磁导率、磁感应强度、水平观测距离和电流. 图6(a), (b), (c)列出了电荷-磁场方法的极限估算结果. 结果表明: 近距离的估算数据偏小, 而远距离的估算结果与其他数值符合较好.
-
根据表3和图6(d)数据, 可以得到如下结论: 1)在58 m处, 三种方法的计算结果与实验值差别较大; 2)在90 m处, 三种计算结果与实验值的差别开始缩小, 其中, FDTD模拟与实验值符合较好; 3)在1.6 km处, 三种计算结果与实验值符合很好. 这侧面说明偶极子方法和电荷-磁场极限估算适合远距离计算. 整体而言, 偶极子方法和电荷-磁场极限估算的数据相近; 而FDTD方法模拟的结果略微与实验值接近, 在大于90 m处的数据表现明显.
-
基于光谱诊断方法确定了广东一次触发闪 电的通道电流的最大值与最小值分别为30.9 kA和25.6 kA. 然后, 采用传输线模型和FDTD方法研究了电场分布特征. 结果表明: 当回击速度取1.3 × 108 m/s时, 辐射电场与实验垂直电场偏差较大, 但与FDTD模拟的结果一致. 另外, 采用FDTD方法、偶极子方法、电荷-磁场极限估算方法研究了58 m, 90 m, 1.6 km的磁场分布. 与实验数据比较发现: 不同计算方法与实验值在58 m和90 m处有一定的偏差, FDTD模拟略微接近实验数据; 但在1.6 km处, 基于FDTD模拟、偶极子方法、极限估算得到的三种计算数据, 能够与实验值很好地符合. 电磁场的其他影响因素(例如地面电导率)将在下一个工作中展开研究. 目前工作提供的方法与测量数据, 对进一步开展闪电电流与电磁场的研究有一定的帮助, 为闪电防护和电磁环境研究也提供了科学参考.
基于光谱诊断和时域有限差分方法计算触发闪电电流与电磁场
Calculation of triggered lightning current and electromagnetic fields based on spectral diagnosis and finite-difference time-domain method
-
摘要: 利用无狭缝摄谱技术获取了中国广东一次人工触发闪电通道等离子体的光谱. 基于光谱诊断方法确定了该触发闪电通道电流的最大值与最小值分别为30.9 kA和25.6 kA, 并采用线性电流衰减传输线模型(modified transmission line with linear current decay, MTLL)对电流进行了模拟. 在此基础上, 采用时域有限差分方法(finite-difference time-domain, FDTD)和传输线模型研究了不同距离处的电场分布特征, 并对58 m处产生的电场进行了比较. 结果发现: 当回击速度取1.3×108 m/s时, 辐射电场与实验垂直电场偏差较大, 但与FDTD方法模拟的垂直电场符合一致. 进一步, 采用FDTD方法、偶极子方法、电荷-磁场极限估算法研究了58 m, 90 m, 1.6 km的磁场分布. 与实验数据比较发现: 不同计算方法与实验值在58 m和90 m处有一定差异, 但在1.6 km处符合一致.Abstract: The channel plasma characteristics of an artificially triggered lightning in Guangdong, China, are analyzed using slit-free spectroscopy technology. Based on spectral diagnostic methods, the maximum and minimum values of the triggered lightning channel current are determined to be about 30.9 kA and 25.6 kA (minimum), respectively, and the current is simulated using a modified transmission line model with linear current decay (MTLL). To investigate the electric field distribution, the finite-difference time-domain (FDTD) method and transmission line (TL) model are employed. At a distance of 58 m, assuming a return stroke velocity of 1.3 × 108 m/s, the TL-predicted radiation electric field deviates from experimental electric field, but is very close to the FDTD-simulation of the vertical electric field. Moreover, the analyses of magnetic fields at 58 m, 90 m, and 1.6 km are compared using FDTD simulations, dipole approximation, and charge magnetic field limit (CMFL) estimation. The discrepancies between calculated value and experimental values appear at 58 m and 90 m, which may be due to the near-field interference and measurement limitation. However, they become small at 1.6 km. This work is helpful for the study of lightning electromagnetic field properties and spectral diagnosis.
-
-
图 1 (a) 触发闪电测量装置示意图; (b) 触发闪电的实验场地; (c) 触发闪电通道示意图; (d) 数值计算模型.
$\otimes $ 表示垂直指向纸上Figure 1. (a) Schematic diagram of triggering lightning measurement device; (b) the experimental site; (c) schematic diagram of lightning channel; (d) numerical calculation model.
$\otimes $ : pointing vertically towards the paper.
图 2 2022年7月5日在中国广东拍摄的某次触发闪电的光谱 (a) 触发闪电通道和衍射光谱; (b) 为触发闪电的分析光谱
Figure 2. The spectrum of a triggered lightning captured on July 5th, 2022 in Guangdong, China: (a) Trigger lightning channel and its diffraction spectra; (b) spectral analysis for triggering lightning.
图 3 电流测量过程. X, Y, Z轴对应于电导率、通道半径、电流. 通道半径和电导率的交点位置对应的电流即为测量电流. Exp.Shen 2024引自文献[9]
Figure 3. Measurement process of Current. X, Y and Z axes correspond to electron conductivity, channel radius, and current. The current corresponding to the intersection of channel radius and electron conductivity is the measured current. Exp. Shen 2024 cites from Ref.[9].
表 2 基于实验电流得到的传输线模型和FDTD模拟的电场
Table 2. The electric fields for the transmission line model and FDTD simulation based on experimental currents.
峰值电流/kA 距离/m 电场/(kV·m–1) 类型 $i_{\text{p}}^{{\text{min}}}$ $i_{\text{p}}^{{\text{max}}}$ D TL model FDTD Erad (v1)c Erad (v2)c Ez Er 本文工作 25.6 30.9 38 18.2—21.9 33.6—40.7 58 11.9—14.4 22.0—26.7 10.1—12.0 0.9—1.0 78 8.8—10.7 16.4—19.8 90 7.7—9.2 14.2—17.2 102 6.7—8.2 12.5—15.1 1000 0.4—0.7 1.3—1.5 1600 0.4—0.5 0.8—0.9 2200 0.3—0.4 0.6—0.7 Cai 2021a 12.0 23.6 58 12.6—35.7 Qie 2007b 11.9 60 18.0 注: a, b 引自文献[41]与[44]. c $v_1= 1.3\times10^8 $ m/s; d$v_2= 2.5\times10^8 $ m/s.
下载: 导出CSV
表 1 触发闪电特征谱线的光谱参数[43]
Table 1. Spectral parameters of characteristic spectral lines for triggered lightning[43].
波长/nm 跃迁率 $ {E}_{k}/{{\mathrm{c}}{\mathrm{m}}}^{-1} $ 谱线跃迁 上能级 下能级 N I 493.5 1.76×106 106477 2s22p2(3P)4p $\rm{}^2P^\circ_{1/2}$ 2s22p2(3P)3s 2P3/2 N I 528.1 2.45×105 107037 2s22p2(3P)4p $\rm {}^4P^\circ_{1/2} $ 2s2p4 4P5/2 N II 417.6 1.21×108 210732 2s22p4f F(5/2)3 2s22p3d $\rm{}^1D^\circ_2 $ N II 447.8 6.44×106 188909 2s22p3d $\rm{}^3P^\circ_1 $ 2s22p3d $\rm{}^1D^\circ_2 $ N II 498.7 6.98×107 188937 2s22p3d $\rm{}^3P^\circ_0 $ 2s22p3p 3S1 N II 524.1 6.2×105 221246 2s22p5d $\rm{}^1P^\circ_1 $ 2s22p4p 1P1 N II 568.0 1.78×107 166521 2s22p3p 3D1 2s22p3s $\rm{}^3P^\circ_2 $
下载: 导出CSV
表 3 FDTD模拟、偶极子方法和电荷-磁场极限估算得到的磁场
Table 3. Magnetic field obtained from FDTD simulation, dipole method, and charge-magnetic field limit estimation.
实验峰值
电流/kA距离/m 磁场/μT 类型 $i_{\text{p}}^{{\text{min}}}$ $i_{\text{p}}^{{\text{max}}}$ D FDTD 偶极子
方法BQ 估算 本文
工作25.6 30.9 38 95.3—115.3 58 82.6—98.5 69.8—84.3 62.4—75.5 78 46.4—56.2 90 68.1—77.0 44.6—53.8 40.2—48.7 102 35.5—42.9 1000 3.6—4.4 1600 2.3—2.8 2.3—2.7 2.3—2.8 2200 1.6—2.0 实验测量 Cai[2] 13.0 58 137.8 90 84.9 1600 1.4 Qie[8] 28.1 60 66.3
下载: 导出CSV
-
[1] An Y Y, Shen X Z, Yuan P, Wu Z W 2023 Appl. Phys. Lett. 133 17 doi: 10.1063/5.0138622 [2] Cai L, Li J, Wang J G, Zhou M, Xu F, Li Q X 2020 IEEE Trans. Electromagn. Compat. 63 811 [3] Dong C X, Yuan P, Cen J Y, Wang X J, Mu Y L 2016 Atmos. Res. 178 1 doi: 10.1016/j.atmosres.2016.03.013 [4] Yuan Y M, Shen X Z, Wang H Y, Zhang H M, Zhang Y J, Wang C M, An Y Y, Su M L 2022 Phys. Lett. A 452 128445 doi: 10.1016/j.physleta.2022.128445 [5] Zhang Q L, Qie X S, Wang Z H, Zhang T L, Yang J 2009 Radio Sci. 44 1 doi: 10.1029/2008RS003866 [6] Zhang Y J, Yang S J, Lu W T, Zheng D, Dong W S, Li B, Chen S D, Zhang Y, Chen L W 2014 Atmos. Res. 135 330 [7] Cai L, Li J, Wang J G, Zhou M, Li Q X, Fan Y D 2021 High Volt. 6 337 doi: 10.1049/hve2.12024 [8] Yang J, Qie X S, Zhang G S, Wang H B 2008 Radio Sci. 43 1 [9] Pokharel R K, Ishii M, Baba Y 2003 IEEE Trans. Electromagn. Compat. 45 651 doi: 10.1109/TEMC.2003.819065 [10] Shen X Z, Su M L, Zhang H M, Gao Z G, Xu Y, Wei F 2024 Phys. Plasmas 31 103508 doi: 10.1063/5.0221897 [11] Rubenstein M, Rachidi F, Uman M A, Thottappillil R, Rakov V A Nucci C A 1995 J. Geophys. Ress D: Atmos. 100 8863 doi: 10.1029/95JD00213 [12] Schoene J, Uman M A, Rakov V A, Kodali V, Rambo K J, Schnetzer G H 2003 J. Geophys. Res. D: Atmos. 108(D6) 4192 doi: 10.1029/2002JD002698 [13] Li X, Lu G P, Fan Y F, Jiang R B, Zhang H B, Li D S, Liu M Y, Wang Y P, Ren H 2018 J. Geophys. Res. D: Atmos. 124 3168 doi: 10.1029/2018JD029682 [14] Yee K 1966 IEEE Trans. Antennas Propag. 14 302 doi: 10.1109/TAP.1966.1138693 [15] Cheng L, Zhu G X, Liu G N, Zhu L Q 2020 Mater. Res. Express 7 125009 doi: 10.1088/2053-1591/abd139 [16] Piltyay S, Bulashenko A, Herhil Y, Bulashenko O 2021 IEEE 2nd International Conference on Advanced Trends in Information Theory Kyiv, Ukraine, November 25–27 2020, pp357–363 [17] Su M L, Shen X Z, Wang H Y, Zhang H M, Yuan Y M, An Y Y 2023 Chem. Phys. Lett. 826 140664 doi: 10.1016/j.cplett.2023.140664 [18] Shen X Z, Li J G, Jönsson P, Wang J G 2015 Astrophys. J. 801 129 doi: 10.1088/0004-637X/801/2/129 [19] 申晓志, 袁萍, 李冀光, 董晨钟, 颉录有, 师应龙 2007 物理学报 10 5715 doi: 10.7498/aps.56.5715 Shen X Z, Yuan P, Li J G, Dong C Z, Ji L L, Shi Y L 2007 Acta Phys. Sin. 10 5715 doi: 10.7498/aps.56.5715 [20] 申晓志, 袁萍, 王杰, 郭逸潇, 乔红贞, 赵学燕 2008 物理学报 57 4066 doi: 10.7498/aps.57.4066 Shen X Z, Yuan P, Wang J, Guo X Y, Qiao H Z, Zhao X Y 2008 Acta Phys. Sin. 57 4066 doi: 10.7498/aps.57.4066 [21] Shen X Z, Yuan P, Liu J 2010 Chin. Phys. B 19 053101 doi: 10.1088/1674-1056/19/5/053101 [22] Shen X Z, Liu J, Zhou F Y 2016 Mon. Not. R. Astron. Soc. 462 1203 doi: 10.1093/mnras/stw1648 [23] Shen X Z, Liu J, Sang C C, Jönsson P 2018 Phys. Rev. A 97 012510 doi: 10.1103/PhysRevA.97.012510 [24] Zhang X Y, Shen X Z, Yan P, Feng H 2020 Phys. Rev. A 102 042824 doi: 10.1103/PhysRevA.102.042824 [25] 邱德仁 2002 原子光谱分析(上海: 复旦大学出版社) 第63—64页 Qiu D R 2002 Atomic Spectrometry Analysis (Shanghai: Fudan University Press) pp63–64 [26] Liu J, Shen X Z, Wang K, Sang C C 2020 J. Chem. Phys. 152 204303 doi: 10.1063/5.0007145 [27] D’angola A, Colonna G, Gorse C, Capitell M 2011 Eur. Phys. J. D 65 453 doi: 10.1140/epjd/e2011-20424-5 [28] Devoto R S 1967 Phys. Fluids 10 2105 doi: 10.1063/1.1762005 [29] D’angola A, Colonna G, Gorse C, Capitell M 2008 Eur. Phys. J. D 46 129 doi: 10.1140/epjd/e2007-00305-4 [30] Larsson A, Lalande P, Bondiou-Clergerie A, Lalande P, Delannoy A 2000 J. Phys. D: Appl. Phys. 33 1866 doi: 10.1088/0022-3727/33/15/317 [31] 马文蔚, 周雨清, 解希顺 2016 物理学教程(下册) (北京: 高等教育出版社) 第49页 Ma W W, Zhou Y Q, Xie X S 2016 A Course in Physics (Vol. 2) (Beijing: Higher Education Press) p49 [32] Rakov V A 1998 J. Geophys. Res. D: Atmos. 103(D2) 1879 [33] Yang C, Zhou B 2004 IEEE IEEE Trans. Electromagn. Compat. 46 133 doi: 10.1109/TEMC.2004.823626 [34] Rakov V A 1997 Proc. 12th Int. Zurich Symp. Electromagn. Compat Gainesville, FL, USA February 18–20, 1997 pp59–64 [35] Bruce C E R, Golde R H 1941 J. Inst. Electr. Eng. -Part II: Power Eng. 88 487 [36] Uman M A, McLain D K 1969 J. Geophys. Res. 74 6899 doi: 10.1029/JC074i028p06899 [37] Heidler F 1985 6th Symposium and Technical Exhibition on Electromagnetic Compatibility Zurich, Switzerland March 5–7, 1985 pp157–162 [38] Diendorfer G, Uman M 1990 J. Geophys. Res. D: Atmos. 95 13621 doi: 10.1029/JD095iD09p13621 [39] Shen X, Xu Y, Liu M, Zhang H M, Wang H Y 2025 J. Opt. Soc. Am. B: Opt. Phys. 42 773 doi: 10.1364/JOSAB.547727 [40] Rubinstein M, Uman M A 1989 IEEE Trans. Electromagn. Compat. 31 183 doi: 10.1109/15.18788 [41] Cai L, Hu Q, Wang J G, Zou X, Li Q X, Fan Y D 2021 J. Electrostat. 109 103537 doi: 10.1016/j.elstat.2020.103537 [42] Wei F, Shen X Z, Yuan P, An T T, An Y Y, Su M L 2024 J. Opt. Soc. Am. B: Opt. Phys. 41 2033 doi: 10.1364/JOSAB.532768 [43] Kramida A, Ralchenko Y, Reader J, NIST ASD Team (2024) NIST Atomic Spectra Database (Ver. 5.12) [Online]. [2025, April 1]. National Institute of Standards and Technology, Gaithersburg, MD. [44] Qie X S, Zhang Q L, Zhou Y J, Feng G L, Zhang T L, Yang J, Kong X Z, Xiao Q F, Wu S J 2007 Sci. China Earth Sci. 50 1241 doi: 10.1007/s11430-007-0064-2 -
图( 6) 表( 3)
计量
- 文章访问数: 22
- HTML全文浏览数: 22
- PDF下载数: 1
- 施引文献: 0