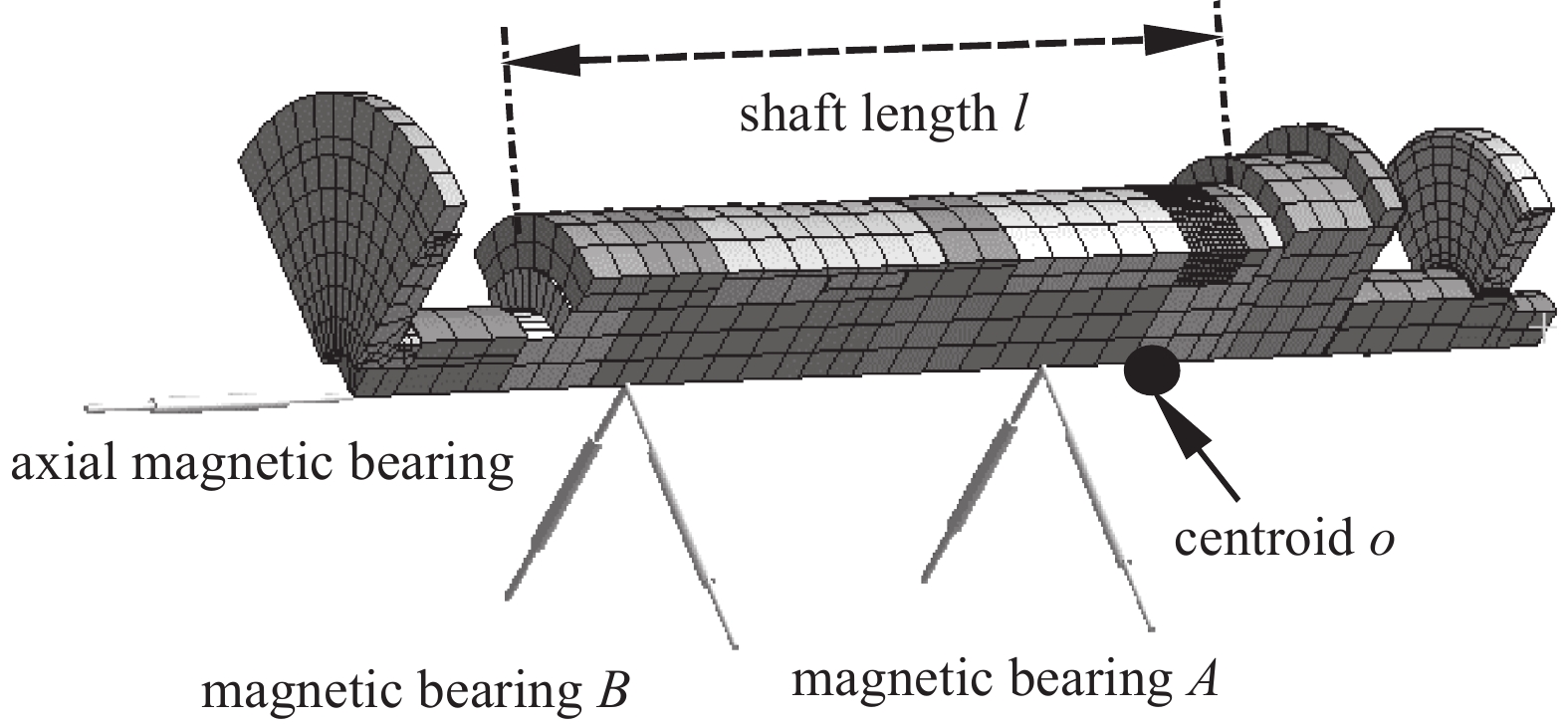
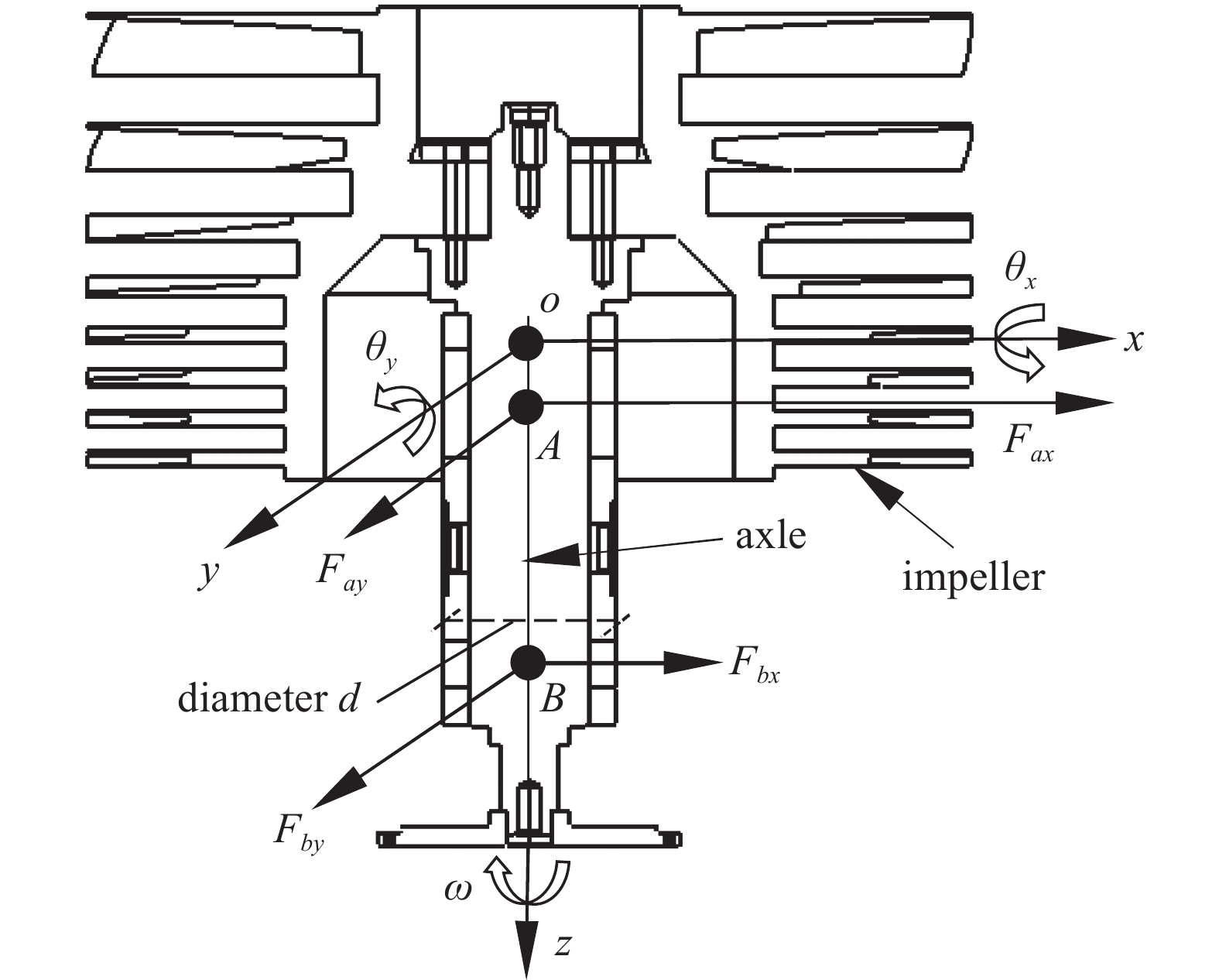
为了描述涡轮转子与磁轴承之间的位置关系，图1给出磁悬浮分子泵的转子与磁轴承关系结构简图，表1给出磁悬浮分子泵的主要参数。以磁悬浮分子泵转子的质心o为原点，建立空间直角坐标系，磁轴承A、B距离转子质心的距离分别为$ {L}_{a} $、$ {L}_{b} $，转子所受由A、B端径向磁悬浮轴承提供的沿x方向与y方向的电磁支承力分别为$ {F}_{ax} $、$ {F}_{bx} $和$ {F}_{ay} $、$ {F}_{by} $。用于限制转子沿x方向与y方向的平动及转动，转子轴向所受力及负载与轴向磁轴承提供的支承力互相平衡，最终实现悬浮和运转。

由于磁悬浮分子泵转子叶片众多，为了简化计算分析过程，可将叶片模态和转子模态分析分开进行计算，在对整个转子进行模态及临界转速分析时，可将叶轮简化成质量块的形式添加到转子结构中，质量块模型与真实叶轮具有相同的重心及转动惯量参数，与真实的转子具有相同的动力学特性，边界条件包括：将磁悬浮轴承均等效成弹簧阻尼单元，进行挠性支承计算，不进行固定约束；整个模型添加转速；打开陀螺效应。磁悬浮分子泵转子主轴直径为d，主轴长度为l，简化后的计算模型如图2所示。

磁悬浮分子泵根据转子动力学建立转子−轴承−系统的数学模型如式（1）所示，

式（1）中，M为质量矩阵，J为陀螺力矩有关的矩阵，K为刚度矩阵，R为外力矩阵，Ω为转动角速度，其中

$ {\boldsymbol{X}=\left\{{x}_{1},{\theta }_{x1},{y}_{1},{\theta }_{y1},\cdots,{x}_{n},{\theta }_{xn},{y}_{n},{\theta }_{yn},{{\textit{z}}}_{n},{\theta }_{{\textit{z}}n}\right\}}^{T} $为各质量块广义位移矩阵。进一步地，为了计算磁悬浮分子泵的临界转速，以质心o的坐标x、y和转角$ {\theta }_{x} $、$ {\theta }_{y} $表示转子在运动过程中任意瞬时的位置。可得到磁悬浮分子泵转子的四个微分方程如式（2）所示，

式（2）中m为转子质量，$ {J}_{P} $为极转动惯量，Ω为转动角速度，$ {J}_{d} $为直径转动惯量，$ {k}_{11} $为转子叶轮质心o在x方向有单位位移时所需加于o点而沿x方向的力，$ {k}_{22} $为转子叶轮质心o在y方向有单位位移时所需加于o点而沿y方向的力，$ {k}_{33} $为转子绕ox轴有单位转角时需对ox轴的力矩，$ {k}_{44} $为转子绕oy轴有单位转角时需对oy轴的力矩，$ {k}_{14} $为转子绕oy轴有单位转角时所需加于o点而沿x方向的力，$ {k}_{23} $为转子绕ox轴有单位转角时所需加于o点而沿y方向的力，$ {k}_{32} $为转子质心o在y方向有单位位移时所需对ox轴的力矩，$ {k}_{41} $为转子质心o在x方向有单位位移时所需对oy轴的力矩。

当磁悬浮分子泵转子质心旋转一个角度θ时，可得到转子质心处位移与磁悬浮轴承处位移的关系为式（3）。式（2）与式（3）联立即可建立磁悬浮分子泵转子平动与转动的四自由度传递函数。

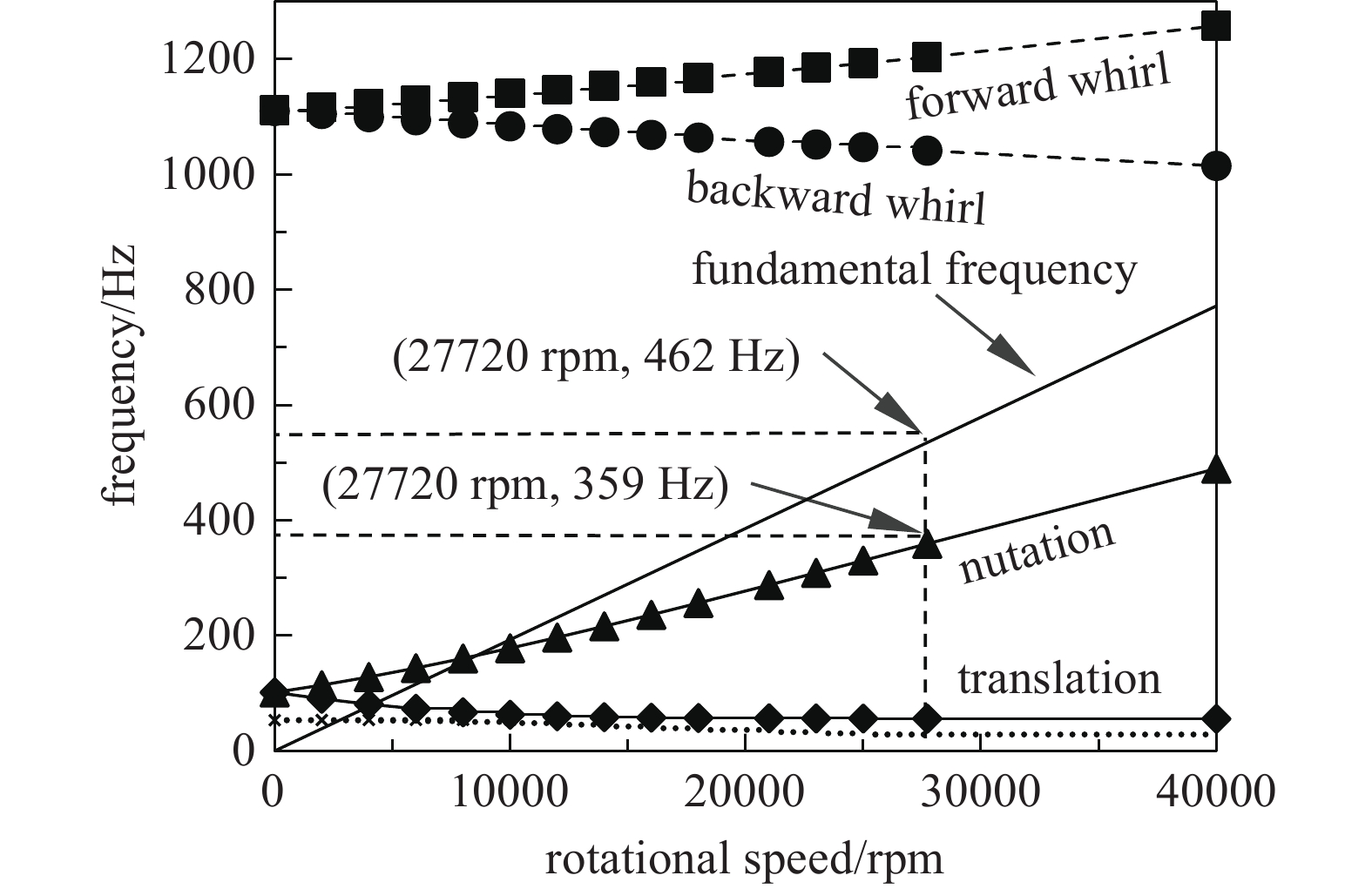
磁悬浮分子泵转子有复杂的动力学特征，包括叶轮叶片振动、转子弯曲振动及刚体振动等等。就转子结构设计而言，为了避免其超越临界转速运行，即保证转子是刚性转子，转子的一阶弯曲频率需远离转子工作频率，以上文图2的计算模型为基础计算得到转子的坎贝尔图如图3所示，为了进行网格无关性验证，本文分别对7 mm、12 mm及20 mm的网格单元进行计算，额定转速下章动频率分别为359.5 Hz、363 Hz及368.5 Hz，可见计算结果与网格大小无关。公式（4）给出了整个磁悬浮分子泵转子涡动频率计算方法，其中$ {\omega }_{r1} $、$ {\omega }_{r2} $分别为转子的正向涡动和反向涡动，$ {k}_{\varphi } $为磁悬浮轴承的支承刚度。

由图3和公式（4）可知，在额定转速范围内，整个磁悬浮分子泵转子整体呈现平动和章动，一阶弯曲频率发生在1092 Hz，随着转速的增加，弯曲模态中，正向涡动频率随转速升高而增加，反向涡动频率随转速升高而减小。一阶弯曲频率远高于额定转速频率，磁悬浮分子泵转子为刚性转子。然而，二阶刚体正向涡动（即刚体章动）频率随转速升高而显著增加，刚体反向涡动（刚体进动）频率趋近于0，当转速升高至27720 r/min时，刚体正向涡动频率为359.5 Hz，此频率非常接近转子额定转速频率462 Hz，此时磁悬浮分子泵转子径向位移波动明显，转子刚体章动频率是导致转子径向位移波动的主要因素。

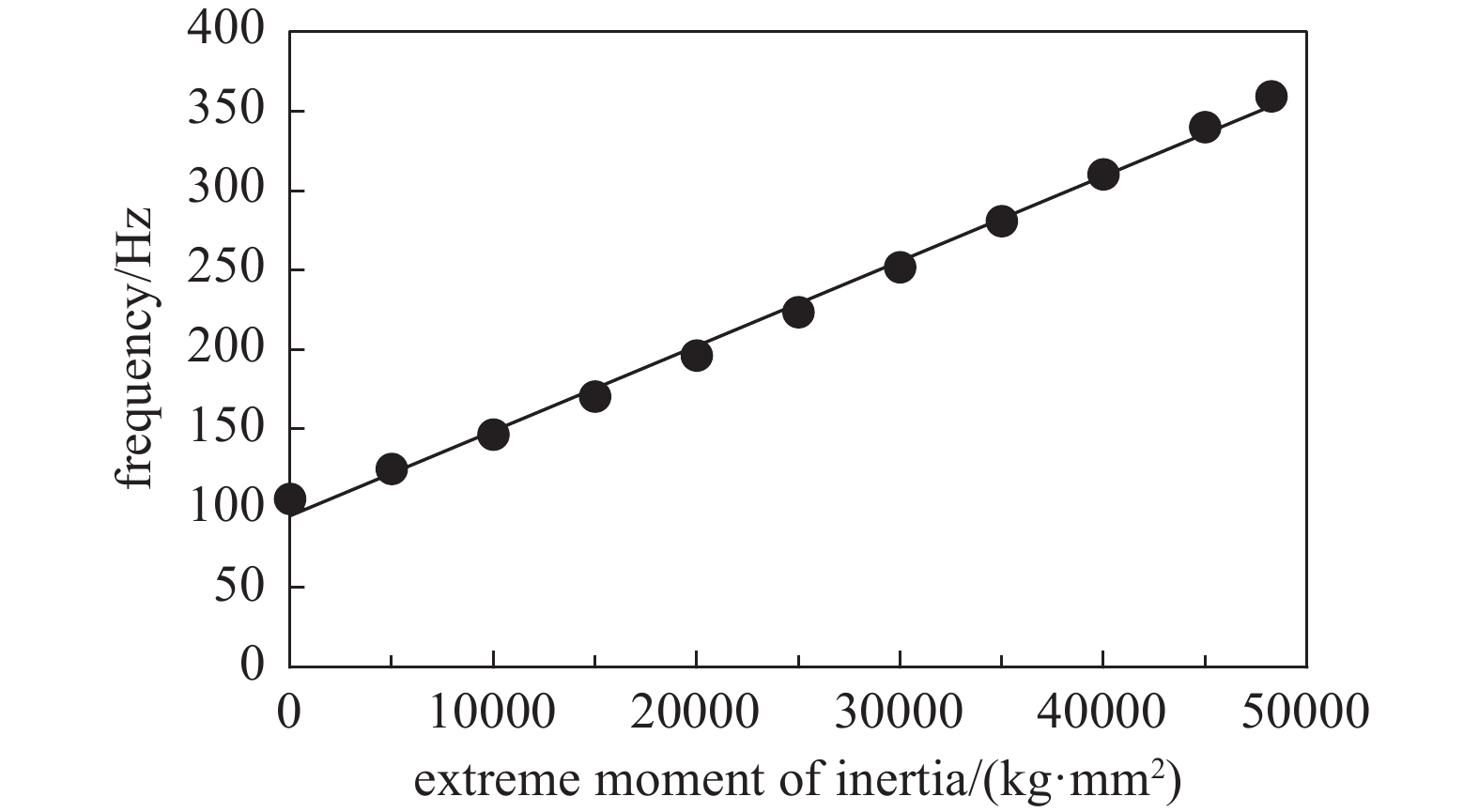
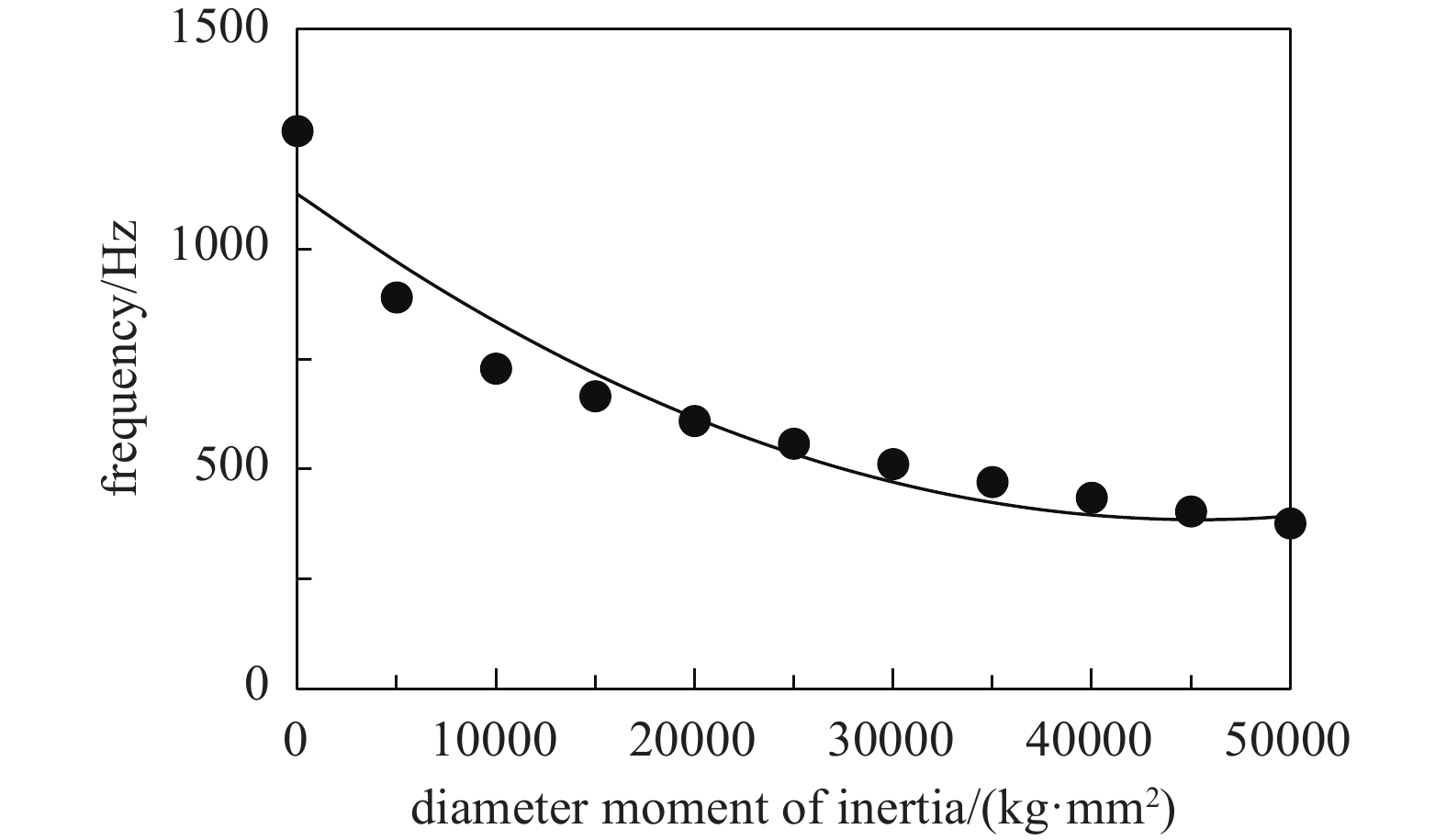
磁悬浮分子泵转子极转动惯量与直径转动惯量的比值较大，转子在高转速下陀螺效应明显，考虑到转子叶轮是整个转子转动惯量的主要贡献单元，为了进一步分析叶轮影响整个转子章动频率升高的灵敏度，本文分别计算叶轮极转动惯量和直径转动惯量对整个转子章动频率的影响如图4、图5所示，叶轮极转动惯量增加会提高整个转子的章动频率，叶轮直径转动惯量增加会减小整个转子的章动频率，故选择较小转动惯量比（极转动惯量与直径转动惯量的比值）的叶轮可有效减小转子的章动频率，但具有小转动惯量比的叶轮会限制磁悬浮分子泵的抽气性能，为了不影响磁悬浮分子泵的抽气性能，通过减小叶轮的转动惯量比的方式抑制整个转子的章动频率显得几无可能。

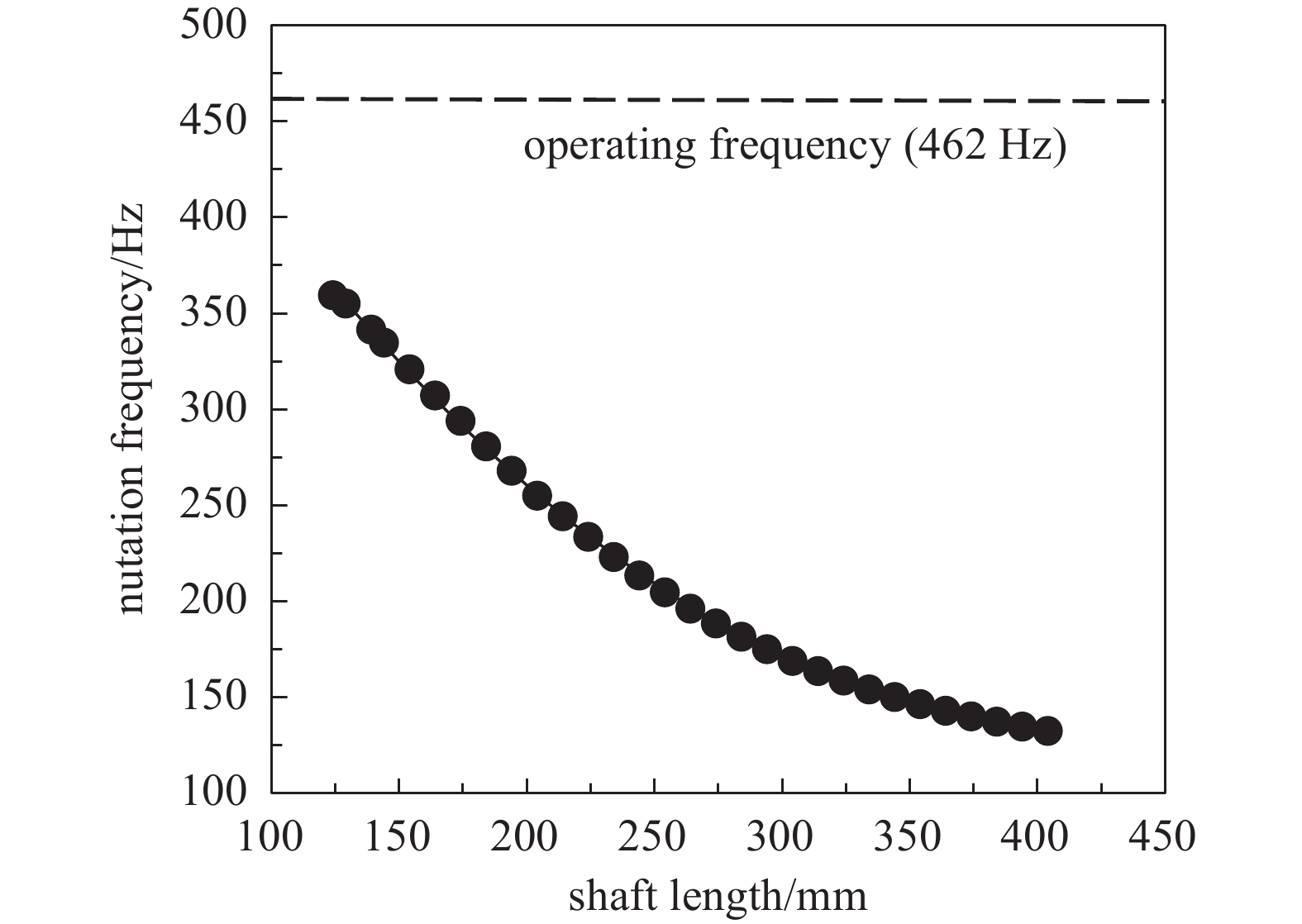
为了有效抑制章动频率对转子径向位移波动的影响，本文通过改变主轴长度l及其所在主轴直径d两个结构对抑制转子章动频率的敏感性进行分析，图6给出了转子主轴长度l变化对转子章动频率的影响关系。

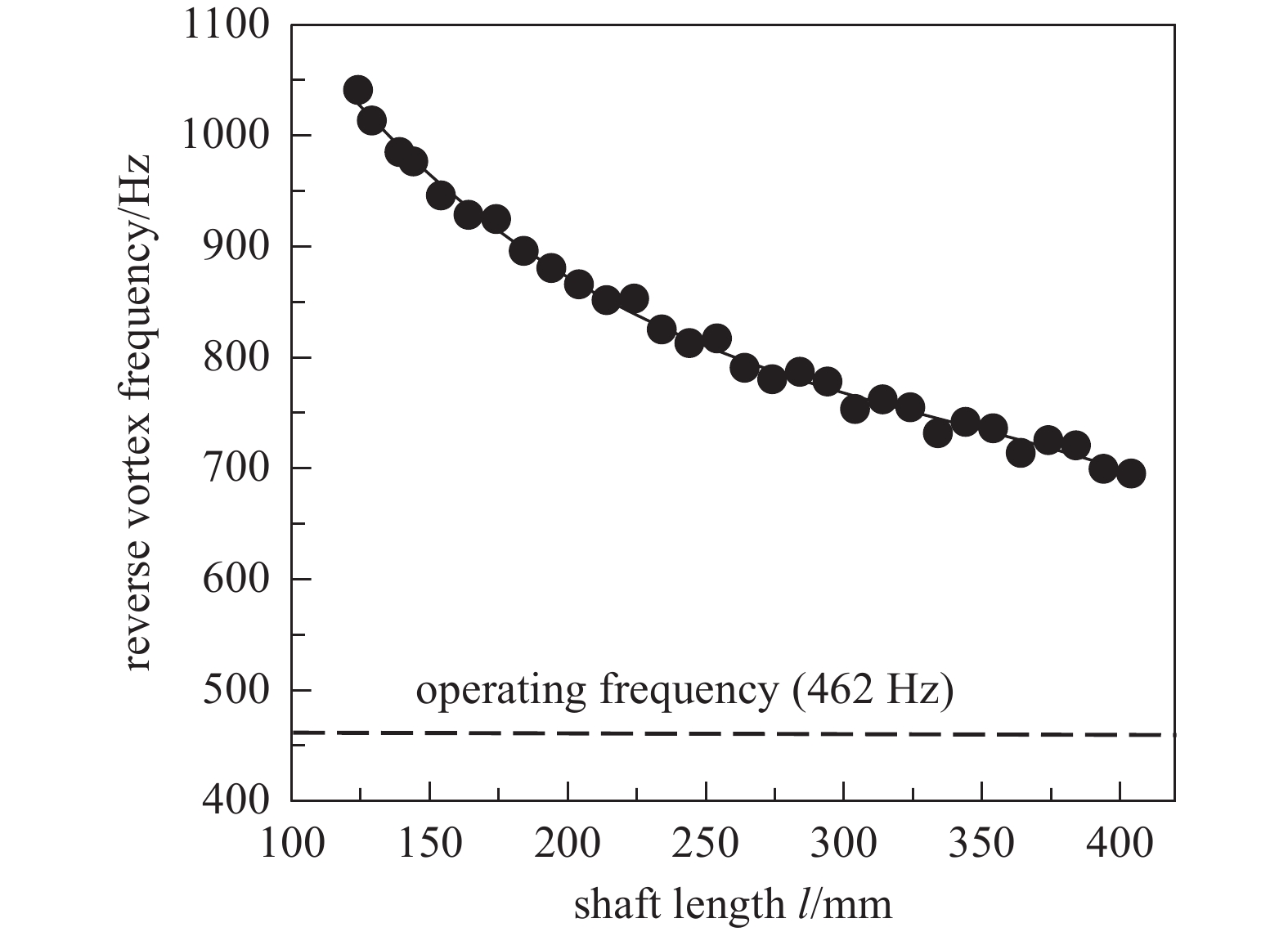
由图6可知增加主轴长度可以抑制整个磁悬浮分子泵转子的章动频率，且抑制效果可达到80 Hz以上，磁悬浮分子泵转子的章动频率对转子长度变化较为敏感。但是增加主轴长度会降低一阶弯曲模态反向涡动频率，图7给出增加主轴长度对一阶弯曲模态反向涡动频率的影响关系，可见，随着主轴长度的增加，一阶弯曲反方向涡动频率会逐渐减小，使其无限接近磁悬浮分子泵转子工作转速频率（462 Hz），激发整个转子的弯曲变形。综上，增加主轴长度60 mm可有效抑制整个转子的章动频率80 Hz，此时一阶反向涡动频率896 Hz，依然远离磁悬浮分子泵转子工作转速频率，不会激发整个转子弯曲变形。

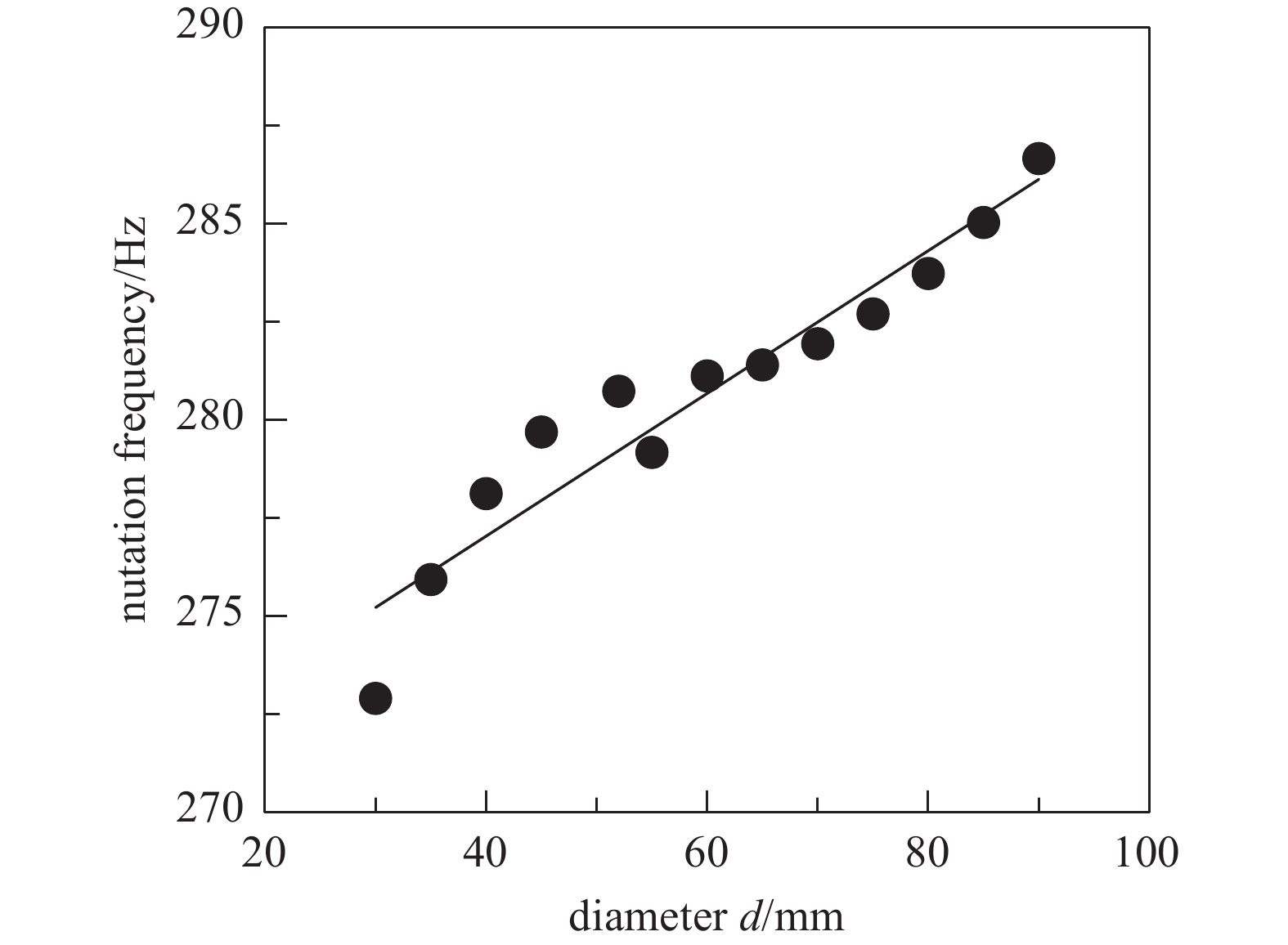
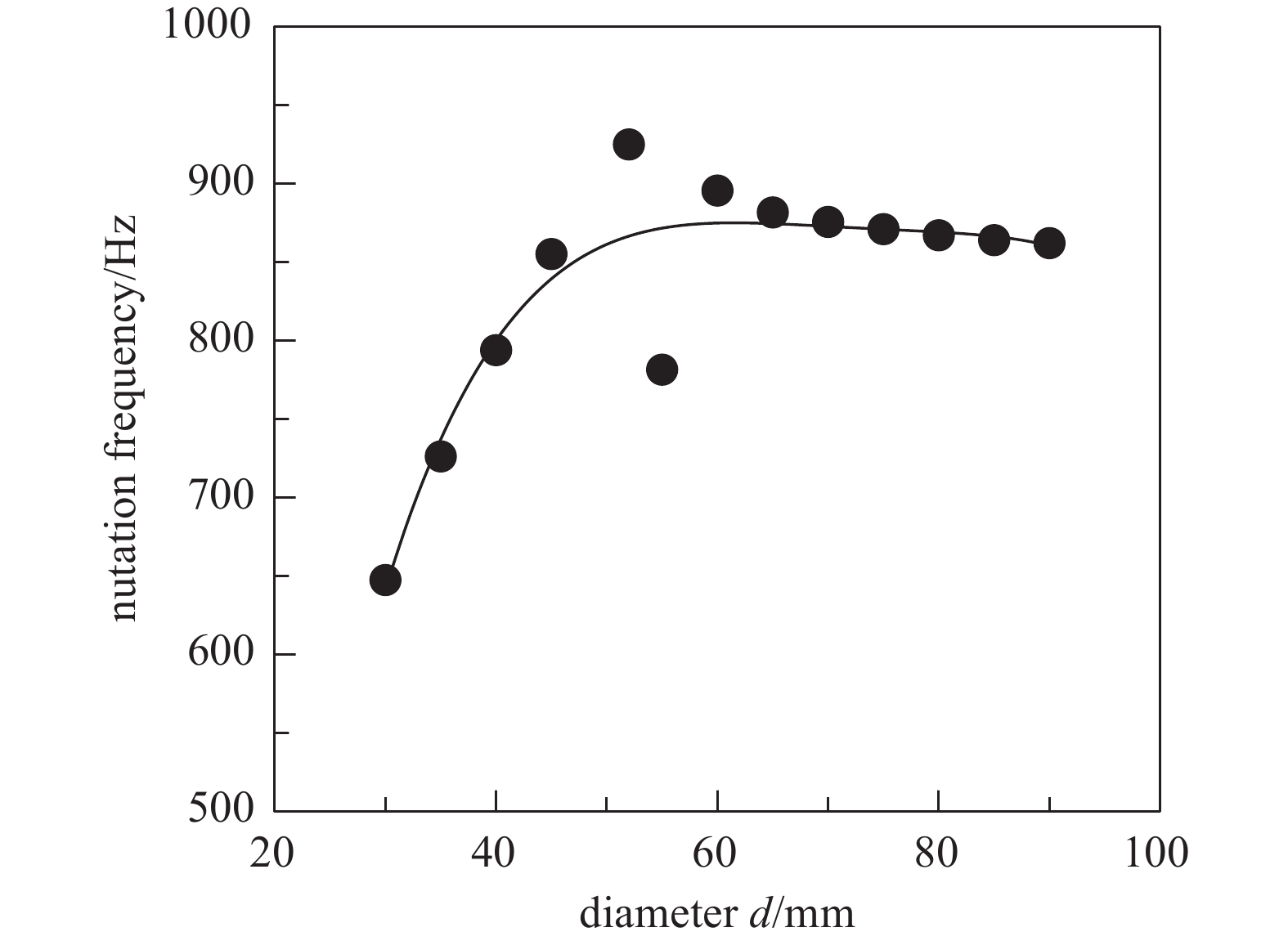
上文验证了增加主轴长度可有效的抑制整个转子的章动频率，为了进一步分析主轴伸长量∆l所在轴段直径d的变化对整个转子章动频率及弯曲频率的影响关系，取主轴伸长量∆l=60 mm（即主轴长度为184 mm），直径d变化范围在30 mm～90 mm之间，图8、图9分别给出了直径d的变化对章动频率和弯曲频率的影响关系，可知章动频率受直径d的变化的影响的敏感性较低，变化范围小于15 Hz，直径d变化对章动频率几乎无影响。但是主轴直径d的增加会有效提高整个转子的一阶弯曲频率，随着直径d的增加，弯曲频率有效的远离工作转速频率，远离趋势先增加后平稳不变。故增加转子长度及直径，可有效抑制章动频率和提高弯曲频率。

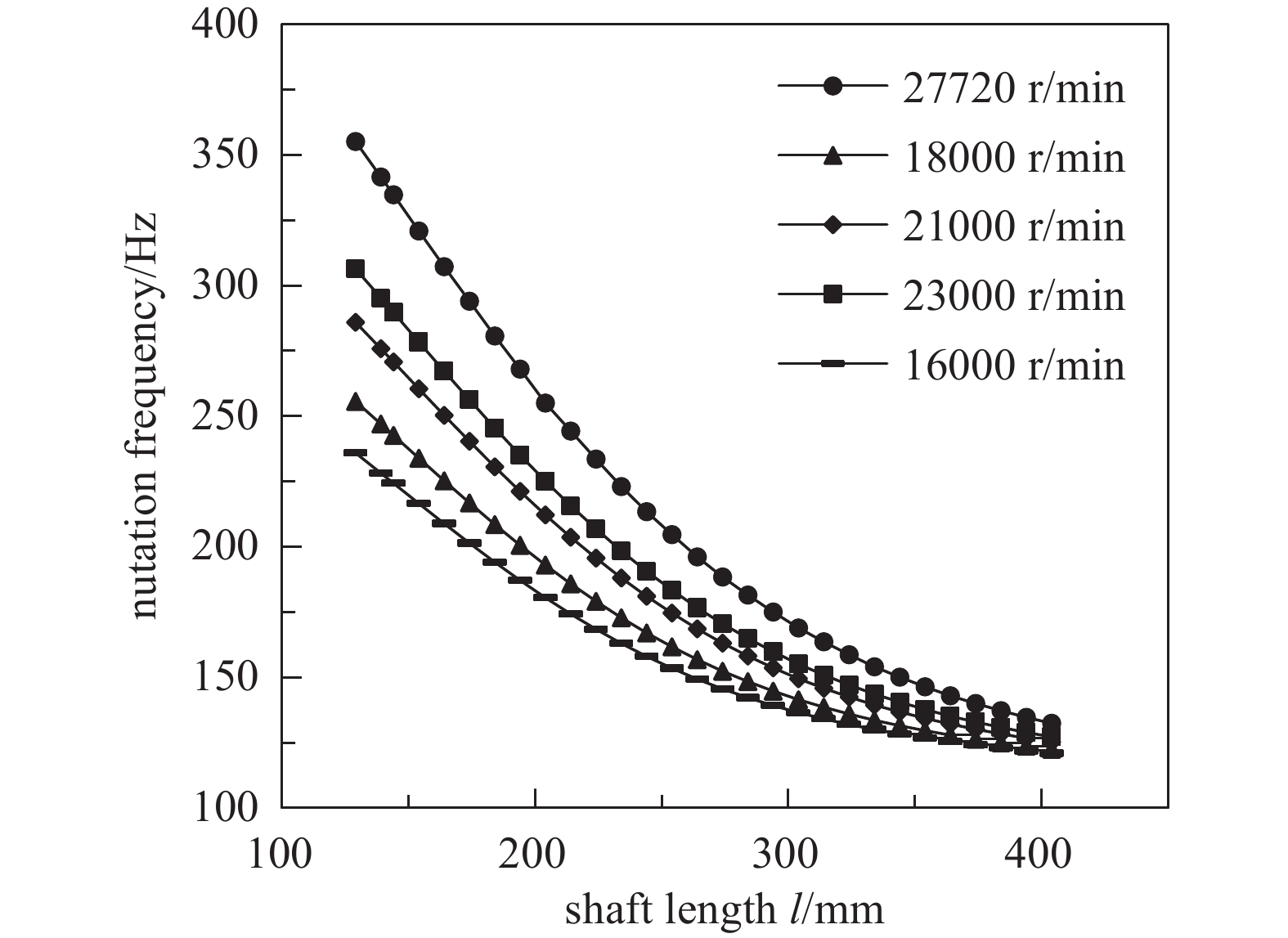
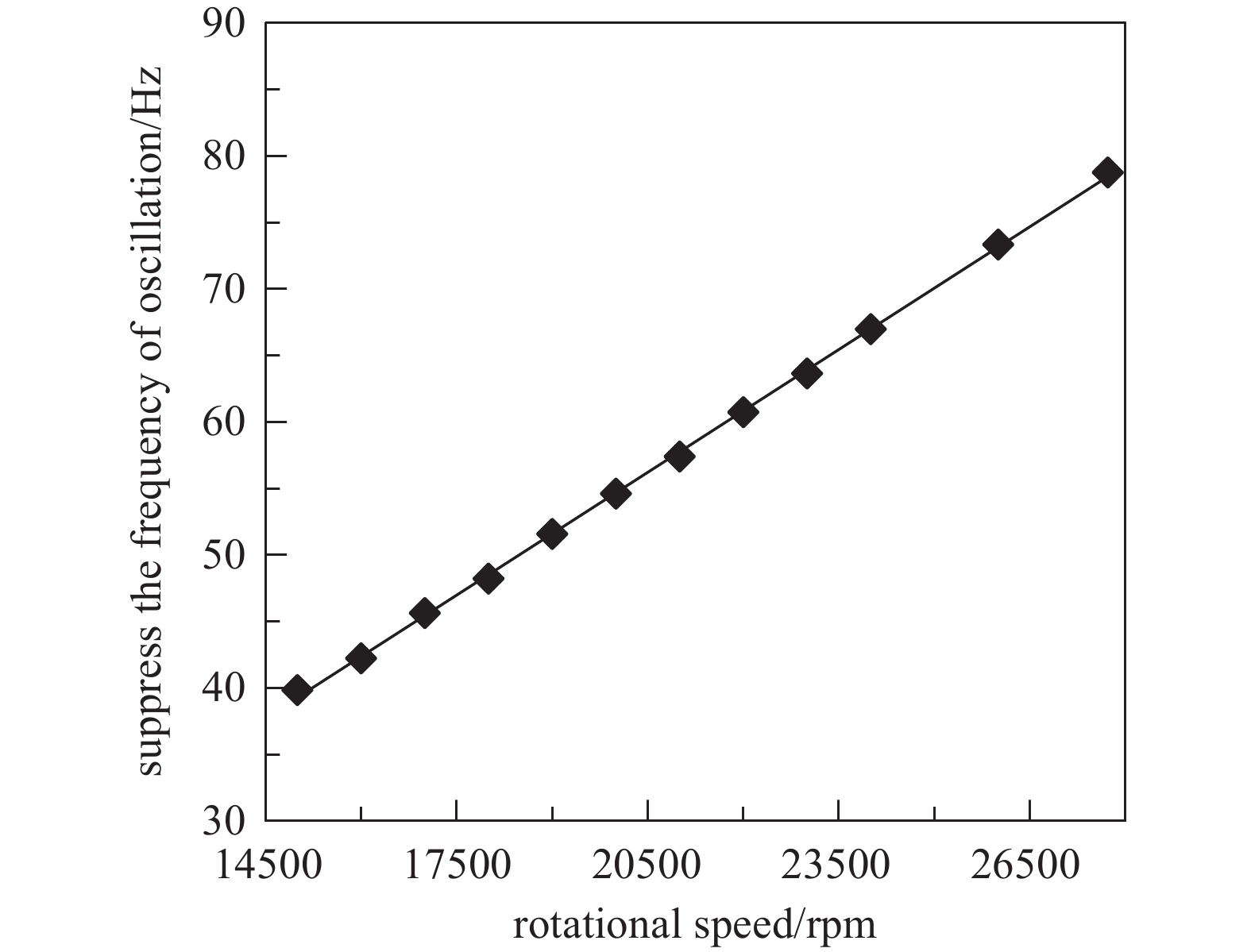
综上，根据主轴长度和直径对抑制章动频率的敏感性分析结果可知，抑制章动频率只与主轴长度有关而与主轴直径无关。结合上文图6主轴长度l对转子章动频率的影响关系，进行二项式拟合并求导，可求得章动频率值$ \mathrm{\delta } $与主轴长度l之间的微分方程如公式（5）所示，其中$ \mathrm{\delta } $为章动频率，l为主轴的长度。

进一步地由公式（4）可知，随着转子转速的升高，涡动频率只与转子的转动惯量比（极转动惯量与直径转动惯量的比值）及转速有关，类似地可探讨转动惯量比和转速对章动的影响规律。因此，在相同转动惯量比时，分别计算了27720 r/min、23000r/min、21000 r/min、18000 r/min及16000 r/min工况下，主轴长度对章动频率的影响如图10所示，可见不同转速下，主轴长度对章动频率的影响呈现为开口向上的抛物线束，图11给出相同主轴长度，不同转速对抑制章动频率变化量的影响关系，可见，转速越高抑制章动频率量越高，即不同转速下，章动频率变化率$ \dot{\delta } $与转速成正比关系。

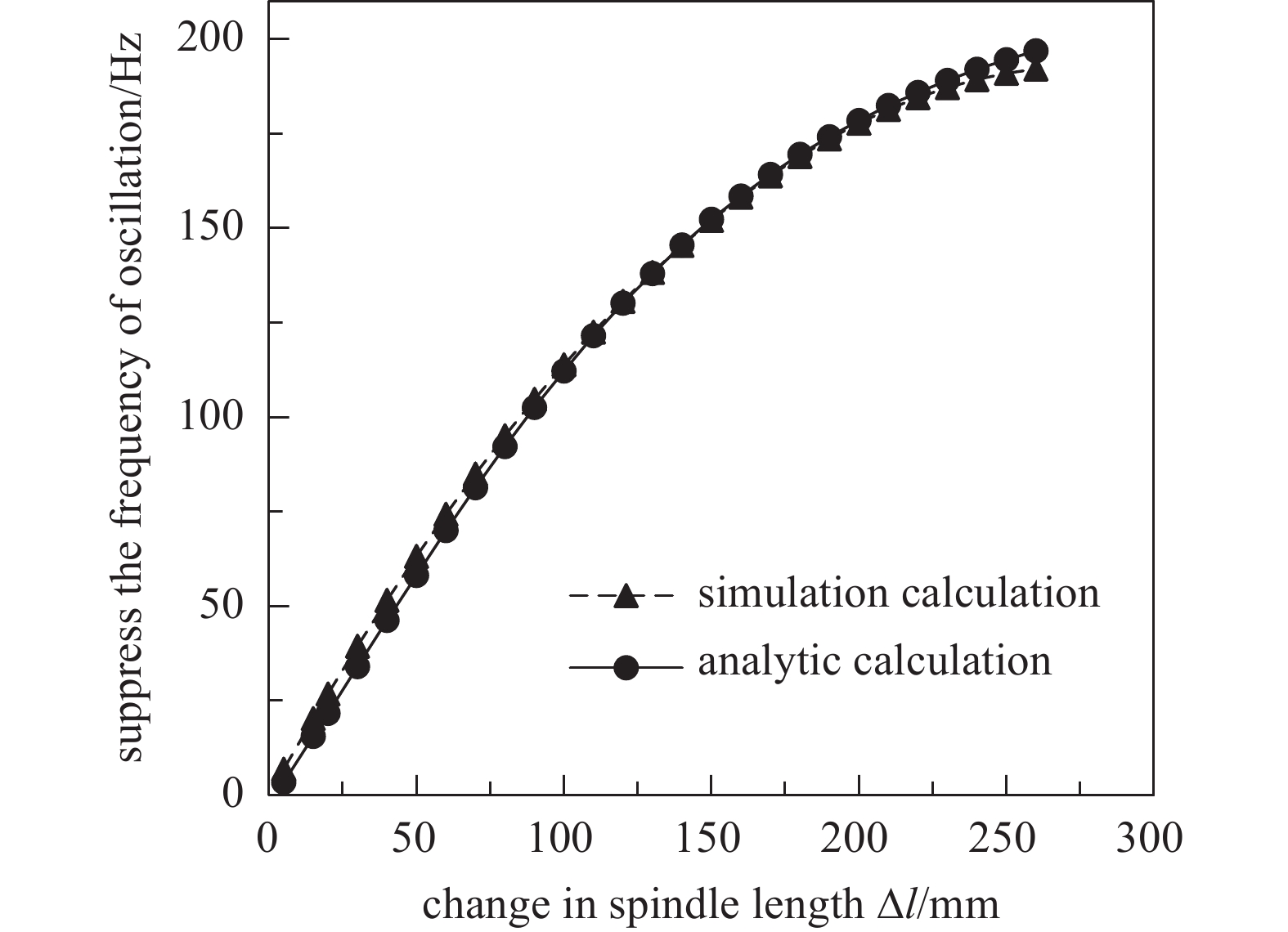
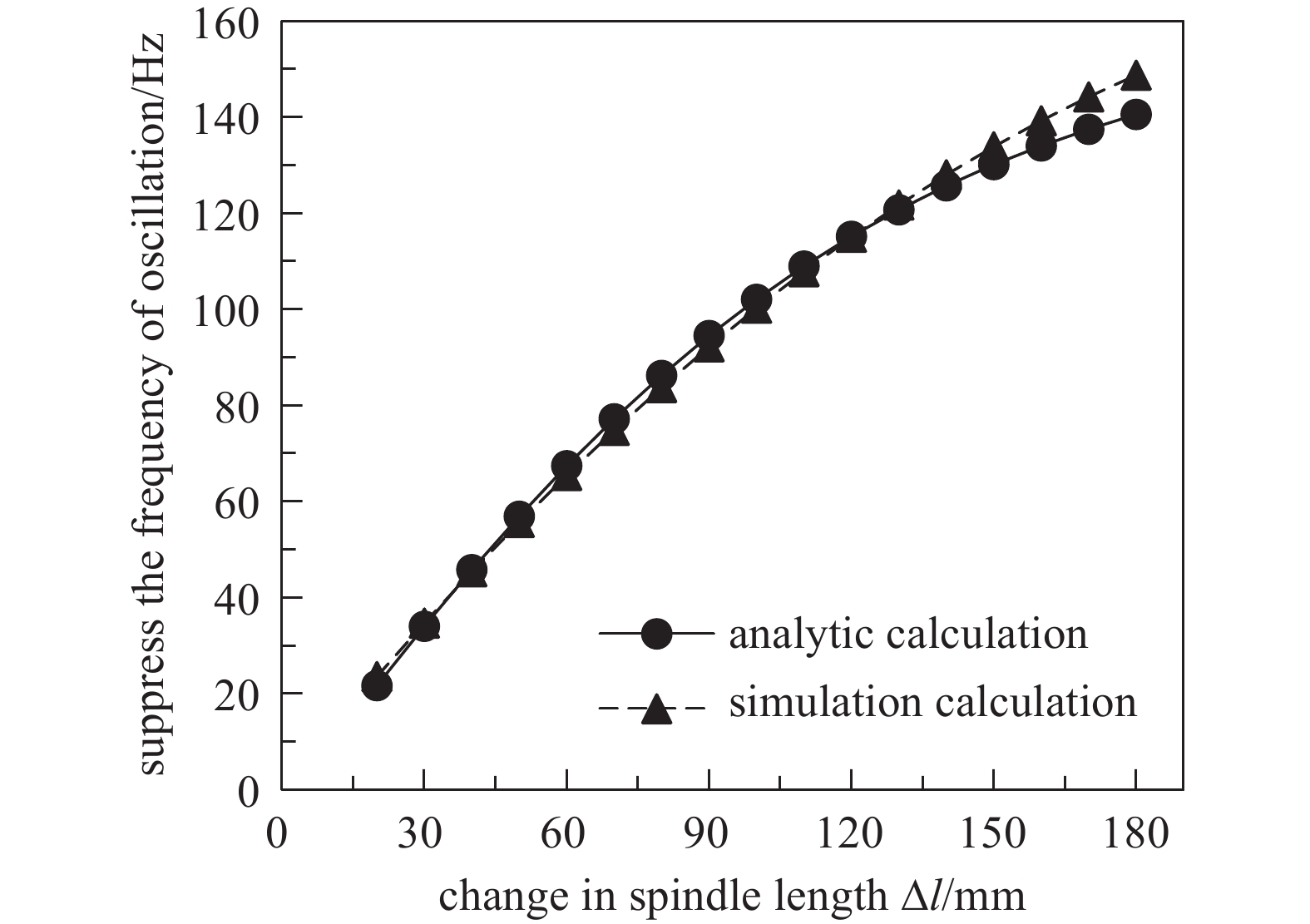
进一步地，结合公式（5）与图11可求得相同转动惯量比时，任意转速下主轴长度对抑制章动频率的微分方程如公式（6）所示，其中$ \dot{{\delta }_{p}} $为任意转速下的章动频率变化率，$ p $为任意转速，单位为r/min。

为了验证公式（6）的正确性，当磁悬浮分子泵转速为25000 r/min时，本文进行了公式（6）解析计算与仿真计算的对比分析如图12所示，可见解析计算结果与仿真计算基本吻合，误差小于5 Hz，公式（6）正确。

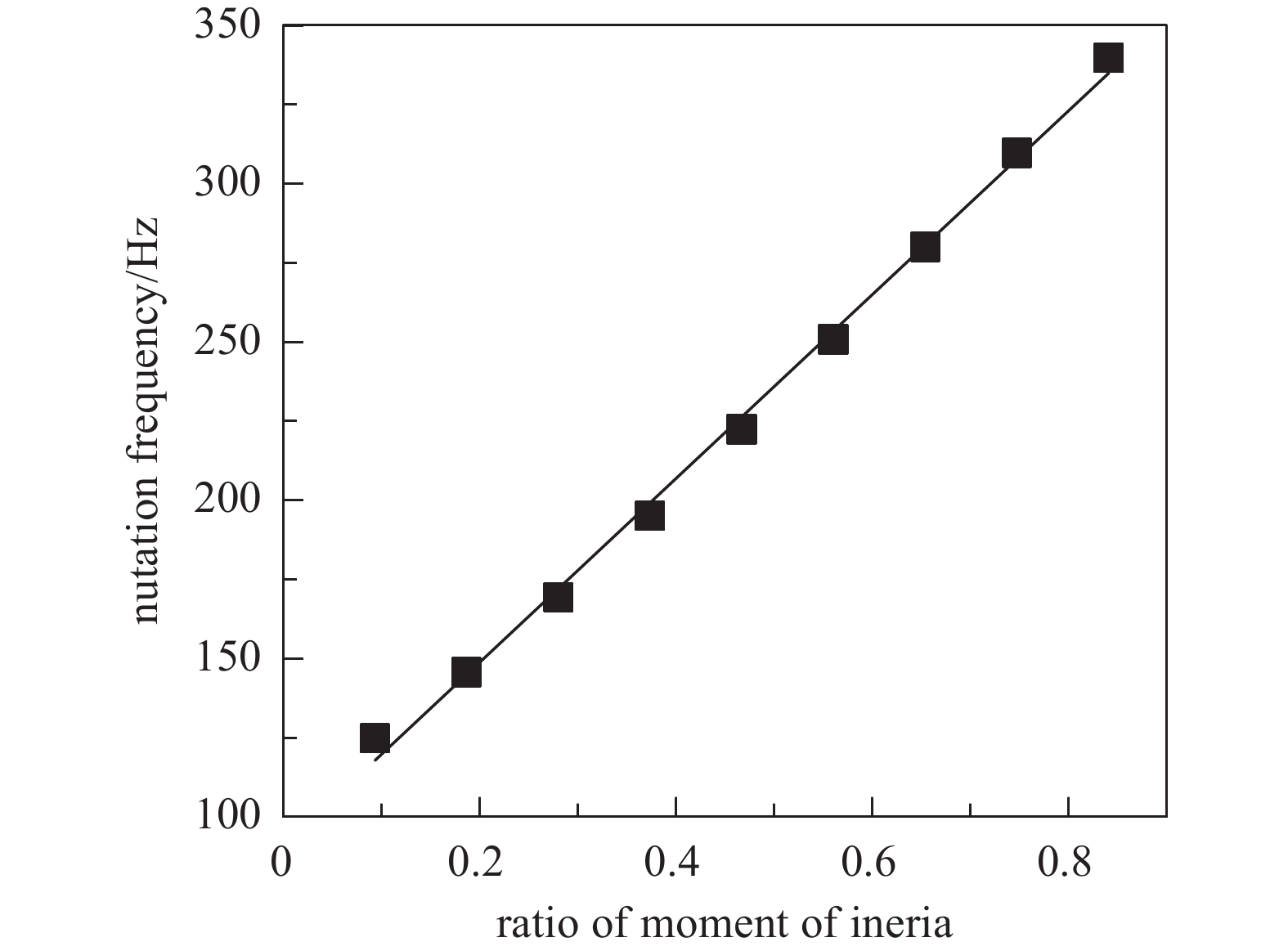
上文给出了相同转动惯量比，任意转速下章动频率与主轴长度的解析关系，为了分析转动惯量比对章动频率的影响，本文计算了不同转动惯量比与章动频率的关系如图13所示，可见，转动惯量比越大，章动频率越大，即转动惯量比与章动频率$ \mathrm{\delta } $成正比关系。

磁悬浮分子泵均采用本文案例所示的扁平转子结构，结合上文的分析结论，可推导出任意转动惯量比、任意转速工况下，主轴长度对抑制章动频率的数学解析关系如公式（7）所示，其中$ \dot{{\delta }_{pn}} $为任意转动惯量比、任意转速的章动频率变化率，n为转动惯量比。

为了验证公式（7）具有通用性，以转子转动惯量比为0.69的磁悬浮分子泵为计算对象进行验证，具体参数如表2所示。图14给出仿真计算与公式（7）解析计算结果对比，可见公式（7）解析计算结果与仿真计算结果两者基本吻合，两者误差平均小于5 Hz，验证了公式（7）的准确性及通用性。

为了验证上文中抑制磁悬浮分子泵转子章动频率方法的正确性及仿真计算的准确性，搭建了磁悬浮分子泵试验平台。磁悬浮分子泵试验平台如图15所示。试验平台由磁悬浮分子泵（参数见表1）、测试罩、真空计、上位机及其他真空辅助设备组成。其中测试罩模拟真空腔体，采用英福康全量程真空规（BPG400，精度15%），抽速30000 L/s的干泵机组（Edwards_iXH1820H）作为磁悬浮分子泵的前级泵，控制器与磁悬浮分子泵为一体式。先启动前级泵，待腔体压力小于10 Pa时，启动磁悬浮分子泵。

工作时，磁悬浮分子泵中的电涡流式非接触位移传感器（ECDS-4-1，精度0.12 μm）检测磁悬浮轴承A、B端位移波动，即传感器可直接检测到转子位移振动，并将位移信号传输至控制器中，经过控制器系统的实时计算，将合适的控制信号传输至功率放大器，再由功率放大器输出合适的控制电流，最终使得磁悬浮轴承产生旋转的电磁力，实现闭环控制。

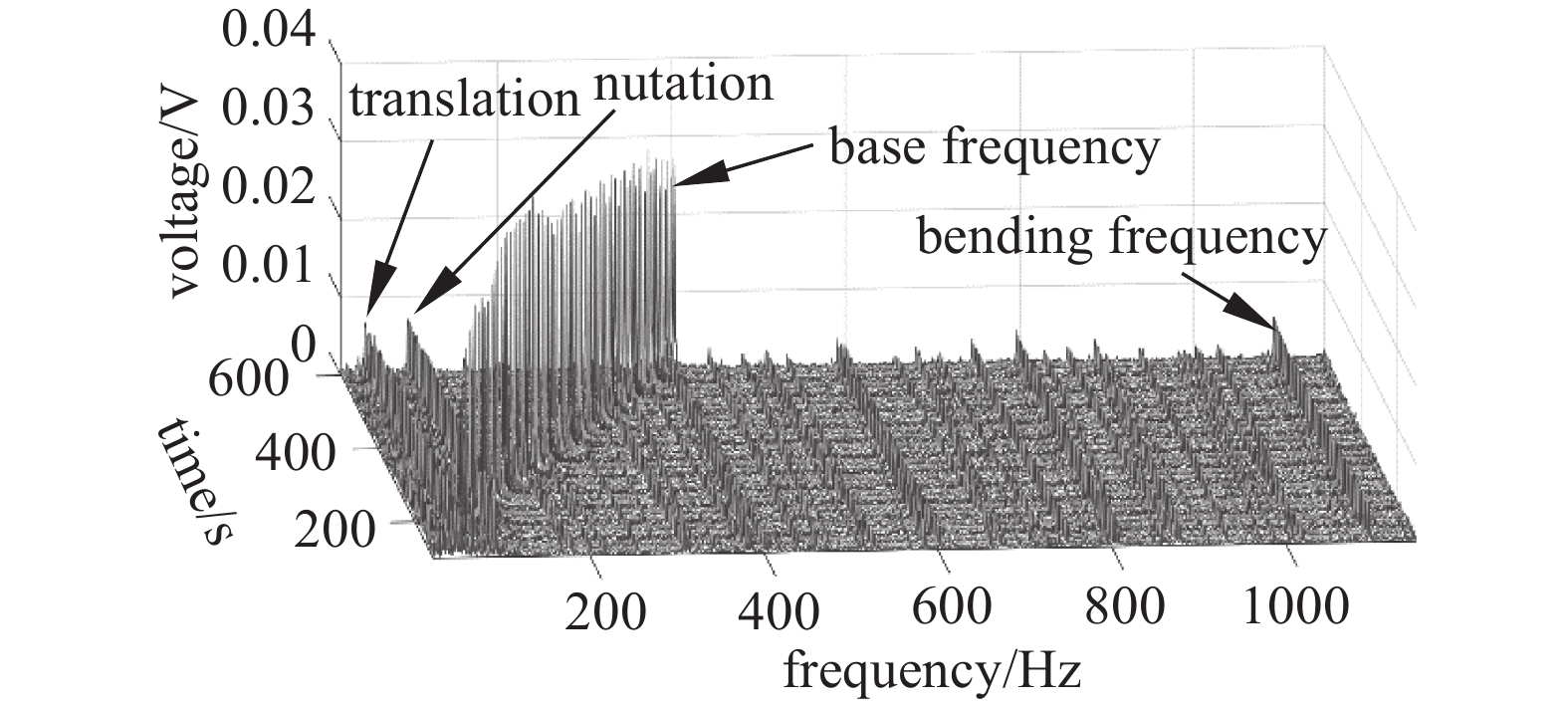
在磁悬浮分子泵升速的过程中，在47 Hz、97 Hz处有明显的振幅，经过信息采集卡（SMACQ，精度4.8 mV）的数据采集，绘制出了磁悬浮分子泵全转速范围内的振动瀑布图如图16所示，图中刚体平动频率和章动频率及弯曲频率均有较高的振幅，与升速过程中位移波动表现一致。表3给出了磁悬浮涡轮分子泵（参数见表1）刚体平动、章动频率与弯曲频率的试验值与计算值（见图3）的数据对比。结果表明两者误差小于5%，验证了计算结果的正确性及抑制章动频率方法的准确性。

（1）本文利用有限元法准确计算了磁悬浮分子泵的刚体振动频率及一阶弯曲频率，刚体章动频率的增加是磁悬浮涡轮分子泵径向位移波动大的主要因素。

（2）针对抑制章动频率，本文给出了增加磁悬浮分子泵主轴长度来抑制章动频率的方法，并给出抑制章动频率量与主轴长度增加量之间的解析关系式。此方法可有效抑制转子章动频率量80 Hz以上。

（3）本文所提出的方法可推广应用于转子具有较大转动惯量比的磁悬浮分子泵，为产品的稳定可靠运行提供了有效的解决方案，本文的研究成果对相关产品的设计具有较大的指导意义和参考价值。