利用仿真软件对真空泵站进行静态结构分析的基本步骤为：

（1） 简化三维模型：基于水平测试平台内部空间大小及各部件安装相对位置，真空泵站的初步设计方案如图1所示。在仿真前，需对真空泵站三维模型进行适当简化，忽略对静态结构分析影响较小的部分（如各法兰上的刀口、法兰孔处的倒角等），以便提高运算速率；而泵站左侧悬挂法拉第筒的长真空管的根部处，在简化时需保留过渡圆角，以解决结构仿真中三维模型几何突变处经常会遇到的应力奇异问题^[28-30]。

（2） 添加材料属性：所用材料为304不锈钢，其材料属性如下：密度为7930 kg/m³，拉伸屈服强度为205 MPa，弹性模量为194 GPa、泊松比为0.3，许用应力137 MPa^[31-33]。

（3） 划分网格：采用分块网格划分的策略，在关键区域（例如泵站左侧悬挂法拉第筒的长真空管的根部处）进行局部加密。为检验网格尺寸设置是否合理，将网格加密部分的单元尺寸依次设置为4 mm，2 mm，1 mm，0.5 mm，0.25 mm并划分网格，通过观察仿真结果的变化趋势检验网格敏感性。

（4） 添加约束和载荷：由于真空泵站的底部安装在离子泵泵口之上，泵站右侧长管与真空插板阀相连，因此对泵站底部的法兰和右侧长管的法兰设置固定约束。由于法拉第筒及其附件的质量为9 kg，重力加速度取g=9.8 m/s²，因此对左侧长管的法兰处施加垂直向下的作用力88.2 N。此外，考虑真空泵站内外压差的作用，对真空泵站外表面施加0.1 MPa的大气压强。

（5） 求解并输出结果：设置好上述约束及载荷后，对真空泵站的变形量及等效应力进行仿真运算并输出结果。

各单元尺寸下网格划分质量与仿真结果如表1所示。从表1可以看出，随着网格不断细化，相邻两次网格步的最大变形量的变化幅度均小于5%，而最大应力值的变化幅度则存在明显的差异。当单元尺寸细化到0.25 mm时，其相邻网格步之间最大变形量的变化幅度约为0.0011%，而最大应力值的变化幅度约为2.03%，由于两者均小于5%的变化阈值，此时可认为仿真结果不再随网格尺寸的减小而发生显著变化，故取单元尺寸0.25 mm的仿真结果进行分析。

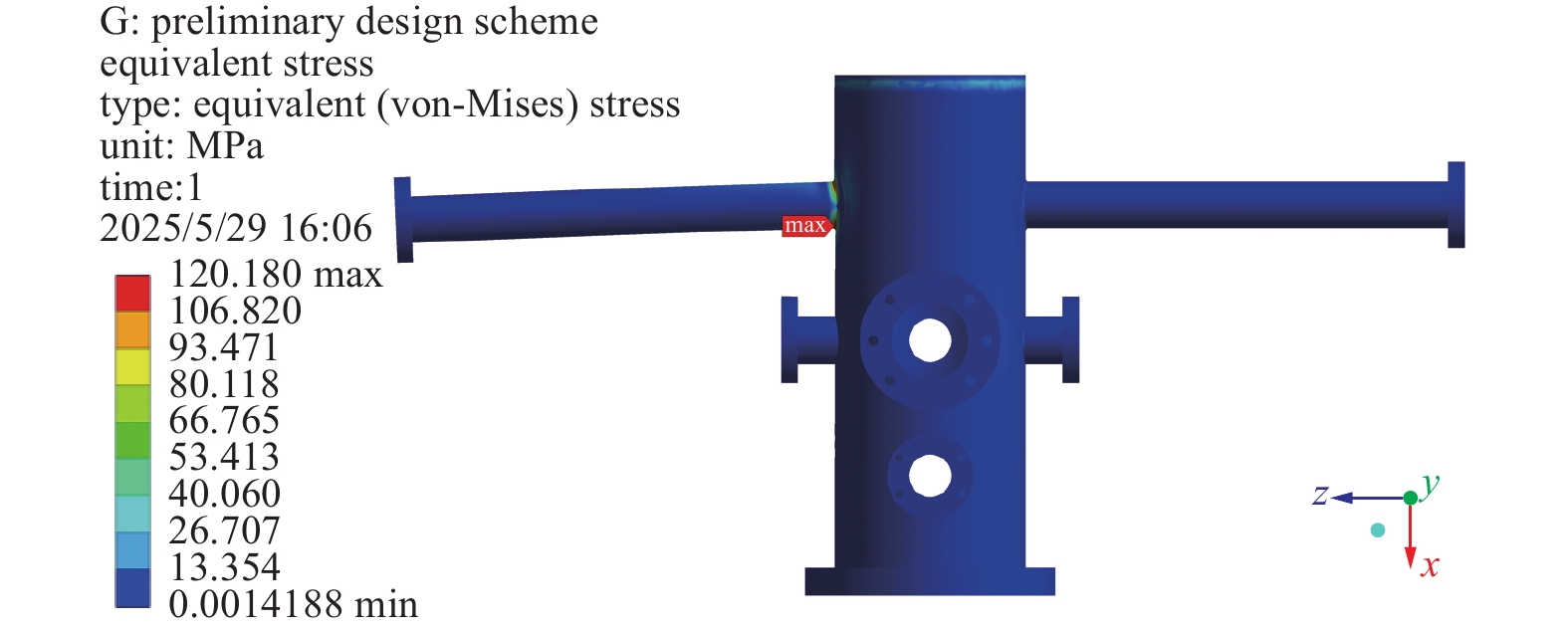
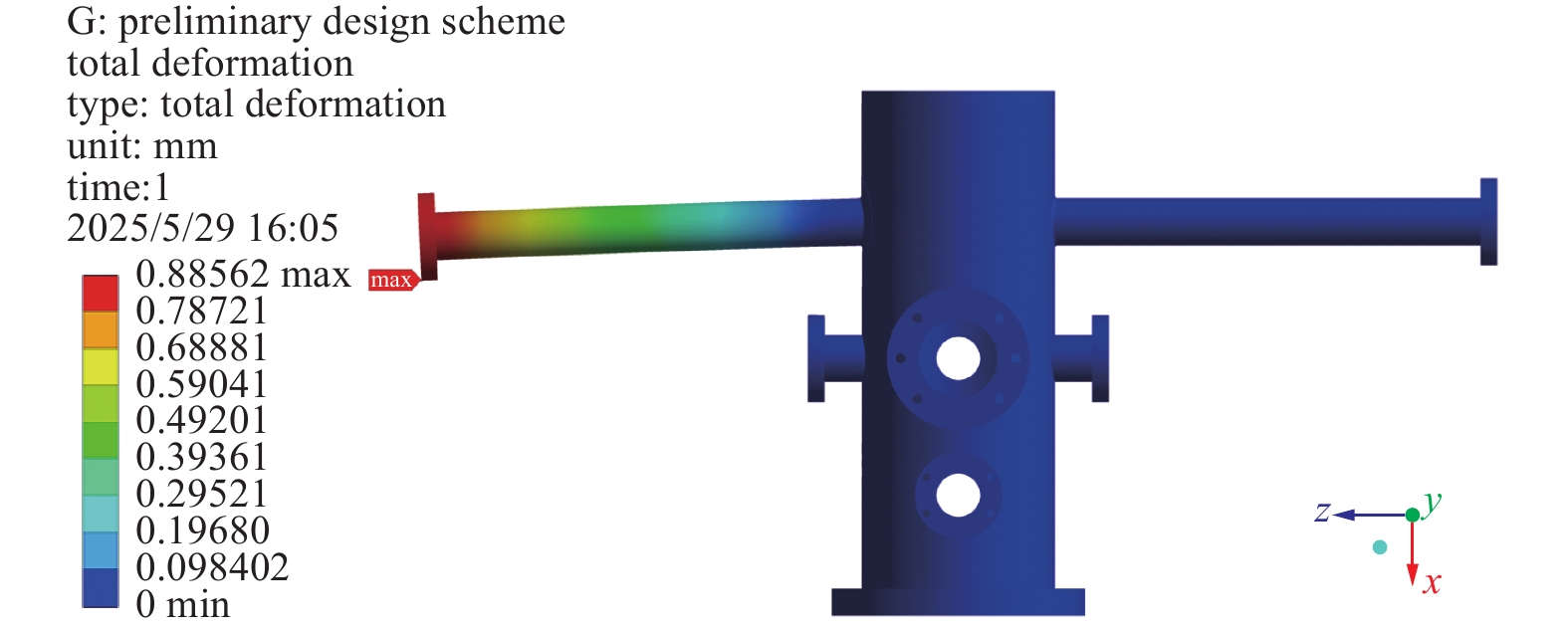
在复杂应力状态下，第四强度理论对塑性材料（如钢、铝等金属）的屈服失效预测精度更高，且在薄壁结构等工况下同实验结果的吻合度更好，因此本文采用第四强度理论（Von Mises理论）进行强度分析。真空泵站初步设计方案的等效应力云图如图2所示，等效应力最大值$ {\sigma _{\max }} $位于悬挂法拉第筒的长真空管的根部位置，其大小为120.18 MPa；而除该长管的根部区域外，真空泵站其余部分的应力值则均小于40 MPa。虽然最大应力值小于材料的许用应力137 MPa，但长管根部仍存在很明显的应力集中问题，需要进一步改善。

真空泵站初步设计方案的变形云图如图3所示，最大变形量$ {\delta _{\max }} $位于悬挂法拉第筒的长真空管的法兰处。为满足悬臂圆管处刚度安全性的需要，本文要求悬臂圆管的最大变形量$ {\delta _{\max }} $须不超过L/500=0.706 mm（其中L为悬臂圆管的长度）。仿真结果显示，悬臂圆管处的最大变形量为0.88562 mm，超出了本文对悬臂圆管变形量的限制要求。综上所述，无论是最大变形量超限还是应力集中问题，都需要对真空泵站结构进行改进和优化。

如果对结构全局求解等效应力，计算量会随着网格的加密呈指数级增长，计算时间也会大幅提高（如表1所示）；而采用子模型技术（Sub-model technology）针对关键区域的应力进行局部高精度仿真，则可避免全局模型计算量过大的问题。子模型的构建依据圣维南原理^[34-36]，该原理指出：当实际分布载荷被等效载荷替代时，应力的改变主要集中在载荷施加的区域。由此可知，若子模型的切割边界远离应力集中区域，则能够通过计算子模型得到较精确的结果。在子模型技术中，全局模型与子模型通过切割边界位移传递实现解耦：先基于较粗的网格求解全局模型，然后从全局模型的结果中提取子模型区域的边界条件，再对子模型构建更精细的高质量网格进行二次分析，重新计算子模型区域的应力，可使局部的仿真结果不受全局模型简化的影响。

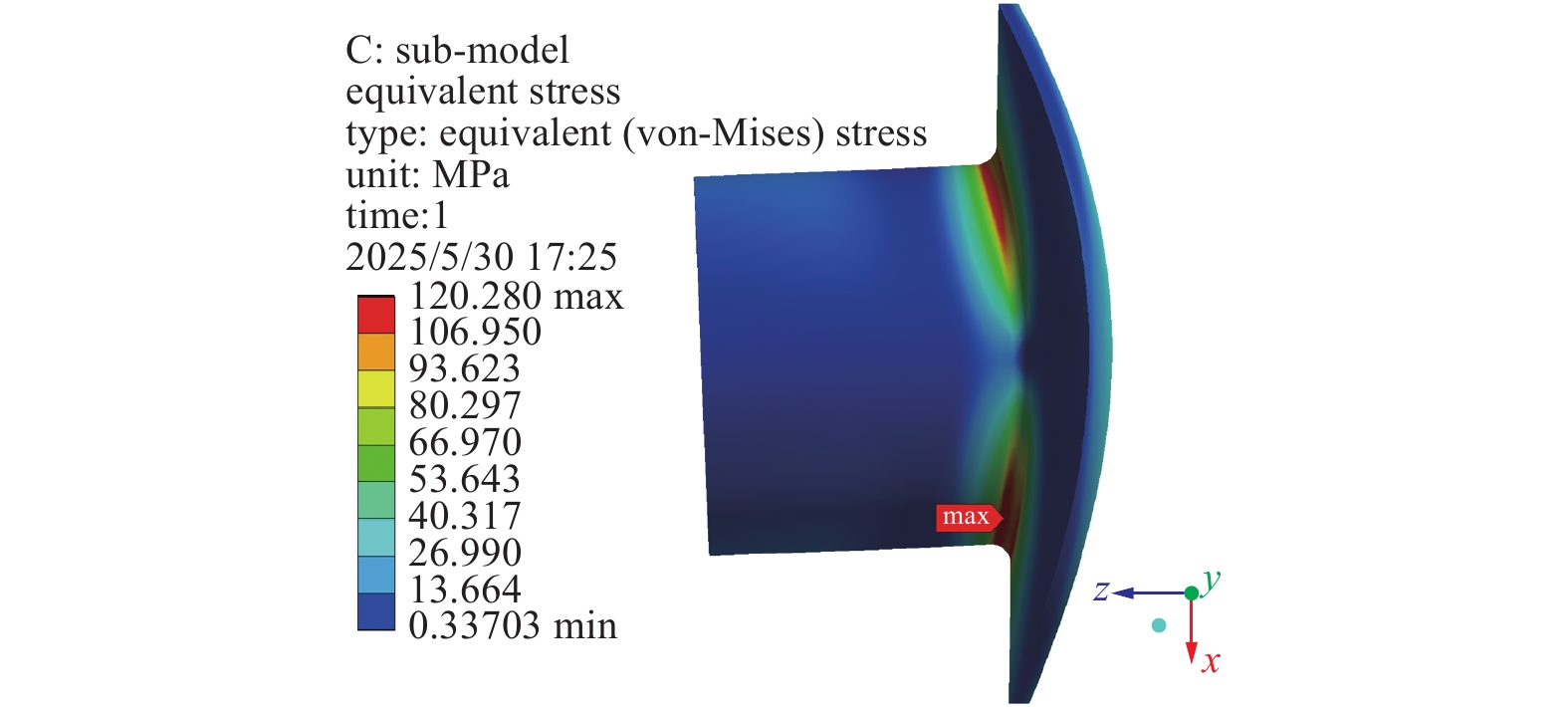
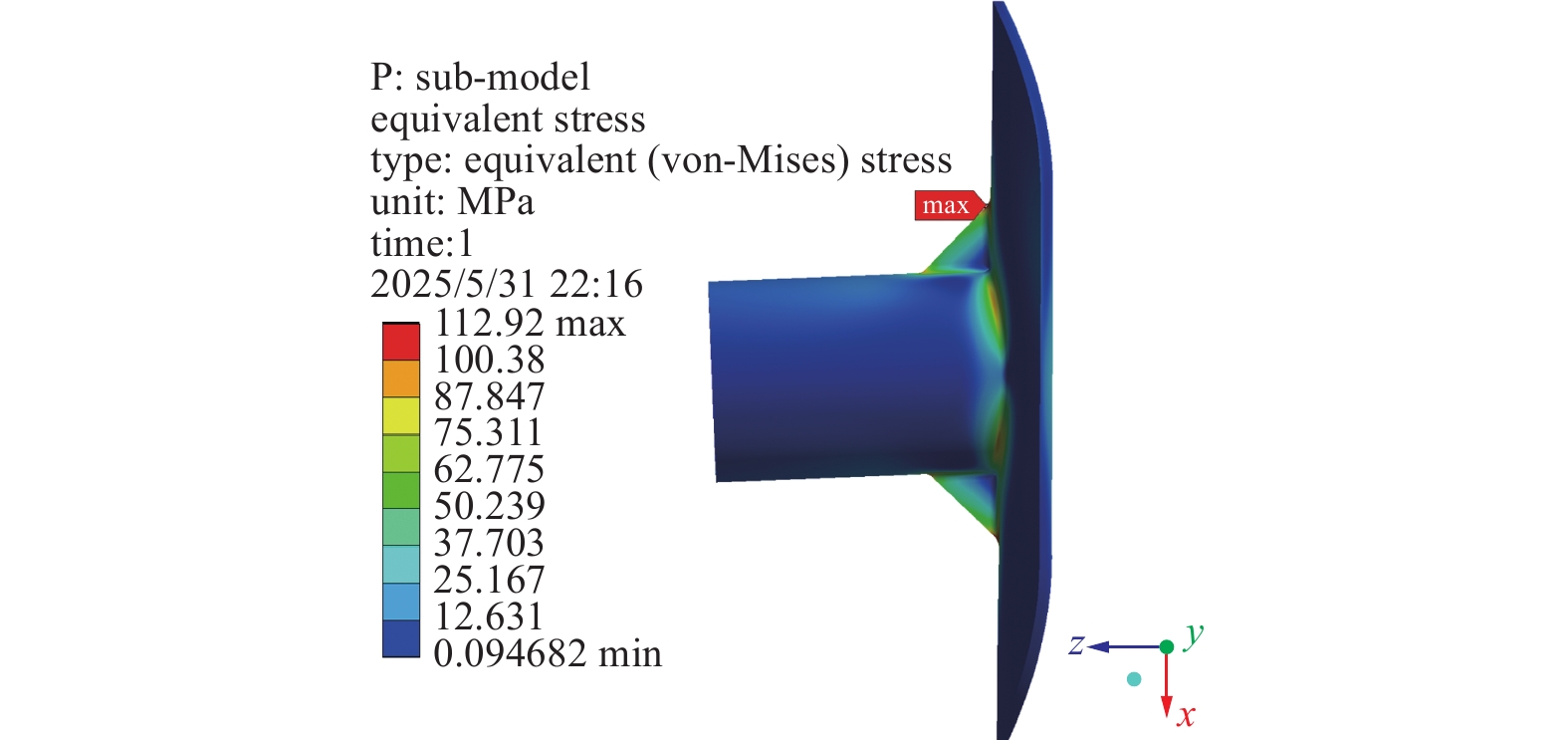
本文选用表1中单元尺寸为1 mm这一中等网格尺寸的仿真结果作为子模型的边界条件，随后对单元尺寸为0.5 mm和0.25 mm的长真空管的根部子模型进行精细化仿真，其网格划分质量与仿真结果如表2所示。从表2可以看出，所求应力结果与表1中的结果相差不大，但运算时长明显下降。图4展示了子模型的几何边界及应力云图，该区域的应力仿真结果与图2相比基本保持一致。由此可见，合理应用子模型技术，可实现计算精度与计算效率的完美平衡。因此，在本文后续的优化设计中，将采用全局模型先计算变形量，而后使用子模型技术求解局部应力，以便快速实现对不同优化方案的精确仿真。

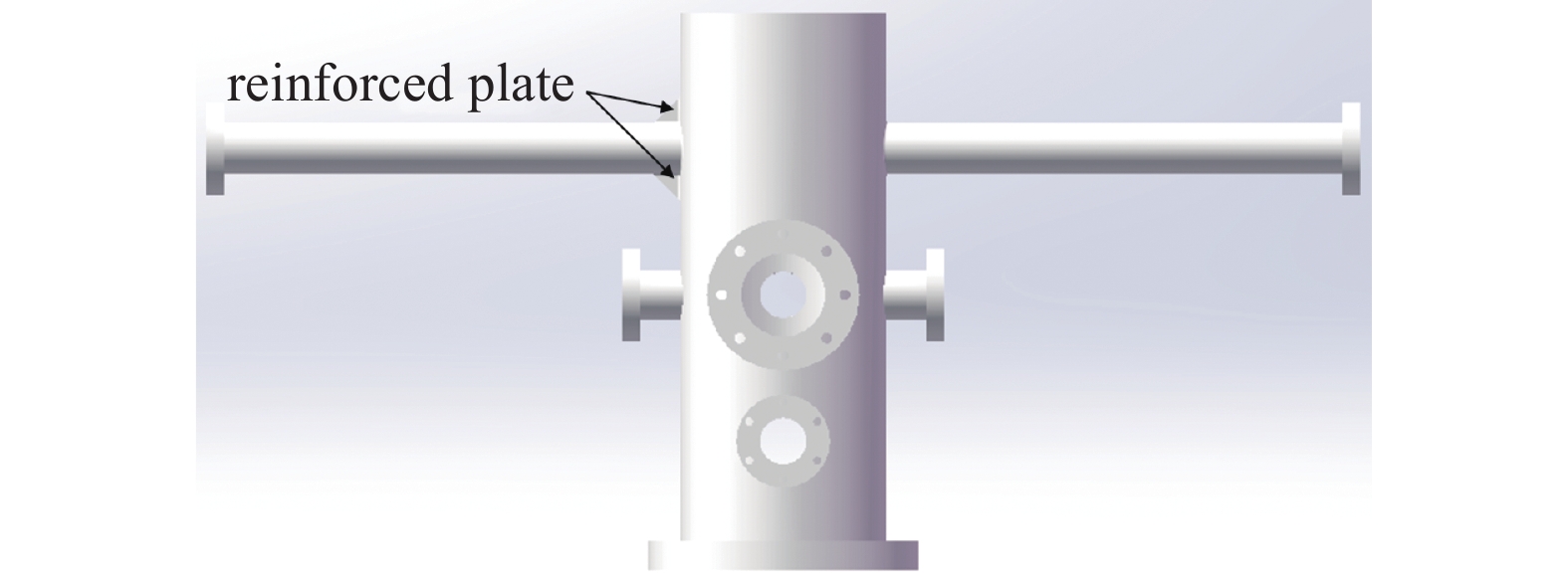
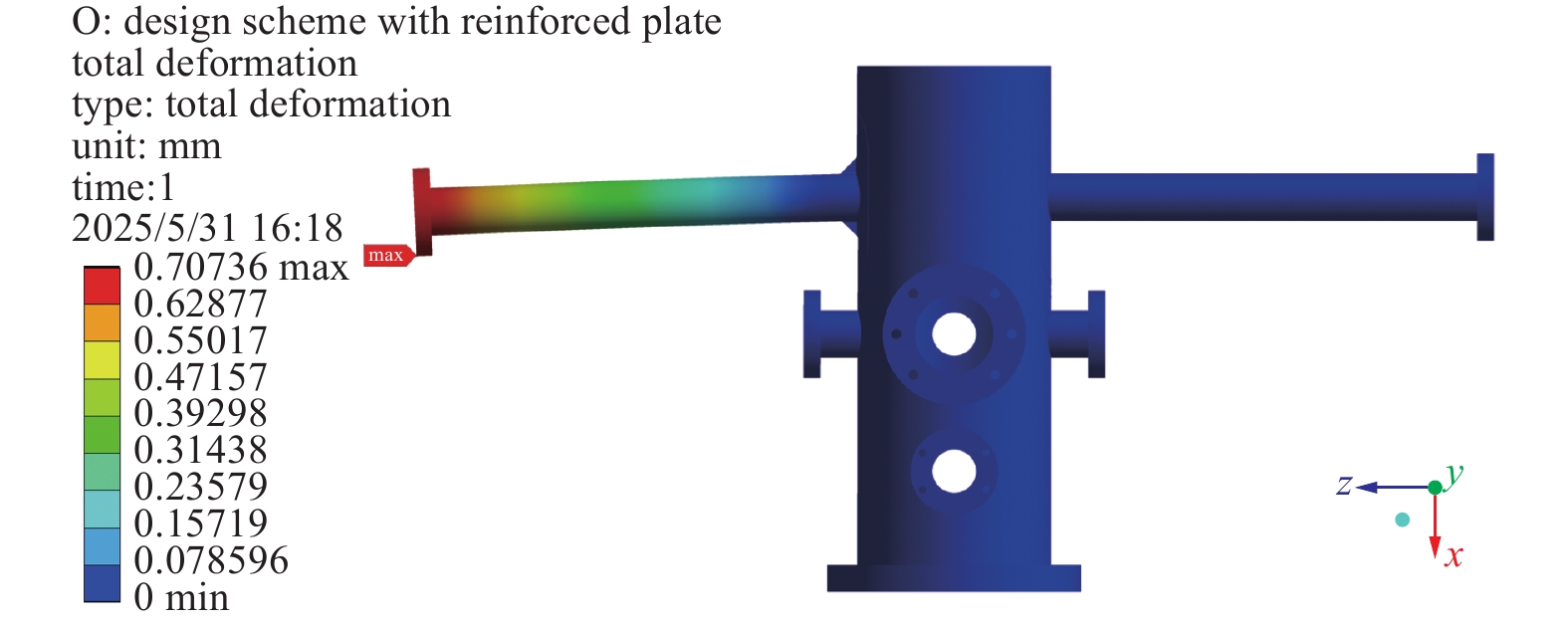
为了解决悬挂法拉第筒一侧长真空管的变形量超限与应力集中问题，决定在此长管根部位置处焊接补强板（如图5所示），以便对此处进行局部补强。在设计方案改进时，需要综合考虑结构安全性与轻量化要求：一方面要降低悬臂圆管的最大应力和变形量，另一方面需控制泵站整体质量的增长幅度。补强板的高度$ {P_1} $、长度$ {P_2} $、半厚度$ {P_3} $分别设计为15 mm，15 mm和1 mm，上下两块补强板大小相等且呈对称分布。对上述改进方案开展仿真分析，采用全局模型计算变形量，利用子模型技术求解局部应力，其变形云图和等效应力云图分别如图6和图7所示。

查看仿真结果发现，由于补强板尺寸取值偏小，泵站总体质量只增加了大约0.03%，因此可认为其质量基本保持不变。虽然实现了结构轻量化的目标，但存在以下关键问题：首先，悬臂圆管法兰口处的最大变形量为0.70736 mm，超出了0.706 mm的设计限值；其次，悬臂圆管根部的最大等效应力为112.92 MPa，仅略低于材料137 MPa的许用应力，安全裕度不足，因此该改进方案在给定载荷工况下仍无法拥有足够的安全性，需要进一步调整补强板的设计参数。然而，针对最大变形量、最大等效应力和泵站质量这三个优化目标，若采用传统的人工调试方法获取最佳设计参数，一方面效率低下且带有较强的主观性，另一方面难以同时兼顾各项优化指标，因此无法在短时间内找到既能有效提升结构刚度和强度，又能合理控制泵站质量的最佳方案。相比之下，多目标优化设计方法通过系统化的参数寻优，可以科学高效地确定最优参数组合，实现安全性与轻量化之间的平衡。

多目标优化设计的总体思路为：以补强板的几何参数为设计变量，以泵站质量、最大变形量和最大应力值为优化目标，采用中心复合设计和参数化仿真获得试验样本空间，建立Kriging模型并进行响应面分析，利用MOGA算法求得Pareto最优解，最后对优选方案进行仿真验证。

根据改进方案的结构特点，以补强板的高度$ {P_1} $、长度$ {P_2} $、半厚度$ {P_3} $作为设计变量$ x $，分别设定其参数变化范围（为减少计算量，上下两块补强板对称分布，对称处的结构参数设置为相同尺寸）；选取真空泵站的最大变形量$ {\delta _{\max }} $、最大应力值$ {\sigma _{\max }} $和质量$ M $作为优化目标；以最大变形量$ {\delta _{\max }} $不超过0.706 mm，最大应力值$ {\sigma _{\max }} $不超过80 MPa作为优化目标约束条件；在保证真空泵站的强度、刚度满足要求的前提下实现轻量化设计。建立真空泵站多目标优化数学模型如下：

中心复合设计（Central Composite Design，CCD ）是最常见的响应面试验设计方法之一，该方法可有效预估因素的主效应、交互作用以及二次效应。在仿真软件中设置补强板各设计变量的取值范围，选用可旋转型中心复合设计方式以保证不同方向上预测精度的一致性，软件会在各设计变量所限定的取值范围内自动生成15个试验样本点。对这些样本点进行参数化建模和仿真迭代求解，利用整体模型求解真空泵站的变形量和质量，利用子模型技术求解补强板处的等效应力，15个样本点及其仿真结果如表3所示。

响应面法（RSM）是一种基于统计学的优化方法，其利用有限的试验数据，通过构建数学代理模型近似表达复杂系统的输入与输出关系，从而预测系统的性能。Kriging代理模型是一种基于随机过程理论的多维插值求解方法，能够同时兼顾全局和局部的共同影响因素，该方法可以显著提升拟合精度，尤其是处理高度非线性优化问题时表现出色。因此，Kriging模型被广泛应用于结构优化设计、材料性能预测等领域。由于Kriging模型是一种近似模型，因此必须对其拟合优度进行评价。Kriging模型的拟合度通常用决定系数$ {R^2} $来判断：

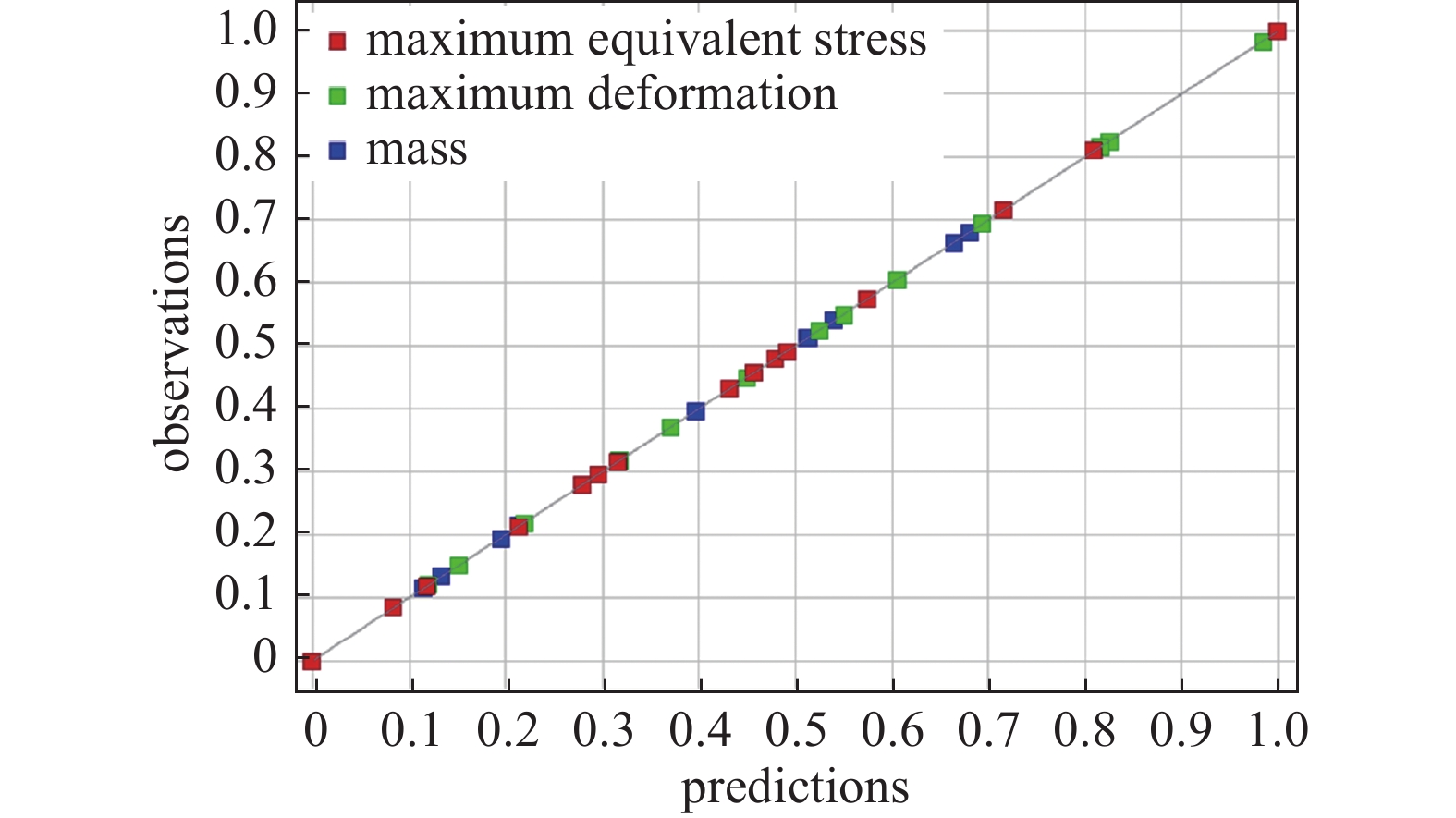
式中，$ {y_i} $是样本点的真实值；$ {\hat y_i} $是响应面模型对样本点的预测值；$ {\bar y_i} $是样本点真实值的平均值。$ {R^2} $越接近于1，说明所构建的响应面函数与设计变量之间的规律拟合得越精确。如果响应面模型达不到预设精度的要求，需要增加试验次数或更换响应面模型来提升响应面拟合的准确性。

求解得到Kriging响应面模型的拟合优度如表4所示。从表中可知， 3个优化目标的响应面拟合度均为1，表明King模型的拟合准确度已达到最优。

Kriging模型的归一化拟合曲线如图8所示。在归一化拟合曲线中，真实值与预测值越接近，即两者越接近45°对角线，响应面模型的拟合效果越准确。从图中可以看出，泵站质量、最大变形量和最大等效应力所对应的点均分布在45°对角线上，表明样本点的真实值与响应面的预测值之间的拟合精度良好，预测准确度高，因此通过Kriging模型得到的响应面符合优化设计需求。

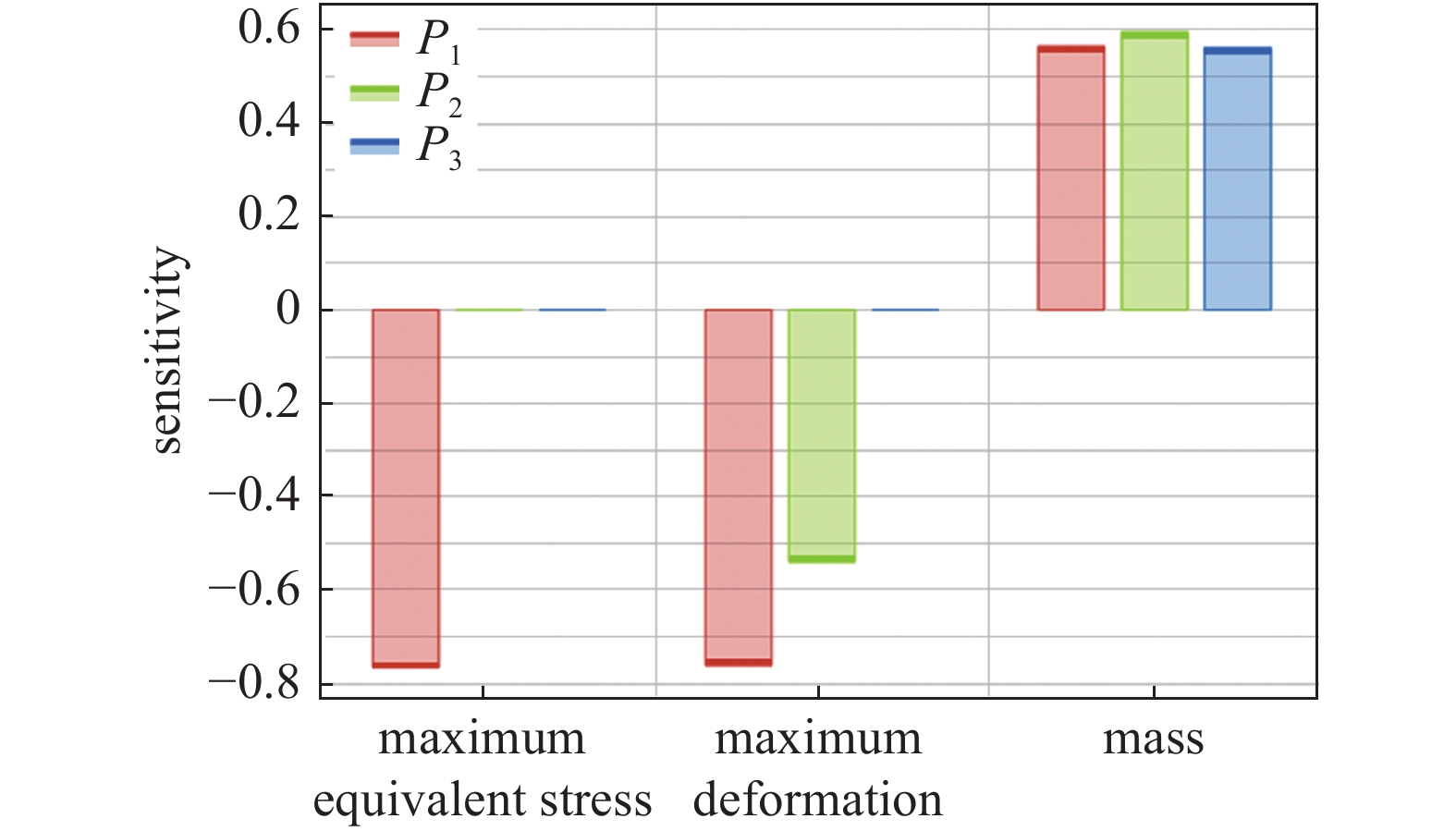
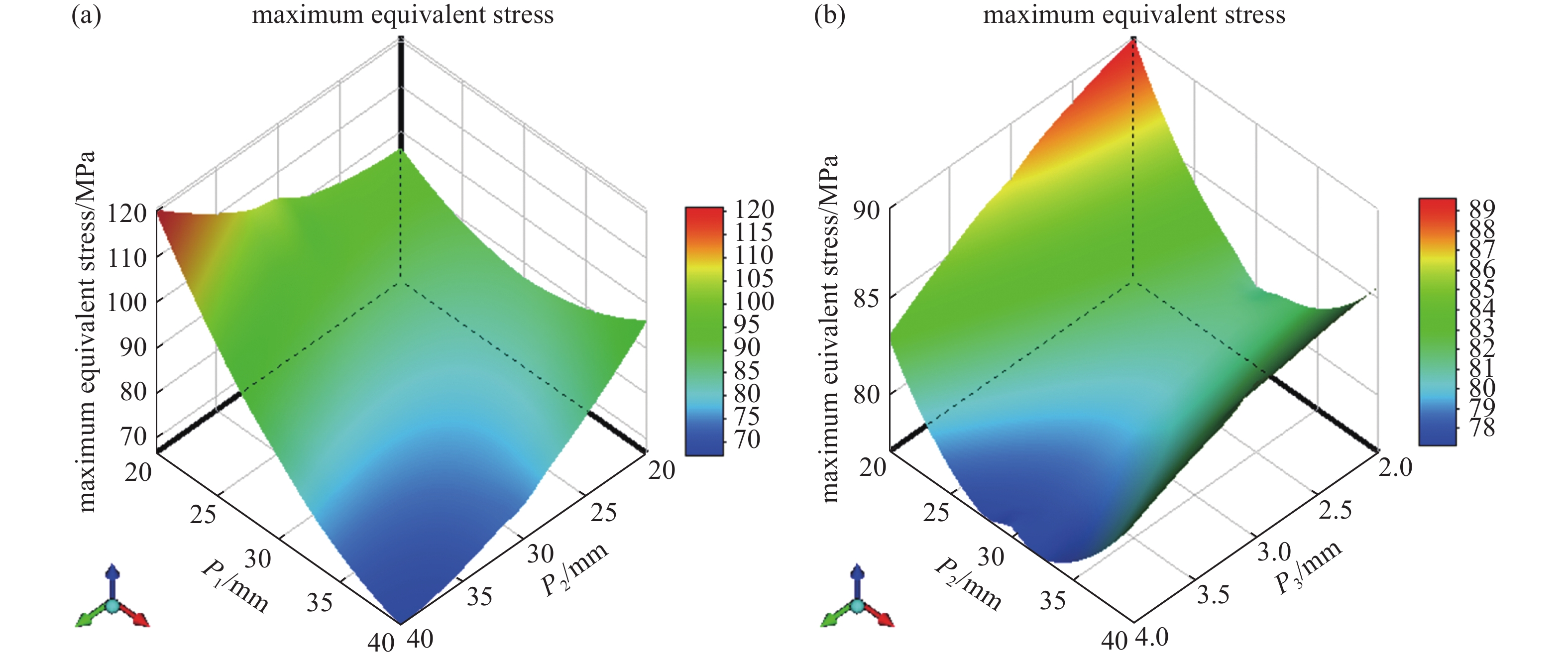
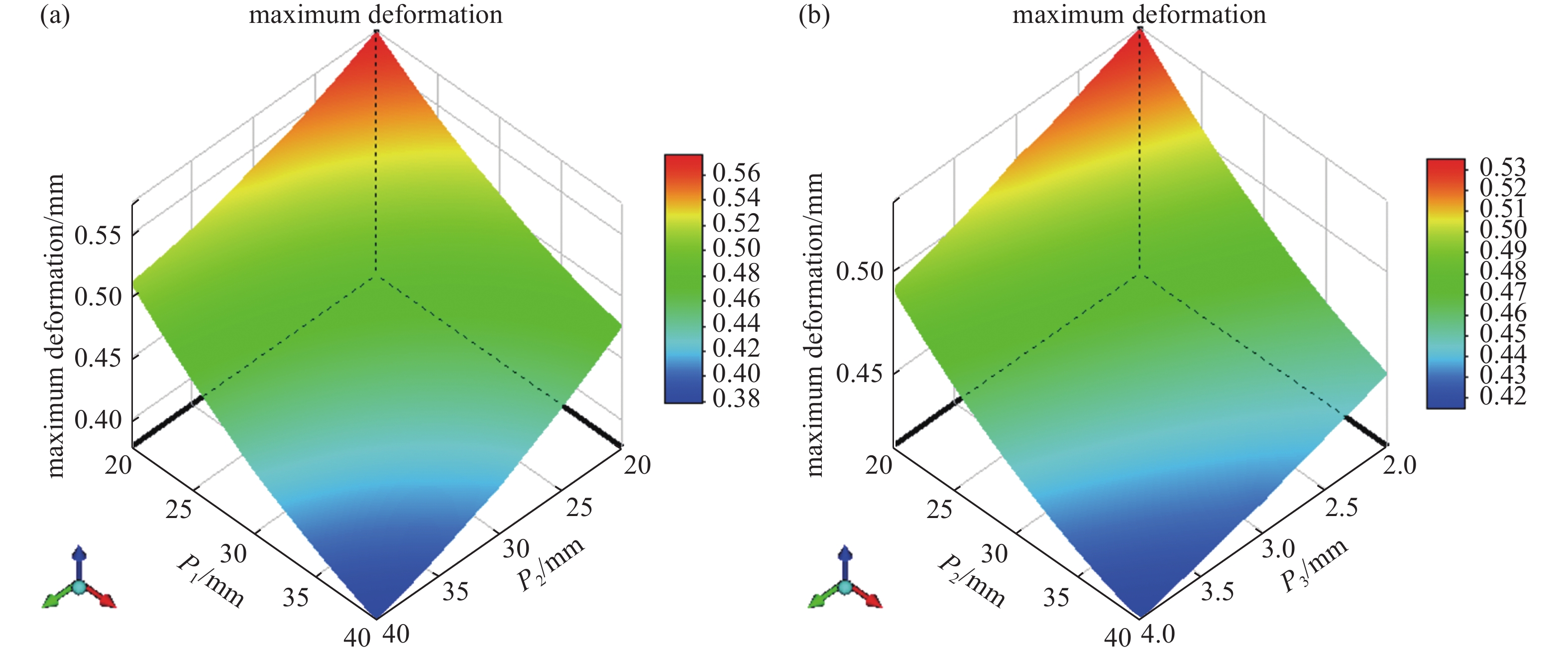
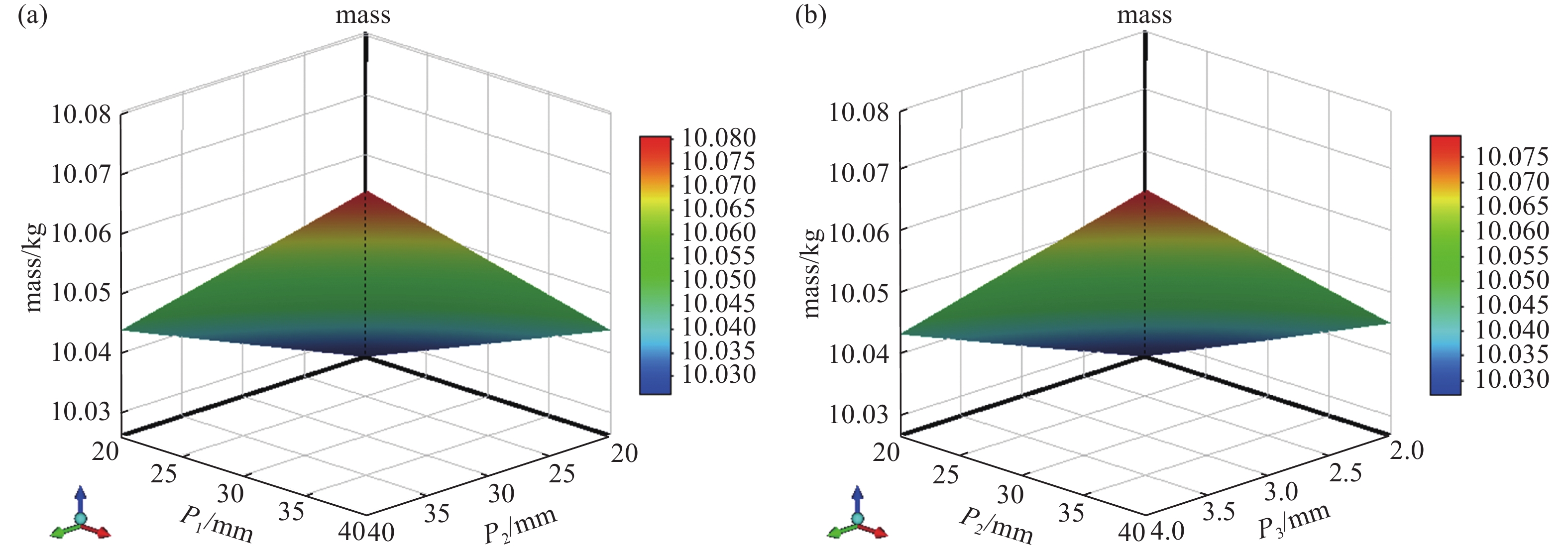
敏感性分析是一种用于评估响应面模型中优化目标对设计变量的敏感程度的方法。在结构优化中，敏感性可有效反映样本拟合后响应面模型的设计变量对于优化目标的影响程度，该值的正负代表设计变量与优化目标的正负相关性。通过敏感性分析，可有效识别出对优化目标影响程度较大的设计变量，为结构优化提供参考。图9展示了补强板3个设计变量对于真空泵站3个优化目标的敏感性。从图中可看出，补强板高度$ {P_1} $对最大等效应力的影响十分明显，且呈负相关；补强板高度$ {P_1} $和长度$ {P_2} $对最大变形量的影响较大，并且这两个变量均与最大变形量呈负相关；补强板的高度$ {P_1} $、长度$ {P_2} $、半厚度$ {P_3} $对质量的影响相对均衡，且均为正相关。

基于Kriging模型，绘制设计变量对优化目标的3D响应面如图10、11、12所示；从图10可看出，补强板的高度$ {P_1} $、长度$ {P_2} $、半厚度$ {P_3} $这3个设计变量与最大等效应力呈非线性关系，且最大应力值的变化比较剧烈。从图11可发现，最大变形量与设计变量之间呈现近似线性关系，并且随着设计变量的增大，最大变形量不断降低。从图12可知，真空泵站的质量随着3个设计变量的增加呈线性增长趋势。由于随着设计变量的增加，最大变形量与几何质量呈相反变化趋势，因此不存在一组设计变量能使真空泵站的3个优化目标同时达到最小，故寻找最优设计变量组合实际上是寻找真空泵站多个优化目标之间的最佳平衡点。

多目标优化问题的求解方法可分为归一化方法和非归一化方法两类。以加权法为代表的归一化方法，通过将多目标函数转化为单目标函数进行求解；然而，加权法在目标权重的分配时，往往受到优化决策者主观判断的影响。相比之下，多目标遗传算法（Multi-objective Genetic Algorithm，MOGA）作为非归一化方法中的典型代表，通过非支配排序（Non-Dominated Sorting）算法和多样性保持策略，生成分布均匀的Pareto前沿。Pareto前沿是全部 Pareto最优解的集合，在多目标优化问题中，由于目标之间相互冲突，无法通过调整设计变量使所有目标同时达到最优，因此Pareto前沿上的最优解实际代表的是不同目标间的最佳平衡点。

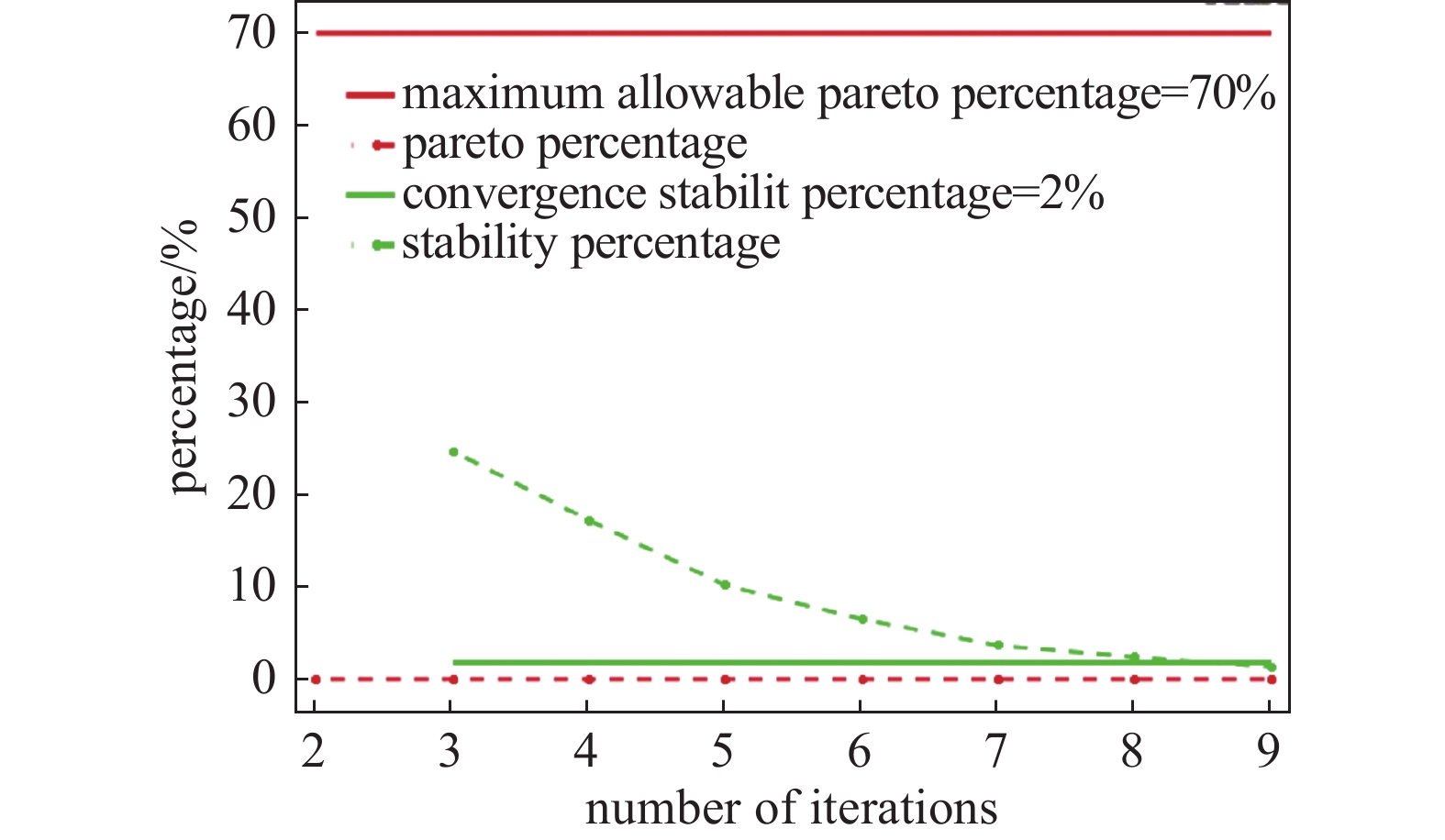
本文将泵站质量、最大变形量、最大等效应力作为优化目标，利用多目标遗传算法（MOGA）进行优化求解。此算法的详细参数设置如表5所示，经过9次迭代7136次评估后基本达到收敛，MOGA优化算法收敛曲线如图13所示。从最优Pareto解集中选出的3组候选点如表6所示。通过观察表6中的数据，3个候选点的参数值比较接近，结合工程实际对于参数尺寸进行圆整，最优设计参数组合$ {P_1} $、$ {P_2} $和$ {P_3} $最终选定为33 mm，29 mm和2 mm。

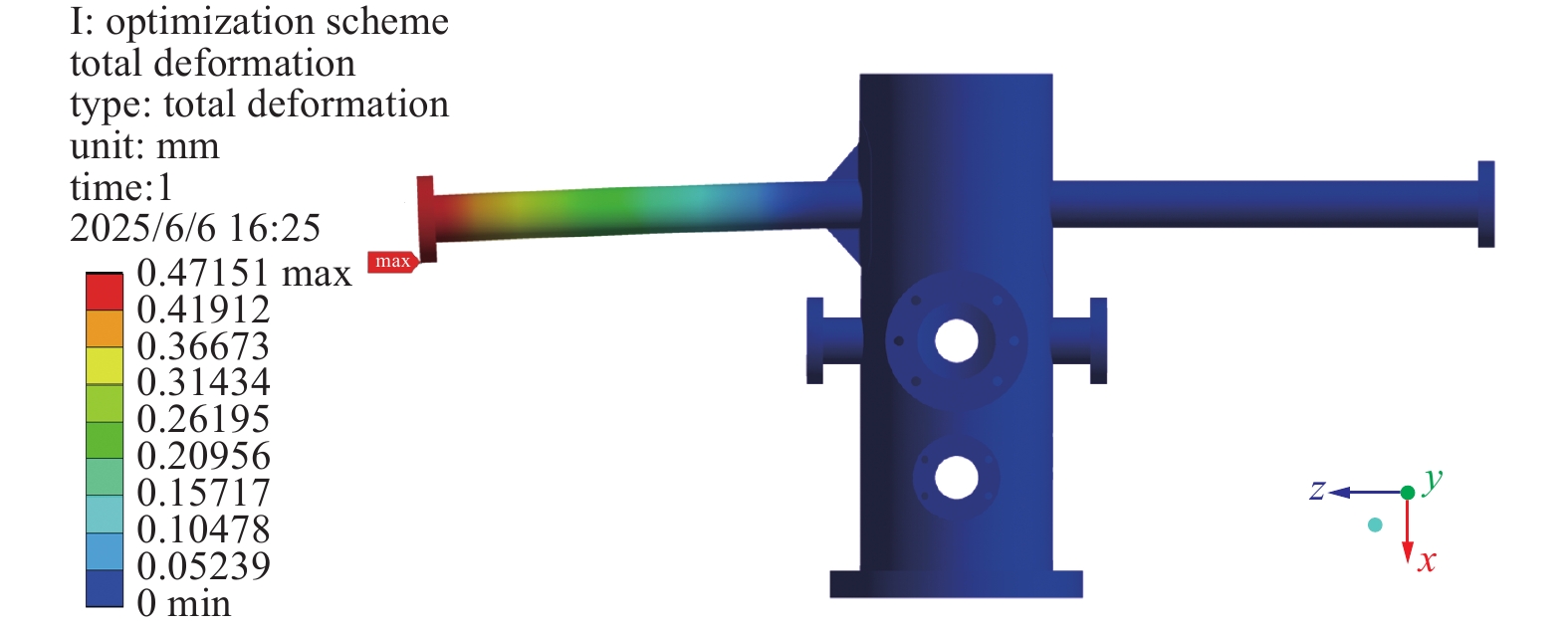
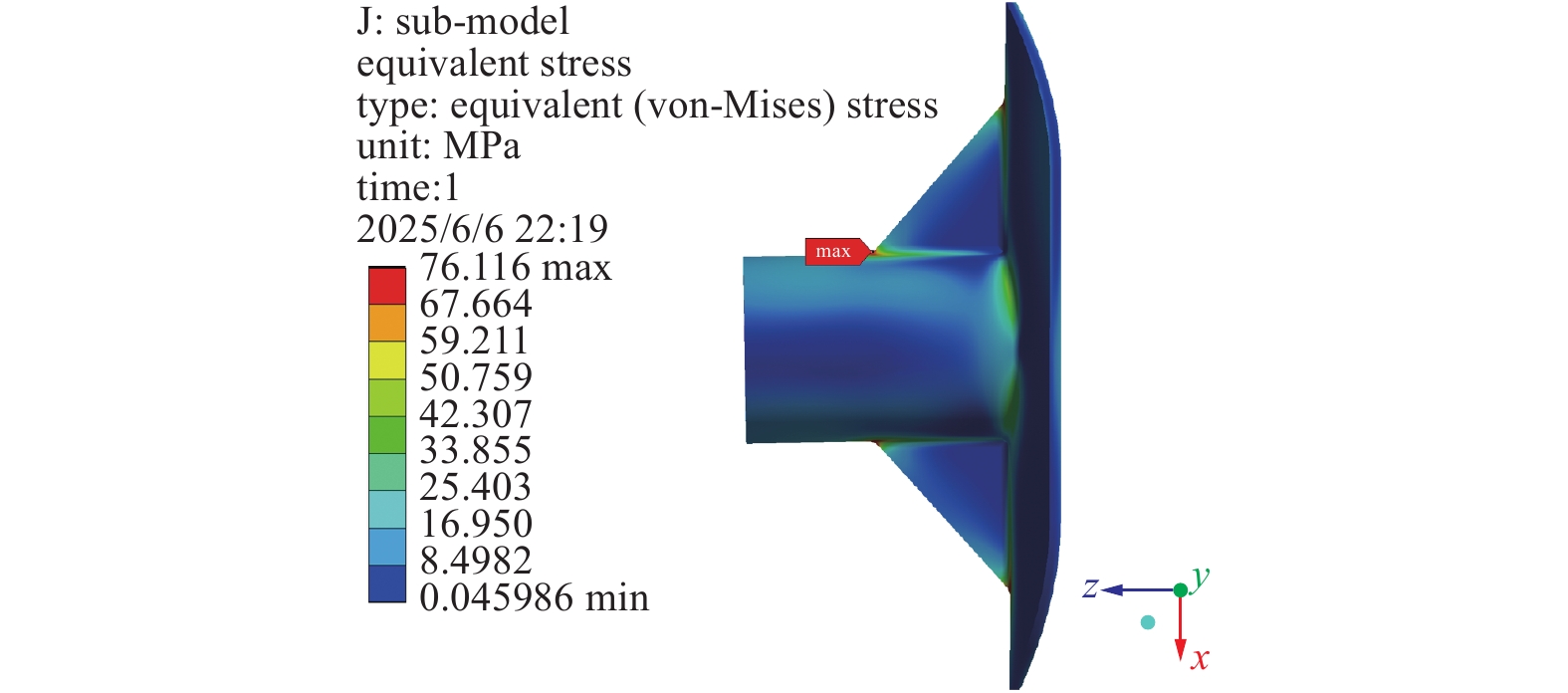
为了验证圆整后所确定的最优设计方案的可行性，还需根据圆整后的优化方案建立相应的三维模型并开展静力学仿真校核。优化后的真空泵站其变形云图及补强板区域的应力云图分别如图14、15所示，优化前后的设计参数和仿真结果列于表7。结合仿真结果对比分析，优化后真空泵站的结构性能得到了显著改善：最大等效应力降低至76.116 MPa，最大变形量减小至0.47151 mm，较优化前分别降低了32.59%和33.34%，有效提升了结构的安全性；同时，泵站质量仅增加了0.25%，满足了轻量化的设计要求。优化结果也表明，综合了参数化建模、试验设计、响应面分析和MOGA算法的多目标优化方法，可以通过科学计算快速获取最优参数组合，实现安全性与轻量化之间的平衡，有效提升了真空腔体的综合性能，这也为加速器领域类似腔体的设计与优化工作提供可靠的理论依据。

本文基于静力学仿真和子模型技术，对真空泵站设计方案进行仿真分析并提出优化方案。为获得补强板各设计参数的最优组合，通过中心复合设计方法和参数化仿真获得试验样本空间，建立Kriging模型并进行响应面分析，采用MOGA算法求得Pareto最优解，最后对优选方案进行仿真验证。结果表明：优化后的真空泵站其最大等效应力为76.116 MPa，最大变形量为0.47151 mm，而泵站质量相比优化前仅增加了0.25%。最终的优化方案既有效提升了结构的安全性，又满足了轻量化的设计要求，实现了安全性与轻量化之间的平衡。本文研究内容也证明了多目标优化设计方法的科学性和可行性，该方法可为真空腔体的设计优化提供理论依据和技术参考，在加速器领域具有广阔的应用前景。