近年来, 双层镍酸盐材料La₃Ni₂O₇在高压条件下(>14 GPa)展现出约80 K的超导转变温度($ T_{\mathrm{c}} $)^[1], 引起了凝聚态物理领域的广泛关注^[2]. 与铜基或无限层镍基超导体相比, La₃Ni₂O₇具有本征的多层耦合与多轨道电子结构, 可能蕴含更丰富的电子关联行为与配对机制. 铜基超导体与无限层镍酸盐中, Cu/Ni离子为$ 3 {\mathrm{d}}^9 $构型, 构成准二维的CuO₂/NiO₂平面, 且其费米面附近的低能电子态主要由单一的$ 3 {\mathrm{d}}_{x^2-y^2} $轨道贡献^[3–5]. 相比之下, La₃Ni₂O₇中的Ni离子呈现名义上为+2.5($ 3 {\mathrm{d}}^{7.5} $)的价态, 其低能电子态同时涉及部分占据的$ 3 {\mathrm{d}}_{x^2-y^2} $与$ 3 {\mathrm{d}}_{3 z^2-r^2} $轨道, 展现出明显的多轨道特征^[1,6]. 此外, 该材料中双层NiO₆八面体通过内层顶点氧相连, 氧的$ 2{\mathrm{ p}}_z $轨道与Ni的$ 3 {\mathrm{d}}_{3 z^2-r^2} $轨道发生强烈的σ型杂化, 形成具有显著层间耦合特性的电子结构. 这种多层耦合不仅改变了费米面的拓扑结构, 也引入了比铜基和无限层镍基体系更复杂的轨道自由度与空间维度. 深入理解这一多层耦合的多轨道电子结构对揭示La₃Ni₂O₇的电子行为并探索其非常规超导机制具有重要意义. 目前, 已有大量理论研究聚焦于La₃Ni₂O₇中低能轨道的电子关联与超导配对机制^[7–28], 并根据不同的模型构建及关联强度提出基于γ带的${\mathrm{ s}}^{\pm} $波配对^[17–21]或α, β带的d波或$ {\mathrm{d+is}} $波配对^[22–25].

另一方面, 在铜基^[4,29] 和无限层镍基^[30–32] 等强关联超导体中, 电荷密度波(CDW)和/或自旋密度波(SDW)等短程有序态常与超导态共存, 并在特定参数区间内呈现出明显的竞争关系. 在La₃Ni₂O₇早期的输运实验中^[33–36], 其电阻-温度曲线曾显示出明显的拐点行为, 可能与CDW或SDW序的形成有关. 光电导率测量也观察到该体系在低温下存在部分能隙打开的现象, 或与密度波序相关^[37]. 近期, 多项实验研究进一步为La₃Ni₂O₇中密度波序的存在提供了更为直接的证据^[38]. 核磁共振(NMR)测量在不同样品中分别观测到明确的SDW序^[39]以及CDW与SDW混合态的迹象^[40]; 缪子自旋弛豫($ \mu^+ $SR)实验亦证实, 氧含量略低的La₃Ni₂O_6.92样品在常压下可形成SDW序^[41]; 共振非弹性X射线散射(RIXS)则探测到动量为$ (\pi/2, \pi/2) $的准二维SDW序, 进一步支持密度波有序态的存在^[42]. 这些密度波序对外部压力高度敏感. 输运实验中, 与密度波相关的拐点结构在高压条件下显著减弱甚至完全消失^[1,43,44], 表明高压可能通过有效抑制这些竞争性有序态为La₃Ni₂O₇高温超导态的稳定提供关键的物理环境.

目前, 关于La₃Ni₂O₇中密度波序的理论研究仍处于初步阶段. 早期工作提出, 费米面嵌套可能导致CDW的形成^[34]. 随后, 多项基于第一性原理与关联效应的计算指出, La₃Ni₂O₇体系的磁化率在特定波矢附近增强, 暗示可能形成SDW或CDW^{[13,18,21,45,46]}. 基于完整Ni-3d和O-2p轨道的关联模型的研究进一步表明, La₃Ni₂O₇中可能存在周期为2、源于高价态Ni氧化物中大量氧空穴短程涨落的CDW, 且在高压与掺杂条件下受到 抑制^[47]. 在对O-2p自由度进行积分、仅保留Ni-$ {\mathrm{d}}_{x^2-y^2} $和$ {\mathrm{d}}_{3 z^2-r^2} $轨道的低能有效模型中, 研究表明非局域库仑作用对CDW形成具有关键作用^[20]: 约束随机相位近似(cRPA)计算也证实了La₃Ni₂O₇中存在显著的非局域库仑相互作用, 基于此的EDMFT计算进一步揭示了体系中周期为2的CDW^[8]. 然而, 目前对于CDW形成对非局域相互作用依赖性的理解仍缺乏系统性的探讨. 基于上述背景, 本工作在密度泛函理论与动力学平均场理论(DFT+ DMFT)框架下, 结合Hartree平均场处理显著的非局域库仑相互作用, 系统考察了非局域库仑相互作用对La₃Ni₂O₇中可能存在的电荷序行为的影响. 特别地, 区别于此前DMFT研究中普遍采用的量子蒙特卡罗(QMC)杂质求解器, 本工作构建了基于矩阵乘积态(MPS)结合密度矩阵重整化群(DMRG)^[48]与含时变分原理(TDVP)^[49,50]方法的高效杂质求解器. 结合杂质模型的自然轨道基矢表示^[51-54], 该方法能够高精度地获取实频谱函数, 为后续相关谱学实验提供可靠的理论参考.

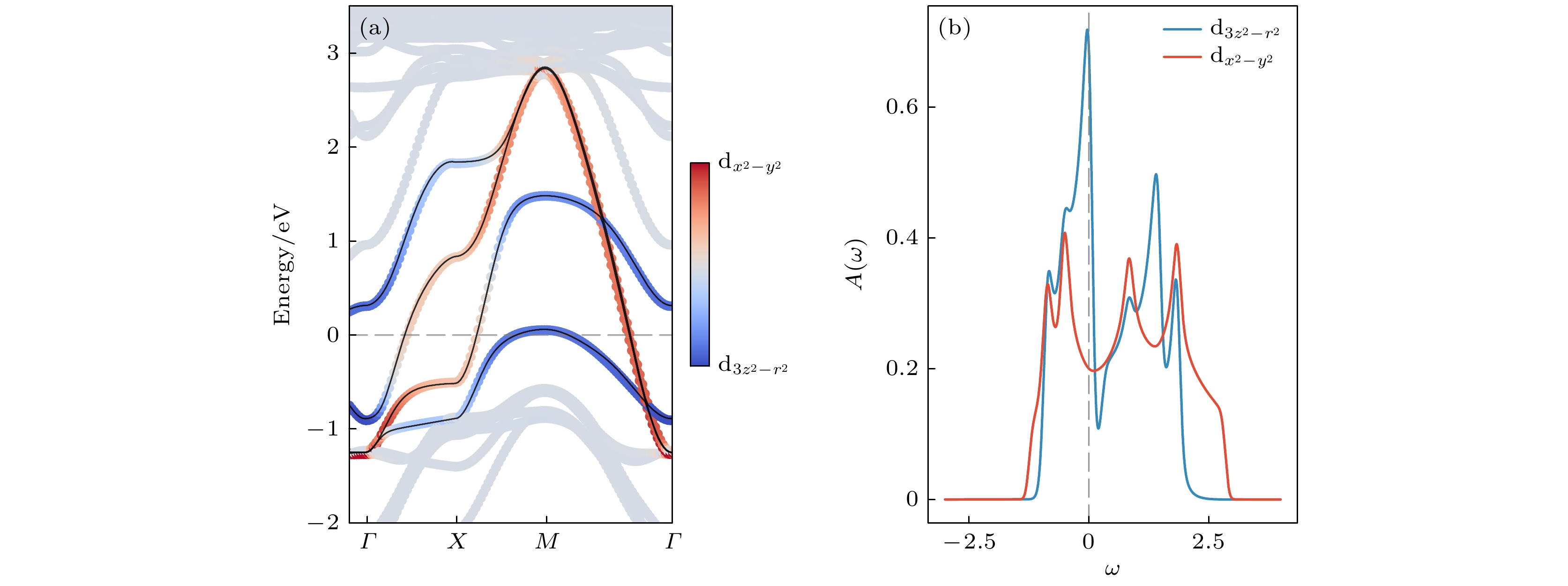
首先, 我们采用VASP程序^[55]对La₃Ni₂O₇在$ P = 20.0 $ GPa下的高对称结构$ I4/mmm $相进行DFT计算. 计算过程中采用PBE(Perdew-Burke-Ernzerhof)交换-关联泛函^[56], 平面波能量截断设置为520 eV, 结构弛豫采用以Γ点为中心的$ 13 \times 13 \times 3 $的k网格, 原子受力和总能量的收敛标准分别为0.001 eV/Å和$ 10^{-6} $ eV. 图1(a)展示了DFT计算得到的能带图. 与文献[1, 6–8, 10, 11, 18, 20]研究一致, 在费米能级$ E_{\mathrm{F}} $附近分布的4条能带主要来源于原胞内两个Ni原子的$ {\mathrm{d}}_{x^2 - y^2} $与$ {\mathrm{d}}_{3 z^2 - r^2} $轨道, 总电子占据数为3/8. 从轨道分布特性定性分析, ${\mathrm{ d}}_{x^2 - y^2} $轨道在晶体面内延展, 层间耦合较弱, 形成两条近似简并的能带(在M-Γ路径上严格简并), 且带宽较大. 而$ {\mathrm{d}}_{3 z^2 - r^2} $轨道则沿垂直方向延展, 与内顶点氧离子的$ 2 {\mathrm{p}}_z $轨道发生强烈σ键杂化, 形成能量劈裂约为1.5 eV的成键与反成键态. 进一步的轨道杂化使这对劈裂态在费米面上下形成带宽相对较窄、由$ {\mathrm{d}}_{3 z^2 - r^2} $轨道主导的能带. 在原子极限近似下, 低能的$ {\mathrm{d}}_{3 z^2 - r^2} $成键轨道被完全占据, 对应$ {\mathrm{d}}_{3 z^2 - r^2} $轨道的1/2填充, 而$ {\mathrm{d}}_{x^2 - y^2} $轨道则保留约1/4填充.

为了进一步刻画La₃Ni₂O₇中多轨道电子关联行为, 我们基于原胞中双层上下两个Ni原子的$ {\mathrm{d}}_{x^2 - y^2} $与$ {\mathrm{d}}_{3 z^2 - r^2} $轨道构建四轨道紧束缚模型, 并在此基础上开展DMFT计算. 利用Wannier90软件^[57]生成最大局域化Wannier轨道^[58,59], 构建得到的紧束缚模型能带与原始DFT结果高度一致, 如图1(a)所示. 该模型计算得到的态密度分布如图1(b)所示, 其中每个Ni上$ {\mathrm{d}}_{x^2 - y^2} $与$ {\mathrm{d}}_{3 z^2 - r^2} $轨道的占据分别为0.32与0.43, 受轨道杂化与能带展宽影响, 略微偏离前述原子极限下1/4与1/2的定性预期. 为得到该模型下的库仑相互作用参数进行了cRPA^[60]计算, 使用以Γ点为中心的$ 5 \times 5 \times 5 $的k网格并考虑能量上限59 eV的未占据态以计算极化函数, 得到有效Kanamori型的旋转不变的库仑相互作用参数$ U=3.4 $ eV以及$ J=0.6 $ eV. 值得注意的是, 可能由于La₃Ni₂O₇准二维电子结构中较弱的电荷屏蔽效应, cRPA计算还显示其存在显著的最近邻Ni原子间的库仑相互作用, 平均为$ V=0.7 $ eV, 与文献[8]报道的结果相当. 在后续计算中, 我们将V作为可调参数, 系统研究其对La₃Ni₂O₇关联电子结构的影响.

我们考虑如下形式的相互作用哈密顿量:

其中, $ H_0 $表示在2.1节中构建的四轨道紧束缚模型, $ H_{\mathrm{U}} $是每个Ni格点上旋转不变的Kanamori型局域库仑相互作用项. 非局域库仑相互作用项$ H_{\mathrm{V}} $的具体形式为

其中$ \hat n_{i\sigma} $为格点i上自旋为σ的总电子数算符, $ \langle ij \rangle $表示在最近邻格点对之间求和, σ和$ \sigma' $表示自旋自由度. 为了简化讨论, 假设面内与面外最近邻Ni-Ni间的非局域库仑相互作用相同, 统一取为V.

在传统的DMFT框架内, 非局域相互作用无法被直接处理. 为此, 采用Hartree平均场的方法对该项进行处理. 由于La₃Ni₂O₇中的双层镍氧结构构成了标准的二分晶格, 两个子晶格(记为A, B)中每个Ni格点受到的平均场可表示为

其中$ z=5 $为每个格点的配位数. 引入上述平均场处理后, DMFT自洽循环作相应调整. 我们以无相互作用格林函数$ {\mathrm{G}}_0(\omega) $作为初始Weiss场$ {\cal{G}}(\omega) $开始自洽求解, 具体步骤如下.

1) 以给定的$ {\cal{G}}(\omega) $分别求解两个Ni原子的杂质模型. 通过DMRG求解得到基态$ |\psi_{0}^l \rangle $, 其中$ l \in (A, B) $. 谱函数通过TDVP计算两个含时格林函数得到:

其中τ集合了轨道与自旋自由度. 由此得到杂质格林函数:

及谱函数$ A^l_\tau(\omega) = -\dfrac{1}{\pi}{\rm{Im}} {\mathrm{G}}^{l}_{\tau}(\omega) $. 系统的总格林函数即为两个杂质格林函数的直和$ {\mathrm{G}}(\omega) = {\mathrm{G}}^{A}_{\tau}(\omega)\oplus {\mathrm{G}}^{B}_{\tau}(\omega) $. 由$ A(\omega) $可得到A, B两个子格点的占据数$ n_{l} =\displaystyle\sum\nolimits_{\tau}\displaystyle\int_{-\infty}^{\mu} {\mathrm{d}}\omega A^{l}_{\tau}(\omega) $, 以此获得格点间库仑相互作用平均场的自能:

2) 通过Dyson方程解得局域Kanamori相互作用的自能:

3) 通过自能与$ {\mathrm{G}}_0 $可得到新的局域格林函数:

其中我们需要寻找合适的化学势μ以保证总占据$ n_{\mathrm{A}} + n_{\mathrm{B}} = 3 $不变.

4) 由Dyson方程得到新的$ {\cal{G}}(\omega) $:

返回步骤1)开始新一轮的循环, 直至结果收敛.

需要注意的是, 在格林函数(4)式与(5)式的计算中, 系统的纠缠熵会随时间演化不断增长, 从而显著增加计算复杂度, 并限制对低频区域的计算精度. 为在保持高精度的同时提高计算效率, 本工作采用了复时间演化方法^[54]. 该方法通过在时间演化中引入部分的虚时分量将量子态投影至低能空间, 能够有效抑制系统纠缠增长, 从而降低准确描述时间演化态所需的键维度. 我们以复时间:

取代实时间t进行演化, 并可通过对$ \alpha_0 $的微扰展开得到实时间($ \alpha_0 = 0 $)的动态关联函数^[54]. 在本文的计算中, 以$ \alpha_0 = 0.2 $、步长$ {\mathrm{d}}t = 0.1 $ eV^–1计算至$ t = 20 $ eV^–1, 并结合线性预测方法外推至$ t = 80 $ eV^–1. DMFT自洽循环中采用的每轨道链长为$ N = 120 $, 最大键维度设为$ \chi_{{\rm{max}}} = 150 $. 在此设置下, DMRG与TDVP的总截断误差分别控制在$ \epsilon_{{\rm{DMRG}}} \sim 10^{-9} $与$ \epsilon_{{\rm{TDVP}}} \sim 10^{-8} $以内. 下文中所有能量单位均采用eV.

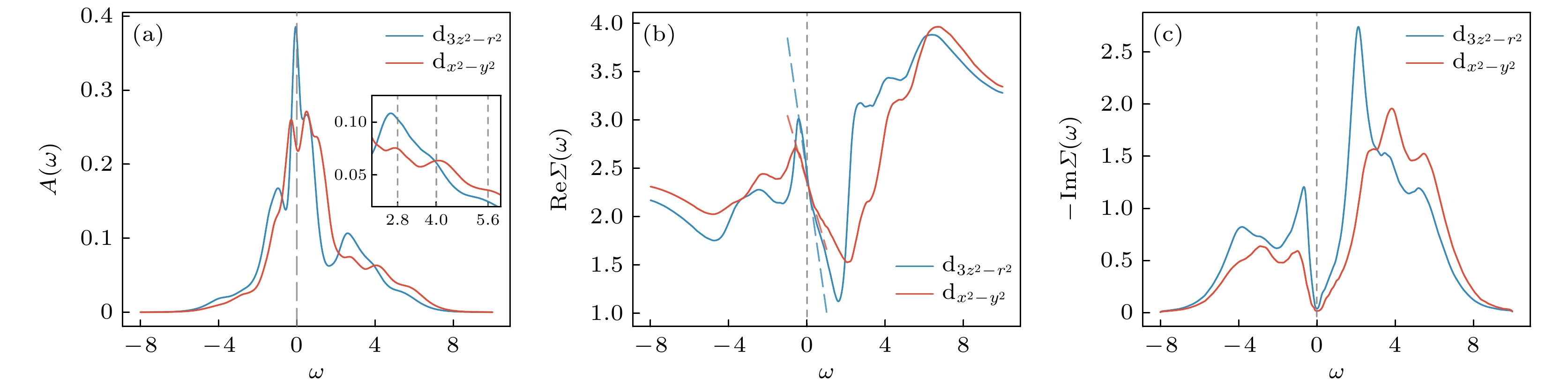
首先讨论$ V = 0 $的情况, 其谱函数如图2(a) 所示, 对应的轨道占据数分别为$ n_{3 z^2 - r^2} = 1.72 $和$ n_{x^2 - y^2} = 1.28 $. 相较于图1(b)中的态密度, 电子关联显著重整化了谱函数的特征结构. 费米能级附近的准粒子能量被压缩, $ {\mathrm{d}}_{3 z^2 - r^2} $轨道的范霍夫奇点变得更加尖锐. 而高能部分特征则因库仑散射而模糊化, 并在ω约为–1.0处与2.0以上出现了典型的Hubbard带. 值得注意的是, 两个轨道的上Hubbard带均显示出明显的多峰劈裂结构, 分别位于$ \omega \approx 2.8 $, 4.0, 5.6, 而这一多峰特征在此前基于虚频轴的DMFT计算中尚未被解析^[8,11,13]. 这些峰位高于无相互作用态密度中相应结构的能量, 表明其来源并非源于单粒子谱的重叠, 而是强关联效应的体现. 该结构可通过相应的原子物理模型加以理解. 对于总占据数为1.5的双轨道系统, 其局域电子排布主要由单占据态与双占据态的叠加构成. 忽略晶体场劈裂的影响, 将每个d轨道单占据时的能量设为$ \epsilon_{\mathrm{d}}=0 $. 在Kanamori相互作用下, 双占据态的能量分别为$ U - 3 J $(三重简并)、$ U - J $(二重简并)和$ U + J $(非简并). 以参数$ U = 3.4 $和$ J = 0.6 $为例, 对于初始为单占据的基态构型, 添加一个电子将激发至双占据态, 对应的激发能量分别为1.6, 2.8和4.0. 其中, 1.6处的激发峰由于能量较低, 与准粒子能带重叠, 可能不易分辨. 类似地, 对于初始为双占据的构型, 若再加入一个电子变为三占据态, 总能量为$ 3 U - 5 J $(四重简并). 相对于双占据基态$ U - 3 J $, 该激发过程的能量差为$ 2 U - 2 J $, 对应谱函数中约5.6处的高能激发峰. 这些能量与图2(a)中观察到的激发峰位置大致一致, 微小的偏差可归因于d电子的在位能$ \epsilon_{\mathrm{d}} $以及系统偏离原子极限所带来的修正. 上述原子极限下的分析同样适用于下Hubbard带的结构理解. 对于电子移除过程, 即从双占据基态激发至单占据态, 或从单占据态激发至空态, 相关激发过程均对应唯一的能量跃迁, 因此理论上不会产生类似上Hubbard带中的多峰劈裂结构. 仅当基态具备更高占据数(如三占据及以上)时, 才可能出现源于多重最终态的能级劈裂. 然而, 在平均占据数为1.5的体系中, 高占据组态所占的谱权重本就较低, 削弱了下Hubbard带中激发结构的可分辨性. 计算结果也未呈现出明显的多峰结构.

电子关联特征还可通过自能进一步揭示, 如图2(b), (c)所示. 在费米能级附近, 自能实部$ {\rm{Re}}\, \varSigma(\omega) $随ω呈线性变化, 虚部$ {\rm{Im}}\, \varSigma(\omega) $则呈现出对ω的平方依赖, 两者均展现出典型的费米液体行为. 根据自能实部的重整化因子计算结果:

$ Z_{{\mathrm{d}}_{3 z^2 - r^2}} \approx 0.41 $显著小于$ Z_{{\mathrm{d}}_{x^2 - y^2}} \approx 0.59 $, 表明前者受到更强的关联重整化. 相应地, 自能虚部显示, 在费米能级附近, $ {\mathrm{d}}_{3 z^2 - r^2} $轨道的准粒子激发寿命明显短于$ {\mathrm{d}}_{x^2 - y^2} $, 进一步反映出轨道间关联强度的差异. $ {\mathrm{d}}_{3 z^2 - r^2} $更强的关联效应一方面源于其轨道接近半填充状态, 另一方面则与其在费米能级附近的范霍夫奇点有关. 此前研究指出, 费米面附近的高态密度特征可显著增强局域电子关联效应^[61,62].

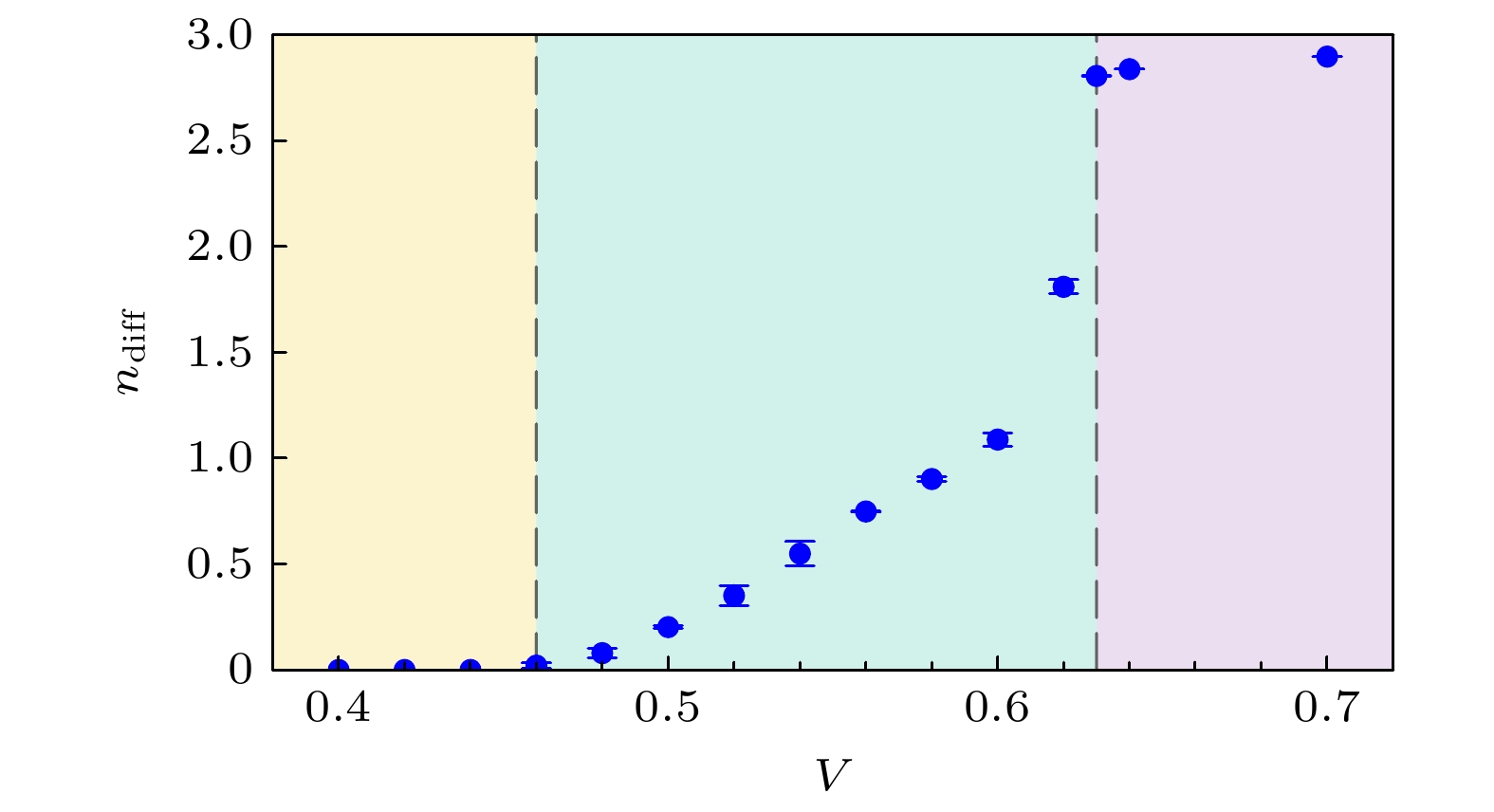
在讨论了$ V = 0 $情况下的关联电子结构之后, 我们进一步引入有限近邻库仑相互作用V, 以探究其对电子态的影响. 图3展示了A与B两个子格点间的密度极化随近邻库仑相互作用强度V的演化, 其中密度差定义为$ n_{{\rm{diff}}} = n_{A} - n_{B} $(以下默认A(B)为多数(少数)占据子格点, 即$ n_{A} \geqslant n_{B} $).

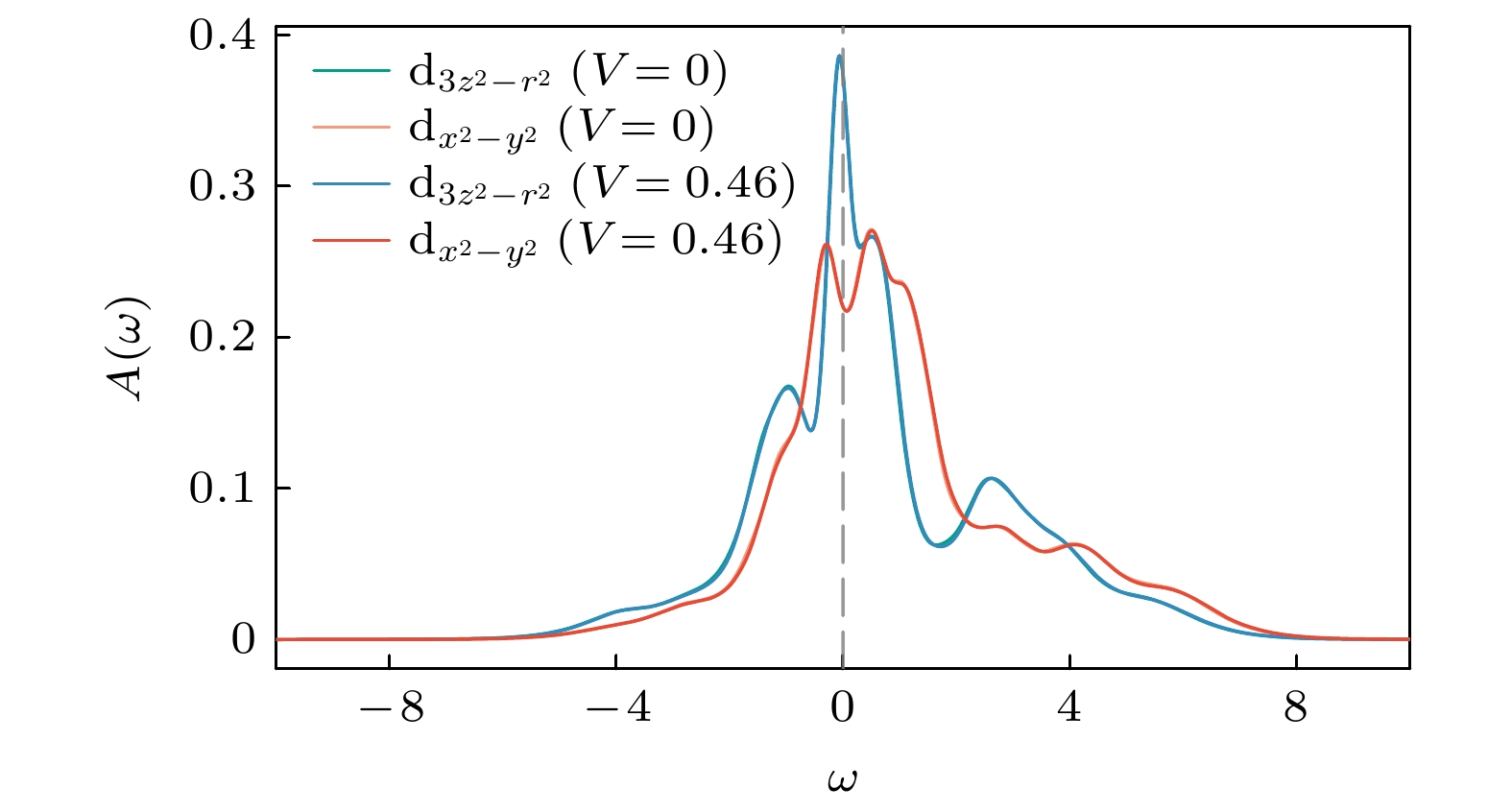
可以看出, $ n_{{\rm{diff}}} $随V的变化大致可分为3个阶段. 在较小的V区间($ V \leqslant V_{{\mathrm{c}}1} \approx 0.46 $)内, 体系对密度扰动表现出较强的鲁棒性, 子格点间对称性仍然保持, 局域谱函数与$ V = 0 $的结果在数值误差范围内一致(图4). 此时, 近邻库仑相互作用主要导致能带相对化学势的整体平移, 对电子关联性质影响甚微.

当$ V > V_{{\mathrm{c}}1} $时, 相邻格点之间交替的高低电荷密度分布所带来的V项能量增益, 超过了克服局域U排斥所需的能量, 从而引发体系电荷密度极化, 标志着电荷有序态的形成. 随着V的进一步增大, 极化程度单调增强, 最终在临界值$ V_{{\mathrm{c}}2} \approx 0.63 $处达到完全极化状态. 此时一个子格点几乎处于空态, 另一子格点的电子占据数约为3.0, 其轨道占据分别为$ n_{3 z^2 - r^2} = 1.65 $, $ n_{x^2 - y^2} = 1.35 $, 相比$ V = 0 $时两轨道的占据更为接近.

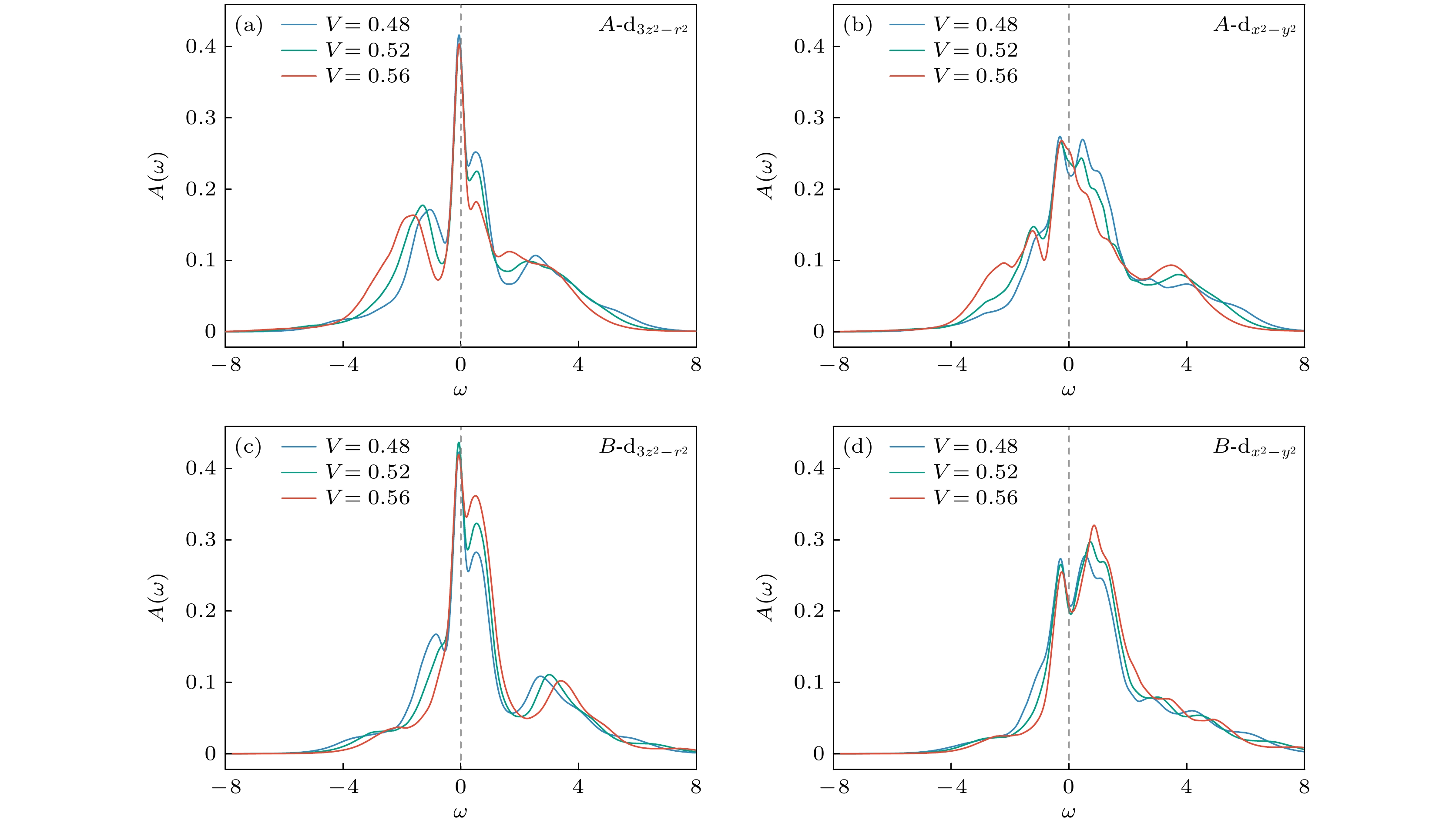
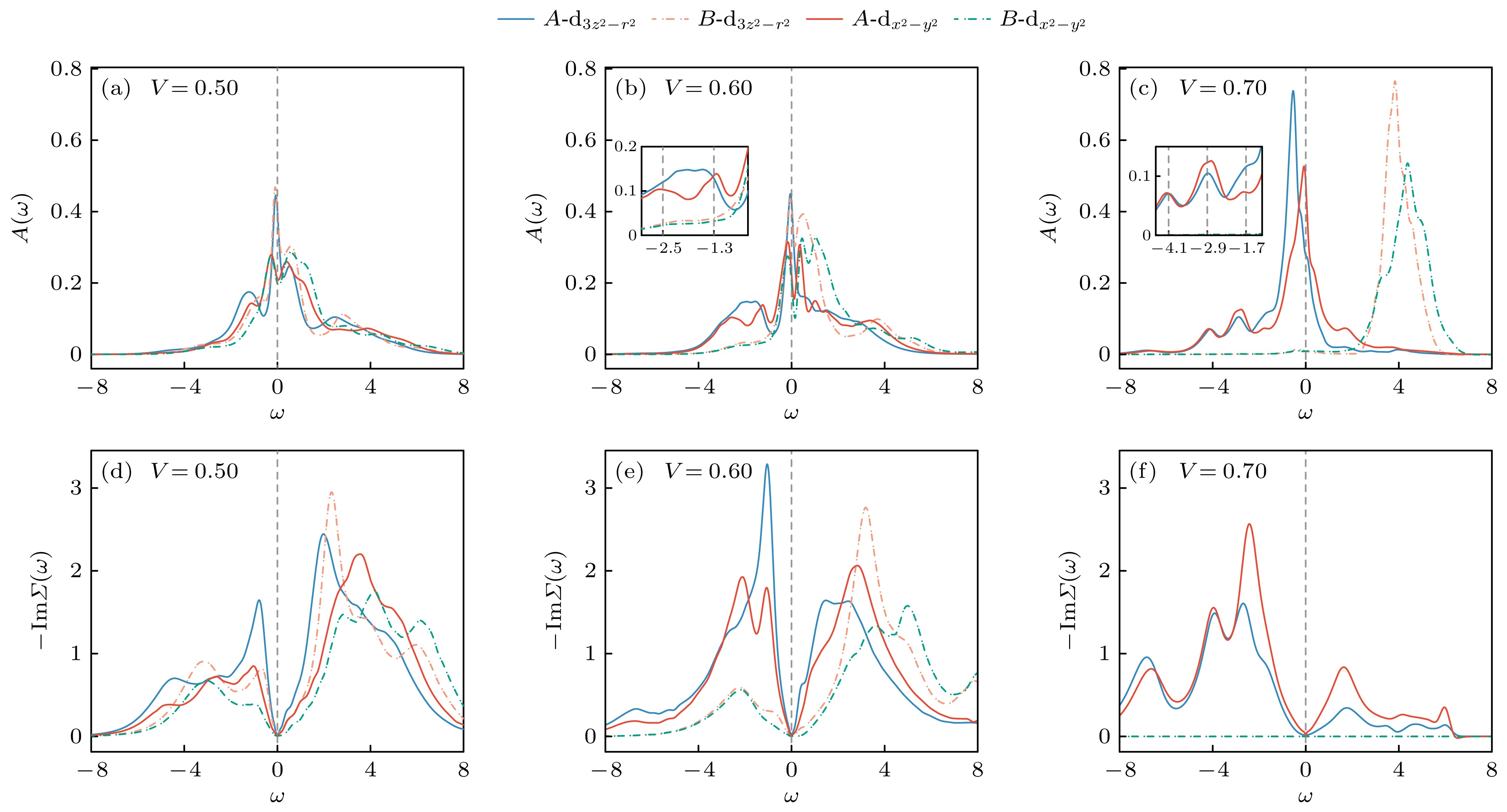
图5展示了在电荷极化程度较低的区间$ 0.48 \leqslant V \leqslant 0.56 $内谱函数的演化行为. 随着V的增大以及极化程度的增强, 多数占据的子格点A上的谱函数在$ \omega < 0 $区域的权重逐渐增大, 整体呈现向低能方向移动的趋势(图5(a), (b)). 与之相对, B子格点的谱函数(图5(c), (d))则表现出相反的演化特征. 与此同时, A(B)格点上对应的Hubbard带及其多峰劈裂结构也随V增大而整体向低能(高能)方向偏移, 反映出不同子格点上激发能量在V增强下的重整化效应. 相较于$ V = 0 $的情形(参见3.1), 对于给定的密度极化$ n_{\rm{diff}} $, 在A和B子格点上添加一个电子所需的激发能量之差为$ \delta \omega = -zV n_{\rm{diff}} $. 以$ V = 0.56 $, $ n_{\rm{diff}} \approx 0.75 $为例, 对应能量差为$ \delta \omega \approx 2.1 $, 这与图5(a), (c), 图5(b), (d)中所观察到的Hubbard峰之间的相对能量位移呈良好的一致性.

图6(a)—(c)展示了在更大V值范围内谱函数的演化行为. 随着V及密度极化$ n_{\rm{diff}} $的进一步增强, 谱函数相较于$ V = 0 $时发生了显著重构. 与较小V情况下主要表现为谱权重平滑转移不同(图6(a)), 当$ V = 0.6 $时, 谱函数结构本身已发生明显变化(图6(b)), 特别是在下Hubbard带中也出现了清晰的多峰特征. 此时体系的密度极化达到$ n_{\rm{diff}} \approx 1.1 $, 多数子格点A上的电子数接近$ n_{A} \approx 2.05 $, 基态中三占据等高占据组态的权重显著上升. 根据前述原子极限分析, 从三占据态移除一个电子将产生一组能量间隔为$ 2 J = 1.2 $ eV的激发峰, 这可能对应于下Hubbard带中观察到的$ \omega \approx -2.5 $和$ \omega \approx -1.3 $的双峰结构. 两峰之间另一个相对清晰的激发峰则可能来源于受V重整化后的双占据组态的电子移除过程. 相比之下, 上Hubbard带中的多峰结构更为复杂, 反映出多个基态占据组分的协同激发所引起的多重能量结构. 对于少数占据格点B, 其占据数$ n_{B} \approx 0.95 $, 因而电子移除过程观察不到明显的下Hubbard带. 当V进一步增强时, 其引入的有效晶体场作用驱动体系进入完全电荷极化态. 从图6(c)中的谱函数可以看出, B子格点的谱权重从费米能附近完全移除, 表明该子格点处于近乎空态. 与此同时, A子格点在费米能附近的谱权重也发生变化, 由此前主要由${\mathrm{ d}}_{3 z^2 - r^2} $轨道主导转变为由$ {\mathrm{d}}_{x^2 - y^2} $轨道占主导地位. 同时, 下Hubbard带中的多峰结构(分别位于$ \omega = -4.1 $, –2.9, –1.7)变得更加清晰, 表明A子格点上的电子关联强度进一步增强, 体系行为更接近局域的原子极限.

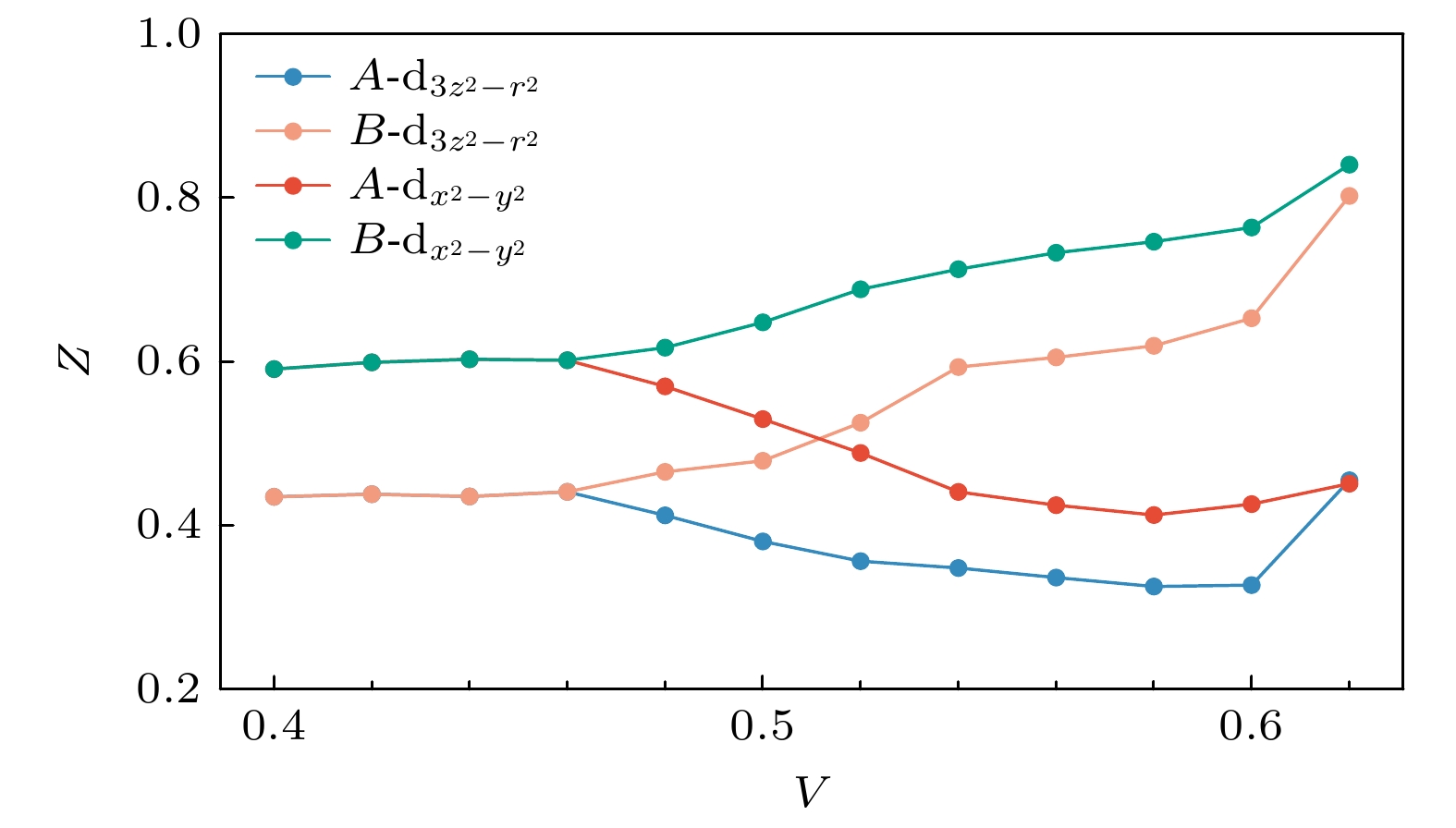
图6(d)—(f)展示了与图6(a)—(c)中谱函数相对应的自能, 进一步揭示了V对不同子格点轨道关联效应的调制作用. 在体系进入完全极化、导致少数占据格点B的自能趋近于零之前, 在数值误差范围内, 各轨道自能的虚部$ {\rm{Im}}, \varSigma(\omega) $在$ \omega = 0 $附近均呈现出典型的$ \omega^2 $频率依赖, 表明A与B子格点在不同V条件下均保持费米液体行为. 总体而言, 多数占据格点A上的准粒子激发寿命始终短于B, 且该差异随极化程度增强而进一步扩大. 这一趋势与A格点比B始终更接近半填充状态相一致, 符合关联效应在轨道接近半填充时最为显著的一般预期^[63].

图7总结了不同子格点、不同轨道的准粒子重整化因子Z随V的演化行为. 随着V的增大, 少数占据层中两个轨道的重整化因子呈单调增加趋势, 表明关联效应逐渐减弱. 而多数占据层的轨道则表现出非单调变化, 在极化初期, Z随V增大而减小, 反映出关联效应的增强, 而在$ V \geqslant 0.6 $后, Z值开始回升, 显示出关联程度有所减弱.

值得注意的是, $ V = 0.58 $和$ V = 0.6 $时体系的密度极化分别达到$ n_{\rm{diff}} \approx 0.9 $与$ n_{\rm{diff}} \approx 1.1 $, 即A子格点占据分别为1.95和2.05, 最接近半填充状态, 两者的Z值在误差范围内相当接近, 对应的关联效应达到最大. 这一结果也与图6中的自能的表现一致. 在完全极化后, A格点自能虚部在$ \omega = 0 $附近相较$ V=0.6 $时变得更加平缓, 表明准粒子激发寿命随之延长.

本文基于DFT+DMFT的理论框架, 并结合Hartree平均场处理近邻格点间库仑作用, 系统研究了La₃Ni₂O₇中非局域库仑相互作用驱动的电荷序行为及其对轨道选择性电子关联效应的影响. 在不包含非局域库仑相互作用时, 体系呈现典型的多轨道强关联费米液体特征, 谱函数与自能均表现出显著的轨道依赖性重整化行为, 揭示了由顶点氧诱导的$ {\mathrm{d}}_{3 z^2 - r^2} $成键轨道相较于$ {\mathrm{d}}_{x^2 - y^2} $轨道具有更强的关联效应. 此外, 通过高精度的实轴谱函数计算, 我们首次解析出源于原子多重态结构导致的Hubbard能带劈裂. 引入近邻库仑作用V后, 体系从子格点间对称态逐步演化为电荷极化态, 最终进入完全极化相, 伴随谱函数结构的显著重构与局域关联强度的重新分布. 在$ V \leqslant V_{{\mathrm{c}}1} \approx 0.46 $ eV区间内, 体系保持子格点对称性, 电子关联特性基本不变; 当$ V > V_{{\mathrm{c}}1} $时, 对称性被打破, 体系进入电荷有序相, 极化程度随V增大而持续增强, 并在$ V_{{\mathrm{c}}2} \approx 0.63 $ eV时达到完全极化状态. 值得注意的是, 计算得到的临界值$ V_{{\mathrm{c}}2} $与此前cRPA方法估算的近邻相互作用强度相当; 但鉴于Hartree平均场往往高估有序态的稳定性, 计算中出现的完全极化电荷序在真实材料中实现的可能性较低, 其实际存在性仍有待进一步检验. 计算结果显示, 在极化演化过程中, Hubbard带的能量位置及其多峰结构随V呈现系统性变化, 这一特征有望为后续实验提供谱学判据, 以反演材料中实际的非局域相互作用强度与电荷序程度.

本研究明确揭示了近邻非局域库仑作用在驱动电荷序形成与调控电子关联中的关键作用, 为理解高压条件下La₃Ni₂O₇中超导的竞争序态提供了新视角. 需要指出的是, 受限于本工作采用的原胞尺寸, 我们得到的电荷序周期为2, 对应波矢为$ (\pi, \pi) $的棋盘状或者$ (\pi, 0)/(0, \pi) $的条纹状电荷序, 尚无法探讨更长周期电荷序的稳定性与竞争态势, 未来工作可进一步扩展至包含更大周期或非平凡对称破缺的有序构型, 以全面揭示该体系中密度波与超导态之间的相互作用与调控机制.