高级搜索

合并束冷碰撞的单量子态氦原子束研究

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

魏龙, 杜小娇, 温金录, 董俊峰, 孙羽, 胡水明. 合并束冷碰撞的单量子态氦原子束研究[J]. 物理学报, 2025, 74(18): 183103-1. doi: 10.7498/aps.74.20250812
引用本文: 魏龙, 杜小娇, 温金录, 董俊峰, 孙羽, 胡水明. 合并束冷碰撞的单量子态氦原子束研究[J]. 物理学报, 2025, 74(18): 183103-1. doi: 10.7498/aps.74.20250812
shu
Long WEI, Xiaojiao DU, Jinlu WEN, Junfeng DONG, Yu SUN, Shuiming HU. Preparation of single-quantum-state-selected helium for neutral atom-molecule merged-beams collisions[J]. Acta Physica Sinica, 2025, 74(18): 183103-1. doi: 10.7498/aps.74.20250812
Citation: Long WEI, Xiaojiao DU, Jinlu WEN, Junfeng DONG, Yu SUN, Shuiming HU. Preparation of single-quantum-state-selected helium for neutral atom-molecule merged-beams collisions[J]. Acta Physica Sinica, 2025, 74(18): 183103-1. doi: 10.7498/aps.74.20250812
shu

合并束冷碰撞的单量子态氦原子束研究

  • 1.

    深圳先进光源研究院, 深圳　518107

  • 2.

    中国科学技术大学, 合肥国家实验室, 合肥　230088

    • 作者简介: 魏龙: weilong@mail.iasf.ac.cn .
    通讯作者: E-mail: sunyu@mail.iasf.ac.cn; 

  • 中图分类号: 31.70.-f, 24.30.-v, 25.40.Kv, 07.77.Gx

Preparation of single-quantum-state-selected helium for neutral atom-molecule merged-beams collisions

  • 1.

    Institute of Advanced Science Facilities, Shenzhen 518107, China

  • 2.

    Hefei National Laboratory, University of Science and Technology of China, Hefei 230088, China

    • Corresponding author: E-mail: sunyu@mail.iasf.ac.cn; 

  • MSC: 31.70.-f, 24.30.-v, 25.40.Kv, 07.77.Gx

  • 摘要: 量子态选择的低温原子分子反应动力学研究是从原子分子层面探究分子间及分子内的微观反应机理, 理解散射量子效应的关键研究手段之一. 合并束低温碰撞实验方法通过将一反应物偏转后与沿直线飞行的另一反应物发生共线碰撞, 获得毫开尔文量级的冷碰撞实验条件, 并开展毫开尔文至百开尔文碰撞能的反应动力学研究. 本文采用自主发展的永磁体“磁导”引导特定量子态的中性原子偏转后与分子束共线, 通过对氦原子穿过磁导的通量测量, 实验实现了三重态亚稳态23S1氦原子约10°角度偏转, 并制备了$ {M_J} = + 1 $ 磁子能级激发态氦原子. 本工作为发展亚稳态氦原子与分子低于开尔文量级的量子态选择激发态冷碰撞研究提供实验基础, 可以促进对激发态反应在星际介质演化中重要贡献的理解以及化学反应调控的研究. 本研究中发展的“磁导”也在原子速度滤波和冷原子输运等领域具有重要的应用前景.
    Abstract: Studying low-temperature atomic and molecular reaction dynamics in quantum state selection is one of the key research methods for exploring the collision reaction mechanisms and revealing quantum effects in scattering processes. The merging beam collision experimental method is a powerful approach to achieving cold collisions of mK collision energy, by deflecting one reactant beam to collide with another reactant beam in a collinear manner.In this work, based on the Zeeman effect, the interaction between atomic magnetic moments and a magnetic field, a permanent-magnet “magnetic guide” system is developed to deflect metastable helium atom beams, with the aim of achieving collinear transport of neutral helium atoms and molecules in cold merged-beams collisions. Metastable helium atoms He(23S1) are produced through RF discharge. Utilizing this “magnetic guide”, the quantum-state-resolved neutral helium atoms (He(23S1), $ {M_J} = + 1 $) are prepared. Helium flux measurements demonstrate about 10°deflection of metastable helium atoms with a flux exceeding 106 atoms/s, accompanied by successful preparation of $ {M_J} = + 1 $ magnetic sublevel helium atoms. Furthermore, by combining the magnetic field measurements and magnetic force calculations for 23S1 metastable helium atom, the simulated trajectories propagating through the magnetic guide are analyzed.This work lays an experimental foundation for quantum-state-resolved cold collisions between excited-state helium and molecules below 1 K, advancing the understanding of cold reaction mechanisms governing the evolution of interstellar media and promoting chemical reaction control. The developed magnetic guidance technology in this study also has important application prospects in fields such as atomic velocity filtering and cold atom transport.In the future, optical pumping experimental methods will be employed to pump 23S1 helium atoms into the $ {M_J} = + 1 $ magnetic sublevel helium atoms, enhancing the population of single quantum state. Moreover, two-dimensional magneto-optical traps and optical molasses will be implemented to optimize beam, which is expected to further improve the beam flux of helium atoms.
  • 加载中

  • 图 1  (a) 亚稳态氦原子束线平台示意图. 黑色虚线框内为合并束的永磁体“磁导”装置; (b) 氦原子能级结构图; (c) 磁导三维图

    Figure 1.  (a) Schematic drawing of metestable helium atoms beam, dashed box is the “magnetic guide” system; (b) energy level diagram of helium atoms; (c) 3D schematic of the magnetic guide.

    下载: 全尺寸图片 幻灯片

    图 2  激光系统部分的光路示意图(AMP, 放大器; LPF, 低通滤波器; PBS, 偏振分束镜; GT, 格兰泰勒棱镜; EOM, 电光调制器; LO, 本地振荡信号)

    Figure 2.  Schematic drawing of optical layout. AMP, amplifier; LPF, low-pass filter; PBS, polarizing beam splitter; GT, Glan-Taylor prism; EOM, electro-optic modulator; LO, local oscillator.

    下载: 全尺寸图片 幻灯片

    图 3  (a) 单个磁组件的结构示意图; (b) 单个磁组件的实物图; (c) 单个磁组件的径向磁场分布模拟结果

    Figure 3.  (a) Schematic diagram of the magnetic assembly; (b) photograph of magnetic assembly; (c) simulated 2D magnetic field distribution.

    下载: 全尺寸图片 幻灯片

    图 4  (a) 磁组件的一维径向磁场曲线图, 其中红色空心圆点为有限元模拟结果, 蓝色和黑色曲线为实验测量的磁场分布曲线; (b) 磁组件的径向磁场梯度分布

    Figure 4.  (a) Radial magnetic field of the magnetic assembly, where red open circles denote the simulation results, and blue/black curves represent measured magnetic field; (b) radial magnetic field gradient of the magnetic assembly.

    下载: 全尺寸图片 幻灯片

    图 5  800 m/s的$ {M_J} = - 1 $磁子能级亚稳态氦原子在单个磁组件内的运动轨迹模拟

    Figure 5.  Simulated trajectory of metastable helium atoms (23S1, $ {M_J} = - 1 $) propagating through the magnetic assembly at 800 m/s.

    下载: 全尺寸图片 幻灯片

    图 6  800 m/s的$ {M_J} = + 1 $磁子能级亚稳态氦原子穿过磁导的运动轨迹模拟

    Figure 6.  Simulated trajectory of $ {M_J} = + 1 $ 23S1 metastable helium atoms propagating through the magnetic guide at 800 m/s.

    下载: 全尺寸图片 幻灯片
  • [1] Herbst E, Yates J T 2013 Chem. Rev. 113 8707 doi: 10.1021/cr400579y
    [2] Roueff E, Lique F 2013 Chem. Rev. 113 8906 doi: 10.1021/cr400145a
    [3] Gerlich D, Jusko P, Roučka Š, Zymak I, Plašil R, Glosík J 2012 J. Astrophys. 749 22 doi: 10.1088/0004-637X/749/1/22
    [4] Stuhl B K, Hummon M T, Ye J 2014 Annu. Rev. Phys. Chem. 65 501 doi: 10.1146/annurev-physchem-040513-103744
    [5] Perreault W E, Mukherjee N, Zare R N 2017 Science 358 356 doi: 10.1126/science.aao3116
    [6] Amarasinghe C, Suits A G 2017 J. Phys. Chem. Lett. 8 5153 doi: 10.1021/acs.jpclett.7b02378
    [7] Ni K K, Ospelkaus S, Wang D, Quéméner G, Neyenhuis B, Miranda M H G De, Bohn J L, Ye J, Jin D S 2010 Nature 464 1324 doi: 10.1038/nature08953
    [8] Karman T, Tomza M, Pérez-Ríos J 2024 Nat. Phys. 20 722 doi: 10.1038/s41567-024-02467-3
    [9] Lavert-Ofir E, Shagam Y, Henson A B, Gersten S, Kłos J, Żuchowski P S, Narevicius J, Narevicius E 2014 Nat. Chem. 6 332 doi: 10.1038/nchem.1857
    [10] Yang T, Huang L, Xiao C, Chen J, Wang T, Dai D, Lique F, Alexander M H, Sun Zh, Zhang D H, Yang X, Neumark D M 2019 Nat. Chem. 11 744 doi: 10.1038/s41557-019-0280-3
    [11] Yang X, Zhang D H 2008 Acc. Chem. Res. 41 981 doi: 10.1021/ar700258g
    [12] 杨威, 孙大立, 周林, 王谨, 詹明生 2014 物理学报 63 153701 doi: 10.7498/aps.63.153701 Yang W, Sun D L, Zhou L, Wang J, Zhan M S 2014 Acta Phys. Sin. 63 153701 doi: 10.7498/aps.63.153701
    [13] Bethlem H L, Berden G, Meijer G 1999 Phys. Rev. Lett. 83 1558 doi: 10.1103/PhysRevLett.83.1558
    [14] Hutzler N R, Lu Hsin-I, Doyle J M 2012 Chem. Rev. 112 4803 doi: 10.1021/cr200362u
    [15] Lemeshko M, Krems R V, Doyle J M, Kais S 2013 Mol. Phys. 111 1648 doi: 10.1080/00268976.2013.813595
    [16] Egorov D, Lahaye T, Schöllkopf W, Friedrich B, Doyle J M, 2002 Phys. Rev. A 66 043401 doi: 10.1103/PhysRevA.66.043401
    [17] Jongh T de, Besemer M, Shuai Q, Karman T, van der Avoird A, Groenenboom G C, van de Meerakker S Y T 2020 Science 368 626 doi: 10.1126/science.aba3990
    [18] Qiu M, Ren Z, Che L, Dai D, Harich S A, Wang X, Yang X, Xu C, Xie D, Gustafsson M, Skodje R T, Sun Z, Zhang D H 2006 Science 311 1440 doi: 10.1126/science.1123452
    [19] Yang T, Yang X 2020 Science 368 582 doi: 10.1126/science.abb8020
    [20] Henson A B, Gersten S, Shagam Y, Narevicius J, Narevicius E 2012 Science 338 234 doi: 10.1126/science.1229141
    [21] Shagam Y, Narevicius E 2013 J. Phys. Chem. C 117 22454 doi: 10.1021/jp4045868
    [22] Klein A, Shagam Y, Skomorowski W, Zuchowski P S, Pawlak M, Janssen L M C, Moiseyev N, van de Meerakker S Y T, van der Avoird A, Koch C P, Narevicius E 2017 Nat. Phys. 13 35 doi: 10.1038/nphys3904
    [23] Shagam Y, Klein A, Skomorowski W, Yun R, Averbukh V, Koch C P, Narevicius E 2015 Nat. Chem. 7 921 doi: 10.1038/nchem.2359
    [24] Paliwal P, Deb N, Reich D M, van der Avoird Ad, Koch C P, Narevicius E 2021 Nat. Chem. 13 94 doi: 10.1038/s41557-020-00578-x
    [25] Jankunas J, Bertsche B, Osterwalder A 2014 J. Phys. Chem. A 118 3875 doi: 10.1021/jp502989g
    [26] Gordon S D S, Omiste J J, Zou J, Tanteri S, Brumer P, Osterwalder A 2018 Nat. Chem. 10 1190 doi: 10.1038/s41557-018-0152-2
    [27] Harada Y, Masuda S, Ozaki H 1997 Chem. Rev. 97 1897 doi: 10.1021/cr940315v
    [28] Kishimoto N, Oda T, Ohno K 2004 J. Electron. Spectrosc. Relat. Phenom. 137 319 doi: 10.1016/j.elspec.2004.02.066
    [29] Yamakita Y, Ohno K 2009 J. Phys. Chem. A 113 10779 doi: 10.1021/jp9038978
    [30] Henson B M, Ross J A, Thomas K F, Kuhn C N, Shin D K, Hodgman S S, Zhang Y H, Tang L Y, G. Drake W F, Bondy A T, Truscott A G, Baldwin K G H 2022 Science 376 199 doi: 10.1126/science.abk2502
    [31] Chen J J, Sun Y R, Wen J L, Hu S M 2020 Phys. Rev. A 101 053824 doi: 10.1103/PhysRevA.101.053824
    [32] Even U 2015 EPJ Tech. Instrum. 2 17 doi: 10.1140/epjti/s40485-015-0027-5
    [33] 孙羽, 冯高平, 程存峰, 涂乐义, 潘虎, 杨国民, 胡水明 2012 物理学报 61 170601 doi: 10.7498/aps.61.170601 Sun Y, Feng G P, Cheng C F, Tu L Y, Pan H, Yang G M, Hu S M 2012 Acta Phys. Sin. 61 170601 doi: 10.7498/aps.61.170601
    [34] Cheng C F, Jiang W, Yang G M, Sun Y R, Pan H, Gao Y, Liu A W, Hu S M 2010 Rev. Sci. Instrum. 81 123106 doi: 10.1063/1.3520133
    [35] 陈娇娇, 孙羽, 温金录, 胡水明 2021 物理学报 70 133201 doi: 10.7498/aps.70.20201833 Chen J J, Sun Y, Wen J L, Hu S M 2021 Acta Phys. Sin. 70 133201 doi: 10.7498/aps.70.20201833
  • 加载中
图( 6)
计量
  • 文章访问数:  204
  • HTML全文浏览数:  204
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-06-21
  • 刊出日期:  2025-09-20

合并束冷碰撞的单量子态氦原子束研究

    通讯作者: E-mail: sunyu@mail.iasf.ac.cn; 
    作者简介: 魏龙: weilong@mail.iasf.ac.cn
  • 1. 深圳先进光源研究院, 深圳　518107
  • 2. 中国科学技术大学, 合肥国家实验室, 合肥　230088
  • 收稿日期:  2025-06-21

摘要: 量子态选择的低温原子分子反应动力学研究是从原子分子层面探究分子间及分子内的微观反应机理, 理解散射量子效应的关键研究手段之一. 合并束低温碰撞实验方法通过将一反应物偏转后与沿直线飞行的另一反应物发生共线碰撞, 获得毫开尔文量级的冷碰撞实验条件, 并开展毫开尔文至百开尔文碰撞能的反应动力学研究. 本文采用自主发展的永磁体“磁导”引导特定量子态的中性原子偏转后与分子束共线, 通过对氦原子穿过磁导的通量测量, 实验实现了三重态亚稳态23S1氦原子约10°角度偏转, 并制备了$ {M_J} = + 1 $ 磁子能级激发态氦原子. 本工作为发展亚稳态氦原子与分子低于开尔文量级的量子态选择激发态冷碰撞研究提供实验基础, 可以促进对激发态反应在星际介质演化中重要贡献的理解以及化学反应调控的研究. 本研究中发展的“磁导”也在原子速度滤波和冷原子输运等领域具有重要的应用前景.

English Abstract

    全文HTML

    1.   引　言

    • 低温原子分子碰撞过程广泛存在于冷星际介质, 是宇宙中最普遍的物理及化学反应之一, 吸引着科学家们极大的兴趣[1–8]. 随着反应体系碰撞能量的降低, 量子隧穿、Feshbach共振、形貌共振及电子态的非绝热跃迁等导致反应速率出现显著的、数量级的急剧增强, 并占据反应通道的主导地位[9–11]. 接近绝对零度的极低温原子分子碰撞实验成为实验室内研究量子效应并探究星际演化的重要实验方案之一.

      目前, 一些实验方法通过Stark减速、Zeeman减速以及缓冲气体冷却等实验技术降低原子分子的速度, 实现冷原子分子的制备, 进而开展开尔文甚至百毫开尔文的低温反应实验研究[12–16]. 例如2020年, Jongh等[17]基于交叉分子束实验技术开展了低至0.3 K的NO和He碰撞实验, 实验中Stark减速产生的一氧化氮分子束和低温阀产生的氦原子束在碰撞中心以5°和8°夹角的小角度碰撞, 获得了碰撞能为0.3—12.3 K的非弹性散射动力学信息, 观测到了多个显著的量子散射共振现象. 这种交叉碰撞实验在量子态分辨反应动力学的研究中取得了很多重要的成果, 但是碰撞能很难进一步降低[18,19]. 除此之外, 共线平行飞行的合并束碰撞(merged-beams collisions)实验方案避免了反应物平动速度减小的技术难点, 在高速运动的实验室坐标系下开展更低温的反应动力学研究, 并可以通过控制碰撞体系的相对碰撞速度来实现不同碰撞能的碰撞实验研究. 合并束实验中一反应物沿直线传输, 而另一反应物被偏转后共线传输, 即偏转后两个反应物近平行重叠飞行碰撞. 理论上, 当碰撞反应的碰撞夹角为零度时, $ {E}_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}=(\mu /2){({v}_{1}-{v}_{2})}^{2} $, 碰撞能$ {E}_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}} $仅与碰撞体系的相对速度$ {v}_{1} $和$ {v}_{2} $有关, 速度相同时反应物碰撞能为0(其中$ \mu $为碰撞体系的约化质量). 2012年, 以色列Weizmann研究所Narevicius课题组[20]将离子-离子和离子-中性碰撞实验中的合并束实验方法成功拓展到中性原子分子碰撞实验, 首次利用合并束碰撞将中性氦原子和氢气及氩的实验碰撞能量降低至mK量级. Narevicius 课题组在mK至百K低温反应动力学实验中, 观测到由共振量子效应机制导致反应概率显著增加的重要实验成果, 并揭示了同位素效应、自旋量子化等机制在冷碰撞反应动力学的重要角色[9,20–24]. 2014年, 瑞士洛桑联邦理工学院Andreas Osterwalder课题组成功实现了亚稳态Ne*原子与氨分子及同位素的中性原子分子合并碰撞实验[25], 随后他们探究了碰撞反应动力学中的量子动力学同位素效应[26]. 由于中性原子分子的操纵和调控较为复杂, 实现中性原子束的偏转共线是实验室内开展极低能量原子分子合并碰撞的关键问题和技术难点, 至今国际上仅有维兹曼研究所和瑞士洛桑联邦理工学院两个研究组实现了中性原子分子合并束冷碰撞实验.

      氦作为最简单的多电子原子, 三重态的23S1亚稳态4He与原子分子发生碰撞时, 由于自身处于电子激发态且携带约20 eV的能量, 能够发生如潘宁电离(Penning ionization)和缔合电离(associative ionization)过程, 形成靶分子离子化. 碰撞电离反应过程可以分别表示为

      其中$ {\mathrm{A}}^{\mathrm{*}} $代表处于电子激发态的原子分子(如亚稳态氦原子), $ \mathrm{B} $代表中性原子或分子, $ {\mathrm{B}}^{+} $为被单电离后的离子产物, $ {\mathrm{e}}^{-} $为碰撞电离过程释放的自由电子, $ {\mathrm{A}\mathrm{B}}^{+} $为缔合电离后形成的离子产物[27–29]. 低碰撞能的激发态原子与分子的潘宁或缔合电离反应速率的测定能够揭示碰撞反应中的量子效应, 并提供重要的动力学参数[9,20,22,24]. 基于原子的塞曼效应, 具有约8000 s长寿命且磁矩不为零的激发态23S1 亚稳态He*原子可在不均匀磁场中受磁场力作用, 这为引导氦原子偏转后与分子的合并束低温碰撞提供了可行性[20]. 此外, 氦原子在精密谱学研究和冷原子研究领域十分重要, 也是发展量子力学基础理论的关键, 其与分子间的低温碰撞反应是研究冷碰撞反应动力学的重要样本之一, 是研究碰撞反应中的量子效应和高精度势能面构建的重要实验支撑[23,30,31]. 开展广泛存在于冷星际介质中的氦原子与分子的碰撞实验研究对理解冷星际化学反应也具有重要的参考意义.

      本文介绍极低能中性原子分子合并束碰撞的单量子态激发态氦原子制备研究. 利用原子与磁场作用的塞曼效应, 不均匀磁场内运动的氦原子受磁场力不同可导致不同磁子能级原子的飞行轨迹发生变化, 由此引导中性氦原子的偏转同时实现氦原子量子态的选态. 本工作利用“磁导”引导顺磁原子传输, 通过亚稳态氦原子穿过磁导的通量测量, 实验实现亚稳态氦束的大角度偏转传输, 并成功地制备了单量子态分辨的23S1亚稳态$ {M_J} = + 1 $磁子能级4He*束. 结合二维激光冷却原子的横向冷却技术, 实验获得>106 atoms/s高通量的量子态选择He*束流. 此外, 通过有限元分析和氦原子运动轨迹的模拟, 进一步探究了塞曼分裂后$ {M_J} = + 1 $量子态氦原子在磁场中的二维运动规律. 该紧凑型永磁体“磁导”结构(长300 mm的弧形磁导)在小空间内实现高梯度的磁场分布(最高达约0.2 T/mm), 高梯度磁场可提供更大磁场力偏转中性原子, 从而在小曲率半径下实现大角度偏转. 同时, 相较于电磁铁/线圈磁场等产生大梯度磁场则需装配冷却系统以减小通电电流引入的发热效应, 永磁体材质不需要额外的冷却系统, 更加的经济适用. 本实验中永磁体“磁导”实现氦原子磁子能级量子态选态的同时, 又能准许不受磁场影响的分子束沿直线顺利穿过, 为开展共线的合并束冷碰撞反应动力学研究提供关键实验基础.

    2.   实验装置

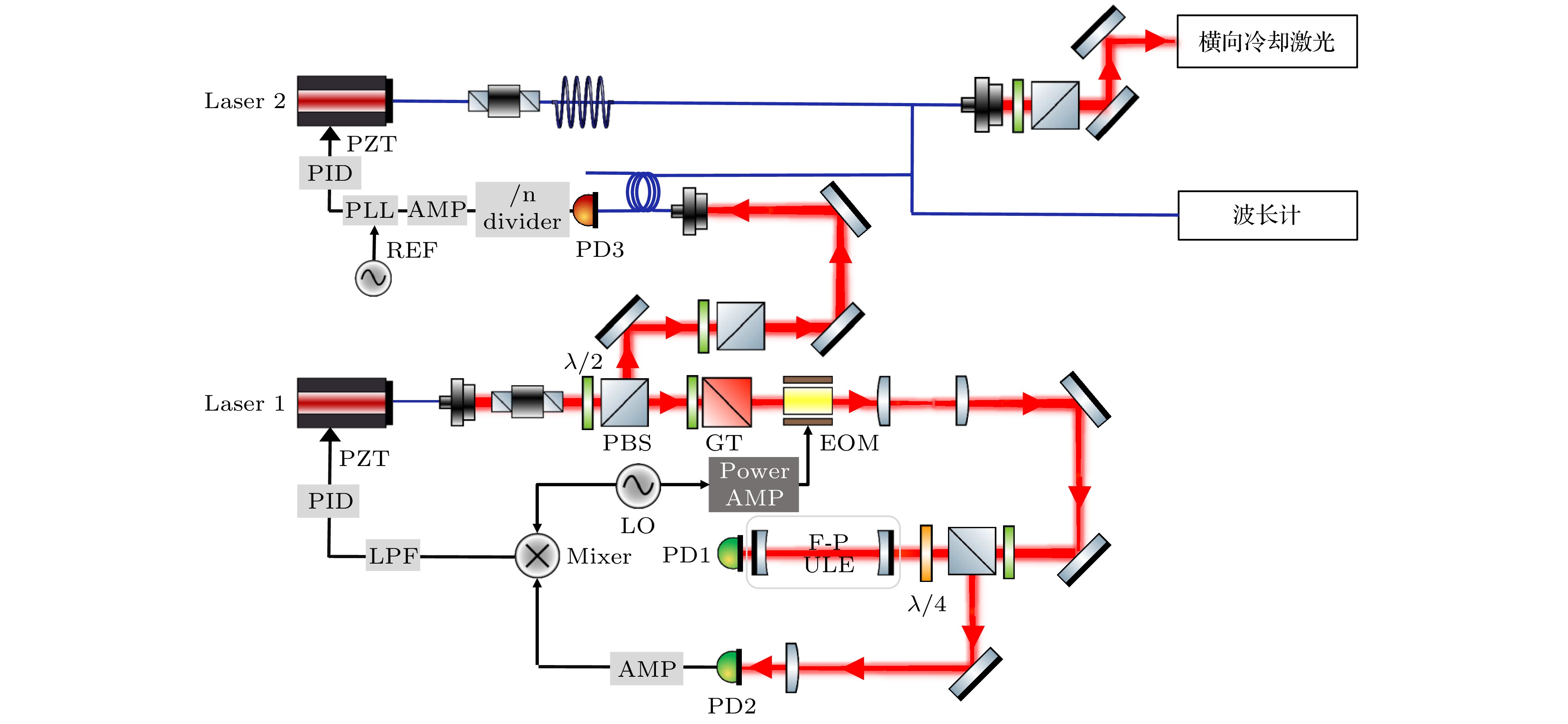
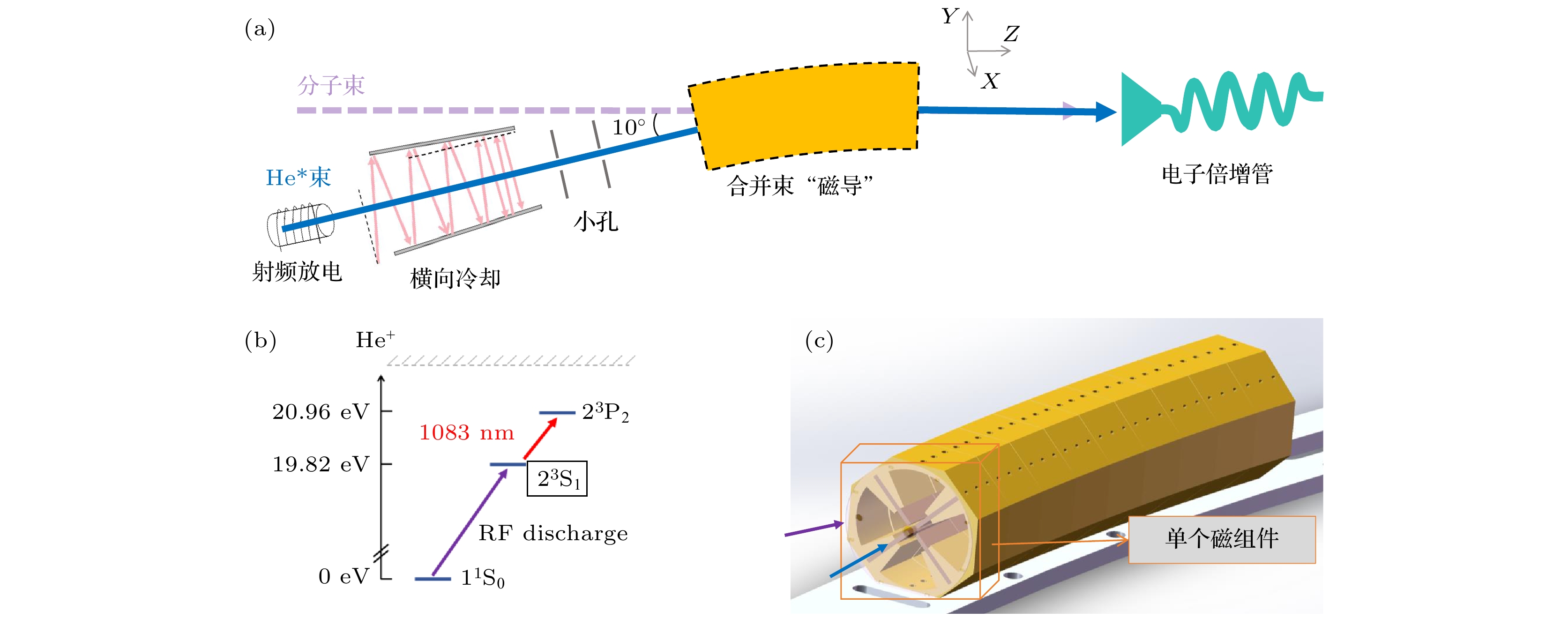
    • 本实验通过磁场引导中性原子偏转, 实现亚稳态氦原子的磁子能级量子态的选态, 同时实现氦束和分子束的共线, 实验装置如图1(a)所示. 实验平台主要由以下部分组成: 亚稳态原子制备的束源部分; 引导中性原子传输的合并束“磁导”部分; 监测原子束流的探测部分; 以及激光系统部分等. 图1中蓝色实线标记为氦束的传输路径, 紫色短线标记为分子束传输的路径, 束流自左向右传输, 氦束和分子束间的初始夹角为10°. 需要说明的是, 本实验聚焦于引导亚稳态原子的偏转和选态, 后续将不讨论沿直线传输的分子束(分子束为Even-Lavie脉冲阀产生的冷分子束[32]).

      实验中自旋三重态23S1亚稳态4He*原子由射频放电技术(RF discharge)激发产生, 经射频信号与共振线圈耦合形成RF放电, 通过减压阀和微漏阀控制扩散进入源腔的氦气量[33,34]. 实验采用液氮冷却方式降低氦束的初始速度, 并防止放电区域温度过高. 为提高放电制备亚稳态氦原子的比重, 实验在进气系统中掺入更低电离能的氪气, 提升23S1亚稳态原子的激发效率. 随后亚稳态氦原子穿过反射镜组成的横向冷却区(transverse cooling, TC), 以减小束流的角发散, 并提高束流强度. 基于激光冷却原子的原理, 1083 nm激光(三重态23S1态和23P2激发态之间的跃迁波长为1083 nm, 氦原子相关能级结构见图1(b))在两组相互垂直的反射镜间多次反射并形成横向冷却场, 对氦原子束进行二维横向冷却[35]. 横向减速后的氦原子依次经过两级小孔准直后垂直进入合并束流磁导装置, 小孔直径为6 mm并相距100 mm, 两个小孔与磁导入口中心位于同一轴线. 合并束流磁导装置为弯曲的弧形结构, 主要由10节永磁体的磁组件构成, 如图1中黑色短线框和图1(c)所示. 永磁体磁导的弧长约为300 mm, 每个磁组件包含四个钕铁硼磁钢, 磁钢以中心对称均匀分布, 形成中心直径6 mm的空隙, 单个磁组件结构如图1(c)中橙色框内所示. 氦原子从中心间隙进入磁导(见图1(c)中的蓝色箭头标识), 塞曼分裂后的$ {M_J} = + 1 $磁子能级23S1氦在磁组件内部磁场作用下, 运动方向被改变, 沿着永磁体磁导轴线传输. 通过约10°大角度偏转后, 23S1($ {M_J} = + 1 $)氦从磁导出口位置的中心隙间飞出. 氦原子的计数利用通道电子倍增管和电子学系统记录, 实验中电子倍增管(CEM4820, Photonis)正对磁导出口处安装. 其可在连续信号和脉冲信号两种模式下工作, 最大增益达108. 经偏转后飞出合并束磁导的氦原子进入电子倍增管, 携带高电子能量的亚稳态氦原子在倍增管入口处电离的电子经倍增后形成脉冲信号. 电子倍增管阳极收集的脉冲信号经放大和甄别(SR445A和SR400, SRS)后被电子学系统记录, 由此获得氦原子束流强度的实时测量. 本实验中束源部分和磁导部分的真空系统采用独立的抽气系统, 由插板阀实现真空的隔离和连通, 并留有一段波纹管连接, 本底真空均好于3 × 10–6 Pa. RF放电时, 源腔的气压为10–4 Pa量级, 磁导腔室的真空为10–5 Pa量级. 高真空环境可降低背景气体的影响, 同时减小亚稳态氦原子在传输过程中因残余粒子碰撞而导致束流强度的损失. 此外, 实验在磁导入口处安装了可移动式法拉第筒, 便于监测和确认亚稳态氦原子是否进入磁导.

      实验的激光系统部分主要由两个独立的光纤激光器光源组成, 如图2所示, 其中Laser 1为参考激光, Laser 2为二维横向冷却光. 两路激光通过锁相环(phase-lock loop, PLL)锁定激光的频率和相位, 激光频率通过Bristol 671A波长计测量确定. 激光器为上海频准激光公司的窄线宽光纤激光器, 输出激光标称线宽<10 kHz, 激光器的压电陶瓷PZT慢调制范围达10 GHz, 且带宽为5 kHz. 实验通过Pound Drever Hall(PDH)稳频技术将Laser 1锁定于法布里-珀罗(Fabry-Perot, F-P)超稳腔的模式上作为参考激光, F-P腔主要由超低膨胀系数(ultra-low expansion, ULE)玻璃和两个高反射平凹反射镜组成. 通过比例-积分-微分(proportion integration differentiation, PID)反馈的温控电路保持F-P腔的温度稳定, 提高锁频的稳定性. 横向冷却激光Laser 2和参考激光Laser 1通过高速光电探测器PD3得到拍频信号, 拍频信号通过除法器后放大进入负反馈的PLL和PID反馈电路, 将拍频信号锁定到参考信号源REF. 由此实现冷却光与参考激光的频率和相位的锁定, 使两个激光间的频率差保持相对稳定, 保证了横向冷却激光的频率稳定性. 横向冷却光最后通过镀高透膜的法兰窗进入真空源腔, 并在腔内安装的反射镜间多次反射, 形成横向冷却区.

    3.   实验结果与分析

    • 开展毫开尔文量级极低能量氦原子与分子合并束冷碰撞的关键实验基础是实验室内实现单一量子态中性氦原子偏转且与分子束共线碰撞. 本实验中, 射频放电激发制备的亚稳态氦原子经磁导(图1(c))传输后, 不仅实现原子磁子能级的分离与选态, 同时使偏转后的单量子态氦束与分子束共线传输. 图3(a)和图3(b)显示了组成磁导的单个磁组件结构, 永磁体磁导由10个磁组件结构两两间隔约1°紧密装配而成如图1(c)中黄色的弧形结构所示. 每个磁组件由四个磁钢组成, 磁钢为N52钕铁硼Nd-Fe-B烧结永磁体, 磁体相互夹角为90°. Nd-Fe-B永磁材料易被氧化和腐蚀, 导致磁性衰减, 为提高磁钢的耐腐蚀性, 本实验采用镀镍+铜+镍的电镀方式进行防腐蚀处理. 氦原子在磁组件中心形成的直径6 mm空隙中传输, 如图3(a)红色圆环标记所示. 分子束则可以通过两个磁钢间的间隙传输. 磁组件中心的XY平面磁场分布如图3(c)所示(X方向为水平方向, Y为竖直方向, Z轴为垂纸面方向), 红色圆环内部为不均匀的磁场分布, 圆心位置是磁势的最低点, 随着离中心圆点距离增加, 磁场越强, 靠近磁钢表面的磁场最高. 磁场分布的模拟结果由有限元分析方法计算获得, 模拟中未考虑杂散磁场以及周围装配件引入的磁场变化. 实验中为尽可能减小磁钢装配件和固定件对磁场分布的影响, 磁钢以外的加工件均采用铜材质和铝合金材质.

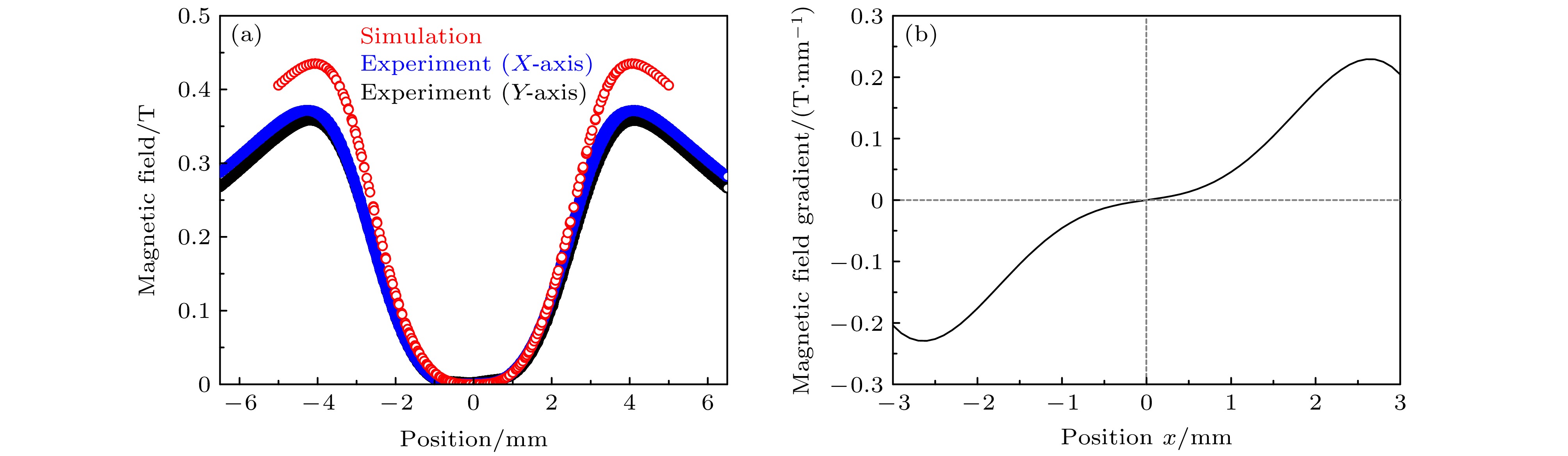
      基于原子与磁场作用的塞曼效应, 不均匀磁场内运动的氦原子受磁场力的不同会导致不同磁子能级氦原子的飞行轨迹被改变. 由此, 为了更仔细地理解原子在磁导内部的运动, 本文开展了氦原子在XZ平面的二维运动轨迹分析. 图4(a)为单个磁组件的一维径向磁场分布, 其中红色空心圆为有限元计算的结果, 蓝色和黑色标记的磁场分布曲线分别为X和Y轴磁感应强度的实验测量值. 实验采用Senis MMS-1A-RS磁场成像测绘系统对磁组件的磁场分布大小进行了测量, 磁场测量的空间分辨率达1 μm, 测量精度优于0.1%. 在正负3 mm范围内, 磁场的实验测量结果和模拟结果符合较好, 其中实验和模拟之间存在的磁场偏差主要来自于磁钢加工的精度、磁偏角及装配过程中存在误差等.

      基于上述的一维磁场分布, 图4(b)计算了X轴不同位置的磁场梯度分布情况, 梯度最高值>0.2 T/mm. 由于具有磁矩的原子在外磁场作用下发生了塞曼能级分裂, 分裂后的不同子能级原子在不均匀磁场中受到的磁场力与磁场梯度相关. 塞曼效应引入的能级分裂$ {W}_{\mathrm{Z}\mathrm{e}\mathrm{e}\mathrm{m}\mathrm{a}\mathrm{n}} $满足关系式(1):

      其中MJ表示亚稳态氦原子的磁子能级, $ {M_J} = - 1, 0, + 1 $; $ {g}_{J} $是朗德因子; $ {\mu }_{\mathrm{B}} $是玻尔磁子; B为外部磁场的磁感应强度大小. 所以原子在外部磁场中受到的沿磁场方向$ r $的磁场力$ {F}_{r} $可以表示为

      因此, 图4(b)中的梯度磁场分布为顺磁原子提供了指向磁组件中心的磁场力作用.

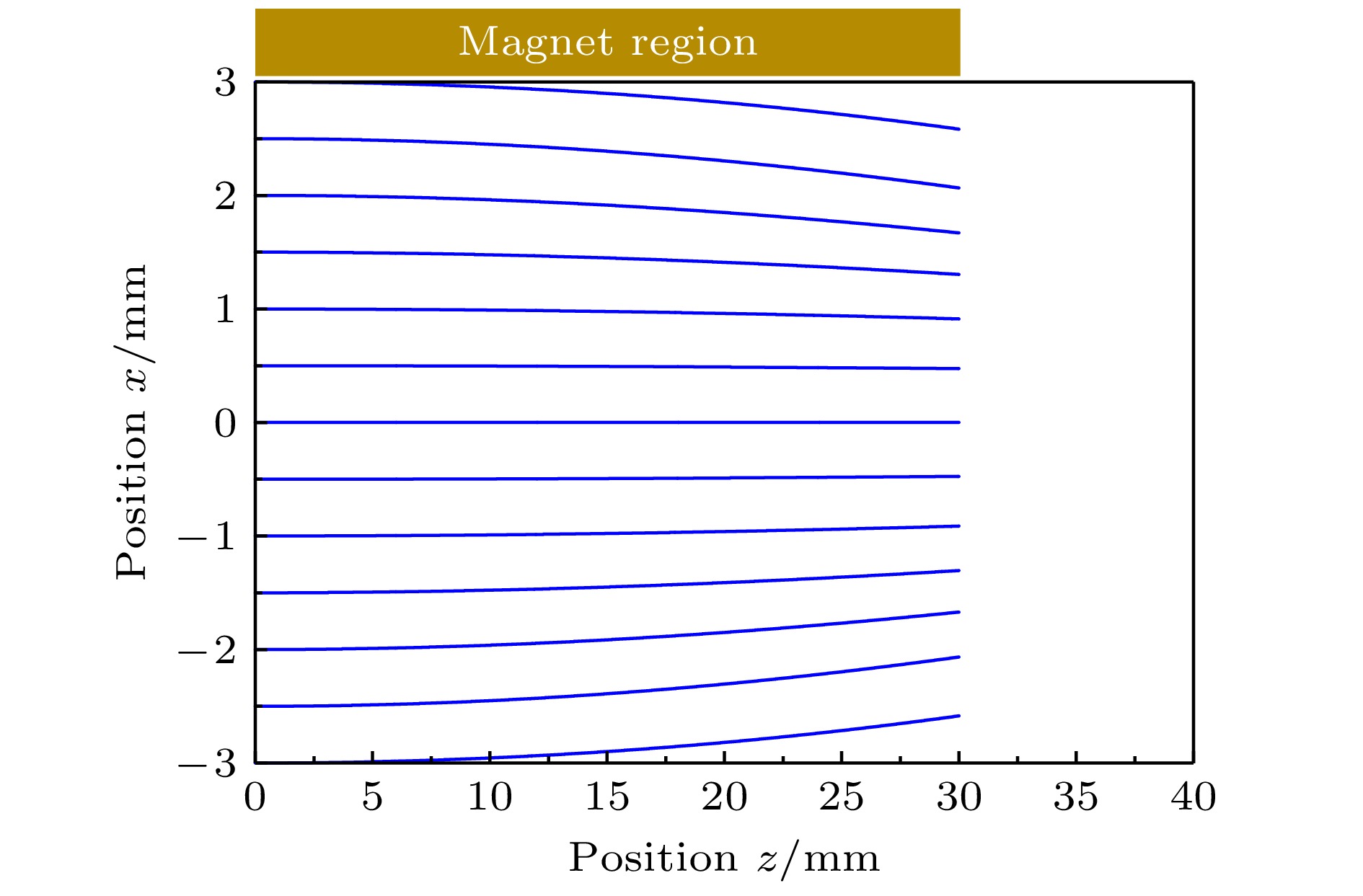
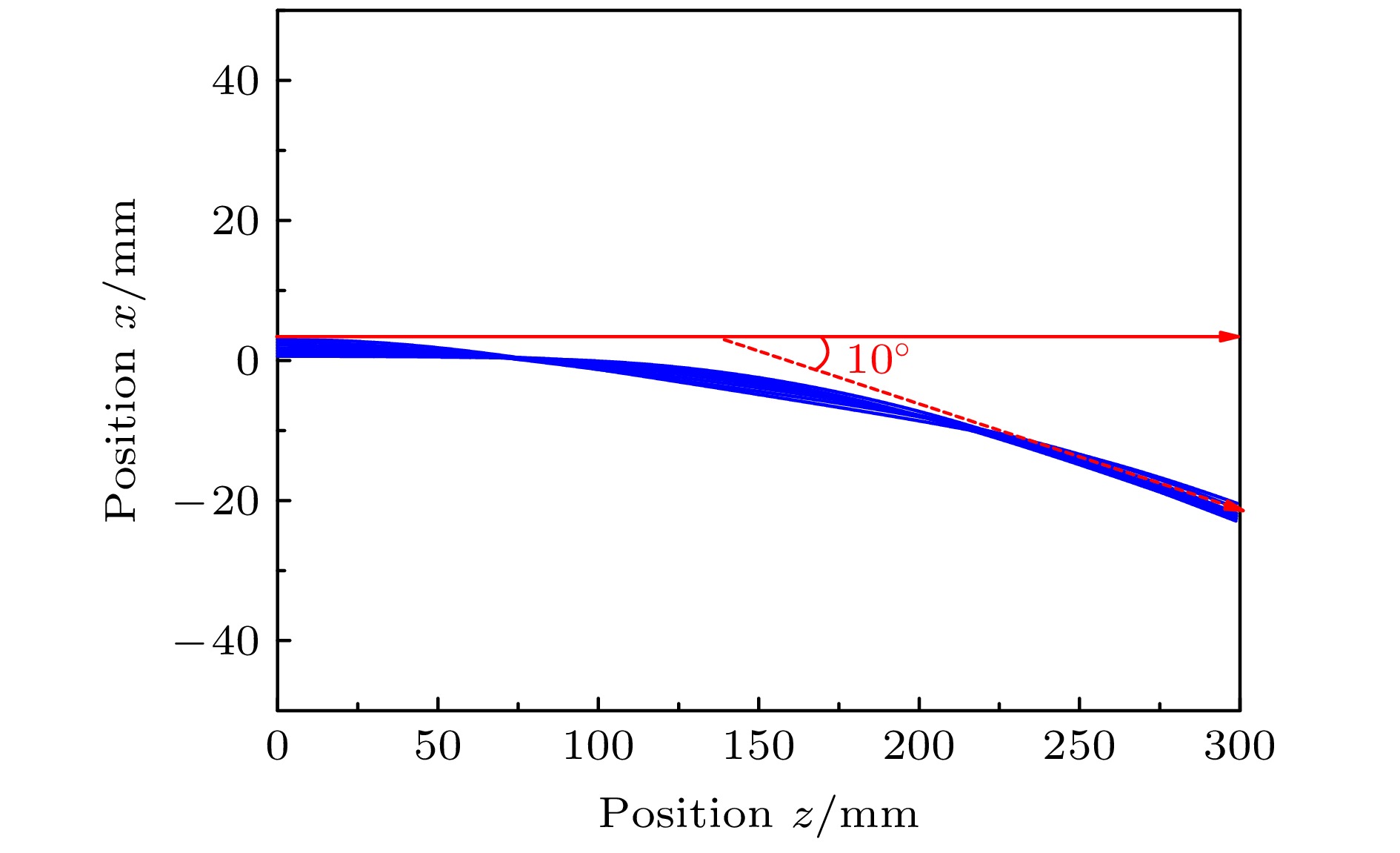
      结合上述磁场分布和(2)式, 图5计算得到了800 m/s的$ {M_J} = + 1 $磁子能级23S1 He*原子在磁组件内的运动轨迹. 从图5可以看出, 单个磁组件对垂直进入磁导中心空隙的$ {M_J} = + 1 $磁子能级的23S1亚稳态氦原子有显著的聚焦效果. 这也表明, $ {M_J} = - 1 $的亚稳态氦原子将表现出相反的运动特征, 即磁导对于$ {M_J} = - 1 $氦原子具有发散效果. $ {M_J} = 0 $的亚稳态氦原子由于受磁场力为零, 在磁组件内将不受影响, 继续沿着初始方向飞行. 本文模拟800 m/s氦原子传输是因为液氮冷却后氦束速度约为800 m/s的原子占比较多, 与脉冲阀产生的超声速氢分子束速度相近(脉冲阀冷泵降温至约40 K), 速度相近的合并束碰撞有利于开展更低碰撞能的低温反应实验.

      图6计算了穿过整个弧形磁导装置的氦原子二维运动轨迹(以800 m/s氦原子为例), 如蓝色曲线所示. 计算结果表明, 氦原子从磁导中心隙间垂直进入磁导装置后, $ {M_J} = + 1 $磁子能级23S1量子态氦原子在不均匀磁场中受“类似向心力”的磁场力作用, 原子的平动运动方向被改变, 不断“扭摆”前进, 最终原子沿着磁组件中心隙间顺利飞出磁导, 实现约10°角的偏转传输. 此外, 不同速度原子穿过磁导的模拟表明, 磁导能够实现纵向速度小于900 m/s原子的偏转传输, 随着原子飞行速度的增加, 原子穿过磁导的传输效率降低. 图6中红色实线箭头表明原子的初始速度方向, 虚线箭头标记的为飞出磁导的原子速度方向(与分子束共线). 此外, 需要说明的是, 本文中引导氦原子偏转的磁导可以有效地剔除杂散粒子进入探测区域: 1) RF射频放电产生的带电粒子可被磁钢的磁场偏转, 轰击在腔壁和其他金属件, 不能进入下游探测器; 2)放电产生的高能光子尽管可以进入磁导, 但沿直线传输的光子轰击在磁组件的固定件上, 而不能从磁导出口出射(磁导出口处安装了6 mm直径的小孔, 仅允许大角度偏转后的束流从中心飞出后进入下游的探测区域); 3) $ {M_J} = 0 $的磁子能级氦原子不受磁场力作用, 沿着入射方向继续飞行, 最终轰击在固定件和腔壁而被淬灭, 不能够顺利通过磁导; 4) $ {M_J} = - 1 $氦原子所受磁场力使其不断偏离磁导轴线飞行, 最终也不能顺利穿过磁导. 由此, 该磁导仅能偏转$ {M_J} = + 1 $的磁子能级氦原子, 保证了后续参加碰撞反应的量子态的单色性.

      本实验通过电子倍增管探测器收集He*原子, 并由计数器获得氦原子计数率. 实验中, 开启射频放电, 亚稳态He*原子产生并顺利进入磁导, 磁导出口处的电子倍增管探测到被偏转的氦束强度为~3.5×105 atoms/s. 需要说明的是, 未开启射频放电时(无亚稳态He*原子产生), 电子倍增管探测器的计数率为1—2 atoms/s, 因此本底噪声引入的统计计数较氦原子束强度可被忽略. 为进一步提高偏转后原子束的品质, 本实验采用二维横向激光冷却方法实现氦原子束流的准直和强度的提升. 利用图2激光光学系统, 调节参考信号REF频率改变冷却光与参考光的拍频差, 并通过PID反馈实现Laser 2冷却光的频率调节. Laser 2冷却光通过光纤放大器进一步放大功率后, 入射至真空腔室内的横向冷却反射镜上, 由此增强激光散射作用力. 同时, 调节冷却光与束流的作用角度, 优化实验条件. 最终, 通过优化横向冷却反射镜的角度、入射激光的角度、入射激光的频率及激光功率等后, 实验测量的束通量约为2.5×106 atoms/s, 束流强度增大约7倍. 实验中, Laser 2冷却光的中心频率为亚稳态氦原子23S1—23P2跃迁的共振频率附近. 冷却光加入后原子束流强度的大幅度提升, 也验证了电子倍增管收集的信号来自于亚稳态氦原子. 因为Laser 2激光频率在23S1—23P2跃迁的共振频率附近, 冷却光仅对23S1亚稳态氦原子起作用, 其他态的氦不吸收该波长光子. 实验采用液氮冷却方式降低射频放电的氦原子速度, 热平衡状态下原子束的速度分布满足玻尔兹曼分布, 氦束的最概然速度约为900 m/s ($v_0= \sqrt{3{k}_{\mathrm{B}}T/M} $, 其中$ {k}_{\mathrm{B}} $玻尔兹曼常数, T气体环境温度, M为原子的质量). 因速度超过900 m/s的氦原子无法通过磁导, 故最终穿过磁导的氦原子速度均低于900 m/s, 且具有较宽的速度分布.

      由此, 本实验采用磁导方法引导氦原子传输, 通过将23S1亚稳态氦原子的不同磁子能级原子分离, 实现$ {M_J} = + 1 $量子态23S14He*激发态原子的选态制备. 结合磁场的有限元分析和原子运动轨迹的模拟表明, $ {M_J} = + 1 $磁子能级态氦原子在磁导内扭摆前进, 最终可实现约10°角的偏转传输. 经偏转后的量子态选择氦束将与沿直线穿过磁导的超声分子束(不受磁场影响的中性分子束)共线传输, 为开展毫开尔文量级氦与分子合并束的极低能量冷碰撞提供必要的实验支撑. 国际上, Narevicius课题组[20]采用Even-Lavie脉冲阀和介质阻挡放电技术产生亚稳态He*原子, 并利用通电导线产生梯度磁场的方法偏转23S1氦原子, 实验中通电导线需施加千安培量级的电流以此产生偏转氦原子所需的磁场, 实验重复频率为10 Hz. 不同的是, 本实验采用射频放电连续He*束流源和永磁体磁导实现氦原子的偏转, 不需要大功率供电和冷却系统, 实验重复频率有望提高(连续氦束和分子束碰撞实验的重复频率与分子束脉冲阀的工作频率相关, Even-Lavie阀无放电时的工作频率可达几百Hz水平[32]).

    4.   结论及展望

    • 本工作设计了一种引导中性原子偏转的磁导, 利用原子的塞曼效应, 通过永磁体磁导引导原子的传输, 实现了三重态23S1亚稳态氦原子的大角度偏转, 并通过磁场调控制备了$ {M_J} = + 1 $磁子能级氦原子He*(23S1, $ {M_J} = + 1 $)单量子态的选态. 实验系统主要包括三个部分: 束源部分、磁导部分及探测部分. 23S1亚稳态氦原子束源是由射频放电激发产生的连续束. 实验通过优化功率和频率等射频放电参数, 结合激光冷却原子的二维横向冷却技术调试了原子束流. 在合并束流的磁导出口处测得>106 atoms/s数量级的亚稳态氦通量, 验证了该磁导引导原子传输的实验方案. 本实验中自主发展的磁导具备以下特点: 1)实现中性亚稳态氦原子束的偏转; 2)实现单一磁子能级氦原子量子态的选态; 3)氦原子传输的同时允许沿直线传输的分子束顺利通过, 并且氦原子束和分子束在装置出口处实现共线传输. 为亚稳态氦原子与分子低于开尔文量级的合并束低温碰撞实验提供了重要的实验基础, 将促进对冷碰撞反应在星际介质演化中重要贡献的理解, 并有助于发展化学反应调控的相关研究. 本文发展的磁导方案也有望在原子的速度滤波和冷原子输运领域得到广泛的应用. 后续研究将在本实验工作基础上, 借助激光与原子的作用, 利用光学抽运方法实现原子磁极化, 将原子泵浦到$ {M_J} = + 1 $磁子能级“暗态”提升单量子态氦原子布居数. 利用激光冷却原子方法(如二维磁光阱、光学黏胶等方法)优化束流品质, 实现更高密度氦原子的制备.

    参考文献 (35)

目录

/

返回文章
返回