行波管作为微波信号放大的核心器件, 由于工作频率高、输出功率大、工作频带宽、抗干扰能力强, 被应用于电子对抗、雷达探测、无线通信、航空航天等领域^[1]. 截至2023年12月, 西安空间无线电技术研究所作为整机集成商的国产化行波管放大器在轨应用数量达到566台, 工作频率包括L频段至Q/V频段, 连续波输出功率包括10 W至200 W^[2]. 行波管的主要组成包括电子枪、慢波结构和收集极, 由电子枪产生的电子注作为行波管中的粒子源, 慢波结构的作用就是使微波信号的相速降下来, 可以使得电子注与微波信号产生有效的相互作用, 收集极的主要功能是接收已经完成与微波信号能量交换的粒子. 聚类算法是机器学习、数据挖掘和模式识别中的一个基本工具, 用于将数据集划分为若干个子集, 使得同一子集中的样本相似, 而不同子集中的样本不相似^[3]. 近年来应用于各种工业场景的聚类算法越来越多也越来越复杂, 例如: 通过密度归一化增强密度峰聚类^[4]、基于网格的密度峰聚类算法^[5]、基于小波变换的负荷曲线聚类算法^[6]等. 其中, K均值聚类算法是最流行、最简单的聚类算法之一, 它最早出现于1955年, 至今已有上千种聚类算法发表, 但K均值聚类算法仍然被广泛使用^[7]. 行波管的注波互作用仿真中通常采用的是均匀理想电子注作为粒子源, 通过设置适合电压、电流、电子注半径等代替实际电子枪, 这样做的好处是缩短注波互作用计算时间. 但是采用理想电子注作为粒子源时, 由于理想电子注上每个粒子的能量以及分布都是均匀的, 往往会忽略了电子注的不均匀性对注波互作用的影响^[8]. 在实际中电子枪设计会存在不足, 不仅会使得电流和电子注半径没有达到良好的预值, 而且由于电子注内各个粒子的能量是存在差异的, 这就导致了每个粒子的初始速度不同, 一部分粒子与微波信号同步, 另一部分粒子与微波信号不同步, 进而会影响整个注波互作用. 采用从电子枪内电子注注腰处的粒子作为注波互作用仿真的粒子源, 行波管的输出特性更接近实际情况, 但是电子注内含有成百上千的粒子使得注波互作用仿真计算量巨大. 因此, 在行波管电子注的仿真分析中引入聚类算法, 使用较为简单的K均值聚类算法将电子枪注腰处的上千个数的粒子进行划分, 简化为数量较少的宏粒子, 保证了宏粒子分布与原始粒子群之间具有相似性, 简化后的宏粒子可以作为行波管互作用区的粒子源进行注波互作用仿真.

在行波管内电子注的层流性会影响周期性聚焦结构中电子注传输的稳定性, 并会影响输出信号的增益^[9]. 电子注层流性主要表现为粒子轨道的交叉程度. 粒子轨道倾角非均匀分布以及粒子产生横向速度分量过大等情况会使得电子注在传输过程中电子轨迹交叉以及部分粒子撞击在行波管螺旋线上, 导致用来与高频场交换能量的粒子数就会减少, 最终影响行波管的增益、带宽和输出功率等关键指标.

近年来, 随着仿真技术和计算能力的提高, 对电子注的研究取得了一系列进展. 在电子光学与注波交互研究领域中, 为了使得行波管的设计结果与实验结果高度一致, 需要建立实际电子情况与注波互作用之间的桥梁, Ge等^[10]使用MATLAB处理腰部位置的宏观粒子数据, 将其作为行波管互作用区仿真的粒子源, 以满足交互计算模型的需求. 由于螺旋线行波管中复杂的电磁环境和阴极发射的随机性, 电子注从电子枪到慢波结构的速度大小和方向是不均匀的, 本课题组前期工作^[11]使用了速度幅值波动范围和速度方向波动范围这两个参数表示建立了不同电子注速度下螺旋线行波管输出特性的仿真模型, 研究分析电子注速度的不均匀性对行波管输出特性产生影响. 在评估电子注质量的研究中, Louksha等^[12]通过不断仿真在距离阴极表面很小的一段距离处的电子注中粒子横向速度v_x的变化来研究回旋管电子光学系统中阴极表面粗糙度对电子束质量的影响. 针对现有的电子光学软件中缺乏对电子层状性质的定量评估指标参数的问题, Zhang等^[13]提出了一个用交叉率和波动率评估电子注层流性的新方法. 仿真结果表明, 该交叉率指数可以准确且定量地评估电子层状性质的质量. 当电子性质的交叉率小于3%时, 且波动率低于30%时, 设计的电子光学系统满足工程要求. David等^[14]研究了用计算机优化技术设计电子枪的问题, 使用MATLAB对仿真结果进行了编程计算, 其中对于电子注层流性参数方面, 提出使用粒子轨迹的一阶导数和二阶导数来组成目标函数, 对仿真的电子注层流性进行优化. Liu等^[15]提出了采用旋转表面阴极的设计方案, 以改善汇聚电子注的层流性, 通过模拟实验, 观察电子枪内电子注电流密度的径向分布图, 说明了旋转表面阴极减弱球面像差, 有助于提高电子注的质量.

上述文献中少有将电子枪和行波管作为一个整体进行仿真研究. 本文对采用三夹持螺旋线慢波结构的某型号行波管^[16]进行仿真分析. 将电子枪注腰处粒子作为行波管的粒子源进行仿真时, 使用K均值聚类算法将电子枪上的初始粒子简化为个数较少的宏粒子, 并以此作为行波管注波互作用仿真的粒子源. 使用径向均方根发射度表征圆柱形电子注的层流性, 而非通过放大观察电子注内的粒子轨道, 主观上判断电子注层流性的好坏. 通过优化电子枪的结构参数, 使得行波管内电子注的层流性得到改善且行波管的输出性能得到提升.

采用相空间模型可以直观地比较层流和非层流的电子注, 在电子注从电子枪产生到传输过程中, 每个粒子的位置和速度都在不断发生变化, 在直角坐标系中每个粒子的运动状态可以用x, v_x, y, v_y, z, v_z的六维相空间来表示. 当电子注截面的粒子分布是圆形对称时, 粒子状态可以用x, v_x的二维相空间来表示, 以x为横坐标, v_x为纵坐标, 就可以勾画出一个包含所有粒子的横向位移和横向速度的相空间分布图^[17]. 电子注的层流性问题, 其实就是电子注在传输的过程中粒子轨道的有序性和无序性的问题.

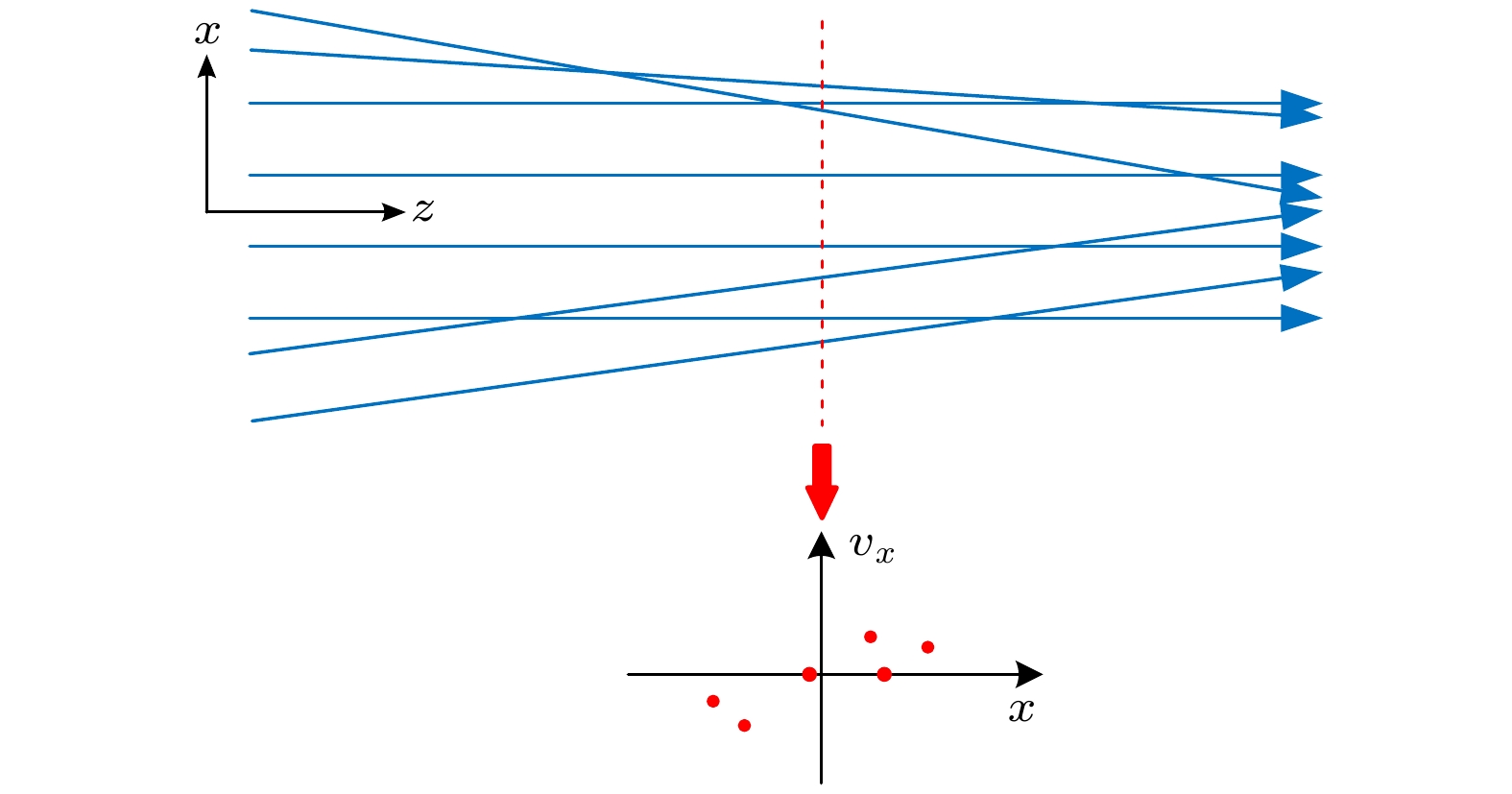
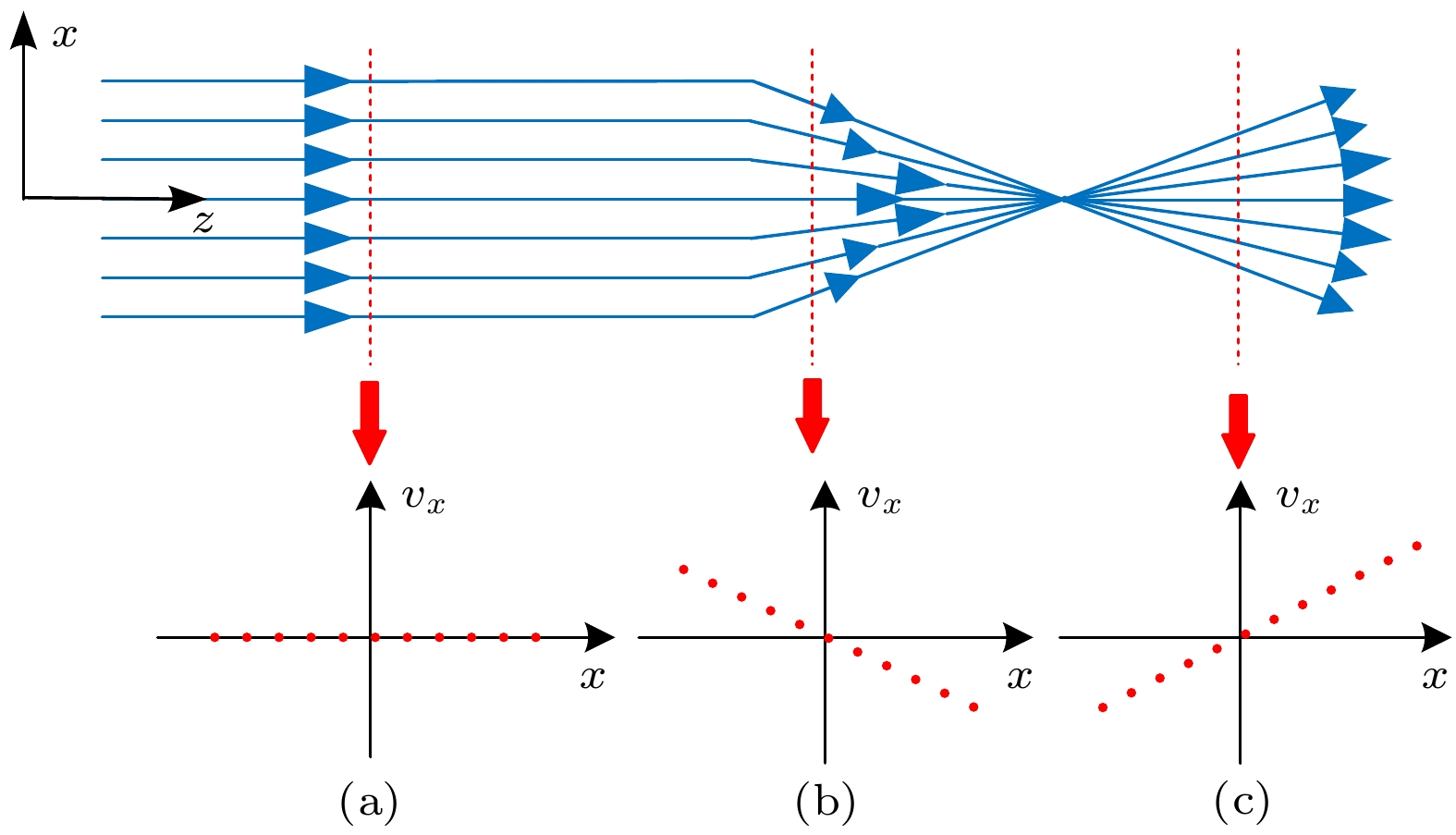
图1为理想的二维电子注模型, 描绘了层流电子注在传输过程中的三种粒子轨道情况以及对应相空间分布图, 模型暂时忽略了空间电荷效应及外力. 电子注在z方向上无限延伸. 选定坐标原点使得x轴的起始端位于电子注的中心, 横向位移的变化率即横向速度v_x.

其中图1(a)是平行电子注, 即所有粒子的横向速度均为0, 这种电子注从产生到传输的过程中粒子轨道按层分布, 不存在交叉的粒子轨道; 图1(b)为汇聚的电子注, 由于粒子的横向位移与横向速度之间成正比关系, 因此所有的粒子轨道会汇聚于一点; 图1(c)是发散的电子注, 粒子的横向位移与横向速度也成正比关系, 即使传输到无限远的距离, 粒子轨道之间也不会发生交叉.

在实际的电子注中, 任意一个横向位置都会存在具有横向速度的粒子, 其在产生与传播的过程中是无序的, 使得粒子轨迹之间会不断相互交叉, 所以实际的电子注均为非层流电子注. 图2所示的非层流电子注, 其在某一位置的相空间分布图像中横向位移与横向速度之间不呈线性关系.

在电子枪的设计过程中利用数值模拟软件计算得到某种结构电子枪的电子运动轨迹图形后, 设计人员凭肉眼观测电子注的层流性好坏^[18]. 这种判断带有很强的主观性, 且注腰处的粒子轨道即使被放大, 但由于粒子轨道数量多, 识别它们的轨道交叉仍然具有挑战性. 因此, 需要利用特定的参数来量化电子注的层流状态.

实验中粒子轨道倾角通常更容易直接测量, 常用横向位移x和横向倾角x' 来计算发射度. 发射度是表征径迹空间(x-x' 平面)内包围粒子分布的椭圆相面积大小的参数, 发射度用字母$\varepsilon $表示, 其单位为mm·mrad, 其值为椭圆面积除以${\pi}$. 椭圆范围的确定具有误差性, 因此基于电子注中的粒子轨迹坐标信息计算得到的发射度表达式更实用, 用统计定义的发射度即全部粒子的横向位移的均方根来描述发射度, 称为均方根发射度${\varepsilon _{{\text{rms}}}}$.

由于在行波管内的电子注为圆柱形电子注, 可使用径向均方根发射度${\varepsilon _{r{\text{-rms}}}}$表征电子注层流性. 将x和y两个方向层流状态耦合则需要将直角坐标转换为极坐标, 因此, 先推导直角坐标系中的x和y方向上的均方根发射度.

x方向上的均方根发射度表达式为^[19]

得到均方根发射度在x方向上的公式, 同理y方向上的均方根发射度公式为

将x与y方向进行耦合, 可以采用径向均方根发射度来表征圆柱形电子注的层流性, 需要将直角坐标系转换为极坐标系.

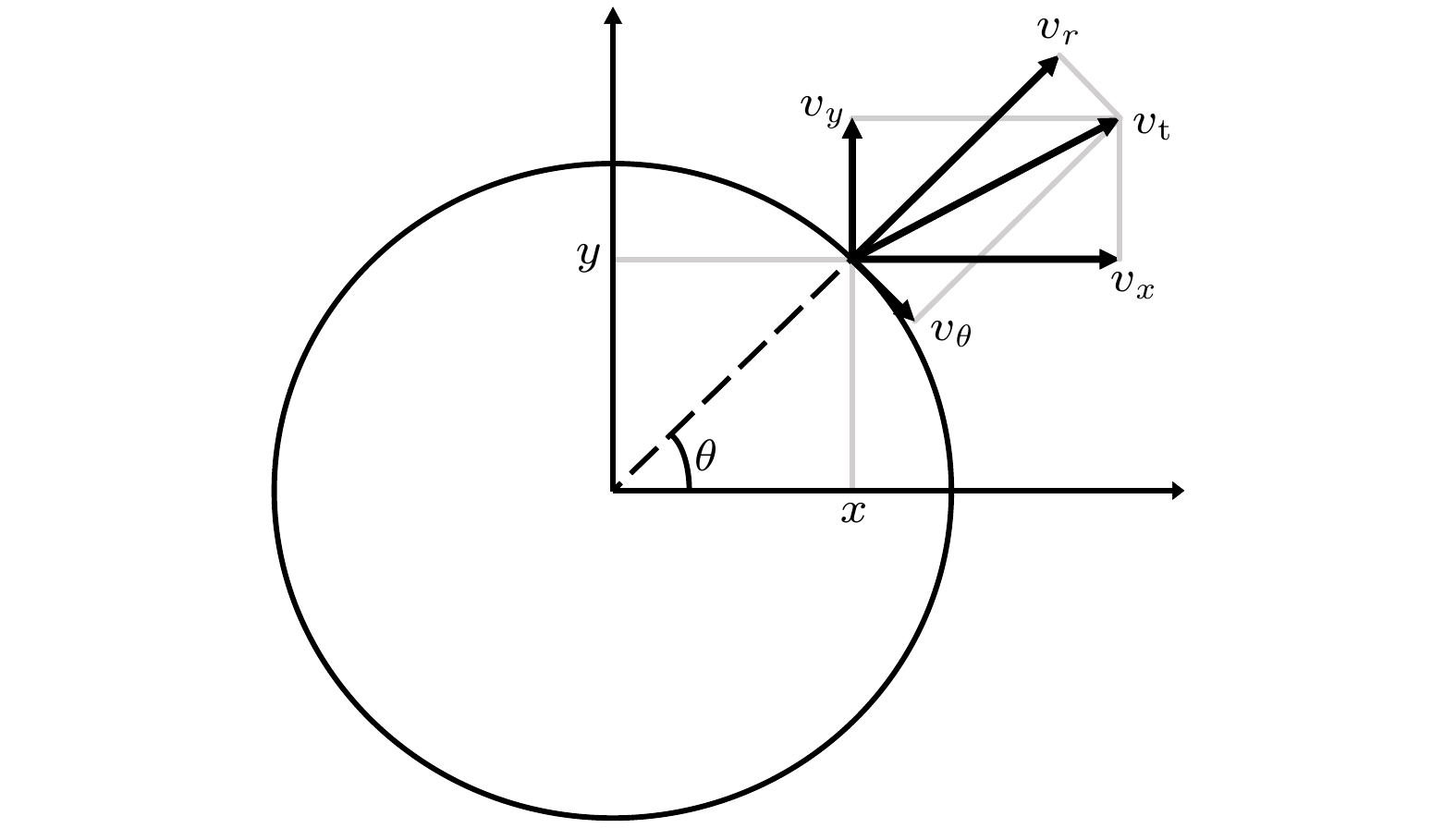
在傍轴近似下, 横向倾角与横向速度的关系是$ x' \approx {{{v_x}} \mathord{\left/ {\vphantom {{{v_x}} {{v_z}}}} \right. } {{v_z}}} $和$ y' \approx {{{v_y}} \mathord{\left/ {\vphantom {{{v_y}} {{v_z}}}} \right. } {{v_z}}} $, 可以得到均方根发射度与横向速度之间的关系式:

图3为粒子速度的矢量图, 其中v_r为径向速度, 而v_θ为角向速度, 使用图3对x, y方向上的速度进行分解, 得到的径向速度和角向速度为

将(5)式和(6)式联立求解可以得到x方向速度与径向和角向速度的关系式:

将(7)式代入(3)式中, 得到:

将(8)式代入(4)式中, 得到:

通过将(9)式和(10)式进一步推导可以求得(11)式, 即为径向均方根发射度表达式^[20]:

本小节阐述了电子注中粒子的状态以及相空间模型, 使用相空间模型举例来区分层流电子注与非层流电子注的不同, 由于在电子枪以及行波管内的电子注为圆柱形电子注, 因此可以使用推导出的径向均方根发射度表征电子注层流状态.

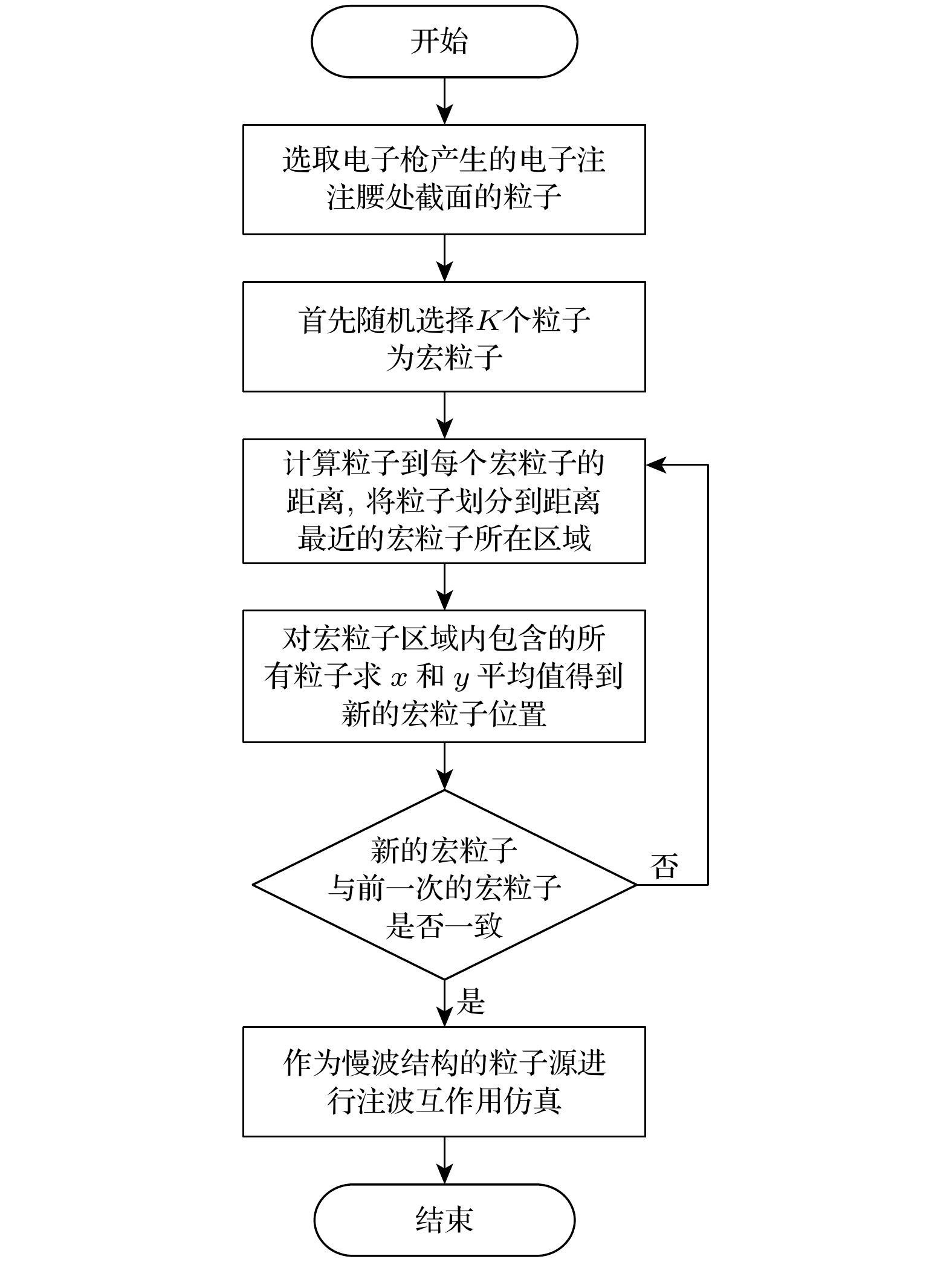
如果将电子枪仿真得到的上千个原始粒子通过粒子导入面法全部导入行波管的粒子源中进行注波互作用计算仿真, 由于计算数据庞大, 会导致计算时间十分漫长, 整个设计优化的工作效率降低. 因此使用K均值聚类算法对电子枪中注腰位置处粒子信息进行处理, 将其简化为个数较少的宏粒子从而缩短仿真时间提高工作效率. 应用于行波管电子注简化的K均值聚类算法流程图如图4所示, 使用该模型将行波管电子注截面粒子简化为宏粒子, 包括以下步骤: 1)使用粒子追踪求解得到电子枪的电子注轨迹, 获取电子注注腰处截面粒子的位置分布、速度、电流等信息; 2)在注腰处截面的粒子中随机选取K个粒子作为宏粒子; 3)计算截面上的粒子到每个宏粒子的距离, 并将粒子划分到距离最近的宏粒子所在区域; 4)对于宏粒子区域内包含的所有粒子, 分别计算x方向、y方向和z方向上的宏粒子位置, 宏粒子在x方向、y方向和z方向的速度、宏粒子的电流值、宏粒子的质量和电荷量; 5)对比通过步骤4)计算得到的新宏粒子的位置信息与前一次宏粒子的位置信息是否一致; 6)如果位置信息不一致, 则要返回步骤3)继续求解新的宏粒子的位置, 直到新的宏粒子信息与前一次宏粒子的位置信息一致时, 便可以结束循环得到的最终宏粒子位置分布; 7)将处理后包含速度、电流值、质量和电荷量的宏粒子作为行波管互作用区的粒子源, 进行注波互作用仿真, 通过对输出结果分析计算可以得到行波管的输出功率.

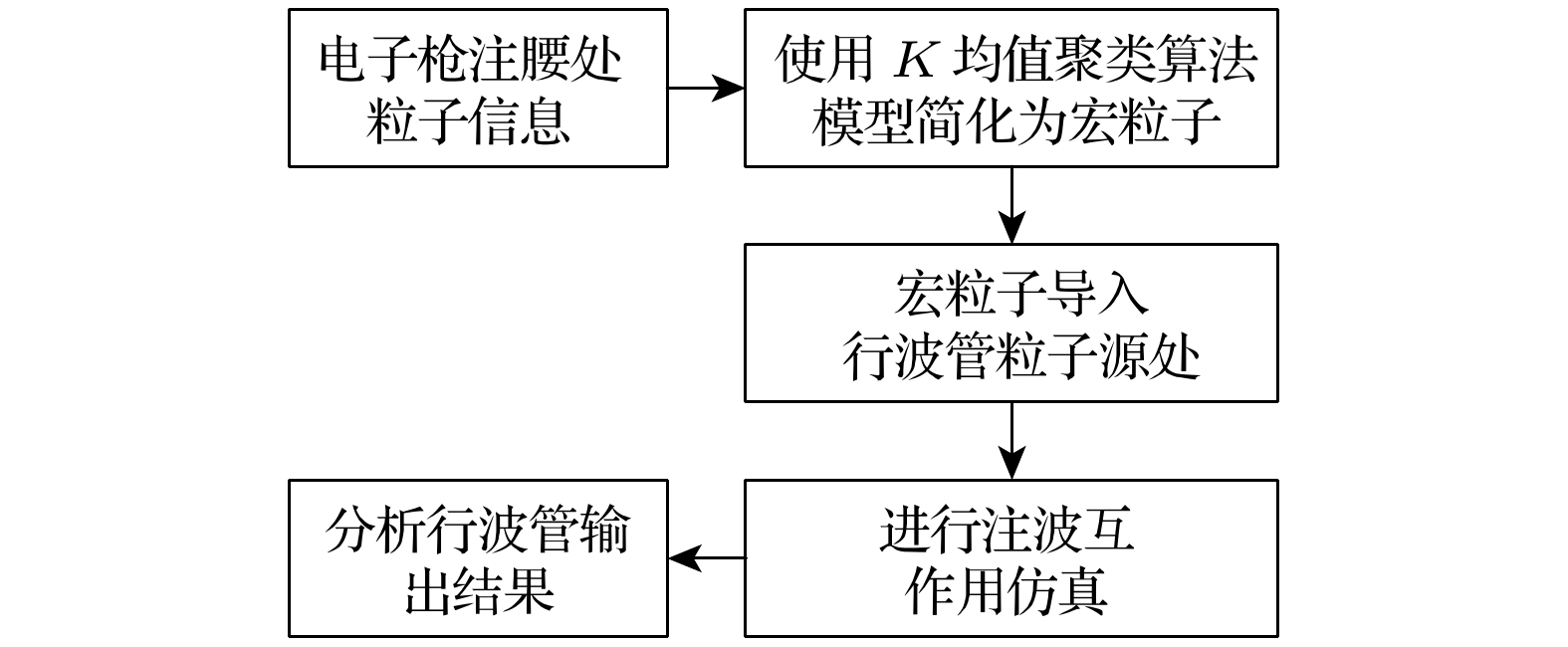
本文的行波管仿真分析时使用了256G内存的计算机, 在CST的仿真分析中使用了GeForce RTX 4090D显卡开启GPU加速. 行波管仿真分析步骤如图5所示, 调节电子枪的参数后, 使用CST的粒子跟踪求解器计算出层流性不同的电子注信息, 并采用径向均方根发射度来表征电子注的层流性; 在MATLAB中使用K均值聚类算法对注腰处的粒子信息进行简化处理, 得到的宏粒子作为行波管互作用区的粒子源, 再使用CST的网格粒子求解器进行注波互作用仿真, 不同层流性的电子注最终会影响行波管的输出特性. 本文中使用的某型号螺旋线行波管参数如表1所列.

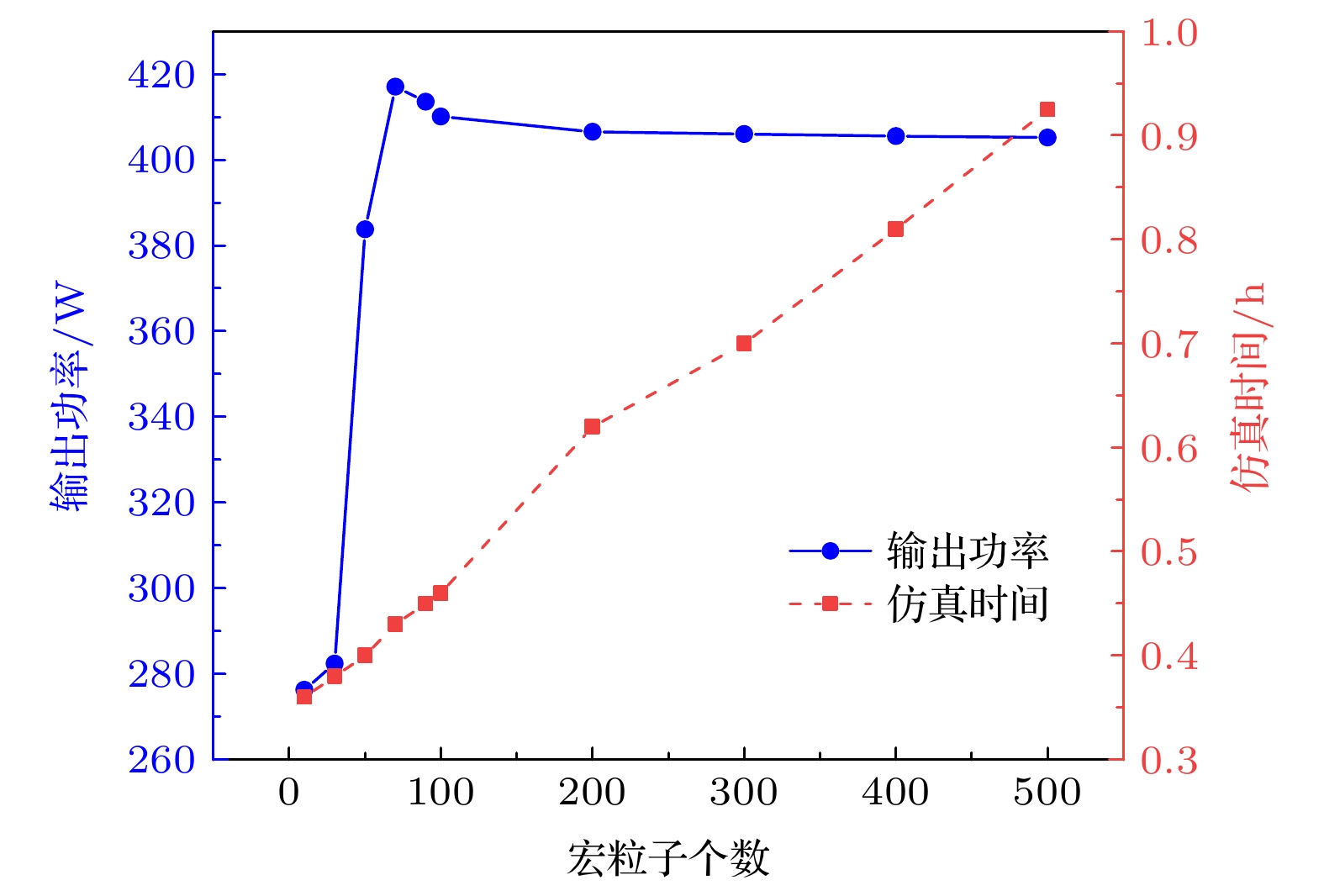
将原始粒子简化为数量不同的宏粒子, 分别作为行波管粒子源进行注波互作用仿真, 得到仿真 后的输出功率以及仿真所消耗的时间, 宏粒子个数取值与行波管输出功率和仿真时间的关系如图6 所示. 由图6可知, 当宏粒子的个数取值在100到 500之间时互作用区的输出功率差距不大. 宏粒子个数越多, 仿真时间越长, 宏粒子个数的取值需要保证在行波管输出功率不变的情况下, 宏粒子数 越少.

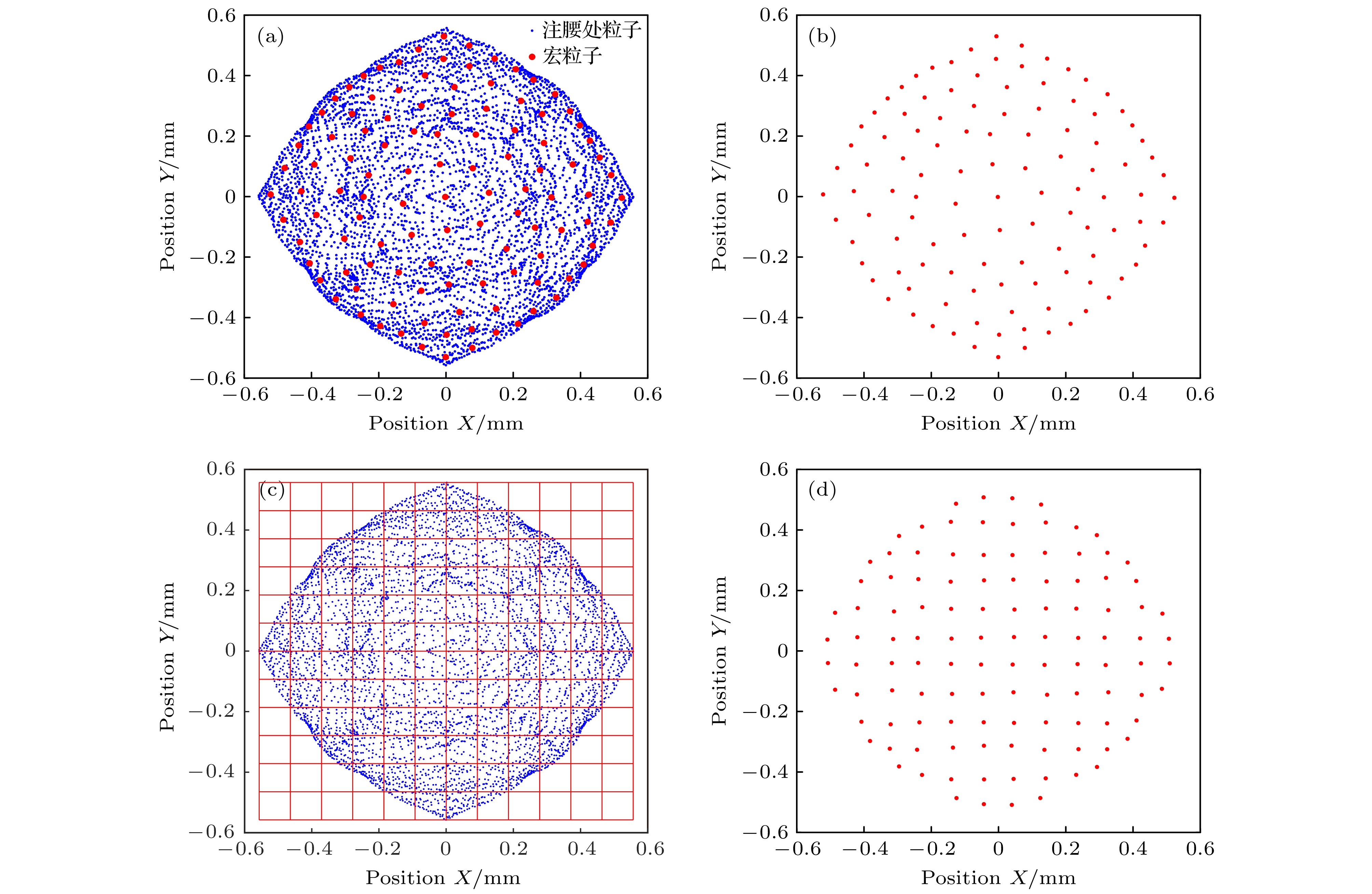
采用K均值聚类算法模型对原始粒子进行简化, 得到简化后的宏粒子如图7(a)和图7(b)所示; 采用网格模型将原始的粒子简化为宏粒子的分布, 在图7(c)中, 将x轴和y轴分别进行12等分, 一共划分为144个等分网格区域, 将每一个小等分网格中的若干粒子参数进行同样的计算处理, 简化为一个新的宏粒子, 最终简化得到的112个宏粒子位置分布如图7(d)所示. 为了与网格模型得到的宏粒子在输出结果上进行对比, 则使用K均值聚类算法的宏粒子个数也为112.

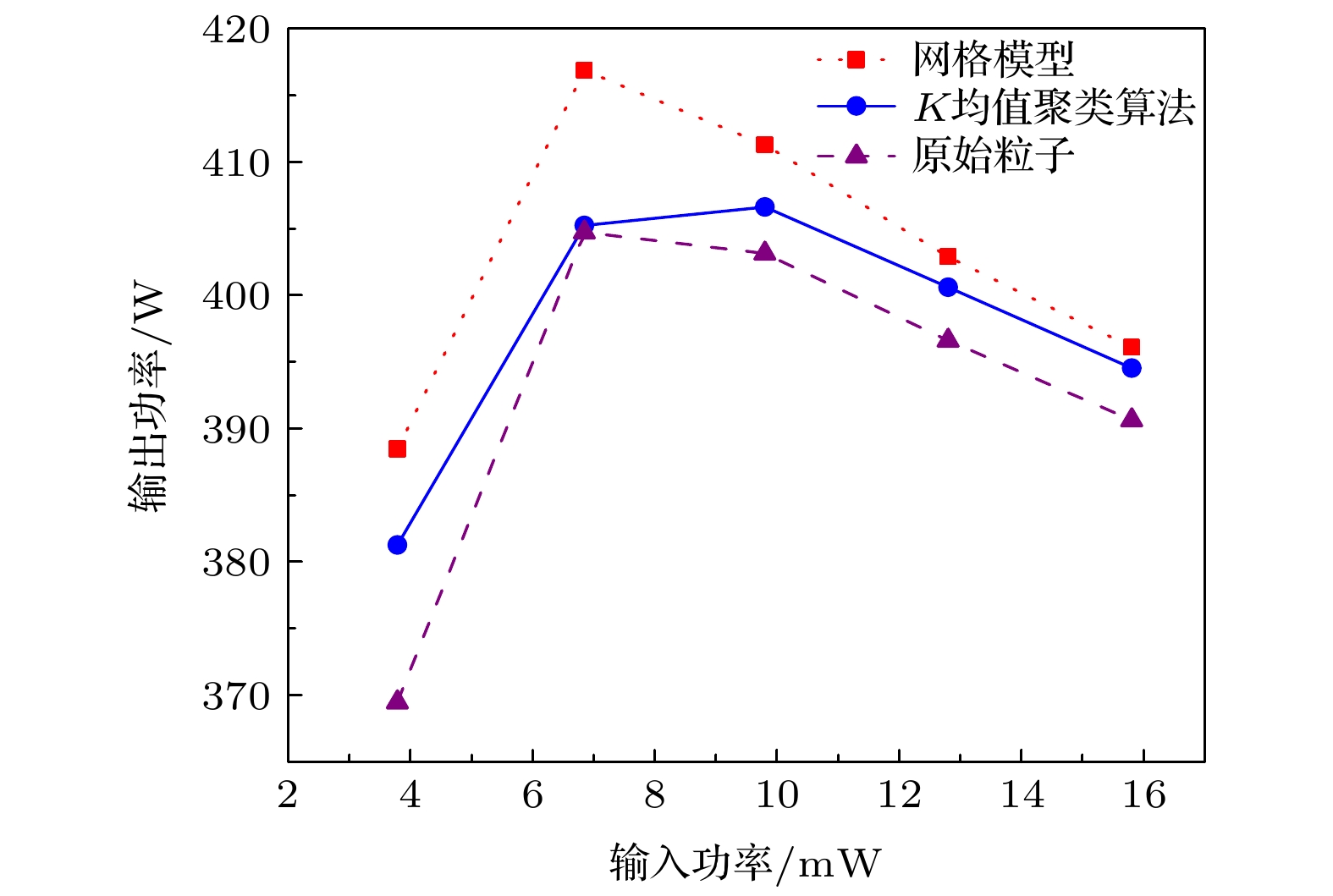
改变行波管输入信号的功率, 分别使用原始粒子、K均值聚类算法简化得到的宏粒子和网格模型简化得到的宏粒子作为粒子源进行注波互作用仿真, 得到了三种粒子在不同输入功率信号下的输出功率, 结果如图8所示, 从图6和图8可以看出, 当输入信号的功率为6.8 mW时, 使用4963个原始粒子, 仿真耗时5.53 h, 输出功率为404.73 W; 使用K均值聚类算法简化后含有112个宏粒子的粒子源时, 仿真耗时0.65 h, 输出功率为405.25 W, 输出功率只比原始粒子的大0.52 W; 使用网格模型简化后含有112个宏粒子作为粒子源, 仿真耗时一样为0.65 h, 但是使用网格模型时行波管的输出功率与使用原始粒子源得到的行波管输出功率相差大, 输出功率为416.88 W, 输出功率比原始粒子的大11.63 W. 从图6和图8还可以看出, 与未简化的原始粒子相比, K均值聚类算法简化原始粒子和网格模型简化原始粒子都极大减少了互作用区仿真的计算量. 与网格模型相比, 使用K均值聚类算法得到宏粒子的注波互作用仿真结果更加接近使用原始粒子的注波互作用仿真结果.

基于K均值聚类算法简化, 使得注腰处的电子注层流性可以方便快速地体现在行波管的注波互作用中. 本文以调节阴极粒子的发散角度和阴阳极间距离这两个参数作为研究电子注层流性的应用举例, 调节这两个参数使得电子注层流性发生改变, 进一步研究电子注层流性对行波管输出性能的影响.

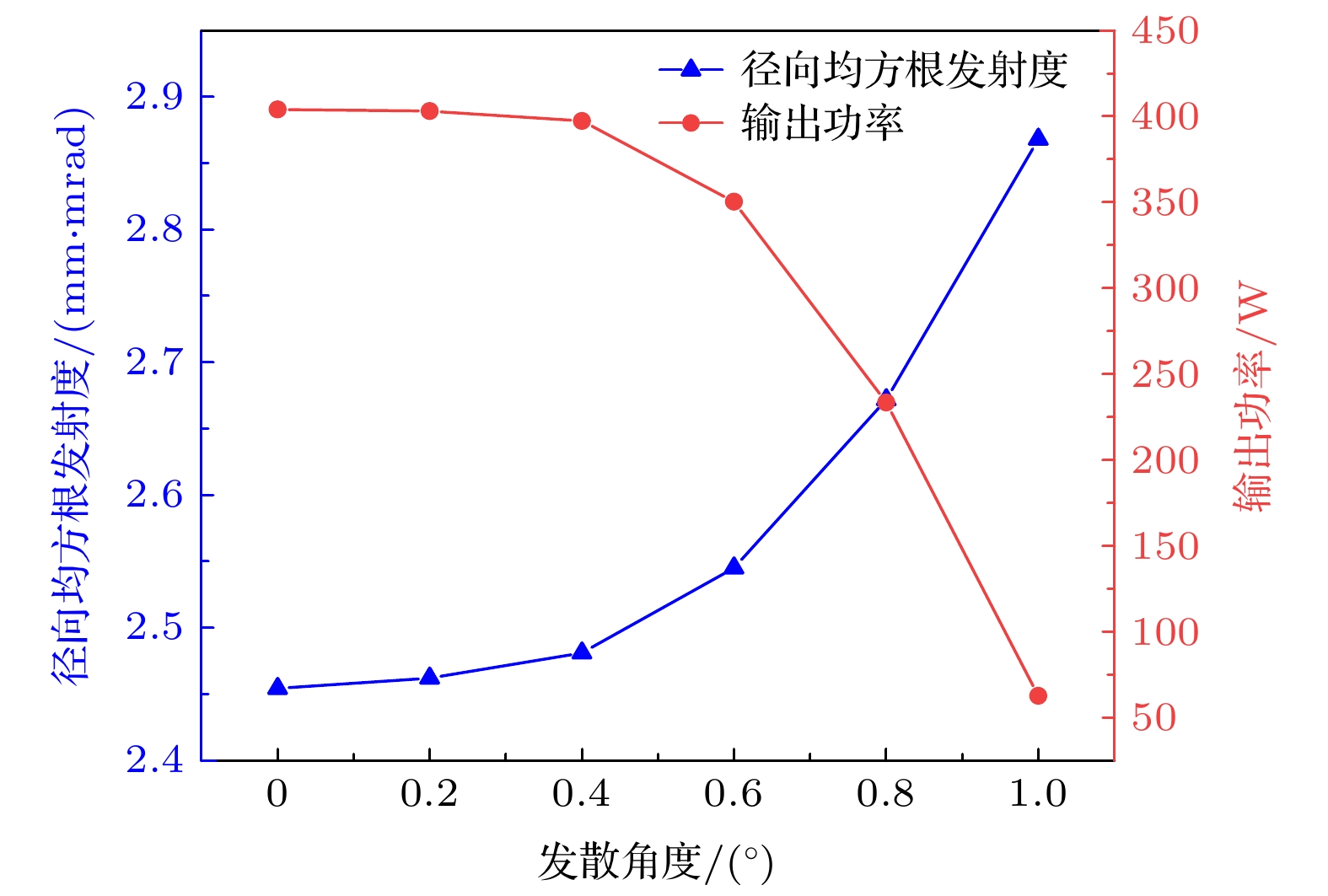
阴极表面的粗糙度影响了电子初始的发射角度, 通过设置电子发散角度的分布来描述阴极粗糙度^[21]. 改变电子枪阴极处发散角度的大小, 将得到的粒子进行注波互作用仿真, 发散角度与行波管输出功率的关系如图9所示. 当阴极表面粗糙到使得粒子源发射的发散角度在0°—0.4°时, 径向均方根发射度变化不大, 电子注层流性变化较小, 行波管输出功率产生较小的衰减, 输出功率均大于390 W; 当阴极表面粗糙到使得粒子源发射的发散角度在0.4°—0.6°时, 径向均方根发射度有明显的增大, 层流性受到影响, 行波管输出功率产生明显的减小, 输出功率开始小于390 W; 当阴极表面粗糙到使得粒子源发射的发散角度由0.6°增加到1°时, 径向均方根发射度增加到最大值, 电子注层流性最差, 输出功率降为63 W. 当阴极表面越粗糙, 即发散角度越大, 表征电子注层流性的径向均方根发射度数值也越大, 电子注层流性就越差, 导致行波管输出功率下降.

对电子枪阴阳极间距离进行调整, 由于阴极和阳极之间距离发生变化, 导致电场强度发生变化, 以及存在空间电荷效应干扰, 进而会影响电子枪内电子注的质量. 在调整电子枪阴阳极间距离时, 会影响发射电流的大小, 进而影响电子枪的导流系数. 为了保持导流系数不变, 通过调整阴极的发射面积, 保持发射电流为0.35 A.

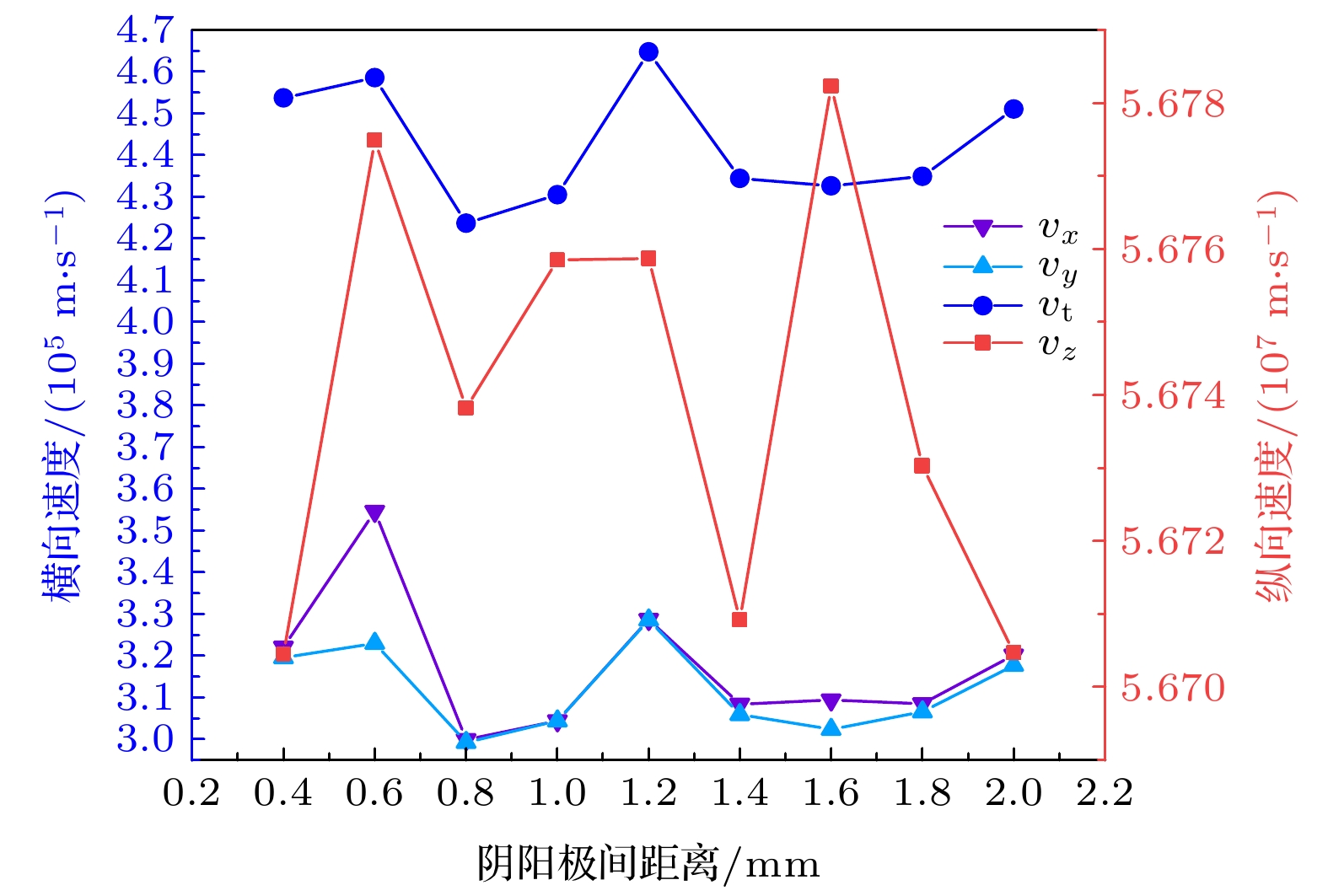
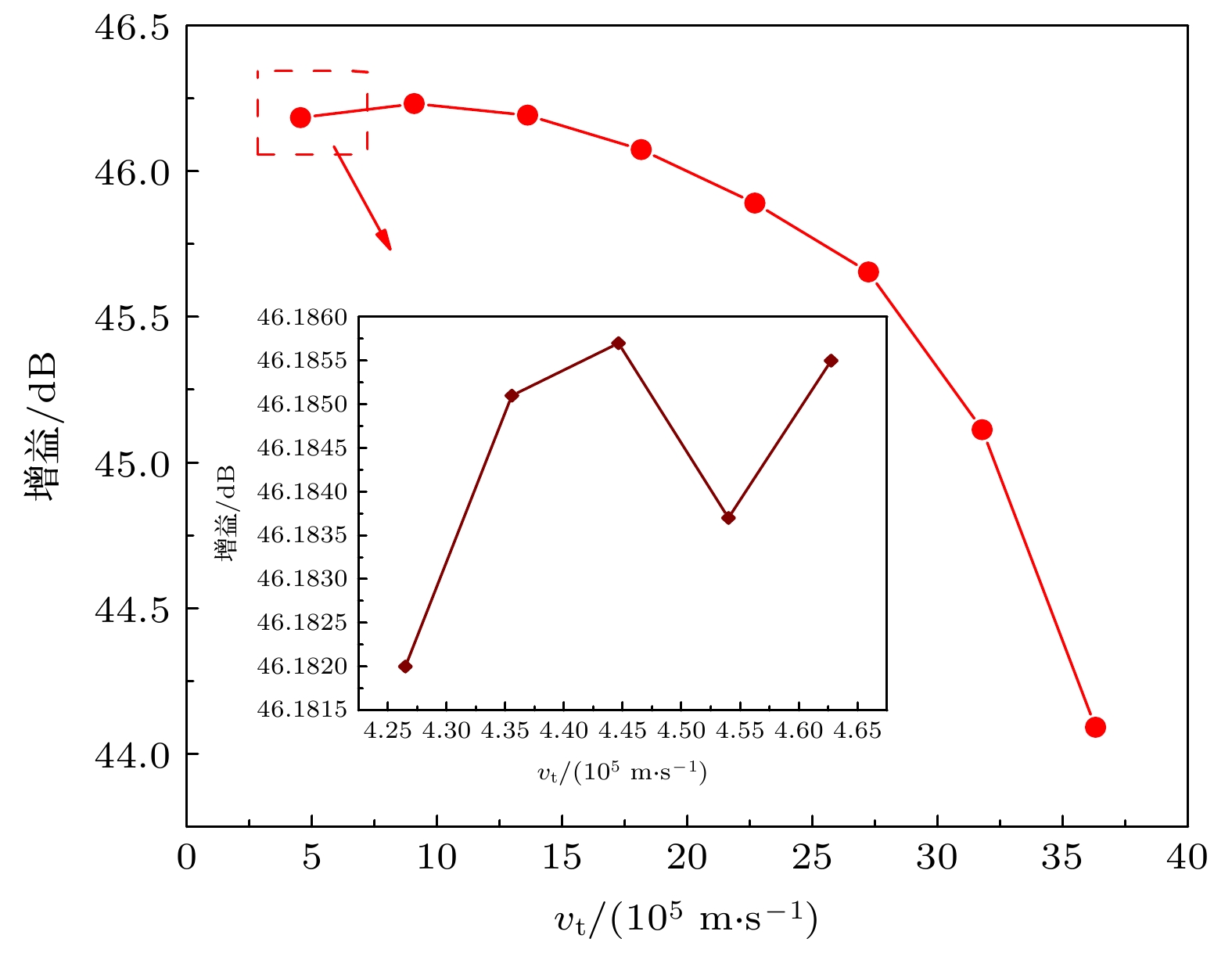
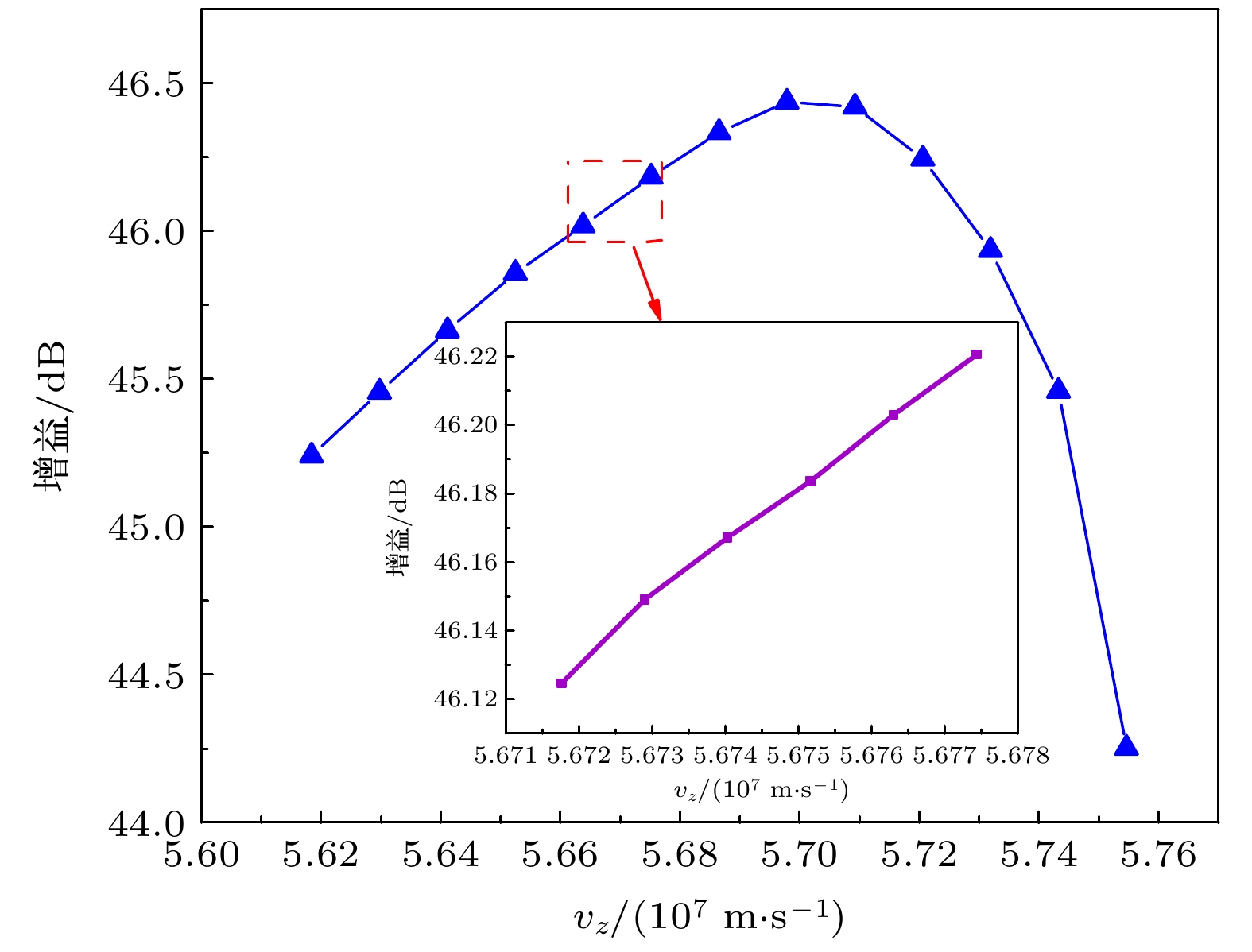
当电子枪阴阳极间距离在0.4—2.0 mm调节时, 进行仿真得到粒子不同的横向速度和纵向速度, 阴阳极间距离对粒子的横向和纵向速度的影响如图10所示. 可以看出, 电子注内的粒子平均横向速度在4.2×10⁵—4.65×10⁵ m/s的范围内波动, 变化范围较小, 其中${v_{\text{t}}} = \sqrt {{v_x^2} + {v_y^2}} $; 电子注内的粒子平均纵向速度在5.670×10⁷—5.678×10⁷ m/s的范围内波动变化, 总的变化范围较小.

当仅改变粒子源处的平均横向速度大小, 进行注波互作用仿真得到的粒子横向速度对行波管输出信号增益的影响如图11所示. 当平均横向速度在4.2×10⁵—3.5×10⁶ m/s的范围内变化时, 行波管增益随横向速度增大而减小. 调节电子枪的阴阳极间距离, 平均横向速度在4.2×10⁵—4.65×10⁵ m/s的范围内波动变化时, 行波管增益的变化约为0.004 dB, 变化较小. 可见当调节电子枪阴阳极间距离时造成的粒子横向速度大小变化对行波管增益的影响有限. 使用MATLAB对粒子信息进行处理, 增大粒子源处的平均纵向速度大小, 进行注波互作用仿真得到的粒子纵向速度对行波管输出信号增益的影响如图12所示. 当粒子平均纵向速度在5.670×10⁷—5.76×10⁷ m/s的范围内波动变化时, 行波管的增益随着纵向速度先增大后减小. 调节电子枪的阴阳极间距离, 粒子平均纵向速度在5.670×10⁷—5.678×10⁷ m/s的范围内波动变化, 行波管的增益均在46 dB以上, 增益变化为0.1 dB. 因此, 当调节电子枪阴阳极间距离时造成的粒子纵向速度大小变化对行波管增益的影响有限. 因此, 当调整电子枪阴阳极间距离时, 单一的横向速度变化和纵向速度变化对行波管的增益影响较小, 需要从电子注层流性的角度进行进一步的仿真研究.

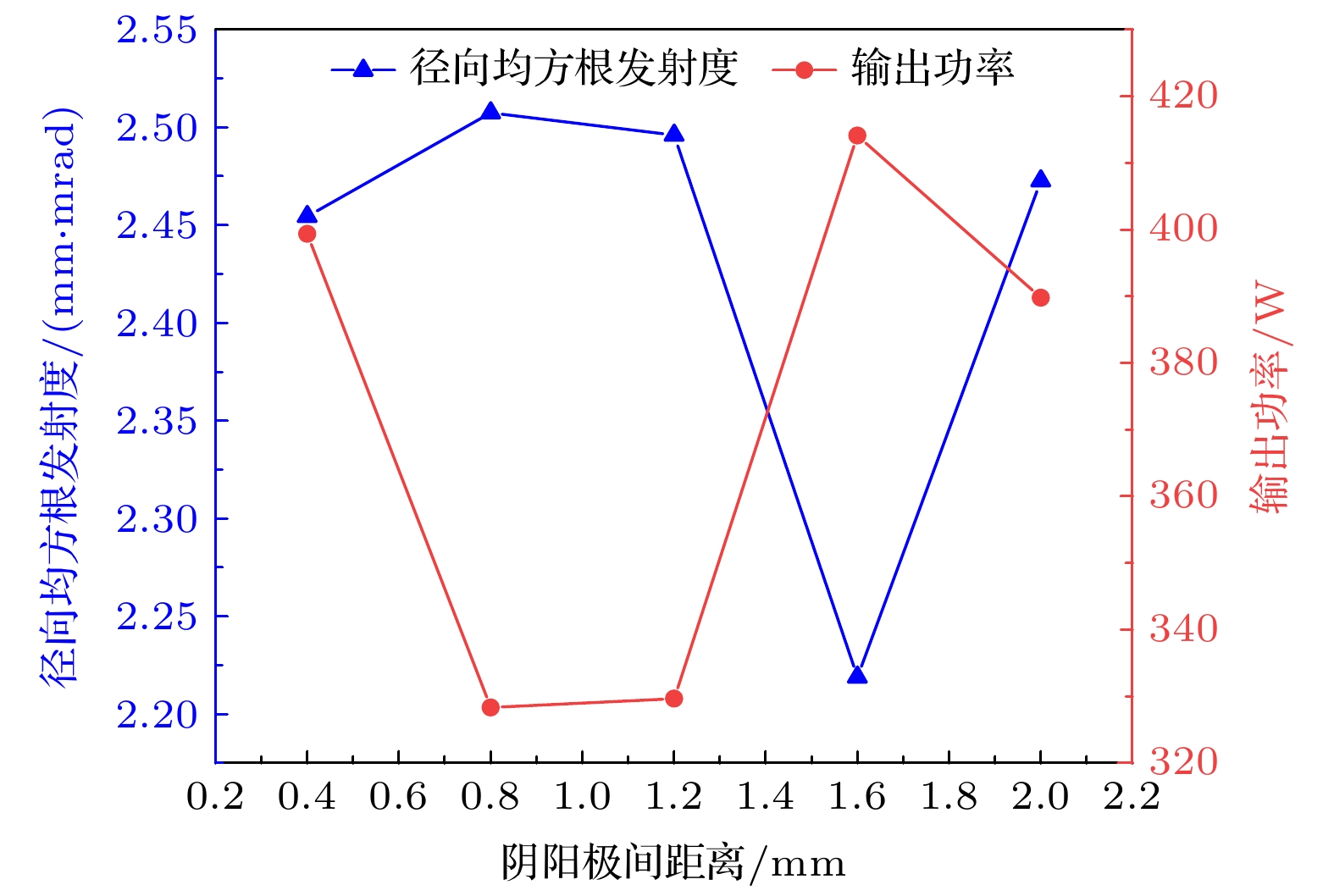
选取阴阳极间距离分别为0.4, 0.8, 1.2, 1.6, 2 mm的5种情况的电子枪, 将其电子注注腰处截面的粒子作为行波管粒子源进行注波互作用仿真, 当输入信号功率为9.8 mW时, 得到的阴阳极间距离与电子注径向均方根发射度和行波管输出功率的关系如图13所示.

当阴阳极间距离为1.6 mm时径向均方根发射度的值最小即电子注层流性最好, 为2.22 mm·mrad, 输出功率最大为414.10 W; 当阴阳极间距离为0.8 mm时径向均方根发射度的值最大即电子注层流性最差, 为2.51 mm·mrad, 输出功率最小为328.34 W. 从图13趋势可以看出, 当电子注的径向均方根发射度的数值越大, 则表征电子注的层流性越差, 此时行波管的输出功率越差.

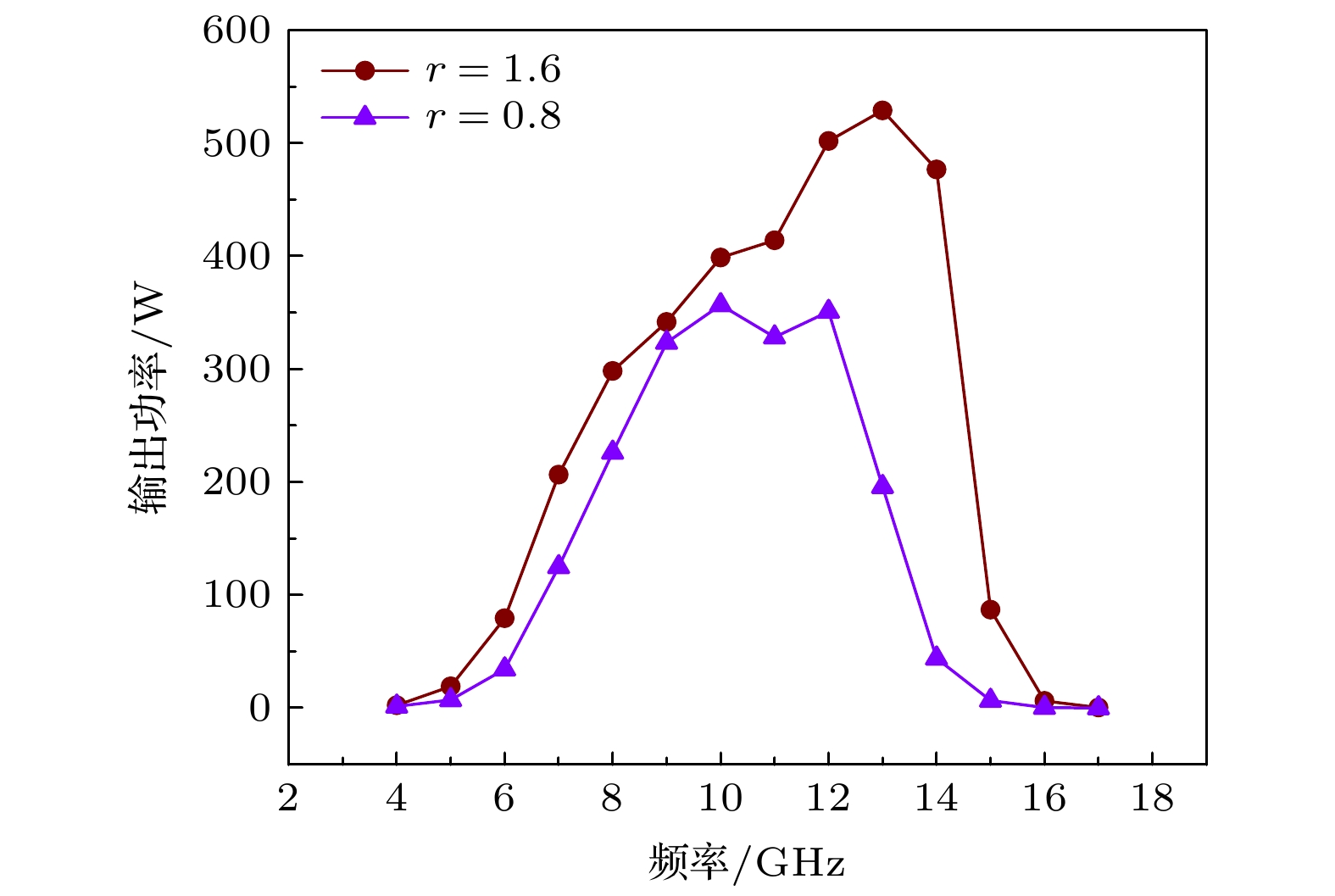
选取图13中电子注层流性最差和最好的两个点(即阴阳极间距离分别为0.8和1.6 mm)作为粒子源, 只改变输入信号的频率大小, 研究使用电子注层流性不同的粒子源进行注波互作用时, 行波管增益和带宽的变化情况. 阴阳极间距离为0.8和1.6 mm时, 输入信号频率与行波管输出功率的关系如图14所示, 层流性好的电子注在各输入信号频率输出功率均较大. 从图14可以看出, 当电子枪优化选用阴阳极间距离为1.6 mm的方案时, 行波管输入信号频率在7—14 GHz的范围内, 输出功率大于200 W, 带宽为7 GHz, 行波管输入信号频率在9—14 GHz的范围内, 输出功率大于300 W, 带宽为5 GHz; 当电子枪优化选用阴阳极间距离为0.8 mm的方案时, 行波管输入信号频率在8—12 GHz的范围内, 输出功率大于200 W, 带宽为4 GHz, 行波管输入信号频率在9—12 GHz的范围内, 输出功率大于300 W, 带宽为3 GHz. 从仿真结果看出, 使用径向均方根发射度表征电子注的层流性, 当电子注的层流性越好则行波管的输出信号增益越大, 输出功率越大, 工作带宽越宽, 使得整个行波管的输出特性不断优化. 使用径向均方根发射度表征电子注层流性在电子枪结构优化设计过程中起到了指导性的作用.

使用K均值聚类算法将电子枪注腰处粒子简化为宏粒子, 粒子数量减少, 使得注波互作用仿真时间由原本的5.53 h减少为0.65 h, 该方法有效地减少注波互作用的仿真时间. 与网格模型相比, 使用K均值聚类算法得到输出结果更加接近原始粒子得到的输出结果. 通过调节电子枪的参数, 得到不同层流特性电子注的注腰处粒子信息. 注波互作用仿真结果表明, 使用径向均方根发射度可以有效地表征圆柱形电子注的层流性. 通过调节电子枪阴阳极间距离, 电子注的层流性得到改善, 径向均方根发射度减小, 空间行波管输出功率由328.34 W上升为414.10 W, 输出功率大于300 W的工作频率带宽由3 GHz拓展为5 GHz. 因此, 电子注层流性变化会影响行波管的输出功率和工作带宽, 依据电子注层流性对行波管性能的影响可以指导电子枪结构参数的优化. 粒子源的发散角度越大, 表征电子注层流性的径向均方根发射度数值越大, 电子注层流性就越差, 导致行波管输出信号的增益下降. 使用K均值聚类算法简化原始粒子, 减少仿真耗时的同时保证了仿真结果的精确度. 考虑到目前使用该聚类算法的作用只是加快了仿真速度, 后续的工作需要实验测试优化后的电子枪和行波管, 进一步调研聚类算法的最新研究, 以提高使用该聚类算法辅助行波管设计和优化的准确度.