首页
登录
注册
-
非晶态二氧化硅(a-SiO2)具有优异的绝缘性能、均匀的无序结构、良好的热稳定性和化学惰性等特性, 是众多半导体器件场氧化层、栅极绝缘层和钝化层的首选材料. 在航空航天领域复杂的宇宙辐射环境中, a-SiO2虽面临陷阱电荷积累和界面退化等问题, 但得益于其本征缺陷密度低、界面稳定性强和工艺灵活性高等特点, 该材料在抗辐射器件的研发与应用中仍具有明显优势. 然而研究发现, 随着辐射总剂量的增加, 材料中具有反应活性的氢释放数量持续上升. 同时, 辐射诱导氧缺陷增多, 也为钝化过程提供了更多的反应位点. 反应生成的氢化氧缺陷在持续辐射下可能再次解离, 释放出活性氢, 形成动态循环过程[1-4]. 此外, 迁移至Si/SiO2界面处的氢会钝化该处的氧空位缺陷并发生堆积, 导致界面态密度上升[5], 引发阈值电压偏移和漏电流增加等问题, 严重威胁航天器的可靠性和服役寿命. 特别是在低剂量率辐射环境下, 双极型器件的性能退化呈现非线性增强的现象, 即存在低剂量率辐射损伤增强效应(enhanced low dose rate sensitivity, ELDRS)[6]. 与传统高剂量率辐射的损伤不同, ELDRS具有时间累积效应和隐蔽性强的特点, 在常规地面加速试验中易被低估[7,8]. 这对采用a-SiO2的航天电子器件的长周期可靠性提出了更严峻的挑战. 学者们经过多年的研究, 提出了多种模型[9-13]来解释这一现象的物理机制. 尽管尚未形成统一定论, 但众多研究普遍指向钝化层和封装层中氢的迁移和扩散行为. 实验结果证实[14-16], 在低剂量率辐照条件下, 残留或扩散的氢与a-SiO2中的氧空位缺陷发生反应, 导致界面和体相中缺陷密度的增大, 这一微观机制被认为是导致ELDRS现象的重要诱因. 类似地, 在卫星和空间站的数据传输系统方面, 光纤因其低衰减、大带宽、轻量化等优势占有较高的使用比重. 而制造工艺和辐射诱发产生的氧空位缺陷, 以及制备过程中残留的氢元素与氧空位形成的Si-H缺陷, 均会导致色心的形成, 从而引起不同频率的光损, 制约光通信系统的稳定性[17-19]. 因此, 探究中性氧空位缺陷并阐明其与氢的微观反应机制, 对理解并抑制ELDRS和辐射致光损至关重要.
Weeks通过电子顺磁共振(electron paramagnetic resonance, EPR)技术率先开展了关于晶态与非晶态二氧化硅材料中辐射诱导缺陷的实验研究, 并将揭示的缺陷标记为
$ {\mathrm{E}}' $ 中心[20–22]. 随着研究热点逐渐转向电子器件中的热氧化物缺陷, 研究人员在a-SiO2中进一步区分出了$ {\mathrm{E}}_{\gamma }' $ 和$ {\mathrm{E}}_{\delta }' $ 等多种顺磁缺陷中心. 其中,$ {\mathrm{E}}_{\gamma }' $ 中心电子顺磁共振谱中呈现特征性响应, 其超精细分裂常数约为42 mT[23]. 此外,$ {\mathrm{E}}_{\gamma }' $ 中心的未配对电子定域在未褶皱硅原子的sp3杂化轨道中, 而带正电荷的Si原子则位于褶皱结构中[24-28]. 对于$ {\mathrm{E}}_{\delta }' $ 中心, 早期研究提出的双硅原子共享未成对电子的模型[29]随着研究的深入逐步发展为二聚体模型[30]. 虽然通过EPR技术能够有效表征带正电的顺磁缺陷中心, 深化对a-SiO2中顺磁缺陷的认识, 但由于中性氧空位缺陷缺乏未配对电子或空穴, 导致其顺磁响应微弱, 难以通过该技术进行有效观测. Imai等[31]提出中性氧空位缺陷可能作为$ {E}' $ 中心的前体, 缺陷的微观结构为硅原子间形成共价键的稳定二聚体. 通过模拟计算, Blöchl[32]给出了两种可能的中性氧空位缺陷, 一种是二聚体构型[SiSi], 形成的二聚体键长较单质硅中Si—Si键仅增加4%; 另一种是中性褶皱构型[Si(3)–+O(3)+], 其中过配位的氧原子上带正电荷, 而欠配位硅原子因孤对电子占据呈现负电荷特性. 光学测量证实, a-SiO2中的不同氧空位缺陷间存在光诱导互相转化现象[33]. 尽管现有研究显示顺磁缺陷与中性氧空位缺陷存在密切关联, 但目前仍欠缺对中性氧空位缺陷本身的微观结构及其演化的清晰认识.在半导体工艺中, 氢被广泛应用于缺陷调控, 其通过饱和悬挂键能够有效降低氧化层以及界面处的缺陷密度, 从而达到提升器件性能的效果. 但在辐照条件下, 氢的扩散与反应会导致点缺陷配位环境和局部电荷态的改变, 这会影响包括载流子迁移率、介电常数和界面态密度在内的电学特性, 最终对器件的长期可靠性及抗辐射性能产生影响[3,34-36]. 研究表明, 氧化层中空穴俘获能够改变缺陷电子分布, 诱导Si—H基团释放氢[37,38]. 解离的质子迁移至Si/SiO2界面既能导致正电性界面缺陷的形成, 又可俘获电子并相互复合后形成氢分子[39]. 在Si/SiO2界面, 氢原子也能够通过失去电子形成含Si—O—H的结构, 该结构可能进一步发生解离, 并伴随H2O的脱附[40-42]. 当前对于氢与氧缺陷反应的研究中, 多聚焦于在缺陷中心位点处的反应, 忽视了a-SiO2无序结构中反应位点可能延伸至缺陷两侧邻近网格中的特性, 导致难以全面反映实际情况下的反应.
本文采用基于密度泛函理论的第一性原理计算方法, 以无缺陷a-SiO2为初始模型, 通过移除氧原子构建中性氧空位缺陷体系, 分析缺陷的微观结构、电子分布和缺陷形成能等. 为探索氢与缺陷的相互作用机制, 进一步在中性氧空位缺陷中分区域引入氢原子, 通过过渡态搜索获得可能的反应路径及能量曲线. 研究结果不仅有助于揭示ELDRS的微观机理, 同时也可为提升半导体器件的抗辐射性能以及低损耗光通信材料的优化设计提供理论依据.
-
本研究基于密度泛函理论, 采用CP2K软件包[43]开展第一性原理计算. 模拟过程中对体系施加三维周期性边界条件, 并启用自旋极化. 使用广义梯度近似 (generalized gradient approximation, GGA)框架下的Perdew-Burke-Ernzerhof (PBE)泛函[44]描述电子交换-关联相互作用. 选用DZVP基组[45]和Goedecker-Teter-Hutter(GTH)赝势[46]描述价电子分布和处理内层电子与原子核的相互作用. 截断能设置为650 Ry以保证计算精度. 在几何优化过程中, 采用Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法[47-50]进行结构弛豫, 该过程中原子力的收敛标准设为0.01 eV/Å. 为探索氢与缺陷的相互作用机制, 采用CINEB (climbing-image nudged elastic band)[51]方法确定反应初态至末态过程中的最小能量路径及能垒. 使用电子定域化函数(electron localization function, ELF)[52,53]描述电子在三维实空间中的局域化程度. 为研究中性氧空位缺陷在非晶态二氧化硅中的热力学稳定性, 体系中氧缺陷的缺陷形成能(
$ E_{\mathrm{{f}}} $ )定义为[54]其中
$ E(V_{\mathrm{O}}) $ 为含有中性氧空位缺陷体系总能量,$ {E(\mathrm{S}\mathrm{i}\mathrm{O}}_{2}) $ 为无缺陷非晶态二氧化硅的体系总能量,$ {E}_{\mathrm{O}} $ 是氧原子的化学势.在顺磁材料缺陷结构的研究中, g张量作为描述未配对电子自旋与外加磁场相互作用的重要物理量, 可以通过以下有效哈密顿量进行表征[55]:
其中,
$ \alpha $ 为精细结构常数,$ \boldsymbol{B} $ 为外加磁场强度, 张量$ {\boldsymbol{A}}_{I} $ 为超精细参数, g为EPR中的g张量,$ \boldsymbol{S} $ 和$ {\boldsymbol{I}}_{I} $ 分别代表总电子自旋和原子核$ I $ 的核自旋. 此外, 顺磁体系的各向同性超精细耦合常数(费米接触)是表征体系磁相互作用的关键参数, 描述了在各向同性平均条件下核自旋和电子自旋之间的耦合强度, 可以表示为[56,57]其中,
$ {\mu }_{0} $ 为真空磁导率,$ {\mu }_{\mathrm{e}} $ 和$ {{g}}_{\mathrm{e}} $ 分别为电子的玻尔磁子和朗德因子,$ {\mu }_{I} $ 和$ {{g}}_{I} $ 为原子核$ I $ 的磁矩和旋磁比,$ {\rho }_{\mathrm{s}} $ 为自旋密度,$ {\boldsymbol{R}}_{I} $ 为原子核的空间位置. 本文采用Quantum-Espresso(QE)软件包[58], 通过GIPAW(gauge including projector augmented wave)方法[59,60], 研究了周期性边界条件下a-SiO2中缺陷的费米接触及g张量. -
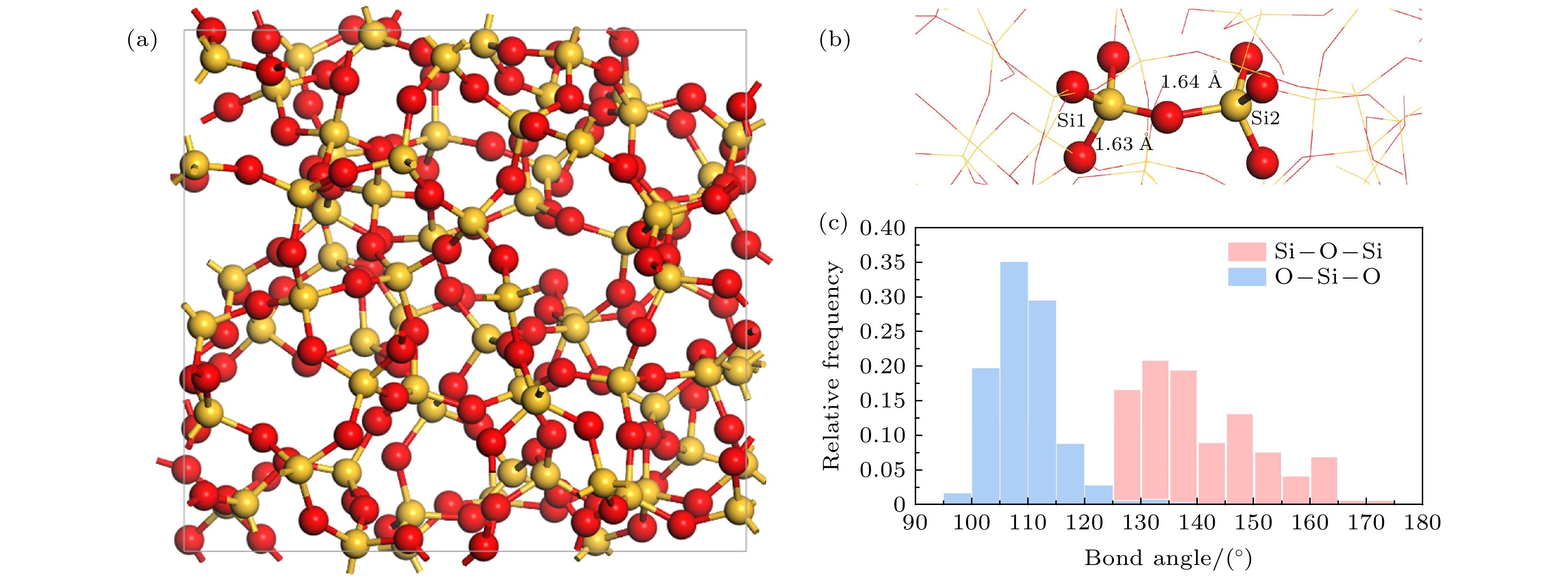
本文所采用的无缺陷a-SiO2模型含有216个原子, 该模型通过分子动力学模拟升温和退火过程生成[27], 其Si—O—Si 键角介于120°—180°之间, O—Si—O 键角分布在95°—135°. 氧原子两侧的Si—O键长存在差异, 为方便讨论, 将具有较短Si—O键长的硅原子标记为Si1, 较长的硅原子标记为Si2, 相应的平均Si—O键长分别为1.63 Å和1.64 Å, 如图1所示. 此外, 基于本原环判据[61-63]对该模型硅原子环分布进行统计, 结果显示六元环和七元环占主导且未观察到二元环, 说明该模型符合非晶结构特征[64].
-
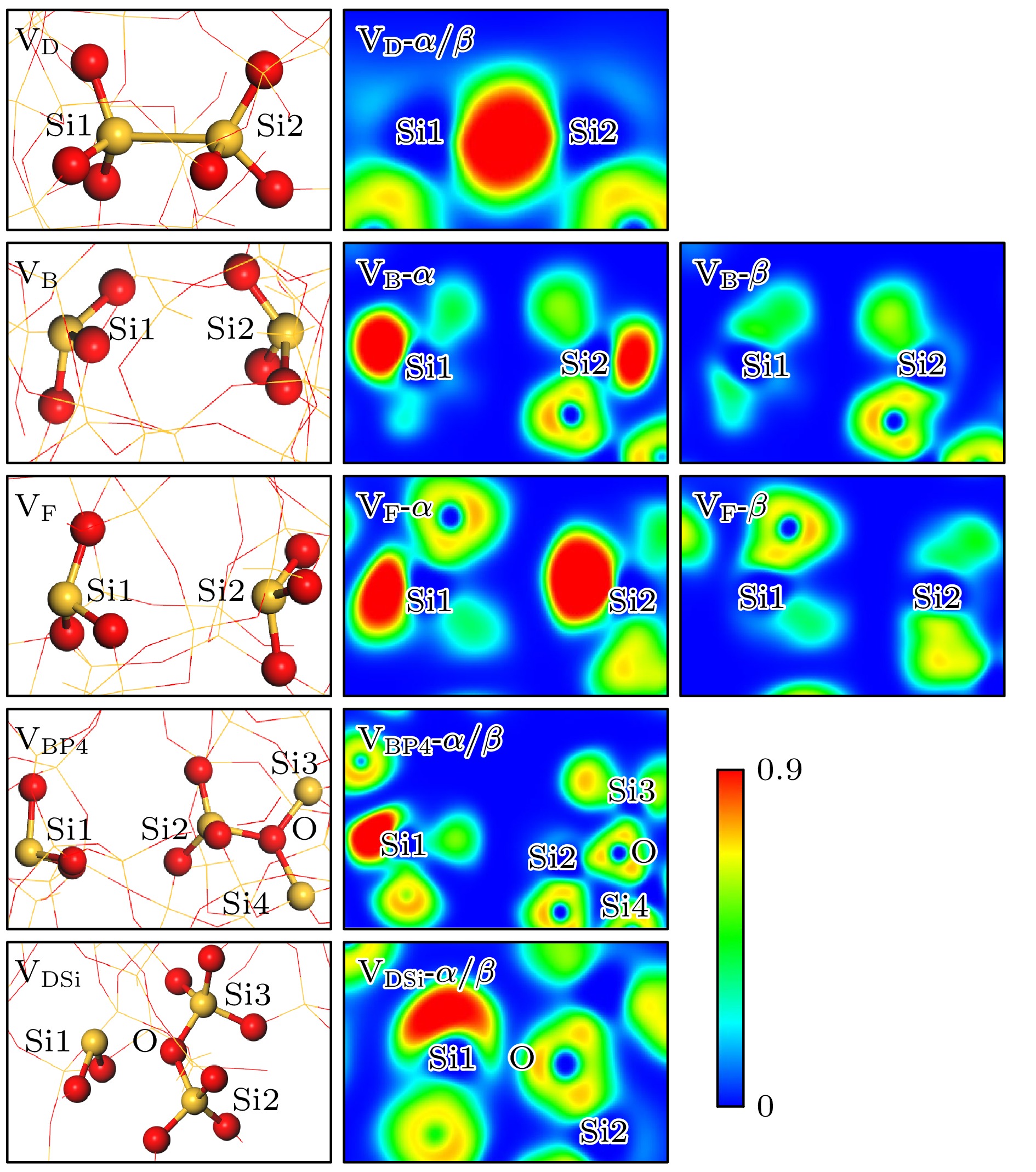
中性氧空位缺陷是从无缺陷a-SiO2中移除两个硅原子之间的一个桥接氧原子, 并对系统进行弛豫优化而产生. 由于二聚体构型和其他构型之间存在能垒, 移除桥接氧原子弛豫优化后得到的中性氧空位缺陷一般都是二聚体构型. 因此, 为获得更多类型的中性氧空位缺陷, 需进一步移动氧空位两侧的硅原子, 使其穿过各自余下的3个配位氧原子所在平面, 再进行弛豫优化. 最终, 我们共获得5种类型的中性氧空位缺陷构型(共48个), 分别为二聚体构型(
$ {\mathrm{V}}_{\mathrm{D}} $ )、后向构型($ {\mathrm{V}}_{\mathrm{B}} $ )、前向构型($ {\mathrm{V}}_{\mathrm{F}} $ )、后向四配位褶皱构型($ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ )和二价硅构型($ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ ), 其典型结构和ELF图如图2所示(悬挂键上含有电子的自旋方向为α, 不含电子的自旋方向为β ).$ {\mathrm{V}}_{\mathrm{D}} $ 构型的结构特征表现为缺陷处的两个硅原子通过共价键形成二聚体, 其Si1-Si2二聚体的平均键长为2.42 Å, 较晶体硅中的Si—Si键长仅增加了3%. ELF分析显示, 在移除氧原子后, Si1和Si2的悬挂键重新键合, 导致二者未成对电子形成配对, 并分布在两个自旋方向上. 受到Si1—Si2共价键的影响, 缺陷处平均O—Si—O键角偏离理想四面体的键角(109.5°), 平均Si—O键长增加至1.66 Å, 如表1所列. 尽管存在氧空位缺陷, 硅氧原子仍维持接近理想四面体的杂化状态, 表明缺陷未显著破坏局域共价键网络. 与$ {\mathrm{V}}_{\mathrm{D}} $ 构型相比,$ {\mathrm{V}}_{\mathrm{F}} $ 和$ {\mathrm{V}}_{\mathrm{B}} $ 构型中Si1和Si2均存在悬挂键, 显著增加了反应的活性位点, 其中$ {\mathrm{V}}_{\mathrm{F}} $ 构型中的两个悬挂键分别指向氧空位及其反方向, 而$ {\mathrm{V}}_{\mathrm{B}} $ 构型的悬挂键则均指向氧空位反方向. 两种构型中的未成对电子仅分布在单一自旋方向上, 并且Si—O键长和O—Si—O键角具有相似的结构参数. 两种构型的O—Si—O键角值均略大于$ {\mathrm{V}}_{\mathrm{D}} $ 构型, 表明其未成对电子对Si—O键的排斥作用要弱于二聚体结构. 虽然$ {\mathrm{V}}_{\mathrm{D}}, {\mathrm{V}}_{\mathrm{F}} $ 和$ {\mathrm{V}}_{\mathrm{B}} $ 三类构型存在结构差异, 但Si1和Si2均表现出明显的sp3杂化特征.在褶皱构型
$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ 中, 缺陷处Si1和Si2分别穿过3个氧原子所在平面, Si1指向氧空位反方向, Si2通过与背后网格中的O相互作用形成四配位结构, 新形成的Si2—O平均键长为1.85 Å. 图2中ELF图显示, 该构型中孤对电子完全定域在Si1上, 并分布在两个自旋方向上. 这极大增强了其对Si1侧成键电子的排斥, 导致Si1侧的Si—O平均键长增至1.80 Å, 平均键角减小至96.27$ ° $ . 褶皱结构处O与3个硅原子之间在两个自旋方向上存在明显的电子定域, 受Si2的影响, Si3和Si4与褶皱结构处O的平均键长增加至1.81 Å.$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ 构型中的Si2通过夺取原本Si1和Si3之间的桥接O, 使其恢复为无缺陷状态, 而Si1转变为正二价态. 结构优化后的Si2与桥接O的键长为1.71 Å, 而Si2原本的Si—O键长并未受到明显的影响, 平均O—Si—O键角增至111.63°. 此外, Si2引起网格结构中应力传递, 使Si3与桥接O的键长从原来的1.65 Å增至1.69 Å. Si1呈现sp2杂化, 孤对电子填充在同一杂化轨道上. 这种高度定域化导致Si1与两个氧原子的平均键长增至1.71 Å, 平均键角减小至99.67°.5种中性氧空位缺陷的缺陷形成能
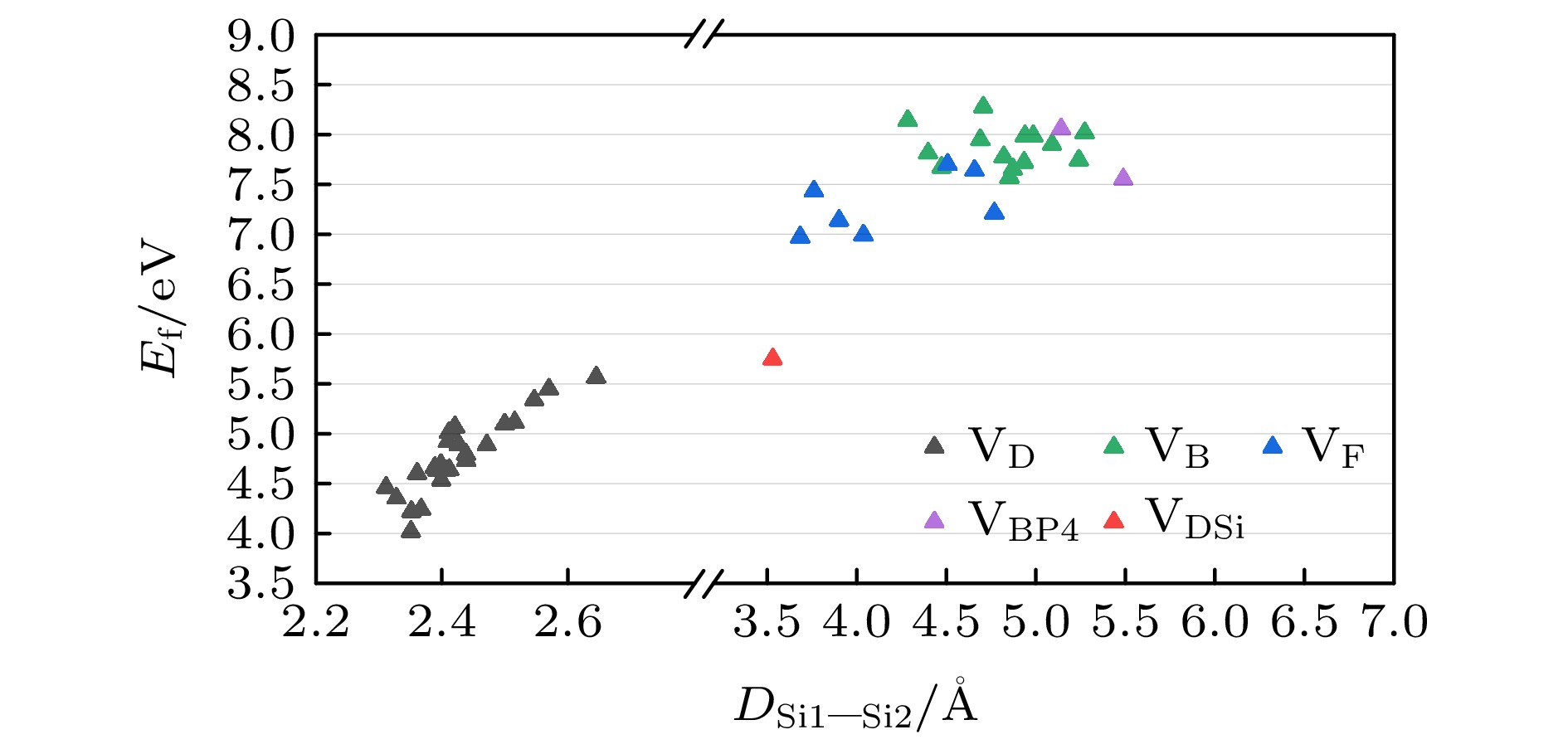
$ E_{\mathrm{\mathit{f}}} $ 随Si1与Si2间距$ {D}_{\mathrm{S}\mathrm{i}1-\mathrm{S}\mathrm{i}2} $ 的变化如图3所示. 可以看出,$ {\mathrm{V}}_{\mathrm{D}} $ 构型具有较低的$ E_{\mathrm{{f}}} $ , 表明其在a-SiO2制备或者辐照过程中更容易出现. 相比之下, 褶皱构型$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ 以及$ {\mathrm{V}}_{\mathrm{F}} $ 和$ {\mathrm{V}}_{\mathrm{B}} $ 构型的形成需要更高的能量, 在a-SiO2中缺陷密度相对较低. 总体上,$ E_{\mathrm{{f}}} $ 与$ {D}_{\mathrm{S}\mathrm{i}1-\mathrm{S}\mathrm{i}2} $ 具有显著的正相关性(Person相关系数为0.96). 在之前对正电性氧缺陷的研究中发现,$ {D}_{\mathrm{S}\mathrm{i}1-\mathrm{S}\mathrm{i}2} $ 的增大会促使体系通过形成褶皱或双褶皱构型来维持缺陷的稳定性并释放局部应力[65,66],$ E_{\mathrm{{f}}} $ 随着$ {D}_{\mathrm{S}\mathrm{i}1-\mathrm{S}\mathrm{i}2} $ 的增加呈现先增大后减小的趋势, 拐点出现在约4.5 Å处[27]. 在本研究中, 尽管未观察到$ E_{\mathrm{{f}}} $ 的明显拐点, 但并不排除中性氧空位缺陷也可能具有类似的变化趋势, 即$ {D}_{\mathrm{S}\mathrm{i}1-\mathrm{S}\mathrm{i}2} $ 也是影响中性氧缺陷$ E_{\mathrm{{f}}} $ 的重要因素之一. -
对于中性氧空位缺陷, 选取每种构型中
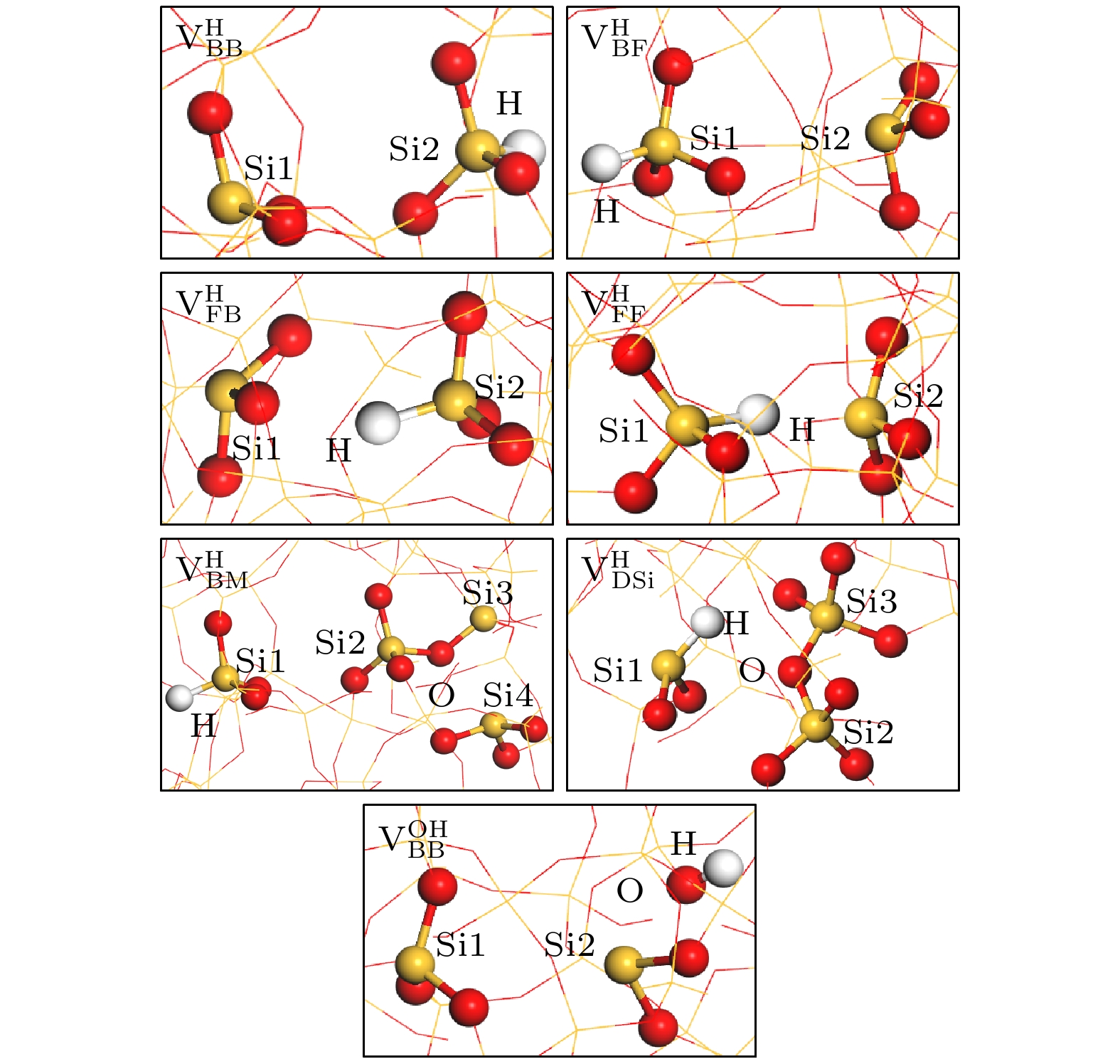
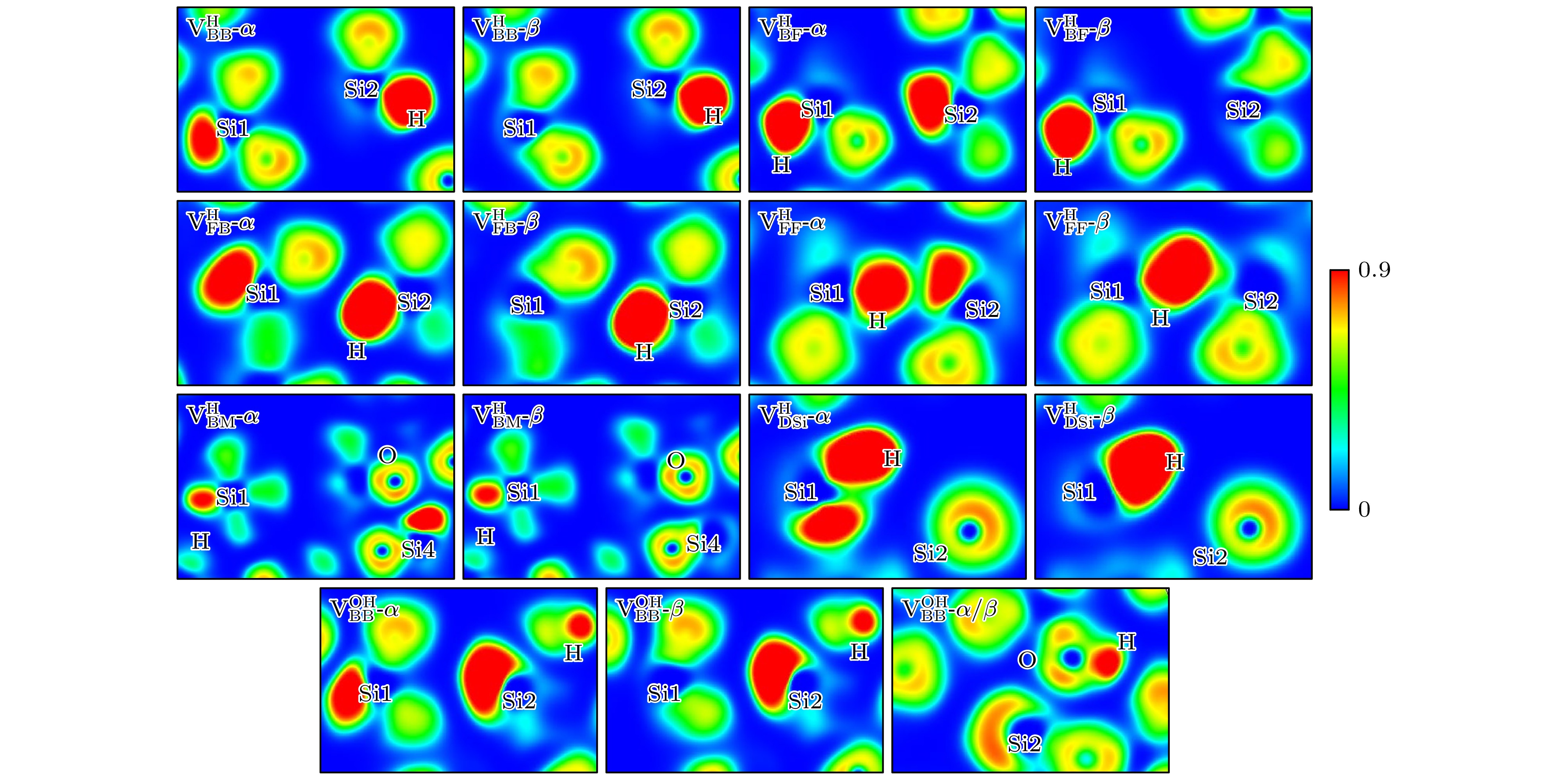
$ E_{\mathrm{{f}}} $ 最小的结构与氢原子进行反应. 考虑到中性氧空位缺陷构型的对称性, 研究中将氢原子与缺陷的反应位点进一步分类. 在具有近似对称结构的$ {\mathrm{V}}_{\mathrm{D}} $ 和$ {\mathrm{V}}_{\mathrm{B}} $ 构型中, 反应位点分为中间位点(middle site, M)和侧方位点(side site, S). M位点位于Si1和Si2原子之间的中心区域, S位点位于Si1或Si2外侧临近的区域. 针对$ {\mathrm{V}}_{\mathrm{F}} $ 和$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ 非对称构型, S位点进一步细分为邻近Si1外侧和邻近Si2外侧的S1和S2. 由于$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ 构型中仅存在一个缺陷硅原子, 因此只划分出S位点.在上述反应位点引入氢原子, 弛豫优化后共得到7种不同的中性氢化氧空位缺陷构型, 其结构和ELF图分别如图4和图5所示. 总体上, 中性氢化氧空位缺陷可分为
$ {\mathrm{V}}^{\mathrm{H}} $ 和$ {\mathrm{V}}^{\mathrm{O}\mathrm{H}} $ 两大类构型. 在$ {\mathrm{V}}^{\mathrm{H}} $ 构型中, 氢原子通过形成Si—H键实现对缺陷硅原子的钝化, 同时存在悬挂键. 而$ {\mathrm{V}}^{\mathrm{O}\mathrm{H}} $ 构型的结构则以硅羟基(Si—O—H)和悬挂键共存为特征. 根据Si—H键(或Si—O—H)和悬挂键的空间朝向差异可对缺陷构型进行进一步细分, 当其背向氧空位时记为后向(backward, B), 反之则归类为前向(forward, F). 构型下标两个字母依次对应 Si—H键(或Si—O—H键)和悬挂键的朝向. 在$ {\mathrm{V}}^{\mathrm{H}} $ 构型中, 当Si—H键和悬挂键分布在不同的缺陷硅原子上时, 根据其朝向可划分为$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{B}\mathrm{F}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{F}\mathrm{B}}^{\mathrm{H}}$ 和$ {\mathrm{V}}_{\mathrm{F}\mathrm{F}}^{\mathrm{H}} $ 四类构型. 另外, 还有一种由缺陷跨网格迁移(migration, M)后形成的$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 构型. 当Si—H键和悬挂键出现在同一缺陷硅原子上时, 该构型定义为$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}}^{\mathrm{H}} $ 构型.$ {\mathrm{V}}^{\mathrm{O}\mathrm{H}} $ 构型中, 目前仅观察到$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{O}\mathrm{H}} $ 构型, 其特征表现为Si—O—H和悬挂键均朝向氧空位反方向.中性氢化氧空位缺陷的结构参数显示
$ {\mathrm{V}}_{\mathrm{F}\mathrm{F}}^{\mathrm{H}} $ 构型具有最小的缺陷硅原子间距(3.39 Å),$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 构型则表现出最大间距(8.18 Å),$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ 构型以4.93 Å次之, 其余构型包括$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{O}\mathrm{H}} $ 在内的缺陷硅原子间距在3.39—4.93 Å内. 在$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{B}\mathrm{F}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{F}\mathrm{B}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{F}\mathrm{F}}^{\mathrm{H}} $ 及$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 构型中, 氢原子钝化后形成的Si—H平均键长为1.45 Å. 被钝化硅原子的Si—O平均键长为1.65 Å, 较未被钝化一侧的键长缩短了0.01 Å. 钝化后的O—Si—O平均键角为109.35°, 相比未钝化的108.25°更接近理想四面体角度. 这表明氢钝化能够缓解上述构型中悬挂键与邻近Si—O键之间的电子排斥作用. 并且通过ELF分析发现, 氢原子通过与$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{B}\mathrm{F}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{F}\mathrm{B}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{F}\mathrm{F}}^{\mathrm{H}} $ 及$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 构型缺陷硅原子形成共价键, 两个未成对电子重新分布在同一sp3轨道的两个自旋方向上. 而在未被钝化一侧, 硅原子的电子分布未发生明显改变. 特别的是在$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}}^{\mathrm{H}} $ 构型中, Si1原子从sp2杂化转变为sp3杂化, 使其O—Si—O键角由99.67°增至107.95°. 原sp2杂化轨道中的两个电子, 一个参与Si—H键的形成, 另一个重新定域形成新的悬挂键, 且仅存在于单一自旋轨道中. 悬挂键的存在也对$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}}^{\mathrm{H}} $ 构型中参与形成Si—H键的成键电子产生排斥作用, 使Si—H键长增至1.48 Å.在
$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{O}\mathrm{H}} $ 构型中, Si2—O键断裂并形成O—H键, 其键长为0.98 Å. 并引发Si2的杂化方式由sp3变为sp2, 其孤对电子填充在同一sp2杂化轨道上, 增加对Si2成键电子对的排斥, 使其O—Si—O键角减小至95.42°, Si—O键长增大到1.71 Å. 该结构特征与$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ 中二价硅原子一致. 未被钝化的Si1仍占据一个未成对电子, 该侧键长和键角与$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ 等钝化构型的相似.在中性氧空位缺陷中,
$ {\mathrm{V}}_{\mathrm{F}} $ 和$ {\mathrm{V}}_{\mathrm{B}} $ 构型的悬挂键含有未成对电子, 其波函数在原子核附近具有非零概率密度, 对费米接触产生贡献, 平均值如表2所列. 由于这两个构型的悬挂键存在于sp3杂化硅原子上, 该结构特征与$ {\mathrm{E}}_{\mathrm{\gamma }}'$ 中心相似, 因此$ {\mathrm{V}}_{\mathrm{F}} $ 和$ {\mathrm{V}}_{\mathrm{B}} $ 构型的费米接触也与$ {\mathrm{E}}_{\mathrm{\gamma }}'$ 的相近.$ {\mathrm{V}}_{\mathrm{D}} $ ,$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ 和$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ 构型中由于电子成对定域在缺陷硅原子上并在两个自旋方向上分布, 因此费米接触为零. 但当这些中性氧空位缺陷失去一个电子转变为正电性氧缺陷后, 成对电子被破坏, 未配对电子仅存在于单一自旋方向上, 从而产生费米接触[66], 这意味着中性氧空位缺陷可以作为前体结构通过电子转移过程演化为正电性顺磁缺陷. 中性氢化氧空位缺陷虽均含有悬挂键, 但$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}}^{\mathrm{H}} $ 构型的特殊性在于Si—H键和悬挂键位于同一硅原子上, 该空间分布导致其费米接触明显区别于其他构型. 相比之下,$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{B}\mathrm{F}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{F}\mathrm{B}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{F}\mathrm{F}}^{\mathrm{H}} $ ,$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 及$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{O}\mathrm{H}} $ 构型中悬挂键均独立存在于sp3杂化的硅原子上, 且其配位原子均为氧原子, 这种结构一致性使其费米接触呈现相近的结果. 此外, 由于$ {\mathrm{V}}_{\mathrm{F}\mathrm{F}}^{\mathrm{H}} $ 构型具有最小缺陷硅原子间距, 未成对电子也会对构成Si—H键的硅原子产生影响, 其费米接触为–16.55 mT.实验测量的
$ {\mathrm{E}}_{\gamma }'$ 中心的g因子为: g1 = 2.0018, g2 = 2.0006, g3 = 2.0003, 其与$ {\mathrm{V}}_{\mathrm{F}} $ 和$ {\mathrm{V}}_{\mathrm{B}} $ 构型的模拟计算结果存在显著差异, 而更接近于$ {\mathrm{V}}^{\mathrm{H}} $ 构型的结果, 尤其是$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ 和$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 构型. 造成此差异的原因在于$ {\mathrm{E}}_{\mathrm{\gamma }}^{\prime} $ 中心仅含有单个悬挂键, 而$ {\mathrm{V}}_{\mathrm{F}} $ 和$ {\mathrm{V}}_{\mathrm{B}} $ 构型中存在两个悬挂键导致其局域环境复杂化, 且电子不对称分布会进一步增强自旋-轨道耦合, 从而引起较大的g因子偏离, 但这一偏离可能在$ {\mathrm{V}}_{\mathrm{F}} $ 和$ {\mathrm{V}}_{\mathrm{B}} $ 构型失去一个电子转变为含有单一悬挂键的正电性氧缺陷后而得到消除.$ {\mathrm{V}}^{\mathrm{H}} $ 构型中虽然也只存在一个悬挂键, 但是邻近Si—H键的存在也会对其自旋-轨道耦合产生影响, 而随着$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ 和$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 构型中Si—H键和悬挂键距离的增大, 影响逐渐减弱, 使得其EPR参数趋近于$ {\mathrm{E}}_{\mathrm{\gamma }}'$ 中心. 这一结果表明, 在实验观测中氢原子钝化后的中性氧空位缺陷可能对$ {\mathrm{E}}'$ 中心的识别产生干扰. -
为探究氢原子在a-SiO2中与中性氧空位缺陷的相互作用, 采用CINEB方法进行过渡态计算. 反应初态的构建是先在无缺陷a-SiO2网格中选取20个不同的位点依次放置氢原子, 要求与最近邻氧原子的距离大于1 Å以确保初期氢原子处于非键合状态. 对此进行结构优化后, 发现氢原子均未与氧原子或硅原子成键, 其稳定位点均位于a-SiO2网格间隙中, 且与最近邻硅、氧原子间距分别超过1.90 Å和2.19 Å. 随后在所选中性氧空位缺陷体系中, 从上述确定的稳定位点中选择与两个缺陷硅原子平均距离短的位点引入氢原子, 通过二次结构优化得到反应初态模型. 反应末态的构建则是将氢原子引入到所选中性氧空位缺陷的M或S反应位点区域, 以促进反应的发生, 最终经弛豫优化获得反应末态结构.
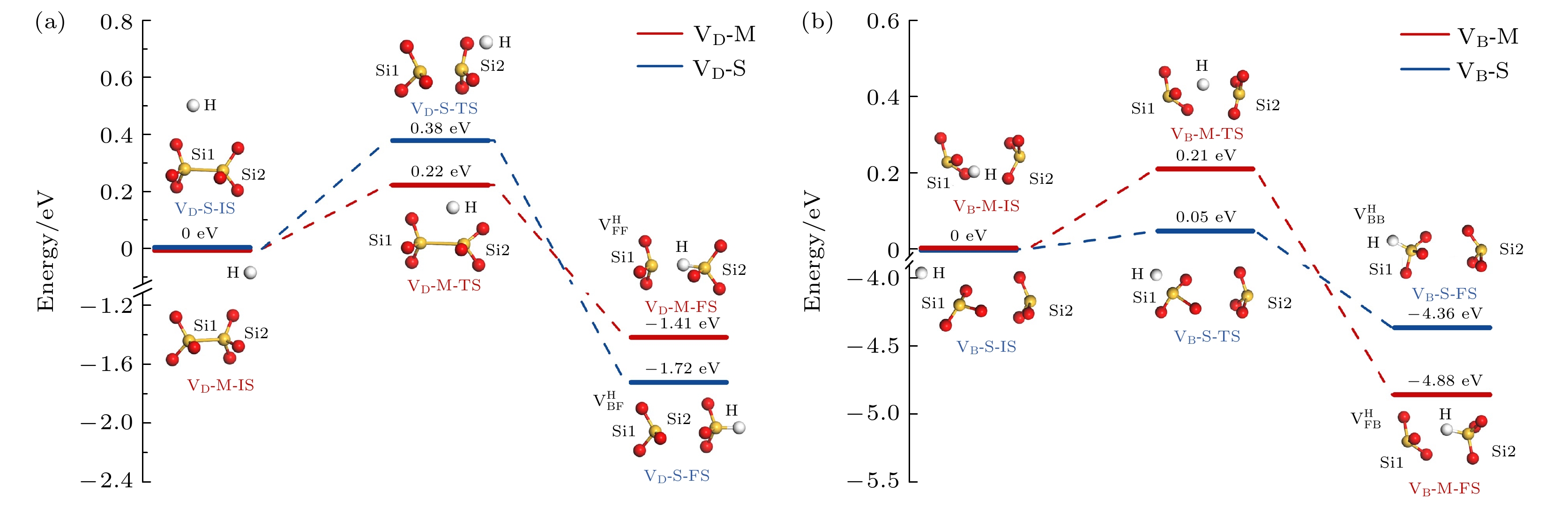
$ {\mathrm{V}}_{\mathrm{D}} $ 和$ {\mathrm{V}}_{\mathrm{B}} $ 构型中具有最小形成能的结构分别与氢原子反应的路径和能量曲线如图6所示. 在$ {\mathrm{V}}_{\mathrm{D}} $ 构型的反应中, 氢原子最终处于两个缺陷硅原子中间区域的路径$ {\mathrm{V}}_{\mathrm{D}} $ -M表现出较低的反应能垒(0.22 eV), 氢原子通过破坏Si1—Si2共价键实现对Si2原子的钝化, 形成$ {\mathrm{V}}_{\mathrm{F}\mathrm{F}}^{\mathrm{H}} $ 构型并伴随1.41 eV的能量释放. 而$ {\mathrm{V}}_{\mathrm{D}} $ -S路径的反应(氢原子最终处于Si2侧区域)需要Si2穿过其配位氧原子所在平面才能实现钝化, 导致反应能垒较$ {\mathrm{V}}_{\mathrm{D}} $ -M路径高出0.16 eV, 但形成$ {\mathrm{V}}_{\mathrm{B}\mathrm{F}}^{\mathrm{H}} $ 构型具有较高的反应放能(1.72 eV). 对$ {\mathrm{V}}_{\mathrm{B}} $ 构型, 沿$ {\mathrm{V}}_{\mathrm{B}} $ -M路径的反应同样因为需要Si2穿过配位氧平面, 反应能垒较高(0.21 eV), 而$ {\mathrm{V}}_{\mathrm{B}} $ -S路径的反应因无需此过程, 其反应能垒显著降低至0.05 eV. 反应产物方面,$ {\mathrm{V}}_{\mathrm{B}} $ -M路径反应生成$ {\mathrm{V}}_{\mathrm{F}\mathrm{B}}^{\mathrm{H}} $ 构型释放4.88 eV的能量, 高于$ {\mathrm{V}}_{\mathrm{B}} $ -S路径生成$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ 构型的4.36 eV. 综合氢原子与$ {\mathrm{V}}_{\mathrm{D}} $ 和$ {\mathrm{V}}_{\mathrm{B}} $ 构型的反应, 无需缺陷硅原子穿过配位氧平面的反应路径($ {\mathrm{V}}_{\mathrm{D}} $ -M和$ {\mathrm{V}}_{\mathrm{B}} $ -S)具有更低的反应能垒, 但涉及缺陷硅原子穿过配位氧平面并生成$ {\mathrm{V}}_{\mathrm{F}\mathrm{B}}^{\mathrm{H}} $ 或$ {\mathrm{V}}_{\mathrm{B}\mathrm{F}}^{\mathrm{H}} $ 构型的反应路径($ {\mathrm{V}}_{\mathrm{D}} $ -S和$ {\mathrm{V}}_{\mathrm{B}} $ -M)在热力学上更有优势.具有最小形成能的非对称构型
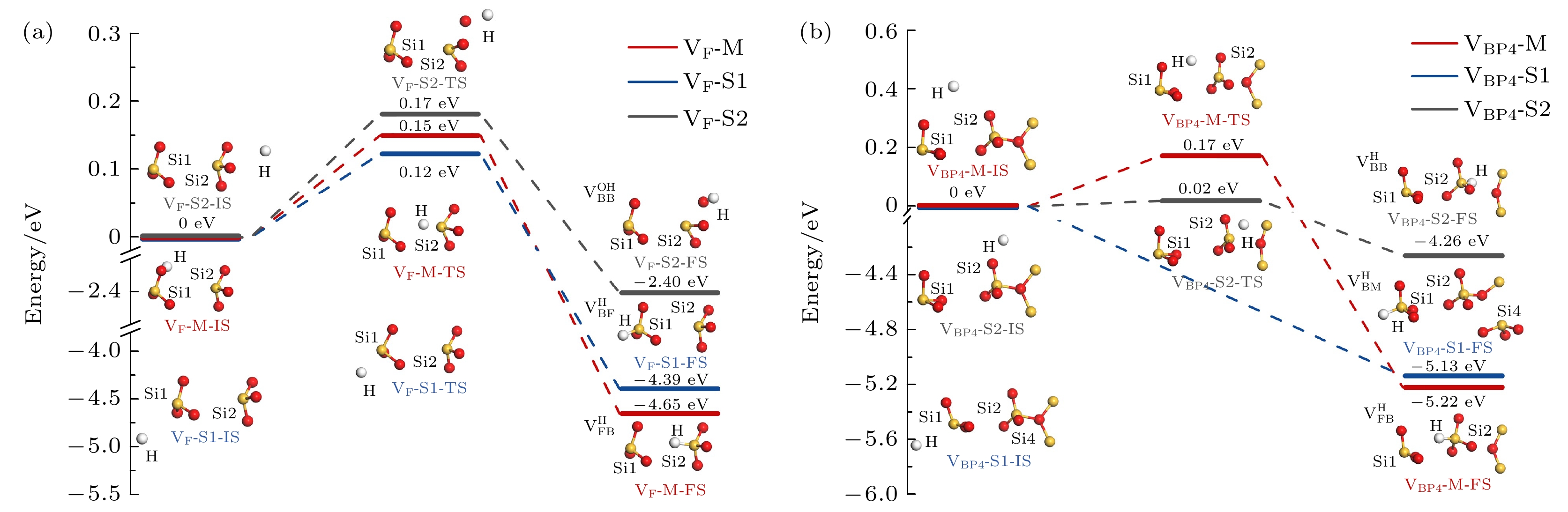
$ {\mathrm{V}}_{\mathrm{F}} $ 和$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ 分别与氢原子反应路径和能量曲线如图7所示. 对$ {\mathrm{V}}_{\mathrm{F}} $ 构型, 沿$ {\mathrm{V}}_{\mathrm{F}} $ -M和$ {\mathrm{V}}_{\mathrm{F}} $ -S1路径反应时, 氢原子的电子直接填充到缺陷硅原子的悬挂键轨道中, 分别形成$ {\mathrm{V}}_{\mathrm{F}\mathrm{B}}^{\mathrm{H}} $ 和$ {\mathrm{V}}_{\mathrm{B}\mathrm{F}}^{\mathrm{H}} $ 构型. 这两个反应具有相似的反应能垒(0.15 eV和0.12 eV), 并且释放能量也相近(4.65 eV和4.39 eV). 而沿$ {\mathrm{V}}_{\mathrm{F}} $ -S2路径反应时, 氢原子的逐渐靠近使Si2原子的一个Si—O键断裂, 继而在相邻硅原子处形成Si—O—H键, 最终生成含有硅羟基的$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{O}\mathrm{H}} $ 构型, 该过程能垒为0.17 eV, 释放能量为2.40 eV. 需注意的是, 产生的硅羟基可能进一步与邻近的质子或氢原子反应, 释放水分子, 这一过程可为SiO2氧化层或Si/SiO2界面处水分子的生成提供理论支持[67].在氢原子与
$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ 构型沿$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ -M路径的反应中, 随着氢原子的靠近, Si2原子与背后网格中O原子的Si—O键发生断裂且Si2穿过配位氧平面, 该过程的反应能垒为0.17 eV, 生成$ {\mathrm{V}}_{\mathrm{F}\mathrm{B}}^{\mathrm{H}} $ 构型并释放5.22 eV的能量. 对于沿$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ -S2路径的反应, 氢原子钝化Si2的反应能垒降低至0.02 eV, 这一过程同样伴随Si2原子的Si—O键断裂, 但未涉及Si2原子穿越配位氧平面的情况. 反应最终生成$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ 构型并放能4.26 eV. 而沿$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ -S1路径的反应中未观测到能垒, 氢原子直接钝化Si1原子, 同时三配位氧原子中的Si4—O键发生断裂, 导致原本位于Si2位点的缺陷转移到Si4位点, 形成$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 构型并释放5.13 eV的能量. 与之前的工作中由电荷态转变实现的缺陷迁移机制不同, 这种氢钝化诱导缺陷跨网格迁移是一种独立且重要的机制, 二者共同解释了缺陷迁移的多种可能性. 通过对比3种路径的反应可见,$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ -S1路径较大的反应放能和缺陷跨网格迁移后生成$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 构型的零反应能垒特性, 使其具有明显的热力学和动力学优势.氢原子与
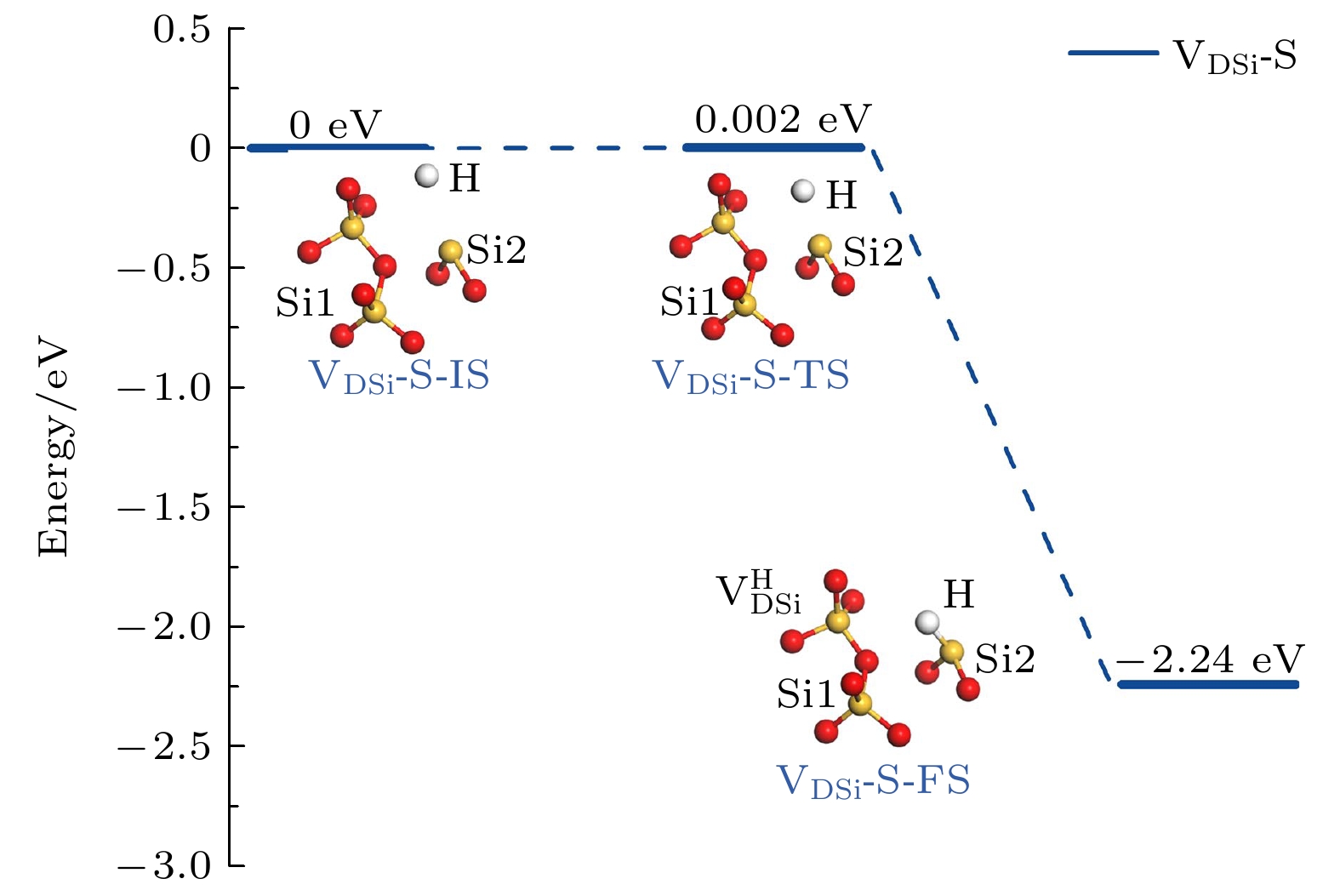
$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ 构型的反应能垒极低, 仅为0.02 eV, 反应后生成$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}}^{\mathrm{H}} $ 构型, 末态比初态能量低2.24 eV, 反应路径及其能量曲线如图8所示. 在此过程中, 氢原子与sp2杂化的Si2发生键合, 使其杂化方式由sp2转为sp3, 残余未成对电子形成悬挂键, 并对Si2—H键起到排斥作用. 尽管该反应生成了新的化学键, 实现了总能量下降, 但未配对电子导致产物仍具备一定的反应活性. -
本研究基于密度泛函理论计算, 研究了a-SiO2中性氧空位缺陷的结构特征及其与氢的相互作用机理. 计算结果表明, 中性氧空位缺陷在a-SiO2中具有多种构型, 相应的缺陷形成能
$ {E}_{\mathrm{f}} $ 与缺陷硅原子间距$ {D}_{\mathrm{S}\mathrm{i}1-\mathrm{S}\mathrm{i}2} $ 呈显著正相关.$ {\mathrm{V}}_{\mathrm{D}} $ 因其较低的$ {E}_{\mathrm{f}} $ 是辐照或制备过程中最易生成的缺陷类型.$ {\mathrm{V}}_{\mathrm{F}} $ ,$ {\mathrm{V}}_{\mathrm{B}} $ 构型的费米接触与$ {\rm E}_{\gamma }' $ 中心相近, 但因含有两个悬挂键导致g因子与$ {\rm E}_{\gamma }' $ 中心的显著差异.$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ 和$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ 构型中电子局域化特性表明两者均可能成为正电性顺磁缺陷的前体.氢原子钝化中性氧空位缺陷后形成的Si—H键有效缓解了悬挂键引起的局域排斥, 降低局部晶格畸变, 而残余悬挂键仍使氢化氧缺陷存在反应活性.
$ {\mathrm{V}}^{\mathrm{H}} $ 构型的EPR参数与$ {\mathrm{E}}_{\mathrm{\gamma }}' $ 中心接近, 特别是$ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ 和$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 构型, 这意味着中性氢化氧空位缺陷可能会对$ {\mathrm{E}}^{\mathrm{\text{'}}} $ 中心的准确EPR表征产生干扰.研究还发现氢原子通过两种钝化机制与缺陷发生反应, 其一为Si—H钝化, 即氢原子填充缺陷硅原子的悬挂键形成 Si—H 键. 其二为形成硅羟基, 表现为氢原子导致缺陷硅的Si—O键断裂继而在相邻硅原子处形成Si—O—H键. 该机制生成的硅羟基可能继续参与反应在SiO2氧化层或Si/SiO2界面处形成水分子. 在同种中性氧缺陷的钝化中, Si—H钝化方式能量释放较高, 硅羟基钝化方式能量释放相对较少. 氢钝化缺陷形成
$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 构型具有显著热力学优势, 为氢诱导缺陷跨网格迁移提供了新机制. 总体上看, 氢钝化中性氧缺陷具有双重作用, 一方面钝化原始缺陷, 通过Si—H键或硅羟基的生成消除中性氧空位的活性位点(如悬挂键); 另一方面诱发次生缺陷, 其中硅羟基可促使水分子的形成,$ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ 构型使钝化缺陷获得跨网格迁移, 而$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}}^{\mathrm{H}} $ 构型则会产生新的悬挂键.本研究揭示了a-SiO2中性氧空位缺陷特征和氢的钝化机制及其双重作用, 研究结果可为低剂量率辐射损伤增强效应提供微观理论依据.
非晶态二氧化硅中性氧空位缺陷的氢钝化机理与反应路径的研究
Hydrogen passivation mechanism and reaction pathways of neutral oxygen vacancies in amorphous silica
-
摘要: 本文基于第一性原理方法研究了非晶态二氧化硅中性氧空位缺陷及其与氢原子的反应机理. 结果显示, 非晶态二氧化硅中存在5种稳定中性氧空位缺陷构型, 相应的缺陷形成能与缺陷硅原子间距呈现显著正相关关系. 其中, $ {\mathrm{V}}_{\mathrm{D}} $构型因形成能最低可能是辐照或制备过程中的主要缺陷, $ {\mathrm{V}}_{\mathrm{F}} $和$ {\mathrm{V}}_{\mathrm{B}} $构型的费米接触与$ {\mathrm{E}}_{\gamma }'$中心相近, 而$ {\mathrm{V}}_{\mathrm{D}} $, $ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $和$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $构型因电子成对存在导致费米接触为零. 氢原子与中性氧空位缺陷通过形成Si—H键或硅羟基两种钝化方式可产生两类共7种中性氢化氧空位缺陷. 电子定域化函数与EPR模拟分析发现, $ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}}\mathrm{和}{\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}}$构型与$ {\mathrm{E}}_{\gamma }' $中心的EPR参数高度接近, 表明氢钝化过程可能干扰$ {E}' $中心的识别. $ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{O}\mathrm{H}} $构型中硅羟基的生成可为氧化层和界面处水分子的形成提供理论依据. 研究获得了氢诱导缺陷跨网格迁移以及生成硅羟基的路径, 并揭示了氢原子具有钝化原始缺陷和诱发次生缺陷的双重作用. 这些发现可为双极型器件低剂量率辐射损伤增强效应提供微观机理解释.Abstract: Amorphous silica (a-SiO2) with excellent insulating properties, uniform disordered structure, and good thermal stability, is the preferred material for field oxide layers, gate insulation layers and passivation layers in many semiconductor devices. However, in space environments, the oxygen vacancies generated by high-energy particle radiation and their interaction with hydrogen atoms in a-SiO2 can lead to enhanced low-dose-rate sensitivity, potentially causing threshold voltage to shift and leakage current to increase in semiconductor devices. These seriously threaten the operation safety of spacecraft, and the exploration of related reaction mechanisms is crucial. A first-principles calculation is employed to investigate the neutral oxygen vacancies in amorphous silica and their reaction mechanisms with hydrogen atoms. Five types of neutral oxygen vacancies are identified, namely $ {\mathrm{V}}_{\mathrm{D}} $, $ {\mathrm{V}}_{\mathrm{B}} $, $ {\mathrm{V}}_{\mathrm{F}} $, $ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ and $ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ configurations. A significant positive correlation is observed between the defect formation energy and the distance between two defective silicon atoms. Due to the lowest defect formation energy, the $ {\mathrm{V}}_{\mathrm{D}} $ configuration may become the main type of defect in irradiation or fabrication.$ {\mathrm{V}}_{\mathrm{F}} $ and $ {\mathrm{V}}_{\mathrm{B}} $ configurations display comparable Fermi contacts to those of $ {\mathrm{E}}_{\mathrm{\gamma }}' $ centers. The presence of electron pairs leads to zero fermi contacts in $ {\mathrm{V}}_{\mathrm{D}} $, $ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ and $ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ configurations. Previous studies have often focused more on the reaction between oxygen vacancies and hydrogen atoms at the middle-sites of oxygen vacancies. And, a critical characteristic of the disordered a-SiO2 structure is neglected by this approach: the reactions may extend into the neighboring network and occur at side-sites of oxygen defects. For a full understanding of actual reactions, both the middle-sites and side-sites are considered for hydrogen atoms in present investigations. It’s revealed that hydrogen atoms passivate neutral oxygen vacancies through two distinct mechanisms: Si−H bond formation or silanol group generation. These processes yield two classes of neutral hydrogenated oxygen vacancies, $ {\mathrm{V}}^{\mathrm{H}} $ and $ {\mathrm{V}}^{\mathrm{O}\mathrm{H}} $ configurations, which can be further classified into seven distinct configurations based on the orientation of dangling bonds and Si−H bonds. By combining the analyses of ELF maps and EPR simulations, it is demonstrated that $ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ and $ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ configurations have EPR parameters comparable to those of $ {\mathrm{E}}_{\mathrm{\gamma }}' $ center, implying that hydrogen passivation processes may interfere with the identification of $ {\mathrm{E}}' $ center. The formation of silanol group in $ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{O}\mathrm{H}} $ configuration provides theoretical bases for explaining water molecules formation within oxide layers and at interfaces. This study elucidates the hydrogen-induced cross-network migration and silanol group formation pathway, collectively revealing the dual role of hydrogen in passivating defects and inducing secondary defects. A microscopic explanation is derived from these findings for the enhanced low dose rate sensitivity in bipolar devices.
-
Key words:
- neutral oxygen vacancy /
- hydrogen atom /
- passivation /
- first-principles .
-
-
图 2 a-SiO2中5种中性氧空位缺陷的典型结构(红色为氧原子、黄色硅原子)和ELF图
Figure 2. Typical configurations and ELF maps of five types of neutral oxygen vacancies in a-SiO2 (red spheres: oxygen atoms; yellow spheres: silicon atoms).
图 4 a-SiO2中7种中性氢化氧空位缺陷的典型结构(红色为氧原子、黄色硅原子、白色为氢原子)
Figure 4. Seven typical configurations of neutral hydrogen-passivated oxygen vacancies in a-SiO2 (red spheres: oxygen atoms; yellow spheres: silicon atoms; white spheres: hydrogen atoms).
图 5 a-SiO2中7种中性氢化氧空位缺陷的ELF图
Figure 5. ELF maps of seven neutral hydrogen-passivated oxygen vacancies in a-SiO2.
图 6 (a)
$ {\mathrm{V}}_{\mathrm{D}} $ 和(b)$ {\mathrm{V}}_{\mathrm{B}} $ 构型与氢原子的反应路径和能量曲线Figure 6. Reaction pathways and energy curves of (a)
$ {\mathrm{V}}_{\mathrm{D}} $ and (b)$ {\mathrm{V}}_{\mathrm{B}} $ configurations with hydrogen atoms.
图 7 (a)
$ {\mathrm{V}}_{\mathrm{F}} $ 和(b)$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ 构型与氢原子的反应路径和能量曲线Figure 7. Reaction pathways and energy curves of (a)
$ {\mathrm{V}}_{\mathrm{F}} $ and (b)$ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ configurations with hydrogen atoms.
图 8
$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ 构型与氢原子的反应路径和能量曲线Figure 8. Reaction pathway and energy curve of
$ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ configuration with a hydrogen atom.表 1 五种中性氧空位缺陷的结构参数
Table 1. Structural parameters of five types of neutral oxygen vacancies.
种类 数量 平均
DSi1—Si2/Å平均Si—O
键长/Å平均O—Si—O
键角/(°)Si1 Si2 Si1 Si2 $ {\mathrm{V}}_{\mathrm{D}} $ 24 2.42 1.66 1.66 106.95 107.34 $ {\mathrm{V}}_{\mathrm{F}} $ 7 4.19 1.66 1.66 108.52 108.91 $ {\mathrm{V}}_{\mathrm{B}} $ 14 4.81 1.66 1.66 109.31 108.19 $ {\mathrm{V}}_{\mathrm{B}\mathrm{P}4} $ 2 5.32 1.80 1.60 96.27 114.07 $ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}} $ 1 3.53 1.71 1.66 99.67 111.63 
下载: 导出CSV
表 2 中性氧空位缺陷和中性氢化氧空位缺陷的平均费米接触和g因子
Table 2. Average Fermi contacts and g values of neutral oxygen vacancies and neutral hydrogen-passivated oxygen vacancies.
缺陷构型 费米接触/mT g1 g2 g3 Si1 Si2 $ {\mathrm{V}}_{\mathrm{B}} $ –38.10 –40.69 2.0006 1.9988 1.9981 $ {\mathrm{V}}_{\mathrm{F}} $ –41.79 –42.95 2.0005 1.9986 1.9979 $ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{H}} $ –39.29 –0.00 2.0017 2.0006 2.0002 $ {\mathrm{V}}_{\mathrm{B}\mathrm{F}}^{\mathrm{H}} $ –0.03 –45.07 2.0017 2.0002 1.9998 $ {\mathrm{V}}_{\mathrm{F}\mathrm{B}}^{\mathrm{H}} $ –44.27 –0.12 2.0017 2.0003 2.0000 $ {\mathrm{V}}_{\mathrm{F}\mathrm{F}}^{\mathrm{H}} $ –16.55 –41.14 2.0014 2.0002 1.9997 $ {\mathrm{V}}_{\mathrm{B}\mathrm{M}}^{\mathrm{H}} $ –0.01 –0.27 (–41.72 a) 2.0016 2.0004 2.0001 $ {\mathrm{V}}_{\mathrm{D}\mathrm{S}\mathrm{i}}^{\mathrm{H}} $ –22.89 –0.02 2.0021 2.0020 2.0005 $ {\mathrm{V}}_{\mathrm{B}\mathrm{B}}^{\mathrm{O}\mathrm{H}} $ –43.75 –0.60 2.0016 2.0005 1.9998 注: a 表示Si4费米接触.
下载: 导出CSV
-
[1] Kajihara K, Miura T, Kamioka H, Aiba A, Uramoto M, Morimoto Y, Hirano M, Skuja L, Hosono H 2008 J. Non-Cryst. Solids 354 224 doi: 10.1016/j.jnoncrysol.2007.07.038 [2] Füssel W, Schmidt M, Flietner H 1992 Nucl. Instrum. Meth. B 65 238 doi: 10.1016/0168-583X(92)95041-O [3] Bunson P E, Di Ventra M, Pantelides S T, Fleetwood D M, Schrimpf R D 2000 IEEE Trans. Nucl. Sci. 47 2289 doi: 10.1109/23.903767 [4] Yue Y L, Wang J W, Zhang Y Q, Song Y, Zuo X 2018 Physica B 533 5 doi: 10.1016/j.physb.2017.12.056 [5] Shen X, Puzyrev Y S, Fleetwood D M, Schrimpf R D, Pantelides S T 2015 IEEE Trans. Nucl. Sci. 62 2169 doi: 10.1109/TNS.2015.2470665 [6] Enlow E W, Pease R L, Combs W, Schrimpf R D, Nowlin R N 1991 IEEE Trans. Nucl. Sci. 38 1342 doi: 10.1109/23.124115 [7] Pershenkov V S, Petrov A S, Bakerenkov A S, Ulimov V N, Felytsyn V A, Rodin A S, Belyakov V V, Telets V A, Shurenkov V V 2017 Microelectron. Reliab. 76–77 703 doi: 10.1016/j.microrel.2017.07.025 [8] Zhou H, Song Y, Liu Y, Zhang Y 2020 Eur. Phys. J. Plus 135 909 doi: 10.1140/epjp/s13360-020-00938-z [9] Hjalmarson H P, Pease R L, Devine R A B 2008 IEEE Trans. Nucl. Sci. 55 3009 doi: 10.1109/TNS.2008.2007487 [10] Hjalmarson H P, Pease R L, Witczak S C, Shaneyfelt M R, Schwank J R, Edwards A H, Hembree C E, Mattsson T R 2003 IEEE Trans. Nucl. Sci. 50 1901 doi: 10.1109/TNS.2003.821803 [11] Rashkeev S N, Cirba C R, Fleetwood D M, Schrimpf R D, Witczak S C, Michez A, Pantelides S T 2002 IEEE Trans. Nucl. Sci. 49 2650 doi: 10.1109/TNS.2002.805387 [12] Witczak S C, Lacoe R C, Mayer D C, Fleetwood D M, Schrimpf R D, Galloway K F 1998 IEEE Trans. Nucl. Sci. 45 2339 doi: 10.1109/23.736453 [13] Fleetwood D M, Kosier S L, Nowlin R N, Schrimpf R D, Reber R A, DeLaus M, Winokur P S, Wei A, Combs W E, Pease R L 1994 IEEE Trans. Nucl. Sci. 41 1871 doi: 10.1109/23.340519 [14] Messina F, Cannas M 2007 J. Phys. Chem. C 111 6663 doi: 10.1021/jp0705727 [15] Pease R L, Adell P C, Rax B G, Chen X J, Barnaby H J, Holbert K E, Hjalmarson H P 2008 IEEE Trans. Nucl. Sci. 55 3169 doi: 10.1109/TNS.2008.2006478 [16] Chen X J, Barnaby H J, Vermeire B, Holbert K, Wright D, Pease R L, Dunham G, Platteter D G, Seiler J, McClure S, Adell P 2007 IEEE Trans. Nucl. Sci. 54 1913 doi: 10.1109/TNS.2007.909708 [17] Morana A, Cannas M, Girard S, Boukenter A, Vaccaro L, Périsse J, Macé J R, Ouerdane Y, Boscaino R 2013 Opt. Mater. Express 3 1769 doi: 10.1364/OME.3.001769 [18] Tomashuk A L, Zabezhailov M O 2011 J. Appl. Phys. 109 083103 doi: 10.1063/1.3561435 [19] Saito K, Ito M, Ikushima A J, Funahashi S, Imamura K 2004 J. Non-Cryst. Solids 347 289 doi: 10.1016/j.jnoncrysol.2004.07.079 [20] Weeks R A 1956 J. Appl. Phys. 27 1376 doi: 10.1063/1.1722267 [21] Nelson C M, Weeks R A 1960 J. Am. Ceram. Soc. 43 396 doi: 10.1111/j.1151-2916.1960.tb13681.x [22] Weeks R A, Nelson C M 1960 J. Am. Ceram. Soc. 43 399 doi: 10.1111/j.1151-2916.1960.tb13682.x [23] Griscom D L 1984 Nucl. Instrum. Meth. B 1 481 doi: 10.1016/0168-583X(84)90113-7 [24] Griscom D L 1985 OPL 61 213 doi: 10.1557/PROC-61-213 [25] Boero M, Oshiyama A, Silvestrelli P L 2004 Mod. Phys. Lett. B 18 707 doi: 10.1142/S0217984904007256 [26] Boero M, Oshiyama A, Silvestrelli P L 2003 Phys. Rev. Lett. 91 206401 doi: 10.1103/PhysRevLett.91.206401 [27] Wang Y, Zhao Y, Chen Z, Jia Z, Tong D, Nie S, Han Z 2024 J. Chem. Phys. 161 034705 doi: 10.1063/5.0206938 [28] Yue Y, Song Y, Zuo X 2017 AIP Adv. 7 015309 doi: 10.1063/1.4975147 [29] Chavez J R, Karna S P, Vanheusden K, Brothers C P, Pugh R D, Singaraju B K, Warren W L, Devine R A B 1997 IEEE Trans. Nucl. Sci. 44 1799 doi: 10.1109/23.658945 [30] Mukhopadhyay S, Sushko P V, Mashkov V A, Shluger A L 2005 J. Phys.: Condens. Matter 17 1311 doi: 10.1088/0953-8984/17/8/009 [31] Imai H, Arai K, Imagawa H, Hosono H, Abe Y 1988 Phys. Rev. B 38 12772 doi: 10.1103/PhysRevB.38.12772 [32] Blöchl P E 2000 Phys. Rev. B 62 6158 doi: 10.1103/PhysRevB.62.6158 [33] Skuja L 1998 J. Non-Cryst. Solids 239 16 doi: 10.1016/S0022-3093(98)00720-0 [34] Pantelides S T, Rashkeev S N, Fleetwood D M, Schrimpf R D 2000 IEEE Trans. Nucl. Sci. 47 2262 doi: 10.1109/23.903763 [35] McLean F B 1980 IEEE Trans. Nucl. Sci. 27 1651 doi: 10.1109/TNS.1980.4331084 [36] Saks N S, Klein R B, Griscom D L 1988 IEEE Trans. Nucl. Sci. 35 1234 doi: 10.1109/23.25445 [37] El-Sayed A M, Wimmer Y, Goes W, Grasser T, Afanas’ev V V, Shluger A L 2015 Phys. Rev. B 92 014107 doi: 10.1103/PhysRevB.92.014107 [38] El-Sayed A M, Watkins M B, Grasser T, Afanas’ev V V, Shluger A L 2015 Microelectron. Eng. 147 141 doi: 10.1016/j.mee.2015.04.073 [39] Rivera A, van Veen A, Schut H, de Nijs J M M, Balk P 2002 Solid-State Electron. 46 1775 doi: 10.1016/S0038-1101(02)00150-8 [40] Kato K 2012 Phys. Rev. B 85 085307 doi: 10.1103/PhysRevB.85.085307 [41] Yao P, Song Y, Zuo X 2021 Superlatt. Microstruct. 156 106962 doi: 10.1016/j.spmi.2021.106962 [42] Hong Z C, Yao P, Liu Y, Zuo X 2022 Chin. Phys. B 31 057101 doi: 10.1088/1674-1056/ac3506 [43] VandeVondele J, Krack M, Mohamed F, Parrinello M, Chassaing T, Hutter J 2005 Comput. Phys. Commun. 167 103 doi: 10.1016/j.cpc.2004.12.014 [44] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865 [45] VandeVondele J, Hutter J 2007 J. Chem. Phys. 127 114105 doi: 10.1063/1.2770708 [46] Goedecker S, Teter M, Hutter J 1996 Phys. Rev. B 54 1703 doi: 10.1103/PhysRevB.54.1703 [47] BROYDEN C G 1970 IMA J. Appl. Math. 6 222 doi: 10.1093/imamat/6.3.222 [48] Fletcher R 1970 Comput. J. 13 317 doi: 10.1093/comjnl/13.3.317 [49] Goldfarb D 1970 Math. Comp. 24 23 doi: 10.1090/S0025-5718-1970-0258249-6 [50] Shanno D F 1970 Math. Comp. 24 647 doi: 10.1090/S0025-5718-1970-0274029-X [51] Henkelman G, Uberuaga B P, Jónsson H 2000 J. Chem. Phys. 113 9901 doi: 10.1063/1.1329672 [52] Becke A D, Edgecombe K E 1990 J. Chem. Phys. 92 5397 doi: 10.1063/1.458517 [53] 卢天, 陈飞武 2011 物理化学学报 27 2786 doi: 10.3866/PKU.WHXB20112786 Lu T, Chen F W 2011 Acta Phys. Chem. Sin. 27 2786 doi: 10.3866/PKU.WHXB20112786 [54] Freysoldt C, Grabowski B, Hickel T, Neugebauer J, Kresse G, Janotti A, Van de Walle C G 2014 Rev. Mod. Phys. 86 253 doi: 10.1103/RevModPhys.86.253 [55] Pickard C J, Mauri F 2002 Phys. Rev. Lett. 88 086403 doi: 10.1103/PhysRevLett.88.086403 [56] Yazyev O V, Tavernelli I, Helm L, Röthlisberger U 2005 Phys. Rev. B 71 115110 doi: 10.1103/PhysRevB.71.115110 [57] Bahramy M S, Sluiter M H F, Kawazoe Y 2007 Phys. Rev. B 76 035124 doi: 10.1103/PhysRevB.76.035124 [58] Giannozzi P, Baroni S, Bonini N, Calandra M, Car R, Cavazzoni C, Ceresoli D, Chiarotti G L, Cococcioni M, Dabo I, Corso A D, Gironcoli S de, Fabris S, Fratesi G, Gebauer R, Gerstmann U, Gougoussis C, Kokalj A, Lazzeri M, Martin-Samos L, Marzari N, Mauri F, Mazzarello R, Paolini S, Pasquarello A, Paulatto L, Sbraccia C, Scandolo S, Sclauzero G, Seitsonen A P, Smogunov A, Umari P, Wentzcovitch R M 2009 J. Phys.: Condens. Matter 21 395502 doi: 10.1088/0953-8984/21/39/395502 [59] Charpentier T 2011 Solid State Nucl. Mag. 40 1 doi: 10.1016/j.ssnmr.2011.04.006 [60] Pickard C J, Mauri F 2001 Phys. Rev. B 63 245101 doi: 10.1103/PhysRevB.63.245101 [61] Le Roux S, Petkov V 2010 J. Appl. Cryst. 43 181 doi: 10.1107/S0021889809051929 [62] Goetzke K, Klein H J 1991 J. Non-Cryst. Solids 127 215 doi: 10.1016/0022-3093(91)90145-V [63] Yuan X, Cormack A N 2002 Comput. Mater. Sci. 24 343 doi: 10.1016/S0927-0256(01)00256-7 [64] Van Ginhoven R M, Jónsson H, Corrales L R 2005 Phys. Rev. B 71 024208 doi: 10.1103/PhysRevB.71.024208 [65] Mukhopadhyay S, Sushko P V, Stoneham A M, Shluger A L 2004 Phys. Rev. B 70 195203 doi: 10.1103/PhysRevB.70.195203 [66] Giacomazzi L, Martin-Samos L, Boukenter A, Ouerdane Y, Girard S, Richard N 2014 Phys. Rev. B 90 014108 doi: 10.1103/PhysRevB.90.014108 [67] Pantelides S T, Tsetseris L, Rashkeev S N, Zhou X J, Fleetwood D M, Schrimpf R D 2007 Microelectron. Reliab. 47 903 doi: 10.1016/j.microrel.2006.10.011 -
图( 8) 表( 2)
计量
- 文章访问数: 31
- HTML全文浏览数: 31
- PDF下载数: 2
- 施引文献: 0