高级搜索

硫掺杂氧化锌纳米线电子性质和光学性质的第一性原理研究

,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

黄俊刚, 方艺梅, 江银河, 郑凯, 陈凯轩, 程梅娟, 林秋宝. 硫掺杂氧化锌纳米线电子性质和光学性质的第一性原理研究[J]. 物理学报, 2025, 74(18): 186302-1. doi: 10.7498/aps.74.20250495
引用本文: 黄俊刚, 方艺梅, 江银河, 郑凯, 陈凯轩, 程梅娟, 林秋宝. 硫掺杂氧化锌纳米线电子性质和光学性质的第一性原理研究[J]. 物理学报, 2025, 74(18): 186302-1. doi: 10.7498/aps.74.20250495
shu
Jungang HUANG, Yimei FANG, Yinhe JIANG, Kai ZHENG, Kaixuan CHEN, Meijuan CHENG, Qiubao LIN. First-principles study of electronic and optical properties of sulfur-doped zinc oxide nanowires[J]. Acta Physica Sinica, 2025, 74(18): 186302-1. doi: 10.7498/aps.74.20250495
Citation: Jungang HUANG, Yimei FANG, Yinhe JIANG, Kai ZHENG, Kaixuan CHEN, Meijuan CHENG, Qiubao LIN. First-principles study of electronic and optical properties of sulfur-doped zinc oxide nanowires[J]. Acta Physica Sinica, 2025, 74(18): 186302-1. doi: 10.7498/aps.74.20250495
shu

硫掺杂氧化锌纳米线电子性质和光学性质的第一性原理研究

  • 1.

    集美大学理学院, 厦门　361021

  • 2.

    厦门乾照光电股份有限公司, 厦门　361101

    • 作者简介: 黄俊刚: 202312854018@jmu.edu.cn .
    通讯作者: E-mail: meijuan@jmu.edu.cn.;  E-mail: lqb@jmu.edu.cn.

  • 中图分类号: 63.20.dk, 74.25.Gz, 31.15.E-, 77.55.hf

First-principles study of electronic and optical properties of sulfur-doped zinc oxide nanowires

  • 1.

    School of Science, Jimei University, Xiamen 361021, China

  • 2.

    Xiamen Changelight Co. Ltd., Xiamen 361101, China

    • Corresponding authors: E-mail: meijuan@jmu.edu.cn.;  E-mail: lqb@jmu.edu.cn.

  • MSC: 63.20.dk, 74.25.Gz, 31.15.E-, 77.55.hf

  • 摘要: 基于密度泛函理论的第一性原理计算, 硫掺杂氧化锌纳米线的电子与光学性质研究揭示了掺杂对材料性能的调控机制. 硫的引入导致ZnO晶格发生局部畸变, 形成替位式掺杂结构, 显著改变了其本征能带结构, 费米能级向导带底偏移, 禁带宽度出现红移. 分轨道能带图表明, 硫的3p轨道在价带顶附近形成杂质能级, 增强了载流子浓度和迁移率. 硫原子的掺杂也诱导纳米线在光学性质方面发生显著变化, 比如, 介电函数实部和虚部展现了新的特征峰, 吸收系数显著提高, 且随着掺杂浓度的增大, 光学性质的变化更加显著. 该研究为硫掺杂氧化锌纳米线在光电探测器、发光二极管等器件中的性能优化提供了重要的理论支撑, 揭示了微观电子结构与宏观光学响应之间的内在关联机制.
    Abstract: Based on first-principles calculations within the framework of density functional theory, the structural features, electronic and optical properties of sulfur-doped ZnO nanowires are systematically investigated in this work, revealing the regulation mechanism of doping on material performance. The results show that sulfur incorporation induces local lattice distortions in ZnO, resulting in a substitutional doping structure. These structural modifications significantly affect the electronic properties, causing the Fermi level to shift toward the bottom of the conduction band and a redshift in the band gap. Importantly, the orbital-projected band structures reveal that the 3p orbitals of sulfur generate impurity states near the top of the valence band, thereby enhancing both carrier concentration and mobility. Furthermore, sulfur doping leads to a notable change in the optical properties, including the emergence of new characteristic peaks in both the real and imaginary parts of the dielectric function, as well as considerable increases in optical parameters such as the absorption coefficient, extinction coefficient, and reflectivity. Moreover, as the doping concentration increases, the changes in optical properties become more pronounced. Overall, this investigation offers valuable theoretical insights into optimizing the performance of sulfur-doped ZnO nanowires in optoelectronic applications, such as photodetectors and light-emitting diodes, revealing the intrinsic correlation mechanism between the microscopic electronic structure and the macroscopic optical response.
  • 加载中

  • 图 1  4种纳米线结构　(a) 六边形氧化锌纳米线结构; (b) 六角星形氧化锌纳米线结构; (c) 12个硫掺杂的六角星形纳米线结构(ZnSO); (d) 24个硫掺杂的六角星形纳米线结构(ZnSSO); 其中红球代表O原子, 灰球代表Zn原子, 黄球代表S原子

    Figure 1.  Four nanowire configurations: (a) Hexagonal ZnO; (b) star-shaped ZnO; (c) 12 S-doped star ZnO (ZnSO); (d) 24 S-doped star ZnO (ZnSSO). Atomic colors: O (red); Zn (gray); S (yellow).

    下载: 全尺寸图片 幻灯片

    图 2  各高对称点Γ, Z, R对应的布里渊区位置, 轴向方向为(0001)

    Figure 2.  Locations within the Brillouin zone corresponding to the high-symmetry points Γ, Z, and R, with the axial direction along (0001).

    下载: 全尺寸图片 幻灯片

    图 3  能带结构　(a) 六角星形氧化锌纳米线能带结构; (b) 12个硫掺杂的六角星形氧化锌纳米线结构(ZnSO); (c) 24个硫掺杂的六角星形氧化锌纳米线结构(ZnSSO); 高对称点Γ, Z, R对应的布里渊区位置分别为Γ (0, 0, 0), Z (0, 0, 0.5), R (0.5, 0.5, 0.5); s纳米线的轴向方向为(0001)

    Figure 3.  Band structures: (a) Star-shaped ZnO nanowire; (b) 12 S-doped star-shaped nanowire (ZnSO); (c) 24 S-doped star-shaped nanowire (ZnSSO). The high-symmetry points Γ, Z, and R correspond to the following positions in the Brillouin zone: Γ (0, 0, 0), Z (0, 0, 0.5), and R (0.5, 0.5, 0.5). The axial direction of the nanowire is (0001).

    下载: 全尺寸图片 幻灯片

    图 4  GGA+U计算的能带结构　(a) 六角星形氧化锌纳米线能带结构; (b) 12个硫掺杂的六角星形氧化锌纳米线结构(ZnSO); (c) 24个硫掺杂的六角星形氧化锌纳米线结构(ZnSSO); 高对称点Γ, Z, R对应的布里渊区位置分别为Γ (0, 0, 0), Z (0, 0, 0.5), R (0.5, 0.5, 0.5); 纳米线的轴向方向为(0001)

    Figure 4.  Band structure of GGA+U calculations: (a) Star-shaped ZnO nanowire; (b) 12 S-doped star-shaped nanowire (ZnSO); (c) 24 S-doped star-shaped nanowire (ZnSSO). The high-symmetry points Γ, Z, and R correspond to the following positions in the Brillouin zone: Γ (0, 0, 0), Z (0, 0, 0.5), and R (0.5, 0.5, 0.5). The axial direction of the nanowire is (0001).

    下载: 全尺寸图片 幻灯片

    图 5  六角星形ZnO纳米线的原子轨道投影能带结构, 其中(a)为总的, (b)为O原子, (c)为Zn原子; 六角星形ZnSO纳米线的原子轨道投影能带结构, 其中(d)为总的, (e)为O原子, (f)为Zn原子, (g)为S原子; 六角星形ZnSSO纳米线的原子轨道投影能带结构, 其中(h)为总的, (i)为O原子, (j)为Zn原子, (k)为S原子. 高对称点Γ, Z, R对应的布里渊区位置分别为 Γ (0, 0, 0), Z (0, 0, 0.5), R (0.5, 0.5, 0.5); 纳米线的轴向方向为(0001)

    Figure 5.  Orbital-projected band structures of hexagonal star-shaped: (a)–(c) ZnO nanowire (total, O, Zn); (d)–(g) ZnSO nanowire (total, O, Zn, S); (h)–(k) ZnSSO nanowire (total, O, Zn, S). The high-symmetry points Γ, Z, and R correspond to the following positions in the Brillouin zone: Γ (0, 0, 0), Z (0, 0, 0.5), and R (0.5, 0.5, 0.5). The axial direction of the nanowire is (0001).

    下载: 全尺寸图片 幻灯片

    图 6  介电函数(实部和虚部)　(a) 六边形氧化锌纳米线; (b) 六角星形氧化锌纳米线; (c) 12个硫掺杂的六角星形纳米线(ZnSO); (d) 24个硫掺杂的六角星形纳米线(ZnSSO)

    Figure 6.  Dielectric functions (real and imaginary parts): (a) Hexagonal ZnO nanowire; (b) hexagonal star-shaped ZnO nanowire; (c) 12 S-doped star-shaped nanowire (ZnSO); (d) 24 S-doped star-shaped nanowire (ZnSSO).

    下载: 全尺寸图片 幻灯片

    图 7  六边形ZnO与六角星形ZnO, ZnSO, ZnSSO纳米线的折射率随入射光能量的变化

    Figure 7.  Refractive indices of hexagonal ZnO nanowire, hexagonal star-shaped ZnO nanowire, 12 S-doped star-shaped nanowire (ZnSO), 24 S-doped star-shaped nanowire (ZnSSO) as a function of incident photon energy.

    下载: 全尺寸图片 幻灯片

    图 8  六边形ZnO与六角星形ZnO, ZnSO, ZnSSO纳米线的消光系数随入射光能量的变化

    Figure 8.  Extinction coefficients of hexagonal ZnO nanowire, star-shaped ZnO nanowire, 12 S-doped star-shaped nanowire (ZnSO), 24 S-doped star-shaped nanowire (ZnSSO) as a function of incident photon energy.

    下载: 全尺寸图片 幻灯片

    图 9  六边形ZnO与六角星形ZnO, ZnSO, ZnSSO纳米线的吸收系数

    Figure 9.  Absorption coefficients of hexagonal ZnO nanowire, star-shaped ZnO nanowire, 12 S-doped star-shaped nanowire (ZnSO), 24 S-doped star-shaped nanowire (ZnSSO).

    下载: 全尺寸图片 幻灯片

    图 10  六边形ZnO与六角星形ZnO, ZnSO, ZnSSO纳米线的反射率

    Figure 10.  Reflectance spectra of hexagonal ZnO nanowire, star-shaped ZnO nanowire, 12 S-doped star-shaped nanowire (ZnSO), 24 S-doped star-shaped nanowire (ZnSSO).

    下载: 全尺寸图片 幻灯片

    表 1  星形氧化锌纳米线(ZnO Star)、12个硫掺杂的六角星形纳米线(ZnSO)以及24个硫掺杂的六角星形纳米线结构(ZnSSO)的结构参数

    Table 1.  Structural parameters for hexagonal star-shaped ZnO, 12 S-doped star ZnO (ZnSO) and 24 S-doped star ZnO (ZnSSO).

    Structural parameters ZnO Star ZnSO ZnSSO
    Lateral dimensions
    a, b/Å    		 33.0×33.0 33.0×33.0 30.0×30.0
    Axial dimension c/Å 5.2065 5.2065 5.2065
    Unit cell volume/ų 5673.5 5673.5 4685.9
    Number of O atoms 102 90 78
    Number of S atoms 0 12 24
    Number of Zn atoms 102 102 102
    下载: 导出CSV
  • [1] Djurišić Dr A B, Leung Y H 2006 Small 2 944 doi: 10.1002/smll.200600134
    [2] Foreman J V, Li J Y, Peng H Y, Choi S, Everitt H O, Liu J 2006 Nano Lett. 6 1126 doi: 10.1021/nl060204z
    [3] Foreman J V, Everitt H O, Yang J, Liu J J 2007 Appl. Phys. Lett. 91 011902 doi: 10.1063/1.2753540
    [4] Özgür Ü, Alivov Y I, Liu C L, Teke A, Reshchikov M A, Doğan S, Avrutin V, Cho S J, Morkoç H 2005 J. Appl. Phys. 98 041301 doi: 10.1063/1.1992666
    [5] Triboulet R, Perrière J 2003 Prog. Cryst. Growth Charact. Mater. 47 65 doi: 10.1016/j.pcrysgrow.2005.01.003
    [6] Greene L E, Law M, Tan D H, Montano M, Goldberger J, Somorjai G, Yang P D 2005 Nano Lett. 5 1231 doi: 10.1021/nl050788p
    [7] Huang M H, Wu Y, Feick H, Tran N, Weber E, Yang P 2001 Adv. Mater. 13 113 doi: 10.1002/1521-4095(200101)13:2<113::AID-ADMA113>3.0.CO;2-H
    [8] Huang M H, Mao S, Feick H, Yan H Q, Wu Y Y, Kind H, Weber E, Russo R, Yang P D 2001 Science 292 1897 doi: 10.1126/science.1060367
    [9] Li S Y, Lin P, Lee C Y, Tseng T Y 2004 J. Appl. Phys. 95 3711 doi: 10.1063/1.1655685
    [10] Liu C H, Zapien J A, Yao Y, Meng X M, Lee C S, Fan S S, Lifshitz Y, Lee S T 2003 Adv. Mater. 15 838 doi: 10.1002/adma.200304430
    [11] Yao B D, Chan Y F, Wang N 2002 Appl. Phys. Lett. 81 757 doi: 10.1063/1.1495878
    [12] Guo M, Diao P, Cai S M 2005 J. Solid State Chem. 178 1864 doi: 10.1016/j.jssc.2005.03.031
    [13] Hartanto A B, Ning X, Nakata Y, Okada T 2004 Appl. Phys. A: Mater. Sci. Process. 78 299 doi: 10.1007/s00339-003-2286-2
    [14] Liu B, Zeng H C 2003 J. Am. Chem. Soc. 125 4430 doi: 10.1021/ja0299452
    [15] Park W, Jun Y, Jung S, Yi G C 2003 Appl. Phys. Lett. 82 964 doi: 10.1063/1.1544437
    [16] Yu W D, Li X M, Gao X D 2004 Appl. Phys. Lett. 84 2658 doi: 10.1063/1.1695097
    [17] Delin A, Ravindran P, Eriksson O, Wills J M 1998 Int. J. Quantum Chem. 69 349 doi: 10.1002/(SICI)1097-461X(1998)69:3<349::AID-QUA13>3.0.CO;2-Y
    [18] Ravindran P, Delin A, Johansson B, Eriksson O, Wills J M 1999 Phys. Rev. B 59 1776 doi: 10.1103/PhysRevB.59.1776
    [19] Lucarelli A, Lupi S, Calvani P, Maselli P, De Marzi G, Roy P, Saini N L, Bianconi A, Ito T, Oka K 2002 Phys. Rev. B 65 054551 doi: 10.1103/PhysRevB.65.054511
    [20] Karazhanov S Z, Ravindran P, Kjekshus A, Fjellvåg H, Svensson B G 2007 Phys. Rev. B 75 155104 doi: 10.1103/PhysRevB.75.155104
    [21] Kong F J, Jiang G 2009 Physica B 404 2340 doi: 10.1016/j.physb.2009.04.041
    [22] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188 doi: 10.1103/PhysRevB.13.5188
    [23] Schmidt-Mende L, Macmanus-Driscoll J L 2007 Mater. Today 10 40 doi: 10.1016/S1369-7021(07)70078-0
    [24] Choi A, Kim K, Jung H I, Lee S Y 2010 Sens. Actuat. B 148 577 doi: 10.1016/j.snb.2010.04.049
    [25] Shi L H, Chen J, Zhang G, Li B W 2012 Phys. Lett. A 376 978 doi: 10.1016/j.physleta.2011.12.040
    [26] Zhao Q D, Xie T F, Peng L L, Lin Y H, Wang P, Peng L, Wang D J 2007 J. Phys. Chem. C 111 17136 doi: 10.1021/jp075368y
    [27] Mousavi S H, Haratizadeh H, Kitai A H 2011 Mater. Lett. 65 2470 doi: 10.1016/j.matlet.2011.05.027
    [28] Cho J, Lin Q B, Yang S, Simmons J G, Cheng Y W, Lin E, Yang J Q, Foreman J V, Everitt H O, Yang W T, Kim J, Liu J 2012 Nano Res. 5 20 doi: 10.1007/s12274-011-0180-3
    [29] Lin Q B, Wu S Q, Zhu Z Z 2016 AIP Adv. 6 095219 doi: 10.1063/1.4963742
    [30] Kresse G, Hafner J 1993 Phys. Rev. B 48 13115 doi: 10.1103/PhysRevB.48.13115
    [31] Kresse G, Furthmüller J 1996 Comput. Mater. Sci. 6 15 doi: 10.1016/0927-0256(96)00008-0
    [32] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865
    [33] Perdew J P, Wang Y 1992 Phys. Rev. B 45 13244 doi: 10.1103/PhysRevB.45.13244
    [34] Ma Y, Yan H, Yu X X, Gong P, Li Y L, Ma W D, Fang X Y 2024 J. Appl. Phys. 135 054101 doi: 10.1063/5.0187116
    [35] Goh E S, Mah J W, Yoon T L 2017 Comput. Mater. Sci. 138 111 doi: 10.1016/j.commatsci.2017.06.032
    [36] Harun K, Salleh N A, Deghfel B, Yaakob M K, Mohamad A A 2020 Results Phys. 16 102829 doi: 10.1016/j.rinp.2019.102829
    [37] Hu J Q, Xu L H, Wu S Q, Zhu Z Z 2019 Curr. Appl. Phys. 19 1222 doi: 10.1016/j.cap.2019.07.014
    [38] Gajdoš M, Hummer K, Kresse G, Furthmueller J, Bechstedt F 2006 Phys. Rev. B 73 045112 doi: 10.1103/PhysRevB.73.045112
    [39] Hu J Q, Shi X H, Wu S Q, Ho K M, Zhu Z Z 2019 Nanoscale Res. Lett. 14 288 doi: 10.1186/s11671-019-3105-9
    [40] Yang L Z, Liu W K, Yan H, Yu X X, Gong P, Li Y L, Fang X Y 2024 Eur. Phys. J. Plus 139 66 doi: 10.1140/epjp/s13360-024-04883-z
    [41] Ould Ne M L, El Hachimi A G, Boujnah M, Benyoussef A, El Kenz A 2018 Optik 158 693 doi: 10.1016/j.ijleo.2017.12.089
  • 加载中
图( 10) 表( 1)
计量
  • 文章访问数:  23
  • HTML全文浏览数:  23
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-04-16
  • 刊出日期:  2025-09-20

硫掺杂氧化锌纳米线电子性质和光学性质的第一性原理研究

    通讯作者: E-mail: meijuan@jmu.edu.cn.; 
    通讯作者: E-mail: lqb@jmu.edu.cn.
    作者简介: 黄俊刚: 202312854018@jmu.edu.cn
  • 1. 集美大学理学院, 厦门　361021
  • 2. 厦门乾照光电股份有限公司, 厦门　361101
  • 收稿日期:  2025-04-16

摘要: 基于密度泛函理论的第一性原理计算, 硫掺杂氧化锌纳米线的电子与光学性质研究揭示了掺杂对材料性能的调控机制. 硫的引入导致ZnO晶格发生局部畸变, 形成替位式掺杂结构, 显著改变了其本征能带结构, 费米能级向导带底偏移, 禁带宽度出现红移. 分轨道能带图表明, 硫的3p轨道在价带顶附近形成杂质能级, 增强了载流子浓度和迁移率. 硫原子的掺杂也诱导纳米线在光学性质方面发生显著变化, 比如, 介电函数实部和虚部展现了新的特征峰, 吸收系数显著提高, 且随着掺杂浓度的增大, 光学性质的变化更加显著. 该研究为硫掺杂氧化锌纳米线在光电探测器、发光二极管等器件中的性能优化提供了重要的理论支撑, 揭示了微观电子结构与宏观光学响应之间的内在关联机制.

English Abstract

    全文HTML

    1.   引　言

    • 氧化锌(ZnO)作为Ⅱ–Ⅵ族直接带隙的半导体材料[1–3], 大多数晶体类型为六边纤锌矿结构和立方闪锌矿结构, 结构特点为: 每个阴离子被四面体角上的4个阳离子包围, 或者4个阴离子结合成四面体, 而阳离子处在四面体的中心. 这种四面体配位兼具典型的$ \mathrm{s}{\mathrm{p}}^{3} $杂化共价键和离子键, 因此ZnO离子性介于共价半导体和离子半导体之间. 在室温条件下, 具有热力学稳定性的相为六边纤锌矿结构, 而立方闪锌矿结构只能通过在立方衬底上稳定生长以及比较罕见的氯化钠式八面体结构只能在相对较高的压力下得到[4]. 相比于其他材料, 氧化锌禁带宽度高达3.37 eV[4], 这使得其对可见光几乎无响应, 而对紫外光特别敏感, 因此在紫外探测器、紫外LED等领域有着较为广阔的应用前景. 此外, 氧化锌还具有优异的抗氧化能力、良好的热稳定性、高的机械强度、高比表面积和高活性、相当大的激子结合能 (60 meV)、低成本、对生态友好等特性. 还可以用于其他多方面, 如压电换能器、光波导、表面声波器件、压敏电阻、荧光粉、透明导电氧化物、化学和气体传感器、自旋功能器件、紫外线发射器等[1,4,5].

      ZnO的纳米结构形态多种多样, 如纳米线[6–11]、纳米棒[12–16]和纳米带状[17–20]等. 制备ZnO纳米结构的方法也具有多样性, 如热蒸发[9,21]、金属有机气相外延(MOVPE)[22]、水热合成[12,14]和基于模板的合成[10]. 各种纳米结构中, ZnO纳米线由于其准一维结构具有量子约束效应和高表面体积比而备受关注. ZnO纳米线可以看作是电子、空穴和光子的吸收、发射和输运的一维通道. 这种特殊的几何结构可以导致对载流子和光子的强限制效应, 从而获得各种新颖的光学和电学性质的器件应用, 如短波长LED和纳米尺寸的激光器[1]. 氧化锌纳米线通常具有较高的长径比, 直径通常在几纳米到几十纳米之间, 长度可以达到几微米或更长. 近年来, 氧化锌纳米线已经在多个领域展现出广泛的应用前景, 例如: 电子器件中的染料敏化太阳能电池[23]、化学和生物传感器[24]以及压电和热电器件[25]等. 不同几何形状的ZnO纳米结构在上述器件的实际应用中起着非常关键的作用[26].

      氧化锌纳米线通常条件下是六边形[27], 不同形状的ZnO纳米线具有不同的性能, 展现不同的应用潜力. 要制备出新型异形氧化锌纳米线, 元素替换掺杂是很好的方法. 而S和O是同族元素且相邻最近, S元素的掺杂是一个很好的选择. Cho等[28]采用低温水热生长法制备了ZnO纳米结构, 当生长溶液添加来自硫脲[SC(NH2)2]中的硫掺杂剂时, ZnO纳米线的横截面由六边形转变为六角星形. 通过对未掺杂和掺硫氧化锌的X射线光发射光谱和光致发光光谱的比较, 证实了硫是导致这种新形貌形成的原因. 此外, 通过第一性原理计算揭示, 硫的加入引起了电荷分布的局部变化, 这种变化在顶点处比在边缘处更强烈, 进而导致发生从六边形到六角星形纳米结构的转变. 基于密度泛函理论, 本文通过从头计算[29]研究了ZnO纳米线的形状转变机理, 证实了一定量的S原子掺杂可以使六边形纳米线转变为六角星形纳米线, 六角星ZnO纳米线的形成强烈依赖于纳米线表面O原子被S原子取代的比例. 电子性质的计算结果表明, 掺杂硫的六角星形ZnO纳米线是一种间接带隙半导体, 其带隙小于相同尺寸的六边形ZnO纳米线, 并且随着S掺杂比例的增大, 带隙减小. 电子性质的改变往往诱发光学性质发生显著的变化, 然而六角星形ZnO纳米线的光学性质仍然没有得到研究, 其很可能具有更加强烈的光学响应. 因此, 本文通过第一性原理计算, 对硫掺杂氧化锌的结构特征、电子性质、介电函数等光学性质展开深入的研究, 以揭示六角星形氧化锌纳米线是否在光电子器件领域表现出更大的应用潜力.

    2.   计算原理方法

    • 本文的从头计算是通过维也纳原子尺度材料模拟的计算程序模拟包VASP [30,31]进行, 该程序使用投影缀加波的密度泛函理论. 基于Perdew, Burke和Ernzerhof [32]的广义梯度近似(GGA)用于描述交换关联能[33]. 确定原子位置的收敛标准设置为: 作用在所有原子上的力小于0.001 eV/Å, 平面波截断能量设为360 eV. 对于自洽电子结构的计算, 总能量收敛要求设为10–4 eV. 采用1× 1×22的Monhkorst-Pack格式的k点网格进行布里渊区采样. 所有计算采用高斯展宽σ = 0.03 eV.

    3.   结果与讨论

      3.1.   结构和电子性质

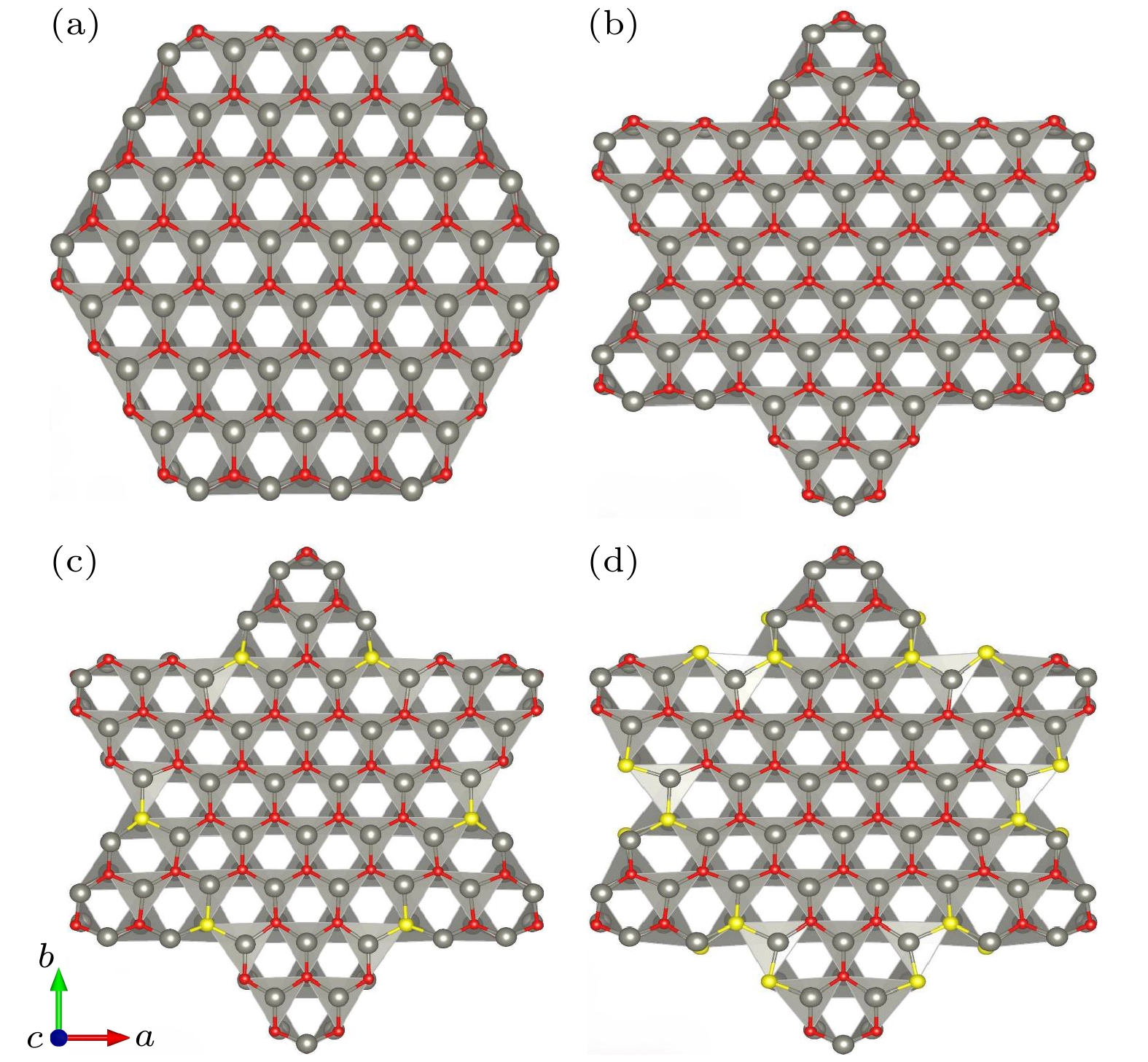
    • 纳米线超胞模型原子位置的建立基于晶格常数为a = b = 0.33 nm和c = 0.521 nm的ZnO纤锌矿结构(空间群C 6mc), a和b方向设置足够大的真空层厚度, 即a = b = 3.3 nm, c = 0.521 nm, α, β, γ为90°. xy平面内设置33 Å周期性距离, 相邻表面原子最小间距0.673 nm, 有效消除了镜像相互作用[34]. 如图1(a)所示, 典型的ZnO纳米线呈六边形纤锌矿结构, 由ZnO结构极性(0001)平面生长得到. 这种结构是ZnO纳米线最常见的形态, 也是ZnO最稳定的晶体形态, 其规则的六边形截面和高对称性使其在光电子器件中表现出优异的性能. 当S原子作为掺杂剂加入到生长溶液中时, 非极性侧面(10$ \overline{1} $0)变得不稳定, 可以形成新的侧面. 如上述提及的, 实验上通过来自于硫脲 ([SC(NH2)2]) 的S掺杂, 最终形成六角星形纳米结构(见图1(c), (d))[28]. 与六边形ZnO纳米线结构相比, 星形结构具有更大的表面积和更多的边缘活性位点, 可以显著增强光散射效应, 从而提高材料的光吸收效率. 掺杂不仅可以改变纳米线的化学组成, 还可能改变ZnO的电子结构, 从而影响其光学、电学性能. 为了探究横截面形状、S掺杂浓度对纳米线电子性质和光学性能的影响, 对图1四种纳米线结构进行优化并计算其电子结构和光学性质. 典型的六边形氧化锌纳米线结构(图1(a)), 由192个原子构成, 其中氧原子和锌原子各占96个. 图1(b)为六角星形氧化锌纳米线结构, 其由204个原子构成, 即102个氧原子和102个锌原子. 在六角星形ZnO纳米线结构基础上, 边缘的12个氧原子被硫原子取代, 得到包含102个锌原子、90个氧原子和12个硫原子的硫掺杂六角星形纳米线结构(称为ZnSO), 如图1(c). 进一步增大硫掺杂的浓度, 即用24个硫原子替换氧原子, 得到高浓度硫掺杂六角星形纳米线结构ZnSSO(由102个锌原子、78个氧原子和24个硫原子构成), 见图1(d). 星形ZnO纳米线以及掺杂硫原子的星形ZnSO和ZnSSO的晶格常数等结构参数见表1.

      在文献[28,29]中, 以六边形ZnO纳米线(基体结构)为起点, 实验生长合成了S掺杂的六角星结构(如图1(b)—(d)所示). 实验和理论计算共同表明, 将六边形ZnO纳米线边缘位置的O原子替换成S原子有助于纳米线的稳定生长, 同时促使其形貌演变为稳定的六角星结构. 而S原子会优先取代六边形ZnO纳米线边缘位置角位点的O原子, 这主要源于角位O原子的取代能垒较低, 电荷转移小, 使得该位置易于发生S掺杂. S占据角位点后, 抑制了角位的生长, 并驱动纳米线边缘发生楔形向外生长, 最终导致了六角星形结构的形成. 理论计算进一步证实了角位是能量最稳定的掺杂位置. 顶角替位构型的总能量显著低于棱边替位构型的总能量, 表明S原子取代角位O原子的构型在能量上更有利(即能量最低构型). 差分电荷密度分析为此提供了证据: 相较于棱边替位, 顶角替位时S原子周围的电荷密度更高, 表明此位置形成的Zn—S键更强, 这与理论计算得出的结论一致.

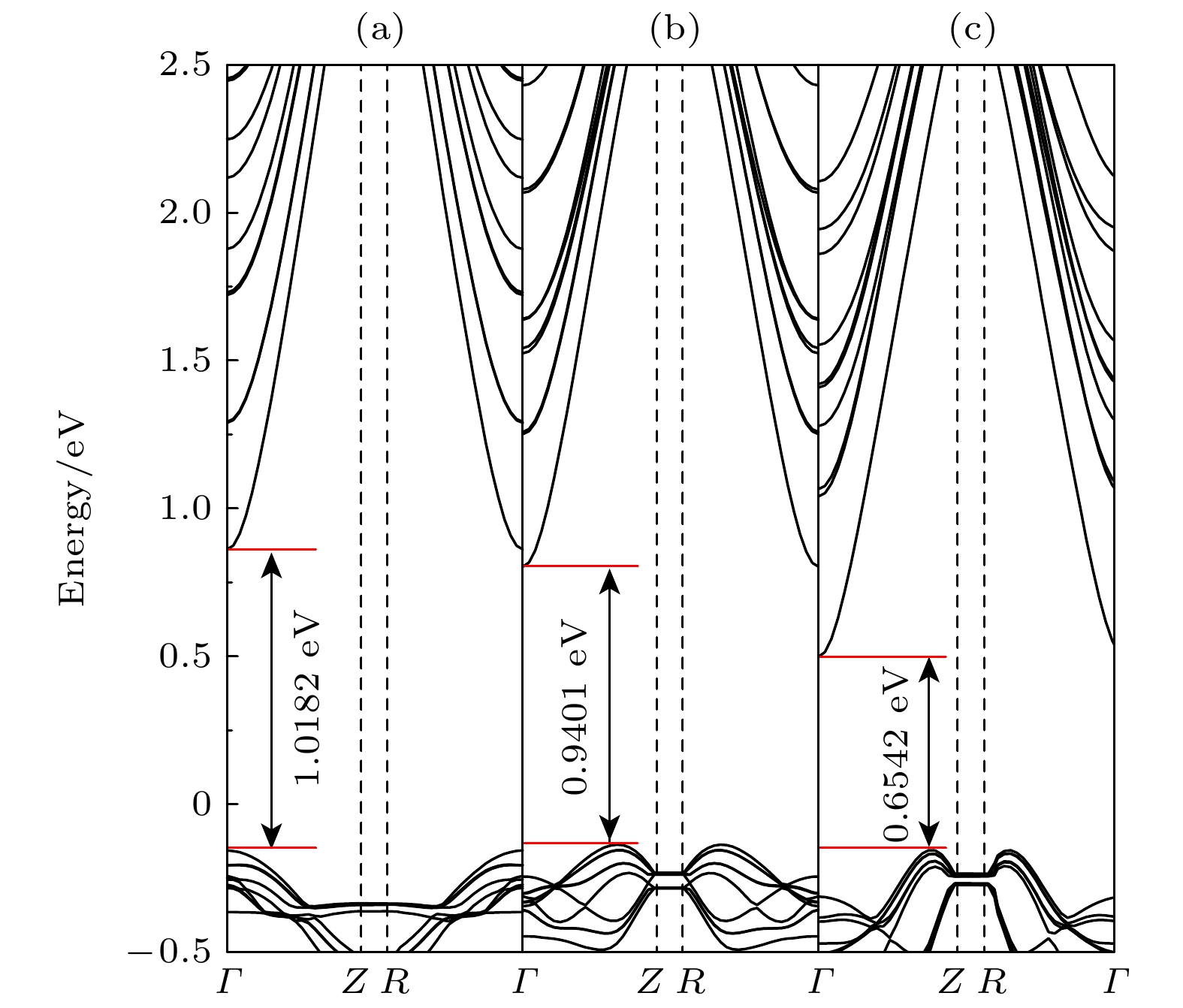
      此外, 我们还计算了不同原子数和结构(基体结构、中间结构、六边形和六角星形)的纳米线在不同S浓度掺杂下每个生长原子的平均形成能$ {\bar E_{{\text{grow}}}} =\left( {E-{E_{{\text{base}}}}} \right) / {N_{{\text{grow}}}} $[29]. 这些形成能可用于比较不同侧平面形状的纳米线的结构稳定性. 如果六角星形结构中每生长一个原子的平均形成能高于六边形结构, 那么在纳米线的生长合成中, 六角星形结构就更稳定, 且更容易形成. 当未掺杂时, 六边形结构的平均形成能 (4.456 eV) 略高于六角星结构(图1(b))的4.409 eV, 此时六边形结构更稳定. 当掺杂12个S原子时, 六边形结构的平均形成能(4.378 eV)比六角星结构(图1(c))的4.314 eV更高, 说明此时还是六边形结构更稳定. 当掺杂增加到24个S原子时, 六角星结构(图1(d))的平均形成能(4.050 eV)反而比六边形结构(3.984 eV)更高, 此时六角星结构更稳定, 侧平面更容易形成六角星形状. 所有S掺杂结构的$ {\bar E_{{\text{grow}}}} $均低于未掺杂, 这说明S原子替代O原子引入晶格畸变, 通常会降低结构的整体稳定性. 随着S浓度的增大, 电荷从S向Zn的转移, S—Zn键强度削弱, 键长伸长, 促使原子优先在角间平面生长, 形成六角星结构[29]. 态密度分析表明: 在低S掺杂的六角星结构中, Zn原子结合强度增强, 晶格稳定性提升. 而在高S掺杂时, S原子3p轨道能级下移, 键合增强, 虽然有助于结构稳定, 但是过度的键长拉伸会削弱整体稳定性. 对比图1的4种纳米线结构, 图1(a)稳定性最好($ {\bar E_{{\text{grow}}}} $ = 4.456 eV), 其次是图1(b), 再是图1(c), 最后是图1(d).

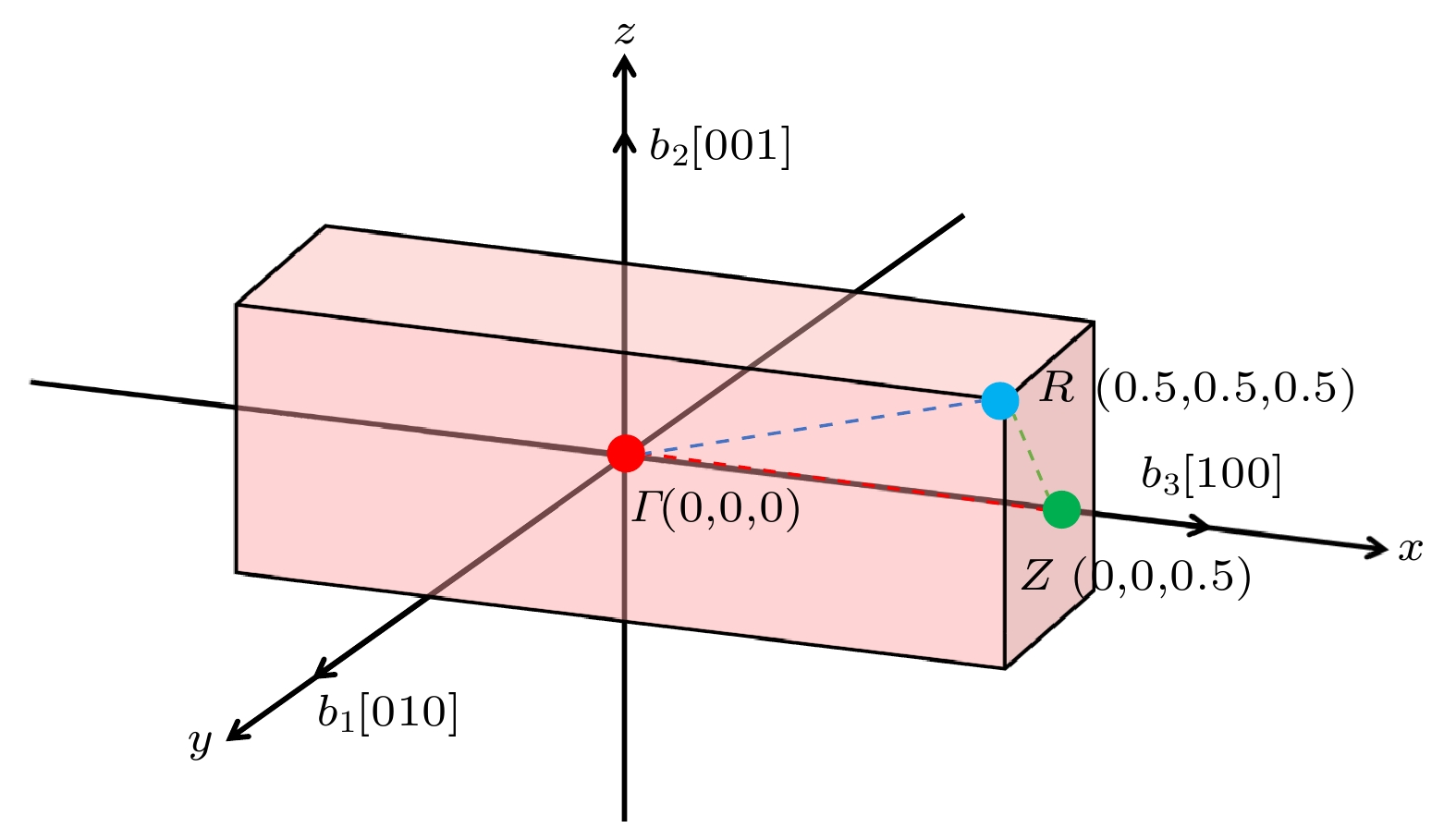
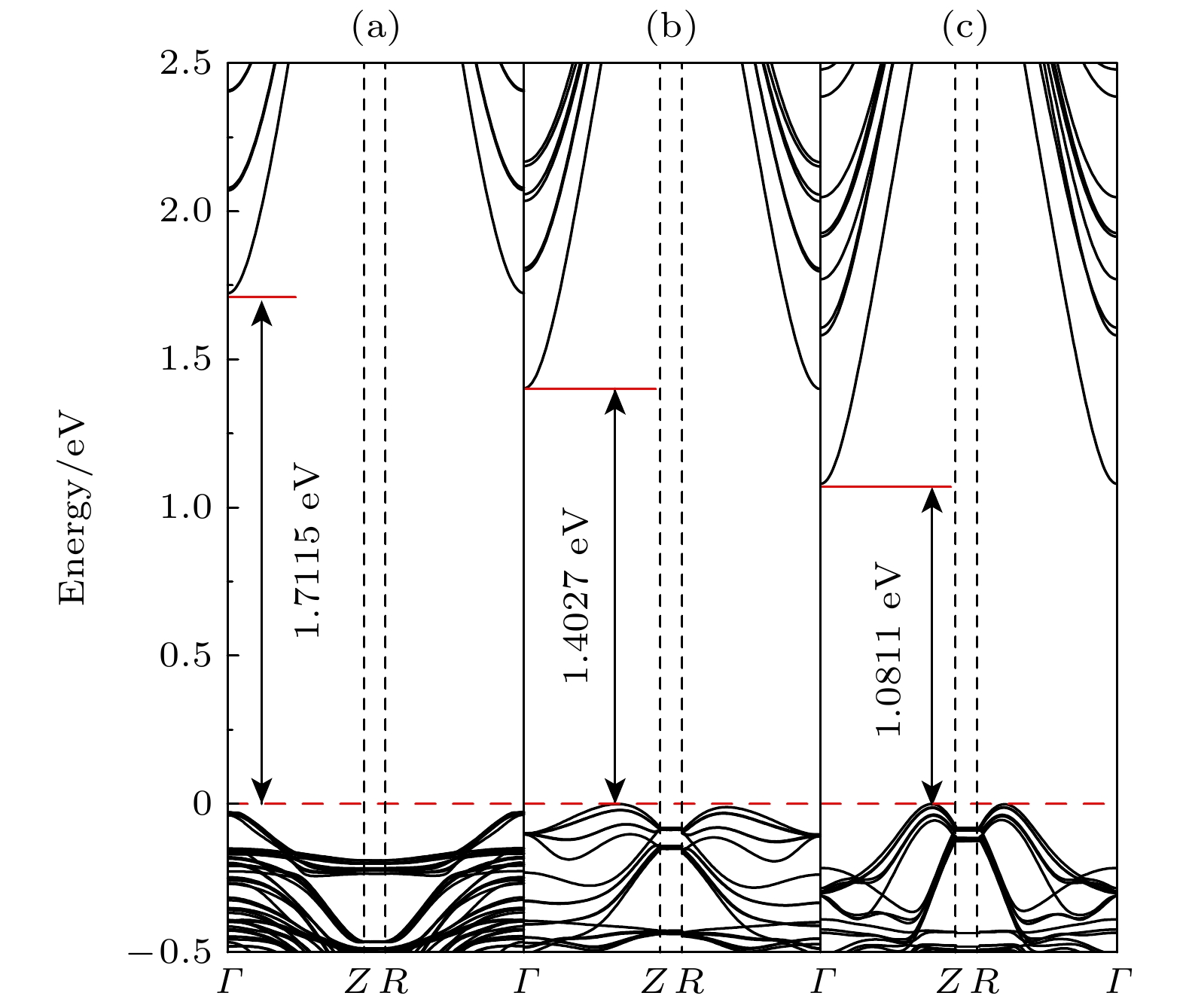
      没有硫掺杂的六边形ZnO纳米线结构是直接带隙的半导体, 其带隙为1.03 eV[29]. 而六角星形ZnO纳米线结构、掺杂硫的六角星形纳米线结构ZnSO和ZnSSO带隙分别为1.0182 eV, 0.9401 eV和0.6542 eV. 相比于六边形ZnO, 六角星形ZnO的电子性质基本上没有发生变化, 价带顶和导带底均在高对称点$ \varGamma $. 但是掺杂硫元素的六角星形纳米线结构带隙降低, 并且随着掺杂硫浓度的增大, 带隙降低更显著. 各高对称点Γ, Z, R对应的布里渊区位置如图2所示. 此外, 如图3能带结构所示, 掺杂硫原子后纳米线结构变成了间接带隙的半导体. 随着硫浓度的增大, 价带顶位置逐渐移向对称点$ {Z} $, 导带底仍处在高对称点$ \varGamma $, 但是导带底的位置逐渐降低, 从而形成了更小带隙的间接带隙半导体. 这是因为掺入硫原子后, 硫会占据氧的位点, 形成了新的能级. 这些能级会出现在ZnO的禁带中进而影响电子的跃迁, 纳米线的能带结构也因此发生变化. 带隙的降低会使得纳米线结构吸收更低能量的光子, 光学性质发生红移. 因此, 掺杂硫元素不仅仅会改变纳米线的能带结构, 还会影响其光学性质. 我们可以通过不同浓度的硫原子掺杂来调控纳米线的电子性质和光学性质, 进而拓展纳米线的应用前景. 比如在光电器件领域, 通过掺杂调节纳米线的带隙增强其光电转换效率. 选择不同浓度的硫原子掺杂, 调节带隙进而改变光吸收范围甚至调整其发光特性, 使得纳米线在光电子器件、场发射器件等领域的应用潜力更加广泛. 因此, 理论上深入研究掺杂对六边形ZnO纳米线性质的影响有利于推动ZnO材料的实验研究和实际应用.

      由于上述计算采用了GGA近似方法, 而GGA泛函通常会低估材料的带隙值. 因此, 我们用GGA+U的方式来计算星形结构的能带进行对比, 能带结构见图4, 其中UZn-d 设置为8 eV[35,36]. 研究发现, 六角星形ZnO纳米线结构、掺杂硫的六角星形纳米线结构ZnSO和ZnSSO带隙分别为1.7115 eV, 1.4027 eV和1.0811 eV. 与GGA-PBE相比, 能带结构的整体形状保持不变, 但带隙变大. 准确的能带结构会对光学参量数值大小产生一定的影响, 同时峰值所在的能量位置也会发生一些变化. 然而, 在本工作中, 我们计算的体系为原子数较多的纳米线结构, 无法通过“剪刀算子”修正等方法得到准确的数值结果. 但是本文计算仍然具有很大的意义, 因为光谱形状没有改变, 从而确保关于光学性质的定性趋势和物理结论依然有效.

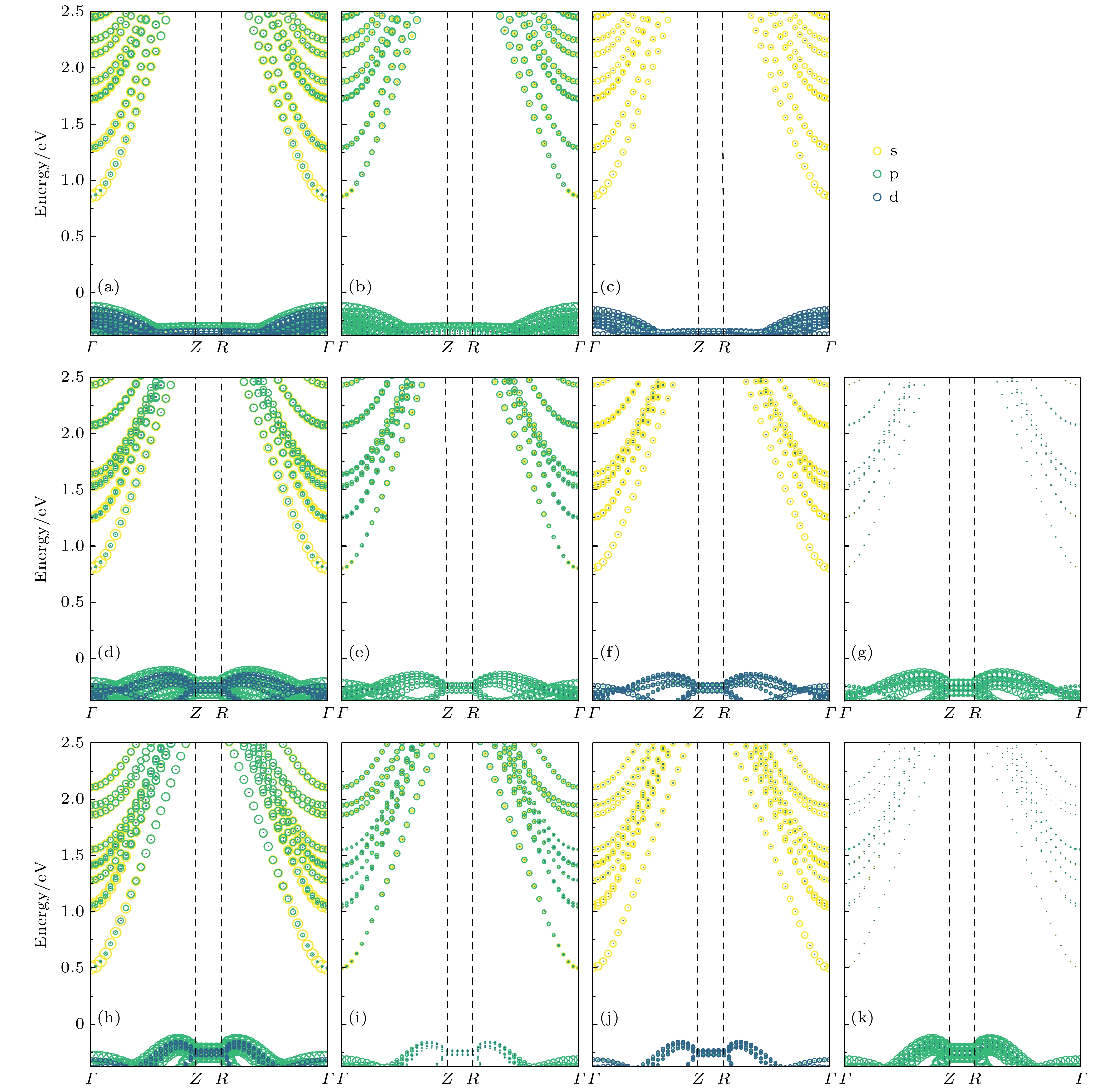
      为了深入了解掺杂硫元素后纳米线电子性质变化的根源, 我们计算并绘制了原子轨道投影的能带结构, 如图5所示. 六角星形ZnO, ZnSO, ZnSSO纳米线结构的导带底均来自于Zn原子$ \mathrm{s} $轨道的贡献. 对于价带顶, 六角星形ZnO主要产生氧原子p轨道的贡献, 而分别掺杂12个与24个硫原子的ZnSO, ZnSSO则是归因于硫原子p轨道的贡献. 这表明, 掺入硫原子后, 在带隙间出现新的能级, 即杂质能级. 此外, 从图5可以看出, 六角星形ZnO, ZnSO, ZnSSO纳米线结构的能带起伏较大, 说明处于这些带中的电子有效质量较小、非局域的程度较大、组成这些能带的原子轨道扩展性较强. 导带中的能带形状近似于抛物线形状, 为类$ \mathrm{s}\mathrm{p} $带.

      • 3.2.   光学性质

      3.2.1.   介电函数

    • 介电函数是描述物质对外电场响应的重要物理量, 由实部和虚部组成. 当物质处于外电场时, 原子中的正负电荷发生相对位移, 从而诱发电偶极矩的形成, 即发生极化现象. 而介电函数实部反映了极化强度的大小, 实部越大, 则代表物质的极化响应越强烈. 介电函数的虚部则代表了物质在外电场中的能量损耗情况. 给定频率下的介电函数$ \varepsilon \left(\omega \right) = {\varepsilon }_{1}\left(\omega \right) + {\mathrm{i}\varepsilon }_{2}\left(\omega \right), $ ${\varepsilon }_{1}\left(\omega \right) $和${\varepsilon }_{2}\left(\omega \right) $分别为介电函数的实部和虚部, $ \omega $为光子频率. 介电函数$ \varepsilon \left(\omega \right) $来自于带内跃迁和带间跃迁两部分的贡献. 对于金属材料, 带内跃迁是重要的, 而对于半导体材料, 带内跃迁贡献较小. 带间跃迁可分为直接跃迁和间接跃迁. 间接带间跃迁涉及声子的散射, 一般对$ \varepsilon \left(\omega \right) $的贡献很小, 可以忽略[21]. 通过占据态到非占据态直接跃迁的求和, 得到介电函数虚部$ {\varepsilon }_{2}\left(\omega \right) $[37,38]:

      利用计算得到的介电函数虚部$ {\varepsilon }_{2} (\omega) $, 通过Kramer-Kronig变换[37,39]计算得到介电函数的实部$ {\varepsilon }_{1} (\omega ) $:

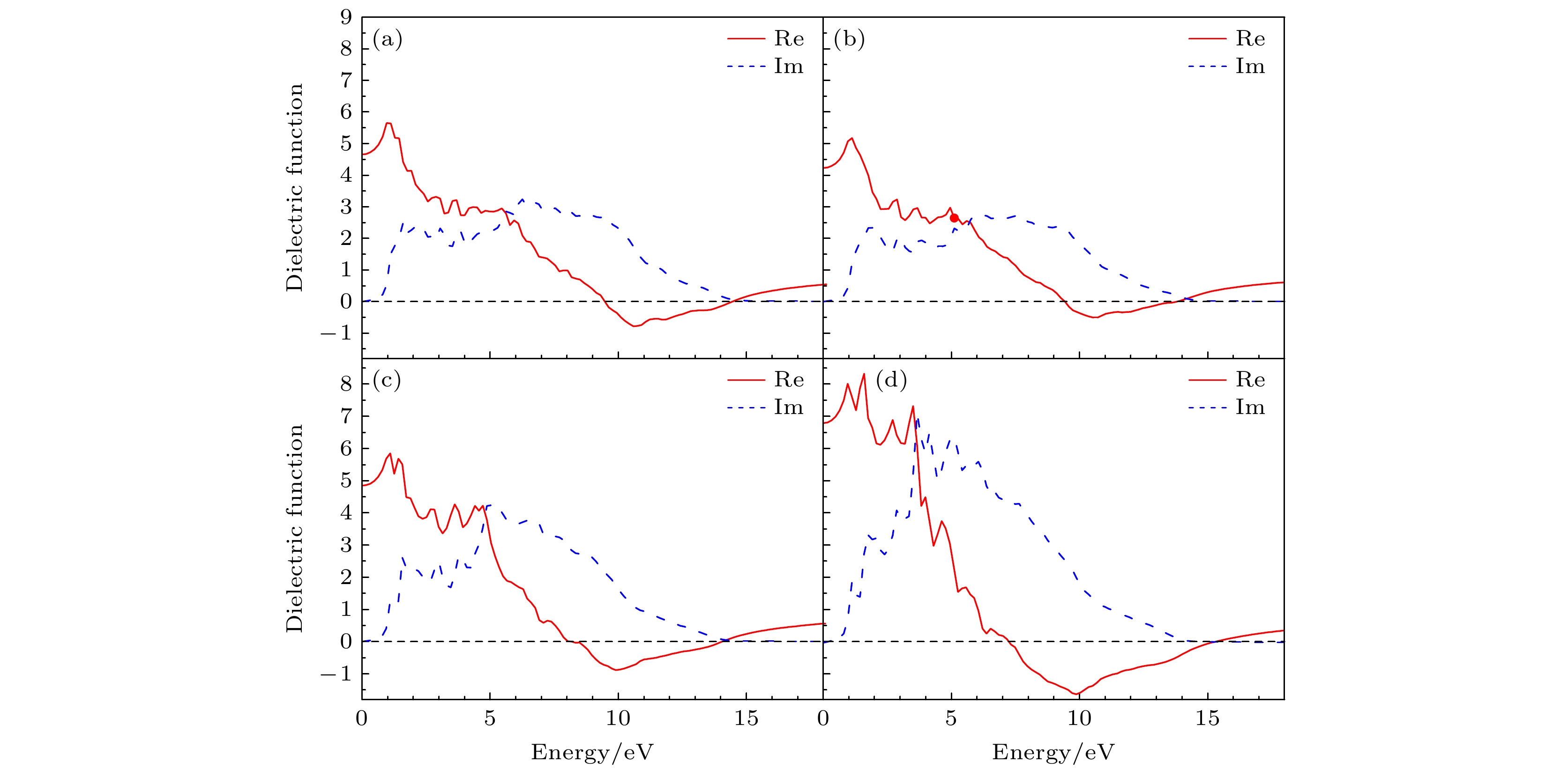
      (1)式和(2)式中的下标c, v分别表示导带和价带; $ \varOmega $为原胞体积; $ \langle{u}_{ck+{e}_{\alpha q}}|{u}_{vk}\rangle $是由自洽能带结构得到的偶极跃迁矩阵元; P表示柯西主值积分; $ \alpha $和$ \beta $为笛卡尔分量; $ {\varepsilon }_{ck} $和$ {\varepsilon }_{vk} $分别是导带和价带的能量; $ \eta $由参数CSHIFT来确定. 图6分别为六边形ZnO、六角星形ZnO、六角星形ZnSO和ZnSSO的介电函数实部与虚部随入射光子能量的变化, 这里仅展示光偏振方向平行于c轴的部分(纳米线方向). 计算得到的六边形ZnO、六角星形ZnO、六角星形ZnSO和ZnSSO的静态介电常数分别为4.66, 4.23, 4.85和6.95. 介电函数实部随光子能量的变化呈现先上升后下降到零以下, 之后再上升的趋势. 介电函数实部在特定光子能量范围出现负值, 呈现出类金属特性, 这源于各结构氧化锌纳米线在该能量区存在强烈的光吸收(图9中的吸收系数也证实了这一点). 这种强吸收是光电效应的结果, 即光子能量足以将价带电子激发到导带, 产生高浓度的光生电子-空穴对. 这些激发的自由载流子(电子)在光照下, 会发生集体性的等离子体振荡. 根据Kramers-Kronig关系, 介电函数虚部强吸收峰的高能侧, 由光生载流子主导的等离子体响应会迫使介电常数实部急剧下降并穿越零点变为负值[40]. 4种结构中, 六角星形ZnSSO展现的极大值最大, 为8.52, 相比于六边形ZnO(5.65), 会发生更强的极化效应. 介电函数虚部反映物质对光的吸收情况, 其峰值是由价带和导带之间的电子跃迁形成的. 六边形ZnO有两个主要的峰, 分别在1.60 eV和6.26 eV处(图6(a)). 六角星形ZnO的两个主要峰分别在1.92 eV与5.91 eV(图6(b)). 而六角星形ZnSO的两个主要峰分别在1.89 eV与5.03 eV(图6(c)). ZnSSO纳米线介电函数虚部谱线发生较大的抖动, 其主峰对应的光子能量为3.66 eV. 对比图6(a)与图6(b)—(d)可知, 六角星形以及S原子的存在, 会使得纳米线结构的介电函数虚部主峰值向能量更低的位置移动, 即发生红移. 相比于六边形ZnO纳米线, 六角星形ZnO介电函数实部和虚部谱线形状发生较小的变化, 而掺硫的六角星形ZnSO和ZnSSO发生明显的变化, 并且硫原子浓度越大, 产生的变化越显著. 如图6(d)所示, 掺杂24个硫原子的六角星形ZnSSO纳米线的介电函数数值明显增大, 并且实部和虚部谱线发生更剧烈的抖动, 这表示ZnO纳米线中掺杂硫原子有利于增加物质对外电场的响应.

      • 3.2.2.   折射率

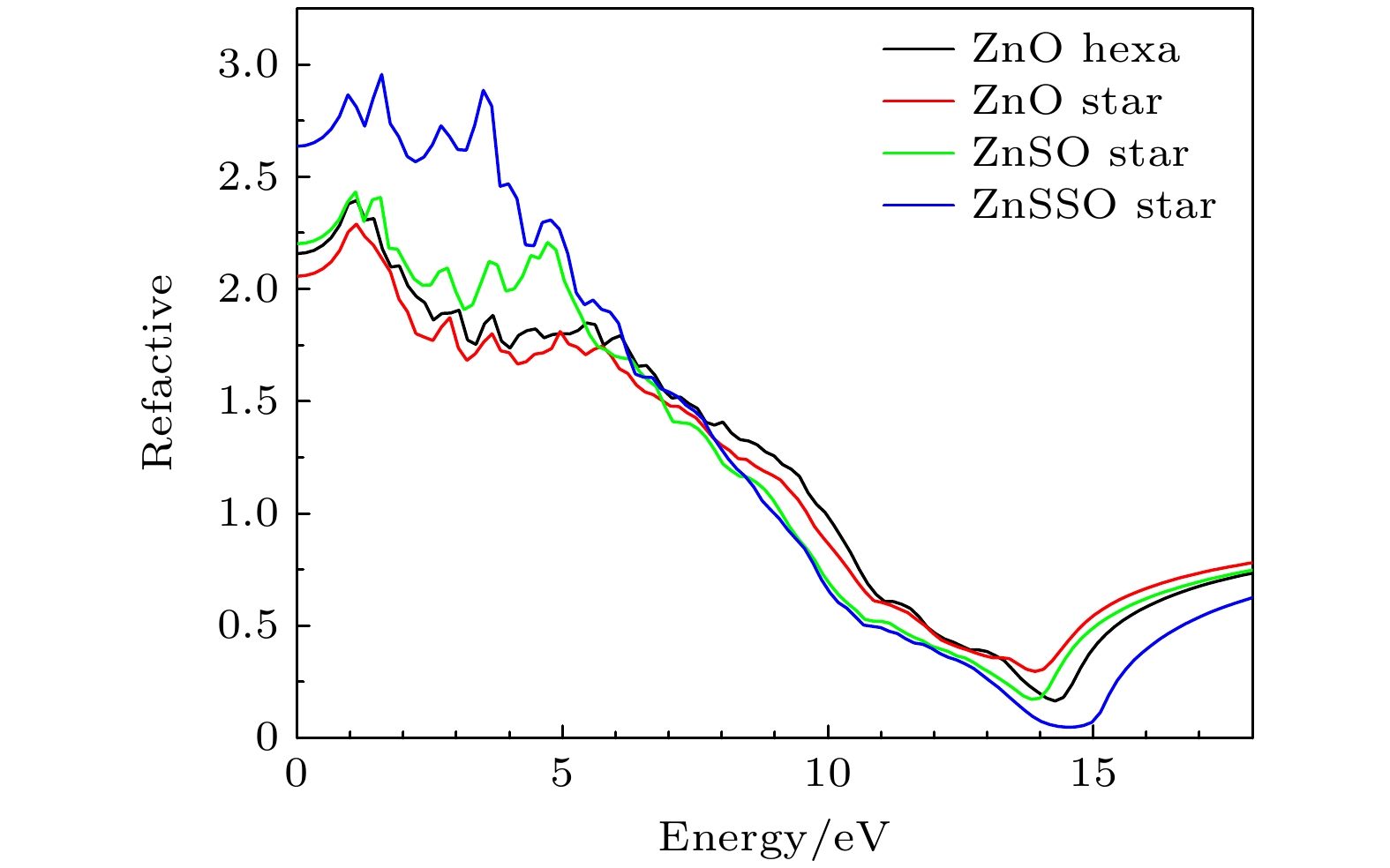
    • 折射率是线性光学领域的一个重要参数, 其用来描述光在真空和某种介质之间传播时速度的变化程度, 即真空中传播速度和该介质中传播速度之比. 晶体的折射率与电子极化率和晶体内部的局部场密切相关. 由介电函数实部和虚部可以得到折射率$ n $[20]:

      如图7所示, 当光子的能量为零时, 六边形ZnO与六角星形ZnO, ZnSO, ZnSSO的静态折射率分别为2.16, 2.06, 2.20和2.64. 相比于六边形ZnO, 六角星形ZnO静态折射率稍微降低, 而掺杂硫的六角星形ZnSO和ZnSSO的静态折射率增大, 并且随着掺杂浓度的增大, 折射率增大更加显著. 类似于介电张量实部, 折射率谱线分布在较宽的频率范围内, 并且呈现先增大后降低的趋势. 0—2 eV的范围内, 4种纳米线结构出现了最大折射率. 当光子能量分别为14.28 eV, 13.89 eV, 13.84 eV和14.49 eV时, 六边形ZnO与六角星形ZnO, ZnSO, ZnSSO折射率分别达到最低, 表示此时入射光发生折射的能力最弱.

      • 3.2.3.   消光系数

    • 消光系数是描述光在物质中传播时, 由于材料内部吸收或散射作用而减弱的光强与入射光强之比. 消光系数作为重要的光学参数, 涉及光的传播、吸收和散射等物理过程. 不同材料和不同环境下的消光系数一般不同, 其大小直接影响材料的透明度、颜色等光学性能. 类似于折射率, 消光系数也可以通过介电函数实部虚部得到[20]:

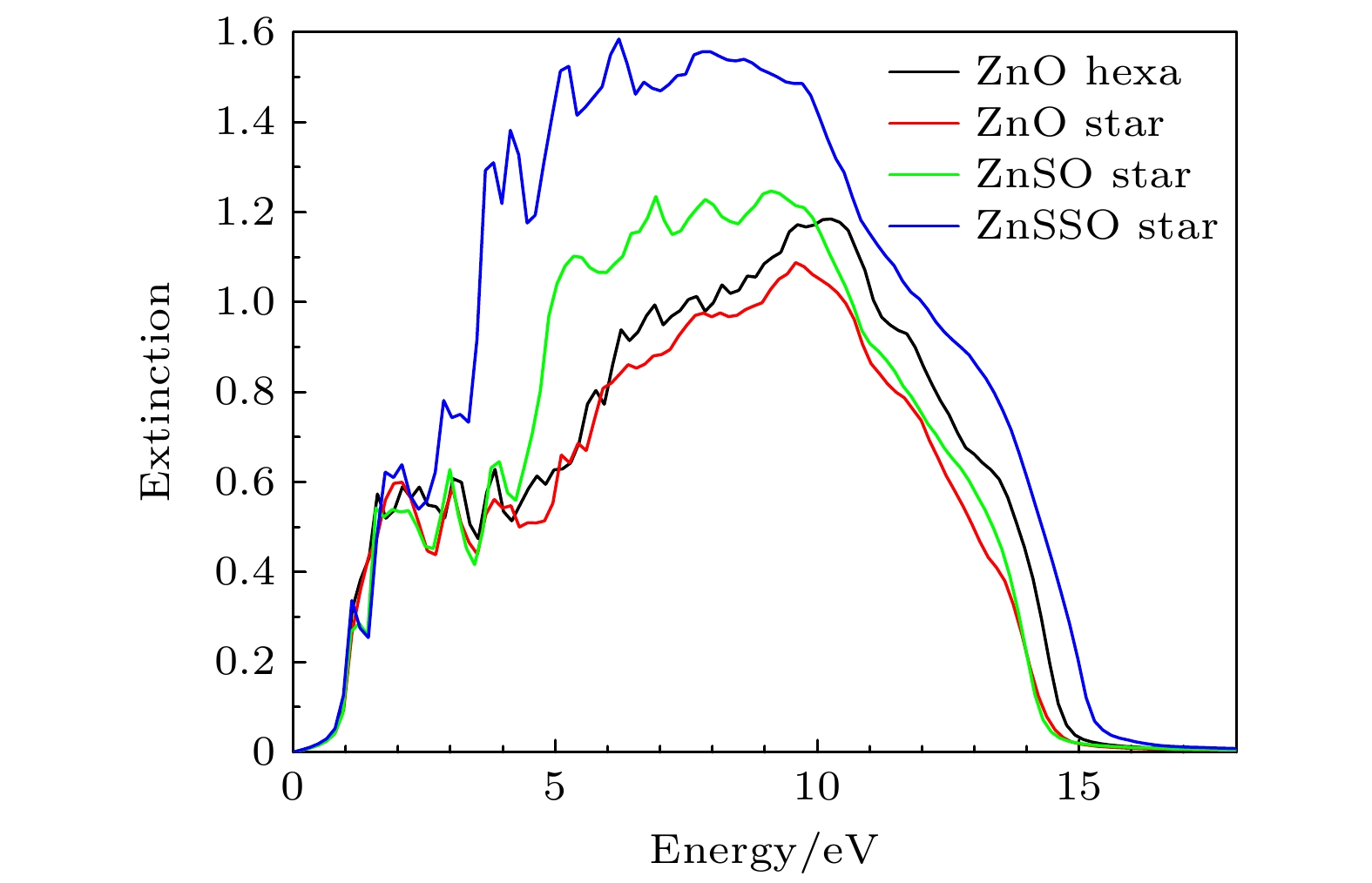
      如图8所示, 4种纳米线结构的消光系数随着能量的增加呈现出先增大后减小, 最后都趋近于0的趋势. 六边形ZnO结构的消光系数在能量为10.27 eV时达到最大值1.19. 六角星形ZnO结构的消光系数相对减小, 在9.59 eV处达到最大值1.09. 与其他光学性质参数类似, 掺杂硫的六角星形ZnSO和ZnSSO结构的消光系数都比六边形ZnO大, 最大值分别为1.25和1.58. 这表示掺杂硫原子的六角星形纳米线材料对光的吸收和散射能力更强, 光在材料中的传播距离更短, 并且硫原子掺杂浓度越大, 材料受到光照射时光能衰减程度越大. 尽管硫原子的掺杂会使得消光系数有所提高, 但是掺杂24个硫原子的ZnSSO纳米线结构的消光系数与ZnO纤锌矿结构是可比的, 并且低于ZnS, ZnSe, ZnTe纤锌矿结构[20]. 这意味着掺硫的六角星形ZnSSO纳米线材料可以用于制造光学器件, 电子显示屏和光导纤维等, 在光学、电子等领域将展现出广泛的应用前景.

      • 3.2.4.   吸收系数

    • 由(5)式计算吸收系数[37,41]:

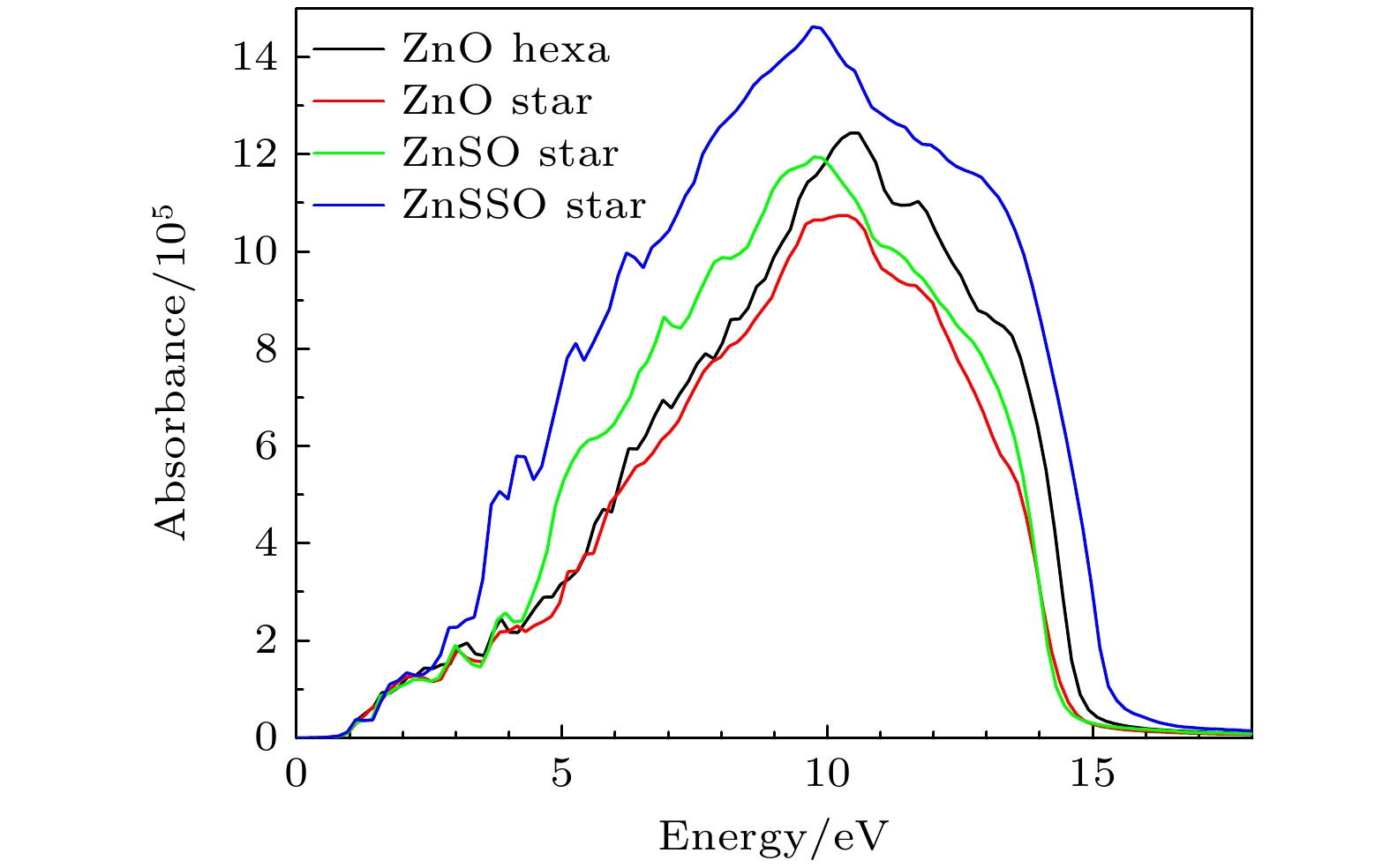
      计算结果如图9所示, 4种结构的光吸收边大约为0.28 eV, 该能量对应于电子从价带顶到导带底的跃迁. 4种结构的最大吸收峰分别位于: 六边形ZnO为10.43 eV, 六角星形ZnO为10.22 eV, ZnSO为9.75 eV, ZnSSO为9.71 eV, 这表明星形纳米线的最大吸收峰发生红移, 并且随着S原子的增加, 红移现象更为明显. 相比六边形ZnO, 六角星形ZnO和ZnSO对应的吸收峰值有所降低, 而六角星形ZnSSO的吸收峰显著增加. 相较于六边形结构, 纳米星结构在低能区都发生了红移, 原因可能是与二者的表面体积比有关. 加入24个S原子的六角星形纳米线光吸收最强, 归因于其带隙显著小于其他3种纳米线材料, 带隙的减小使得电子从价带跃迁到导带所需的能量减小, 有利于电子的跃迁.

      • 3.2.5.   反射率

    • 由复介电函数与反射率的关系, 即(6)式[20]:

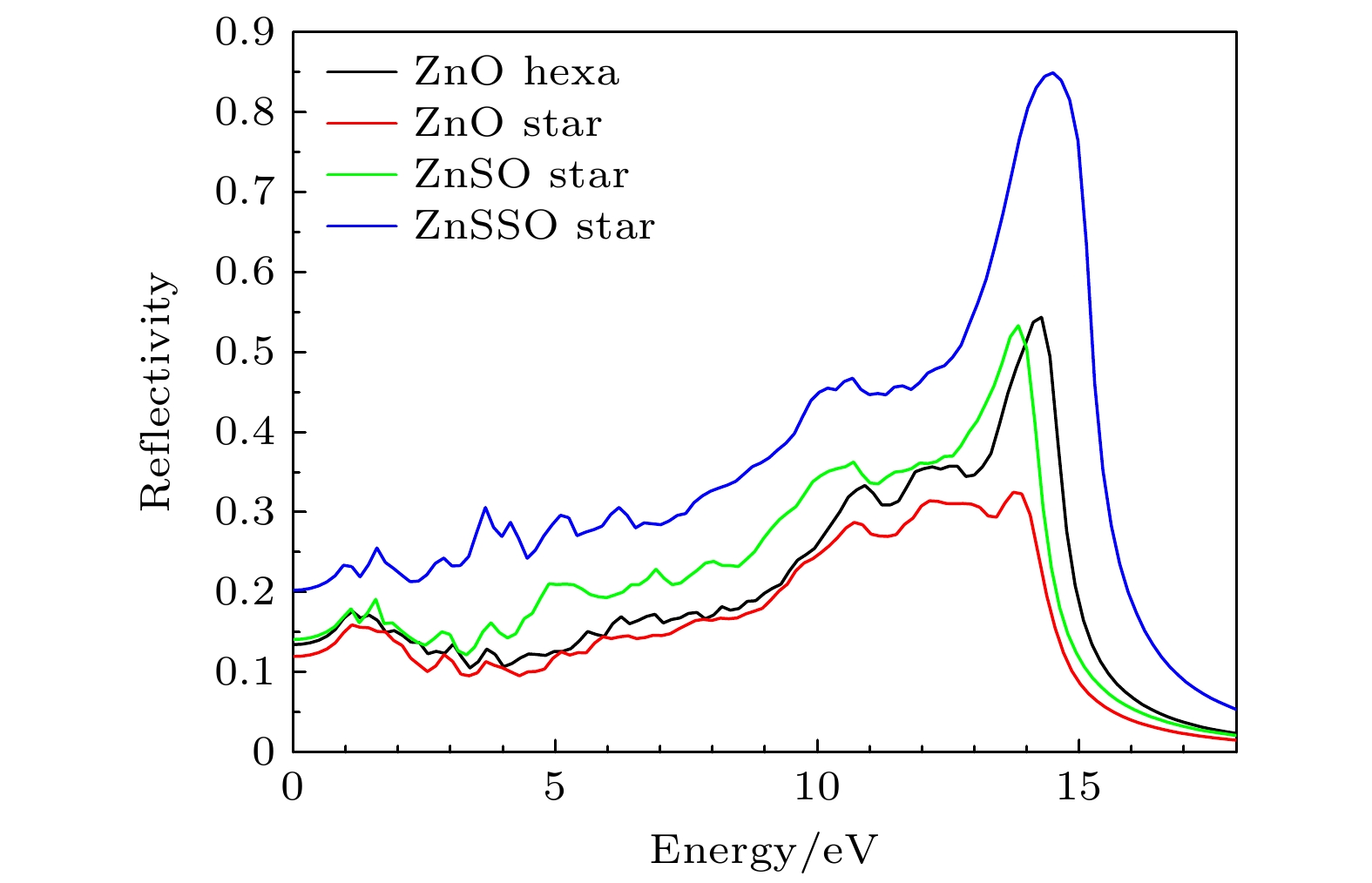
      得到反射率与入射光能量的关系. 反射率与光吸收谱线一致, 吸收强的体系反射也强. 反射率变化曲线如图10所示, 可以看出4种结构的静态反射率: 六边形ZnO为0.13, 六角星形ZnO为0.12, 六角星形ZnSO和ZnSSO分别为0.14和0.20. 当入射光子能量分别达到14.28 eV, 13.74 eV, 13.84 eV和14.49 eV时, 4种结构到达最大反射率, 分别为0.54, 0.33, 0.53和0.85. 六边形与六角星形ZnO结构相比, 六边形ZnO结构的反射率更大, 但随着星形结构中S原子替换O原子的数目增大, 反射率明显提高, 反射性质进一步增强. 之后反射率随着光子能量增加迅速减少并趋于零. 光反射、光吸收和光透射三者遵从能量守恒定理, 因此, 光吸收系数与反射率越大, 那么透射越弱. 结合光吸收谱与反射率图可知, 六角星形ZnO纳米线的透光率最高, ZnSSO的透光率最低.

    4.   结　论

    • 本研究基于密度泛函理论的第一性原理计算, 系统分析了硫掺杂对氧化锌纳米线电子与光学性质的调控机制. 硫掺杂诱导ZnO纳米线表面形成稳定的六角星形结构. 掺杂后体系由直接带隙(未掺杂六角星形ZnO: 1.02 eV)转变为间接带隙半导体(高掺杂ZnSSO: 0.65 eV), 且带隙随硫浓度增大显著减小. 硫的3p轨道在价带顶附近形成杂质能级, 导致费米能级向导带偏移, 有效提升载流子浓度与迁移率. 光学性质的计算结果显示: 硫掺杂显著改变介电函数响应, 实部峰值增至8.52(ZnSSO), 虚部主峰红移至3.66 eV, 表明材料极化响应与光吸收能力增强. 在吸收特性方面, 掺杂后吸收边红移, 低能区光吸收效率提升, 归因于带隙减小及表面缺陷态增加. 此外, 高掺杂浓度下消光系数与反射率显著提高, 表明光散射与界面反射增强, 适用于高灵敏度光电探测器件. 因此, 硫掺杂六角星形ZnO纳米线因带隙可调、光吸收增强及高载流子迁移率, 在紫外-可见光探测器、发光二极管及光伏器件中将展现出重要应用价值. 其表面活性位点与高比表面积的特性, 还可拓展至传感器与催化领域.

      本研究从电子结构-光学响应关联机制出发, 为硫掺杂ZnO纳米线的可控合成与器件设计提供了理论依据. 未来工作可结合实验验证掺杂浓度梯度对性能的优化, 并探索其在柔性光电子器件中的集成潜力.

    参考文献 (41)

目录

/

返回文章
返回