-
网络科学在过去十年间蓬勃发展, 吸引了社会学、物理学、医学、生物学和经济学等众多学科的关注[1–4]. 在现实世界中, 大量复杂系统, 如社会系统、生物系统、基础设施系统和技术系统等, 都可以被建模为复杂网络, 其中实体被视为节点, 实体之间的关联则表示为连边. 节点在网络中的作用往往各不相同, 如何设计有效的算法来识别有影响力的节点, 对于我们更好地应对诸多实际问题至关重要, 比如控制传染病的暴发、优化有限资源利用以促进信息传播、开展电商网络的精准营销、制定策略防止电信网络通信瘫痪, 以及传播新思想、新技术以推进社会化进程等[5–10].
在网络中有效识别多个有影响力的用户, 以最大化特定信息传播范围的过程, 被称为影响力最大化[11]. Kempe等[12]证明了影响力最大化问题是一个NP (non-deterministic polynomial)难的优化问题. 近几十年来, 出现了许多不同的影响力最大化方法. 例如, 贪心算法[13–15]通过迭代选择影响力最大的节点来解决该问题, 虽然准确性高, 但时间复杂度也很高. 尽管有大量研究致力于提高其性能, 但在处理大型复杂网络时, 它们仍然非常耗时. 由于典型的信息最大化问题是NP难点, 因此大多数已知的工作都试图找到问题的近似解而不是精确解. 启发式算法是所有近似算法中最常见的, 例如, 根据节点的度数或其他中心性指标对所有节点进行排序, 并直接选取排名前k的节点, 这是一种简单但广泛用于影响最大化问题的启发式算法. 当前, 中心性指标这些方法大致可分为两类: 一类是基于邻居的中心性指标, 如度中心性[16]、k-壳分解指 标[17]、H指数[18]等; 另一类是基于路径的中心性指标, 包括离心率中心性(ECC)[19]、中介中心性[20]、接近中心性[21]、katz中心性[22]等. 这些指标考虑了节点的位置或邻居的影响, 并选择排名靠前的节点作为种子节点. 然而, 这些指标仅适用于选择单个传播源的情况. 在大多数实际场景中, 传播过程是由多个初始传播者同时发起的, 而单纯利用这些中心性指标挑选排名靠前的节点作为种子节点存在“富俱乐部效应”, 会导致传播影响力的重叠, 并且在不同网络上的表现存在差异[23,24]. 为有效解决种子集合的传播重叠问题, Chen等[25]开创性地提出了一种度折扣算法, 其准确性几乎与贪心算法相同, 但比最快的贪心算法快一百万倍以上. 近年来, 学术界还提出许多基于混合方法的影响力最大化算法. Berahmand等[26]提出了DCL算法, 该算法考虑了节点的位置参数, 如度、邻居的度、节点与其邻居之间的公共链接以及逆聚类系数. Salavati等[27]提出了GLR算法, 该算法利用节点的局部网络结构改进了接近中心性的计算, 然后根据节点的潜在影响力对其进行评分. Wen和Deng[28]提出了一种通过局部信息维度识别有影响力传播者的方法, 该方法考虑了中心节点周围的局部结构属性, 通过香农熵来度量盒子内节点的信息. Yang等[29]提出一种基于新型重力中心性和递归排序策略的自适应算法AIGCrank, 用于识别有影响力的种子节点集. 具体而言, 通过重力中心性结合节点的邻域、网络位置和拓扑结构信息, 评估节点被选为种子的潜力. 并设计递归排序策略, 用于逐个识别种子节点.
复杂网络的生成与人类生产生活密切相关, Zhang等[30]模拟现实社会选民投票过程, 提出一种基于人类社会投票规则的VoteRank方法来选择关键节点. VoteRank是一种局部化算法, 通过投票选举多个关键节点, 将当选节点的投票能力置零, 并在每轮投票后迭代更新, 以确保传播源的分散性. 该算法以O(n)时间复杂度实现高效计算, 但其存在两大局限: 其一, 投票过程中默认邻居节点无保留将票投给候选人, 实际上在人类社会真实投票场景中, 是否给候选人投票往往受投票人与候选人的关系亲近程度所影响, 投票人与候选人关系越亲近, 越有可能把选票投给候选人, VoteRank方法默认邻居节点无保留将票投给候选人, 未量化邻居节点与候选人之间的亲密度, 不符合现实情况. 其二, VoteRank算法在抑制邻居节点影响力时, 没有充分利用节点之间的差异. 它采用统一的方式削弱邻居节点的投票能力, 没有考虑到不同节点在网络中的重要性和角色差异[31]. 在实际网络中, 不同节点对信息传播的贡献不同, 这种 “一刀切”的衰减策略无法精准地反映节点对于目标节点信息传播的贡献, 难以有效地抑制种子节点的传播重叠现象. 由于VoteRank算法精度相对较高且改进潜力较大, 许多学者对该方法进行了深入研究. Sun等[32]提出了WVoteRank方法, 将VoteRank方法应用于加权网络. Kumar等[33]在上述两种方法的基础上提出了基于核数的改进VoteRank方法(NCVoteRank), 该方法认为节点的投票能力应取决于其在网络中的拓扑位置, 通过将节点的投票能力与邻居核度值[34]相乘并归一化, 使处于网络核心区域、邻居核心度值高的节点在投票过程中拥有更大的影响力, 效果优于原始方法. Liu等[35]提出了考虑节点投票能力差异的VoteRank++方法, 该方法通过迭代选择有影响力的节点, 在考虑节点投票能力差异、节点间亲疏关系的基础上, 有效地抑制了邻居节点的影响, 同时提高了算法效率. Wang等[36]引入了投票能力自适应调整方法来动态调整节点的投票能力, 该方法具有较高的准确性和有效性. 最近, Li等[31]从网络局部结构出发识别网络多影响力节点, 通过融合节点边权重、区域影响因子和节点相似度, 模拟人类投票行为, 提出了一种VoteRank方法的改进算法(EWV).
针对VoteRank方法的固有缺陷, 本文提出一种改进投票模型的IMVoteRank算法, 算法突破传统均等投票假设, 将邻居节点的投票贡献分成两类, 一类是直接连接贡献, 另一类是领域相似性贡献, 前者直接投给候选节点, 后者主要考虑邻居节点和目标节点的亲密度, 如果邻居节点和目标节点的共同邻居越多, 两个节点应该越亲密, 这部分选票越有可能投给候选人; 其次, 引入动态群组隔离策略, 在迭代过程中以种子节点为核心检测紧密连接群组, 通过抑制群组内节点投票能力并断开其连接, 保证多个传播源在网络中的分散性. 通过对多个真实网络进行信息传播实验来验证IMVoteRank方法的有效性. 分别与度中心性、k-壳中心性、VoteRank、NCVoteRank[33]、VoteRank++[35]、AIGCrank算法[29]和EWV[31]算法7种方法进行比较. 实验结果表明, IMVoteRank方法在识别网络多影响力节点方面比其他7种方法提供了更优的结果.
-
考虑一个无向无权复杂网络
$ G = (V, E) $ , 其中$V$ 和$E$ 分别代表网络的节点和连边, 且$ \left| V \right|{\text{ }} = N $ . 网络邻接矩阵用$ A = {\text{ }}{\left( {{a_{ij}}} \right)_N}_{ \times N} $ 表示, 当节点i和j相连的时候aij = 1, 否则aij = 0.本文从两方面对VoteRank算法进行改进, 一是设计了基于结构亲密度的投票贡献机制, 将邻居节点的投票贡献分解为直接连接贡献与结构相似性贡献; 二是设计了动态群组隔离策略, 保证所选出来的种子节点不仅是重要的, 而且种子节点之间在网络中是相对分散的.
-
VoteRank算法假设投票时, 一个节点对其每个邻居的投票都是一样的. 然而节点与其邻居之间的关系, 如相似性[37]和吸引力[38], 通常是不同的. 因此一个节点可以给它的邻居不同数量的投票. 在IMVoteRank中, 我们将相邻节点对目标节点的投票贡献分为直接连接贡献和结构相似性贡献. 直接连接贡献表示如果两个节点之间存在连接, 那么邻居节点就会将手中这部分选票直接投给候选节点; 结构相似性贡献是邻居节点手中另一部分选票, 这部分选票是否完全投给候选节点取决于邻居节点和候选节点之间的结构相似性, 如果邻居节点和候选节点之间的结构相似性越高, 这部分选票越有可能投给候选节点. 由此, 给定一个节点u, v从u处得到的选票VP(u, v)定义为
这里,
$ N(u) $ 表示节点u的邻居,$ {k_v} $ 表示节点v的度值. Va(u)表示节点u的投票能力, 我们沿用了VoteRank算法的设定, 将节点初始投票能力设为1. θ参数用于调节节点u投票给节点v时直接连接贡献和结构相似性贡献的比例, 定义为θ参数的值是动态变化的. θ值反映了对于候选节点其度越大, 邻居对其投票时直接连接贡献占比越大; 候选节点的度越小, 则结构相似性贡献占比越大. 参数设计依据为: 通常共同邻居占比低(如社交网络中的名人, 其关注者之间关联性弱), 此时直接连接贡献占主导地位(1 – θ趋近于1). 而网络中低度数邻居节点的信息传播更依赖于和候选节点的共同邻居, 当节点u和节点v之间共同邻居数越多, 越容易传递影响. 因此当节点之间的结构相似性高, 节点u的这部分投票越可能全部投给v.
-
IMVoteRank算法引入动态群组隔离策略, 以解决VoteRank算法采用的邻域均质化投票衰减策略难以有效抑制种子节点传播影响重叠的问题. 在迭代选择种子节点的过程中, 每次选定一个种子节点vmax后, 按以下步骤进行操作.
1)确定初始群组: 以种子节点vmax为核心, 找出与其连接紧密的邻居节点组成初始群组OG. 判断规则为: 对于种子节点vmax的邻居节点u, 假如
$ \left| {N\left( {{v_{{\text{max}}}}} \right) \cap N\left( u \right)} \right|/\left\langle k \right\rangle \geqslant 1 $ 时, u被加入OG.2)扩展群组: 对初始群组OG进行扩展, 按照度从大到小遍历初始群组的所有邻居节点, 将符合条件的邻居节点加入OG中. 判断规则如下: 对于OG的每个邻居节点i, 将其总度ki分解为连接到OG内节点的边数
$ k_i^{{\text{in}}}({\text{OG}}) $ 和连接到网络其余部分的边数$ k_i^{{\text{out}}}({\text{OG}}) $ . 按照度的降序将每个邻居节点和OG比较, 若$ k_i^{{\text{in}}}({\text{OG}}) $ ≥$ k_i^{{\text{out}}}({\text{OG}}) $ , 则将节点i加入到OG. 这个过程可以将与初始群组连接紧密的节点纳入到群组中, 从信息传播的角度, 信息在这部分连接紧密的群组里可以有效地扩散.3)隔离群组: 确定最终的紧密连接群组后, 将群组内所有节点的投票能力设为0, 并将该群组从网络中断开. 对于vmax其他不在群组中的邻居节点, 将这些节点的投票能力削减一半.
-
根据上述分析, IMVoteRank算法步骤如下:
1)将所有节点的元组(S(u), Va(u))都设置为(0, 1), 其中S(u)表示节点u从邻居获得的投票得分, Va(u)表示节点u能给邻居的投票能力;
2)投票, 根据(2)式, 节点为其邻居投票, 同时也会收到邻居的投票. 投票结束后, 计算每个节点的投票得分.
3)计算每个节点的得分, 选择得分最高的vmax节点, 以vmax为中心寻找连接紧密的邻居节点扩展群组.
4)将群组内所有节点的投票能力设为0, 并将该群组从网络中断开; 对于vmax其他不在群组中的邻居节点, 将这些节点的投票能力削减一半.
5)重复步骤1至步骤4, 直到选出r个种子节点.
其具体计算步骤如表1所列.
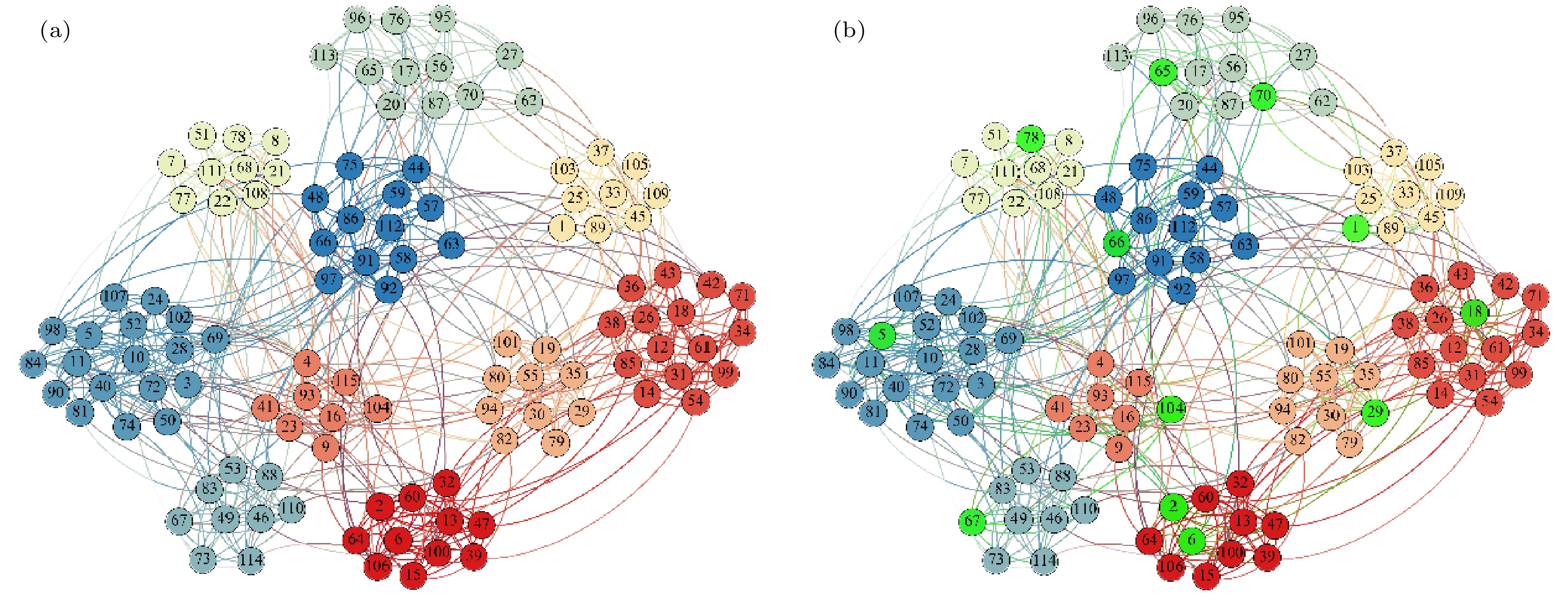
为验证IMVoteRank算法的有效性, 本文以Football网络[39](一种典型的社交网络数据集, 包含多个社区结构)为例, 详细阐述算法的执行过程. 假设初始传播源数量r = 12, 具体步骤如下.
1) 节点投票得分计算: 基于2.1节提出的结构亲密度投票机制, 首先计算所有节点的投票得分. 以节点1为例, 根据(1)式和(2)式, 其每个邻居节点的投票贡献由直接连接和结构相似性共同决定. 经计算, 节点1的累计得分为10.12. 遍历网络所有节点后, 节点67以最高得分被选为第一优先级种子节点.
2) 动态群组隔离策略应用:
①初始群组确定: 以节点67为核心, 检测其邻居节点是否满足初始群组加入条件
$ \left| N\left( {{v_{{67}}}} \right) \cap N\left( u \right) \right|/\left\langle k \right\rangle \geqslant 1 $ . 经判定, 其邻居节点均不满足该条件, 因此初始群组仅包含节点67自身.②群组扩展尝试: 根据2.2节策略, 需对初始群组进行扩展. 以度降序遍历节点67的邻居节点, 并检查每个邻居节点i的度分布条件
$ k_i^{{\text{in}}}({\text{OG}}) $ ≥$ k_i^{{\text{out}}}({\text{OG}}) $ . 结果显示, 所有邻居节点的$ k_i^{{\text{in}}}({\text{OG}}) $ 均小于$ k_i^{{\text{out}}}({\text{OG}}) $ , 故无新增节点加入群组.③群组隔离与投票能力调整: 最终群组仍仅包含节点67. 将其邻居节点的投票能力削减50%, 以抑制后续传播重叠.
3) 迭代选种与结果分析: 重复上述过程, 依次选出12个种子节点: [67, 1, 5, 6, 18, 66, 78, 65, 29, 2, 70, 104], 如图1(b)所示(绿色节点为所选种子), 这些节点在Football网络中呈现显著的空间分散性, 分布于不同社区的核心位置. 此分布特性与算法设计目标一致: 一方面, 种子节点自身具有较高的拓扑重要性; 另一方面, 动态群组隔离策略通过削弱局部密集区域的节点投票能力, 确保了种子间的低冗余性. 从这些分散且高影响力的节点发起信息传播, 可有效地覆盖网络全局, 减少传播盲区, 验证了IMVoteRank在平衡节点重要性与分布分散性上的优势.
-
为进一步验证所提方法的有效性, 本文选用了9个来自不同领域的真实数据集进行实验, 分别是: ECON-WM1经济网络[40]、Slavo Zitnik的Facebook朋友圈关系数据[41]、USAir美国航空运输网络[40]、Celegans秀丽隐杆线虫的代谢网络[42]、冰与火之歌网络ASOIAF[43]、邮件网络Dnc-corecipient[40]、ERIS1176网络[40]、DNC-emails网络[43]以及Facebook-combined社交关系网络[44]. 为了保证一致性, 只取每个网络的最大子图, 确保实验结果更具统计意义. 各网络的统计参数如表2所列: 其中N表示网络节点数量, E表示网络连边个数,
$\left\langle d \right\rangle $ 表示网络平均最短路径长度,$\left\langle k \right\rangle $ 表示网络平均度, C表示网络聚类系数, ksmax和ksmin分别表示网络最大和最小k-壳值,$ {\beta _{{\text{th}}}} = \langle k \rangle /\langle {{k^2}} \rangle $ 表示信息传播阈值,$ \left\langle {{k^2}} \right\rangle $ 表示节点二阶平均度. -
为了衡量所提算法的性能, 本文使用易感-感染-恢复(susceptible-infected-recovered, SIR)信息传播模型来模拟所识别出的有影响力节点的传播能力. 此外, 为了评估所识别出的有影响力节点的分散分布程度, 本文还采用了传播者之间的平均最短路径长度这一指标[30].
-
SIR模型[45]是一种著名的传染病传播模型, 用于衡量网络中的疾病传播效率. 由于其在传染病传播过程中的简单性和良好的模拟能力[46], SIR模型经常被用于评估多影响力节点识别算法的性能[47,48]. 在SIR模型中, 每个节点有三种状态: 易感(S)、感染(I)和恢复(R). 一开始, 初始种子集中的节点处于感染状态, 其他节点处于易感状态. 在每个时间步, 每个感染节点以概率β随机感染其易感邻居, 被感染邻居的状态变为I. 同时, 感染节点以概率μ转变为恢复状态R, 在本文中设置μ = 1. 传播过程持续进行, 直到达到稳定状态. 基于SIR模型, 节点的传播能力可以通过网络中最终处于恢复态R的节点总数来定义.
-
除了SIR模型, 本文采用传播者之间的平均最短路径长度Ls来评估传播者的分散程度. Ls越大, 意味着所选的有影响力节点分布得越分散, 有利于扩大受影响的范围. Ls的数学表达式为
其中,
$ \left| {SN} \right| $ 表示种子节点数, luv表示从节点u到v的最短路径长度. -
我们将所提方法与度、k-壳分解算法、VoteRank、NCVoteRank、VoteRank++、AIGCrank和EWV方法在9个真实网络和3个模拟数据集中通过SIR信息传播模型进行有效性比较. 其中, k-壳分解对比算法在对节点影响力做排序时, 对于k-壳值相同的节点我们优先选择其中度值较大的节点作为种子节点.
-
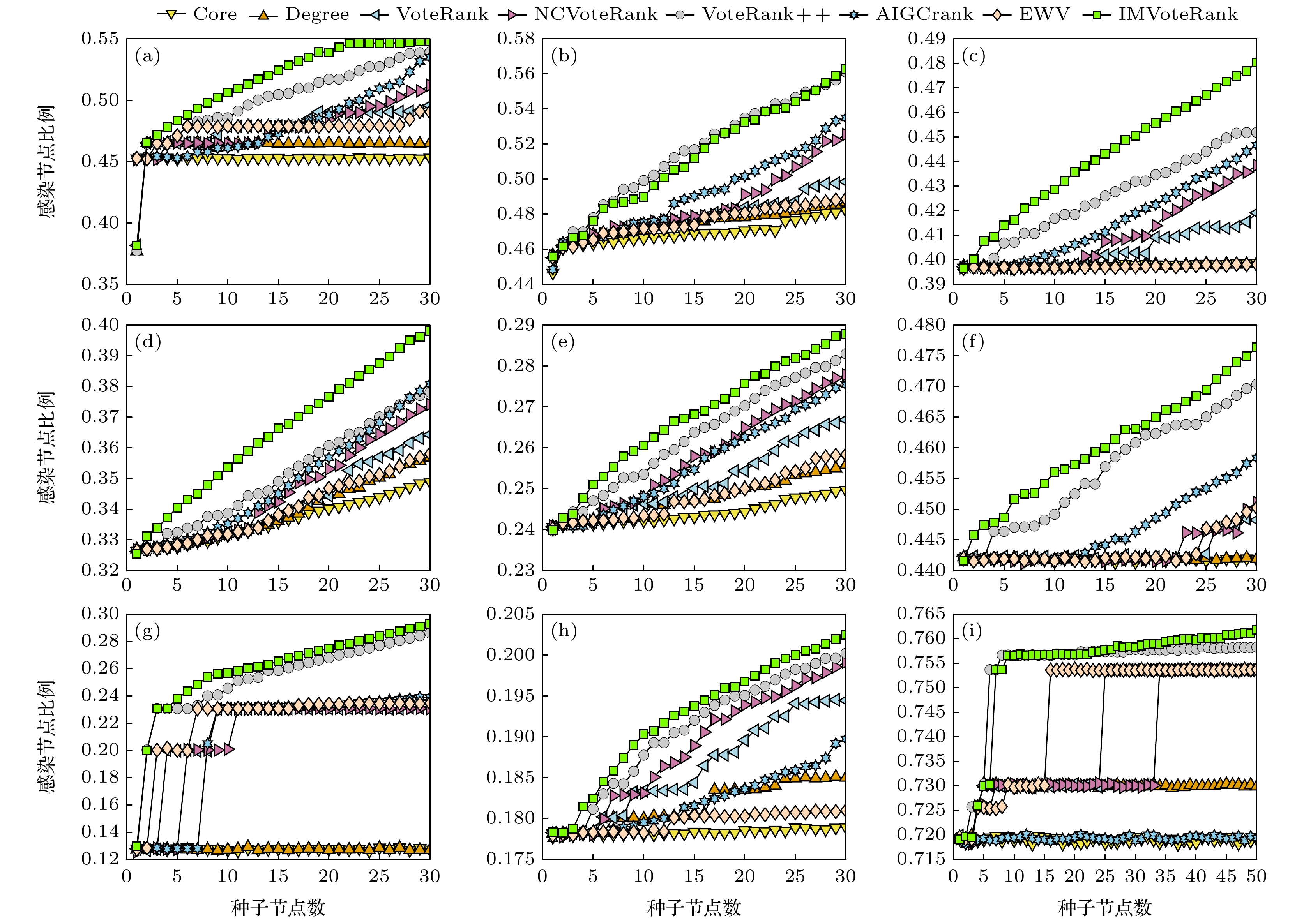
对于网络规模较大的网络Facebook-combined, 初始传播者数量从1到50取值; 对于其他8个网络, 初始传播者数量从1到30取值. 考虑到传播概率β的选择既不能太小也不能太大. 如果β过小, 信息无法在网络中传播; 反之, 如果β太大, 信息很容易在网络中广泛传播, 导致不同算法之间的差异很小, 因此信息传播概率统一设置为β = 0.1. 通过SIR传播模型模拟实验独立进行5000次, 取最终感染规模的平均值. SIR模型的最终感染规模如图2所示. 在相同数量的初始传播者情况下, 所提方法在促进影响最大化方面优于度、k-壳分解算法、VoteRank、NCVoteRank、VoteRank++、AIGCrank和EWV. 所提方法的最终感染规模随着初始传播者数量的增加而持续增长, 而其他方法的增长则相对较弱. 这表明所提方法选择的初始传播者能更好地减少传播冗余. 即使在初始传播者数量较少的情况下, 所提方法在大多数网络上也具有相对较好的性能, 这意味着该方法能很好地确保单个节点的影响力.
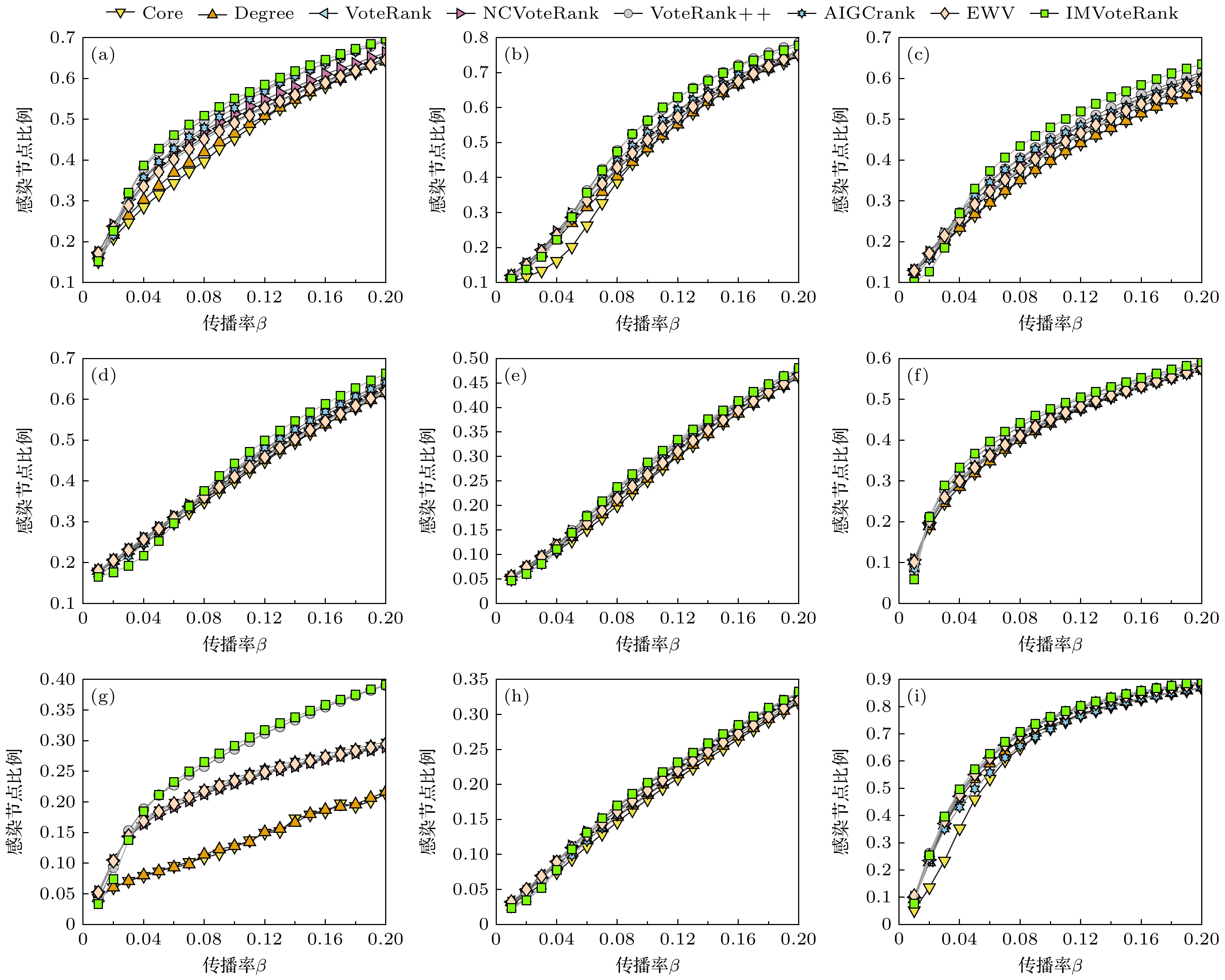
为了使实验更具说服力, 图3展示了当传播源数量固定时, 不同算法感染网络节点比例与SIR疾病传播率之间的关系. 同样地, 对于网络规模较大的网络Facebook-combined, 种子节点数量取50; 对于其他8个网络, 种子节点数量设置为30. 如图3所示, 显然所有方法的最终感染规模都会随着β的增加而上升. 与其他六种算法相比, 在相同数量的初始传播源但不同传播概率的情况下, 本文所提方法在大多数情况下都具有优势.
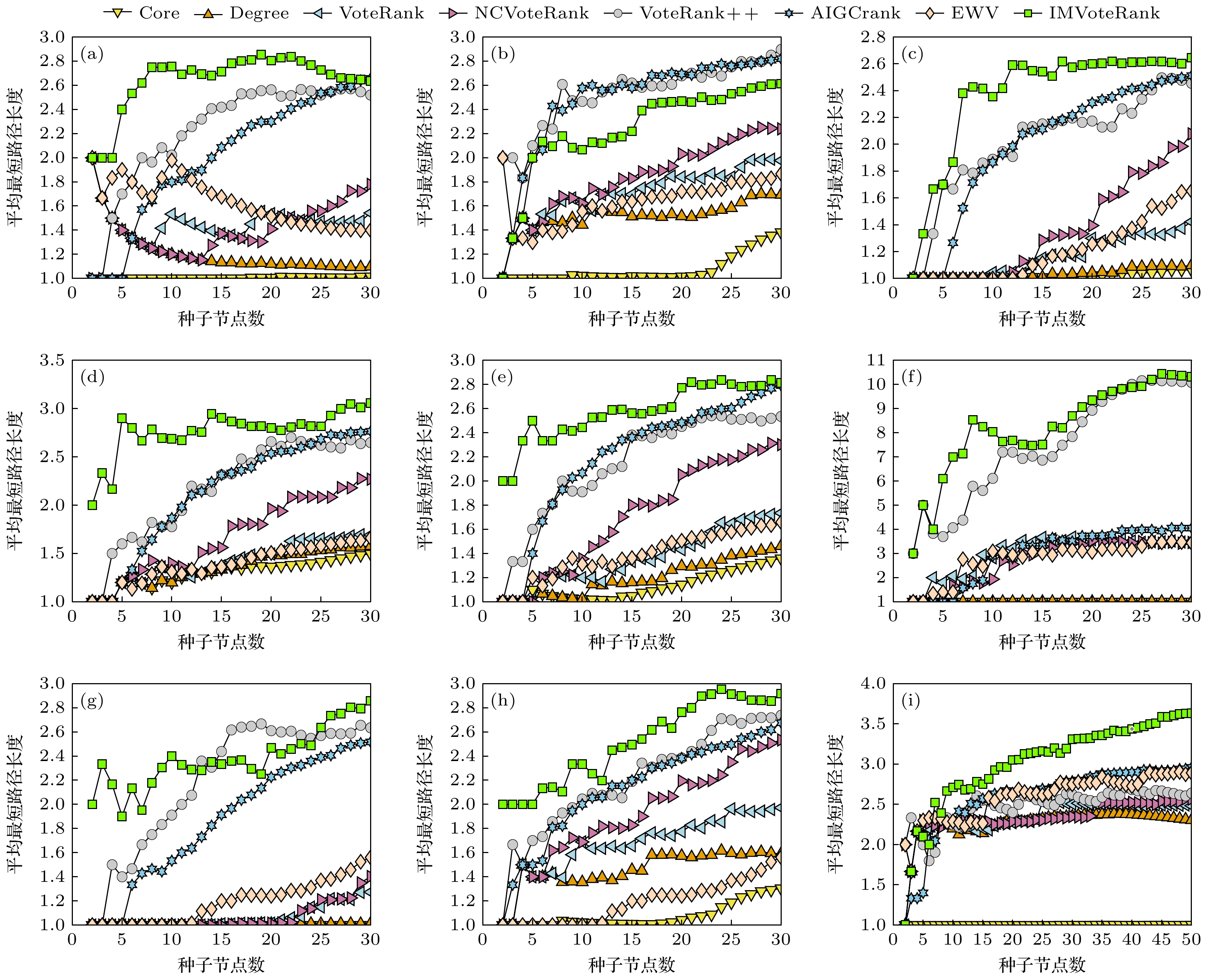
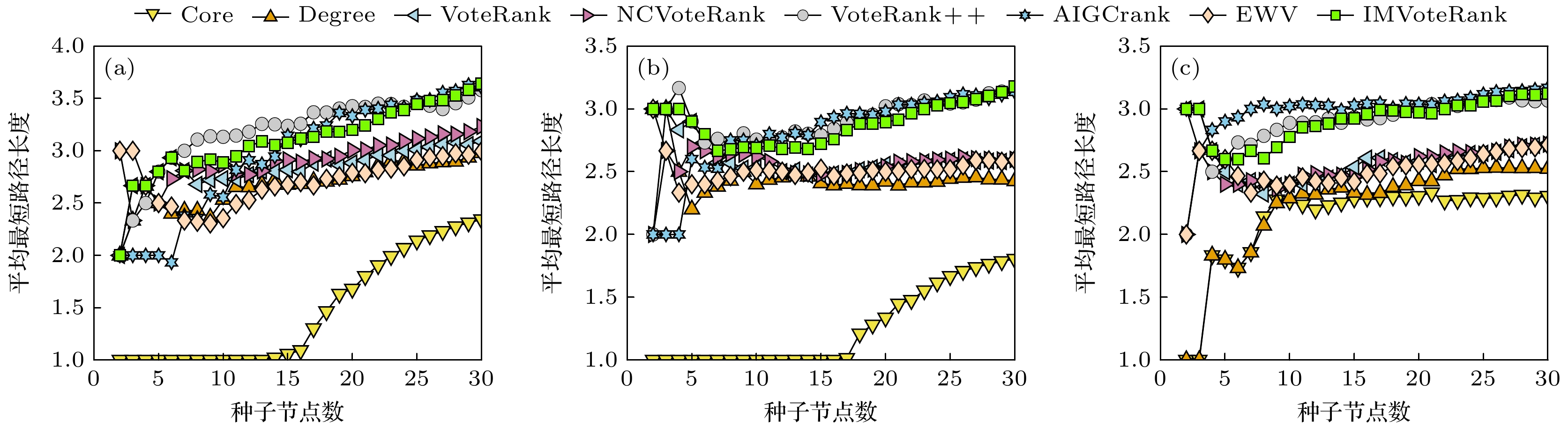
此外, 本文还研究了不同方法选取的传播源之间的平均路径长度与传播源数量间的关系. 如图4所示, 可以发现除了Facebook-SZ网络, IMVoteRank方法在其他网络如ECON-WM3, USAir, Celegans, ASOIAF, Dnc-emails和ERIS1176中所挑选出的传播源节点之间的平均最短路径值比其他方法更大. 而在Dnc-corecipient和Facebook-combined网络中, IMVoteRank方法识别出的传播源节点间的平均距离相比其他方法在多数情况下也更大一些. 结合上述SIR模型模拟实验的结果会发现, IMVoteRank方法不仅保证了源节点本身具有较高的重要性, 还确保了源节点之间在网络中的分散性.
-
除真实数据集外, 本文还采用了 Lancichinetti-Fortunato-Radicchi (LFR)基准模型[44]生成人工网络数据集. 通过调控LFR模型的参数设置, 可构造具有不同拓扑特征的网络结构. 具体参数配置如下: 网络节点数N = 1000, 社区规模范围[cmin, cmax] = [20,50], 最大节点度kmax = 50, 混合参数μ = 0.1. 为考察网络密度变化的影响, 通过设置网络平均度
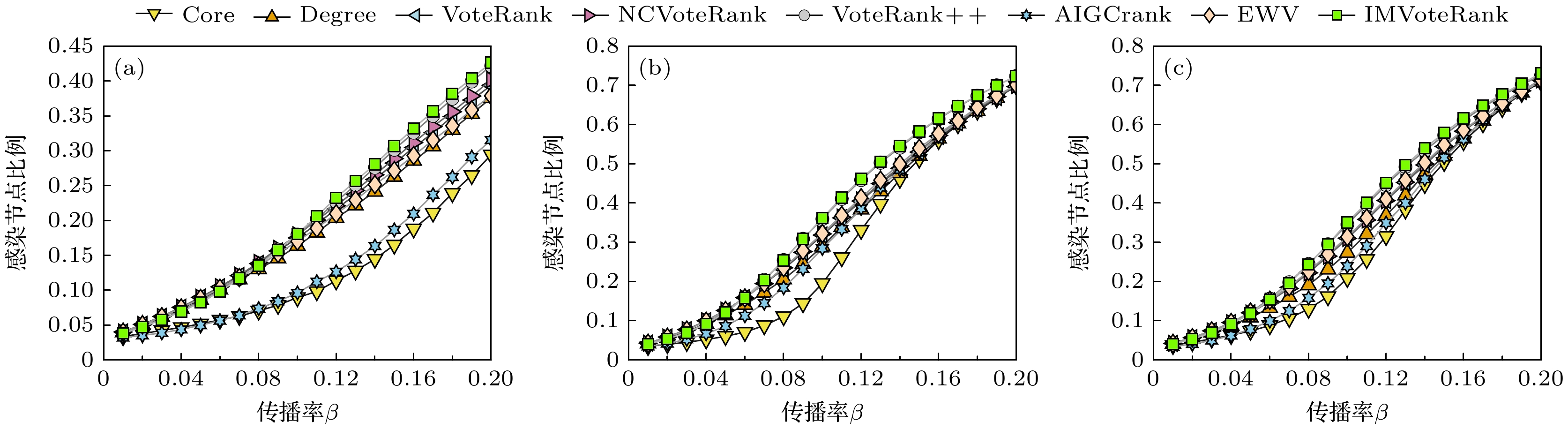
$\left\langle k \right\rangle $ 为5, 10和15, 生成了3个不同紧密程度的人工数据集, 3个网络的信息传播阈值分别为0.075, 0.0571, 0.0598, 3个模拟数据集上的实验结果如图5所示.实验结果揭示了种子节点感染比例对网络稀疏性(
$\left\langle k \right\rangle $ )和传播率的依赖性. 在三个LFR人工网络中, 传播率低于阈值阶段, IMVoteRank的性能优势有限, 这与真实数据集结论相符. 其根本原因在于低传播率下信息难以突破种子节点的局部邻域, 此时依赖局部连接性(如度中心性)的算法更为有效. 相反, 当传播率提升至阈值以上, IMVoteRank在多数场景下表现更佳. 该优势源于该方法所选种子兼具高传播潜力及良好的网络拓扑分散性, 有效地避免了激活重叠区域, 实现了更广泛的覆盖. 图6展示了不同方法所选传播源之间的平均最短路径长度与传播源数量的关系. 可以看到, 我们提出的算法能有效保证种子节点在拓扑结构上的分散性. -
多影响力节点识别问题在许多研究领域都备受关注. 传统策略通过简单的中心性方法选择排名靠前的有影响力节点作为源传播者, 面临着富人俱乐部效应的问题. 在本文中, 本文设计了一种改进的基于投票模型的IMVoteRank算法, 该算法与其他改进的VoteRank算法(如NCVoteRank和VoteRank++)的核心不同之处在于: 1)基于结构亲密度的投票贡献机制: 不同于传统算法中节点对邻居的均质化投票, IMVoteRank将投票贡献分解为直接连接贡献和结构相似性贡献, 通过参数θ动态调整两者比例. 这一机制更贴合真实网络中节点间关系的异质性, 尤其关注低度数节点依赖共同邻居传播的特性, 而NCVoteRank仅依赖邻居核度值, VoteRank++则侧重节点度的对数比例; 2)动态群组隔离策略: 通过识别并隔离与种子节点紧密连接的群组(而非简单衰减邻居投票能力), 有效抑制了种子节点影响力的重叠. 相比VoteRank++对一阶/二阶邻居的固定折扣或NCVoteRank的两跳范围更新, 该策略更精准地分散种子节点位置, 提升全局传播覆盖. 因此IMVoteRank通过结合局部结构相似性与动态群组划分, 在保留投票机制高效性的同时, 进一步优化了种子节点的多样性和传播效率. 在9个真实网络上基于SIR传播模型的实验表明, 所提方法相比其他6种方法(度、k-壳分解算法、VoteRank、NCVoteRank、VoteRank++和AIGCrank)表现更出色. 将来的工作将在以下几个方面进行. 首先, 当前所提算法随着初始传播者数量的增加, 运行时间会变长. 后续工作将研究如何提高算法效率, 使其更好地应用在大规模网络中. 其次, 从中观尺度, 复杂网络往往存在群组、社区结构, 未来将进一步研究群组、社区结构这一特性对多影响力节点识别的影响.
基于改进投票模型识别复杂网络上的多影响力节点
IMVoteRank: Identifying multiple influential nodes in complex networks based on an improved voting model
-
摘要: 在复杂网络中高效识别一组关键传播节点对信息扩散与谣言控制至关重要. 对于多传播源节点选取问题, 一种有效的方法不仅要考虑种子节点自身的影响力, 还要考虑其分散性. 传统投票模型算法VoteRank假设一个节点对其每个邻居的投票都是一样的, 忽视了拓扑相似性对投票倾向的影响; 其次, 采用邻域均质化投票衰减策略, 难以有效地抑制种子节点的传播范围重叠. 本文提出一种改进的基于VoteRank的复杂网络多影响力节点识别算法IMVoteRank, 通过双重创新提高算法效果: 首先, 设计基于结构相似性的投票贡献机制, 模拟真实世界中选民更倾向于投票给自己关系相近的人, 算法认为节点之间拓扑结构越相似邻居节点越有可能将票投给对方, 因此将邻居节点的投票贡献拆分为直接连接贡献与拓扑相似性贡献, 通过动态权重平衡二者的贡献从而优化投票精准度; 其次, 引入动态群组隔离策略, 在迭代过程中以种子节点为核心检测紧密连接群组, 通过抑制群组内节点投票能力并断开其连接, 保证种子节点的空间分散性从而有效克服了传播范围重叠问题. 在多个真实数据集上基于易感-感染-恢复模型的传播实验证明, 所提方法能更有效识别网络中多影响力节点.Abstract: Efficiently identifying multiple influential nodes is crucial for maximizing information diffusion and minimizing rumor spread in complex networks. Selecting multiple influential seed nodes requires to take into consider both their individual influence potential and their spatial dispersion within the network topology to avoid overlapping propagation ranges (“rich-club effect”). Traditional VoteRank method has two key limitations: 1) the voting contributions from a node is assumed to be consistent to all its neighbors, and the influence of topological similarity (structural homophily) on the voting preferences observed in real-world scenarios is neglected, and 2) a homogeneous voting attenuation strategy is used, which is insufficient to suppress propagation range overlap between selected seed nodes. To address these shortcomings, IMVoteRank, an improved VoteRank algorithm featuring dual innovations, is proposed in this work. First, a structural similarity-driven voting contribution mechanism is introduced. By recognizing that voters (nodes) are more likely to support candidates (neighbors) with stronger topological relationships with them, the voting contribution of neighbors is decomposed into two parts: direct connection contribution and a structural similarity contribution (quantified using common neighbors). A dynamic weight parameter θ, adjusted based on the candidate node’s degree, balances these components, significantly refining vote allocation accuracy. Second, we devise a dynamic group isolation trategy. In each iteration, after selecting the highest-scoring seed node vmax, a tightly-knit group (OG) centered around it is identified and isolated. This involves: 1) forming an initial group based on neighbor density shared with vmax, 2) expanding it by merging nodes with more connections inside the group than outside, and 3) isolating this group by setting the voting capacity (Va) of all its members to zero and virtually removing their connections from the adjacency matrix. Neighbors of vmax not in OG have their Va values reduced by half. This strategy actively forces spatial dispersion among seeds. Extensive simulations using the susceptible-infected-recovered (SIR) propagation model on nine different real-world networks (ECON-WM3, Facebook-SZ, USAir, Celegans, ASOIAF, Dnc-corecipient, ERIS1176, DNC-emails, Facebook-combined) demonstrate the superior performance of IMVoteRank. Compared with seven benchmark methods (Degree, k-shell, VoteRank, NCVoteRank, VoteRank++, AIGCrank, EWV), IMVoteRank consistently achieves significantly larger final propagation coverage (infected scale) for a given number of seed nodes and transmission probability (β = 0.1). Furthermore, seeds selected by IMVoteRank exhibit a consistently larger average shortest path length (Ls) in most networks, which proves their effective topological dispersion. This combination of high personal influence potential (optimized voting) and low redundancy (group isolation) directly translates to more effective global information dissemination, as evidenced by the SIR results. Tests on LFR benchmark networks further validate these advantages, particularly at transmission rates above the epidemic threshold. IMVoteRank effectively overcomes the limitations of traditional voting models by integrating structural similarity into the voting process and employing dynamic group isolation to ensure seed dispersion. It provides a highly effective and physically reliable method for identifying multiple influential nodes in complex networks and optimizing the trade-off between influence strength and spatial coverage. Future work will focus on improving the computational efficiency of large-scale networks and exploring the influence of meso-scale community structures.
-
Key words:
- complex network /
- multiple influential nodes /
- voting model /
- isolation strategy .
-

-
图 1 Football网络中的多影响力节点识别结果 (a) 网络划分情况, 不同社区用不同颜色表示; (b) 绿色节点为IMVoteRank方法选取的12个初始传播源
Figure 1. Identification results of multiple influential nodes in the Football network: (a) Network partitioning, with different communities represented by different colors; (b) the green nodes are the 12 initial propagation sources selected by the IMVoteRank method.
图 2 SIR疾病传播率β = 0.1时, 不同算法感染网络节点比例与传播源数量之间的关系 (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined
Figure 2. Relationship between the proportion of network nodes infected by different algorithms and the number of transmission sources when the SIR disease transmission rate β = 0.1: (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined.
图 3 传播源数量固定时, 不同算法感染网络节点比例与SIR疾病传播率之间的关系(Facebook_combined网络中初始传播源数量为50, 其他8个网络的传播源节点数量为30) (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined
Figure 3. Relationship between the proportion of network nodes infected by different algorithms and the SIR disease transmission rate when the number of transmission sources is fixed: (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined. The initial number of propagation sources in the Facebook_combined network is 50, while the number of propagation source nodes in the other eight networks is 30.
图 4 七种方法选取的传播源之间的平均路径长度与传播源数量间的关系 (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined
Figure 4. Relationship between the average path length and the number of propagation sources selected by seven methods: (a) ECON-WM1; (b) Facebook-SZ; (c) USAir; (d) Celegans; (e) ASOIAF[43]; (f) Dnc-corecipient; (g) ERIS1176; (h) DNC-emails; (i) Facebook-combined.
图 5 LFR 人工数据集中各方法所选初始种子节点在不同信息传播率β下感染节点比例对比 (a)
$\left\langle k \right\rangle = 5$ ; (b)$\left\langle k \right\rangle = 10$ ; (c)$\left\langle k \right\rangle = 15$ Figure 5. Comparison of the proportion of infected nodes selected by each method as initial seed nodes in the LFR artificial dataset under different information transmission rates: (a)
$\left\langle k \right\rangle = 5$ ; (b)$\left\langle k \right\rangle = 10$ ; (c)$\left\langle k \right\rangle = 15$ .图 6 LFR人工数据集中8种方法选取的传播源之间的平均路径长度与传播源数量间的关系 (a)
$\left\langle k \right\rangle = 5$ ; (b)$\left\langle k \right\rangle = 10$ ; (c)$\left\langle k \right\rangle = 15$ Figure 6. Relationship between the average path length of the spread sources selected by eight methods in the LFR artificial dataset and the number of spread sources: (a)
$\left\langle k \right\rangle = 5$ ; (b)$\left\langle k \right\rangle = 10$ ; (c)$\left\langle k \right\rangle = 15$ .表 1 计算步骤
Table 1. Step of the calculation.
输入: 网络 $ G\left( {V, E} \right) $ , 需要选择的种子节点数r, 调节参数θ
输出: 包含r个有影响力节点的集合SN//初始化
1 foreach v in V do
2 (S(u), Va(u)) = (0, 1)
3 end foreach
//迭代选择种子节点
4 while$ \left| {SN} \right| < r $ do
5 foreach u in V do
6 foreach v in N(u) do
7$ VP(u, v) = (1 - \theta ){V_{\text{a}}}(u) + \theta {V_{\text{a}}}(u) {{|N(u) \cap N(v)|}}/{{{k_v}}} $
8$ S\left( v \right) = S\left( v \right) + VP\left( {u, v} \right) $ //节点v收到的投票得分增加
9 end foreach
10 end foreach
11$ {v_{{\text{max}}}} = {\text{ argmax}}(S\left( v \right)) $ //选择投票得分最高的节点vmax
// 动态群组隔离策略
12 OG = {vmax}
13 foreach u in N(vmax) do
14 if$ \left| {N\left( {{v_{{\text{max}}}}} \right) \cap N\left( u \right)} \right|/\left\langle k \right\rangle \geqslant 1 $ then
15 OG = OG∪{u}
16 end if
17 end foreach
// 扩展群组
19 foreach i in sort(N(OG), by degree desc) do
20 if$ k_i^{{\text{in}}}({\text{OG}}) $ ≥$ k_i^{{\text{out}}}({\text{OG}}) $ then
21 OG = OG ∪{i}
22 end if
23 end foreach
// 隔离群组
24 foreach node i in OG do
25 Va(i) = 0//将群组内所有节点的投票能力设为0
//将网络邻接矩阵中该节点对应的行和列置为0
26 foreach j in V do
27 adj_matrix[i][j] = 0
28 adj_matrix[j][i] = 0
29 end foreach
30 end foreach
31 foreach neighbor j of vmax not in OG
32$ {V_a}(j) = {V_a}\left( j \right)/2 $
33 end foreach
34 SN = SN ∪{vmax}
35 end while
36 return SN
表 2 真实网络参数描述
Table 2. Parameters description of real networks.
网络 N E $\left\langle d \right\rangle $ $\left\langle k \right\rangle $ C βth ksmax ksmin ECON-WM3 257 2379 2.6147 18.5136 0.2653 0.0207 33 1 Facebook-SZ 324 2218 3.0537 13.691 0.4658 0.0466 18 1 USAir 332 2126 2.738 12.807 0.6252 0.0225 26 1 Celegans 453 2025 2.6638 8.9404 0.6465 0.0249 10 1 ASOIAF 796 2823 3.4162 7.093 0.4859 0.0336 13 1 Dnc-corecipient 849 10384 2.7595 24.4617 0.5072 0.0107 74 1 ERIS1176 1174 8687 12.0591 14.799 0.4327 0.0190 79 1 DNC-emails 1833 39264 3.3695 4.7938 0.2157 0.0135 17 1 Facebook-combined 4039 88234 3.6925 43.691 0.6055 0.0094 115 1 -
[1] Watts D J, Strogatz S H 1998 Nature 393 440 doi: 10.1038/30918 [2] Barabasi A L, Albert R 1999 Science 286 509 doi: 10.1126/science.286.5439.509 [3] Liu Y Y, Slotine J J, Barabasi A L 2011 Nature 473 167 doi: 10.1038/nature10011 [4] Yang Z, Li Y, Liu J 2021 Proceedings of the 15th EAI International Conference on Communications and Networking (ChinaCom 2020) Shanghai, China, November 20–21, 2020 p766 [5] Li Y G, Xiao Z L, Gao A, Wu W N, Pei E R 2025 Knowl-Based Syst. 317 113434 doi: 10.1016/j.knosys.2025.113434 [6] Lin Y G, Wang X M, Hao F, Jiang Y C, Wu Y L, Min G Y, He D J, Zhu S C, Zhao W 2019 IEEE Trans. Syst., Man, Cybern.: Syst. 51 3725 doi: 10.1109/TSMC.2019.2930908 [7] Olasupo T O, Otero C E 2017 IEEE Trans. Syst., Man, Cybern.: Syst. 50 256 doi: 10.1109/TSMC.2017.2737473 [8] Laitila P, Virtanen K 2018 IEEE Trans. Syst., Man, Cybern.: Syst. 50 1943 doi: 10.1109/TSMC.2018.2792058 [9] Yang J, Yao C, Ma W, Chen G 2010 Physica A 389 859 doi: 10.1016/j.physa.2009.10.034 [10] Morone F, Makse H A 2015 Nature 524 65 doi: 10.1038/nature14604 [11] Guo C, Li W M, Liu F F, Zhong K X, Wu X, Zhao Y G, Jin Q 2024 Neurocomputing 564 126936 doi: 10.1016/j.neucom.2023.126936 [12] Kempe D, Kleinberg J, Tardos É 2003 Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Washington, DC, USA, August 24–27, 2003 p137 [13] Leskovec J, Krause A, Guestrin C, Faloutsos C, VanBriesen J, Glance N 2007 Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining San Jose, CA, USA, August 12–15, 2007 p420 [14] Ou Z, Wang S 2024 Swarm Evol. Comput. 87 101542 doi: 10.1016/j.swevo.2024.101542 [15] Kumar S, Mallik A, Panda B S 2023 Expert Syst. Appl. 212 118770 doi: 10.1016/j.eswa.2022.118770 [16] Albert R, Jeong H, Barabási A L 1999 Nature 401 130 doi: 10.1038/43601 [17] Kitsak M, Gallos L K, Havlin S, Liljeros F, Muchnik L, Stanley H E, Makse H A 2010 Nat. Phys. 6 888 doi: 10.1038/nphys1746 [18] Lü L Y, Zhou T, Zhang Q M, Stanley H E 2016 Nat. Commun. 7 10168 doi: 10.1038/ncomms10168 [19] Hage P, Harary F 1995 Soc. Netw. 17 57 doi: 10.1016/0378-8733(94)00248-9 [20] Dolev S, Elovici Y, Puzis R 2010 J. ACM 57 25 doi: 10.1145/1734213.173421 [21] Opsahl T, Agneessens F, Skvoretz J 2010 Social Networks 32 245 doi: 10.1016/j.socnet.2010.03.006 [22] Katz L 1953 Psychometrika 18 39 doi: 10.1007/BF02289026 [23] Wang Y, Zheng Y N, Shi X L, Liu Y G 2022 Physica A 588 126535 doi: 10.1016/j.physa.2021.126535 [24] Zhao Z L, Liu X P, Sun Y, Zhao N N, Hu A H, Wang S L, Tu Y Y 2025 Chaos, Solitons Fractals 193 116078 doi: 10.1016/j.chaos.2025.116078 [25] Chen W, Wang Y J, Yang S Y 2009 Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Paris, France, June 28–July 1 p199 [26] Berahmand K, Bouyer A, Samadi N 2019 Computing 101 1711 doi: 10.1007/s00607-018-0684-8 [27] Salavati C, Abdollahpouri A, Manbari Z 2019 Neurocomputing 336 36 doi: 10.1016/j.neucom.2018.04.086 [28] Wen T, Deng Y 2020 Inf. Sci. 512 549 doi: 10.1016/j.ins.2019.10.003 [29] Yang P L, Zhao L J, Dong C, Xu G Q, Zhou L X 2023 Chin. Phys. B 32 058901 doi: 10.1088/1674-1056/ac8e56 [30] Zhang J X, Chen D B, Dong Q, Zhao Z D 2016 Sci. Rep. 6 27823 doi: 10.1038/srep27823 [31] Li H Y, Wang X, Chen Y, Cheng S Y, Lu D J 2025 Sci. Rep. 15 1693 doi: 10.1038/s41598-025-85332-4 [32] Sun H L, Chen D B, He J L, Ch’ng E 2019 Physica A 519 303 doi: 10.1016/j.physa.2018.12.001 [33] Kumar S, Panda B S 2020 Physica A 553 124215 doi: 10.1016/j.physa.2020.124215 [34] Bae J H, Kim S W 2014 Physica A 395 549 doi: 10.1016/j.physa.2013.10.047 [35] Liu P, Li L, Fang S, Yao Y K 2021 Chaos, Solitons Fractals 152 111309 doi: 10.1016/j.chaos.2021.111309 [36] Wang, G. Alias S B, Sun Z J, Wang F F, Fan A W, Hu H F 2023 Heliyon 9 e16112 doi: 10.1016/j.heliyon.2023.e16112 [37] Jeh G, Widom J 2002 Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining Edmonton, Canada, July 23–26, 2002 p538 [38] Chi K, Yin G S, Dong Y X, Dong H B 2019 Knowl-Based Syst. 181 104792 doi: 10.1016/j.knosys.2019.05.035 [39] Rossi R, Ahmed N 2015 Proceedings of the 29th AAAI Conference on Artificial Intelligence Austin, TX, USA, January 25–30, 2015 p4292 [40] Batagelj V, Mrvar A 1998 Connections 21 47 [41] Blagus N, Šubelj L, Bajec M 2012 Physica A 391 2794 doi: 10.1016/j.physa.2011.12.055 [42] Jeong H, Tombor B, Albert R, Oltvai Z N, Barabási A L 2000 Nature 407 651 doi: 10.1038/35036627 [43] Kunegis J 2013 Proceedings of the 22nd International Conference on World Wide Web Rio de Janeiro, Brazil, May 13–17, 2013 p1343 [44] McAuley J, Leskovec J 2012 Advances in Neural Information Processing Systems (Lake Tahoe, USA: NIPS) p539 [45] Pastor-Satorras R, Vespignani A 2001 Phys. Rev. Lett. 86 3200 doi: 10.1103/PhysRevLett.86.3200 [46] Ruan Y R, Liu S Z, Tang J , Guo Y M, Yu T Y 2025 Expert Syst. Appl. 268 126292 doi: 10.1016/j.eswa.2024.126292 [47] Yu E Y, Wang Y P, Fu Y, Chen D B, Xie M 2020 Knowl-Based Syst. 198 105893 doi: 10.1016/j.knosys.2020.105893 [48] Zhang M, Wang X J, Jin L, Song M, Li Z Y 2022 Neurocomputing 497 13 doi: 10.1016/j.neucom.2022.05.010 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: