Structure and Vibrational Spectroscopy of 2-Methylallyl Alcohol

Intramolecular hydrogen bonding plays an important role in stabilizing various molecular compounds. Extensive researches, encompassing both experimental and theoretical approaches, have been conducted to investigate different types of intramolecular hydrogen bonds [1-8]. The hydrogen bond is well understood within the X–H···Y framework, where a hydrogen atom acts as a bridge between a proton donor X and a proton acceptor Y. Typically, X and Y are electronegative atoms, with the acceptor Y possessing at least one lone pair of electrons. It is widely recognized that X can belong to a range of elements, including F, N, O, C, P, S, Cl, Se, Br, and I, while Y can encompass these elements as well as π electrons [9].

π electrons are typically found in the aromatic system of a benzene ring or the π-system of multiple bonds [3, 10-13]. It has been established that π electrons can act as weak proton acceptors in X–H···π hydrogen bonding systems [14-16]. These X–H···π hydrogen bonds are prevalent in chemistry and biology, playing a crucial role in the structural organization of proteins and DNA, as well as in drug-receptor binding and catalysis [10, 17]. Rotational studies on dimers formation from benzene with various partner molecules have provided evidence for the proton acceptor capabilities of π systems. Examples include C₆H₆···HF [18], C₆H₆···HCl [19], C₆H₆···H₂O [20], and C₆H₆···NH₃ [21], where the partner molecules are positioned above the benzene plane, and the acidic hydrogen atoms are directed towards the π cloud. Additionally, several examples of intramolecular hydrogen bonding have been reported in the literatures, involving XH donors such as OH [3, 15, 22], NH [12], and SH [16], and π-electron acceptors such as alkene [3, 15], alkyne [3, 16, 22], and aryl [12, 15] groups.

The intramolecular O−H···π hydrogen bond has been extensively investigated in unsaturated alcohols [3, 14, 23-26]. Miller et al. [3] measured the OH stretching vibrational overtone spectra and performed atoms in molecules (AIM) and non-covalent interactions (NCI) calculation. Their findings indicated the presence of a weak O−H···π intramolecular hydrogen bond in allyl carbinol (CH₂=CH–CH₂–CH₂–OH) and propargyl carbinol (H–C≡C–CH₂–CH₂–OH). However, they found that the identification of O−H···π intramolecular hydrogen bonds in allyl alcohol (CH₂=CH– CH₂–OH) and propargyl alcohol (H–C≡C–CH₂–OH) remains uncertain or debatable. In a separate study, Mackeprang et al. [14] investigated the third OH stretching overtone region of vapor-phase allyl carbinol and methallyl carbinol (CH₂= C(CH₃)–CH₂–CH₂–OH). They observed that the inductive effect of the methyl group increased the strength of the O−H···π intramolecular hydrogen bond and resulted in significant redshifts of the v_OH frequency.

2-Methylallyl alcohol (MAA, CH₂=C(CH₃)–CH₂–OH) is a significant compound in the industrial sector, finding applications as a monomer in polymer synthesis and as a starting material for the production of pharmaceuticals, pesticides, and other allyl compounds [27, 28]. MAA shares a structural similarity with methallyl carbinol, suggesting the presence of an intramolecular hydrogen bond between the OH group and the π-electrons of the C=C double bond. Caminati et al. [25, 29] conducted the microwave spectra measurement on MAA and assigned the spectrum to two conformers, characterized by an O−H···π hydrogen bond, where the oxygen atom is either skew or syn with respect to the C=C double bond. However, previous studies on MAA have primarily focused on the kinetics of its reactions with important atmospheric oxidants such as Cl atom, OH, O₃, and NO₃ radicals. To the best of our knowledge, there have been no reports on the infrared (IR) spectra investigation of MAA, except for the data available at the National Institute of Standards and Technology (NIST) [30].

In this study, we investigate the gas-phase vibrational spectra of both neutral and cationic MAA under jet-cooled conditions using the non-resonant ionization detected IR spectroscopy (NRID-IR) method. Using the time-of-flight mass spectrometry (TOF-MS), we detect the signal of the fragment (m/z=57) and the parent (m/z=72) ions, from the variation of which upon the resonance absorption of IR radiation, the IR spectra were obtained. Comparing the experimental IR spectra with the DFT-simulated ones, we propose the main spectral carriers for neutral and cationic MAA. In addition, electron density distribution calculations were performed to analyze the structure and IR spectra of neutral and cationic MAA. Furthermore, natural bond orbital (NBO) analyses and interaction region indicator (IRI) theory were used to characterize the intramolecular OH···π hydrogen bonding in MAA.

A detailed description of the experimental apparatus can be found elsewhere [31]; here, we provide a concise overview. The IR absorption spectra of both neutral and cationic MAA were acquired, using TOF mass spectrometry, by detecting the variation of the signal intensities of MAA cation (m/z=72) and the dissociative ionization product [C₃H₅O]⁺ (m/z=57) as the wavelength of the IR radiation was scanned. The IR laser was fired 50 ns prior to the VUV laser for the measurement of neutral MAA IR spectra, and 50 ns after the VUV laser for that of cationic MAA. The VUV laser (118 nm) was generated by tripling the frequency of a 355 nm laser (40 mJ per pulse) in a gas cell filled with Xe and Ar (with a pressure ratio of 1:10) at a pressure of 300 Torr. The 355 nm laser was tripled in frequency from the output of a Nd: YAG laser (Beamtech, SGR-20, 10 Hz). Subsequently, the 118 nm laser was focused into the center of the ionization region using a convex MgF₂ lens mounted at the end of the gas cell.

The tunable IR radiation utilized in this study was generated from the idler/signal output of an optical parametric oscillator/amplifier (OPO/OPA) system (Laser Vision). The OPO/OPA system (linewidth of 0.9 cm⁻¹) was pumped by an unseeded Nd:YAG laser (Continuum, Surelite EX), operated at 5 Hz, and the typical pulse energy was 630 mJ. The pulse energy of the IR laser was about 10 mJ at the entrance of the vacuum chamber. A CaF₂ lens (focal length of 500 mm) was employed to focus the IR laser into the ionization region.

Helium was directed through a room temperature bubbler that contained anhydrous MAA (99%, Sigma-Aldrich), and the gas mixture was fed to a pulsed solenoid valve (Parker, General Valve Series 9, 0.5 mm orifice, backing pressure of 25 psi). The molecular beam, generated by the solenoid valve, was subsequently collimated by a skimmer (1.5 mm diameter) positioned 2 cm downstream on the path of the molecular beam. The counter-propagated VUV laser and IR laser were intersected perpendicularly by the molecular beam in the ionization region. The signal from the mass spectrometry was amplified with a broadband amplifier (SR445A) and subsequently recorded on a multichannel scaler (MCS6A, FAST ComTec).

We used the Molclus program to investigate the structure of the MAA molecule [32]. We further optimized its geometry by using Grimme's dispersion-corrected density functional theory (DFT) with Becke-Johnson damping and three-body terms D3(BJ) [33-35] at the B3LYP/def2-SVP level, employing the Gaussian 16 program suite [36]. In addition, the calculated five most stable conformers of MAA were optimized at the B3LYP-D3(BJ)/def2-TZVPP level. We determined the three lowest energy structures of cationic MAA with the same method.

The anharmonic IR spectra were computed using the vibrational second-order perturbation theory (VPT2) approach implemented in the Gaussian 16 programs. Specifically, calculations were performed at the B3LYP-D3(BJ)/def2-TZVPP level of theory. The single-point energy was computed at the DLPNO-CCSD(T)/aug-cc-pVTZ//B3LYP-D3(BJ)/def2-TZVPP level with zero-point energy correction, utilizing the ORCA program [37].

The Mayer bond order was demonstrated with the Multifunctional Wavefunction Analyzer (Multiwfn) program [38], utilizing the wavefunction from the Gaussian16 program. The IRI of neutral MAA was calculated at the B3LYP/def2-SVP level, and the visualization analysis was carried out using both Multiwfn and Visual Molecular Dynamics (VMD) [39] programs.

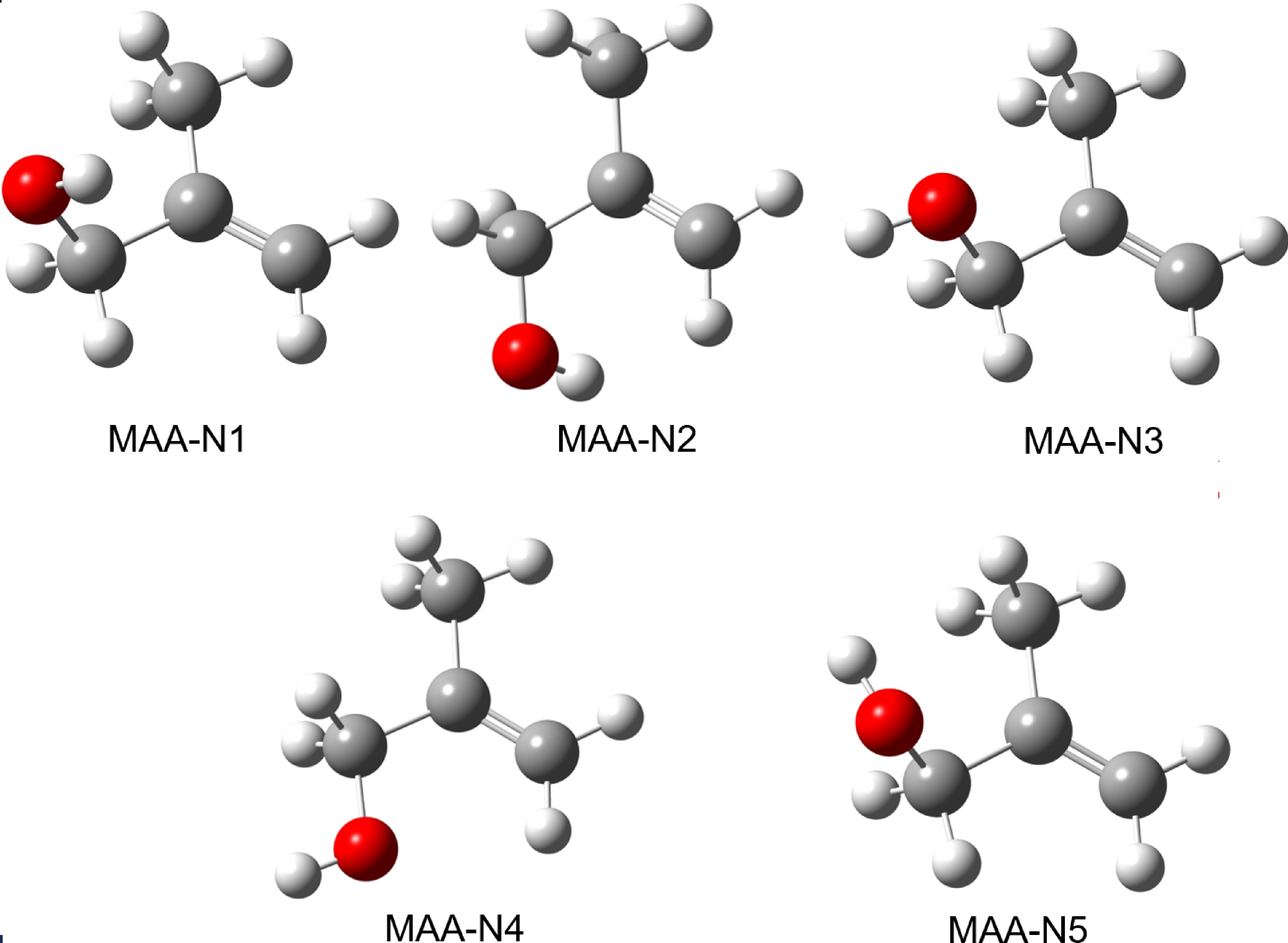
Previous studies on MAA have rarely conducted structural searches. In this study, we calculated the potential structures of neutral and cationic MAA using the B3LYP-D3(BJ)/def2-TZVPP level of theory. FIG. 1 illustrates the five most stable structures of neutral MAA, denoted as MAA-Nm, where “m” represents the stability ranking of each conformer. Table I provides the calculated OH-bond length, zero-point energy (ZPE) corrected relative electronic energy (ΔE), Gibbs free energy (ΔG), and the Boltzmann populations for the five conformers of neutral MAA at 298 K.

Among the conformers, MAA-N1 exhibits the highest stability, the second most stable conformer is MAA-N2 with an energy only 0.15 kJ/mol higher than the MAA-N1. Furthermore, the energy difference between MAA-N1 and MAA-N5 is 4.88 kJ/mol. Boltzmann population shows that neutral MAA is dominated by conformer MAA-N1 (36%) and MAA-N2 (32%), although the contributions of MAA-N3 and MAA-N4 should not be disregarded. Regarding the identification of conformers in the microwave spectra, it is worth noting that Caminati et al. initially identified the MAA-N1 conformer [25], followed by the identification of the MAA-N2 conformer [29]. Our calculated Boltzmann population is consistent with the observation [25, 29], which indicates that these two conformers are the most abundant.

Notably, in both MAA-N1 and MAA-N2, the H atom of the OH group is positioned towards the C=C double bond. Additionally, these conformers exhibit the longest OH bonds, suggesting the presence of intramolecular hydrogen-bonding interaction between the OH group and the π electron of the C=C double bond. This interaction has been demonstrated to play a significant role in stabilizing organic molecules [3, 15].

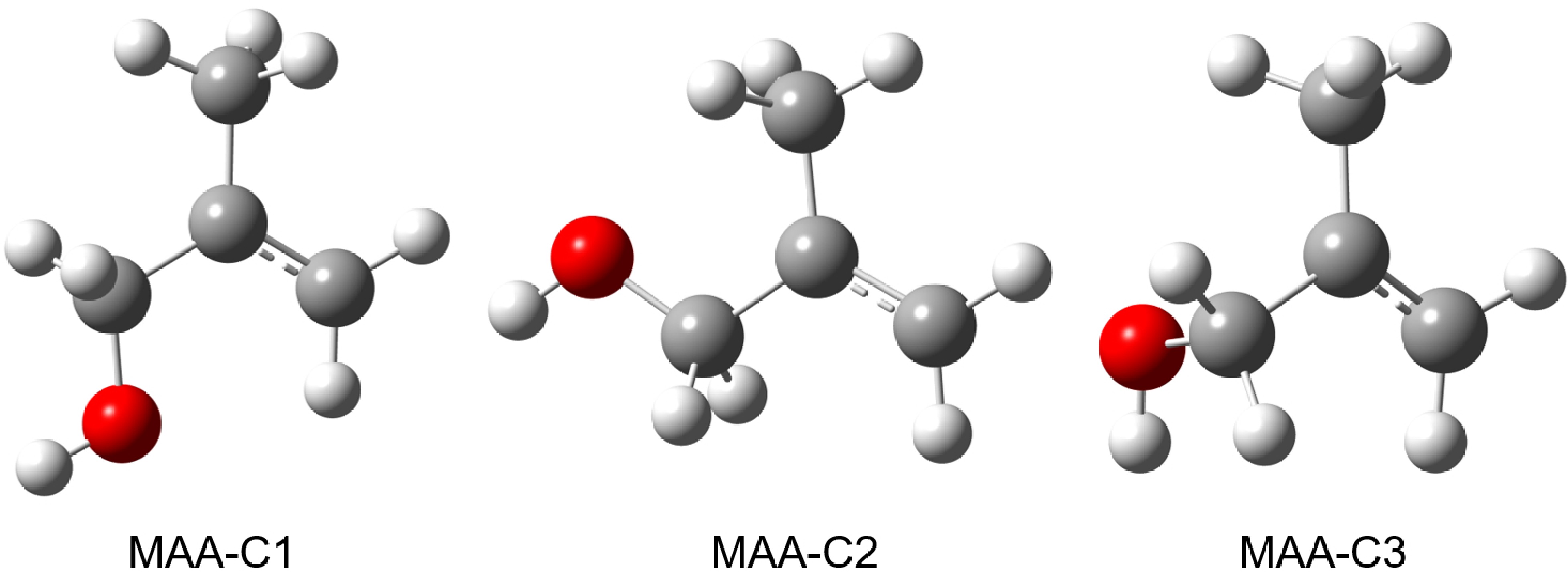
FIG. 2 displays the three stable conformers of cationic MAA, denoted as MAA-C1, MAA-C2, and MAA-C3. The calculated OH-bond length, zero-point energy (ZPE) corrected relative electronic energy (ΔE), and Gibbs free energy (ΔG) are presented in Table II. The most stable conformer is MAA-C1, the second most stable conformer MAA-C2 has an energy of 0.22 kJ/mol higher than MAA-C1.

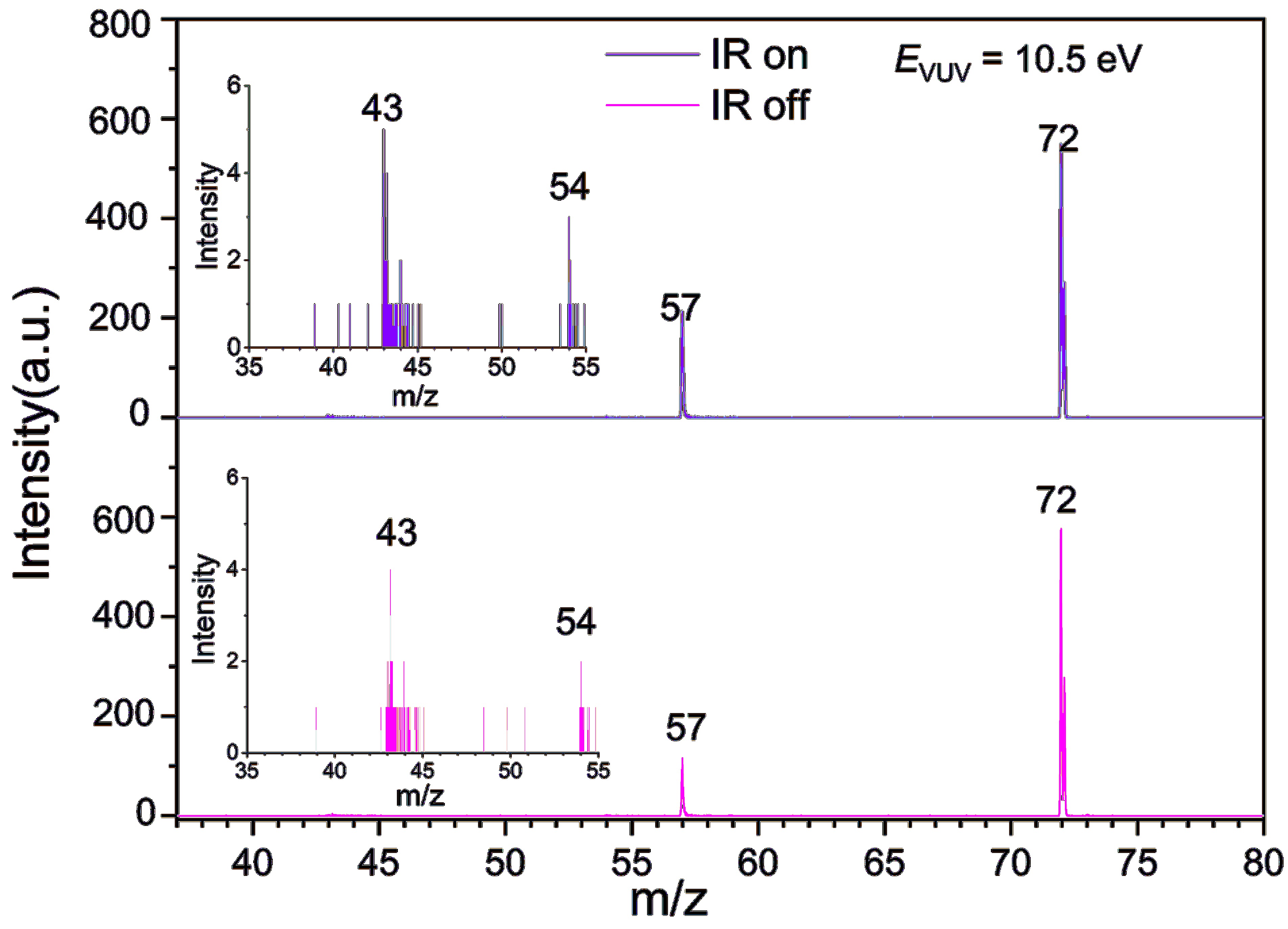
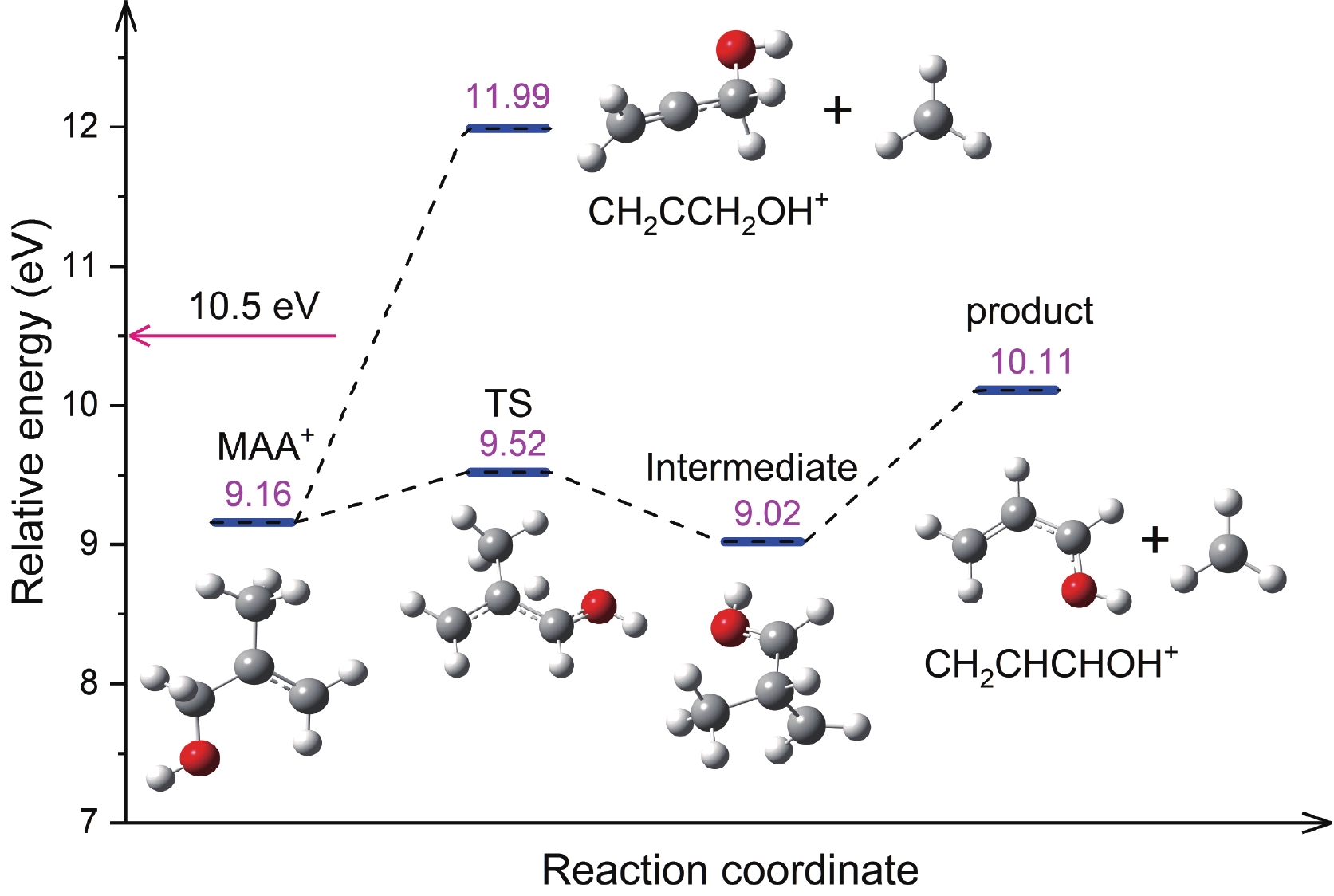
FIG. 3 shows a representative TOF mass spectrum of MAA ionized by 118 nm VUV radiation and the corresponding mass peak assignments based on the mass-to-charge ratio (m/z). The mass spectrum reveals the presence of cationic MAA at m/z=72, as well as several dissociation products at m/z=57, 54, and 43. Under the VUV radiation energy of 10.5 eV, the parent ion and the fragments at m/z=57 dominate the spectrum. The ionization energy (IE) of MAA has been previously reported to range from 9.20 eV to 9.28 eV using electron ionization [40] and photoionization [41, 42] methods. The appearance energies of dissociation products at m/z=57, 54, and 43 are in the range of 9.74–9.77 eV [42].

Upon introduction of IR radiation (2930 cm⁻¹) 50 ns before the VUV laser, as depicted in the top panel of FIG. 3, the signal intensity of m/z=72 decreases, while that of m/z=57 increases, due to the higher photon energy (VUV + IR vs. VUV) absorbed by MAA, leading to an enhanced dissociative ionization efficiency. In contrast, the signals of m/z=54 and 43 show no significant changes following the introduction of IR radiation.

The m/z=57 ion corresponding to the chemical formula C₃H₅O⁺ represents the primary dissociative photoionization product of MAA below 15.5 eV [42]. FIG. 4 shows the calculated dissociation pathways leading to the formation of the m/z=57 cation. One pathway is the direct cleavage of the C–C bond, resulting in the loss of a CH₃ group and the formation of CH₂CCH₂OH⁺; as the calculated AE for this cation is as high as 11.99 eV, which exceeds the photon energy of the current experiment, we exclude this pathway. The other pathway involves the transfer of an H atom from the CH₂ group adjacent to the OH group to the central C atom before the cleavage of the C–C bond. This pathway leads to the formation of the CH₂CHCHOH⁺, which is the most likely isomer of the m/z=57 cation. The calculated AE for this cation is 10.11 eV, which agrees with the experimental result of 9.77 eV [42]. The fragment cations at m/z = 54 and 43 can be assigned to CH₂CHCHCH₂⁺ and CH₃CO⁺, respectively, with calculated AEs of 9.74 eV and 9.61 eV, respectively [42].

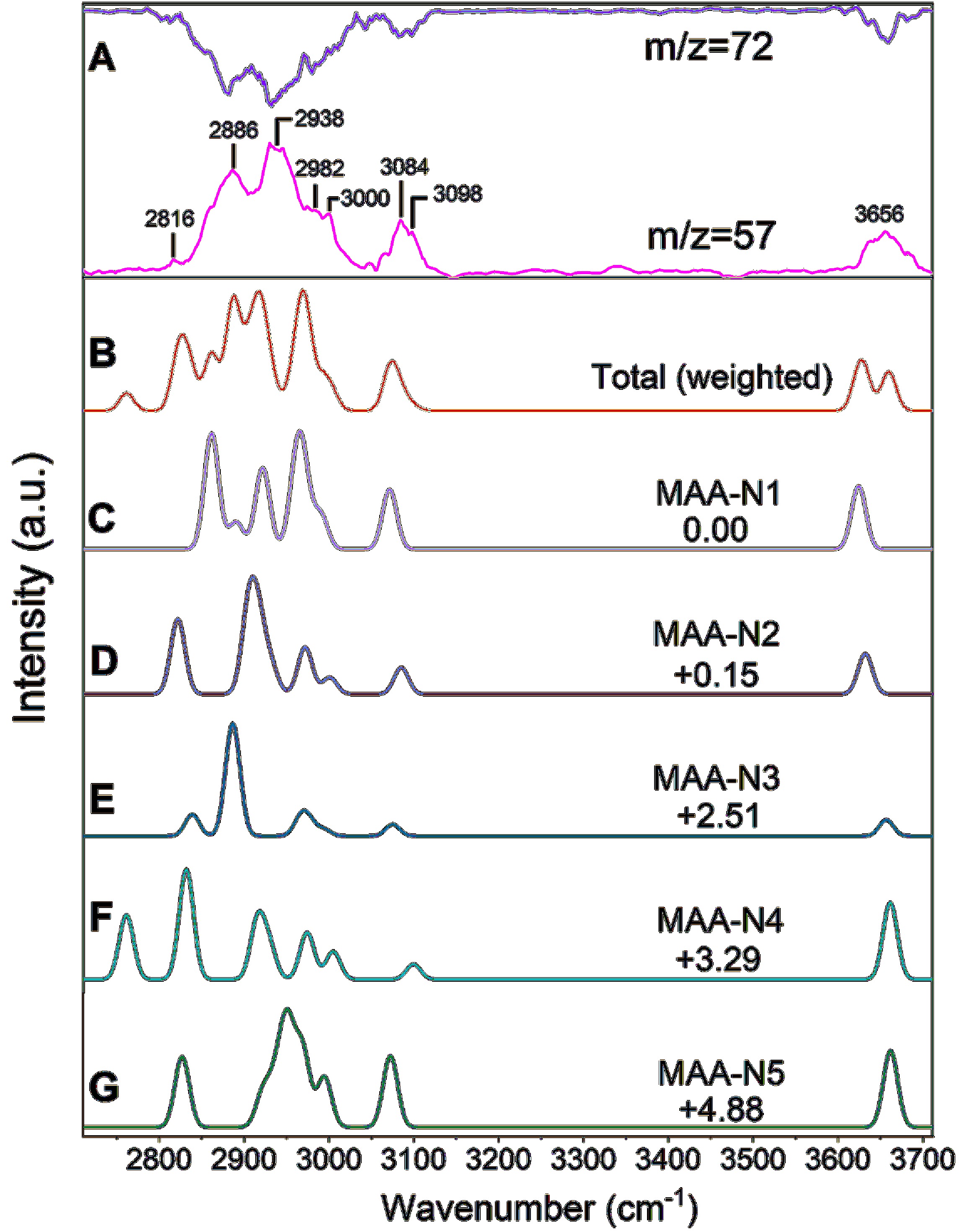
The vibrational spectra of neutral and cationic MAA were obtained using the NRID-IR method. In the NRID-IR spectroscopy method, the signal of the target species changes upon resonant absorption of infrared radiation when detected by nonresonant ionization. In the case of MAA, the absorption of infrared radiation facilitates the dissociative ionization process upon absorbing the 118 nm radiation. As a result, the detected MAA cation signal decreases, while the signal of the fragmentation product cation increases. These changes correspond to the IR dip and enhancement spectra, respectively. FIG. 5 presents the IR spectra of neutral MAA from both experimental measurement and theoretical calculation. FIG. 5(A) demonstrates the IR dip spectrum from monitoring MAA (m/z=72) and the IR enhancement spectrum from monitoring dissociation ionization product (m/z=57).

Since the neutral MAA can exist in five conformers, each contributing to the observed IR spectral with varying Boltzmann populations (as listed in Table I), the total anharmonic IR spectra of neutral MAA (FIG. 5(B)) were simulated by weighting the spectra of the five conformers according to their Boltzmann populations at 298 K. The transition states between the conformers are shown in FIG. S1 in Supplementary materials (SM). We assume that the interconversion between conformers is negligible during the supersonic expansion, which converts the internal energy to the translational energy.

The simulations were performed at the B3LYP-D3(BJ)/def2-TZVPP level of theory. The anharmonic simulated stick spectra of the five conformers are convoluted by Gaussian function (20 cm⁻¹ FWHM), and the resulting spectra are shown in FIG. 5(C–G). It is worth noting that the enhancement spectra exhibit a higher signal-to-noise ratio compared to the dip spectra, and our discussion mainly focuses on the former spectra. In addition, significant efforts were made to obtain the overtone IR spectra, but no obvious peak was observed.

In the frequency range of 2700–3200 cm⁻¹, a broadband with two prominent peaks at about 2886 and 2938 cm⁻¹ was observed, accompanied by several shoulder peaks at 2816, 2982, and 3000 cm⁻¹ (refer to FIG. S1(a) in SM for detailed information). Additionally, a relatively narrow peak centered at 3084 cm⁻¹ was also observed.

In this region, seven CH fundamental stretching transitions are predicted, with three corresponding to the antisymmetric modes of CH₂ and CH₃ groups, and the remaining four symmetric modes of CH₂ and CH₃ stretch. In addition, several combination and overtone bands with comparable absorption intensities are predicted, exemplified by the MAA-N1 conformer. These bands include 2v₁₀, 2v₁₂, v₁₁ + v₁₀, and v₁₇ + v₉, primarily involving CH₃ and/or CH₂ bending vibrations and the C=C stretchin modes. It is worth noting that the simulated total anharmonic IR spectra exhibit good agreement in terms of profile and absorption intensity ratios among different peaks when compared to the observed spectra.

Considering the peak position, absorption intensity, and the Boltzmann populations of the five conformers, we propose that the feature at approximately 2886 cm⁻¹ primarily originates from the v₆ mode (the antisymmetric modes of CH₂ group adjacent to OH) of the MAA-N3 conformer. Another prominent peak centered at ~2938 cm⁻¹ can be assigned to the combined contribution from the v₅ mode (the antisymmetric modes of the CH₃ group) of MAA-N2 and MAA-N4 conformers, as well as the v₆ and v₁₁ + v₁₀ modes of MAA-N1. The lower frequency shoulder peak at ~2816 cm⁻¹ originates from the symmetric modes of the CH₂ group adjacent to OH (v₈ mode) of conformers MAA-N2 and MAA-N3, as well as the symmetric modes of the CH₃ group of MAA-N4. The two higher frequency shoulders at ~2982 and 3000 cm⁻¹ are mainly contributed by the v₄ and v₃ modes, which correspond to the antisymmetric mode of the CH₃ group and the symmetric mode of the CH₂ group, respectively. FIG. S1 in SM shows that the distinct band centered at ~3084 cm⁻¹ is exclusively attributed to the antisymmetric stretching vibration of the CH₂ group on the double bond (v₂).

The observed band of the OH first fundamental stretch (v₁) is centered at 3656 cm⁻¹, which is similar to those of other gas-phase enols, such as allyl alcohol (~3650–3689 cm⁻¹) [43] and crotyl alcohol (3665 cm⁻¹) [30]. However, the observed frequency of MAA is slightly lower than that of the free OH stretch in gas-phase alcohols, such as the methanol (~3683 cm⁻¹) [44] and ethanol (~3667 and 3682 cm⁻¹) [45], but higher than those of ether alcohol molecules with significant intramolecular hydrogen bonds, such as 2-methoxyethanol (~3635 cm⁻¹) [31] and tetrahydropyran-2-methanol (~3614 cm⁻¹) [46]. This suggests the possible existence of weak intramolecular hydrogen bonding in one or more conformers of MAA. Theoretical calculations predicted that the OH fundamental stretching frequencies of MAA-N1 (3625 cm⁻¹) and MAA-N2 (3632 cm⁻¹) are lower than those of the other three conformers (~3660 cm⁻¹) by about 30 cm⁻¹. The difference may be attributed to weak OH···π intramolecular hydrogen bonds in the MAA-N1 and MAA-N2 conformers. The details of this OH···π interaction will be discussed in Section III.E.

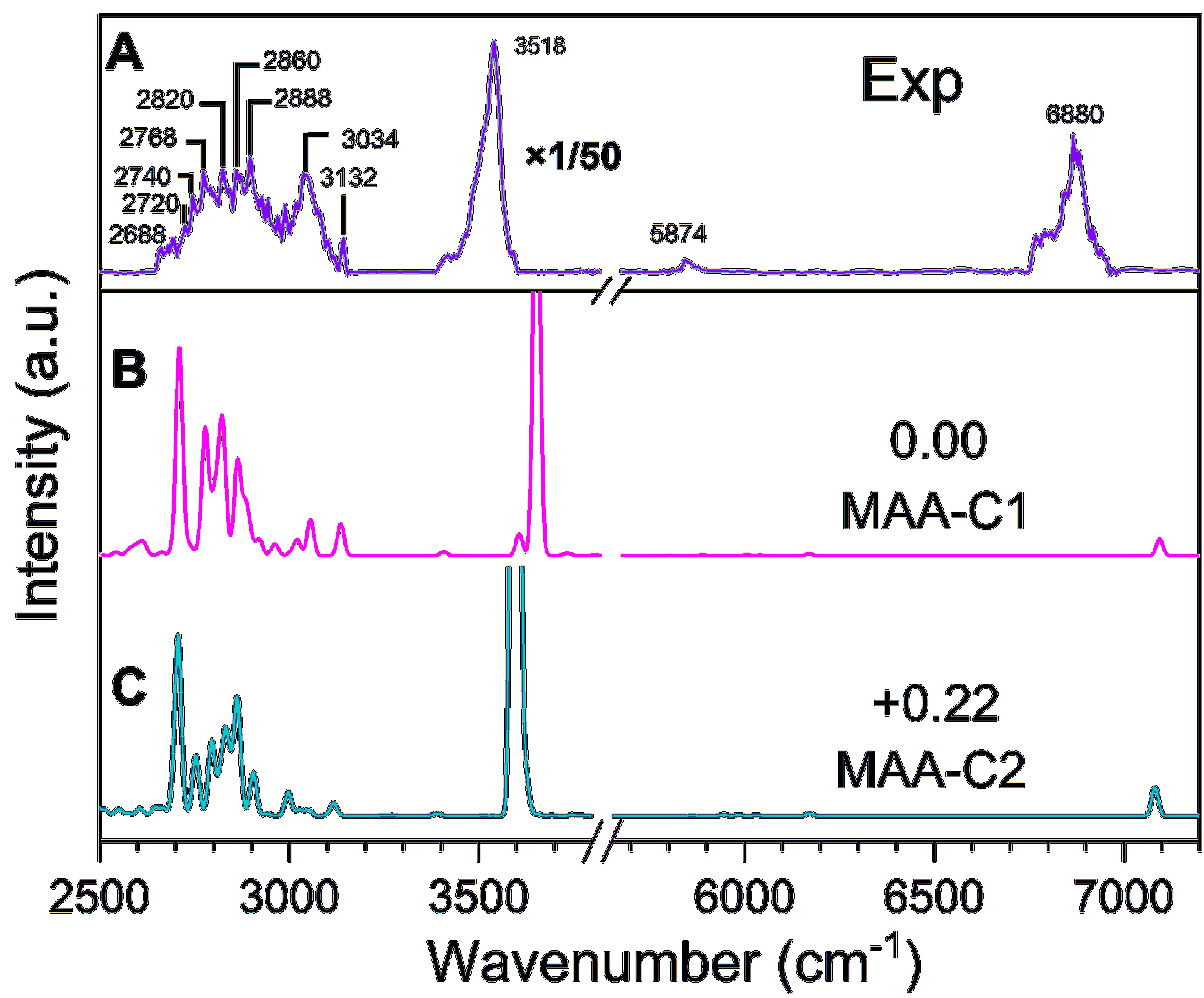
FIG. 6(A) shows the observed IR spectral of the cationic MAA. FIG. 6(B, C) depict the simulated individual anharmonic IR spectra (convoluted with a Gaussian profile of 20 cm⁻¹ FWHM). The predicted stick IR spectra are shown in FIG. S2 (SM).

In the 2600–3200 cm⁻¹ range, three distinct features are observed. The broadband in the 2600–2950 cm⁻¹ region exhibits several shoulder peaks that are not completely resolved. Upon careful comparison with the simulated IR spectrum (see FIG. S2 in SM), these peaks can be tentatively assigned as follows: (i) the features at 2688 and 2720 cm⁻¹ are attributed to the antisymmetric (v₈) and symmetric (v₇) C–H stretching mode of the CH₂ group adjacent to the OH group, respectively; (ii) the peak centered at 2740 cm⁻¹ can be assigned to the combination band of v₁₆ + v₉ of MAA-C1 conformer, and (iii) the band at 2768 cm⁻¹ is assigned to the combined contribution from the combination bands of v₁₆ + v₉ and v₃₃ + v₈ of the MAA-C2 conformer, as well as the overtone band of the 2v₁₁ mode; (iv) the three higher frequency shoulder peaks at about 2820, 2860, and 2888 cm⁻¹ mainly arise from the v₆ mode of the MAA-C1 conformer and 2v₁₁ mode of the MAA-C2 conformer, v₁₁ + v₁₀ mode of the MAA-C2 conformer, and 2v₁₀ mode of MAA-C2 conformer, respectively. The peak at 3034 cm⁻¹ arises from the combined contribution of the 2v₉ mode of MAA-C1 and the v₃ mode (antisymmetric C–H stretch) of MAA-C2. Similar to the neutral MAA, the relatively narrow band centered at 3132 cm⁻¹ is exclusively assigned to the antisymmetric stretching vibration of the CH₂ group on the double bond (v₂). The observed band of the OH first fundamental stretch (v₁) of the cationic MAA is centered at 3518 cm⁻¹, indicating a redshift of about 140 cm⁻¹ relative to neutral MAA. The observed peaks at 5874 and 6880 cm⁻¹ arise from the first overtone stretches of the CH (2v_CH) and OH bonds (2v_OH), respectively.

The highest occupied molecular orbital (HOMO) of neutral MAA is localized on the π bonding orbital of C=C, as shown in FIG. S3 (SM). Upon electron removal from the HOMO, the C=C bond elongates from 1.33 Å to 1.41 Å, accompanied by a slight shortness of the two neighboring C–C bonds from 1.50 Å to 1.47 Å. Additionally, the Mayer bond order of C=C decreases from 1.81 to 1.2, consistent with the predicted about 160 cm⁻¹ red-shifted in the C=C stretching vibrational (v₉) of the cationic MAA in comparison with neutral MAA. In contrast, the ionization process barely affects the OH and CH stretching vibrational frequencies. However, it is unexpected that the OH fundamental stretching mode of the cationic MAA experiences a red shift of about 140 cm⁻¹ relative to the neutral MAA, significantly larger than the theoretical predictions of a red-shifted about 35 cm⁻¹. Similarly, for the CH stretch, taking =CH₂ as an example, the observed antisymmetric C–H stretch (v₂) of the cationic MAA is blue-shifted by about 48 cm⁻¹ in comparison with the neutral MAA.

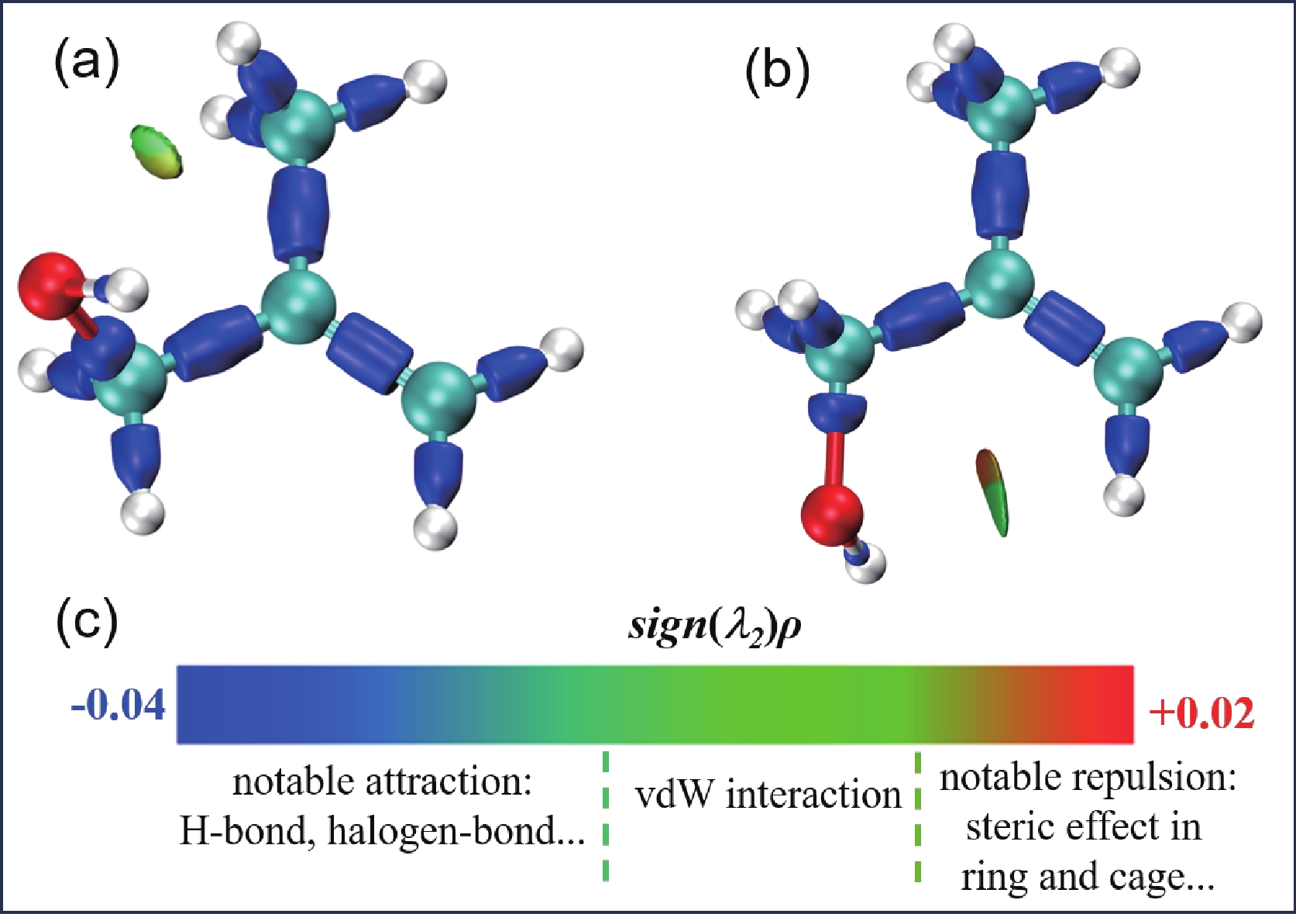
As presented in Table I, the OH bond lengths for the five conformers of neutral MAA were calculated at the B3LYP-D3(BJ)/def2-TZVPP level of theory. The calculated OH lengths of MAA-N1 and MAA-N2, which possess structures that potentially facilitate an intramolecular hydrogen bond between the OH group and the π-electrons of the C=C double bond, are 0.9617 and 0.9615 Å, respectively. These values are approximately 0.0015 Å longer than those of the other three conformers, where the OH-group points away from the π-electron cloud of the C=C double bond. The interaction region indicator (IRI) approach [47] was employed to analyze interactions in MAA-N1 and MAA-N2. FIG. 7(A, B) illustrate the result of the IRI maps for MAA-N1 and MAA-N2. It can be observed that a weak interaction (IRI=1.1) corresponding to the CH···O intramolecular hydrogen bonding interaction was identified. However, no IRI critical points were found between the OH group and the π-electron cloud of the C=C double bond. This suggests that the O−H···π interaction in MAA-N1 and MAA-N2 is too weak to be observed.

To further investigate the strength of O−H···π interaction, a natural bond orbital (NBO) analysis was also performed. In the NBO analysis, the second-order perturbation stabilization energy gained from the hydrogen bond interaction, denoted as E(2), can be utilized to quantify the interaction strength. The calculated E(2) values for the interaction between the C=C π-orbital and the antibonding OH σ-orbital are 0.21 and 0.67 kJ/mol for MAA-N1 and MAA-N2, respectively. These values are relatively small, particularly when compared to the intramolecular O−H···O hydrogen bonding interaction systems, where the stabilization energies are calculated to be above 83.7 kJ/mol [48, 49].

Mackeprang et al. conducted a study on the O−H···π interaction in methallyl carbinol (CH₂=C(CH₃) –CH₂–CH₂–OH, MAC) and allyl carbinol (CH₂=CH–CH₂–CH₂–OH, AC), which have similar structures to MAA. The NBO analysis revealed that the stabilization energies associated with the O−H···π interaction were also very small, and the values are 3.72 and 2.85 kJ/mol for MAC and AC, respectively [14]. Additionally, their NCI analysis identified two troughs for both MCA and AC, indicating the presence of intramolecular O−H···π hydrogen bonding. Based on these findings, it can be concluded that the O−H···π interaction in MAA is weaker compared to that in MCA and AC. In summary, the NBO analysis further confirms the weak O−H···π strength in MAA-N1 and MAA-N2, consistent with the IRI analysis. This also explains the extremely small energy difference between the O−H···π hydrogen bonding conformers (MAA-N1, MAA-N2) and the other three conformers.

The gas phase IR spectra of neutral and cationic MAA were measured utilizing the IR-VUV NRID-IR method. In addition, quantum chemical calculations suggest that the two most stable conformers of neutral MAA were expected to be stabilized by an intramolecular hydrogen bond (OH···π). However, the interaction region indicator (IRI) analysis revealed no critical point between the OH group and the π-electron cloud of the C=C double bond, suggesting that the OH···π interaction is extremely weak. Furthermore, the NBO analysis showed that the second-order perturbation stabilization energy (E(2)) of the interaction between the C=C π-orbital and the antibonding OH σ-orbital is negligible. These theoretical findings collectively suggest that the OH···π interaction in MAA is not as significant as initially anticipated. This is consistent with the experimental observation that the observed OH fundamental stretching frequency of neutral MAA (3656 cm⁻¹) is slightly lower than that of the free OH stretch of gas-phase alcohols.

The observed OH fundamental stretch of cationic MAA exhibits a substantial redshift of about 140 cm⁻¹ in comparison with that of neutral MAA, which is greater than predicted. This unexpected result is surprising since the removal of an electron from the HOMO was predicted to have a minimal impact on the OH stretch. In short, the present work provides a compelling example illustrating the exceptionally weak nature of the OH···π intramolecular hydrogen bond in unsaturated alcohols, particularly when compared to aromatic and OH···O systems.

Supplementary materials: Observed and predicted IR spectra of neutral and cationic MAA in CH stretch region; calculated HOMO of the neutral MAA; fundamentals (frequency and intensity) of neutral and cationic MAA are available.