Machine Learning Approach Accelerates Search for Solid State Electrolytes

With the current rapid development of electric vehicles and electrochemical energy storage technologies [1], solid-state battery [2] technology has received great attention from the industry due to its promising future. In particular, solid-state electrolytes (SSE) [3], as the core component, are becoming a key research area for next-generation battery technology due to their significant advantages in safety [4, 5], energy density [6, 7] and lifetime. The research and development of solid-state electrolytes is an important step toward the commercialization of solid-state batteries, which involve a number of aspects such as material discovery and performance optimization. Solid-state electrolytes are divided into three main categories: polymer solid-state electrolytes [4, 8–10], inorganic solid-state electrolytes, and organic-inorganic hybrid solid-state electrolytes [11]. Although polymer and organic-inorganic hybrid electrolytes have potential in some applications due to their unique properties, they face many challenges in practical applications. For example, the complex chemical structure of these materials not only increases the difficulty of optimizing the design of the materials, but also faces the problems of uncontrollable lithium dendrite growth and lower ionic conductivity, which limit their application in high performance batteries. Therefore, the focus of this study has shifted to the development and optimization of inorganic solid-state electrolytes. Inorganic solid-state electrolytes are considered key materials for realizing high-performance, long-life solid-state batteries due to their excellent chemical stability, high ionic conductivity, and excellent mechanical strength [12]. In addition, compared with organic materials, inorganic solid-state electrolytes are better at preventing lithium dendrite penetration, which greatly improves battery safety.

Good solid-state electrolyte [13] materials must have low electronic conductivity [14, 15], specifically an electronic conductivity (σ_e) of less than 3.6 × 10⁻³⁰ S/cm or a band gap greater than 4.0 eV, which allows the material to exhibit excellent insulating properties, effectively blocking the passage of electrons. This is particularly important because when the ionic conductivity of the electrolyte is high, electrons can easily pass through the electrolyte, leading to self-discharge, which not only depletes the battery’s energy storage, but also causes the formation of dangerous lithium dendrites, which can compromise battery performance and safety. In addition, solid-state electrolytes must have good thermal stability, especially at room temperature, to ensure stable operation under normal use conditions. This means that ideal solid-state electrolytes must excel in both structural and phase stability [16–18]. Specifically, these materials should have a low formation energy [14, 19] (formation_energy_per_atom), which indicates that the material is more stable and less likely to decompose during preparation. At the same time, they should also have a low convex hull energy [20–22] (e_above_hull), which indicates that the material is more thermodynamically stable and less likely to transform into other phases. Such properties help ensure that the electrolyte maintains its chemical and physical properties throughout the battery’s life cycle, providing long-lasting and reliable performance.

Both experimental and computational methods have contributed to the targeted exploration of inorganic structures; in particular, first-principles calculations based on density functional theory (DFT) [23–25] can provide information about the energy bands of the structure, the formation energies, as well as stabilization information. However, the very large search space of inorganic materials is very time-consuming, and in experiments where the synthesis and testing of a solid electrolyte consumes a lot of time and resources, traditional experimental methods are very inefficient. Theoretical computational methods can speed up the discovery of new materials to some extent, but they are still limited by computational complexity and accuracy. Complex battery systems and a large number of possibilities make traditional theoretical computational methods limited in dealing with practical problems. In this context, machine learning methods have emerged as a new way to discover and optimize solid-state electrolytes. Machine learning (ML) [26, 27] has breathed new life into materials science research by analyzing the properties and structures of a large number of inorganic structures, discovering potential laws, and making intelligent predictions. And we can often access these properties very quickly through machine learning methods to further determine whether these structures are candidates for ideal solid-state electrolyte structures.

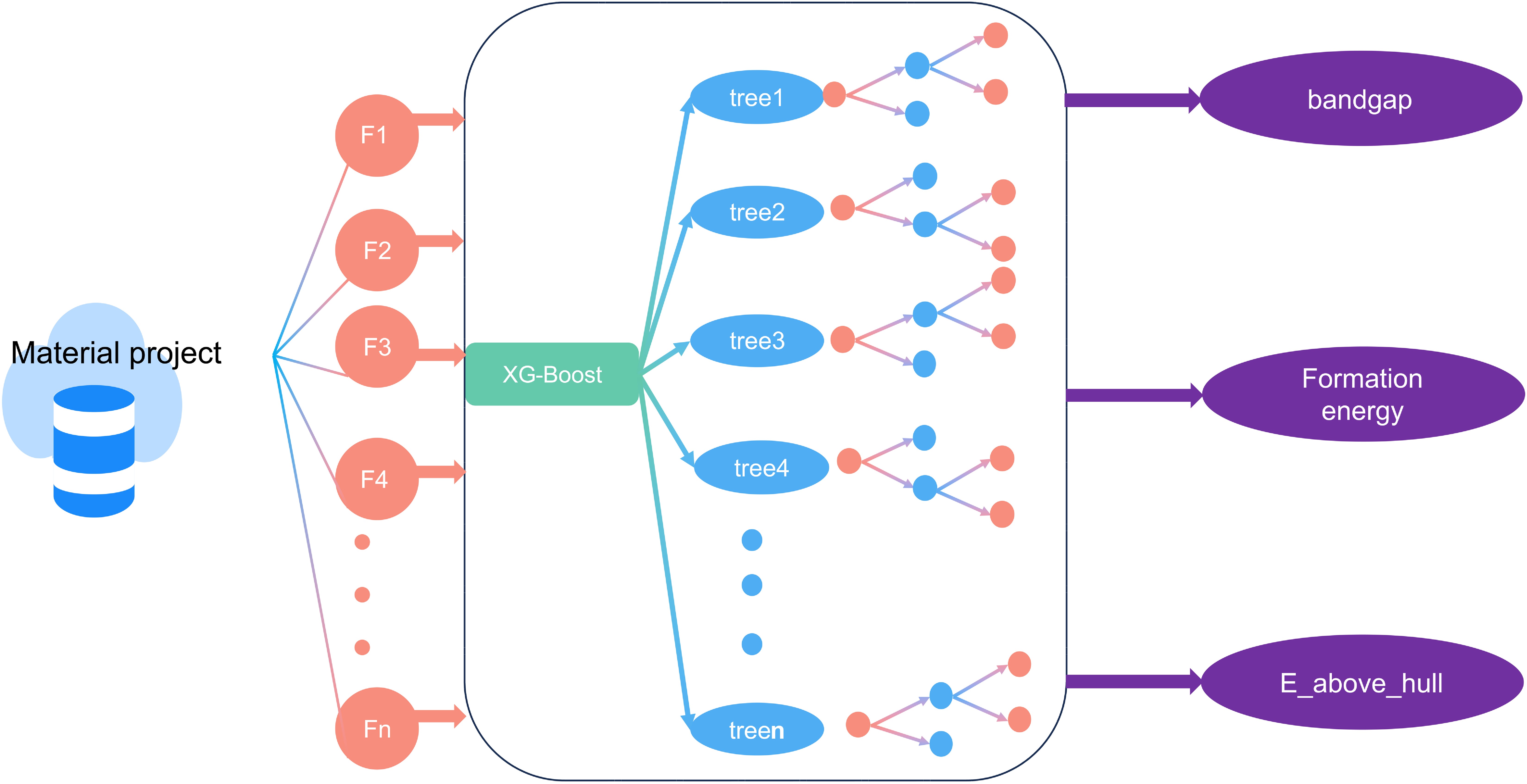
We have successfully applied XGBoost [28], an advanced gradient descent based algorithm, to predict the energy band structure and stability of materials in the Materials Project database [29], an achievement that marks a major breakthrough in the field of materials science. By collecting and analyzing the elemental correlation characteristics of various materials and their crystal structure properties, our model shows excellent performance in predicting the bandgap and formation energies of materials, with regression R² score values of 0.88 and 0.94, respectively, demonstrating a high degree of consistency between the model predictions and the actual data. More impressively, our classification model also achieved an accuracy of 84% in terms of structural phase stability, demonstrating its strong capability in material classification problems. Most importantly, our model significantly reduces the time cost and improves the efficiency by 5 orders of magnitude compared to the traditional density functional theory (DFT) computational method. This not only means that a great deal of time and resources can be saved in the process of materials research and development, but also greatly accelerates the process of discovery and application of new materials, which is of great significance in advancing the development of materials science.

The machine learning model in this work is implemented by the classification model (XGB-C) and regression model (XGB-R) [30], which are all based on the extreme gradient boosting (XGBoost) algorithm. Overall, the model between the predicted value ${Y}_{i}^{\rm{pred}}$ and input $ {X}_{i} $ can be mathematically as:

where $ k $ is the number of decision trees, and $ f $ is a function in the functional space. The loss function that contains the gradient boosting algorithm loss and regularization term in the training process is defined as:

where $ \rho $ is the number of leaf nodes in the decision tree, and $ \omega $ is the score of leaf nodes. $ \psi $ and $ \lambda $ are the default coefficients of the regularization term to limit the number of leaf nodes and smooth the score of leaf nodes.

While building accurate algorithms and applying computational skills is part of machine learning, data are also an essential and valuable resource for each ML process. A good ML model should be based on the correct and reasonable use of data sets. The data set in this work contains 13000 inorganic solid electrolytes from Materials Project database. All properties were obtained by theoretical calculations and are available in the database, about 60% of the structures have band gap values in the range 0–1 eV. A large amount of narrow band gap data will interfere with the model, which is not conducive to find materials with wide band gaps. Therefore, it is necessary and reasonable to establish a classification model (XGB-C) to exclude garnets with band gaps less than 1 eV.

We then build the XGB-R model to implement regression operations for structures with band gaps greater than 1 eV. For the prediction of formation energies we use direct regression (XGB-R). Finally the classification of phase stability is achieved by the XGB-C model. The ratio of training to test sets for all models is 8:2.

To obtain the optimal model, the determination of hyper-parameters is essential. In both the XGB-C and XGB-R models, the hyper-parameters (the maximum number of trees, the step size of each iteration, the percentage of samples that are randomly sampled per tree, the percentage of features sampled at random per tree, and the maximum depth of the tree) are selected by the grid search method.

The framework of our overall work is shown in FIG. 1, first we obtain a large number of solid electrolyte structures from the database, the structure generally consists of three parts, A (cation), B (transition metal ions), and X (anion); and according to the anion, we classify the structure into halide oxides and sulfides. Due to the differences in the anionic part, the three types of solid electrolytes will show large differences in electronic conductivity as well as stability properties. Therefore, we first analyze the band gap, formation energy, and phase stability of the three structures to explore the influence of the anions on the overall properties, and then extract the properties of the elements corresponding to these three positions (ionic radius [32], electronegativity [33], first ionization energy [34], atomic radius, dipole polarizability [35, 36], mole fraction, atomic mass, and elemental valence), and add additional features of the space group and crystal system as input features of the model in the form of one_hot coding. With the extracted input features, we build four sets of training models corresponding to phase stability classification, narrow and wide band gap classification, wide band gap regression, and formation energy regression.

In this work, we collected more than 6000 structures of ternary or more complex compounds containing Na⁺ and Li⁺. By extracting the elemental and crystal system-related features of these structures, we constructed classification and regression models, respectively. First, we performed classification prediction for wide band gap [37] (band gap > 1 eV) and narrow band gap [38] (band gap < 1 eV) structures. Then we performed regression prediction for wide bandgap structures. In addition, we predicted the stability (e.g., formation energy) and phase stability (e.g., above convex packet energy) of the structures based on the XGB regression (XGB-R) and XGB classification (XGB-C) models, respectively. By predicting this set of properties, we found only 120 structures that met both the low electronic conductivity and stability requirements. As a result, we used machine learning algorithms to narrow down our search by more than 95%, greatly accelerating the development of solid-state batteries.

In order to thoroughly investigate the effect of anion type on the performance of solid-state electrolytes, we have meticulously analyzed the three key metrics, namely band gap, formation energy, and e_above_hull, for three types of electrolyte materials, namely oxides, halides, and sulfides. Examining FIG. 2(a), it is evident that the band gap size plays a crucial role in determining the electronic properties of the material and significantly influences the formation energy distribution pattern. It is interesting to note in FIG. 2(b) that oxide and halide structures with band gaps larger than 4 eV, as well as sulfide structures with band gaps larger than 2 eV, tend to have relatively low average formation energies, which may indicate the advantages of these materials in certain applications. In addition, analysis of sulfides shows that they typically have relatively high formation energies. This property contrasts with oxides and halides, indicating that sulfides have some disadvantages in terms of structural stability due to differences in anion type. This finding suggests the need for further studies on the relationship between band gap size and formation energy and the phase stability of materials. To gain a deeper understanding of these relationships, we have meticulously tabulated the distribution of the properties of the three solid-state electrolytes in FIG. 2 (c), (d), and (e), respectively. Strikingly, in the unstable structure, most of the material is distributed in the region where the energy of formation is greater than −1 eV and where the band gap is less than 1 eV. In contrast, for the stabilized structures, the distribution of band gap and formation energy appears to be more uniform. This observation strongly suggests that structures with lower band gaps and higher formation energies are usually unstable in terms of phase stability, which is an important guideline for the design and development of new solid-state electrolyte materials.

The next phase of our research was dedicated to building an efficient machine learning model using carefully selected structural feature descriptors to further understand and predict the properties of solid-state electrolytes. To select the most effective features, we first focused on the correlation coefficients between features, a step that is crucial because it reveals the linear relationship between different features. FIG. 3(a) clearly shows the distribution of the correlations between these features, and a notable finding is that the correlation coefficients of most of the features are below 0.4, indicating a weak linear association. It is noteworthy that the correlation of features between anions is generally higher than that between cations as well as transition metal ions, a finding that can be an important guide for subsequent model construction.

We then shifted our focus to regression analysis of bandgap and formation energy for all data. As shown in FIG. 3 (c) and (d), the bandgap regression achieves an R² of 0.96 and 0.88 on the training and test sets, respectively, demonstrating the high accuracy of the model in predicting the bandgap. In particular, in regions with large bandgap values, we observe a significant reduction in the error between predicted and actual values. This phenomenon is consistent with our previous observation of the distribution of bandgap properties: in regions with bandgaps larger than 3 eV, the data are more uniformly distributed, and thus the model is able to show better prediction performance. Similarly, due to the uniform distribution property of the formation energy data, our model also exhibits very high accuracy in predicting the formation energy, with R² of 0.99 and 0.96 for the training and test sets, respectively, corresponding to RMSE (root mean square error) of 0.06 eV and 0.13 eV.

To further explore the effect of anions on the model performance, we performed a feature importance analysis on the results of band gap regression, formation energy regression, and phase stability classification, and the results are shown in FIG. 3(e). In the feature importance ranking, we found that the elemental properties associated with the anion position occupy a significant position in the model, which further emphasizes the significant impact of anion variability on the model performance.

Having completed the prediction of the fundamental properties, our next step is to use this predictive model for more in-depth screening and analysis of the properties of solid-state electrolytes. This will not only help us better understand the fundamental properties of the materials, but will also help us make more informed decisions in future research and applications.

Having ensured the relatively low linear correlation between the features, we proceeded to perform a classification operation on the model with the aim of distinguishing between wide and narrow band gaps as well as structures with different phase stability. The ROC (Receiver Operating Characteristic) curves shown in FIG. 3(b) demonstrate the excellent performance of the model in this regard: the accuracy of bandgap and phase stability classification reaches 88% and 84%, respectively, and the area of the ROC curves is even as high as 0.96 and 0.94, which are significant indications of the model’s efficient classification capability.

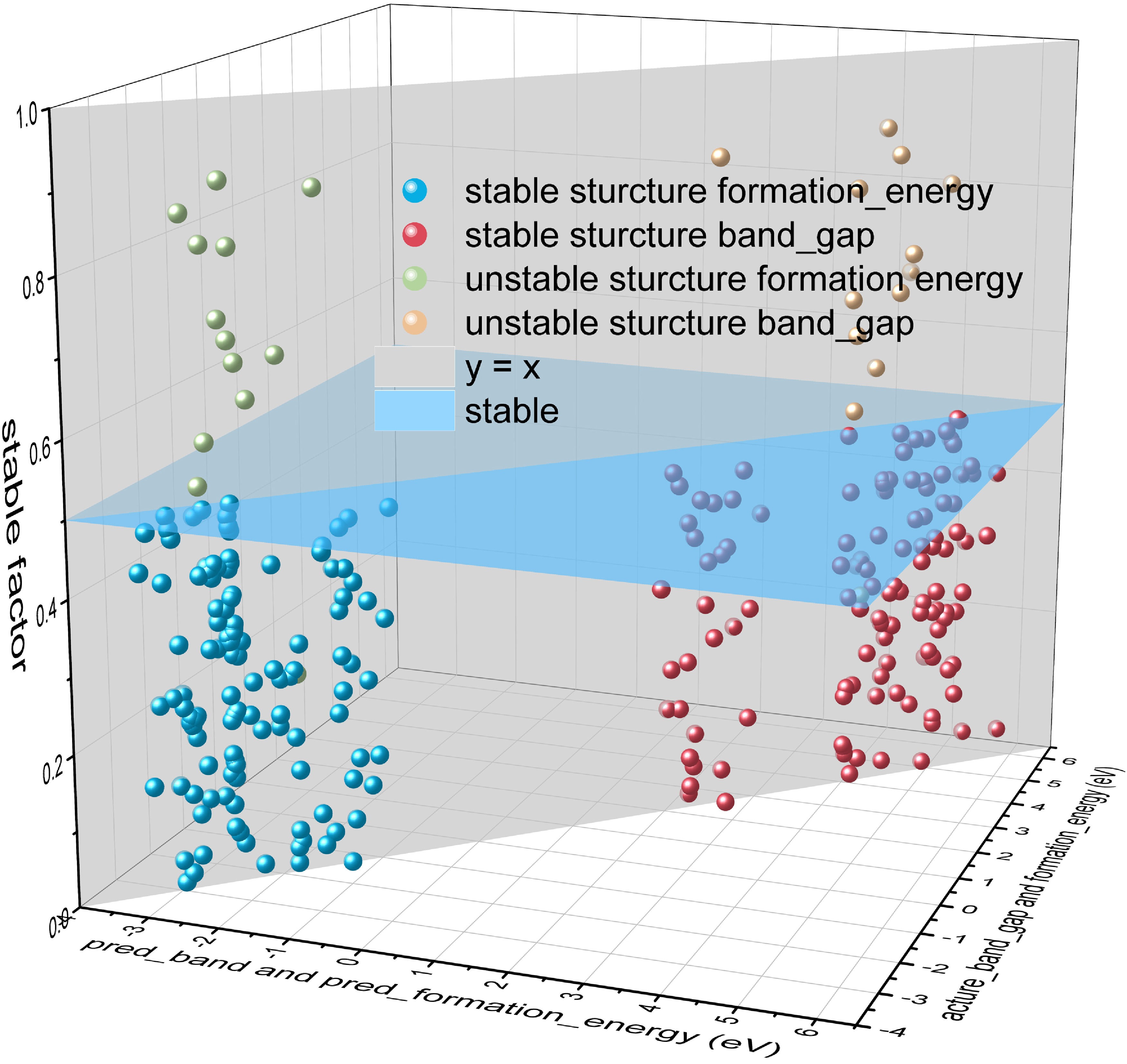
In our study, we successfully screened out 194 ideal solid-state electrolyte structures from a large number of candidate structures by accurate predictions of the machine learning model, and this result marks a significant progress in our research. As clearly shown in FIG. 4, our model performs well in predicting phase stability (in terms of e_above_hull > 0.01 eV). Of all the solid-state electrolytes predicted to be phase-stable, only 8% of the structures actually behave in an unstable state, meaning that our overall prediction accuracy is as high as 92%. In addition, the accuracy of our predictions for band gap and energy of formation is equally commendable. For these two key parameters, our model not only predicts them accurately, but also has a very high consistency between the actual and predicted values, with R² values of 0.92 and 0.96, respectively, which exceeds the average prediction of the model and demonstrates the power of the XGBoost algorithm in dealing with high bandgap and stable structures.

This work demonstrates the successful prediction of the energy band structure and stability of solid-state electrolytes using a gradient descent-based decision tree algorithm (XGBoost). The algorithm utilized feature descriptors to characterize solid state electrolyte structures and built classification and regression models from data collected in a database. The search scope was reduced by more than 95% through machine learning, resulting in a significant improvement in the discovery efficiency of solid state electrolytes. By analyzing the band gap, formation energy, and phase stability, it is evident that sulfides exhibit distinct band gap and formation energy properties compared to oxides and halides. It is also shown through modeling that variances in anions can lead to huge differences in the properties of solid-state electrolytes, which gives us some ideas for designing ideal solid-state battery structures. The model successfully screened out 194 ideal solid-state electrolyte structures with an overall prediction accuracy of 92%. The XGBoost algorithm accurately predicts the energy band structure and stability characteristics of solid-state electrolytes and efficiently screens out the most promising candidate materials from a large number of structures. The efficient screening capability greatly accelerates the discovery process of new materials. It provides strong scientific support for the application and development of solid-state electrolytes. This result will be crucial for future materials design and optimization, providing new material options for the development of key technologies such as energy storage and conversion. We can deepen our understanding of materials and open up new opportunities for more efficient and sustainable energy use.

Supplementary materials: Details of the specific meaning of element-related feature descriptors and setting of XGBoost-related parameters are shown.