HTML
-
Polymer-bonded explosives (PBX) are composite materials formed by binding high-energy explosive particles together using polymeric materials, offering high energy density, excellent mechanical properties, explosive performance, and safety.[1–6] Octogen (HMX) is widely utilized in military explosives and solid rocket propellants for its high energy density and exceptional thermal stability, key factors in managing thermal loads during detonation processes.[7–9] However, despite its favorable thermal properties, localized heat accumulation in HMX-based PBX can lead to safety concerns, necessitating effective thermal management strategies.[10–12] Therefore, optimizing the thermal conductivity of PBX materials through advanced fillers, such as graphene, has become a promising approach to enhance heat dissipation and mitigate the risk of hotspot formation.
High energy, high safety, and strong environmental adaptability have put forward higher requirements for high-performance PBX.[13,14] Its development must take into account the performance in multiple aspects such as energy, safety, mechanical properties, and environmental adaptability. Thermal conductivity[15–17] is one of the key properties of PBX, and enhancing it is beneficial for reducing thermal stress, increasing shape stability, and improving safety. It is one of the important ways to improve the comprehensive performance of PBX. Therefore, conducting research on thermal conductivity enhancement of PBX is of great significance for improving equipment performance.
In recent years, research on carbon-based materials such as graphene and carbon nanotubes has surged, driven by their unique thermal and structural properties. These materials have the potential to significantly enhance the thermal conductivity of composites, thereby improving the thermal management of related systems.[18–20] The dispersion of graphene thermal conductive fillers greatly influences the thermal conductivity of composite materials. Uniform dispersion of these fillers can create an efficient thermal conduction network, substantially improving the composite’s thermal conductivity. Conversely, uneven dispersion leads to aggregation, disrupting thermal conduction pathways and reducing the composite’s overall thermal conductivity. Thus, ensuring the uniform dispersion of graphene fillers in composite materials is crucial for achieving high thermal conductivity.[21]
The degree of aggregation of thermal conductive fillers has a significant impact on the thermal conductivity and local hot spots of composite materials. When the fillers are evenly dispersed within the composite material, they can form an efficient thermal conduction network, thereby enhancing the overall thermal conductivity of the material.[22,23] This uniform distribution helps to evenly transfer heat, reducing the formation of local hot spots, and thus avoiding the risk of performance degradation or damage in localized areas due to overheating. Conversely, if the fillers aggregate, they may create thermal resistance, hindering the transfer of heat and leading to the accumulation of heat in certain areas, forming local hot spots. These hot spots can negatively affect the performance and lifespan of the equipment. Therefore, optimizing the dispersion of fillers is one of the key strategies to improve the thermal conductivity and thermal stability of composite materials.[21,24,25]
Recent studies suggest that improving the dispersion of carbon-based fillers within HMX-based PBX significantly boosts its thermal management capabilities and mitigates the risk of local overheating.[26] Nonetheless, a comprehensive understanding of how varying degrees of filler aggregation impact the thermal conductivity of HMX-based PBX is still missing. To address this gap, the present investigation utilizes finite element simulations to explore the influence of graphene filler distribution on thermal conductivity and the temperature of hotspots in HMX-based PBX composites. Through the utilization of metrics such as the coefficient of variation of the Voronoi tessellation (CV-area) to quantify spatial clustering, the research examines the correlation between hotspot temperature and the degree of aggregation. Ultimately, drawing from the simulation data collected, strategies to enhance the dispersion of carbon-based materials within the composite were proposed.
-
We initially construct diverse configurations of graphene fillers dispersed within a polymer matrix, each with a distinct spatial distribution. The detailed procedure starts by designating the geometric centre points of the graphene fillers as sampling points. Subsequently, we designated the geometric centre points of the graphene fillers as sampling points and employed a point-by-point insertion technique to generate a two-dimensional (2D) Voronoi diagram within the matrix boundary of 1 mm×1 mm, incorporating 100 graphene fillers. This method[27] facilitates the creation of a Voronoi tessellation, or Thiessen polygon, which serves to partition the entire spatial area under investigation. Consequently, this approach enables us to measure the level of aggregation of the graphene fillers throughout the matrix.
In Fig. 1, the red discrete points signify the geometric centres of the graphene fillers. These points are used to generate the corresponding Voronoi diagrams, also known as Thiessen polygons, within the defined boundary through the application of the Voronoi partitioning algorithm. The boundary of each polygon is determined by the spatial distance relationships among the geometric centre points and their neighbouring points, ensuring that any point within a polygon is closer to its central point than to any other. This spatial partitioning technique effectively captures the distribution of the graphene fillers, depicting their dispersion within the material matrix. The creation of Thiessen polygons offers a visual depiction of the filler distribution and quantitatively reflects the spatial relationships between different geometric centres. This insight is crucial for understanding how the distribution of fillers impacts heat diffusion and the management of hotspots.
Based on the relationship between the area of the Thiessen polygons and the spatial aggregation intensity of the sample points, the following indicators were constructed to characterize the degree of spatial aggregation of the sampling points[28]
Here, μ represents the average sampling area, Si represents the area of the Thiessen polygon generated by the i sampling point, N is the total number of sample points, and CV-area is the coefficient of variation of the Thiessen polygon area, which describes the level of aggregation of the sample points. When the sample points are uniformly distributed, CV-area approaches 0; when there is spatial aggregation of the sample points, CV-area > 0. The greater the spatial aggregation, the larger the CV-area value becomes. By examining the CV-area value, which serves as an aggregation descriptor, we can investigate the relationship between the degree of spatial aggregation of graphene in HMX-based PBX and the temperatures of local hotspots.
-
In this section, we utilize the finite element method (FEM) to evaluate and compare the heat dissipation performance of six models of graphene-filled HMX-based PBX, each with different levels of aggregation. The simulations were performed using the COMSOL multiphysics software, and the parameters of physical properties of graphene and PBX were obtained from relevant literatures, as summarized in Table 1. This study utilized COMSOL multiphysics software to model and analyze the simulation process. Since COMSOL software cannot directly simulate the thermal coupling between graphene and PBX, a thin-layer model with a thickness of 10 nm, mimicking an interfacial thermal resistance[29] of 6 × 10−9 m2⋅K/W was introduced at the interface. This model effectively captures the interfacial thermal transport behavior, providing a more accurate representation of the heat transfer process between graphene and PBX. To better reflect the heat dissipation characteristics of graphene in practical applications, this study employed the thermal conductivity values for supported 2D materials. To facilitate the simulations, 2D models were used in the finite-element simulations, and only the in-plane thermal conductivity of graphene was considered.
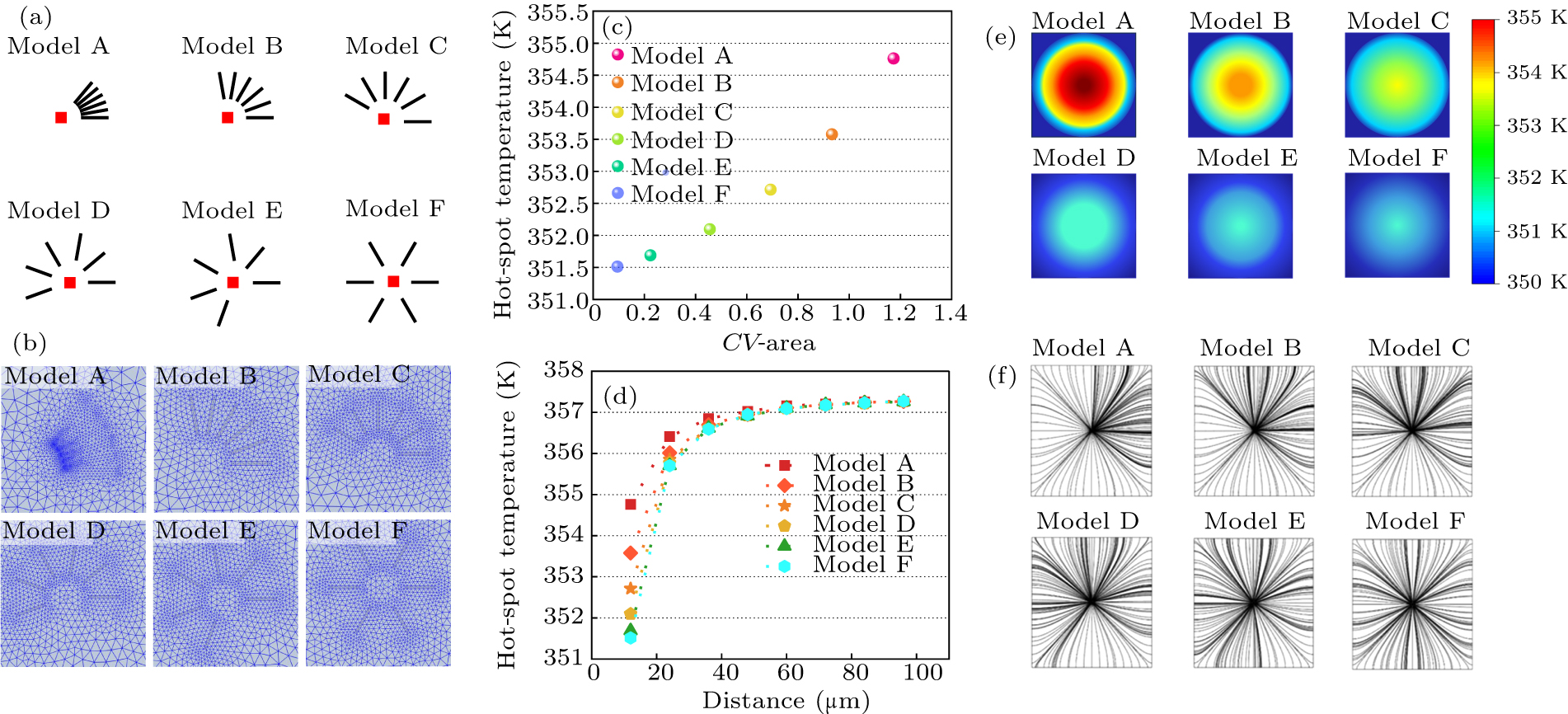
Figure 2(a) illustrates six models with different spatial configurations of graphene in the composites (model A to model F), in which the geometric center of the graphene fillers maintains a constant distance of 12 μm from the heat source. The angular separation between the fillers in the models increases in increments of 10°, starting from 10° in model A and ending at 60° in model F. The dimensions of the models are 1 mm×1 mm, encompassing a central heat source measuring 7.37 μm×7.37 μm, with the graphene fillers arranged in a concentric configuration, each with fixed dimensions of 1 μm×10 μm. The heat source is positioned at the center of the model, with a heat flux density of 200 W/m2. The thickness of the model is 0.34 nm. Triangular meshes (shown in Fig. 2(b)) were generated for the models, with typical dimensions ranging from 12 nm to 70 μm.
The thermal diffusion process is simulated through the numerical solution of the classical heat conduction equation
where T is temperature, ρ is density, C is heat capacity, κ is thermal conductivity, and q is heat generated. The four edges of the model, with a length of L = 1 mm, were subjected to temperature boundary conditions (Dirichlet boundary conditions) at 293.15 K.
Figure 2(c) illustrates the correlation between the central hotspot temperature and the degree of graphene spatial aggregation, quantified by the coefficient of variation of the Thiessen polygon area (CV-area), across the six models. It is evident that there is a consistent increase in the central hotspot temperature as the degree of graphene spatial aggregation intensifies. At a heat flux density of 200 W/m2, the temperature difference between the central hotspots in model A and model F is observed to be 3 K. Notably, the figure also indicates a substantial decrease in hotspot temperature at very low concentrations of graphene fillers within the PBX matrix. The temperature distribution depicted in Fig. 2(e) for the corresponding models suggests that heat diffusion intensifies as we progress from model A to model F, aligning with the trend observed in Fig. 2(c) where the hot-spot temperature decreases in response to the more uniform dispersion of graphene fillers.
Figure 2(d) illustrates the relationship between the hotspot temperature and the distance from the hotspot to the center of graphene fillers across various models. In each model, the temperature at the hot spot increases with distance, but the sensitivity to distance diminishes once the distance reaches 50 μm. It can be inferred that the thermal management at the hot spot is significantly influenced by the proximity to the thermally conductive fillers. Additionally, a comparison of the different models reveals that heat dissipation is more effective when the fillers are more uniformly distributed rather than being clustered.
To delve deeper into the thermal conduction mechanisms at play, we conducted analyses focusing on heat flux density across the models. Figure 2(f) visually demonstrates the increasing density of heat flux lines from model A to model F, which corresponds to a more uniform distribution of heat flux. This suggests that a more uniform dispersion of graphene fillers facilitates better phonon propagation within the matrix, leading to the establishment of efficient thermal conduction pathways. The results underscore that even at very low concentrations of graphene, the arrangement of these fillers can substantially impact heat dissipation pathways and, consequently, the thermal management performance of the device.
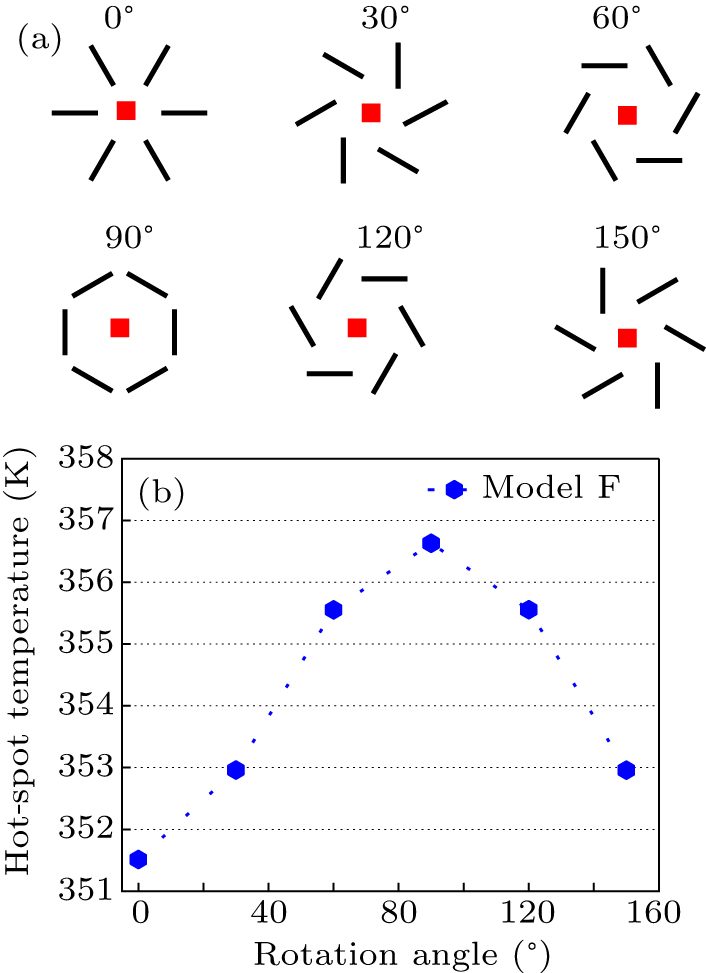
We conducted a detailed investigation into the impact of graphene filler orientation on the temperature at the hotspot. As depicted in Fig. 3(a), we developed six distinct models, each with a unique orientation of graphene fillers, by rotating the initial configuration (model F) by a defined angle. Figure 3(b) illustrates that the initial configuration (model F) exhibits the most effective heat dissipation properties in relation to the hotspot. With an increase in the rotation angle, the temperature at the hotspot also increases, culminating in a peak at 90°. Beyond this point, further increments in the rotation angle lead to a decrease in temperature, attributed to the symmetrical nature of the models.
-
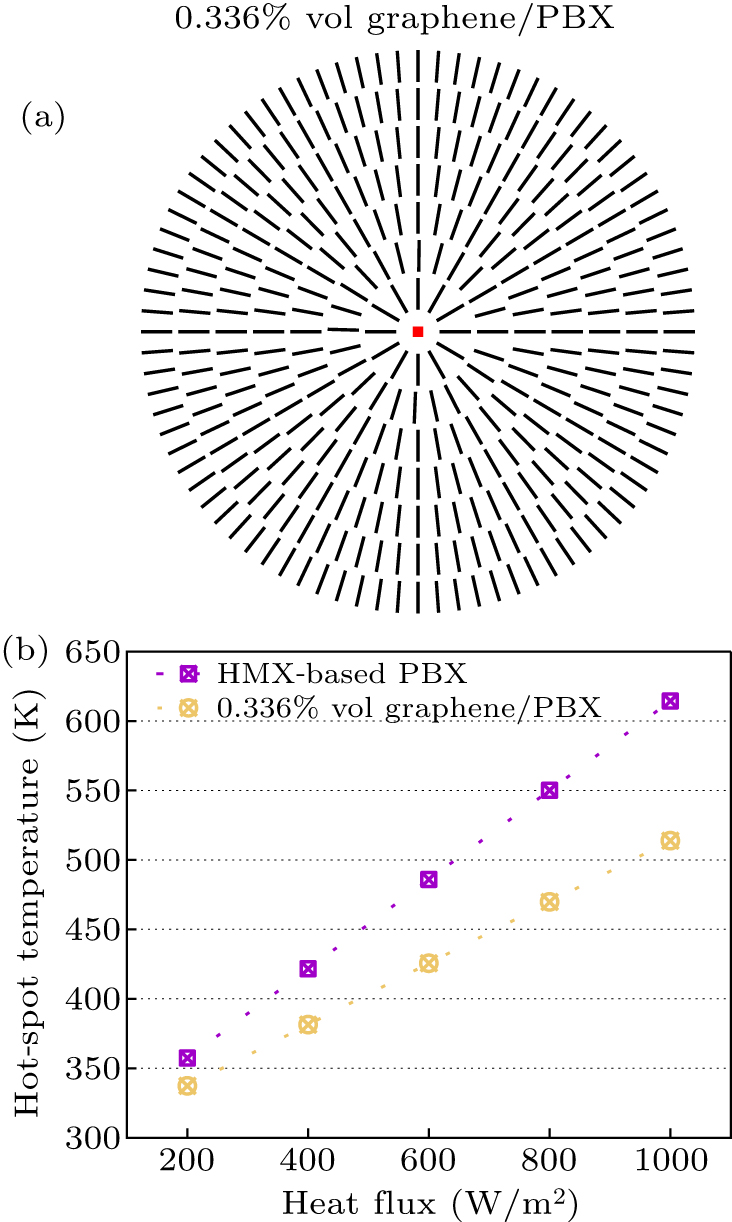
To investigate the capacity of low-concentration graphene-enhanced PBX for mitigating localized high-temperature zones, we introduce an optimized model of graphene-embedded PBX. This model incorporates considerations of the spatial distribution of graphene fillers (in terms of coefficient of variation of the area), their orientation, and proximity to the central heat source. A minimal graphene filler concentration of 0.336% was applied in our design.
As depicted in Fig. 4(a), graphene fillers measuring 1 μm×10 μm are symmetrically distributed around a central heat source, which is 7.63 μm×7.63 μm. The multi-layered arrangement is meticulously designed to ensure uniform and efficient heat transfer from the centre outwards. The innermost graphene layer is positioned 12 μm from the heat source, with the angle between fillers calculated by dividing 360° by the number of fillers. For instance, the innermost layer has 12 fillers, each separated by an angle of 30°. In each subsequent layer, the distance from the heat source increases by 12 μm, maintaining the same angular arrangement for consistent symmetry and distribution. This configuration forms a mesh-like diffusion pattern, enhancing heat dissipation across the material matrix. The graphene fillers account for a volume fraction of 0.336%, and their geometric arrangement is optimized to maximize thermal conductivity in the HMX-based PBX composite material. As shown in Fig. 4(b), the central hotspot temperature varies with the applied heat flux density, revealing a linear relationship between temperature and the applied heat flux. In the case of graphene-filled PBX, the maximum temperature reduction of 100 K occurs when the heat flux density reaches 1000 W/m2.
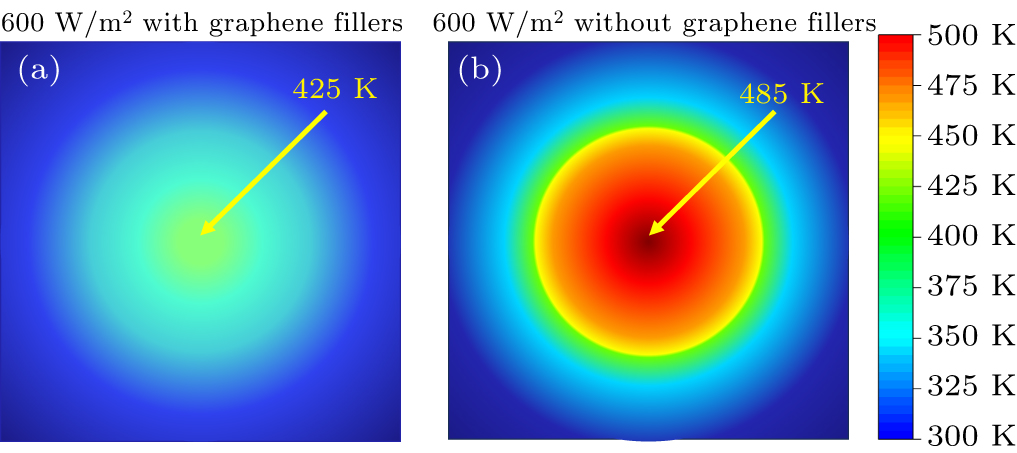
To better understand the mechanisms behind these phenomena, the temperature distribution of graphene-filled PBX was plotted and compared with systems without graphene fillers, as shown in Fig. 5. In the graphene-filled PBX model, due to the high in-plane thermal conductivity of graphene, heat can propagate along the graphene planes from the central heat source (Fig. 5(a)). In contrast, in the model without graphene-filled PBX, heat is confined around the central heat source (Fig. 5(b)). This demonstrates that the graphene heat fillers provide additional pathways for heat propagation, contributing to the reduction of hot-spot temperature. The model, through precise geometric design, enables the graphene fillers to be uniformly distributed within the PBX matrix, optimizing the overall thermal conductivity of the material. This layered and uniformly distributed configuration allows the model to minimize the accumulation of heat in any particular region, ensuring that heat is evenly distributed throughout the composite matrix. This design strategy offers a method to maximize thermal transport optimization while maintaining the material’s thermal properties and a low filler ratio.
3.1. Impact of graphene filler aggregation on heat dissipation
3.2. Optimized graphene-filled PBX model for efficient thermal management
-
This study employed finite element simulation to quantitatively assess how the spatial distribution of graphene impacts the localized hotspots in HMX-based PBX explosives. The findings reveal that the strategic orientation, aggregation, and positioning of graphene relative to the heat source can markedly lower the hot-spot temperature. Specifically, under a heat flux of 600 W/m2, a graphene-enhanced PBX model with a 0.336% volume fraction of graphene can reduce the local hotspot temperature by about 60 K. This demonstrates not only the efficacy of graphene fillers at minimal concentrations but also underscores the importance of precise geometric arrangement in enhancing the thermal management capabilities of HMX-based PBX materials.
These insights provide a theoretical foundation for refining the thermal management design of HMX-based PBX explosives and are anticipated to spur further research on integrating graphene into high-energy explosives. Future research can be further expanded in the following aspects: Experimental validation by fabricating graphene-filled composite materials in actual PBX systems and utilizing experimental techniques, such as laser flash analysis or infrared thermography, to measure local hotspot temperatures and verify the accuracy of the simulation results. Additionally, the expansion of filler types can be explored by investigating the effects of other high-thermal-conductivity fillers, such as carbon nanotubes, boron nitride, on the thermal management performance of PBX, as well as evaluating the synergistic effects of different fillers.

 首页
首页 登录
登录 注册
注册



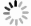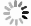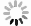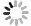
 DownLoad:
DownLoad: