Experimental study on the regulation of radiative heat flux by coating SiC film

The increasing demand for sustainable energy motivates many researchers to investigate the various energy harvesting methods. When the gap distance between two objects is smaller than the characteristic wavelength of thermal radiation, Wien’s displacement law^[1] applies. As a result, the evanescent waves start to dominate, making the radiative energy transfer exceed the black-body limit.^[2–4] Near-field thermal radiation has attracted intensive attention with the development nanotechnology and micro-processing technology due to its great energy transport rate.^[5,6] This phenomenon has been demonstrated both theoretically and experimentally. It shows that photon tunneling can travel through micro/nanoscale distance.^[7–14] This has recently aroused significant interest in some applications,^[15,16] such as thermophotovoltaic (TPV) energy conversion,^[17–20] near-field imaging,^[21] near-field thermal switch^[22,23] and nano-lithography.^[24]

Based on the fluctuation electrodynamics theory proposed by Rytov et al. and Polder and van Hove, most of the theoretical studies focus on the near-field radiative flux.^[25,26] In addition, experimental research on near-field thermal radiation has so far been focused on different geometric objects. The experimental shapes of tip–plane and sphere–plane have been reported, which have advantages and drawbacks.^[27–31] As mentioned above, the geometries easily precisely control the gap distance, but it is difficult to analyze the complicated data. There are also various studies on plane–plane experiments with near-field radiative heat flux. Great progress has been achieved in the plane–plane experiments, but the most difficult issue is how to control the gap distance and sample flatness. In Ref. [32], the measurement of near-field thermal radiation between two glass samples was carried out, and 1 μm polystyrene particles of a certain scale were used as supporting pillars to keep a micron-size gap distance. The near-field radiative heat flux of doped-Si parallel plates is reported by Zhang et al., and the array of SiO₂ posts which was fabricated on the sample through ultraviolet photolithography is used to maintain the desired gap distance.^[11] The dynamic measurement of near-field radiative flux between the glasses is presented in Ref. [13], and the gap distance is separated by micro/nano particle spacers. The precise measurement of the near-field thermal radiation between macroscale single-crystalline quartz plates is proposed by Park et al., and a nanopositioning platform was used to control the gap distance down to 200 nm.^[12]

Although the near-field thermal radiation has been confirmed by many researchers, thermal radiation regulation after coating has not been investigated by experiments. In this paper, we present the measurement of SiC thin film and optical glass heat radiative flux. As demonstrated in this study, the radiative flux decreases with increasing thickness of the SiC film on the hot side. The optimal thickness of the SiC film is about 1 μm. We use small polystyrene particles to maintain the gap distance, which is the same as mentioned in Refs. [8,13]. To the best of our knowledge, the experimental measurement of validation of coating-regulated radiative heat flux is reported for the first time.

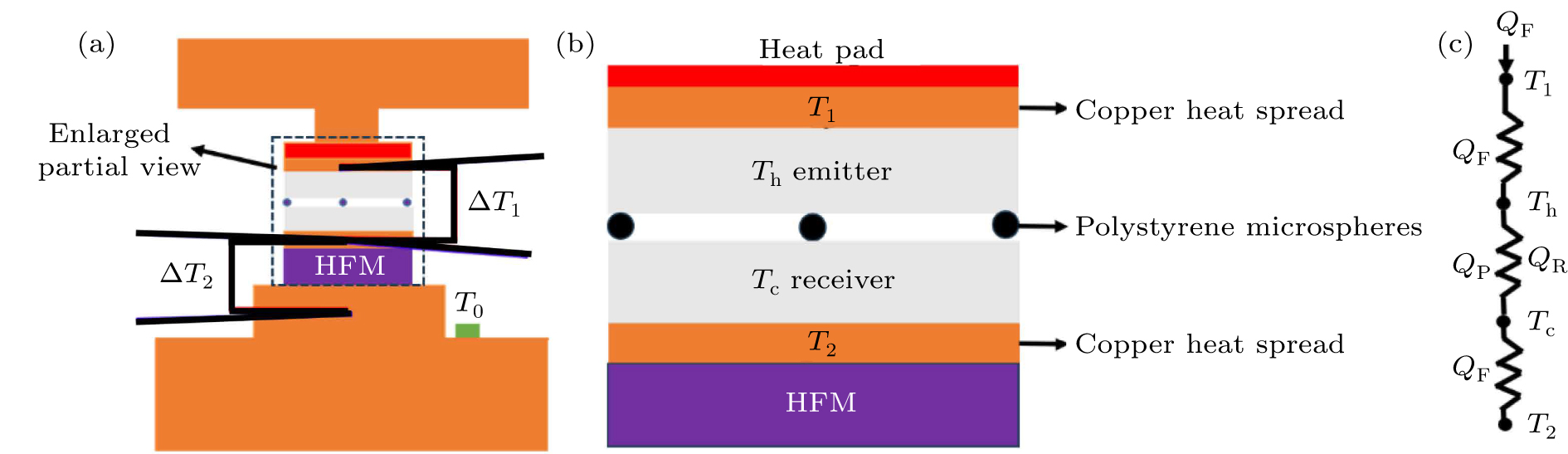
A schematic diagram of the experimental setup is shown in Fig. 1(a). A copper weight of 67.8 g is pressed onto the stack of layers of a copper base station, and almost one-dimension heat transfer can be assumed. A resistance heater (in red color online) with a size of 1 cm × 1 cm is laid on the top stack of layers, and there is a 2 mm thick, 1 cm × 1 cm copper plate (in orange) on the bottom of the heater. The sample (in transparent color) is sandwiched between two copper plates to homogenize the temperature over the sample surface. To ensure good thermal contact, we use thermal grease between the copper and the sample to reduce the thermal contact resistance. A heat flux meter (HFM) is laid on the very bottom stack of layers, and it is positioned between the copper plate and the copper base. The heat-flow contact area of the heat flux meter is square, with a side length of 10 mm. In order to allow a thermocouple to measure the temperature, we drilled a tiny halfway-drilled hole in the side of two pieces of copper. After that, the thermocouple is inserted into the hole to measure the temperature of the sample on the hot side and cold side, T₁ and T₂, respectively. When DC power is applied to the heater, a temperature difference (ΔT₁ = T₁ − T₂) is generated between two identical copper plates. To obtain the absolute temperature of copper base T₀, a thermistor is mounted on the heat sink, which is a copper plate. The thermocouple wires measure the temperature difference, ΔT₂ = T₂ − T₀. When we measure the temperature of heat sink T₀, the hot side and cold side temperature, T₁ and T₂, can respectively be determined. From the temperature T₁ and T₂, the temperature of the hot and cold surfaces can be derived by solving the one-dimensional conduction problem. The emitter temperature of the hot surface is given by T_h = T₁ − qd_glass/λ_glass, where q is measured by heat meter flux, and λ_glass and d_glass are the thermal conductivity and thickness of the optical glass, respectively. Similarly, the receiver temperature of the cold surface is given by T_l = T₂ + qd_glass/λ_glass. It is worth noting that the thermal resistance of copper plates is negligible. In addition, the temperature differences ΔT₁ and ΔT₂ have an uncertainty of 1 K. The near-field radiative flux can be quantified by

where Q_F is the measured energy and Q_P is the heat conduction energy of polystyrene, λ_glass = 0.18 W·m⁻¹·K⁻¹.^[33] Here, the polystyrene particles are assumed to be cylindrical in order to calculate the thermal conduction.

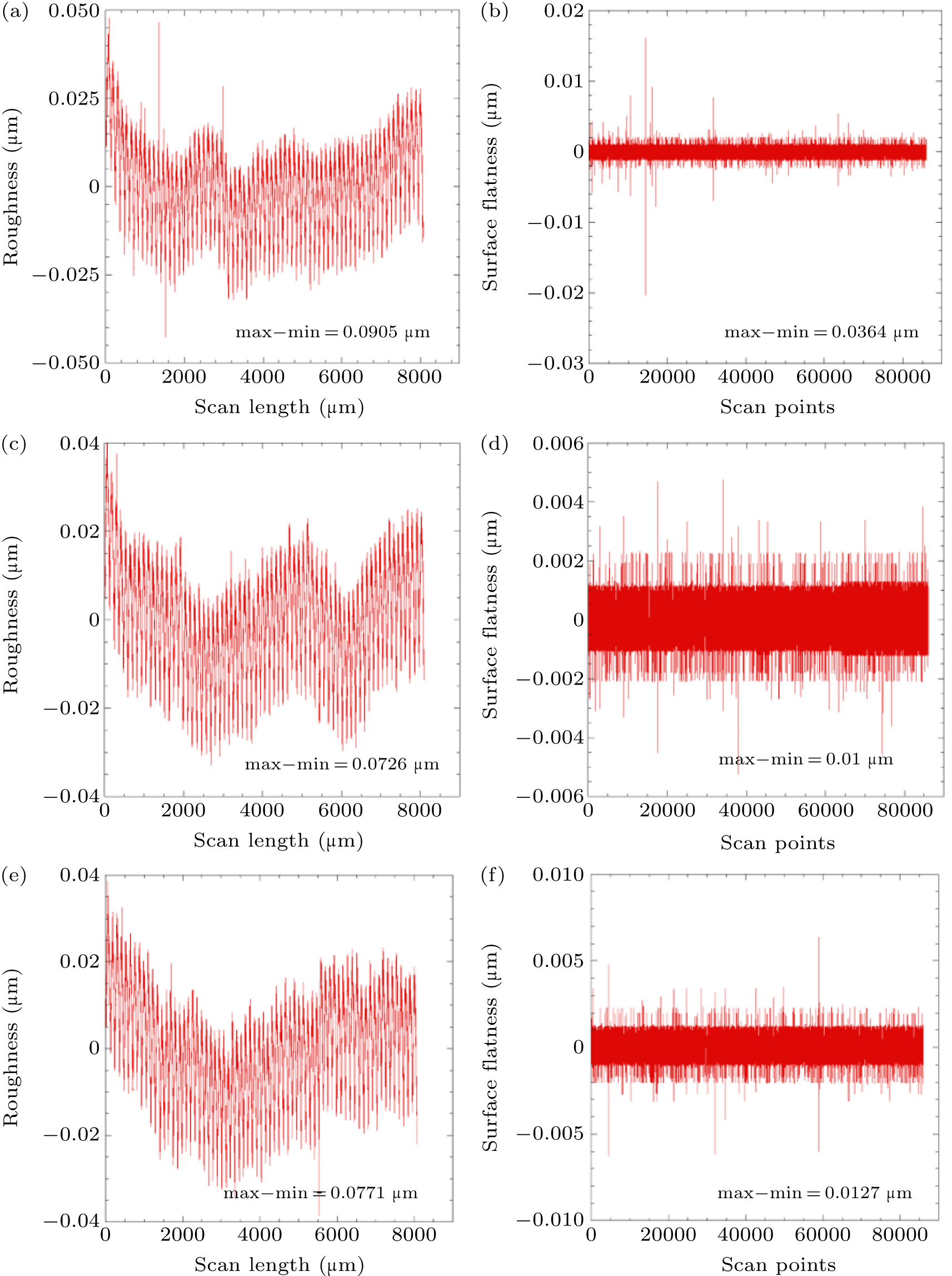
The two identical precision optical glasses (Edmund product) are used as the sample with 10 mm diameter and 3 mm thickness. The optical flats are provided by the manufacturers as follows: the glasses with λ/10 (λ = 633 nm) peak-to-valley for smaller gaps, and the parallelism is 5 arcseconds. For the surface flatness of the glass measurements, we used an optical microscope to verify the accuracy of the number. The flatness of optical glass, as shown in Fig. 2, and the three directions on its surface were scanned on a piece of glass. Figure 2 shows that the optical glasses fully meet the measurement requirements.

To verify the accuracy of the experimental setup, the near-field thermal radiation between the two samples was measured. First, we measured the glass-glass near-field thermal radiation. Second, 50 nm and 100 nm SiC films were coated on the hot side of the optical glass by a coating machine. We then measured the near-field thermal radiation flux between the optical glass coated with a 50 nm SiC film and the flat glass. The gap distance was created by the following procedure. First, the optical glasses are ultrasonically cleaned with acetone, after ultrasonication in ethanol, and then deionized water. Second, the glasses are blown dry with nitrogen or left to dry naturally in a clean room. An aqueous suspension is then prepared by diluting the polystyrene particles in deionized water. To ensure the consistency of the size of polystyrene spheres, we had the supplier provide high-quality products. Meanwhile, we also selected a small number of samples and observed them under an electron microscope. As shown in Figs. 3(b) and 3(c), the particle sizes have very little difference, being approximately 1 μm. Using a small pipette, three small droplets are placed on the cold side. After the water is evaporated, only the polystyrene particles remain over the surface of the cold side. Finally, the emitter is carefully placed on top of the receiver. Note that we conducted the operations in a clean room to eliminate dust particles. In addition, the total number of polystyrene particles, which is an estimated value, is placed at multiple positions between the receiver and emitter. As shown in Fig. 3(a), the black dots are the particles. In order to obtain a uniform distribution of the polystyrene particles, there are three small droplets on the receiver.

Since any experiment has uncertainty, it is necessary to quantify the errors and uncertainties. In this paper, the uncertainty of the device measurements and the errors of each device are discussed. As shown in formula (1), the uncertainty of the measured radiative flux depends on the total heat flux and the estimated heat conduction energy of polystyrene. The error transfer formula was used to evaluate the effect of uncertainty on heat transfer. Here, the uncertainty of the heat flow meter is about 5%, and the uncertainty of the thermocouple is 1 K. In addition, the uncertainty of the number of polystyrene particles is 300, and the uncertainty of the thermistor is ignored. The measured radiative flux is obtained by excluding the heat conduction of polystyrene from the total heat flux. It can be expressed by

where λ_ps is the thermal conductivity of polystyrene, d is the diameter of the polystyrene particles, N is the estimated number of polystyrene particles spread on the optical glass sample and A is the area of the optical glass. According to formula (2), the value of independent measurement is Q_F, N, and ΔT₁.

Because the uncertainty value of the near-field heat radiation is roughly calculated and analyzed according to the error transfer formula, it is assumed that a measured value is obtained through the indirect measurement y = f(x₁,x₂,…,x_n), where x₁,x₂,…,x_n are the measured values that are independent of each other, and h is the spreading factor. The approximate calculation of the error transfer formula can be expressed as

Therefore, the uncertainty value of the measured near-field thermal radiation can be expressed as

It is worth noting that we have only roughly calculated the uncertainty value of the near-field thermal radiation measurement. The errors caused by the inconsistency of particle size, the thermal conductivity of polystyrene particles, glass size, glass thermal conductivity and the influence of the parallelism between samples were not considered, etc. The polystyrene particle was calculated as a 1 μm cylinder. It is worth noting that when polystyrene particles are calculated as cylinders, the cross-sectional area for heat conduction is assumed to be πd²/4. However, in reality, the heat-conduction cross-sectional area is much smaller than πd²/4 because the contact between the sphere and the surface is point contact.^[32] The size of the glass and each thermal conductivity were calculated according to the determined value, and the impact of contact resistance and heat loss through the side was not considered.

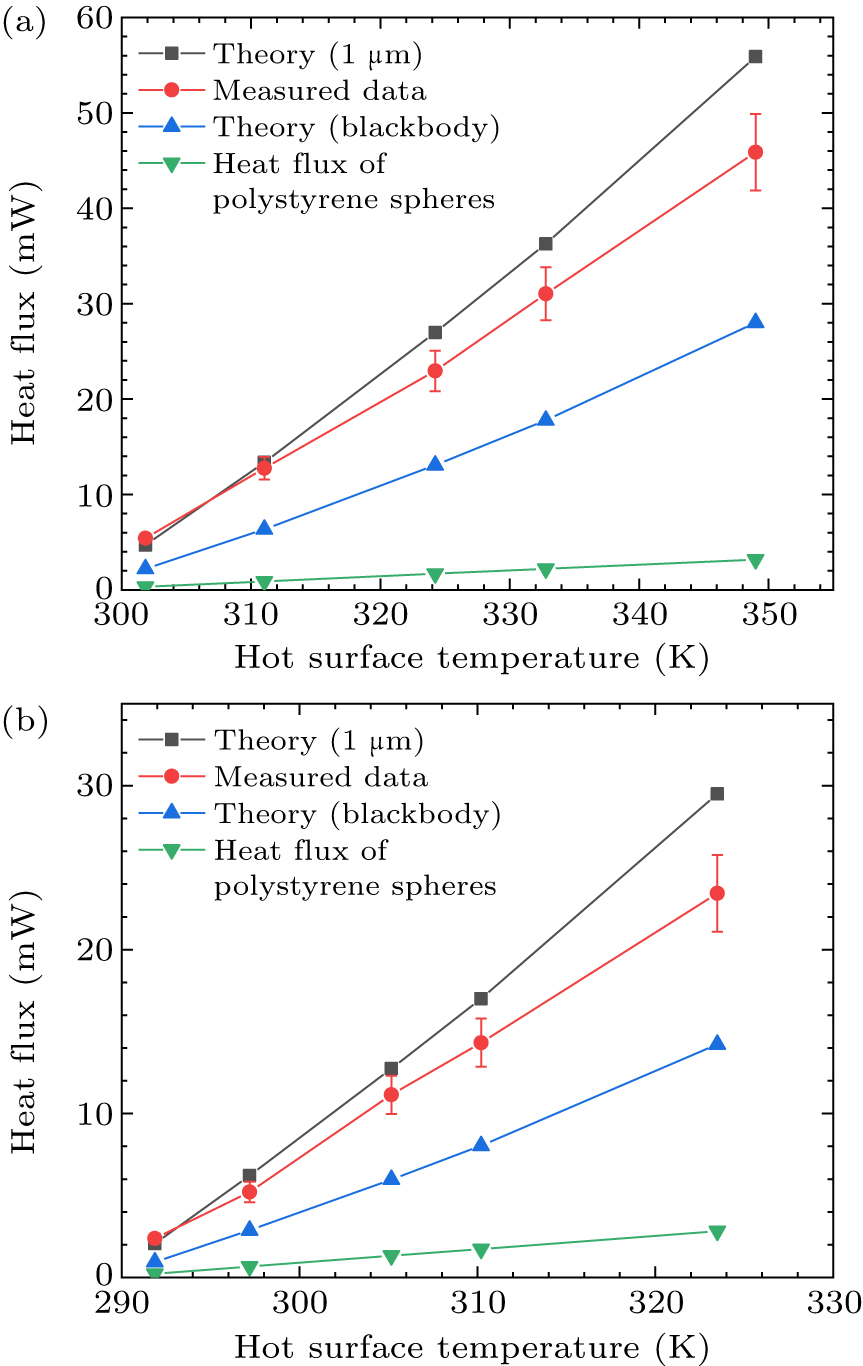
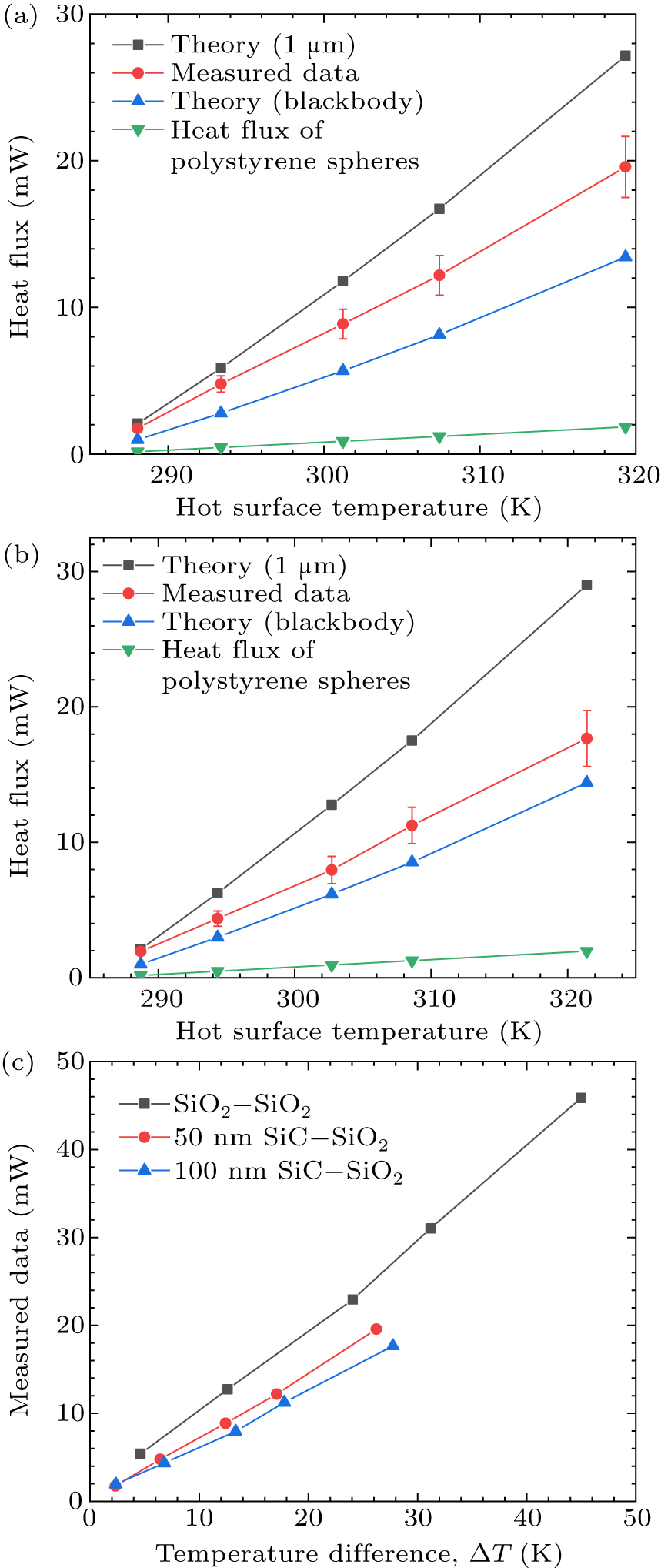
To measure the near-field radiative heat transfer, the thermal radiation should be a dominant transfer mode in this experiment. The whole device is installed in a vacuum chamber below 3 × 10⁻⁴ Pa, which eliminates the effect of air conduction across the sample. The measured thermal radiation between optical glasses is presented in Fig. 4. Figure 4 illustrates the variation of the heat flux with the temperature of the hot side for four different values. The line marked with red solid-circle symbols represents the measured values, and the error bars show their uncertainties. The black line with quadrangle symbols represents the theoretical calculated value for a 1 μm gap. The blue line marked with solid oblique triangles represents the black-body heat flux, and the green line marked with solid downward-pointing triangles represents the heat flux of polystyrene spheres. As shown in Fig. 4, the near-field heat flux exceeds the black-body limit. These data have been adjusted by taking into account a heat-spreading factor of 4/π between the circular optical flat and the square flux meter.^[32] Although it clearly demonstrates the near-field thermal radiation phenomenon, and the measured value is far greater than the black-body radiation heat flux, the measured data do not fully coincide with the theoretical values. This is caused by factors such as the inconsistency of particle size and the presence of dust particles. Here, calculations were done using the theoretical value of 1 μm. However, under actual conditions, the presence of dust particles larger than 1 μm in the environment leads to incomplete agreement between the measurement results and the experimental results. Nevertheless, these data can fully reflect the existence of the near-field thermal radiation phenomenon and that it is far higher than the black-body radiation heat flux.

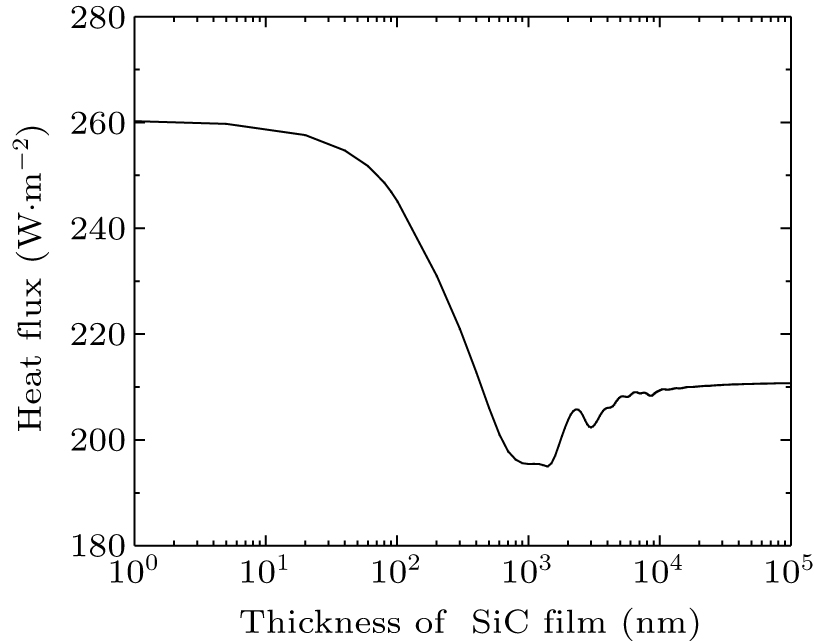
Assuming the emitter side and receiver side temperatures are 310 K and 290 K, respectively, and the gap distance is 1 μm, we coat the SiC film on the hot side as the emitter and the optical glass as the receiver. As shown in Fig. 5, the radiative fluxes at different thicknesses of SiC film, which range from 10 nm to 100 μm, are used to illustrate the regulation of the heat flux by coating the SiC film. There exists an optimal-thickness film of about 1 μm. In this case, for a fixed gap, the radiative flux reaches the minimum value.

To examine the heat-flux control effect, the upper optical glass is coated with 50 nm and 100 nm silicon carbide (SiC) films as heat emitters, and the lower optical glass is used as a receiver. By measuring the near-field thermal radiation data between the SiC films and the optical glass, it is found that near-field thermal radiation can also be observed. Figure 6 shows the near-field thermal radiation data between the SiC films and the glass. It can be seen from the figure that when the glass is coated with SiC films, the near-field thermal radiation effect exceeds the black-body radiation limit, and as the thickness of the SiC films increases, the heat flux decreases. However, when a 1 μm SiC film is coated, the surface flatness cannot be guaranteed. Since the coating thickness and the gap are of the same order of magnitude at this time, a more precise nanometer-scale moving platform is required to adjust the gap. This experiment verifies the influence of the gap between glasses and the 50 nm and 100 nm coatings on the heat flux. It can also be seen from the figure that when the SiC films are coated, the radiative heat flux decreases, which also verifies the previous theory.

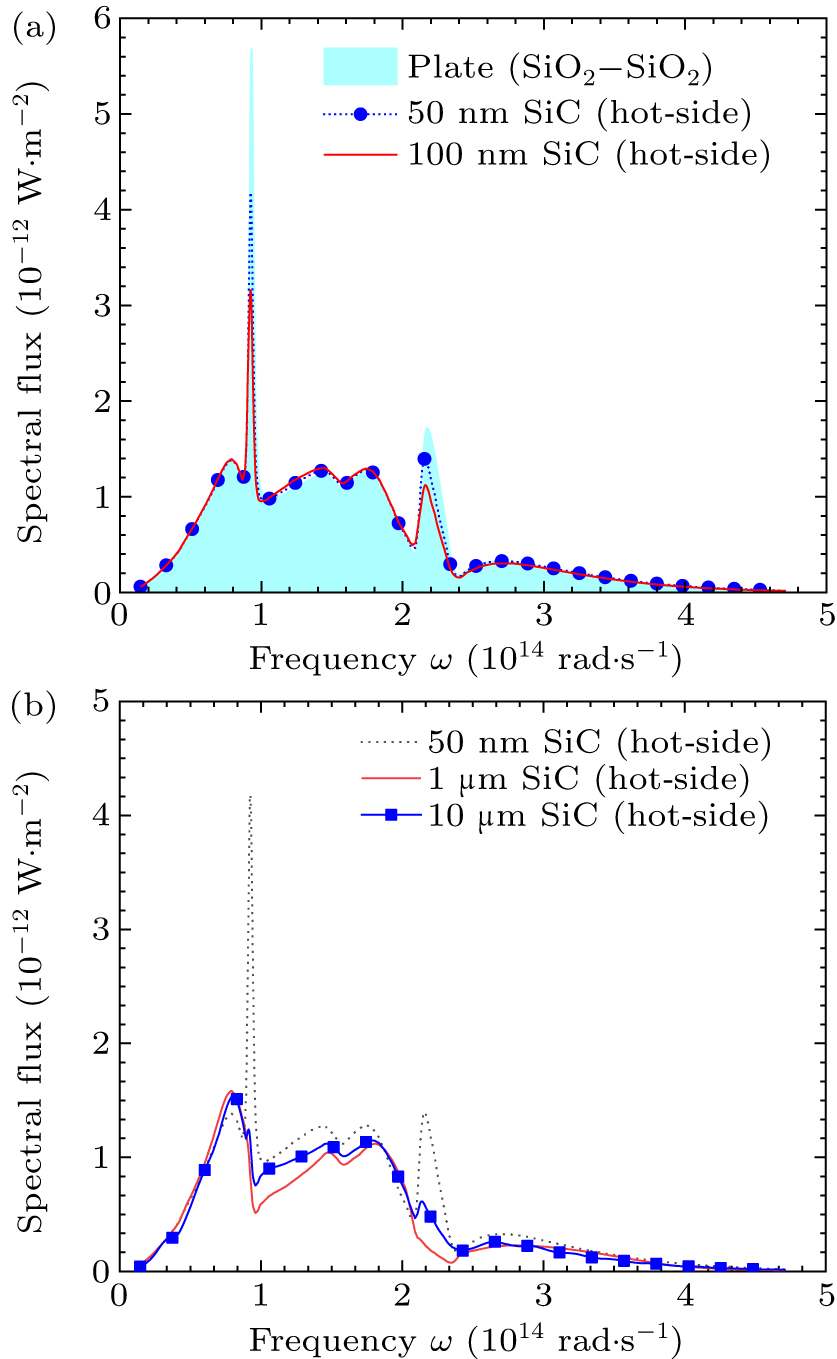
To analyze the variation characteristics of the spectrum after coating SiC film on the glass, figure 7(a) presents the calculated spectral radiative heat fluxes between the two surfaces of the glass and two SiC films with different thicknesses. As mentioned previously, the gap distance is 1 μm, and the temperatures of the emitter side and the receiver side are 310 K and 290 K, respectively. It can be observed from Fig. 7 that when the SiC film is thin, the peak position of the spectral heat flux is approximately at a frequency of 1 × 10¹⁴ rad/s. As the thickness of the SiC film increases, the spectral heat flux at the peak position decreases. In addition, figure 7(b) shows the spectral radiative heat fluxes of three SiC films with different thicknesses. When the film thickness increases from 50 nm to 1 μm, the heat flux decreases with the increase in the SiC film thickness. However, if the film thickness is further increased, the heat flux will increase.

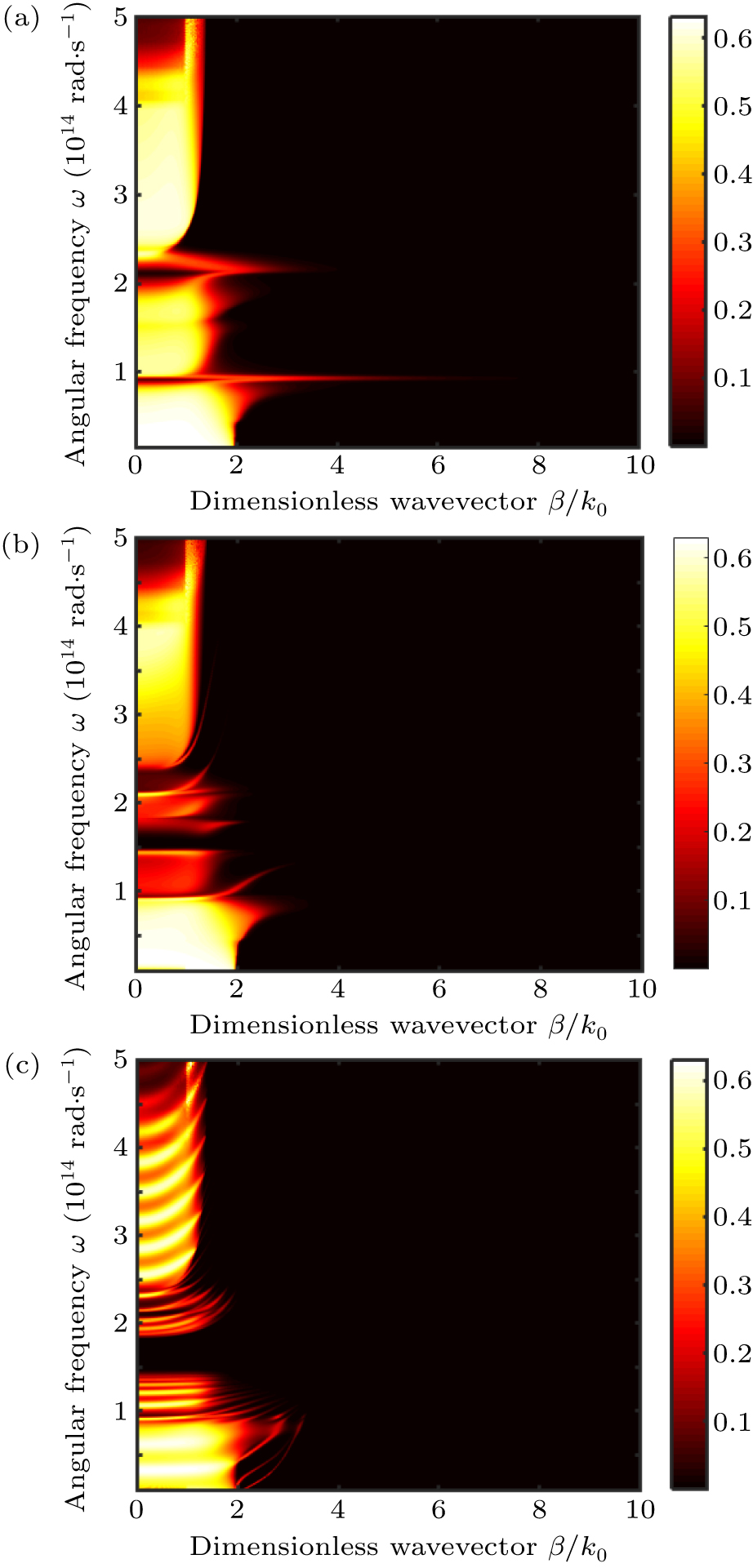
In order to understand this peak, it is necessary to explore the transmission coefficient versus angular frequency and dimensionless wavevector. This is shown in Fig. 8 where the dimensionless wavevector decreases with the increase in the thickness of the SiC film on the hot side. When the dimensionless wavevector declines, the evanescent wave propagating decreases. Because the evanescent wave received by the cold side is reduced, the radiative heat flux is decreased. This is exactly the same as the experimental data.

In summary, first, the experimental results demonstrated the near-field thermal radiation phenomenon between the flat glasses. Second, we conducted an experiment in which different thicknesses of SiC films were coated on one side of the hot optical glass. It was demonstrated that the increase in the thickness of the SiC film reduced the radiative heat flux, thus achieving the effect of regulating the radiative heat flux. Compared with the experiment of near-field radiation data, the theoretical results were in high agreement with the experimental data. Through theoretical analysis, it was found that there exists an optimal film thickness.