-
随着石油、煤炭等传统能源的枯竭,以太阳能、地热能、风能、海洋能、生物质能和核聚变能等为主的新能源研究迫在眉睫,“能量”的利用效率作为新能源的衡量指标,已成为最热门、最受关注的研究内容之一[1-3]。结合能作为能量最基本的单位,是单个原子结合成相应材料时所放出的能量,放出的能量越多,则材料的结构越稳定,反之,越不稳定。另外,原子能够结合为晶体的根本原因在于,原子结合后整个系统具有更低的能量。因此,以性质最稳定的稠密惰性元素原子(晶体)作为研究对象,对结合能进行深入研究是一项艰巨而重要的任务。结合能作为稠密惰性元素(Rare-Gas Solid,RGS)原子的一个重要物性,可推导出稠密惰性元素原子的许多特性,如热力学参数、弹性系数、熔化曲线、弹性常数和高压压缩特性等[4-8]。另外,通过对原子结合能的理论研究也可以得到物理学、化学、能源学和晶体材料学的许多物质特性,如密度泛函理论[9]、从头算自洽场[10]、单双(三)重激发耦合簇理论CCSD(T)[11-12]、半经验及经验势函数[13-18]等。因此,能否得到简便、准确的结合能对研究其他物性至关重要。近年来,对结合能的研究已趋于白热化,大量文献报道了有关结合能的研究进展及成果[4-11],如通过结合能的能量曲线反转得到原子对势的相互作用、三体相互作用、弹性常数、熔化曲线以及各种体系的密度相关势能等。截至目前,在众多结合能的研究中,有两种典型的结合能公式被广泛应用:一种是基于从头算法的多体势能的简单叠加[10-12],此方法在求晶格原子结合能时只有当多体展开式满足收敛性并达到一定的截断精度时,所得的结合能才是准确、可靠的,因此仅适用于较低压强的稠密惰性元素;另一种是通过能带理论和密度泛函理论得到[19],虽然可应用于更高密度范围,但是准确度不高,而且所得的结合能考虑到温度的影响,情况更加复杂[20]。通过研究发现,宇宙当中,金星、木星和土星等恒星的内部成分中包含大量的惰性元素,其内部压强高达数百吉帕,甚至上千吉帕,因此研究结合能对稠密惰性元素高压压缩特性的影响具有潜在的应用价值。
基于此,运用原子簇理论和量子力学理论,结合两体势的从头算方法和薛定谔方程,本研究提出一种计算RGS(RGS=He,Ne,Ar,Kr)原子结合能的新势函数,并运用新表达式研究结合能对高压稠密惰性元素状态方程的影响。其中新表达式只用到两体相互作用势U2和总原子相互作用势Vn,避免了对各多体项的分别计算,大大减少了计算量,并且由于U2和Vn的收敛最快,所需考虑的近邻原子数较少,因此计算的繁琐程度减轻,计算时间缩短。这些优点将便于我们处理复杂情况下(包括高温、高压、等离子体状态等)的多体相互作用并进行分子动力学模拟。本工作旨在用最简单的势函数解决较复杂的问题,在此过程中两体和总原子势能都得到了合理的强调,同时它也是准确理解压缩特性、光谱散射和体积数据的关键。希望新方案能适用于所有电中性或离子气体系统、固体和液体等。
全文HTML
-
基于原子团簇理论,对任意一个由n个原子组成的惰性元素原子团簇(RGS)n (RGS=He,Ne,Ar,Kr),该团簇的总相互作用势能Vn为
式中:E0为稠密惰性元素孤立原子的基态能量,En(r1,r2,···,rn)代表团簇中n个原子处于r1,r2,···,rn位置时团簇体系的基态总能量,可通过求解团簇体系的薛定谔方程得到,即
式中:
$\hat H$ 表示n个惰性元素原子所构成团簇的哈密顿算符,可表示为式中:MI、ZI分别为第I个惰性元素原子核的质量和核电荷数,ZJ为第J个原子核的核电荷数,rIJ为第I个原子核与第J个原子核之间的距离,rij为第i个电子与第j个电子之间的距离。利用Louwdin法求解团簇的总波函数
$\psi \left( r \right)$ 。若第I个原子基态单电子轨道波函数为${\varphi _1}\left( r \right)$ ,则团簇的总波函数$\psi \left( r \right)$ 为N个惰性元素原子中2N个单电子自旋轨道波函数所构成的反对称Slater行列式(4)式中选取的双Slater基态单电子解析波函数为
-
基于多体展开方法和第一性原理的从头算法[6-7, 11-12, 21],也可得到 (RGS)n中任意一个中心原子M的多体相互势能Un和总相互作用势能Vn,即
式中:Uk(M)代表k体项的总和,高阶项很小,在这里予以忽略。u2、u3、u4分别表示团簇中任意两个原子、3个原子和4个原子间的两体势、三体势和四体势,表达式如下
本研究中,所有多体势u2(i, M)、u3(i, j, M)、u4(i, j, k, M)等的计算是基于第一性原理,运用GAMESS计算程序下的从头算方法得到。本研究只用到收敛最快、计算最省时、计算精度最高的两体相互作用势能U2(M),即
-
温度为T时,稠密惰性元素原子的压强P的表达式为[22]
式中:Pn代表由多体相互作用引起的压强;Pzp表示由零点振动引起的压强;Pth表示由温度引起的压强,通过Debye-Mie-Grüneisen模型获得[23];
$\gamma $ 为Grüneisen参数;$\varTheta $ 为德拜温度[16],不同体积下的德拜温度$\varTheta $ 可根据线性公式[24]和Grüneisen参数$\gamma $ 得到[22];Ezp为晶格的零点振动能,通过德拜近似模型得到。
1.1. 总相互作用势能
1.2. 两体相互作用势能
1.3. 压 强
-
一般而言,只有当多体项Uk(M)在一定的截断精度下收敛时,多体展开方法才能准确地得到结合能E(M)。然而,随着近邻原子的增加,结合能E(M)的展开和计算变得越来越复杂和繁琐。为了解决该问题,本研究根据几何关系,建立了一个计算结合能的新势函数。
稠密惰性元素原子的结合能E(M)可表示为[6]
根据(12)式,利用多项式函数的特性,构造一个多项式函数f(x),将总原子相互作用势能Vn(M)与结合能E(M)联系起来,即
式中:f(x)是变量x 的多项式函数,各项系数Uk(M)(k=2,3,4,5,···)为各多项式的值。
通过比较(6)式、(12)式和(13)式,有
因此,任意一个中心原子M对团簇体系结合能的贡献E(M)对应着f(x)在[0,1]区间的积分,即
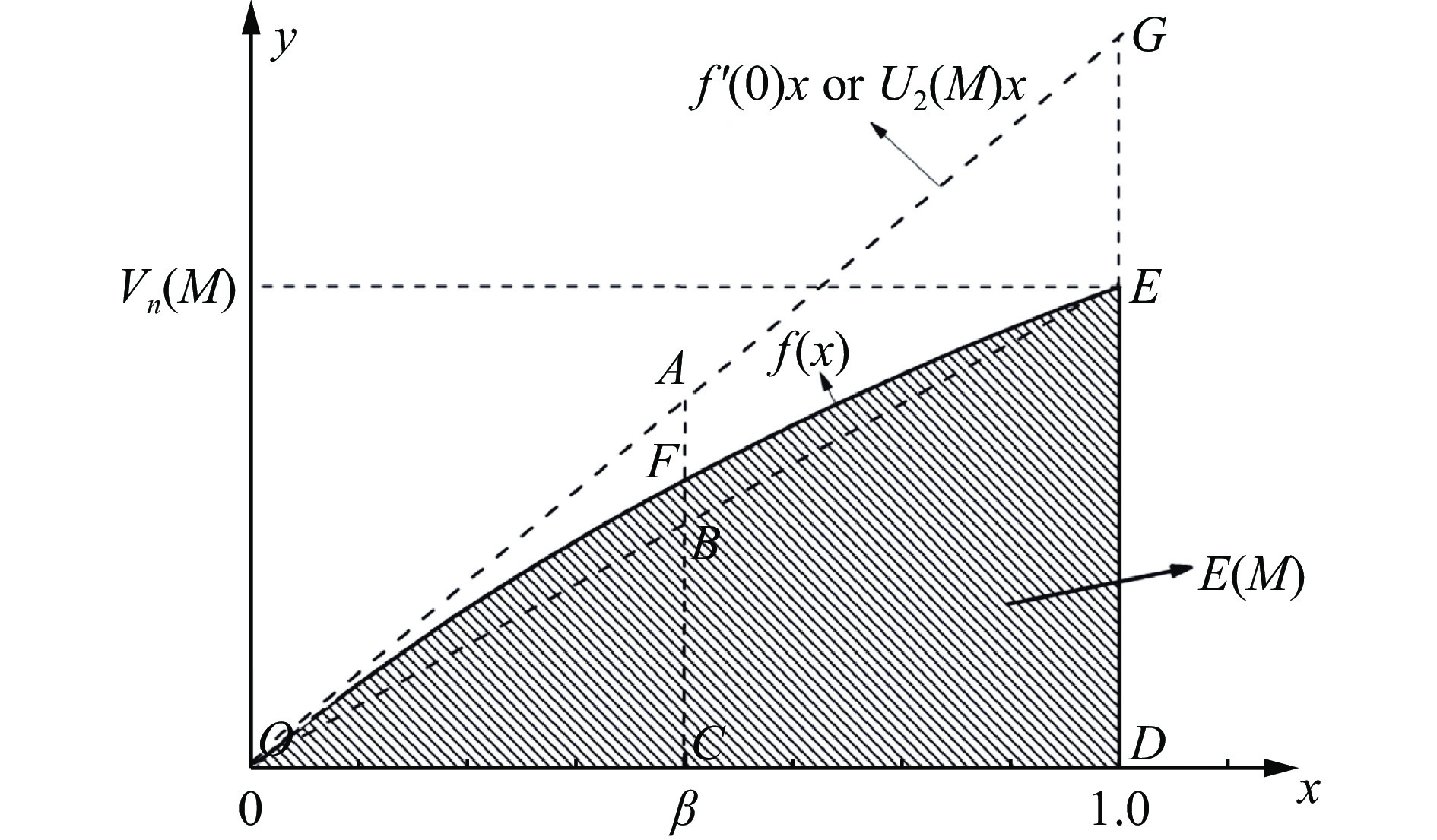
联立(12)式~(16)式,利用几何关系和定积分的物理意义,通过数据分析软件Origin 8.0得到U2(M)、Vn(M)和E(M)三者之间的关系,如图1所示。
在图1中,过点C做直线OD的垂线交OG于A点,使
${\text{△}}OAF$ 和${\text{△}}EBF$ 的面积相等,即${S_{{\text{△}}OAF}} = {S_{{\text{△}}EBF}}$ ,则阴影面积SOFED可转化为${\text{△}}AOC$ 和梯形BCDE的面积之和,即结合(17)式,通过几何关系,得到一个计算积分(16)式的近似公式。该近似公式通过点O和点C的距离参数
$\beta $ 来表示,即结合能E(M)的表达式为(18)式即为稠密惰性元素原子结合能的新势函数。由图1可以看出,当总原子势能Vn(M)已知时,结合能E(M)的值可以得到。
-
稠密惰性元素原子结合能的新势函数为
(19)式是关于参数
$\beta $ 的新势函数,来自两部分贡献:第1部分是由从头算方法计算得到的两体势${\beta ^2}{U_2}\left( M \right)$ ,对应着图1中的${\text{△}}OGD$ 的面积;第2部分是通过求解薛定谔方程得到的总多体势$\left( {1 - {\beta ^2}} \right){V_n}\left( M \right)$ ,对应着图1中的${\text{△}}OED$ 的面积。由图1和(19)式可以得到:若
$\beta $ =1,则(19)式变为传统的两体相互势能的一半,此时图1中OE与OG重合,这显然高于E(M)的实际值;若$\beta $ =0,则(19)式变为平均总相互作用势能,此时对应图1中的E点,其值低于E(M)的实际值。在精确度要求较低的情况下,这两种方法可以粗略地计算原子的结合能。本研究通过第一性原理的从头算法计算发现,结合能E(M)的准确值介于以上两种情况之间,对应的$\beta $ 介于0和1之间,与图1中的阴影区域有关。由于U2(M)和Vn(M)的收敛速度非常快,近邻原子的数量也不大,所以相比传统方法的计算时间很短,以便在任何温度下研究多体相互作用和分子动力学模拟。 -
由于总相互作用势能Vn(M)是一个交错级数,因此通过比较(12)式、(16)式和(18)式发现,如果只考虑两体势,忽略三体及以上多体势,结合能E(M)是参数
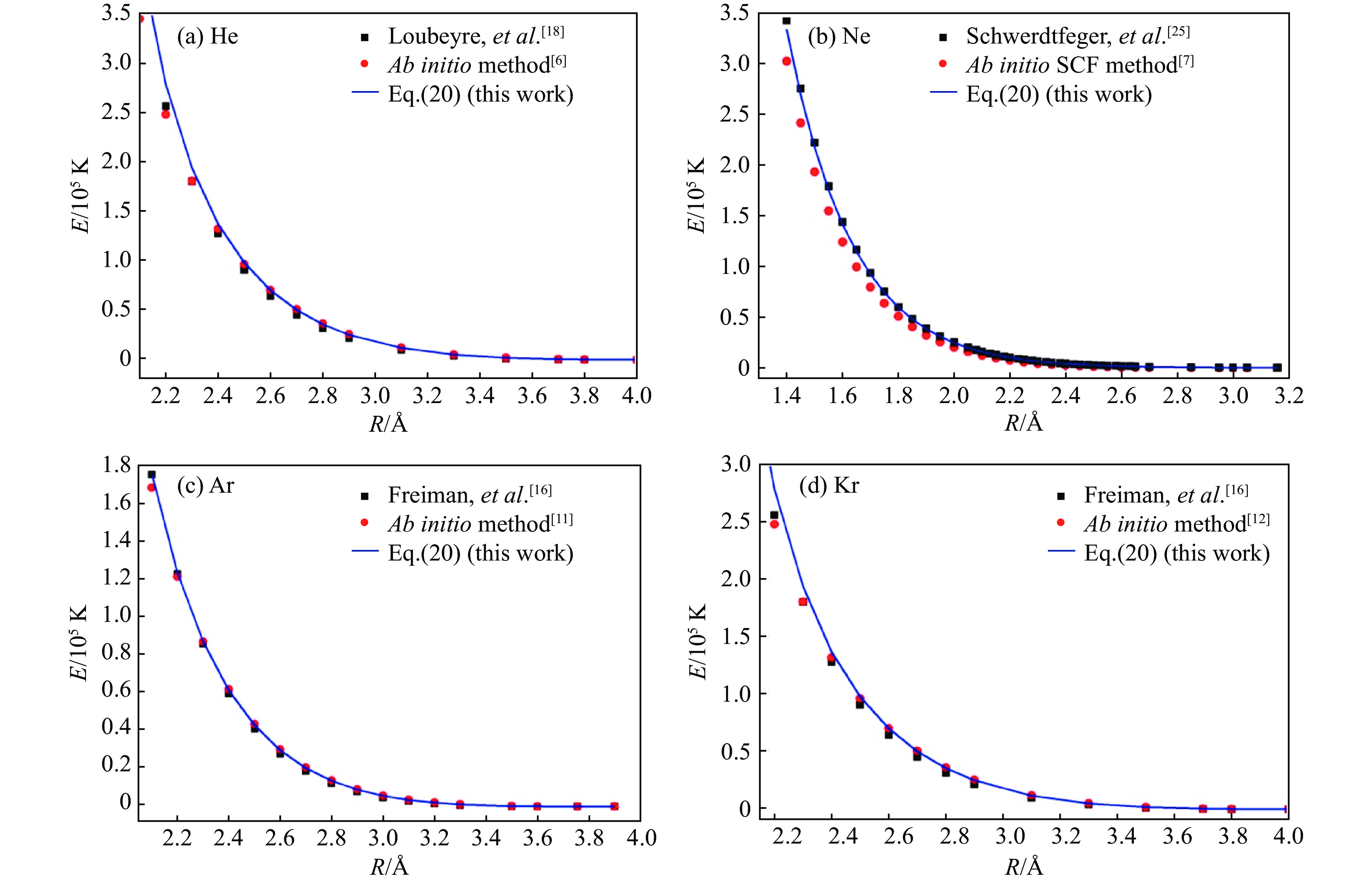
$\beta $ 的独立函数,此时$\beta $ =1,这也是求解结合能的传统方法;如果考虑两体势和三体势,忽略四体势及四体以上势,可以推导出$\beta $ =(1/3)1/2=0.577;如果考虑两体、三体和四体势,忽略五体及五体以上势,则有0<$\beta $ <0.577。随着更高多体势被考虑,$\beta $ 值就越接近0.5。也就是说,可以得到参数$\beta $ 的一个近似值($\beta $ =0.5),它适用于所有的稠密惰性元素原子的结合能。因此,结合能的表达式可简化为在这个新的结合能公式中,U2(M)可以通过从头算法或者Aziz对势准确得到,且只占结合能E(M)的25%;Vn(M)可通过求解薛定谔方程得到,且占结合能E(M)的75%。利用新公式,得到了结合能E(M)的数值,并将数值结果与前人的理论计算结果、实验值[6-7, 11-12, 16, 18, 25]进行了比较,如图2所示。
结果表明,新的结合能E(M)与参考文献中的实验结果吻合较好,平均相对误差在3%以内,个别在3%~5%范围内。综上所述,新结合能的表达式具有如下优点:
(1)新表达式能够更广泛地应用到基于RHF理论的分子体系密度范围之内;
(2)由于原子多体相互作用势中的坐标独立性,新表达式对于原子晶体的结构转变、相变、弹性系数和高压熔化线等的理解具有特殊的价值;
(3)依据新表达式的理论计算方法,一些简单的理论和表达式也可以很容易地扩展到原子多体展开理论或分子势理论,如流体微扰理论[19-20]等;
(4)对于短程排斥势,一些离子体系和分子体系的情况与原子体系的情况类似,因此新表达式和该方案有望应用于这些体系。
-
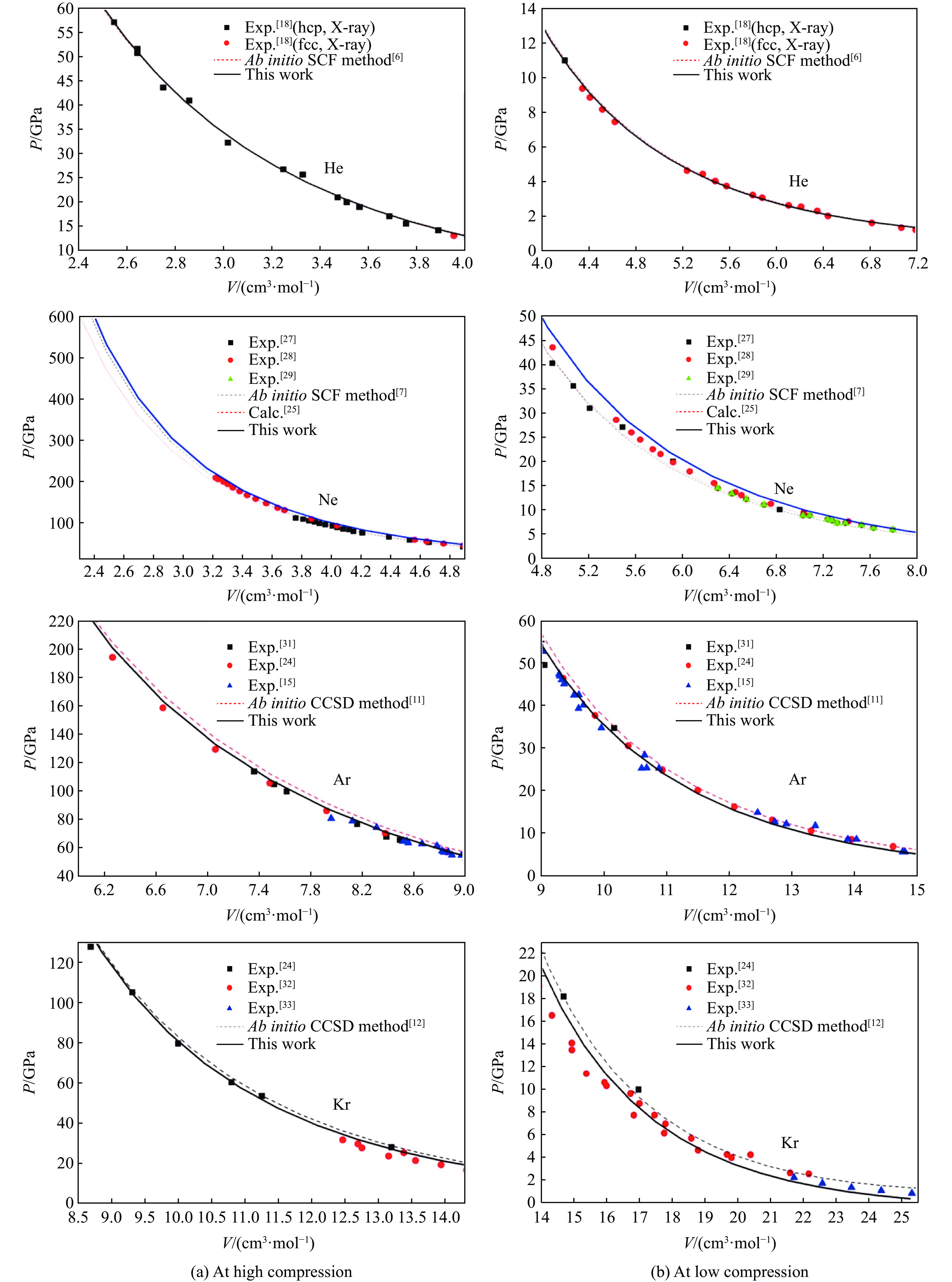
根据新结合能的计算结果,运用(11)式可得到稠密惰性元素原子的新结合能对高压压缩特性的影响,并与前人通过从头算理论得到的计算结果[6-7, 11-12, 26]、实验值[15, 18, 24, 27-33]进行比较,如图3所示,其中R、V分别为原子间距和对应的摩尔体积。数值结果表明,本研究的数值结果与从头算法结果相近,在目前的实验范围内与实验结果基本一致(氦1~60 GPa[6],氖1~238 GPa[30],氩1~114 GPa[31],氪1~128 GPa[24]),且平均相对误差都在3%以内,极个别在3%~5%。
为了进一步验证本研究提出的理论,表1列出了固氩的实验压强值、理论计算值,以及本研究的计算值与实验值的相对误差。可以看出,本研究的计算结果与实验值[24]基本吻合,平均相对误差小于3%,说明新方案是可行的。在此工作中,结合能的新表达式准确地解释了惰性元素物质在高压高密度下的稠密特性。
2.1. 结合能的新势函数
2.2.
参数${\,\beta}$![]()
![]()
2.3. 新的结合能
2.4. 新结合能对高压压缩特性的影响
-
基于量子理论和原子团簇理论,运用多体展开方法和第一性原理的从头算方法,提出了一种新的计算稠密惰性元素(RGS=氦,氖,氩和氪)原子结合能的经验势函数,运用新经验势研究了结合能对高压稠密惰性元素状态方程的影响。此经验势函数由两部分组成:一部分是由从头算法计算得到的两体相互作用势能,另一部分是通过求解薛定谔方程得到的总相互作用势能。此函数引入了一个新的物理参量
$\beta $ (其值为0.5),使得结合能的经验表达式更加简单、准确。比较结果表明:结合能的新经验势函数能够准确地描述多体相互作用对结合能的贡献,且相对误差在5%以内,能够更广泛地应用到基于RHF理论的分子体系密度范围之内,对原子晶体的结构转变、相变、弹性系数和高压熔化线的理解具有特殊的价值;运用新经验势的理论计算方法,可以将一些简单的理论、表达式很容易地扩展到原子多体展开理论或分子势理论;此外,此表达式和方案做法有望应用于一些离子体系和分子体系的短程排斥势情况。在高压区域,结合能的新势函数对高压压缩特性的影响在当前实验范围内(氦1~60 GPa,氖1~238 GPa,氩1~114 GPa,氪1~128 GPa)做出了令人满意的描述,数值结果与实验结果、理论计算结果基本吻合,平均相对误差在3%以内。最后,以固氩的压强数据为例,验证了该势函数的准确性。该经验势函数不仅适用于更宽的密度和压强范围,而且对所有惰性元素原子的各种状态的高压压缩特性研究具有重要的指导意义。

 首页
首页 登录
登录 注册
注册






 下载:
下载: