首页
登录
注册
-
C3N4具有优异的化学稳定性和独特的电子能带结构，在诸多领域有着广泛应用，如作为超硬材料[1–2]、光催化材料[3]以及环境污染物降解的催化剂[4–5]。另外，新型富氮含能材料5,5′-联四唑-1,1′-二氧二羟铵（TKX-50）[6]的反应产物中可能含有碳氮化合物[7–9]，C3N4可能是其中之一。C3N4的高温高压物性对其应用有重要的影响。目前，针对C3N4在高温高压下的物性和相变研究较多，但认识仍不够深入，一些结论存在矛盾。Han等[10]在300 K下对石墨相C3N4（g-C3N4）进行了高压原位电阻测试，发现了2个异常电阻变化，由此认为g-C3N4在10 GPa以内较为稳定，在10 GPa左右转变成为立方相，20 GPa时转变为未知相；李雪飞等[11–12]在300 K下通过同步辐射X射线衍射（X-ray diffraction，XRD）和金刚石对顶砧（diamond anvil cell，DAC）实验发现，g-C3N4在10 GPa以内不稳定，在6.6 GPa转变为三斜相。Gao等[13]在17.0～62.1 GPa压力下对含铜和不含铜的g-C3N4开展了冲击加载和回收实验，分析认为，g-C3N4在22.4 GPa下转变为未知相。马海云等[14]和Wang等[1]通过分析冲击回收样品，认为在接近Gao等[13]的冲击压力下合成了第一性原理计算预测的超硬β相C3N4（β-C3N4）[15–16]；但是，Kojima等[17]通过激光加热金刚石对顶砧（laser-heated diamond anvil cell，LHDAC）和平顶对顶砧实验，发现g-C3N4在30 GPa、
1600 K的条件下转变为正交相C3N4（O-C3N4），且该正交相在高达125 GPa、3000 K的压力温度范围内均稳定，该实验结果与马海云等[14]和Wang等[1]的结论不一致。Ming等[18]在21～38 GPa、1600 ～3000 K的压力温度范围内利用LHDAC和同步加速器XRD技术，发现g-C3N4在压力高于21 GPa、温度高于1800 K的条件下转变为立方相；然而，Fang等[19]开展了多次高温高压卸载实验，未发现C3N4存在任何高压相。邹广田等[20]利用六面顶压机对g-C3N4进行了高温高压相变研究，在5.2 GPa、1073 K下发现了稳定的g-C3N4结构；Gao等[13]开展了g-C3N4的冲击回收实验，认为g-C3N4应该在17 GPa、1943 K条件下存在；但是，根据Kojima等[17]总结的相图，邹广田等[20]和Gao等[13]的实验区已经越过了g-C3N4的分解边界，此时g-C3N4应该已经分解为氮气和碳。最近，Laniel等[21]通过LHDAC在高于100 GPa的条件下合成了新型碳氮化合物tI14-C3N4和hP126-C3N4，这些化合物在常温常压的空气中稳定。在理论方面，很多学者通过第一性原理研究了C3N4的物性。Manyali等[22]通过密度泛函理论计算了石墨型和超硬结构C3N4的模量和力学特性；Lanzilotto等[23]和Ugolotti等[24]通过密度泛函理论计算了g-C3N4的结构、电子和光谱特性；Fang等[19]采用第一性原理，研究了压力对C3N4的结构、电子、光学、力学、热力学性质的影响规律。热化学状态方程具备描述物质热力学量的能力，可用于深入研究C3N4的高温高压物性。第一性原理计算一般得到离散的热力学状态点，无法形成热化学状态方程，并且其计算可靠性还需要实验检验。例如：阮林伟[25]计算的g-C3N4的Grüneisen系数随压力的升高而增大，而实验结果显示，Grüneisen系数随着压力的升高而减小[26]；Ruan等[27]计算的g-C3N4在0 K下的冷压线与常温下实验压缩线[11]的差异高达65%，根据常见物质的等压膨胀系数范围[28]，可估算常温与0 K下的初始密度差异约为0.3%，无法解释此显著误差。因此，C3N4的热化学状态方程研究不能完全依赖计算，基于可靠的实验结果建立C3N4的热化学状态方程具有重要意义。
为定量研究C3N4的热化学状态方程，本研究利用已知的相分解边界和等温压缩线，提出一种高精度、低成本的新方法；利用建立的C3N4热化学状态方程，对争议点的相态进行初步判断；同时，尝试将C3N4热化学状态方程加入新型富氮炸药TKX-50的爆轰性能研究中，以期为以TKX-50为代表的新型炸药爆轰参数计算研究提供新的参考方向。
-
为研究Helmholtz能（A），建立C3N4的热化学状态方程
式中：
$ T $ 为温度，$ V $ 为比容，$ E $ 为内能，$ S $ 为熵。利用热力学基本关系，由$ A $ 求出剩余所有的热力学量，如压强p。根据经典三项式热化学状态方程，内能E和熵S由3部分贡献组成
式中：下标c表示冷压贡献，n表示晶格热运动贡献，e表示电子贡献。0 K时熵很小[29]，即Sc取零。由于本研究涉及的温度不高，因此，忽略电子贡献项。
冷压项采用Murnahan方程
式中：
$ {V_{{\text{0\,K}}}} $ 为0 K下的比容，$ {B_0} $ 和$ {B_1} $ 分别为零压下的体弹模量及其对压力的一阶导数。晶格振动贡献由德拜模型描述式中：n为体系中的原子数目；kB为玻尔兹曼常数；Eref和Sref为常数修正项；Θ为德拜温度，是比容的函数；
$ \zeta $ 为德拜函数。德拜温度Θ是定量计算晶格贡献的关键因素，目前关于Θ的计算模型较多[30–31]，本研究采用Xian等[32]的模型
式中：
$ {\mathrm{\hbar}} $ 为约化普朗克常量；veff为有效声速，是德拜温度的核心控制因素。Xian等[32]、Luo等[33]的研究表明，声速与体积具有良好的线性关系。本研究采用Luo等[33]的假设式中：c1和c2为常数。尽管声速与体积的线性关系假设的普遍性还需要更多研究验证，但是该假设对于C3N4的可靠性可由以下计算结果与实验结果的良好吻合来证明。
由于实验无法达到0 K，直接用室温实验结果代替0 K实验结果会导致一定的误差，因此，本研究考虑了温度变化导致的比容变化，由此修正此误差
式中：V0为室温下的比容，α为常压下的体积膨胀系数，T0为室温。因此，只要标定
$ {V_{{\text{0\,K}}}} $ 、B0、B1、c1、c2、Eref、Sref、α这8个量，就可以完全确定热化学状态方程。 -
为了构造物质在高温高压下的热化学状态方程，理论上需要通过实验获得若干(p, T, V)点以标定热化学状态方程的8个参数，从而确定热化学状态方程。然而，基于实验结果标定热化学状态方程普遍存在数据缺乏问题，因为一般的实验方法难以同时得到p、T、 V数据，而利用LHDAC和同步加速器XRD技术获取(p, T, V)数据的成本十分高昂。已发表的常见数据是通过常温压缩实验获得的(p, V, T0)点以及高温高压实验获得的相边界(p, T)点。常温压缩线可以很好地反映冷压项的贡献，但相边界数据由于缺乏体积信息一般难以支撑关于热贡献的定量计算，除非相分解的产物状态信息已知。
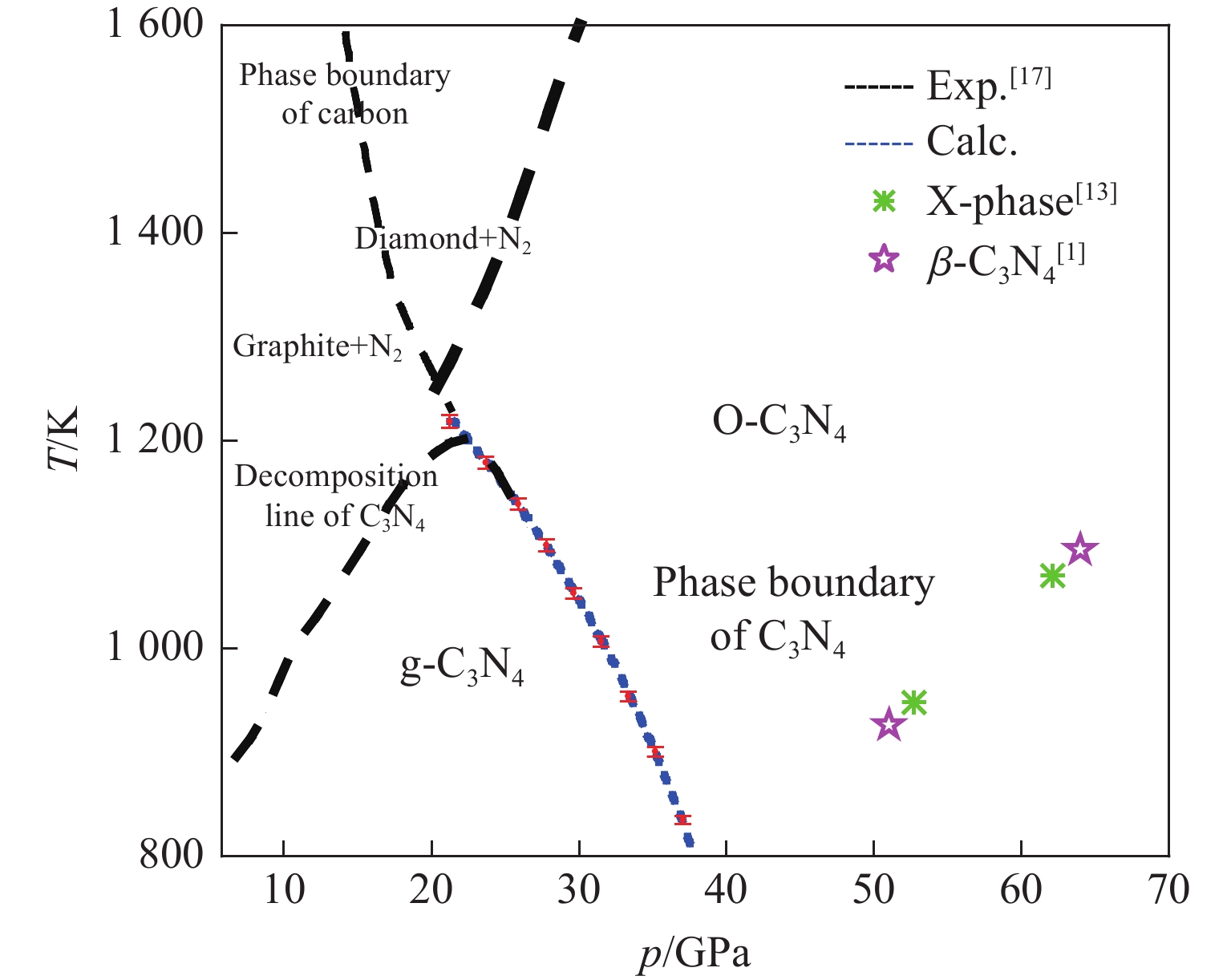
利用已知的C3N4分解产物的热化学状态方程，计算了C3N4相边界上的(p, T, G)数据（G为Gibbs能），结合已发表的常温压缩实验数据(p, V, T0)，可高精度、低成本地定量研究C3N4的热化学状态方程。Kojima等[17]通过实验得到的g-C3N4高压相图（见图1）被广泛接受，他们发现，g-C3N4在20 GPa左右转变为正交相O-C3N4，而O-C3N4直到150 GPa都非常稳定；他们还研究了高温下g-C3N4和 O-C3N4的分解线，发现g-C3N4在高温下主要分解为石墨和N2，而O-C3N4主要分解为金刚石和N2。目前，人们对石墨、金刚石和N2的高温高压状态的认识比较深刻，已经获得了可靠的热化学状态方程。因此，利用石墨、金刚石和N2的热化学状态方程，可以计算出C3N4相边界上的(p, T, G)数据。由于相边界上具有Gibbs能相等的特征，因此，计算出的(p, T, G)数据同样适合C3N4，可以支撑关于热贡献的定量计算。李雪飞等[11]和Kojima等[17]实验研究了g-C3N4和 O-C3N4的常温压缩线，可以支撑关于冷压项的定量计算。
N2在高温高压下的热化学状态方程[34]基于MCR（molecular crystalline renormalization[35]理论计算。MCR理论以分子相互作用势（Φ）为基础
式中：r为分子间的距离；ε、
$ r^* $ 、α为势参数，取值分别为293、0.389和11.5[36]。Fried等[37]提出的碳（C）的四相（石墨、金刚石和2个流体相）热化学状态方程被证明可靠性较高[38]。本课题组编写了DLCHEQ热化学程序[39–40]，其中包含N2和C的热化学状态方程，可以通过p、T方便地推导出C+N2的Gibbs能。
-
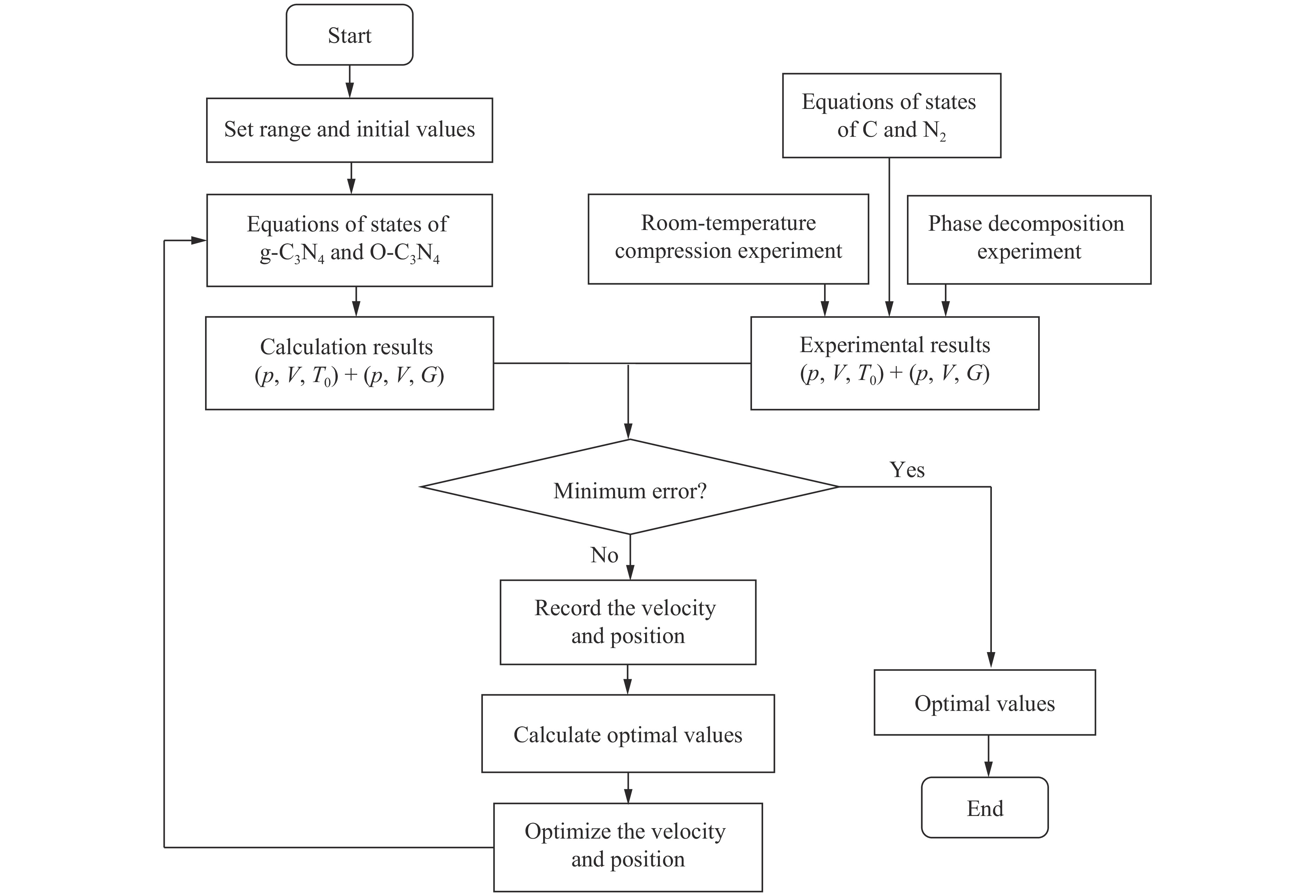
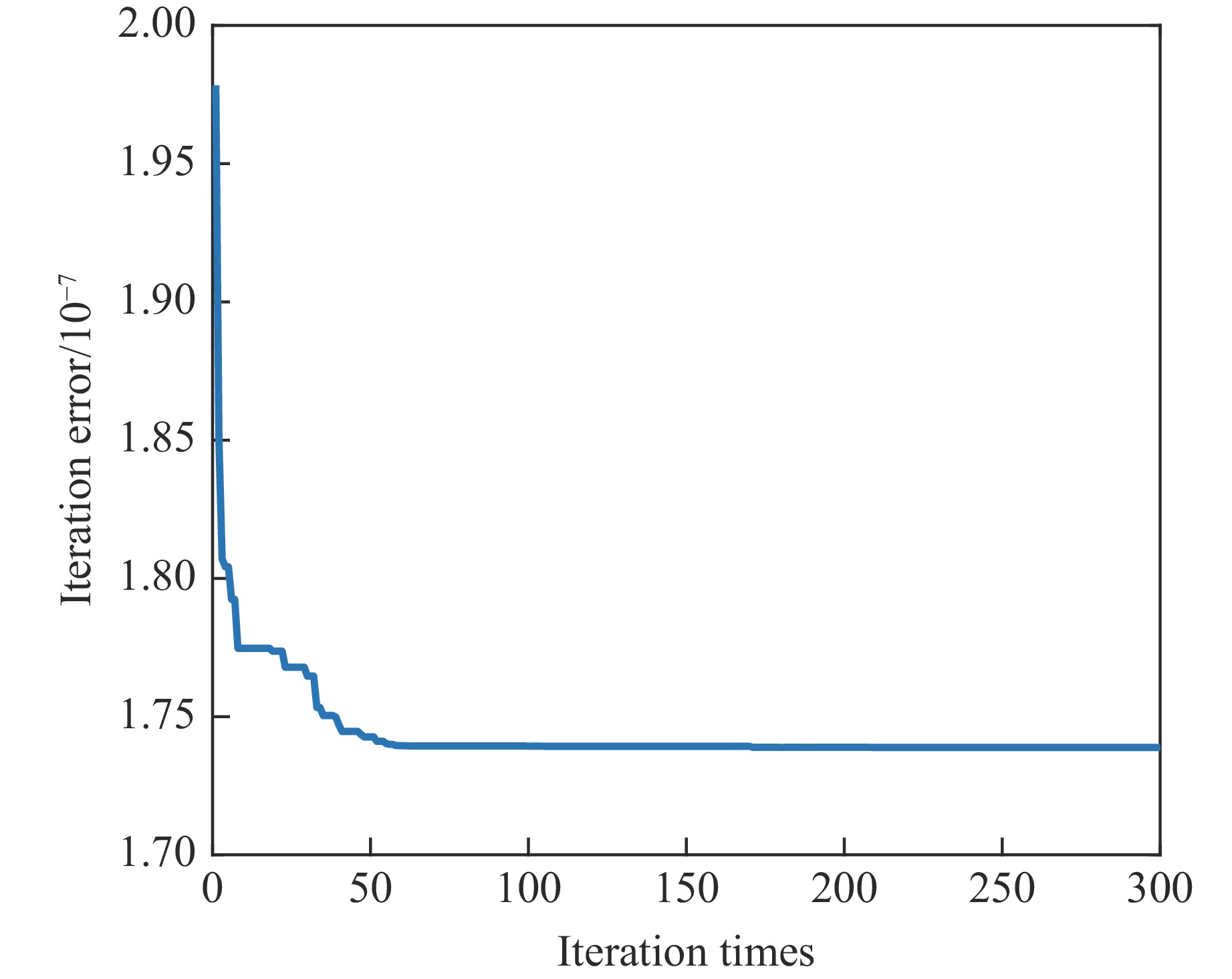
基于多个数据点标定热化学状态方程的8个参数，本质上是多参数求极值问题。人工求多参数极值问题费时费力且难以保证计算效果。为此，研究人员常用遗传算法[41]开展标定工作，本研究采用粒子群算法。粒子群算法[42]是一种智能优化的随机搜索算法，能以较大的概率收敛于全局最优解，适合在动态、多目标优化环境中寻优，与传统优化算法相比，其更新优化参数位置的速度更快，拥有更好的全局搜索能力。采用粒子群算法标定热化学状态方程的流程如图2所示，其标定误差随迭代次数的变化如图3所示。由图3可知，8参数的极值求解在50次迭代后基本收敛，效率较高。标定的常温压缩线的平均相对误差不超过1.85%，Gibbs能的平均相对误差不超过0.50%。平均相对误差δave的公式为
式中：N为数据点个数，xfit,i和xexp,i分别为标定点和实验点数据。
-
本研究标定的g-C3N4和O-C3N4的热化学状态方程参数如表1所示。g-C3N4和 O-C3N4的热化学状态方程的可靠性可以通过对比各物理量的第一性原理计算值或实验值得到。
首先，标定的g-C3N4的
$ {V_{{\text{0\,K}}}} $ 为0.449 cm3/g，第一性原理计算结果为0.433 cm3/g[25]，相对误差为3.56%，在可接受范围内。其次，热化学状态方程计算的g-C3N4和O-C3N4的常温压缩线与实验数据的吻合度较高，如图4所示，平均相对误差约为1.85%。根据比定容热容（cV）的定义，计算了O-C3N4的cV，与Cang等[43]的第一性原理计算结果具有较高的一致性（平均相对误差为2.27%），如图5所示。
最后，通过相边界上Gibbs能相等的特点，计算g-C3N4和O-C3N4的相边界，结果如图6所示。考虑到热化学状态方程标定时Gibbs能的平均相对误差不超过0.50%，因此，计算的相边界误差棒对应的Gibbs能上下限误差为0.50%。本研究计算的g-C3N4和O-C3N4相边界压强范围接近40 GPa，其中26 GPa以下的部分与Kojima等[17]由实验得到的相边界吻合得很好，相同压强下温度的最大误差仅为1.44%。
-
本研究尝试通过新建立的g-C3N4和O-C3N4相边界，对争议温度压力区域的C3N4相态进行初步鉴别。如图6所示，绿色点表示Gao等[13]通过g-C3N4冲击回收实验得到的未知相，紫色点表示Wang等[1]通过冲击回收实验得到的超硬预测相β-C3N4。根据本研究计算的相边界可知，绿色点和紫色点都位于O-C3N4范围内，如果Gao等[13]和Wang等[1]发现的相为非亚稳相，那么它们应该是O-C3N4。
2012年，Fischer等[44]设计并合成了TKX-50炸药，理论预测其具有高爆轰的Chapman-Jouguet（CJ）爆轰参数[45]，实验研究发现，其撞击感度、摩擦感度、静电感度较低，因此，TKX-50作为一种综合性能优异的炸药备受关注。后续的计算模型都表明，TKX-50具有较高的CJ爆轰参数，但是与实验结果相比存在系统性偏大。造成该差异的原因目前还不明确，因而阻碍了富氮炸药的爆轰机理研究。一些研究表明，TKX-50的产物中可能存在CN组分[7–9]。据此，本研究认为，经典方法的计算误差可能源于未考虑TKX-50的富氮特性，导致产物中可能存在CN凝聚态组分，如C3N4。为了验证此假设，将g-C3N4和O-C3N4的热化学状态方程加入热化学程序DLCHEQ[40]中，建立了TKX-50炸药产物的热力学模型。DLCHEQ程序根据系统Gibbs能最小来确定产物组分，由此计算TKX-50产物的Hugoniot线和CJ爆轰参数[46–47]。研究发现，直接用g-C3N4和O-C3N4的热化学状态方程计算时，在炸药常见的爆轰压力范围（42～26 GPa）内，C3N4主要以O-C3N4相存在，但含量较少。若TKX-50产物中存在C3N4，那么它可能经历从小到大的生长过程，从而拥有团簇生长和表面悬挂键等特征，致使其能量、体积等性质与块体材料存在差异。为了模拟TKX-50产物中C3N4的性质，改变O-C3N4的
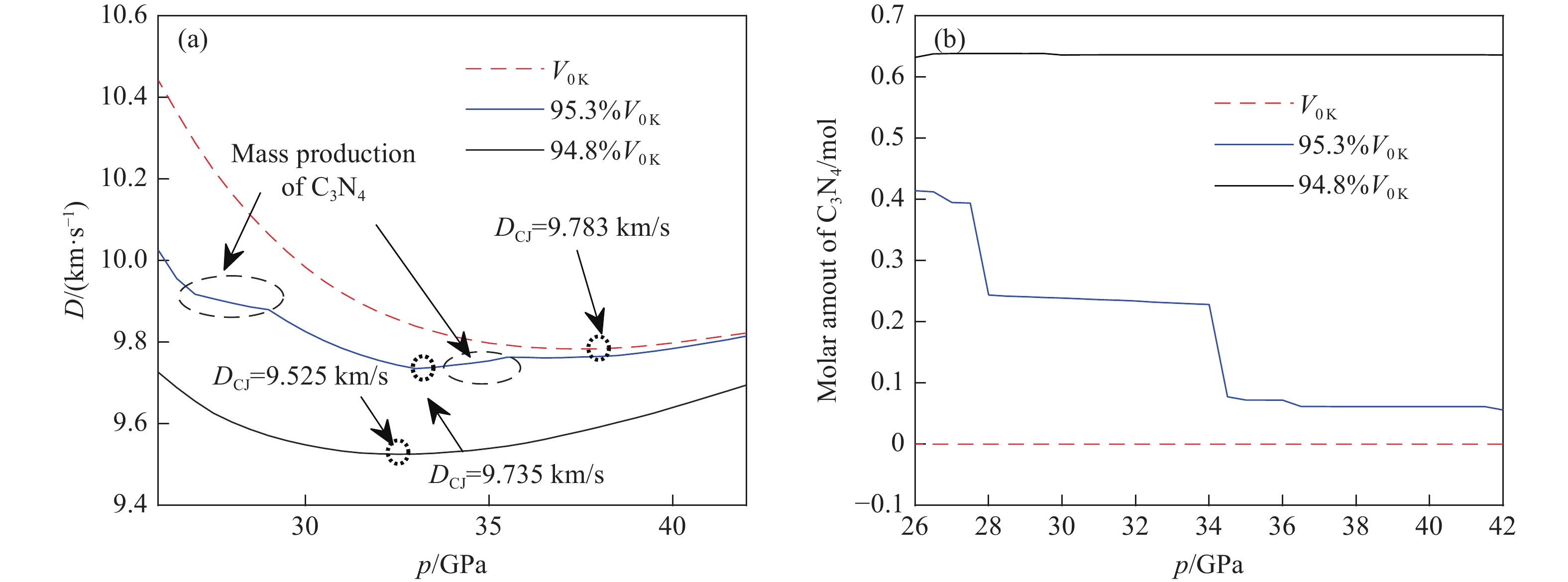
$ {V_{{\text{0\,K}}}} $ ，设置$ {V_{{\text{0\,K}}}} $ （36.9 cm3/mol）、95.3%$ {V_{{\text{0\,K}}}} $ （35.2 cm3/mol）、94.8%$ {V_{{\text{0\,K}}}} $ （35.0 cm3/mol）3种梯度，反映TKX-50产物组分的3种典型状态。计算得到的D-p形式的Hugoniot线如图7所示，其中，D为爆轰波爆速。由图7(a)可知，改变$ {V_{{\text{0\,K}}}} $ 对于TKX-50产物的Hugoniot状态具有显著影响，Hugoniot线总是随着$ {V_{{\text{0\,K}}}} $ 的下降而下降。$ {V_{{\text{0\,K}}}} $ 条件下，产物Hugoniot状态中的凝聚态组分以石墨为主。在95.3%$ {V_{{\text{0\,K}}}} $ 条件下，Hugoniot线在36 GPa以下显著下降，并且在36～34 GPa和29～27 GPa区间存在2个显著的转折，如图7(b)所示，此时生成了大量O-C3N4，即在94.8%
$ {V_{{\text{0\,K}}}} $ 条件下，整个Hugoniot状态中都不存在石墨，凝聚态组分一直以O-C3N4为主。生成C3N4是一个吸热且总体积减小的反应，因此，TKX-50产物中的C3N4含量越大，则系统内能和气体含量越少，导致爆轰性能下降。本研究对$ {V_{{\text{0\,K}}}} $ 的体积修正不超过5.2%，与体积标定的相对误差接近；由于O-C3N4的体积占TKX-50产物体积不超过10%，因此，$ {V_{{\text{0\,K}}}} $ 修正对总体积的影响最大约为2%。综上，可以认为，修正$ {V_{{\text{0\,K}}}} $ 后的O-C3N4热化学状态方程仍具有物理意义，计算得到的C3N4在 TKX-50产物中可能存在的结论具有合理性。根据CJ理论模型[45]，Hugoniot线中D最小值对应的点为CJ爆轰点，由此得到CJ爆轰参数。本研究总结了不同实验和计算得到的TKX-50炸药的CJ爆轰参数[44, 46, 48–51]，如表2所示，其中：DCJ、pCJ、TCJ分别为CJ 爆速、CJ 爆压和CJ 温度。由表2可知，对于经典的计算方法，无论是著名的热化学程序Explo 5、CHEETAH，还是经验公式，在TKX-50炸药的理论密度（1.877 g/cm3）下预测的CJ爆速（9.650～9.735 km/s）和CJ爆压（42 GPa左右）都比现有炸药更具优势，这也是研究人员一直认为TKX-50炸药拥有较高潜力的原因。实验上，Gottfried等[48]发现，理论密度下TKX-50炸药的CJ爆速（9.432 km/s）稍小于计算值。刘佳辉等[49]和Tan等[50]通过实验发现，当TKX-50炸药的密度稍低于理论密度时，其CJ爆速和CJ爆压远小于计算值。由于实验上钝感炸药的CJ点并不明显，因此，测试的TKX-50炸药的CJ压力差异较大。本研究的计算结果表明：TKX-50炸药爆轰产物中O-C3N4的含量越多，计算的CJ爆速和CJ爆压越接近实验值；当取94.8%
$ {V_{{\text{0\,K}}}} $ 时，计算的CJ爆速、CJ爆压与Tan等[50]获得的实验值的相对误差分别为5.24%和7.20%，远低于经典模型。由表2可知，随着$ {V_{{\text{0\,K}}}} $ 的下降，TKX-50炸药的CJ爆速下降约3%，CJ爆压下降约16%，CJ温度下降约7%。这说明TKX-50炸药的CJ爆压和CJ温度对凝聚态产物组分变化非常敏感，而CJ爆速则不太敏感，该结论对于TKX-50炸药的爆轰性能研究具有重要价值。本研究的计算结果表明，C3N4可能存在于TKX-50炸药的爆轰产物中，计算值与实验值的差异说明TKX-50炸药爆轰产物中可能还存在其他凝聚态组分。 -
利用实验测试的分解相边界及常温压缩线，提出了一种新的高精度、低成本的热化学状态方程研究方法。根据新方法，对g-C3N4和 O-C3N4建立了经典的三项式热化学状态方程，计算了初始比容、体弹模量等物理量，与实验值及第一性原理计算值的对比结果表明，由热化学状态方程得到的初始比容、冷压线、比定容热容和相边界均与第一性原理计算值及实验值吻合良好，相对误差分别为3.50%、1.85%、2.27%和1.44%，证明了利用新方法研究热化学状态方程的可靠性和准确性。
采用热化学状态方程计算了g-C3N4和O-C3N4的相边界，判断研究人员在50～70 GPa压力下通过冲击实验发现的未知相为O-C3N4。将C3N4热化学状态方程应用在TKX-50炸药的爆轰参数计算研究中，发现O-C3N4有可能存在于TKX-50炸药的爆轰产物中，并且O-C3N4的存在大幅降低了CJ参数计算值与实验值的误差，为以TKX-50炸药为代表的新型富氮炸药的爆轰参数计算研究提供了新的理论依据和研究方向。
C3N4热化学状态方程的研究及应用初探
Study and Preliminary Application of the Thermochemical Equation of State of C3N4
-
摘要: C3N4在超硬材料合成和光催化等领域具有广泛的应用，然而，其在高温高压下的相变和物理行为尚未完全清楚，研究其热化学状态方程十分必要。利用分解相边界及常温压缩线数据，提出了一种定量研究C3N4热化学状态方程的高精度、低成本的新方法。对C3N4的石墨相和正交相建立了三项式热化学状态方程，由此计算的诸多物理量与第一性原理计算结果及实验结果吻合良好，证明了热化学状态方程的可靠性。利用C3N4热化学状态方程，对特定温度压力下C3N4的争议相进行了初步判断。此外，将C3N4热化学状态方程加入新型富氮炸药5,5′-联四唑-1,1′-二氧二羟铵（TKX-50）的爆轰参数计算中，显著降低了TKX-50爆轰参数计算值与实验值之间的误差，为新型炸药爆轰机理研究提供了新的参考方向。Abstract: C3N4 has a wide range of applications in the synthesis of superhard materials and photocatalysis materials, but its phase transitions and physical behaviors under high pressure and high temperature conditions are not fully understood. Therefore, it is necessary to study its thermochemical equation of state. In this paper, we propose a novel, high-precision and low-cost method for quantitatively determining the equation of state of C3N4, based on decomposition phase boundary and compression line at room temperature. We constructs the equation of state for two phases of C3N4, and the corresponding physical quantities match well with first-principles calculations and experimental values, proving the reliability of the equation of state. Based on the equation of state of C3N4, we make a preliminary judgment on the phase state of the controversial points. Furthermore, this study attempts to incorporate the equation of state of C3N4 into the research on the detonation mechanism of novel nitrogen-rich explosives. It significantly reduces the long-standing errors between the calculated values and experimental values of the detonation parameters of the explosives, and provides a new reference direction for the research on the detonation parameter calculations of new explosives.
-
Key words:
- C3N4 /
- thermochemical equation of state /
- phase boundary /
- nitrogen-rich explosive .
-
-
图 1 C3N4的相图[17]（圆形、正方形、菱形和三角形分别表示石墨、O-C3N4、金刚石和g-C3N4，实线表示石墨与金刚石的边界，虚线表示C3N4的分解相边界）
Figure 1. Phase diagram of C3N4[17] (Circles, squares, diamonds and triangles denote graphite, O-C3N4, diamond and g-C3N4, respectively. Thick solid line represents the boundary between graphite and diamond, and the dashed line indicates the decomposed phase boundary of C3N4.)
图 2 粒子群算法原理示意图
Figure 2. Schematic diagram of the particle swarm optimization algorithm
图 3 粒子群算法的迭代误差随迭代次数的变化
Figure 3. Variation of iteration error with iteration times in particle swarm optimization algorithm
图 4 标定的常温压缩线与实验结果的对比
Figure 4. Comparison of calculated compression lines with experimental results under room temperature
图 6 g-C3N4和O-C3N4的相边界计算结果（误差棒对应的Gibbs能误差上下限为0.50%）
Figure 6. Calculated phase boundary between g-C3N4 and O-C3N4 (The corresponding Gibbs energy error limits for the error bars are 0.50%.)
图 7 TKX-50产物的Hugoniot线：(a) D-p曲线，(b) 1 mol TKX-50炸药产物中C3N4的物质的量的变化
Figure 7. Hugoniot lines of TKX-50 detonation products: (a) D-p curves; (b) change of the molar amount of C3N4 in the products of 1 mol TKX-50 explosive
表 1 g-C3N4和O-C3N4的热化学状态方程参数
Table 1. Thermochemical equation of state parameters of g-C3N4 and O-C3N4
Material B0/GPa B1 $ {V_{{\text{0\,K}}}} $ /(cm3·g−1)Eref/(kJ·mol−1) Sref/(kJ·mol−1·K−1) c1/(mm·s−1) c2/(mm·s−1) α/(cm3·g−1·K−1) g-C3N4 163.62 5.40 0.449 89.86 3.40×10−2 1.39 −1.07 4.41×10−6 O-C3N4 244.12 4.08 0.401 111.85 8.76×10−2 1.15 −0.47 4.19×10−6 
下载: 导出CSV
表 2 实验和计算得到TKX-50炸药的CJ爆轰参数
Table 2. CJ parameters of TKX-50 explosives obtained by experiments and calculations
Method ρ0/(g·cm−3) DCJ/(km·s−1) pCJ/GPa TCJ/K Exp. (detonation test)[48] 1.877 9.432 Exp. (damage test)[49] 1.86 9.037 26.40 Exp. (DRZ test)[50] 1.85 9.050 35.04 Calc. ( $ {V_{{\text{0\,K}}}} $ )1.85 9.783 38.20 3161.9 Calc. (95.3% $ {V_{{\text{0\,K}}}} $ )1.85 9.735 33.30 3030.9 Calc. (94.8% $ {V_{{\text{0\,K}}}} $ )1.85 9.525 32.50 2953.9 Calc. (Explo 5.05)[44] 1.877 9.698 42.40 3954 Calc. (CHEETAH 8.0)[48] 1.877 9.735 42.40 2845 Calc. (empirical code)[51] 1.877 9.650 41.90 3724
下载: 导出CSV
-
[1] WANG Y G, LIU F S, LIU Q J, et al. Recover of C3N4 nanoparticles under high-pressure by shock wave loading [J]. Ceramics International, 2018, 44(16): 19290–19294. doi: 10.1016/j.ceramint.2018.07.155 [2] LANIEL D, TRYBEL F, ZHOU W J, et al. High-pressure synthesis of oP28-C3N4 recoverable to ambient conditions [J]. Advanced Functional Materials, 2025, 35(11): 2416892. doi: 10.1002/ADFM.202416892 [3] SONG X L, CHEN L, GAO L J, et al. Engineering g-C3N4 based materials for advanced photocatalysis: recent advances [J]. Green Energy & Environment, 2024, 9(2): 166–197. doi: 10.1016/j.gee.2022.12.005 [4] MUHMOOD T, AHMAD I, HAIDER Z, et al. Graphene-like graphitic carbon nitride (g-C3N4) as a semiconductor photocatalyst: properties, classification, and defects engineering approaches [J]. Materials Today Sustainability, 2024, 25: 100633. doi: 10.1016/j.mtsust.2023.100633 [5] YU X N, NG S F, PUTRI L K, et al. Point-defect engineering: leveraging imperfections in graphitic carbon nitride (g-C3N4) photocatalysts toward artificial photosynthesis [J]. Small, 2021, 17(48): 2006851. doi: 10.1002/smll.202006851 [6] KLAPÖTKE T M. TKX-50: a highly promising secondary explosive [M]//TRACHE D, BENALIOUCHE F, MEKKI A. Materials Research and Applications: Select Papers from JCH8–2019. Singapore: Springer, 2021: 1–91. [7] WANG X H, HAO G Z, XIAO L, et al. Review on the thermal decomposition of dihydroxylammonium 5, 5′-bistetrazole-1, 1′-diolate (TKX-50) [J]. Thermochimica Acta, 2023, 719: 179393. doi: 10.1016/J.TCA.2022.179393 [8] ZHAO C D, CHI Y, PENG Q, et al. A study on the comprehension of differences in specific kinetic energy of TKX-50 and HMX from the perspective of gas products [J]. Physical Chemistry Chemical Physics, 2019, 21(12): 6600–6605. doi: 10.1039/C8CP07487A [9] REN X, HE R N, WANG X H, et al. A comprehensive experimental and theoretical study of thermal response mechanisms of TKX-50 and HMX [J]. Fuel, 2024, 375: 132623. doi: 10.1016/j.fuel.2024.132623 [10] HAN Y H, LUO J F, GAO C X, et al. Phase transition of graphitic-C3N4 under high pressure by in situ resistance measurement in a diamond anvil cell [J]. Chinese Physics Letters, 2005, 22(6): 1347–1349. doi: 10.1088/0256-307X/22/6/014 [11] 李雪飞, 张剑, 刘伟, 等. 氮化碳的高压同步辐射研究 [J]. 高压物理学报, 2009, 23(1): 71–74. doi: 10.11858/gywlxb.2009.01.012 LI X F, ZHANG J, LIU W, et al. Synchrotron radiation X-ray diffraction of carbon nitride under high pressure [J]. Chinese Journal of High Pressure Physics, 2009, 23(1): 71–74. doi: 10.11858/gywlxb.2009.01.012 [12] 李雪飞, 马艳梅, 沈龙海, 等. 石墨相C3N4压致结构相变研究 [J]. 高压物理学报, 2010, 24(1): 67–70. doi: 10.11858/gywlxb.2010.01.012 LI X F, MA Y M, SHEN L H, et al. Study on the pressure-induced phase transition of g-C3N4 [J]. Chinese Journal of High Pressure Physics, 2010, 24(1): 67–70. doi: 10.11858/gywlxb.2010.01.012 [13] GAO X, YIN H, CHEN P W, et al. Shock-induced phase transition of g-C3N4 to a new C3N4 phase [J]. Journal of Applied Physics, 2019, 126(15): 155901. doi: 10.1063/1.5111710 [14] 马海云, 刘福生, 李永宏, 等. 强冲击压缩条件下g-C3N4向β-C3N4直接转化 [J]. 高压物理学报, 2012, 26(3): 319–324. doi: 10.11858/gywlxb.2012.03.012 MA H Y, LIU F S, LI Y H, et al. Strong shock-compression of g-C3N4 precursor for direct synthesis of β-C3N4 [J]. Chinese Journal of High Pressure Physics, 2012, 26(3): 319–324. doi: 10.11858/gywlxb.2012.03.012 [15] TETER D M, HEMLEY R J. Low-compressibility carbon nitrides [J]. Science, 1996, 271(5245): 53–55. doi: 10.1126/science.271.5245.53 [16] LIU A Y, COHEN M L. Prediction of new low compressibility solids [J]. Science, 1989, 245(4920): 841–842. doi: 10.1126/science.245.4920.841 [17] KOJIMA Y, OHFUJI H. Structure and stability of carbon nitride under high pressure and high temperature up to 125 GPa and 3000 K [J]. Diamond and Related Materials, 2013, 39: 1–7. doi: 10.1016/j.diamond.2013.07.006[18] MING L C, ZININ P, MENG Y, et al. A cubic phase of C3N4 synthesized in the diamond-anvil cell [J]. Journal of Applied Physics, 2006, 99(3): 033520. doi: 10.1063/1.2168567 [19] FANG L M, OHFUJI H, SHINMEI T, et al. Experimental study on the stability of graphitic C3N4 under high pressure and high temperature [J]. Diamond and Related Materials, 2011, 20(5/6): 819–825. doi: 10.1016/j.diamond.2011.03.034 [20] 邹广田, 李雪飞, 杨大鹏, 等. 石墨相C3N4的高温高压研究 [J]. 原子与分子物理学报, 2009, 26(4): 705–707. doi: 10.3969/j.issn.1000-0364.2009.04.024 ZOU G T, LI X F, YANG D P, et al. Study on the pressure-induced phase transition of g-C3N4 [J]. Journal of Atomic and Molecular Physics, 2009, 26(4): 705–707. doi: 10.3969/j.issn.1000-0364.2009.04.024 [21] LANIEL D, TRYBEL F, ASLANDUKOV A, et al. Synthesis of ultra-incompressible and recoverable carbon nitrides featuring CN4 tetrahedra [J]. Advanced Materials, 2024, 36(3): 2308030. doi: 10.1002/adma.202308030 [22] MANYALI G S, WARMBIER R, QUANDT A, et al. Ab initio study of elastic properties of super hard and graphitic structures of C3N4 [J]. Computational Materials Science, 2013, 69: 299–303. doi: 10.1016/j.commatsci.2012.11.039 [23] LANZILOTTO V, SILVA J L, ZHANG T, et al. Spectroscopic fingerprints of intermolecular H-bonding interactions in carbon nitride model compounds [J]. Chemistry–A European Journal, 2018, 24(53): 14198–14206. doi: 10.1002/chem.201802435 [24] UGOLOTTI A, DI VALENTIN C. Ab-initio spectroscopic characterization of melem-based graphitic carbon nitride polymorphs [J]. Nanomaterials, 2021, 11(7): 1863. doi: 10.3390/nano11071863 [25] 阮林伟. g-C3N4光催化材料的第一性原理研究 [D]. 合肥: 安徽大学, 2015: 42–56. RUAN L W. First-principles study of g-C3N4 photocatalytic materials [D]. Hefei: Anhui University, 2015: 42–56. [26] ZHAO Y R, ZHANG H R, ZHANG G T, et al. First-principles investigation on elastic and thermodynamic properties of Pnnm-CN under high pressure [J]. AIP Advances, 2016, 6(12): 125040. doi: 10.1063/1.4972775 [27] RUAN L W, ZHU Y J, QIU L G, et al. First principles calculations of the pressure affection to g-C3N4 [J]. Computational Materials Science, 2014, 91: 258–265. doi: 10.1016/j.commatsci.2014.04.058 [28] PRIBYLOV A A, POSTNIKOV E B. Thermodynamic curvature and the thermal expansion isolines [J]. Journal of Molecular Liquids, 2021, 335: 115994. doi: 10.1016/j.molliq.2021.115994 [29] RIBEIRO M, HENRIQUES T, CASTRO L, et al. The entropy universe [J]. Entropy, 2021, 23(2): 222. [30] BLANCO M A, FRANCISCO E, LUAÑA V. GIBBS: isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model [J]. Computer Physics Communications, 2004, 158(1): 57–72. doi: 10.1016/j.comphy.2003.12.001 [31] LUO Y F, LI M K, YUAN H M, et al. Predicting lattice thermal conductivity via machine learning: a mini review [J]. NPJ Computational Materials, 2023, 9(1): 4. doi: 10.1038/s41524-023-00964-2 [32] XIAN Y T, XIANG S K, LIU L, et al. Accurate equation of state of rhenium as pressure scale up to 130 GPa and 3200 K [J]. AIP Advances, 2022, 12(5): 055313. doi: 10.1063/5.0089292[33] LUO Y, XIANG S K, LI J, et al. Equation of state of MgO up to 345 GPa and 8500 K [J]. Physical Review B, 2023, 107(13): 134116. doi: 10.1103/PhysRevB.107.134116[34] KRUKOWSKI S, STRĄK P. Equation of state of nitrogen (N2) at high pressures and high temperatures: molecular dynamics simulation [J]. The Journal of Chemical Physics, 2006, 124(13): 134501. doi: 10.1063/1.2185096 [35] 杨金文, 施尚春, 李巧燕, 等. 高温高密度液氦冲击压缩特性理论研究 [J]. 爆炸与冲击, 2007, 27(6): 557–561. doi: 10.11883/1001-1455(2007)06-0557-05 YANG J W, SHI S C, LI Q Y, et al. Theoretical research on shock compression properties of liquid helium at high temperature and density [J]. Explosion and Shock Waves, 2007, 27(6): 557–561. doi: 10.11883/1001-1455(2007)06-0557-05 [36] 赵艳红. 基于统计物理和化学平衡的爆轰产物物态方程 [D]. 绵阳: 中国工程物理研究院, 2015: 21–46. ZHAO Y H. The equation of state of detonation products based on statistical physics and chemical equilibrium [D]. Mianyang: China Academy of Engineering Physics, 2015: 21–46. [37] FRIED L E, HOWARD W M. Explicit Gibbs free energy equation of state applied to the carbon phase diagram [J]. Physical Review B, 2000, 61(13): 8734–8743. doi: 10.1103/PhysRevB.61.8734 [38] JAWORSKI Z, ZAKRZEWSKA B, PIANKO-OPRYCH P. On thermodynamic equilibrium of carbon deposition from gaseous C-H-O mixtures: updating for nanotubes [J]. Reviews in Chemical Engineering, 2017, 33(3): 217–235. doi: 10.1515/revce-2016-0022 [39] 王中友, 李星翰, 甘云丹, 等. 爆热弹中产物组分演化的计算研究 [J]. 火炸药学报, 2022, 45(2): 229–242. doi: 10.14077/j.issn.1007-7812.202112008 WANG Z Y, LI X H, GAN Y D, et al. Study on thermodynamic evolution of detonation products in the detonation bomb test [J]. Chinese Journal of Explosives & Propellants, 2022, 45(2): 229–242. doi: 10.14077/j.issn.1007-7812.202112008 [40] LI X H, YI Z C, LIU Q J, et al. Research of detonation products of RDX/Al from the perspective of composition [J]. Defence Technology, 2023, 24: 31–45. doi: 10.1016/j.dt.2022.11.016 [41] KATOCH S, CHAUHAN S S, KUMAR V. A review on genetic algorithm: past, present, and future [J]. Multimedia Tools and Applications, 2021, 80(5): 8091–8126. doi: 10.1007/s11042-020-10139-6 [42] WANG D S, TAN D P, LIU L. Particle swarm optimization algorithm: an overview [J]. Soft Computing, 2018, 22(2): 387–408. doi: 10.1007/s00500-016-2474-6 [43] CANG Y P, LIAN S B, YANG H M, et al. Predicting physical properties of tetragonal, monoclinic and orthorhombic M3N4 (M= C, Si, Sn) polymorphs via first-principles calculations [J]. Chinese Physics Letters, 2016, 33(6): 066301. doi: 10.1088/0256-307X/33/6/066301 [44] FISCHER N, FISCHER D, KLAPÖTKE T M, et al. Pushing the limits of energetic materials: the synthesis and characterization of dihydroxylammonium 5, 5′-bistetrazole-1, 1′-diolate [J]. Journal of Materials Chemistry, 2012, 22(38): 20418–20422. doi: 10.1039/C2JM33646D [45] SUCESKA M, TUMARA B S, DOBRILOVIC M, et al. Estimation of detonation front curvature radius by empirical equations [J]. Journal of Energetic Materials, 2024, 42(2): 169–186. doi: 10.1080/07370652.2022.2052207 [46] SAIF M, WANG W T, PEKALSKI A, et al. Chapman-Jouguet deflagrations and their transition to detonation [J]. Proceedings of the Combustion Institute, 2017, 36(2): 2771–2779. doi: 10.1016/j.proci.2016.07.122 [47] 杨舒棋, 张旭, 彭文杨, 等. 钝感炸药冲击起爆反应过程的PDV技术 [J]. 高压物理学报, 2020, 34(2): 023402. doi: 10.11858/gywlxb.20190856 YANG S Q, ZHANG X, PENG W Y, et al. PDV technology of shock initiation reaction process of insensitive explosive [J]. Chinese Journal of High Pressure Physics, 2020, 34(2): 023402. doi: 10.11858/gywlxb.20190856 [48] GOTTFRIED J L, KLAPÖTKE T M, WITKOWSKI T G. Estimated detonation velocities for TKX-50, MAD-X1, BDNAPM, BTNPM, TKX-55, and DAAF using the laser-induced air shock from energetic materials technique [J]. Propellants, Explosives, Pyrotechnics, 2017, 42(4): 353–359. doi: 10.1002/prep.201600257 [49] 刘佳辉, 范桂娟, 卢校军, 等. TKX-50基混合炸药的爆轰及安全性能 [J]. 含能材料, 2019, 27(11): 902–907. doi: 10.11943/CJEM2019052 LIU J H, FAN G J, LU X J, et al. Detonation and safety performance of TKX-50 based PBX [J]. Chinese Journal of Energetic Materials, 2019, 27(11): 902–907. doi: 10.11943/CJEM2019052 [50] TAN K Y, HAN Y, LIU J H, et al. Detonation reaction zone and acceleration ability of a TKX-50 based polymer bonded explosive [J]. Propellants, Explosives, Pyrotechnics, 2023, 48(1): e202100367. doi: 10.1002/PREP.202100367 [51] KESHAVARZ M, ABADI Y H, ESMAEILPOUR K, et al. Novel high-nitrogen content energetic compounds with high detonation and combustion performance for use in plastic bonded explosives (PBXs) and composite solid propellants [J]. Central European Journal of Energetic Materials, 2018, 15(2): 364–375. doi: 10.22211/cejem/78091 -
图( 7) 表( 2)
计量
- 文章访问数: 33
- HTML全文浏览数: 33
- PDF下载数: 0
- 施引文献: 0