-
近些年,基于大Piwinski角的“Crab-Waist”对撞方案被提出[1]并成功被验证[2],实现更高的对撞亮度变成了可能。在陶粲能区内,相应地提出了超级陶粲装置(STCF)概念。世界范围内,目前俄罗斯[3]、意大利[4]和中国[5]各自提出了建造STCF的计划,并开展了概念性设计和前期预研工作。中国的STCF作为继第二代北京正负电子对撞机(BEPCII)之后的下一代对撞机,其总体设计方案为[6-7]:极化电子源产生极化束,经直线加速器加速后满能量注入到储存环;储存环运行质心能量范围为2~7 GeV,采用双环、完全对称结构和单个对撞点,并基于大Piwinski角的Crab-Waist对撞方案来压制束束耦合共振,从而保证亮度;在束流能量为2 GeV下,希望得到峰值对撞亮度为1.0×1035 cm−2·s−1和束流极化度85%以上,并实现纵向极化对撞。其中,束流极化作为STCF追求目标之一将在概念设计的第二阶段重点考虑,且相关研究实际上与高亮度储存环lattice设计同步展开。
纵向极化束的需求基本贯穿整个陶粲能区。利用极化束对撞可以探索陶轻子衰变的电荷共轭-宇称(CP)破坏机制、测试陶轻子衰变的标准模型、探索粲粒子衰变的CP破坏,以及在高精度前沿寻找超出标准模型的新物理等等[3]。因此,在陶粲能区内实现束流纵向极化对撞有重要研究价值和意义。然而,储存环中存在各种退极化扰动会影响束流极化。这些扰动通常很小,但是当自旋进动频率与这些扰动调制频率的线性组合相等时,扰动将相干叠加并发生自旋共振[8-9],从而使束流极化度无法维持。目前,在整个能区内克服自旋共振从而得到纵向极化束最有效的方法是在储存环中等方位角度间隔安装奇数个西伯利亚蛇装置[10-11]。西伯利亚蛇是人为引入的有益的强扰动,束流经过它时各个粒子的自旋绕一水平面上的轴线(称作“蛇轴”)转动180°,而对轨道的总体影响相当于单位映射,不影响本来的束流光学性质。通过使粒子在每相邻两圈的绕环运动中其自旋处于反相状态,从而破坏各种自旋共振的形成。西伯利亚蛇主要有螺线管蛇和弯铁蛇两种。螺线管蛇由螺线管提供纵向磁场,操纵自旋绕纵向轴旋转180°;弯铁蛇由水平和垂直弯铁以一定方式排列组合,形成自旋绕某个水平轴旋转180°的等效操纵效果。不管是哪一种蛇装置,对轨道的扰动都应控制在蛇装置内部,而尽量对蛇装置以外的束流光学不造成影响。在STCF能区,螺线管蛇是比较理想的蛇装置,相比于弯铁蛇具有这些优点[12]:首先,对轨道扰动小,不会造成设计闭轨畸变;其次,不会增加附加的同步辐射;最后,不像弯铁蛇那样容易造成束流垂直发射度增加和亮度降低。因此,它非常适合低发射度、高亮度模式下对束流极化的需求。但是,螺线管会引入轨道运动的横向耦合,需用四极铁加以补偿。为了维持束流极化的同时尽量不影响束流亮度,对蛇装置进行精心设计是十分重要的。
本文介绍了螺线管蛇作为中国STCF束流极化的维持装置所做的相关物理设计,并对设计结果进行了展示。设计过程中,粒子群算法被用来寻找和优化蛇装置的元件参数。结果表明粒子群优化算法与西伯利亚蛇物理设计的有效结合,能够使蛇装置的设计达到很高精度,从而对储存环原有光学特性尽量不造成影响。
-
储存环中的粒子自旋运动由Thomas-BMT方程[13-14]描述,即
式中:S为自旋矢量;t为时间;e为基元电荷;m0为静止电子质量;γ为相对论Lorentz因子;c为光速;v为粒子速度,B⊥和B//为垂直和平行于速度方向的磁场,E为电场,a=
0.00115965 为电子反常磁矩。对于满强度螺线管蛇,需要归一化积分场强度为π以满足对自旋180°的旋转操作,即式中:ks为螺线管归一化磁感强度参数;L为螺线管长度。束流能量为2 GeV时,要求积分场强达到
20.9336 T·m,若螺线管总长3.6 m,则所需磁感应强度为5.8149 T。由于螺线管会引入轨道运动的横向耦合,为了补偿引入的横向耦合和光学函数变化,通常需要加一组四极铁用于去耦合和匹配。文献[15]中提到的去耦合方案被广泛采用,本文也将采用这种方案。设计中需考虑以下几个因素:对环上除蛇装置以外其他部分的轨道扰动,特别是对撞点的β函数尽量做到无影响,从而保证对撞亮度。因此,蛇装置的去耦合和光学匹配需要做到足够精准;在保证光学性质的前提下,蛇装置尽量紧凑,从而节省安装空间和成本;螺线管和补偿四极铁的磁感应强度要合理。目前超导螺线管的磁场在10 T以下技术和工艺上是没问题的;对自旋要透明,即不同运动状态的粒子经过蛇装置,它们的自旋受到的作用差异要尽量小,从而有利于高极化度。接下来根据物理问题提炼出数学问题。环形加速器中粒子的轨道运动状态以闭轨为参考,并由六维相空间中的6×1状态矢量描述径向、垂直和纵向运动。以下采用x表示径向,y表示垂直方向,s表示纵向。当粒子经过线性磁铁元件时,轨道运动状态的变化可以由相应的6×6传输矩阵来表示,其中4×4的子矩阵用来描述横向运动。漂移段、正四极铁和螺线管的横向传输矩阵可分别表示为[16]
式中:D是与漂移段长度相关的2×2矩阵;E、F是与四极铁参数相关的2×2矩阵;A、B是与螺线管参数相关的2×2矩阵,矩阵B表征螺线管引入的横向耦合。
假设n块四极铁与n+1个漂移段交替相连,则整个四极铁和漂移段组合(QD)的传输矩阵为
式中:2×2矩阵
$ \boldsymbol{T}_x $ 和$ \boldsymbol{T}_y $ 是各个漂移段和四极铁参数变量的函数。假设有N(N≤2n+1)个待定参数k1、k2、…、kN,则把满强度螺线管等分为两半(此时A=B),加到QD组合的左右两边,总的传输矩阵变为
容易看出,只要QD组合满足
$ {{\boldsymbol{T}}_x} = - {{\boldsymbol{T}}_y} $ ,整个蛇装置的矩阵肯定是去耦合的形式,并且具有以下特点式中:H也是各个漂移段和四极铁参数变量的函数,一般希望把它调节成如式(12)所示的目标矩阵形式。我们把
$\boldsymbol{O}=\left(\begin{array}{*{20}{c}}1 & 0 \\ 0 & 1\end{array}\right) $ 情况对应的蛇装置称为±I蛇,$\boldsymbol{O}=\left(\begin{array}{*{20}{c}}1 & L' \\ 0 & 1\end{array}\right) $ 对应的蛇装置称为±L蛇。式中:L′为整个蛇装置的总长度。因此,蛇的设计问题相当于寻找一组合适的元件参数
$ ({k_1},{k_2}, \cdots ,{k_N}) $ ,使得以下8个非线性方程构成的方程组成立由于传输矩阵受保辛特性(行列式等于1)的约束,式(13)中第一个表达式中只有3个方程是独立的,第二个表达式也只有3个方程是独立的。因此,总的独立方程个数为6。在实际设计和应用中,通常把装置设计成中心对称的结构,这样的好处是粒子不管从装置的哪一端进入,效果大致是一样的。当QD组合关于中心对称设计时
此时必有
$ {{\boldsymbol{T}}_{x(1,1)}} \equiv {{\boldsymbol{T}}_{x(2,2)}} $ 和$ {{\boldsymbol{H}}_{1,1}} \equiv {{\boldsymbol{H}}_{2,2}} $ 。因此,对称性设计使得问题的维度再减去2。此时,为了得到合适的蛇装置,应取N≥4。由于蛇装置最终是安装在储存环上的特定位置,需要或不需要用到它时,只是将螺线管启动或关闭,并重新给定一组磁铁元件参数使整个传输段始终保持固定矩阵形式,而不可能再去改变元件的位置。因此,实际设计时其实只有四极铁参数可当作搜索变量。依照上面分析步骤可知,当螺线管关闭时,同样需要N≥4的变量调节来满足整个传输段仍为本来的矩阵形式。如果装置对称中心为四极铁,则至少需要7块四极铁来匹配蛇装置;如果装置对称中心为漂移段,则至少需要8块四极铁。用7块四极铁匹配蛇装置的设计方案如图1所示。早期一些用于粒子物理实验的机器,如阿姆斯特丹脉冲拉伸器(AmPS)[17]和麻省理工学院贝茨南大厅环(SHR)[18],由于在建造时未设计和安装蛇装置,在后期需要极化束时只能寻求在本来机器的长直线节上安装蛇装置的可行性。这种情况下往往把蛇装置设计成±L蛇形式,因为这样原先的储存环lattice结构无需重新设计,添加蛇装置进去以后,粒子径向轨道振荡tune分数部分不会改变,垂直方向轨道振荡tune分数部分变化0.5,横向运动的光学特性整体变化不大。而如今新建或者准备建造的机器,若对极化束有需求则在概念设计阶段都会把蛇装置的设计一并考虑进去,并且通常设计成±I形式。因为±I形式一方面对整个储存环lattice设计和调节非常便利,并且它不改变轨道横向振荡的tune,从而对亮度的影响能做到最小;另一方面对自旋运动更加自旋透明[19]。所以,在STCF的储存环设计中也将采用±I蛇装置。剩下的问题则是如何精准快速地设计±I蛇装置。
-
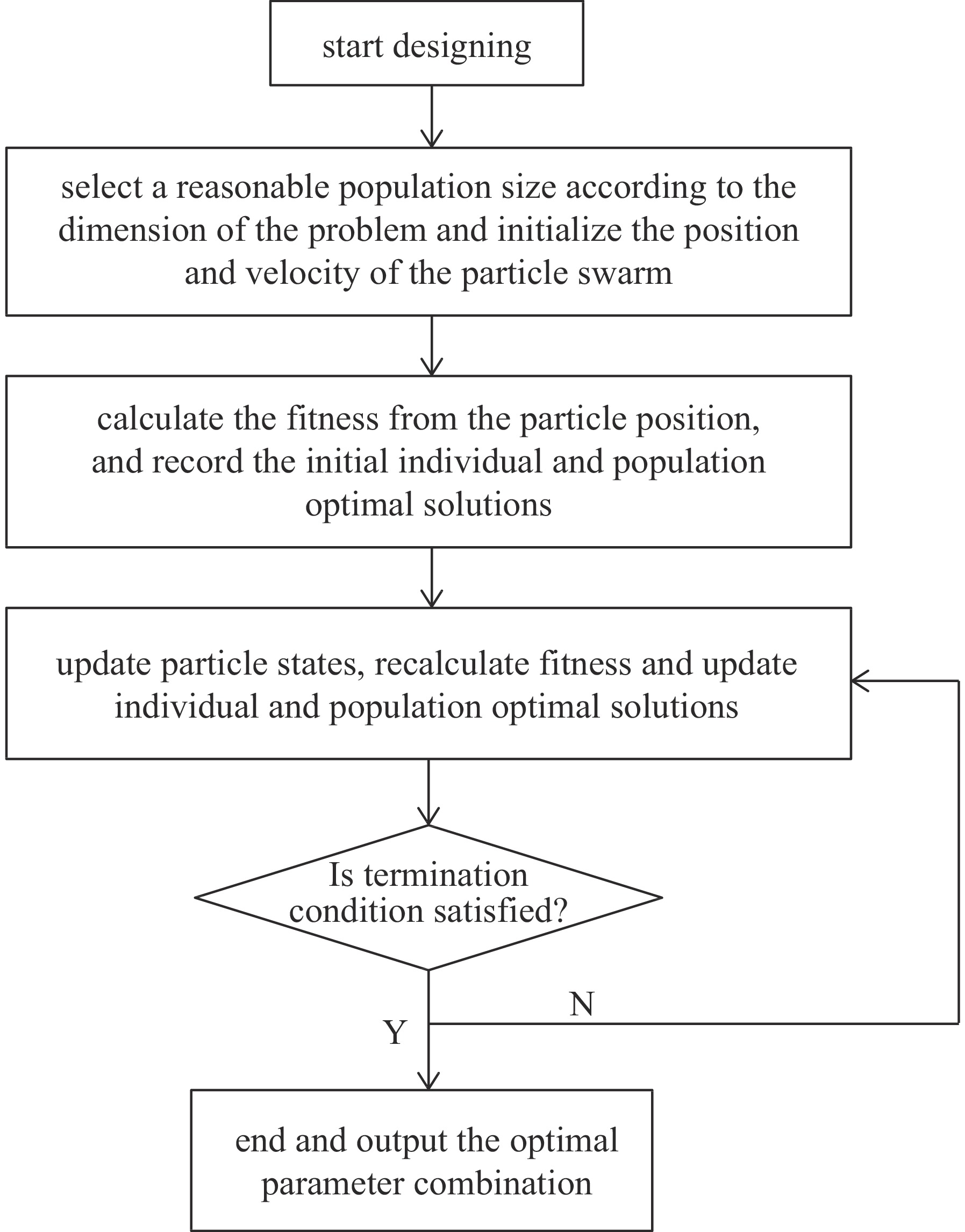
本文采用粒子群优化算法来快速设计和优化螺线管蛇装置的参数。粒子群优化算法[20]是群体智能算法的一种,思想源自于对鸟群捕食时通过个体协作和信息共享使群体达到最优目的的行为方式的研究。它具有寻优能力强、收敛速度快、设置参数少等优点,已被广泛应用于现代工程设计,在加速器领域也有相关的应用案例[21-22]。设计流程如图2所示。
首先,根据问题的维度选取合理的种群大小即粒子数,并初始化粒子群位置x和速度v。位置即一组四极铁参数取值,速度则表示各个参数的搜索快慢,它们都是抽象空间的多维矢量。对称性蛇装置设计问题维度为4,选取种群大小为它的50倍,即粒子数为200。待定四极铁参数表示为{k1, k2, k3, k4},每个粒子的位置对应一组参数取值。设定各维度的搜索范围,即给定各块四极铁参数取值范围ki∈[kimin, kimax],并在范围内初始化粒子群位置。设定粒子每个维度搜索的最大速度Vi,该值不能太小,否则算法搜索太慢容易陷入局部最优;也不能太大,否则粒子容易飞过最优解。每个粒子的速度{v1, v2, v3, v4}在vi∈[−Vi, Vi]区间随机初始化。
接着,由初始粒子位置坐标即四极铁的参数组合计算蛇装置的轨道传输矩阵,与优化目标式(11)和式(12)相比较,计算出每个粒子的适应度F,并记录初始的个体最优解pbest和群体最优解gbest。适应度通常表示当前计算结果与优化目标之间的差值,而在实际算法设计中,还会考虑到某些约束条件。本文的设计按式(15)定义执行计算,其中,Pf为根据匹配段计算结果与某些设定约束值(比如匹配段的x、y两个方向最大β函数限制等)的差值产生的罚函数。
然后,根据式(16)和式(17)更新粒子的位置和速度,若粒子位置或速度超出设定边界,则把它拉回限制值。其中,上标j表示迭代的次数,下标i表示粒子编号。w称为惯性因子,该值在搜索过程中取变化的量,一开始取0.9,使得全局优化能力较强;随着迭代的深入,w值线性递减从而使得迭代后期局部优化能力变强,直到最后取0.4。c1和c2为学习因子,一般取固定值2。r1和r2为[0,1]区间产生的随机数。由新的粒子位置即新的一组四极铁参数重新计算适应度,并更新个体最优解pbest和群体最优解gbest。
迭代过程中,判断是否满足终止条件,如迭代次数大于设定的最大迭代次数或群体最优适应度小于设定的适应度值。若满足,则终止迭代并最终输出群体最优解。否则继续执行上一步更新迭代步骤。为了使蛇装置的匹配和设计精度足够高,这里将迭代终止的适应度判据取得足够小,如10−7。当螺线管关闭时,类似地也按以上步骤优化整个传输段使其仍为±I形式。
-
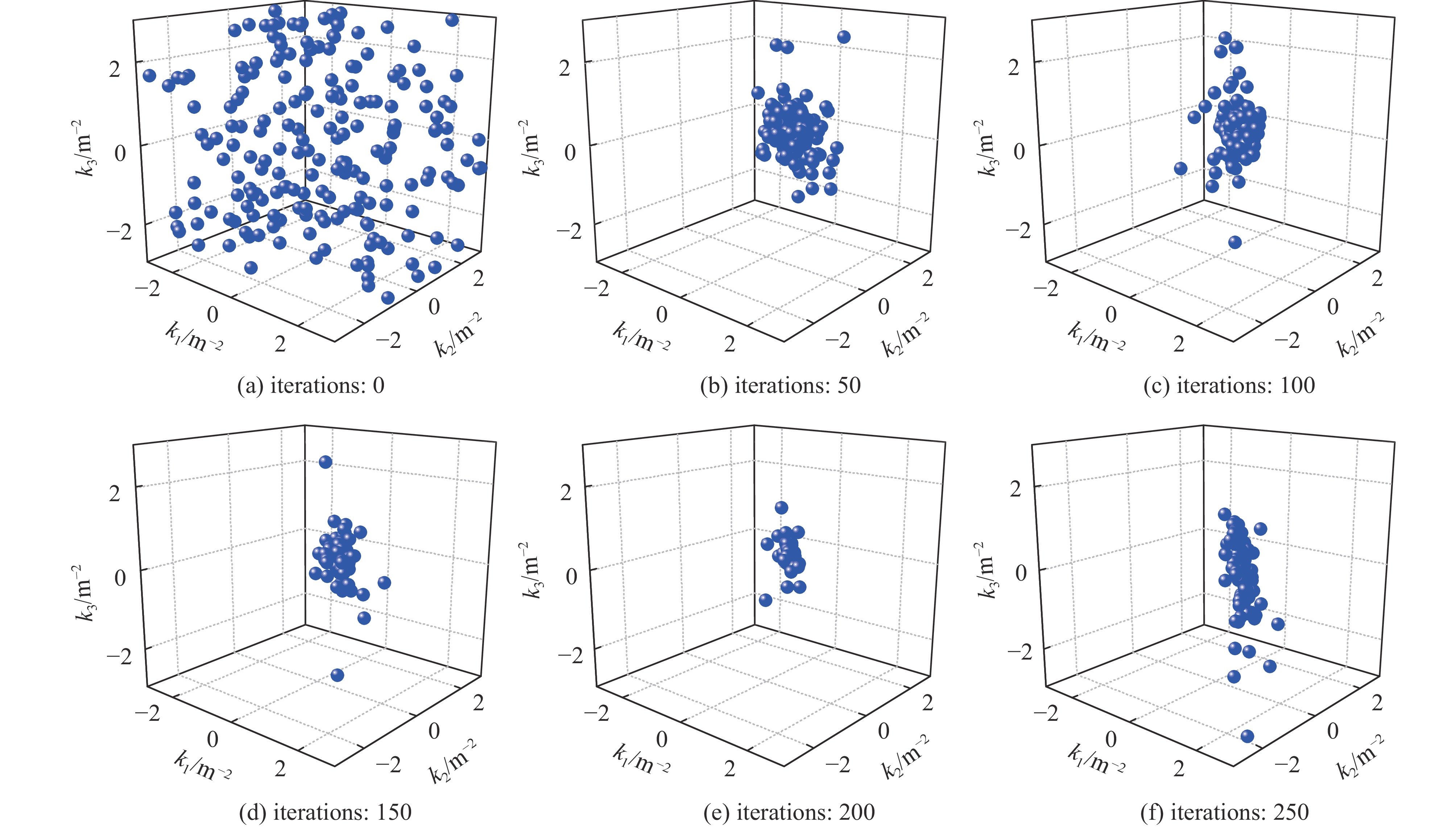
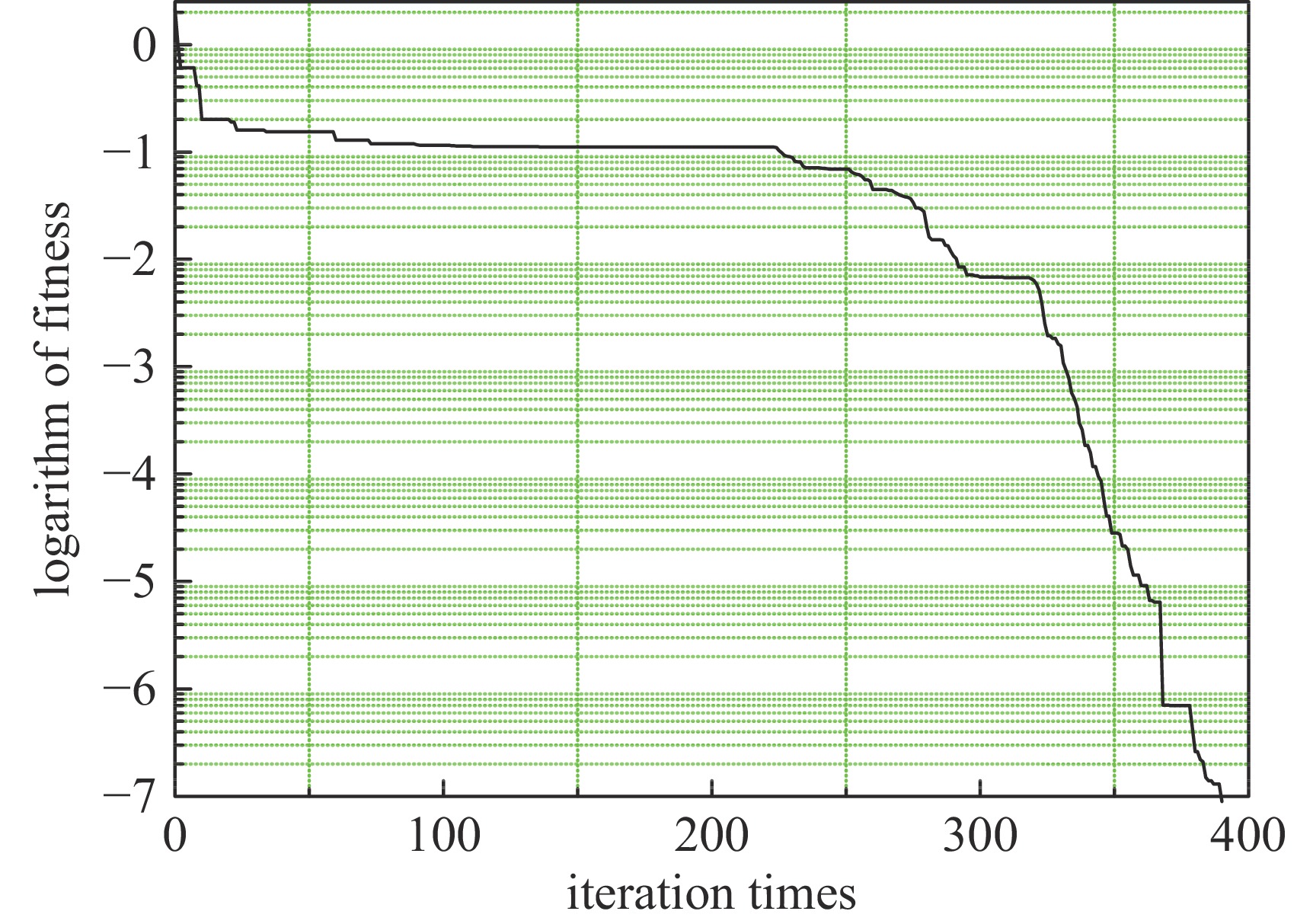
按照以上粒子群算法优化设计步骤,迭代次数每隔50次输出粒子群(其中的三个维度)分布情况如图3所示。优化过程中适应度随迭代次数的变化情况如图4所示。整个优化设计过程十分快速,且达到很高的设计精度(约10−7)。最终得到设计参数如表1所示,其中K1是四极铁强度参数。蛇装置总长10.1 m,整体比较紧凑,且元件磁场参数合理。不管螺线管开启或关闭,整个传输段的匹配结果均能快速达到约10−7的设计精度。
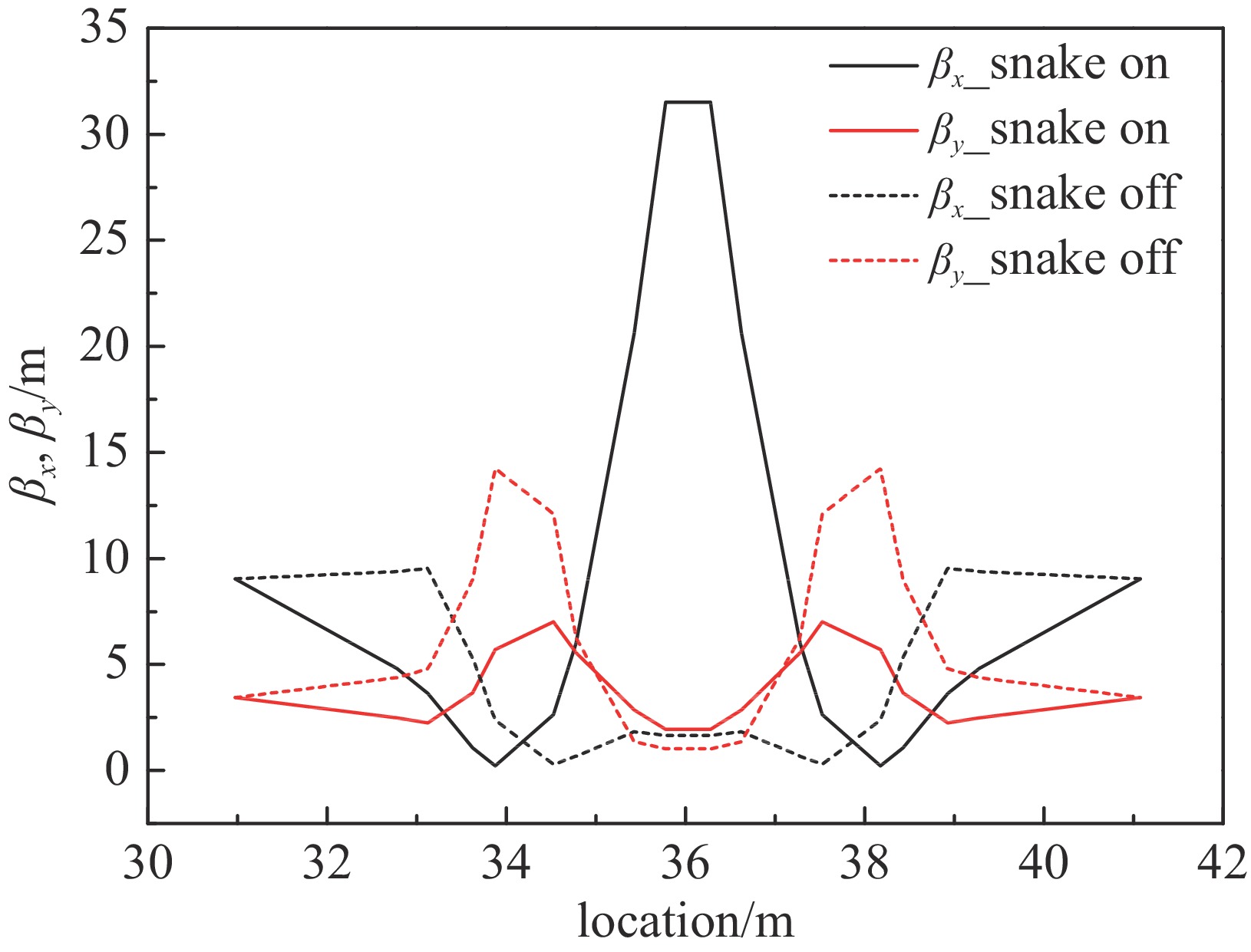
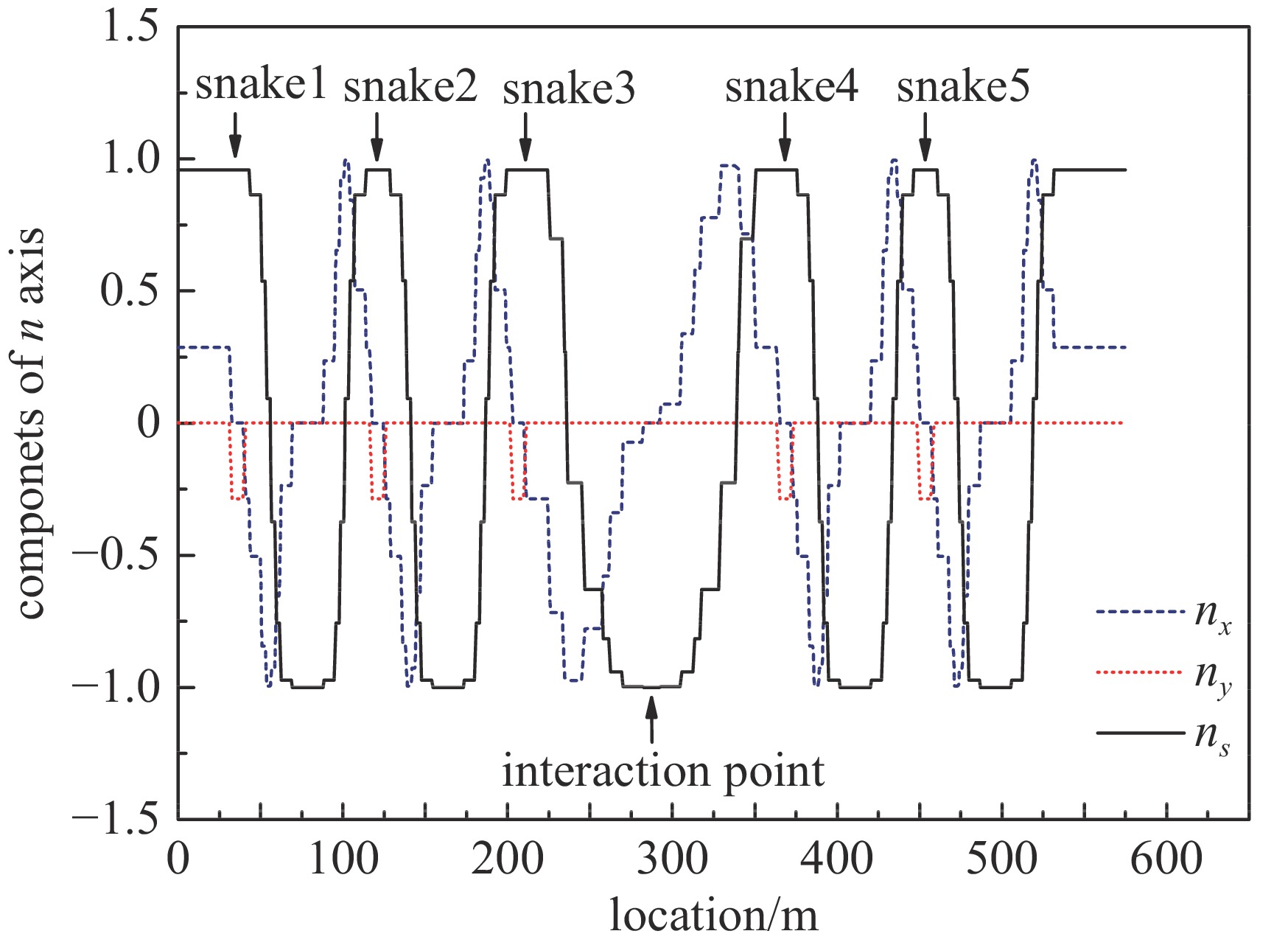
将设计好的蛇装置等方位角每间隔72°加到STCF储存环中(具体布局见文献[23]),结果显示除了蛇装置内的lattice函数有变化,如图5所示,装置以外其它部分的光学特性未受影响,表明去耦合和匹配设计足够精准,效果良好。图6显示了稳定自旋方向(通常记作n轴),即束流极化能够稳定维持的方向单位矢量的各分量沿环分布情况,并把蛇装置和对撞点所在位置标出。可以清楚看到,通过把奇数个蛇装置关于对撞点对称且等方位角分布安装,可以在对撞点位置准确得到纵向极化。
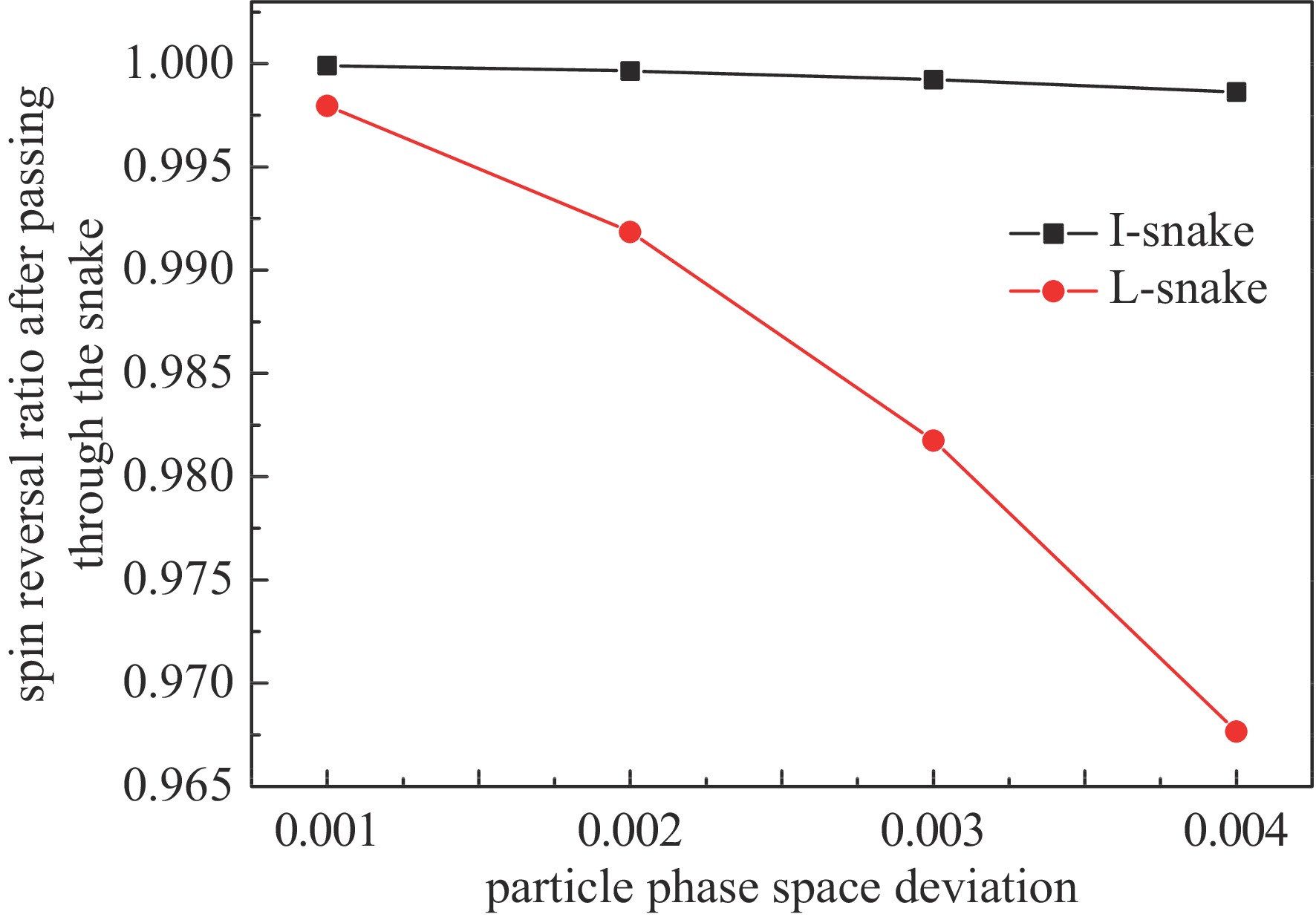
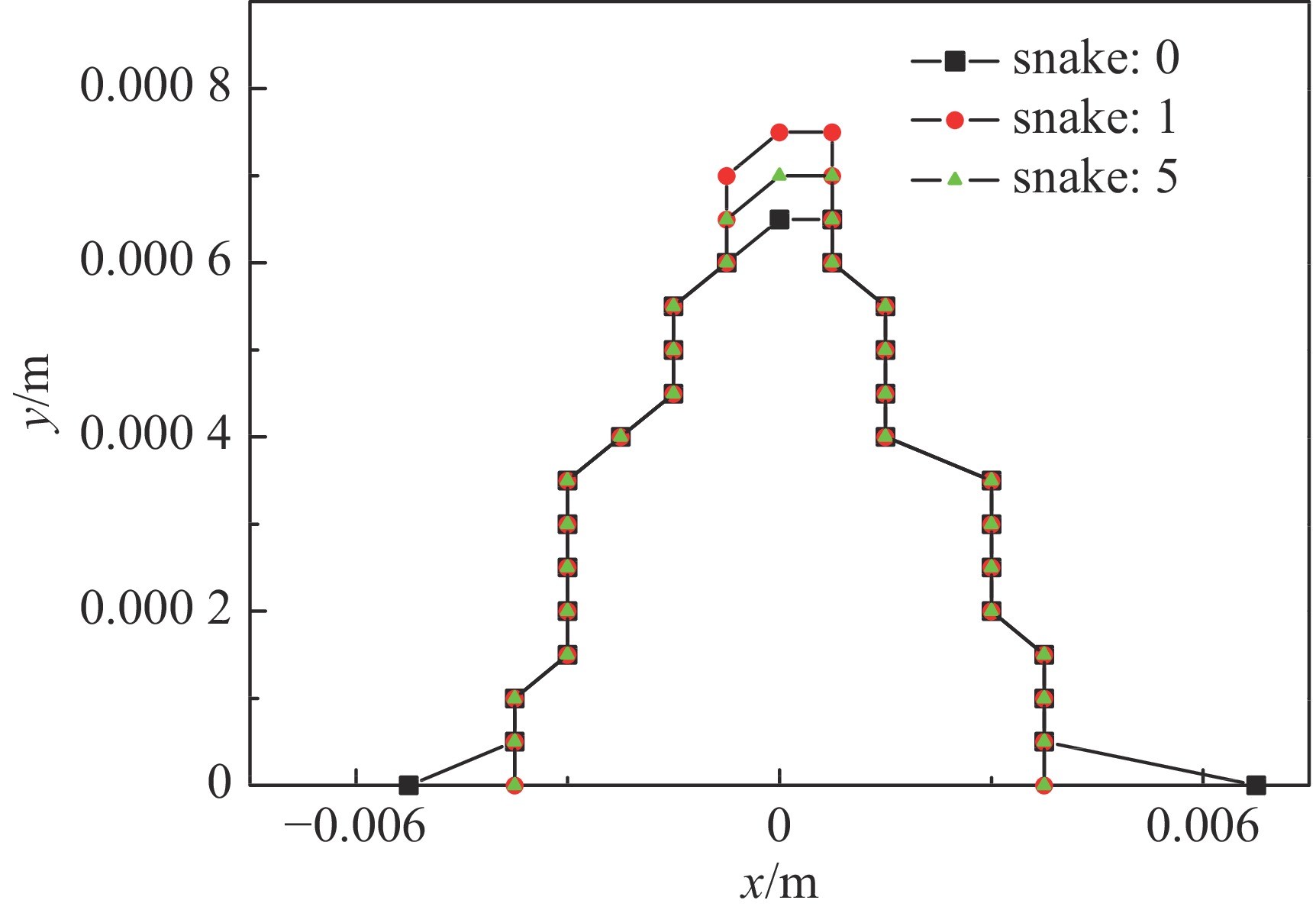
以上关于±I蛇的设计过程同样适用于±L蛇,只不过在优化过程中需要将优化目标做相应的修改,文中不再重复叙述。为了显示±I蛇的自旋透明特性,本文对不同运动状态的粒子通过±I蛇和±L蛇时的自旋转动情况进行了对比研究。将粒子进入蛇装置前的横向轨道运动相空间坐标设置为一定的数值,得到通过蛇装置后自旋方向的变化情况如图7所示。反转比率为1表示蛇装置对自旋的转动角度为精准的180°,反转比率偏离1越多则表示蛇装置对不同运动状态粒子的自旋转动角度偏离180°越多。结果显示,±I蛇明显比±L蛇对自旋运动更加自旋透明。此外,为了考察蛇装置对储存环轨道运动非线性表现的影响,在六极铁参数保持不变的情况下,对蛇装置关闭以及蛇装置打开1个、5个时的动力学孔径进行了跟踪对比,结果如图8所示。可以看出,蛇装置打开和关闭两种情况下动力学孔径差别不大。这主要由于整个传输段在蛇装置打开或关闭时均精准设计成±I形式,未对轨道振荡的tune造成改变。
-
本文选取螺线管型西伯利亚蛇作为超级陶粲装置中维持束流极化的装置,并采用等方位角间隔安装的方式来实现对撞点位置纵向极化。通过分析螺线管蛇设计中的去耦合和光学匹配问题,确定优化目标和所需调节的元件参数变量个数,详细介绍了应用粒子群优化算法对它进行快速精准设计的过程。结果显示,粒子群优化算法与西伯利亚蛇物理设计的有效结合,能够使蛇装置的设计达到很高精度,从而对储存环原有光学特性尽量不造成影响。这对超级陶粲装置所追求的高极化度和高亮度是至关重要的。本文中的问题分析和解决方法也可为加速器设计中的其他多参数优化问题提供参考。
致 谢 感谢自旋动力学专家S. R. Mane给予的帮助和讨论。
基于粒子群优化算法设计超级陶粲装置中的螺线管蛇装置
Design of solenoid snake for Super Tau-Charm Facility based on particle swarm optimization algorithm
-
摘要: 在环形对撞机中等方位角间隔安装奇数个西伯利亚蛇是用来获得纵向极化束对撞的通常方案。根据超级陶粲装置的特点,选取螺线管型西伯利亚蛇作为维持束流极化的装置。详细介绍了如何把粒子群优化算法与螺线管蛇去耦合和光学匹配问题相结合,对它进行快速优化设计,并对设计结果进行了展示。结果显示,基于粒子群算法的螺线管蛇优化设计有效且高效。Abstract: Installing an odd number of Siberian snakes at equal azimuth intervals in a circular collider is a common scheme for obtaining longitudinally polarized beam collisions. In this paper, the solenoid Siberian snake is selected as the device to preserve beam polarization in the Super Tau-Charm Facility according to its characteristics. The paper introduces in detail how to combine particle swarm optimization algorithm with decoupling and optical matching problem of solenoid snake to design it quickly and optimally, and presents the design results. The results show that the optimization design of solenoid snake based on particle swarm optimization algorithm is effective and efficient.
-
Key words:
- solenoid snake /
- particle swarm optimization /
- Super Tau-Charm Facility /
- longitudinal polarization /
- decoupling .
-

-
表 1 ±I螺线管蛇装置主要设计参数
Table 1. Main design parameters of ±I solenoid snake
solenoid ks /m−1 solenoid L/m K1/m−2 Q1 Q2 Q3 Q4 snake on 0.8722 1.8×2 2.38494523 − 1.78215169 0.12879834 2.08811998 snake off 0 1.8×2 2.24210204 − 2.69629201 2.93748997 0.07303464 -
[1] Raimondi P. Status on super-b effort[C]//3rd Workshop on Super Flavor Factory based on Linear Collider Technology (Super B III). 2006. [2] Zobov M, Alesini D, Biagini M E, et al. Test of “crab-waist” collisions at the DAΦNE Φ factory[J]. Physical Review Letters, 2010, 104: 174801. doi: 10.1103/PhysRevLett.104.174801 [3] Anashin V V, Anisenkov A V, Aulchenko V M, et al. Super charm-tau factory conceptual design report part two (collider, injector)[R]. Novosibirsk, Russia: BINP SB RAS, 2018. [4] Biagini M E, Boni R, Boscolo M, et al. Tau/Charm factory accelerator report[R]. Frascati: INFN, 2013. [5] Zhao Zhengguo. Introduction to future high intensity collider @ 2-7 GeV in China[C]//Workshop on Physics at Future High Intensity Collider @ 2-7GeV in China. 2015. [6] 黄光顺, 李澄, 李海波, 等. 2~7GeV高亮度正负电子对撞机的物理研究[J]. 科学通报, 2017, 62(12):1226-1232 doi: 10.1360/N972016-00398 Huang Guangshun, Li Cheng, Li Haibo, et al. Physics on the high intensive electron position accelerator at 2~7 GeV[J]. Chinese Science Bulletin, 2017, 62(12): 1226-1232 doi: 10.1360/N972016-00398 [7] Luo Qing, Xu Derong. Progress on preliminary conceptual study of HIEPA, a super Tau-Charm factory in China[C]//9th International Particle Accelerator Conference. 2018: 422-424. [8] Lee S Y. Spin dynamics and snakes in synchrotrons[M]. River Edge: World Scientific Press, 1997. [9] Mane S R, Shatunov Y M, Yokoya K. Spin-polarized charged particle beams in high-energy accelerators[J]. Reports on Progress in Physics, 2005, 68(9): 1997-2265. doi: 10.1088/0034-4885/68/9/R01 [10] Derbenev Y S, Kondratenko A M, Serednyakov S I, et al. Radiative polarization: obtaining, control, using[J]. Particle Accelerators, 1978, 8: 115-126. [11] Mane S R, Shatunov Y M, Yokoya K. Siberian Snakes in high-energy accelerators[J]. Journal of Physics G: Nuclear and Particle Physics, 2005, 31(9): R151-R209. doi: 10.1088/0954-3899/31/9/R01 [12] Kondratenko A M, Kovalenko A D, Kondratenko M A, et al. Comparison of solenoid, helix and dipole Siberian snake in the NICA collider[C]//Joint Institute for Nuclear Research XV Workshop on High Energy Spin Physics. 2013. [13] Thomas L H. The motion of the spinning electron[J]. Nature, 1926, 117: 514. [14] Bargmann V, Michel L, Telegdi V L. Precession of the polarization of particles moving in a homogeneous electromagnetic field[J]. Physical Review Letters, 1959, 2(10): 435-436. doi: 10.1103/PhysRevLett.2.435 [15] Zhelents A A, Litvinenko V N. On the compensation of solenoid field effects by quadrupole lenses[R]. DESY L-TRANS-289, 1984: 1-8. [16] Iselin F C. The MAD program (methodical accelerator design) version 8.13 physical methods manual[M]. Geneva: Eurpean Organization for Nuclear Research, 1994. [17] Liujckx G, Van Amersfoort P W, Boer-Rookhuizen H, et al. Polarized electrons in the AmPS storage ring[C]//Proceedings of the 1997 Particle Accelerator Conference. 1997: 1063-1065. [18] Zwart T, Ivanov P, Shatunov Y, et al. A spin control system for the south hall ring at the bates linear accelerator center[C]//Proceedings of the 1995 Particle Accelerator Conference. 1995: 600-602. [19] Koop I A, Otboev A V, Shatunov P Y, et al. Spin transparent Siberian snake and spin rotator with solenoids[J]. AIP Conference Proceedings, 2007, 915(1): 948-954. [20] Kennedy J, Eberhart R C. Particle swarm optimization[C]//IEEE International Conference on Neural Networks. 1995: 1942-1948. [21] Zhang Tong, Huang Xiaobiao. Numerical optimization of a low emittance lattice cell[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2019, 923: 55-63. [22] Jiao Yi, Xu Gang. Optimizing the lattice design of a diffraction-limited storage ring with a rational combination of particle swarm and genetic algorithms[J]. Chinese Physics C, 2017, 41: 027001. doi: 10.1088/1674-1137/41/2/027001 [23] Lan Jieqin, Luo Qing, Zhang Chun, et al. Design of beam optics for a super tau-charm factory[J]. Journal of Instrumentation, 2021, 16: T07001. doi: 10.1088/1748-0221/16/07/T07001 -


 首页
首页 登录
登录 注册
注册



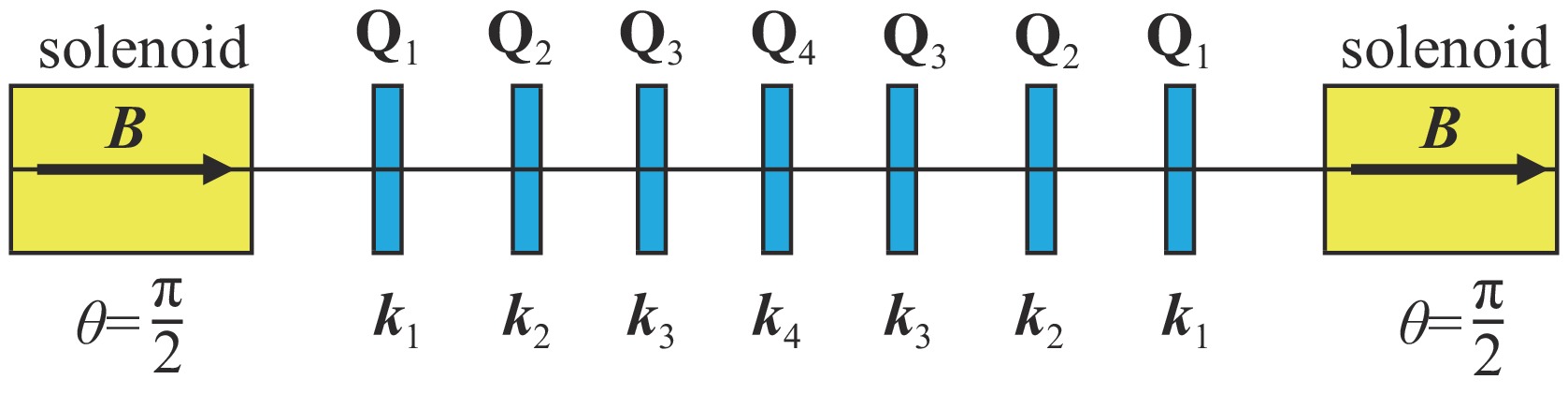
 下载:
下载: