近年来, 在海洋地震勘探和水声学研究中广泛使用低频和甚低频段声波, 随着频率的降低深层海底对声传播的影响越来越大。对地声环境建模时通常采用简化的等效海底模型, 以便在保证精度的情况下预报海洋中的声场^[1-2]。然而, 对特定频率等效海底模型需考虑的海底深度却缺少深入研究。地声环境模型需考虑的有效海底深度, 取决于水下声场对特定深度上的海底参数是否敏感。因此, 需建立水下声场对底质参数敏感特性的分析方法, 在不同频段、不同距离上给出典型环境下的地声参数敏感特性。

水声学研究中, 典型海洋环境如Pekeris波导^[3]、深海SOFAR信道^[4]和距离有关楔形波导^[5]等均将海底视为半无限, 在中高频段声场预报中取得了较好的结果^[6]。Fokina等^[7]指出, 在甚低频段传统的Pekeris海底模型得到的传播损失结果与实验结果不一致, 因为对于甚低频信号, 海底引起的能量损失不可忽略。因此, 为了更准确地预报声场, 使理论与实验得到的传播损失曲线符合得更好, 需考虑疏松沉积层的吸收衰减和海底分层结构的影响。近年来, 甚低频水下声场特性的研究中, 越来越关注海底分层结构的影响^[8-11]。

现有关于地声参数敏感特性的研究主要围绕地声参数反演, 即分析反演中代价函数对待反演地声参数的敏感性, 如在选定环境模型基础上, 改变单一的待反演参数, 通过代价函数随地声参数的变化分析其对该参数的敏感性^[12]。Zheng等^[13]在半无限海底环境下, 以实测声压场与拷贝场的差值构建代价函数, 通过仿真代价函数随单一参数的变化分析了代价函数对地声参数的敏感性。基于Bayesian反演的后验概率密度也可反映代价函数对待反演参数的敏感性^[14]。Li等^[15]利用Scholte波频散特性反演海底横波声速剖面时, 估计模型参数的边缘概率分布, 对比了以基阶Scholte波和多阶模态频散特性作为代价函数进行反演的地声模型参数的敏感性。郭晓乐等^[16]等根据模态频散时间差反演海底声速和密度, 根据传播损失反演海底衰减。模型参数的边缘概率分布表明, 代价函数对沉积层和基底层声速的敏感性较强, 对沉积层厚度、沉积层密度和基底层密度敏感性较差, 反演的海底声速的可信度最高。

地震成像中通常采用时延敏感核分析介质声速变化对地震波传播时间的影响, 近年来关于敏感核的研究逐渐发展到水声学领域, 并应用于海洋声层析及水下目标定位等。敏感核的概念最早来自地震学^[17-18], 应用于走时层析成像, 常用的敏感核可分为两大类, 射线走时敏感核和有限频走时敏感核。有限频敏感核考虑实际声波频率的有限性而非射线理论的高频近似, 即声波在介质中传播时存在散射及衍射效应, 认为声波的传播时延对本征声线以外的结构(第一菲涅尔带)同样敏感, 是波动方程的一阶Born近似^[19]。Skarsoulis等^[20]在二维和三维水声环境中利用抛物近似计算了波动理论传播时延敏感核, 研究了其随传播距离增加的变化情况, 并与射线理论及其相应的菲涅尔带进行了比较。温凤丹等^[21]分析了距离有关的水声波导中的传播时延敏感核。但上述研究仅分析了水体中的敏感核, 考虑了不同的水下声速剖面环境以及海洋中尺度现象的距离有关环境, 没有包含海底分层结构。

针对不同频段需建立怎样的底质环境模型尚无定论。本文结合我国周边浅海海域历史调查数据, 建立了典型水平分层浅海环境模型。在该环境模型基础上, 利用声压敏感核的幅度分析水下声场对海底底质参数的敏感程度。当海底地声环境中存在声速扰动时, 声信号的幅度、相位、传播时间等代价函数会随之发生变化, 敏感核显示了引起这种变化的空间位置和强弱分布, 可用于直观研究水下声场对海底环境参数的敏感特性。水声工程应用包括声呐方程中多以声强衡量信号强弱, 因此本文目标函数选择频域声压。稳态声场对海底地声参数的声压敏感核考虑了所有多途共同作用的稳态声场对海底地声参数的敏感特性, 可以明确海底对甚低频声波导的贡献, 为海底地声参数的获取以及甚低频声探测等提供参考。

地球物理学研究表明, 受压实效应的影响, 地层声速与深度的变化成正比关系, 即地层声速随深度的增加而增加。海底介质往往表现为具有垂向对称轴的横向各向同性特征(即水平分层介质), 导致体波和面波的正折射和反射。因此声信号特别是低频和甚低频声信号可以返回至水体中。在这种情况下, 简化模型^[3-5]框架下预测的在水体中传播的不同类型的波的能量将不再准确。

为分析水下声场海底地声参数的敏感特性, 根据实际底质演变规律建立海底底质基本规律模型, 如图1所示, 在构建该模型时使用了文献[22]报道的数据。地球结构分为地核、地幔和地壳, 在不同海域地壳的厚度不同。在深海区域, 厚度约为7 km, 而在大陆架区域, 厚度可达25~70 km。而水声研究中所关心的声源通常为微弱信号, 即使频率较低其能量也无法达到地壳以下, 因此本文仅考虑地壳。除地层厚度和介质声速外, 介质对声波的吸收衰减系数也是地声环境的重要参数, 本文以经验公式确定吸收衰减系数, 低频段(<1 kHz)海底吸收衰减随频率近似线性变化^[23]:

其中, $ \delta $为每1 kHz声波的标准对数衰减系数。

Helmholtz方程的解可以表示为分离的深度方程解的波数积分形式^[24]。在水声学中, 采用快速傅里叶变换进行波数的积分计算也叫快速场理论(FFM); 在地震学中, 通常称为反射法或离散波数方法。

对Helmholtz方程应用汉克尔变换, 可得深度分离的波动方程:

式(2)的解即为深度有关格林函数$ \psi \left( {{k_r},{\textit z}} \right) $, 水声学中通常采用全局矩阵法、传递矩阵法等求解该式。

特定接收距离r和深度z上的声场$ P(r,{\textit z}) $可写为对水平波数的积分形式, 即数值计算深度z处深度分离波动方程解的反汉克尔变换:

其中, 贝塞尔函数$ {{\rm J} _m}({k_r}r) $的阶数为$m = 0$。首先将贝塞尔函数表示为汉克尔函数:

其中, $ {\rm H} _m^1\left( {{k_r}r} \right) $对应于前向传播声波, $ {\rm H} _m^2\left( {{k_r}r} \right) $对应于后向传播声波。后一项仅在表示极短范围内的驻波场时较为重要, 此时被忽略。用渐近形式代替$ {\rm H} _m^1\left( {{k_r}r} \right) $:

得到汉克尔反变换的渐近表达式:

式(6)为傅里叶变换形式, 可以经过离散转化成离散傅里叶变换形式, 采用快速傅里叶变换(FFT)算法进行声场的快速求解。本文采用OASES声场计算软件, 使用波数积分结合直接全局矩阵求解来模拟水平分层波导中的声波传播。

用来描述水下声场的谐和点源的格林函数$ G\left( {{\boldsymbol{r}}|{{\boldsymbol{r}}_s}} \right) $满足以下Helmholtz方程:

其中, $ {\boldsymbol{r}} $表示空间位置矢量, $ {{\boldsymbol{r}}_s} $为声源位置, $ \omega $表示声源的角频率, $ c\left( {\boldsymbol{r}} \right) $表示空间声速分布, $ \delta $表示Dirac函数。

任意空间分布的声源函数$ S\left( {\boldsymbol{r}} \right) $激发的声场$ P\left( {\boldsymbol{r}} \right) $满足Helmholtz方程:

且声场$ P\left( {\boldsymbol{r}} \right) $可以表示为格林函数和声源函数乘积的积分:

引入散射理论中的一阶Born近似, 认为声速的小扰动$ \Delta c $将引起格林函数的小扰动$ \Delta G $, 扰动后的格林函数$ G + \Delta G $满足

式(10)减去式(7), 等号两侧同时加$ {{{\omega ^2}\Delta G} \mathord{\left/ {\vphantom {{{\omega ^2}\Delta G} {{c^2}}}} \right. } {{c^2}}} $, 可得

比较式(11)和式(8), 可将式(11)等号右侧项当成一扰动声源的声源函数$ S\left( {\boldsymbol{r}} \right) $, 散射场由此扰动声源激发, 利用式(9)可得格林函数扰动$ \Delta G $的表示式:

忽略式(12)中$ \Delta c $的高阶项, 仅保留其一阶项, 可得格林函数扰动的一阶函数:

频域声压扰动可记为$\Delta P\left( {{\boldsymbol{r}}|{{\boldsymbol{r}}_s}} \right) = \Delta G\left( {{\boldsymbol{r}}|{{\boldsymbol{r}}_s}} \right)$。敏感核反映了有限频近似下目标函数对模型扰动的敏感程度, 其本质上是目标函数(声压幅度)对模型参数(速度)的一阶偏导数(Fréchet导数), 根据敏感核定义式^[25]:

频域声压幅度敏感核

是声速扰动和声场变化量之间的关系量。声速变化引起的声场扰动可以通过敏感核对整个声场的体积分得到, 即如果已知灵敏度核函数及海底声速扰动, 目标函数的扰动量就可根据式(14)求得, 式(14)也体现了敏感核的应用意义。须注意的是, 基于一阶Born近似推导的敏感核只适用于弱散射介质情况, 根据参考文献[26-27], 一阶Born近似有限频理论允许的最大速度扰动为10％。本文后续关于地声参数的影响分析所得结论仅适用于声速的小扰动情况, 对于速度变化剧烈的介质突变环境不适用。

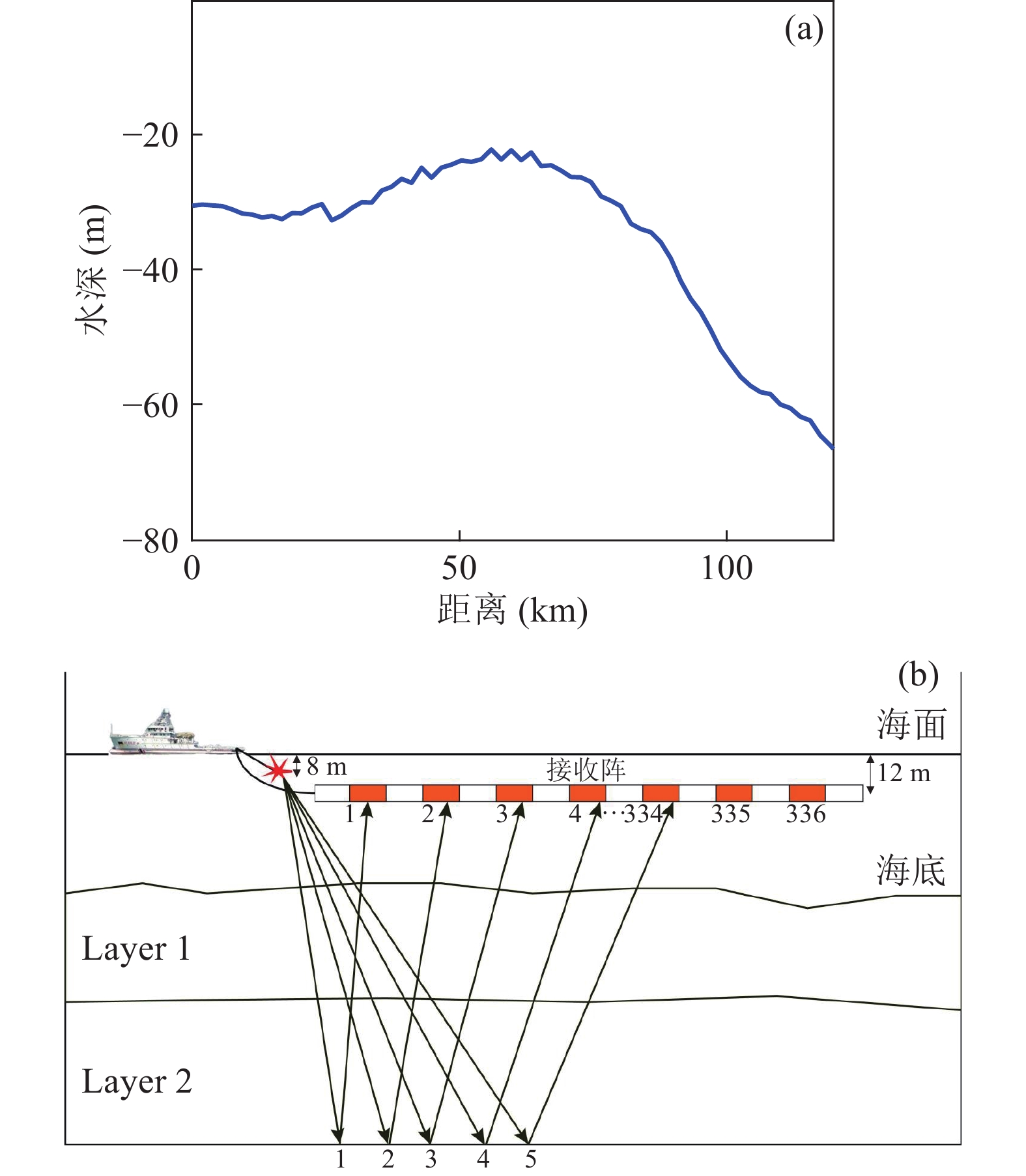
本节首先结合南黄海一次多道地震勘探实验数据, 对本文提出的地声参数敏感性分析方法进行验证。实验测线全长超过100 km, 测线自东向西水深变化如图2(a)所示, 水深在22~70 m之间。调查船和实验设备的布置见图2(b)。地震拖缆长4187.5 m, 共336个接收器, 在水深12 m处拖曳, 接收数据以SEG-D格式记录, 采样间隔为2 ms, 数据长度为8 s。声源为总容量2940 in³的气枪阵列, 由18个气枪组成, 拖曳深度为8 m, 发射间隔为37.5 m。

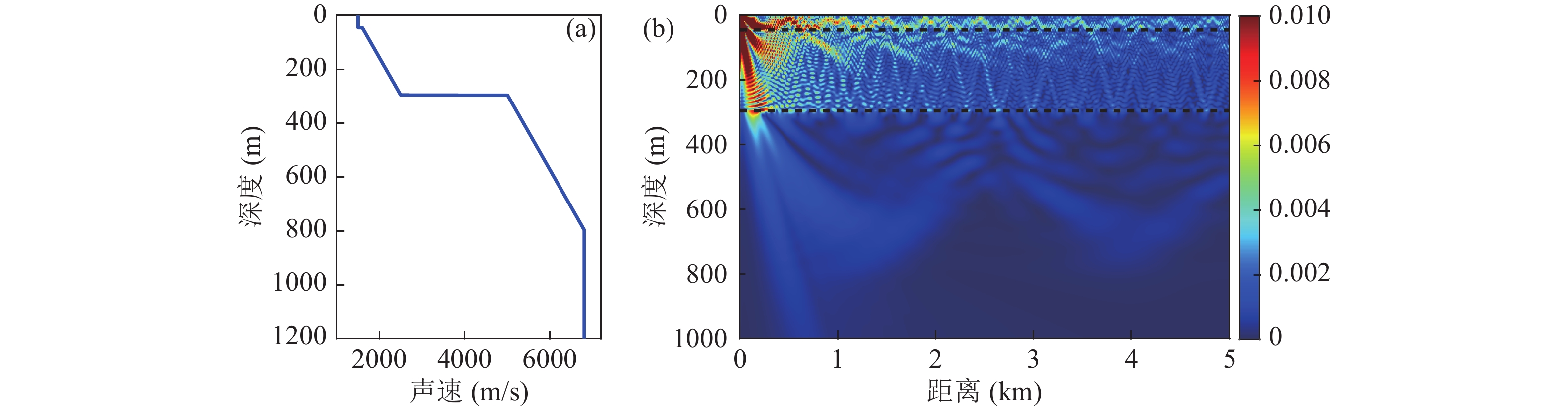
首先根据地质勘探结果, 建立南黄海底质环境模型, 计算声压幅度敏感核分析水下声场的地声环境敏感特性。图3是对应测线的多道地震成像结果, 实验海域岩石层埋深较浅, 自西向东沉积层厚度由100 m变化到400 m, 岩石层上界面双程走时由0.2 s变化到0.5 s。此外, 南黄海历史调查数据显示, 海底沉积层并非均匀介质, 南黄海诸盆地内砂、泥岩地层存在100~600 m/s的速度差, 能形成较好的反射。因此, 实验海域环境既有明显的分层结构, 在层内又有较大的声速梯度。综上, 建立南黄海实验海域环境模型, 如图4(a)所示, 海水深度和沉积层厚度取平均值, 分别设为45 m和250 m, 声速梯度则为地震剖面处理流程中正常时差校正时获得的叠加速度谱。

利用OASES计算的声场格林函数, 如图4(b)所示, 海底界面反射波和海底反转波能量均可以返回水体中, 由水中的传感器接收。沉积层和岩石层由于存在声速梯度都有声线反转, 反转深度分别为150 m和680 m。该环境下, 沉积层和岩石层速度差较大, 界面阻抗大, 因此能形成较好的反射, 海底分层的反射信号相较于反转信号能量更强。

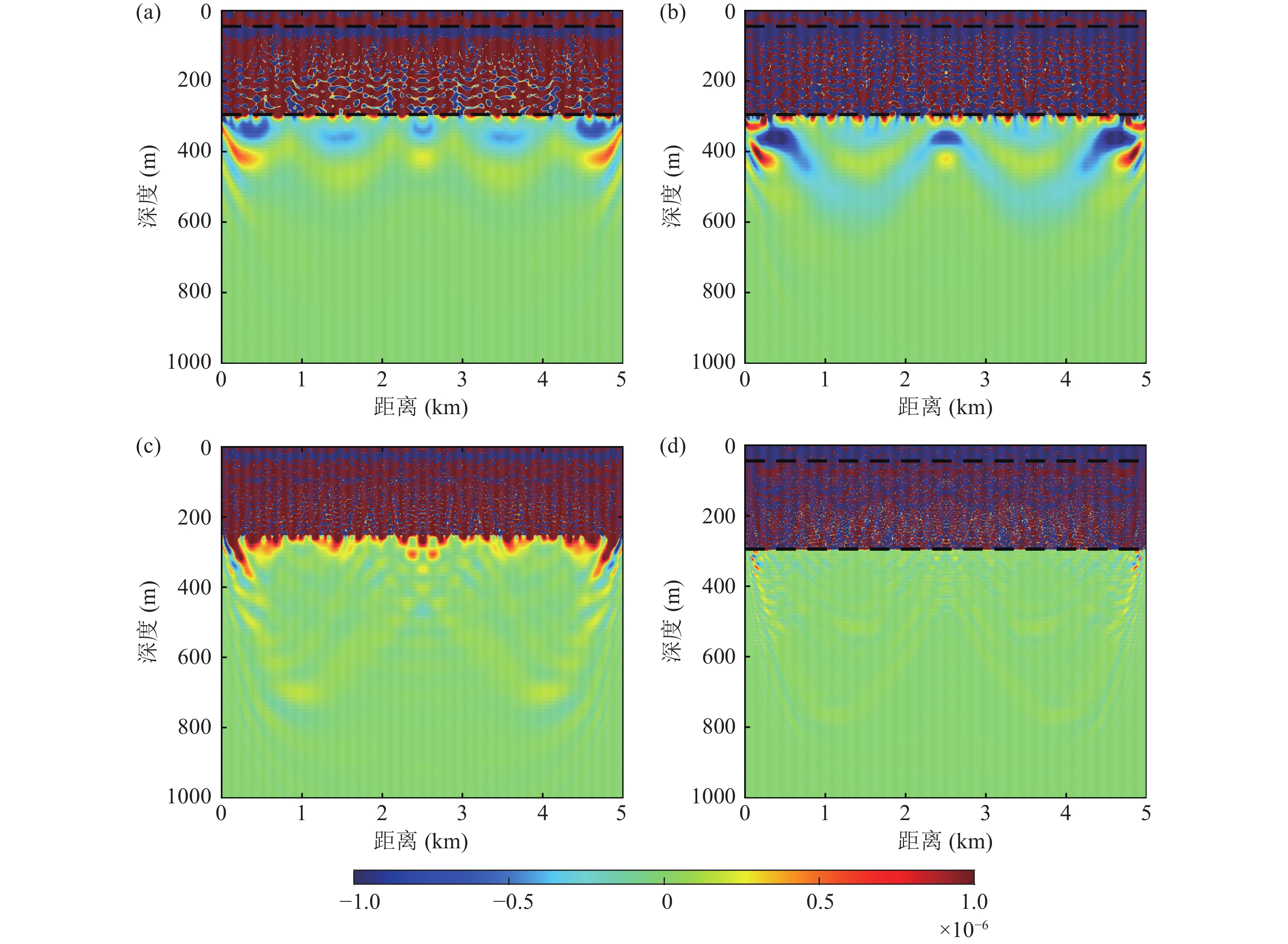
图5为不同频率下声压敏感核的分布, 由于气枪声源为低频声源, 因此这里只对200 Hz以下的频段进行地声参数敏感性分析。频率低于100 Hz时, 岩石层仍有敏感度, 但敏感核在分层界面以下比较微弱, 这是因为该环境下岩石层十分坚硬, 沉积层和岩石层阻抗差较大导致界面反射系数较大, 大部分能量都经界面反射; 同时也导致该环境下, 水中声压对沉积层内的地声参数敏感度较高。

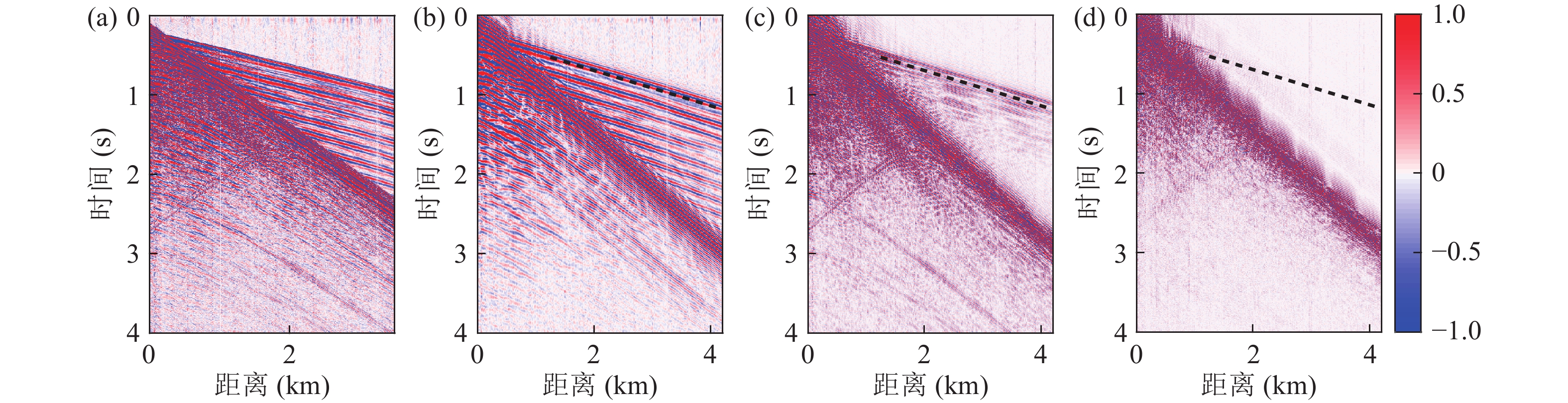
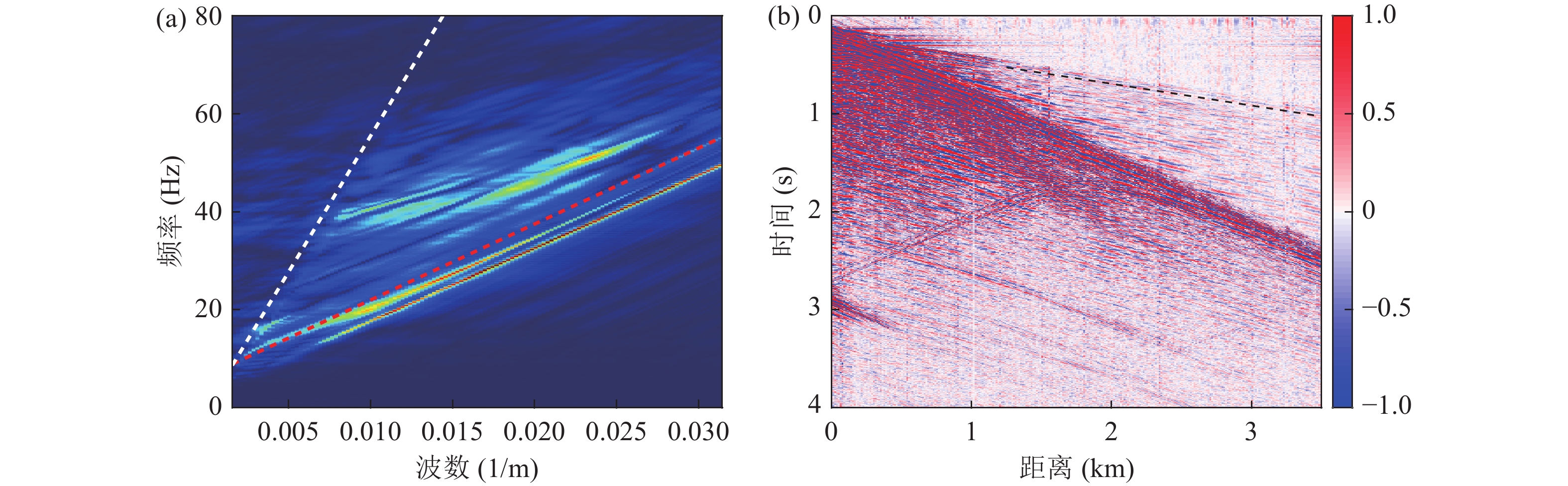
侧面波不受频率影响, 只要入射角达到临界角全频段皆可激发, 更适合用于衡量不同频段信号在海底的渗透情况。南黄海实验海域环境下, 基岩埋深较浅且速度高, 更易激发沿岩石层传播的侧面波, 可作为衡量岩石层对水下接收声场影响的指标。图6为第200炮接收信号的频率扫描结果, 在0~100 Hz频段内声源级高于200 dB, 声源频谱平缓。图中白色虚线给出了岩石层层海底侧面速度为4500 m/s, 如图3所示第200炮所在位置沉积层厚度约为250 m。如图6(b)(c)(d)所示, 随着频率的升高, 侧面波逐渐减弱, 即频率越低水中接收的声压信号受岩石层影响越大。

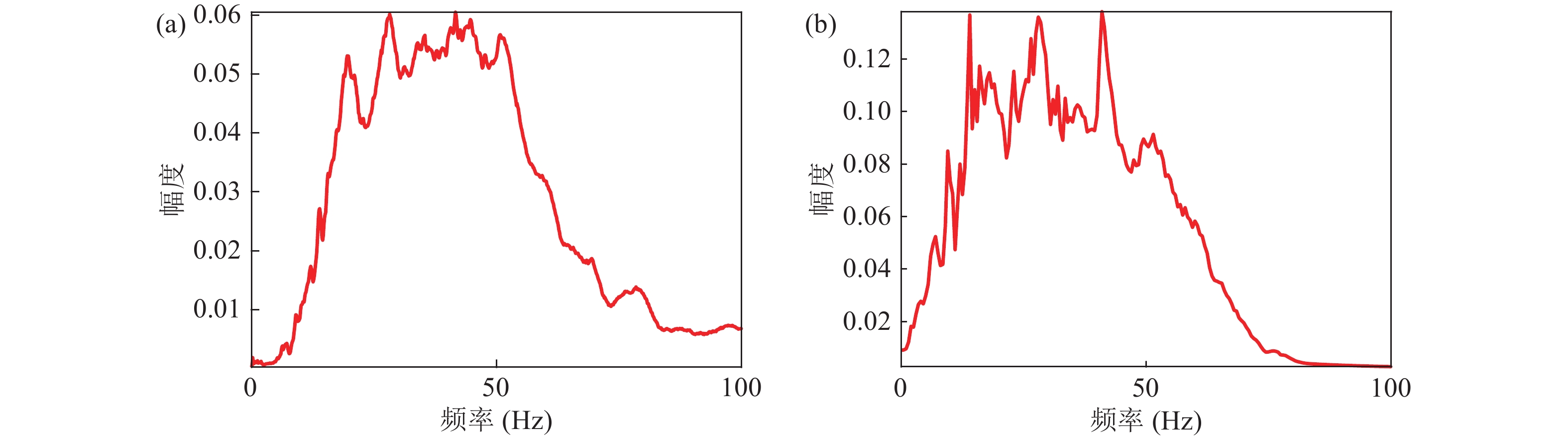
为进一步分析不同频段的海底影响深度, 在频率波数域滤除水声信号及侧面波信号, 仅保留海底底层反射及反转波数据。通过二维傅里叶变换将图6(a)所示时间−距离域声压数据变换至频率−波数域, 如图7(a)所示。该炮点所在海域水深45 m, 在选定频段(0~80 Hz)仅支持2阶水中模态传播, 图中红色虚线以下为水中模态, 图中白色虚线对应速度为4500 m/s, 即侧面波速度。在频率−波数域设计滤波器, 将红色虚线以下的水声信号区域以及白色虚线处的侧面波信号设为0滤除, 其中侧面波信号的滤波器宽度设置为$ \pm 10$ m/s, 滤波后的数据如图7(b)所示。

滤波后的数据仅包含地声信号, 对其分时段进行频谱分析, 可近似为不同深度反射信号的频谱, 图8为滤波后数据的分时段平均频谱。实验海域数据浅层频带宽, 中深层衰减较快, 频带窄。浅层0~0.5 s有效频宽为20~60 Hz; 0.5~1.0 s有效频宽为10~40 Hz; 更深层数据信号微弱、信噪比较低, 甚低频段受本底噪声干扰严重, 这里不做分析。根据图3所示地震剖面, 0.5 s对应于岩石层界面的双程走时, 1.0 s则约为岩石层反转信号的双程走时, 因此南黄海实验海域考虑沉积层的频带约在60 Hz左右, 而40 Hz以下则须考虑岩石层的声速梯度, 这一结论与上一节仿真结果相符。

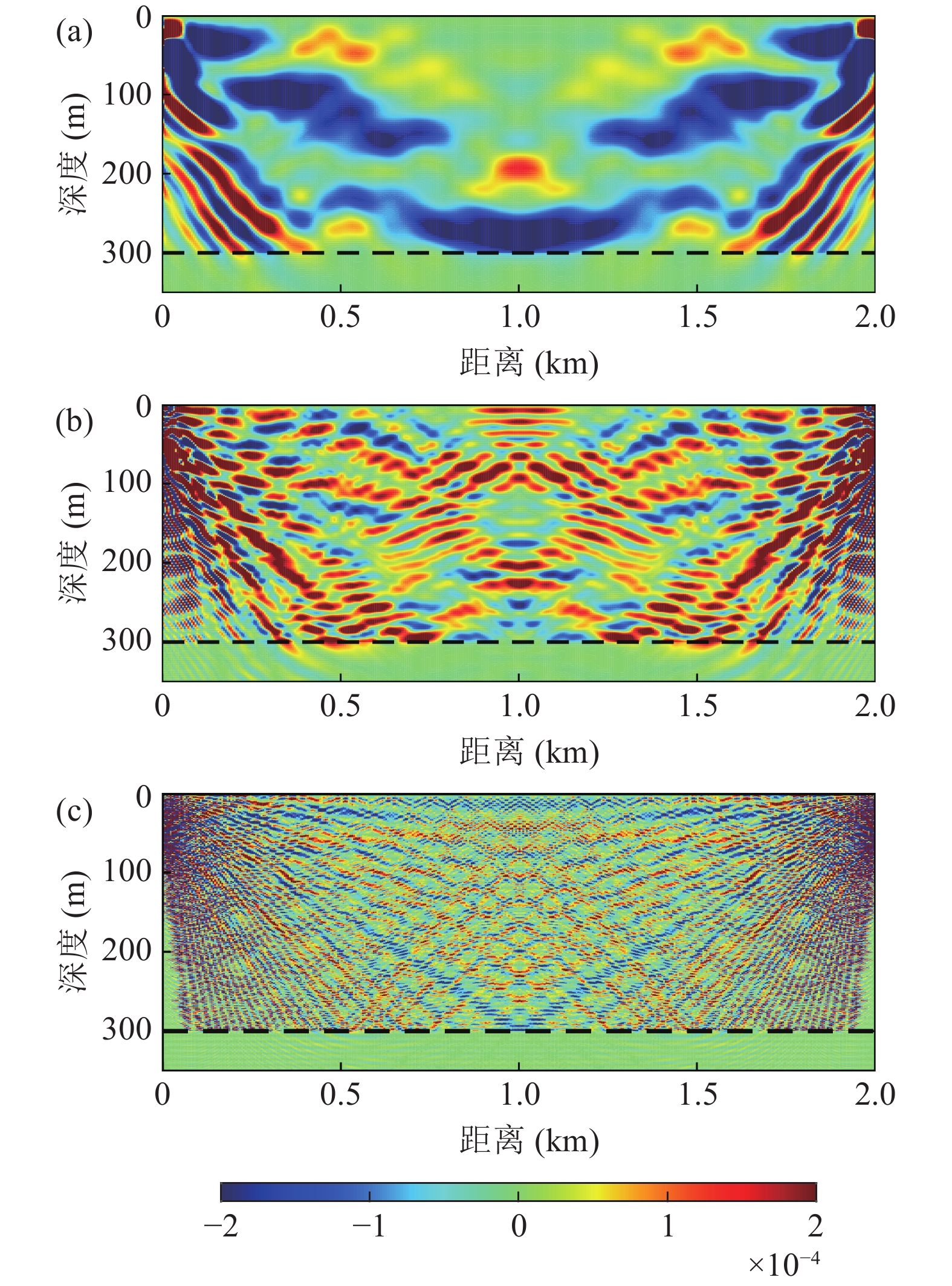
首先在水声学中经典的Pekeris波导和具有沉积层的理想环境下, 分别以50 Hz, 100 Hz, 500 Hz为例进行地声参数敏感特性分析, 声源和接收深度设为50 m, 使用波数积分程序OASES计算格林函数。图9为经典的Pekeris波导传播距离2 km条件下的声压敏感核的分布, 虚线为海底界面。水深300 m, 半无限流体海底声速为1800 m/s。图中敏感核为负的区域表示该区域的声速增大相应的声压会减小, 敏感核为正则表示声速增加会使接收点处的声压增大。也就是说, 声压敏感核可以反映海底声速变化是否会对接收点处的声压产生影响。

如图9所示, 由于海底为半无限, 进入海底的声能无法再由接收点接收, 这里仅给出水中声压对海水声速的敏感性。三个频点下均可看到, 沿着声源与接收点间的本征声线上声速对声压的影响最强, 这说明当本征声线上的声速发生微小扰动时, 接收点处可能出现截然不同的结果, 中高频段(500 Hz)这一现象更为明显。但在低频甚低频段(50 Hz, 100 Hz), 本征声线以外的参数敏感性也很显著, 声线路径并不明显。这也是射线理论不再适用低频和甚低频段的声场分析的原因, 此时使用波动理论分析。此外, 对于低频甚低频段, 声线反射位置处海底界面以下的地声参数也会对接收点处的声压产生较大影响。

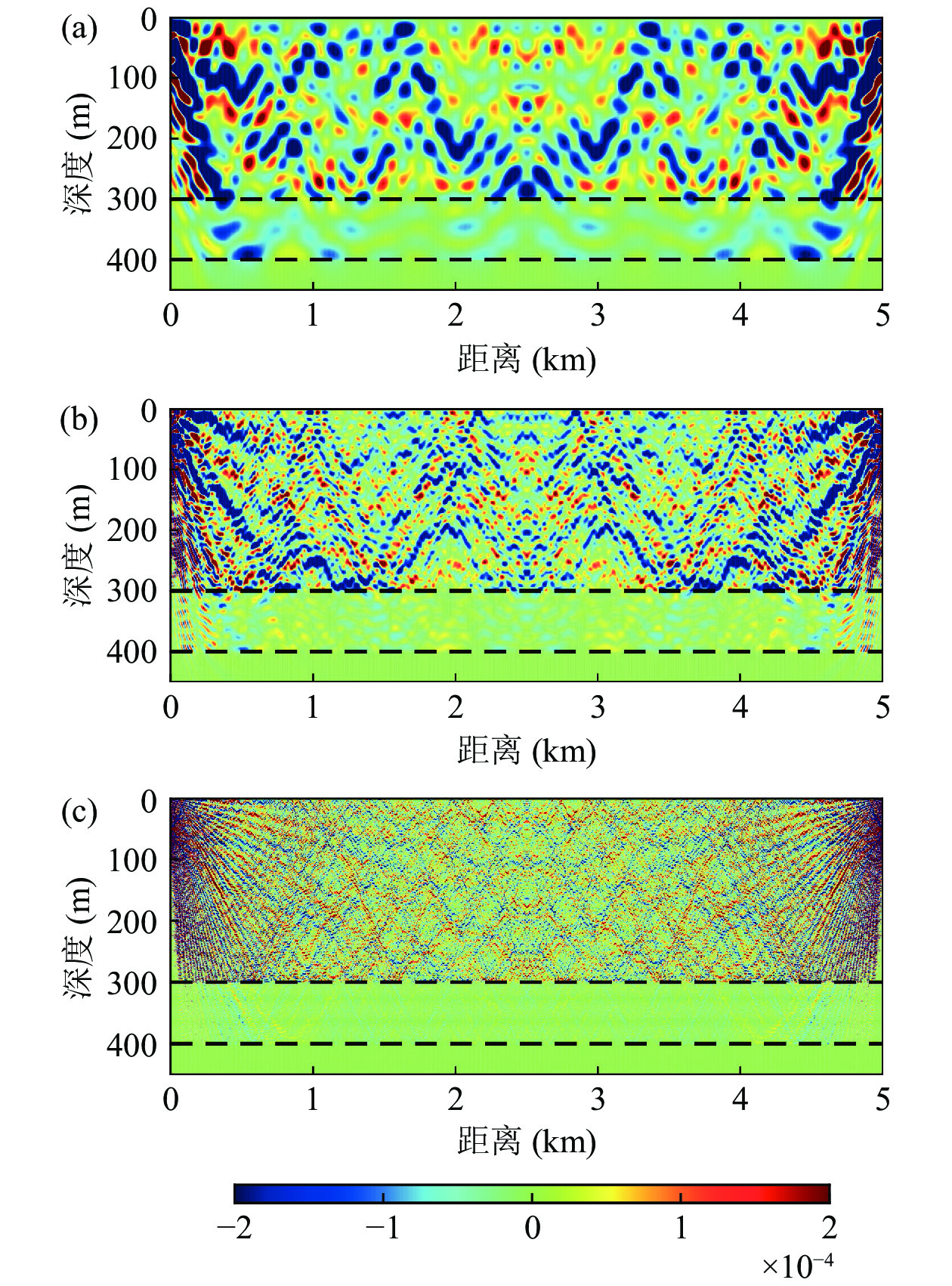
图10为理想的沉积层波导、传播距离5 km条件下的声压敏感核的分布, 虚线为海底分层结构。水深300 m, 沉积层厚度为100 m, 声速为1800 m/s; 半无限基底声速为2400 m/s。由上至下, 声源频率分别为50 Hz, 100 Hz, 500 Hz。图中不仅给出水中声速的影响, 由于沉积层中声信号经沉积层下界面反射后可返回水体中, 因此接收点处的声压会受沉积层的参数影响。如图10所示, 随着频率的升高, 沉积层对接收声压的影响逐渐减弱, 中高频段可以忽略沉积层的影响, 传统的Pekeris波导仍然适用。

在1.1节所述基本规律下, 根据海底底质历史调查资料, 建立典型浅海水平分层环境模型, 模型参数见表1。如图1所示, 地壳可分为沉积层和岩石层, 沉积层由浅至深又可以分为松散沉积层、固结沉积层和致密沉积层三大类, 实际海底环境并非均包含三类沉积层, 由于地壳运动、火山活动等会造成某些地层的缺失, 水声学中所说的沉积层通常指松散沉积层。本文计算频段范围20~1000 Hz, 海底考虑到1 km深度处, 以下为半无限空间。海水深度100 m, 其下设置三层沉积层, 沉积层总厚度为400 m; 两层岩石层, 分别设置为火山熔岩和花岗岩; 半无限基底设为片麻岩, 即图1中的花岗岩层, 该层厚度可达10~15 km, 未考虑玄武岩层。

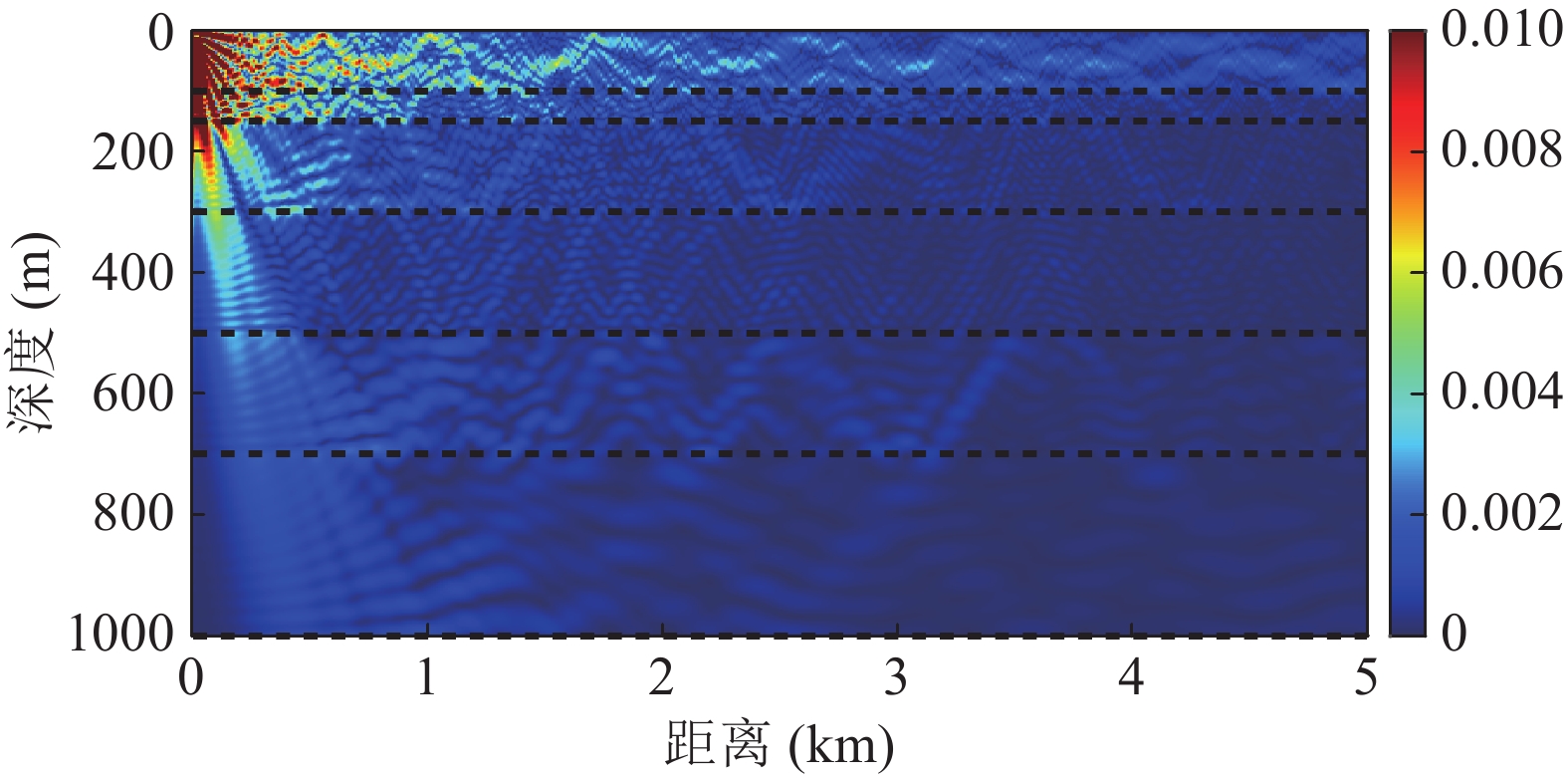
首先通过计算声场格林函数对该环境下的声场分布进行简要分析。图11为声源频率100 Hz的声场格林函数分布, 黑色虚线为海底分层结构。由图可见, 直到深度1000 m的地层仍有回波能量可返回水体中, 由水中的传感器接收。随着水下微弱信号检测技术的发展, 包含环境信息和声源信息的深层海底回波信号的处理也是参数反演与目标参数估计等应用的重要内容。

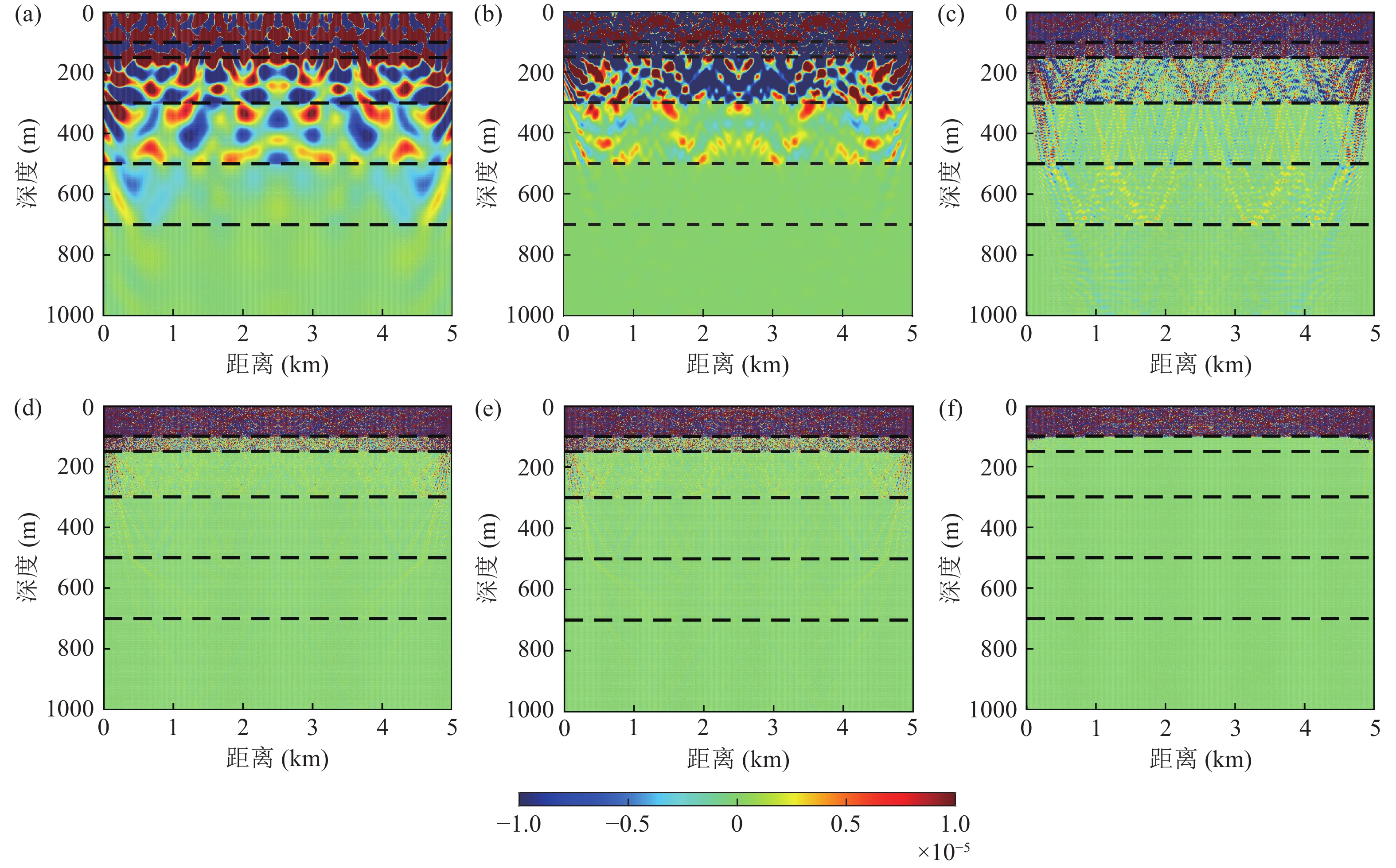
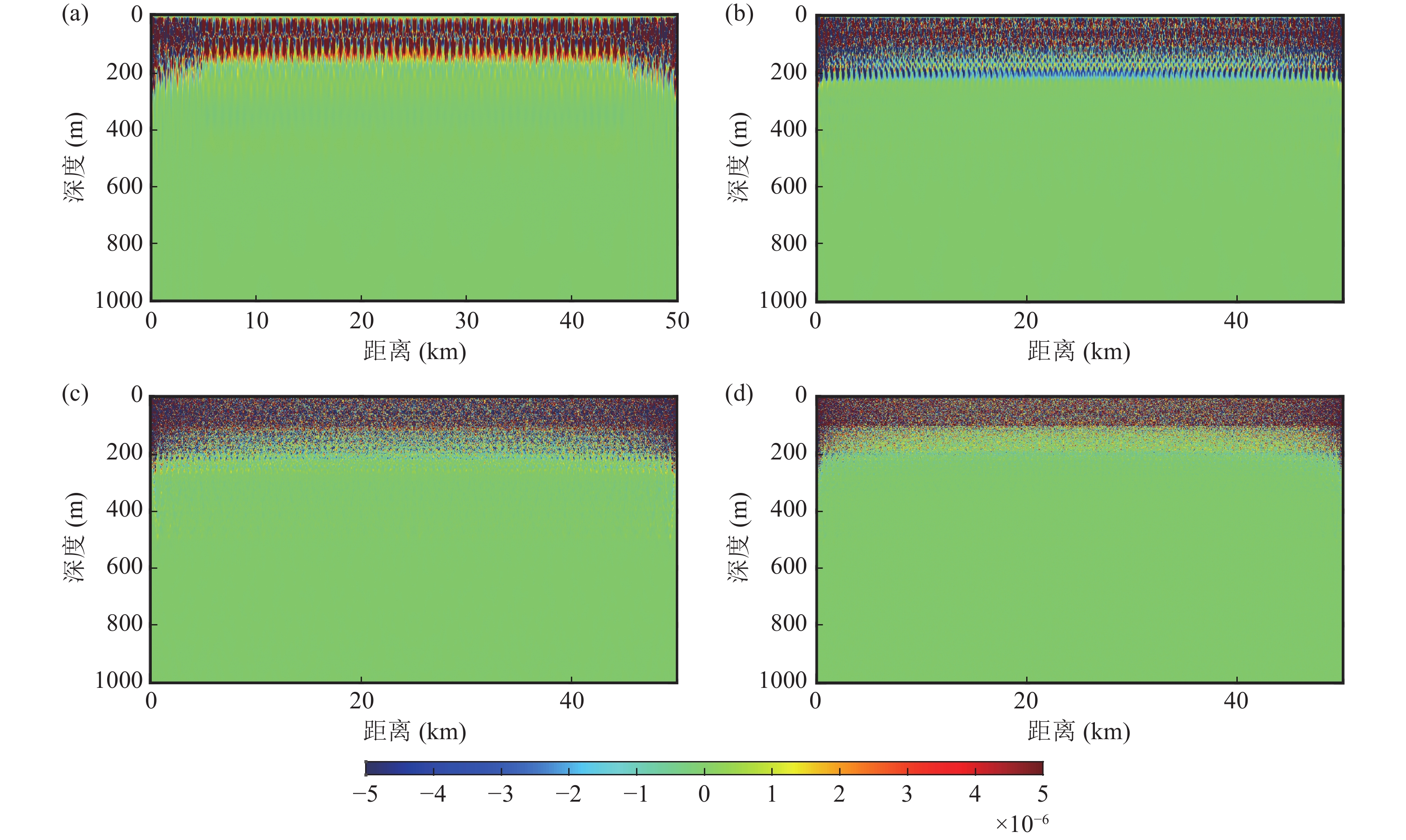
图12为不同频率下声压敏感核的分布, 随着频率的升高, 海底影响深度越浅, 20 Hz时700 m以下深度层仍有敏感度, 但敏感核在700 m以下就十分微弱了, 这表明该深度处声波向海底透射但无法反射回海水中, 不会对水中声场能量产生影响; 而800 Hz时仅海水层和疏松沉积层敏感。此外, 虽然海底设置了50 m的疏松沉积层, 但无论是格林函数还是敏感核的分布结果都表明低频段海底界面作用不明显。这是由于海水中的低频截止效应, 声场能量更易向海底耦合, 而且海底界面上下介质阻抗差较小, 反射系数小, 界面反射作用不明显。

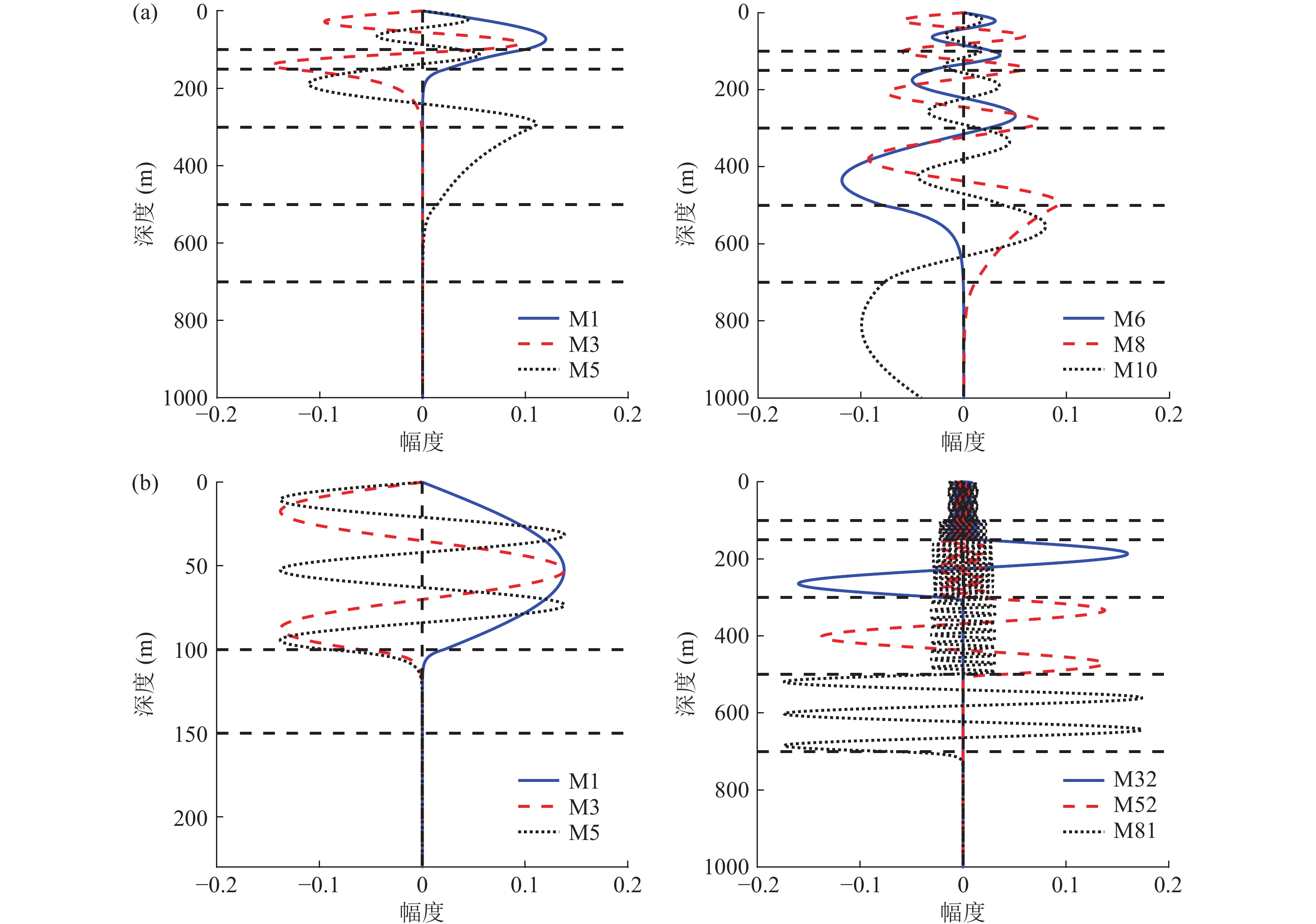
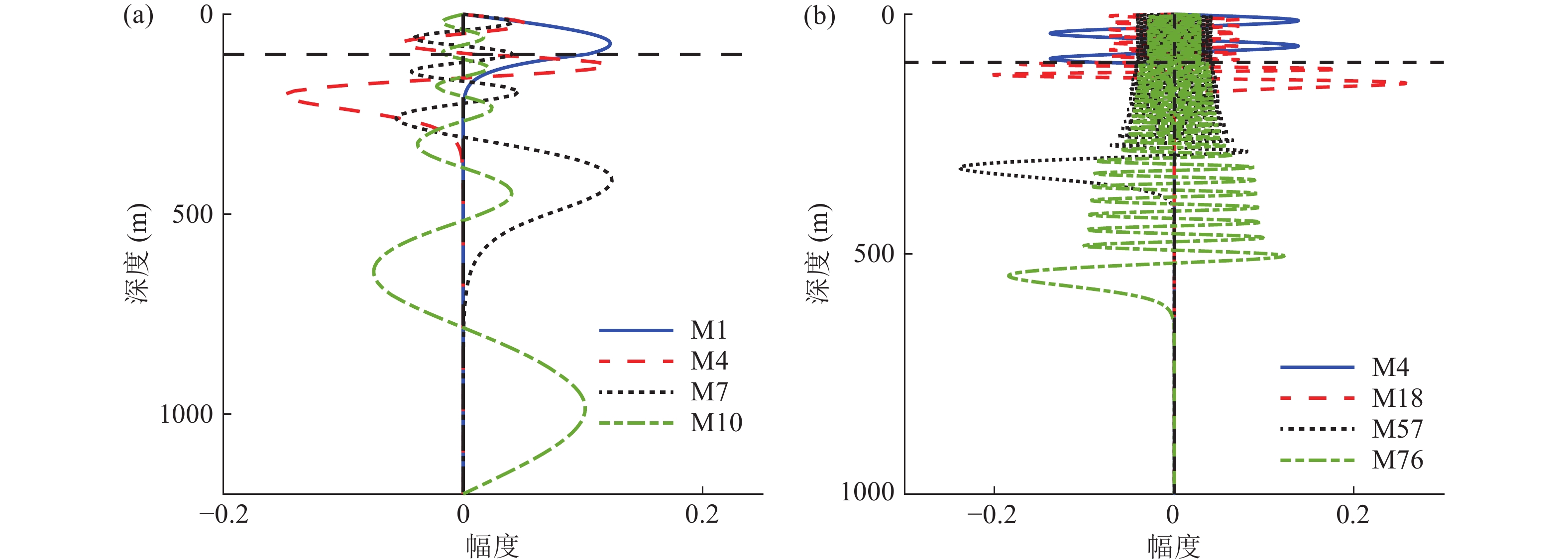
大掠射角出射的声信号经多次海面、海底反射和折射, 传播损失较大, 无法远距离传播, 小掠射角信号更易远程传播。因此远距离声传播条件下, 深层海底的影响减弱, 需考虑的海底深度将有所改变。浅海远程传播以模态分析更为方便, 高阶模态相当于大掠射角出射的声信号, 低阶模态更易远程传播, 相当于小掠射角出射的声信号。这里首先给出不同频率下, 表1所示地声环境下的简正波模态分布。如图13所示, 以20 Hz和200 Hz为例分析不同频段声波模态分布。20 Hz仿真环境下可激发17阶模态, 而200 Hz可激发173阶模态, 图中分别给出低阶模态(第1, 3, 5阶)和较为典型的高阶模态, 随着阶数的升高也就是掠射角的增大, 模态分布的海底地层越深, 对应不同地层的海底捕获模态。此外, 对比两频率下的低阶模态, 频率越低同阶模态受海底影响越深, 20 Hz下第5阶模态函数分布深至500 m, 而200 Hz频率下第5阶模态仍为水声模态, 几乎不受地声参数变化影响。

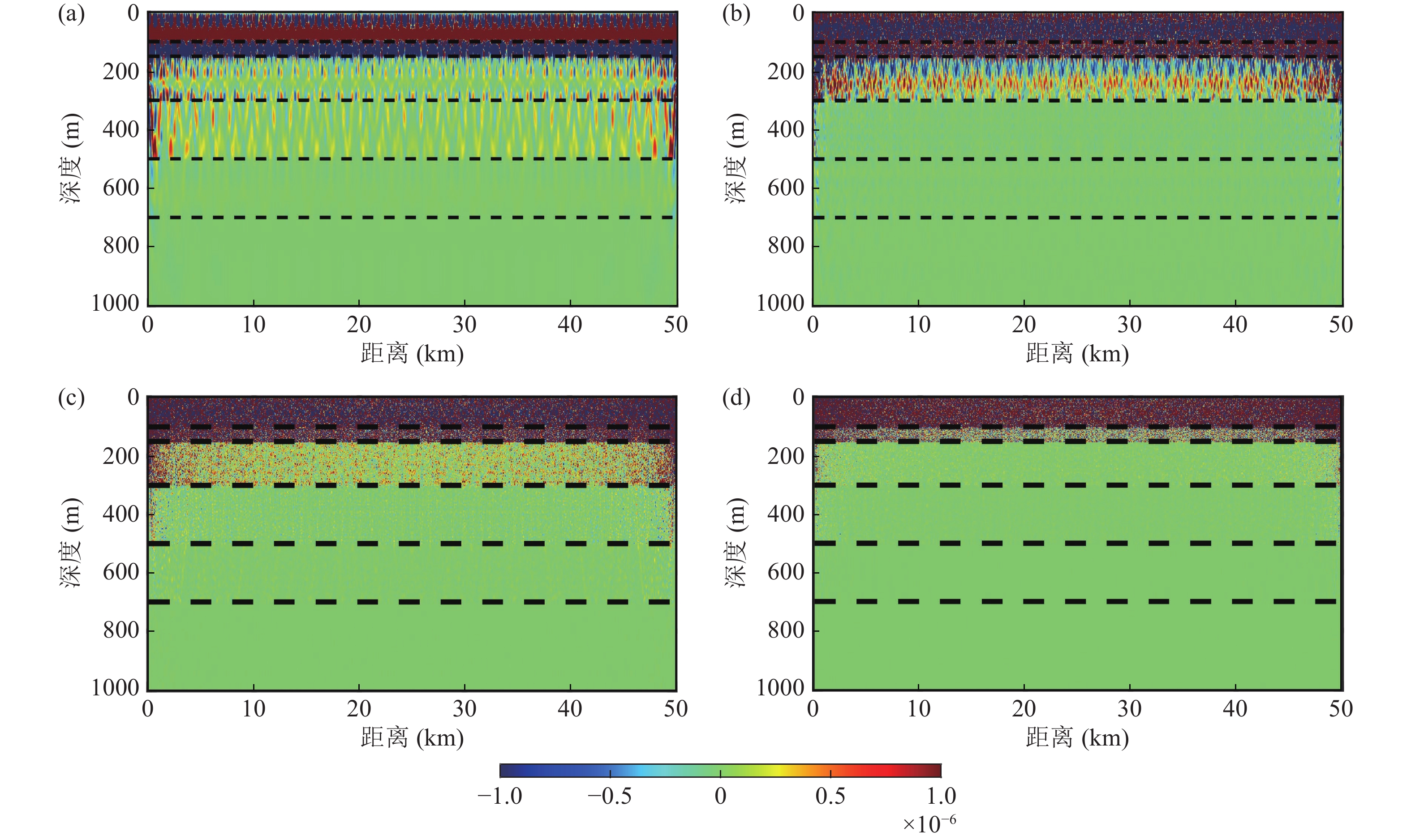
图14和图15分别为不同频率下传播距离为25 km和50 km的声压敏感核分布。对比图12与图14可见, 25 km距离内敏感核分布的地层与5 km计算结果相似, 即传播距离小于25 km时, 可近似认为水下声场对海底地声参数的敏感特性不随传播距离的增大而改变。对比图12与图15可见, 当传播距离达到50 km时, 相比于近距离传播, 对水下声场有影响的海底层数明显减少。

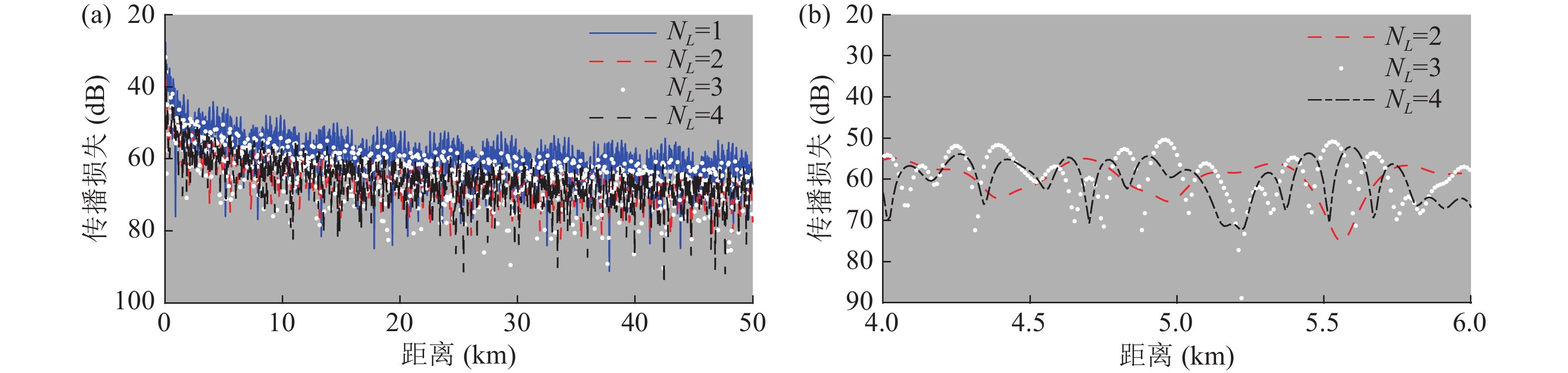
图16为50 Hz频率下仅考虑最为敏感的前四层海底的传播损失的对比, 分别给出了0~50 km传播损失和4~6 km内的放大图, 图中N_L表示海底层数。当将松散沉积层设为半无限(N_L=1)时, 与其他模型相比传播损失的幅度相差较大; 考虑至少两层海底后, 传播损失的幅度变化不大, 但传播损失曲线细节相差较多, 如干涉结构、干涉距离和干涉周期均明显不同。因此, 当仅需考虑传播损失量级时, 考虑两层海底即可; 当需要考虑声场特性以及传播衰减的细节规律时, 则须考虑多层海底的影响。

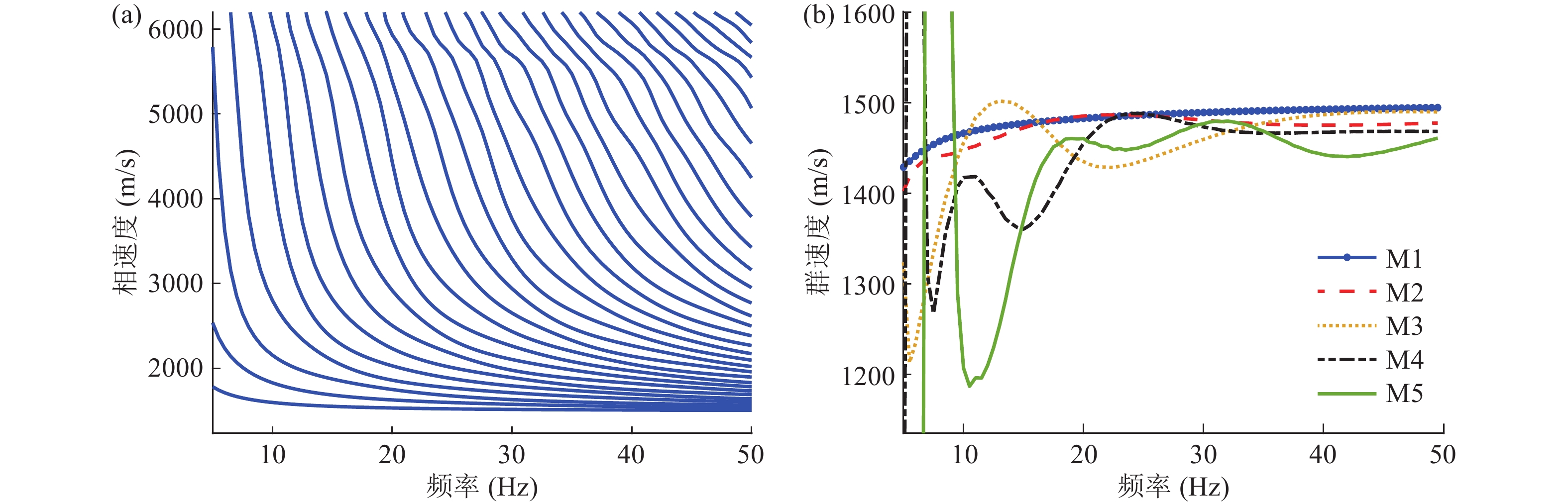
不同深度海底对水下声场的影响不仅体现在声压上, 如目标参数估计、地声参数反演中常用的时频特性也受海底影响较大。图17分别给出了考虑三层海底(蓝实线)和五层海底(红虚线)情况下的相速度与群速度频散曲线的对比, 由于群速度频散变化较为复杂, 为清晰对比这里仅给出前5阶。由图可见, 对于单阶模态, 在频率低于Airy频率的底波部分, 两环境频散特性差别较大, 底波的频散特性也是地声参数影响的体现。由不同阶模态相速度频散的对比可见, 两环境下低阶模态符合较好, 而由于高阶模态受海底影响较大, 两模型高阶模态频散曲线差别较大。

综上所述, 对于分层海底模型近距离传播条件下(<25 km), 甚低频段(20~100 Hz)需考虑五层海底, 深度达1 km处; 低频段(100~500 Hz)需考虑三层海底及半无限空间; 中高频段(500~1000 Hz)则需考虑衰减沉积层及半无限海底; 频率高于1 kHz时, 经典的半无限Pekeris波导仍然适用。而对于远距离传播(>50 km), 所需考虑的海底层数及深度可根据敏感核的分布相应减小。

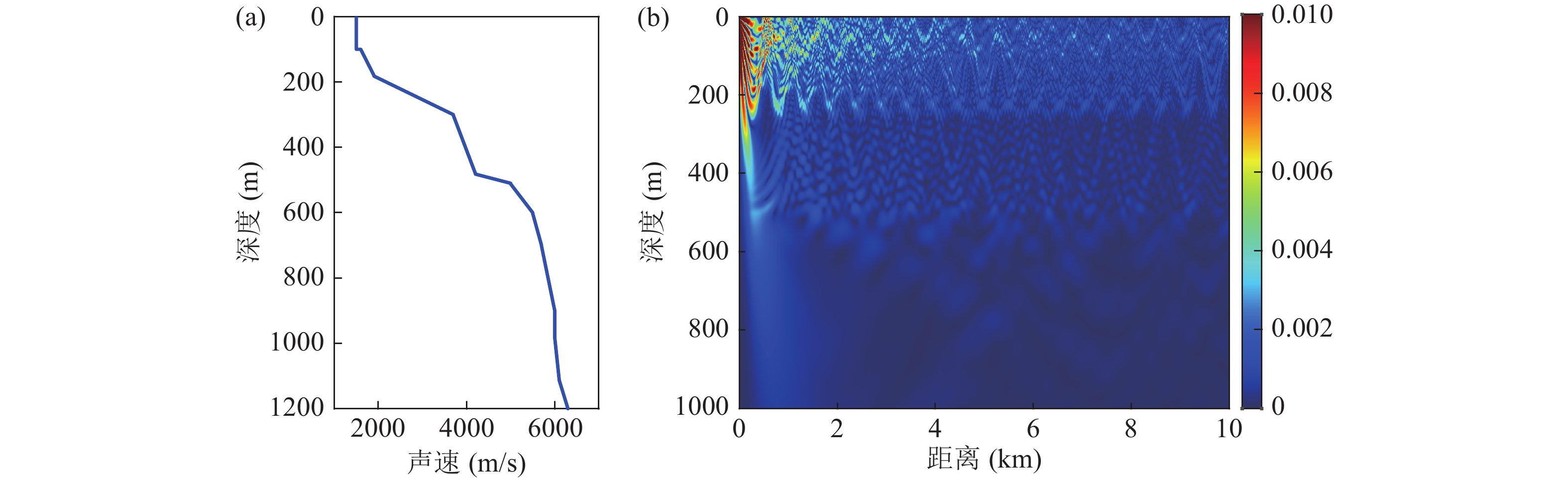
在实际的海洋环境中, 部分海域海底声速是随深度以一定梯度连续变化的, 声速变化仍符合图1所示的基本规律。建立典型浅海梯度海底环境模型, 如图18(a)所示。水深为100 m, 海水层声速均匀设置为1500 m/s; 深度100~300 m区间声速小于3700 m/s, 梯度变化符合图1所示沉积层的声速变化规律; 深度300~1000 m区间, 梯度变化符合图1所示花岗岩层的声速变化规律。

计算声场格林函数, 如图18(b)所示, 对该环境下的声场分布进行简要分析。由图可见, 直到深度1000 m的地层仍有海底反转波能量可以返回水体中, 由水中的传感器接收。由于声线进入海底的出射角度不同, 该环境下在1000 m内共形成三个反转深度, 分别为230 m, 520 m, 790 m。小掠射角入射的反转波声线跨度大, 海底反转深度更深, 受海底影响更大。

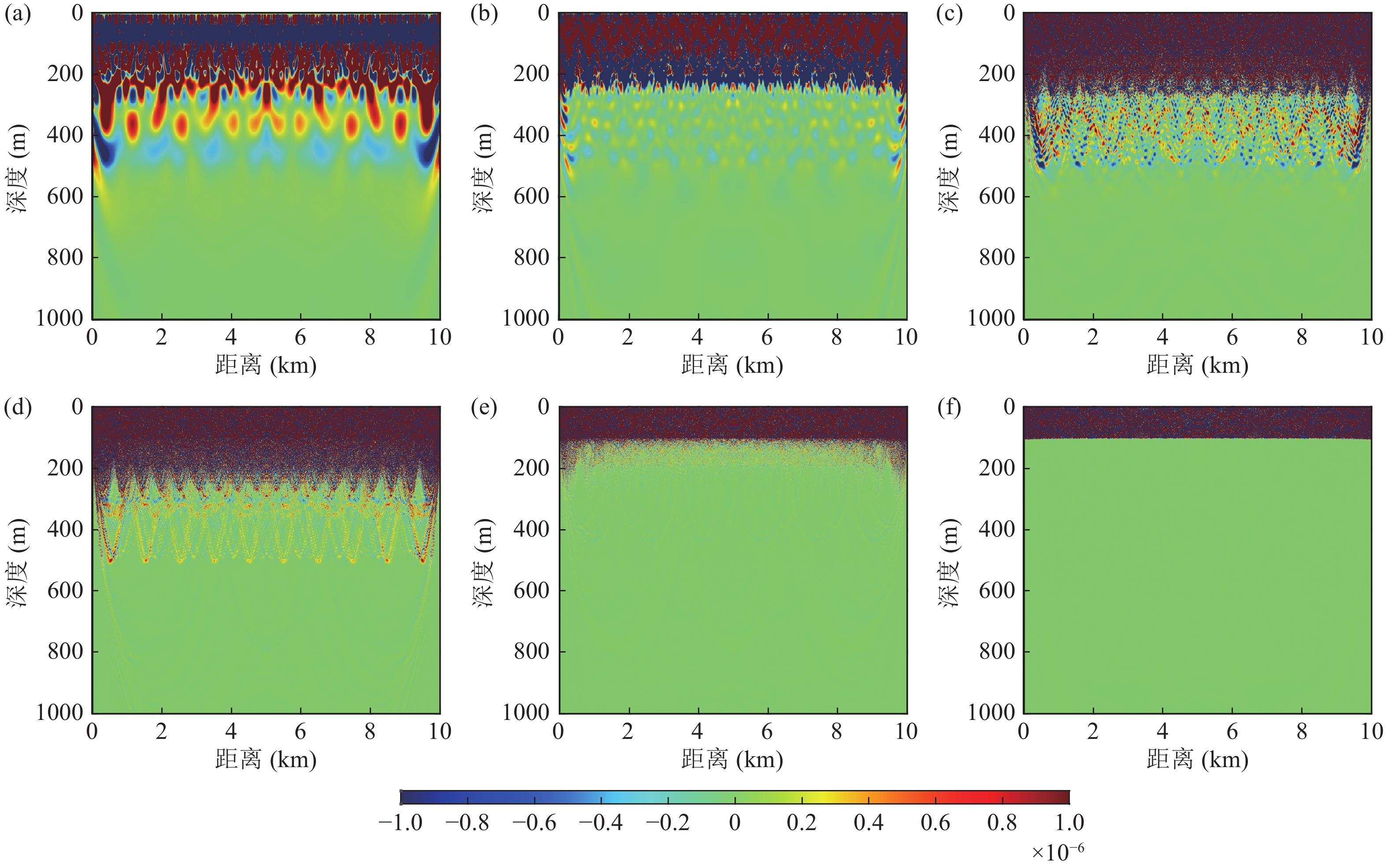
图19为声速梯度海底环境下不同频率的声压幅度敏感核的分布, 为保证大跨度的海底反转信号被接收, 水平传播距离设置为10 km。与分层海底所得结论不同, 790 m深度处反转的地声信号对声压幅度的影响十分微弱, 低频和甚低频段(0~500 Hz)梯度海底环境下需考虑的海底深度约500 m。与分层海底环境相同的是, 频率高于1 kHz时, 经典的半无限Pekeris波导仍然适用。分层海底由于界面作用可在海底形成波导支持低频和甚低频地声信号的远距离传播; 而梯度海底则类似深海声道, 由反转声线形成的会聚效应使得地声信号可以远距离传播, 但高频段海底吸收衰减较大, 因此声速梯度海底环境更利于中低频段地声信号的传播。中低频段, 即如图19所示200 Hz和500 Hz情况, 对海底地声环境更加敏感。

分析梯度海底环境下的模态和远距离海底参数敏感特性。图20为20 Hz和200 Hz频率下的典型模态的空间分布, 两频率下的4阶模态分别对应水声模态和第1~3个反转点对应模态。高频情况下低阶均为远程传播的水声模态, 海底反转模态则为更高阶。

如图21所示, 远距离传播条件下, 即使在最敏感的中低频段也仅第一个反转深度处的地声参数变化会对水中声压幅度产生影响。图22为声速梯度海底环境下的相速度和群速度频散曲线, 相速度频散曲线与分层海底环境下的结论相同, 仅在低于Airy频率的底波部分和高阶模态可见地声参数的影响。而群速度频散则与分层海底环境相差较多, 通常较高频率处各阶模态群速度频散较为规律, 随着频率的升高趋向于水中声速1500 m/s (图17), 梯度海底环境对这一部分频散产生较大影响, 导致不同阶模态的群速度频散曲线频繁交叉, 这也将导致模态间干涉条纹结构的变化^[28]。

本文通过复声压敏感核建立了水下声场对海底分层结构及底质参数敏感特性的分析方法。敏感核的分布和大小可反映背景速度场上的速度扰动引起的散射波对观测量的影响大小, 据此可分析不同频段的信号受海底深度的影响。

利用所提方法分析分层海底和声速梯度海底环境下地声参数敏感性, 仿真结果表明, 近距离传播条件下, 分层海底地声环境下甚低频(20~100 Hz)需考虑四层海底, 深度达1 km处, 低频(100~500 Hz)需考虑三层海底及半无限空间, 中高频段(500~1000 Hz)则需考虑衰减沉积层及半无限海底; 声速梯度海底环境下, 甚低频段须考虑至少第三个反转深度处, 中高频段仅需考虑到第一个反转深度。远距离传播条件下, 所需考虑的海底层数及深度可根据敏感核的分布相应减小。不同分层海底传播损失的分析结果表明, 当仅需考虑传播损失量级时, 考虑两层海底即可; 当需考虑声场特性以及传播衰减的细节规律时, 则须考虑多层海底的影响。此外, 文中还分析了典型地声环境下地声参数对时频特性的影响, 仿真结果表明, 低于Airy频率的底波部分以及高阶模态对海底地声参数更加敏感。