水下目标的辐射噪声是无源声呐的主要探测对象。目标辐射噪声的功率谱由宽带连续谱和叠加在其上的低频窄带线谱分量构成^[1-5]。与宽带连续谱信号相比, 低频窄带线谱信号具有更高的单位带宽强度和更好的稳定性。因此, 低频线谱信号的检测对安静型水下目标的远程探测具有十分重要的意义。

受嘈杂海洋环境的影响, 无源声呐通常工作在低信噪比环境下。为提高线谱信号的信噪比, 自适应线谱增强器(ALE)在无源声呐中得到了广泛应用, 常作为线谱检测前的预处理手段。自适应线谱增强器利用了窄带周期性线谱信号的时间相关半径大于宽带随机噪声的特性, 通过对自适应线谱增强器的输入数据样本进行时间延迟, 使延迟前后数据样本中的宽带噪声成分不相关而线谱成分仍保持相关, 进而利用最小均方误差(MMSE)准则进行权值的自适应迭代, 在保留线谱信号的同时抑制宽带噪声成分^[5-8]。常规自适应线谱增强器受稳态自适应权值噪声的影响, 输出信噪比增益不够理想, 为抑制稳态自适应权值噪声, 稀疏驱动自适应线谱增强器受到了学者们的关注。金盛龙等^[1]利用线谱信号在频域的稀疏性, 在自适应线谱增强器的惩罚函数中引入频域权向量的l_1/2稀疏范数, 降低了常规自适应线谱增强器中的额外稳态误差; Hao等^[8]将l₀范数引入频域权值向量的稀疏范数, 进一步抑制了稳态自适应权值噪声。罗斌等^[9]结合频域批处理技术, 提出了归一化频域批处理最小均方算法, 能够兼顾收敛速度和稳态误差, 同时减少了自适应算法的运算量。

上述自适应线谱增强器算法都假设噪声服从高斯分布, 基于均方误差这一全局二阶统计量设计自适应滤波器。依据中心极限定理, 海洋环境噪声服从高斯分布是合理的。然而在实际中, 受自然现象或人为干扰的影响, 海洋环境噪声往往具有非高斯统计特性, 这一现象在受工业噪声和航船噪声影响的近海海域以及受冰层融化噪声影响的极地海域尤为明显^[10-14]。非高斯噪声不具有有限二阶统计特性, 因此基于最小均方误差准则的常规自适应线谱增强器在非高斯噪声背景下的性能会急剧下降甚至完全失效^[11,15]。针对该问题, Sanei等^[16]提出了基于奇异谱分析的自适应线谱增强器(SSA-ALE)。SSA-ALE将输入数据样本的轨迹矩阵进行分解和重构, 首先利用奇异值分解得到轨迹矩阵的主要特征值和相应的特征分量, 从而得到数据样本的趋势项和周期项; 然后构建本征三元组, 重构满足特征值约束条件的子空间, 使其互不相关。SSA-ALE的参考数据样本是输入数据样本的延迟, 惩罚函数为参考数据样本构成的Hankel矩阵与重构得到的子空间之差的Frobenius范数。不同于常规自适应线谱增强器, SSA-ALE通过迭代更新自适应权值向量, 最小化惩罚函数得到与参考数据样本的Hankel矩阵最相似的子空间, 进而得到目标线谱信号。相较于常规自适应线谱增强器仅能够在高斯噪声条件下应用, SSA-ALE还能够应用于非高斯噪声环境中。然而, SSA-ALE的分解和重构过程计算量巨大, 且奇异值分解效果受输入数据样本的信噪比影响大, 导致该方法不适用于实际工程应用。Hao等^[17]提出了基于香农熵的自适应线谱增强器(Shannon-ALE)。香农熵是随机变量概率分布的函数, 概率分布的不确定性越大, 其熵值越大。Shannon-ALE不依赖于输入信号的全局二阶统计特性, 而是利用香农熵能够度量时间序列无序性的性质, 在惩罚函数中引入香农熵, 沿逆梯度方向迭代更新来抑制信号的脉冲分量。然而, 香农熵本质上是对随机信号平均信息量的度量, 其受到平滑参数和窗口长度影响, 会不同程度地“展宽”瞬态脉冲性噪声^[18], 从而对后续的线谱检测造成负面影响。

与常规自适应线谱增强器不同, 本文方法通过相关熵来描述线谱信号与宽带噪声的相关性差异。相关熵是一种局部相似性测度, 在测量噪声为非零均值、非高斯、离群值较大等情况下均有很好的鲁棒性^[15]。由于再生核的存在, 相关熵对数据样本中的瞬态成分有着很好的抑制作用, 适合于描述和度量数据样本的相关性^[19]。借助上述性质, 本文提出基于最大相关熵准则的自适应线谱增强器(Maximum Correntropy Criterion-based ALE, MCC-ALE), 将自适应线谱增强器中自适应滤波器的惩罚函数定义为参考与输出的相关熵, 通过最大化惩罚函数完成对自适应权值的迭代更新, 保留数据样本中广义时间相关半径较大的窄带线谱分量, 抑制广义时间相关半径较小的宽带噪声分量, 以实现非高斯噪声背景下的线谱增强, 提升信噪比增益。仿真结果表明, MCC-ALE可在非高斯噪声背景下有效增强线谱信号的输出信噪比, 且增强效果优于SSA-ALE和Shannon-ALE。北极海域采集的实验数据处理结果也验证了MCC-ALE的可行性和可靠性。

线谱信号的时间相关半径大于宽带噪声的时间相关半径, 常规自适应线谱增强器利用该特性, 基于自适应滤波器完成线谱增强。自适应滤波器的输入数据是参考数据$ x(k) $经过解相关延迟后得到的延迟数据向量$ {\boldsymbol{x}}(k - \varDelta ) $:

其中, $ L $为自适应滤波器阶数, $ \varDelta $为解相关延迟点数, ${\left[ \cdot \right]^{\rm T}}$表示转置运算。常规自适应线谱增强器的输出为

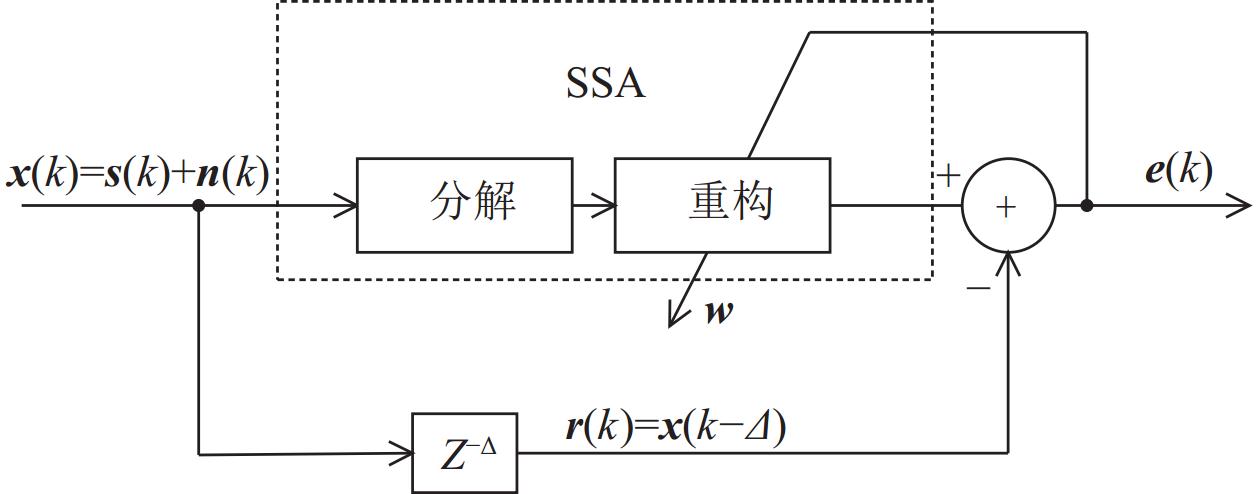
其中, $ {\boldsymbol{w}}(k) $是自适应滤波器在k时刻的$ L $维权值向量。参考数据$ x(k) $与输出数据$ y(k) $相减得到误差$ e(k) $:

$ e(k) $作为系统反馈对自适应滤波器的权值进行调整。整个过程中, 若$ \varDelta $大于宽带噪声的时间相关半径, 且小于线谱信号的时间相关半径, 则系统参考数据中的宽带噪声分量和输入数据中的宽带噪声分量将不相关, 而二者的线谱信号分量依然保持相关^[7]。基于此, 系统对输入数据进行$ \varDelta $步的前向预测, 宽带噪声会被抑制, 线谱信号得到增强。自适应线谱增强器的系统框图如图1所示。

自适应线谱增强器基于MMSE准则对自适应滤波器的权值进行自适应调整。常规自适应线谱增强器的惩罚函数$J(k)$定义为参考$ x(k) $与输出$ y(k) $的均方误差, 即误差$ e(k) $的二阶矩:

利用式(4)进行自适应权值的迭代更新需要比较大的计算量, 实际中, 通常采用最小均方算法, 即利用误差的瞬时平方对均方误差进行近似:

式(5)表示的惩罚函数相对于自适应权值的梯度为

对自适应权值向量进行沿逆梯度方向的迭代更新, 其过程表示为

其中, $ \mu $为自适应学习的步长。

在高斯噪声背景下, 常规自适应线谱增强器能够有效实现线谱信号增强。然而, 均方误差作为一种基于全局二阶统计量的函数, 其对于远离分布中心的误差会显著放大, 即在误差分布非对称、非零中心及有异常值时不能实现最优。受人为干扰与自然环境尤其是冰致噪声的影响, 海洋环境噪声中常常存在一些瞬态的冲激性成分, 使得噪声不再满足高斯分布。$\alpha $稳定分布模型可以对非高斯海洋环境噪声进行建模^{[10-11, 20-21]}。设随机变量$ \eta $服从$\alpha $稳定分布, 即

其中, $ \alpha $为特征指数, 描述$\alpha $稳定分布的拖尾厚度; $ {{ - 1}} \leqslant \beta \leqslant {{1}} $为对称参数, 表示分布的对称程度; $ {{ - }}\infty \leqslant m \leqslant \infty $为位置参数, 确定分布的中心位置; $ \gamma > 0 $为分散参数, 表征了分布的离散程度。对于随机变量$ \eta $, 有

式(9)表明, 对于满足$\alpha $稳定分布的随机变量, 其全局二阶统计量是发散的。因此, 当背景噪声满足$\alpha $稳定分布时, 基于全局二阶统计量的常规自适应线谱增强器的性能将会显著退化, 甚至会导致错误的结果。

SSA-ALE和Shannon-ALE分别基于不同的原理来解决非高斯噪声背景下的自适应线谱增强问题, SSA-ALE利用奇异谱分析, 将输入数据分解重构, 构建自适应线谱增强器; Shannon-ALE将香农熵作为惩罚函数构建自适应线谱增强器。

SSA具有可分离性, 它表征了不同信源的信号在噪声中可分离的程度。Sanei 等^[16]利用SSA的特性设计了一种自适应线谱增强器。输入数据通过SSA的分解和重构步骤, 能够利用其轨迹矩阵得到输入数据的估计值, 基于此, SSA-ALE以最小化参考数据与输入数据的估计值的残差设计自适应线谱增强器, SSA-ALE的系统框图如图2所示。

SSA在分解阶段中将输入数据x(k)依观察窗分解并组成轨迹矩阵H。对$ {\boldsymbol{H}}{{\boldsymbol{H}}^{\rm T}} $进行奇异值分解, 得到特征值$ {\lambda _i} $和相应的左奇异向量$ {{\boldsymbol{u}}_i} $、右奇异向量$ {{\boldsymbol{v}}_i} $, 其中左奇异向量$ {{\boldsymbol{u}}_i} $满足$ {\boldsymbol{H}}{{\boldsymbol{H}}^{\rm T}}{{\boldsymbol{u}}_i} = {\lambda _i}{{\boldsymbol{u}}_i} $, 右奇异向量$ {{\boldsymbol{v}}_i} $满足$ {{\boldsymbol{H}}^{\rm T}}{\boldsymbol{H}}{{\boldsymbol{v}}_i} = {\lambda _i}{{\boldsymbol{v}}_i} $。令d为特征值大于0的个数, 那么H的奇异值分解结果为

在重构阶段中, 将初等矩阵分为多个子矩阵, 每个子矩阵的大小由先验信息确定, 重构矩阵由轨迹矩阵的分解结果表示为$ {\boldsymbol{H}} = \sum\nolimits_{j = {I_1}}^{{I_m}} {{{\widehat {\boldsymbol{H}}}_j}} $, $ {\widehat {\boldsymbol{H}}_I} = \sum\nolimits_{j = {i_1}}^{{i_p}} {{{\boldsymbol H}_j}} $, 集合$ {I_1},{I_2}, \cdots, {I_m} $被称为三特征分组。

在重构过程中, 式(11)描述的代价函数被最小化, 以确保选择正确的三特征分组来重构周期信号。

其中, $ {\left\| \cdot \right\|_{\rm F}} $为F范数, $ {\boldsymbol{U}} $, $ \boldsymbol\varLambda $ (特征值构成的对角阵)和$ {\boldsymbol{V}} $是由式(10)得到的元素构成的矩阵, ${\boldsymbol{ W}} $为自适应权值$ {w_{ij}} $构成的对角阵。采用梯度下降法最小化惩罚函数, 得到SSA-ALE的权值迭代公式为

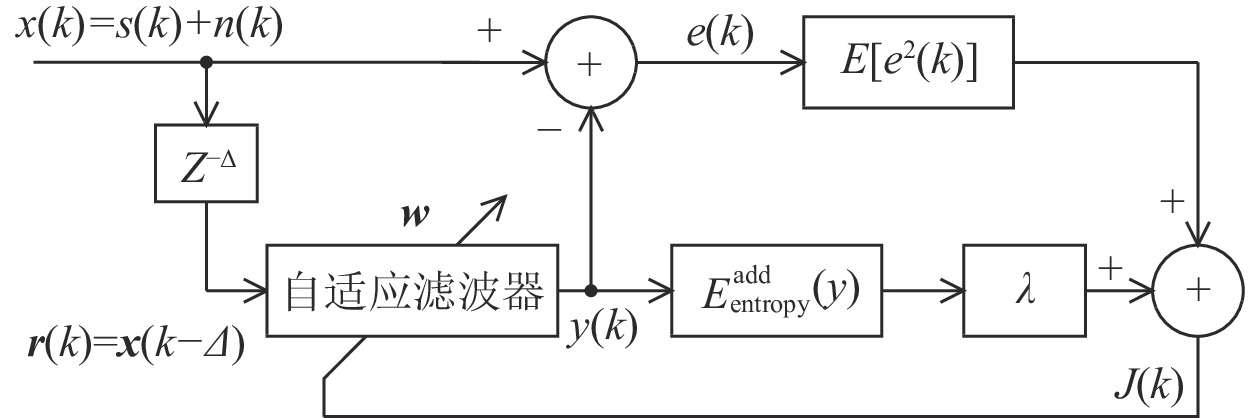
香农熵能够描述时间序列的复杂性, 香农熵的值越大, 表示信号的无序程度越严重。Qiu等^[17]利用香农熵构建了一种非高斯背景噪声下的自适应线谱增强器, 其原理框图如图3所示。

香农熵定义为$ {E_{\rm entropy}}(y) = - \sum\nolimits_{k = 1}^N {p(k)\ln p(k)} $, 其中$ p(k) $表示输出数据$ y(k) $的输出序列的能量占比。$ {E_{\rm entropy}} $不是一个加性函数, 为方便将香农熵引入惩罚函数中, 定义非归一化香农熵为

将具有拉格朗日乘子$ \lambda $的非标准香农熵引入惩罚函数中

为了使得惩罚函数最小, 权值向量沿着性能表面负梯度方向迭代, 在每次迭代更新中, 惩罚函数的梯度采用了近似处理。则权值向量表示为

SSA-ALE和Shannon-ALE都能够有效增强非高斯噪声条件下的线谱信号, 然而SSA-ALE需要足够的先验信息和输入信噪比来区分子空间且矩阵运算量巨大, Shannon-ALE本质上是对平均信息量的度量, 会不同程度展宽冲激性噪声, 可能加剧对弱线谱信号的影响。因此两种自适应线谱增强器在实际应用时仍然面临很大挑战。

针对常规自适应线谱增强器在非高斯噪声背景下失效的问题, 本文提出MCC-ALE。MCC-ALE利用相关熵对自适应线谱增强器输出数据和参考数据的广义时间相关性进行度量, 根据线谱信号与非高斯噪声在广义时间相关半径上的差异, 基于MCC准则设计自适应滤波器, 保留广义时间相关半径较大的线谱成分, 抑制广义时间相关半径较小的宽带非高斯随机噪声, 从而实现线谱的自适应增强。

定义两个随机变量X, Y, 其相关熵表示为

其中, $ {f_{X,Y}}(x,y) $表示X和Y的联合概率密度函数, $ {\kappa _\sigma }(x - y) $表示核函数, $ \sigma $表示核宽度。$ {\kappa _\sigma }(x - y) $通常采用高斯核函数进行度量, 表示为

在实际应用中, $ {f_{X,Y}}(x,y) $难于获取, 且通过采样只能获得有限的M组数据$\left\{ {{x_i},{y_i}} \right\}_{i = 1}^M$, 因此在实际应用中常采用相关熵的样本估计, 表示为

其中, M表示样本数量。

由式(17)和式(18)可知, 相关熵本质上是将随机变量X和Y通过高斯变换映射到再生核希尔伯特空间, 进而求得二者的相似性。相关熵对异常值不敏感, 当存在瞬态噪声时, 相关熵是一种理想的衡量随机变量相关性的广义相关函数^[22-27]。

由于非高斯噪声不存在有限二阶矩, 基于最小均方误差准则的常规自适应线谱增强器的性能会在该噪声背景下严重下降。为解决该问题, 本文基于MCC准则设计自适应线谱增强器。MCC-ALE的结构与常规自适应线谱增强器相同, 使用一个自适应滤波器对延时信号进行处理, 其输出信号表示为

线谱信号具有周期性, 其广义时间相关半径远大于宽带非高斯噪声。基于此, MCC-ALE采用输出数据与参考数据的相关熵作为惩罚函数, 并以最大化相关熵为准则对自适应滤波器权值进行迭代更新, 使广义时间相关半径较大的线谱信号得以保留, 广义时间相关半径较小的非高斯噪声得到抑制, 进而实现非高斯噪声背景下的线谱自适应增强。MCC-ALE的惩罚函数表示为

其中, M为当前时刻的样本数量。式(20)相对于自适应权值的梯度为

MCC-ALE的自适应权值采用小步长搜索进行迭代更新, 沿性能表面梯度方向上升, 迭代过程表示为

式(22)基于梯度算法, 每次计算权值向量时需要付出巨大的计算量。受随机梯度下降法的启发^[28], 利用当前值(令$ i = k $, 即$ M = 1 $)对式(22)近似求和:

需要说明的是, 引入随机梯度下降法是必要的。相较于梯度算法, 随机梯度下降法在大规模数据集上比较高效, 其每次迭代只使用一个样本。虽然引入随机梯度下降法会带来额外的误差, 但是高斯核函数能够有效抑制该误差。这些特点使得随机梯度下降法十分适用于自适应线谱增强器。

常规自适应线谱增强器利用LMS算法进行自适应权值迭代, 当非高斯噪声中的瞬态成分出现时, 预测误差$ e(k) $会异常放大, 使自适应权值在迭代过程中发散, 常规自适应线谱增强器性能失效。对比式(6)与式(23)可知, 与常规自适应线谱增强器相比, MCC-ALE的权值在每次迭代更新时额外增加了异常值抑制因子$ \exp ( - {e^2}(k)/2{\sigma ^2}) $, 该因子可有效解决这一问题。当瞬态噪声成分出现时, 该因子的值将显著减小, 进而减少预测误差$ e(k) $放大带来的负面影响。另外, 相较于梯度法而言, 虽然引入随机梯度下降法可能会导致异常值抑制因子中出现极大的误差$ e(k) $, 但是该因子对异常值不敏感, 极大的误差会使该因子的值趋向于零, 避免了错误的估计值。基于上述原因, MCC-ALE对非高斯背景噪声具有鲁棒性。

在开始仿真实验前, 有必要对自适应滤波器的阶数$ L $进行分析。文献[29]针对常规自适应线谱增强器, 提出分割稳态均方误差的概念, 用以衡量自适应滤波器的阶数对滤波器收敛性能的影响。文献[30]在高斯核函数的基础上, 定义MCC-ALE的分割稳态相关熵为

其中, $ L $为当前的阶数, $ e_g^{(L)} = {e^{(L)}}(1:g) $,$ 1 \leqslant g \leqslant L $, 随着误差趋近于零, 分割稳态相关熵应趋近于1, 当自适应滤波器阶数趋近于最佳值时, 分割稳态相关熵变化量应趋于稳定, 那么MCC-ALE的最佳阶长应满足:

式中, $ 1 \leqslant \varDelta g \leqslant L $且取值为正整数。

最后分析MCC-ALE的计算复杂度。文献[31]基于自适应滤波器实现过程中实数乘法运算的总次数来评估自适应滤波器的计算复杂度。本文使用相同的方法来评估MCC-ALE的计算复杂度。假设MCC-ALE使用的自适应滤波器阶数为$ L $, 式(19)需$ L $次实数乘法运算, 同时式(23)也需约$ L $次实数乘法运算, 因此MCC-ALE的总计算复杂度为2$ L $, 与常规自适应线谱增强器的计算复杂度一致^[32]。

需特别说明的是, 由于 Alpha 稳定分布噪声下二阶统计量不再收敛, 传统的信噪比失去了意义, 因此重新定义信噪比为^[33]

其中, $ \delta _s^2 $为信号的平均功率。信噪比增益为输出信噪比与输入信噪比之差。

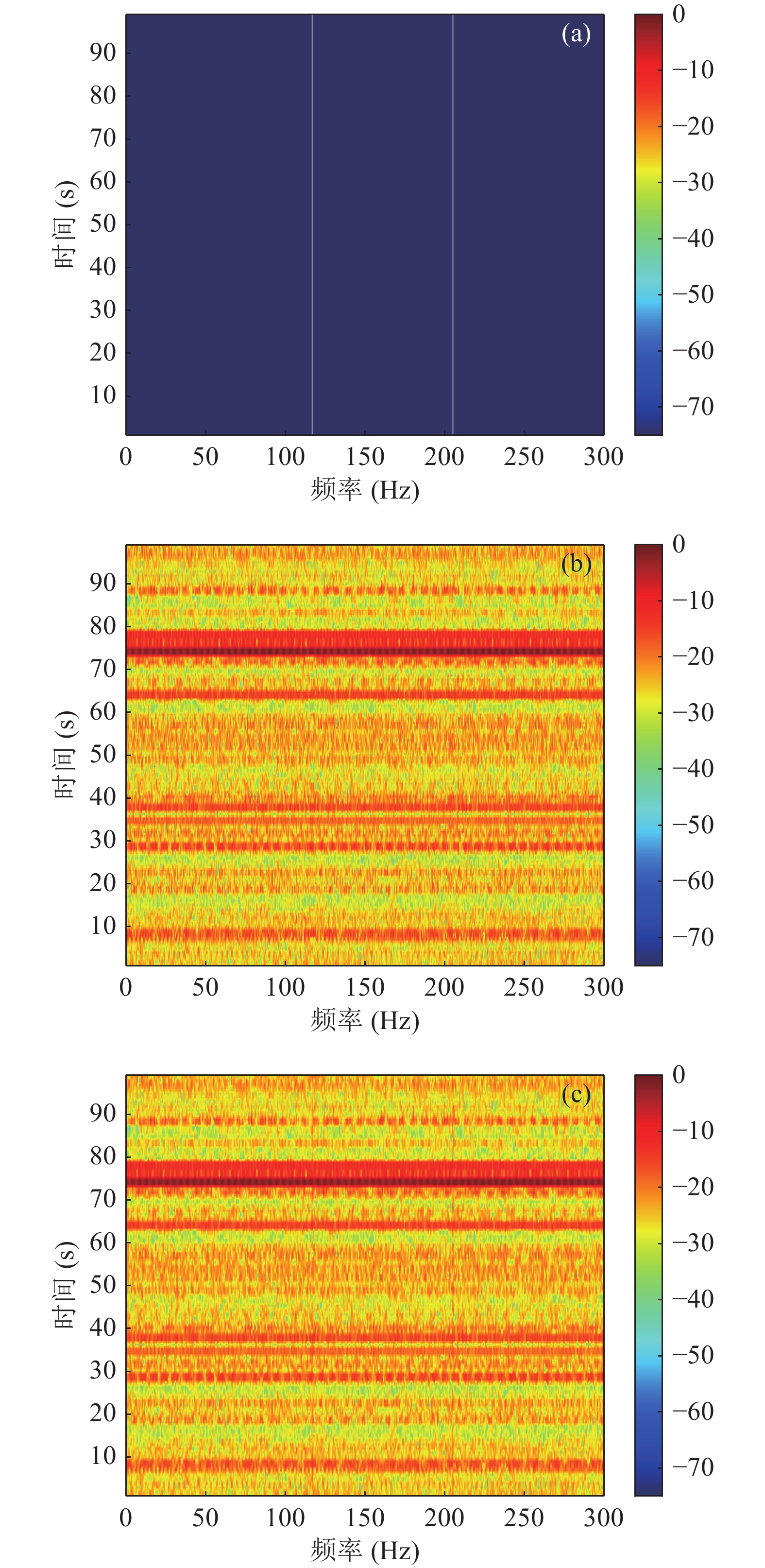
利用仿真实验对MCC-ALE的性能进行验证。假设自适应线谱增强器的输入由频率分别为117 Hz和205 Hz的两条线谱以及非高斯背景噪声构成。非高斯背景噪声采用Alpha稳定噪声模型描述, 特征指数$ \alpha = 1.34 $, 偏斜指数$ \beta = 0.5 $, 分散系数$ \gamma = 0.05 $, 位置参数$ m = 1 $。输入信噪比设置为−25 dB, 采样频率为2 kHz, 仿真数据长度为100 s。线谱信号、噪声和自适应线谱增强器的输入信号的LOFAR谱如图4所示。LOFAR谱由长度为2 s的短时傅里叶变换(STFT)和长度为1 s的数据重叠产生。

阶数设置为10: 3000, 分割稳态相关熵近似为

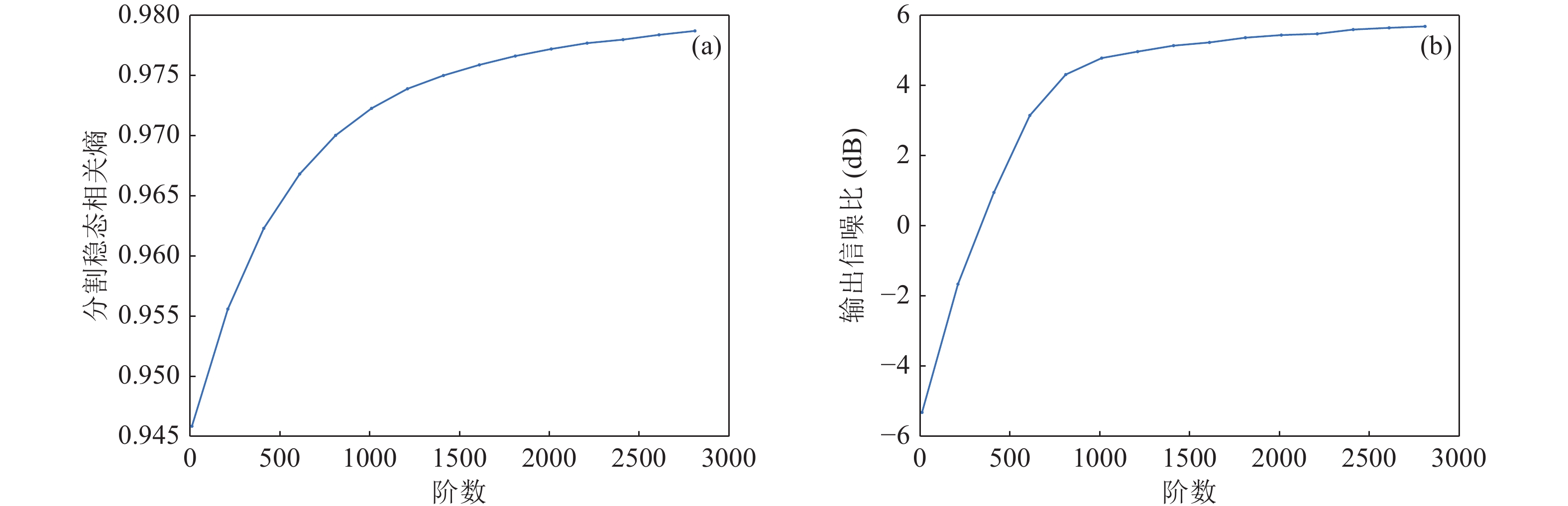
基于式(25)、式(27)和式(26), 利用仿真实验确定MCC-ALE在上述实验条件下的阶数最佳值。

图5(a)中, 阶数为2000左右时, 稳态相关熵的变化量较小且趋于平缓, 过高的阶数会带来过大的计算量。图5(b)中, 阶数较小时输出信噪比较低, 阶数到达1000以后, 输出信噪比稳定在5 dB附近。本次仿真实验中, 在不影响滤波器性能的条件下, 应尽量减少计算量, 设定自适应滤波器阶数为2000。

在上述实验条件下, 利用常规自适应线谱增强器、SSA-ALE、Shannon-ALE和MCC-ALE分别对构造的自适应线谱增强器输入信号进行处理。延迟量设置为100, MCC-ALE的高斯核宽度不敏感^[19], 文献结果表明高斯核宽度取值为0.1~2.0时, 基于高斯核函数的相关熵都能取得近似最佳核宽度的处理结果。本文仿真实验中高斯核宽度取0.84。图6给出了4种自适应线谱增强器方法输出信号的LOFAR谱。LOFAR谱的产生方式与图4相同。如图6(a)所示, 常规自适应线谱增强器对瞬态噪声成分缺乏鲁棒性, 瞬态噪声的出现导致常规自适应线谱增强器的自适应权值迭代过程发散, 自适应线谱增强器完全失效, 无法检测到目标线谱信号。如图6(b-d)所示, SSA-ALE、Shannon-ALE和MCC-ALE均可在非高斯噪声背景下实现对线谱的有效增强, LOFAR谱都能够清晰表现出117 Hz和205 Hz频率处的两条线谱。在仿真过程中, 为了更贴近实际应用的条件, SSA-ALE没有使用输入信号的先验信息, 子空间的预设大小和重构阶数并不能保证是最优解, 因此与图6(c)(d)相比, 图6(b)中对非高斯噪声的抑制效果并不理想, 75 s时, SSA-ALE受到强冲激性噪声影响, 无法有效增强目标线谱信号。Shannon-ALE的平滑参数和窗口长度选取不合适, 又会导致如图6(c)中75 s处的非高斯噪声“展宽”的问题。与SSA-ALE和Shannon-ALE相比, 本文提出的MCC-ALE的性能最优, 瞬态噪声成分得到了最有效的抑制。

计算3种自适应线谱增强器在不同输入信噪比下的输出信噪比。其他参数与上述仿真实验相同, 在不同输入信噪比条件下进行仿真实验。图7是3种自适应线谱增强器的输出信噪比随输入信噪比的变化, 图中每个输入信噪比对应的输出信噪比均通过100次蒙特卡罗实验取平均得到。3种自适应线谱增强器均能有效提升线谱信号的信噪比, 3种自适应线谱增强器中, MCC-ALE可提供最高的信噪比增益。输入信噪比为−25 dB时, 相较于SSA-ALE和Shannon-ALE, MCC-ALE可将输出信噪比分别提升约12 dB和5 dB。

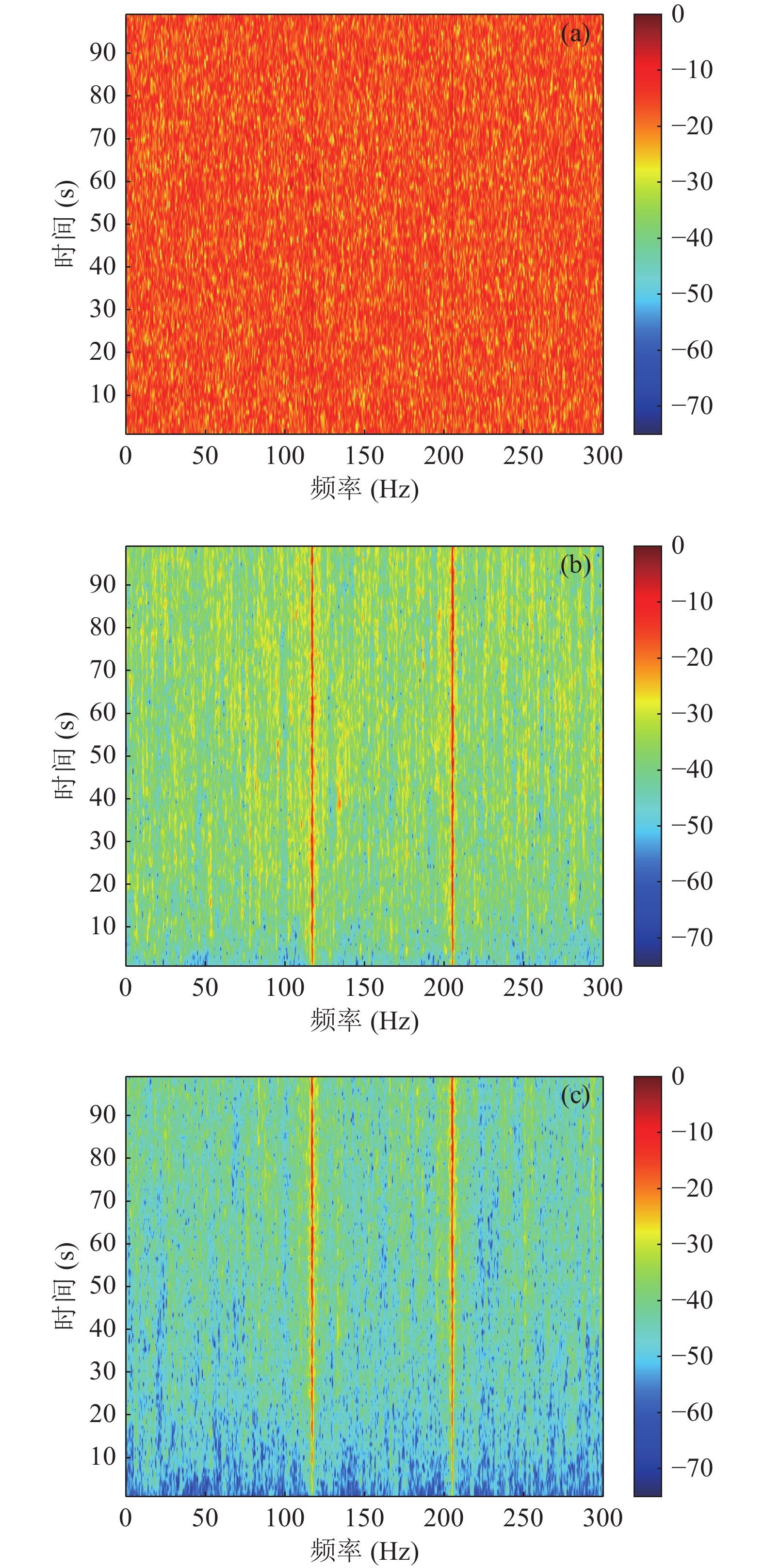
上述仿真实验均在非高斯噪声条件下进行, 为进一步验证MCC-ALE的应用范围, 将噪声设定为高斯白噪声, 其他条件不变, 分析验证在高斯白噪声影响下MCC-ALE的性能。图8(a)是自适应线谱增强器输入的LOFAR谱, 图8(b)和图8(c)分别是该输入条件下, 经过常规自适应线谱增强器和MCC-ALE的输出信号LOFAR谱。

图8(a)中目标线谱被高斯白噪声淹没。图8(b)(c)中, 常规自适应线谱增强器和MCC-ALE都能够有效增强117 Hz和205 Hz两处的目标线谱, 且MCC-ALE具有更好的抑制高斯白噪声的能力。上述结果表明, 在高斯和非高斯噪声背景下, MCC-ALE都具有良好的线谱增强性能; 在不同实验条件下, MCC-ALE具有鲁棒性。

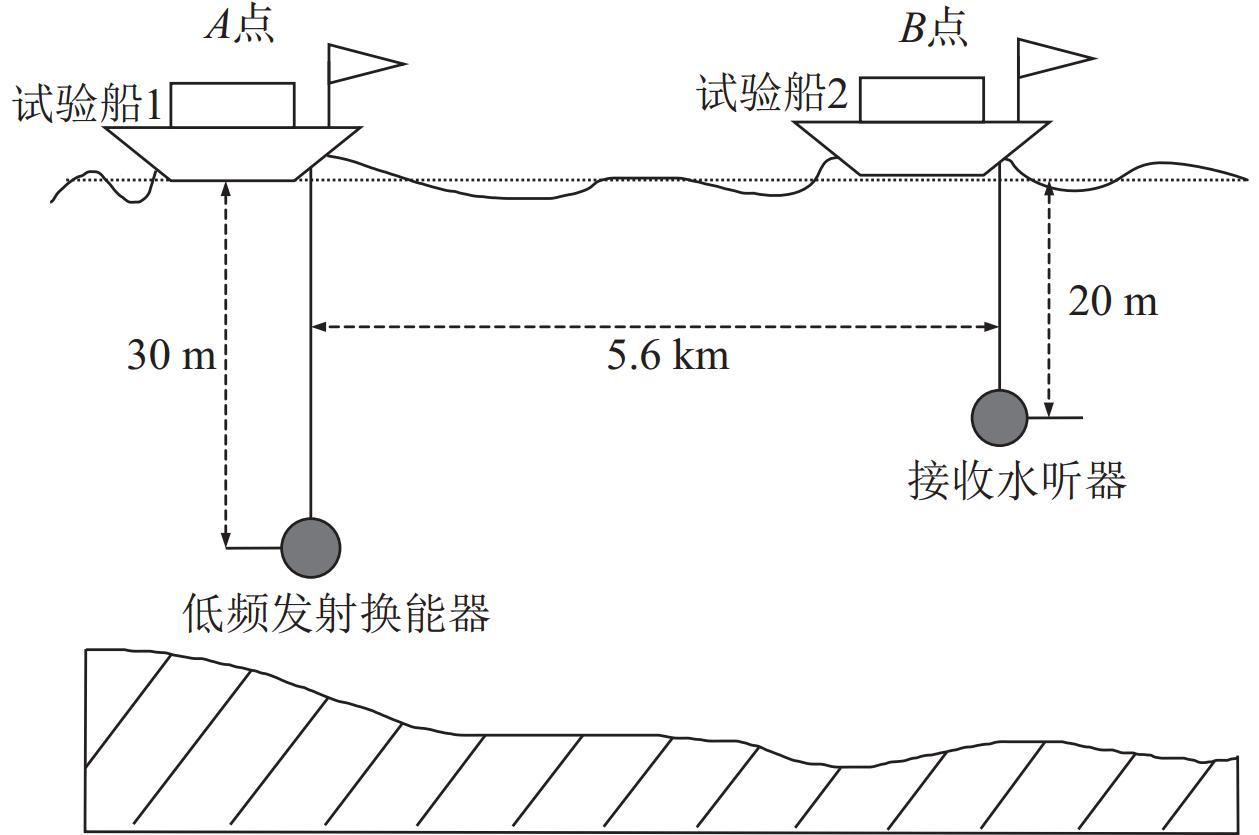
通过海试数据处理结果验证MCC-ALE的性能。试验数据在某浅海海域采集, 海试态势如图9所示。试验海域平均水深约200 m。试验船1锚定于A点, 吊放低频发射换能器, 深度30 m, 发射频率为117 Hz和205 Hz的线谱信号。试验船2锚定于B点, 吊放接收水听器, 深度20 m。A点与B点间水平距离为5.6 km。采样率为100 kHz。

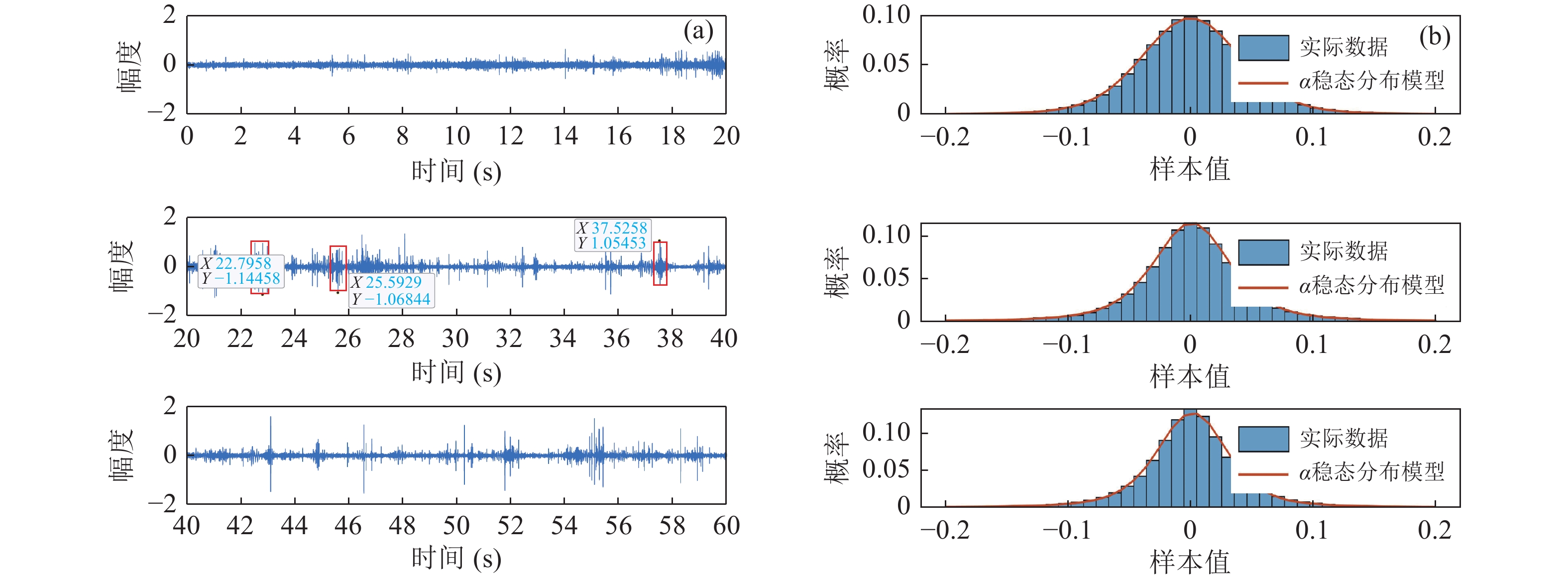
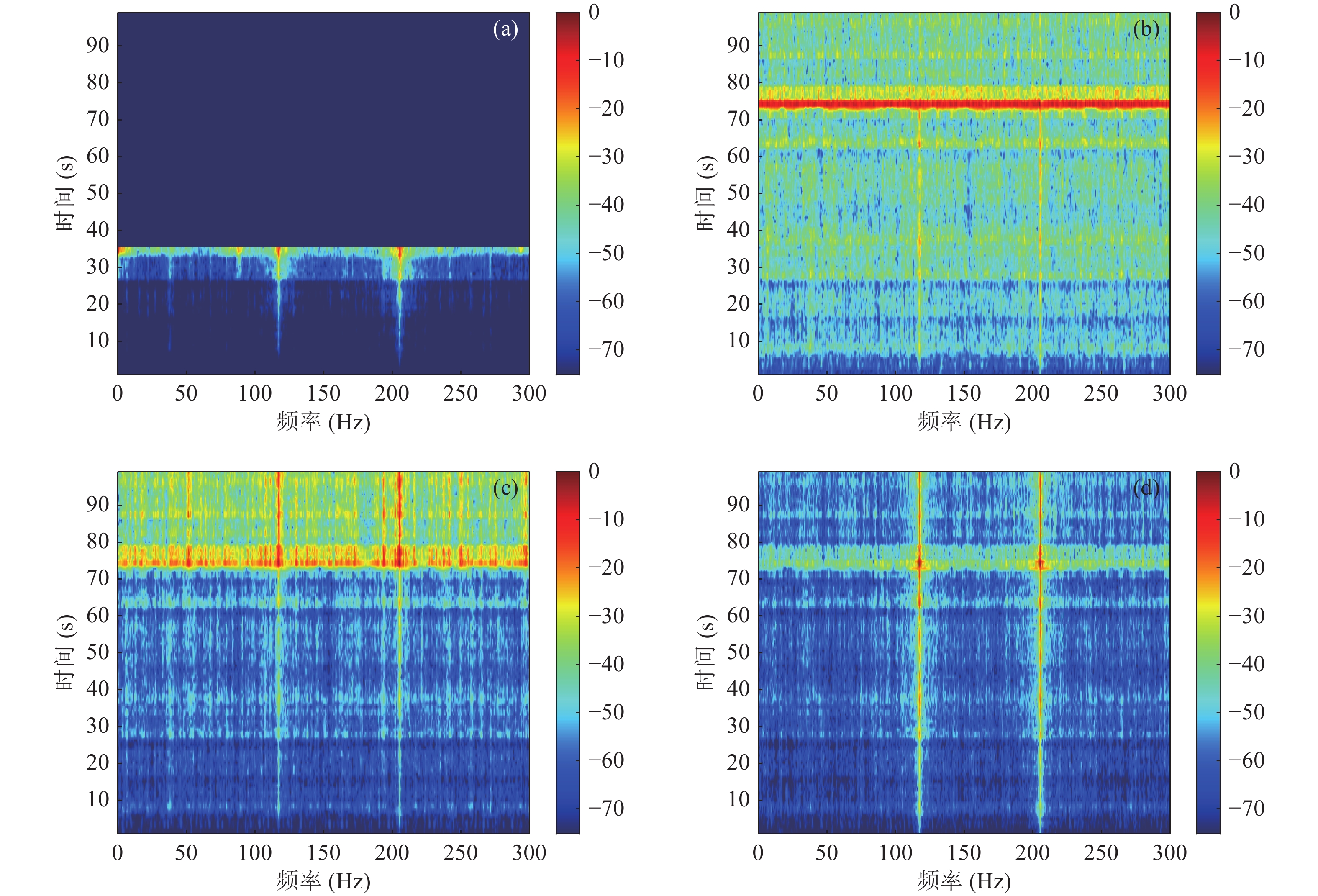
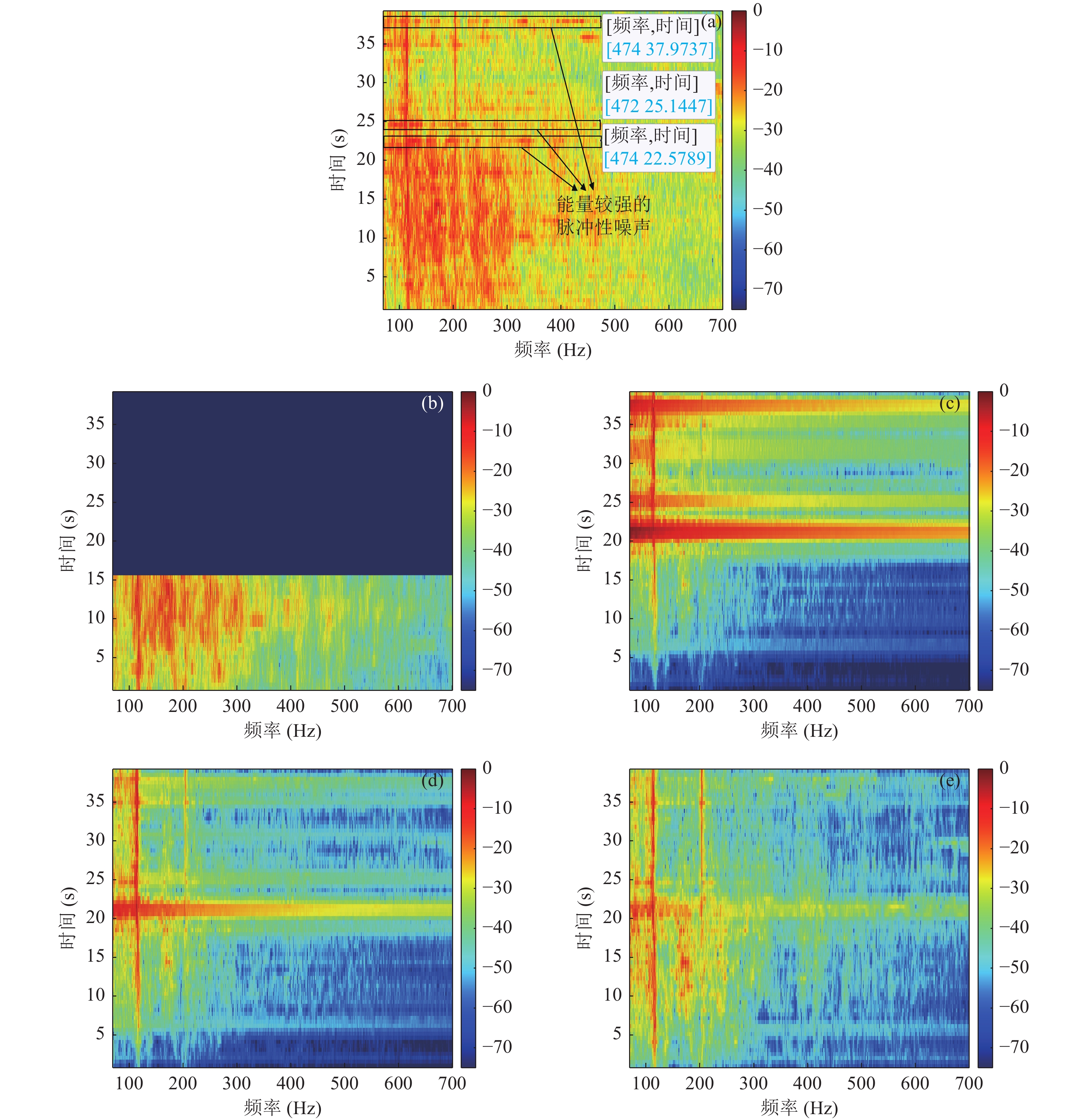
首先采集浅海环境下的声信号。图10(a)是3组长度为20 s的接收数据样本的时域波形, 其具有明显的非高斯特性。将接收数据样本与$\alpha $稳定分布进行参数拟合, 结果如图10(b)所示, 其中特征指数$\alpha $分别为1.7376, 1.4406, 1.5074, 即实际浅海噪声特征指数$ \alpha \in (1,2] $ 。

取40 s低频换能器发射状态下的接收数据, 分别利用常规自适应线谱增强器、SSA-ALE、Shannon-ALE和MCC-ALE进行处理。图11是4种ALE输出信号的LOFAR谱, 并与ALE输入信号的LOFAR谱进行了对比。

图11(a)中, 存在频率分别为117 Hz和205 Hz的线谱信号, 方框内标记了几处能量较强的非高斯噪声。常规自适应线谱增强器在迭代过程中发散, 无法增强目标线谱信号。SSA-ALE能够在非高斯噪声背景下实现线谱增强, 但是SSA-ALE得到理想结果的前提是能够人工预先选择合适的子空间进行重构。图11(c)中, 由于缺少先验信息, 子空间的不适配不仅导致难以抑制如23 s处、25 s处和38 s处能量较强的非高斯噪声, 还使得205 Hz处的线谱能量减弱, 难以检测到目标信号。图11(d)中, Shannon-ALE相较于SSA-ALE而言, 25 s处和38 s处的非高斯噪声得到了进一步抑制, 线谱能量被抑制的问题也得到了改善, 然而Shannon-ALE受到平滑参数和窗口长度的影响, 输入信号20~25 s处的瞬态脉冲性噪声被展宽, 将影响后续进一步的线谱检测与频率估计。图11(e)中MCC-ALE有效抑制了非高斯噪声, 实现了对线谱信号的有效增强, 其增强效果优于SSA-ALE和Shannon-ALE。从信噪比的角度分析, 在70~700 Hz带宽范围内, 输入信号的信噪比约为−2.28 dB, 经4种自适应线谱增强器处理后, 常规自适应线谱增强器不收敛, SSA-ALE的输出信噪比约为1.16 dB, Shannon-ALE的输出信噪比约为7.61 dB, MCC-ALE的输出信噪比约为8.62 dB。为进一步比较Shannon-ALE与MCC-ALE对目标线谱的增强能力, 在70~250 Hz范围内再次计算二者的输出信噪比, 其中Shannon-ALE的输出信噪比为17.46 dB, 而MCC-ALE的输出信噪比为21.38 dB, 因此MCC-ALE在上述4种自适应线谱增强器中具有最好的处理增益。

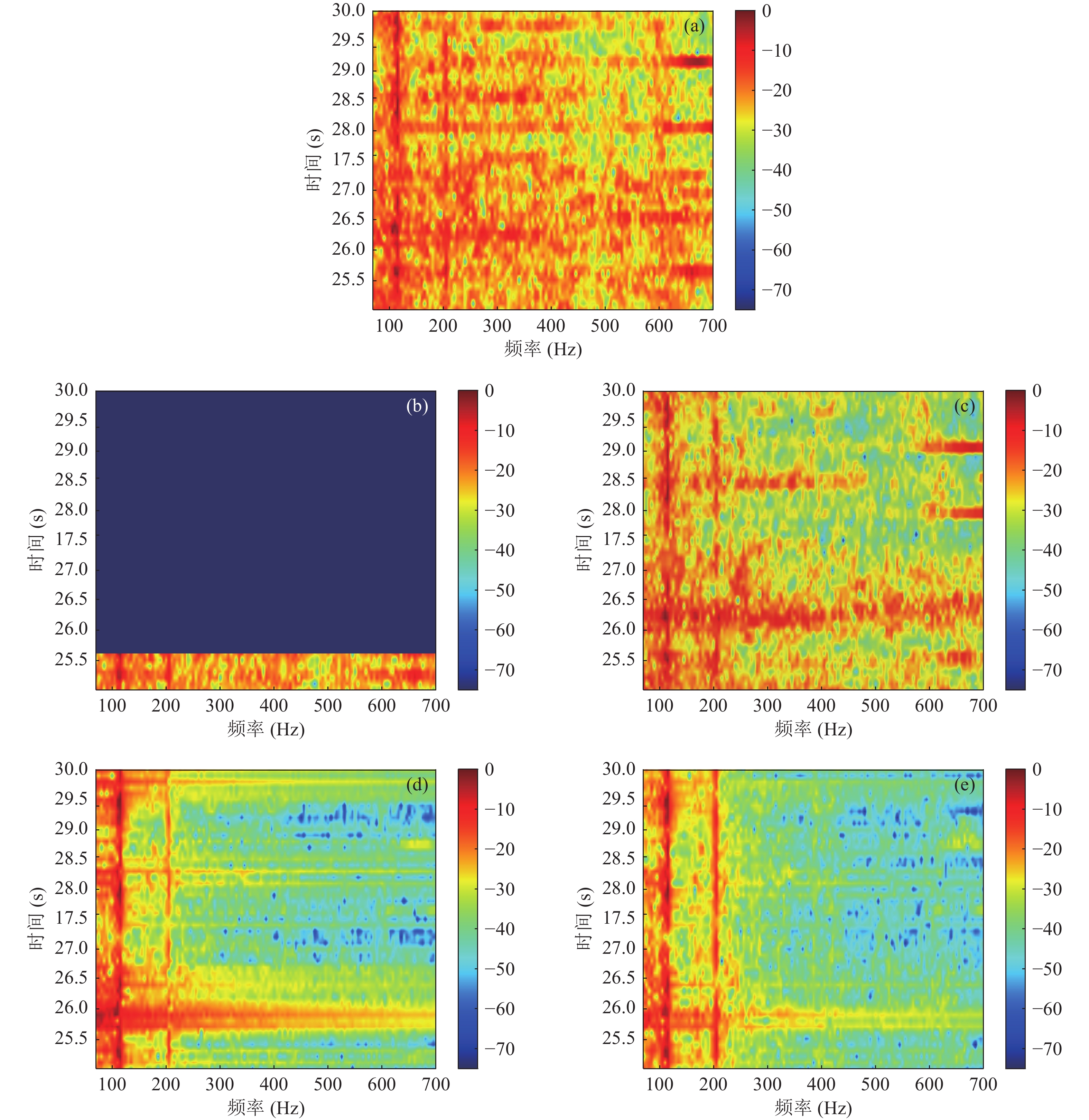
上述实验针对40 s的实测数据进行了分析, 工程应用中自适应线谱增强器往往需要在数据量较少的情况下工作, 因此为进一步验证MCC-ALE的性能, 展开如下仿真条件下的实验: 取25~30 s低频换能器发射状态下的接收数据作为系统的输入, 其他条件不变, 分别利用常规自适应线谱增强器、SSA-ALE、Shannon-ALE和MCC-ALE进行处理。图12是4种自适应线谱增强器输出的LOFAR谱, 并与自适应线谱增强器输入的LOFAR谱进行了对比。

图12(a)为25~30 s的接收信号LOFAR谱, 存在频率为117 Hz和205 Hz的线谱信号。输入信号中两处线谱信号淹没于噪声中, 在25.5 s, 26 s, 28 s, 29 s等处有多条能量较强的非高斯噪声。常规自适应线谱增强器受非高斯噪声影响, 迭代发散。相较于图12(d)(e), 图12(c)中SSA-ALE的处理效果不理想, 其原因在于该实验中数据量相对较小且输入信噪比较低, SSA-ALE分解重构的过程中无法得到有效的重构矩阵。虽然图12(d)中Shannon-ALE有效增强了两处目标线谱信号, 但是相较于图12(e), Shannon-ALE展宽了26 s处的非高斯噪声, 且205 Hz的目标线谱信号能量相对于图12(e)中MCC-ALE更低。综上, 数据量较少的情况下, 4种方法中MCC-ALE也具有最好的性能。

针对非高斯噪声的二阶矩发散导致基于最小均方误差准则的常规ALE性能失效的问题, 提出了一种基于MCC准则的自适应线谱增强器算法。基于线谱与非高斯噪声在广义时间相关半径上的差异, 采用MCC准则构造惩罚函数对自适应线谱增强器自适应权值进行迭代更新, 以抑制瞬态噪声成分带来的负面影响。仿真和海试数据处理结果表明, 在强非高斯噪声背景下, 本文算法可以实现弱线谱信号的有效增强, 处理增益显著优于现有方法, 且在高斯噪声背景下仍可实现弱线谱信号的有效增强, 具有鲁棒性; 数据量有限时, 本文算法仍有较好的线谱增强性能, 具有工程应用价值。本文算法与常规自适应线谱增强器类似, 也存在收敛速度和稳态失调的矛盾, 当收敛速度增大时, 稳态失调量也会增大。针对高斯背景噪声环境下常规自适应线谱增强器收敛速度和稳态失调间的矛盾, 目前已有学者提出了有关算法进行优化, 未来研究中可考虑利用相关算法进一步优化线谱增强性能。