波束形成是实现目标波达方向(DOA)估计的关键技术^[1-2]，较为常用的波束形成方法包括常规波束形成 (CBF) ^[3]、基于数据自适应的最小方差无失真响应(MVDR) ^[4]、匹配波束处理(MBP)^[5]。CBF与MVDR获取波束谱的谱峰位置确定来波方向, 端射方向性能下降明显。MBP与声场特性相关, 对端射方向的估计偏差有修正作用, 但拷贝场模型失配会导致性能严重不足。因此, 传统DOA估计算法亟需进一步优化。

近年来, 人工智能技术已成为各领域关注焦点^[6-8], 在水声探测、定位等领域得到了广泛应用^[9-11]。2020年, Elbir^[12]设计了一种CNN与多重信号分类(MUSIC)算法结合的信号DOA估计框架, CNN模型的输入是阵列接收到数据的协方差矩阵, 通过学习相应角度子区域的MUSIC谱进行DOA估计。2021年, Liu等^[13] 以接收阵列中水听器个数为目标设计多种CNN模型, 输入为实数与虚数协方差矩阵, 实现了目标方位的高效识别。2021年, 曹怀刚^[14]将CNN应用于单个矢量传感器目标DOA估计, 实现了多目标分辨。综上, 深度学习在目标定位研究中, 重点关注学习算法、数据集、特征选择和实际应用等。卷积神经网络(CNN)^[15]模型是基于共享卷积核的一种深度神经网络模型, 常规波束形成技术表征DOA信息具有一定的优势, 将CNN与常规DOA估计方法结合有望提高DOA估计性能, 而相比于网络本身, 数据集与特征选取往往影响更大。

基于深度学习的DOA估计模型多使用单一目标特征样本作为输入, 然后针对单一特征设计回归器或分类器, 目标的不同特征量对DOA特性有不同程度的描述, 这些特征量可能存在一致性和互补性。模式识别领域中，特征融合技术已广泛应用, 水下目标识别领域特征融合策略也获得了很好的效果。2018年, Zhang等^[16]提出了一种基于长短期记忆网络(LSTM)的多特征融合的目标识别方法, 融合了时域时间序列数据、频谱特征数据和Mel倒谱系数特征数据三种特征, 对水下目标辐射噪声识别的效果优于单一特征或者组合两种特征的分类效果。2020年, Ke等^[17]应用二维特征融合技术进行水下目标识别, 显著提高了识别精度。上述水声目标识别任务, 通过对目标的不同特征进行融合处理, 实现了特征间的表征能力互补或者增强特征表达。将多种特征进行联合表征, 目的是学习到更多关于目标的综合信息, 实现分类或者回归的学习任务^[18]。

本文首先探讨了传统DOA估计算法的特点及不足, 给出数值仿真示例分析; 然后结合CNN, 引入特征融合技术, 利用水平阵实现了目标DOA估计, 提出了CNN-CBF、CNN-MVDR和基于CBF和MVDR两种特征融合的CNN-Ⅱ三种估计算法。针对CBF和MVDR两种波束域特征展开了数值仿真分析, 在不同阵元间隔及不同信噪比下讨论CNN模型的DOA估计性能; 利用海试数据对本文算法进行了性能评价。

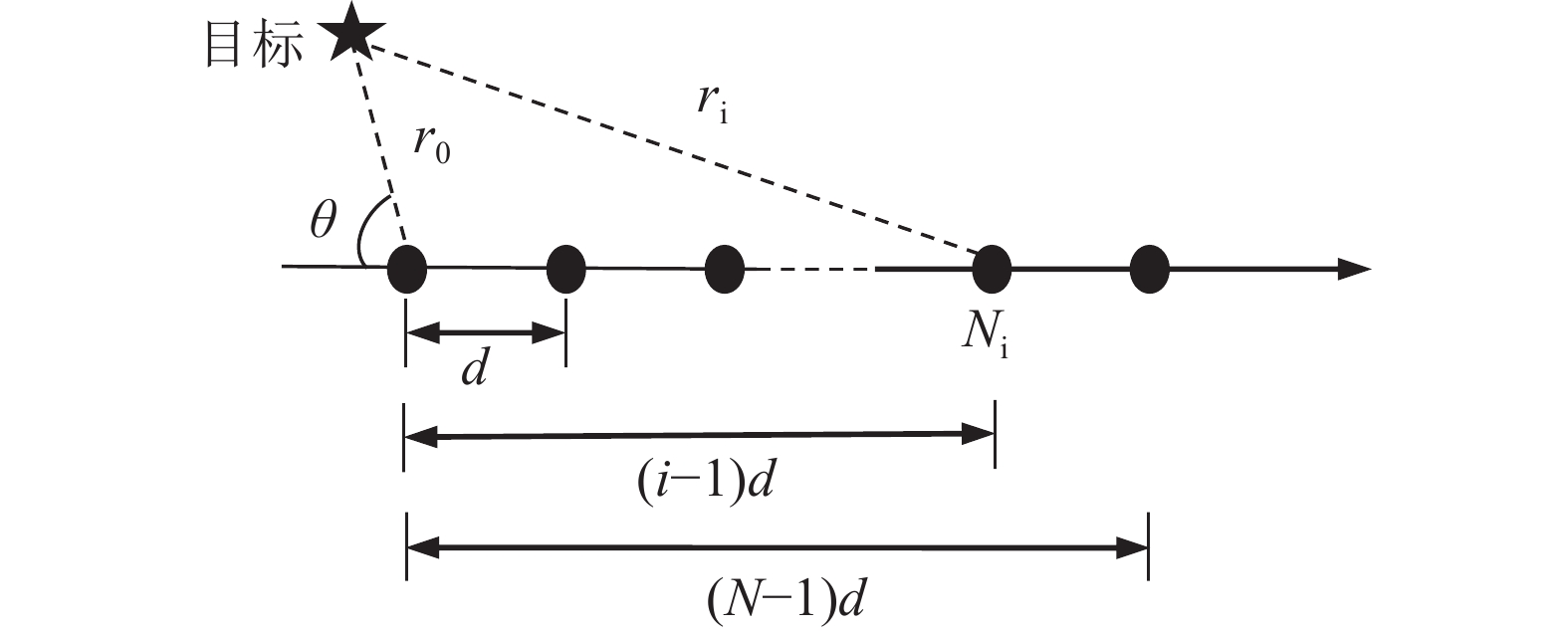
首先建立单条水平线阵列接收信号模型, $N$个水听器以间隔$d$均匀分布。假设单声源情况, 中心频率为$f$的信号$s(t)$以来波方向$\theta $入射到线列阵上, 信号满足远场窄带假设条件, 信号包络在通过阵列期间不会发生改变, 设$ {\boldsymbol{x}}(t) = {[{x_1}(t),{x_2}(t), \cdots ,{x_N}(t)]^{\rm T}} $为各个阵元接收信号, 一般包含经信道传播后的声源信号和噪声信号, 则阵列接收信号模型可以表示为

其中, ${\boldsymbol{n}}(t)$为噪声矩阵, ${\boldsymbol{a}}(f,\theta )$为阵列流形向量矩阵:

其中, ${p_i}$为阵元位置, $i = 1, \cdots ,N$, ${\boldsymbol{k}}$为波数向量, ${\boldsymbol{k}} = (2\pi f/c){\boldsymbol{\nu}} (\theta )$, ${\boldsymbol{\nu}} (\theta )$为声信号传播方向的单位向量, $c$为信号的传播速度。

实际中假设${\boldsymbol{x}}$是遍历的, 数据的互谱密度矩阵${\boldsymbol{R}}$通常使用一段快拍样本进行估计, 多快拍估计下互谱密度矩阵可以表示为

其中, $M$表示数据的频域快拍数, ${x_f}(m)$为每个快拍下$N$个阵元接收声场信号的频域数值, ${\rm H}$表示共轭转置。

CBF的基本原理为: 对线列阵每个阵元所处位置的接收信号进行处理, 按照指定方向作一定的时延补偿, 使期望方向上信号加强, 并抑制噪声和干扰。CBF扫描波束谱为

其中, ${{\boldsymbol{w}}_{{\text{CBF}}}}(f,\theta ) = {\boldsymbol{a}}(f,\theta )/\sqrt N $为CBF的加权向量。

波束谱最大模值对应的角度${\widehat \theta _{\text{C}}}$即为DOA估计角度:

其中, ${\theta _{\text{C}}} = {\theta _1},{\theta _2}, \cdots ,{\theta _{L1}}$为波束谱扫描的角度范围。

当目标来波方向为${\theta _0}$时, 衡量DOA分辨率的波束宽度为

其中, $\lambda $为波长。

从式(6)可以看出, 对于多目标分辨, 若信号频率相同, 入射到阵列的DOA的间隔小于波束宽度, CBF将不能准确分辨目标实际的DOA, 这是CBF存在的固有瑞利准则局限性, 一般通过增加阵元间隔和增加阵元个数提高角度分辨率, 在实际应用中阵列孔径的增加有所限制。

MVDR的基本原理为: 使得期望方向上的信号具有无失真输出的同时最小化噪声方差, 且在理想状态下旁瓣更窄, 主瓣更高, 但稳健性不足。基于对角加载的MVDR是指在样本互谱密度矩阵上添加对角矩阵项, 在模型失配情况下, 可以提高MVDR的输出性能。对角加载MVDR扫描波束谱为

其中

为对角加载后的MVDR的加权向量, $\rho $为对角加载系数, $\rho $的选取一般没有严格的标准, $I$为单位矩阵。

波束谱最大模值对应角度${\widehat \theta _{\text{M}}}$即为DOA估计角度:

其中, ${\theta _{\text{M}}} = {\theta _1},{\theta _2}, \cdots ,{\theta _{L2}}$为波束谱扫描的角度范围。

MBP进行目标DOA估计的基本原理为: 将阵列实际接收数据与所有可能的目标来波方向上产生的拷贝场数据的常规波束响应进行匹配。MBP需要已知声场先验知识, 通过参数不断调整寻求最优解或通过提高信号处理器的性能缓解环境失配问题, 但增加了计算量。MBP的目标函数为

其中, ${{{\boldsymbol{B}}}_{{\text{CBF}}}}({\text{data}};\alpha {|_{\theta = {\theta _k}}})$和${{{\boldsymbol{B}}}_{{\text{CBF}}}}(s;\alpha {|_{\theta = {\theta _l}}})$分别为测量场和拷贝场的波束响应, ${\theta _k}$为目标的来波方向, ${\theta _l}$为设置的匹配波束扫描方向, ${\theta _l}$遍历某个DOA可能的范围, $\alpha $是计算CBF波束响应时扫描的角度范围, 在本文$\alpha $取值范围为1°~180°, 取值间隔为1°。

根据${\boldsymbol{ B}}(s;\alpha {|_{\theta = {\theta _l}}}) $即可确定目标方向${\widehat \theta _{{\text{MBP}}}}$:

其中, ${\theta _{{\text{MBP}}}} = {\theta _1}, \cdots ,{\theta _l}, \cdots , {\theta _L}$为匹配波束扫描的角度范围。

在典型的浅海环境下, 接收阵为水平线列阵时, 对CBF、MVDR对角加载以及MBP三种算法的DOA估计性能进行数值仿真分析。

声源频率为100 Hz, 声源深度为20 m, 单条水平线列阵(32阵元, 阵元间隔1.5 m)深度为50 m, 目标声源距离水平阵参考阵元的距离为4.5 km。采用两层海底模型, 设置声场环境参数为: 水深为100 m, 沉积层厚度为6 m, 沉积层和基底层声速分别为1600 m/s和1800 m/s, 沉积层和基底层密度分别为1.7 g/cm³和1.8 g/cm³, 沉积层和基底层衰减均为0.5 dB/λ, 海水声速为1500 m/s, DOA扫描范围为1°~180°, 扫描角度间隔为1°。利用声场仿真软件KRAKENC进行声场数据仿真。沉积层和基底层参数范围设定时参照文献[19] 1.6节中的表1.3。

定义本节三个性能评估参数: DOA估计准确度$ {\rm Acc}_{5^ \circ } $(预测DOA与真实DOA的绝对误差小于等于5°的百分率)、波束谱主瓣宽度${B_{ - 3{\;{\mathrm{dB}}} }} = |\theta _{ - 3}^ + - \theta _{ - 3}^ - |$(波束谱中的主瓣对应的波束谱强度下降到−3 dB时对应的两方向间的夹角, $\theta _{ - 3}^ + $表示主瓣波束谱下降到−3 dB时主瓣右侧对应角度, $\theta _{ - 3}^ - $表示主瓣波束谱下降到−3 dB时主瓣左侧对应角度)和水平接收阵阵输出主旁瓣比${G_{{\text{HLA}}}}$(主瓣峰值与第一旁瓣峰值对应波束谱强度之差)。

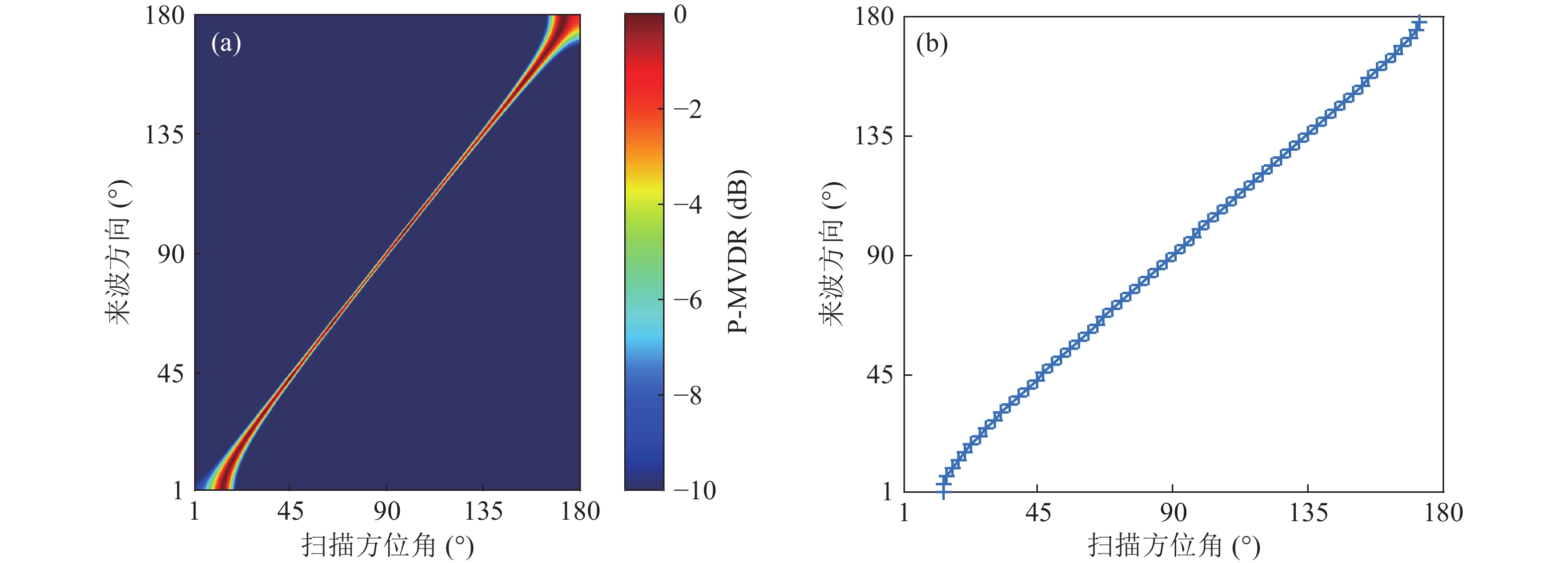
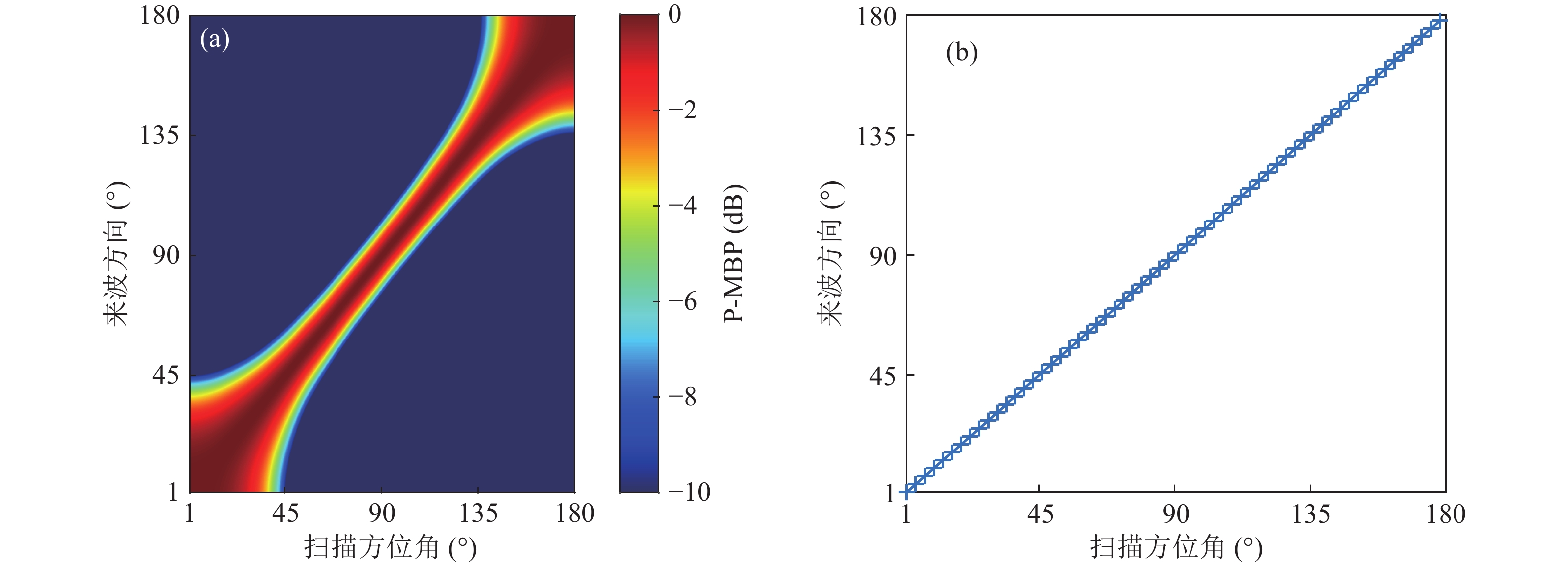
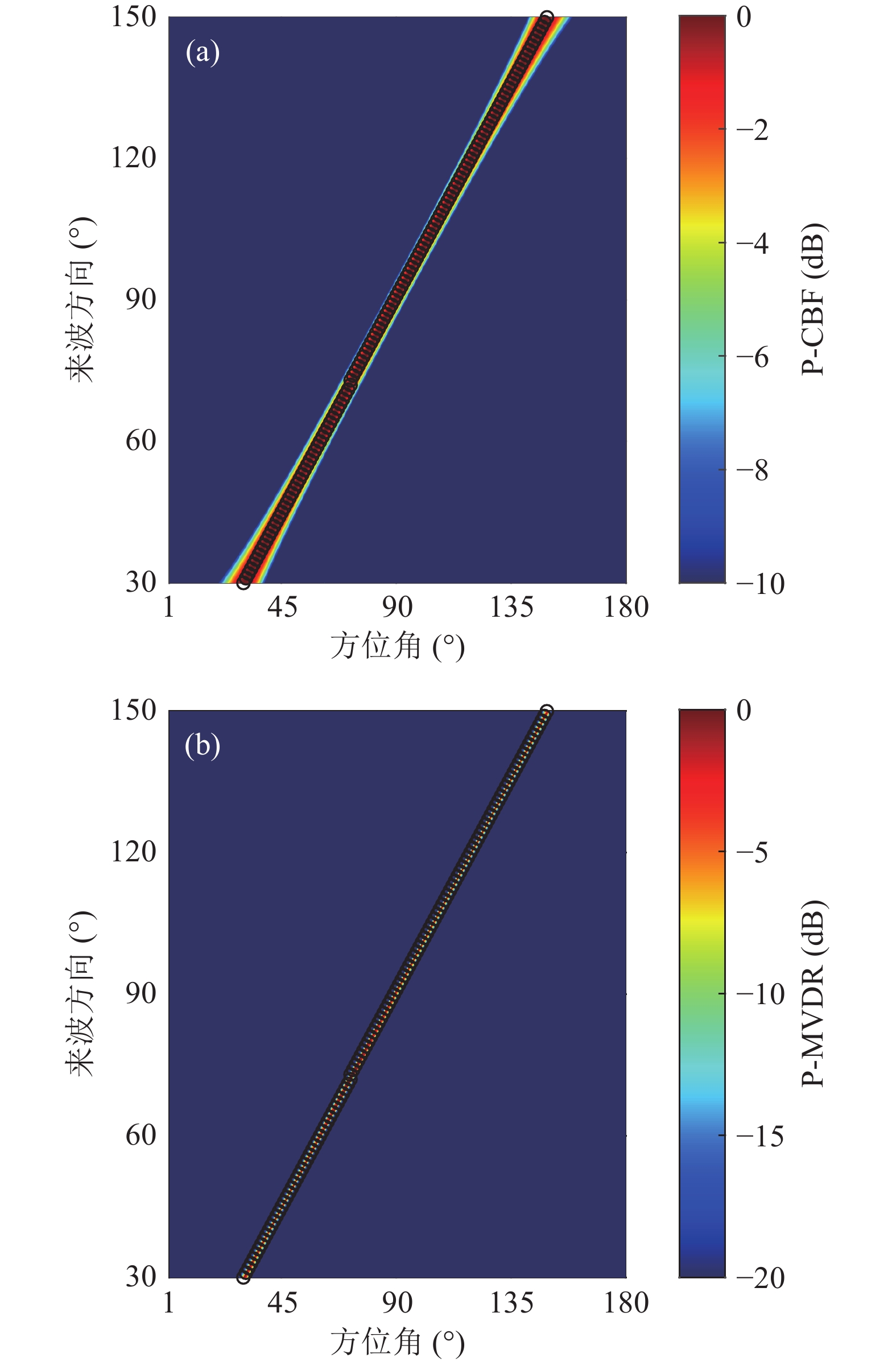
使用MBP时, 拷贝场参数设置严格与测量场仿真参数一致, DOA扫描角度范围为1°~180°, 扫描角度间隔为1°。CBF、MVDR对角加载(对角加载系数为0.01)、MBP处理结果分别如图1—图3所示。

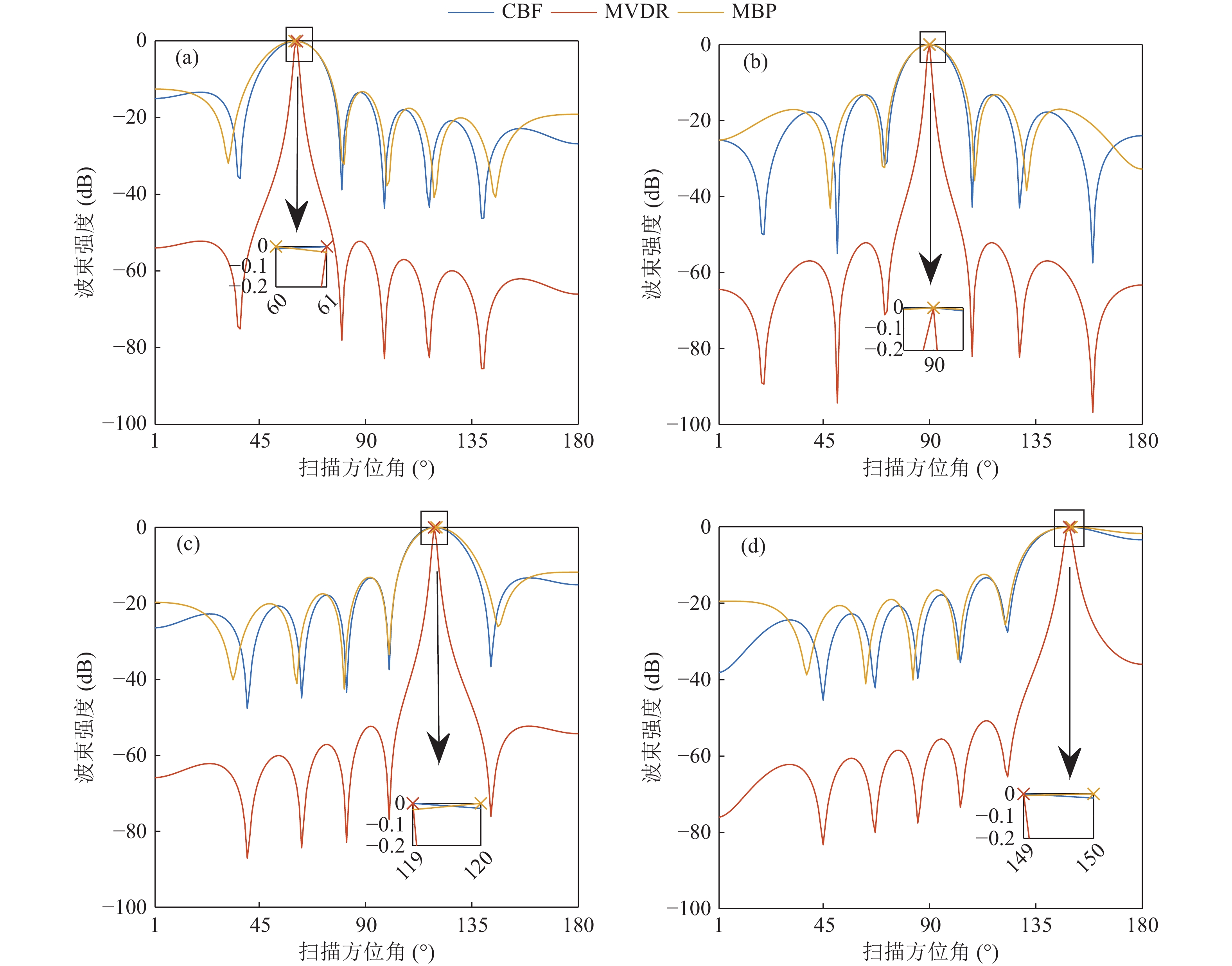
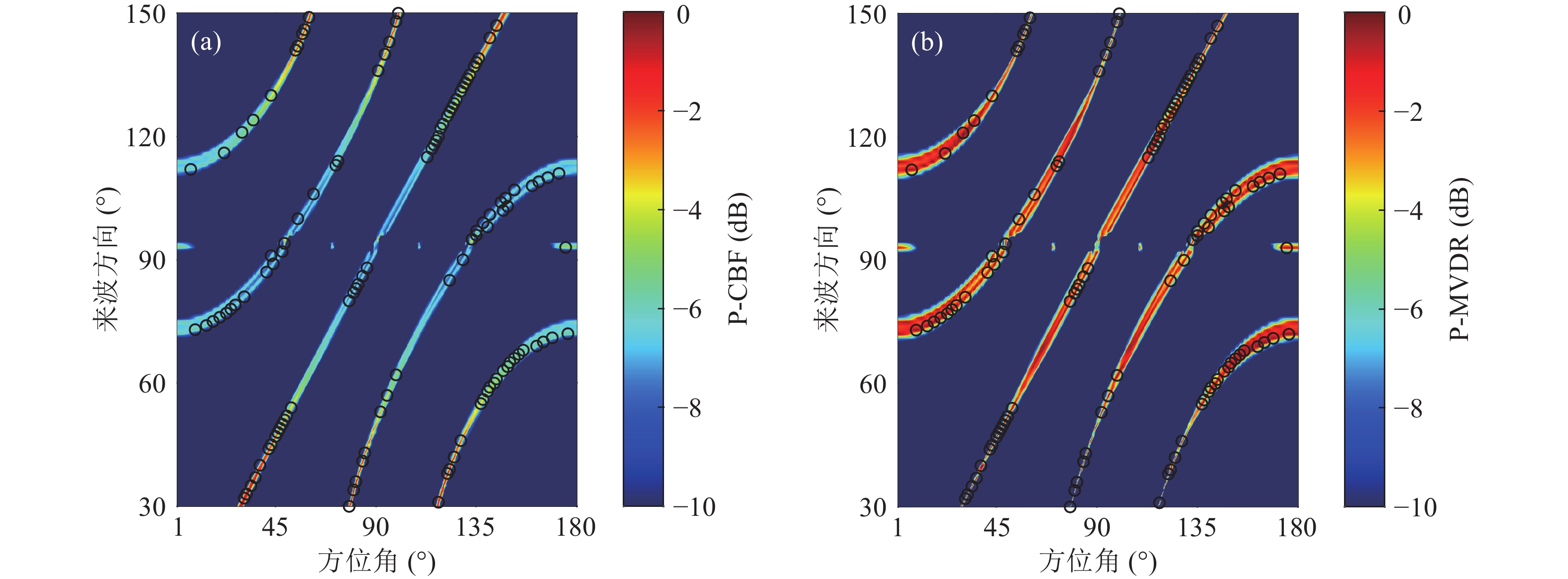
分析非端射方向主瓣宽度和阵输出主旁瓣比。当来波方向为60°, 90°, 120°, 150°时, CBF、MVDR和MBP处理结果的波束谱扫描图如图4所示。波方向为60°, 90°, 120°, 150°时的${B_{ - 3\;{\rm dB} }}$和${G_{{\text{HLA}}}}$数值分别列于表1和表2。

从图1—图3的方位历程图可明显看出, 对比三种方法的主瓣宽度, MVDR有最窄的主瓣, CBF和MBP的主瓣相当。MBP方法的$ {\rm Acc}_{5^ \circ } $为100%, CBF和MVDR的$ {\rm Acc}_{5^ \circ } $均为90.56%, CBF和MVDR估计方法在端射方向失效, 出现较大DOA估计偏差, MBP方法性能仍然保持精准, 这是因为端射方向波束输出的宽度增加导致角度分辨能力下降, 匹配波束在理想的模拟仿真下, 通过全声场处理可以有效解决端射方向DOA估计问题。在本节设置仿真参数下, 从表1可以看出MBP对应主瓣宽度稍大于CBF, MBP方法在保证了DOA估计精度的同时损失了很小的阵输出主旁瓣比。

分析三种算法的原理, CBF和MVDR在浅海水平阵下的应用与环境参数关联性不强, 并不需要提前获得声场环境参数的先验知识, 直接利用线性加权可以计算出波束谱, 直接根据波束谱峰值对应角度确定估计的来波方向。MBP技术从原理来看可以视为一个相关处理器, 基于物理原理, 在已知测量场相关信息后, 可以准确进行DOA估计。具体实测数据下性能需要进一步分析。

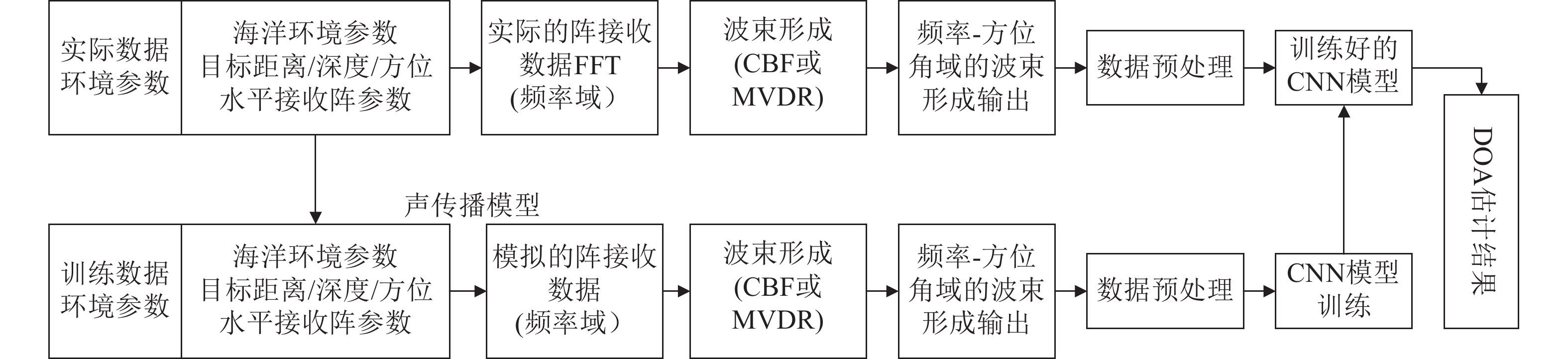
图5是本文将卷积神经网络方法应用于水声目标DOA估计的流程图。具体实现过程可以分为五个环节: 声场数据仿真、波束形成处理、数据集预处理、网络模型训练、DOA估计。

特征融合方式可以分为基于特征级的前端融合、中间融合, 以及基于决策级的后端融合。前端融合指在网络的样本输入层上做相关融合操作, 最简单的就是将两个特征矩阵进行垂直连接; 中间融合是指先将不同特征通过神经网络转变为高维特征表达, 在网络模型的隐含层做融合操作, 再去训练实现分类或回归; 后端融合指在网络输出层融合, 针对不同的特征分别训练网络模型, 针对模型输出的预测结果, 将不同的预测的结果通过某些融合机制进行融合。

本文进行简单的尝试, 将前端特征融合应用到水下目标DOA估计中。3.1.1节所述的DOA估计流程是指通过对阵列接收数据进行波束形成处理, 再利用CNN进行目标DOA估计, 输入到网络中的数据集特征是单一波束域特征。为了学习到更多关于目标DOA的相关信息, 通过不同的波束形成处理得到关于目标的两种波束域特征量, 采用统一的数据集预处理方法, 将两种特征进行前端特征矩阵垂直连接融合, 融合后的数据输入到网络中。多特征融合技术目标DOA估计具体流程如图6所示。

针对水听器阵列获取的实测声场数据量不足以支撑网络模型训练的问题, 本节建立了实际声场无源声呐阵列接收信号模型。

根据简正波理论^[19], 水平均匀波导环境中线列阵各个阵元所接收到的声场数据是各阶简正波模态加权求和的结果:

其中, ${r_i}$为接收距离, ${{\textit z}_r}$为接收深度, ${{\textit z}_s}$为声源深度, $\rho ({{\textit z}_s})$是声源深度上的介质密度, $M$是有效简正波的阶数, ${Z_m}({{\textit z}_s})$和${Z_m}({{\textit z}_r})$是第$m$阶简正波相应的本征函数, ${k_{rm}}$是本征函数对应的本征值, 即第$m$阶简正波水平波数。${S}(f)$为信号经傅里叶变换后在对应频段内的频谱, ${{P}_{\text{H}}}({r_i},{{\textit z}_r},f)$为各阵元感兴趣频段内利用声场计算软件计算出的若干离散频率的频域信道传输函数, 频点与信号频点对应, 且与距离有关。

目标来波方位为$\theta $时无源声呐阵列接收信号模型可以表示为

其中, ${r_i},i = 1,2, \cdots ,N$为目标到各阵元距离, ${{\textit z}_r}$为接收线列阵布放深度。

目标信号传播至接收线列阵处的声场为${{P}_{\text{E}}}(f,\theta ,{N_i})$, 其中${N_i}$为阵元编号, $i = 1,2, \cdots ,N$, ${{P}_{\text{E}}}(f,\theta ,{N_i})$与DOA信息有关, 与距离有关, 则有

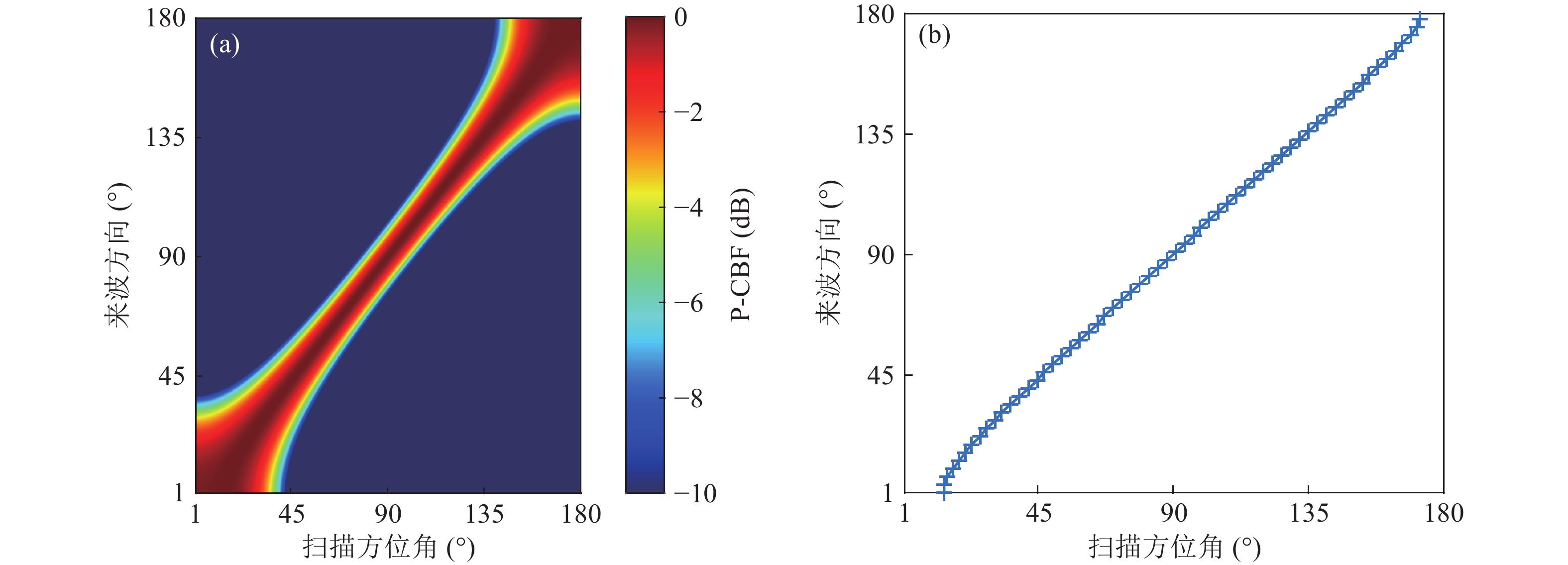
其中, ${r_0}$为目标到接收线列阵参考阵元的距离, ${r_i},{\text{ }}i = 1,2, \cdots ,N$为目标到各阵元的距离。式(15)的计算示意图如图7所示, $N$个阵元以间隔$d$均匀分布。

通过扫描DOA可能存在的角度范围得到单频CBF波束谱为

其中

${{\boldsymbol{R}}_x}$为接收信号的互谱密度矩阵, ${{\boldsymbol{R}}_n}$为与${{\boldsymbol{R}}_x}$尺寸一样的单位噪声矩阵, ${R_{{\text{SN}}}}$表示信噪比。

信噪比定义如下:

其中, ${R_{{\text{SN}}}}$定义为第一阵元接收信号与噪声方差的比值, $\sigma _s^2 = {{\boldsymbol{R}}_x}(1,1)$为信号方差, $\sigma _n^2$为零均值的高斯白噪声方差。

通过扫描DOA可能存在的角度范围得到单频对角加载MVDR波束谱为

其中, 不添加噪声时, ${\boldsymbol{R}} = {{\boldsymbol{R}}_x} + \rho{\boldsymbol{ I}}$, $\rho $为对角加载量。

根据上述建立的实际声场无源声呐阵列接收信号模型, 利用声场计算软件KRAKENC可以进行数据集的大量生成, 满足深度学习算法的训练数据量需求。

本文实测数据处理方式与仿真数据归一化方式保持一致, 根据阵元域接收声场数据计算出互谱密度矩阵:

添加噪声后的互谱密度矩阵${\boldsymbol{R}}$归一化为

统一将CBF和MVDR的波束谱写为$ {{\boldsymbol{P}}_{\mathrm{B}}}(f,\theta ) $:

波束谱取模值就可以表征DOA信息, 归一化并取模值后的波束谱$ {{\boldsymbol{P}}_{\mathrm{B}}}(f,\theta ) $的维度为${N_f} \times {N_\theta }$, 以此作为神经网络的输入, 其中${N_f}$为频点个数, ${N_\theta }$为波束形成时扫描角度个数。每一个样本对应输入矩阵的形式为

将CBF和MVDR两种波束域特征进行特征融合, 根据3.1.2节所述流程具体实现如下: 对于每一个样本, 分别进行CBF、MVDR波束形成处理, ${\widetilde {\boldsymbol{P}}_{\text{C}}}(f,\theta )$为CBF处理结果, ${\widetilde {\boldsymbol{P}}_{\mathrm{M}}}(f,\theta )$为MVDR处理结果, 将两个矩阵进行垂直拼接, 得到每个输入样本特征为

目标的DOA通常具有空间相关性, 而分类问题的输出中不同的类别所对应的空间DOA并无关联; 回归问题的输出则是用于预测连续的数值且网络的输出可以回归到多个值。结合分类输出中不同神经元位置代替目标的DOA值和回归输出中通过输入预测输出数值的特点, 本文将目标的DOA估计看作分类与向量回归的联合问题^[20]。先对目标的DOA可能存在的角度范围进行分类, 再对目标的DOA在每个类别上的概率进行回归, 根据DOA估计概率分布确定DOA数值。这种情况下采用高斯编码将DOA在角度域的表示进行预处理, 得到每个样本DOA对应的正态分布。

设目标DOA为${\theta _k}$, $k = 1,2, \cdots ,K$, 对扫描角度范围以间隔$\Delta \theta $等间隔划分为$N$份, 每一个输入矩阵$ {{\boldsymbol{P}}_{\mathrm{B}}}(f,\theta ) $, 对应一个标签向量为${{\boldsymbol{t}}_k}$:

其中, $k$为样本的标签序数, ${\theta _{kj}} = j\Delta \theta $为第$j$个划分角度, $j$为各划分角度的序数, ${\theta _{kr}}$为第$k$个样本对应的真实DOA, 对应到测试样本则是根据GPS记录计算出的真实DOA值, $\sigma $为DOA正态分布的标准差, 表征真实DOA与预测出的DOA之间的偏差, 与波束宽度有关, $\sigma $越大代表了对DOA估计误差容忍度越大, 但$\sigma $不是无限大, 超过一定界限DOA估计精度会下降, 在实际中为可调参数。

本文利用CNN网络进行DOA估计时, 扫描角度范围为1°~180°, 取值间隔为1°, 输出层节点对应的角度值为

当模型训练完成时, 将测试集样本输入至训练好的模型中进行测试。每一个样本分别与输出层输出的$1 \times 180$的向量相对应, 将输出向量经过处理后转换为有关各测试样本所对应的角度向量${{\boldsymbol{t}}_k}$, 估计的DOA值${\theta _{ek}}$就是${{\boldsymbol{t}}_k}$最大值位置所代表角度值, 即

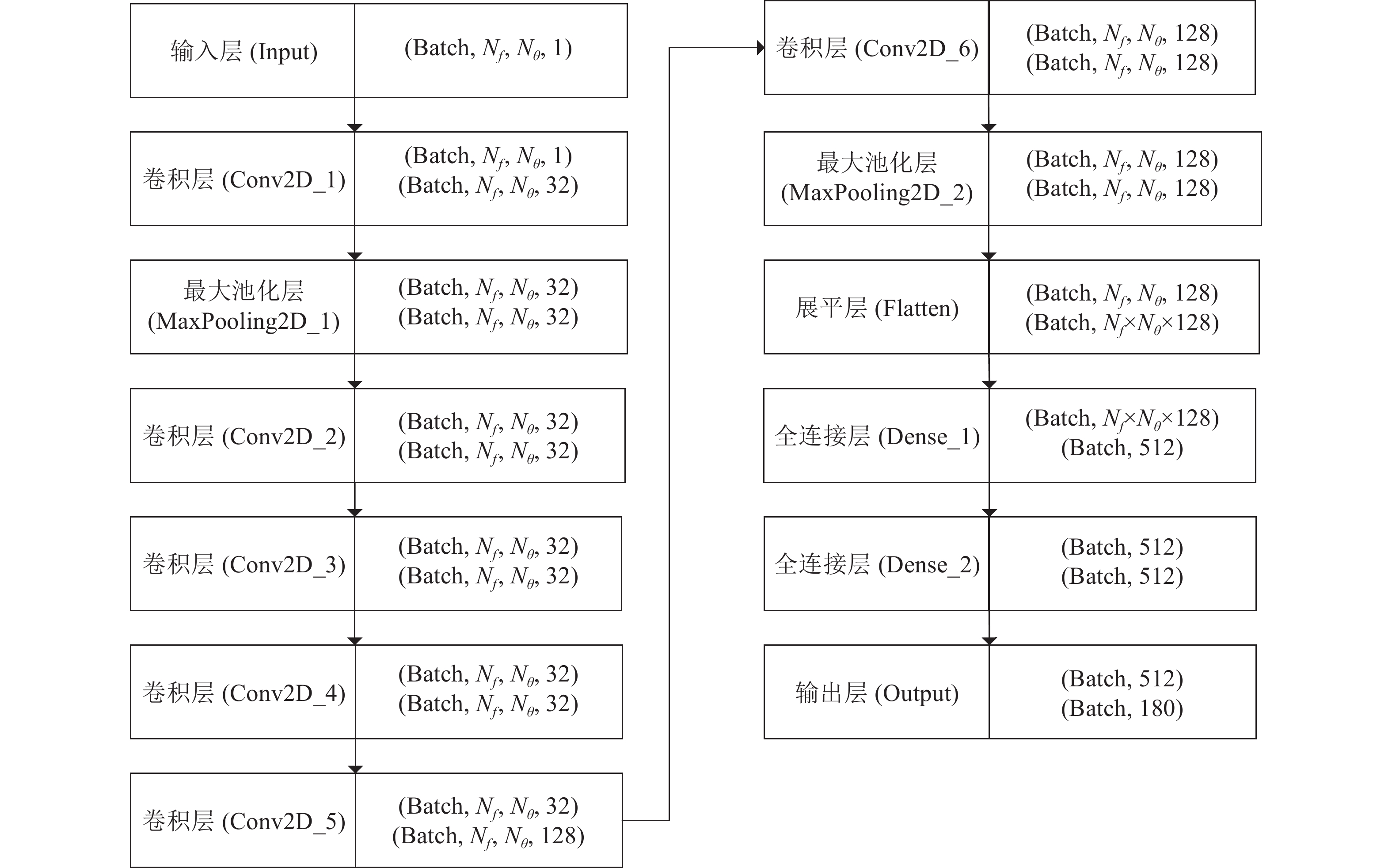
图8为本文所采用CNN模型网络结构, 其中Batch表示批量样本数目。所用模型包含6层卷积核尺寸为$3 \times 3$的卷积层, 包含输出层在内的3层全连接层和2层池化层。每层卷积核个数设置值依次为32, 32, 32, 32, 128, 128, 分别在第1层卷积层和第6层卷积层后加入1层核为$2 \times 2$的池化层, 设置的3层全连接层神经元数量分别为512, 512, 180。使用Dropout正则化方法, 第6层卷积层之后将Dropout设置为0.7。卷积层所采用的激活函数都设定为ReLU激活函数, 损失函数选用最小均方误差函数。优化算法选用Adam, 初始学习率设置为0.0001, CNN的训练过程包含500个epoch, 批量样本数目为32。

CNN训练过程分为前向传输预测阶段和后向传输更新权重阶段。首先, 预处理后的数据集经各层网络变换传输到输出层进行预测输出, 网络训练结束后的预测阶段也是如此; 然后, 根据样本数据的对应标签与模型的预测输出进行最小均方误差计算; 随后计算每个权重的梯度, 利用Adam优化器更新权重。

为了定量评估不同DOA估计算法下的定位性能, 定义可靠测向概率(PCDE)为DOA估计结果的绝对误差小于5°的概率, 可以反映实际各种算法预测出的DOA结果的可靠性; 均方根误差(RMSE)用于衡量预测出的DOA与真实DOA之间的偏差, 即

其中, ${N_{{\text{test}}}}$是待估计样本总数, $\eta (k) = 1$时表示第$k$个样本的DOA被有效估计出。${\theta _{rk}}$是第$k$个样本根据GPS计算出的真实DOA, ${\theta _{ek}}$是第$k$个样本根据DOA估计算法预测出的DOA。

采用Pekeris型浅海波导, 设置声场参数: 海底的声速、密度和衰减分别为1600 m/s, 1.5 g/cm³, 0.2 dB/λ, 声速剖面呈等声速梯度并设置为1500 m/s, 32阵元接收阵, 目标的DOA取值范围为30°~150°。来波信号半波长条件约束为阵元间隔$d \leqslant c/2f$, 其中$c$为接收阵所在深度上的声速, $f$为信号频率, 信号频率取值范围为100~200 Hz, 则$d \leqslant $3.75 m。训练集和测试集参数设置分别如表3和表4所示。训练集样本数据量为$121 \times 5 \times 8 \times 6 = 29040$, 输入CNN网络的特征维度为$11 \times 180$, 不同信噪比对应下每组测试集样本数据量为$121 \times 1 \times 8 \times 6 = 5808$, 输入CNN网络的特征维度为$11 \times 180$。

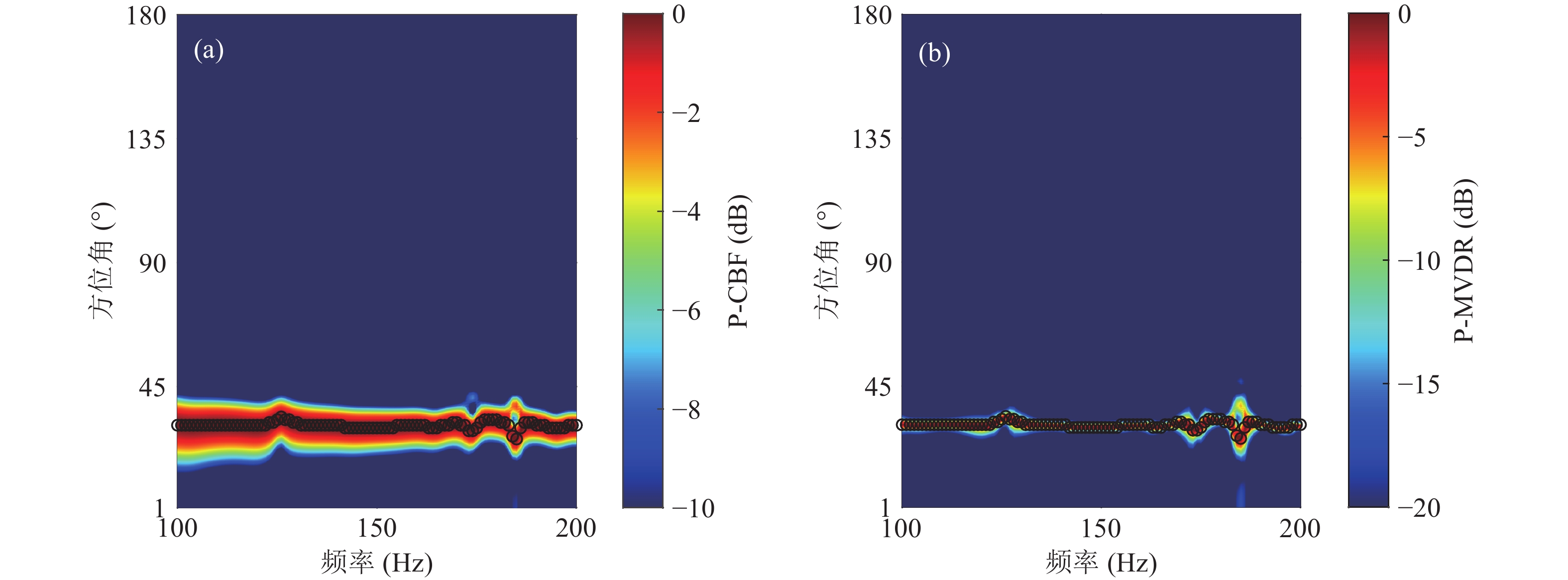
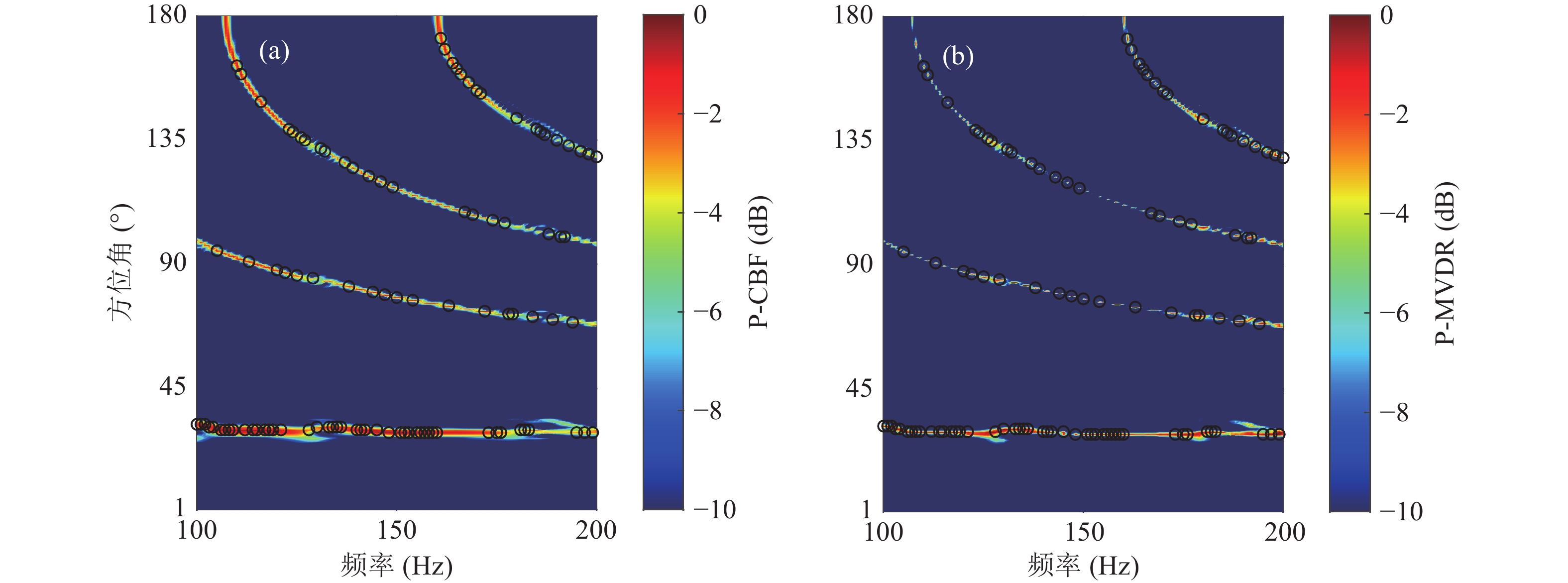
设置声源深度20 m, 声源到参考阵元距离为4 km, 水平线列阵接收深度为50 m, 水深为60 m。当$f$= 150 Hz, 阵元间隔$d$= 3 m, 来波方向取值范围为30°~150°, 取值间隔为1°时, CBF和MVDR输出特征见图9; 改变阵元间隔为$d$= 15 m, 结果见图10。当$f$取值范围为100~200 Hz, 取值间隔为1 Hz, 来波方向为30°时, 阵元间隔$d$= 3 m, 频率−波束谱结构见图11; 改变阵元间隔为$d$= 15 m, 结果见图12。最高能量点在图中均用黑色圆圈标出。

如图9和图11所示, 在$d$= 3 m时, CBF和MVDR估计结果最高能量输出点指示DOA估计结果, 主瓣强度最高, 几乎无旁瓣的干扰, MVDR拥有窄的主瓣宽度。当$d$= 15 m时, 如图10和图12所示, 二者波束谱不仅包含DOA方位输出信息, 还包含多个强度很高的栅瓣信息, 这将造成很大的干扰, 波束图指示的最高能量点发生改变, 不是完全处于来波方向误差范围内, CBF和MVDR不能正确估计DOA。

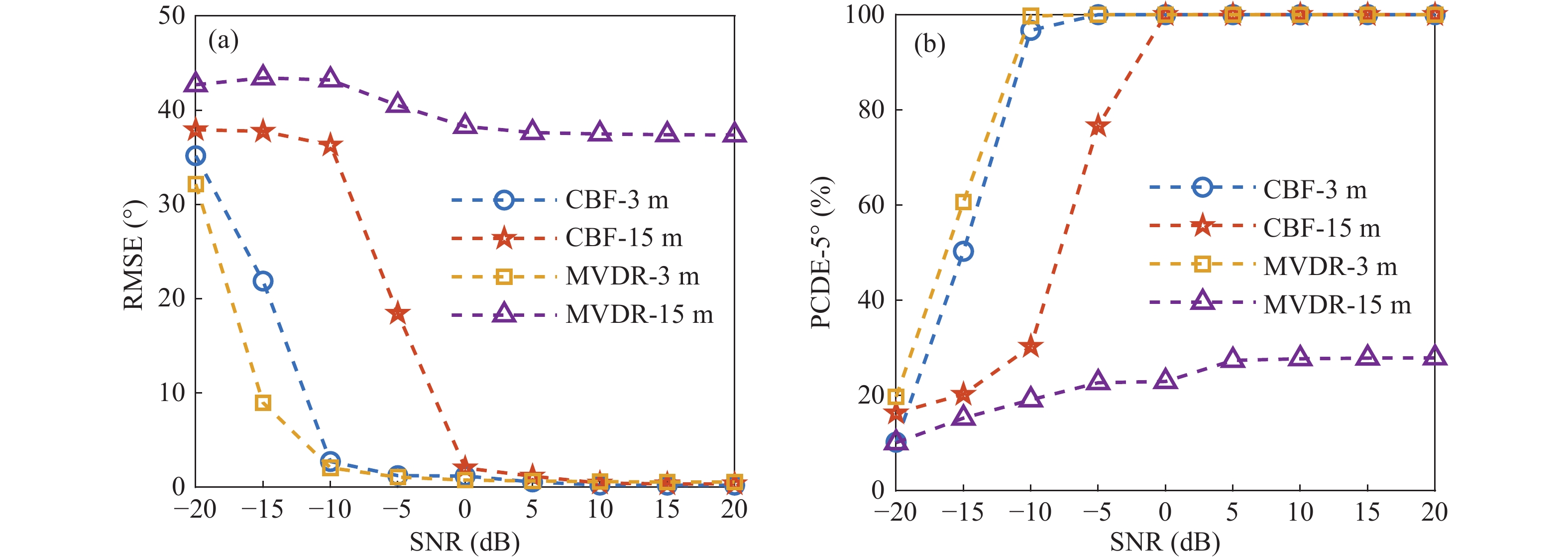
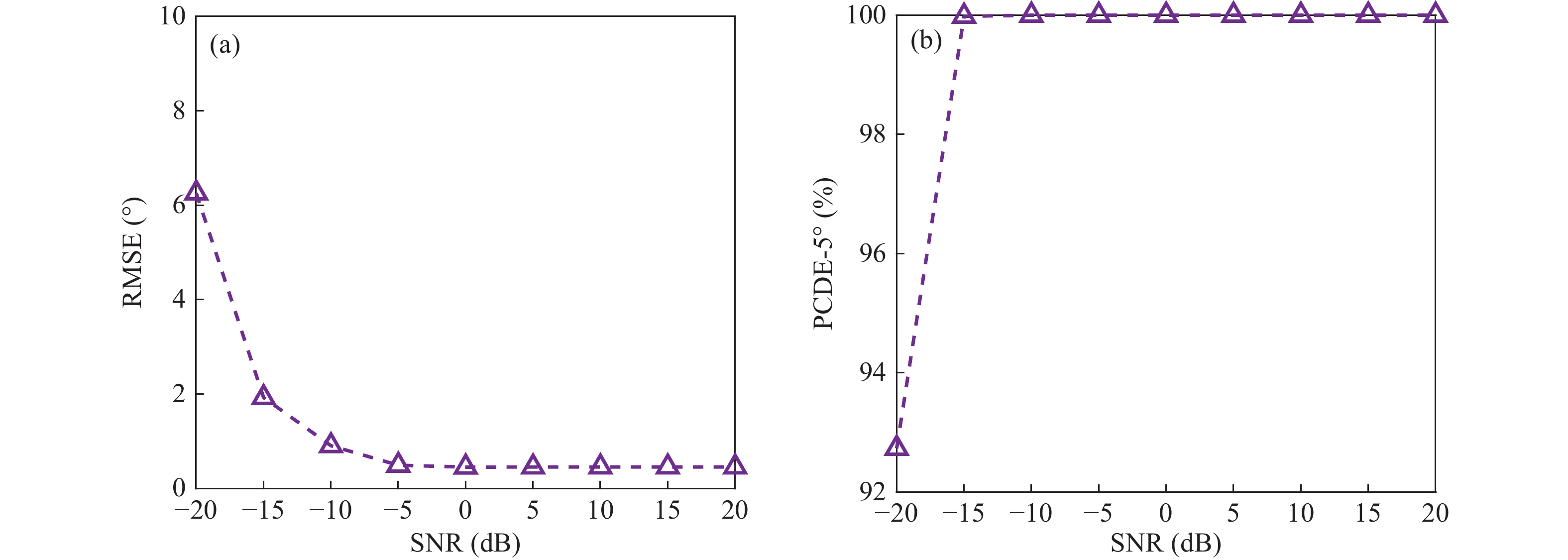
波长的变化会引起波束谱能量分布发生变化。分别在满足半波长条件($d$= 3 m)和不满足半波长条件($d$= 15 m)下进行训练和测试, 训练集中均未加入噪声, MVDR训练集采用对角加载方式生成(对角加载量为0.01), 设置对应波长条件下CBF和MVDR测试集信噪比取值范围为−20~20 dB, 取值间隔为5 dB, 在不同信噪比对应测试集下, 测试不同阵元间隔下模型的性能, 比较RMSE和PCDE-5°。

网络模型结构和训练参数与3.4.1节保持一致, 迭代的最大次数为500, 信噪比取值范围为−20~20 dB时, 取值间隔为5 dB, 定义以CBF和MVDR波束谱作为特征输入时模型为CNN-CBF和CNN-MVDR, 则在不同阵元间隔条件下CNN-CBF、CNN-MVDR模型预测结果的RMSE和PCDE-5°随信噪比变化如图13所示。

由图13可见, 当$d$= 3 m时, CNN-CBF和CNN-MVDR性能表现差别不大, CNN-MVDR估计结果在信噪比小于−5 dB时略优于CNN-CBF。在信噪比大于等于−10 dB时, 两种估计方法的PCDE-5°均逼近100%并趋于稳定, RMSE下降到2°以下趋于稳定, 都能准确估计出DOA。两种方法对于信噪比都具有很强的宽容性。

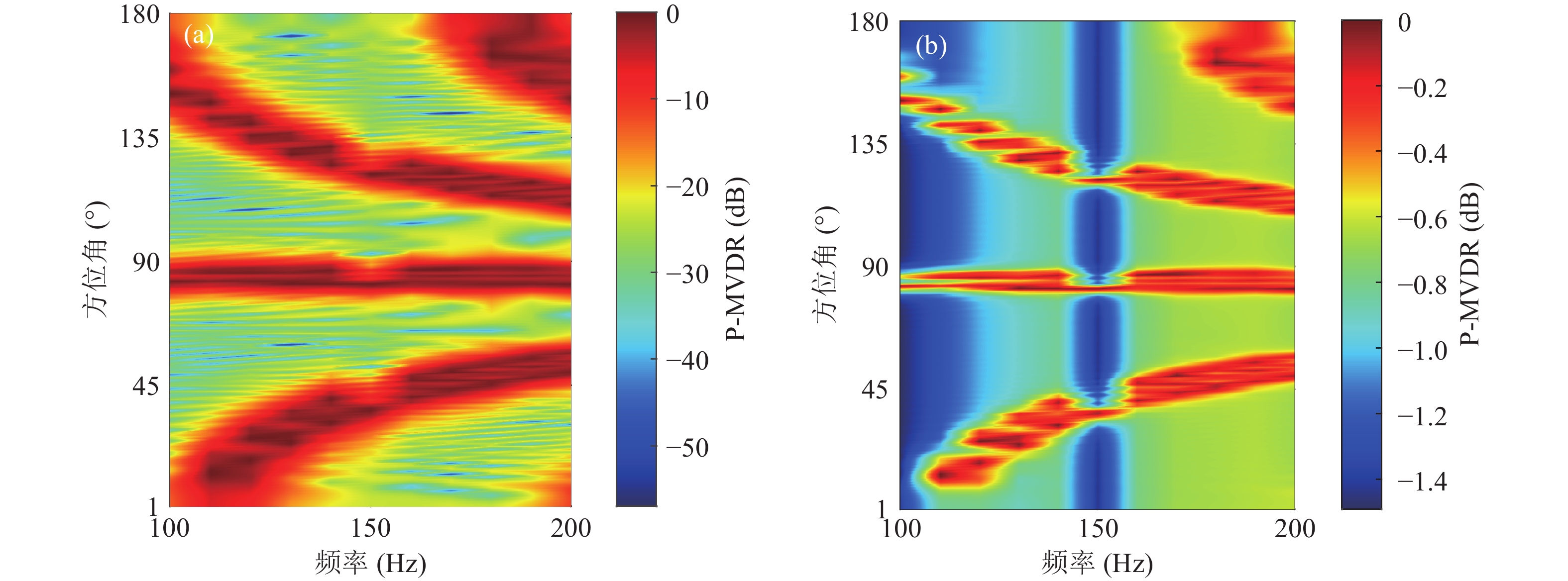
当$d$= 15 m时, 在设定的信噪比范围内, CNN-MVDR模型预测结果的PCDE-5°均在30%以下, RMSE最小也在35°以上, 可以视为估计方法失效。当信噪比大于等于0 dB时, CNN-CBF模型预测结果的PCDE-5°达到100%趋于稳定, RMSE也下降到2°以下并趋于平稳, 说明CNN-CBF方法对于阵元间隔具有一定的宽容性。当阵元间隔不满足半波长条件时, CNN仍能够从CBF特征量上学习到关于真实DOA的信息, 栅瓣的存在一定程度上降低了CNN-CBF对于信噪比的鲁棒性。

分析$d$= 15 m时CNN-MVDR失效的原因, 以及训练集和带噪声的测试集的特征分布。仿真时, 声场环境参数一致, 来波方向为90°, 训练样本及测试样本的频率−波束谱输出特征结构如图14所示。在训练集无噪声情况下进行了对角加载(加载量为0.01); 测试集在进行仿真时, 在互谱密度矩阵上加入噪声(信噪比为5 dB)。

由图14可见, 两子图特征分布存在一定差异。MVDR加权向量与数据的互谱密度矩阵相关, 带噪声条件下互谱密度矩阵的误差会增加, 训练样本的互谱密度矩阵进行了对角加载, 对角加载量的选取本身没有严格的标准, 存在特征差异分布不一致的问题, 从而导致测试结果的误差。

针对上述问题, 可以根据具体使用情景使用带噪训练集训练模型。在MVDR训练集样本数据中加入随机的高斯白噪声, 随机信噪比的取值范围为0~20 dB, 测试集信噪比取值范围为−20~20 dB, 取值间隔为5 dB。CNN-MVDR模型测试结果的RMSE和PCDE-5°随信噪比变化如图15所示。

由图15可见, 训练集中加入一定的信噪比后, 网络模型在测试集上的预测结果显著提高且具有规律性。信噪比大于等于−20 dB的估计结果均可靠。这也验证了上述在对角加载下的CNN算法失效的原因, 特征分布存在很大的差异性会带来测试误差。阵元间隔失配下CBF和MVDR两种特征量均可以有效地被用于训练和测试, 并且在训练集中加入一定噪声, 网络模型的性能有明显的提升。

S5测线是指SWellEx-96实验期间沿等深线拖曳的声源的实验轨迹, S5测线实验不存在干扰源, 源船速度为5 kn, 深源拖曳深度为54 m。

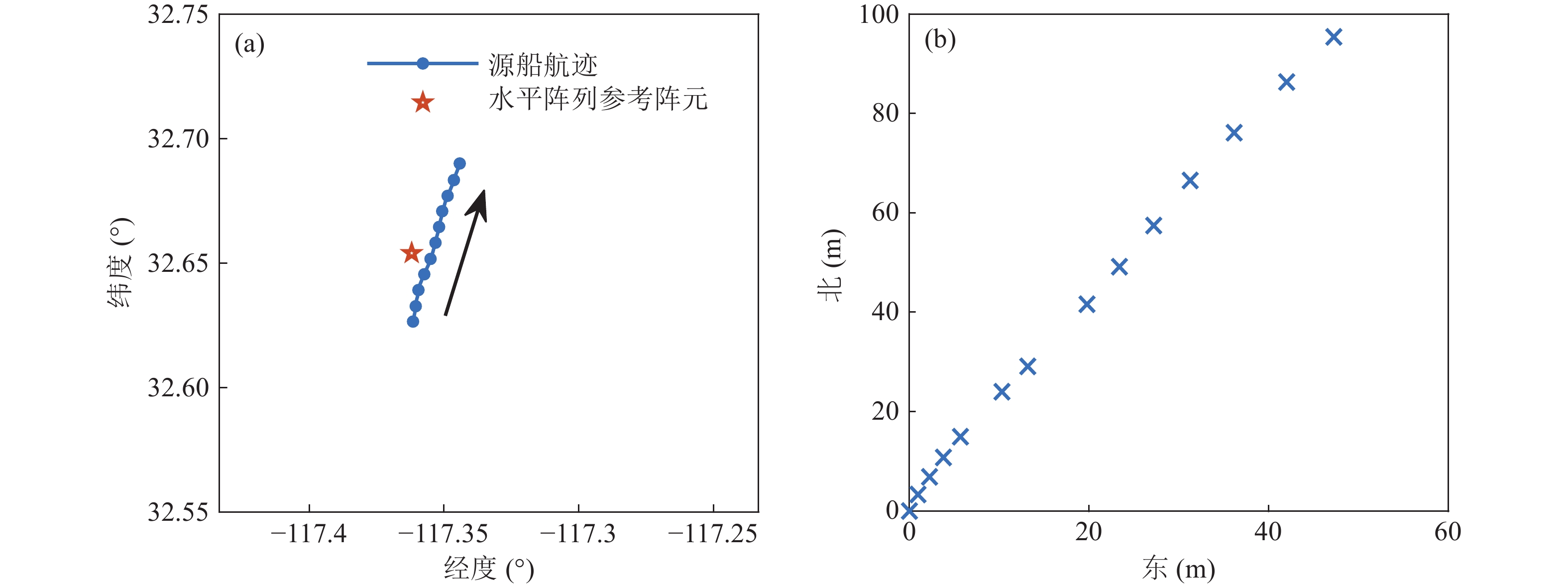
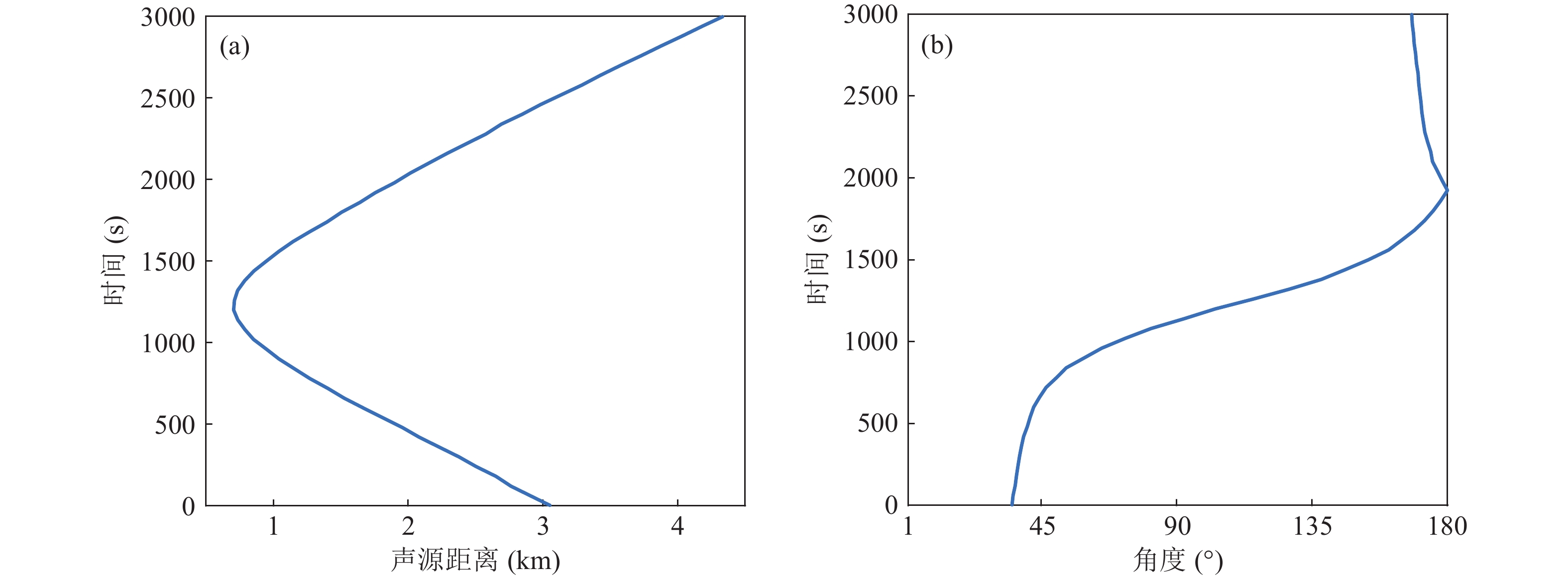
水平阵HLAN接收数据共持续50 min。源船的经纬度坐标变化如图16 (a)所示, 接收阵列位于213 m的海底, 孔径大小为240 m, 阵元个数为32 (有效个数27, 损坏5个), 阵型从形状来看呈弓形, 以前14个阵元作为子阵1, 子阵1各阵元位置如图16 (b)。声源到参考阵元(水平阵HLAN第一个阵元为(0, 0)位置, GPS已知)的距离及DOA随时间变化如图17所示, GPS记录为每1分钟记录一次, 采用插值方法计算整体真实距离及DOA数值。

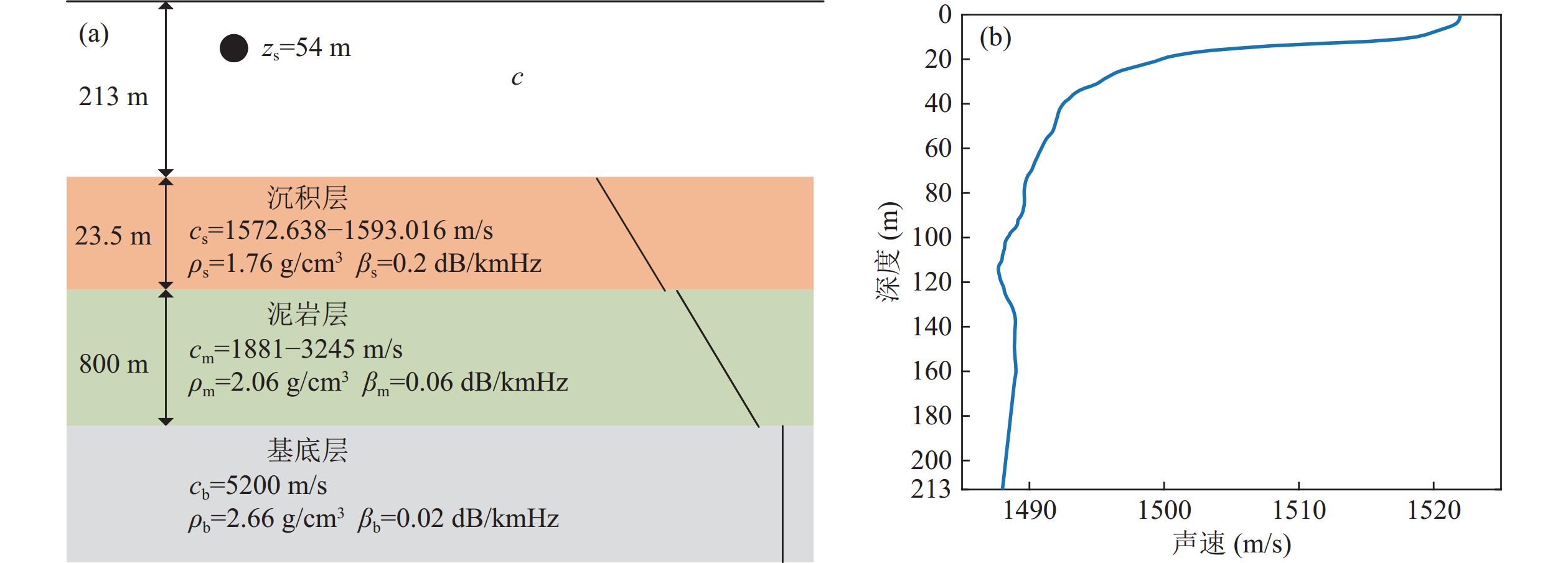
S5测线的环境模型(距离无关的浅海波导)如图18 (a)所示, 水深为213 m, 三层海底模型, 声源位于54 m。沉积层厚度为23.5 m, 沉积层顶部和底部的声速分别为1572.368 m/s和1593.016 m/s, 沉积层的密度和衰减分别为1.76 g/cm³和0.2 dB/(km·Hz)。泥岩层顶部和底部的声速分别为1881 m/s和3245 m/s, 泥岩层的密度和衰减分别为2.06 g/cm³和0.06 dB/(km·Hz)。基底层的声速、密度和衰减分别为5200 m/s, 2.06 g/cm³, 0.06 dB/(km·Hz)。声速剖面如图18 (b)所示, 为CTD记录的真实数据。

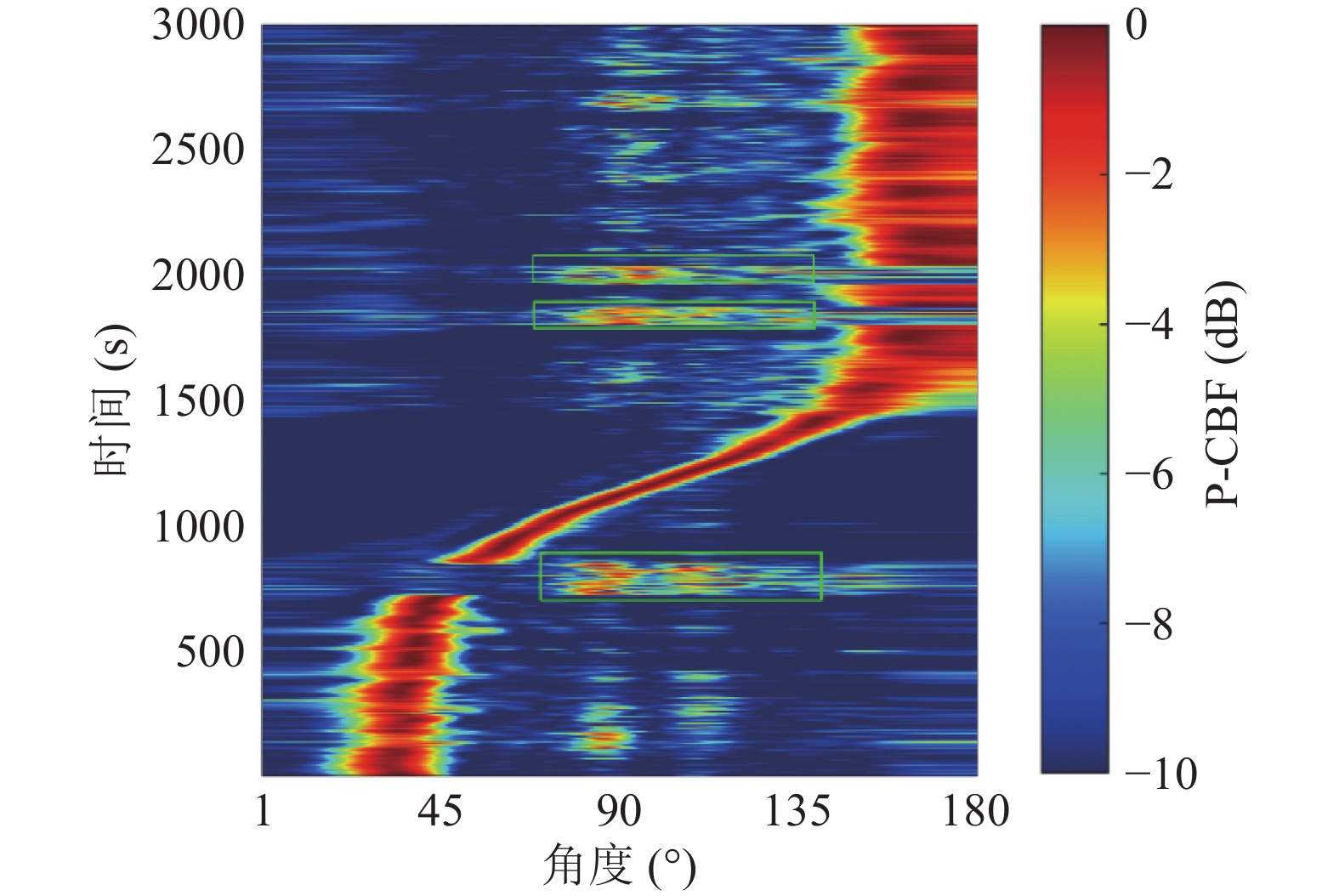
水听器采样率为3276.8 Hz, 声源信号为单频脉冲信号, 高电平信号对应频率为49 Hz, 64 Hz, 79 Hz。首先, 将水平阵数据转化为整数倍采样, 采样率扩大10倍为32768 Hz, 以1.25 s脉冲宽度进行采样, 共得到2400个样本; 然后, 对2400个样本进行单快拍CBF处理。源船方位历程图如图19所示, 其中圈出的三部分是源船拖曳时的停止发射深源信号段, 去除这三段停止发射信号段样本, 共得到2090个有效样本。

本节训练数据仿真参照图18 (a)环境模型。采用3.2节无源声呐阵列接收信号模型, 利用声场仿真软件KRAKENC计算声压。$S(f)$线谱幅值设为1。参考实验相关参数的训练集相关声学参数范围设置如表5所示, 声速剖面参考实测声速剖面如图18 (b)所示。

训练集个数为$180 \times 11 \times 8 \times 3 = 47520$, 输入CNN网络的特征维度为$3 \times 180$。对仿真的数据集, 利用3.3节中选择的预处理方式进行数据及标签的预处理。训练集样本中未添加噪声, 将仿真训练集数据按照7∶3进行划分训练集和验证集, 网络模型采用图8所示结构。在训练和测试时, 分别对单频或综合多个频率对应数据进行训练和测试。

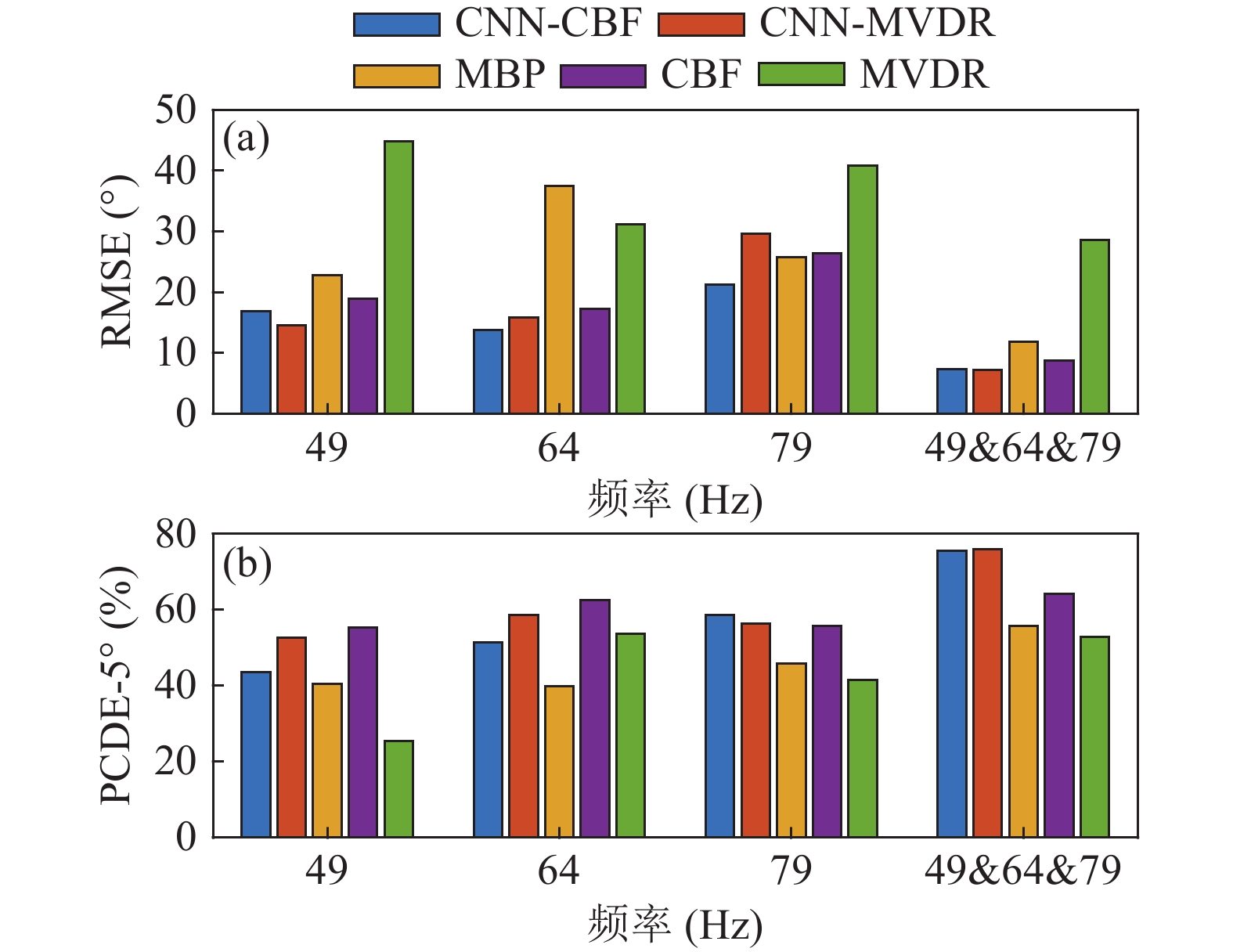
将CNN-CBF和CNN-MVDR方法应用到5.1节实际测线实验中, 进行目标的DOA估计, 测试样本数为2090。对测试样本数据进行单快拍CBF处理和MVDR对角加载处理, 得到的频率−波束输出特征分别作为CNN网络输入特征进行测试。训练集样本标签标定时设定的标准差$\sigma = 20$, 在训练过程中针对不同频点, 网络模型的相关参数设置都是相同的, 在训练过程中未出现误差反增情况, 训练模型有效, 未出现过拟合现象, 验证集误差最小时保存最佳模型。

利用3.4.2节定义的RMSE和PCDE-5°进行各算法性能评价。将CNN、MBP、CBF和10个快拍下对角加载MVDR的DOA预测结果的相关性能评价标准列于表6, 其中包括单频49 Hz, 64 Hz, 79 Hz训练的测试结果的性能评价, 以及三个频点{49 Hz, 64 Hz, 79 Hz}综合训练的测试结果的性能评价, 柱状图对比如图20所示。

分析表6统计结果。在综合频点{49 Hz, 64 Hz, 79 Hz}条件下, 五种方法的DOA估计性能均比单频条件下有很大提升。传统波束形成方法及MBP方法的PCDE-5°不超过65%, CNN方法相比其提高了10%以上; CNN方法的RMSE也有所降低。

CBF作为常规的处理方法, 在综合频点下DOA估计结果的RMSE为8.76°, PCDE-5°为64.21%; 给出的对角加载MVDR在10个快拍条件下的性能表现严重下降, RMSE为28.53°, 偏离真实值的离散点增多, PCDE-5°下降为52.92%。MVDR在多快拍情况下, 估计性能并没有得到明显的提升, 这可能是因为源船在拖曳过程中的DOA随时间变化太大, 各个快拍相关性表现均不同, 互谱密度矩阵估计误差增大, 多快拍下的估计效果并不理想。

MBP和CNN方法在数据处理阶段都应用了波束形成技术, 详细对比MBP与CNN的性能评价结果。MBP在单频49 Hz, 64 Hz, 79 Hz和所有频点{49 Hz, 64 Hz, 79 Hz}四种条件下, RMSE测向误差分别为22.78°, 37.53°, 25.72°, 11.78°, PCDE-5°分别为40.57%, 39.86%, 45.84%, 55.74%。CNN-CBF相比MBP在上述四种条件下的RMSE测向误差分别降低了5.92°, 23.84°, 4.47°, 4.52°, CNN-CBF相比MBP在上述四种条件下的PCDE-5°分别提高了3.02%, 11.58%, 12.72%, 19.91%。CNN-MVDR估计方法的DOA估计性能与CNN-CBF相似, 其PCDE-5°也都高于MBP且RMSE明显降低。

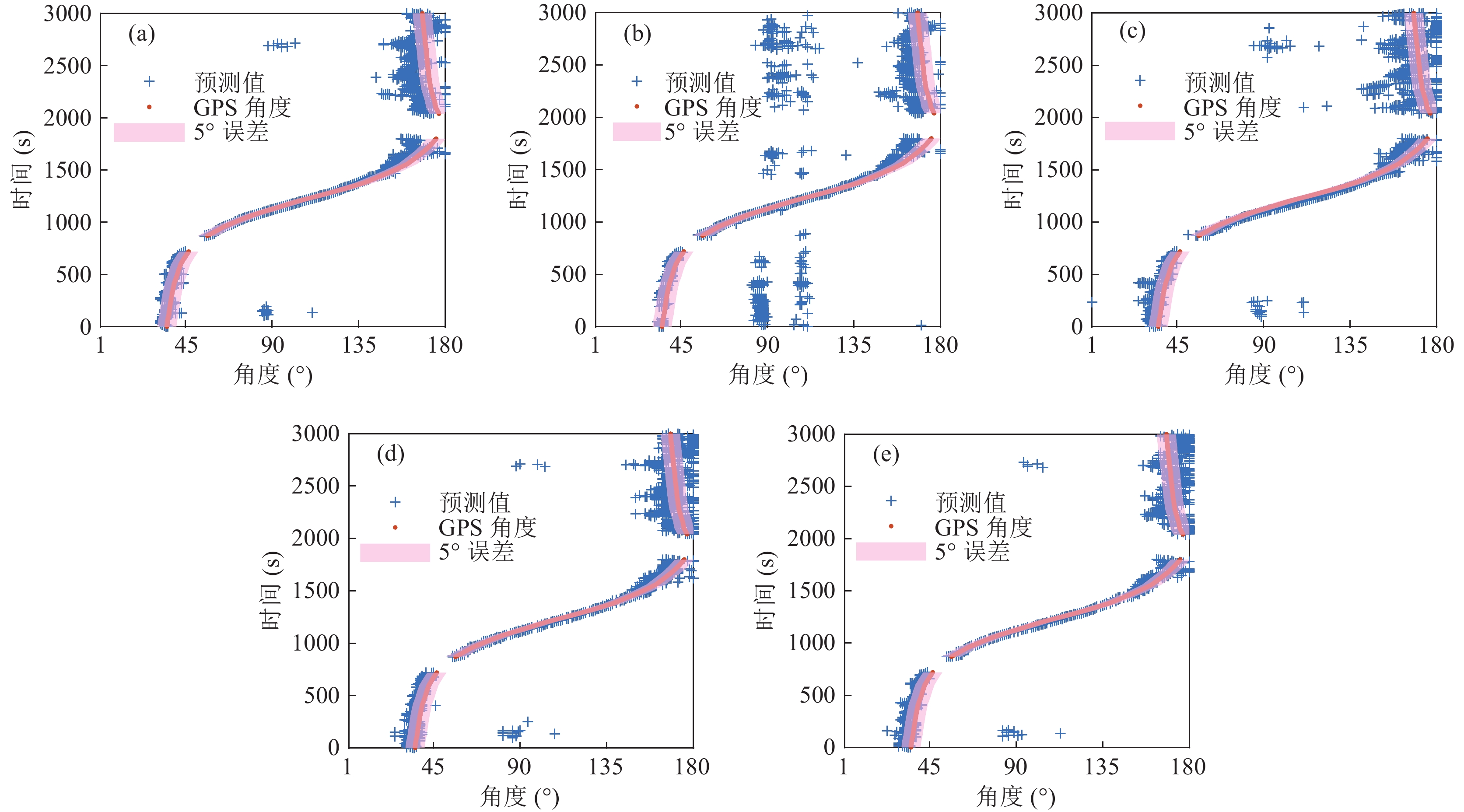
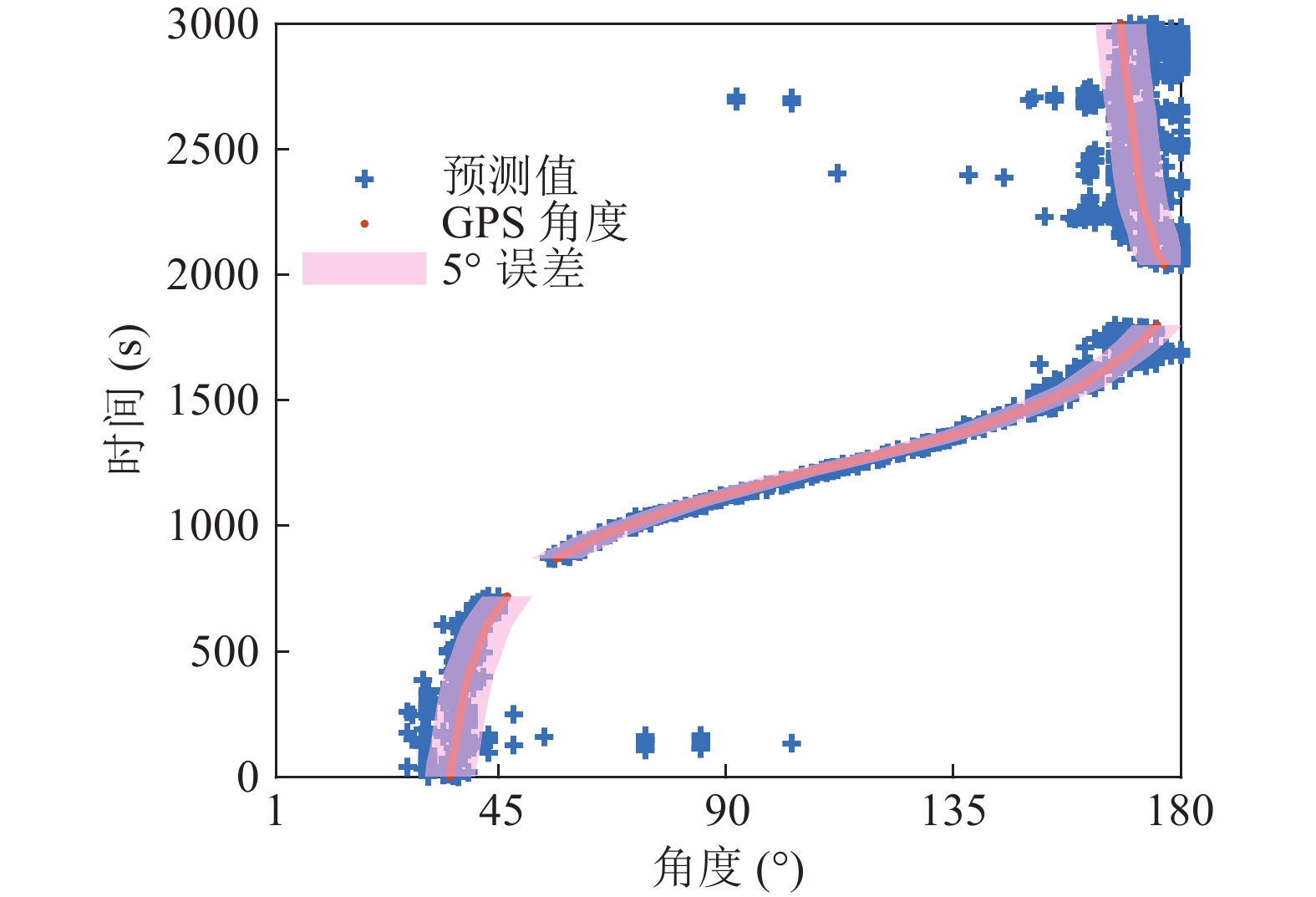
综合频点{49 Hz, 64 Hz, 79 Hz}下CBF、10个快拍下对角加载MVDR、MBP、CNN-CBF和CNN-MVDR的估计结果与真实角度的散点图如图21所示。CNN-CBF和CNN-MVDR总体拟合效果优于CBF、MVDR和MBP三种方法。五种方法估计结果特点总结来看: 在中间时间段的DOA估计性能优于开始一段时间和最后一段时间, 中间时间段的DOA估计结果与真实DOA拟合程度更高。从CNN-CBF和CNN-MVDR两种方法在端射方向估计结果来看, 估计值更加聚集于真实值附近, 端射方向的估计性能获得很大提升。

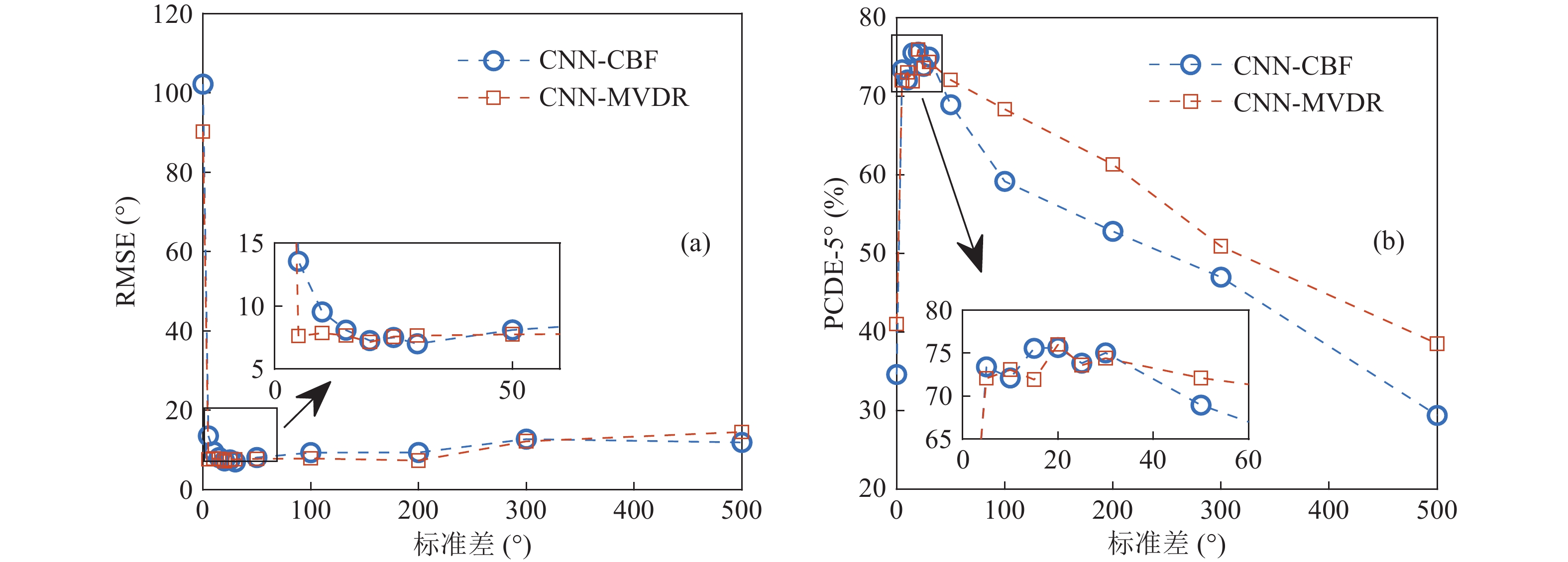
采用高斯输出层时, 根据式(25)可知, 针对不同实际情况, 角度划分间隔${\theta _{kj}}$和标准差$\sigma $要自行设置。${\theta _{kj}}$决定了网络输出神经元个数, $\sigma $表示预测DOA与真实DOA间允许的最大误差。为了研究不同标准差设定值对DOA估计性能的影响, 通过设置不同的$\sigma $值, 其他训练参数保持一致, 在相同的训练数据集和训练迭代次数下比较测试结果的RMSE和PCDE-5°的变化, 如图22所示。RMSE随着$\sigma $的增大不断减小至最佳预测位置后趋于稳定后开始回涨, RMSE更能反映估计中出现的离散点的偏离程度, 说明偏离真实值的点数增多。随着$\sigma $的不断增大, PCDE-5°不断增大后趋于稳定。当$\sigma $值超过一定界限时, 从原理上看预测对于真实DOA附近角度的宽容性变大, 可以容忍更大误差范围的DOA进入预测区间, 导致预测结果偏差增大, PCDE-5°开始下降。

在基于单特征的CNN算法基础上, 进行特征融合时, 输入CNN特征维度为$6 \times 180$, 训练数据集参数设置与5.2节保持一致, 训练集个数为$180 \times 11 \times 8 \times 3 = 47520$。利用3.3节数据预处理方式, 训练集和验证集按照7∶3的比例进行划分, 网络模型依旧采用图8结构, 相关超参数设置不变, 将这种特征融合方法命名为CNN-Ⅱ。

对5.1节中S5测线实验样本数据进行测试, 基于CNN-Ⅱ的目标DOA估计结果与真实角度的散点图如图23所示。CNN-Ⅱ预测结果的PCDE-5°提升到了79.78%, RMSE降低到6.95°, 相比较单特征估计方法CNN-CBF和CNN-MVDR, CNN-Ⅱ的PCDE-5°分别提高了4.13%和3.82%, RMSE分别降低了0.31°和0.19°。证明特征融合方法对于DOA估计性能提升是有效的。

通过对比, 融合两种特征的深度学习算法在本文DOA估计任务中的PCDE-5°最高且RMSE最低, 融合后效果优于单独使用CBF和MVDR特征的训练测试结果, 且垂直连接的操作简单易实现。分析其原因可能是: CBF特征反映了扫描DOA范围内的波束谱的整体差异性, 旁瓣信息更加丰富, 主瓣更宽, 特征结构上信息量更多; 而MVDR特征在目标的真实DOA上信息更加集中, 单一的特征对于相近的不同DOA的差异的表征能力存在局限性。将CBF和MVDR两种特征按照通道数方向垂直连接起来, 可以综合利用不同特征表征出的DOA对应波束谱的敏感度信息, CNN模型可以同时学习到两个特征包含的目标方向的信息, 从而获得更完整、更准确的目标方向信息, 进一步影响DOA估计的性能。因此, 融合两种特征的CNN估计方法可以获得更好的性能。

本文所用数据处理操作系统为Windows 11。GPU配置为NVIDIA GeForce RTX 3080, CPU配置为酷睿i7-12700KF。采用统一计算架构为CUDA 11.7和TensorFlow 2.7深度学习库, 集成开发环境为Anaconda 22.9.0, 使用Spyder集成开发环境, 编程语言采用Python (Ver. 3.8)。使用MATLAB软件对线阵列接收信号进行波束形成处理。

CNN、MBP、CBF和10个快拍下对角加载MVDR的处理速度如表7所示。处理速度评估结果是指每种算法对总的测试样本处理的平均时间。CNN方法的处理时间包含了数据样本的特征提取与测试的总时间。CBF、MVDR和MBP的GPU版的处理速度为空。

实验数据处理时CNN模型的训练是利用GPU完成的。使用GPU的训练时间: CNN-CBF模型训练时间为3742.60 s, CNN-MVDR模型训练时间为3846.65 s, CNN-Ⅱ模型训练时间为5907.33 s, 特征融合方法增加了输入特征的维度, 训练模型速度会降低。

由表7可见, 传统的波束形成方法速度最快, 但其性能表现并不是最优的; 匹配场方法处理速度最慢, 在实际应用中优势不大; CNN方法可以在已知预训练模型时, 快速高效地应用于真实环境中未知数据的实时处理, 在今后还可以考虑改用其他语言将数据矩阵处理模块与CNN测试模型进行联合部署, 提高处理速度。

水平线列阵DOA估计的数值仿真分析表明, 仅依赖于数据的波束形成DOA估计方法在端射方向上会产生大的角度偏差, 而MBP技术能够较好地解决理想条件下端射估计准确度不高的问题。然而MBP在实际应用中则需要更精确的声场模型参数, 由于真实海洋环境中的不确定性, 使得真实环境相关知识的获取困难, 这可能会导致拷贝场模型失配, MBP的性能也会大幅度降低, 在实测海试数据下性能不如常规波束形成。

本文提出了一种利用卷积神经网络模型进行DOA估计的方法, 该方法将水平线列阵接收数据的波束域特征输入到网络模型中。通过数值仿真验证, 以单一波束域特征数据作为CNN模型的输入时, 模型对信噪比具有一定的鲁棒性, 对阵元间隔具有一定的容忍性。在阵元间隔不能满足半波长情况下, 波束谱存在栅瓣的影响, CNN仍能学习到输入数据的相关DOA信息来估计目标DOA。海试数据处理结果表明, 采用CNN的估计方法性能比传统的MBP方法以及波束形成方法有较大提升, 端射方向估计也有较大改善。简单实现的多特征融合的DOA估计方法在海试数据下5°误差内可靠测向概率最高且均方根误差最低, 比单一特征训练测试表现好, 这也说明了对于目标的多个特征可考虑合适的融合处理以取得更高的估计精度。