阵列信号处理中, 波达方向估计(DOA)被广泛应用于雷达、声呐、通信、探测以及医学工程等领域^[1]。随着减振降噪技术的发展, 目标辐射噪声强度及特征线谱频率不断降低^[2]; 受实际工程应用条件限制, 有限的阵列孔径使得低频波束宽度较宽, 空间分辨能力受限^[3-4]。为了提高对低频目标的方位分辨能力, 通常的手段为改进信号处理算法^[5]。

多重信号分类(MUSIC)算法最早由Schmidt提出^[6], 将信号的协方差矩阵分解为信号子空间与噪声子空间, 利用子空间正交性估计目标的到达角。该算法具有高性能和高分辨率的优点; 但需预先知道目标数量, 并对信噪比有一定的要求^[7-8]。Hoffman提出的特征子空间(Eigenspace)算法利用相关矩阵的特征结构进行方位估计^[9]。该算法将最小方差无失真响应(MVDR)算法的扫描向量投影到信号子空间, 得到该算法的扫描向量, 并将该扫描向量代入常规波束形成(CBF)公式中得到方位估计结果^[10]。近年来, 该算法在超声领域得到了广泛应用, 其不仅能够同时提高超声成像的分辨率和对比度, 且具有较强的鲁棒性^[11]。此外, 该算法较经典的MUSIC等方法具有更低的旁瓣和更高的方位估计精度^[12]。由于投影的MVDR扫描向量涉及的求逆运算具有不稳定性, 且对导向矢量误差较为敏感, 通过结合对角加载或减载方法, 可提高该算法的鲁棒性或计算性能^[13-14]。也可以通过校正预设导向矢量提高该算法对指向误差的鲁棒性^[15]。结合后置维纳滤波, 则能够提高超声成像对比度和成像分辨率^[16]。仿真研究表明, 该算法也可应用于水声阵列中, 结合后置维纳滤波的方式使得该算法具有极低的旁瓣水平^[17]。通过结合空间平滑技术, 即可实现对相干多目标声源的高分辨估计^[18]。

综上所述, 基于扫描向量投影到信号子空间的Eigenspace算法具有较窄的波束宽度, 能够同时提高空间方位谱的分辨率并压低其旁瓣水平。为了提高该算法的鲁棒性与计算性能, 通常在计算流程中引入其他约束条件^[19]。根据Eigenspace算法的计算流程, 可从波束形成公式的角度改进该算法, 如函数波束形成(FB)算法通过控制指数的方式, 在保证信号方向幅值不变的前提下调整旁瓣高度。当指数取1时, 该方法衍变为CBF方法; 当指数取−1时, 该方法衍变为MVDR方法, 可以看作是CBF等方法的一般形式^[20]。

本文基于改进的方位估计算法, 为提高特征子空间算法的分辨性能, 在计算流程中引入FB算法, 使其兼具FB算法的指数控制与子空间分解算法的高分辨率的优点, 从而在不影响算法抗噪性能的前提下进一步提高了算法的计算性能。

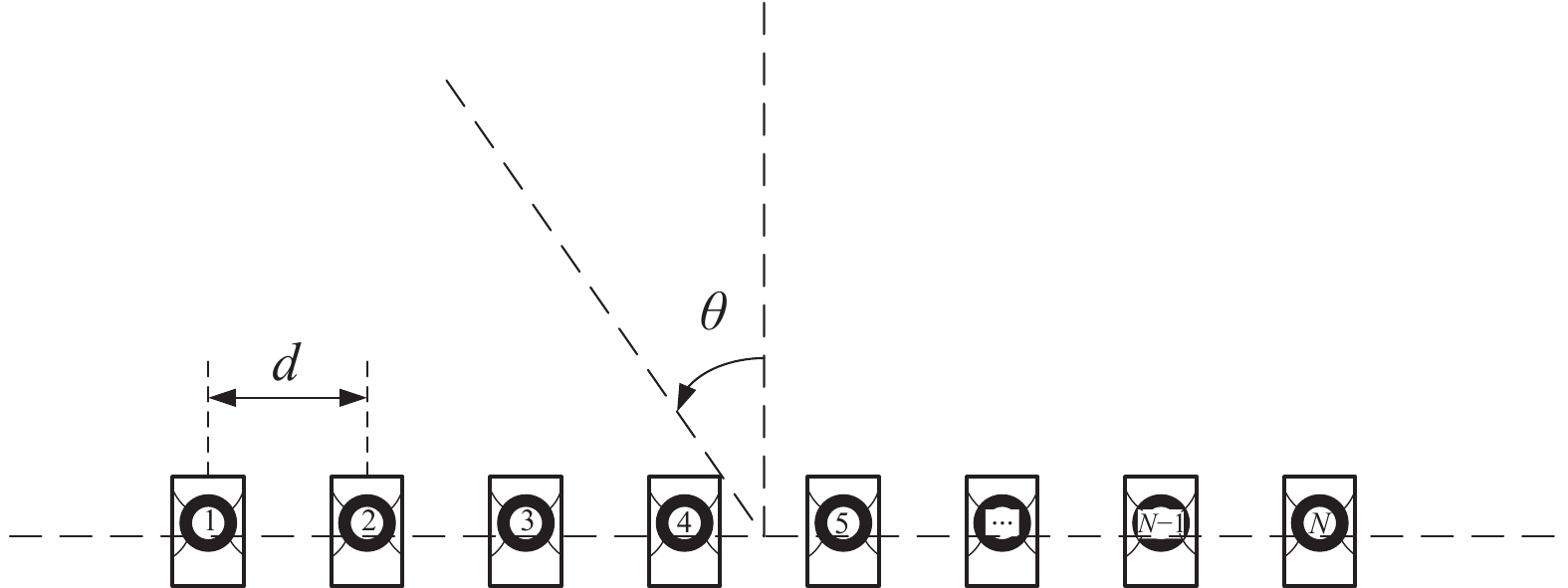
根据特征子空间方位谱估计技术, 阵元域数据投影至阵列接收的特征空间, 水声接收阵列可有效实现空域滤波, 并以较高精度获得目标到达角度等信息。以图1所示N阵元的水声阵列为例, 远场声波入射时, 对于阵列接收信号$ {\boldsymbol{x}}(t) = [{x_1}(t),{x_2}(t),\cdots , {x_N}(t)]^{\rm H} $, 其在导向角$ \theta $方向上的方位谱估计公式为

其中, $ {\boldsymbol{w}}(\theta ) = [{w_1}(\theta ),{w_2}(\theta ), \cdots ,{w_N}(\theta )] $为方位谱估计的扫描向量, $\boldsymbol{T} $为阵列接收信号的协方差矩阵。根据已知信源数, 可以对协方差矩阵进行奇异值分解, 并将其分解为彼此互相正交的信号子空间(下标S表示)与噪声子空间(下标N表示):

其中, $ {{\boldsymbol{\varLambda }}_{\text{S}}} $和$ {{\boldsymbol{\varLambda }}_{\text{N}}} $分别对应信号子空间与噪声子空间的特征值矩阵, 则$ {{\boldsymbol{V}}_{\text{S}}} $和$ {{\boldsymbol{V}}_{\text{N}}} $分别对应该特征值矩阵$ {{\boldsymbol{\varLambda }}_{\text{S}}} $和$ {{\boldsymbol{\varLambda }}_{\text{N}}} $的特征向量矩阵。

根据MVDR扫描向量推导结果, 对于导向角$ \theta $, 其Eigenspace扫描向量为^[17]

其中, $ \boldsymbol{w}(\theta) $为投影的MVDR扫描向量, $ \widehat{\boldsymbol{g}}(\theta)=[\widehat{g}_{1}(\theta), \widehat{g}_{2}(\theta), \ldots, \widehat{g}_{N}(\theta)]^{\rm H} $为导向角$ \theta $的导向矢量。取$ \mu = 1/ [{\boldsymbol{\widehat g}}^{\text{H}}{{\text{(}}\theta {\text{)}}}{{\boldsymbol{T}}^{ - 1}}{\boldsymbol{\widehat g}}{\text{(}}\theta {\text{)}}] $, 考虑信号子空间与噪声子空间的正交性, 可得

将式(4)所示Eigenspace扫描向量$ {{\boldsymbol{w}}_{\text{E}}}{\text{(}}\theta {\text{)}} $代入方位谱估计式(1), 可得特征子空间的方位谱输出:

在式(5)所示的Eigenspace方法中, 已区分了信号子空间与噪声子空间。然而, 在计算扫描向量时, 子空间的正交关系并未得到充分利用。根据式(2)中信号协方差矩阵的分解, 参数$ \mu $可表示为$ \mu = 1/({\boldsymbol{\widehat g}}^{\rm H}{(\theta )}({{\boldsymbol{V}}_{\text{S}}}{\boldsymbol{\varLambda }}_{\text{S}}^{ - 1}{{\boldsymbol{V}}_{\text{S}}} + {{\boldsymbol{V}}_{\text{N}}}{\boldsymbol{\varLambda }}_{\text{N}}^{ - 1}{{\boldsymbol{V}}_{\text{N}}}){\boldsymbol{\widehat g}}(\theta )) $。考虑到信号子空间的特征向量与噪声子空间正交性, 导向矢量的信号模型主要与信号子空间有关, 为了使分母上的因子最小化, 取$\mu = 1/[{\boldsymbol{\widehat g}}^{\rm H}{(\theta )}{\boldsymbol{V}}_{\text{N}}^{\rm H}{{\boldsymbol{V}}_{\text{N}}}{\boldsymbol{\widehat g}}(\theta )]$, 代入式(4), 可得该参数$ \mu $形式下的特征子空间方位谱输出:

式(5)和式(6)具有相同的分子形式, 但分母有一定差异, 分别为MVDR与MUSIC的形式。通过对Eigenspace算法表达式的化简, 可将Eigenspace算法分为两步: 首先通过MVDR/MUSIC方法对导向矢量进行加权; 然后再将其投影到信号子空间中进行方位谱估计计算。在已知信源数量的条件下, 通过导向矢量加权可获得更高的空间增益, 可以理解为基于特征子空间的导向矢量预滤波。因此, 基于导向矢量预滤波的理论基础, 可通过结合函数波束形成方法进一步改进算法, 即本文所提FB-Eigenspace方位谱估计算法, 其综合了FB方法和Eigenspace方法的优点, 从而提升了目标方位分辨能力。

在传统常规波束形成基础上, 通过控制指数$k$的引入, 可获得函数波束形成方法。根据接收阵列信号协方差矩阵T的奇异值分解$ {\boldsymbol{T}} = {\boldsymbol{V\varLambda }}{{\boldsymbol{V}}^{\text{H}}} $, 考虑导向矢量$ {\boldsymbol{\widehat g}}(\theta ) $协方差矩阵中对应于信号的特征向量与$ {\boldsymbol{V}} $中相应特征向量平行, 函数波束形成表示为^[20]

其中, ${\boldsymbol{\varLambda }}$对应于协方差矩阵$ {\boldsymbol{T}} $的特征值矩阵, 可根据特征值大小或已知信源数划分信号子空间与噪声子空间, $ {\boldsymbol{V}} $对应于该特征值矩阵${\boldsymbol{\varLambda }}$的特征向量矩阵。函数波束形成算法中$1/k$次幂的引入,可在理论上增加主瓣与旁瓣之间的差异, 提升分辨能力; 同时, 特征值矩阵中$k$次幂的存在, 又使其输出功率与常规波束形成相同, 使波束形成的输出结果具有实际意义。当$ k = 1 $时, FB算法的表达式转化为常规波束形成(CBF)算法; 当$ k = - 1 $时, FB算法的表达式转化为MVDR算法。

尽管通过控制FB算法的指数项可以提高算法的分辨能力, 但较大的指数项值会导致算法在计算多目标时过度降低次要目标的主瓣高度, 从而无法实现多目标的分辨。此外, 过多的乘幂运算也会降低算法的稳定性。因此, 为了进一步提高算法的分辨能力, 需考虑与其他方法相结合, 如式(6)所示的特征子空间方法。基于函数波束形成过程, 结合式(2)与式(3), 特征子空间方法的扫描向量可表示为

其中, 参数$ \mu $为扫描向量归算系数, 根据不同的算法, 将获得不同的扫描向量及方位谱输出, 如经典的MVDR和MUSIC方法, 其分别取$\mu = 1/[{\boldsymbol{\widehat g}}^{\text{H}}{(\theta )}{{\boldsymbol{T}}^{ - 1}}{\boldsymbol{\widehat g}}(\theta )]$或$\mu = 1/[{\boldsymbol{\widehat g}}^{\text{H}}{(\theta )}{\boldsymbol{V}}_{\text{N}}^{\text{H}}{{\boldsymbol{V}}_{\text{N}}}{\boldsymbol{\widehat g}}(\theta )]$; $ k $为函数波束形成的控制指数, 可通过调整其数值控制方位谱输出结果; 在函数波束形成计算过程中涉及乘幂操作, 将控制指数分为大于0与小于0两种情况进行讨论: 当控制指数大于0时, 信号特征值占特征值矩阵的主要成分; 当控制指数小于0时, 噪声特征值占特征值矩阵的主要成分。与式(3)不同, 函数−特征子空间方位谱估计算法的扫描向量需根据不同指数参数取值来分析对方位谱估计的贡献。由于信号子空间与噪声子空间的特征值大小存在差异, 当$ k $取正值时, 信号子空间在协方差矩阵中占主要成分; 当$ k $取负值时, 噪声子空间在协方差矩阵中占主要成分, 因此将式(8)所示的FB-Eigenspace扫描向量$ {{\boldsymbol{w}}_{\text{FB-E}}}(\theta ) $代入方位谱估计表达式(式(1)), 可以得到与式(6)结构相似的表达式, 保留其分母形式, 为了方便讨论指数参数k的影响, 并使分子表达式存在实际意义, 将分子表达形式化简并与式(7)统一, FB-Eigenspace的方位谱估计表达式可表示为

由式(9)可以看出, FB-Eigenspace方法兼具了函数波束形式和Eigenspace方法的优点, 即在Eigenspace方法的基础上进行了拓展, 使其表现形式更加灵活多样。可根据实际需要选择不同的权值来进一步优化算法的计算性能。根据信号子空间与噪声子空间在算法中的贡献程度,当k取正值时, 算法的抗噪声能力较好, 当k取负值时, 算法的谱峰较为尖锐; 而k越接近于0, 对旁瓣的压制能力越强。

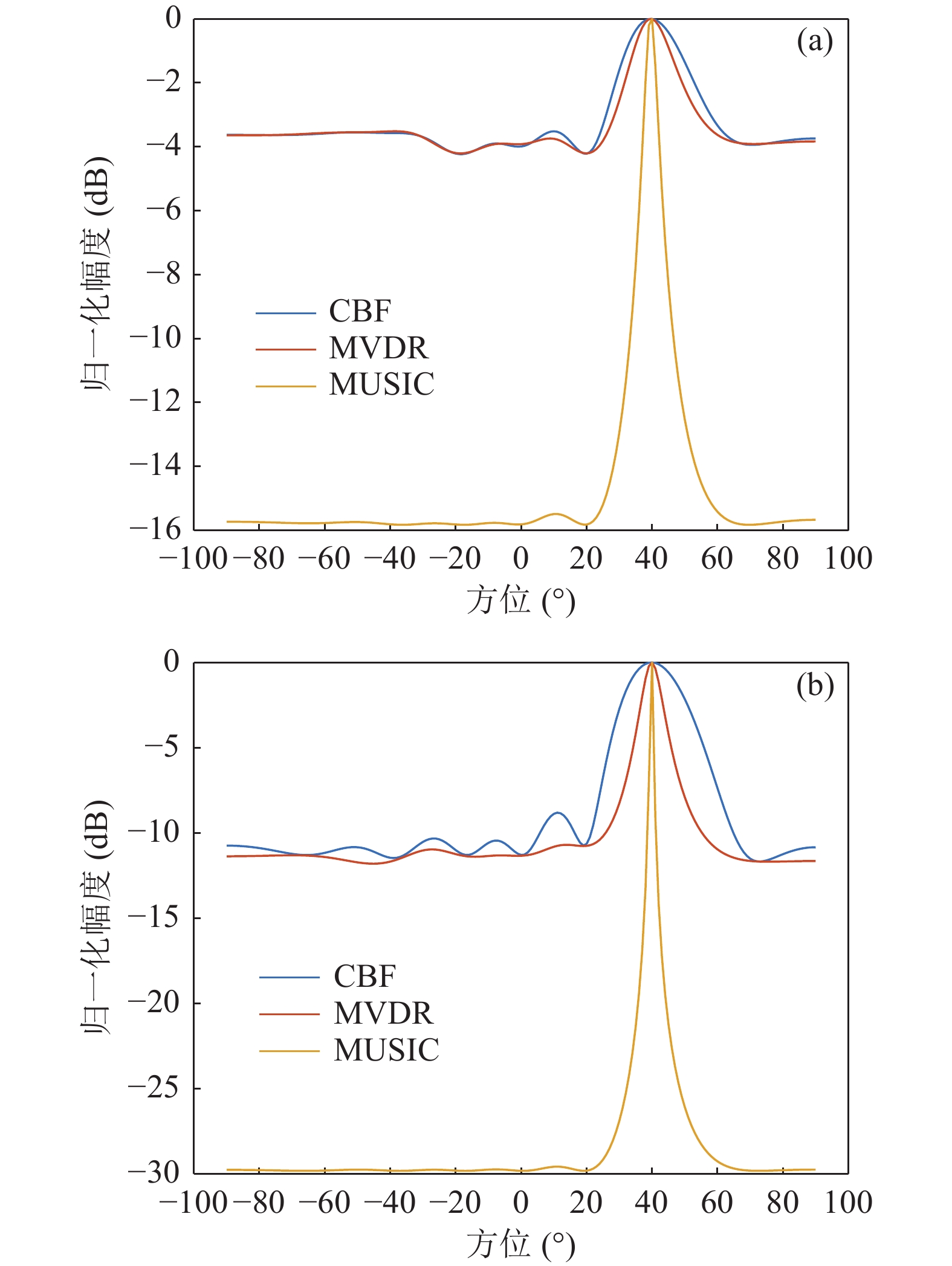
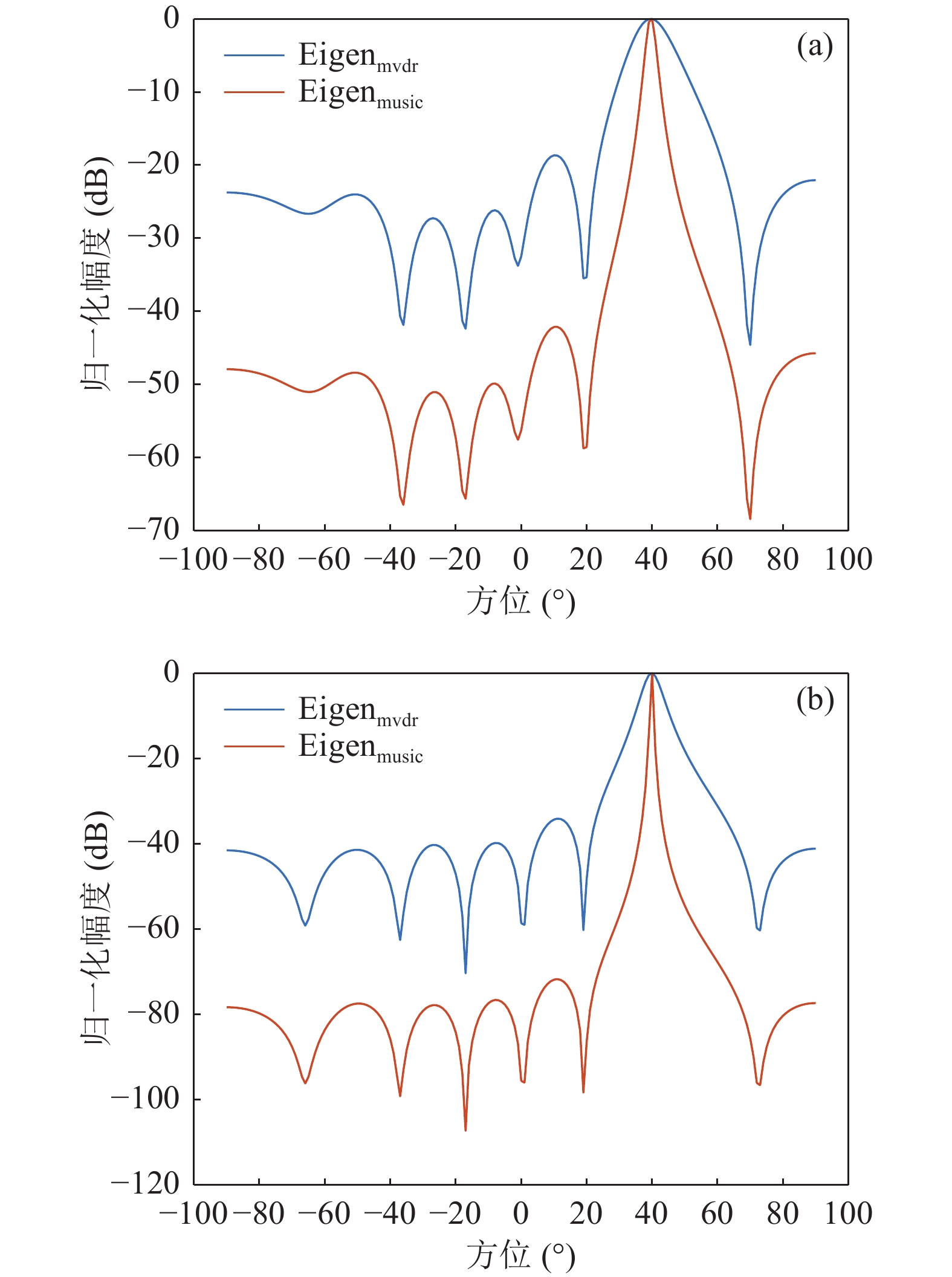
在本文所提的FB-Eigenspace方位谱估计算法中, 参数$ \mu $的不同取值形式在式(9)中给出, 将导致不同的波束形式输出形式, 这对于FB-Eigenspace方位谱估计方法的性能具有至关重要的影响。为此, 考虑经典的MVDR和MUSIC方法建立参数$ \mu $的表达形式, 并与常规波束形成形式给出的参数$\mu = {\boldsymbol{\widehat g}}^{\text{H}}{(\theta )}{\boldsymbol{T\widehat g}}(\theta )$形式进行对比。在仿真中, 采用阵元间距为10 m 的8元声压阵, 以10 kHz的采样频率和总计320快拍(快拍数为40乘以阵元个数)来接收远场60 Hz单频信号, 并设定声波从40°角度入射, 同时加入高斯白噪声, 在信噪比5 dB与−5 dB情况下分别计算参数$ \mu $的归一化幅度, 计算结果如图2所示。同时, 避免k值引入的复杂性, 暂仅考虑常规特征子空间方位谱估计方法(式(5)和式(6)), 分析MVDR和MUSIC方法给定参数$ \mu $对方位谱输出的影响, 信噪比分别取5 dB与−5 dB的情况下计算结果如图3所示。

根据图2可知, 不同算法给出的参数$ \mu $具有显著的差异。在小快拍数条件下, 相较于CBF、MVDR算法给出的参数$ \mu $幅度, 无论是信噪比为正值还是负值, MUSIC算法给出的参数$ \mu $幅度具有更为尖锐的谱峰, 即拥有更为有效的分辨能力, 此情况与图3所示的两种导向矢量加权方式下波束输出图结果一致。同时, 由图2可以看出, 相较于MUSIC算法形式, MVDR算法形式的参数$ \mu $值受信噪比影响更大。对于高信噪比(SNR = 5 dB)情况, MVDR算法给出的参数$ \mu $幅度具有较为尖锐的谱峰分布, 明显优于CBF算法; 对于低信噪比(SNR = −5 dB)情况, MVDR算法给出的参数$ \mu $幅度分布则趋于平滑, 与CBF算法几乎一致, 即通过MVDR算法给出的参数$ \mu $未获得额外的方位估计能力提升。

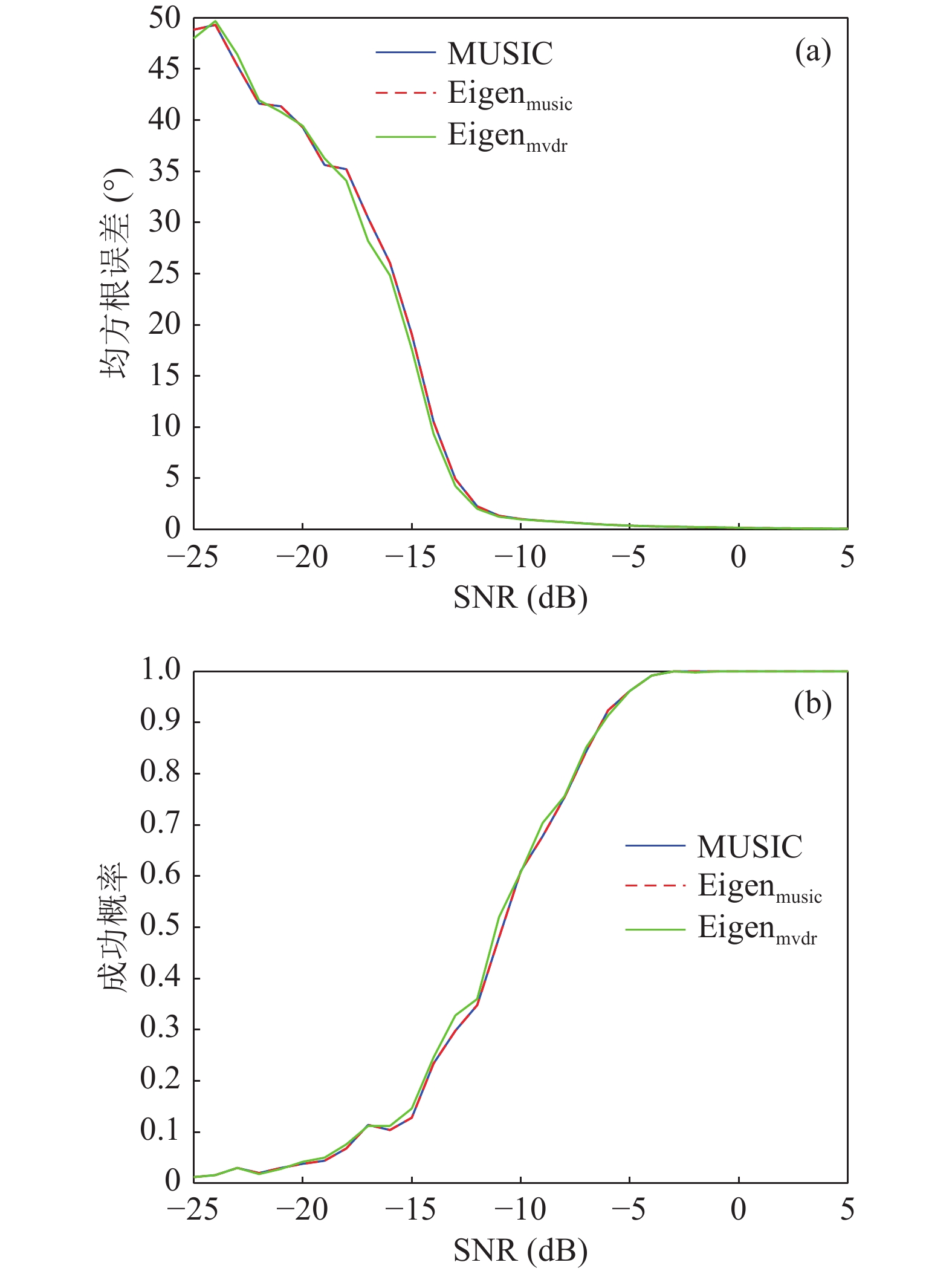
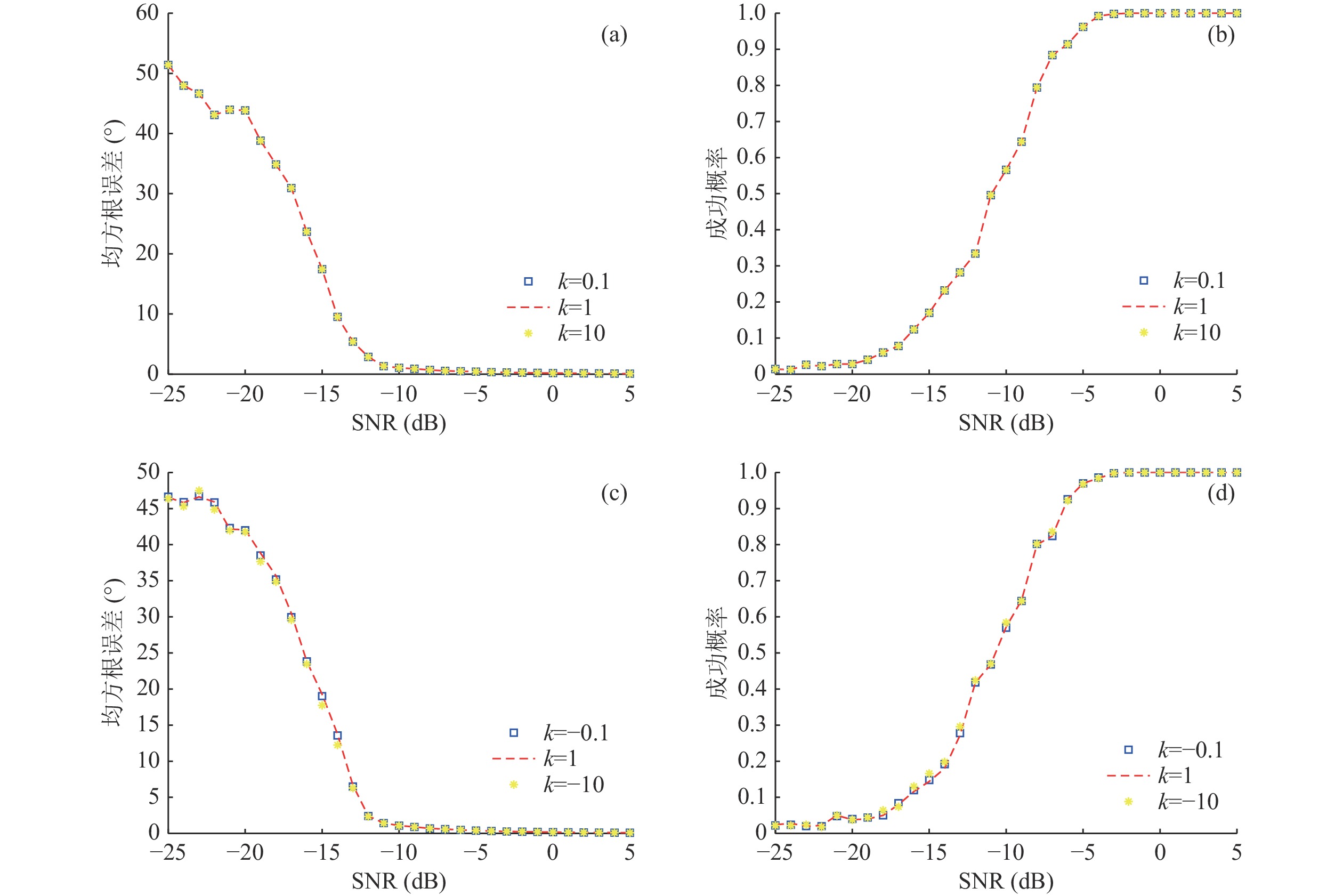
为进一步阐述参数$ \mu $的作用, 采用与图3相同频率单声源仿真条件, 在信噪比变化范围为−25~5 dB的情况下, 参数$ \mu $选取MVDR算法和MUSIC算法形式, 进行了500次的蒙特卡罗仿真试验, 然后将参数$ \mu $下的特征子空间方位谱输出与典型的MUSIC方位谱输出进行对比, 通过均方根误差和DOA估计成功概率(以±1°为估计成功的阈值)来评估结果, 如图4所示。

如图4所示, 基于MUSIC算法的方位谱输出与采用MUSIC算法对导向矢量加权的Eigenspace方位谱输出在均方根误差与估计成功概率方面呈现出相似的结果。该结果进一步表明, Eigenspace方位谱输出性能主要与导向矢量的加权方式有关, 即参数$ \mu $的选取形式对Eigenspace方位谱输出至关重要。同时, 受限于子空间划分的基本原理, 参数$ \mu $以及Eigenspace方位谱输出受信噪比影响显著。当信噪比大于−10 dB时, 根据两种算法选取参数$ \mu $及方位谱输出, 其均方根误差均小于1°; 当信噪比小于−10 dB时, 均方根误差显著增加, 而估计成功概率明显下降。

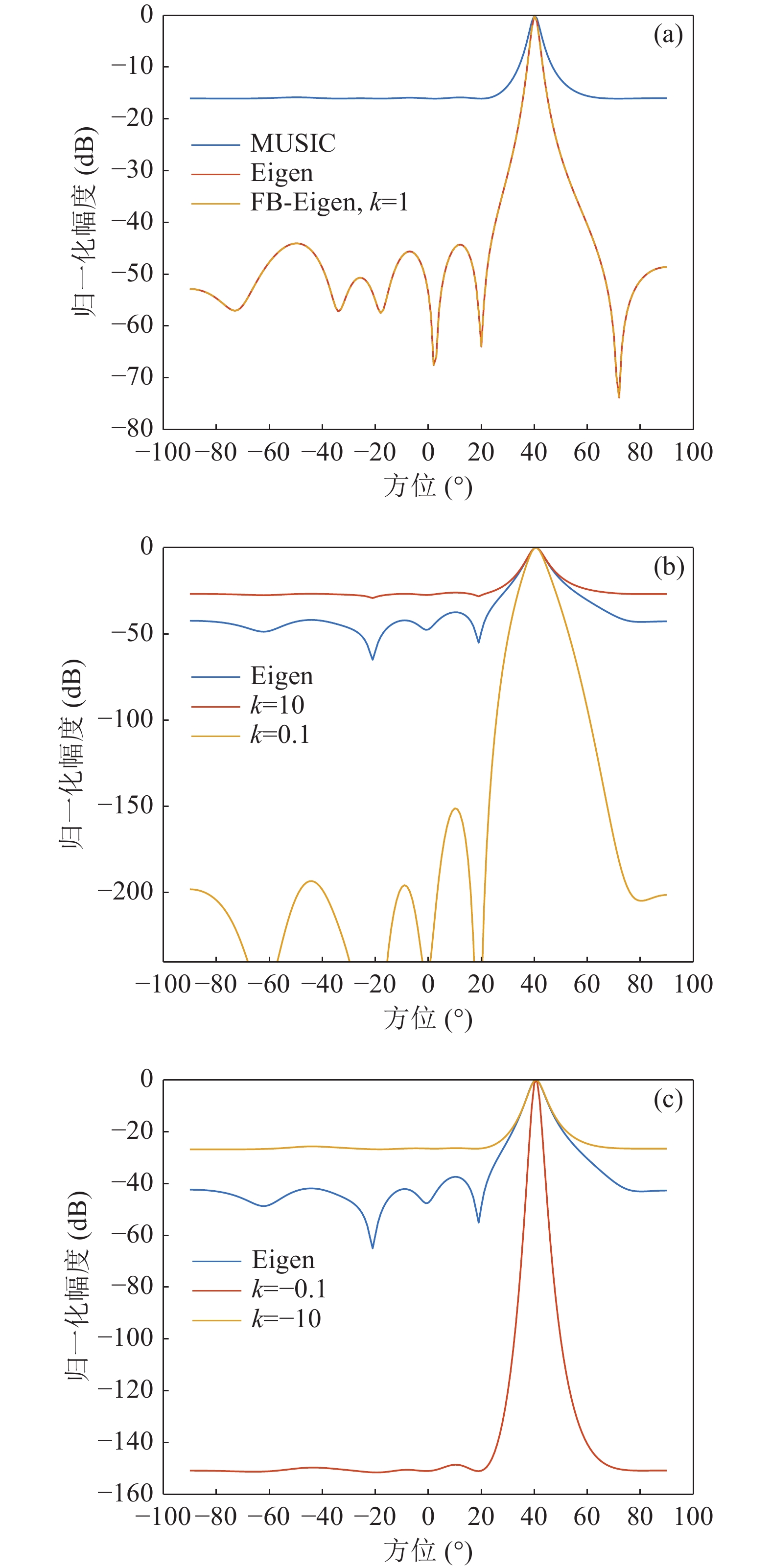
根据上述分析, 当信噪比较高时, 采用MUSIC方法对导向矢量进行加权可以获得更窄的主瓣和更低的旁瓣。因此, 在FB-Eigenspace方位谱计算过程中, 本文选取基于MUSIC方法的参数$ \mu $形式。然而, 除了参数$ \mu $的形式, 如式(9)所示的指数k也对本文所建立的FB-Eigenspace方位谱计算有重要影响。因此, 考虑采用阵元间距为10 m 的8元声压阵, 以10 kHz的采样频率和总计320快拍(快拍数为40乘以阵元个数)来接收远场60 Hz单频信号, 并设定声波从40°角度入射, 同时加入信噪比−5 dB的高斯白噪声, 参数$ \mu $取为MUSIC形式, 计算不同指数k值的FB-Eigenspace方位谱输出, 并与MUSIC方位谱输出、Eigenspace方位谱输出进行对比, 结果如图5所示。

由图5可知, 当指数k取值为1时, Eigenspace方位谱和FB-Eigenspace方位谱的性能一致, 二者方位谱输出曲线完全重合。当指数k取值为0.1和10时, FB-Eigenspace方位谱输出曲线呈现出较大的性能差异, 尤其在对旁瓣的压制效果上。指数k值越接近0, 则对旁瓣的压制能力越强。当指数k取值为−0.1和−10时, FB-Eigenspace方位谱输出曲线的主瓣变窄, 旁瓣起伏降低, 方位谱输出性能依赖于所选择的指数k值, 指数k越接近0, 主瓣的变窄程度越大。为进一步分析指数k值的影响, 在图5仿真参数下, 选取蒙特卡罗仿真次数为500次, 计算不同k值下的FB-Eigenspace方位估计, 其均方根误差和DOA估计成功概率(以±1°为估计成功的阈值)结果如图6所示。

由图5和图6可见, 指数k值对算法的定位精度无明显影响, 结合式(9)可知, 这是因为指数k值通过乘幂运算影响算法的主旁瓣比, 而不会影响最大谱峰的位置, 在低信噪比情况下(小于−10 dB), 正值且较大的指数k值使算法具有更好的鲁棒性。通过上述仿真结果, 验证了FB-Eigenspace方位估计方法性能及其参数选取的影响, 在较高信噪比的情况下, 不同的指数k值取值仅影响算法的谱峰尖锐度, 而不会影响算法的方位估计精度, 即本文所提FB-Eigenspace算法具有与Eigenspace算法相当的方位估计能力, 但可通过控制指数k值来获得更加尖锐的谱峰, 具有更强的多目标分辨能力。

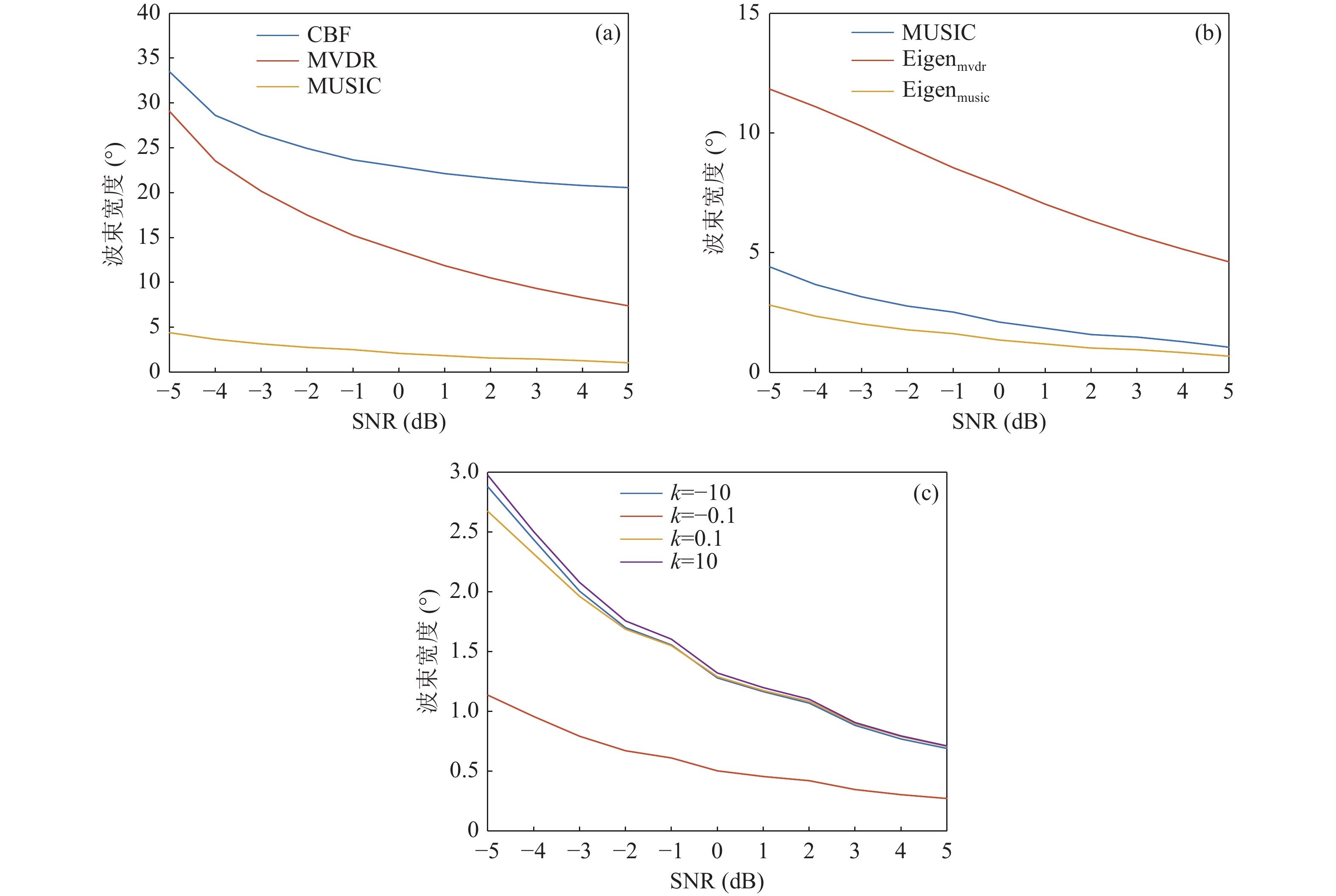
由于多目标的分辨力约等于1.3倍主瓣宽度^[21], 因此通过主瓣宽度对多目标分辨力进行初步的仿真分析。不同信噪比下的主瓣宽度比较结果如图7所示。可以看到, MUSIC算法具有比CBF与MVDR算法更窄的主瓣宽度, 这使得基于MVDR加权的Eigenspace算法的主瓣宽度仍大于MUSIC算法, 而本文所提FB-Eigenspace算法具有比MUSIC算法更窄的主瓣宽度, 当指数参数k远大于1时, 算法的主瓣宽度表现趋同, 这是因为在此情况下, FB-Eigenspace算法主要受参数$\mu $的影响; 当指数k接近于0时, 主瓣宽度进一步大幅度降低, 且指数k取负值时主瓣宽度最小, 仿真结果与对式(9)的理论分析一致。

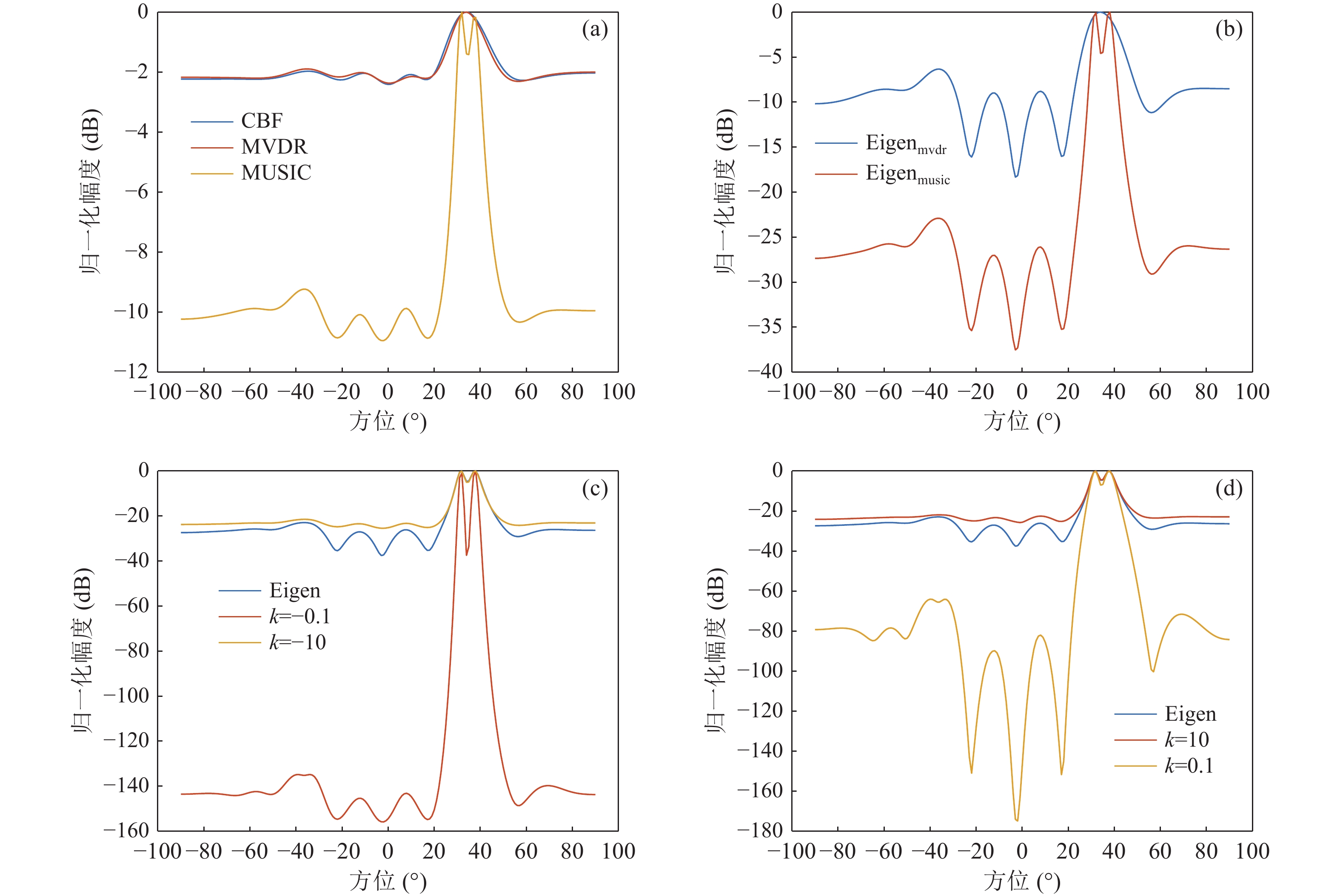
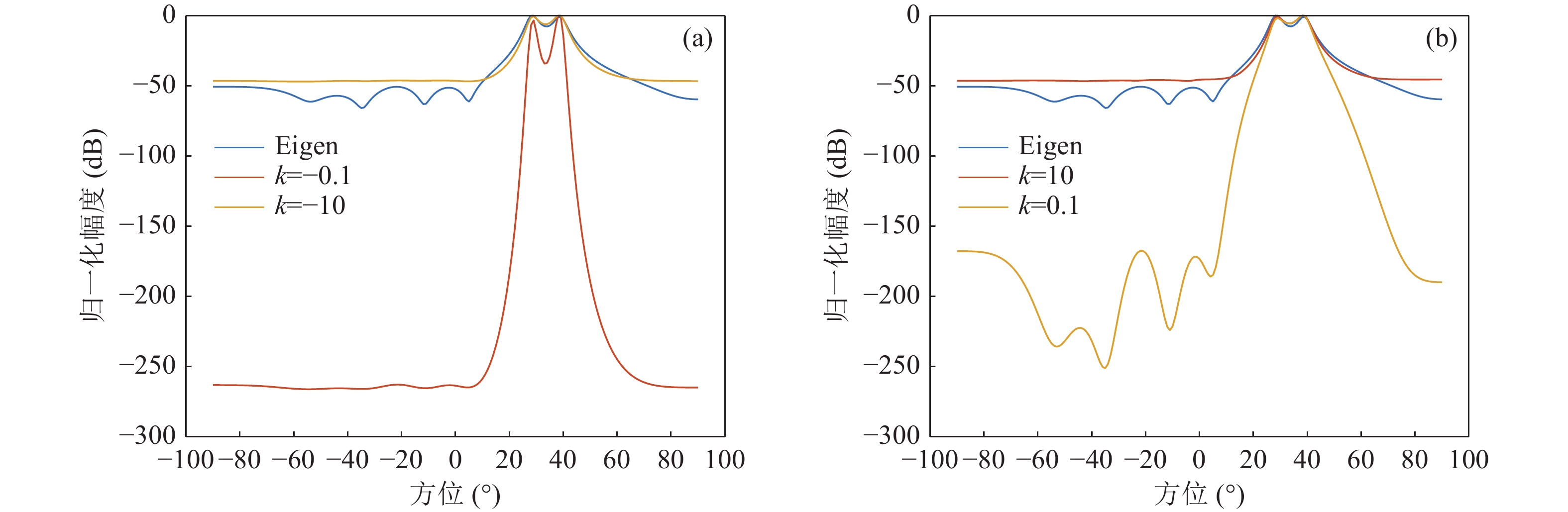
为分析本文所建立的FB-Eigenspace方位估计算法对多目标的分辨能力, 以及阐述指数k值对多目标分辨能力的影响, 阵列接收条件与上一节单声源仿真条件相同, 目标频率设定为60 Hz和70 Hz, 远场入射的角度分别是30°和40°。接收信号中加入高斯白噪声, 信噪比设定为−5 dB与−10 dB。 计算不同指数k值下FB-Eigenspace方位谱输出, 并与CBF、MVDR、MUSIC算法及文中所提两类导向加权Eigenspace算法方位谱输出进行对比, 结果如图8和图9所示。

由图8可以看出, MUSIC算法的方位谱曲线具有尖锐的谱峰, 因而MUSIC方位估计、基于MUSIC算法对导向矢量加权的Eigenspace方位估计和基于MUSIC算法对导向矢量加权的FB-Eigenspace方位估计皆可实现两个目标的有效分辨。同时, 由于指数k的引入, 使得主瓣与旁瓣差异增加, 多目标分辨能力更强。当指数k取值为负时, 主瓣宽度变得更窄, 即FB-Eigenspace算法具有更强的多目标分辨能力。当指数k取值为正时, 从归一化幅度上看, 主旁瓣差异显然优于其他情况, 但主瓣宽度不如指数k为负情况下尖锐。因此, 在多目标分辨方面, FB-Eigenspace的指数更宜取负数。

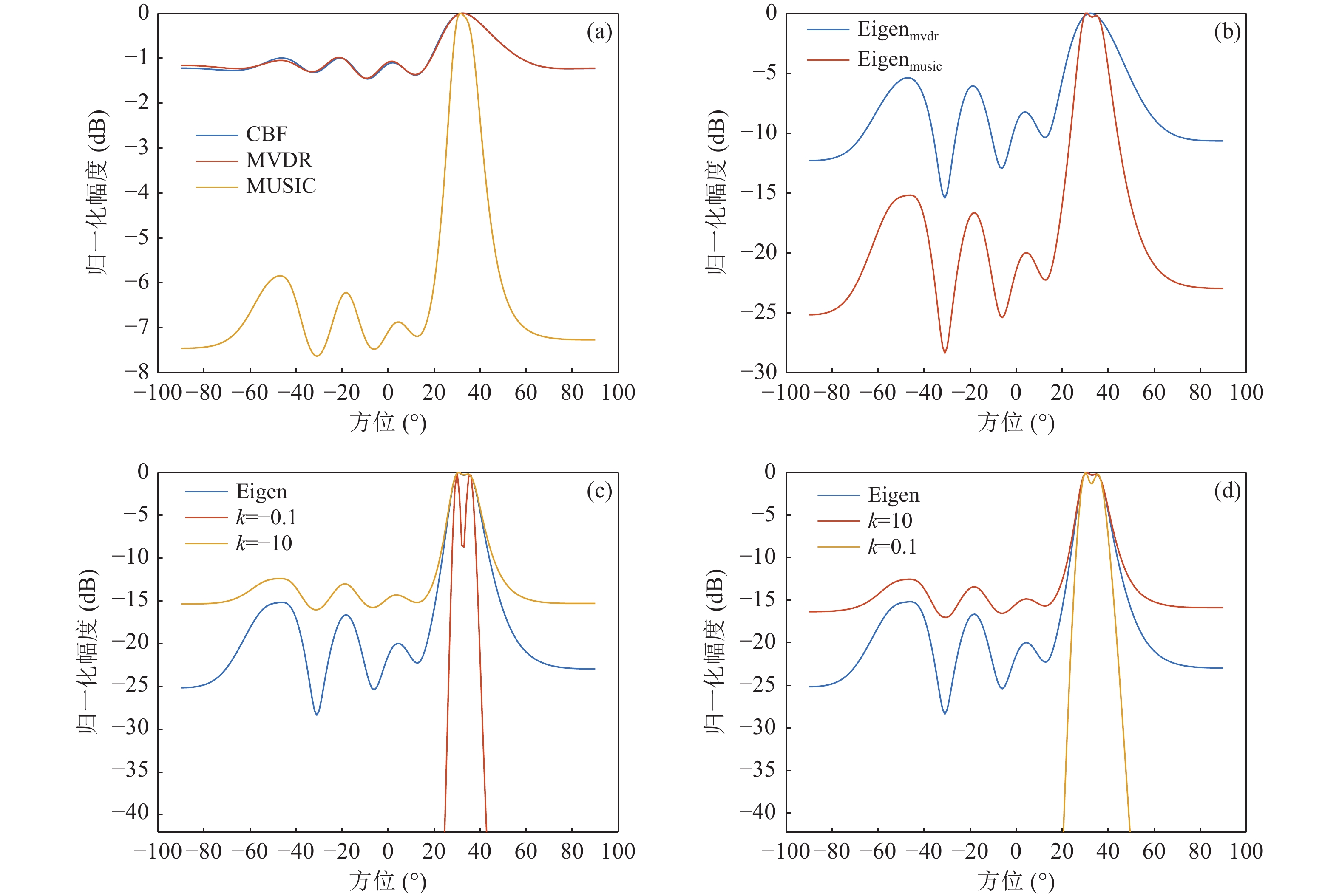
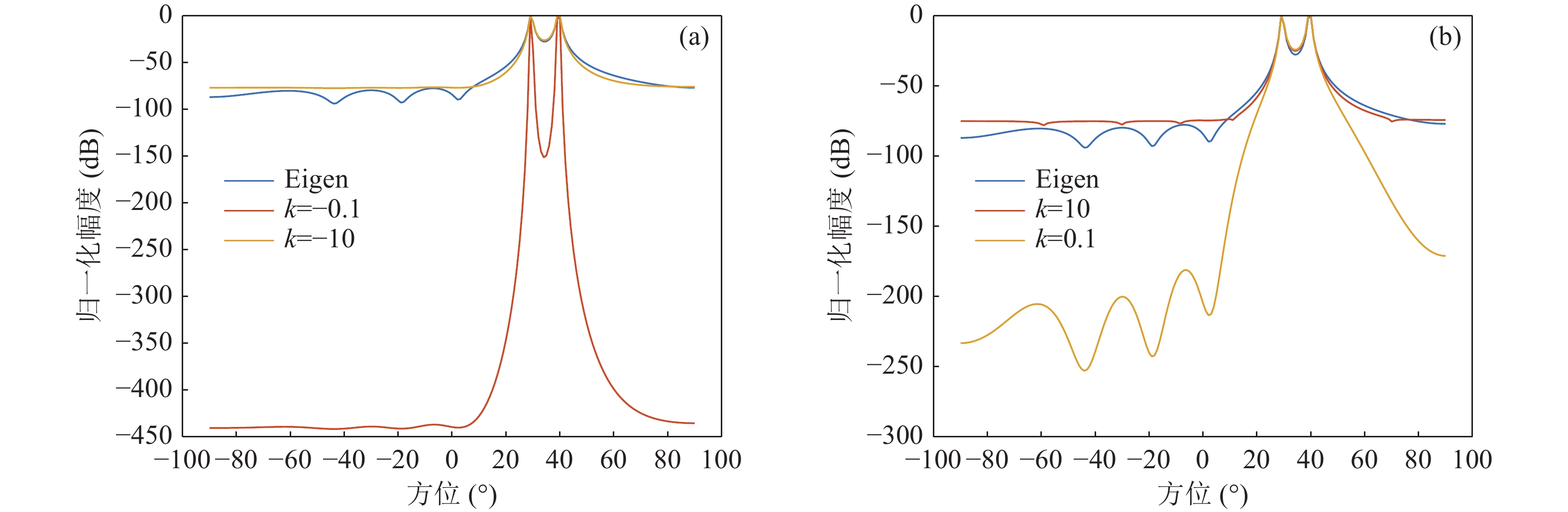
由图9可以看出, 当信噪比进一步降低时, 所有算法的分辨能力皆有所下降。甚至相较于SNR = −5 dB时, MUSIC方位估计与基于MUSIC算法的导向矢量加权Eigenspace方位估计算法也已无法实现多目标的分辨, 这可以用特征子空间划分和MUSIC算法采用的子空间形式解释。但对于本文所提FB-Eigenspace方位估计算法, 虽然其分辨能力下降, 但当指数$ k = - 0.1 $和指数$ k = 0.1 $时, 即指数k取值接近0, 特别k值取值为负数, 其仍具有多目标分辨能力。因此, 通过合理的指数k取值, FB-Eigenspace方位估计算法在低信噪比环境下仍然比CBF、MUSIC方位估计算法和Eigenspace方位估计算法具有更优的多目标分辨能力。

上述多目标仿真计算中, 不同目标具有不同的频率特征。为进一步分析本文所提FB-Eigenspace方位估计算法在多目标分辨方面的能力, 考虑两声源同频相干的情况。在同频相干声源情况下, 为保证阵列接收矩阵满秩的需求, 采用空间平滑的方式进行处理。将阵列拆分或看作若干彼此重叠的子阵, 子阵数目与目标数有关, 取各子阵协方差矩阵和的平均且作方位谱估计计算。与上述仿真计算条件相似, 假设同频相干双目标的频率均为60 Hz, 远场入射的角度分别是30°和40°。接收信号中加入高斯白噪声, 信噪比取5 dB, 计算不同指数k值下无空间平滑和空间平滑处理的FB-Eigenspace方位谱曲线, 并与Eigenspace方位谱曲线对比, 其结果分别如图10和图11所示。

根据图10和图11, 相较于Eigenspace方位谱估计曲线, 本文所提FB-Eigenspace方位谱估计曲线具有更好的分辨能力。但即便在较高信噪比的条件下, 对于相干声源的多目标问题, 方位估计算法的分辨能力显著下降。当采用空间平滑技术时, 其多目标分辨能力得到了明显提升。特别是指数$ k = - 0.1 $时, FB-Eigenspace方位谱估计曲线具有极窄的主瓣宽度, 实现了30°与40°入射角度上相干声源的分辨。虽然空间平滑方法牺牲了一定空间孔径, 但该方法对协方差矩阵秩的补足在一定程度上缓解了方位估计算法本身以及指数乘幂次数过多引起的次要目标主瓣高度过度降低的问题, 因此在确定目标数量的情况下需要采用空间平滑方法。

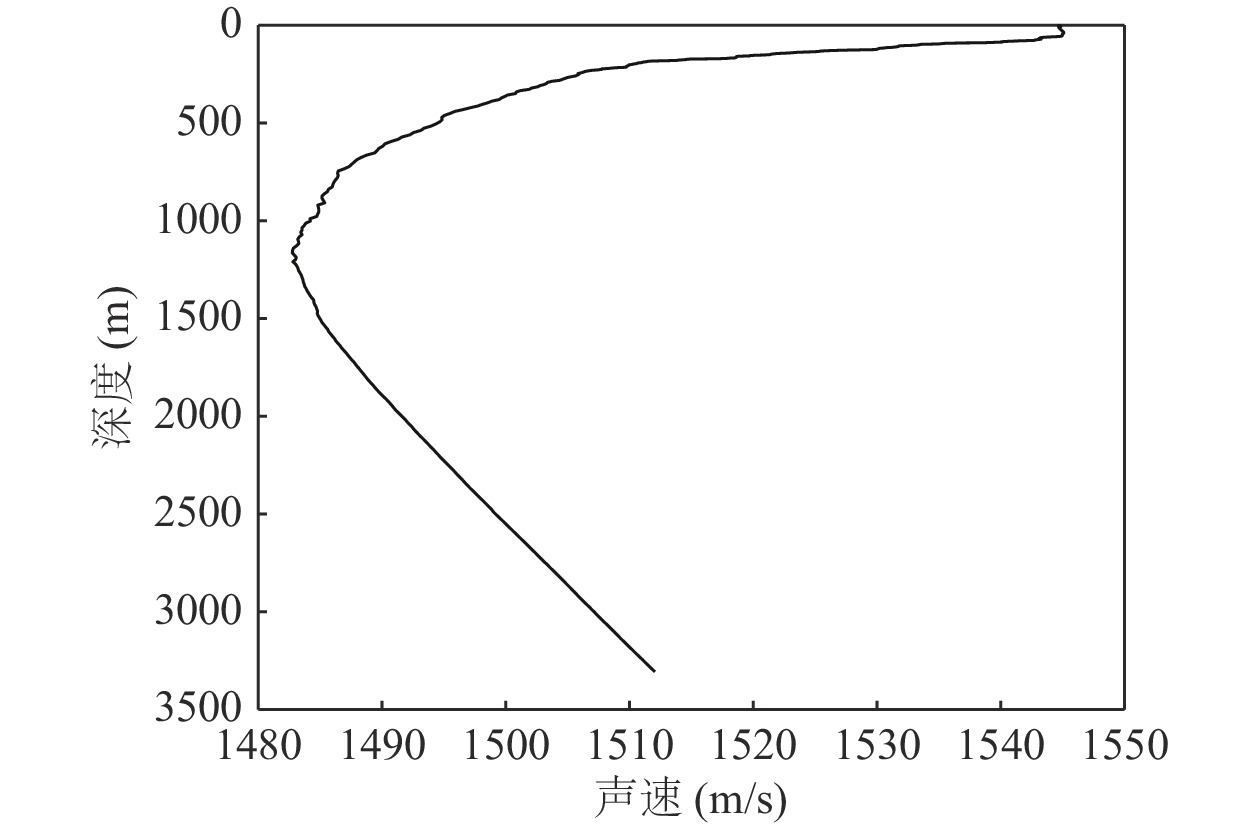
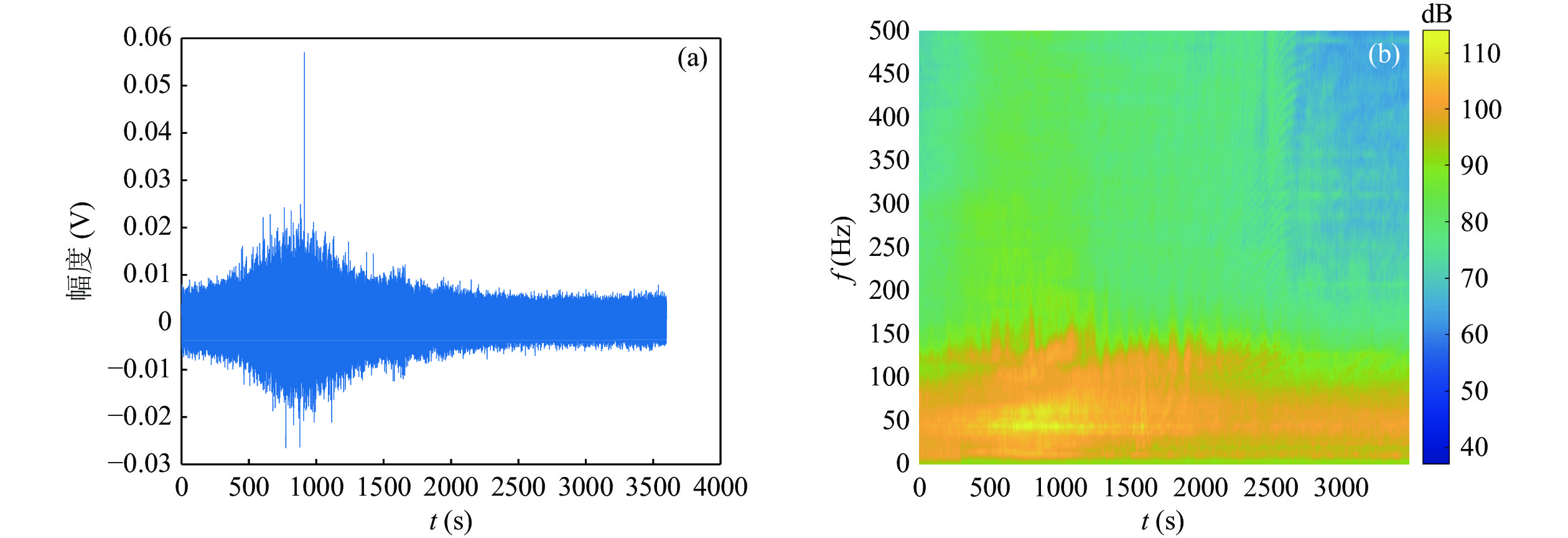
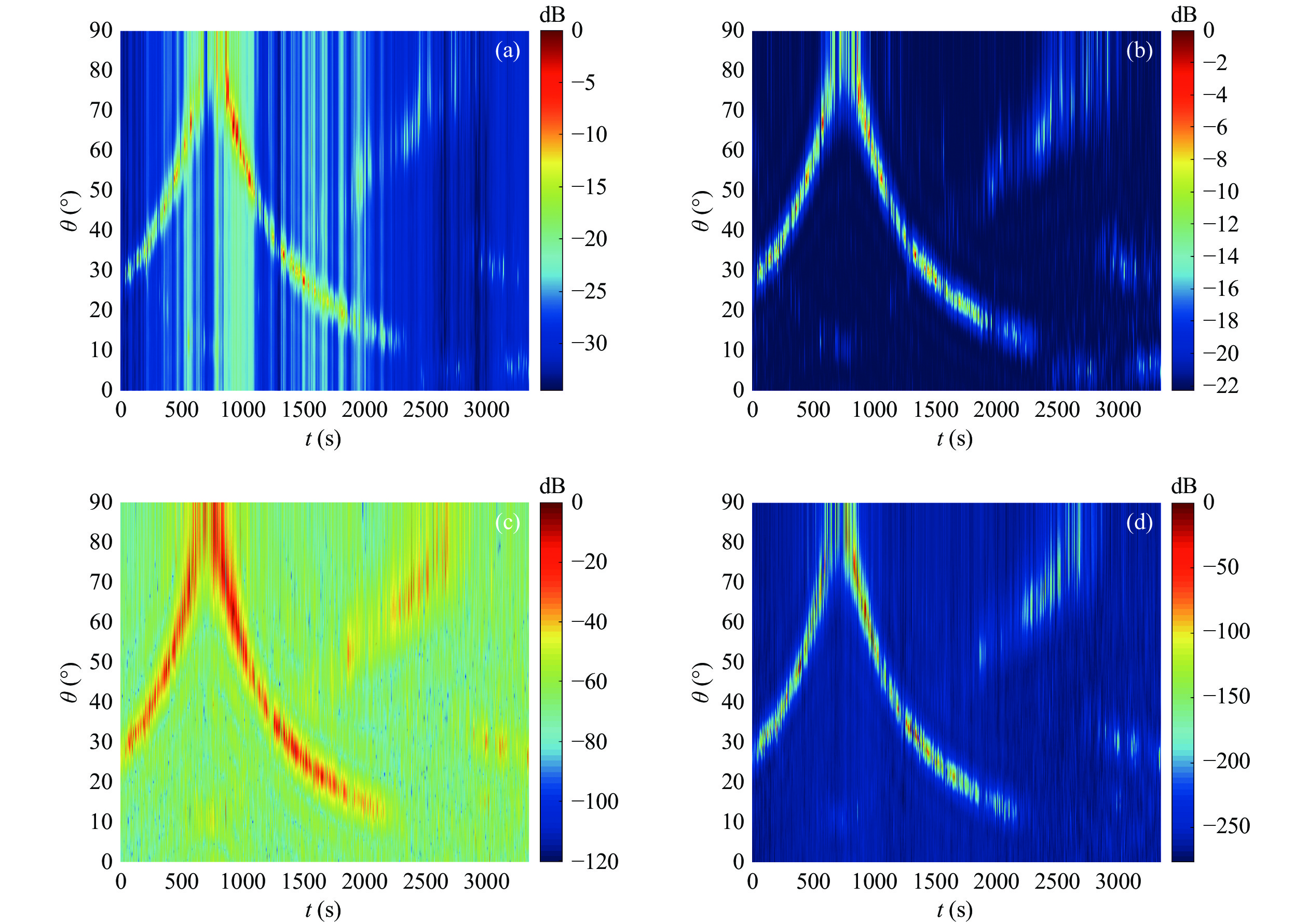
根据与经典CBF、MVDR、MUSIC和导向矢量加权Eigenspace结果对比分析, FB-Eigenspace算法具有更为优良的方位分辨能力, 其方位分辨能力同时受导向矢量加权参数$ \mu $的形式和指数k选取数值影响。当导向矢量加权参数$ \mu $选取MUSIC形式, 指数k数值选取−0.1时, FB-Eigenspace算法具有极窄的主瓣宽度和极佳的多目标分辨能力。为进一步验证FB-Eigenspace算法性能, 分析处理南海南部海域的垂直阵水声探测试验数据。试验海域水深约3300 m, 海底地形平坦, 典型的深海声速剖面, 声速剖面如图12所示。采用布放于海底且阵元间距为10 m的8元垂直阵进行接收, 8元垂直阵距离海底约300 m, 以第4通道为例, 其接收信号如图13所示, 已知确定信号频率为126 Hz。

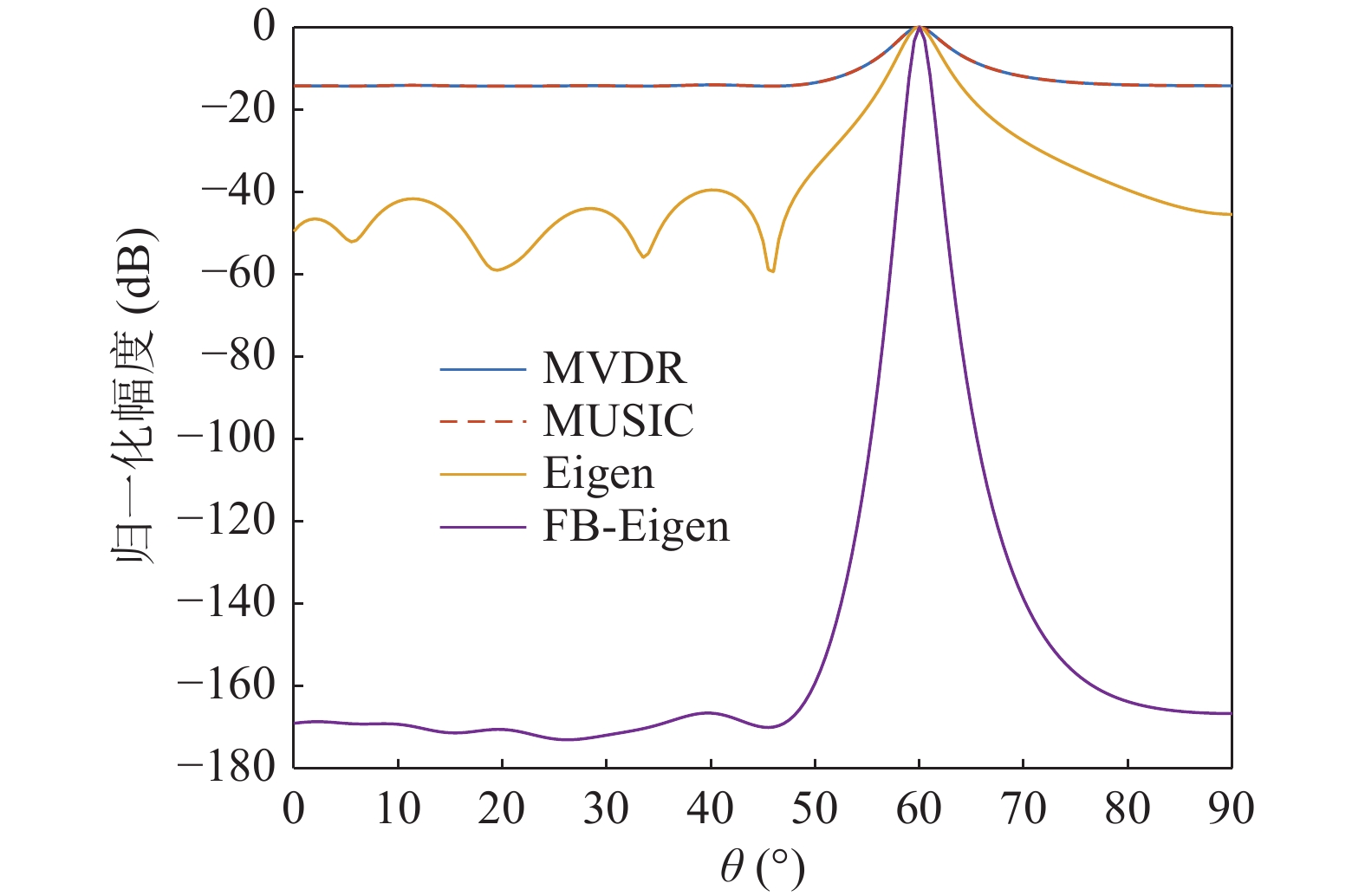
通过时域波形可见, 本次试验为一次过顶航行, 即航船由远及近再及远, 在700 s左右距离最近。由于确定信号频率较高, 未满足空间半波长采样条件, 在进行方位谱估计时发生了混叠, 为避免歧义且阵列位于海底, 仅0°~90°探测区间有效。因此, 后续的方位估计结果仅展示0°~90°区间。针对本次垂直阵探测试验, 导向矢量加权参数$ \mu $选取MUSIC形式, 指数k数值选取−0.1, 计算本文FB-Eigenspace算法的时间−方位历程, 并与MVDR、MUSIC、Eigenspace算法进行比较, 计算结果如图14所示。为便于观察各算法计算获得的时间−方位历程, 并未采用一致的色棒颜色显示范围。从时间方位历程图的视觉效果上看, 所采用的四种算法均正确估计出了目标方位, 但MVDR算法出现了方位估计不稳定的情况。相较于Eigenspace算法, MUSIC算法与参数$ \mu $选取MUSIC算法形式、指数$ k = - 0.1 $的FB-Eigenspace算法效果更佳且二者几乎一致, 明显地给出了该目标的时间−方位历程。而从显示范围上看, 显然FB-Eigenspace算法明暗差异更大, 即声源目标分辨效果将更佳。

为避免颜色显示范围不同所导致的视觉效果问题, 取第1000秒的方位谱估计计算结果剖面, MVDR、MUSIC、Eigenspace算法与本文所提FB-Eigenspace算法的比较结果如图15所示。由于信号到达时间段内, 存在较多干扰, 使得MUSIC算法计算性能下降, 无论是采用MVDR算法, 还是MUSIC算法, 其方位谱曲线几乎一致。以MUSIC形式为导向矢量加权的Eigenspace算法, 在MUSIC基础上, 进一步应用信号子空间与噪声子空间的正交性, 获得更优的角度分辨能力, 但存在额外的旁瓣。在MUSIC形式为导向矢量加权的Eigenspace算法基础上, 通过函数波束形成指数k的引入, 本文所提FB-Eigenspace算法具备更佳的角度分辨能力, 如图15所示, 在信号到达时刻处, FB-Eigenspace算法主瓣宽度极小, 峰值尖锐, 几乎未有旁瓣, 更为准确地获得了到达角度。

针对低频条件下小尺寸阵列波束形成的波束宽度宽、分辨能力弱、无法满足多目标分辨需求这一问题, 本文在综合分析函数波束形成与特征子空间方位谱估计理论基础上, 将以特征子空间算法表征的扫描向量归算系数与函数波束形成的控制指数控制技术相融合, 提出了一种函数−特征子空间方位估计方法, 即FB-Eigenspace方法, 理论上兼具了表现形式灵活与多目标分辨能力等优点。

改进传统 Eigenspace 算法的扫描向量归算系数仿真结果表明, 选取MUSIC 形式作为Eigenspace算法的扫描向量归算系数能使该算法具有最佳分辨力。在此基础上, 将函数波束形成的控制指数引入Eigenspace算法的计算流程中, 可进一步提升算法的分辨力。不同控制指数下 FB-Eigenspace算法具备不同的能力, 当控制指数取值小于 1且为负数时, 该算法的多目标分辨能力明显优于其他算法。同时, 也可根据对算法的鲁棒性需求选取其他合适的控制指数, 控制指数取值为正数时, 算法的多目标分辨能力有所降低, 但鲁棒性得到了提升。海试结果进一步验证了 FB-Eigenspace 算法的声源分辨能力, 能够较好地获取多个声波到达角。

致谢　感谢“实验1”科考船为获取试验数据提供的支持。