-
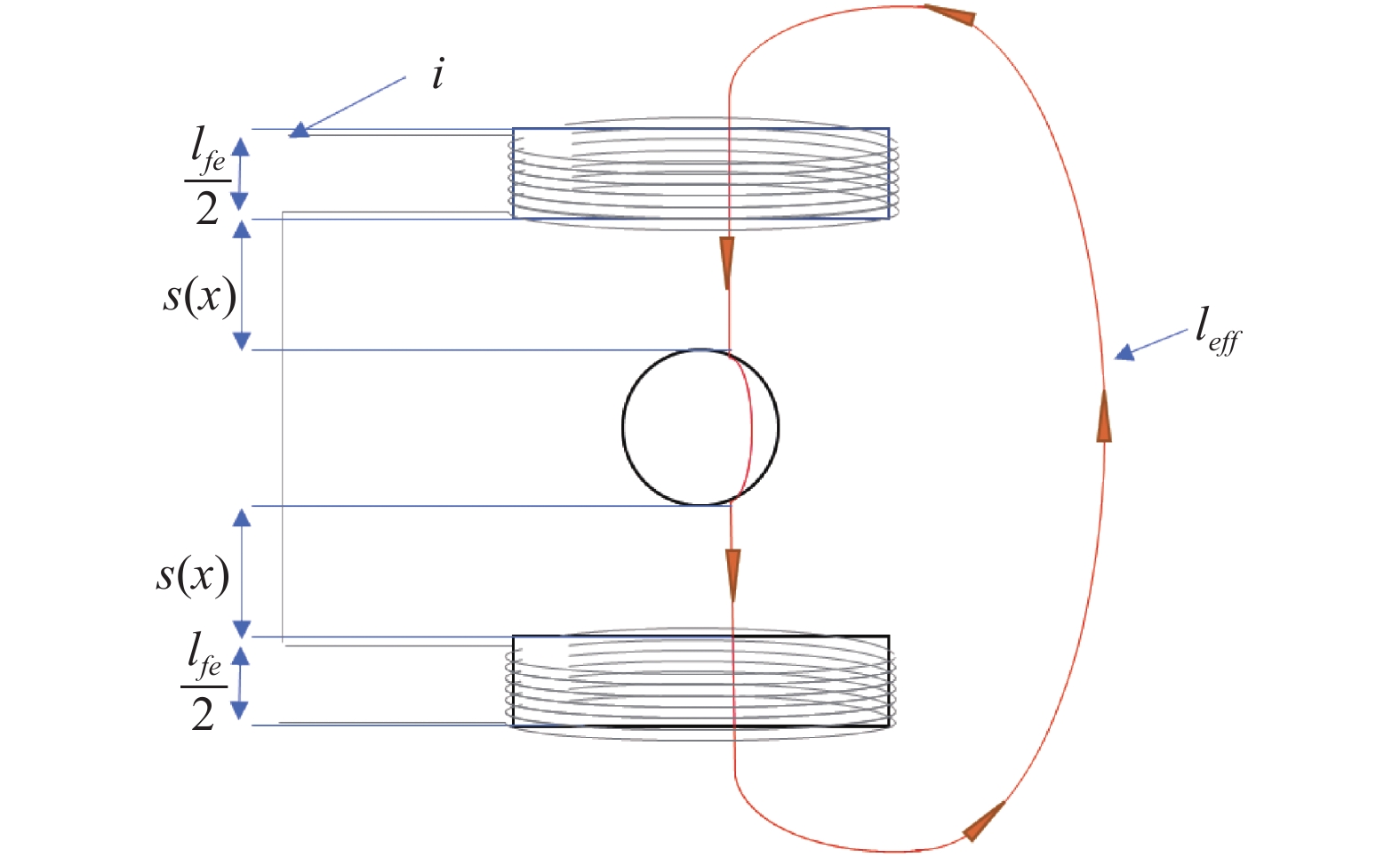
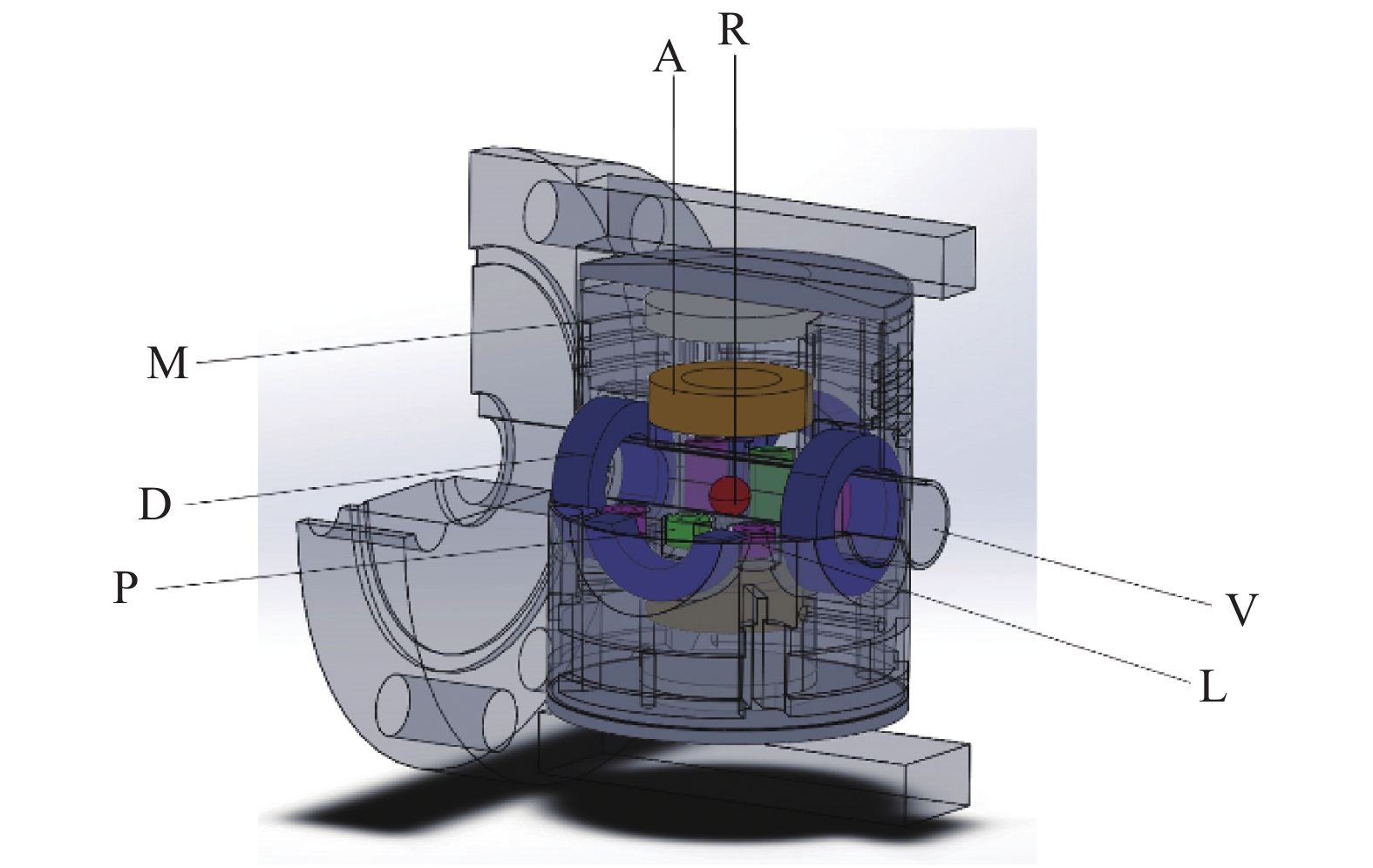
磁悬浮转子真空计是一种精密的黏滞型真空计,以其优良的计量特性成为国际公认的高真空范围溯源/传递标准及真空计量标准装置的主标准器,常用于真空量值的国际比对以及各国真空量值溯源及传递体系的构建[1-6]。磁悬浮转子真空计采用永磁-电磁合力实现混合磁悬浮。转子稳定悬浮在真空中时,转子与不与传感器中的任何结构件产生接触,凭借测量气体分子对旋转转子的阻尼作用的大小来测量真空度,磁悬浮转子真空计相比于有旋转轴线的阻尼测量装置,具有更低的测量下限。磁悬浮转子真空计结构如图1所示,真空计中心位置为转子R,水平方向上有两对相对布置的驱动线圈D,转子轴向上下有一对悬浮线圈A,转子水平面上四周有两对起横向稳定作用的线圈L,转子工作状态下的转速由一对感应转子磁场变化的拾取线圈P组成[7]。
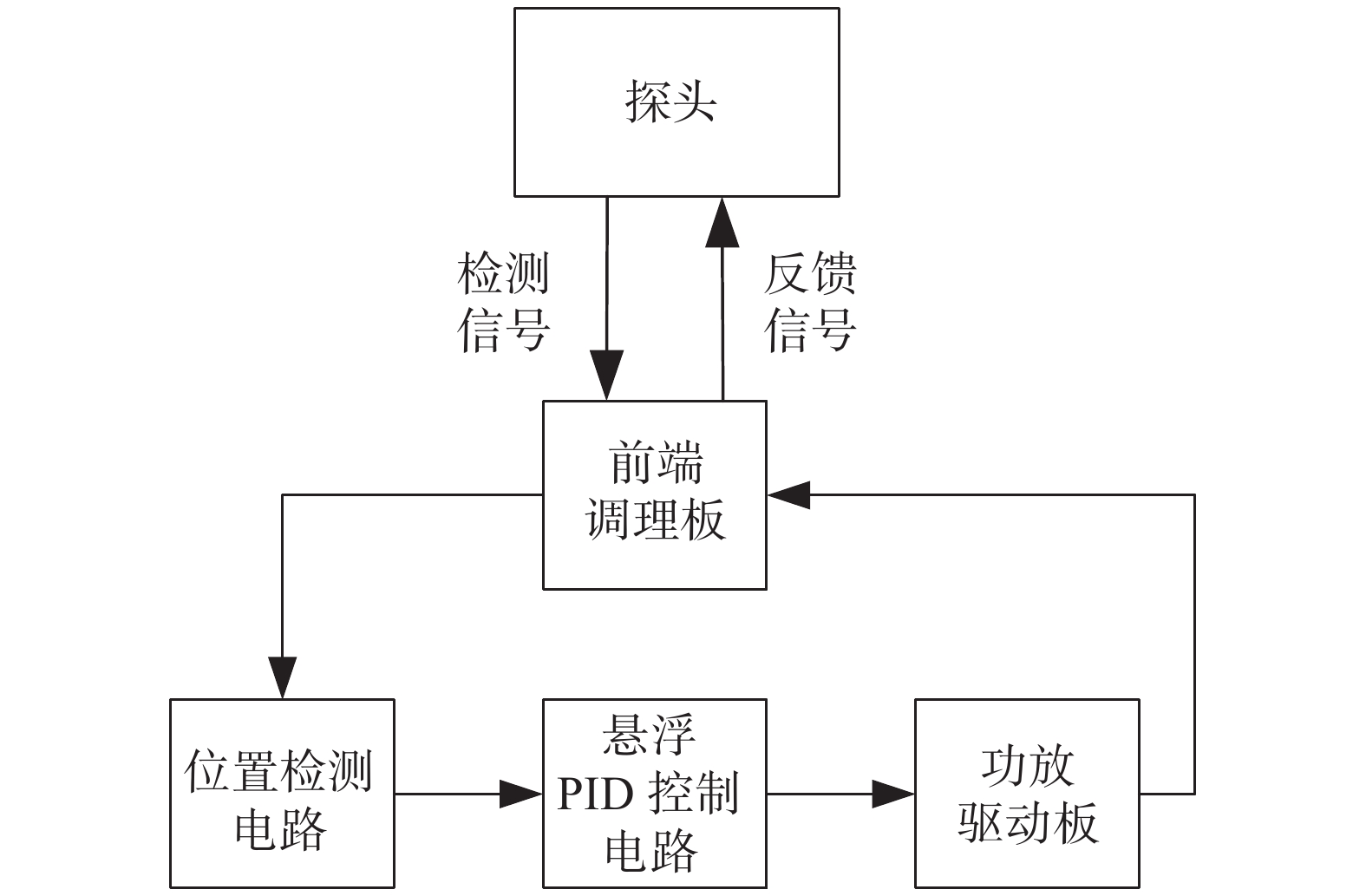
转子的悬浮稳定性决定着阻尼作用的测量准确度,因此在悬浮轴向上,需要精密的位移传感器对转子的悬浮位置进行精确的实时测量,以达到更稳定的悬浮控制效果。位移传感器的检测结果作为悬浮闭环控制的输入,影响着磁悬浮转子真空计转子轴向控制精度,从而影响真空度的测量[8-10]。电涡流传感器的工作原理是基于互感效应,通过测量线圈上的高频激励,在被测物上产生涡流互感,影响激励线圈的阻抗,从而在实现距离的测量。在磁悬浮转子真空计的应用中,测量真空度的转子轴向位移检测对电涡流传感器有更特殊的要求。通常电涡流传感器采用几十千赫兹到数兆赫兹的激励频率,以提高其测量灵敏度,但是在磁悬浮转子真空计的设计中,为满足真空漏率要求,采用全金属设计,要求在其中工作的电涡流传感器的激励频率不可太高,过高的激励频率会由于屏蔽效应导致信号无法穿透内部金属结构件,无法准确测量到转子的位移,而过低的激励频率则会降低位移测量的精度。另一方面,悬浮在真空中的转子无法通过对流和热传导散热,只能通过缓慢的热辐射降温,电涡流传感器的参数选择也应考虑涡流效应引起的转子发热。此外,受限于磁悬浮转子真空计测量头小体积、高度紧凑的结构设计,悬浮系统使用了位移传感器与悬浮执行器复用的解决方案,在同一对轴向线圈上加载交流激励信号使其作为电涡流位移传感器,同时在线圈上加载直流信号使其作为磁悬浮控制的电磁力执行器。在实际磁悬浮转子真空计轴向线圈设计中,应该综合考虑以上因素[11-13]。
全文HTML
-
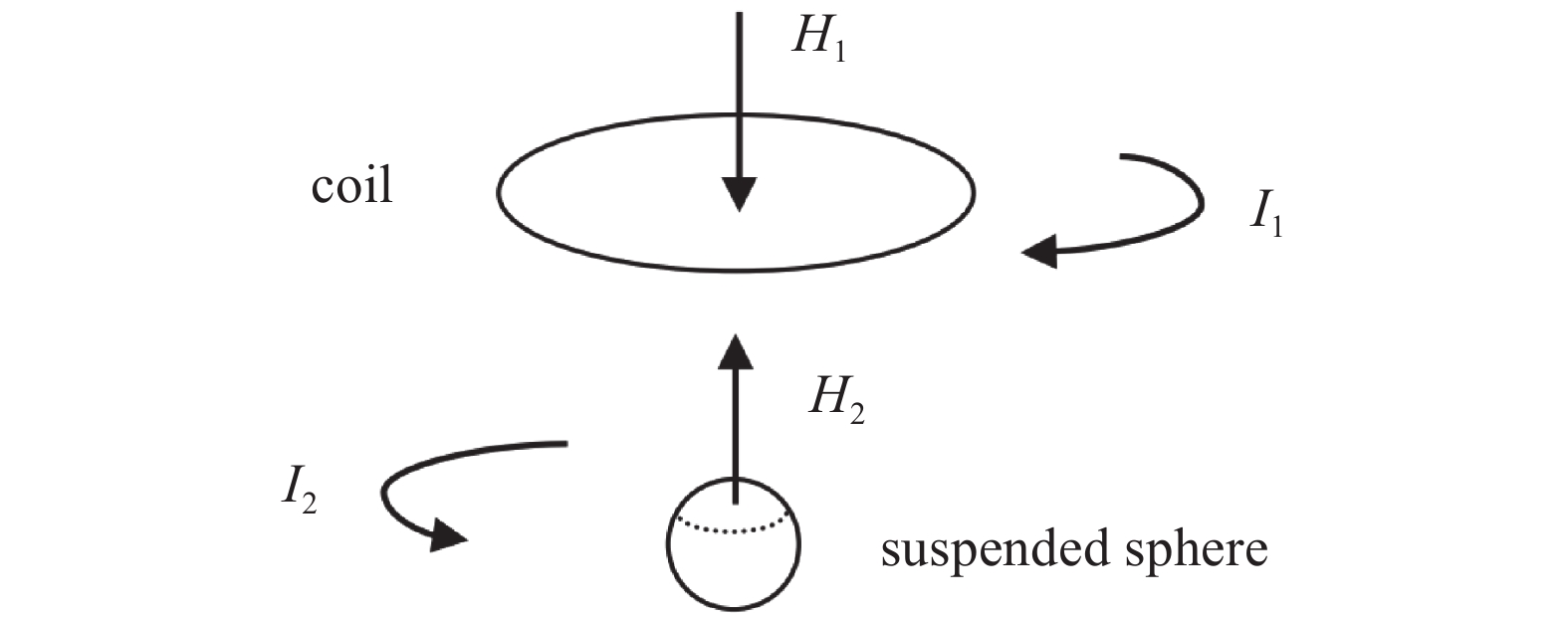
电涡流传感器的工作状态下的互感原理如图2所示。电涡流传感器的基本原理是电涡流效应,被测物体表面产生的涡流来自于探测线圈上加载的高频激励。电涡流位移传感器的主要构件是传感器线圈,对被测物体的要求是金属导体。传感器进行位移检测时,在传感器线圈上加载一定频率的的交流激励I1,加载了交流激励的线圈会在周围空间产生一个交变磁场H1。交变磁场会在线圈一端的金属导体表面产生小型电涡流I2,金属导体表面处的电涡流I2会产生与传感器线圈的磁通H1方向相反的磁通H2,抵消传感器线圈的部分磁场。根据传感器线圈与金属导体间的距离变化,导致传感器线圈的电感L、阻抗Z和品质因数Q发生对应改变,从而通过换算得到金属导体的位置信息。因此,线圈参数是导体参数的函数[14-18]。
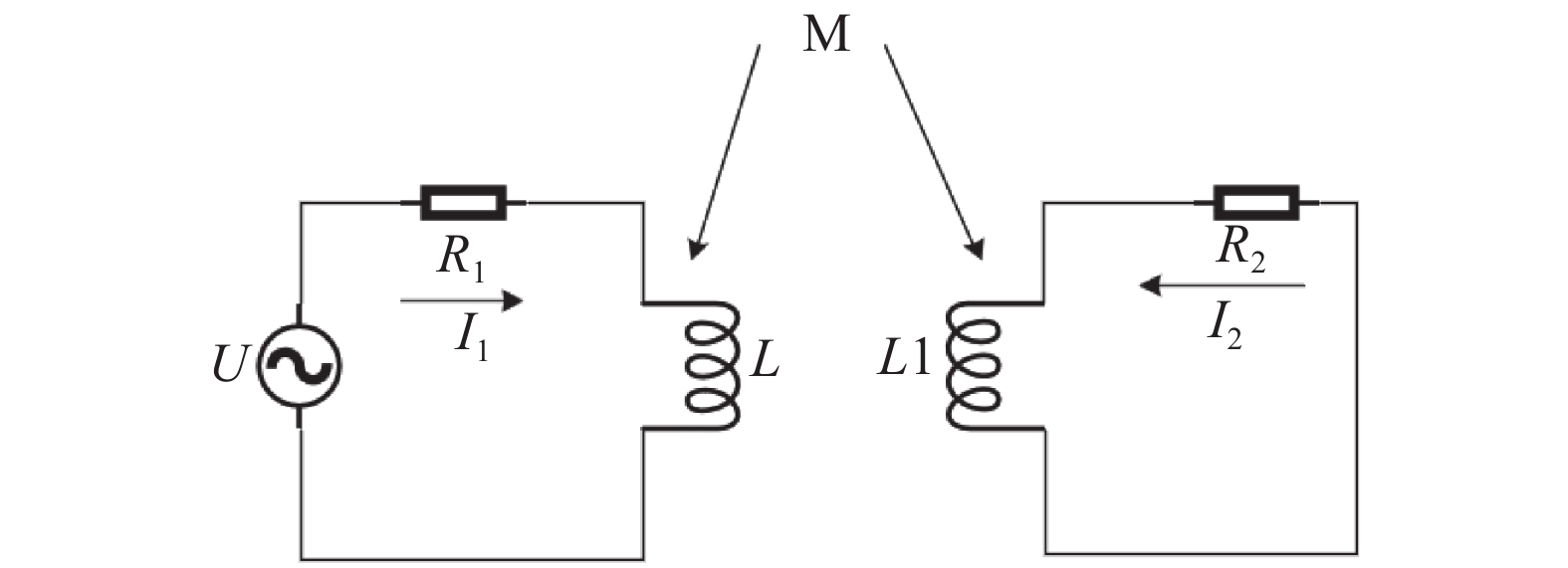
将被测导体,即转子看作产生涡流的电感,此时图一中的原理图可以简化为如图3所示的等效电路,由一对有互感M的线圈组成。
由基尔霍夫电压定律,可得平衡电压方程式
求解方程组可以得到电流表达式
式(2)中,I1为激流交流电流;I2为线圈变化的磁通在转子上感生出的电涡流;L为线圈等效电感;R1为线圈电阻;L1为转子等效电感;R2为转子等效电阻;ω为角频率;jωL为电感阻抗;M为L与L1之间的互感系数;U为激励电压。
因此传感器线圈的等效阻抗Z为
也可以写为式(4),等效电感Leq和等效电阻Req
根据上述推导,电涡流传感器线圈的等效阻抗可以简化为如下表达式
式中,ω 为线圈中激励电流频率;μ 为被测金属导体磁导率;ρ 为被测金属导体电阻率;x 为线圈与被测金属导体的距离。对于磁悬浮转子真空计中的应用,需将转子的轴向位移变化转变为测量线圈等效阻抗Z的变化。通过改变转子与测量线圈之间的轴向距离与测量线圈的激励频率,即得到等效阻抗与两者距离x之间的关系。其中阻抗变化范围越大,电涡流传感器的位移检测灵敏度越高。
-
根据前一节的电涡流传感器工作原理的分析,在线圈加载特定的交流激励时,磁悬浮转子位移改变使位移测量传感器的等效阻抗发生改变,但是阻抗值难以直观的显示或者测量,因此需要转换电路将阻抗变化转换为对应的电压或者电流变化。
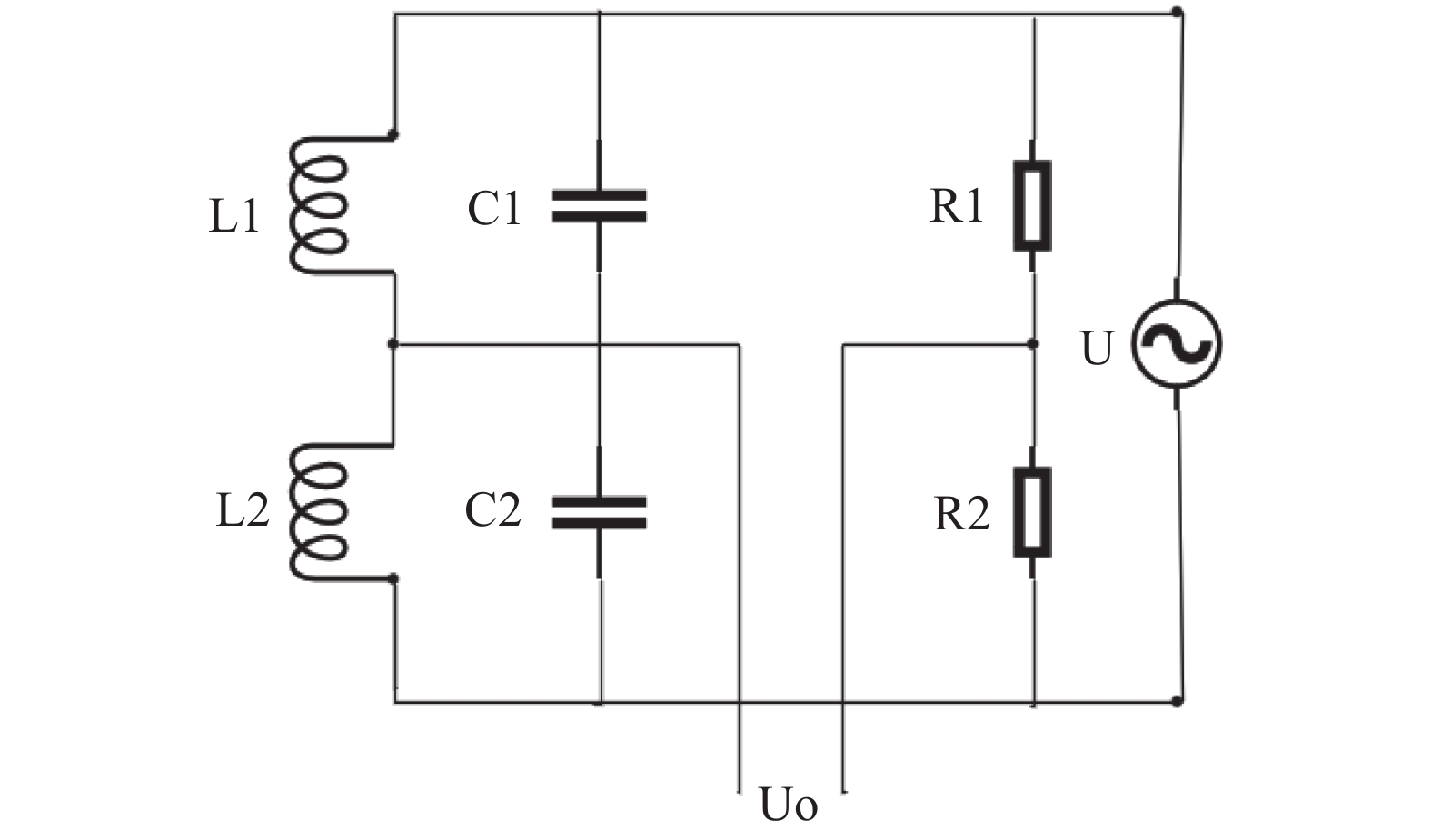
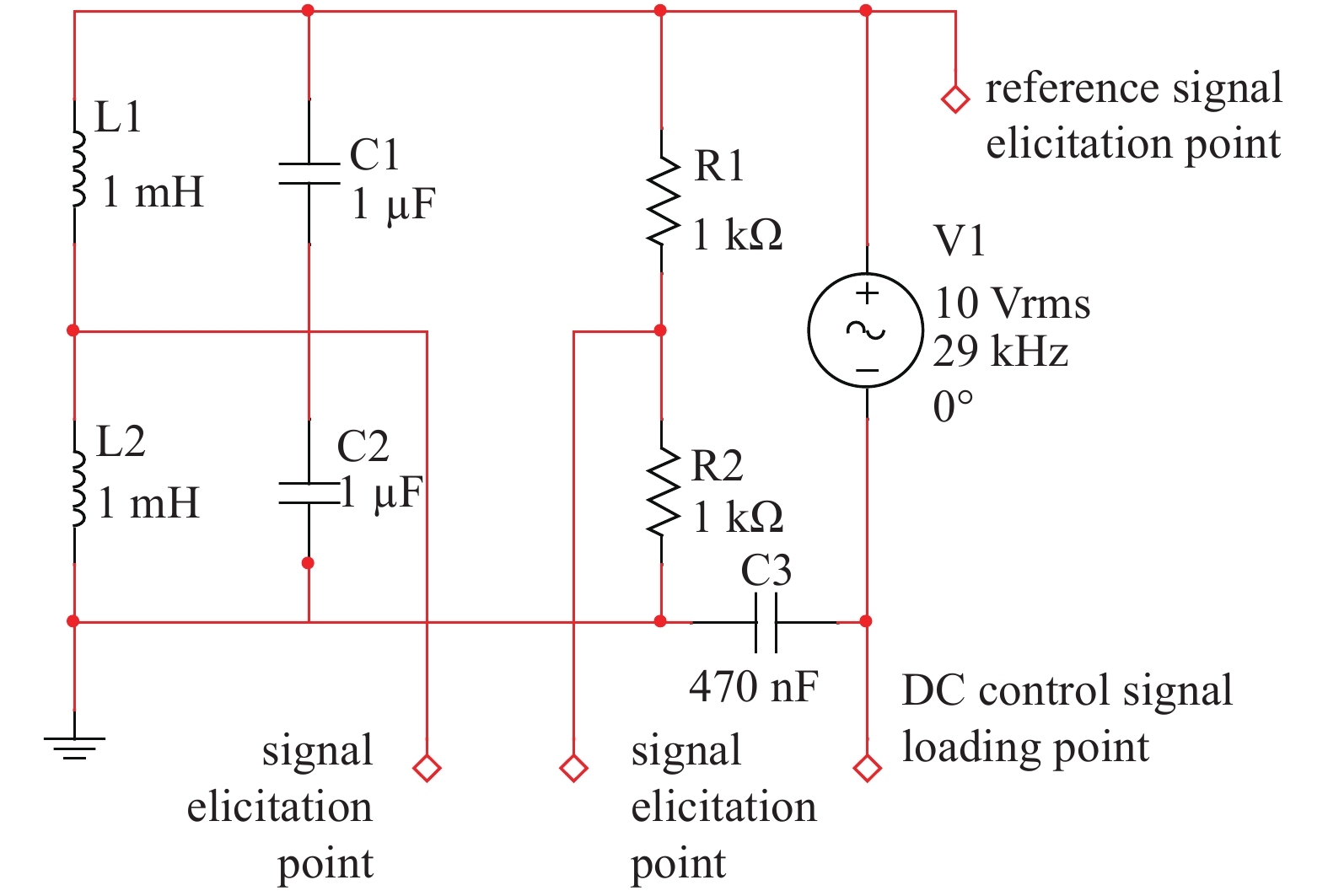
在磁悬浮转子真空计的实际应用中,使用交流电桥法进行阻抗——电压的转换。电桥原理图如图4所示,使用差动式测量线圈组成电桥的两臂,当转子位移发生变化,会引起两个差动布置的传感器同时发生等效阻抗的变化,电桥的平衡被打破,此时对输出信号Uo进行处理,即可实现对位移的检测。经过处理后的电压信号与转子位移对应。位于上下线圈中间位置时电压为0,上下极限位置处对应电压分别为+2 V与−2 V。
为提高输出信号的线性度,在电涡流传感器的应用中,采用并联LC回路,并且使电涡流传感器工作在谐振频率,即并联LC回路对外呈现纯电阻电路特性。LC回路在29 kHz频率下处于谐振状态,故选取该频率作为工作频率
-
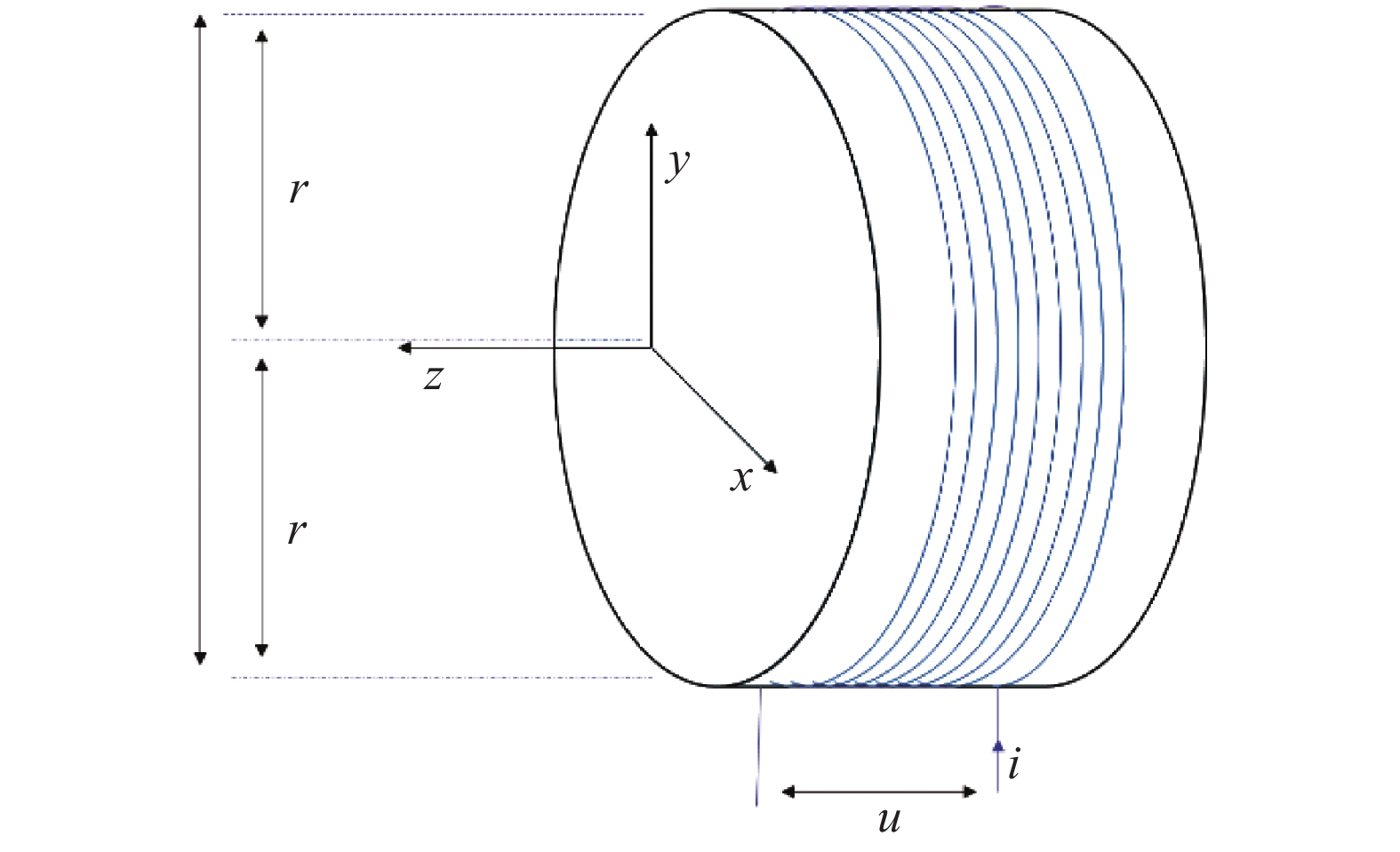
磁悬浮系统中使用的电磁铁原理如图5所示,图中u为激励线圈的端电压;i为电磁线圈的电流;r为铁芯半径,在磁悬浮转子真空计的实际应用中,线圈上不仅要加载直流电压,还有作为电涡流传感器而加载的交流激励,此时若在线圈上加载正弦电流,产生的电场强度为[19]
式中
$\sigma $ 与$\mu $ 分别为铁芯的电导率与磁导率。经过Laplace变换变量,式(6)可变为已知磁感应强度B与磁场强度H之间的关系为
磁通量与磁感应强度的关系为
由式(7)−式(9)可以得到磁通量的表达式
式中A为线圈截面积,根据安倍环路定理,如磁路示意图6所示。
表面磁场强度
${H_0}$ 可以表示为式中,
${l_{{\text{eff}}}}(x)$ 是电磁线圈的有效长度,s(x)是气隙总长度,${\mu _{\text{r}}}$ 为铁的磁导率,${\mu _{\text{r}}}$ >>1;${l_{{\text{fe}}}}$ 为铁芯气路长度,N为线圈匝数。简化式(11),得到
结合式(10),(12),得到磁通量与线圈电流在频域上的关系式
将式(13)线性化,级数展开,高次项产生的非线性对于一次项可以忽略不计,保留一次项,得到磁通量频域表达式
式(14)可以写为时域表达式
此时可以看出,在线圈中加入交流项后,磁通量与电流的微分项相关。
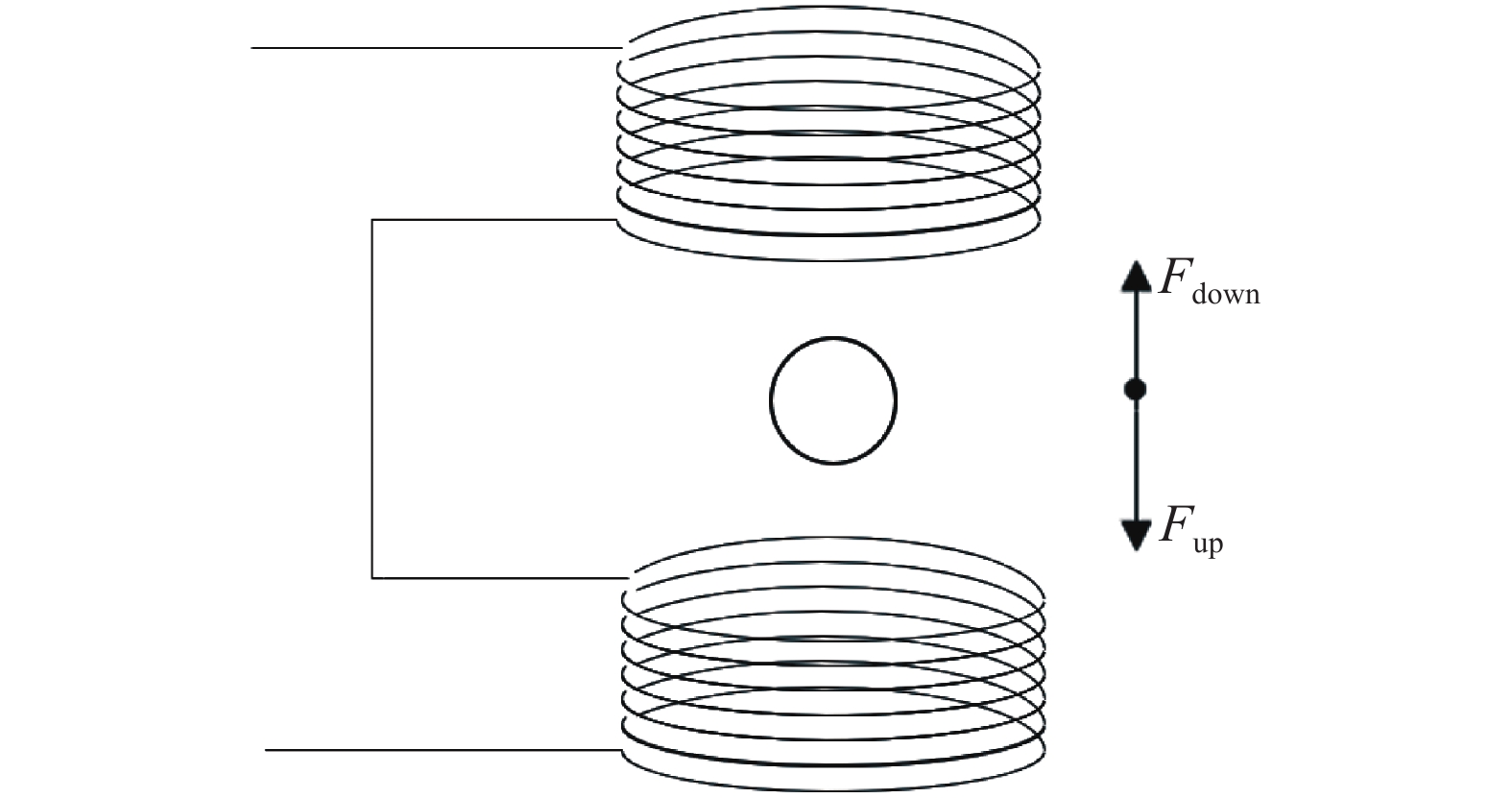
对于磁悬浮转子真空计,上下线圈采用串联结构,由一对电磁线圈产生磁力Fup与Fdown共同作用在转子上,如图7所示,因此考虑差动模式的线圈电磁力,总电磁力可以写为转子位移与线圈电流的函数
由式(15)可知,线圈铁芯材质确定后,铁芯电导率与磁导率同时确定,视为常数项,此时可取
$ \alpha = \dfrac{1}{3}\sigma \mu {r^2} $ ,将式(15)与式(18)联立得到方程组式中,
$ {\phi _ + } $ 与$ {\phi _ - } $ 分别为上下线圈的磁通量,$ {i_0} $ 与$ {s_0} $ 为偏置电流与悬浮设定位置,α为交流影响因子。由(19)式可以看出,涡流效应引起的电流微分项产生了非线性,其非线性程度取决于交流影响因子α的大小。转子的轴向磁悬浮动力学模型为
采用比例-微分控制器进行控制,电流模型为
kp为比例系数;kD为微分系数。式(21)带入(20),联立式(19),可得微分方程组
模型参数如表1所示。
由 式(22)可以看出,交流激励相比于直流激励,多出了以α为系数的微分项,由此可知交流电加载在线圈上对电磁力产生的影响是产生了一个电流的微分项,而影响作用的大小取决于系数α的大小,而α是与线圈参数电导率、磁导率和线圈截面大小有关的量,代入实际线圈参数,改变α的值,即可得到交流项对悬浮响应的影响。
-
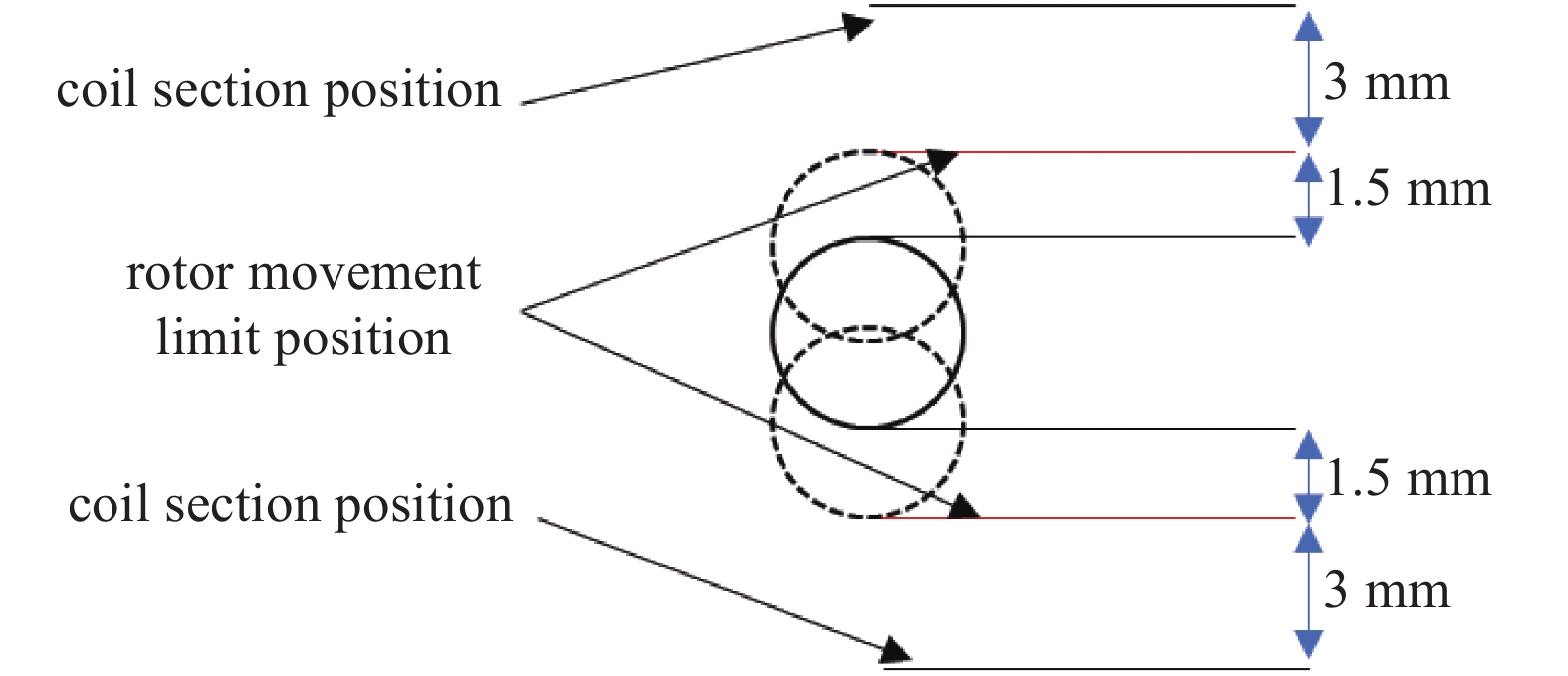
在磁悬浮转子真空计中,转子安装在法兰管中,法兰管连接至真空系统,因此转子的运动范围受限于法兰管的内径。实际工况中,转子运动范围如图8所示。
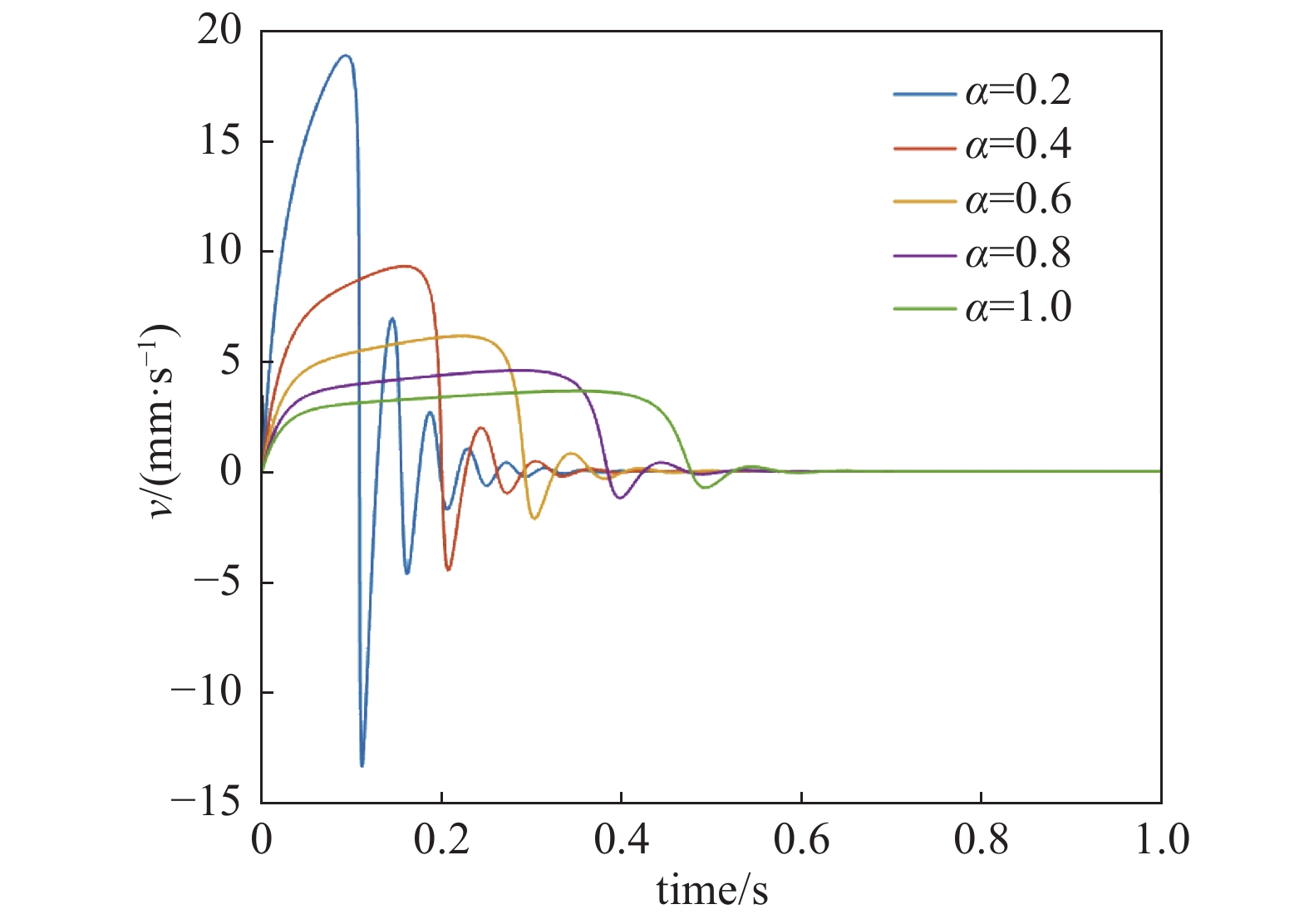
使用四阶龙格-库塔法解微分方程组(22)。设置微分方程组初始值,转子初始位置为3 mm,初始速度为0 mm/s,目标位置为4.5 mm处。设置控制输入项电流系数为kp=150,kD=10,以达到较为稳定的控制效果,便于测试影响因子α的变化对悬浮系统的影响。
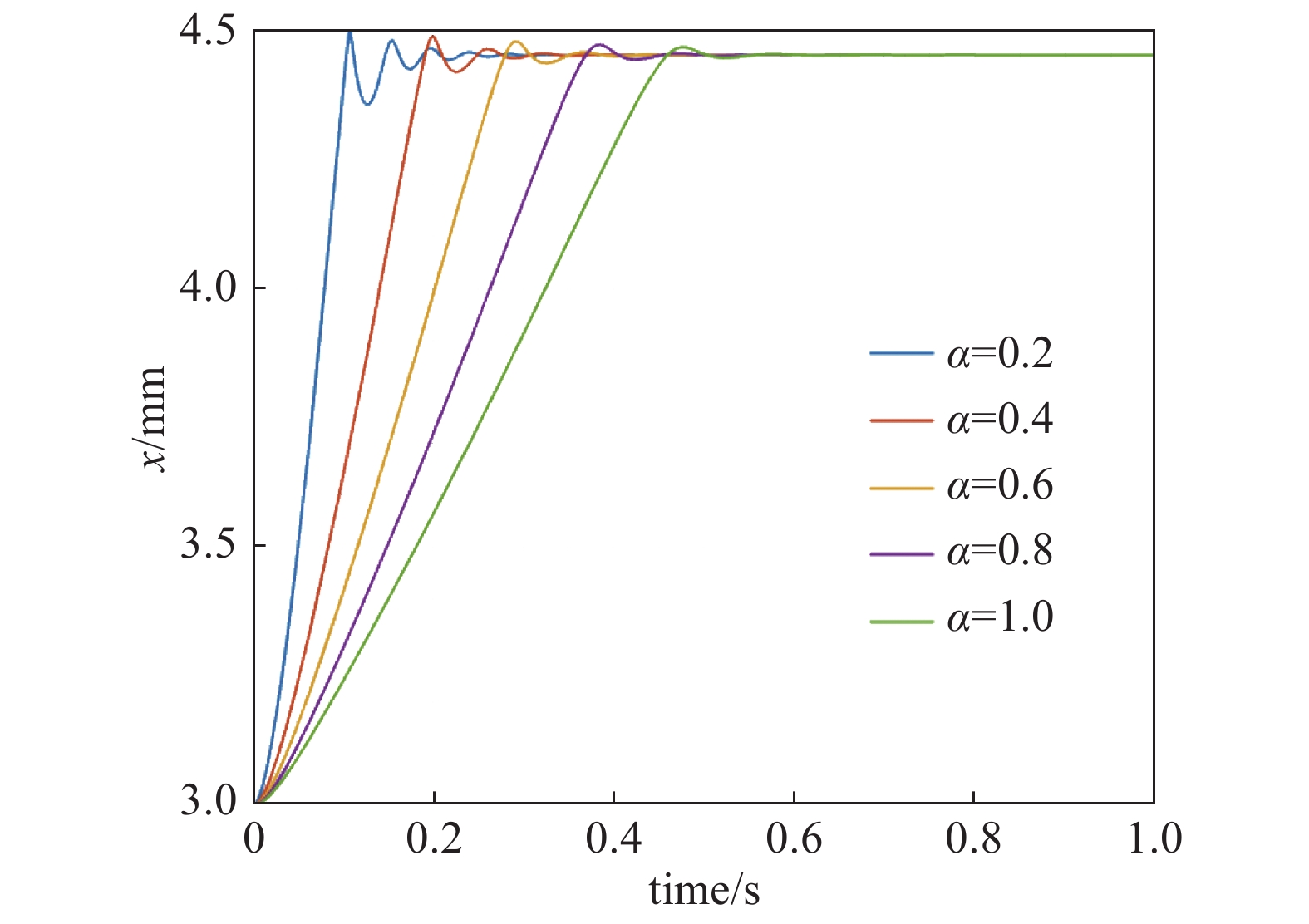
线圈参数的变化对应着影响因子α的变化,具体体现在线圈截面积的变化。代入绕制的不同半径的线圈对应的截面积,得到交流影响因子α从0.1−0.8变化。解微分方程组得到时域响应结果如图9、图10所示。
从计算结果可以看出,加入交流因素后,在适当的比例微分参数下,随着α值的增加,悬浮响应过程超调量变小,振荡次数减少,系统呈现出更强的阻尼性;从悬浮速度响应曲线来看,随着α值的增加,悬浮过程中的转子运动速度变慢,α=0.2时转子悬浮过程中最大运动速度达到18.73 mm/s,以较快的速度达到悬浮位置,且经历了多次振荡。α=1时转子悬浮过程中最大运动速度仅为3.57 mm/s,以较低速度达到悬浮位置,且悬浮过程经历较少振荡。
仿真结果显示,磁悬浮线圈加载交流电流后悬浮过程受到影响,随着交流影响因子的增大,转子悬浮的响应超调减小,稳定过程中轴向运动速度减小。对于位移检测来说,转子的速度变化平缓且速度波动范围小有利于悬浮位移的检测。更缓慢的位移变化降低了对电涡流传感器位移检测的要求,有利于线圈作为电涡流传感器的位移检测工作。
从仿真结果可以看出,随着交流影响因子α的增加,悬浮过程变得“缓慢”,α=0.2时与α=1时的稳定时间相差约0.2 s,在实际使用中对此性能损失可以忽略不计。在计量仪器的使用中,更关心工作状态的稳定性,因此选取交流影响因子时,选α=1的计算模型,使系统具有更强的阻尼性。在仿真中使用了比例−微分控制器,不可避免地产生了稳态误差,因此在实际电路设计时应考虑加入积分控制。
-
磁悬浮转子真空计的悬浮电路设计中,电路的重要部分就是轴向悬浮电磁铁与电涡流传感器的复用设计,轴向悬浮线圈上既加载使转子悬浮的直流信号,也加载了使线圈作为电涡流传感器的交流激励信号。针对这一特定应用,设计悬浮线圈上信号复用的电路如图11所示。
-
在式(22)的推导中使用了比例−微分控制器,在实际的此悬浮电路设计中,考虑后续改进,设计模拟比例−积分−微分控制电路。控制器框图如图12所示。
-
由式(22)可知,改变参数α即可测试交流作用的影响。线圈材料确定后电导率与磁导率即可固定,在实际实验中,通过改变线圈截面积达到改变α的目的。
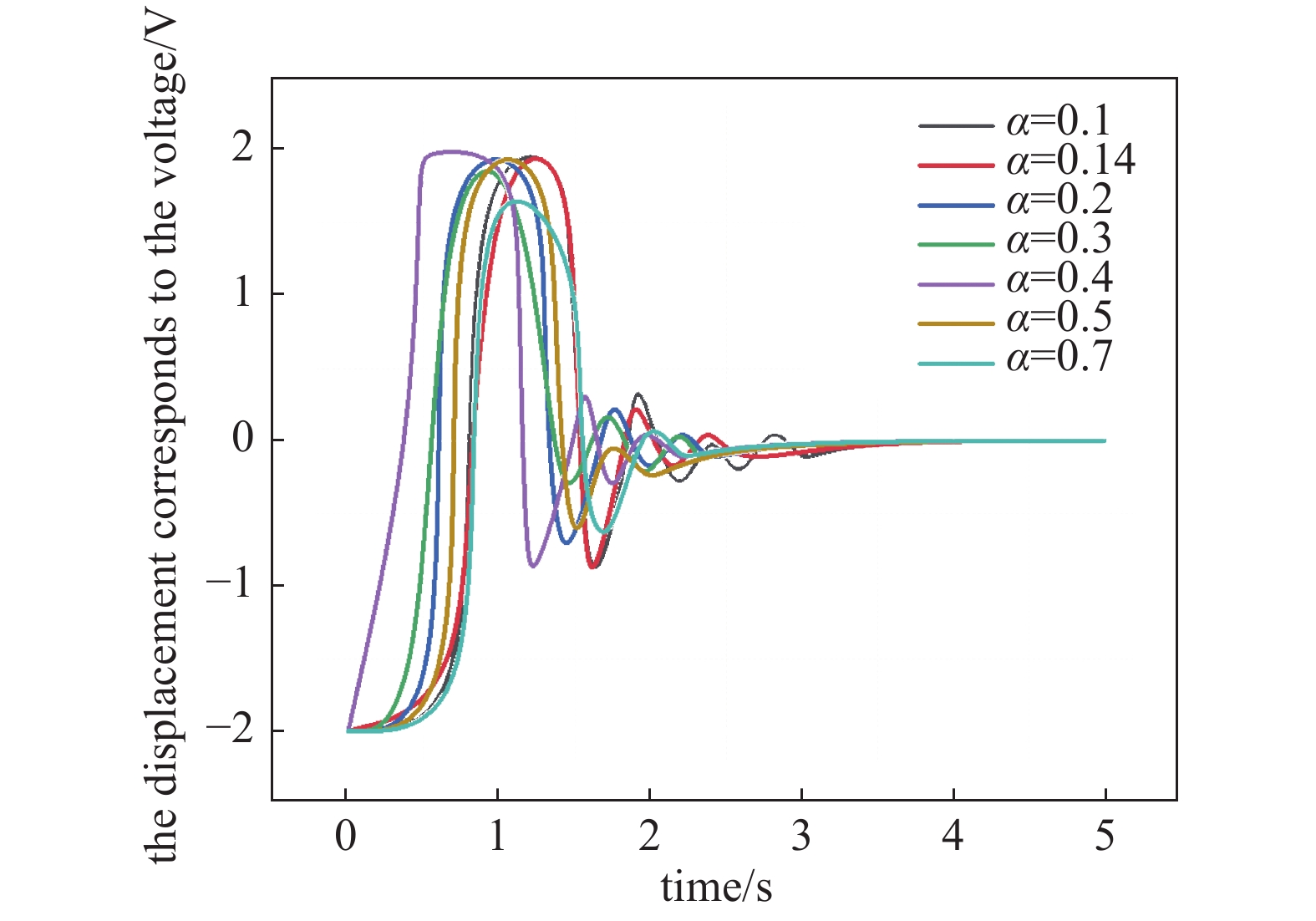
绕制截面半径为2.5 ,3 ,4 ,5 ,6 ,7 mm的线圈进行实验,分别对应α值约为0.1,0.14,0.2,0.4,0.5,0.7。PID参数不变,仅更换线圈,实际悬浮实验结果如图11所示。
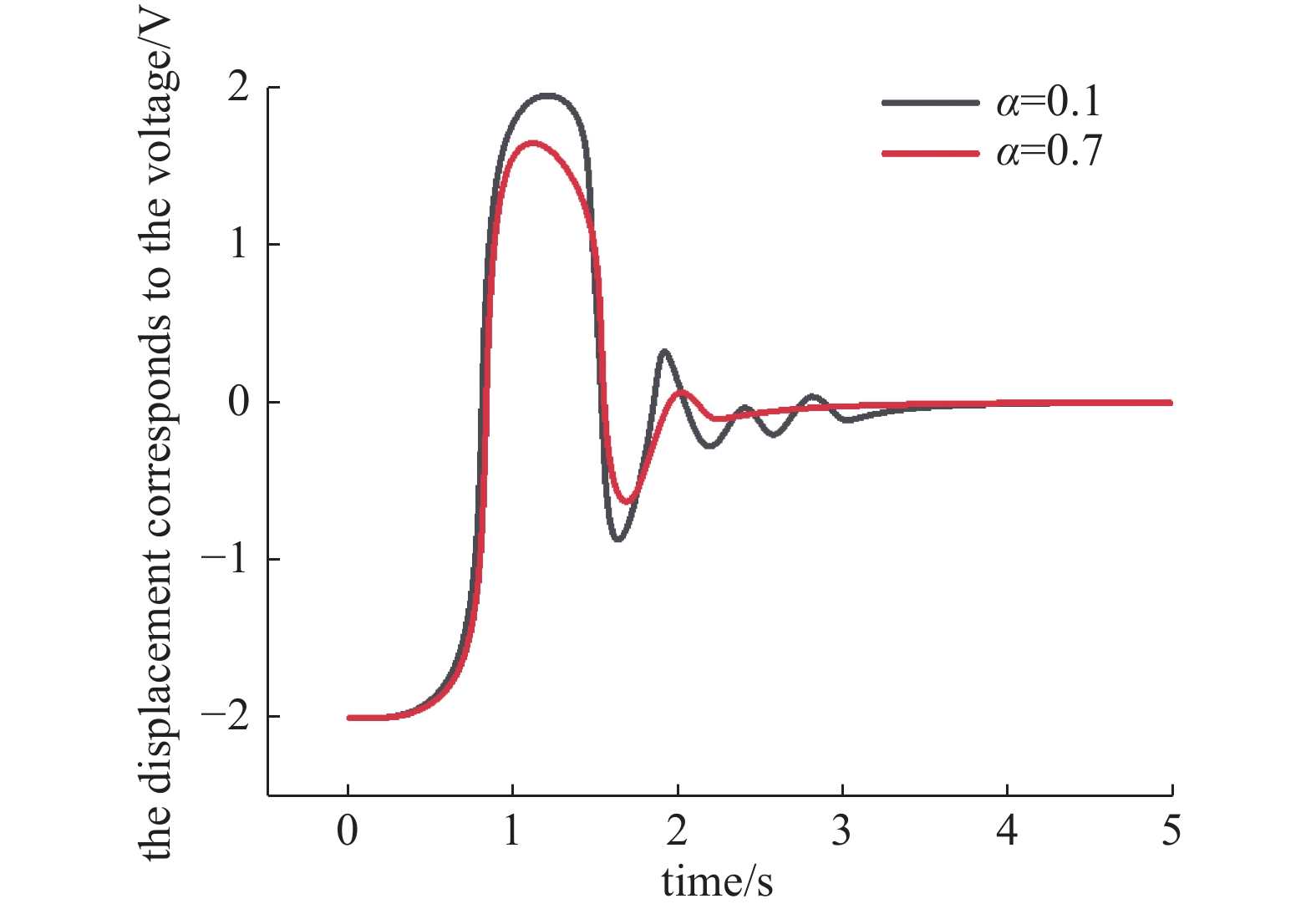
从图13可以看出,影响因子大小直接影响了磁悬浮稳定过程的超调量与振荡次数,为更清晰的展示其作用,取上图中α=0.1和α=0.7两条曲线进行对比,如图14所示。
取α=0.1与α=0.7两种状态下的情况进行对比,通过改变线圈参数,悬浮响应过程的超调量与振荡次数都发生了变化。使用交流影响因子较大的线圈时,系统显示出较强的阻尼性,超调量更小且经更少的振荡到达稳定,这也印证了前方的推导。即加入交流信号后,交流信号产生的磁通量变化在磁悬浮的控制过程中,影响了的悬浮过程。
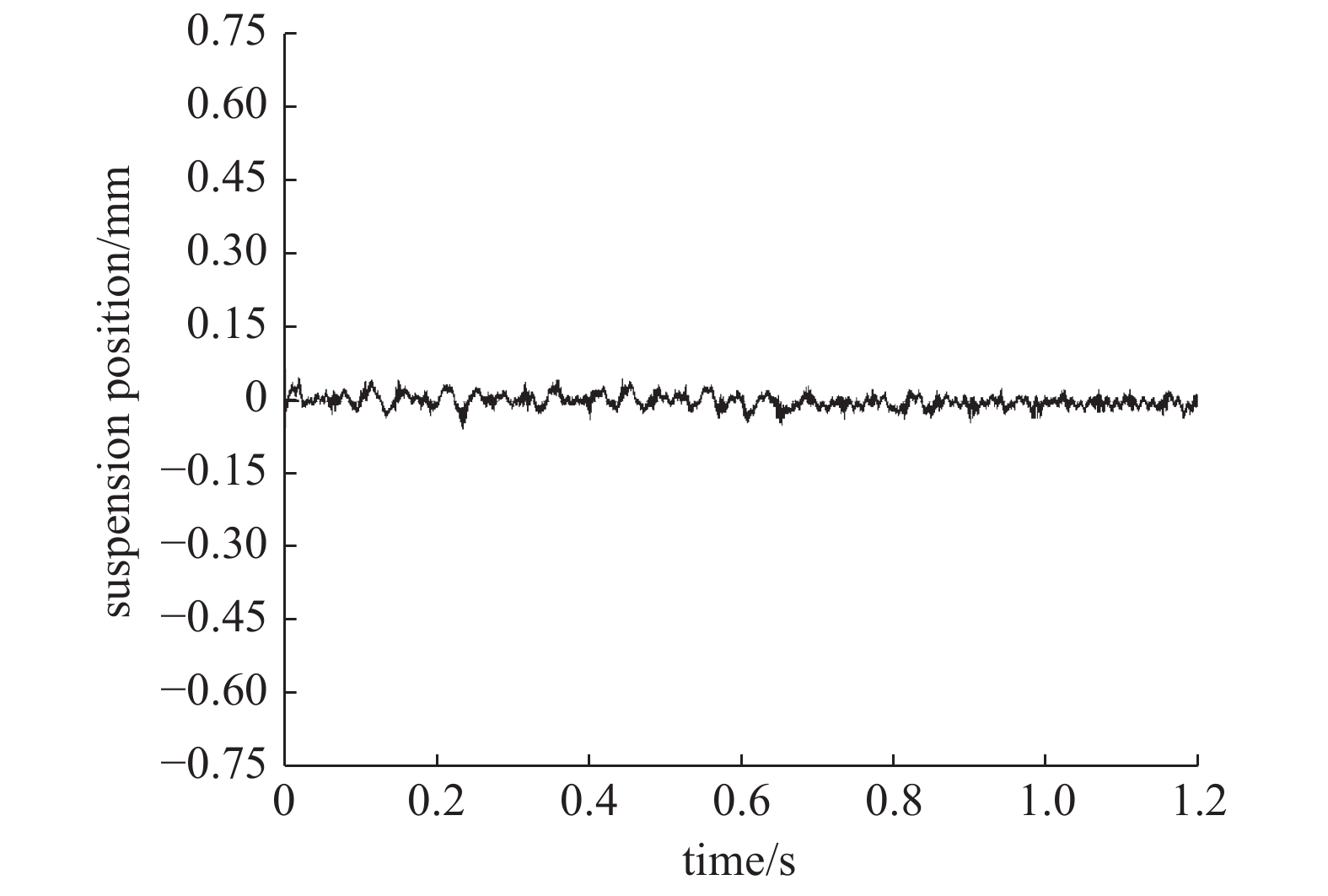
在实验中可以通过线圈参数的优化来控制交流信号的影响。根据实验结果,最终选取交流影响因子α=0.7的线圈作为磁悬浮转子真空计的轴向线圈。悬浮效果如图15所示,悬浮位移示波器输出如图16所示。
由图16可知悬浮位置在±0.05 mm内微弱震动,实验结果证明此悬浮效果已达到计量级别的稳定性,满足了真空计的计量要求[20]。
5.1. 电磁铁-电涡流传感器复用装置设计
5.2. 磁悬浮控制电路设计
5.3. 实验数据
-
在传统的传感器与执行器相互独立的磁悬浮动力学模型中,未涉及用于位移传感器的交流激励引入。 在磁悬浮转子真空计的应用中,由于真空计结构设计的特殊性,轴向线圈必须既作为轴向位移检测的电涡流传感器,又作为提供使转子悬浮的电磁力的电磁线圈。因此交流激励的加载是必要的,只能通过对悬浮系统的设计与优化来控制其影响。
通过对线圈半径参数进行优化与选取,实现了对交流作用所产生影响的控制。减小了响应过程的超调,减少了振荡频次。为磁悬浮转子真空计的优化设计提供了理论指导。

 首页
首页 登录
登录 注册
注册




 下载:
下载: