首页
登录
注册
-
在相变、凝结换热、降水等研究领域，电荷诱导气体分子成核受到越来越多关注[1]。1897年Wilson就已经发现带电粒子上水蒸气凝结现象[2]。从宏观方面对此过程的经典理论是将电场能作为吉布斯自由能的补充项，即经典Kelvin-Thomson方程（CKT）[3-5]。2002年Lapsin[6]等人将极性分子介电泳力对CKT方程进行修正。2005年Yu[7]详细推导了团簇增大过程中逐个分子增加带来的自由能变化，获得MKT方程。不过目前该方程仍有争议。2018年Tauber等[8]研究离子引起正丁醇蒸汽凝结过程，发现MKT理论明显低估了凝结所需的起始过饱和度。2019年Duft等[9]采用1~3 nm的Fe2O3诱导结冰实验，发现凝结起始过饱和度与颗粒半径的关系不符合Yu和Lapshin模型，仍然与CKT模型预测结果接近。总体而言，以经典成核模型为框架的理论方法，都以宏观角度为基础。然而直径为nm或Å量级的团簇与宏观液滴截然不同，宏观参数如表面张力等在微观上不存在，甚至微小团簇中很难区分表面和液滴内部。因此经典成核理论在处理极微小团簇时往往与实验难以相符。
另一类做法是从分子动力学出发，从分子层面模拟研究电荷增强凝结过程。Znamenskiy V等[10]模拟了荷电水分子纳米液滴的蒸发过程，结果显示离子会被十个左右的中性水分子包裹从液滴中蒸发出来。倪中华等[11]研究了介电泳驱动纳米胶体分离的分子动力学模型。王跃社等[12]模拟了几种荷电原子诱导水蒸气核化过程，指出当离子存在时成核过程的诱导阶段缩短，核化速率增大。Shi等[13]将量子力学计算与分子动力学计算进行对照，分析OH−(H2O)n (n = 1~8, 10, 15, 23)团簇结构和电荷分布等。Zhang等[14]采用从头算分子动力学计算了在超临界水中Na+-F−离子对周围分子的缔合作用。这一类计算中，需要首先确定离子的力场参数，才能得到合理的模拟结果。在成熟的力场参数中通常没有这些特定离子的力场参数。
在电荷增强凝结的研究中，产生电荷的主要方法是非平衡态等离子体放电。典型的非平衡态放电包括常压下的电晕放电、介质阻挡放电等。在这些等离子体中，通常电子温度可以高达上万K，但是中性分子和离子的温度仅有几百K。两者形成巨大温度差，处于典型的非平衡状态。在实验方面Reznikov等[15]采用丝状电极产生电晕放电诱导过热蒸汽凝结。2015年顾璠等[16]提出利用非平衡态等离子体诱导凝结，将部分汽化潜热转化为气体动能的设想。但是由于观测尺度极小，电荷增强水分子凝结过程通常难以直接进行实验观测，目前微观实验数据仍非常匮乏，同时带电液滴的行为和等离子体形成的机制也存在争议。
但是目前尚无从分子动力学角度研究水蒸气等离子体诱导凝结的研究。本文基于水蒸气非平衡态等离子体过程，采用Dmol3从头算方法计算荷电粒子的电荷分布；采用分子动力学方法，对非平衡态等离子体促进成核过程进行数值模拟研究。
-
目前在水蒸气中进行电荷诱导凝结的实验都采用非平衡态等离子体[5]，例如电晕放电。等离子体中存在大量的电子碰撞反应和化学反应，使理论模拟过程过于复杂。表1中汇总了产生荷电粒子的主要反应。
其中反应1为e和H2O碰撞电离过程，产生H2O+；反应2中H2O*为H2O的激发态，该反应的激发能量为8.445 eV；反应3为激发态电离过程；反应4和5都是分解吸附过程，形成OH−和O−。
文献[5]对Reznikov等典型的水蒸气放电器进行一维数值模拟研究。该反应器为90 mm长的线-筒式等离子体放电器，其中电晕线电极直径为75 μm，外壁筒电极半径8 mm。模拟结果指出水蒸气等离子体中最主要的荷电粒子为O−，OH−和H2O+。根据计算结果，当施加在线电极上的电压范围为+4000 V至+8000 V时，等离子体体中具有最高数密度的离子为H2O+，最大值从7.5×1015 m−3增加至8.5×1016 m−3，另外两种负离子数密度较小。当施加在线电极上的电压在−4000 V至−8000 V时，等离子体体中具有最高数密度的离子是OH−, 最大数密度从2.8×1016 m−3增加至1.33×1017 m−3，O−的数密度略小于，也可以达到1016 m−3，此时正离子数密度均较小。 此外其他过程还会产生H2+、H+、H−、O2+、O+等多种荷电粒子，但是根据计算它们的数密度远小于O−，OH−和H2O+三种离子。
后文将对这三种离子引起的凝结情况进行分子动力学模拟。其他离子在水蒸气等离子体中占比较少，因此不作为本文模拟研究的重点。
-
CKT模型中假设每一个凝结液滴中仅有一个电荷，液滴是球形，则水蒸气荷电凝结系统中气相和液相的吉布斯自由能为[8]：
式中，S为过饱和度；vl为水分子体积；Tg为气体温度；σW为水的表面张力系数；r为凝结液滴半径；Ri为荷电粒子半径；εl和εg分别为液态气态介电常数。(1)式对应极大值ΔG*处的解为临界半径r*。当液滴半径r>r*时ΔG将趋于下降，液滴半径r趋于增大，即发生凝结现象。该理论可以基本描述较大液滴的变化规律。但是团簇形成初期仅有几个分子组成，通常不可能是球形。所以CKT模型无法描述荷电粒子诱导成核和增长的早期过程。
-
本计算采用含长程库仑力的Lennard-Jones 12-6势函数来描述原子间的相互作用势。
式中，下标i和j分别代表不同的粒子，q为粒子所带电荷，r为粒子间距离，σ和ε为粒子间的LJ势能参数，ε0为真空介电常数。不同粒子间LJ势能参数采用Lorentz-Berthelot混合法计算：
本计算中水分子采用SPC/E模型。中性水分子中O原子带电荷−0.8472 e，H原子带电荷0.4236 e。O−、OH−和H2O+三种离子的电荷分布在下一节中进行计算。
本文采用LAMMPS软件进行分子动力学模拟。根据上一节计算，水蒸气等离子体放电中荷电粒子占比实际上非常小（~10−8）。因此当模拟体系较小时体系中离子数量也是非常少的。本文对含有1000个水分子系统进行模拟，在这样体系中最多含有1个离子。即本文关注围绕在离子周围非常小的空间中系统的变化过程。在模拟的初始阶段，使用NPT系综，使水蒸气分子在373.15 K和1 atm下，通过200 ps松弛达到平衡。采用速度标定法进行降温将系统的温度标定为362 K，采用Nose-Hoover热浴使温度保持稳定。此时水蒸气过饱和度为S=1.5。本文采用Stillinger方法定义团簇，采用Merikanto等提出的O-O中等间距rneigh=3.8 Å为团簇判据。
-
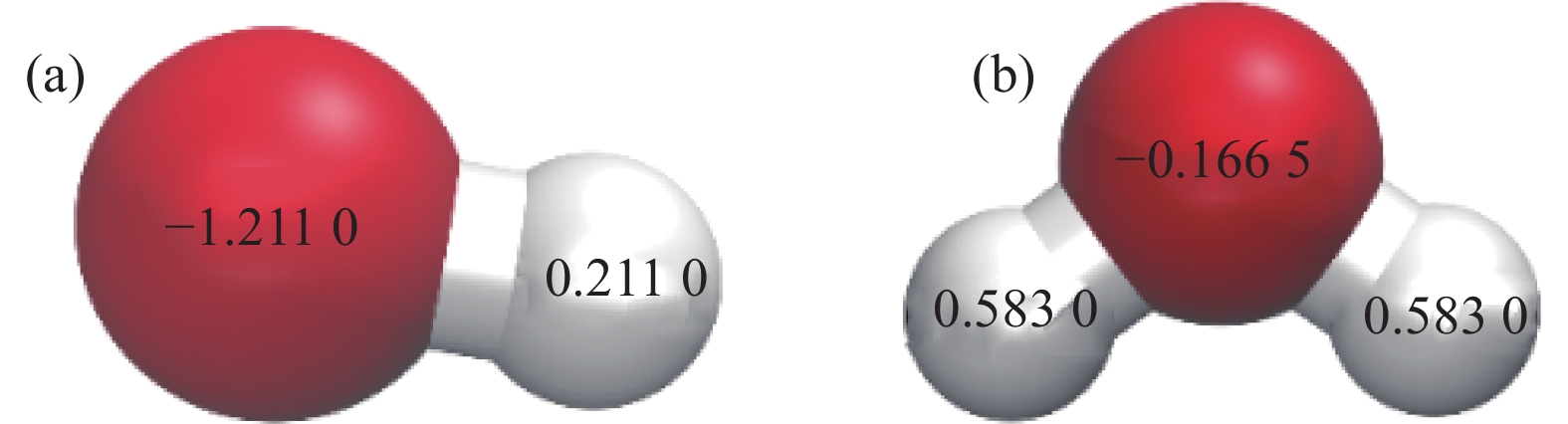
在分子动力学计算中考虑电荷的长程力作用，需要给每一个原子上赋一个电荷数。本文采用Materials Studio中Dmol3模块局域密度近似（LDA）泛函 PWC方法，采用精度较高的广义梯度近似方法(GGA)，PW91泛函，采用DND基组对OH−和H2O+两种离子的电荷分布进行计算。离子中的电荷分布采用Mulliken分布。这种方法在计算中性H2O电荷分布为O电荷−0.810 e，H原子带电荷0.405 e，与SPC力场最为接近。考虑到水蒸气放电产生的离子仍以H、O元素组成，因此各原子的势能参数同样采用SPC/E参数。OH−和H2O+两种离子的电荷分布如图1所示。
-
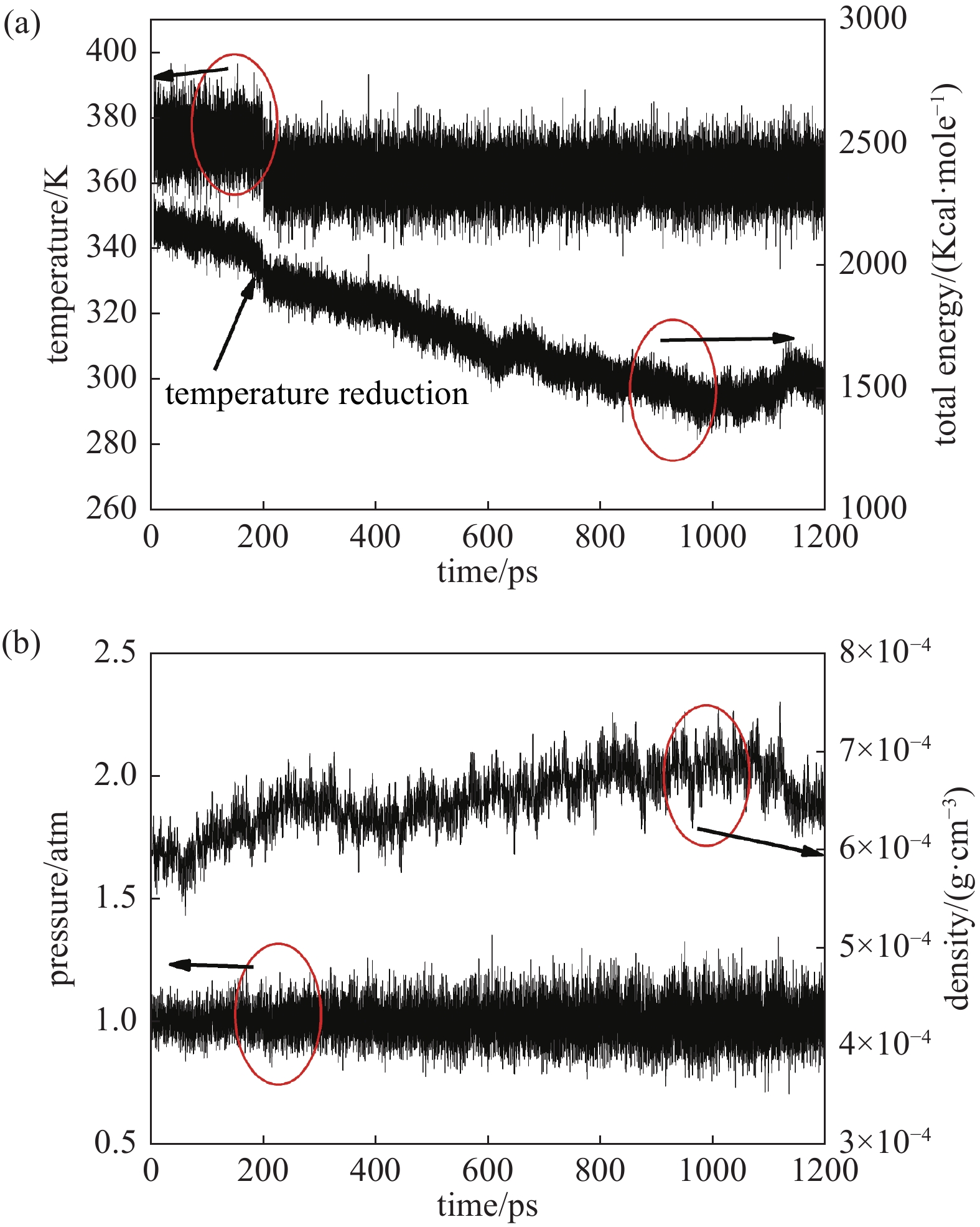
图2给出了含O−体系主要参数随时间的变化规律。因为本文算例体系较小，不同离子对体系影响较小，三种算例主要体系参数变化规律非常接近。从图2中可见，在200 ps前温度压力基本平稳，总能基本达到稳定。200 ps后，压力保持不变，过饱和度达到1.5，体系总能开始下降，至1000 ps处达到最低值，系统再一次达到稳定。对比200 ps和1200 ps两处分子位置，可以得到离子对成核的影响规律。
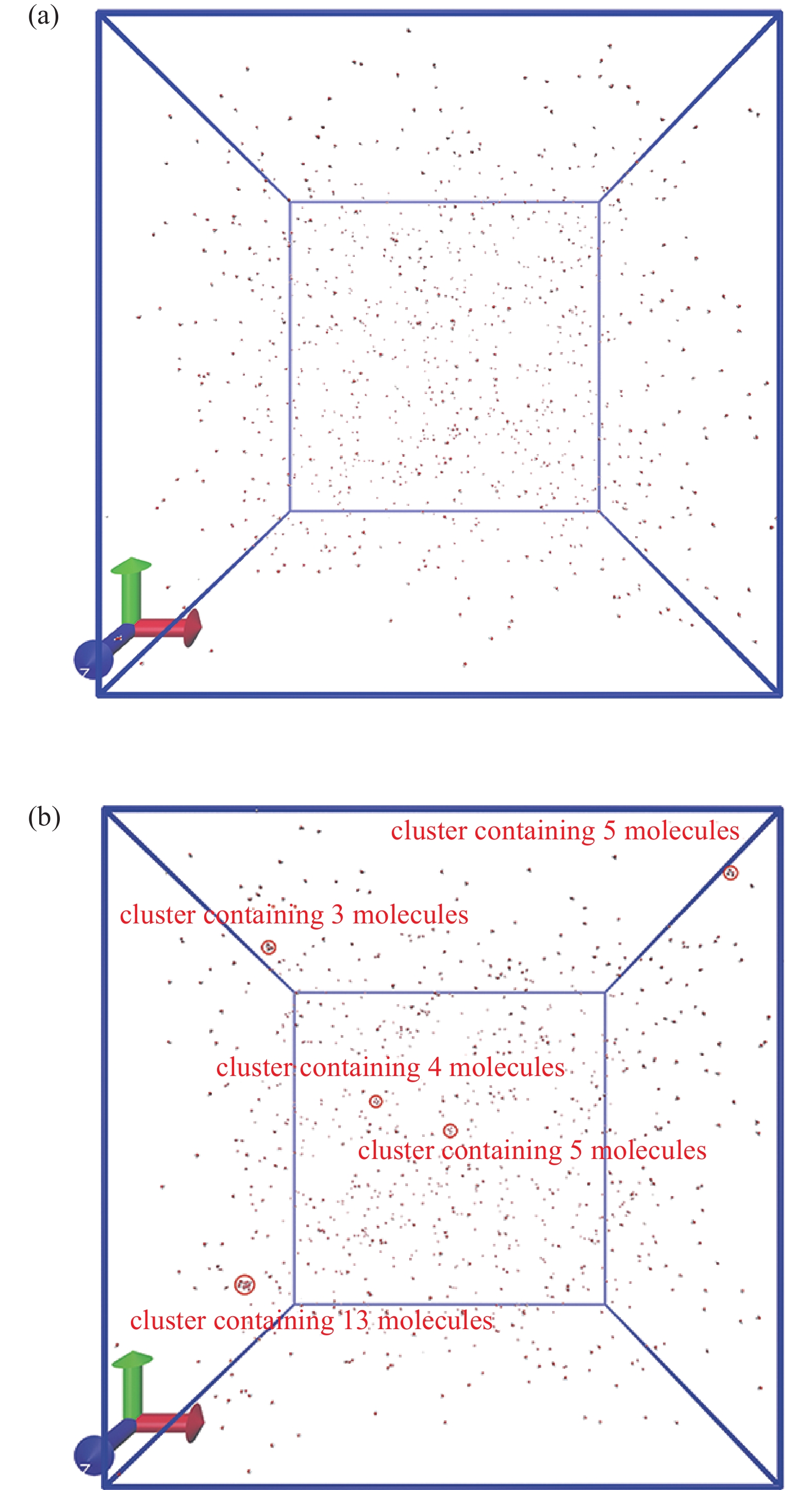
图3显示了200 ps和1200 ps时含O−体系分子位置的变化情况。在图3(a)中，分子基本上为均匀分布，仅有极少数双分子偶尔靠近形成团簇，没有更大尺寸的团簇形成。在图3(b)中，形成了1个以O−为核心由13个水分子组成的大团簇，另外形成了1个5分子团簇，4个4分子团簇和7个3分子团簇。以离子为核心诱导成核效果显著。
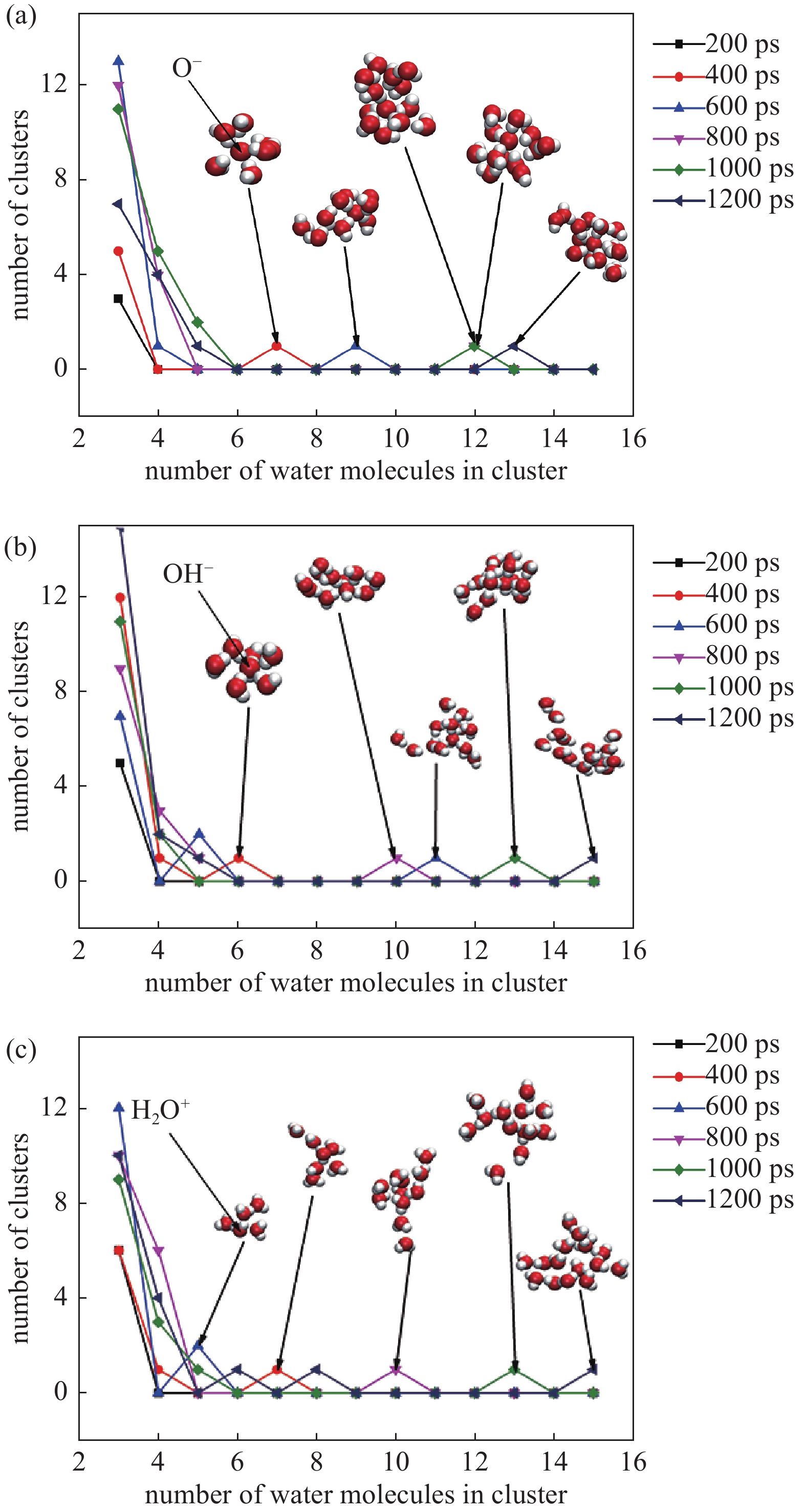
图4给出不同体系下各种尺寸分子团簇变化的统计规律。考虑到小分子团簇随机生成和离解，图中小于2分子团簇不予统计。从图4(a)-(c)中可见，由O−，OH−和H2O+等等离子体荷电粒子引起的团簇在降温后显著增大，从6~7分子的小团簇开始，逐步增加到10~15分子的较大团簇。而均相凝结团簇始终较小，而且增长较慢，如图4(c)中1200 ps曲线所示均相团簇仅含有8个水分子。这是因为本算例中，体系过饱和度非常小仅为S=1.5，在该过饱和度下均相凝结过程很难发生。通常在均相凝结中，要达到显著凝结S应该在5~20之间，即参数应该达到Wilson点凝结过程才能快速发生。通过对比，显然等离子体过程可以明显实现诱导凝结。对比图4中三组图片，可见当凝结核心为单原子离子O−时，由于离子结构简单，形成的团簇也更接近球形。OH−和H2O+由于在微观上并非球形，其诱导形成的团簇形状更加复杂。其中H2O+形成的团簇中很常见长臂状结构，显然不再是球形结构。因此经典CKT模型不适合对微观团簇进行描述。
-
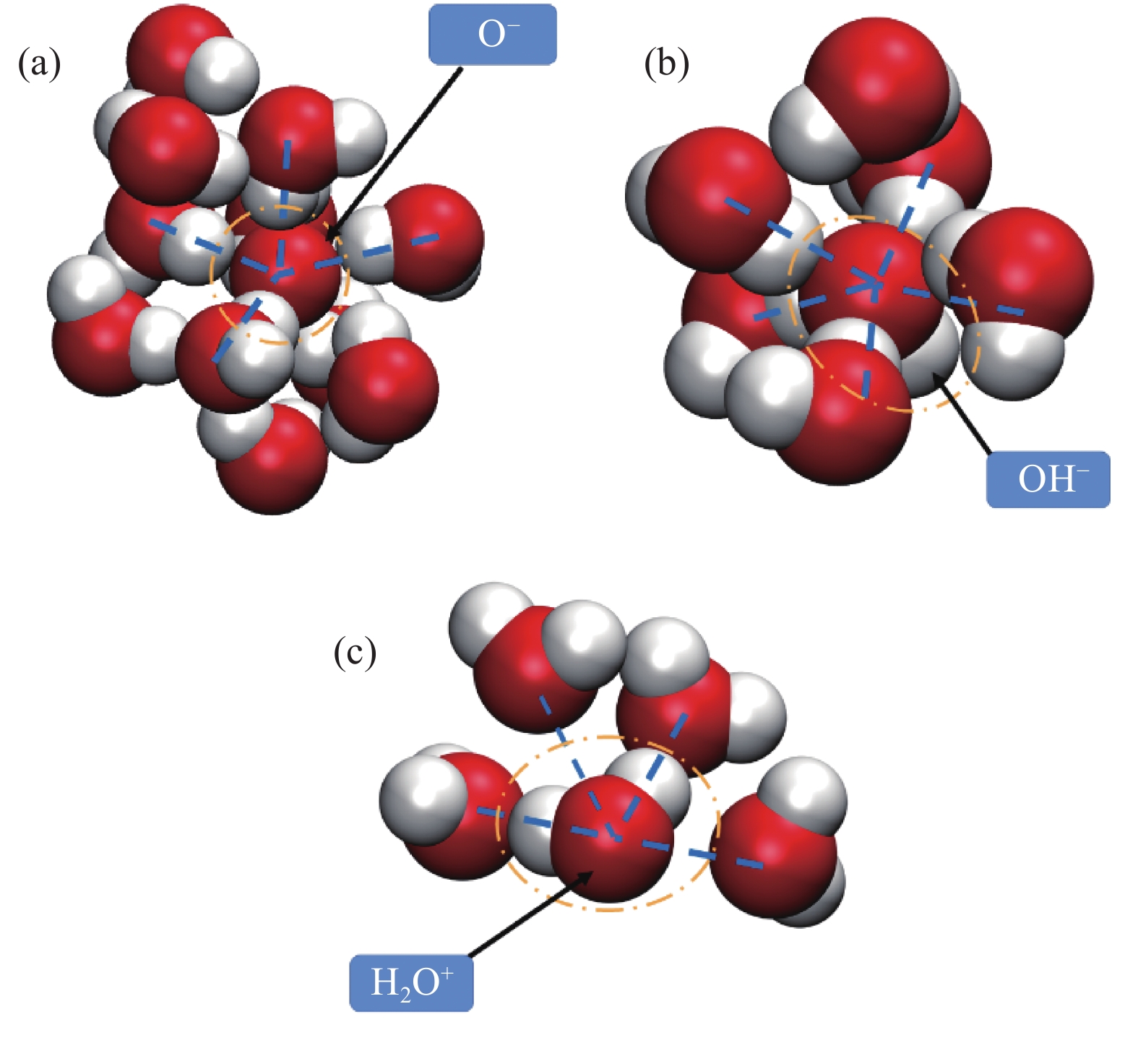
图5为不同荷电粒子诱导形成团簇核心处的分子结构图。从图5(a)和(b)中可见，以O−或OH−为核心时，周边水分子均将1个H原子指向OH−的O原子。在图5(c)中水分子带正电荷，周边水分子均将各自O原子指向H2O+。电荷诱导凝结过程中，荷电粒子电场影响极大。核心处分子受到离子电场影响发生偏转，并聚集到离子周围，形成了最初的凝结核心。
-
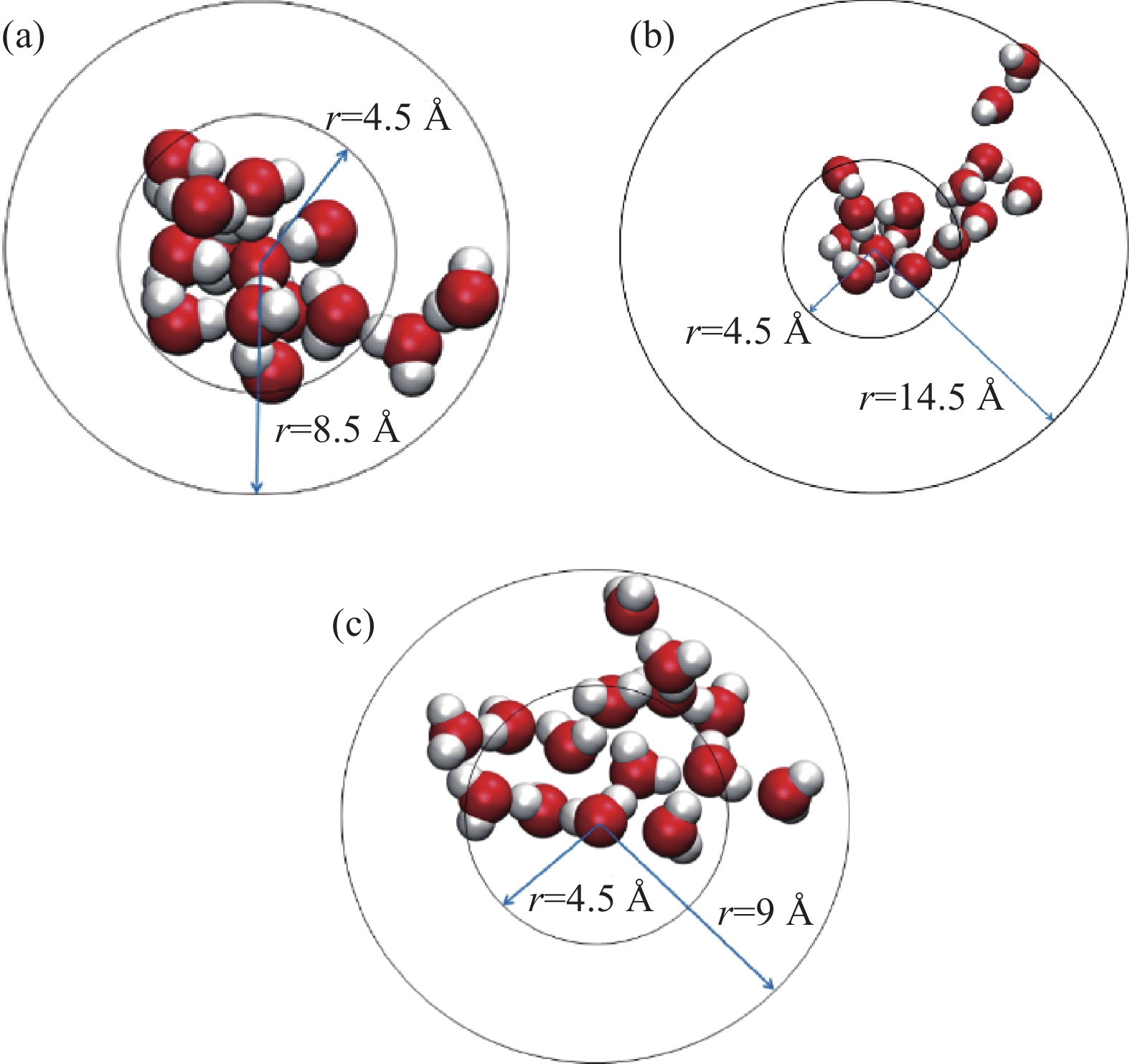
图6为1200 ps时不同荷电粒子诱导形成团簇的尺寸。图6(a)中以O−为核心的13分子团簇，该团簇最远端距离O−核心约为8.5 Å，核心处团簇近似为球形，该球形半径约为4.5 Å。图6(b)为以OH−为核心的14分子团簇，核心处团簇近似为球形，该球形半径约为4.5 Å，该团簇最远端距离OH−核心约为14.5 Å，该团簇整体形态远远偏离球形。图6(c)为以H2O+为核心的14分子团簇，该团簇最远端距离OH−核心约为9 Å，H2O+在该团簇的外侧，团簇并非以H2O+为核心。从图中可见，微观分子团簇几乎都不是球形。该几种团簇也无法区分团簇表面和内部，与CKT模型并不一致。
图7为三类荷电粒子诱导形成团簇的变化规律。从200 ps开始荷电离子诱导形成了小型团簇。从200 ps~800 ps间，这些团簇快速增大。从800 ps~1200 ps该团簇增长明显放慢。对三组数据进行拟合，拟合曲线指出这几组团簇的最大分子数应为14~16个水分子。
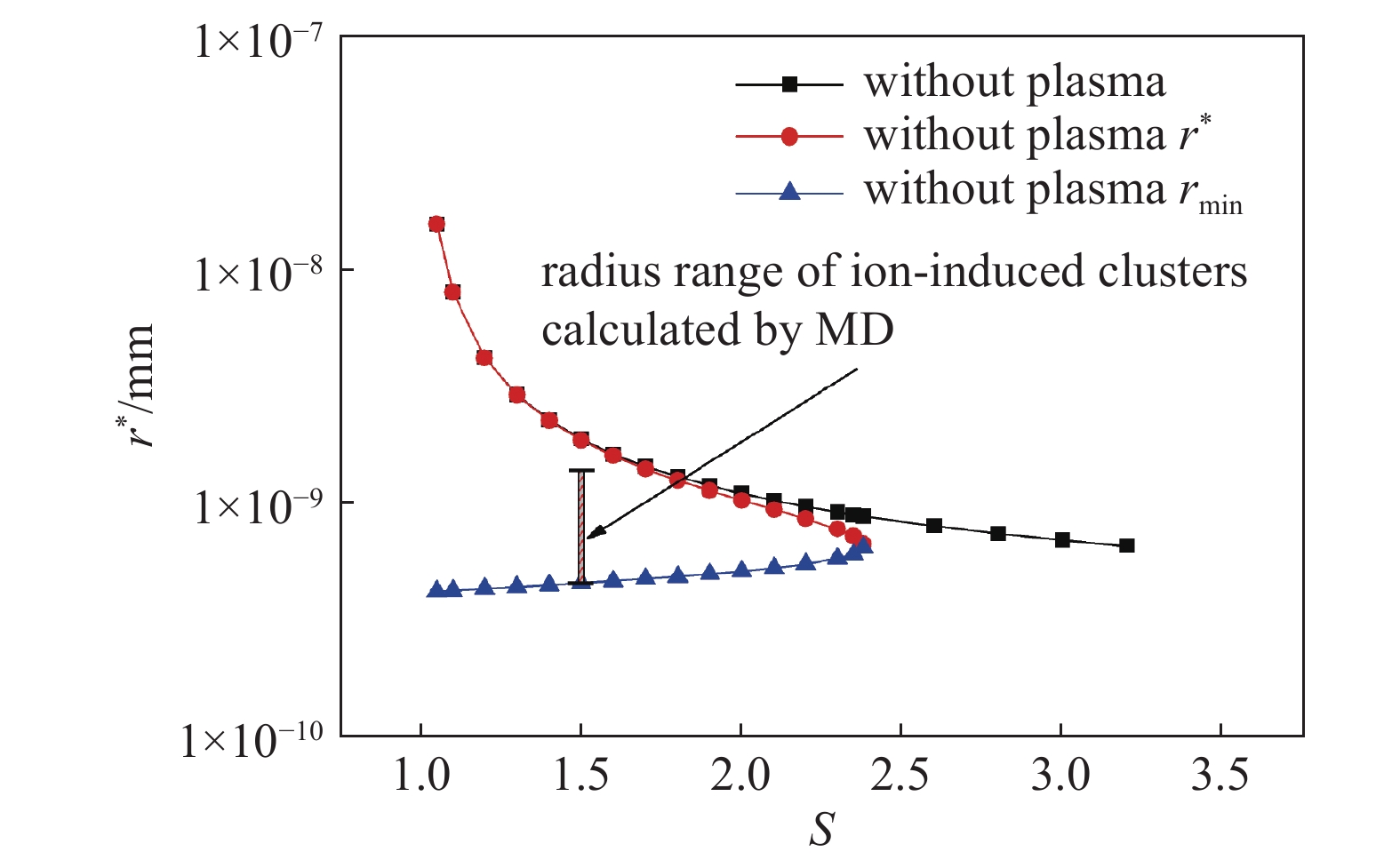
图8中画出了不同理论分析中团簇临界半径的变化规律。当水蒸气中无等离子体影响时，对Gibbs自由能求极值可以得到团簇临界半径，显然当过饱和度S的值较低时，尽管已经达到相变温度，也需要非常大的临界半径才能发生凝结过程。当水蒸气中存在等离子体时，对式(1)求极值会获得两个根，其中较大根为临界半径r*，而较小的根rmin为团簇达到自由能极小值时的半径。CKT模型指出电荷诱导的团簇较小时会快速增大，使团簇自由能到达极小值。仅有团簇尺寸大于r*的才可能最终增大出现凝结过程。如图8所示，当过饱和度S的数值较小时，r*和rmin差距明显，即使电荷诱导形成了少量团簇，也仅有其中尺寸较大的才可能形成明显的凝结过程。当S>2.38之后，团簇Gibbs自由能只有单调的下降趋势，不存在极值。此时所有离子诱导形成的团簇都将持续增长，进而全部形成液滴。通过分子动力学计算出的团簇范围约为4.5 Å~14.5 Å，图8中也画出了该范围区间，略大于CKT模型预测rmin的情况。但是考虑到微观团簇通常不是紧密排列，两者结果比较接近。
-
电荷增强水分子凝结的现象可以应用于多种领域。目前荷电粒子的形成和增强凝结的机理目前尚存在争议。本文采用分子动力学方法初步讨论了水蒸气非平衡态等离子体形成机理和增强凝结机理。根据水蒸气放电机理获得水蒸气非平衡态等离子体中的主要荷电粒子种类。采用Dmol3从头算方法计算荷电粒子的电荷分布。凝结过程采用分子动力学方法进行数值模拟，其中水分子采用SPC/E模型，荷电粒子主要包括O−、OH−和H2O+。分别计算在凝结过程中，这些荷电粒子诱导成核的增长过程。在该过程中，由于电荷存在，极性的水分子会发生偏转和聚集，形成了最初的凝结核心。该凝结核心会首先达到14~16个分子团簇的自由能极小值。将该微观过程与宏观理论相对照，本文分子动力学模拟过程和宏观CKT模型基本保持一致。本文的分子动力学研究描述了诱导凝结的微观过程，补充了CKT模型中对微观描述的不足。
水蒸气等离子体诱导凝结分子动力学研究
Molecular Dynamics Study on Condensation Induced by Water Vapor Plasma
-
摘要: 本文采用分子动力学方法初步讨论了水蒸气非平衡态等离子体形成机理和增强凝结机理。非平衡态等离子体放电部分建立水蒸气放电模型，基于该过程获得等离子体中的主要荷电粒子类型为O−，OH−和H2O+。采用密度泛函理论OH−和H2O+的电荷分布进行理论计算。采用SPC/ E力场对凝结过程进行分子动力学模拟。分别计算在凝结过程中，这些荷电粒子诱导成核的增长过程。将该微观过程与宏观理论相对照，初步获得等离子体诱导蒸汽凝结的微观机理。Abstract: The formation mechanism and enhanced condensation mechanism of water vapor nonequilibrium plasma are discussed by the molecular dynamics method. In the nonequilibrium plasma discharge part, the water vapor discharge model is established. Based on this process, the main types of charged particles in the plasma are O−, OH− and H2O+. The density functional theory is used to calculate the charge distribution of OH− and H2O+. The SPC/E force field was used to simulate the condensation process. The nucleation process induced by these charged particles in the condensation process is calculated, respectively. Compared with the macroscopic theory, the microscopic mechanism of plasma-induced vapor condensation is obtained.
-
Key words:
- Plasma /
- Vapor condensation /
- Nucleation /
- Molecular dynamics .
-
-
图 1 两种离子的电荷分布。 (a)OH−电荷分布 ， (b) H2O+电荷分布
Figure 1. Charge distribution of two ions. (a) Charge distribution of OH−， (b)Charge distribution of H2O+
图 2 含O−体系参数随时间变化。 (a) 温度和总能随时间变化，(b) 压力和密度随时间变化
Figure 2. Parameters of O− containing system change with time. (a) Temperature and total energy change with time, (b) Pressure and density change with time
图 3 含O−体系不同时刻分子位置。 (a) 200 ps时, (b) 1200 ps时
Figure 3. Molecular position of O− containing system at different times. (a) At 200 ps, (b) at 1200 ps
图 4 荷电粒子诱导团簇变化规律。 (a) 含O−体系，(b) 含OH−体系，(c) 含H2O+体系
Figure 4. Changes of clusters induced by charged particles. (a) System containing O−, (b) system containing OH−, (c) system containing H2O+
图 5 荷电粒子诱导核心分子团簇结构。 (a) 含O−体系，(b) 含OH−体系，(c) 含H2O+体系
Figure 5. Core molecular cluster structure induced by charged particles. (a) System containing O− , (b) system containing OH− , (c) system containing H2O+
图 6 电荷诱导团簇半径。 (a) 含O−体系，(b) 含OH-体系，(c) 含H2O+体系
Figure 6. Radius of charge induced clusters. (a) System containing O−, (b) system containing OH-, (c) system containing H2O+
图 7 电荷诱导团簇分子数变化规律
Figure 7. The change rule of charge induced cluster molecular number
表 1 H2O等离子体中的产生荷电粒子的主要反应机理
Table 1. Main reaction mechanism of producing charged particles in H2O plasma
No. Reaction Type 1 e+H2O=>2e+H2O+ 电离 2 e+H2O=>2e+H2O* 激发 3 e+ H2O*=>2e+H2O+ 激发态电离 4 e+H2O=>H+ OH− 分解吸附 5 e+H2O=>H2+ O− 分解吸附 
下载: 导出CSV
-
[1] Reznikov M,Salazar M,Page M,et al. Further progress in the electrostatic nucleation of water vapor[J]. IEEE Transactions on Industry Applications,2018,54(1):591−598 doi: 10.1109/TIA.2017.2755579 [2] Wilson C T R. On the Comparative efficiency as condensation nuclei of positively and negatively charged ions[J]. Philosophical Transactions of the Royal Society B Biological Sciences,1900,193:289−308 [3] Reznikov M. Electrically enhanced condensation I: effects of corona discharge[J]. Industry Applications IEEE Transactions on,2015,51(2):1137−1145 doi: 10.1109/TIA.2014.2354734 [4] 崔可. 电荷作用对湿蒸汽流中非均质凝结影响研究[D]. 哈尔滨: 哈尔滨工业大学, 2016 Cui K. The influence of charge-effect on the heterogeneous condensation in wet steam flow[D]. Harbin: Harbin Institute of Technology, 2016 [5] Li S,Wang X,Liu Y,et al. Numerical analysis of the influence of nonequilibrium plasma on the nucleation rate of supersaturated steam[J]. AIP Advances,2020,10(2):25322 doi: 10.1063/1.5143917 [6] Lapshin V B,Yablokov M Y,Palei A A. Vapor pressure over a charged drop[J]. Russian Journal of Physical Chemistry,2002,76(10):1727−1729 [7] Yu F. Modified Kelvin–thomson equation considering ion-dipole interaction: comparison with observed ion-clustering enthalpies and entropies[J]. The Journal of Chemical Physics,2005,122(8):84503 doi: 10.1063/1.1845395 [8] Tauber C,Chen X,Wagner P E,et al. Heterogeneous nucleation onto monoatomic ions: support for the kelvin-thomson theory[J]. ChemPhysChem,2018,19(22):3144−3149 doi: 10.1002/cphc.201800698 [9] Duft D,Nachbar M,Leisner T. Unravelling the microphysics of polar mesospheric cloud formation[J]. Atmospheric Chemistry and Physics,2019,19(5):2871−2879 doi: 10.5194/acp-19-2871-2019 [10] Znamenskiy V,Ioan M A,Vertes A. Solvated ion evaporation from charged water nanodroplets[J]. Journal of Physical Chemistry A,2003,107(38):7406−7412 doi: 10.1021/jp034561z [11] Ni Z H,Zhang X J,Yi H. Molecular dynamics simulation of nanocolloid separation driven by dielectric electrophoresis[J]. Scientia Sinica(Technologica),2009,39(6):1152−1158 (倪中华,张鑫杰,易红. 介电泳驱动纳米胶体分离的分子动力学模拟[J]. 中国科学E:技术科学,2009,39(6):1152−1158(in chinese) Ni Z H, Zhang X J, Yi H. Molecular dynamics simulation of nanocolloid separation driven by dielectric electrophoresis[J], Scientia Sinica(Technologica) , 2009, 39(6): 1152-1158 [12] Zhang C,Wang Y S,Li C P. Molecular dynamics simulation of water vapor nucleation induced by ions[J]. Journal of University of Chinese Academy of Sciences,2016(02):228−233 (张超,王跃社,李晨沛. 离子诱导水蒸气核化过程的分子动力学模拟[J]. 中国科学院大学学报,2016(02):228−233(in chinese) Zhang C, Wang Y S, Li C P．Molecular dynamics simulation of water vapor nucleation induced by ions［J］．Journal of University of Chinese Academy of Sciences, 2016, 33(2):228-233 [13] Shi H,Gong L,Liu C,et al. ABEEM/MM OH- models for OH-(H2O)n clusters and aqueous OH-: structures, charge distributions, and binding energies[J]. The Journal of Physical Chemistry A,2020,124(28):5963−5978 doi: 10.1021/acs.jpca.0c03941 [14] Zhang W,Yan T. Molecular dynamics simulation on Na+−F− ion-pair association from ambient to supercritical water[J]. Fluid Phase Equilibria,2020:112615 [15] Salazarm M,Minakata K,Reznikov M. Electrically enhanced condensation II: effects of the electrospray[J]. IEEE Transactions on Industry Applications,2015,51(2):1146−1152 doi: 10.1109/TIA.2014.2344508 [16] 李森. 一种新型非平衡态等离子体热电转换系统及关键问题研究[D]. 南京: 东南大学, 2015 Li S. Study on a new type of non-equilibrium plasma thermoelectric conversion system and the key issues[D]. Nanjing: Southeast University, 2015 -
计量
- 文章访问数: 199
- HTML全文浏览数: 199
- PDF下载数: 1
- 施引文献: 0