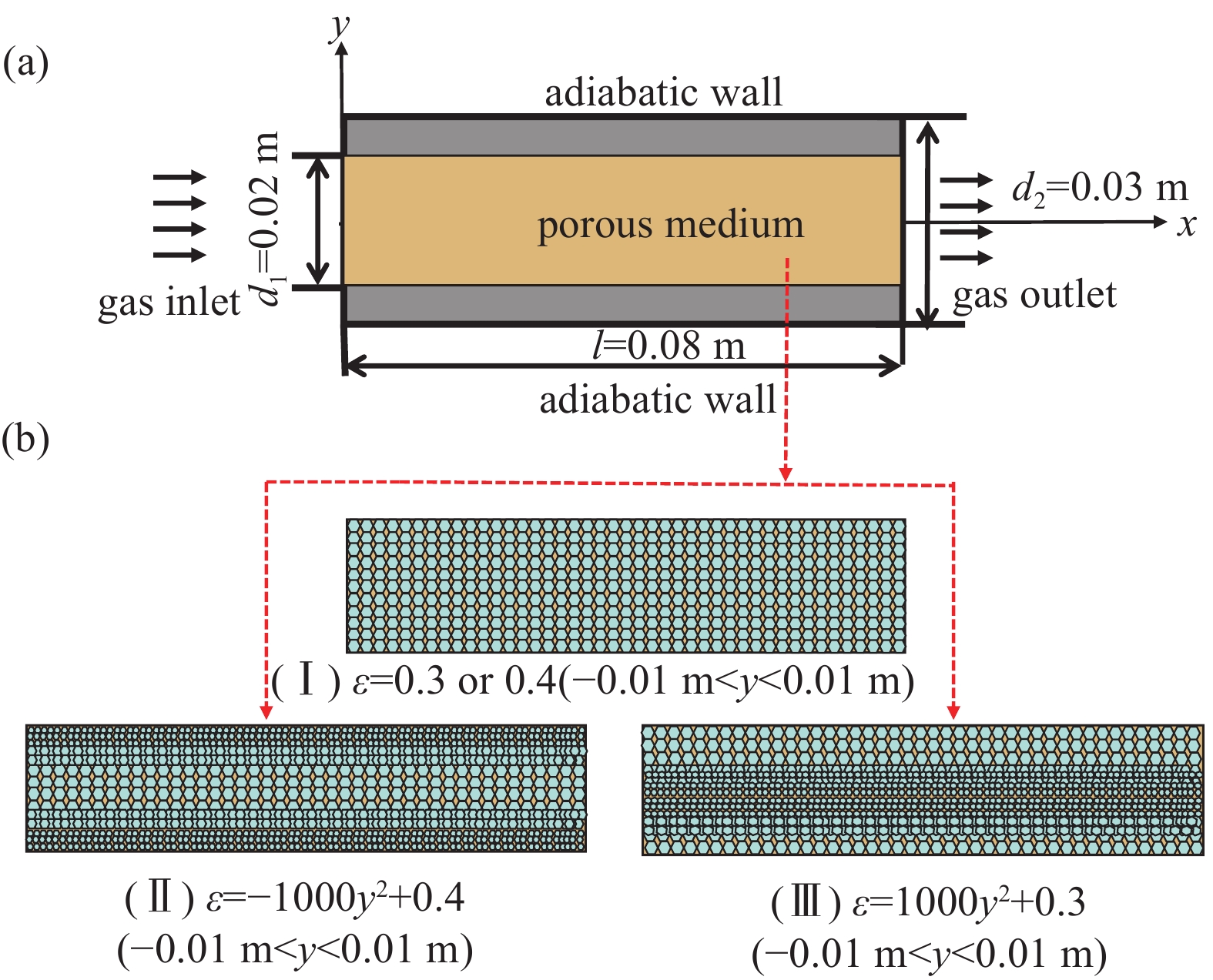
通道型正压标准漏孔的物理模型如图1所示。 如图1(a)，不同类型的气体包括：Air、He、D₂、H₂，从直径d₁=0.02 m正压标准漏孔的进口端进入由微米级多孔泡沫金属填充的正压标准漏孔内部，多孔泡沫金属的孔径$ {d}_{\mathrm{p}} $分别为6 μm，8 μm，10 μm，其中通道型正压标准漏孔的长度l分别设定为0.08 m，0.12 m，0.16 m，最后气体从正压标准漏孔出口端排出，通过监测出口的质量流量从而计算出漏率的大小。多孔泡沫金属孔隙率的变化如图1(b)所示，多孔泡沫金属分别具有恒定的孔隙率ε=0.3或0.4，先增后减以及先减后增变化的孔隙率。不同类型的气体的物性参数如下表1所示。

本文主要研究Air、He、D₂、H₂通过多孔介质填充的正压标准漏孔内部机理进行探讨，由于不同压力下通过漏孔所获得的流态不同，因此，需要通过克努森数^[9]来判断气体的流态。

$ {K}_{\mathrm{n}} $表示分子自由程与几何特征尺度之比。其中式(1)中，$ \lambda $为气体分子平均自由程，$ L $为几何特征尺度，本文中几何特征尺度为正压标准漏孔的直径d₁；式(2)中，$ {K}_{\mathrm{b}} $为Boltzmann常数，T为气体热力学温度298 K，d为气体分子直径，p为进出口的压力差。

当$ {K}_{\mathrm{n}} $ < 0.001时，流体的流动可以看作连续介质流动，具有无滑移边界条件，即为粘滞流；当0.001 <$ {K}_{\mathrm{n}} $ < 0.1时，经过无滑移边界条件处理，可以看作连续介质流动；当0.1 <$ {K}_{\mathrm{n}} $ < 10时，为过渡流；当$ {K}_{\mathrm{n}} $ > 10时，为分子流。

针对100 Pa−40000 Pa压力下气体通过正压标准漏孔流态进行判断如下：经过计算可得到， 当气体为空气且进口压力p > 300 Pa时， $ {K}_{\mathrm{n}} $ < 0.001，为粘滞流；当气体为氢气且进口压力p > 600 Pa时， $ {K}_{\mathrm{n}} $ < 0.001，为粘滞流；当气体为氦气且进口压力p > 800 Pa时， $ {K}_{\mathrm{n}} $ < 0.001，为粘滞流；当气体为氘气且进口压力p > 1000 Pa时， $ {K}_{\mathrm{n}} $ < 0.001，为粘滞流。本文主要假设流体为粘滞流条件下展开研究。因此，选取进口气体压力范围1000 Pa-40000 Pa进行分析。

根据目前所研究的通道型正压标准漏孔漏率的问题，作以下假设：

(1) 在通道型正压标准漏孔内的流动为二维稳态、不可压缩流体；

(2) 多孔泡沫金属是均匀的、各向同性、流体与固体间为无热量的传递；

(3) 流体的性质恒定，忽略重力的影响；

(4) 泡沫金属内部流体流动为粘滞流状态，惯性阻力被忽略。

基于以上假设，流体在通道型正压标准漏孔泡沫金属区域的控制方程如下^[10]：

在式(3)-(5)中，${u}_{{\rm{f}}}$和${v}_{{\rm{f}}}$分别代表$ x $和$ y $方向上的速度，单位：m/s，${\rm{f}}$表示流体。ε表示孔隙率，$ \rho $表示流体的密度，单位：kg/m³；$ p $表示压力，单位：N/m²；$ \mu $表示动力粘度，单位：kg/(m·s)；其中$ K $为泡沫金属内部的渗透率，单位：m²，具体公式如下：

式(6)中， ${d}_{{\rm{p}}}$为多孔泡沫金属的孔径，单位：μm；ε为无量纲数，表示泡沫金属的孔隙率。

边界条件:

(1) 气体进口：$ \dfrac{\partial u}{\partial x}=\dfrac{\partial v}{\partial y}=0, p=p $,$ \dfrac{\partial p}{\partial y}=0 $

(2) 气体出口：$ \dfrac{\partial u}{\partial x}=\dfrac{\partial v}{\partial y}=0 $ ,$ \dfrac{\partial p}{\partial x}=\dfrac{\partial p}{\partial y}=0 $

本文的控制方程和边界条件采用 SIMPLE 算法进行数值计算，动量方程采用二阶迎风格式，其中非线性变化的孔隙率采用用户自定义函数 (UDFs)来实现，同时，设置收敛标准为10⁻⁶，采用标准初始化。

在模拟的过程中，计算域中使用非结构化网格。如表2所示，为了验证网格的质量，采用四种不同的网格数来分析网格数对通道型正压标准漏孔漏率的影响。从表2中可以发现，随着网格数从741改变为1127，漏率值变化了0.004%；网格数从1127继续增大到12243，漏率值变化了0.002%；继续增大网格数至237303，漏率值变化了0.001%。为了节省计算时间和成本，选取网格数为12243进行计算和分析。

通道型正压标准漏孔的形状极为复杂，对其进行准确的测量极为困难，其中涉及漏孔内部金属孔隙以及金属丝的直径等多方面影响。为了验证目前的数学模型以及方法的正确性，分别将数值模拟结果与已发表的两篇实验文章[7,11]进行对照。

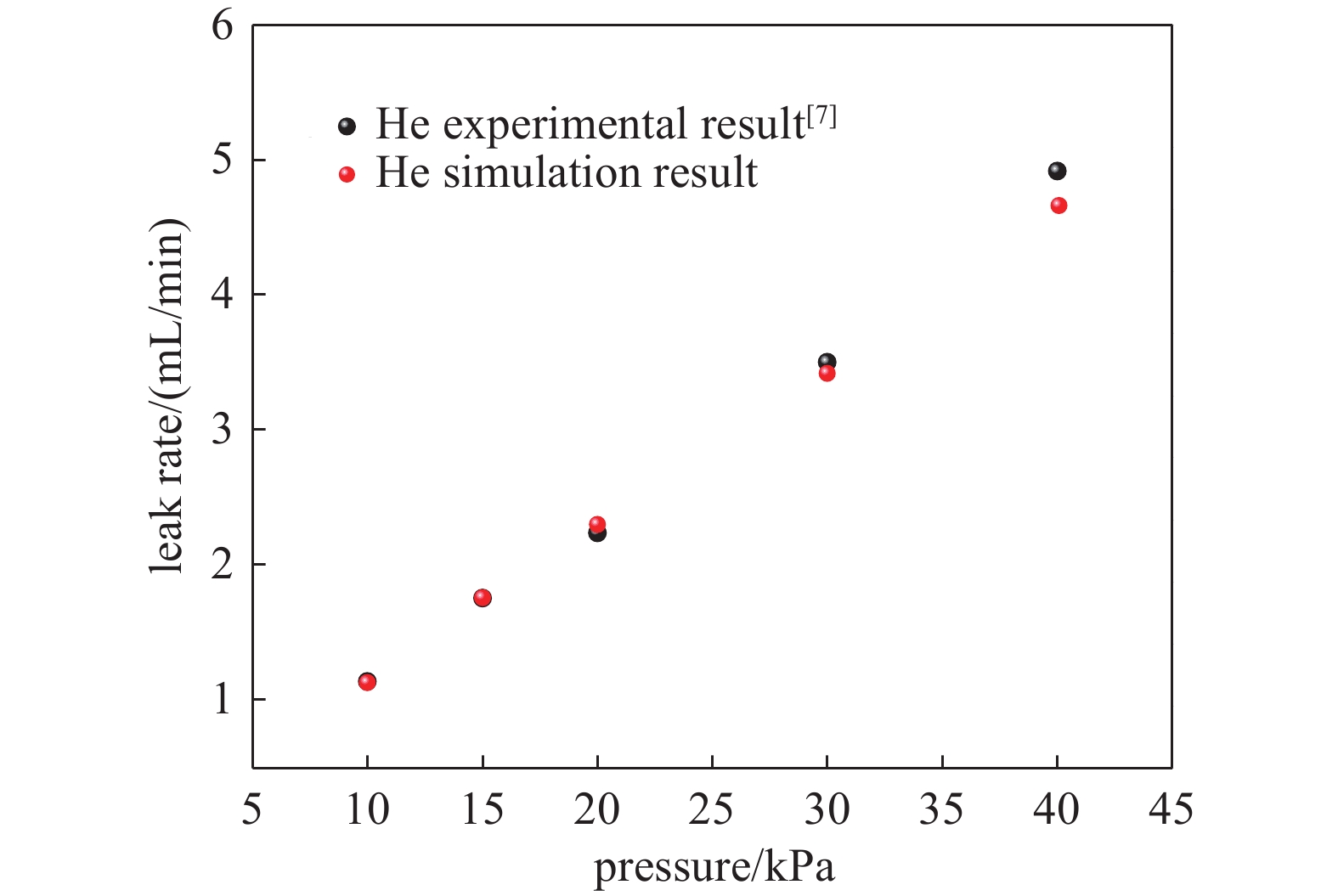
(1) 在气源压力10 kPa-40 kPa的实验条件下，研究高纯He通过通道型正压标准漏孔漏率的变化规律。如图2所示，实验漏率值与模拟结果进行比较，可获得的最大相对误差为8.17%。

(2)在气源为Air 且选取三种不同气源压力值，研究不同的正压标准漏孔的漏率变化，正压标准漏孔的实验漏率值与模拟结果如表3所示。从表3中可以看出，实验结果与模拟结果的最大相对误差为8.58%。

由此可见，数值模拟结果与实验结果基本吻合，说明以上提及的数学方法和模型是可行的。

本文主要采用多孔泡沫金属填充通道型正压标准漏孔并建立数学模型。主要研究了在气源压力：1000 Pa−40000 Pa条件下，不同气体类型、孔隙率以及孔经$ {d}_{p} $=6 μm, 8 μm, 10 μm，漏孔长度、内部速度场分布等参数对通道型正压标准漏孔漏率的影响。

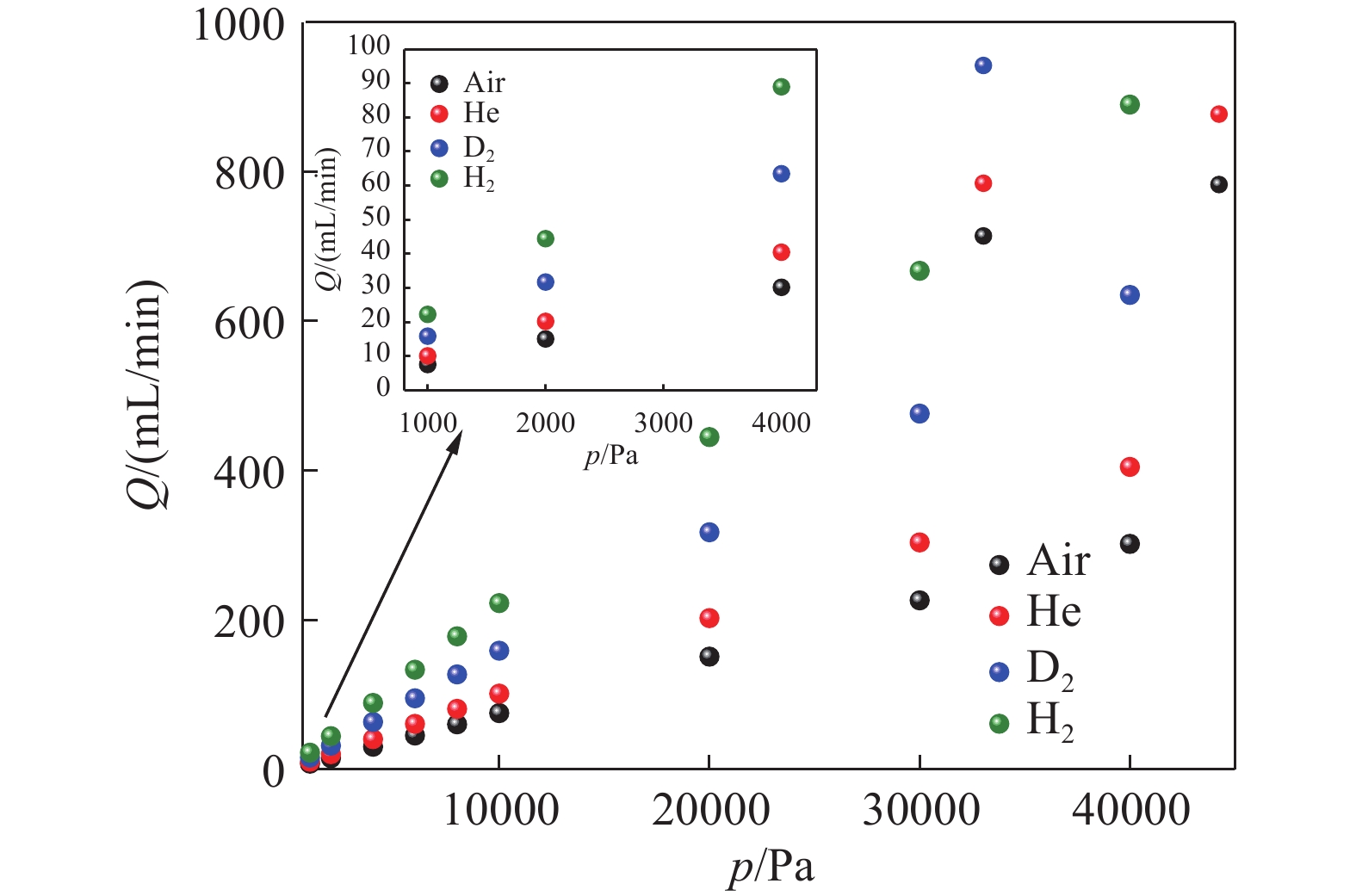
图3主要分析了在恒定孔隙率ε=0.3，恒定的通道型正压标准漏孔长度l=0.08 m, 不同Air、He、D₂、H₂以及在不同压力条件下通道型正压标准漏孔漏率的变化。从图3中可以看出，通道型正压标准漏孔的漏率随着气源压力的增大而增大，与此同时，在相同的气源压力下，与Air、He以及D₂相比，H₂获得的漏率最大。在相同气源压力下，He获得的漏率比Air提高34.18%，D₂比Air的漏率提高110.40%，H₂获得的漏率比Air提高194.84%，这主要是因为在相同的环境温度条件下，不考虑通道型漏孔壁面热量的传递，H₂的动力粘度最小，从而在泡沫金属内部获得的渗透率最大，这导致更多的H₂更易通过泡沫金属内部而释放到漏孔外部。此外，还可以发现在本次气源压力范围内，通道型正压标准漏孔的漏率与压力成线性关系。

不同类型的气源对正压标准漏孔漏率的影响很大，气体的粘性越小，在相同的气源压力下获得的漏率越大。但是，在实际生产和密封系统设计中，漏率并非越大越好。因此，选择粘性较大的气源类型以减少泄漏率，这对于密封系统性能的优化和设计提供指导，同时，这对于计量方面的检漏工作，选择合适的气源类型也具有重要意义。

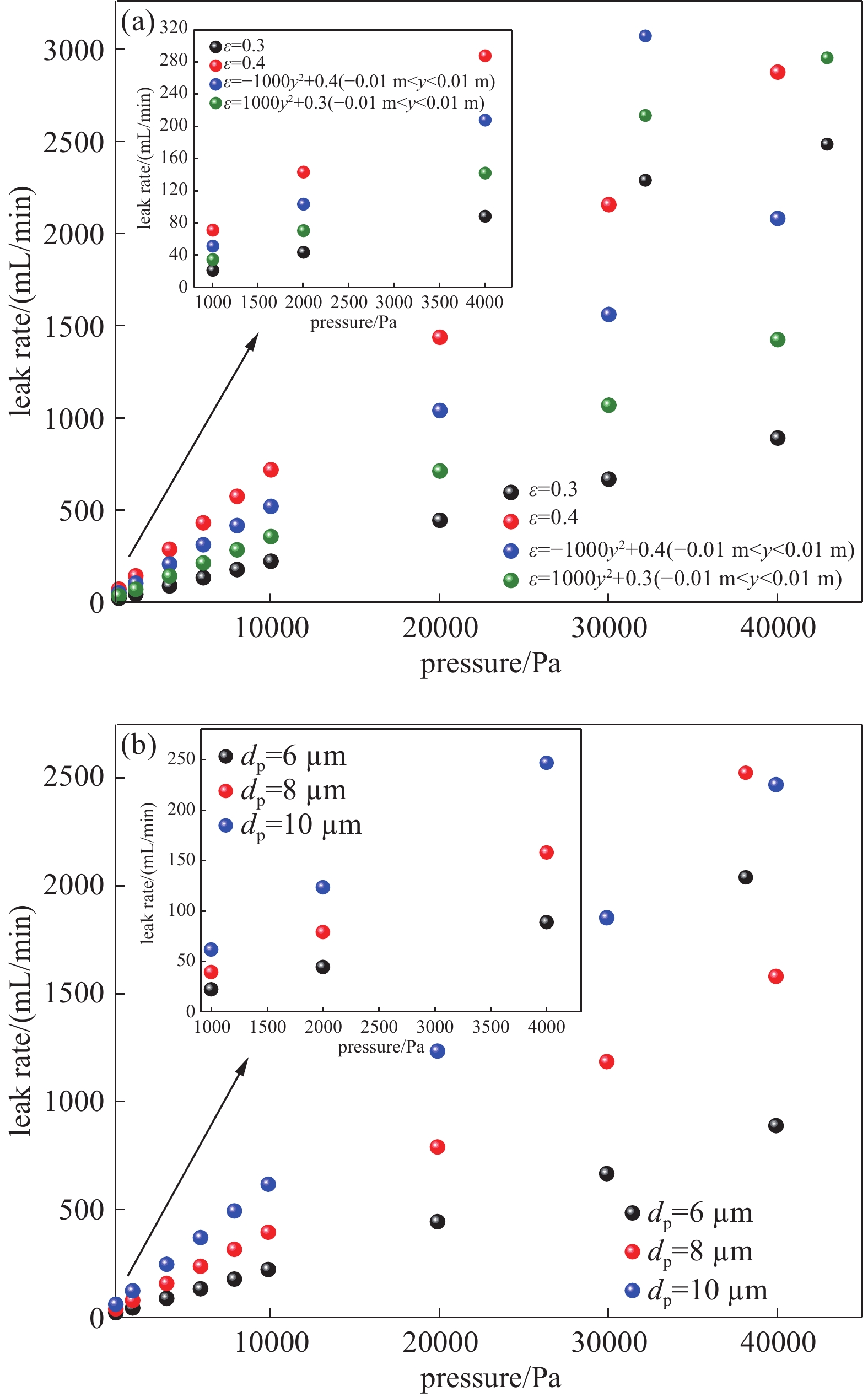
如图4所示，在气源为H₂且通道型正压标准漏孔长度l=0.08 m条件下,分别研究恒定变化孔隙率和非线性变化孔隙率以及不同孔径在不同压力下通道型正压标准漏孔漏率的变化。从图4(a)中可以看出，在相同的气源压力条件下，随着孔隙率从0.3增加至0.4，通道型正压标准漏孔获得的漏率明显增大。这主要是因为在相同的孔径条件下，孔隙率的增大，渗透率增大，气体的流动阻力降低，气体更容易通过泡沫金属间隙，从而获得较大的漏率。对于非线性变化的孔隙率，在泡沫金属内部孔隙率沿着纵轴方向从0.3逐渐变化到最大0.4再逐渐降低到0.3的过程中，在通道型正压标准漏孔的中轴线孔隙率最大为0.4，由于靠近壁面的孔隙率相对于中间区域的孔隙率较小，从而两边获得的流速相对较小，中间获得的流速较大。然而，与孔隙率为0.3的泡沫金属相比，孔隙率ε = −1000y²+0.4 (−0.01 m<y<0.01 m) 获得的漏率最大。对于非线性孔隙率ε = 1000y²+0.3 (−0.01 m<y<0.01 m)，在接近壁面处获得的孔隙率较大，在泡沫金属内部中间区域获得的孔隙率较小，更多的气体会从两边沿着壁面流向出口，由于曲率的差异，孔隙率ε=1000y²+0.3 (−0.01 m<y<0.01 m)获得的漏率较小。从整体来看，非线性孔隙率的变化介于ε =0.3和ε =0.4之间，因此，较大孔隙率获得漏率最大，非线性变化的孔隙率可以有效控制漏孔漏率的大小。

在相同的孔隙率条件下，不同的孔径对通道型正压标准漏孔漏率的影响，如图4(b)所示。从图4(b)中可以看出，在相同的气源压力条件下，通道型正压标准漏孔的漏率随孔径$ {d}_{\mathrm{p}} $的增大而增大，随着气源压力的逐渐提高，漏率呈现上升的趋势。这主要是因为在相同的气源压力以及孔隙率条件下，泡沫金属内部的渗透性随孔径的增大而增大，气体在内部的流动阻力减小，从而获得更多的动能。此外，在相同的孔径条件下，气源压力与获得的漏率成正比关系，在相同的粘滞力条件下，压力越大获得的动能越大。

因此，由泡沫金属填充的通道型正压标准漏孔，在相同的孔径$ {d}_{\mathrm{p}} $=6 μm条件下，正压标准漏孔的漏率值随着孔隙率的增大而增大，非线性孔隙率ε = −1000y²+0.4 (−0.01 m<y<0.01 m)和ε =1000y²+0.3 (−0.01 m<y<0.01 m)获得的漏率值介于恒定孔隙率0.3和0.4之间获得的漏率值。在相同的孔隙率ε=0.3条件下，通道型正压标准漏孔的漏率随孔径的增大而增大。

不同的孔隙率或孔径能够有效控制正压标准漏孔的漏率。较大的孔隙率或孔径能够加速气体通过漏孔的速度，线性变化的孔隙率这对与通道型正压标准漏孔未来结构的设计以及漏率的控制具有一定的指导意义。

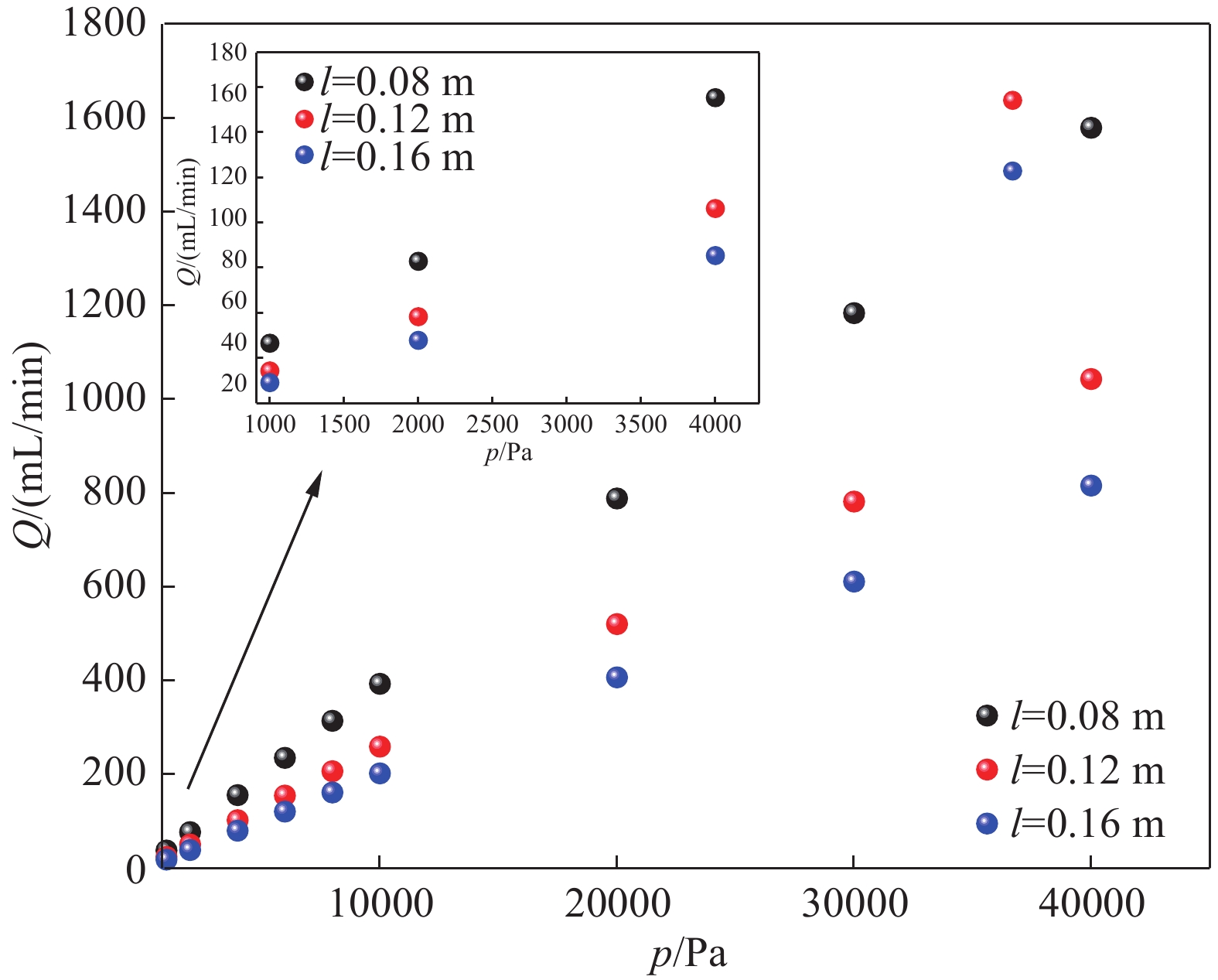
图5主要分析了在恒定的孔隙率$ \varepsilon =0.3 $和恒定孔径$ {d}_{\mathrm{p}}=8 $ μm以及相同的气源H₂条件下，不同的通道型正压标准漏孔长度在不同进气压力下获得漏率的变化趋势。从图5中可以看出，在气源压力40000 Pa的条件下，漏孔长度由l=0.08 m增加到l=0.12 m, 在出口监测到的漏率降低了33.89%，随着漏孔长度增加至l=0.16 m，在出口监测到的漏率比l=0.12 m下的漏率降低了21.74%。在相同的进气压力条件下，随着漏孔长度的增加，在出口获得的漏孔漏率逐渐越小。这主要是因为漏孔长度的增加，气体通过漏孔的阻碍程度随之增加，气体分子碰撞次数增多，H₂在通道型标准漏孔中停留的时间相对延长，从而获得漏率减小。

因此，正压标准漏孔的长度对漏率的影响较大，在实际的工业生产中，可根据需求设计和生产不同长度的漏孔，这对设备的密封性测试以及不同场所的应用具有指导意义。

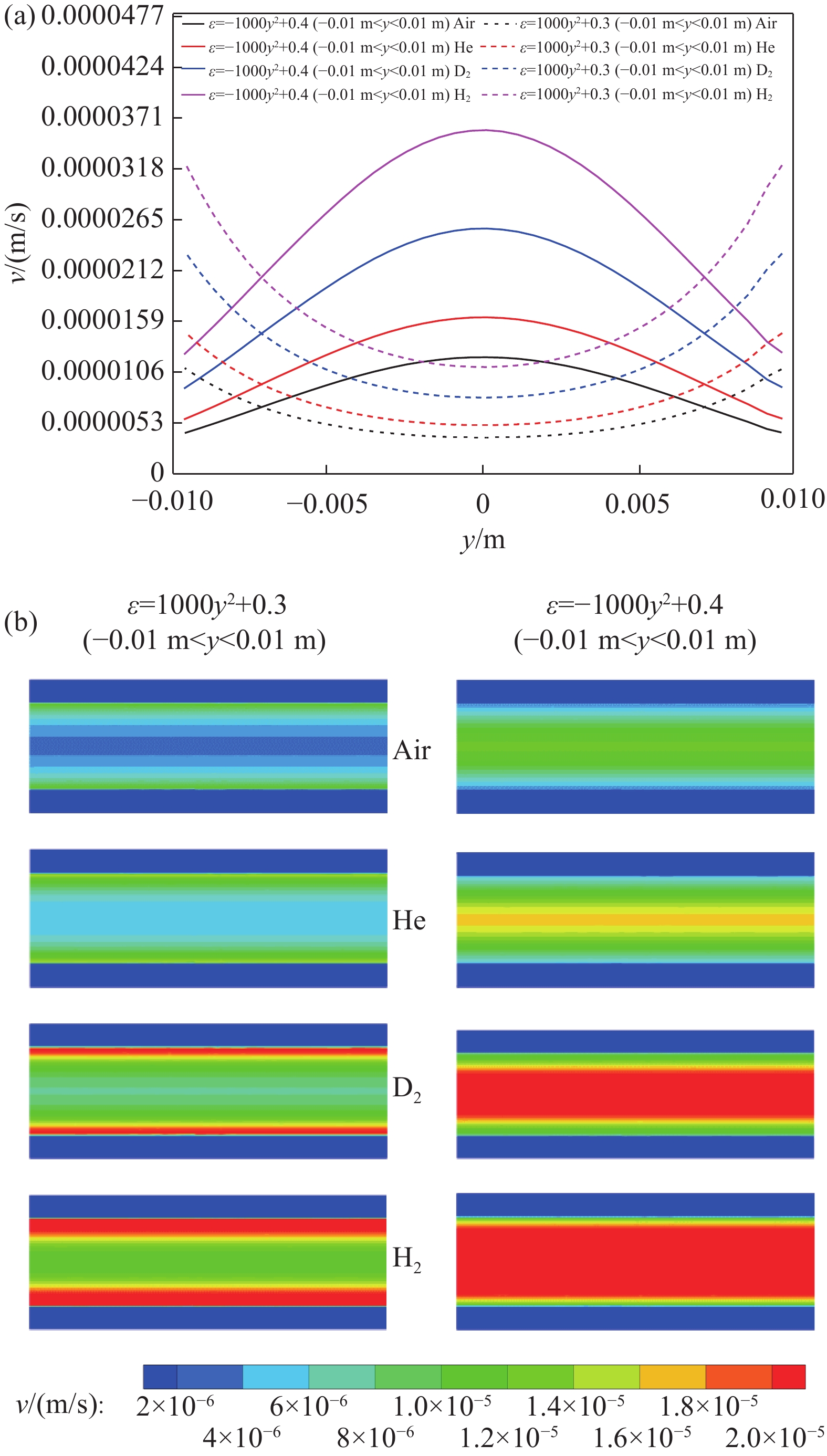
在恒定的孔径$ {d}_{\mathrm{p}} $=6 μm条件下,不同气源在泡沫金属内部沿着y方向速度场的变化如图6(a)所示。从图6(a)中可以发现，对于开口向下的抛物线形变化的孔隙率，与空气相比，H₂在泡沫金属多孔层中获得的流速较大。在$ -0.01 \; \mathrm{m} < {y} < -0.005 \; \mathrm{m} $和$ 0.005 \; \mathrm{m} < {y} < 0.01 \; \mathrm{m} $ 之间，流速的变化相对于中间区域较小，这主要是因为流体在流道内流动边界层出存在粘滞力，另一方面中间区域孔隙率最大，获得的流动阻力相对减小，导致更多的流体更易通过。与此同时，相对于孔隙率的非线性变化，流体的性质占据主导地位。从图6(b)的速度场分布中可以发现，与Air、He、D₂相比，在气源为H₂且填充的泡沫金属孔隙率 $ \varepsilon =1000{y}^{2}+0.3(-0.01 \; \mathrm{m} < {y} < 0.01 \; \mathrm{m}) $条件下，在通道型正压标准漏孔两侧区域流速较大；填充$ \varepsilon =-1000{y}^{2}+0.4(-0.01 \; \mathrm{m} < {y} < 0.01 \; \mathrm{m}) $条件下，在通道型正压标准漏孔中间区域流速较大。这表明泡沫金属内部速度的大小与气体的粘度有关，粘度的大小会直接影响正压漏孔的漏率。

本文主要将多孔泡沫金属填充于通道型正压标准漏孔内部，通入不同类型的气体，采用数值模拟的方法，研究其内部机理并建立数学模型。分别分析了不同类型的气源，孔隙率、孔径、正压标准漏孔长度等参数对漏率的影响，并给出了非线性变化孔隙率内部速度场分布。得到的主要结论如下：

(1) 在恒定的气源压力条件下，与Air、He以及D₂相比，H₂获得的漏率最大。不同的气体类型通入通道型正压标准漏孔中对其漏率有较大的影响。气体的粘性越大，在相同的气源压力下获得的漏率越小，这是因为粘性的增大，导致流动阻力增大，从而在出口获得的气体量减少。因此，在实际生产和密封系统设计中，选择粘性较大的气源类型以减少泄漏率，这对于优化和设计密封系统具有指导意义。此外，对于计量方面的检测，明确气体类型也是十分重要的。

(2) 通道型正压标准漏孔的漏率随着孔径或孔隙率的增大而增大，不同的孔隙率或孔径能够有效控制正压标准漏孔的漏率。线性变化孔隙率对通道型正压标准漏孔结构上的设计以及漏率的控制具有一定的参考意义。

(3) 通道型正压标准漏孔的漏率随其长度的增加而降低，这主要因为漏孔长度的增加，导致气体分子碰撞次数增多，气体不能及时从出口排出。这对于漏孔内部结构的优化和设计提供帮助。

综上所述，对于同种型号的正压标准漏孔，明确气体类型对计量方面的检漏工作是十分重要的。此外，控制和调节孔隙率、孔径、漏孔长度等参数，能够改变正压标准漏孔漏率的大小，这对于未来漏孔生产的发展以及密封系统性能的优化和设计提供有价值的参考意义。