人们对具有电磁特性的人工合成材料的探索，最早可以追溯到1898年Bose^[5]和Lindman^[6]开展的关于毫米波和微波波段人工手性结构的研究。然而，一直到20世纪40−60年代，随之开创性的“人工电介质”材料发现，具有特定电磁特性的人工材料的研究才真正得到人们的重视并逐渐发展起来。早期研究中，人们试图通过复制已知的材料参数来合成人工电介质，以开发用于射频和微波波段的轻质材料。20世纪60年代末，Veselago^[7]从理论上首次预言了介电常数和磁导率都为负值的材料的电磁性质，超材料的概念由此诞生。1987年，Yablonovitch和John发现介电函数呈周期性排列的光子结构具有操控光流的能力，他们将这种结构命名为“光子晶体”^[2]。2006年，Pendry等^[8]提出了“变换光学”理论，即可以通过设计超材料，实现电磁波的任意调控。随后，Smith等^[9]首次实现了可以在微波波段诱导电磁波转向的隐身超材料。随着微纳光子学领域的发展，人们通过人工设计微结构阵列，获得了在自然材料中难以实现的奇特电磁参数，极大地丰富了人们对光传输行为的调控能力。许多新奇的光学材料和现象，包括人工手性介质、人造磁性介质、负折射率材料、超透镜、光学黑洞以及超分辨成像等，都得到了广泛的研究。

在过去十年中，对人工光子学结构的探索代表了微纳光子学研究的中心主题。例如，光子晶体可以实现完全的光子带隙，使光以近乎完美的传输效率在这种晶体包围的一个急弯处无泄漏传输^[2]。通过合理的结构设计，超材料表现出特殊的性质，例如负折射率。这种特性使光可以折射到负方向，这与基于Snell定律的正常折射相反^[1,10]。由不同尺寸和几何形状组成的金属纳米颗粒，可以突破经典的衍射极限，将光波的作用范围控制到纳米尺度，在单分子水平上实现光发射^[11]。通过在微型光散射体和超表面中引入几何结构的空间变化，在光波的相位、幅度、偏振和角动量等信息中可以产生可控的变化，实现任意的波前整形。总之，微纳光子学人工结构对光波调控的独特能力为其广泛应用提供了新的可能和机遇。

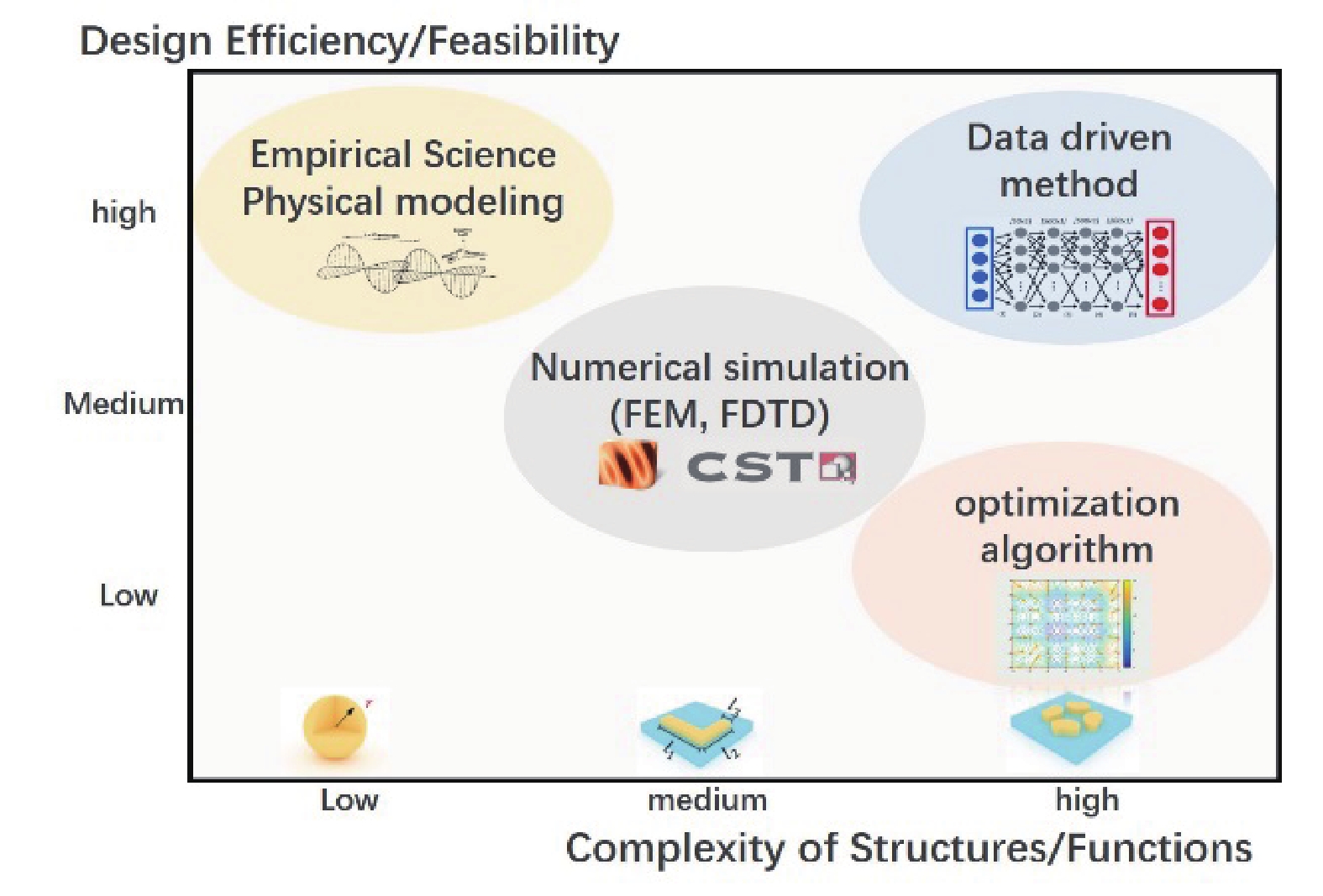
微纳光子学结构设计主要分为正向预测光谱和逆向设计结构两种思路，图2比较了各种设计方法的复杂度和设计效率。到目前为止，具有特定功能的光子学结构主要是以“自下而上”的正向预测方式设计的，可分为基于物理的方法和基于数值模拟的电磁建模方法。其中前者是以科学经验和基本的物理理论为指导的简化建模分析，后者包括有FEM和FDTD等模拟方法。早期光子学的设计原型大多基于简单的几何结构，如球体、圆柱体、分裂环、V型天线、和十字形等，通常结构的可调自由度较小（自由度小于3）。此外，设计过程中需要进行大量的建模、扫参数和在试错中不断优化结构的过程，尤其在对复杂结构的设计中，建模和调参的过程复杂而繁琐。与此同时，这种传统的设计方法会受到人为引导误差的影响及经验知识的固有限制，其设计结果往往会止步于局部最优解。因此，具有非常规功能和极高效率的光子器件结构很难从人们凭直觉猜测的几何体中发现。

为了解决微纳光子学设计的困难，逆向设计方法正逐渐成为近年来光子学研究的主题之一。逆向设计直接从所需要的光学特性出发，通过相关优化算法和仿真模拟方法同时优化多个设计参数，直接反向计算所需的光学结构，即“自上而下”的方式。由于这种方法需要在设计空间中探索更大的自由度，因此更具挑战性。为此，逆向设计过程通常是由包括基于梯度的(拓扑优化、伴随方法和水平集方法等)和基于进化(遗传算法和粒子群算法等)的优化算法指导。优化算法的加持有助于找到性能显著优于一般结构的非直觉的、形状不规则的光子学结构。然而，它们本质上仍是基于规则的方法，每个案例都包含复杂的迭代搜索步骤，强烈依赖于每个阶段中的数值模拟来生成有助于修改搜索策略的中间结果。同时，这些算法受限于其随机搜索性质，不足以在多约束问题上进行复杂的设计^[12-13]。如多参数问题，用遗传算法求解需要复杂的计算模型、强大的计算能力和大量时间，并且随着问题规模和复杂性的增加，计算参数与时间将呈指数增长。

深度学习主要是通过构建类似人脑的多层神经元结构来自动捕获高维数据之间的内在规律和基本特征，极大地改变了数据处理的范式。它的本质是对训练数据进行分层特征表示，逐层将数据的低级特征抽象成高级特征表示。作为人工智能和机器学习的一个子领域，深度学习在计算机视觉、语音识别和自然语言处理等方面取得了巨大的成功，受到了越来越多的关注。特别是在一些以前被认为仅人类可以掌握的领域，例如复杂的策略游戏和医学图像诊断等，深度学习都己经表现出、有时甚至高于人类专家的水平。

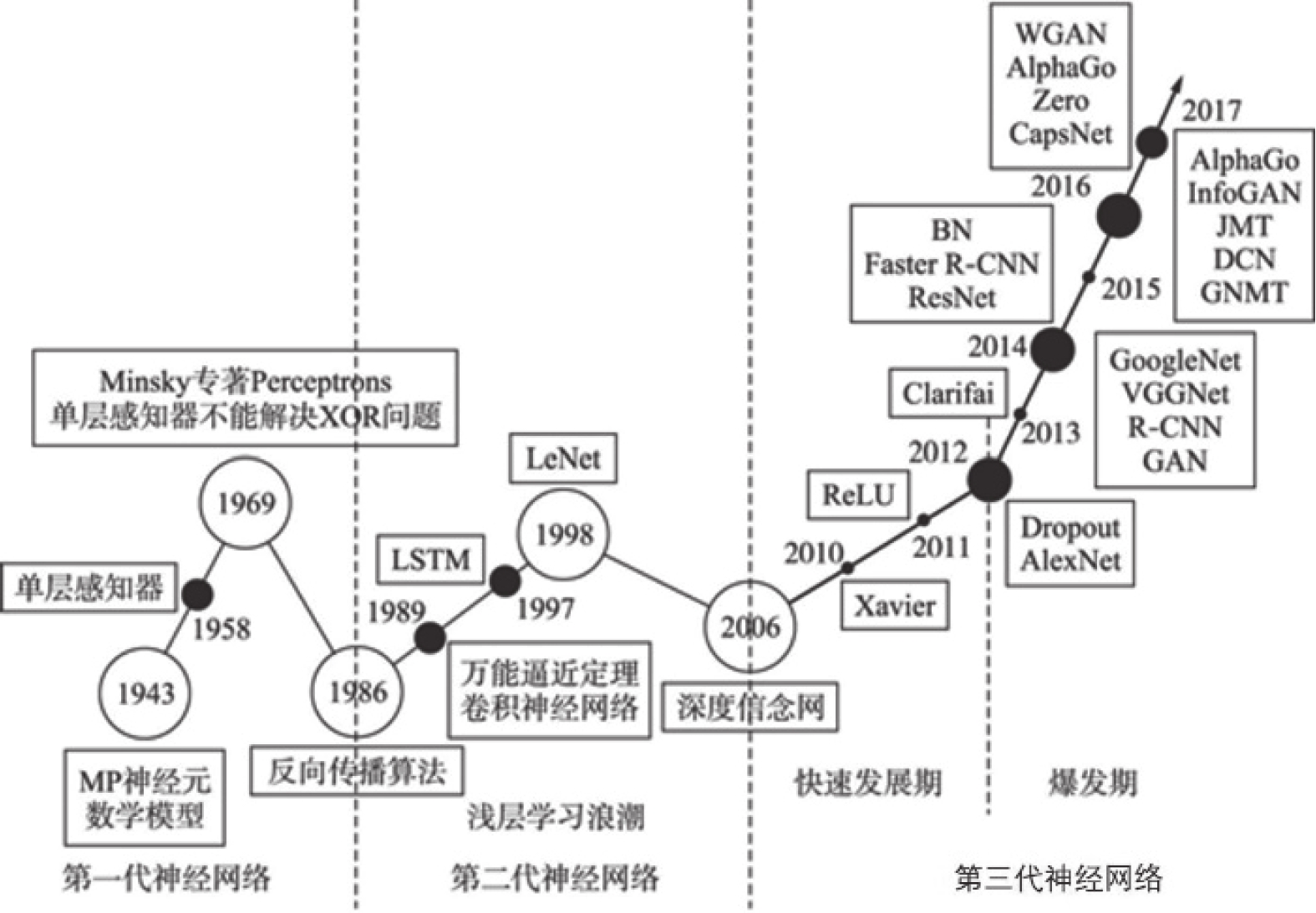
从历史上看，深度学习可以追溯到20世纪40年代，它经历了许多不同的名称，最终以现在的名称广为人知，图3描述了深度学习的发展历程。自20世纪80年代以来，深度学习也被称为人工神经网络(artificial neural networks，ANNs)。最初的一些学习算法始于1890年美国心理学家James对于人脑结构与功能的研究，他模拟了人类大脑的学习过程。半个世纪后，1958年，Frank提出了单层感知机(monolayer perceptron)的概念。然而，1969年，Minsky在书Perceptrons中指出了上述的感知机的研究瓶颈，提出理论上还无法证明将单层感知机模型扩展到多层网络是否有意义。直至2006年，Hinton教授提出深度学习方法并改进了模型的训练方法，即由一系列受限玻尔兹曼机(Restricted Boltzmann machine, RBM)组成的深度置信网络(Deep Belief Networks)和无监督逐层贪婪预训练算法(greedy layer-wisepre-training)，消除了上述神经网络发展的瓶颈，感知机的应用效果才取得突破性进展。随后，Ruslan提出的深度玻尔兹曼机重新点燃了人工智能领域的神经网络和玻尔兹曼机的热情，掀起了深度学习的浪潮。研究人员已经能够训练出比以前更深的神经网络，并且从理论上认识到模型架构深度的重要性。从目前最新的研究进展来看，只要数据量充足、隐藏层足够深，即便不加预处理，深度学习也可以取得很好的结果，这反映了大数据和深度学习之间相辅相成的潜在联系。因此，在这个信息爆炸的大数据时代，深度学习将继续引领人工智能研究的热潮方向。

近十年来，深度学习逐渐兴起并快速发展，对众多研究主题产生了前所未有的影响。凭借其在高维参数空间中高效搜索并解决问题的非凡能力，受到世界各国研究人员和高科技企业的高度重视。同时，随着ReLU、activation^[14]、dropout^[15]和batch normalization^[16]等新的训练方法和正则化技术的发明，研究人员已经可以在大数据集上设计和训练越来越深，越来越大的神经网络。因此，深度学习的相关技术被认为是新材料、^[17]药物研发^[18-19]、生物医疗、光子学逆向设计^[20-21]等拥有海量数据领域最有前途的候选方法。此外，深度学习可以与传统优化方法交互，提升算法性能。在光子学结构的逆向设计中，无需猜测物理机理，直接聚焦于预期的电磁响应，从而解决设计问题。这种设计思想主要基于高级的算法和电磁仿真软件相结合，寻求一种解决模型，通过反复训练以最小化目标距离（或最大化设计指标）。在整个参数空间进行搜索时，训练好的模型往往能够找到不直观但性能优异的设计方案。尽管训练之前首先要建立一个足够大的数据库，但训练一旦完成，模型几乎可以立即解决逆向设计问题。而对于传统的光子学结构设计团队，只有合理收集和处理已有的仿真结果和设计方案，并利用计算机对其进行二次利用和挖掘，才有发现潜在的物理机制。因此，将深度学习引入到光子学结构设计过程中，自动挖掘结构电磁响应背后的物理内涵，针对特定设计目标实现按需设计具有很强的现实意义。

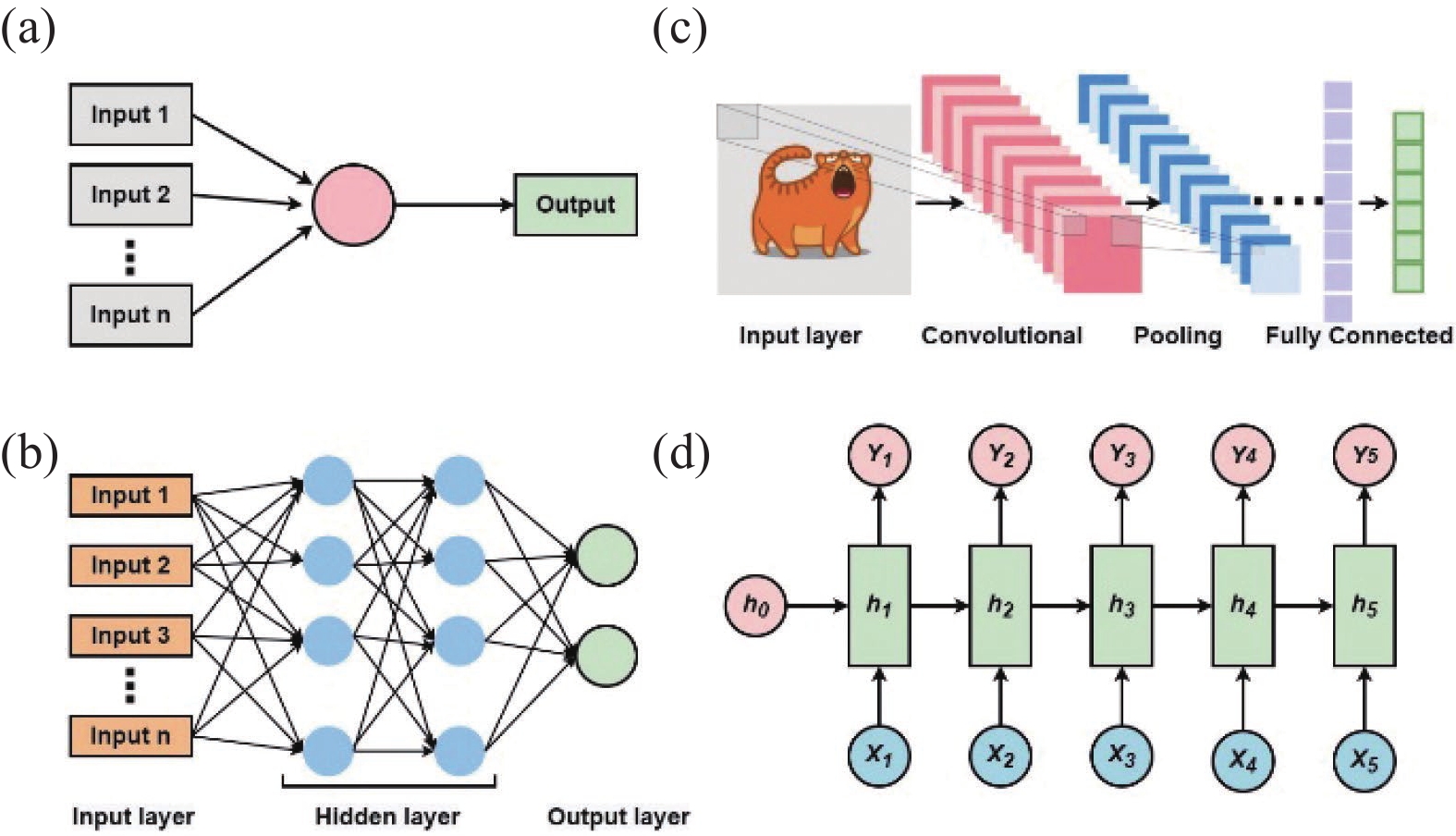
根据中间功能层的不同，神经网络主要可以分为以下几种：

（1）感知机

感知机的结构如图4(a)所示，每个神经网络单元可以用抽象的数学模型表示，也被称为单层神经网络，是最简单的神经网络结构。它接收多个输入，计算其权重值，然后通过激活函数sign(z)生成一个输出。这类似于神经末梢感受到外部刺激，生成了能够传导到神经细胞（又叫神经元）的电信号。但是，这种体系的结构过于简单，处理问题能力有限，只能用于二元分类问题，无法学习处理复杂的非线性模型。

（2）多层感知机

在现实世界中，实际的决策模型往往是由多个感知机组成的多层全连接网络。图4(b)是一个经典的神经网络模型–多层感知机(Multilayer perceptron, MLP)。MLP主要做了三个扩展：(1)添加隐藏层，多层隐藏层增强了模型的表达能力和复杂度；(2)输出层有多个输出神经元，增加了模型的应用场景，可以灵活应用于分类、回归、降维和聚类等问题；(3)扩展激活函数，MLP中的激活函数有Sigmoid, tanh, softmax和ReLU等。通过使用不同的激活函数，神经网络的表达能力进一步增强。因此MLP具有比感知机更强的处理能力。MLP利用反向传播的监督学习技术进行训练，理论上已经证明MLP是一个通用的逼近器，可以用有限个神经元拟合任意连续函数。但是这种模型的效果在很大程度上受限于不成熟的训练策略、不充足的数据和浅层的模型架构，同时“全连接性”易使模型过拟合。

（3）卷积神经网络

卷积神经网络（Convolutional neural network，CNN）是计算机视觉中最重要的神经网络类型之一，在计算机视觉中取得了巨大的成功，例如图像识别、图像分割、视频识别和医疗诊断中肿瘤的检测等。对于经典的MLP，读取图像需要将全部像素点作为输入（即全连接的方式），图像的尺寸越大，它连接的参数越多，计算量就越大。受到动物视觉皮层中可以检测边缘、形状、深度和运动的神经元的启发，1962年，Hubel和Wiesel首次提出了一种新的概念“感受野”(Receptive Field)。一个神经元只对其局部视野中一个感受野的刺激做出反应，不同神经元的感受野部分重叠，可以覆盖整个视野。因而，模型没必要感知全部图像，只需感知局部像素(图4(c))，提取有效特征即可。这个过程也可以解释为使用过滤器（卷积核）来过滤图像的各个小区域，获取各个小区域的有效特征值。CNN卷积层的过滤器是它与其它神经网络的主要区别，通过损失函数不断迭代优化过滤器，网络就能够实现特定的任务。

（4）循环神经网络

经典的人工神经网络如MLP、CNN，输入的数据维度相同，而且输入和输出在各个时刻都是相互独立的，每个神经元的信号只能向后传播，在每个节点上具有不同的权重。而现实生活中的绝大多数情况并不都适用这样的模型，例如在演讲过程中进行语音识别，因为演讲者讲的每一句话的时间都不相同，而识别的内容还必须要按照时间顺序进行关联识别。这就需要有一种能力更强的模型，具有能存储模型的前几个学习阶段的记忆能力，并且能够按时序依次处理任意长度的信息，这就是如图4(d)所示的循环神经网络（Recurrent neural network, RNN）。RNN是一种利用顺序数据或时间序列数据的人工神经网络，它们从先前的输入中获取信息，以影响当前的输入和输出，即输出取决于序列中的先验元素。RNN需要考虑习语中每个单词的位置，并使用该信息来预测序列中的下一个单词。因此，RNN通常用于连接序列应用，如语言翻译、自然语言处理、时间信号处理、图像字幕和音乐生成等。

通过巧妙地改变结构单元的几何形状、尺寸和排布规律等，研究人员可以在波长尺度甚至亚波长尺度上对电磁场实现灵活有效的操控，例如降低电磁场群速度，将电磁场限制在亚波长空间范围内，以及获得高品质的光学共振等等^[26]。这种研究策略在现代光学工程领域具有广阔的应用前景，如消色差超透镜、结构色和多功能全息成像等。复杂多功能器件需要更高效的设计方法，深度学习便是最有前景的候选方法。深度学习模型通过建立几何结构与其光学响应之间复杂非线性关系，能实现振幅、相位^[27]、偏振、非线性和近场分布^[28]等多自由度参量的快速预测。例如，Peurifoy等^[29]使用全连接神经网络构建了多层同心球壳结构的正向预测模型，该网络接收多层壳的层厚度作为输入，并预测在多个波长点的散射截面光谱图像。对于训练过程中没有见过的结构，训练有素的神经网络模型也能准确预测其散射截面。这项研究为如何利用神经网络设计微纳光子学器件提供了一个极好的例子。

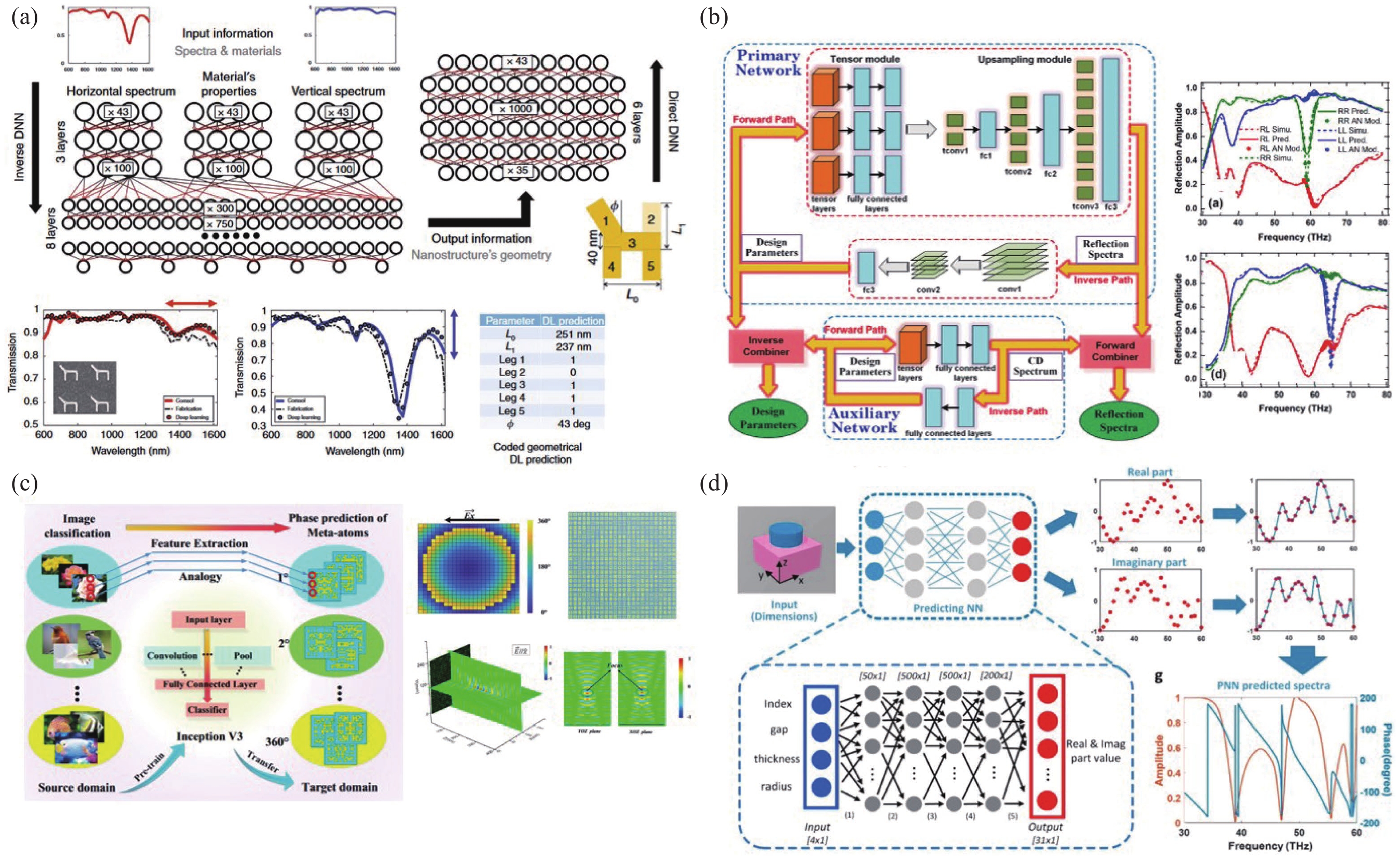
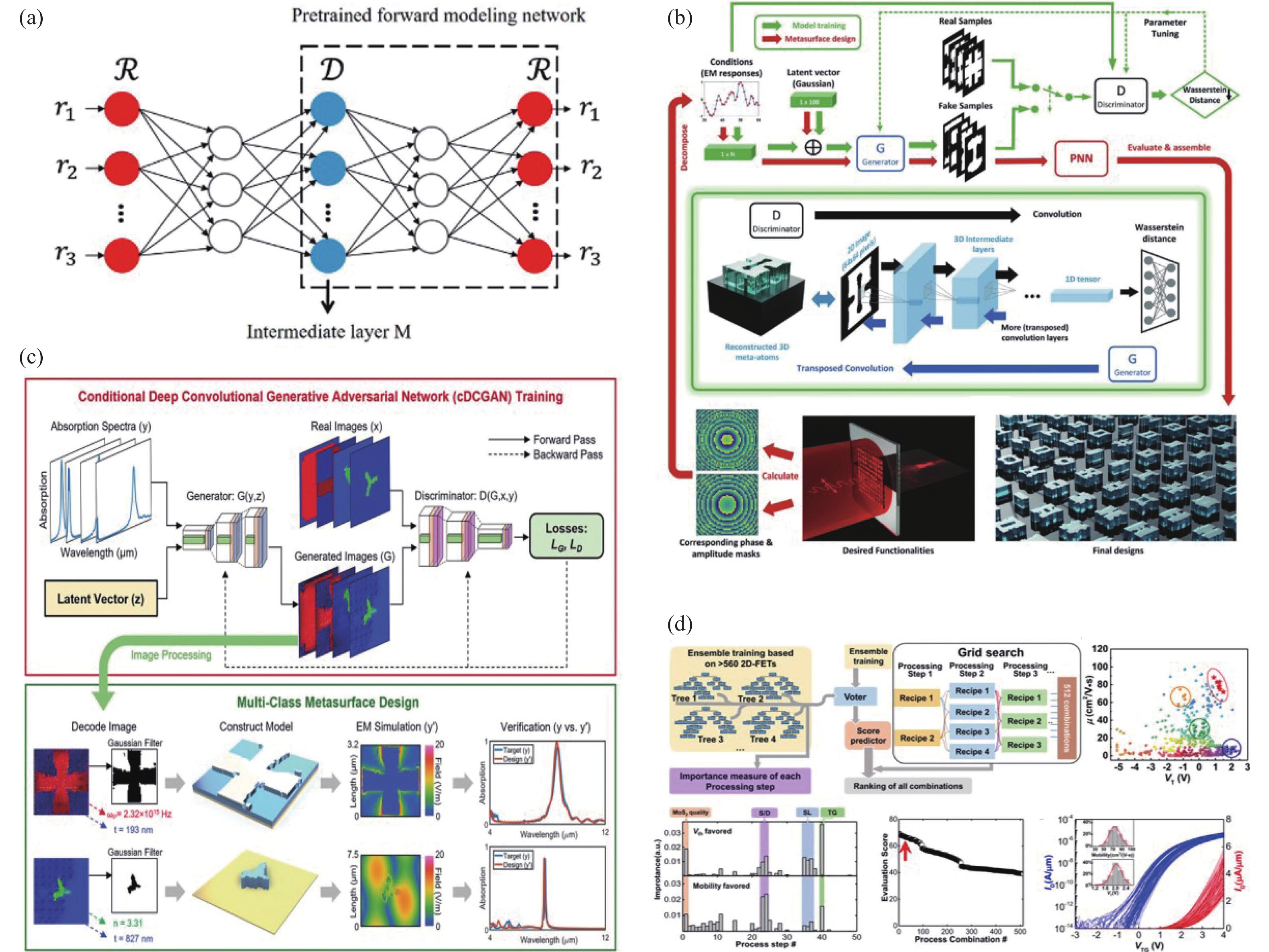
深度神经网络也已经成功用于微纳光子学中各种物理量的预测，例如，各种光谱(反射、透射、散射、吸收等)振幅和相位。光谱振幅可以方便地离散为向量(单光谱)或矩阵(多光谱)，因此可以很容易地纳入深度学习模型。2018年，Malkiel等^[22]提出一种深层全连接网络，用于预测等离激元纳米结构的光谱。等离激元纳米结构是如图5(a)所示的H型金属结构，具有臂长、宽和旋转角度三个连续参数和五个臂的存在与否的二元参数。材料属性(如氧化铟锡粘结层和金属材料的介电常数)表示为具有25个参数的向量。设计目标为两个正交偏振方向的反射光谱，离散为具有43个参数的向量。该研究在1.8万个样本数据上训练一个6层的频谱预测网络，训练好的模型相当于一个快速的“模拟器”。然而，多数光谱的正向预测网络都存在在共振峰附近谱线的预测误差较大的缺点，主要原因是光谱共振峰附近的采样点数不足。为了解决这个问题，Ma等^[23]在手性共振型器件的正向预测网络中添加了一个辅助神经网络，如图5(b)所示，针对共振峰超过一定数值的频谱范围，单独提取数据并选择更小的采样间隔进行再次训练。最后，将将两次训练结果合并输出。结果表明，辅助网络的加入极大的提高了网络预测谱线的精度，损失函数均方误差小于0.0008。

除了振幅，相位也是光场自由度的重要信息之一。相较于光谱振幅调控，相位调控的应用领域更加广泛，实现方式也相对更复杂^[30-31]。受到深度学习图像识别领域的启发，研究人员将相位预测问题转化为类图像分类问题。如图5(c)，类比图像分类，将每个角度也分为一个类，共360类。并将图像识别分类能力优异的InceptionV3网络迁移到相位的分类问题上^[24,32]。这种高效、准确的相位设计方法可以更加灵活的设计多功能集成器件，如偏振复用光束偏折器、频率复用信息加密器件和空间偏振频率复用全息图等。最后，为了能够实现对光场全方位信息的同时控制，我们需要建立具有更多光场自由度的网络模型。这将有利于开发新的光子学器件，其中包括但不限于在不同波长下显示不同图像的多维超全息成像、用于不受缺陷影响的对光传输鲁棒的拓扑光子晶体波导，以及增强单量子发射的可控纳米点等。目前研究人员^[25,33]通过建立两个相同的全连接网络分别预测透射系数的实部与虚部，再通过公式转换成振幅和相位，可以实现共振结构光谱振幅和相位的准确预测，预测准确率分别为99.4%和99.3%，如图5(d)所示。利用优化算法对目标振幅与相位对应的结构进行全局搜索后，可以根据期望的振幅、相位分布对不同结构单元进行有序排列，从而实现偏转器、透镜等多种器件。

在过去相当长的一段时间里，微纳光子学器件的设计方法都是基于简化物理模板的经验建模式方法和基于规则的试错模拟式方法。深度学习的兴起，一种新兴的“自上而下”的逆向设计方法开始受到微纳光子学研究人员的重视。不同于传统优化算法指导的逆向设计，训练完成的深度神经网络模型，能在极短的时间内，直接得到所需的结构参数。这种设计方法可以提供更系统、更全面的器件特性优化，甚至创生出全新的器件构型，对微纳光子学的器件的发展具有极其重要的指导价值。值得注意的是，除了结构的几何形状，光学响应还强烈依赖于材料组成和制备工艺。因此，为了应对此类优化挑战，为实现光子学器件的最佳性能奠定基础，将进一步发展先进的光子学器件的全局优化方案。不同于正向预测网络，由于数据库中存在多个满足相似需求但几何参数非常不同的候选结构，逆向网络模型往往无法收敛。为了解决这个问题，Liu等^[34]提出了一种串联训练方法。如图6(a)所示，首先训练一个从结构参数到光学响应的正向预测网络，然后将这个预训练的正向网络连接到逆向设计网络的输出，监督的损失函数为输入与输出之间的均方误差。通过这种串联方式的间接训练后，逆向网络的输出将被迫收敛到由正向模型指导的唯一一种可能解，有效地解决了逆向设计问题中非唯一解所导致的数据不一致问题。

大多数微纳光子学结构都是基于固定的、规则的形状，其设计潜力仍有很大的发掘空间。深度学习为突破传统的设计约束并充分发掘设计潜力提供了途径。An等^[35]提出了一种生成对抗网络，可以生成满足多功能设计目标的超原子结构。该网络结构具有鲁棒的训练过程，与设计目标的复杂性无关，因此非常适合多功能器件的设计。此外，该网络生成的具有相似电磁响应但不同物理特征、不同类型结构的能力可以提供额外的自由度，来考虑其他因素，如制造约束和公差。图6(b)为双焦点超透镜、偏振复用光束偏转器、偏振复用超透镜和偏振无关超透镜，展示了该网络具有产生多种多功能超表面器件的能力。Yeung等^[36]通过特殊的折射率编码方式，设计了一个能够预测超表面拓扑结构、材料性质和面外结构参数的框架（图6(c)）。框架以条件深度卷积生成对抗网络和多参数编码策略为中心，将金属谐振器的单层电介质材料的实际折射率、几何形状与厚度分别编码到代表颜色的RGB三个通道中。同时，考虑加入控制超表面光学行为的全局参数，包括材料、结构和器件类别或制造工艺。该模型性能的评估结果表明，它不仅能够从训练和验证数据集生成准确和独特的解决方案，而且能够利用生成对抗网络的“一对多”映射功能，为单个目标生成多个替代方案和材料建议。Chen等^[37]提出通过使用机器学习算法来评估影响MoS₂顶栅场效应晶体管电学特性的关键工艺参数，如图6(d)所示。通过机器学习结合网格搜索算法指导晶圆级制造工艺，共同优化器件性能，包括迁移率、阈值电压和亚阈值摆幅。对MoS₂FET进行了62级的SPICE建模，得出最优的制造工艺流程，并进一步成功用于构建功能性的数字、模拟和光电检测电路。总之，深度学习不仅可以对结构进行优化，还可以提供最优的材料组成方案，甚至可以指导制造工艺，以实现目标器件的最佳性能，验证了深度学习辅助的器件优化强大能力。

深度学习的快速发展为解决光子学设计问题提供了全新的途径。“大数据”是深度学习的催化剂，它使人工智能的研究继续发生革命性的变化，但同时也导致计算能力和能耗的指数增长。目前，大多数深度学习算法都部署在具有冯·诺依曼架构的传统计算机中，其串行性是神经网络高效运行的内在障碍。因此，在速度和功耗方面都优于电子平台，包括纳米光子散射体^[38]、集成硅光子芯片^[39-40]和3D打印衍射层^[41]等用于深度学习的光子平台正在积极研究中。深度学习模型在光学平台上运行的巨大优势在于其对光信号的并行处理能力，用于光学平台的非线性激活函数可以通过使用二维材料的可饱和吸收^[42]、硅^[43]中的非线性电光调制或简单的外部数字处理器^[39]以固定或可重新编程的方式实现^[44]。光学元件不需要在ANN中进行矩阵乘法和非线性激活等数学操作，其本身就代表了一种数学运算操作。例如光脉冲神经网络利用片上光学元件，如波导、波分复用器和环形谐振器^[40,43,45]自然地模拟了生物神经元的基本集成和发射功能。这些神经形态的光子平台在处理信息时具有速度和并行性上的压倒性优势。新的光子学结构和深度学习之间的相互作用可能会克服当前计算方法和系统的限制，并潜在地将人工智能研究引向新的视野。事实上，已经证明逆向设计的超材料可以利用电磁场^[46]求解积分方程。另一方面，波动物理学也可以看作是一个模拟递归神经网络^[47]。深度学习技术已经展示了其在整个光学系统优化上的巨大潜力，并将继续探索新的方法来加速光学测量，甚至发现新的光学效应。总之，新的光子学结构实现非常规计算和人工智能技术的潜力还值得进一步探索。

本综述介绍了用于光子设计的正向预测与逆向设计的深度学习方法。这些显著的发展都在过去几年中得到了证明，随着不同背景的研究人员对这一新兴领域的贡献，人们期待着进一步的飞跃性进展。人工智能研究人员应该与光学科学家一起协同合作，开发非传统的、物理驱动的算法，这些算法和网络不仅具有鲁棒性、生成性和可解释性，同时使用更少的数据，可以提供了实现无与伦比的光学功能器件的非常规方法。这种融合人工智能、微纳光子学的跨学科方法将允许具有独特功能的大规模光子学结构设计以及新的光学表征方法，为高速超分辨成像、实时探测和操控、高效的能量转换系统以及量子测量和计量领域的变革性进展铺平道路。在这条道路上，光子学界应该以构建一个包含光子概念、架构、组件和光子材料的综合数据集为最终目标。