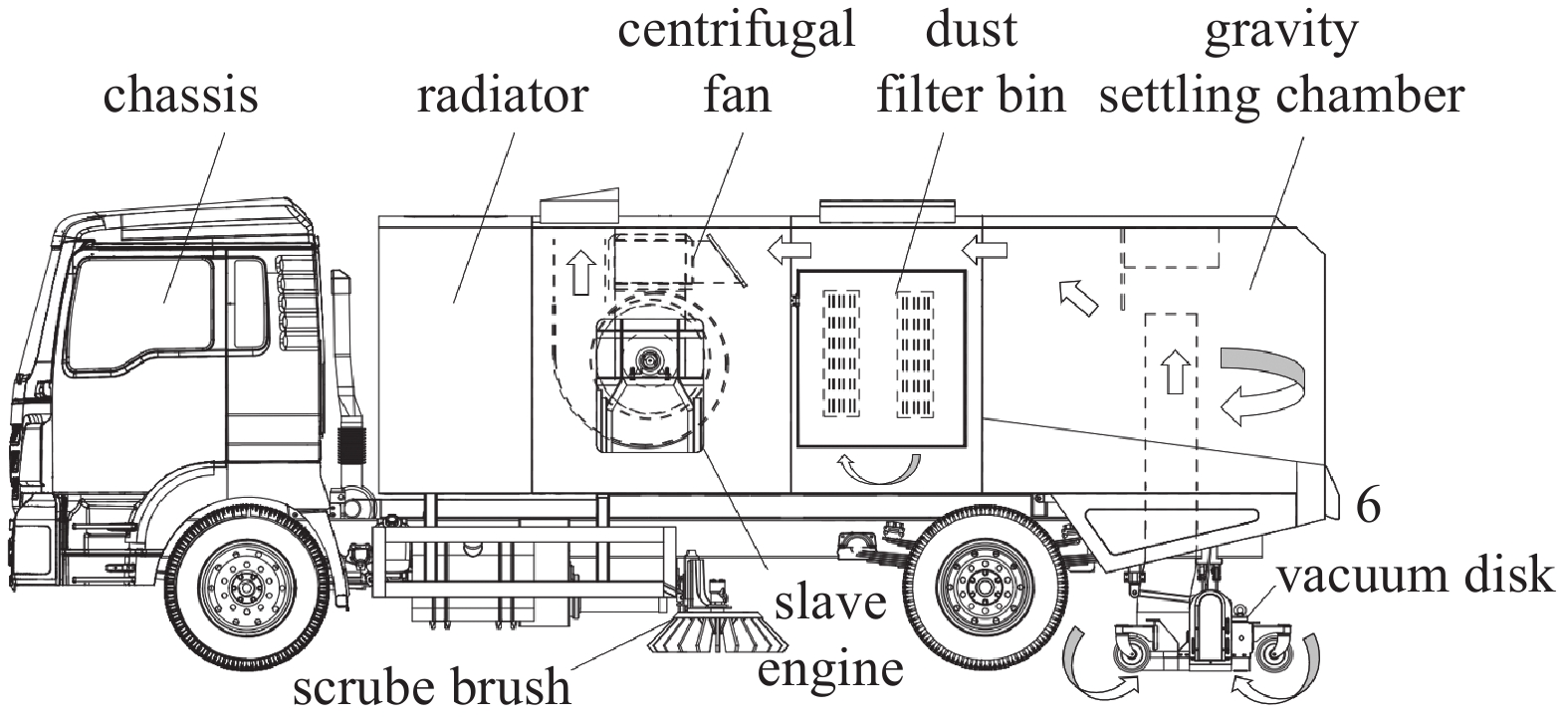
如下图1所示，道路上的尘粒被吸尘盘吸起后，经气力输送管道进入重力沉降室中，在沉降室中依靠自身重力沉降与气流分离^[9]。

尘粒沉降的过程中，竖直方向主要受到自身重力$G$、气流动力${F_{\rm{D}}}$和气流浮力${F_{\rm{f}}}$（即上升力）的作用^[10-11]。对于大质量的金属颗粒物、石块、树枝等，气流对它们的气流动力和浮力远小于它们自身的重力，这些垃圾会在降落过程中保持加速运动直至接触沉降室底部；粒径极小、质量极低的灰尘颗粒所受的气流动力和浮力大于其自身重力，难以依靠自身重力下落，会随气流被输送至滤尘仓内被滤筒吸附^[12-13]。

对于质量相对较小的细小尘粒，其自身重力与气流动力和气流浮力的大小相当，细小尘粒的沉降过程按其受力不同主要分为以下三个阶段：

（1）初始状态：尘粒从静止开始向下做自由落体运动，此时尘粒的速度${v_{\rm{c}}}$为0，尘粒所受气流动力${F_{\rm{D}}}$为0。尘粒受到自身重力$G$和极小的气流浮力${F_{\rm{f}}}$共同作用获得竖直向下的加速度$a$，所受合力${F_{\rm{H}}} = G - {F_{\rm{f}}} = {m_{\rm{c}}}a$。

（2）加速沉降：尘粒竖直向下做加速运动，气流动力增大，此时所受合力${F_{\rm{H}}} = G - {F_{\rm{f}}} - {F_{\rm{D}}} = {m_{\rm{c}}}a$，尘粒竖直向下的加速度因气流动力的增大而逐渐减小。

（3）匀速沉降：随着尘粒气流动力继续增大，当竖直方向上合力${F_{\rm{H}}}$为0时，尘粒的加速度$a$减小为0，气流动力不再变化，尘粒进入匀速沉降阶段。各力大小及尘粒所受的合力表达式分别如下：

式中，${C_{\rm{f}}}$为气动阻力系数，湍流时取值为0.44；${v_{\rm{c}}}$为气流与尘粒的相对速度，${\text{m/s}}$；${d_{\rm{D}}}$为尘粒的当量粒径，${\text{m}}$；$\rho $为空气密度，${\text{kg/}}{{\text{m}}^{\text{3}}}$；${\rho _{{r}}}$为尘粒的真实密度，${\text{kg/}}{{\text{m}}^{\text{3}}}$；${m_{\rm{c}}}$为尘粒的质量，${\text{kg}}$；$g$为重力加速度，${\text{m/}}{{\text{s}}^{\text{2}}}$。

由式（1）~（4）可推导得到尘粒能够依靠自身重力匀速沉降的临界风速：

本文所研究的清扫车滤尘仓可以过滤和吸附当量粒径在0.5 mm以内的灰尘颗粒，为了确保沉降室内当量粒径大于0.5 mm的尘粒都能依靠自身重力沉降，取当量粒径${d_{\rm{D}}} = 0.5{\text{ mm}}$，路面典型尘粒^[14]中砂石的真实密度为1500~2000 kg/m³，这里取最小值${\rho _{\rm{r}}}$=1500 kg/m³，将数据代入式（5）计算出：

因此当沉降室底部风速$v \leqslant 4.15 \; {\text{m/s}}$时，当量粒径大于0.5 mm的尘粒到达沉降室底部后不会被气流再次吹起，均可以依靠自身的重力沉降。

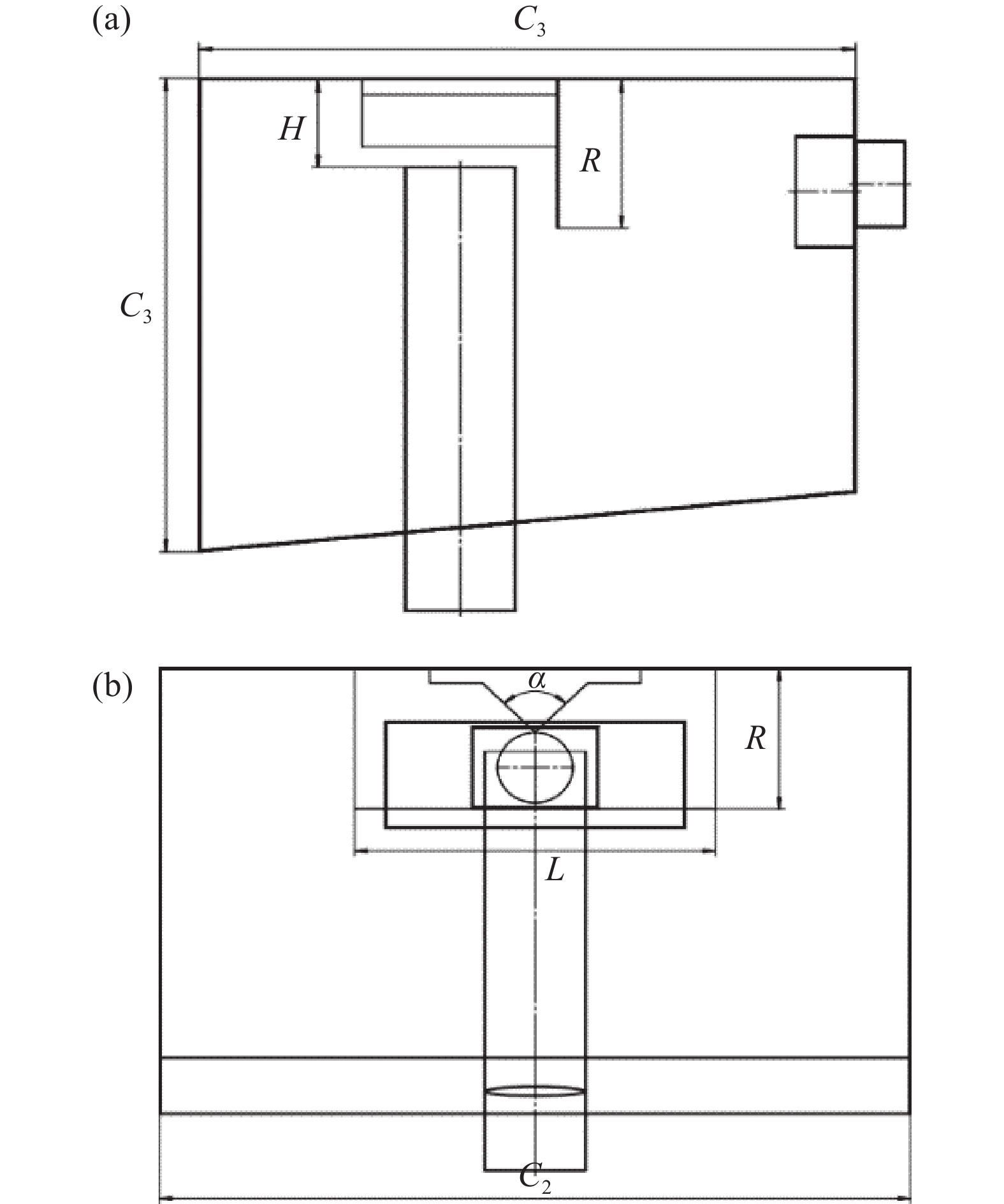
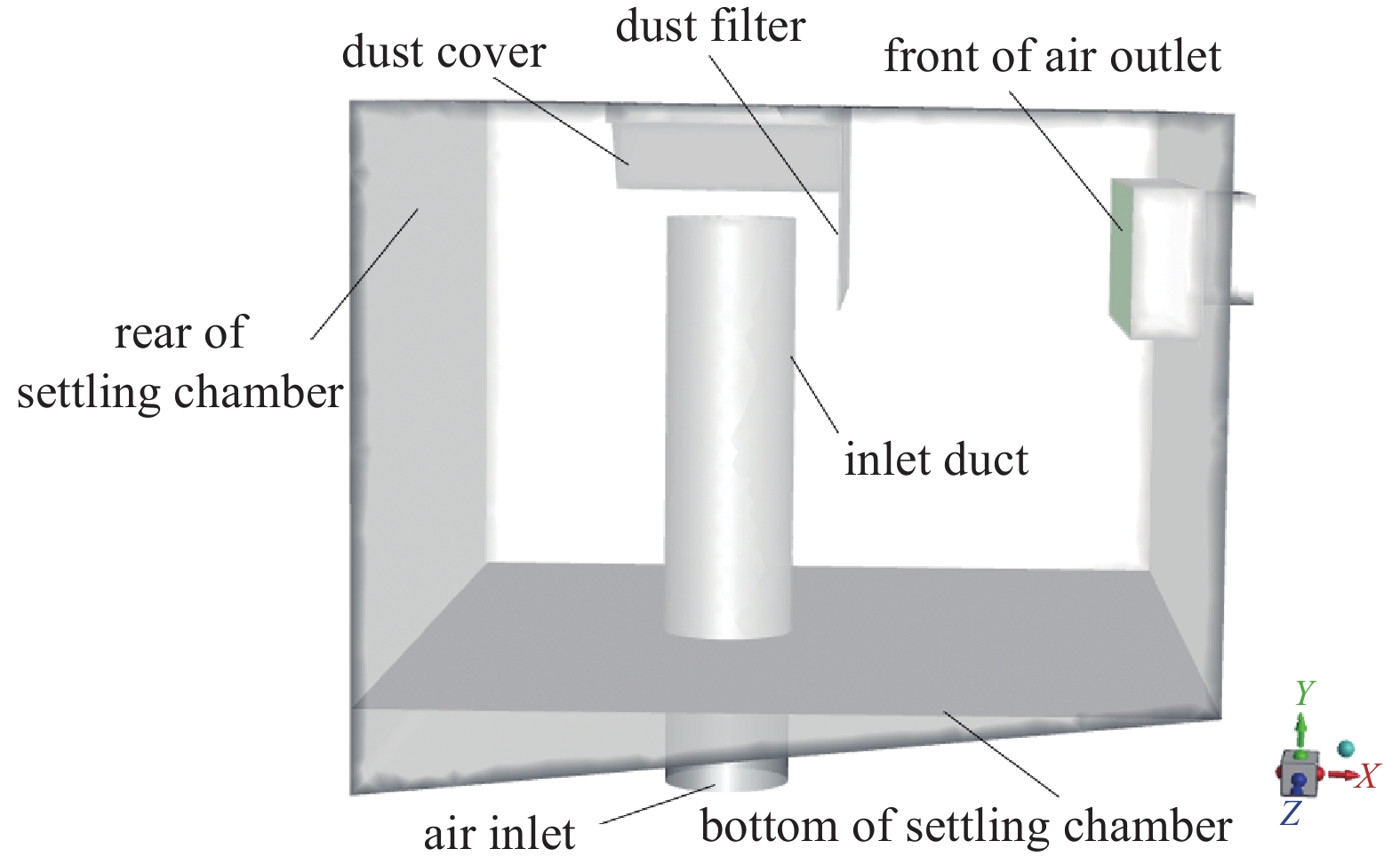
重力沉降室是清扫车除尘系统中用于沉降和分离尘粒的核心部件，依靠沉降室中的挡尘罩、挡尘板等惯性除尘器对携尘气流进行阻挡与分流，能够更好的促使尘粒分离沉降。沉降室结构如下图2所示，主要结构参数包括：沉降室长度${C_{\text{1}}}$、宽度${C_{\text{2}}}$、高度${C_{\text{3}}}$、进风管出口距顶部距离H，挡尘罩夹角$\alpha $，挡尘板宽度L，挡尘板高度R。

重力沉降室是在清扫车的二类底盘基础之上进行安装调试的，二类底盘上需同时布置离心风机、水箱、液压系统、滤尘仓和沉降室等，当底盘型号确定后，沉降室箱体的长度、宽度和高度一般就不做改变^[15]。因此本文主要研究挡尘罩夹角$\alpha $、挡尘板宽度$L$和进风管出口距沉降室顶部距离$H$对沉降室沉降特性的影响。

利用FLUENT对尘粒在沉降室内的运动过程进行模拟，采用欧拉-拉格朗日方法，建立颗粒相的DPM模型。假设离散相颗粒不发生形变，与沉降室内的空气不存在耦合作用，将其简化为气固两相流问题，即离散相颗粒在重力沉降室内的连续相空气流域内的颗粒流动问题。

重力沉降室的流场仿真采用速度入口（Velocity-inlet）和速度出口（Velocity -outlet）边界条件。道路清扫车正常工作时风机转速为1800 r/min，风机流量为11510 m³/h，利用毕托管风速测量仪测得重力沉降室的进风口速度为35 m/s，出风口速度为11 m/s。

环境温度设置为25℃，时间响应为稳态求解，重力沉降室内部的空气流动为不可压缩流动，即空气密度恒定。选用标准k-ε湍流模型，有限体积法（FVM）模拟重力沉降室工作时的内部流场。

沉降室沉降性能评价指标参考面如下图3所示。本文主要分析挡尘罩夹角$\alpha $、挡尘板宽度$L$和进风管出口距沉降室顶部距离$H$对沉降室沉降特性的单因素影响。选择重力沉降室底部平均速度${Y_1}$、出风口前部平均速度${Y_2}$（${Y_2}$越小，则携尘气流在沉降室内部运动的时间越长，尘粒依靠自身重力沉降的可能性就越大。 ）和沿程压力降${p_0}$（沉降室的进风口至出风口的压强差，反映沿程压力损失的大小）作为重力沉降室沉降特性的评价指标。

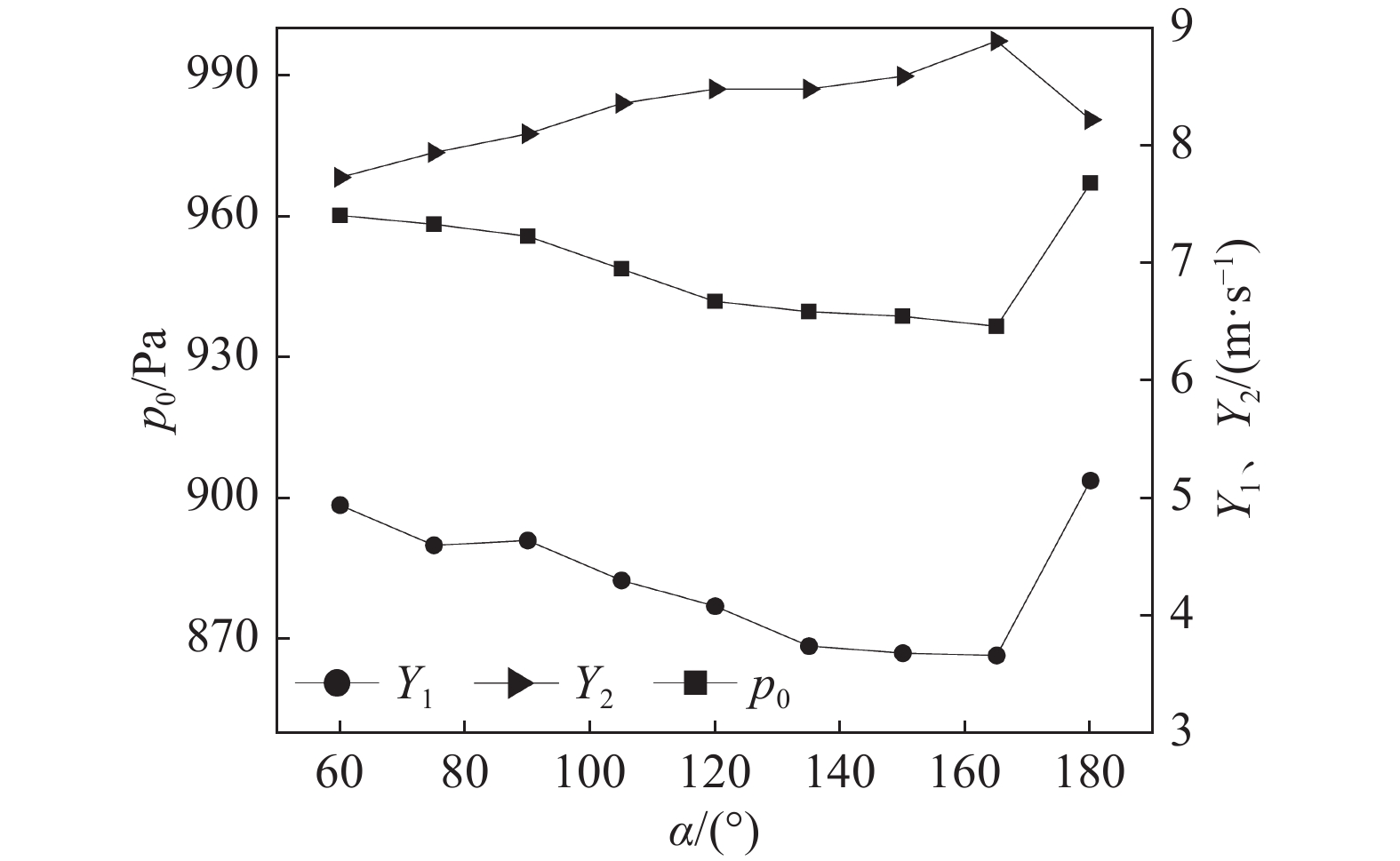
设定进风管出口距沉降室顶部距离$H$为300 mm，挡尘板宽度$L$为1000 mm，改变挡尘罩夹角$\alpha $，对应${Y_1}$、${Y_2}$和${Y_3}$的变化规律如下图4所示。

由图4可知：随着$\alpha $从60°逐渐增大至180°，${Y_1}$和${p_0}$先减小后增大，${Y_2}$先增大后减小。这是由于$\alpha $较小时，沿进风管出口排出的气流经由挡尘罩分流，折射部位主要集中在沉降室顶部和侧壁的中下部，此时沉降室底部受到折射气流的影响较大；随着$\alpha $逐步变大，气流的折射部位逐渐集中在沉降室顶部和侧壁的上部，减少了对沉降室底部的扰动，${Y_1}$逐渐减少，${Y_2}$逐渐增大。同时气流在沉降室侧壁折射位置的上移，使气流从进风管出口至沉降室出风口的路径变短，沿程气力损耗降低，进而${p_0}$逐渐减小。

$\alpha $继续增大至180°的过程中，挡尘罩的形状趋近于平面，逐渐失去了分流作用。大部分气流经沉降室顶部折射后直接向下对底部空间造成较大扰动，此时${Y_1}$增大，出风口前部受到气流的扰动影响减小，${Y_2}$减小。同时气流在从进风管出口至沉降室出风口的路径变长，沿程气力损耗增加，进而${p_0}$增大。为确保${Y_1}$小于4.15 m/s，挡尘罩夹角$\alpha $的调整范围为120°~150°。

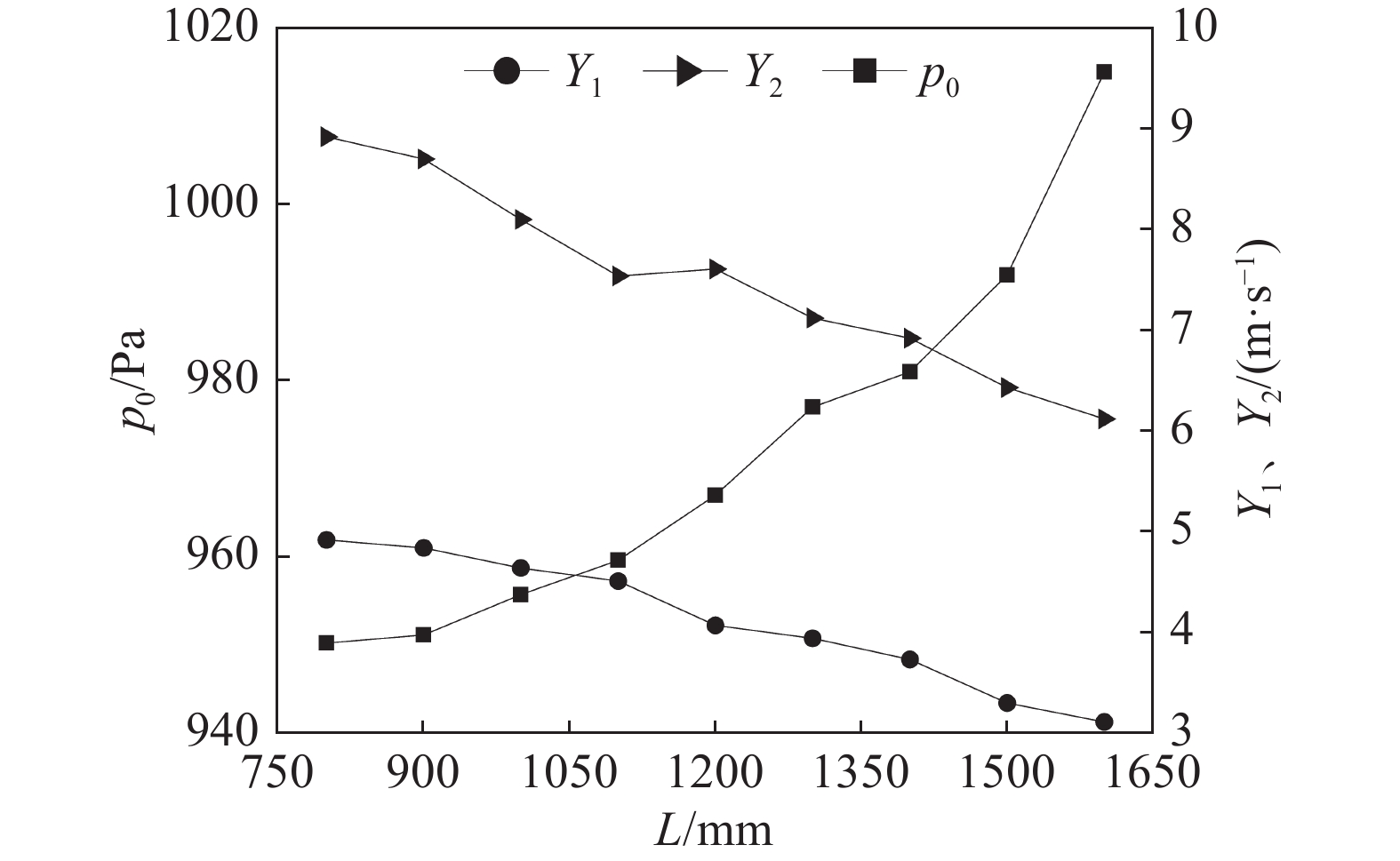
设定挡尘罩夹角$\alpha $为90°，进风管出口距沉降室顶部距离$H$为300 mm，改变挡尘板宽度$L$，对应${Y_1}$、${Y_2}$和${p_0}$的变化规律如下图5所示。

随着L从800 mm逐渐增大至1600 mm，${Y_1}$和${Y_2}$均逐渐减小，而${p_0}$逐渐增大。这是由于进风管出口排出的气流在平行于进风管纵截面方向上经由挡尘罩分流，而平行于进风管横截面方向的气流则被挡尘板阻碍分流，防止携带尘粒的气流从进风管排出后直接进入沉降室出风口，造成尘粒排放的二次污染。而L的增加意味着挡尘板对气流的阻碍分流作用增强，气流从进风管出口至沉降室出风口的沿程气力损耗增加，进而${p_0}$增大。同时沉降室上部受到气流的扰动影响也因为挡尘板宽度的增加而减小，${Y_1}$和${Y_2}$均减小。

适当增加L，虽然会增加气力输送过程中的沿程损耗，即${p_0}$，但是可以有效降低${Y_1}$和${Y_2}$，提高沉降室的降尘能力，挡尘板宽度$L$的调整范围为1200~1400 mm。

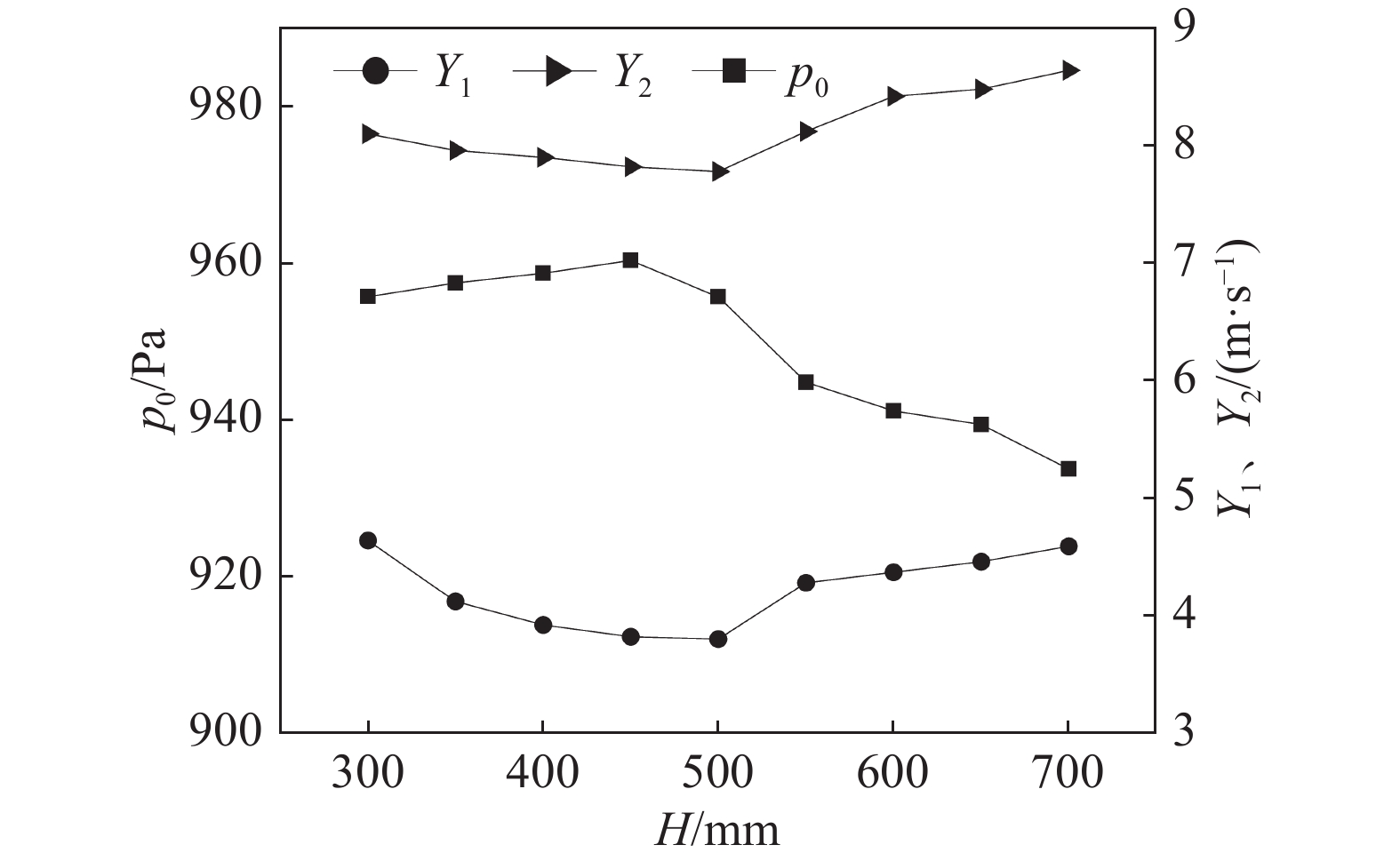
设定挡尘罩夹角$\alpha $为90°，挡尘板宽度$L$为1000 mm，改变进风管出口距沉降室顶部的距离$H$，对应${Y_1}$、${Y_2}$和${Y_3}$的变化规律如下图6所示。

随着$H$从300 mm逐渐增大至700 mm，${Y_1}$和${Y_2}$先减小后增大，沿程压力降先增大后减小。在$H$为300~500 mm时，进风管出口位置高于挡尘板最下端，气流从进风管出口流出后，呈发散辐射的趋势，随后受到挡尘罩和挡尘板的阻碍分流。$H$越来越大时，气流受到挡尘罩和挡尘板的阻碍前辐散的程度越大，气力损耗越大，速度下降得越快。此时气流到达挡尘罩时速度下降，因此${Y_1}$和${Y_2}$减小，${p_0}$增加。

当$H$超过500 mm后，进风管出口位置低于挡尘板最下端，此时气流从进风管出口流出后，一部分发散辐射的气流直接从挡尘板下部通过进入沉降室出风口。随着$H$的增加，更多气流直接从挡尘板下部通过，挡尘板的阻碍分流作用大幅下降，气流的沿程气力损耗减小，${p_0}$减小，同时${Y_1}$和${Y_2}$均增大。为确保${Y_1}$小于4.15 m/s，进风管出口距沉降室顶部距离H的调整范围为400~500 mm。

上节的单因素试验已对挡尘罩夹角$\alpha $、挡尘板宽度L、进风管出口距沉降室顶部距离H进行了参数的初步优选，有效减少了后续试验的次数，提高试验设计的效率。因此针对单因素优选后的范围值，设计三因素三水平的Box-Behnken试验，因素水平设置入下表1所示。

根据软件Design-Expert生成的Box-Behnken试验设计表进行仿真模拟试验，以沉降室各结构参数为自变量，以沉降室底部平均速度${Y_1}$、出风口前部平均速度${Y_2}$和沿程压力降${p_0}$作为评价指标，试验结果如下表2所示。

根据表2的数据样本，通过软件Design-Expert分别得到${Y_1}$、${Y_2}$和${p_0}$与结构参数:$\alpha $、L和H的三元二次回归方程：

在模型的显著性检验中，模型的P值越小（P＜0.05），且失拟项不显著（P＞0.05），则该模型的拟合精度越高，响应面拟合模型能够更好地解释因变量的变异。

沉降室底部平均速度${Y_1}$回归模型的方差分析结果如下表3所示。回归模型的P值为0.0038（＜0.05）；同时失拟项的P值为0.0750（＞0.05），表明${Y_1}$的回归模型显著且拟合精度较好。由$\alpha $、L、H的P值可判断：各结构参数对${Y_1}$的影响程度从大到小依次为$L$＞$H$＞$\alpha $。

出风口前部平均速度${Y_2}$回归模型的方差分析结果如下表4所示。回归模型的P值小于0.0001；同时失拟项的P值为0.5933（＞0.05），表明${Y_2}$的回归模型显著且拟合精度较好。由$\alpha $、L、H的P值可判断：各结构参数对出风口平均速度${Y_2}$的影响程度从大到小依次为$L$＞$\alpha $＞$H$。

沿程压力降${p_0}$回归模型的方差分析结果如下表5所示。回归模型的P值小于0.0001；同时失拟项的P值为0.4307（＞0.05），表明${Y_3}$的回归模型显著且拟合精度较好。由$\alpha $、L、H的P值可判断：各结构参数对沿程压力降${p_0}$的影响程度从大到小依次为$L$＞$\alpha $＞$H$。

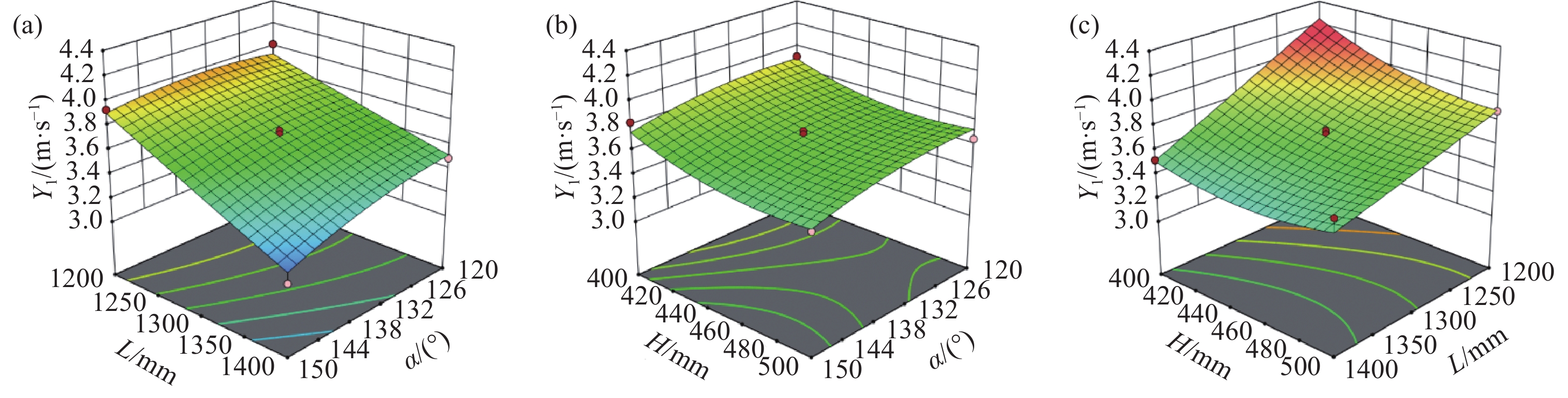
根据回归模型的分析结果，利用Design-Expert绘制各因素的3D交互响应曲面图。结构参数：挡尘罩夹角$\alpha $、挡尘板宽度L、和进风管出口距沉降室顶部距离H对沉降室底部平均速度${Y_1}$、出风口前部平均速度${Y_2}$和沿程压力降${p_0}$的因素交互响应曲面分别如下图7、8和9所示。

（1）沉降室底部平均速度${Y_1}$的响应面分析

从图7 (a)可以看出随着L和$\alpha $的增加， ${Y_1}$越来越小，$\alpha $对${Y_1}$的影响程度随着L的增加而增加；从图7(b)可以看出，随着$\alpha $和H的增加，${Y_1}$略微减小，当H较小时，$\alpha $对${Y_1}$的影响程度很小；如图4所示，L越大，${Y_1}$越小，H对${Y_1}$的影响程度随着L的增加而减小。

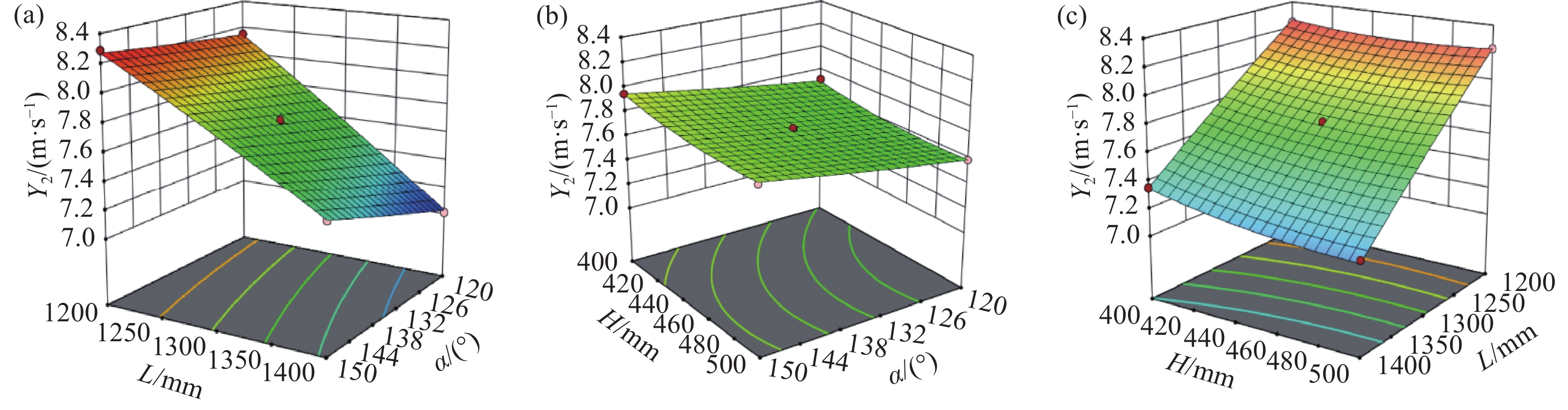
（2）出风口前部平均速度${Y_2}$的响应面分析

由图8(a)可知L越大，$\alpha $越小，${Y_2}$越小，$\alpha $对${Y_2}$的影响程度随着L的增加而增加；由图8(b)可知随着$\alpha $的增加，${Y_2}$略微增大，同时H对${Y_2}$的影响程度很小；如图8(c)所示，L越大，${Y_2}$越小，同时H对${Y_2}$的影响程度很小。

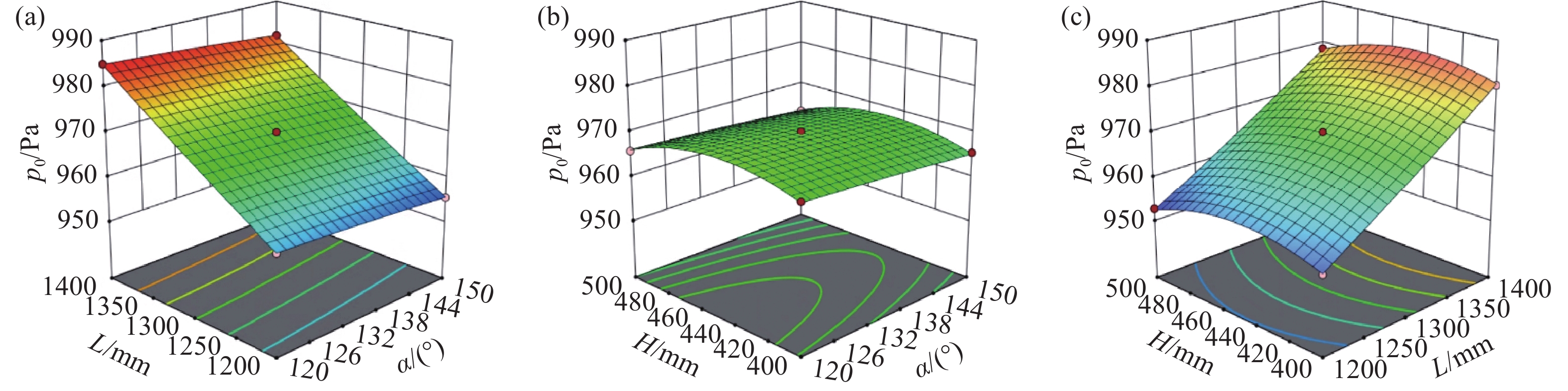
（3）沿程压力降${p_0}$的响应面分析

由图9(a)可知：L越小，${Y_3}$越小，同时$\alpha $对${Y_3}$的影响程度很小；由图9(b)可知随着H的增加，${Y_3}$先增大后减小，而此时$\alpha $对${Y_3}$的影响程度很小；如图9(c)所示，L越大，${Y_3}$越大，${Y_3}$随着H的增加呈现出先增大后减小的趋势。

针对${Y_1}$、${Y_2}$和${p_0}$的回归模型，以${Y_1}$、${Y_2}$和${p_0}$同时取最小值为约束条件，运用Design-Expert软件的Optimization功能进行多目标响应面优化。

求解回归模型得到的重力沉降室最优参数为：$\alpha $=150°、L=1360 mm、H=500 mm。最优参数下的${Y_1}$=3.39 m/s， ${Y_2}$=7.57 m/s， ${p_0}$=971.53 Pa。

为验证响应面优化参数的可靠性，在最优参数条件下进行Fluent仿真试验，仿真结果为${{{Y}}_{\text{1}}}$=3.54 m/s， ${{{Y}}_2}$=7.41 m/s， ${p_0}$=965.44 Pa。响应面优化得到的近似值与仿真计算结果的误差率分别为4.23%，2.16%和0.63%，表明该响应面优化得到的参数具有较高的可靠性。

根据上文对沉降室的单因素分析与多目标响应面优化，对沉降室参数进行改进：$\alpha $由90°调整为150°，L由1000 mm调整为1360 mm， H由300 mm调整为500 mm。为了验证沉降室优化后的沉降特性，对其内部流场和颗粒相运动情况进行分析。

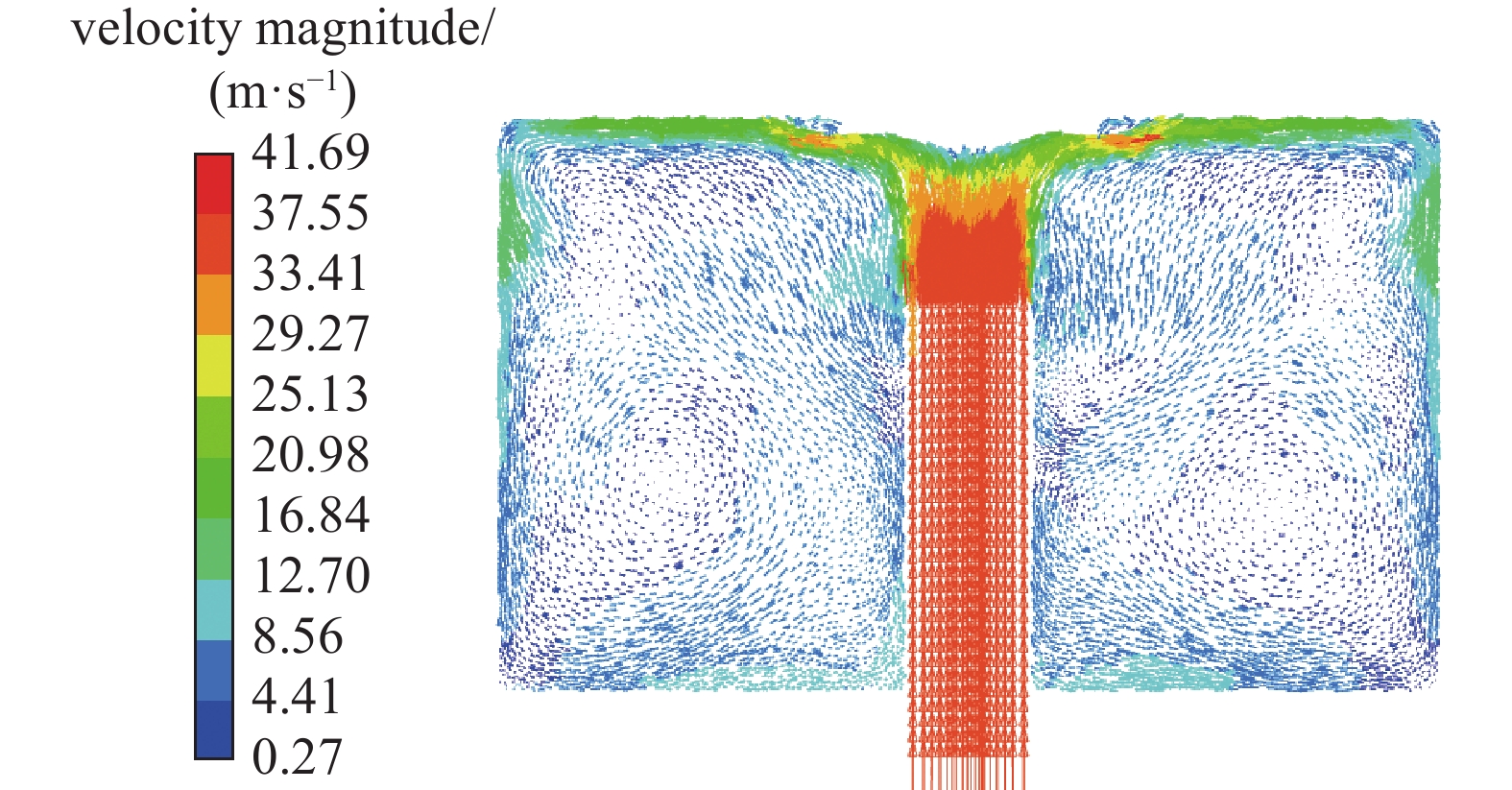
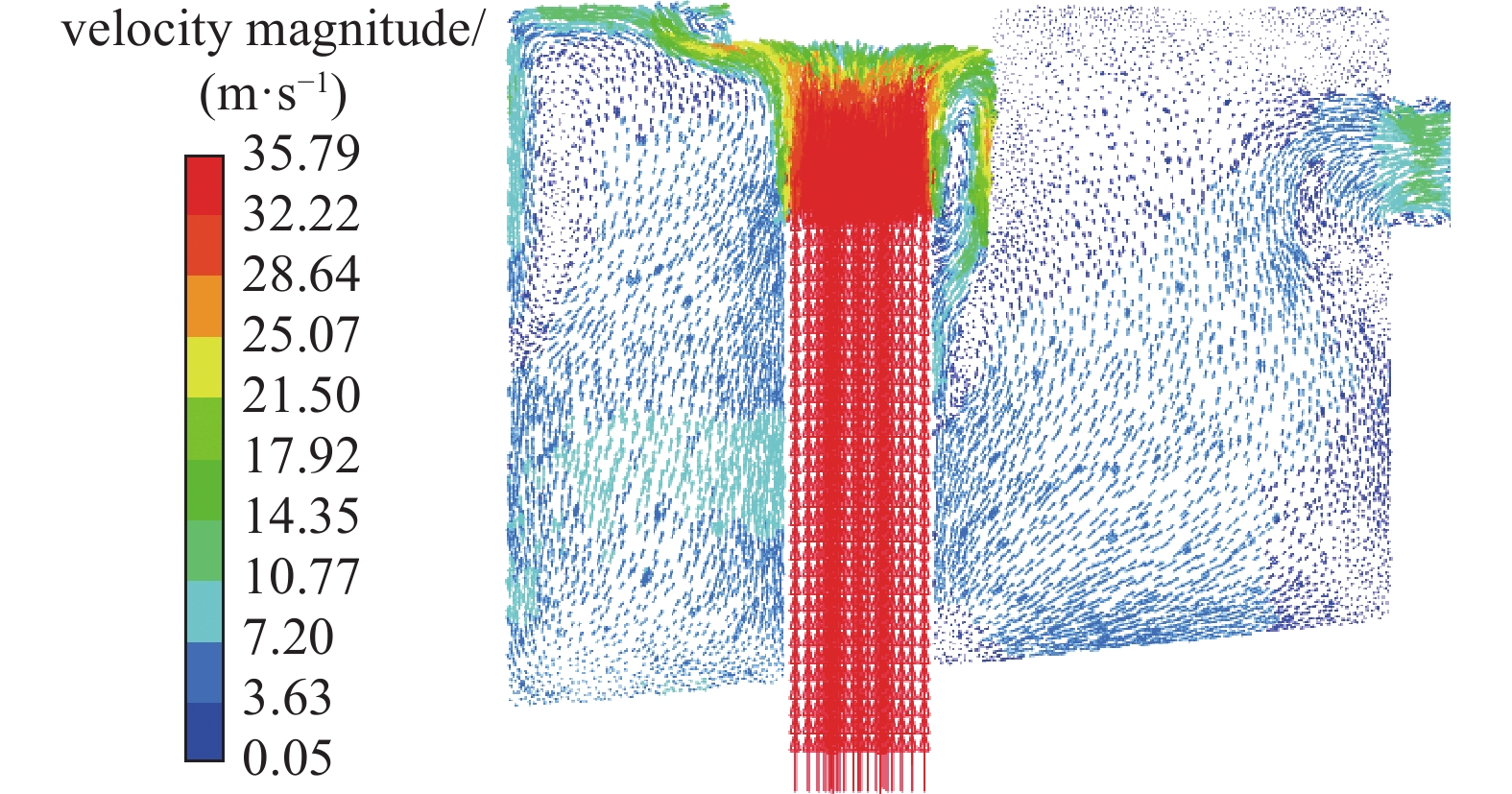
优化后的重力沉降室沿进风管横截面速度分布情况如下图10所示。从图中可以看出，在进风管的横截面，气流从进风管出口高速流入沉降室后发生辐散，气流两侧区域速度迅速下降，与挡尘板接触时气流速度已下降至13~18 m/s；由于H和L的增大，气流与挡尘板接触后，挡尘板充分发挥了阻碍和导流作用，将部分气流引向沉降室后部，此时气流速度稳定在7~10 m/s，无涡流产生。${{{Y}}_{\text{1}}}$、${{{Y}}_2}$较优化前均下降至3.5 m/s 和7 m/s左右，均有利于尘粒在沉降室依靠自身重力进行沉降。

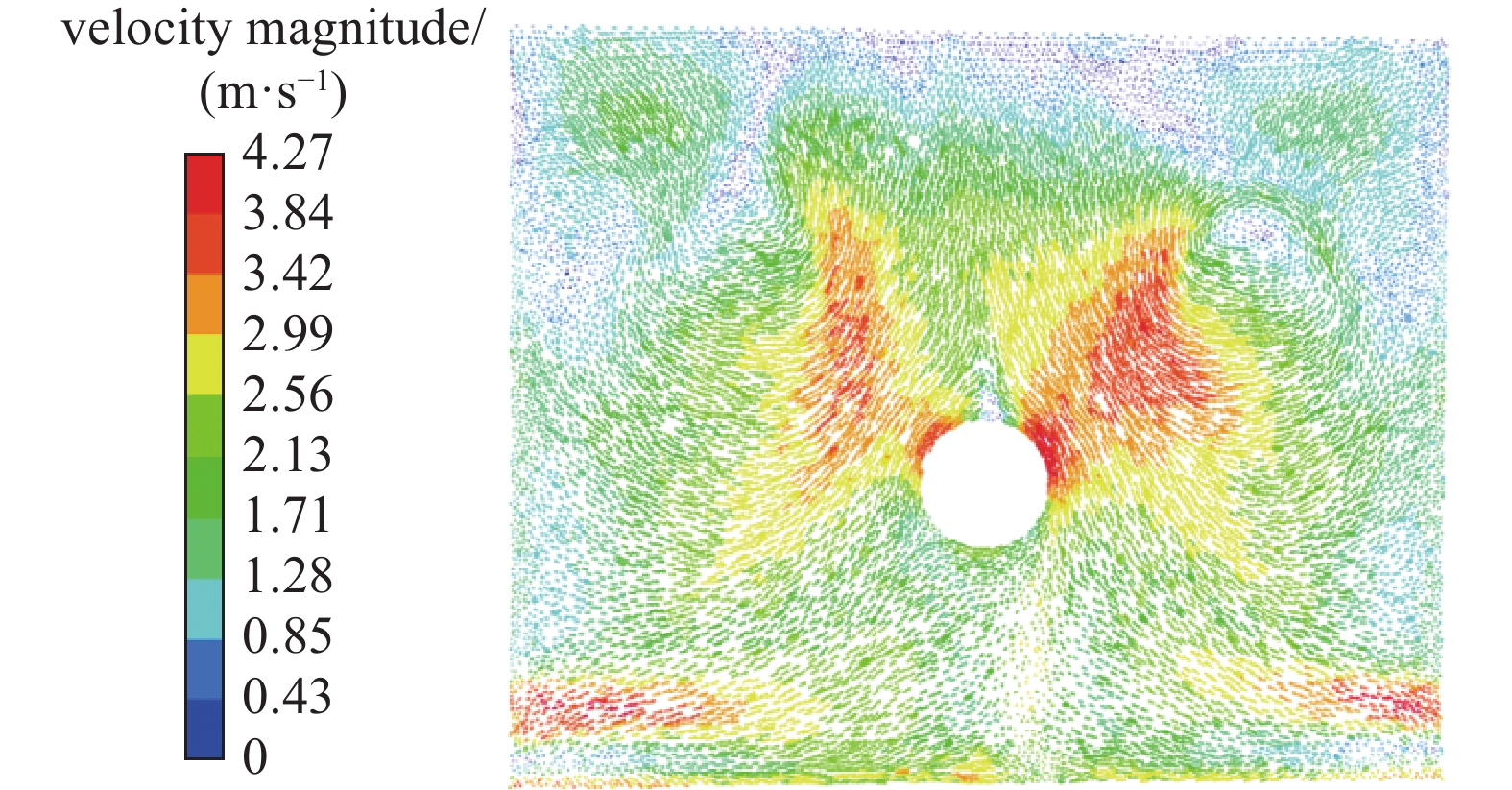
优化后的重力沉降室沿进风管纵截面速度分布情况如下图11所示。从图中可以看出，在进风管的纵截面，从进风管出口高速流出的气流受到了挡尘罩的阻碍和分流作用；由于$\alpha $增加，气流的折散部位较优化前发生了上移，主要集中在沉降室顶部和两侧壁的上部，此处的速度下降至12~17 m/s；此时沉降室底部受到两侧壁的折散气流扰动大幅下降，气流速度下降至3~4 m/s，气流对尘粒的沉降过程影响较小。

优化后的重力沉降室底部速度分布情况如下图12所示。从图中可以看出，气流主要从沉降室两侧壁后方的向沉降室中前部运动，速度基本呈现对称分布；风速较高的区域较优化前大幅减小，主要集中在进风管与挡尘板附近和沉降室尾部侧壁，最大速度为4.27 m/s，绝大部分区域风速在4 m/s以下。优化后的进风管、挡尘板和挡尘罩的结构及布置合理，使挡尘板和挡尘罩能够起到充分的阻碍与分流作用，到达沉降室底部的气流速度较优化前大幅下降，有利于尘粒的沉降。

将尘粒描述为离散的DPM颗粒相模型，模拟颗粒相在优化后的沉降室连续相流体域内的运动情况。颗粒相的特征参数如表6所示。

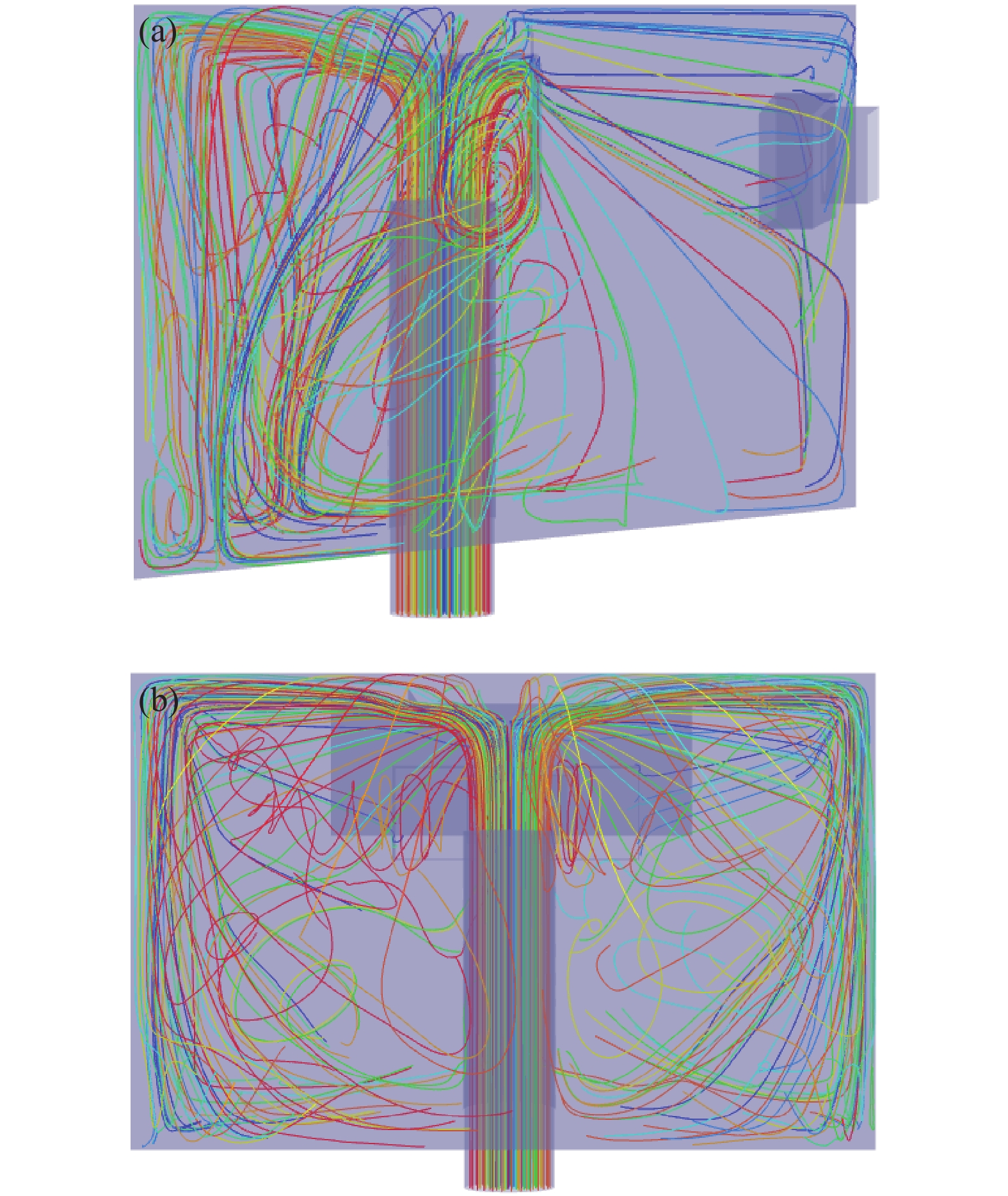
颗粒在优化后沉降室内部的运动轨迹如下图13所示。从图可知，尘粒经进风管进入沉降室后，在挡尘罩和挡尘板的分流阻碍作用下，绝大部分尘粒被气流带向沉降室底部，尘粒在自身重力的作用下开始沉降；由于沉降室底部气流速度较优化前大幅降低至4 m/s，大部分尘粒到达沉降室底部后不会再被气流吹起，极小一部分尘粒在沉降室底部重新被高速气流带起向出风口聚集并逃逸，优化后的沉降室具有较优的沉降效果。

利用DPM Iteration统计当量粒径0.5 mm的尘粒在重力沉降室内的沉降效率。重力沉降室的进风口注入尘粒数为1792个，优化前：沉降室出风口的尘粒逃逸数为274个，沉降效率为84.71％；优化后：沉降室出风口颗粒逃逸数为104个，沉降效率提升至94.20％。

优化后沉降室的沉降特性较优化前显著改善，主要体现在：在${p_0}$略微增加的前提下，${Y_1}$从4.84 m/s下降至3.54 m/s，降低26.86%；${Y_2}$从8.4 m/s下降至7.41 m/s，降低11.79%；当量粒径0.5 mm的尘粒在沉降室中的沉降效率从84.71%提升至94.20%。以上对比分析表明，优化后的重力沉降室对当量粒径0.5 mm以上的尘粒有较优的沉降效果，达到了流场特性优化的目的。

本文利用FLUENT研究了重力沉降室的挡尘罩夹角$\alpha $，挡尘板宽度L和进风管出口距沉降室顶部距离H对沉降特性的影响，具体结论如下：

（1）对沉降特性进行单因素分析，获得了沉降性能较优的参数取值范围： $\alpha $为120°~150°， L为1200~1400 mm， H为300~500 mm；

（2）利用Box-Behnken设计和响应面分析得到重力沉降室的最优结构参数： $\alpha $为150°， L为1360 mm， H为500 mm；

（3）优化后的重力沉降室较优化前：沿程压力降${p_0}$略微增加，${Y_1}$降低26.86%，${Y_2}$降低11.79%，尘粒的沉降效率提升至94.20%；

本文提出的清扫车沉降室的结构优化设计思路（参数化建模、流场仿真、多目标响应面优化、气固两相流验证）可用于指导实际生产中清扫车沉降室结构的研发设计。