高级搜索

大气压双频Ar/O2放电等离子体特性的数值模拟

, 

downloadPDF

上一篇

下一篇

崔明晨, 王一男. 大气压双频Ar/O2放电等离子体特性的数值模拟[J]. 真空科学与技术学报, 2023, 43(11): 977-986. doi: 10.13922/j.cnki.cjvst.202301008
引用本文: 崔明晨, 王一男. 大气压双频Ar/O2放电等离子体特性的数值模拟[J]. 真空科学与技术学报, 2023, 43(11): 977-986. doi: 10.13922/j.cnki.cjvst.202301008
shu
Mingchen CUI, Yinan WANG. Numerical Simulation of the Characteristics of Dual Frequency Ar/O2 Discharge Plasma at Atmospheric Pressure[J]. zkkxyjsxb, 2023, 43(11): 977-986. doi: 10.13922/j.cnki.cjvst.202301008
Citation: Mingchen CUI, Yinan WANG. Numerical Simulation of the Characteristics of Dual Frequency Ar/O2 Discharge Plasma at Atmospheric Pressure[J]. zkkxyjsxb, 2023, 43(11): 977-986. doi: 10.13922/j.cnki.cjvst.202301008
shu

大气压双频Ar/O2放电等离子体特性的数值模拟

  • 1.

    辽宁石油化工大学理学院 抚顺 113001

  • 2.

    共青科技职业学院 九江 332020

    • 通讯作者: E-mail: ynwang1985@hotmail.com

  • 中图分类号: O539

Numerical Simulation of the Characteristics of Dual Frequency Ar/O2 Discharge Plasma at Atmospheric Pressure

  • 1.

    College of Science, LiaoNing Petrochemical University, Fushun 113001, China

  • 2.

    GongQing Institute ofScience and Technology, Jiujiang 332020, China

    • Corresponding author: Yinan WANG, ynwang1985@hotmail.com

  • MSC: O539

  • 摘要: 文章采用等离子体流体理论模型，研究了双频容性耦合放电中高频源频率对大气压氩气与氧气混合气体放电等离子体的各类粒子密度与各项等离子体参数的影响。通过模拟不同高频源频率的放电，得到了放电空间中各类粒子的密度、电子温度、电场等参数的一维时空分布，进一步了解了双频放电中高频源频率对等离子体特性的影响作用。研究结果表明：当放电电压固定时，随高频源频率的升高，电子密度逐渐增大；电子温度、电场与电势有下降的趋势；各类氩离子密度与氩原子的亚稳态密度随高频源频率的升高而增大；随高频源频率的升高，各类氧离子密度增大，氧原子密度先减小后增大，氧分子的亚稳态密度先增大后减小。电子压力加热、电子欧姆加热、电子加热和能量损失受高频源频率的影响均逐步升高。此外，有效电流密度与有效功率密度随高频源频率的升高大体增加。
    Abstract: Based on the plasma fluid theory, the effects of high-frequency source frequency in dual frequency capacitive coupling discharge on the various particles’ density and plasma parameters of argon oxygen mixture discharge plasma at atmospheric pressure were studied. We simulate the discharge in different high-frequency source frequencies and have achieved the one-dimensional space-time distribution of the various particles’ density, electron temperature, electric field and other parameters, and a better understanding of the influence of high-frequency source frequency on plasma characteristics in dual frequency discharge. The results show that when the discharge voltage is fixed, the electron density increases with the increase of the high-frequency source frequency; The electron temperature, electric field and potential have a downward trend; The density of various argon ions and sub argon atoms increases with the increase of high-frequency source frequency; With the increase of high-frequency source frequency, the density of various oxygen ions increases, the density of oxygen atoms decreases first and then increases, and the metastable density of oxygen molecules increases first and then decreases. Electronic pressure heating, electronic ohmic heating, electronic heating and energy loss are gradually increased due to the influence of high-frequency source frequency. In addition, the effective current density and effective power density generally increase with the increase of high-frequency source frequency.
  • 加载中

  • 图 1  装置结构示意图

    Figure 1.  Schematic diagram of device structure

    下载: 全尺寸图片 幻灯片

    图 2  单周期内放电电流密度与电压波形

    Figure 2.  Waveform of the discharge current density and voltage in one cycle

    下载: 全尺寸图片 幻灯片

    图 3  不同高频源频率下的时间平均的(a)电子密度、(b)电子温度、(c)电场强度和(d)电势的空间分布

    Figure 3.  Spatial distribution of time averaged (a) electron density, (b)electron temperature, (c) electric field and (d) potential at different high-frequency source frequencies

    下载: 全尺寸图片 幻灯片

    图 8  不同高频源频率下的时间平均的(a) PH、(b) PP、(c) PC、(d) PL的空间分布图

    Figure 8.  Spatial distribution of time averaged (a) PH、(b) PP、(c) PC、(d) PL at different high-frequency source frequencies

    下载: 全尺寸图片 幻灯片

    图 4  不同高频源频率下的时间平均的(a)Ar2+粒子密度、(b)Ar+粒子密度和(c)Ar*粒子密度的空间分布

    Figure 4.  Spatial distribution of time averaged (a) Ar2+ particle density、(b) Ar+ particle density and (c) Ar* particle density at different high-frequency source frequencies

    下载: 全尺寸图片 幻灯片

    图 5  不不同高频源频率下的时间平均的(a) O2+粒子密度、(b) O− 粒子密度、(c) O原子密度和(d) O2*粒子密度的空间分布

    Figure 5.  Spatial distribution of time averaged (a) O2+ particle density、(b)O− particle density、(c) O atom density and (d) O2* particle density at different high-frequency source frequencies

    下载: 全尺寸图片 幻灯片

    图 6  放电达到稳态时放电空间中心区域(a)电子密度与O− 粒子密度、(b) O2*粒子密度与O原子密度随高频源频率的变化图

    Figure 6.  Changes of (a) electron density and O− particle density, (b) O2* particle density and O atom density in the central area of the discharge space with high-frequency source frequency when the discharge reaches a steady state

    下载: 全尺寸图片 幻灯片

    图 7  不同高频驱动源下的(a)电子密度、(b) O−粒子密度、(c) O原子密度和(d) O2*粒子密度的最大值随时间的变化图

    Figure 7.  Variation of time the maximum of (a) electron density, (b) O− particle density, (c) O atom density and (d) O2* particle density at different high-frequency driving sources

    下载: 全尺寸图片 幻灯片

    图 9  有效电流密度Irms、有效功率密度Prms随高频源频率的变化图

    Figure 9.  Variation of effective current density Irms and effective power density Prms with high-frequency source frequency

    下载: 全尺寸图片 幻灯片

    表 1  氩氧混合气体放电中的反应过程

    Table 1.  Reaction process in argon oxygen mixture discharge

    反应过程 反应系数/cm3·s−1
    1. $e+{\rm{Ar}}\to { {\rm{Ar} } }^{+}+2{\rm{e}}$ $ {k}_{1}=1.235\times {10}^{-7}\mathrm{e}\mathrm{x}\mathrm{p}(18.6/{T}_{e}{)} $[17]
    2. ${\rm{e}}+{\rm{Ar}}\to {{\rm{Ar}}}^{*}+{\rm{e}}$ $ {k}_{2}=3.71\times {10}^{-8}\mathrm{e}\mathrm{x}\mathrm{p}(-15.06/{T}_{e}{)} $[17]
    3. ${\rm{e}}+{{\rm{Ar}}}^{*}\to {{\rm{Ar}}}^{+}+2{\rm{e}}$ $ {k}_{3}=2.05\times {10}^{-7}\mathrm{e}\mathrm{x}\mathrm{p}(-4.95/{T}_{e}{)} $[17]
    4. ${{\rm{Ar}}}^{*}+{{\rm{Ar}}}^{*}\to {{\rm{e}}+{\rm{Ar}}}^{+}+{\rm{Ar}}$ $ {k}_{4}=1.2\times {10}^{-9}(300/{T}_{g}{)} $[18]
    5. ${{\rm{Ar}}}^{+}+2{\rm{Ar}}\to {{\rm{Ar}}}_{2}^{+}+{\rm{Ar}}$ $ {k}_{5}=2.5\times {10}^{-31}\mathrm{e}\mathrm{x}\mathrm{p}(-18.6/{T}_{e}{)} $[18]
    6. ${\rm{e}}+{{\rm{Ar}}}_{2}^{+}\to 2{{\rm{Ar}}}^{*}$ $ {k}_{6}=5.4\times {10}^{-8}{{T}_{e}^{-0.66}} $[18]
    7. ${\rm{e} }+{ {\rm{O} } }_{2}\to {{\rm{O}}}_{2}^{+}+2{\rm{e} }$ $ {k}_{7}=9.0\times {10}^{-10}{T}_{e}\mathrm{e}\mathrm{x}\mathrm{p}(-12.6/{T}_{e}{)} $[19]
    8. ${\rm{e}}+{{\rm{O}}}_{2}\to {{\rm{O}}}^{-}+{\rm{O}}$ $ {k}_{8}=8.8\times {10}^{-11}\mathrm{e}\mathrm{x}\mathrm{p}(-4.4/{T}_{e}{)} $[19]
    9. ${{\rm{O}}}^{-}+{{\rm{O}}}_{2}^{+}\to {{\rm{O}}}_{2}+{\rm{O}}$ $ {k}_{9}={{10}^{-13}} $[19]
    10. ${\rm{e}}+{{\rm{O}}}^{-}\to {\rm{O}}+2{\rm{e}}$ $ {k}_{10}=2.7\times {10}^{-7}\mathrm{e}\mathrm{x}\mathrm{p}(-5.5/{T}_{e}{)} $[19]
    11. ${{\rm{Ar}}}^{*}+{{\rm{O}}}_{2}\to {{\rm{O}}}_{2}+{\rm{Ar}}$ $ {k}_{11}={{1.1\times 10}^{-9}} $[18]
    12. ${{\rm{Ar}}}^{*}+{\rm{O}}\to {\rm{O}}+{\rm{Ar}}$ $ {k}_{12}={{8.1\times 10}^{-12}} $[18]
    13. ${{\rm{Ar}}}^{+}+{{\rm{O}}}_{2}\to {{\rm{O}}}_{2}^{+}+{\rm{Ar}}$ $ {k}_{13}={{1.2\times 10}^{-11}} $[18]
    14. ${ {{\rm{Ar}}}_{2}^{+}+{{\rm{O}}}_{2}\to {\rm{O}}}_{2}^{+}+2{\rm{Ar}}$ $ {k}_{14}={{1.0\times 10}^{-10}} $[18]
    15. ${{\rm{e}}+{{\rm{O}}}_{2}\to {\rm{O}}}_{2}^{*}+{\rm{e}}$ $ {k}_{15}={{1.7\times 10}^{-9}{e}^{-3.7/{T}_{e}}} $[18]
    16. ${{\rm{O}}+{{\rm{O}}}_{2}\to {\rm{O}}}_{2}^{*}+{\rm{O}}$ $ {k}_{16}={{1.2\times 10}^{-16}} $[18]
    17. ${ {\rm{e} }+{\rm{} }{\rm{O}}}_{2}^{*}\to { {\rm{O} } }^{-}+{\rm{O} }$ $ {k}_{17}={{1.2\times 10}^{-16}} $[18]
    18. ${{\rm{e}}+{\rm{O}}}_{2}^{*}\to 2{\rm{O}}+{\rm{e}}$ $ {k}_{18}={{2.4\times 10}^{-15}} $[18]
    19. ${\rm{Ar}}+{{\rm{O}}}_{2}^{+}\to {{\rm{O}}}_{2}+{{\rm{Ar}}}^{+}$ $ {k}_{19}={{5.5\times 10}^{-11}} $[18]
    20. ${{\rm{Ar}}}^{+}+{{\rm{O}}}^{-}\to {\rm{O}}+{\rm{Ar}}$ $ {k}_{20}={{2.8\times 10}^{-15}} $[18]
    下载: 导出CSV

    表 2  模型中的边界条件

    Table 2.  Boundary conditions in the model

    边界 $ x=0 $ $ x=L $
    电子通量 ${J}_{{\rm{e}}}={k}_{{\rm{s}}}{n}_{{\rm{e}}}-\gamma \left(\displaystyle \sum _{i}{J}_{+,i}+{J}_{-}\right)$ $J_e=k_s n_e-\gamma\left(\displaystyle \sum_i J_{+, i}+J_{-}\right)$
    正离子通量 ${J}_{+,{\rm{i} } }=\pm {\mu }_{{\rm{i}}}{n}_{{\rm{i}}}E$ $ {J}_{+,i}=\pm {\mu }_{i}{n}_{i}E $
    负离子密度 $ n=0 $ $ n=0 $
    中性粒子密度 $ n=0 $ $ n=0 $
    电子温度 ${T}_{{\rm{e}}}=0.5 \;{\mathrm{ eV}}$ ${T}_{e}=0.5 \; {\mathrm{eV}}$
    电压 $V={V}_{ {\rm{H} } }\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi {f}_{ {\rm{H} } }t\right)+{V}_{{\rm{L}}}\mathrm{sin}\left(2\pi {f}_{{\rm{L}}}t\right)$ $ V= 0 \;{\mathrm{ V}} $
    下载: 导出CSV
  • [1] Lee J K, Babaeva N Y, Kim H C, et al. Simulation of capacitively coupled single- and dual-frequency rf discharges[J]. IEEE Transactions on Plasma Science,2004,32(1):47−53 doi: 10.1109/TPS.2004.823975
    [2] Makabe T, Petrović Z L. Development of optical computerized tomography in capacitively coupled plasmas and inductively coupled plasmas for plasma etching[J]. Applied Surface Science,2002,192(1):88−114
    [3] Godyak V A, Piejak R B, Alexandrovich B M. Ion flux and ion power losses at the electrode sheaths in a symmetrical rf discharge[J]. Journal of Applied Physics,1991,69(6):3455−3460 doi: 10.1063/1.348530
    [4] Carl D A, Hess D W, Lieberman M A. Oxidation of silicon in an electron cyclotron resonance oxygen plasma: kinetics, physicochemical, and electrical properties [J]. Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films, 1990, 8(3): 2924-2930
    [5] Kitajima M, Kuroki H, Shinno H, et al. Growth of silicon oxide on silicon in the thin film region in an oxygen plasma[J]. Solid State Communications,1992,83(5):385−388 doi: 10.1016/0038-1098(92)90250-D
    [6] Chabert P, Braithwaite N. Physics of radio-frequency plasmas [M]. Cambridge: Cambridge University Press, 2011
    [7] Li X C, Bao W T, Jia P Y, et al. Characteristics of a large gap uniform discharge excited by DC voltage at atmospheric pressure[J]. Chinese Physics B,2014,23(9):095202−6 doi: 10.1088/1674-1056/23/9/095202
    [8] Liu D, Yang A, Wang X, et al. Electron heating and particle fluxes in dual frequency atmospheric-pressure helium capacitive discharge[J]. Journal of Physics D:Applied Physics,2016,49(49):49LT01−7 doi: 10.1088/0022-3727/49/49/49LT01
    [9] Han Q, Wu C, Guo Y, et al. Temporal evolution of atmospheric cascade glow discharge with pulsed discharge and radio frequency discharge[J]. Plasma Science and Technology,2020,22(3):034014−11 doi: 10.1088/2058-6272/ab6760
    [10] Wang Y H, Liu W, Zhang Y R, et al. Fluid simulation of inductively coupled Ar/O2 plasmas: comparisons with experiment[J]. Chinese Physics B,2015,24(09):095203−8 doi: 10.1088/1674-1056/24/9/095203
    [11] Pan G, Tan Z, Pan J, et al. A comparative study on the frequency effects of the electrical characteristics of the pulsed dielectric barrier discharge in He/O2 and in Ar/O2 at atmospheric pressure[J]. Physics of Plasmas,2016,23(4):043508−10 doi: 10.1063/1.4946777
    [12] Liu J, Zhang Q Z, Liu Y X, et al. Measurements of ion energy distributions in a dual-frequency capacitively coupled plasma for Ar/O2 discharges[J]. Journal of Physics D:Applied Physics,2013,46(23):235202−8 doi: 10.1088/0022-3727/46/23/235202
    [13] Booth J P, Curley G, Marić D, et al. Dual-frequency capacitive rf discharges: effect of low-frequency power on electron density and ion flux[J]. Plasma Sources Science and Technology,2010,19(1):015005−7 doi: 10.1088/0963-0252/19/1/015005
    [14] Liu Y, Starostin S A, Peeters F J J, et al. Atmospheric-pressure diffuse dielectric barrier discharges in Ar/O2 gas mixture using 200 kHz/13.56 MHz dual frequency excitation[J]. Journal of Physics D:Applied Physics,2018,51(11):114002−15 doi: 10.1088/1361-6463/aaac73
    [15] Magnus F, Gudmundsson J T. Digital smoothing of the langmuir probe I-V characteristic[J]. The Review of scientific instruments,2008,79(7):073503−8 doi: 10.1063/1.2956970
    [16] Park J, Henins I, Herrmann H W, et al. Discharge phenomena of an atmospheric pressure radio-frequency capacitive plasma source[J]. Journal of Applied Physics,2001,89(1):20−28 doi: 10.1063/1.1323753
    [17] Lymberopoulos D P, Economou D J. Fluid Simulations of glow discharges: effect of metastable atoms in argon[J]. Journal of Applied Physics,1993,73(8):3668−3679 doi: 10.1063/1.352926
    [18] Moravej M, Yang X, Hicks R F, et al. A radio-frequency nonequilibrium atmospheric pressure plasma operating with argon and oxygen[J]. Journal of Applied Physics,2006,99(9):093305−6 doi: 10.1063/1.2193647
    [19] Lieberman M A, Lichtenberg A J. Principles of plasma discharges and materials processing [M]. John Wiley & Sons, Inc: Hoboken, NJ, USA, 2005
    [20] Wang Y N, Cui S Y, Zheng S, et al. Modeling of atmosphere discharge in mixture of nitrogen and oxygen[J]. Frontier of Applied Plasma Technology,2011,4(2):59−64
    [21] Jia F, Ishikawa K, Takeda K, et al. Spatiotemporal behaviors of absolute density of atomic oxygen in a planar type of Ar/O2 non-equilibrium atmospheric-pressure plasma jet[J]. Plasma Sources Science & Technology,2014,23(2):025004−7
    [22] Li S Z, Huang W T, Zhang J, et al. Optical diagnosis of an argon/oxygen needle plasma generated at atmospheric pressure[J]. Applied Physics Letters,2009,94(11):111501−3 doi: 10.1063/1.3099339
    [23] Li S Z, Wu Q, Yan W et al. Influence of oxygen traces on an atmospheric-pressure radio-frequency capacitive argon plasma discharge[J]. Physics of Plasmas,2011,18(10):103502−8 doi: 10.1063/1.3643224
    [24] Yu Y Q, Xin Y, Lu W, et al. Investigation of capacitively coupled argon plasma driven by dual-frequency with different frequency configurations[J]. Plasma Science and Technology,2011,13(5):571−574 doi: 10.1088/1009-0630/13/5/12
  • 加载中
图( 9) 表( 2)
计量
  • 文章访问数:  99
  • HTML全文浏览数:  99
  • PDF下载数:  4
  • 施引文献:  0
出版历程
  • 收稿日期:  2023-01-16
  • 刊出日期:  2023-11-30

大气压双频Ar/O2放电等离子体特性的数值模拟

    通讯作者: E-mail: ynwang1985@hotmail.com
  • 1. 辽宁石油化工大学理学院 抚顺 113001
  • 2. 共青科技职业学院 九江 332020
  • 收稿日期:  2023-01-16

摘要: 文章采用等离子体流体理论模型，研究了双频容性耦合放电中高频源频率对大气压氩气与氧气混合气体放电等离子体的各类粒子密度与各项等离子体参数的影响。通过模拟不同高频源频率的放电，得到了放电空间中各类粒子的密度、电子温度、电场等参数的一维时空分布，进一步了解了双频放电中高频源频率对等离子体特性的影响作用。研究结果表明：当放电电压固定时，随高频源频率的升高，电子密度逐渐增大；电子温度、电场与电势有下降的趋势；各类氩离子密度与氩原子的亚稳态密度随高频源频率的升高而增大；随高频源频率的升高，各类氧离子密度增大，氧原子密度先减小后增大，氧分子的亚稳态密度先增大后减小。电子压力加热、电子欧姆加热、电子加热和能量损失受高频源频率的影响均逐步升高。此外，有效电流密度与有效功率密度随高频源频率的升高大体增加。

English Abstract

    全文HTML

  • 众所周知，等离子体处理技术在全球制造业中发挥着非常重要的作用。容性耦合放电产生的等离子体具有良好的均匀性、等离子体刻蚀与沉积的速率高[1-3]，且容性耦合放电结构相对简单。因此该放电常被应用于工业制造中，如杀菌、材料改性及半导体制造等[4-5]。早期的容性耦合放电是在极板的一侧施加单个射频电源驱动放电，从而获得相对均匀的等离子体。它的缺点在于不能独立控制放电空间中离子能量和通量[6]。随着半导体工业技术发展，双频容性耦合放电出现在大众视野，实现了独立控制离子能量和通量，在等离子体清洁和刻蚀工艺中得到广泛应用[6]。

    早期应用气体放电产生等离子体的工作气体大部分为惰性气体，如氦气、氩气等，对正电性气体放电等离子体特性的认识比较全面，但对电负性气体放电等离子体的特性不够了解[7-9]。在实际的工业刻蚀中使用的工作气体以电负性气体为主，而电负性气体如CF4、SF6、Cl2、O2通常与惰性气体混合放电产生等离子体，其成分十分复杂。因此无论是实验研究还是数值模拟研究，对混合气体放电等离子体特性的研究是必不可少的[10]。结合双频容性耦合放电的优点，双频混合气体放电成为了研究的热点。同时，大气压氩气与氧气混合气体放电产生的非平衡等离子体中包含了大量的活性粒子，能在许多新兴的等离子体材料处理与生物医学中发挥重要作用。例如，在工业中可用于刻蚀工艺与薄膜沉积；在生物医学中包括伤口处理、器械消毒灭菌、皮肤病治疗、牙科护理等方面发挥十分重要的作用[11]。在近期双频混合气体放电等离子体的研究中，Jia Liu等[12]在实验上研究了氩气与氧气双频容性耦合放电等离子体中离子能量分布特征，分析了低频源的频率和功率对离子能量分布的影响。研究发现随着低频功率的增加，高能量峰向高能区移动，高能和低能峰之间的能量宽度也增加；低频源频率的增加导致高能量峰向低能区移动，能量宽度变窄[12]。Booth等[13]研究了双频容性耦合放电中低频功率对电子密度和离子通量的影响。研究发现在低气压氩气与氧气混合放电中，电子密度和离子通量的变化非常相似，这与简单的正电输运理论非常一致；双频频率为27 MHz和2 MHz下的射频功率对等离子体密度和离子通量皆有显著影响[13]。Y Liu等[14]采用200 KHz/13.56 MHz双频氩气与氧气混合气体放电，获得了均匀的大气压介质阻挡放电等离子体，研究了激发动力学和等离子体产生机制。研究结果表明：单个射频放电对激发动力学的调制有限，而双频放电能够通过调制叠加的低频和射频信号的振幅比对电场进行时间调制，从而对激发/电离机制进行调制[14]。

    低气压双频容性耦合放电能够对离子能量和通量独立控制[6]，而大气压双频气体放电主要是借鉴低气压双频容性耦合放电的特征，引入高低频电源，通过控制更多的可调参数来控制等离子体的特性。大气压双频混合气体放电等离子体的特性主要由外部因素决定，如电源参数、腔室几何结构和工作气体等，可调节参数众多。因此想要充分了解等离子体特性，还需进行大量的研究工作。数值模拟方法能够对复杂的气体放电反应过程进行有效的、直观的研究，通过建立模型并对模型数值求解从而获得相应的等离子体状态参数[15]。本文基于一维流体模型，对大气压双频氩气与氧气混合气体放电等离子体进行了数值模拟研究，对等离子体参数的时空演变进行了分析，尤其分析了高频源频率等外部参数对等离子体特性的影响，为大气压混合气体双频放电应用提供一定的理论指导。

1.   模型

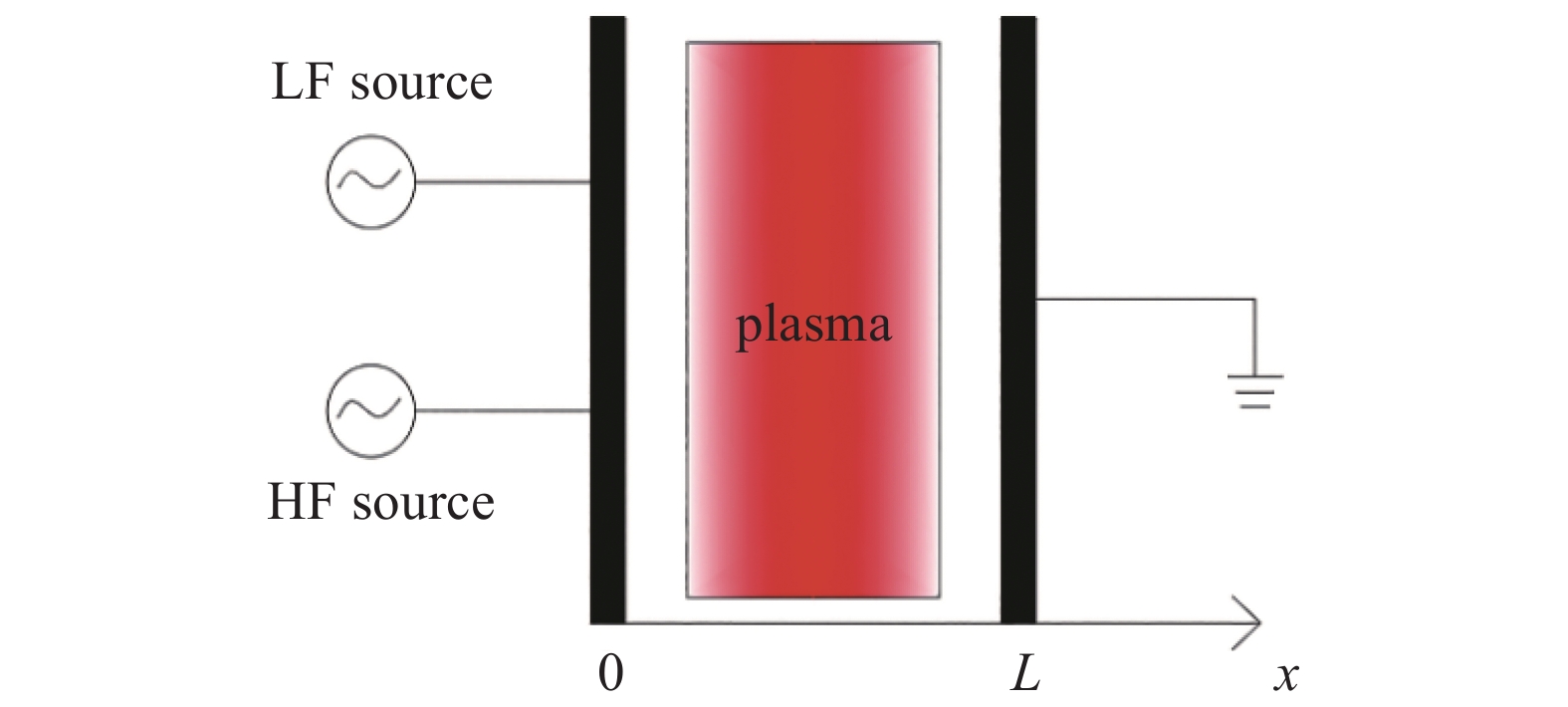
  • 在本文研究中，放电装置为平行板电极结构。电极由两块裸金属平行板组成，左端电极接电源，右端电极接地，其中左端放电电源为双频电源，如图1。

    平行板间充入的气体为氩气与氧气混合气体，其中氧气的占比为0.1%，平行板电极间距L = 0.2 cm。此放电间距对应实验上常用到的电极间距[16]。由于放电间隙远远小于放电电极的尺寸，因此模型中不考虑平行板放电电极的直径大小。放电过程中考虑到的粒子种类为氩离子Ar+和Ar2+、氧离子O−和O2+、氧原子O、亚稳态原子Ar*和O2*以及电子e。放电时粒子间发生的反应过程如表1所示。

    本文采用一维流体模型对放电中的等离子体进行数值模拟研究，可用连续性方程描述粒子的产生和消失。一维模型下电子、离子与亚稳态粒子的连续性方程为:

    式中，$ n $代表粒子密度，下标${{\rm{e}}}_{}、{\rm{i}}$与*分别为电子、离子与亚稳态粒子；气体放电时既有粒子的产生也有粒子的消失，式中的$ S $即为粒子的净产生项；$ J $为粒子流通量，式中的${J}_{{\rm{e}}}{}_{}、{J}_{{\rm{i}}}$与$ {J_{\text{*}}} $可用式（4）−（6）表示：

    上式中的$ E $代表带电粒子在放电空间中产生的电场强度。$ \mu $与$ D $分别代表粒子的迁移率和扩散系数，本文中的迁移和扩散系数来自参考文献[17，20]。电子能量方程为：

    式中，$ {H_j} $与$ {k_j} $分别代表电子非弹性碰撞的能量阈值和电离系数；$ N $代表气体分子数密度；${T_{\rm{e}}}$代表电子温度；$ e $代表电子的电量。${J_{\rm{w}}}$代表电子能量通量，可表示为：

    式(8)中的${W_{\rm{e}}}$为电子能量密度，由${n_{\rm{i}}}{T_{\rm{e}}}$计算获得。泊松方程为：

    式中，下标$+ ,{\rm{i}}$与$- ,{\rm{i}}$代表正离子与负离子；$ {\varepsilon _0} $代表真空介电常数；$ V $代表电势，电势与电场满足关系式：

    模型设定的初始条件，即$ t = 0 $时：电场$ E = 0 $，电势$ V = 0 $，${n_{\rm{e}}} = {n_{\rm{i}}} = {10^6} \; {{\mathrm{cm}}^{ - 3}}$。

    模型中所采用的边界条件如表2所示。表中${k_{\rm{s}}}$和$ \gamma $分别为复合系数和二次电子发射系数，均来自参考文献[20]。

    本文采用有限差分法将以上方程联立进行数值求解，即可获得本文研究所需要的粒子密度、电子温度及电场等物理量的一维时空分布。

2.   结果与分析

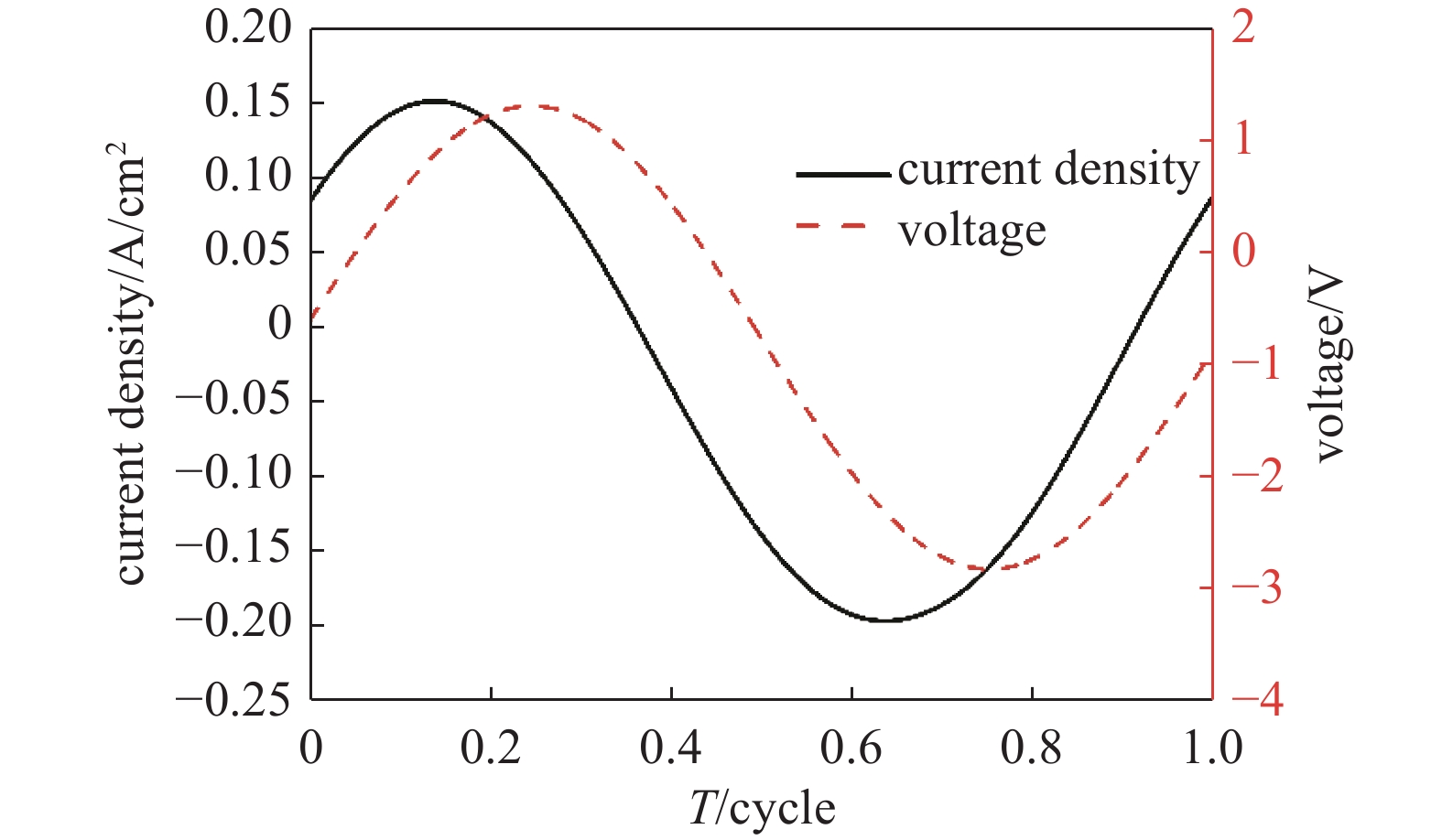
  • 在本节中，主要对双频氩气与氧气混合气体放电等离子体特性进行数值模拟分析。分析过程中重点围绕高频源频率对放电空间中各类粒子的密度、电子温度、电子能量等物理量的影响进行分析。本文在研究过程中采用的驱动源为高低射频源组成的双频电源$V = {V_{\rm{H}}}\sin (2\pi {f_{\rm{H}}}t) + {V_{\rm{L}}}\sin (2\pi {f_{\rm{L}}}t)$，其中高频源频率为14、18、22、26、30 MHz，低频源频率固定在2 MHz。

    图2给出了在本文设置的放电参数下模拟得到的放电电流电压波形。从图中可以看出电流密度与电压波形均为正弦，且电流相位角较电压提前，由此可判断该放电为容性耦合放电。在放电过程中，电子不断吸收能量与背景气体碰撞，碰撞反应在鞘层和主等离子体之间的区域最为激烈，极度消耗电子，同时也促进了Ar+、O2+等粒子的产生。这使电子密度在此区域迅速下降，电子密度最大值出现在放电中心区域。正是由于该区域的特点，影响着众多物理量的分布结构。

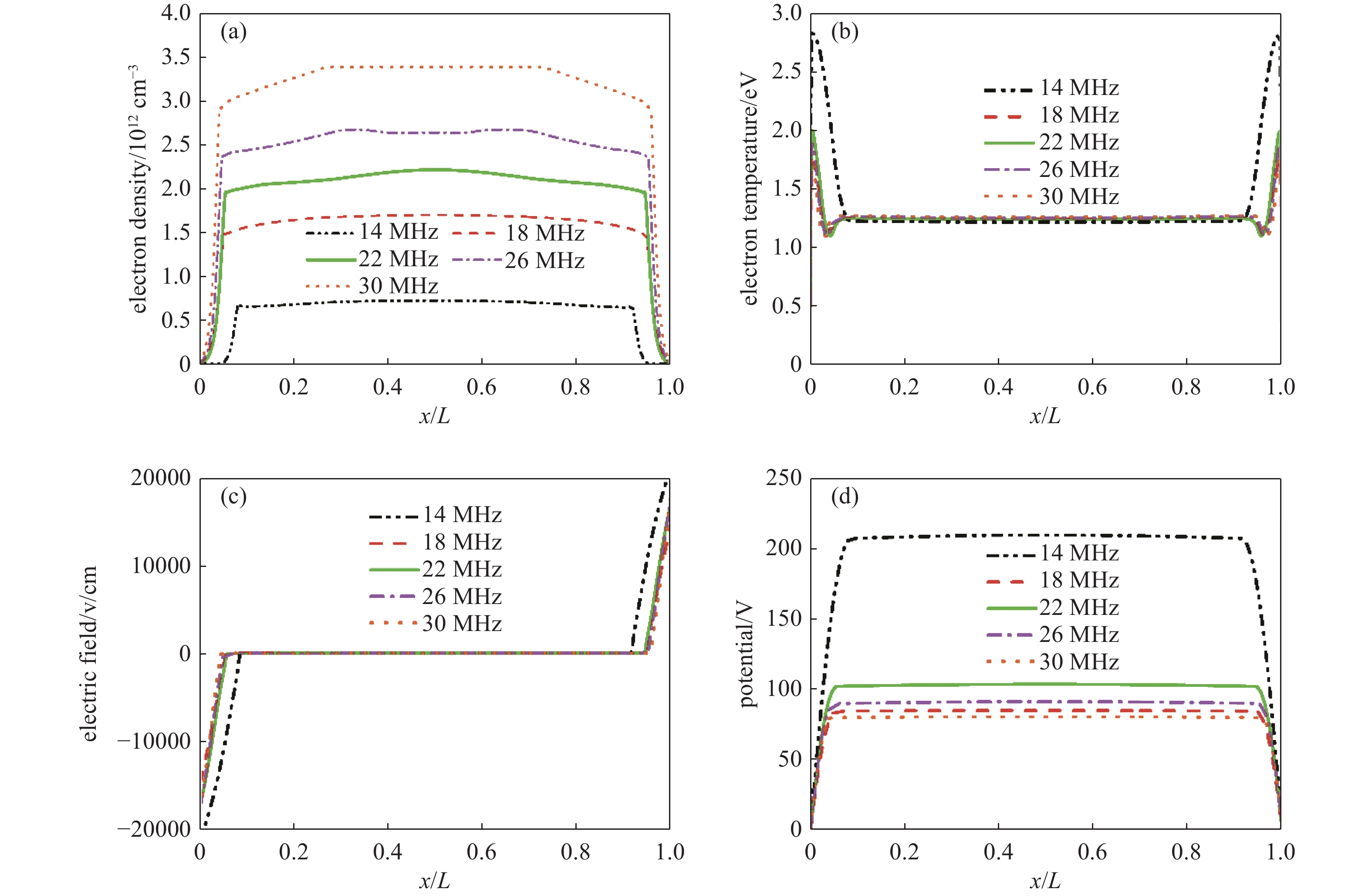
    图3给出了固定低频源频率f L = 2 MHz高频源频率分别为f H = 14、18、22、26和30 MHz下的时间平均的电子密度(a)、电子温度(b)、电场强度(c)和电势(d)的空间分布。从图3(a)中可以看出电子密度随高频源频率的升高明显增大。这是因为在大气压容性耦合放电中，电子主要由粒子间的碰撞电离反应产生，加热机制通常以欧姆加热为主导(见图8)。高频源频率的升高使电子吸收更多的能量，促进中性粒子的电离，电离率升高，从而获得更多的电子。图3(b)中的电子温度曲线在放电空间中呈对称分布，在鞘层区出现双峰。当高频源频率最低时，鞘层区电子温度明显升高，随着高频源频率逐渐升高，鞘层区电子温度有逐渐下降的趋势。这是由于高频源频率的升高导致电子与粒子间碰撞的次数大幅增加，碰撞过程中损失能量使电子温度降低。电场强度与电子温度密切相关，如图3(c)所示，电场在等离子体区不受高频源频率变化的影响，始终为零，而在鞘层区迅速增大。电子受鞘层区内的强电场作用吸收大量能量使电子温度升高，表现与图3(b)电子温度相符。此时鞘层区的等离子体电势快速下降，如图3(d)，这与式(10)相符。

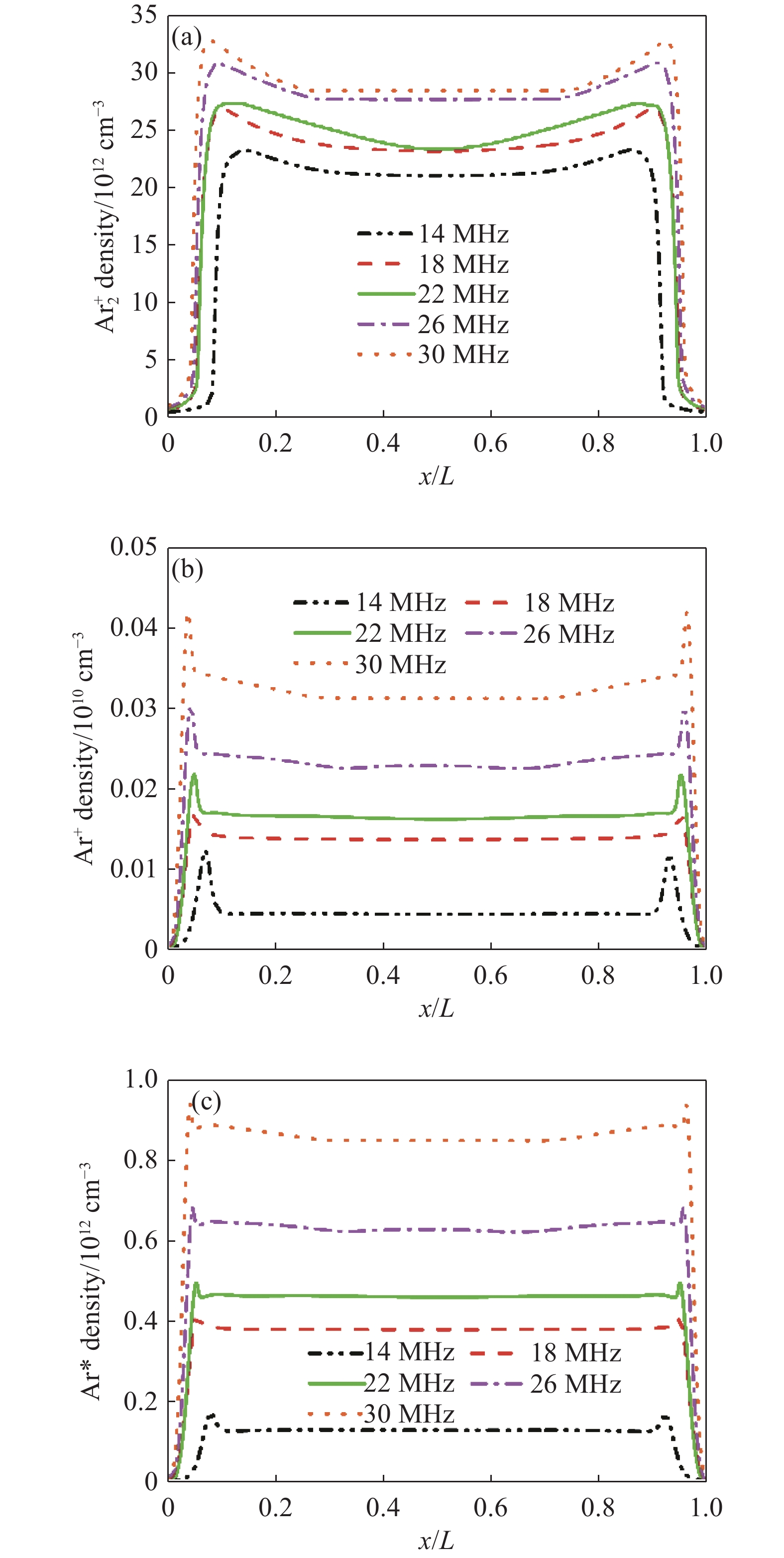
    图4(a)、(b)和(c)分别给出了低频源频率为2 MHz时，高频源频率在14、18、22、26和30 MHz下的时间循环平均的Ar2+、Ar+和Ar*粒子的空间分布。可以看出这三种粒子密度在放电空间中均呈对称分布，在等离子体区分布较为均匀，在鞘层区有不同程度的增长，且在整个放电空间中均随高频源频率升高而增加。其中，Ar2+粒子密度最高，Ar+粒子密度最低。这是因为Ar+粒子主要由电子对Ar原子的直接电离产生，而背景气体存在大量的氩气，电离生成的Ar+粒子与背景气体发生反应生成Ar2+。剩余电子的能量不足以使氩原子发生电离，呈亚稳态的原子居多，因此Ar+粒子密度最低。

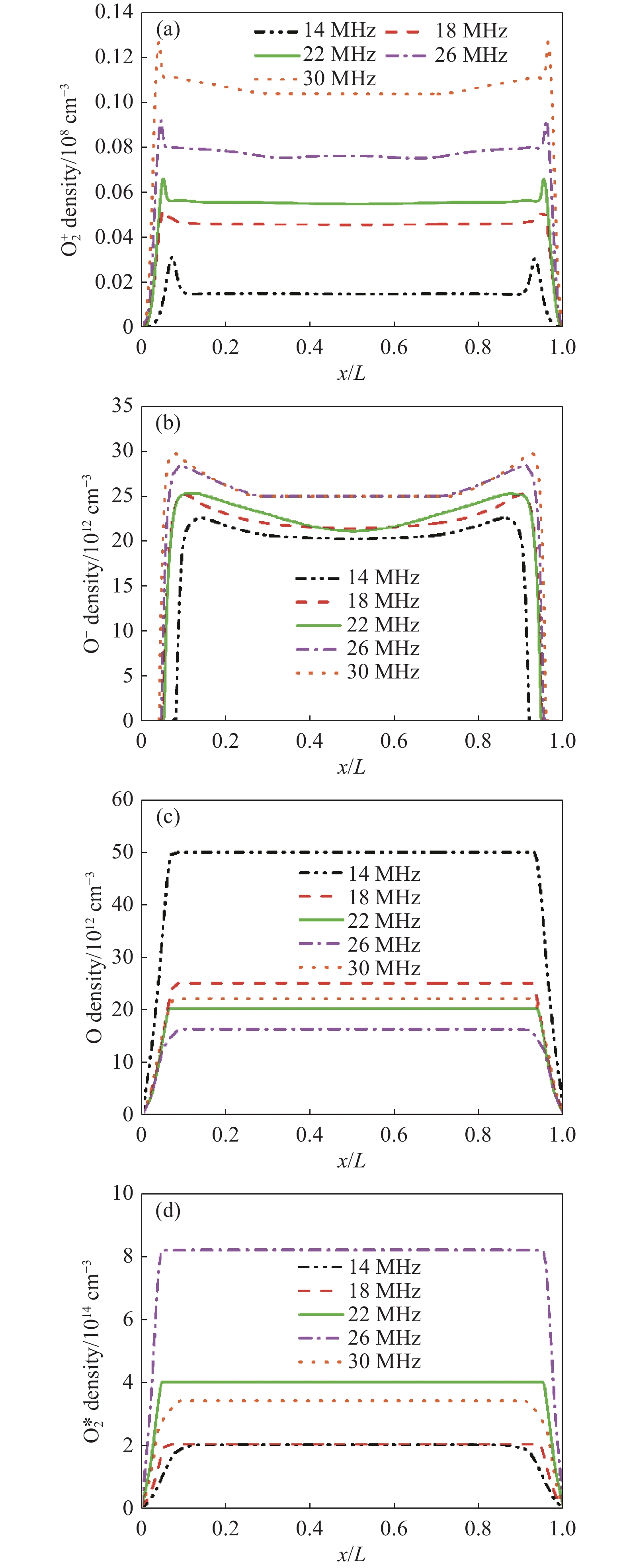
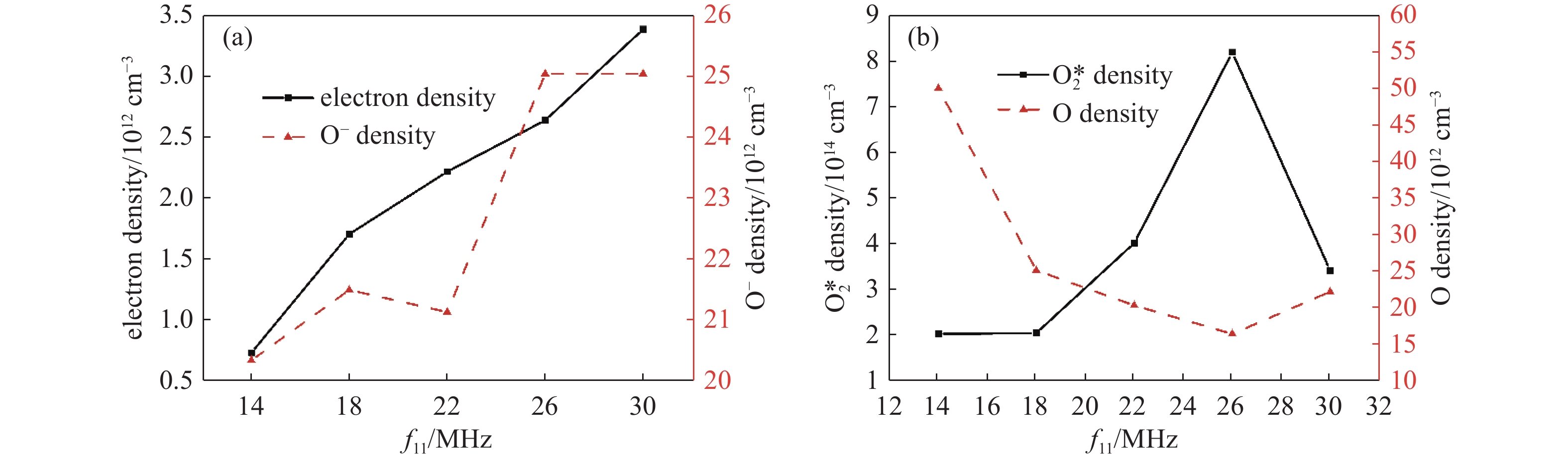
    图5给出了低频源频率f L = 2 MHz时，不同高频源频率f H = 14 MHz、18 MHz、22 MHz、26 MHz和30 MHz下的时间循环平均的O2+(a)、O−(b)、O(c)和O2*(d)粒子密度的空间分布。其中，O2+与O−粒子密度分布在放电空间中存在双峰，且密度随高频源频率的升高而增加。O2+粒子主要由电子与氧气发生电离反应产生，O−粒子主要由电子的附着反应产生，它们的产生均与电子密度有直接的联系，这决定了它们的结构。在图6(a)中给出了随高频源频率的升高电子密度与O−粒子密度的关系，证明了O−粒子密度对电子密度的依赖性。此外，可以看出在极板附近几乎没有O−粒子的出现，这是由于相对于电子，O−粒子质量大，受电场影响，将无法穿透存在强电场的鞘层区，因而被限制在放电中心。图5(c)中的O原子密度随高频源频率的升高逐渐减少，直到高频源频率为30 MHz时粒子密度反增。而O2*粒子密度的变化规律与O原子密度相反，高频源频率的升高使得O2*粒子密度越来越高，直到高频源频率为30 MHz 时粒子密度减少，如图5(d)。由表格1中的反应过程可以看出，这主要是由于O原子与O2*粒子在反应过程中的相互转换的结果，图6(b)很好的证明了这一关系。

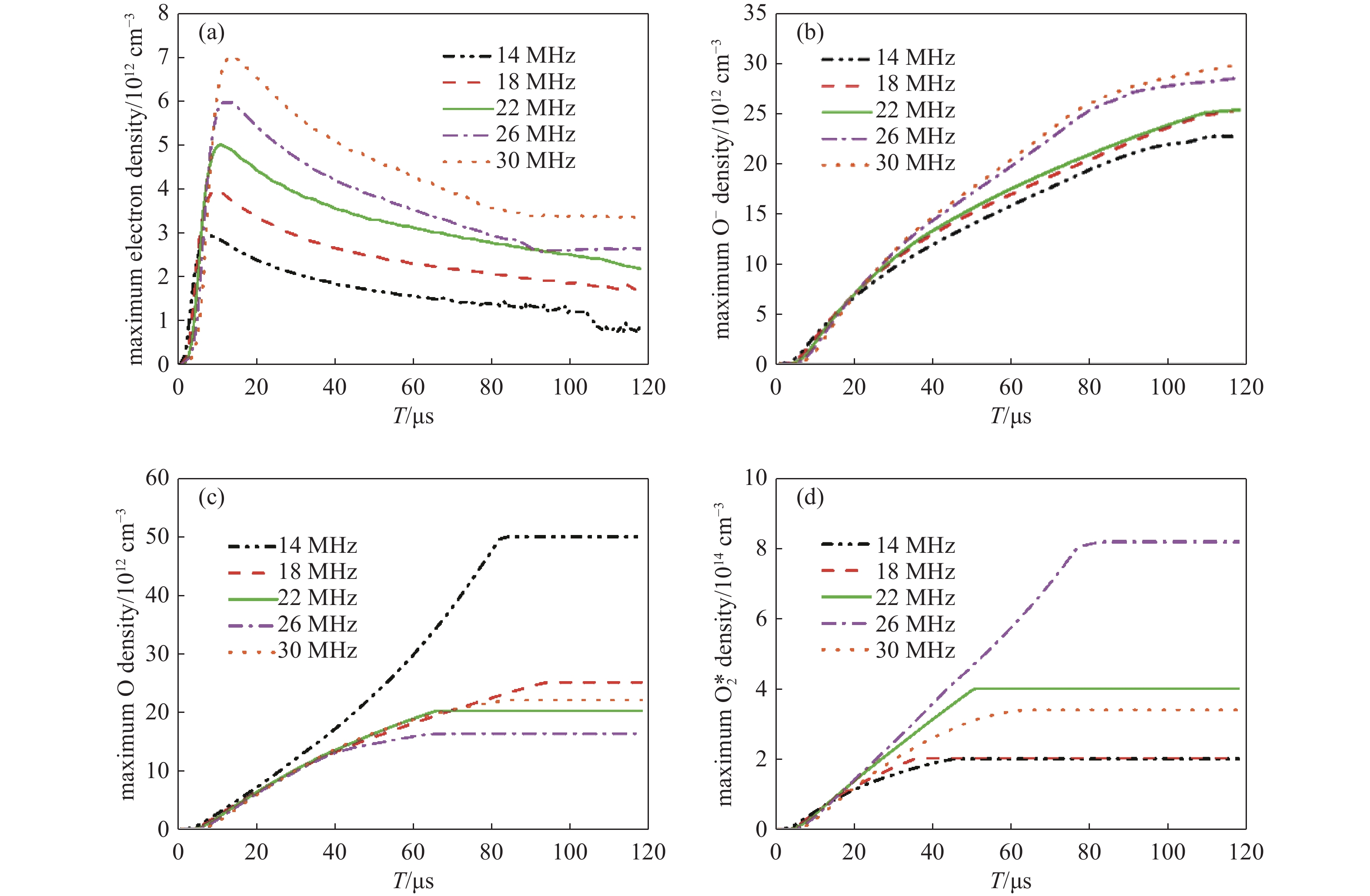
    图7(a)给出了低频源频率固定为2 MHz，高频源频率为14、18、22、26、30 MHz下电子密度的最大值随时间的变化。可以看出在放电初始电子密度急速上升到峰值。这是因为在放电初始，电离率上升，背景气体发生电离反应，瞬间产生大量电子。此后由于电子与Ar2+的复合、与O2的附着等反应的发生，使电子的消耗大于电子的产生，导致电子密度逐渐下降。最后，电子密度最大值趋于稳定，使装置持续放电。由于高频源频率的升高使电子获得更多的能量，粒子间碰撞更加剧烈，电子密度最大值峰值与放电达到稳态时电子密度最大值均明显升高，这与图3(a)中的电子密度空间分布相符。但高频源频率的升高也导致了电子密度达到峰值的时间越来越长。同样，O−粒子密度最大值随高频源频率的升高而增大，如图7(b)所示。图7(c)与(d)为O原子密度与O2*粒子密度最大值随时间的变化。从图中可以看出O、O2*粒子密度最大值随时间几乎线性增长，放电达到稳态后不再变化，高频源频率对它们的影响与图5(c)与(d)相同。

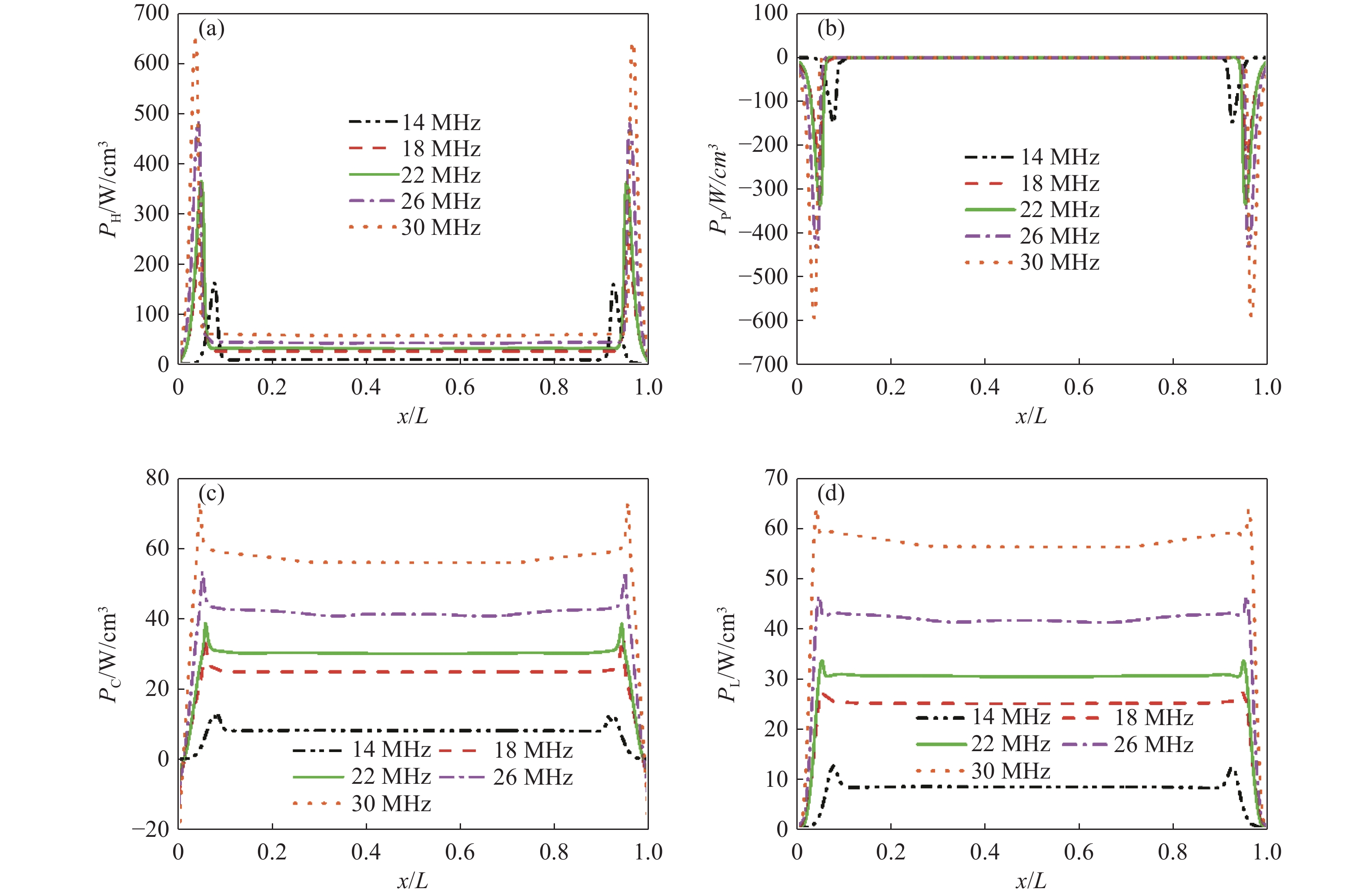
    图8给出了时间平均的PH (欧姆加热)、Pp (压强加热)，PC (电子加热)和PL (能量损失)的空间分布。从图中可以看出PH、Pp、PC和PL均随高频源频率的升高而增加，并在鞘层区出现双峰值。电子加热率的峰值存在于鞘层区，在等离子体区是恒定的。这是由于在放电空间中鞘层区的电场较强，电子温度变化显著，导致电子加热率具有明显变化，证明电子加热率在空间中的分布特点均与电子温度相符。还可以看出随着高频源频率的升高，电子加热率增加，这代表有更多的能量耦合到等离子体中。

    电子加热率包括电子欧姆加热PH和压强加热Pp。从图中可以观察到，在整个放电区电子欧姆加热为正值，电子压强加热为负值，功率的变化主要发生在等离子体鞘层界面，在等离子体区无压强加热。还可以看出在图8(c)中的电子加热PC在等离子体区和鞘层边缘为正值，可得出欧姆加热PH是电子的主要加热机制。但在两个电极附近，电子加热PC为负值，证明在此区域压强加热高于欧姆加热，以压强加热为主。因此，在双频放电中高频电子功率在等离子体区和鞘层区边界处影响最大。图8(d)给出了损失的能量PL的分布，可以看出高频源频率的增加使整个放电空间中的能量损失都增加。

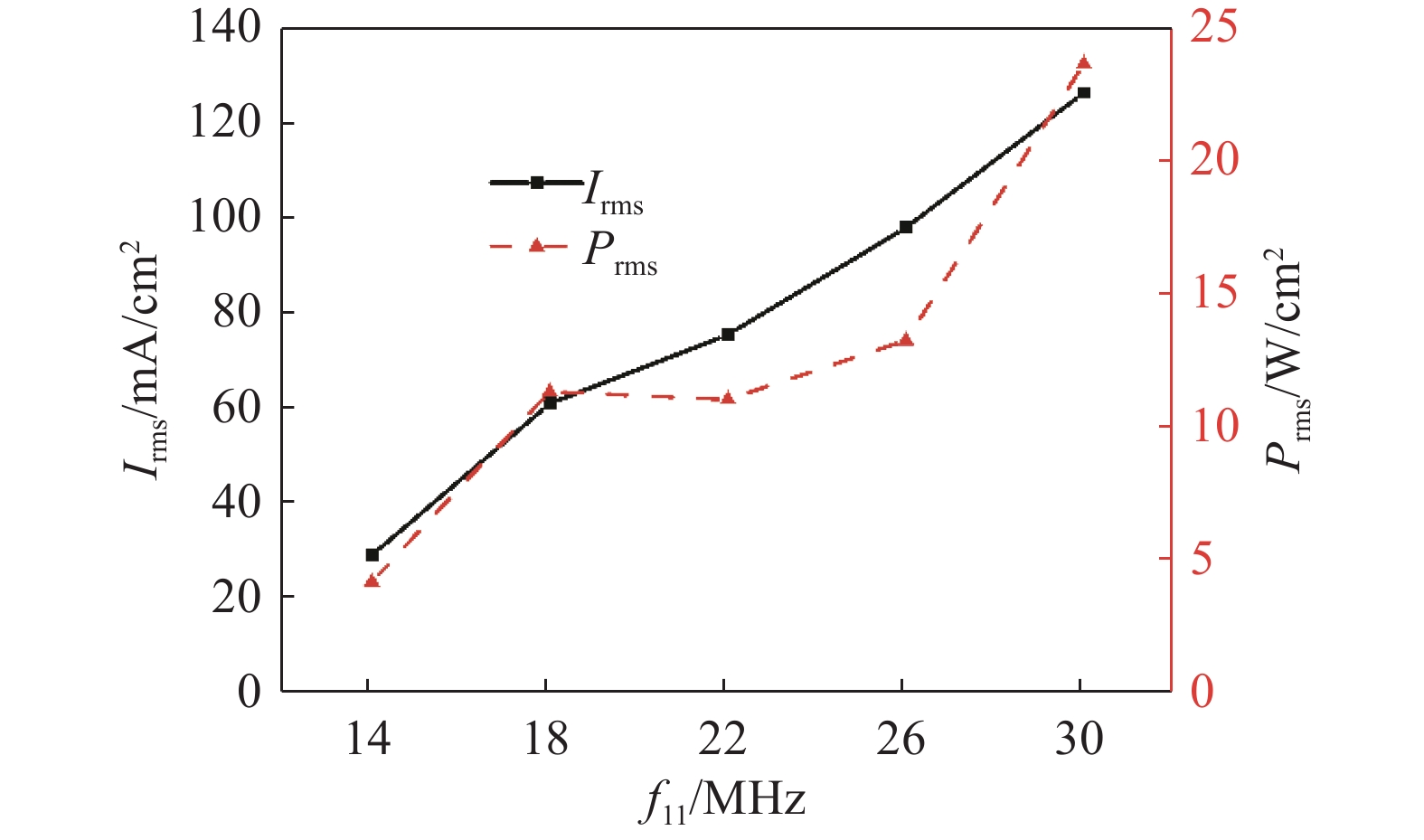
    图9为等离子体中有效电流密度与有效功率密度随高频源频率的变化。其中，有效电流密度由公式${X_{{\rm{rms}}}} = \sqrt {\dfrac{1}{n}\displaystyle \sum\limits_{i = 1,n} {x_i^2} }$求得。由图可知，有效电流密度随高频源频率的升高逐渐增大，从整体上看，有效功率也在增加，这使电子吸收更多能量，粒子碰撞更加剧烈，导致等离子体密度增加。在细节上看，高频源频率从18 MHz变换为22 MHz过程中，有效功率密度稍降，这使各粒子密度的上升速率减慢，在Ar+、Ar*与O2+粒子密度空间分布中尤为明显，同时，电子加热率也出现同样趋势。

3.   对比实验

  • 本文基于上述的流体模型，对大气压双频氩氧混合气体放电进行模拟。模拟结果中得到的部分数据与实验相互验证。实验上通过发射光谱线的强度比来获得大气压放电等离子体的电子密度。采用线比法测量的电子密度范围一般为1012−1016 cm−3[21-23]。本文中获得的电子密度在此范围内。本文中计算得到的O的粒子密度量级为1013 cm−3，与实验参考文献[21]中测得的1014 cm−3量级接近，结果相差较小，主要是由于氧气含量占比所导致的氧粒子密度的不同。文中得到的负离子密度主要为O−离子，而正离子主要为O2+，激发态氧分子密度高等均与实验上得到的结论一致[22-23]。此外，本文得到的电子温度随高频源频率的上升而增加，电子温度则相反，这一结论与参考文献[24]结果一致。考虑到模型中一些外界条件与实验条件不能完全相同，使得结果有些差异，但足以证明本文模型的可靠性。

4.   结论

  • 本文利用自主开发的大气压混合气体放电程序，研究了大气压下高频频率对双频氩氧混合气体放电等离子体特性的影响。比较了不同高频频率下，等离子体特性如电子温度、电子密度、中性粒子密度、电场等物理量的变化趋势。通过研究分析发现，随着高频源频率的增加可以有效的提高放电中种子电子的密度、氧负离子密度以及氩离子密度。针对工业应用中比较关心的亚稳态粒子密度、氧原子密度及激发态氧原子密度的调制存在最佳调制频率。本文也进一步分析了高频源频率对放电加热机制的影响，随着高频源频率的增加，包括电子压力加热机制、欧姆加热机制及等离子体能量损失机制都在增加。此外，通过对高频源频率的调制，可以有效的调节放电时的有效电流密度及有效功率密度，从而进一步影响能量加热损失机制，最终实现对粒子密度的调节。

参考文献 (24)

目录

/

返回文章
返回