-
罗茨真空泵由一对相互啮合的罗茨转子、泵腔、吸气口和排气口组成。罗茨真空泵工作时,两个转子由齿轮驱动,在相反方向上进行同步旋转运动。
罗茨真空泵结构简单、可靠性高、抽速大、效率高,在冶金、化工,以及航空航天、食品工业等领域的各环节中应用广泛。
罗茨转子是罗茨真空泵的关键部件,转子型线设计是提高泵性能的关键因素。徐文兵等[1]提出了一种包含偏心圆弧的转子型线,有面积利用率高、啮合严密的优点。刘林林等[2]提出了一种转子型线,由渐开线、摆线、圆弧组成,提高了转子运行的稳定性。Hsieh C F和Hwang Y W[3-5]将变摆线比的摆线应用于罗茨转子的设计中,并介绍了其无根切型线构建方法,相较传统摆线具有设计多样性,研究表明所提出的变摆线型转子有较高的面积利用系数和密封性。秦丽秋等[6]使用圆弧及其共轭曲线设计了两种罗茨泵圆弧转子型线。王君等[7]提出一种相较圆弧转子有更大面积利用系数的椭圆弧型转子,研究了消除该型线的根切现象和余隙容积的方法。刘厚根等[8]将齿条法应用于罗茨机械的型线设计之中,采用Auto CAD模拟加工以得到转子型线。刘厚根等[9]通过改进传统渐开线转子齿顶圆弧,使渐开线长度增加,理论效率有所提高,改善了啮合重合度。
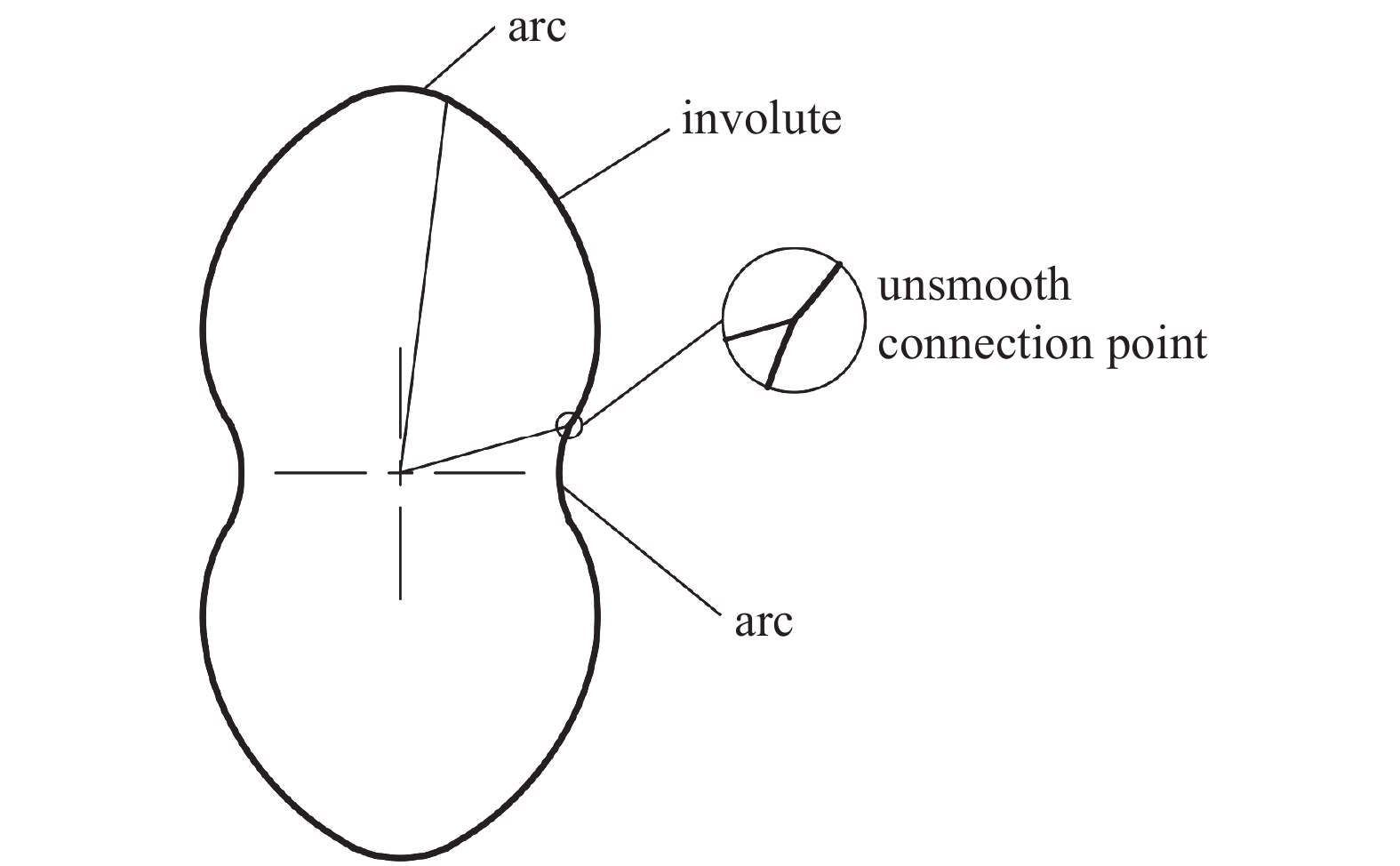
在工作过程中,转子型线的不光滑连接点易于磨损,导致转子的力学性能降低,严重限制了罗茨转子的工作性能和可靠性。李海洋等[10]优化了传统渐开线型罗茨泵的转子型线,避免了叶片间的干涉,提高了转子的径距比和面积利用率。沈浩等[11]采用高次曲线,消除了转子型线的不光滑点,改进后的罗茨真空泵出口处的脉动现象得到了改善。朱超颖等[12]基于传统渐开线型转子,提出了一种由渐开线和多段圆弧组成的新型罗茨转子,新型线光滑性较好,面积利用系数较高。
为研究罗茨转子的工作特性,得到不同型线样式对罗茨转子工作性能的影响规律,刘坤等[13]对圆弧型转子的面积利用率与形状参数等的关系进行了研究;Hsieh C F[14]提出了一种椭圆轮盘转子,研究了不同椭圆轴比对效率、瞬时质量流量、流速、压力脉动的影响。李玉龙等[15]通过改变节圆半径等参数对渐开线转子型线进行了优化。肖芝[16]等利用Fluent软件对改进后的扭叶转子罗茨风机的内部气流流动进行了研究。戴映红[17]设计了用于气冷式罗茨真空泵的罗茨转子,并对其进行了数值模拟。张宇[18]采用了结构化动网格,对空冷罗茨泵进行了数值模拟,研究了不同位置的速度及压力分布,分析了其脉动特性。岳向吉等[19]通过数值模拟研究了罗茨真空内部流场,分析了罗茨真空泵内旋涡的尺寸、方位与强度。陈长琦等[20]建立了罗茨泵间隙泄漏模型,对不同间隙下的部分工作参数进行了理论计算。
渐开线-圆弧型罗茨转子在渐开线与圆弧连接处存在不光滑连接点,长期运行转子易发生磨损,转子的力学性能变差。此外,不光滑连接点的磨损,导致转子间气体泄漏严重,真空泵的性能降低。针对以上问题,本文采用偏心渐开线与齿顶、齿根两段圆弧平滑相连。采用数值模拟对转子几何参数与面积利用率之间的关系进行了研究。对比了罗茨真空泵新型不对称转子与传统带尖点的罗茨转子的内部流动特性。研究内容丰富了罗茨转子型线,对提高罗茨真空泵的性能具有重要意义和价值。
全文HTML
-
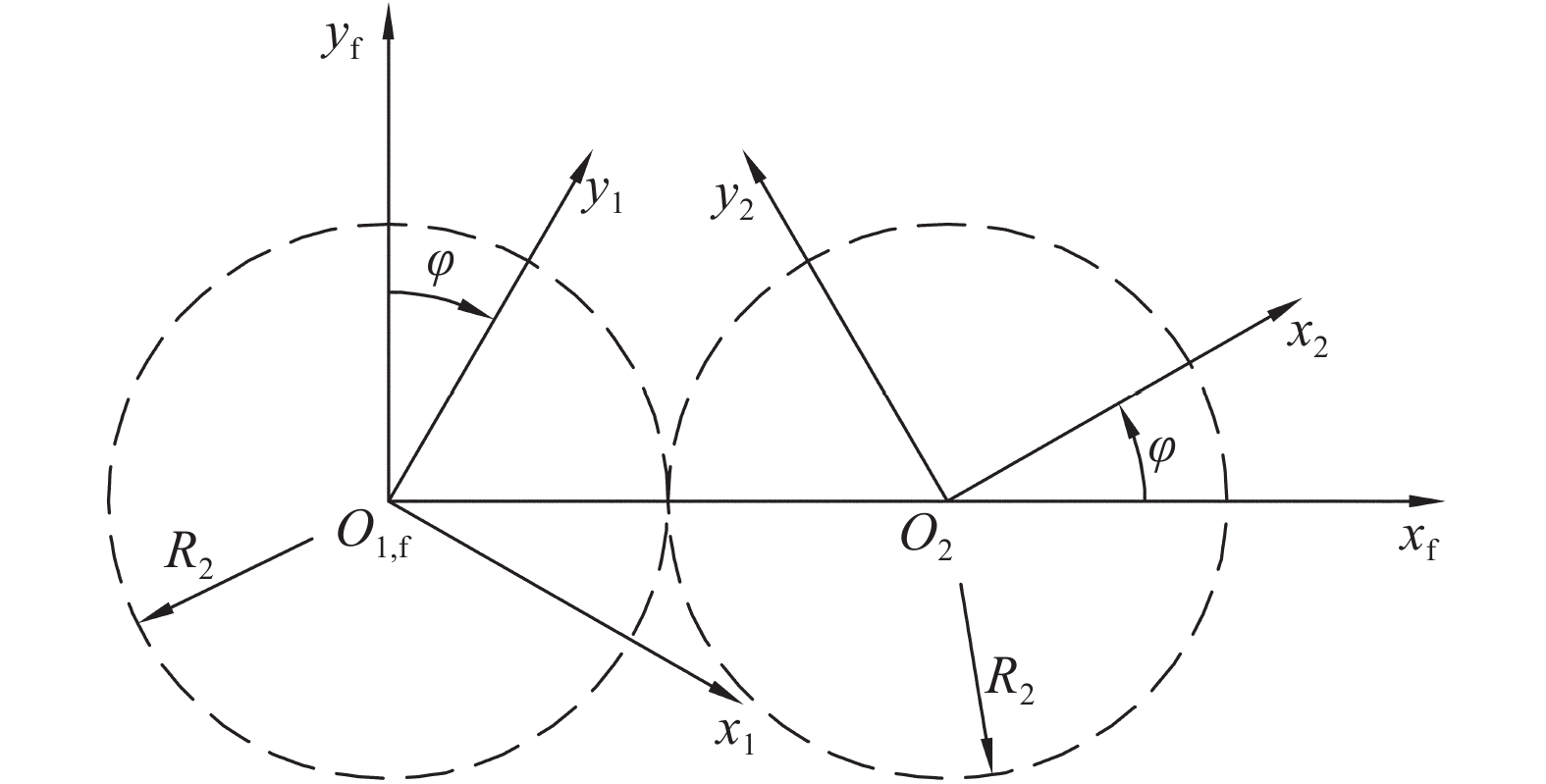
转子动静坐标系如图1所示。左转子型线方程由x1O1y1变换至x2O2y2的方程为:
式中:r1为左转子型线在x1O1y1中确定的方程,r2为左转子型线在x2O2y2中确定的方程。
传统带尖点的渐开线型罗茨转子截面型线如图2所示,为消除尖点构建新型渐开线不对称转子模型。
-
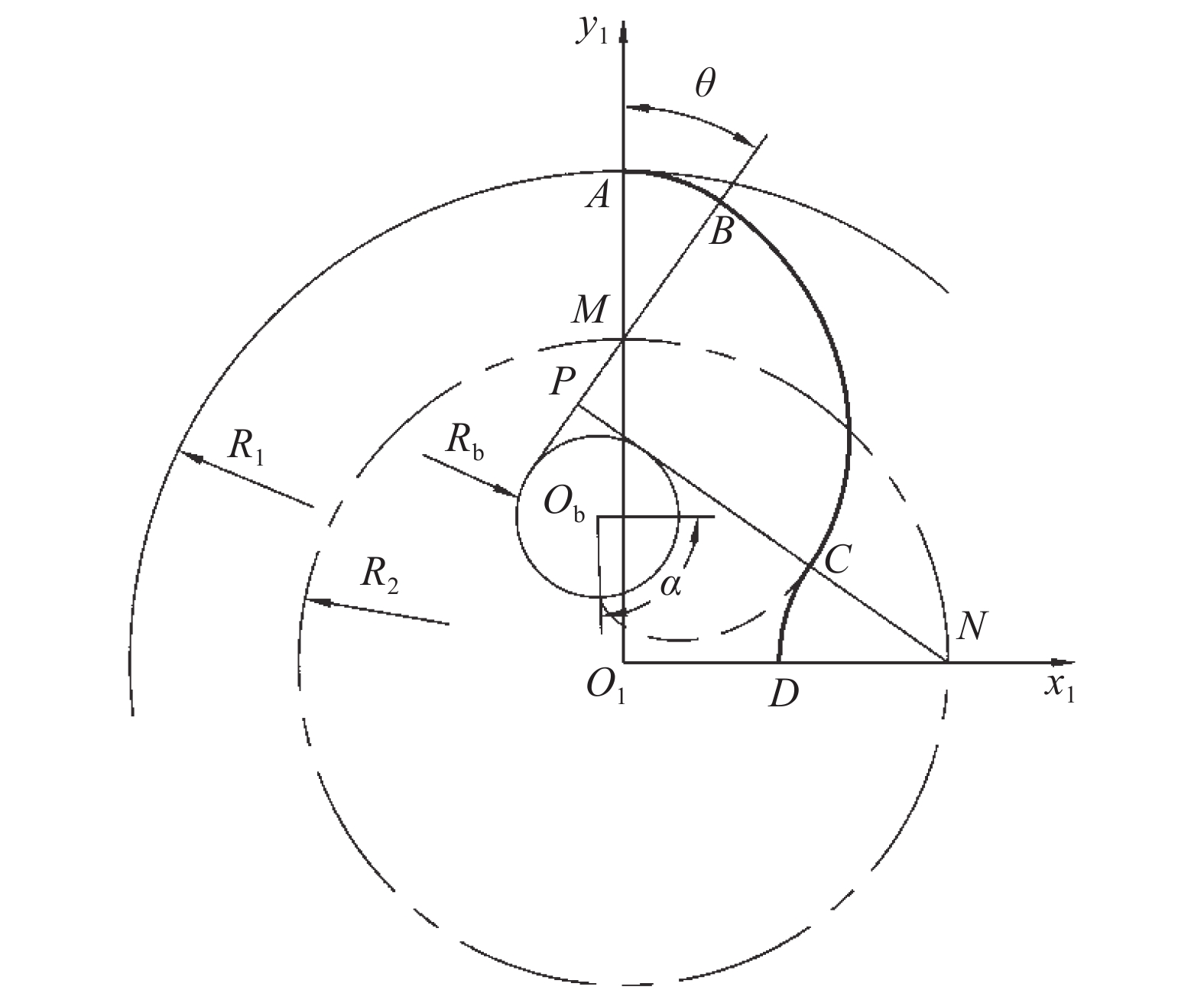
左转子曲线组成如图3所示,转子呈中心对称结构。转子由销齿圆弧AB、CD,偏心渐开线BC组成。圆弧与偏心渐开线连接处可平滑过渡。
各段曲线的方程如下所示。
圆弧AB的方程为:
圆弧CD的方程为:
对于偏心渐开线BC的方程可分为以下三种情况:
延长圆弧AB的半径BM和圆弧CD的半径NC交与点P,得到线段BP、CP。
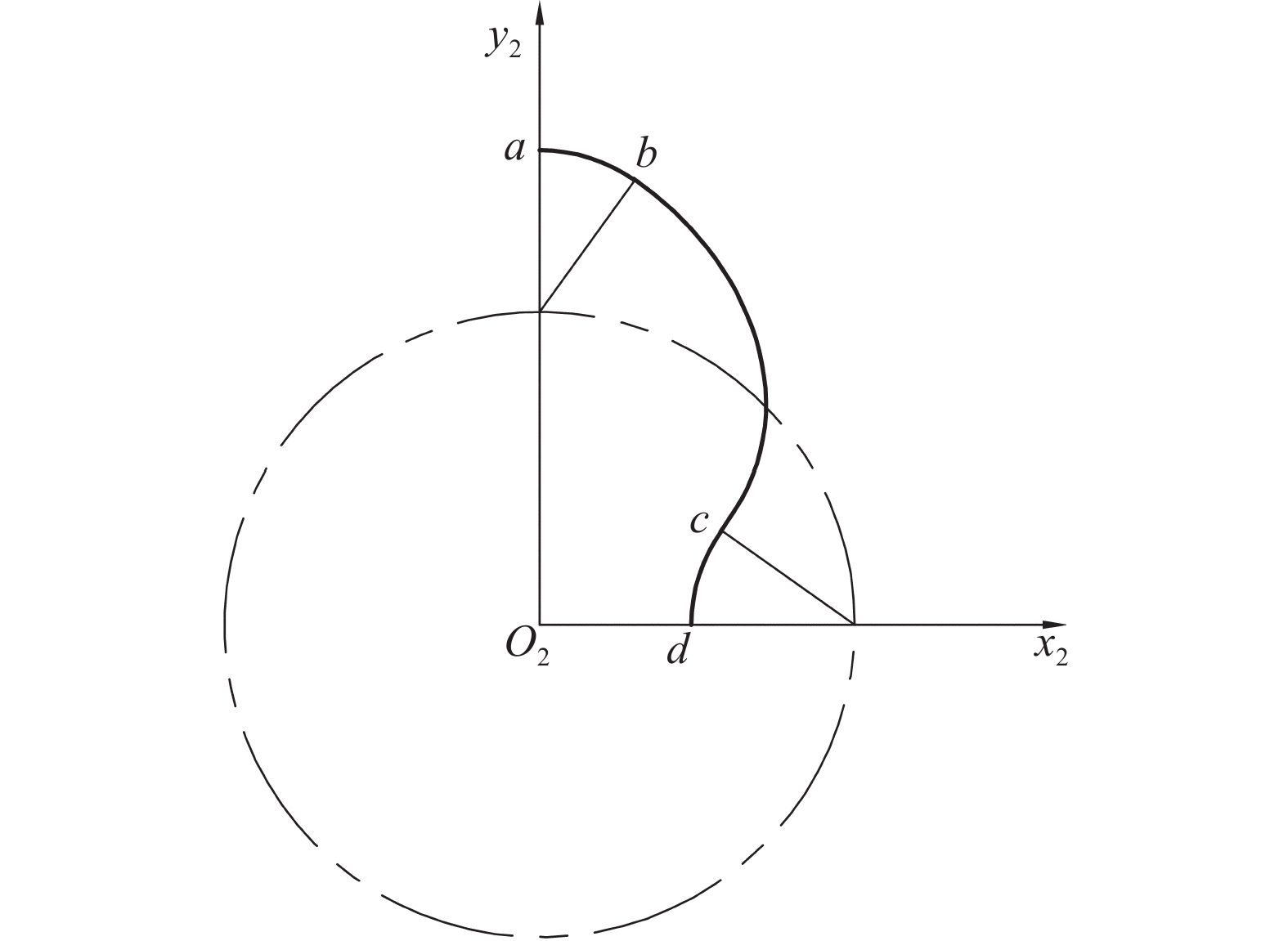
当BP<CP时,渐开线BC基圆圆心Ob在点P之下,此时偏心渐开线沿逆时针方向展开,如图3所示,其方程为:
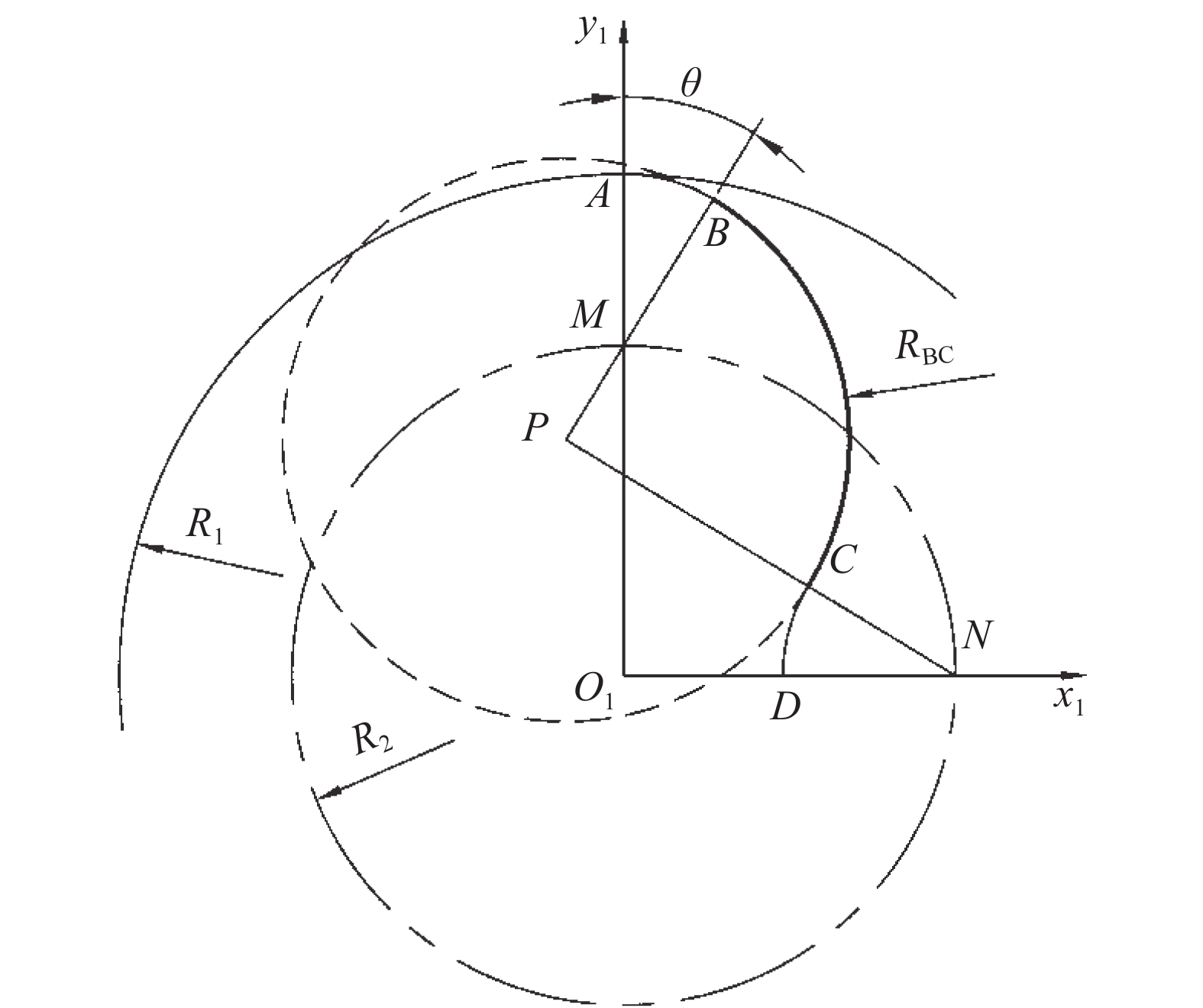
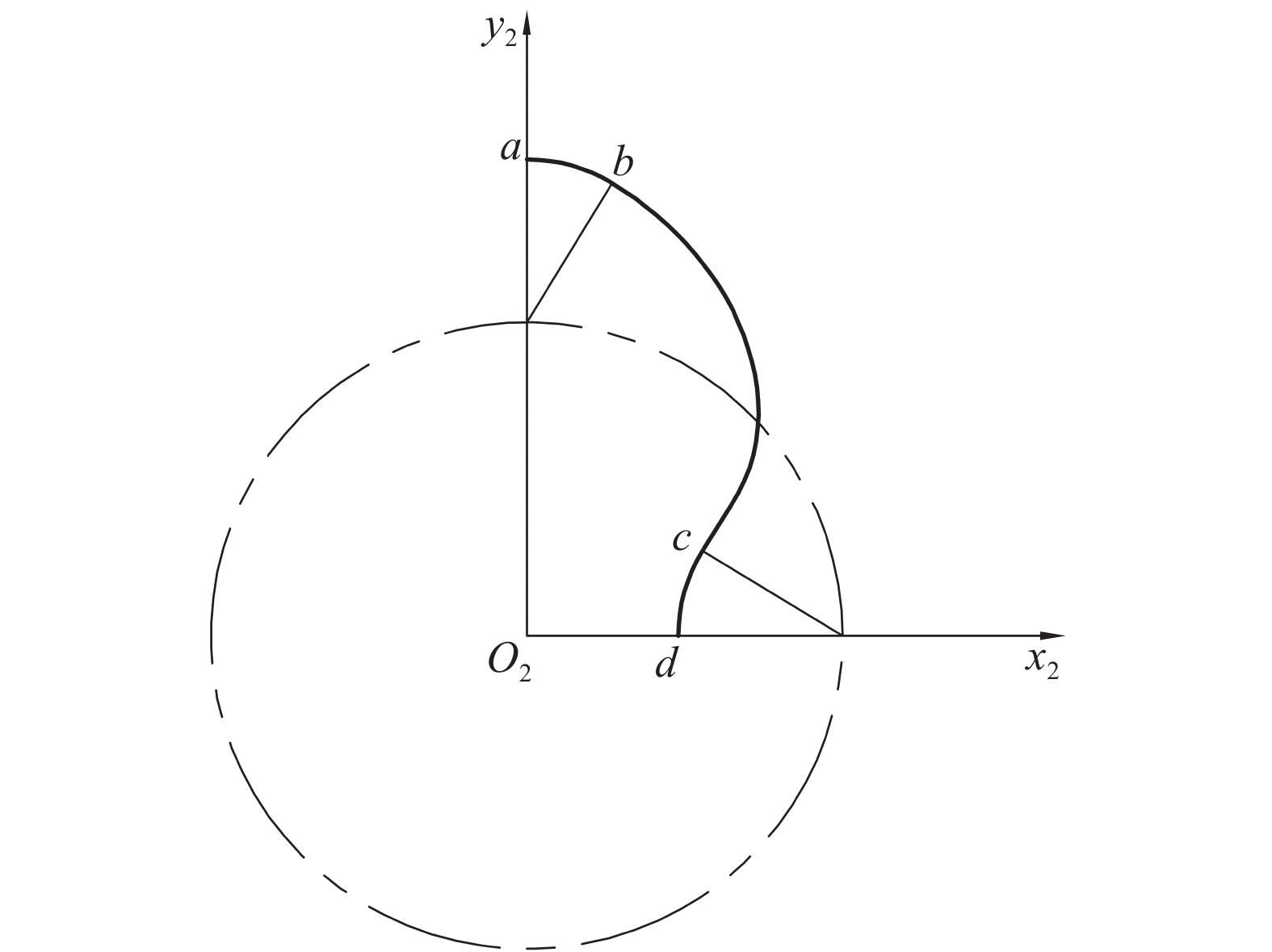
当BP=CP时,渐开线BC变作以点P为圆心的圆弧,如图4所示,其方程为:
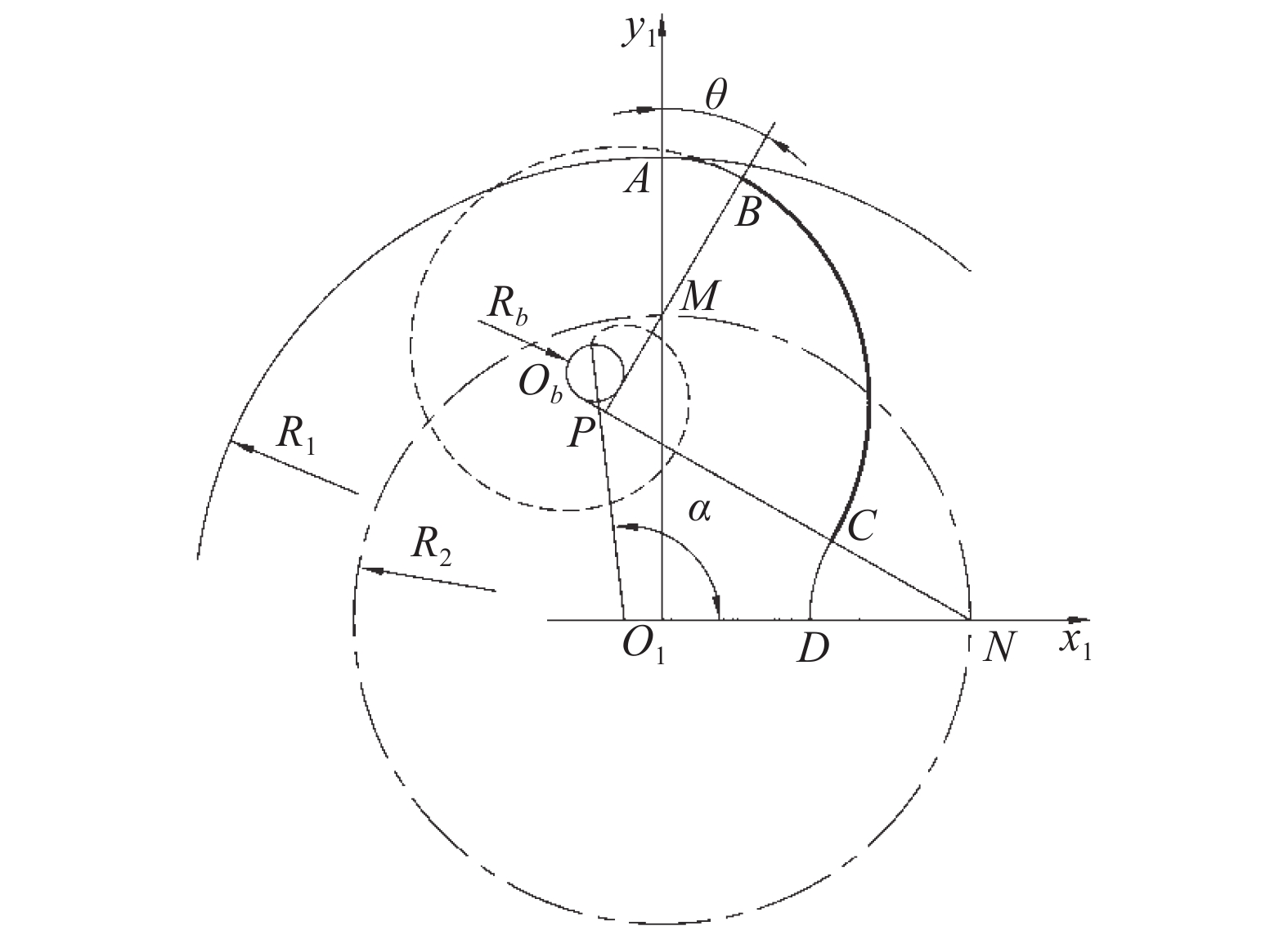
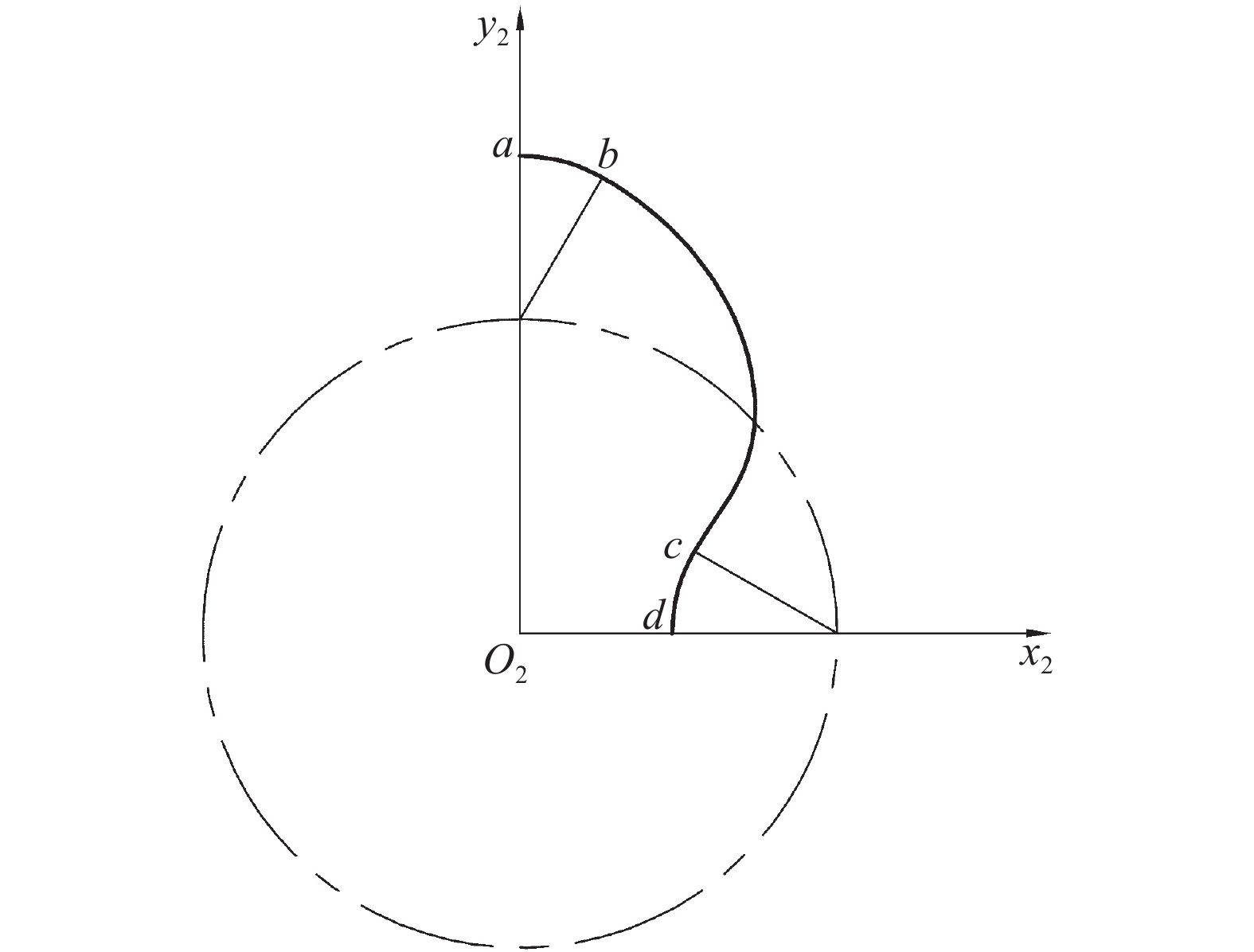
当BP>CP时,基圆圆心Ob在点P之上,此时偏心渐开线沿顺时针方向展开,如图5所示,其方程为:
-
右转子由圆弧和偏心渐开线的共轭曲线组成,右转子齿顶圆弧与左转子齿底圆弧相同,右转子齿底圆弧与左转子齿顶圆弧相同,故求出偏心渐开线的共轭曲线方程即可得到右转子型线。
由啮合原理可知,互为共轭曲线的两曲线一定满足如下啮合方程:
式中,N1为过两曲线啮合点的公法矢量:
$ {\boldsymbol{V}}_1^{(12)} $ 为啮合点处的相对速度矢量:式中:
为了便于计算,取dφ/dt值为1。由此,可化简式(9)得到:
将式(8)和式(13)代入式(7)可得:
将式(4)-(6)分别代入式(14),并进一步化简得到曲线BC及其共轭曲线的啮合条件。
当BP<CP时:
当BP=CP时:
当BP>CP时:
将式(4)-(6)分别代入式(1)可以得到三种情形下的共轭曲线方程:
当BP<CP时:
如图6所示,为BP<CP时的1/4右转子型线。
当BP=CP时:
如图7所示,为BP=CP时1/4右转子型线。
当BP>CP时:
如图8所示,为BP>CP时1/4右转子型线。
1.1. 转子坐标系及渐开线型转子型线
1.2. 新型线的构建
1.3. 求解偏心渐开线的共轭曲线
-
根据渐开线的基本性质,无论BP与CP的长度关系如何,仅当BP、CP和BC的基圆相切时,偏心渐开线可以与圆弧AB、CD平滑连接,且有以下几何关系:
根据图4中的几何关系可知,
$ BP \bot CP $ 。因此,基圆半径为:因存在图5中BP>CP的情况,基圆半径为:
根据图3中的几何关系可知,点B、点C的坐标分别为:
直线BP的方程可表示为:
直线CP的方程可表示为:
将式(27)、(28)联立解得交点P的坐标为:
线段BP、CP的长度分别为:
-
由于BC的基圆和BP、CP都是相切的,所以可将BP、CP平移来求出基圆圆心的坐标。
当BP<CP时,基圆的圆心在P点之下。把直线BP往下平移Rb/sinθ可得:
把直线CP往下平移Rb/cosθ可得:
联立式(31)、(32)可得基圆圆心点Ob的坐标为:
当BP=CP时,点P即为圆弧BC的圆心,其坐标如式(29)所示。
当BP>CP时,基圆的圆心在P点之方。把直线BP往上平移Rb/sinθ可得:
把直线CP往上平移Rb/cosθ可得:
联立式(34)、(35)可得基圆圆心点Ob的坐标为:
-
把发生角为0的渐开线围绕基圆的圆心Ob转动可求出偏心渐开线的发生角。
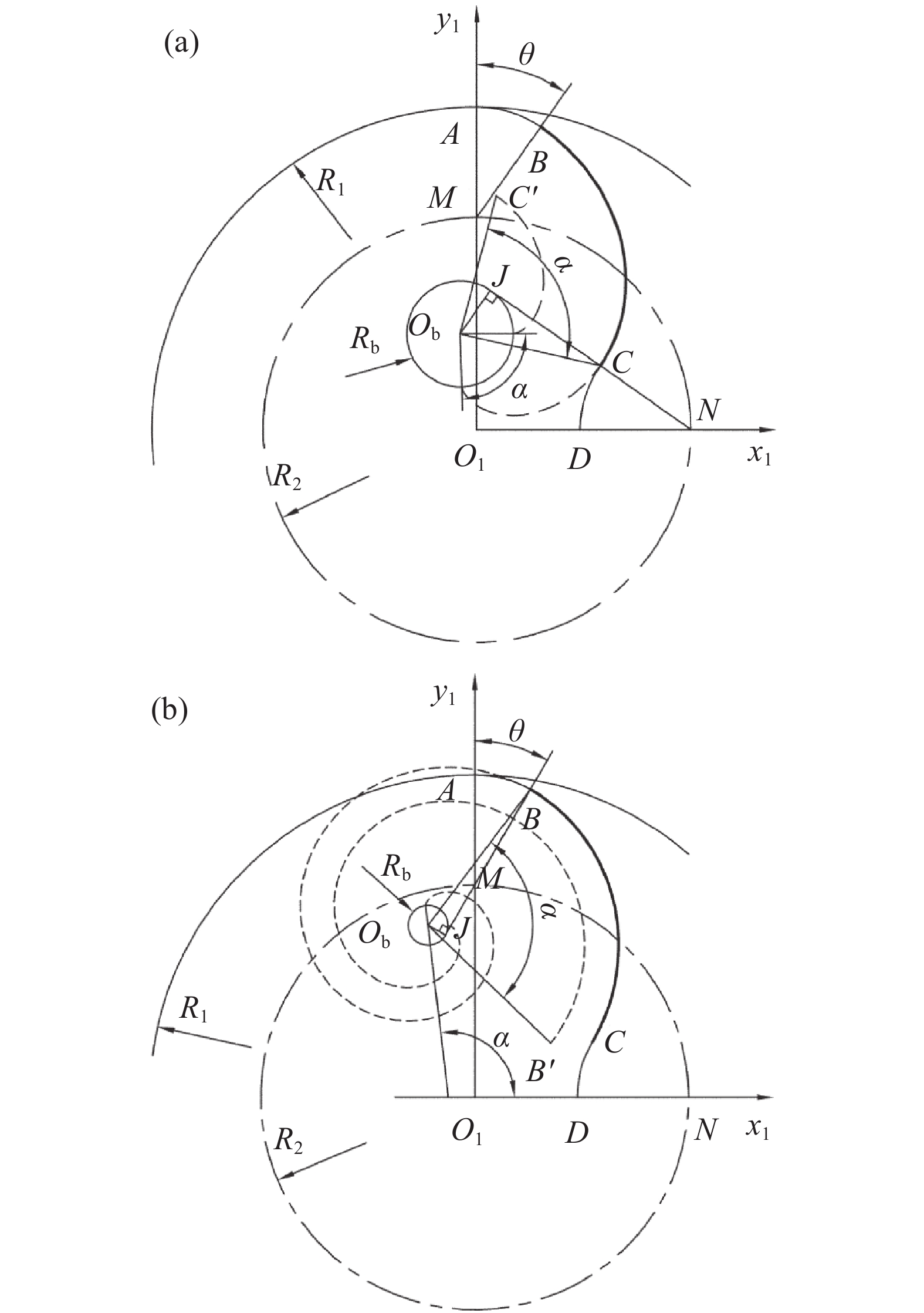
当BP<CP时,如图9(a)所示,在Rt∆CJOb中,根据勾股定理可知:
根据渐开线的基本性质,代入各点的坐标后可得:
联立式(38)、(39)可得:
则角度参数t可取区间为:t∈[t1,t1+π/2]。
因此,C点在渐开线旋转之前的相应点C´坐标:
则可得偏心渐开线的发生角α:
同理,当BP>CP时,如图9(b)所示,可得:
则角度参数t可取区间为:t∈[t1,t1+π/2]。
B点在渐开线旋转之前的相应点B´坐标:
则可得偏心渐开线的发生角α:
-
面积利用系数是指罗茨真空泵每转的排气面积与容腔面积的比值。面积利用系数越高,真空泵的理论吸气量越大。面积利用系数η的表达式如下:
其中,Al表示左转子的截面积,mm2。Ar表示右转子的截面积,mm2。
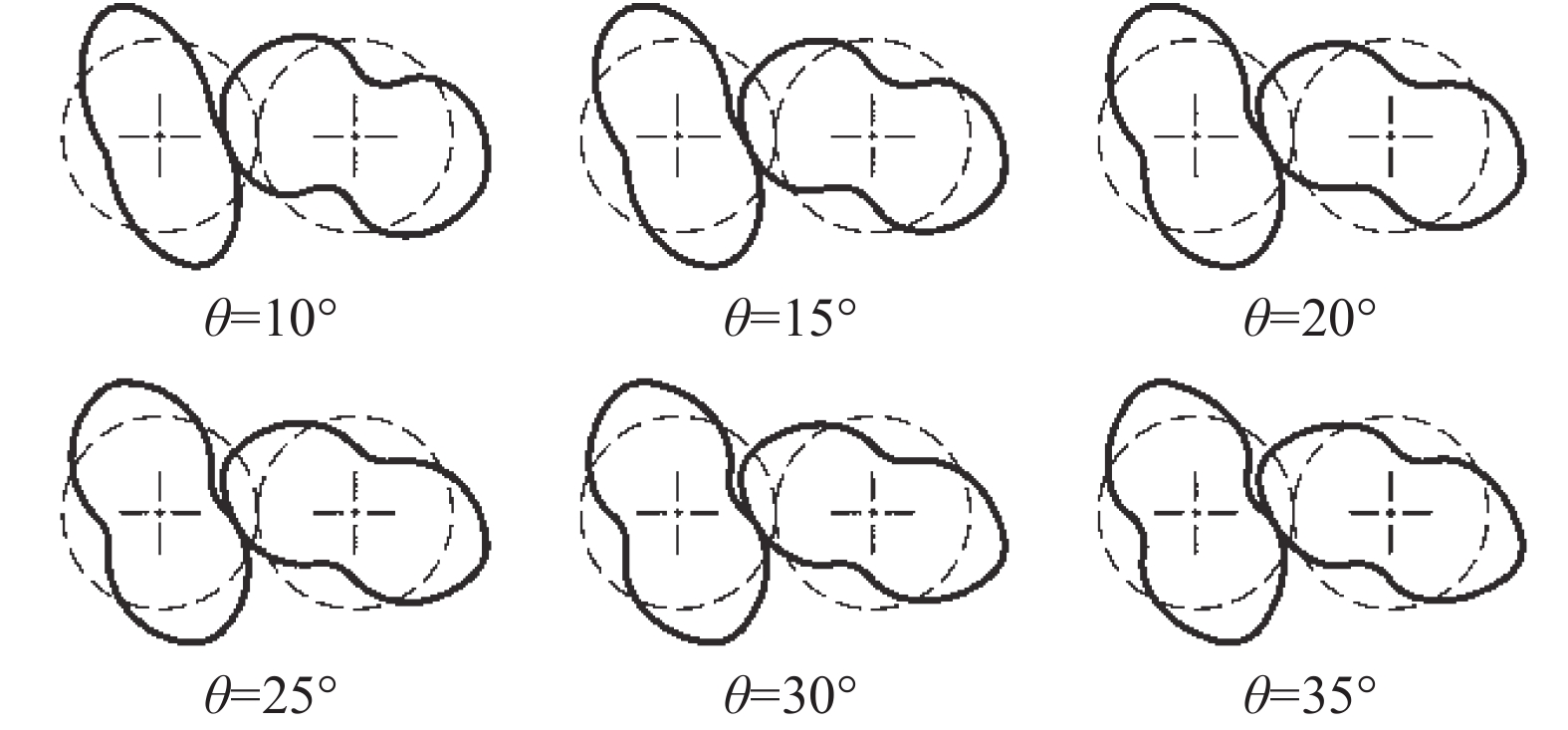
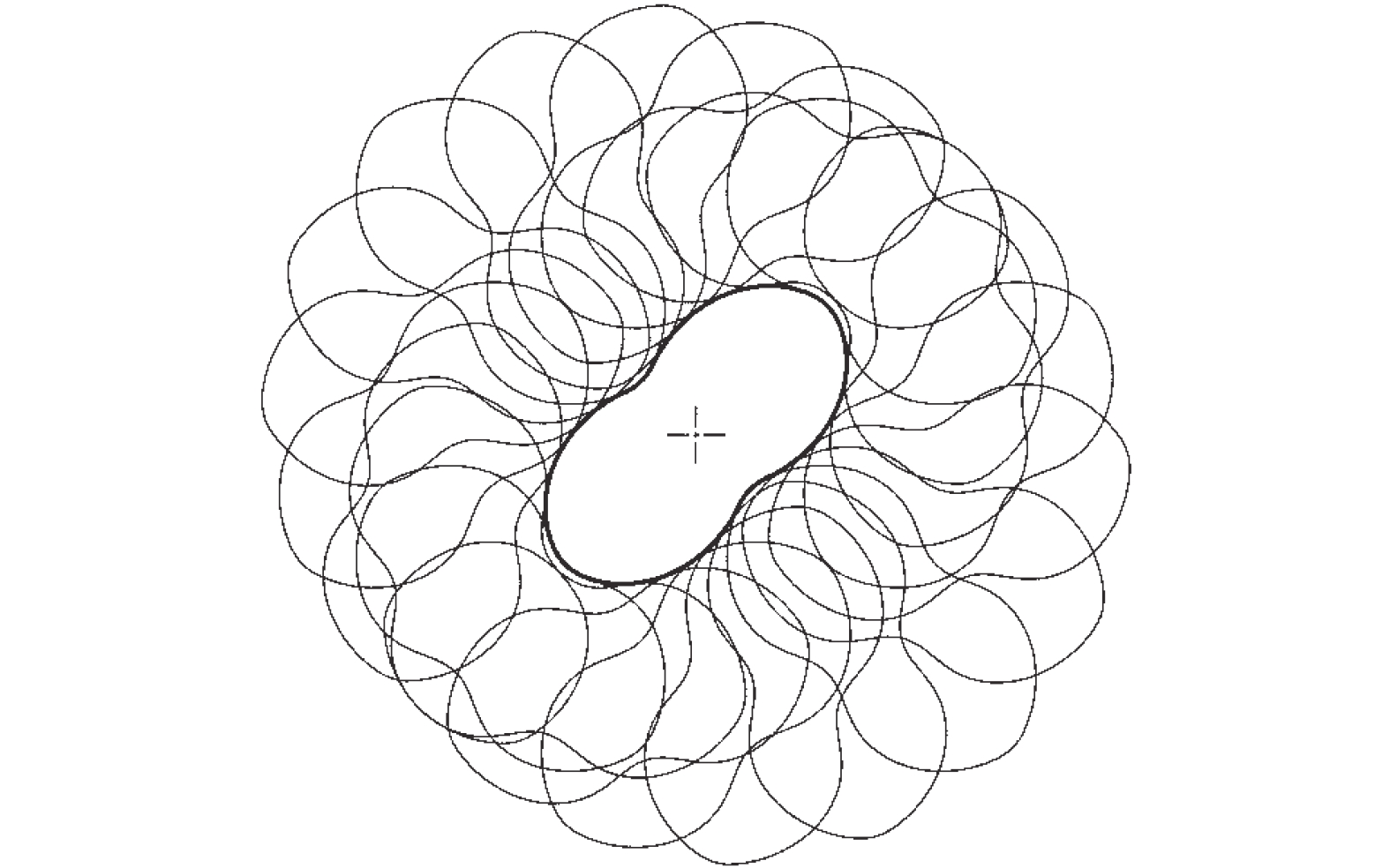
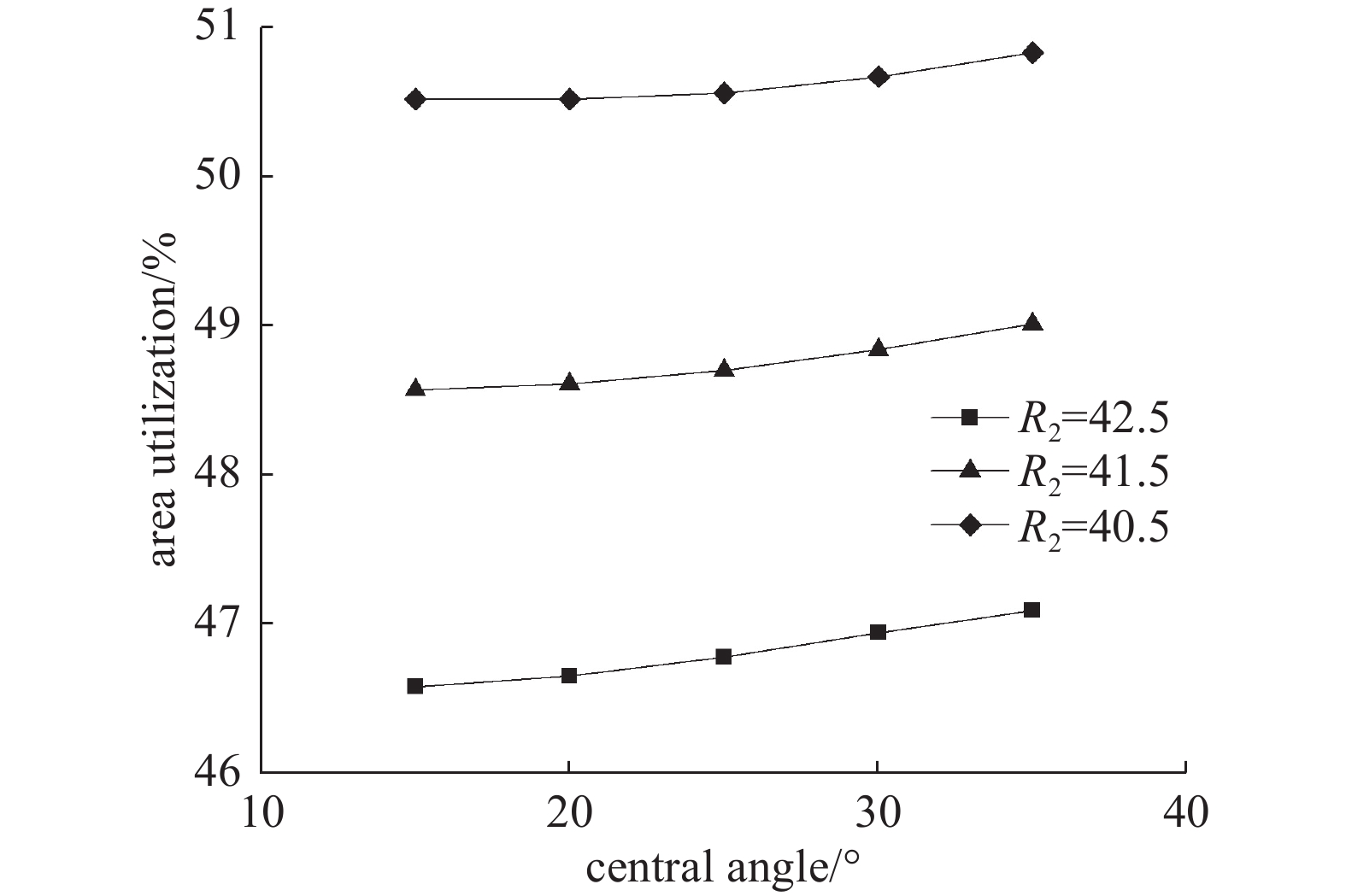
为将圆弧圆心角度θ取不同大小时的转子面积利用率进行比较,设定R1为60 mm和R2为42.5 mm作为参考。圆心角θ取不同数值时的转子截面构建结果如图10所示。转子的运行轨迹如图11所示,两转子可以实现正确啮合。面积利用系数如图12所示,从图中可以看出:当转子外圆半径R1为一固定值时,加大圆心角2θ、减小节圆半径R2,可以使转子面积利用率η得到提高。
2.1. 渐开线基圆半径的确定
2.2. 偏心渐开线基圆的圆心坐标
2.3. 角度参数取值范围及发生角
2.4. 面积利用系数
-
为便于对比分析带尖点的渐开线型和新型不对称渐开线型罗茨真空泵的工作性能,两种转子采用相同的模型参数并设置相同的边界条件。转子的长度l为170 mm,转子的外圆半径R1为60 mm,节圆半径R2为42.5 mm,圆心角θ为25º,转子顶部轮廓与气缸内壁之间的距离β1为0.15 mm,两转子边缘间的距离β2为0.3 mm。工作介质选择理想空气,进口压力为2×104 Pa,出口压力为3×104 Pa,设定进口温度为295 K,采用标准k-ε模型,转速为3000 r/min,设定计算的一个周期为0.06 s。
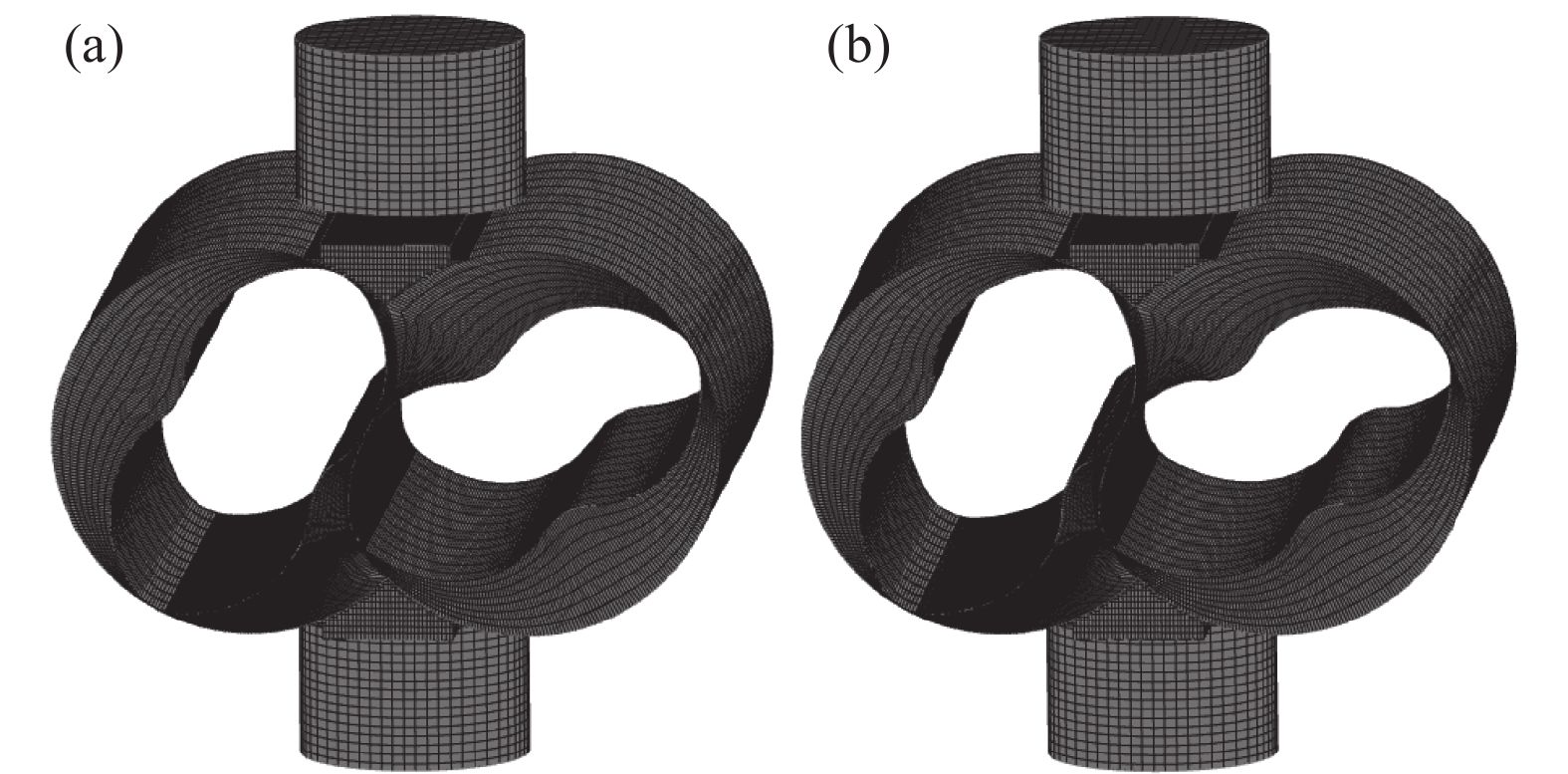
采用四种网格数量对偏心渐开线型罗茨泵开展数值模拟,其中流体域为结构化网格,进出口为非结构化网格,如表1和图13所示:
由表1中计算结果可知,C组求得质量流量与D组相比低1.12%,B组求得质量流量与C组相比低3.95%。可知网格数量高于270385时,网格数量对数值模拟影响较小,为提高计算效率,采用网格数量270385的计算结果进行后续数值分析。
-
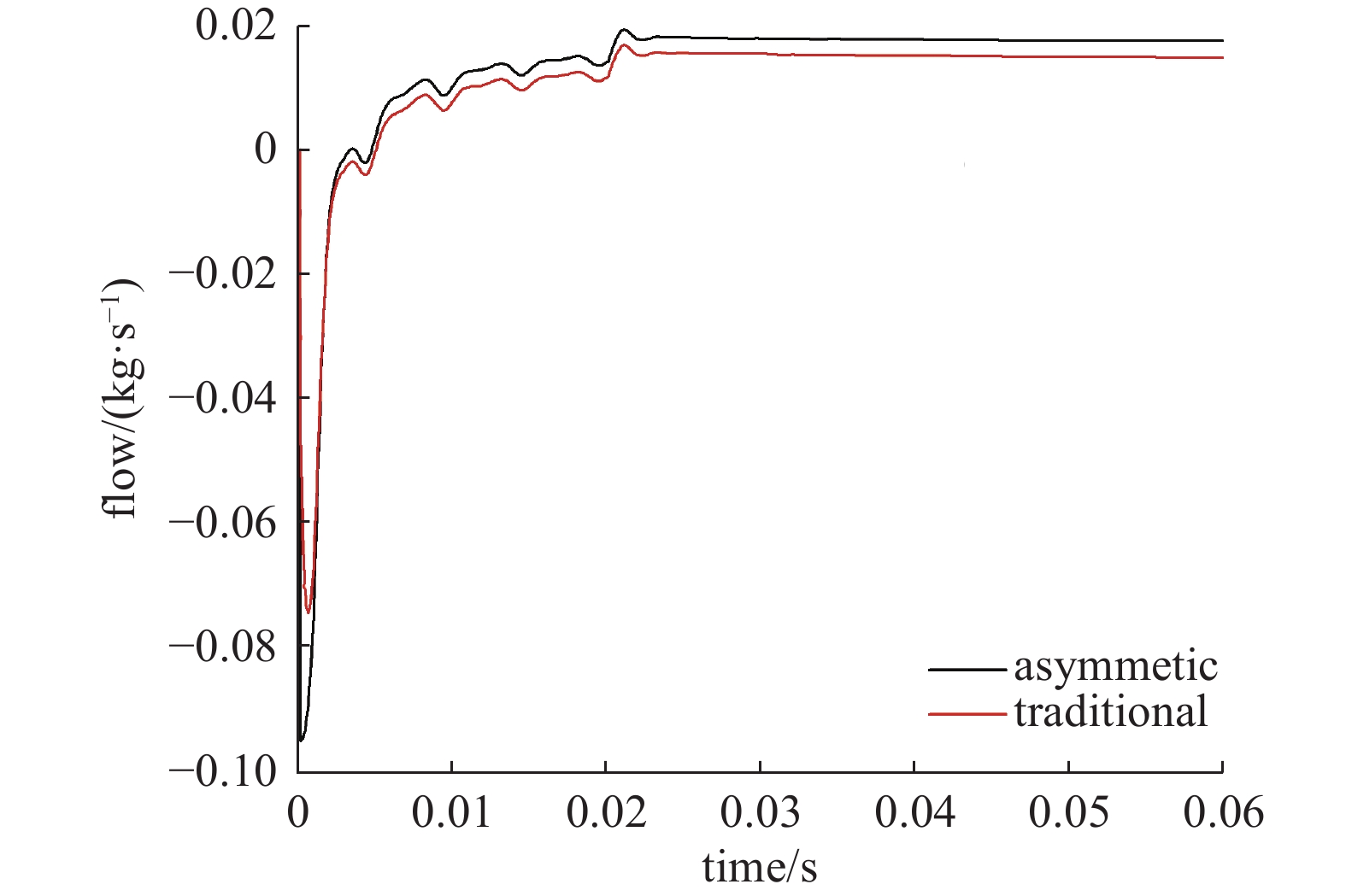
转子区域的面积利用率可以通过出口的平均质量流量来体现。从如图14所示的两类罗茨转子真空泵转子的平均质量流量与时间关系曲线中可以看出,在旋转的第二周(0.02 s),两种转子的出口流量脉动均逐渐变得稳定,至第三周时(0.04 s)便已经稳定,带尖点的渐开线型罗茨转子真空泵和不对称渐开线型罗茨转子真空泵每转平均质量流量分别为:0.0151 kg/s、0.0177 kg/s,不对称渐开线型罗茨转子真空泵每转排量比带尖点的渐开线型罗茨转子真空泵高出约17.2%。
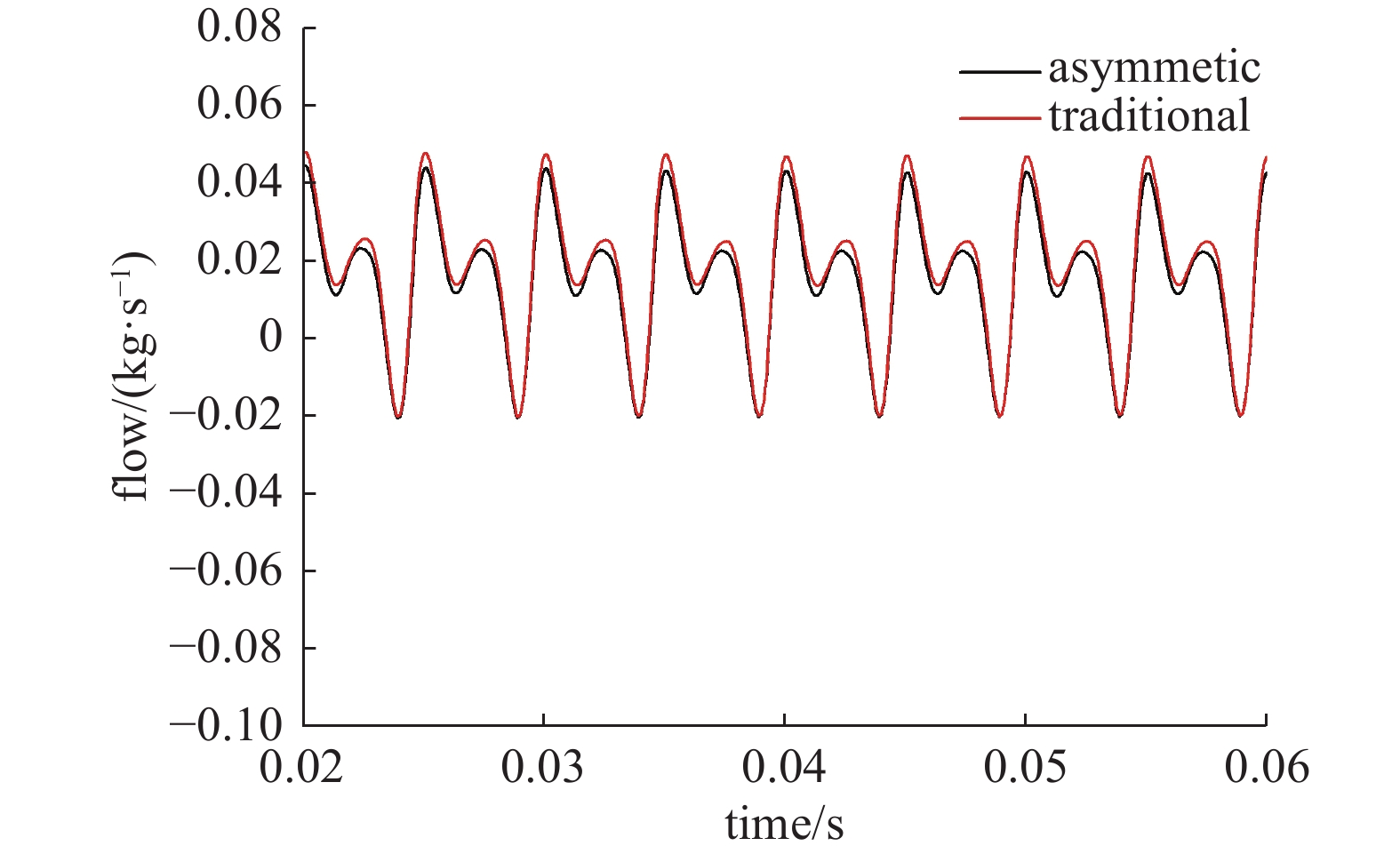
如图15所示,为两种转子在第三转时出口处流量脉动图。从图中可以看出,转子每转动一圈,脉动周期的个数为4。
现定义流量脉动系数F,其计算公式为:
式中:Fmax为质量流量的瞬时最大值,kg/s;Fmin为质量流量的瞬时最小值,kg/s;Fave为质量流量的平均值(每转),kg/s。
带尖点的渐开线型罗茨转子真空泵和不对称渐开线型罗茨转子真空泵出口处的流量脉动系数分别为:4.2089、3.7980,与带尖点的渐开线型罗茨转子真空泵相比,不对称渐开线型罗茨转子真空泵在出口处的流量脉动降低约9.8%。
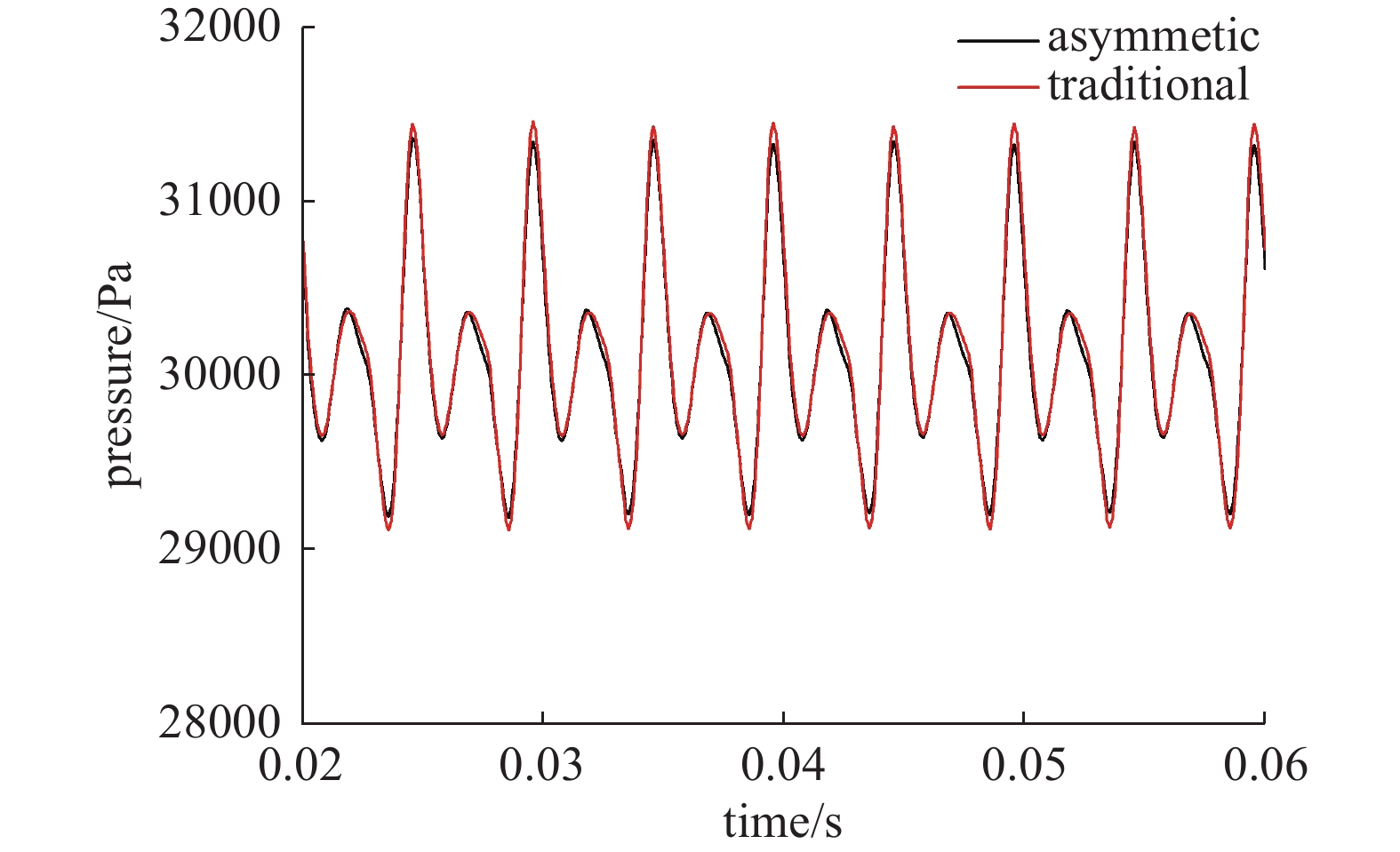
如图16所示,为两种转子在第三转时出口处压力脉动图。从图中可以看出,转子每转动一圈,脉动周期的个数为4。
定义压力脉动系数p,其计算公式为:
式中:pmax为出口压力最大值,Pa;pmin为出口压力最小值,Pa;pave为出口压力均值,Pa。
带尖点的渐开线型罗茨转子真空泵和不对称渐开线型罗茨转子真空泵出口流量脉动系数分别为:0.0777、0.0716,与带尖点的渐开线型罗茨转子真空泵相比,不对称渐开线型罗茨转子真空泵在出口处的压力脉动降低约7.9%。
3.1. 网格划分与边界条件设置
3.2. 流动特性分析
-
(1)为优化罗茨转子型线,提高转子面积利用率,进而提高转子的工作性能,将偏心渐开线与齿顶、齿根圆弧相连实现平滑过渡,减少了转子的不光滑连接点,改善了转子的力学性能。此外转子的型线种类的减少,简化了转子的加工过程,降低了加工成本。运用啮合原理求解了渐开线平移、旋转变换后的共轭曲线,构建了不对称渐开线型转子的数学模型,推导了转子截面型线方程。
(2)得到BP<CP及BP>CP时渐开线角度参数的取值范围及偏心渐开线的发生角。研究了圆弧的圆心角θ与转子面积利用系数之间的关系,发现当外圆半径R1为一固定值时,通过加大圆心角2θ及减小节圆半径R2,可以使转子面积利用率得到提高。
(3)通过数值模拟对比了所提出的不对称渐开线型罗茨转子真空泵和传统渐开线型罗茨空泵的内部流场,发现相较于传统罗茨真空泵:每转排量提升17.2%,出口流量脉动降低9.8%,出口压力脉动降低7.9%。

 首页
首页 登录
登录 注册
注册




 下载:
下载: