首页
登录
注册
下载:
-
射频电源在ICP（Inductively Coupled Plasma）工艺中扮演着关键角色[1-3]。ICP是一种高温、高密度等离子体工艺，常用于半导体制造中的清洗、蚀刻和沉积等工艺。射频电源通过向感应线圈施加高频电磁场，使气体（通常是氩气或氧气）在真空室中电离，形成等离子体，并作用于基底。
与单频射频电源相比，双频射频系统可以提供更精细的等离子体控制，有助于优化工艺参数和提2高加工质量。其结合了低频和高频功率输入，可调节等离子体的密度和能量分布，从而实现更精准的材料处理[4-5]。基于对双频射频电源系统的进一步优化需求，双频匹配器可以实现在不同频率下的阻抗匹配，以确保射频功率被有效地传输到等离子体中，从而提高工艺的稳定性和可控性[6]。
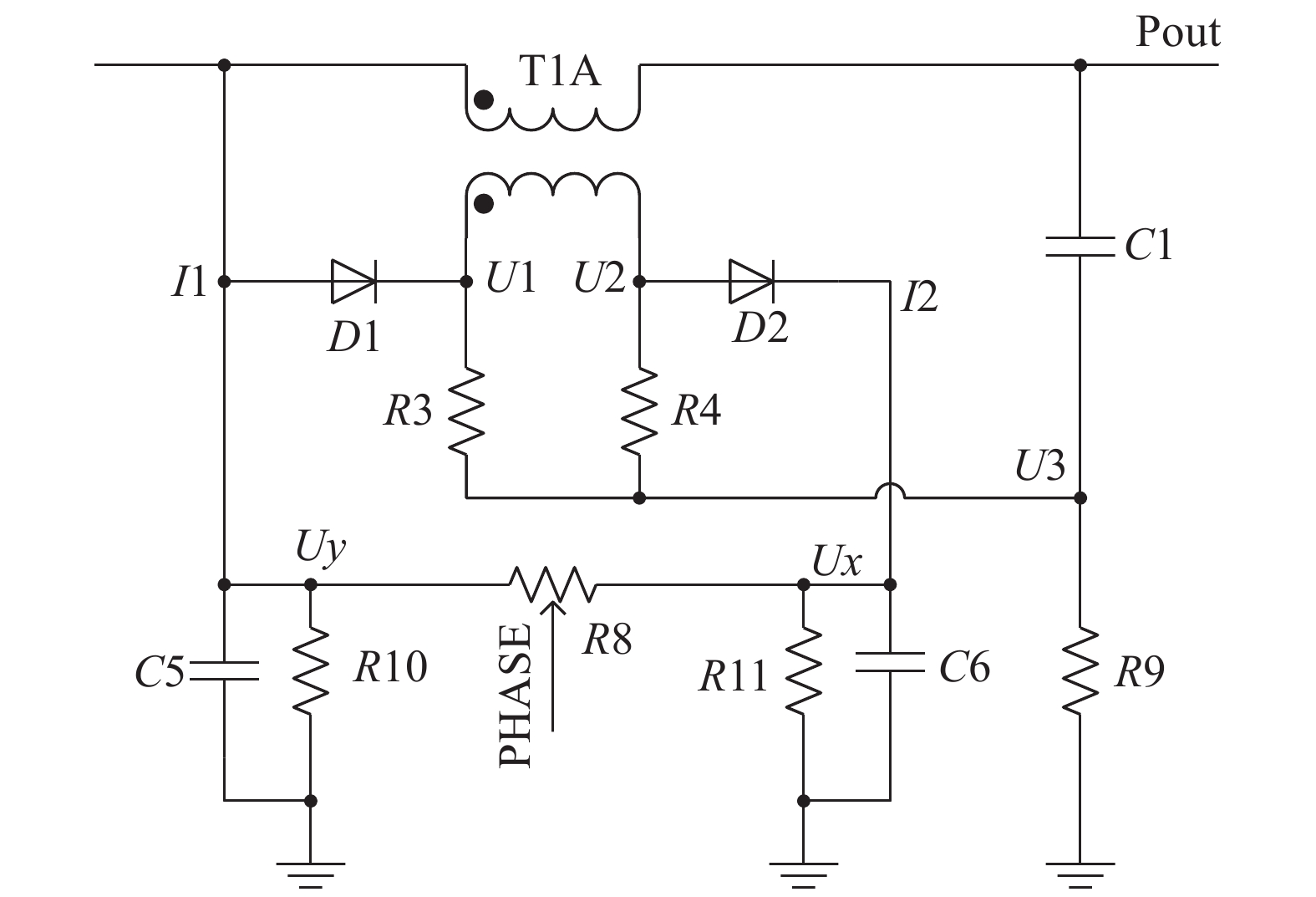
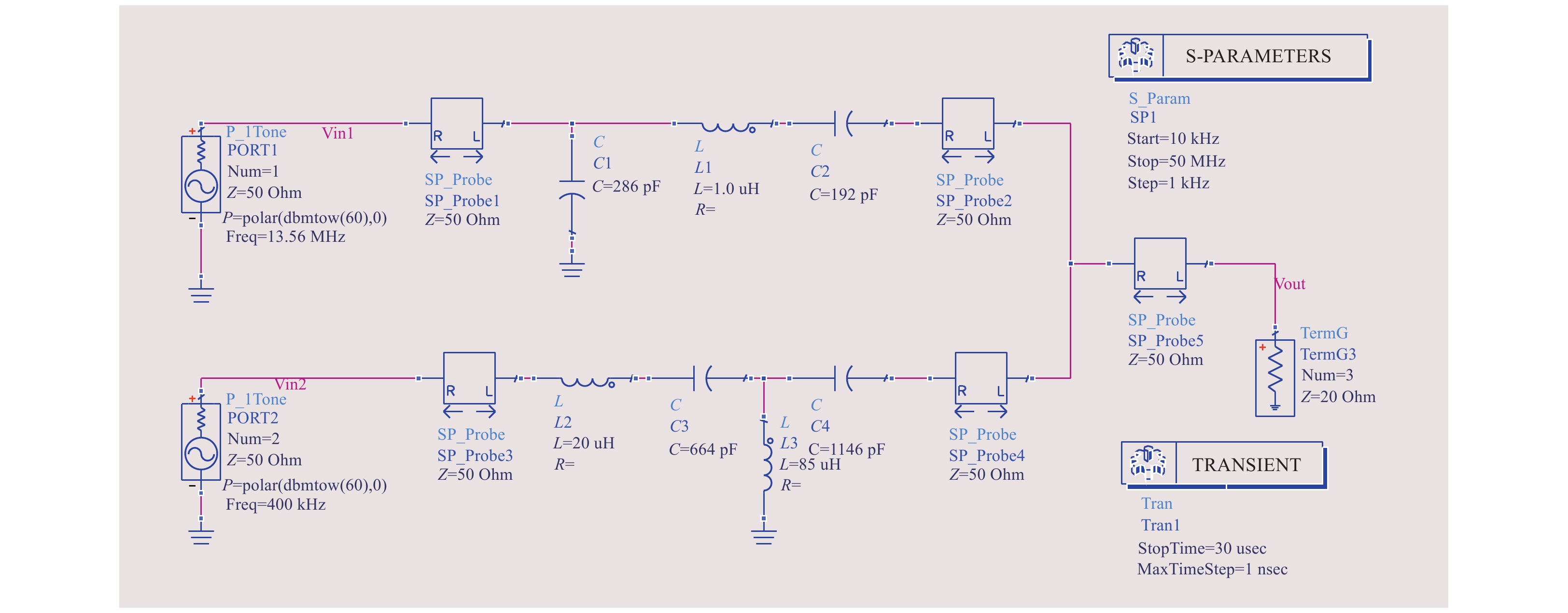
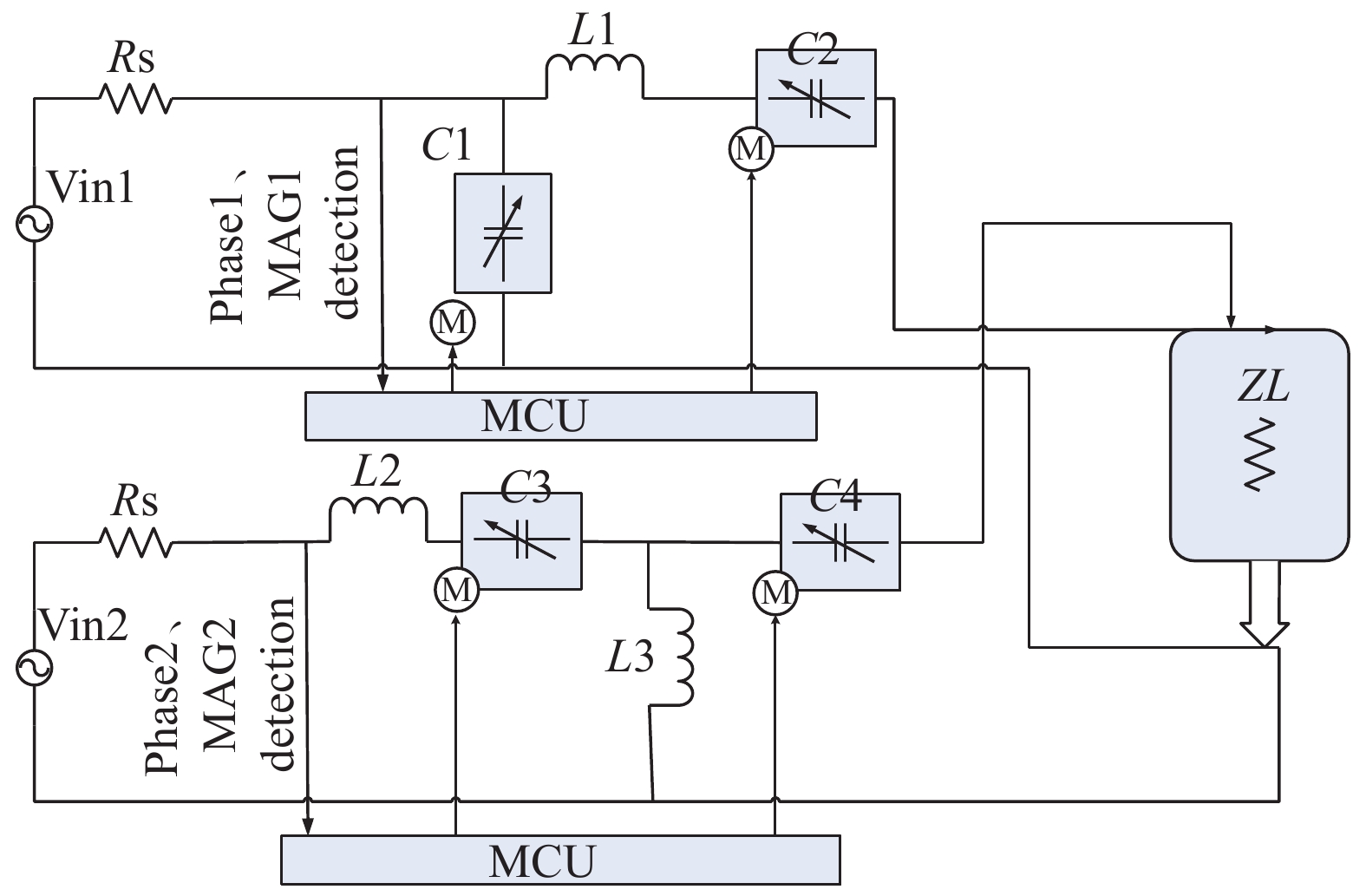
传统匹配箱都是针对当个频点进行匹配，本文设计的基于幅−相检测电路，提出一种双频阻抗匹配器架构，实现在双路同时输入的工况下也能实现双路与腔体之间的共轭匹配，如图1所示。利用输入端的幅值信息和相位信息，通过STM32分别控制可调电容C1和C2以及C3和C4位置，实时采集负载幅值和相位信息，并进行均方根处理
${{{U}}_{{\text{rms1}}}} = \sqrt {{{U}}_{{\text{MAG1}}}^2 + {{U}}_{{\mathrm{Phase1}}}^2} $ ，${{{U}}_{{\text{rms2}}}} = \sqrt {{{U}}_{{\text{MAG2}}}^2 + {{U}}_{{\mathrm{Phase2}}}^2} $ 。当${{{U}}_{{\text{MAG}}}}$ 和相位${{{U}}_{{\text{Phase}}}}$ 均小于设定值时，即${{{U}}_{{\mathrm{rms}}}}$ 小于设定值，就可以代表射频电源和等离子腔体之间实现共轭匹配[7]。 -
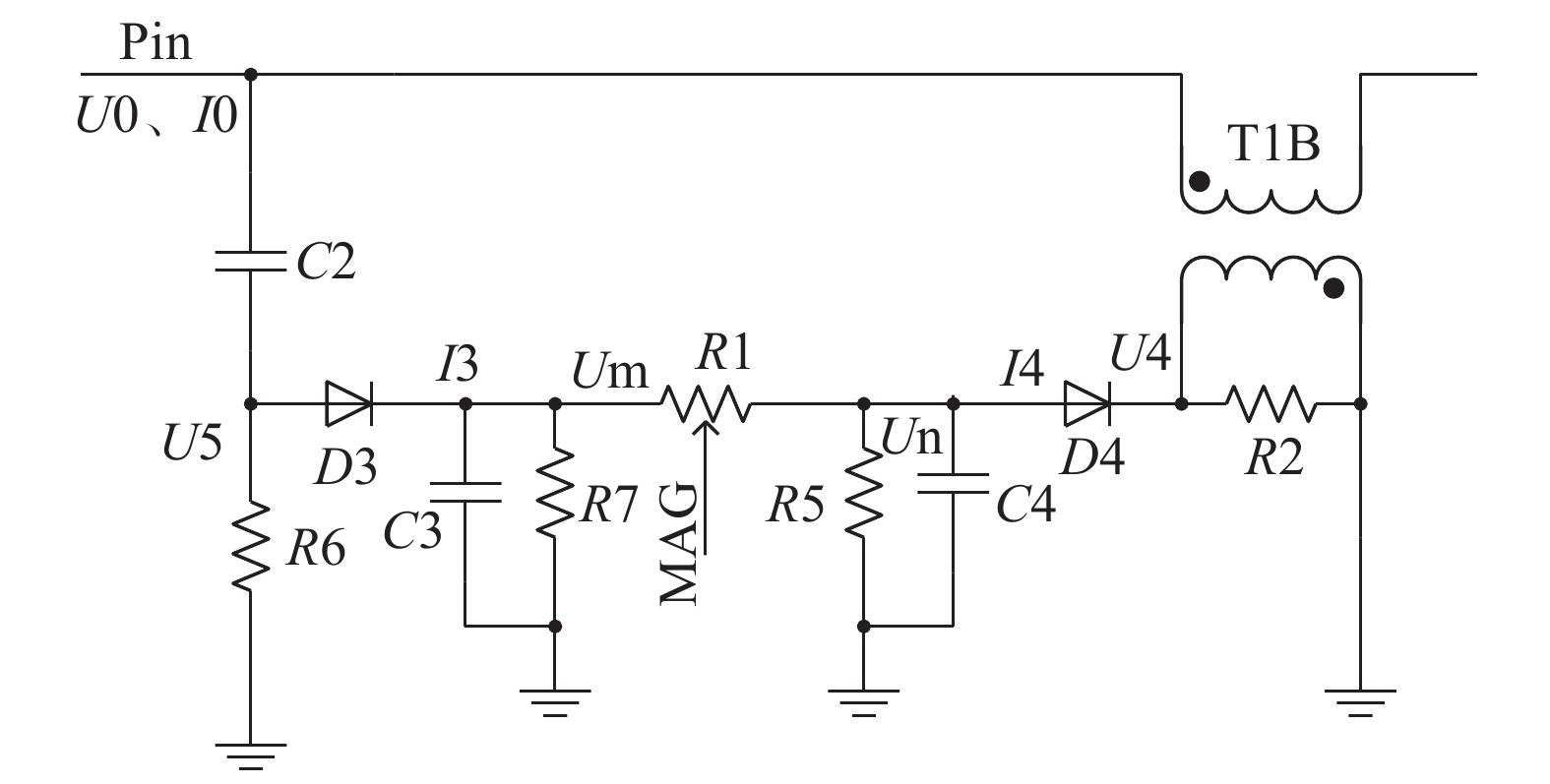
该阻抗幅−相检测系统主要由4部分组成：（1）13.56 MHz匹配模块；（2）MAG-Phase1检测模块；（3）400 kHz匹配模块；（4）MAG-Phase2检测模块。利用以上4个模块就可以搭建双频阻抗匹配器主电路。其中（2）和（4）检测模组原理相一致，适用的频段有区别，（1）13.56 M匹配模组采用的是Gama型匹配网络，（3）400 kHz匹配模组采用的是T型匹配网络。双路射频信号经过合路输出到腔室用于离化等离子体。
负载阻抗的幅值/相位信息与输出电压和输出电流密切相关，利用电流互感器分离主电路电流信息并做进一步电路处理。同时，利用电容分压原理分离主路电压信息，再利用二极管的单向导电性原理以及RC滤波得到
${{{U}}_{{\mathrm{Phase}}}}$ 和${{{U}}_{{\mathrm{MAG}}}}$ [8]。 -
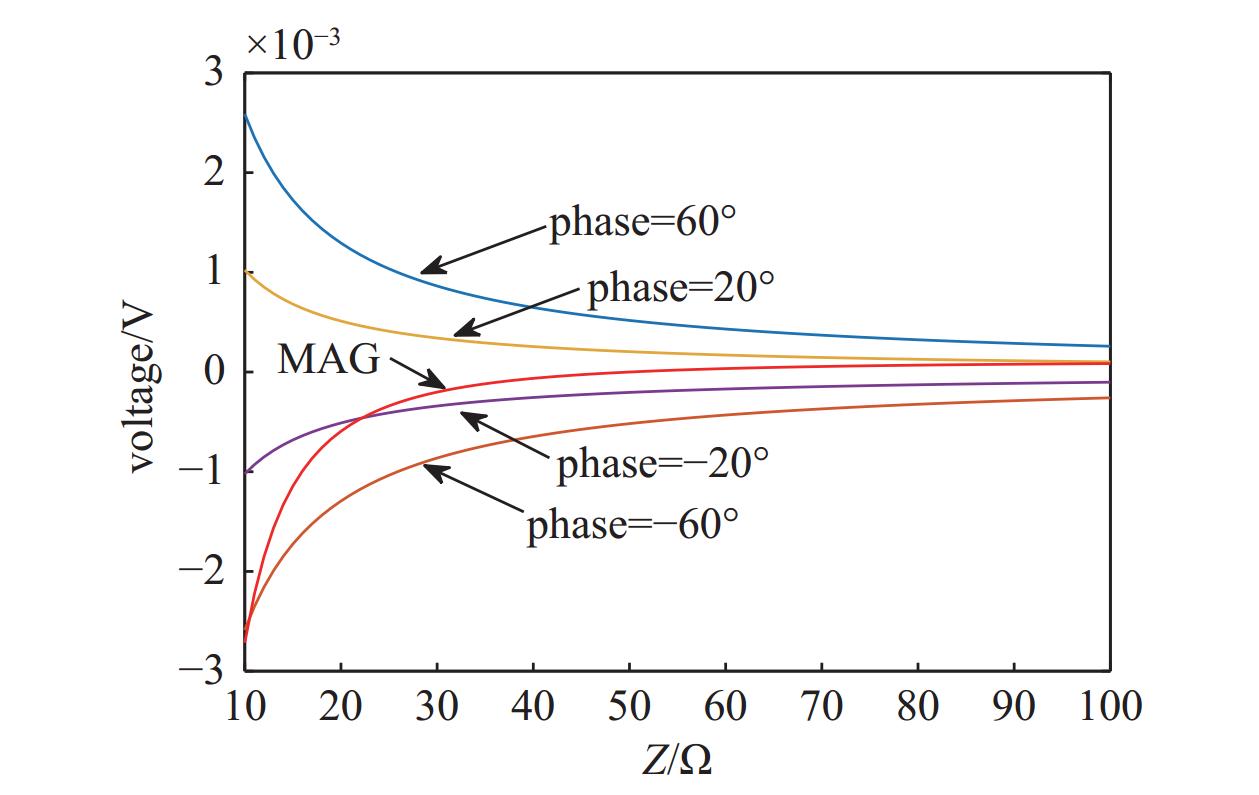
Phase检测电路主要利用电压以及电路信号叠加得到带有相位信息的高频信号，再利用二极管单向导电性，并结合RC滤波电路实现相位信息提取[9-10]，其电路原理框图如图2所示。
MAG检测电路同样主要利用电压以及电路信号叠加得到带有幅值信息的高频信号，再利用二极管单向导电性，并结合RC滤波电路实现幅值信息提取，其技术原理框图如图3所示。
经过数据处理，从而得到表达式:
其中k1为相位检测系数，大小与功率相关且与阻抗幅值成反比；k2为幅值检测系数，大小与功率相关，k3为常数。
当检测两路
${U_{{\mathrm{MAG}}}}$ 和${U_{{\mathrm{Phase}}}}$ 信号数值为0时，等价于该等效负载阻抗的幅值大小等于$ {Z}_0 $ 且相位等于0°，如图4所示。 -
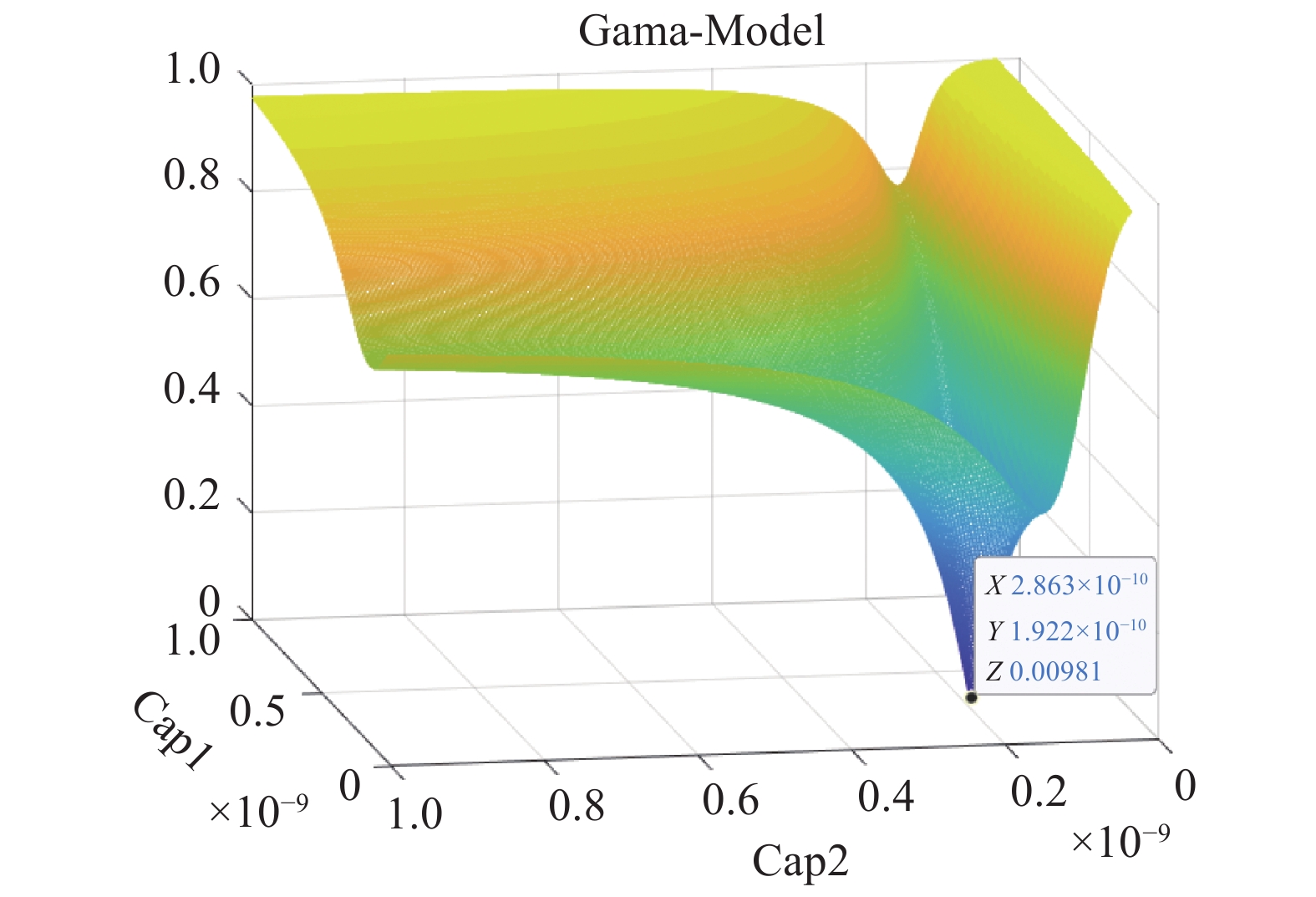
在图1中，Vin1为13.56 MHz射频信号，内阻Rs=50 Ω。针对负载ZL=20 Ω，通过理论计算得到不同容值对应的反射系数，其中C1范围[30,1000]pF、C2范围[30,1000]pF，Gama型匹配网络中串联电感Ls1=1.0 uH，如图5所示。
针对Gama型匹配架构[11]，可以明显发现，当并联电容C1=286 pF,串联电容C2=192 pF时，反射系数为极小值0.0098。此时
${{{U}}_{{\mathrm{rms1}}}}$ 也是极小值，再通过判断${{{U}}_{{\mathrm{rms1}}}}$ 是否小于阈值条件，来判断是否继续调节电容C1和C2。通过重复这样的循环调节就可以实现射频源和腔体之间的阻抗匹配。 -
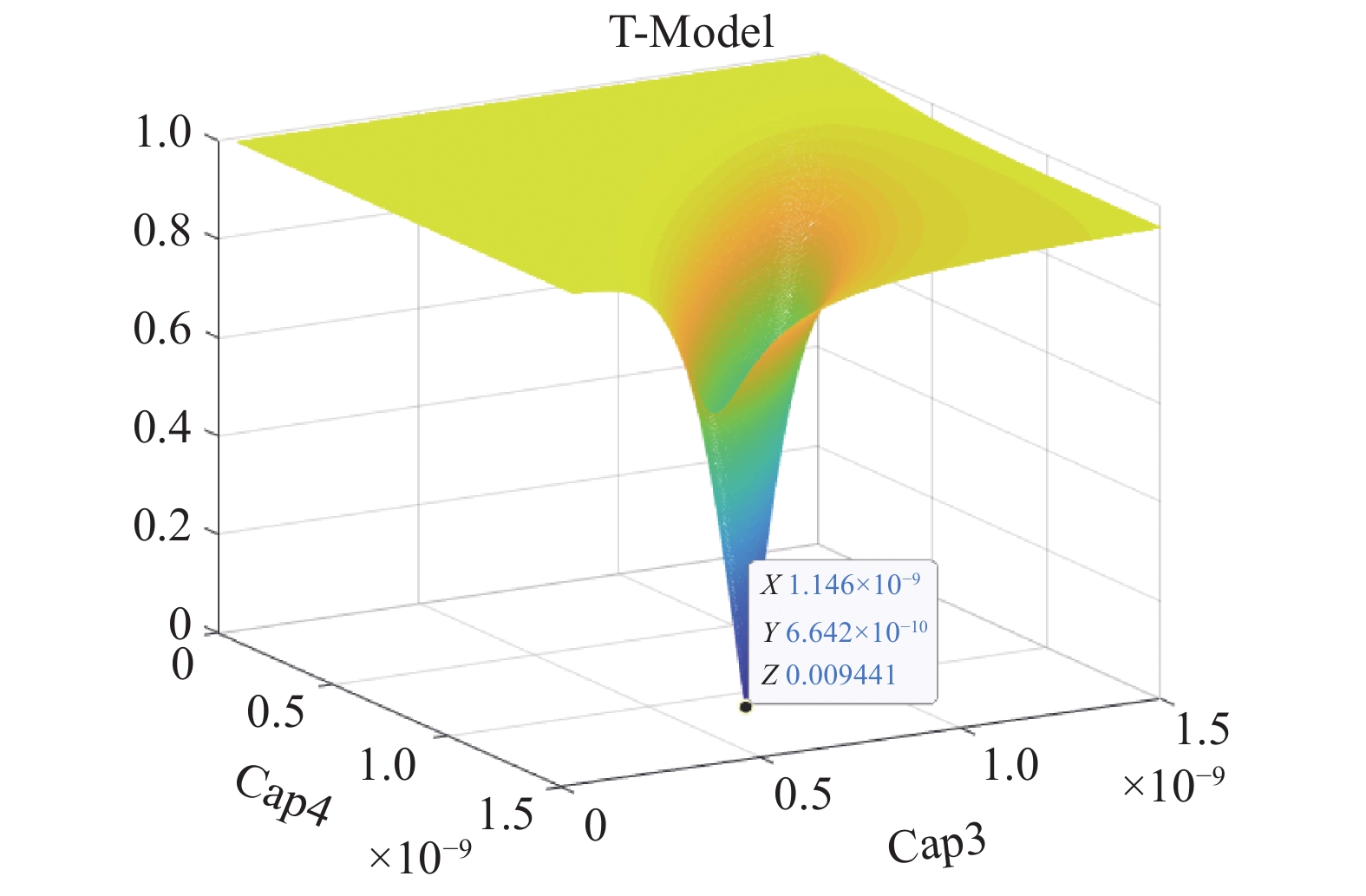
在图1中，Vin2为400 kHz射频信号，内阻Rs=50 Ω。针对负载ZL=20 Ω，通过理论计算得到不同容值对应的反射系数，其中C3范围[30,1500]pF、C4范围[30,1500]pF，T型匹配网络中串联电感Ls2=20 uH，并联电感LS3=85 uH，如图6所示。
针对T型匹配架构，可以明显发现，当并联电容C3=664 pF,串联电容C4=1146 pF时，反射系数为极小值0.009。此时
${{{U}}_{{\mathrm{rms2}}}}$ 也是极小值，再通过判断${{{U}}_{{\mathrm{rms2}}}}$ 是否小于阈值条件，来判断是否继续调节电容C3和C4。通过重复这样的循环调节就可以实现射频源和腔体之间的阻抗匹配。 -
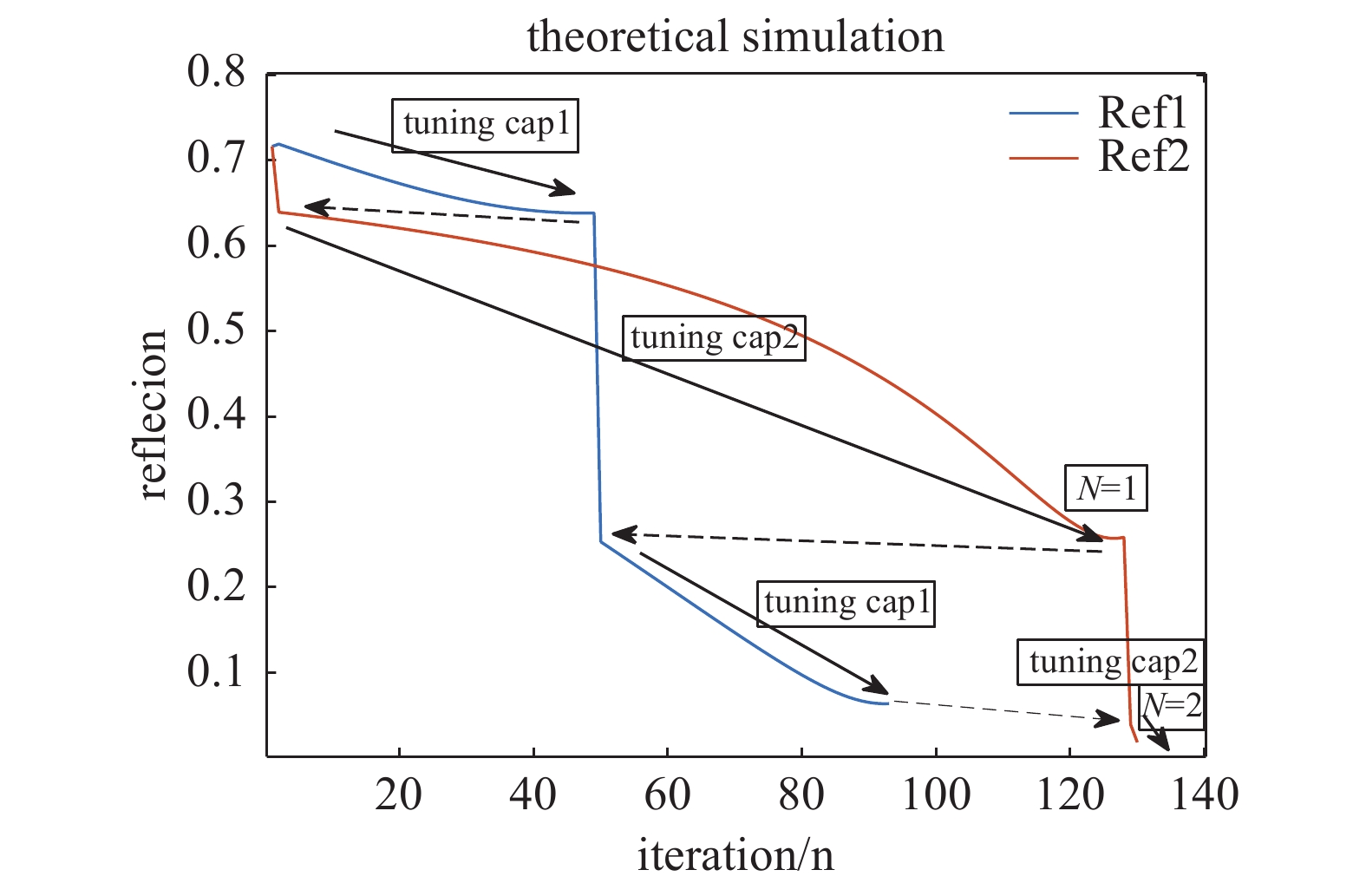
针对13.56 M Gama型匹配架构，当并联电容C1恒定，反射系数随串联电容C2改变，且存在一个极小值，当C2调节到极小值点时，对应
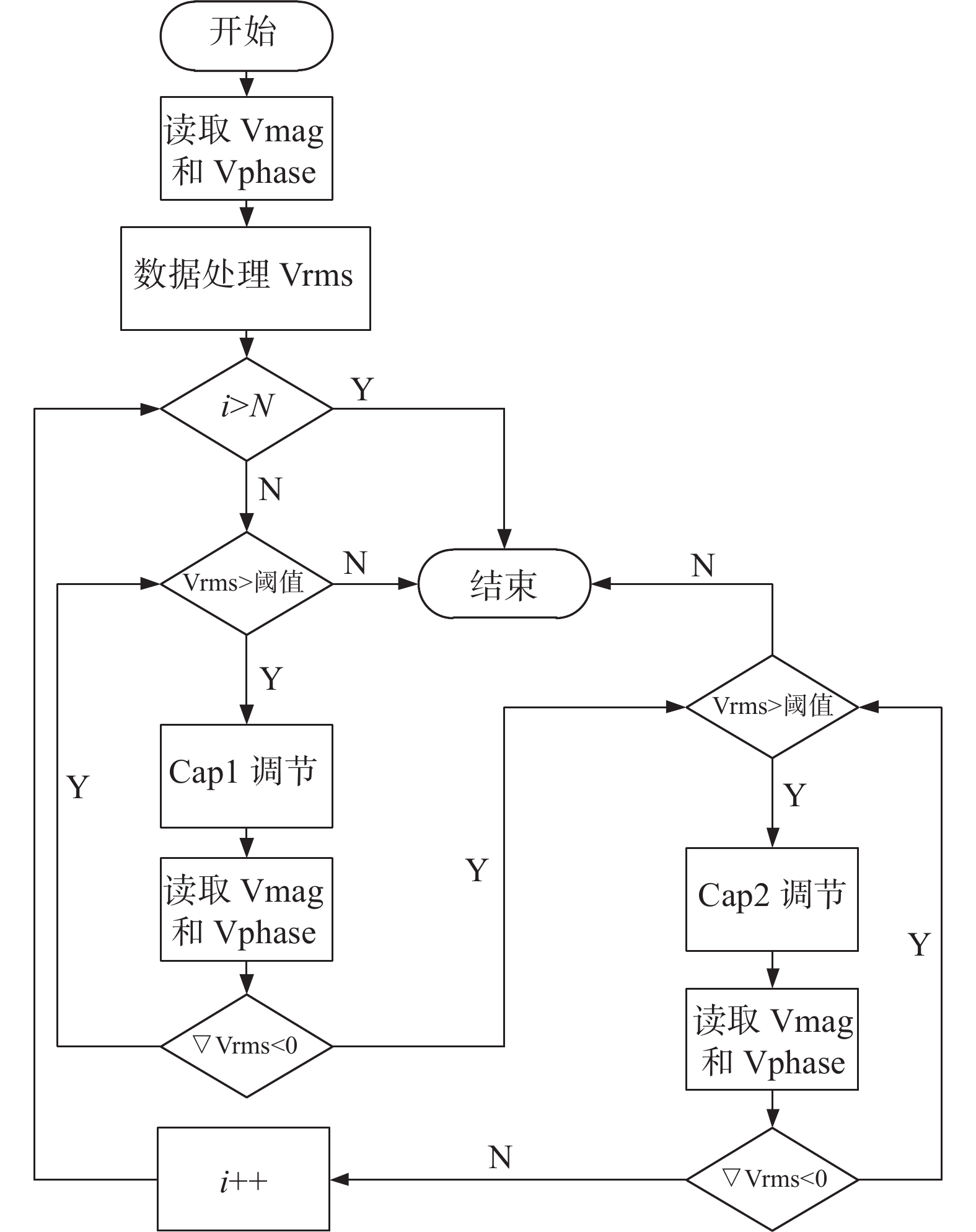
${{{U}}_{{\mathrm{rms1}}}}$ 也是极小值，再通过判断${{{U}}_{{\mathrm{rms1}}}}$ 是否小于阈值条件，来判断是否继续调节串联电容C2；当串联电容C2恒定，反射系数随并联电容C1改变，且同样存在一个极小值，当C1调节到极小值点时，对应${{{U}}_{{\mathrm{rms1}}}}$ 也是极小值，再通过判断${{{U}}_{{\mathrm{rms1}}}}$ 是否小于阈值条件，来判断是否继续调节并联电容C1。因此，通过重复这样的循环调节就可以实现射频源和腔体之间的阻抗匹配。程序原理框图如图7所示，首先设定循环次数N和
${{{U}}_{{\mathrm{rms}}}}$ 的阈值条件，进入程序。针对Gama型匹配网络，控制逻辑如下：（1）读取腔体此时刻的幅值
${U_{{\mathrm{MAG}}}}$ 和相位${U_{{\mathrm{Phase}}}}$ ，并计算${{{U}}_{{\mathrm{rms}}}}$ ，首先判定循环次数i是否超过N，如果超过最大次数就结束调节，否则进行步骤（2）；（2）判定
${{{U}}_{{\mathrm{rms}}}}$ 是否大于阈值，如果${{{U}}_{{\mathrm{rms}}}}$ 超过阈值，则进行步骤（3）,否则结束调节；（3）调节C1电容位置，寻找对应
${{{U}}_{{\mathrm{rms}}}}$ 的极小值点，即反射系数对应电容C1的极小值，再进行步骤（4）；（4）调节C2电容位置，寻找对应
${{{U}}_{{\mathrm{rms}}}}$ 的极小值点，即反射系数对应电容C2的极小值，循环次数i加1，再进行步骤（1）；以上便是Gama型匹配拓扑的控制逻辑，经过2到3次循环就可以找到C1和C2，使得射频源和腔体等效阻抗共轭匹配，T型匹配拓扑控制逻辑同理。
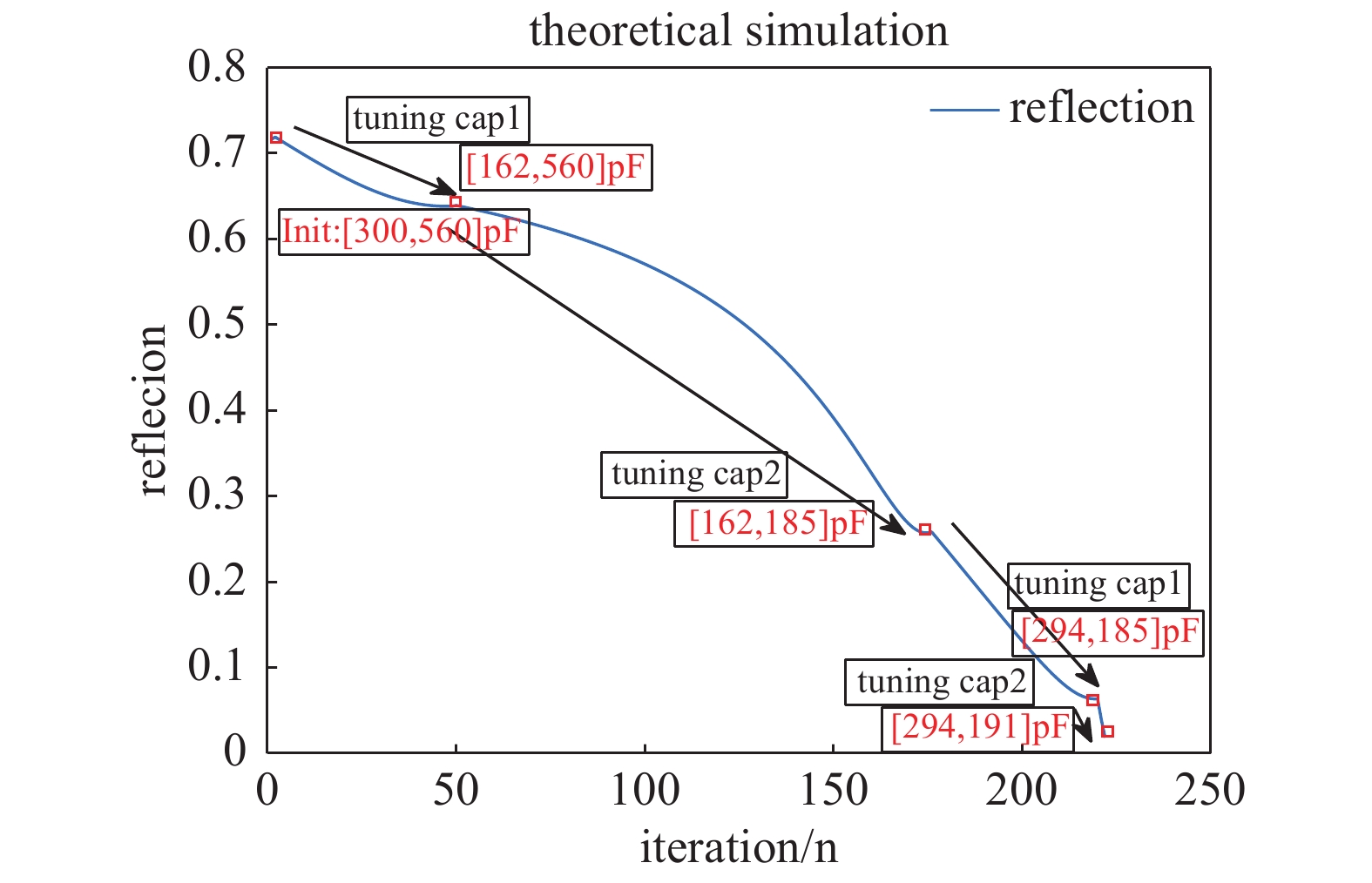
图8是基于MATLAB编程得到对应阻抗Z=20 Ω下，分步调谐的反射系数变化趋势线。反射阈值为0.03，N=3，初始电容Cap=[C1,C2]=[300,560]pF，电容C1和电容C2的步进值均为3pF。（1）调谐并联电容C1，固定串联电容C2，经过49次迭代，找到极小值点组合Cap=[162,560]pF，（2）调谐串联电容C2，固定并联电容C1，经过127次迭代，找到极小值点组合Cap=[162,185]pF，（3）调谐并联电容C1，固定串联电容C2，经过45次迭代，找到极小值点组合Cap=[294,185]pF，（4）调谐串联电容C2，固定并联电容C1，经过2次迭代，找到极小值点组合Cap=[294,191]pF，此时对应反射系数为0.0183小于0.03，满足设定要求结束循环，如图9所示。
因为
${{{U}}_{{\mathrm{rms}}}}$ 和反射系数存在线性关系，当${{{U}}_{{\mathrm{rms}}}}$ 增大时，其物理意义为射频电源与腔体等效负载之间的阻抗偏差越大，当${{{U}}_{{\mathrm{rms}}}}$ 小于设定值0.03时，其代表射频电源和腔体等效负载之间满足阻抗匹配要求，同时射频电压驻波比也将小于1.05。因此，该匹配算法可以快速便捷的实现射频源和负载之间的阻抗匹配。基于幅－相检测实现双频自动阻抗匹配的方式，可以快速响应等离子体腔室由于外部扰动导致的等效阻抗变动，有助于双频信号在半导体工艺场合下的应用能力。 -
对于双频阻抗匹配器，一方面重点考虑射频源和腔体之间的阻抗匹配，另一方面还需要考虑三端口网络之间的隔离度和插损。利用ADS仿真软件搭建双频阻抗匹配系统，如图10所示。其中Vin1为13.56 MHz射频信号，内阻Rs=50 Ω，Vin2为400 kHz低频信号，内阻Rs=50 Ω，负载Z=20 Ω。
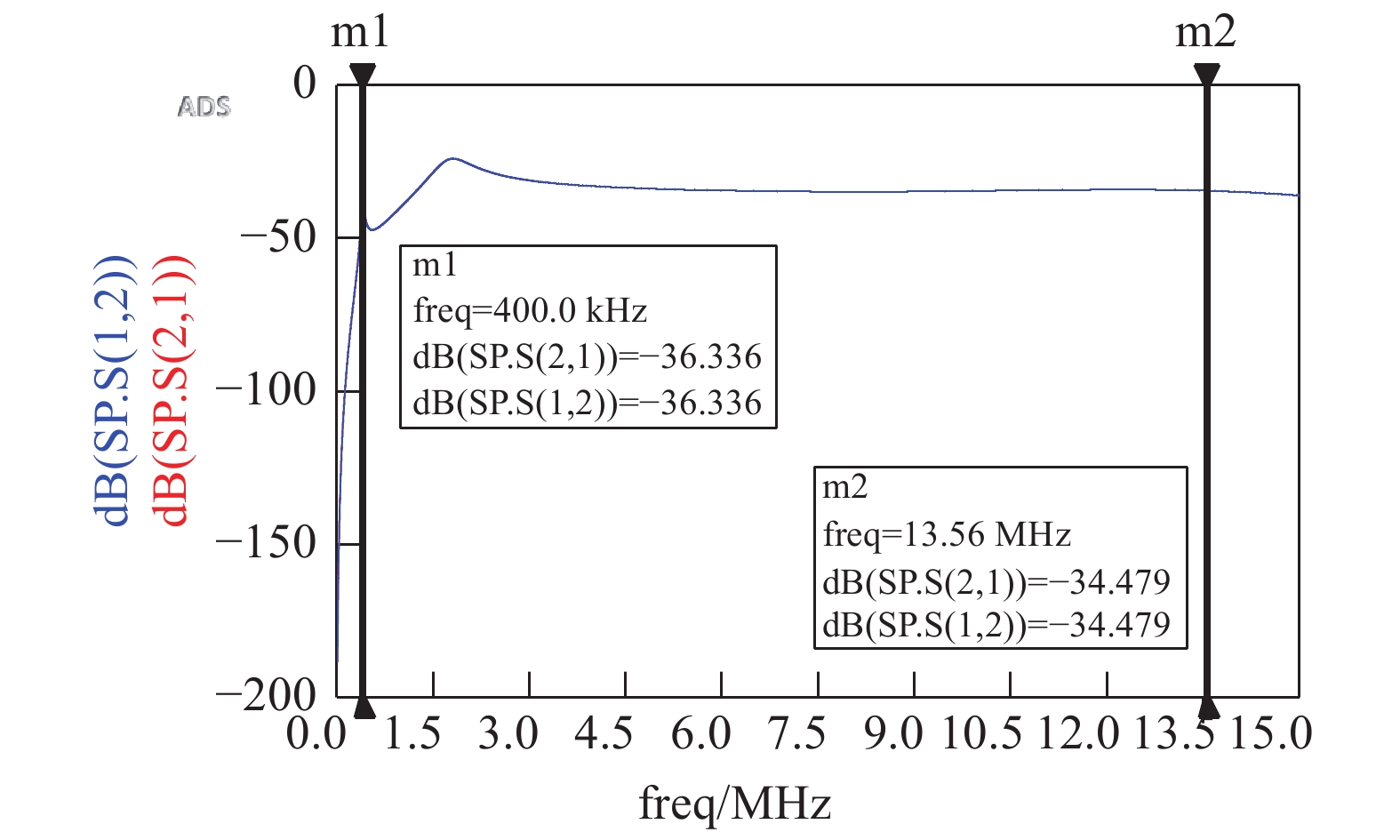
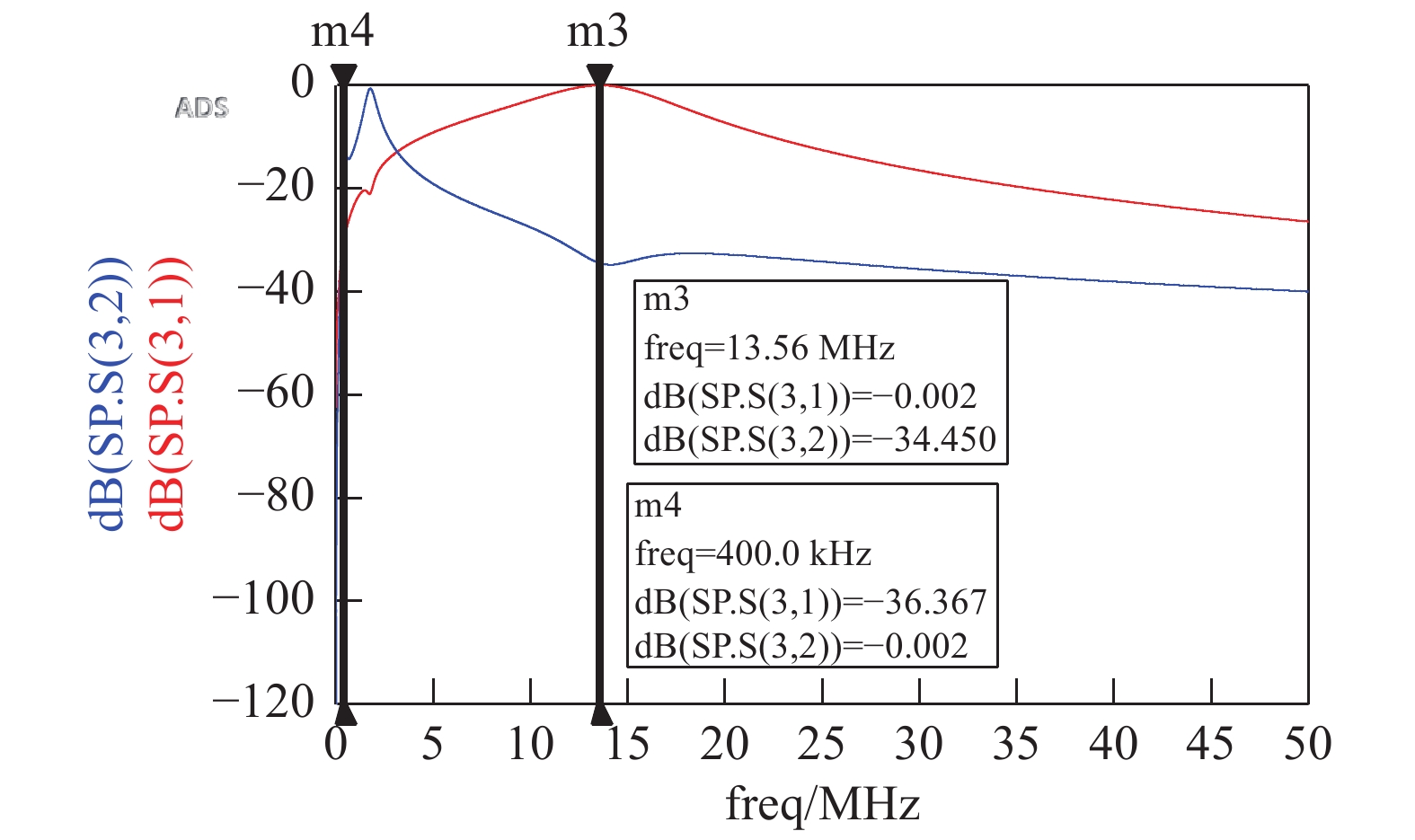
依据理论计算，设置相关集总参数数值，得到Vin1和Vin2以及Vout之间的隔离度和插损，如图11、图12所示。
在400 kHz和13.56 MHz频率下，该匹配架构的S12=−36.3 dB,S21=−34.4 dB，输入1、2端口之间具有较好的隔离度。其相对输出Vout端口的插损分别为S32=−0.002 dB，S31=−0.002 dB，具有较低的插入损耗。因此，该双频阻抗匹配器拓扑具有非常良好的隔离度，保证射频电源之间不会相互影响。同时，射频源到负载之间的插入损耗也非常小，保证各路功率传输时，能量都能被腔室吸收，效率高、反射小。
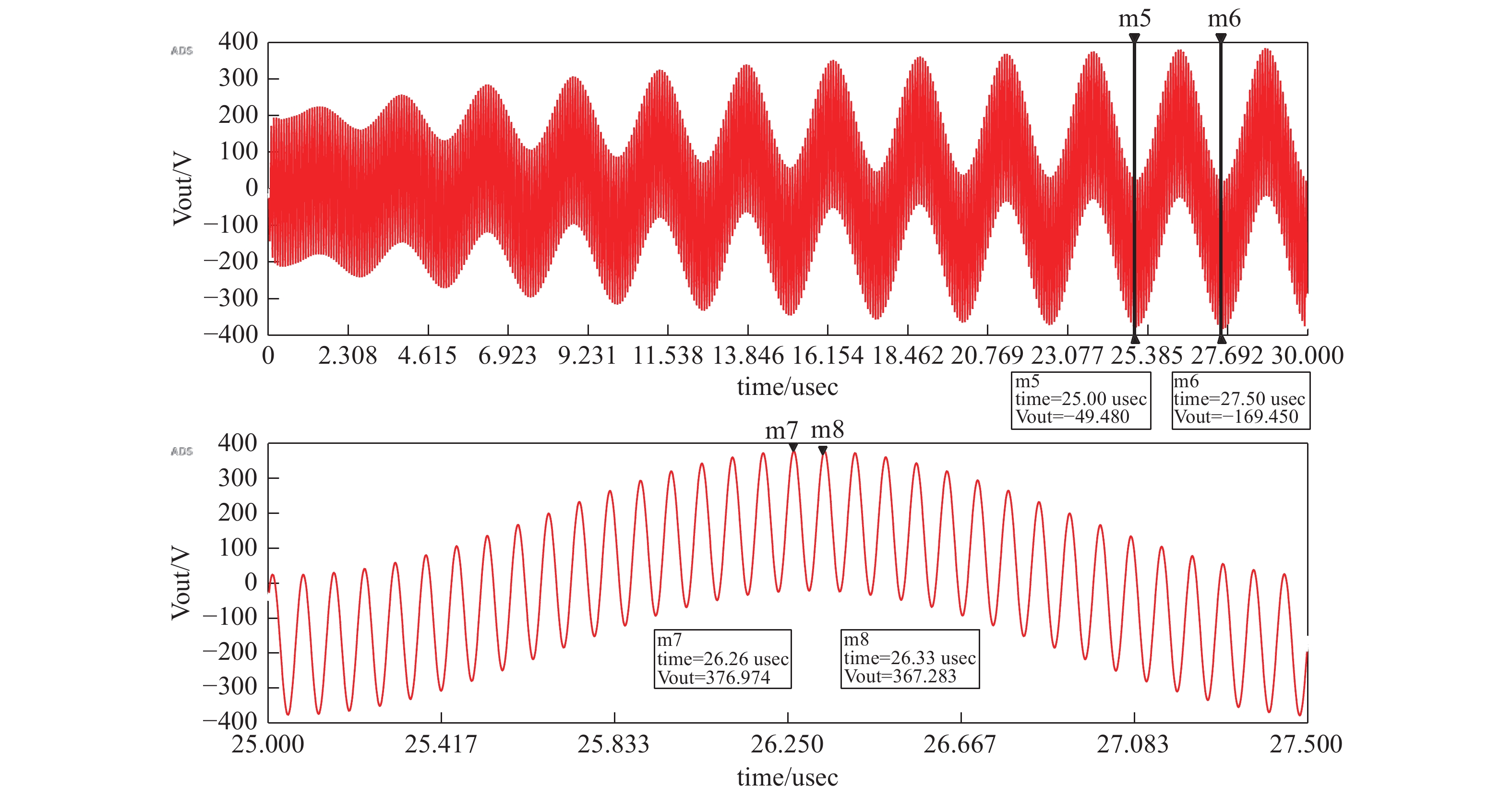
图13为在端口1和2分别输入1 kW功率Vin1和Vin2信号，得到的时域仿真波形。可以看出端口3输出的是载波为400 kHz，并叠加13.56 MHz的高频信号作用于负载。因此，通过分别控制输入Vin1和Vin2的功率，实现腔体离子的离化率和等离子能量的精准控制。
-
本文设计的基于二极管幅−相检测双频阻抗匹配电路，具备电路原理简单，维修方便，成本可控等优势。通过利用高频信号（13.56 M）和低频信号（400 K）进行多路复合输出，进而分别控制等离子体的离化率和轰击能量，从而实现多维度、多角度的等离子体精准控制，适合用于多场合下的阻抗匹配应用环境。
同时，轮换寻优算法迭代效率高，匹配阈值可调，其有力提升匹配器中电机调节效率，当检测
$ {U_{{\mathrm{MAG}}}} $ 和${{{U}}_{{\mathrm{Phase}}}}$ 信号小于设定值时，即可以判定腔室等效负载和射频电源之间实现阻抗匹配。另一方面，该方案采集腔室等效阻抗的相对幅值和相对相位大小，无需进行复杂的物理建模求解腔室等效阻抗真值，也无需进行复杂的可调电容真值曲线拟合，匹配算法基于轮换调谐的方式实现${{{U}}_{{\mathrm{rms}}}}$ 调节操作，从而能高效的实现匹配箱的阻抗匹配。同时，避免因可调电容、工艺调节以及应用环境等外部因素改变而对匹配箱中的调节算法产生较大影响，相对于传统调节方式，该方案更加稳定与高效。
基于幅−相检测双频自动阻抗匹配器仿真分析
Analysis of Dual Frequency Automatic Impedance Matcher Based on Amplitude-Phase Detection
-
摘要: 先进半导体制程中需要对等离子体离化率和轰击能量进行精准控制，传统单频系统难以实现上述目标，进而提出复频信号控制。基于对双频射频电源系统的进一步需求，开发双频匹配器以便实现在不同频率下的阻抗匹配具有重要的意义。文章基于二极管幅−相检测电路，设计一款双频自动阻抗匹配器电路，并分别进行检测模组、匹配架构以及寻优算法等相关机理分析。通过研究表明，Urms可以表征射频电源与腔室之间的匹配程度，Urms越大表征失配程度越大，反之匹配程度越好。针对13.56 M和400 kHz信号分别采用Gama型和T型匹配网络进行匹配输出，仿真结果表明该结构具有很好的传输特性，理论插损小于−0.002 dB以及较高的隔离度，理论隔离度−34.4 dB。同时，轮换寻优算法，具备响应速度快，匹配精度高等特性，可以利用轮换调谐的方式高效实现射频源和腔室之间的阻抗匹配。Abstract: In the advanced semiconductor process, it is necessary to precisely control the plasma ionization rate and ion impact energy, and the traditional single-frequency power supply makes it difficult to achieve the above goals, so a dual-frequency is proposed. It is of great significance to develop dual frequency matchers in order to achieve impedance matching at different frequencies. This article designs a dual frequency automatic impedance matcher based on a diode amplitude-phase detection circuit. Simulation research shows that Urms can represent the matching degree between the RF power and the chamber; the greater the Urms, the greater the degree of mismatch, and vice versa, the better the matching degree. Gama and T-type matching networks are used for matching outputs of 13.56 M and 400 kHz signals, respectively. Simulation results show that the structure exhibits excellent transmission characteristics, with a theoretical insertion loss of less than −0.002 dB and high isolation, with a theoretical isolation of −34.4 dB. The optimization algorithm has the characteristics of fast response and high matching accuracy, and uses this method to achieve impedance matching between the RF source and the chamber.
-
-
图 1 双频自动阻抗匹配器系统框图
Figure 1. System diagram of dual-frequency automatic impedance matcher
图 4 阻抗幅值
${U_{{{{\mathrm{MAG}}}}}}$ 和相位${U_{{{{\mathrm{Phase}}}}}}$ 随阻抗变化趋势Figure 4. The relationship between MAG and Phase with Z0
图 5 Gama型匹配网络，不同容值对应的反射系数
Figure 5. Gama-type network, the relationship between reflection coefficients with capacitance
图 6 T型匹配网络，不同容值对应的反射系数
Figure 6. T-type network, the relationship between reflection coefficients with capacitance
图 8 分步调谐对应反射系数变化趋势
Figure 8. Stepwise tuning corresponds to the trend of reflection coefficient
图 9 反射系数随迭代次数变化趋势
Figure 9. Relationship between Reflection Coefficient and Iteration Times
图 12 Vin1和Vin2端口相对输出Vout端口的插损
Figure 12. Insertion loss of Vin1 and Vin2 ports relative to Vout ports
-
[1] Khan F A, Zhou L, Ping A T, et al. Inductively coupled plasma reactive ion etching of AlGaN for application in laser facet formation[J]. Journal of vacuum science & technology B,1999,17(6):2750−2754 doi: 10.1116/1.591057 [2] Yu K, Feldbaum M, Pandhumsoporn T, et al. Deep anisotropic ICP plasma etching designed for high-volume MEMS manufacturing[J]. Proceedings of SPIE-The International Society for Optical Engineering,1999 doi: 10.1117/12.361224 [3] Lee Y J, Kim K N, Song B K, et al. Internal linear inductively coupled plasma (ICP) sources for large area FPD etch process applications[J]. Materials Science in Semiconductor Processing,2002,5(4-5):419−423 doi: 10.1016/S1369-8001（02）00129-4 [4] Liu Y C, Fu Y P. Inductively coupling plasma (ICP) treatment of propylene (PP) surface and adhesion improvement[J]. Plasma Sci technol,2009(6):5 doi: 10.1088/1009-0630/11/6/13 [5] Mishra A , Yeom G Y. Dual frequency ICP discharges: Effect of pressure and gas ratio on EEPF and discharge parameters[J]. Surface & Coatings Technology,2013,237:440−444 doi: 10.1016/j.surfcoat.2013.09.063 [6] Sun X Y , Zhang Y R , Li X C , et al. Modulations of the plasma uniformity by low frequency sources in a large-area dual frequency inductively coupled plasma based on fluid simulations[J]. Physics of Plasmas,2015,22(5):045020 doi: 10.1063/1.4921670 [7] 姚龙, 李晓峰, 马聪伟, 等. 基于阻抗匹配器的二极管幅−相检测电路设计[J]. 电子技术应用,2023,49(7):120−125 (in Chinese) Yao L, Li X F, Ma C W. Design of amplitude-phase detection circuit for impedance match[J]. Application of Electronic Technique,2023,49(7):120−125 [8] 姚龙, 马聪伟, 侯丽丽. 硬件控制的射频电源功率检测电路仿真研[J]. 真空科学与技术学报,2023,43(4):326−330 (in Chinese) doi: 10.13922/j.cnki.cjvst.202208002 Yao L, Ma C W, Hou L L. Simulation analysis of RF power detection controlled by hardware circuit[J]. Chinese journal of vacuum science and technology,2023,43(4):326−330 doi: 10.13922/j.cnki.cjvst.202208002 [9] 余振坤, 曲文英. 射频大功率测量误差分析[J]. 微波学报,2006(3):55−57+61 (in Chinese) Yu Z K, Qu W Y. Error analysis on high power RF measurement[J]. Journal of microwaves,2006(3):55−57+61 [10] 张新好, 武文, 孙合敏. 射频功率测量误差分析及其精度改善方法[J]. 现代雷达,2003(2):50−53 (in Chinese) Zhang X H, Wu W, Sun H M. Analysis of errors on testing RF power and the method of improving measurement accuracy[J]. Modern radar,2003(2):50−53 [11] Montaser A, Ishii I, Clifford R H, et al. Versatile impedance matching network for inductively coupled plasma spectrometry[J]. Analytical Chemistry,1989,61(22):2589−2592 doi: 10.1021/ac00197a028 -
计量
- 文章访问数: 502
- HTML全文浏览数: 502
- PDF下载数: 3
- 施引文献: 0