首页
登录
注册
下载:
-
W波段行波管（TWT）在卫星地面通信、高分辨率雷达、精确跟踪、电子对抗、深空探测等方面具有广泛的应用前景[1-3]。目前，美国、法国和中国已经开发了W波段脉冲TWT。这些TWT的峰值输出功率在100瓦左右，工作电压和电流均高于21 kV，增益平坦度超过5分贝[4-6]。
折叠波导作为行波管的核心部件器件，对行波管小型化的发展具有重要意义，并且由于其自身的全金属结构，在稳定性、导热性、高可靠性[7-9]等方面具有天然的优势，已经成为W波段行波管首选的慢波结构。为了获得高输出功率，W波段通常选择相对较高的工作电压和电流，这会限制设备的广泛应用。因此，降低工作电压和改善其增益波动成为突破W波段行波管高功率的关键问题。
中国科学院空天信息创新研究院已经成功设计了峰值功率大于233W的W波段同心圆弧非周期折叠波导行波管的高频结构，电子效率可达32.4%[10]。根据慢波结构设计结果，在工作电流6 kV的条件下，需要120 mA的工作电流通过慢波结构。相比于目前所报道的周期折叠波导行波管,非周期折叠波导行波管在工作电压和电子效率等方面具有显著优势。但与此同时，低压的工作条件会导致聚束电子注所需的布里渊磁场变大，这给电子光学磁聚焦设计带来困难。国内各单位目前采用的周期永磁聚焦方式在现有技术指标下极难实现，因此，本文采用均匀永磁聚焦约束电子注的方式，设计一种满足所需高频结构技术指标的均匀永磁聚焦系统。
-
微波器件是通过电子注与电磁波之间进行能量交换，获得高功率电磁波输出的器件。电子枪用于电子注的产生，是微波器件的关键组成部分。设计电子枪的流程一般为先使用皮尔斯法计算出电子枪结构的大致尺寸参数，然后借助三维仿真软件进一步优化设计。
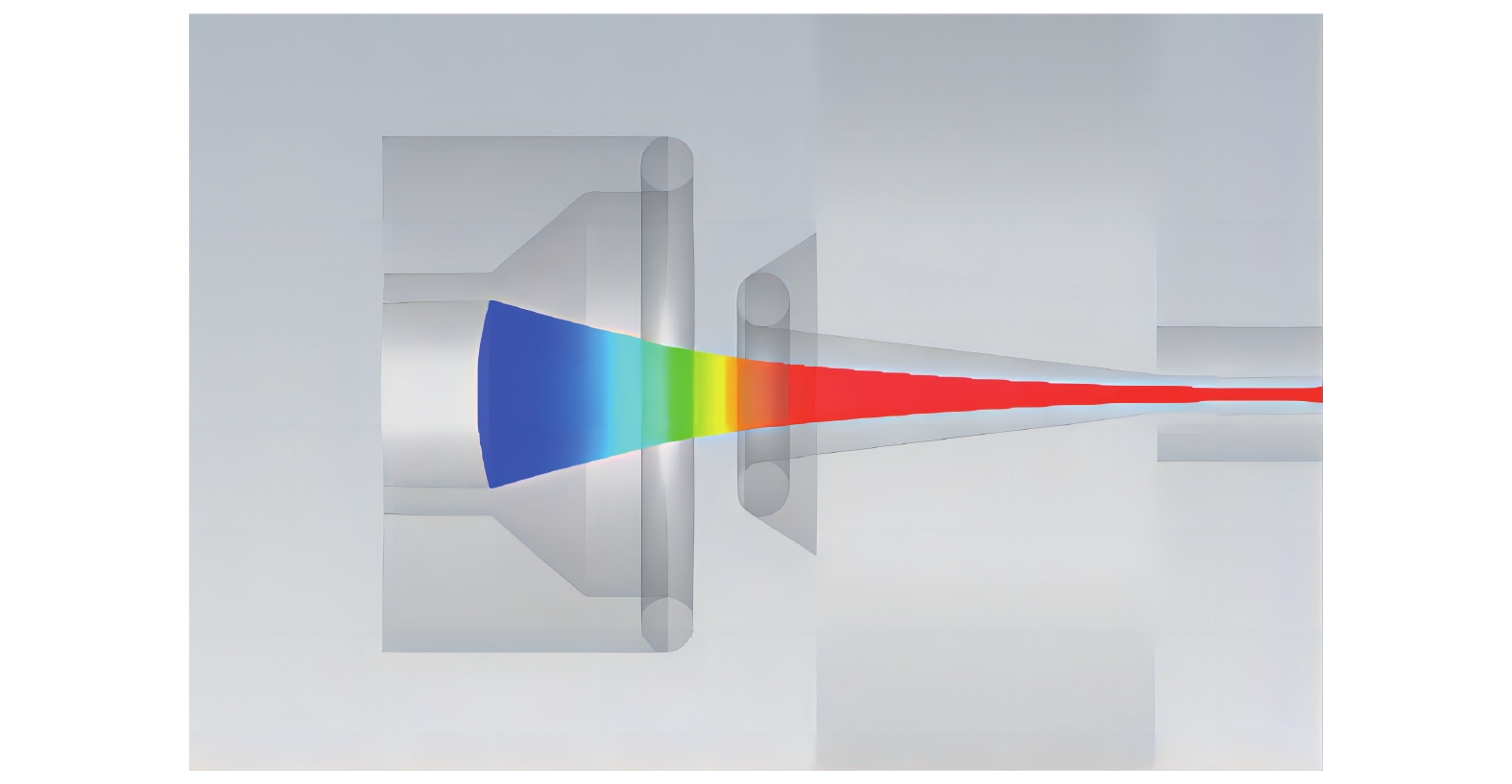
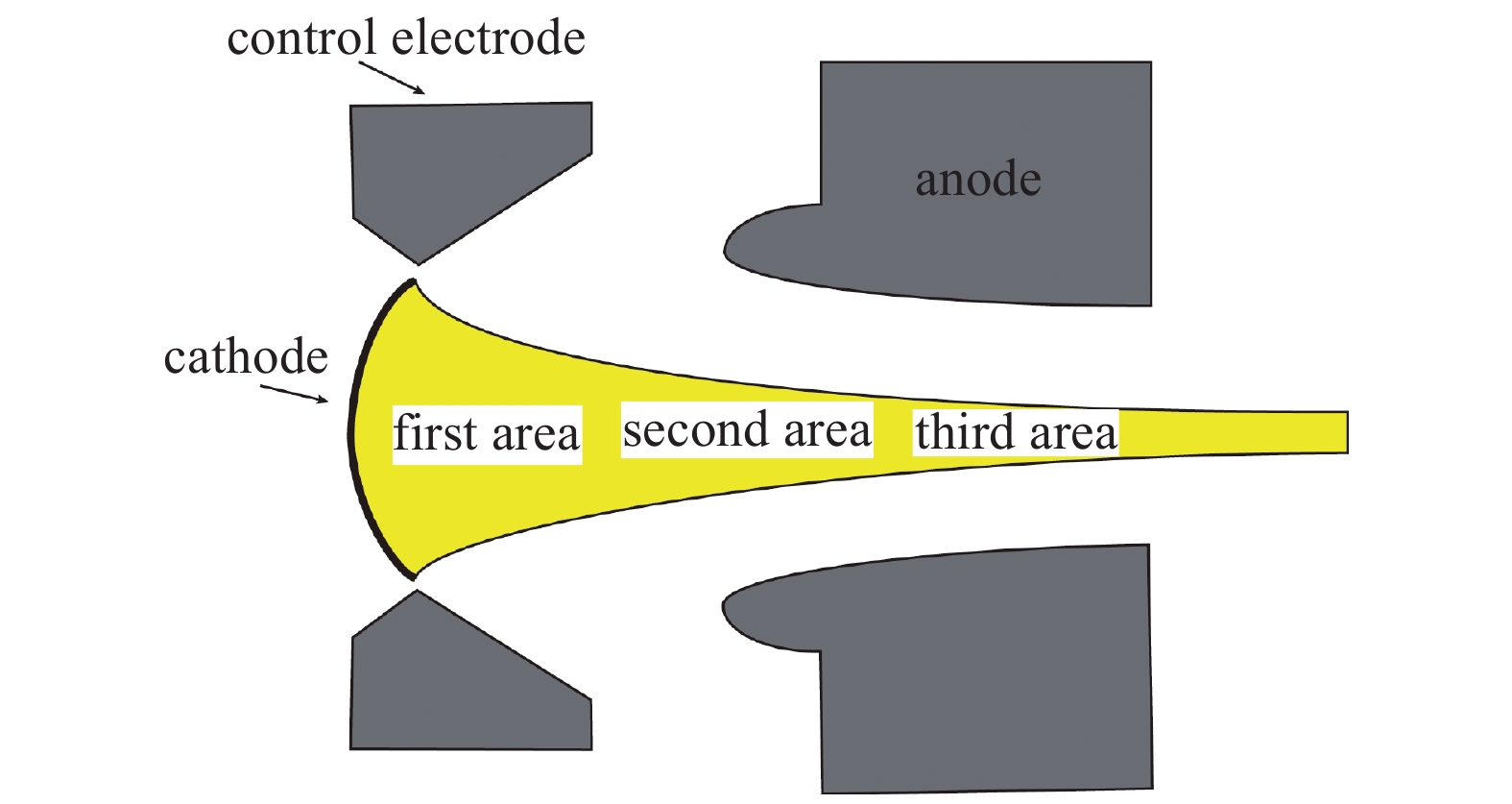
本文中，电子光学的基本设计要求为电子注电压U=6 kV，电子注电流I=120 mA，漂移通道长度L=40.5 mm，电子通道半径r=0.15 mm，填充比为75%。电子枪结构示意图如图1所示，根据以上参数及皮尔斯枪综合计算法，可大致求解电子枪结构[11]。
首先通过式（1）算出导流系数P：
由束腰半径rw和阴极所允许的发射电流密度Jc，用式（2）决定电子枪的压缩比M 2和阴极截面半径rc。
再查询电子枪压缩比设计曲线可得到阴阳极曲率半径之比Rc/Ra，由式（3）可以得到朗谬尔函数
$ - {\alpha _\alpha }$ 的值。结合式(4)即可求出阴极发射面半锥角$ \theta $ 。最后利用方程组（5）求出电子枪的其它结构参数。
通过上述计算，可以求得，球面阴极弦半径为0.7 mm和曲率半径分别为2.5 mm，阳极半径为0.64 mm。
为了方便分析结构尺寸和导流系数，电流，束腰半径的关系，作者还引入了一些新的结构参量，如图2所示。在设计电子枪的过程中，发现影响电子枪电流和束腰半径的两个主要参数是rf和zf。根据仿真分析，P，I和rw，随着rf增大而增大，随着zf增大而减小。在保持其它结构参数不变的情况下，最终优化得到的电子枪及电子注轨迹如图3所示。仿真结果显示，当阴阳极电压差U=6 kV时，发射电流I=120 mA。
-
电子注从电子枪发射出来之后，由于自身的空间电荷力的作用，若无外加力进行聚束，电子会迅速发散，进而轰击到行波管的高频结构，降低器件的性能，降低器件的使用寿命。因此，需要外加聚焦系统来对电子注进行聚束，实现电子注的长距离稳定传输。考虑到本文针对的非周期同心圆弧折叠波导行波管处于低电压的工作条件下这一特点，其所需的聚束电子注的布里渊磁场较大，周期永磁聚焦难以满足技术指标，所以本文采用了均匀永磁聚焦的方法。
首先，由技术指标可知，漂移通道的长度为40.5 mm。根据式（6），可以求得布里渊磁场为2918 Gs，考虑到本次设计中，电子注电流密度较大，电荷间的空间电荷力较强，因此选择峰值磁场为 布里渊磁场的2.0 ~ 2.5倍。
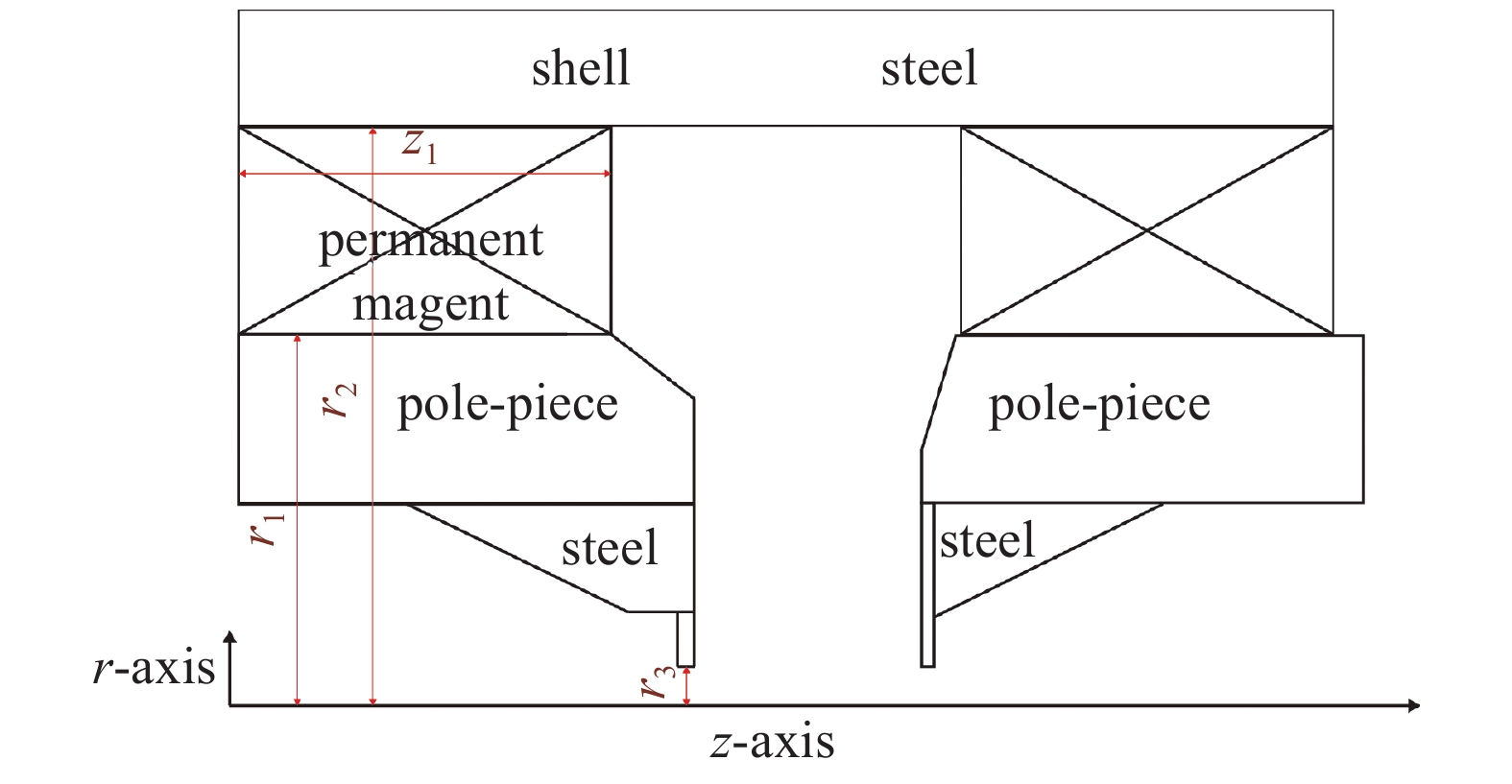
本文采用的聚焦系统是Π型永磁聚焦系统，为了产生均匀磁场，两个磁环在径向的极性方向相反，如图4所示。为了使电子注有良好的传输性，需要调整过渡区及互作用区的磁场曲线，作者发现，较为敏感的几个结构尺寸为r1，r2和r3，其中，r1，r2主要影响互作用区磁场峰值，而r3影响过渡区斜率。通过多次仿真计算，并且综合考虑永磁聚焦结构的体积、重量、电子束填充比、刚度等因素，确定尺寸结构参数为r1=31.7 mm，r2=75.7 mm，r3=2.0 mm。
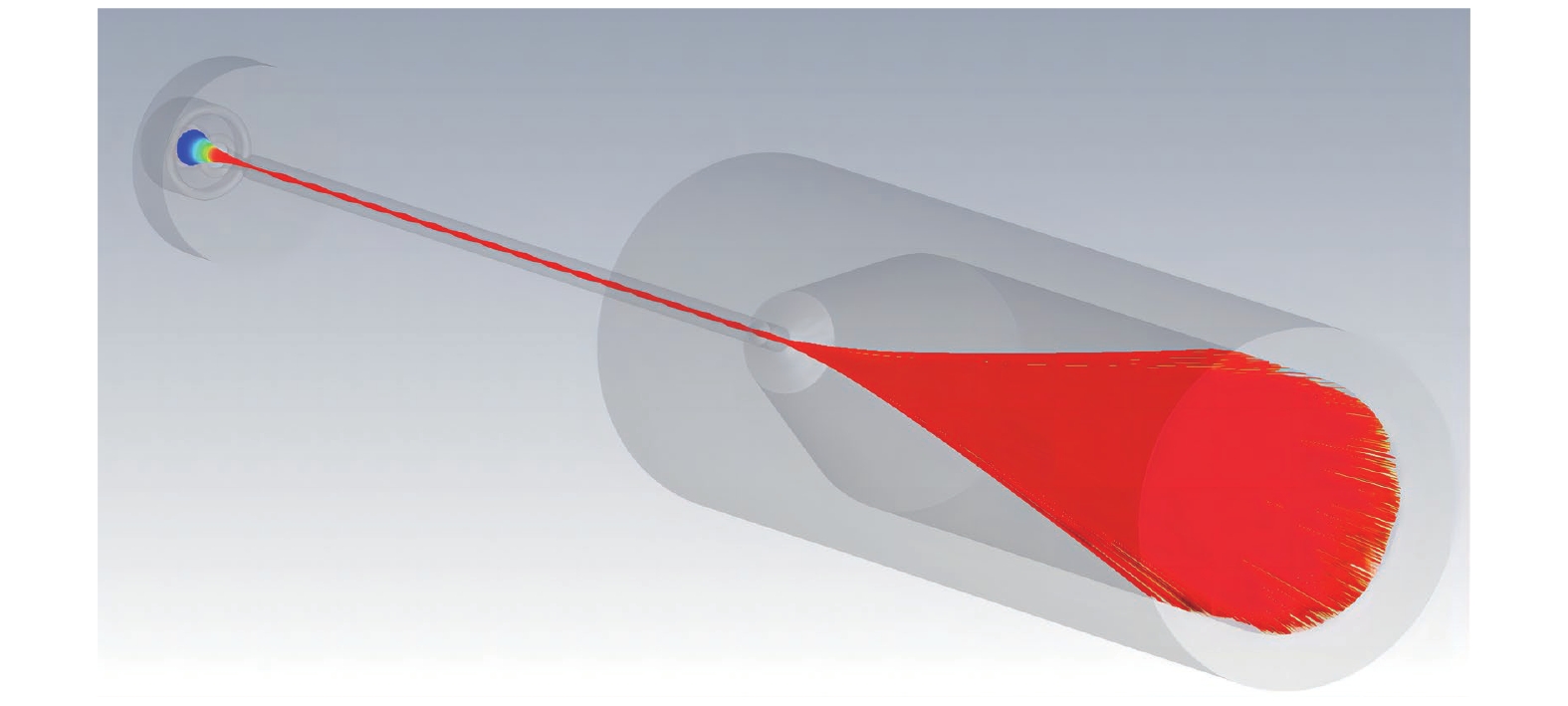
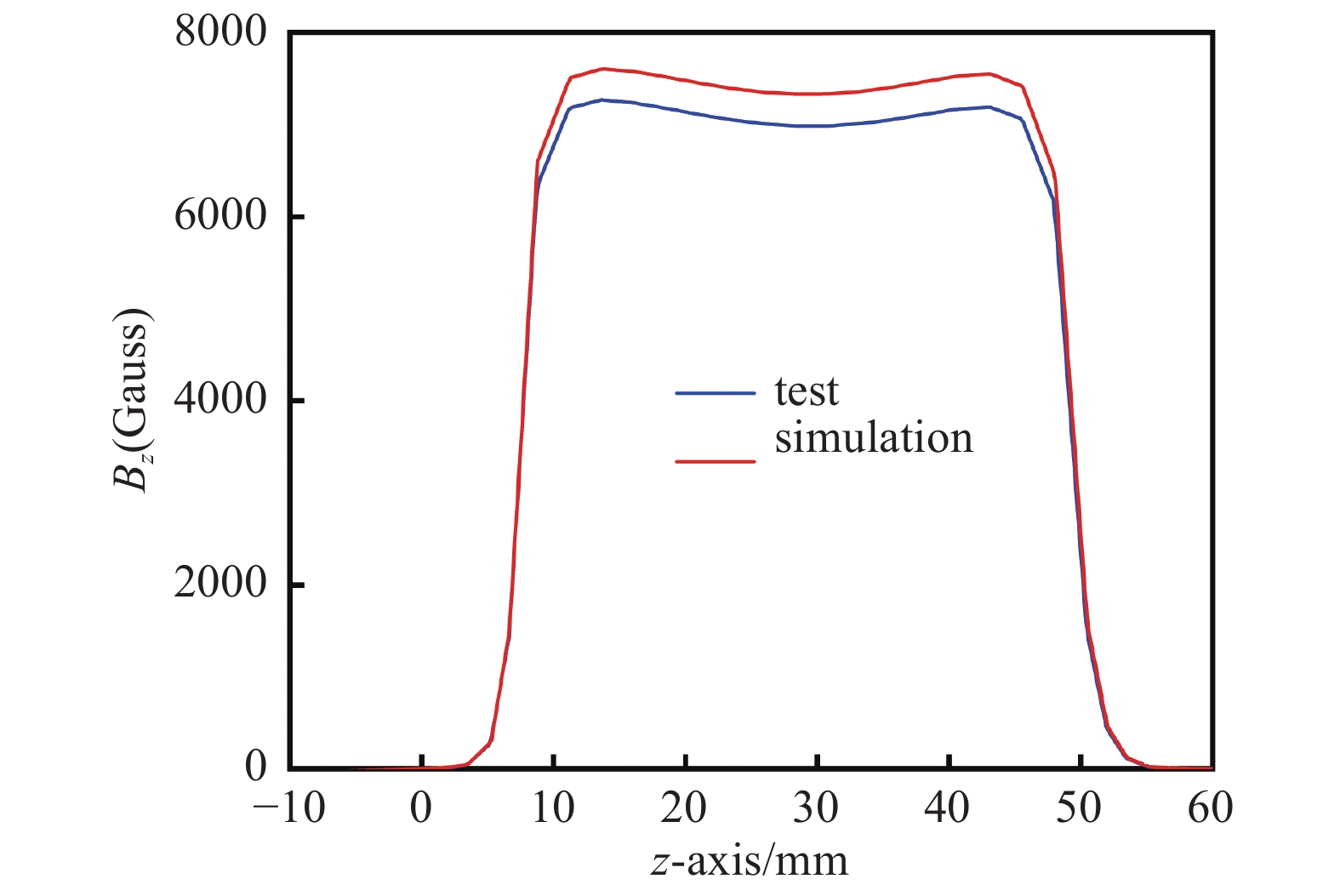
仿真后得到的电子注轨迹如图5所示，由仿真结果可知，在阴阳极电压差为6 kV，发射电流为120 mA时，电子注在漂移通道中的通过率为100%。为了对仿真结果进行验证，作者加工了磁系统。图6为CST仿真结果与实际测试的径向磁场Bz的对比，由图中可以看出，实验测试结果能较好地拟合仿真下的Bz分布曲线，只是峰值略小。
-
为了验证电子光学设计的准确性，作者加工了束管进行冷测试。实验中保持阳极接地，阴极接通负高压的脉冲序列，脉冲宽度为10 μs，如图7所示。最终测试结显示，在阴阳极施加6 kV的电压时，可以产生120 mA的电子注电流,高频截获电流为12 mA，通过计算可知，收集极电流为108 mA。电子通过率为90%。
-
本文根据非周期同心圆弧折叠波导的技术指标要求，设计了电子枪和均匀永磁聚焦系统，并进行了实物加工及测试。仿真结果表明，在电子注通道直径0.3 mm，长度为40.5 mm的条件下，阴阳极电压差为6 kV，可以产生120 mA的电流，电子通过率100%。测试结果表明，在阴阳极施加6 kV的电压时，所产生的电子注电流为120 mA，电子通过率为90%。测试结果能较好地验证实验结果，满足同心圆弧非周期折叠波导行波管的技术指标，为后续非周期折叠波导行波管的研制奠定了基础。
非周期同心圆弧折叠波导行波管的永磁聚焦系统设计
Design of Permanent Magnetic Focusing System of Concentric Arc Folded Waveguide TWT
-
摘要: 开展了对非周期折叠波导行波管永磁聚焦系统的研究。基于W波段非周期折叠波导行波管的技术指标，根据理论分析和电磁仿真，设计了一套均匀永磁聚焦的电子光学系统，并进行了实物加工与测试。仿真结果表明，在电子主通道直径0.3 mm，长度为40.5 mm的条件下，阴阳极电压差为6 kV，可以产生120 mA的电流，电子通过率100%。测试结果表明，在阴阳极施加6 kV的电压时，阴极发射电流为120 mA，电子通过率为90%，满足高频结构设计要求。Abstract: A magnet focusing system for W-band concentric arc folded-waveguide traveling wave tube (TWT) is developed. Based on the technical specifications of W band concentric arc folded waveguide TWT, a uniform permanent magnet focusing system is designed and tested. The beam tunnel is 0.3 mm and the length is 40.5 mm. The simulation result shows that when the voltage between the anode and cathode is 6 kV, a current of 120 mA can be generated, and the beam transmission rate is 100%. The test result is in agreement with the simulation result. The test result shows that the beam transmission rate is 90% with a voltage of 6 kV.
-
-
图 4 均匀永磁聚焦结构示意图
Figure 4. The schematic diagram of the Uniform Permanent Magnetic Focusing System
-
[1] Booske J H, Dobbs R J, Joye C D, et al. Vacuum electronic high power terahertz sources[J]. IEEE Transactions on Terahertz Science and Technology,2011,1(1):54−75 doi: 10.1109/TTHZ.2011.2151610 [2] Chong C K, and Menninger W L. Latest advancements in high-power millimeter-wave helix TWTs[J]. IEEE Transactions on Plasma Science,2010,38(6):1227−1238 doi: 10.1109/TPS.2010.2041940 [3] Sengele S, Jiang H, Booske J H, et al. Microfabrication and characterization of a selectively metallized W-band meander-line TWT circuit[J]. IEEE Transactions on Electron Devices,2009,56(5):730−737 doi: 10.1109/TED.2009.2015416 [4] Gerum W, Malzahn P, Schneider K. 94-GHz TWT for military radar applications[J]. IEEE Transactions on Electron Devices,2001,48(1):72−73 doi: 10.1109/16.892170 [5] Theiss A J, Meadows C J, Freeman R, et al. High-average-power W-band TWT development[J]. IEEE transactions on plasma science,2010,38(6):1239−1243 doi: 10.1109/TPS.2010.2041794 [6] Zhang X, Feng J, Cai J, et al. Design and experimental study of W band pulsed TWT with 8-GHz bandwidth[J]. IEEE Transactions on Electron Devices,2017,64(12):5151−5156 doi: 10.1109/TED.2017.2766664 [7] Na Y H, Chung S W, Choi J J. Analysis of a broadband Q band folded waveguide traveling-wave tube[J]. IEEE transactions on plasma science,2002,30(3):1017−1023 doi: 10.1109/TPS.2002.801638 [8] Han S T, Jang K H, So J K, et al. Low-voltage operation of Ka-band folded waveguide traveling-wave tube[J]. IEEE transactions on plasma science,2004,32(1):60−66 doi: 10.1109/TPS.2004.823978 [9] Sharma R K, Grede A, Chaudhary S, et al. Design of folded waveguide slow-wave structure for W band TWT[J]. IEEE Transactions on Plasma Science,2014,42(10):3430−3436 doi: 10.1109/TPS.2014.2352267 [10] Wen Z, Luo J, Li Y, et al. Beam–wave resynchronization method of the nonperiodic meander line and folded-waveguide SWS for TWTs[J]. IEEE Transactions on Electron Devices,2021,69(2):763−770 [11] Wang J X, Barnett L R, Luhmann N C, et al. Electron beam transport analysis of W-band sheet beam klystron[J]. Physics of Plasmas,2010,17(4):043111 -
图( 7)
计量
- 文章访问数: 140
- HTML全文浏览数: 140
- PDF下载数: 1
- 施引文献: 0