首页
登录
注册
-
负电子亲和势GaAs光电阴极具有量子效率高、暗电流小、平均能量及角分布小的优异特点，在微光像增强器、光电倍增管、真空电子源等光电成像及探测器件具有广泛应用，促进了弱光成像及探测技术的发展[1-5]。然而，与传统超快响应的碱锑阴极和Ag-O-Cs阴极相比，透射式GaAs、InGaAs/InP等负电子亲和势光电阴极具有较长的响应时间，影响了它在超快等领域的应用[6-8]。同时，透射式GaAs等半导体光电阴极的时间响应问题不但涉及超快领域，而且与阴极的量子效率等响应特性有关，因此GaAs光电阴极的时间响应问题研究，对进一步提升光电阴极响应性能，进一步扩展其应用领域，具有十分重要的应用研究价值和科学意义[9-11]。
在超快响应领域应用中，为缩短GaAs等光电阴极的响应时间，研究者采用不同的方法尝试提升负电子亲和势光电阴极的响应速度，以期扩展它在超快响应领域进一步应用[12-13]。所采用的方法主要有两种，施加加速电场和减小阴极厚度。超快应用主要瞄准高速摄影、高速电子源等方面。国外的研究主要集中在电子源方面，主要采用缩短阴极厚度的方法，来以提高阴极的响应速度[12]。国内西安光机所、陕西理工大学均进行了相关研究。郭里辉等[14]、李晋闽等[15]通过引入外偏压的方式，分别讨论了GaAs光电阴极、InGaAsP/InP场助阴极的时间响应特性，大幅提升了阴极的响应速度。蔡志鹏等[16-17]通过引入表面光电子浓度的平均时间衰减常数概念，解决了瞬态响应仿真中，初始条件与边界条件的矛盾，仿真认为，平均时间衰减常数与光电子输运过程的整个过程有关，因此通过平均时间衰减常数，有望获得光电子输运的内在机理等重要信息。近年来，西安光机所、微光夜视技术重点实验室、南京理工大学、陕西理工大学、东华理工大学等单位分别开展了透射式InGaAsP/InP场助阴极、GaAs光电阴极的瞬态响应理论研究[18-23]。
在量子效率应用方面，为提升像增强器的响应特性，南京理工提出利用梯度掺杂的方法[24]，以缩短阴极的响应时间，从而获得了量子效率等响应特性的提高，该方法已经在GaAs、GaN光电阴极方面获得应用，进一步改善了像增强器的响应特性，该方法获得国外同行专家的高度评价[25]。
上述研究表明，梯度掺杂方式能够大幅提升阴极的响应性能，而且，不同的梯度掺杂方式具有不同的响应特性，从而解决不同条件下的阴极应用，因此，为进一步深入研究光电阴极中光电子向阴极表面渡越的内在运动过程及阴极响应性能，本仿真讨论了不同掺杂梯度下，平均时间衰减常数随GaAs阴极吸收层厚度、入射光子能量的变化关系。同时，基于获得的平均时间衰减常数，得到了两种掺杂方式—e指数掺杂、e指数内建电场掺杂下的时间响应特性，为光电阴极中光电子的输运机理研究，以及阴极时间、量子效率等响应过程的分析研究，提供了必要的理论基础和数据支持。
-
本文主要讨论两种掺杂方式的透射式GaAs光电阴极：具有均匀内建电场的e 指数掺杂[17]，具有e指数内建电场的梯度掺杂[23]。
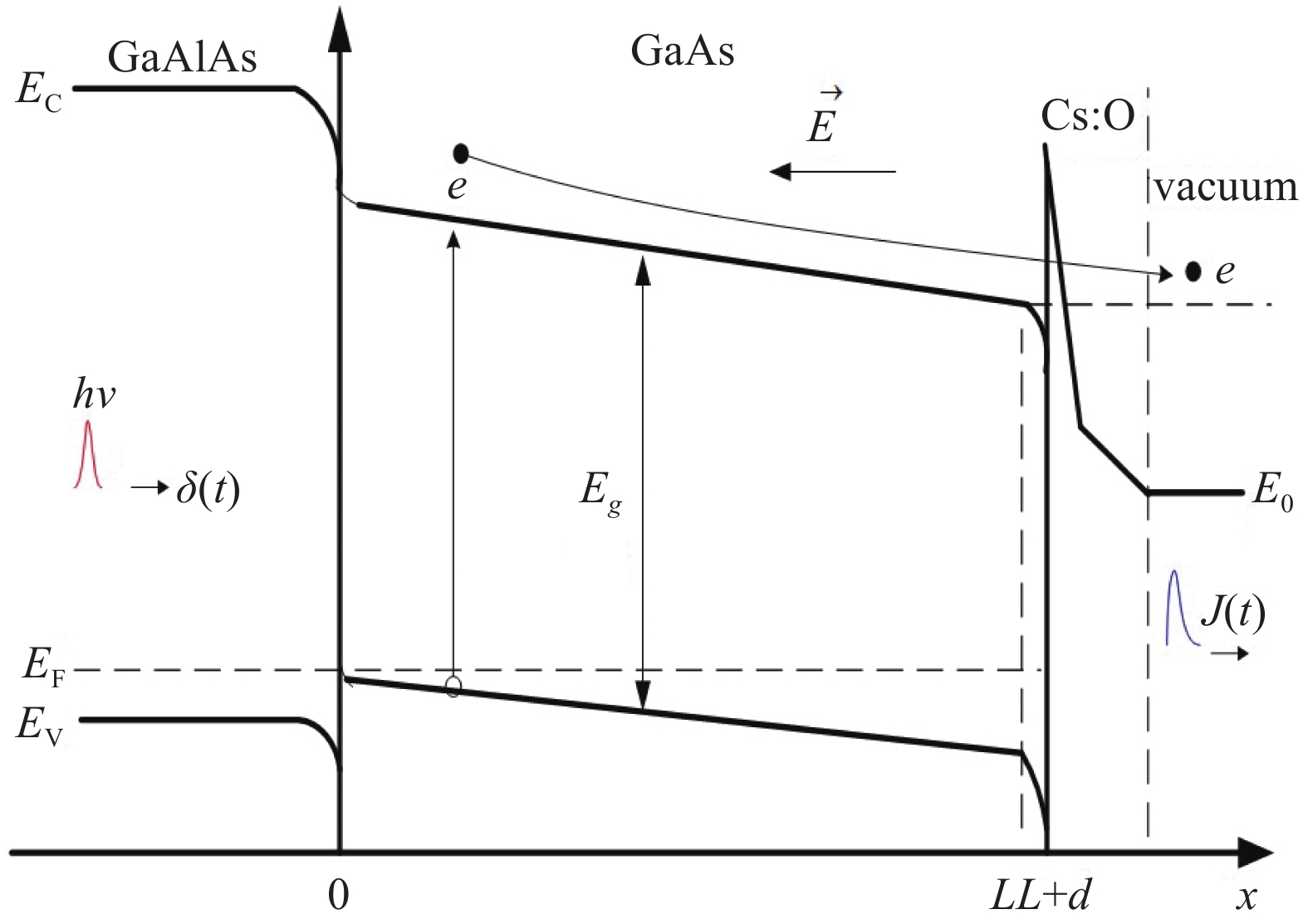
如图1所示，两种透射式GaAs光电阴极的能带结构，由两部分组成：光吸收I区（x：0~L）和表面发射Ⅱ区（x：L~L+d）。其中L是吸收区宽度，d是表面发射区宽度；Eg是GaAs的禁带宽度，Ec、Ev分别为GaAs导带底能级和价带顶能级，EF为Cs: O激活后GaAs阴极的费米能级，E0是真空能级。理想δ(t)脉冲光从缓冲层GaAlAs一侧入射，产生的脉冲光电流J(t)从真空一侧出射。
-
对e指数掺杂：
内建电场场强
对e指数内建电场的掺杂：
内建电场场强
掺杂浓度函数
界面处掺杂浓度：GaAlAs/GaAs边界x=0：N(0)=1019 cm−3, I/II边界x=L：N(L)分为五种情况，并在后续小节分别加以讨论：
1. N(L)=1015 cm −3；2. N(L)=1016 cm −3；3. N(L)=1017 cm −3；4. N(L)=1018 cm −3；5. N(L)=1019 cm −3（为均匀掺杂）；
I区的作用是产生光电子，光电子在内建电场下加速向阴极表面输运。其中，I区GaAs吸收层为p型掺杂，
$ \beta $ 是e指数内建电场时的优化因子。需要说明，不考虑x=0附近重掺杂下的弱简并态。 -
Ⅱ区是p型重掺杂薄层，掺杂浓度NA为1018−1019 cm−3，其作用是Cs：O激活后产生足够高的表面逸出几率。根据半导体理论[9-10, 14]，当Ⅱ区的厚度d为如下式（5）时，在Cs：O激活后，I/Ⅱ区边界处若有突变，则因掺杂浓度突变产生的电子势垒被消除。d的厚度设计如下[17]：
由文献可知，本讨论中的光电阴极，均能形成负电子亲和势表面。在实际设计中Ⅱ区GaAs的厚度均小于d，且满足d≤L，一般地，取d≤10 nm。以保证I/Ⅱ区边界处的“电子势垒”有效消除， 其中, ε是GaAs的介电常数，NA是发射层掺杂浓度，q是单位电荷量，开氏温度T取300 K。同时，由于d<<L，因此在讨论阴极的时间响应时，不考虑光电子在Ⅱ区内的渡越时间。需要说明的是，由于光在阴极内的渡越时间极短，因此忽略光在阴极内的传播时间。
-
信号光入射到GaAs吸收层，激发产生光电子，产生的光电子向表面输运。光电子输运的变系数一维连续性方程表述为[17, 23]：
其中，
$ {D_n}(x) = \dfrac{{kT}}{q}{\mu _n}(x) $ ，Δn(x,t)表示光电子（少子）浓度，Dn(x)、μn(x)、τn(x)分别为光电子的扩散系数、迁移率和寿命，且均为随掺杂浓度变化的函数，g(x,t)是光生函数[17]。 -
在理想δ脉冲瞬态条件下，初值条件表示为
其中α为GaAs的吸收系数，本计算中α值取自文献[26]，I0是入射光强。
其中，τ' 是表面处电子浓度的平均衰减常数，如文献[17, 23]所述。
需要说明的是，光电子在电场中的速度运动公式，用
$ v = {\mu _n}(x)\left| {E(x)} \right| $ 来表示，当$ {\mu _n}(x)\left| {E(x)} \right| \gt v $ 时，用文献[17]中的速度公式替代$ {\mu _n}(x)\left| {E(x)} \right| $ 。尤其地，当L≤0.5 μm时，在较高电场下出现速度过冲效应，漂移速度公式$ v = {\mu _n}(x)\left| {E(x)} \right| $ 即不再适用，需要考虑速度过冲带来的影响，采用如文献[17, 23]所述的过冲速度公式替代$ {\mu _n}(x)\left| {E(x)} \right| $ 。发射向真空的光电子流：
其中，P是阴极表面的电子逸出几率。由式（6）−（10），采用后向差分法求得到方程数值解，并讨论平均时间衰减常数，以及光电阴极的时间响应特性。需要说明的是，本文不再讨论表面逸出几率和量子效率等问题，下面将着重讨论光电阴极的时间响应问题。
-
τ' [17, 23]参数是光电子动态行为在真空发射界面的集中体现，它是通过光电子在真空界面处电子浓度的动态变化来描述光电子的整个动态过程的。文献中τ' 的初次引入，是为了解决光电阴极瞬态过程中，真空边界条件和时间初值条件的矛盾而引入的一个修正因子，它假定发射边界处的电子浓度，与光电子的整个发射过程有关。文献[17, 23]表明，τ' 的引入能够解决边界条件与初值条件之间的矛盾，成功解决了光电阴极瞬态响应仿真的缺陷，证明了该参数引入的必要性。
前期研究讨论了在大梯度掺杂条件下，GaAs吸收层厚度L、入射光子能量Ehv、GaAs/GaAlAs后界面复合速率S等参数对τ' 影响，结果表明，L对τ' 的影响最大且占主导地位，而S的影响可忽略不计[17]，因此本仿真仅讨论在不同梯度掺杂条件下，L与Ehv对τ' 的影响。一般地，若不作特殊说明，则取S=105 cm/s。
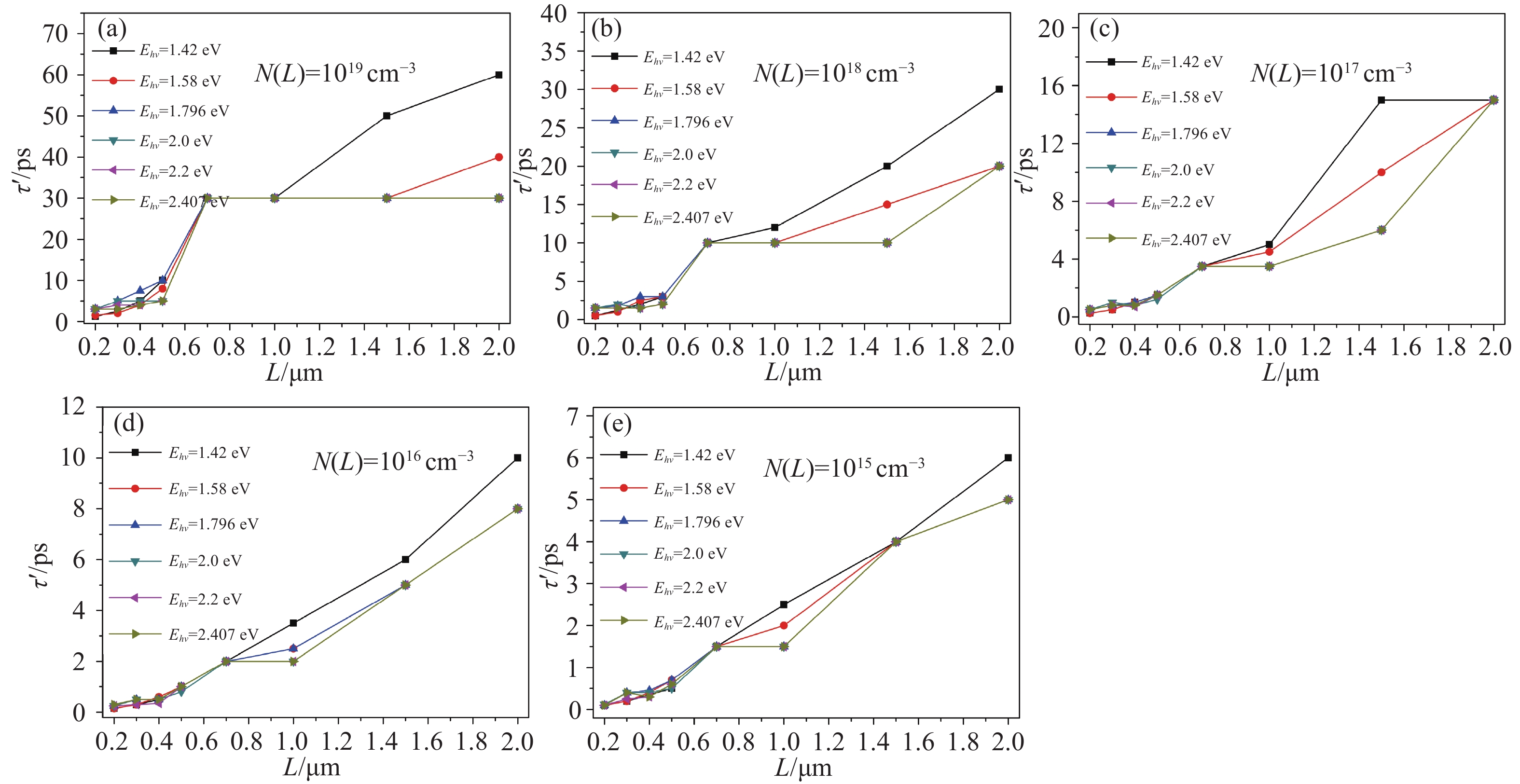
图2是在N(L)=1015~1019 cm−3的掺杂梯度下，获得的τ' 值与L、Ehv的关系。其中，除均匀掺杂外，两种掺杂方式被讨论：即掺杂方式分别为产生均匀电场的e指数掺杂方式（N(L)=1015~1018 cm−3），与产生e指数电场的掺杂方式（N(L)=1015~1018 cm−3），仿真结果表明，在相同掺杂梯度下，这两种掺杂方式下的τ' 值基本相同。结果如图2所示：
图2给出了L~0.2−2.0 µm，N(L)=1015~1019 cm−3范围内的τ' 分布，仿真结果表明：
1. τ' 的值始终低于相对应阴极的响应时间；
2. 相同Ehv条件下，τ' 随N(L)的增大而逐渐减小，随L的增大而增大，且N(L)、L对τ' 值的影响占主导地位；相同N(L)、L条件下，Ehv对τ' 值的影响相对较小；
3. 在相同的N(L)下，不同的掺杂方式τ' 值不变，如产生均匀内建电场的e指数掺杂方式，与产生e指数内建电场的掺杂方式，其中的机理尚不明确。该结论与前期研究一致[17, 23]。
4. 如图2所示，τ' 随N(L)、L、Ehv的变化关系比较复杂，但是，可通过t=0初始时刻的表面电子浓度，与体内电子浓度及分布两个因素进行简化分析。对每一N(L)，分析如下：
（1）当L=0.2 µm时，当Ehv较小，如1.420 eV、1.580 eV，此时由于表面电子浓度小，电子发射及损耗较快，表现为表面电子浓度衰减快，因此τ' 值较小；随Ehv进一步增大，表面电子浓度增大，故其衰减变慢，τ' 值从而增大。根据式（7）获得的表面电子浓度可知，上述τ' 值变化趋势与表面电子浓度变化一致，因此可能得出结论，当L较小时，如L=0.2 µm，初始表面电子浓度对τ' 值的影响和贡献占主要方面，而后者的影响占次要地位或可以忽略。
（2）当L~0.3~0.5 µm，或0.3~0.4 µm时，表面电子浓度与体内电子浓度及分布共同作用，使得τ' 值随Ehv的增大呈多次起伏的复杂变化状态，且在约 1.796 eV或2.000 eV附近达最大值。这可能表明，初始表面电子浓度与体内电子浓度及分布两个因素导致了τ' 值的复杂变化，二者对τ' 的影响均较大。但仅仅根据L=0.3~0.5 µm范围内τ' 的变化，针对不同的Ehv值，难以判断谁的影响更大。关于这一点，将在后续结论中继续分析。
（3）当L~0.7~1.0 µm，或0.5~0.7 µm时，τ' 值基本Ehv不随的变化而变化。这可能表明
初始时刻的表面电子浓度，与体内电子浓度及分布等两个因素达到某种动态平衡所导致的。
（4）当L~1.0~2.0 µm，或1.5~2.0 µm时，随Ehv的增大，Ehv由1.420 eV到1.580 eV时，τ' 值逐渐减小，当Ehv≥1.796 eV后达到稳定值。在N(L)、L相同条件下，由1.420 eV到1.580 eV过程，初始表面电子浓度对τ' 值的影响不可忽略；当Ehv≥1.796 eV时，初始表面电子浓度的影响忽略不计，而体内电子浓度及分布占主要影响地位。
综合上述分析，得出以下结论：
在L~0.2~0.5 µm时，τ' 反映的光电子动态过程信息最为丰富。相同Ehv条件下，当L~0.2~0.5 µm时，初始表面电子浓度对τ' 的影响和贡献占主导，随着L增大，初始表面电子浓度减小，它对τ' 的影响逐渐降低，而体内电子浓度及分布的影响逐渐增大。当L达到0.3~0.5 µm，或0.3~0.4 µm时，τ' 值的多次起伏变化，由初始表面电子浓度占主导逐渐过渡到由体内电子浓度及分布占主导，这种起伏是由二者交替占主导所导致的，这也说明了初始表面电子浓度，与体内电子浓度及分布对τ' 值的影响是复杂的，它们对τ' 值的影响不是二者简单的叠加，而是表现出一种复杂的电子浓度变化过程。
当L~0.7~1.0 µm，或0.5~0.7 µm时，根据上述分析，初始表面电子浓度，与体内电子浓度及分布达到的是一种动态平衡，τ' 值不随Ehv变化。当L继续增大，体内电子浓度及分布的影响逐渐占主导，但由1.420 eV到1.580 eV过程，初始表面电子浓度仍τ' 值具有一定的影响，而随着Ehv进一步增大，初始表面电子浓度的影响逐渐忽略，体内电子浓度及分布开始逐渐占据主导地位。
-
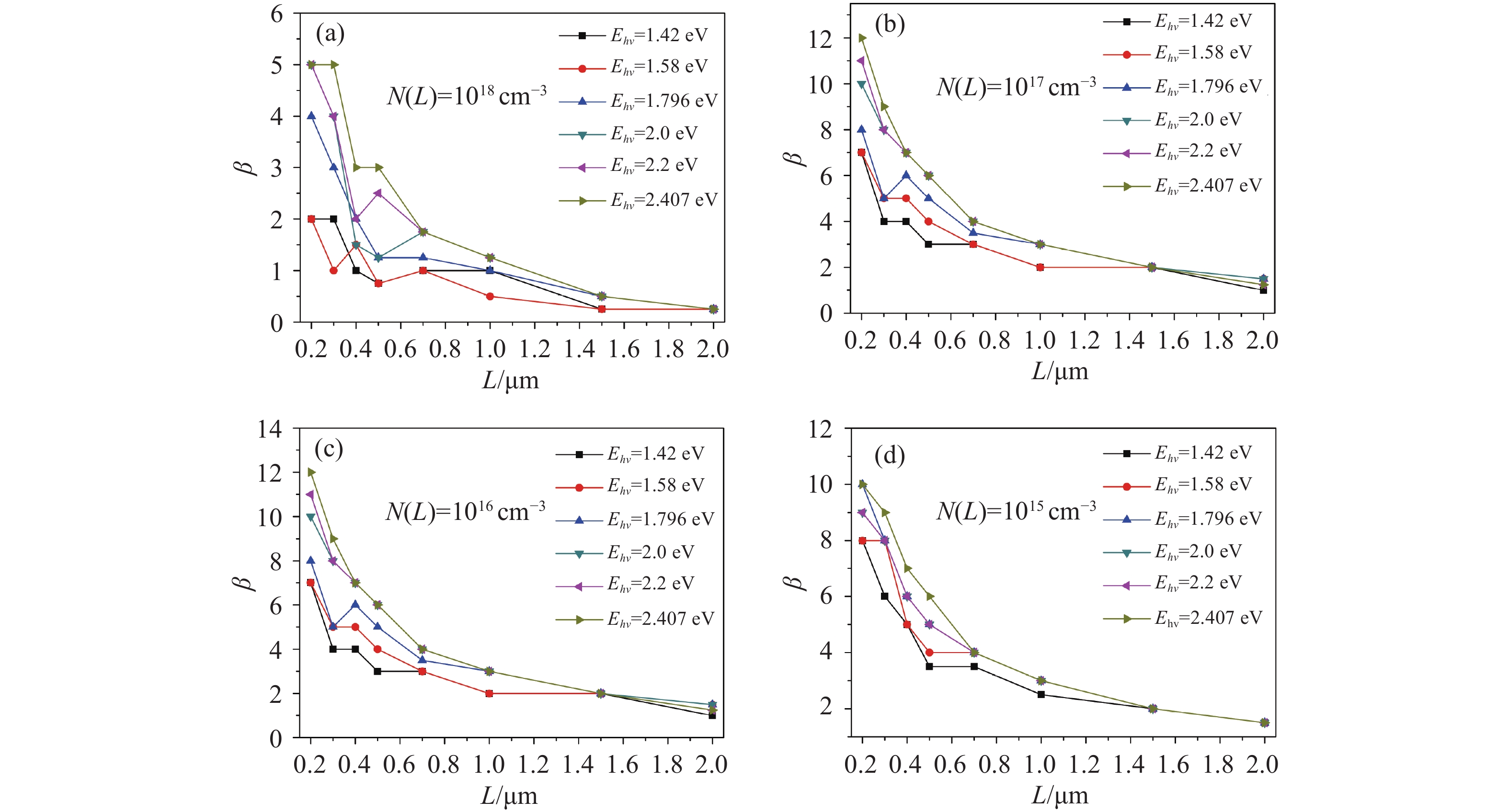
由文献[23]可知，基于上述仿真计算获得的τ' 值，在梯度掺杂形成的e指数内建电场下，能够实现最短响应时间的e指数内建电场分布函数，该e指数电场系数称为最优系数因子β，如式（3）所示。图3给出了L~0.2−2.0 µm，N(L)=1015~1018 cm−3范围内，e指数内建电场条件下的最优化系数因子β分布，仿真结果表明：
1. 图3可知，最优β值基本遵从以下规律：在同一N(L)下，Ehv相同时，最优β值随L增大而逐渐下降；相同L下，随Ehv增大，最优β值缓慢增大，且L越大，最优β值增大越不明显。当L≥1.5 μm或L~2.0 µm时，最优β值基本不变。这与前期研究N(L)=1015 cm−3时的结论是一致的[17]。
但是，上述规律也有少数例外，例如，当N(L)=1018 cm−3时，L~0.4 μm，最优β值先增大后减小；在Ehv ~1.420~2.000 eV，L~0.5~0.7 μm时，除Ehv ~1.796 eV外，最优β值反常增大，而在Ehv ~1.580 eV，L~1.0 μm时，最优β值反常减小。
当N(L)=1017 cm−3时，随Ehv增大，最优β值出现先缓慢增大后减小的趋势。N(L)=1017 m−3时，除Ehv ~1.580 eV，L~2.0 μm时，Ehv ~2.407 eV，L~0.7 μm两个点的微小偏移外，其余均符合上述规律。
总之，N(L)=1018 cm−3时，最优β值的变化最为复杂，这体现了光电子自由扩散和电场加速漂移两种输运机制，对时间响应促进作用的复杂性。随着掺杂梯度的不断增大，加速电场不断增强，最优β值的规律性逐渐增强，这种规律性体现的是，掺杂梯度增大导致光电子漂移机制逐渐占据主导地位，当N(L)=1015 cm−3时，完全具有上述规律性。
2. 相同条件下，随着N(L)的增大，最优β值出现先增大后减小的趋势，且在N(L)=1016 cm−3时达到最大值。当L~0.2~0.5 µm时，最优β值的变化趋势较为复杂，且变化相对较大；当L~0.7~2.0 µm时，变化趋于平缓。
当L~0.2~0.5 µm时，最优β随N(L)增大呈现先增大后减小的趋势，N(L)=1016 cm−3>N(L)=1017 cm−3>N(L)=1015 cm−3>N(L)=1018 cm−3；当L~0.7~2.0 µm时，最优β随N(L)增大呈现先增大后减小的趋势，N(L)=1016 cm−3>N(L)=1015 cm−3>N(L)=1017 cm−3>N(L)=1018 cm−3。这是由于N(L)=1016 cm−3时，通过提高β值以达到更高的场强，进而能够获得更高的响应速度，尤其当L~0.2~0.5 µm时，通过提高β值，使内建电场达到速度过冲，从而实现高响应速度。当N(L)=1018 cm−3时最优β值始终最小，这是由掺杂梯度太小，通过提高β值来提高响应速度，难以达到高N(L)时的过冲速度，因此相比较而言，N(L)=1时最优β值最低。
-
在图2所示的平均时间衰减常数τ' 与L、Ehv的关系，与图3所示的最优系数因子β与L、Ehv的关系条件下，由3.1节及文献所述的后向差分方法，分别在e指数掺杂（均匀电场），以及e指数内建电场掺杂（e指数电场）下，获得了阴极的瞬态响应特性参数—响应时间（响应半峰宽Full Width Half Maximum，简称 FWHM）、响应时间峰值（Tm）与L、Ehv的关系，如表1-4所示。
通过表1-4比较可得，上述两种掺杂条件下，FWHM、Tm均随N(L)增大逐渐减小，随L增大逐渐增大。相同条件下，均匀电场下的FWHM小于e指数电场，且随N(L)的增大而进一步增大，说明e指数内建电场条件下具有更快的响应速度。尤其地，在相同条件下，N(L)~1015 cm−3时，阴极的响应时间缩短1/3以上，说明e指数内建电场的掺杂方式具有更优异的时间响应性能。在Ehv~1.420~2.407 eV范围内，均匀电场下的Tm波动范围大于e指数电场，即在Ehv~1.420~2.407 eV范围内，均匀电场下的Tm最小值小于e指数电场，而最大值高于e指数电场。
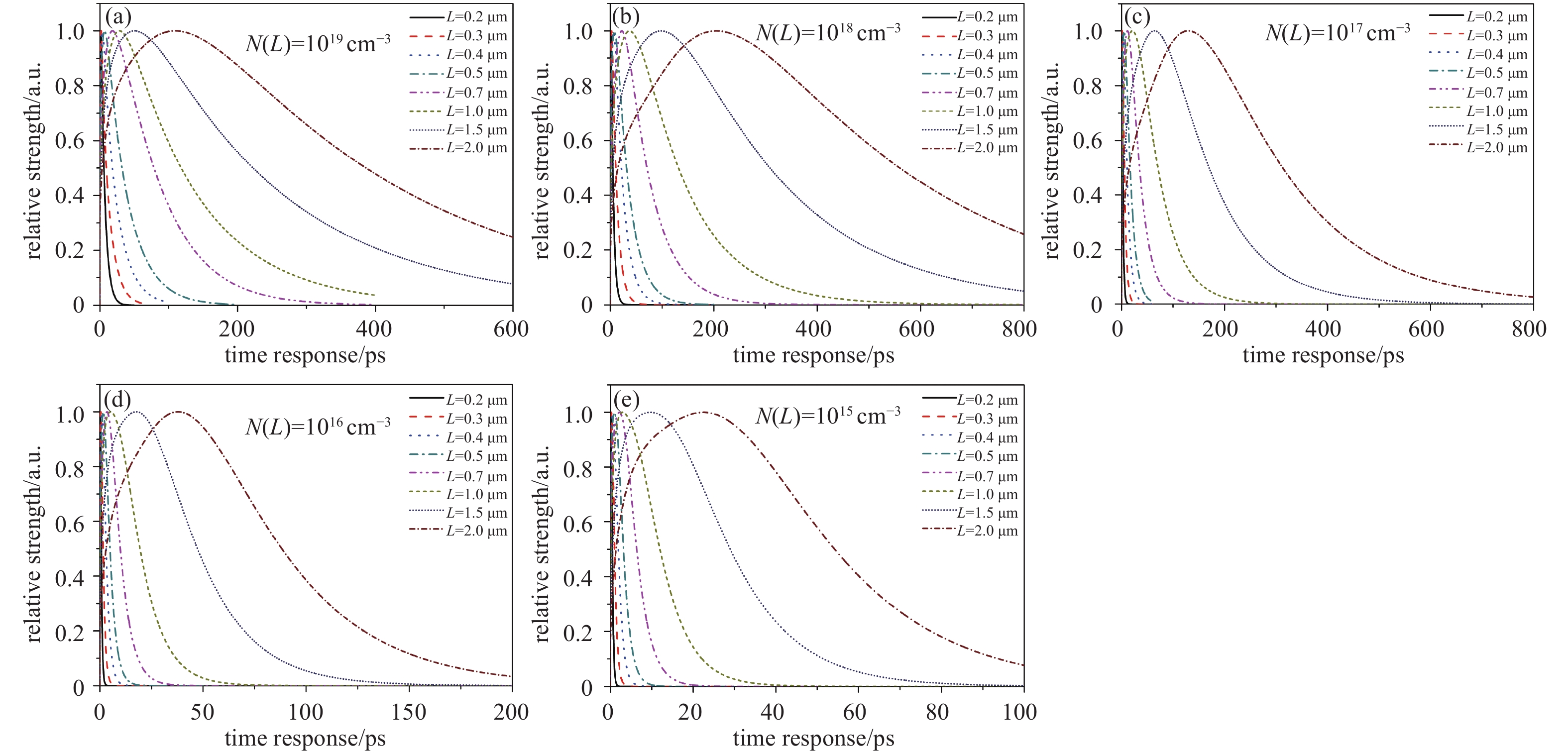
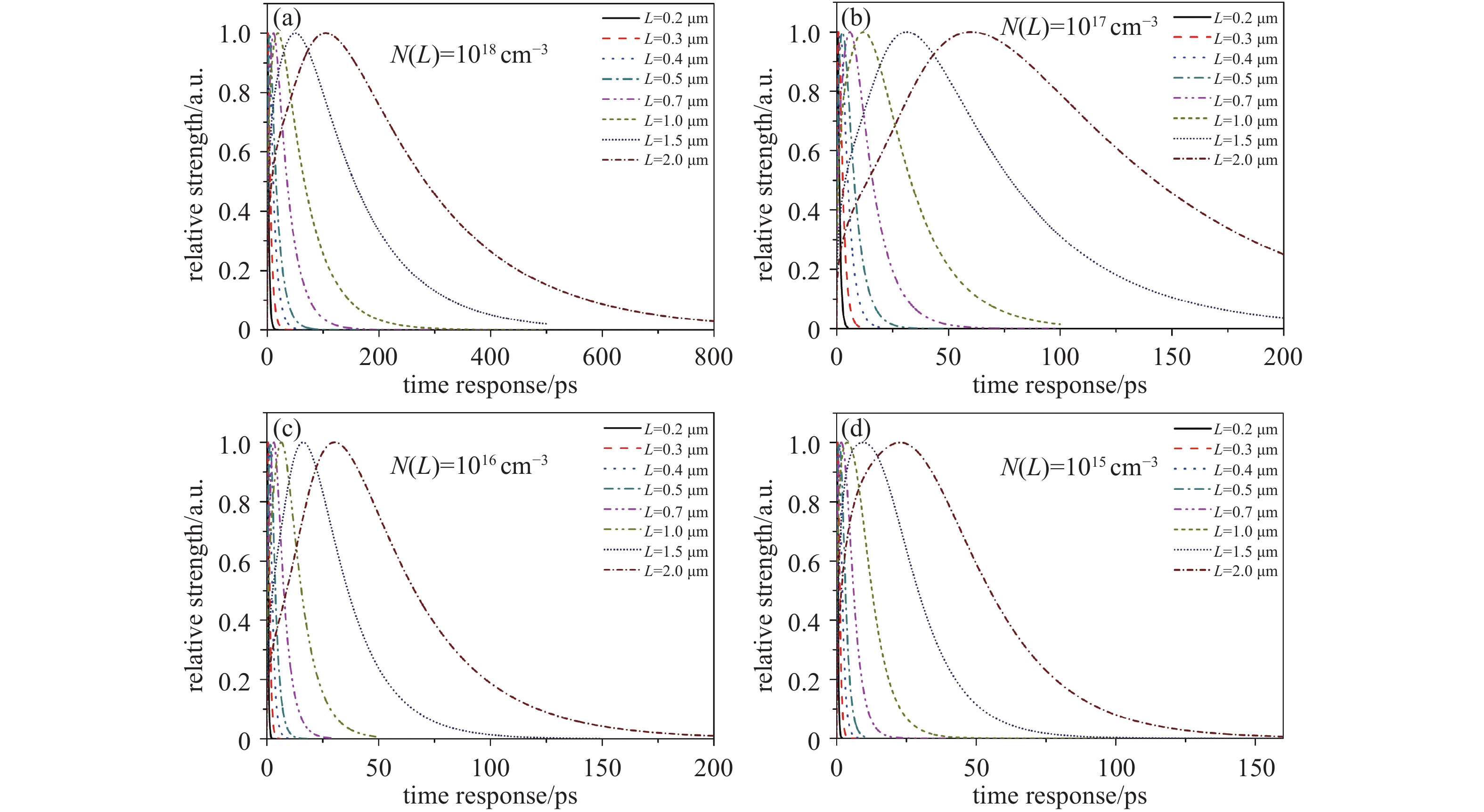
另外，仿真表明，在相同条件下，Tm均随Ehv增大而增大，这一现象是由吸收系数随Ehv增大而增大所导致的：Ehv增大，导致光吸收系数增大，光电子吸收逐渐向后界面靠近，光电子浓度的最大值距离表面越来越远，因此导致响应峰值逐渐增大；而FWHM随Ehv增大而出现复杂的变化关系，即L不同时，FWHM最大值不一定出现在Ehv~1.420 eV处，FWHM最小值不一定出现在Ehv~2.407 eV处，而是随Ehv增大FWHM最大值出现的Ehv位置随之变化，这显示了电子发射过程中，Ehv所导致的光电子浓度及分布、表面电子浓度变化、L的大小等对电子发射的复杂影响，具体表现了电子发射过程中L、Ehv、τ' 三者复杂的相互关系。如图4、5所示。图4、5 分别是在S=105 cm/s，Ehv=1.580 eV条件下，时间响应随N(L)、均匀电场（特别地，图4（a）内建电场为零）、e指数电场的变化关系。图4、5分别体现了表1-4中Tm、FWHM随L、Ehv增大时的变化关系。例如：
由图4，与表1所示，在均匀内建电场条件下，Ehv=1.580 eV时，FWHM 最大值出现在：N(L)~1015 cm−3~1018 cm−3时，L~2.0 μm，N(L)~1016 cm−3时，L~1.5 μm。FWHM 最小值出现在：N(L)~1015 cm−3时，L~0.2~0.3 μm；N(L)~1016 cm−3时，L~0.2 μm。
由图5，与表3所示，在e指数内建电场条件下，Ehv=1.580 eV时，FWHM 最大值出现在：N(L)~1018 cm−3时，L~2.0 μm；N(L)~1017 cm−3时，L~1.0 μm，L~2.0 μm；N(L)~1016 cm−3时，L~1.5 μm；N(L)~1017 cm−3时，L~0.4~0. 7 μm，L~1.5 μm。
总之，仿真结果表明：
1. L与N(L)对τ' 的影响占主要地位，τ' 随掺杂梯度N(L)的增大而减小，但在相同N(L)下，掺杂方式对τ' 的影响可以忽略；而τ' 随L影响的增大而增大；
2. τ' 对时间响应的影响，随L、Ehv的增大而逐渐减小，随L增大，L对时间响应逐渐占据主要地位；
3. 相同N(L)下，e指数内建电场下的瞬态响应特性优于均匀内建电场，FWHM随L、Ehv的变化，FWHM变化的复杂程度远高于Tm。
因此，本研究结果中，N(L)~1015 cm−3~1016 cm−3时，对应用于超快成像、透射式超快电子源等方面的应用更有利；N(L)~1017 cm−3~1018 cm−3时，对透射式光电倍增管，以及微光像增强器方面应有更有利，本研究对不同应用场景下的GaAs光电阴极设计提供了必要的理论数据支持。
-
综合讨论了透射式GaAs光电阴极在不同掺杂梯度下，τ' 与L、Ehv的变化关系，同时基于τ' 值，获得了不同N(L)下、厚度0.2~2.0 μm范围、入射光子能量1.420~2.407 eV波段范围的瞬态响应特性，较为全面地对透射式GaAs光电阴极在高速摄影、光电倍增管、超快电子源以及像增强器等领域的应用研究提供了必要的理论和瞬态响应特征数据支持，也为光电阴极响应特性的进一步深入研究提供了新的借鉴和思路，具有重要的科学意义和应用研究价值。另外，相同掺杂梯度下，τ' 值为什么基本不随掺杂方式的变化而变化，其中的机理，对光电子微观输运过程具有重要意义，是未来研究中需要进一步深入探讨的问题。
不同梯度掺杂透射式GaAs光电阴极的平均时间衰减常数及瞬态响应理论研究
Theoretical Study of the Average Decay Time and Response Characteristics of the Transmission-Mode GaAs Photocathodes with the Different Doping Gradient Distribution
-
摘要: 计算了透射式GaAs负电子亲和势光电阴极在不同掺杂梯度下的平均时间衰减常数τ' ，分析认为，阴极吸收层厚度L、掺杂梯度对τ' 影响占主要地位，且随L、掺杂梯度的增大逐渐减小；仿真涉及的两种掺杂方式，吸收层浓度的e指数掺杂方式和e指数电场掺杂方式，没有发现它们对τ' 的影响。当L~0.2−0.5 µm较小时，光子能量Ehv对τ' 的影响较大。随光子能量Ehv进一步增大，它对τ' 的影响逐渐减小；在L、Ehv变化过程中，发现了L、Ehv对τ' 的影响的动态竞争关系，分析认为，二者竞争的实质是，初时刻表面光电子浓度与体内光电子浓度分布的动态竞争，共同影响了τ' 的变化，且这种竞争关系，不是二者简单的叠加关系，而是出现一种复杂的、交替占主导的、此消彼长的变化关系，随着L增大，Ehv由主导逐渐过渡到占次要地位，而L由次要地位过渡到占主导地位。同时，基于τ' 仿真得到了阴极在不同掺杂方式、不同掺杂梯度下的时间响应特性—Tm和FWHM，它们均随掺杂梯度的增大而逐渐减小，而e指数电场掺杂方式具有优异的响应特性。该仿真结果为透射式GaAs光电阴极在高速摄影、电子源、光电倍增管以及像增强器的应用研究提供了必要的理论基础和数据支持。Abstract: We calculate the average time decay constant τ' of the transmission GaAs NEA cathode under different doping gradients; the analysis suggests that the thickness L of the cathode absorption layer and the doping gradient have a dominant influence on τ' , and τ' gradually decreases with the increase of L and doping gradient. The two doping methods involved in the simulation, the e-index doping method and the e-index electric-field doping method with absorption layer concentration, were not found to have an impact on τ' . When L~0.2−0.5 µm is small, the photon energy Ehv is significant to τ' . As Ehv further increases, the effects of Ehv on τ' gradually decrease. In the process of L and Ehv changes, there is a dynamic competition relationship between the L and Ehv in terms of the influences to τ' . Analyzed that the essence is the dynamic competition between the surface photoelectron concentration at the initial moment and the distribution of photoelectron concentration in the body, which jointly affects the τ' . The competitive relationship is not a simple superposition of the two parameters, but a complex, alternately dominant relationship. As L increases, Ehv gradually transitions from dominant to secondary, while L transitions from secondary to dominant. Meanwhile, based on τ' , the simulation obtained the time response characteristics of the cathode under different doping methods and doping gradients - Tm and FWHM, both of which gradually decrease with the increase of doping gradient, while the e-index electric-field doping method has excellent response characteristics. This simulation result provides the theoretical basis and data support for the application research of transmission GaAs photocathodes in high-speed photography, electronic sources, photomultiplier tubes, and image intensifiers.
-
Key words:
- GaAs photocathode /
- Gradient doping /
- The average decay time /
- Optimal factor /
- Time response .
-
-
图 1 具有内建电场的GaAs光电阴极的能带结构示意图
Figure 1. Schematic diagram of band structure of GaAs photocathode with built-in electric field
图 2 当N(L)=1019 cm−3（a）（均匀掺杂）、1018 cm−3（b）、1017 cm−3（c）、1016 cm−3（d）、1015 cm−3（e）时，τ' 与L、Ehv的关系
Figure 2. The relationship of τ' and L, Ehv when (L)=1019 cm−3(a), 1018 cm−3(b), 1017 cm−3(c), 1016 cm−3(d), 1015 cm−3(e)
图 3 当N(L)=1018 cm−3（a）、1017 cm−3（b）、1016 cm−3（c）、1015 cm−3（d）时，最优系数因子β与L、Ehv的关系
Figure 3. The relationship of β and L, Ehv when (L)=1018 cm−3(a), 1017 cm−3(b), 1016 cm−3(c), 1015 cm−3(d)
图 4 在均匀内建电场下，S=105 cm/s，Ehv=1.580 eV时，时间响应与L、Ehv 、N(L)的变化关系，其中N(L)~1019（a）~1015 cm−3（e）
Figure 4. Under the uniform built-in electric field, the relationship of the time response and L, Ehv from N(L)=1019 cm−3(a) to N(L)=1015 cm−3(e), when S=105 cm/s，Ehv=1.580 eV
图 5 在e指数内建电场下，S=105 cm/s，Ehv=1.580 eV时，时间响应与L、Ehv 、N(L)的变化关系，其中，N(L)~1018（a）~1015 cm−3（d）
Figure 5. Under the exponential built-in electric field, the relationship of the time response and L, Ehv from N(L)=1018 cm−3(a) to N(L)=1015 cm−3(d) when S=105 cm/s，Ehv=1.580 eV
表 1 均匀电场下，FWHM与L、Ehv的关系
Table 1. The relationship of FWHM and L, Ehv in the uniform built-in electric field
L (μm)
FWHM (ps)
N(L)
1019 cm−3
1018 cm−3
1017 cm−3
1016 cm−3
1015 cm−30.2 5.1~8.4 2.3~3.3 1.2~1.6 0.71~0.88 0.36~0.51 0.3 8.3~15.0 5.3~9.8 2.6~5.9 1.53~3.2 1.0~2.0 0.4 20.4~23.4 9.3~11.9 4.9~6.1 2.7~3.5 1.7~2.2 0.5 29.9~43.4 14.4~18.6 7.6~9.5 4.6~5.4 2.0~3.4 0.7 68.9~83.4 33.9~35.6 16.1~20.0 9.4~10.4 6.1~6.6 1.0 110.4~125.3 59.5~71.3 31.2~37.4 18.5~21.3 11.7~13.3 1.5 205.8~250.5 127.1~153.8 70.1~83.4 39.7~46.6 23.9~29.6 2.0 300.5~388.6 236.8~272.6 128.7~151.5 73.0~85.1 44.9~52.8 
下载: 导出CSV
表 2 均匀电场下， Tm与L、Ehv的关系
Table 2. The relationship of Tm and L, Ehv in the uniform built-in electric field
L (μm)
Tm (ps)
N(L)
1019 cm−3
1018 cm−3
1017 cm−3
1016 cm−3
1015 cm−30.2 1.1~1.93 0.61~1.09 0.36~0.64 0.25~0.39 0.15~0.17 0.3 2.3~3.46 1.6~2.16 0.71~1.48 0.49~0.88 0.28~0.56 0.4 4.5~6.66 2.5~4.68 1.45~2.82 0.8~1.64 0.49~1.04 0.5 8.4~11.26 3.8~7.9 2.2~4.76 1.67~2.82 1.0~1.78 0.7 19.66~65.8 10.4~16.9 5.0~17.4 3.3~9.7 2.34~6.1 1.0 24.7~51.6 15.5~36.2 9.2~22.0 5.7~13.3 3.3~8.6 1.5 47.3~115.0 31.4~84.0 18.0~52.3 10.6~32.0 5.6~20.9 2.0 63.7~196.5 56.1~149.0 33.1~93.9 20.5~58.1 12.6~38.2
下载: 导出CSV
表 3 e指数电场下，FWHM与L、Ehv的关系
Table 3. The relationship of FWHM and L, Ehv in the exponential built-in electric field
L (μm)
FWHM (ps)
N(L)
1019 cm−3
1018 cm−3
1017 cm−3
1016 cm−3
1015 cm−30.2 5.1~8.4 2.3~3.2 1.1~1.3 0.55~0.6 0.3~0.35 0.3 8.3~15.0 5.1~6.5 2.5~3.0 1.23~1.34 0.71~0.75 0.4 20.4~23.4 9.2~12.5 4.6~5.2 2.2~2.4 1.28~1.4 0.5 29.9~43.4 14.4~17.8 7.3~8.2 3.5~3.7 2.0~2.1 0.7 68.9~83.4 33.5~40.4 14.8~15.6 6.6~7.2 3.6~4.0 1.0 110.4~125.3 48.2~77.6 26.1~32.2 13.2~15.0 7.5~8.5 1.5 205.8~250.5 130.0~153.7 66.7~75.8 30.8~33.7 16~18 2.0 300.5~388.6 251.5~275.5 117.6~128.4 51.1~59.2 28.5~32.9
下载: 导出CSV
表 4 e指数电场下，峰值 Tm与L、Ehv的关系
Table 4. The relationship of Tm and L, Ehv in the exponential built-in electric field
L (μm)
Tm (ps)
N(L)
1019 cm−3
1018 cm−3
1017 cm−3
1016 cm−3
1015 cm−30.2 1.1~1.93 0.59~1.1 0.34~0.57 0.20~0.28 0.12~0.18 0.3 2.3~3.46 1.25~2.5 0.67~1.34 0.44~0.67 0.3~0.45 0.4 4.5~6.66 2.38~4.66 1.4~2.5 0.7~1.2 0.5~0.8 0.5 8.4~11.26 3.6~7.85 2.1~4.1 1.4~2.0 0.8~1.2 0.7 19.66~65.8 10.4~16.7 5.1~8.6 2.8~4.2 1.7~2.6 1.0 24.7~51.6 12.9~35.8 10.6~18.2 4.7~9.0 3.5~5.5 1.5 47.3~115.0 30.3~83.2 26.6~42.5 13.2~19.4 8.5~13.0 2.0 63.7~196.5 83.0~148.3 46.9~78.8 25.2~39.7 15.6~23.8
下载: 导出CSV
-
[1] Xie H. Overview of the Semiconductor photocathode research in China[J]. Micromachines,2021,12(11):1376−1376 doi: 10.3390/mi12111376 [2] Jani H, Chen L, Duan L. Femtosecond pump-probe study of negative electron affinity GaAs/AlGaAs photocathodes[C]. Ultrafast Phenornena & Nanophotonics XXII, Proceedings of SPIE, 2018, 10530: 105300X [3] Bourree L E, Chasse D R, Thamban P L S, et al. Comparison of the optical characteristics of GaAs photocathodes grown using MBE and MOCVD[J]. SPIE,2003,4796:11−22 [4] Jani H, Chen L, Duan L. Pre-emission study of photoelectron dynamics in a GaAs/AlGaAs photocathode[J]. Journal of Quantum Electronics,2020,56(1):1−8 [5] Dowell D H, Bazarov I, Dunham B, et al. Cathode R&D for future light sources[J]. Nuclear Instruments & Methods in Physics Research,2010,622(3):685−697 [6] Li X M, Zhou L W. Temporal characteristics of GaAs NEA and alkali metal photocathode[J]. Journal of Beijing Institute of Technology,2003,12(4):381−384 [7] La Rue R A, Edgecumbe J P, Davis G A, et al. High quantum efficiency photomultiplier with fast time response[J]. SPIE,1993,2022:64−73 [8] 张益军. 半导体光电阴极的研究进展[J]. 红外技术,2022,44(8):778−791 (in Chinese) Zhang Y J. Progress in reseatch on semiconductor photocathodes[J]. Infrared Technology,2022,44(8):778−791 [9] Karkare S, Dimitrov D, Schaff W, et al. Monte Carlo charge transport and photoemission from negative electron affinity GaAs photocathodes[J]. Journal of Applied Physics,2013,113:104904 [10] Karkare S, Boulet L, Cultrera L, et al. Ultrabright and ultrafast III-V semiconductor photocathodes[J]. Physical Review Letters,2014,112(9):097601 doi: 10.1103/PhysRevLett.112.097601 [11] 岳江楠, 李禹晴, 陈鑫龙, 等. n-InP/p-InP/p-InGaAs场助光电阴极理论建模与仿真[J]. 真空科学与技术学报,2023,43(6):547−553 (in Chinese) Yue J N, Li Y Q, Chen X L, et al. Theoretical modeling and simulation of n-InP/p-InP/p-InGaAs field-assisted photocathode[J]. Chinese Journal of Vacuum Science and Technology,2023,43(6):547−553 [12] Jones L B, Rozhkov S A, Bakin V V, et al. Cooled transmission-mode NEA-photocathode with a band-graded active layer for high brightness electron source[C]. 18th International Spin Physics Symposium, 2009, 1149(1): 1057−1061 [13] Guo L H, Li J M, Hou X. Calculation of temporal response of field-assited transmission-mode GaAs NEA photocathodes[J]. Solid State Electronics[J],1990,33(4):435−439 doi: 10.1016/0038-1101(90)90047-I [14] 郭里辉, 侯洵. 透射式GaAs光电阴极响应时间的理论分析[J]. 电子学报,1989,17(5):118−120 (in Chinese) doi: 10.3321/j.issn:0372-2112.1989.05.020 Guo L H, Hou X. Theoretic analysls of temporal response of transmission mode GaAs photocathodes[J]. Acta Electronica Sinica,1989,17(5):118−120 doi: 10.3321/j.issn:0372-2112.1989.05.020 [15] Li J M, Guo L H, Hou X. Calculation of temporal response for field-assisted InP/InGaAs/InP semiconductor photocathodes[J]. Chinese Science Bulletinm,1992,37(24):2047−2051 [16] 蔡志鹏, 杨文正, 唐伟东, 等. 大梯度指数掺杂透射式GaAs光电阴极响应特性的理论分析[J]. 物理学报,2012,61(18):511−516 (in Chinese) doi: 10.7498/aps.61.187901 Cai Z P, Yang W Z, Tang W D, et al. Theoretical analysis of response characteristics for the large exponential-doping transmission-mode GaAs photocathodes[J]. Acta Physica Sinica,2012,61(18):511−516 doi: 10.7498/aps.61.187901 [17] Cai Z P, Yang W Z, Tang W D, et al. Numerical analysis of temporal response of a large exponential-doping transmission-mode GaAs photocathode[J]. Materials Science in Semiconductor Processing,2013,16(2):238−244 [18] 韩明, 郭欣, 邱洪金, 等. 透射式 GaAs 光电阴极时间分辨特性研究[J]. 红外与激光工程,2022,51(8):20210761−1−5 (in Chinese) doi: 10.3788/IRLA20210761 Han M, Guo X, Qiu H J, et al. Study on the time-resolved characteristics of the transmissionmode GaAs photocathode[J]. Infrared and Laser Engineering,2022,51(8):20210761−1−5 doi: 10.3788/IRLA20210761 [19] 岳江楠, 李禹晴, 陈鑫龙, 等. 场助光电阴极研究进展[J]. 光电子技术,2022,42(4):248−266 (in Chinese) Yue J N, Li Y Q, Chen X L. Development of field assisted photocathode[J]. Optoelectronic Technology,2022,42(4):248−266 [20] 周振辉, 徐向晏, 刘虎林, 等. 高量子效率InP/In0.53Ga0.47As/InP红外光电阴极模拟[J]. 红外与激光工程,2019,48(02):247−253 (in Chinese) Zhou Z H, Xu X Y, Liu H L, et al. High quantum efficiency InP/In0.53Ga0.47As/InP infrared photocathode simulation[J]. Infrared and Laser Engineering,2019,48(02):247−253 [21] Zhou R, Jani H M, Zhang Y J, et al. Dynamic photoelectron transport in stepwise-doped GaAs photocathodes[J]. Scientifc Reports,2022,12:12936 doi: 10.1038/s41598-022-16993-8 [22] Zhou R, Jani H M, Zhang Y J, et al. Photoelectron transportation dynamics in GaAs photocathodes[J]. Journal of Applied Physics,2021,130:113101 doi: 10.1063/5.0057458 [23] 蔡志鹏, 姚军财, 黄文登, 等. 具有e指数内建电场的透射式GaAs光电阴极响应特性的理论分析[J]. 发光学报,2018,39(5):661−667 (in Chinese) doi: 10.3788/fgxb20183905.0661 Cai Z P, Yao J C, Huang W D, et al. Theoretical study of response characteristics of transmission-mode GaAs photocathodes with exponential inner electric field[J]. Chinese Journal of Luminescence,2018,39(5):661−667 doi: 10.3788/fgxb20183905.0661 [24] 邹继军, 常本康, 杨智. 指数掺杂GaAs光电阴极量子效率的理论计算[J]. 物理学报,2007,56(5):2992−2997 (in Chinese) doi: 10.7498/aps.56.2992 Zou J J, Chang B K, Yang Z. Theoretical calculation of quantum yield for exponential-doping GaAs photocathodes[J]. Acta Physica Sinica,2007,56(5):2992−2997 doi: 10.7498/aps.56.2992 [25] 常本康, GaAs基光电阴极[M]. 北京: 科学出版社, 2017 (in Chinese) Chang B K. GaAs-based photocathodes[M]. Beijing: Science Press, 2017 [26] Sadao A. Optical constants of crystalline and amorphous semiconductors: Numerical data and graphical information[M]. Springer Science, 1999 -
图( 5) 表( 4)
计量
- 文章访问数: 36
- HTML全文浏览数: 36
- PDF下载数: 0
- 施引文献: 0