首页
登录
注册
-
喷射器是一种简单的流体机械装置，能将高压流体用于引射和压缩二次流体，常被用于回收低品位热能[1]。
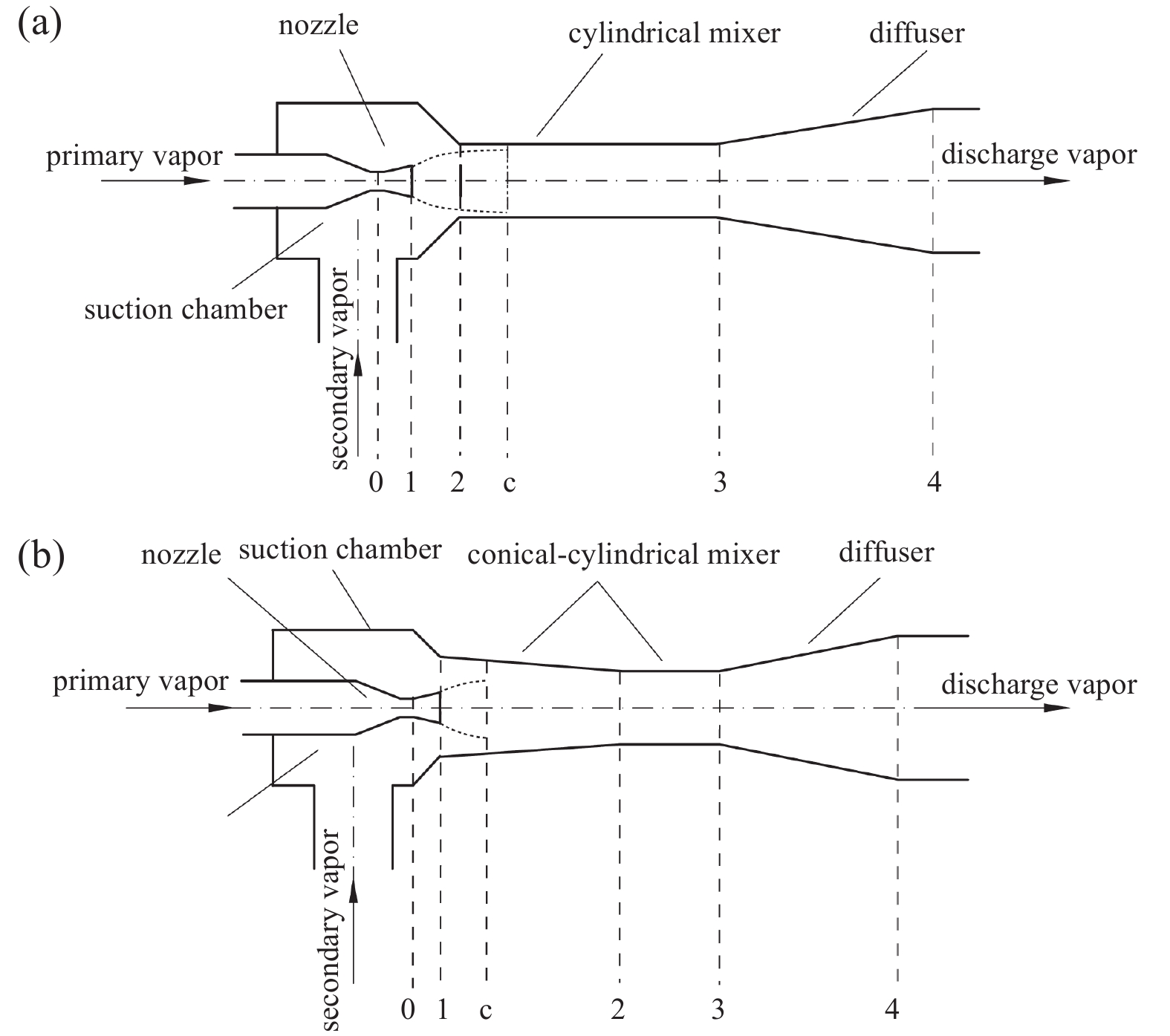
研究已表明混合室结构对喷射器性能具有重要影响[2-4]。如图1所示，根据混合室结构不同，喷射器通常分两种类型：锥−柱形混合室喷射器（CCME）和圆柱形混合室喷射器（CME）[5]。Keenan J H等[6]采用一维分析方法来考虑这两种混合室结构的流体混合，结果显示，锥−柱形混合室喷射器比圆柱形喷射器具有更高的喷射系数。Yapıcı R等[7]研究结果显示，在相同操作条件下，相较于圆柱形混合室喷射器系统而言，锥−柱形混合室喷射器系统的效率更高，但是需要更低的冷凝温度。Petrenko V O等[8]实验结果显示，与圆柱形混合室喷射器相比，具有锥−柱形混合室的喷射器可将临界喷射系数提高25%~35%。Shestopalov K O和Del Valle J G等[9-11]实验对比结果也表明锥−柱形混合室喷射器的临界喷射系数更大，但临界压缩比更小。Chen H J等[12]理论比较分析了圆柱形和锥−柱形混合室喷射器在不同膨胀比和压缩比下的性能差异，为喷射器在实际应用中选择混合室结构提供一定理论依据。Tashtoush B等[13]采用R134a喷射器研究发现在相同的喷射系数下，锥−柱形混合室喷射器可获得比圆柱形混合室喷射器更高的临界压缩比。而Sierra-Pallares J等[14]研究则发现锥−柱形混合室喷射器的熵产率更小。研究上述两种类型喷射器性能对比是优化喷射器设计，提高喷射器性能的有效途径，但这些研究的工况较为单一，以至于不同的研究者得到了矛盾的结论[7, 13]；产生矛盾结论的原因还可能是上述研究是在固定喷嘴距和等混合室截面比的情况下进行的。注意，结合图1所示，本文NXP和Ar定义分别为：
喷嘴距（NXP）即出口截面1至柱形混合室入口截面2之间距离。而截面比（Ar）即柱形混合室出口截面积A3与工作喷嘴喉部截面积A0的比值。
恰当的喷嘴距是保证喷射器高效稳定地运行的重要几何因素，为了避免不同操作条件下喷嘴距偏离设计点时导致喷射器性能严重下降[15-17]，将喷射器喷嘴距设计成可在线调节是一种有效的途径[18-19]。为了实现不同工况下喷嘴距在线调节，Ge J等[20]基于可压缩流体的剪切混合层理论和绝热摩擦流动方程，提出了一种能够预测锥−柱形混合室喷射器最佳喷嘴距的设计模型。而对于截面比Ar而言，其作为影响蒸气喷射器喷射系数的主要尺寸之一，Ar的大小决定了喷射器的双壅塞喷射系数大小；且膨胀比越大，所需截面比越大，双壅塞喷射系数越大；而压缩比越大，则所需截面比越小，双壅塞喷射系数越小[19, 21-22]。而在先前的报道中，合适的喷嘴距和截面比组合可使得锥−柱形混合室喷射器比圆柱形混合室喷射器性能更优的结果已经得到了实验验证[23]。
迄今为止，在可变几何结构喷射器的研究中，针对锥−柱形和圆柱形混合室喷射器的性能差异研究工作仍旧不足，尤其缺乏从综合性能及内部流动特性方面对这两种类型喷射器进行比较的研究。因此，本文基于可变几何结构喷射器实验系统，采用CFD模拟并引入热力学完善度，充分研究不同喷嘴距下，圆柱形和锥−柱形混合室喷射器在相同及不同面积比下的性能差异，通过数值模拟进一步分析喷射器内部流场和熵产率的变化规律，为合理选择混合室结构及其几何参数，减小喷射器的不可逆损失，实现喷射器临界性能的多目标（临界喷射系数和临界冷凝压力）优化提供新指导。
-
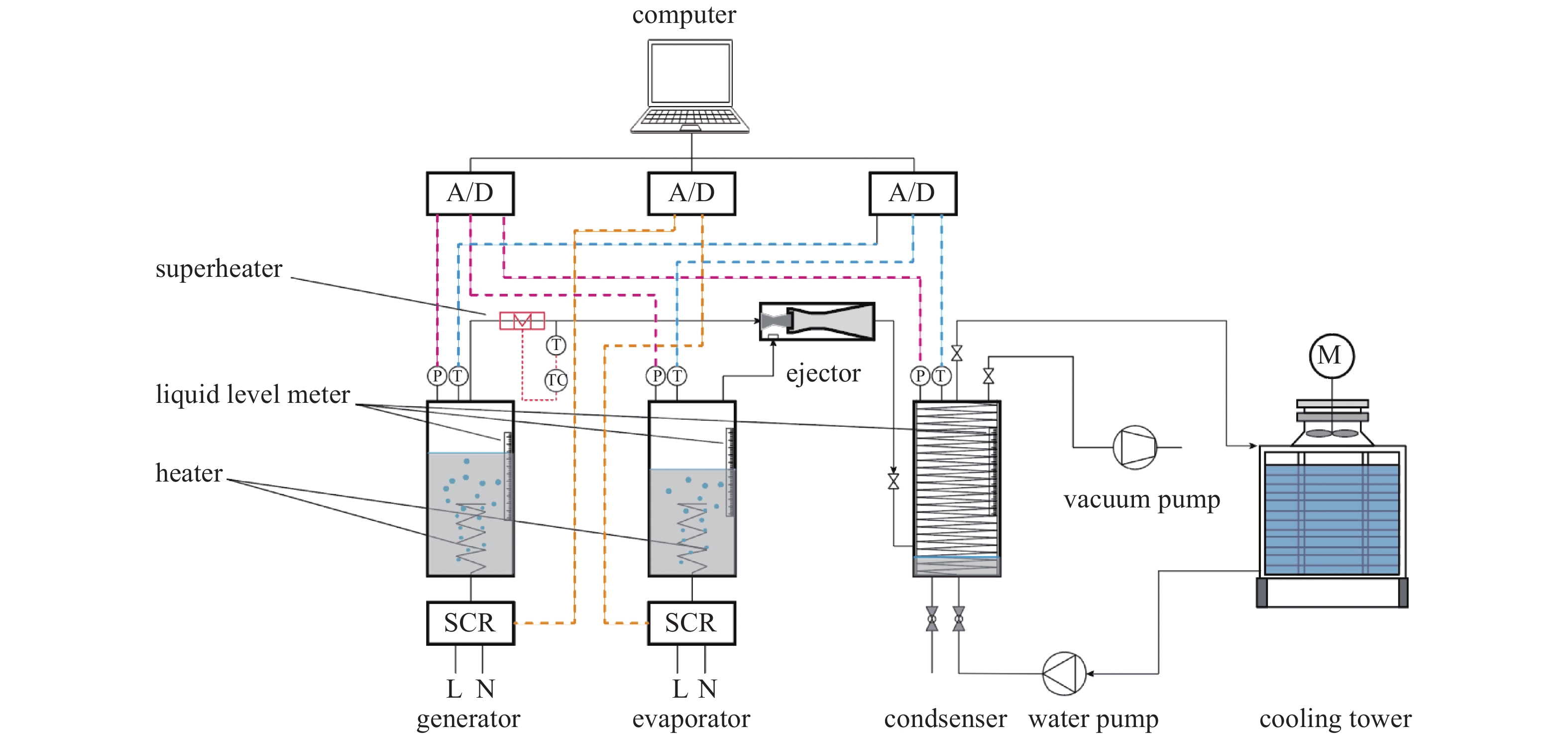
图2为本文实验研究用可调式喷射器实验系统，该实验装置由发生器、蒸发器、冷凝器、喷射器等主要设备及蒸汽过热器、真空泵、循环泵、冷却塔等辅助设备，以及测量系统和PID控制系统组成[23]。
如图1所示，带圆柱形混合室和锥−柱形混合室的喷射器结构主要包括：喷嘴、吸入室、混合室和扩压器。然而，如图3所示，在实验装置中，本文喷射器采用模块化设计，即工作喷嘴、喷嘴座、混合-扩压室以及喷射器主体均为可拆卸式，如图3（c）所示，这样设计的优势在于喷嘴距NXP可通过工作蒸汽管螺纹结构在线调节喷嘴座轴向位置的方式进行，使得喷嘴距调节过程喷嘴距调节机构对喷射器引射性能无影响；而截面比Ar可通过更换不同的混合-扩压室进行改变。发生器和蒸发器内部均设置有电加热器，通过可控硅调节电压来改变热量输入，以控制发生器和蒸发器内饱和温度。发生器、蒸发器和冷凝器的液位通过玻璃管液位计进行测量。过热器为缠绕在发生器出口工作蒸气金属管外的电加热带，其自带温控器，以控制工作蒸气过热度为10 K。真空泵主要作用是实验系统实验前抽真空和系统运行中配合控制系统调节冷凝器压力。测量仪器包括发生器、蒸发器液位测量刻度尺，长度为500 mm，刻度为1 mm；喷嘴距测量刻度尺长度为250 mm，刻度为0.5 mm；压力和温度传感器，具体规格型号如表1所示。数据采集控制单元包括数据采集模块、A/D转换器和自动控制系统[23]。控制系统作用主要包括两个方面：（1）保证发生器、蒸发器内具备稳定的蒸汽压力；（2）配合真空泵使用，保证冷凝器内冷凝压力维持目标值。
-
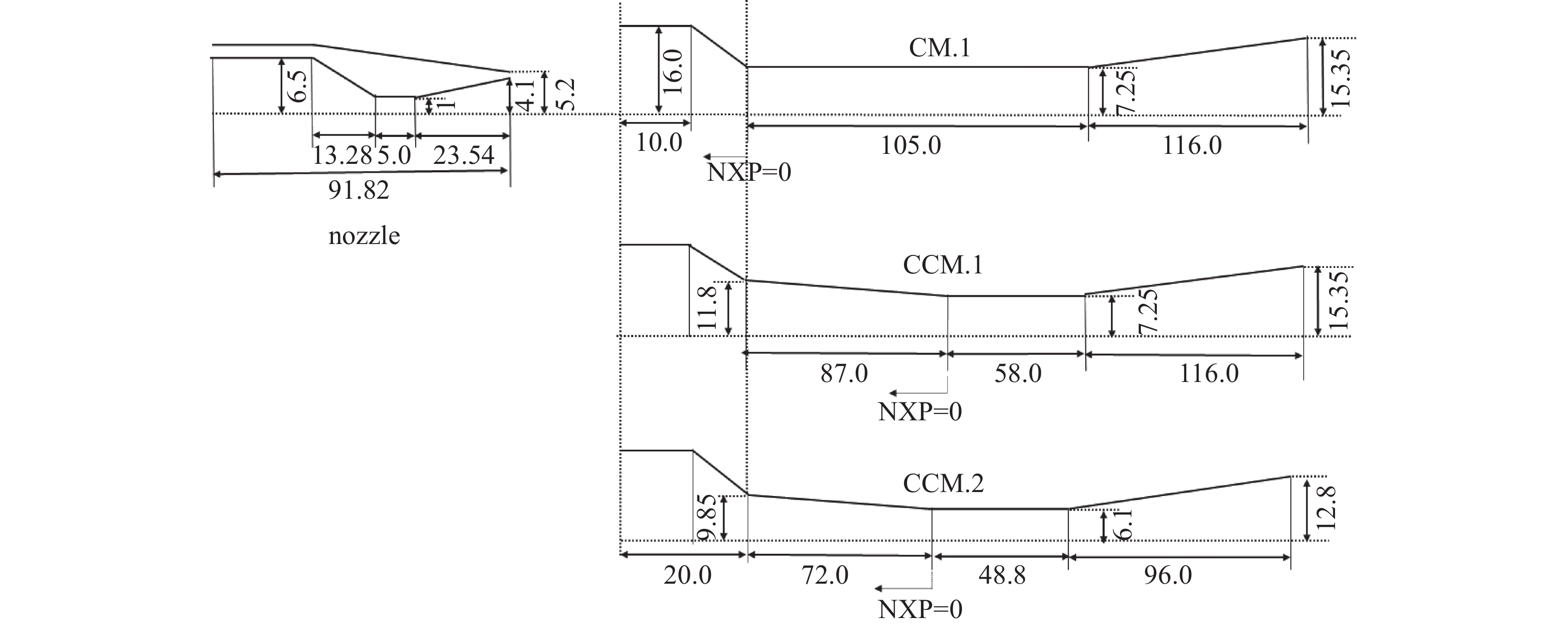
实验工质采用水蒸气，实验工况为发生器压力pp = 143.38 kPa，发生器温度Tp = 393.15 K；蒸发器压力ps = 1.23 kPa，蒸发器温度Ts = 283.15 K。在临界模式下，研究了带圆柱形混合室CM.1、锥−柱形混合室CCM.1和CCM.2三个不同喷射器在不同喷嘴距的临界喷射系数（ucri）和临界冷凝压力（pc, cri）。图4为该三个喷射器的几何尺寸，喷射器CM.1、CCM.1及CCM.2的实验喷嘴距测试范围分别为0.0~52.0 mm、70.0~117.0 mm及65.0~98.0 mm。
喷射器性能参数包括临界喷射系数ucri、临界背压pc, cri和热力学完善度η。根据定义，喷射系数u定义为引射蒸气与工作蒸气质量流量之比[16]。
临界背压为喷射器工作在临界喷射系数前提下所能达到的最高背压。在实验测取时，可以通过不断降低冷凝压力，测取喷射系数曲线转折点对应的背压获得。而热力学完善度为实际临界喷射系数和理想临界喷射系数ui的比值[16]，喷射器在理想状态（等熵过程）下有：
-
采用ICEM软件建立喷射器二维几何模型，并生成结构化网格，如图5所示，喷射器物理模型壁面网格结构均进行了加密处理，并将壁面处第一个网格层的无因次高度Y-Plus值尽可能调节至接近1。由于存在摩擦效应，可压缩性流体有效流通截面积被认为是实际截面积的0.88倍[24]。本文采用SST k-ω湍流模型，原因是其对全局和局部流动现象均具有更高的预测精度[25-26]，SST k-ω湍流模型可描述为：
其中，k为湍流动能，kg/(m·s3)；ω为比耗散率，kg/ (m3·s2)；其他参数解释见文献[27]。
Fluent中边界条件和其他设置：工作蒸气和二次蒸气入口为压力入口；混合蒸气出口为压力出口（模拟过程不考虑喷射器管道阻力损失）；壁面采用绝热无滑移条件；水蒸气采用真实气体属性，选择基于密度的隐式求解器和二阶迎风格式，给工作蒸气增加10 K的过热度[20, 23]。模拟计算过程残差设置小于10−3；且计算结果显示质量流量处于稳定状态时才确认计算收敛。
为检验网格数对数值结果的影响，如表2所示为CM.1喷射器在其最佳喷嘴距ONXP = 48.0 mm时，网格数在40356~196532范围内的临界喷射系数模拟值随网格数变化趋势。由表可知，随着网格数的增加，相对于网格数为40356的模拟结果而言，模拟结果相对变化范围均在±2.42%以内，这表明网格数量在40356至81612之间时已经可以忽略网格数对模拟结果的影响，兼顾计算速度及模拟的精确性，选择网格数为81612进行模拟。
-
单相流体的熵仅为温度和压力的函数，温度和压力在流场中均已知，此时熵可以看作是一个可以确定的后处理量。喷射器内的热耗散和粘性耗散共同构成的喷射器的熵产率[28-29]：
在不考虑喷射器与外界热交换的前提下，喷射器总熵产率可简化为：
其中，T为温度，K；τ为粘性应力张量，N/m2；ν为速度矢量，m/s。
粘性耗散包括平均流场耗散和速度波动引起的耗散[30]：
其中，平均流场熵产率Smean表达为：
而SST k-ω湍流模型由速度湍流波动引起的耗散熵产率Sflu表达为：
通过对式（11）在计算域内进行体积积分得到喷射器熵产率[31]：
-
表3为喷射器CM.1、CCM.1以及CCM.2的模拟值和实验值之间的对比结果。比较结果表明：临界喷射系数模拟值与临界喷射系数实验值相比，临界喷射系数最大相对误差在±16.36%以内，而两者的相对偏差绝对值的平均值为7.29%；临界冷凝压力的模拟值与其实验值的最大误差则在±20.86%以内，而两者相比的相对偏差绝对值的平均值为11.78%。Ruangtrakoon N等[35]报告指出，实验值与模拟值存在差异的原因包括：首先，数值计算的流体流动过程作了绝热光滑壁面假设，忽略了喷射器内部壁面的粗糙度造成的不可逆损失；其次，实验喷射器尺寸设计加工过程错在误差，尤其加工过程可能存在偏差；此外，尽管较多的文献报道显示相对于其它湍流模型，SST k-ω湍流模型对局部和全局流动均具有较好的准确度，然而，SST k-ω湍流模型仍然不能完全处理湍流的复杂性[36]。综上，在所述误差范围内，本文数值模型对临界喷射系数和临界冷凝压力的预测值可认为合理，计算方案具有准确性。
-
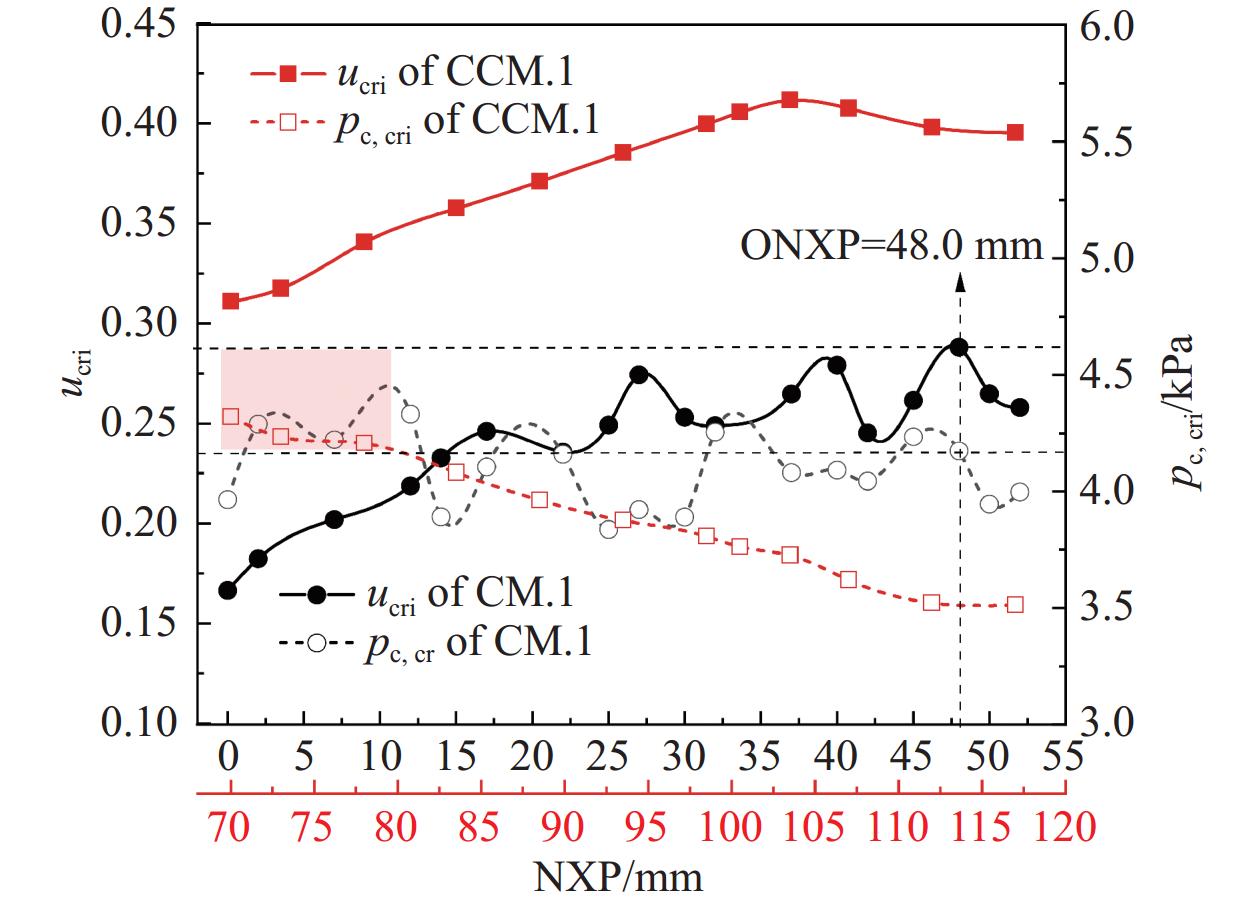
图6为等截面比（Ar = 52.6）下，圆柱形混合室喷射器CM.1和锥−柱形混合室喷射器CCM.1的性能对比：一方面，如黑色实线所示，CM.1在喷嘴距NXP从0.0 mm增加到17.0 mm时，临界喷射系数则从0.167逐渐增加至0.247，而喷嘴距在22.0~52.0 mm时，临界喷射系数在0.247~0.289之间波动，并在喷嘴距为48.0 mm 时达最大值0.289；此外，如黑色虚线所示，随着NXP的增加，CM.1的临界冷凝压力则在3.84~4.29kPa之间波动。上述现象说明：在一定的喷嘴距范围内，改变NXP对圆柱形混合室喷射器临界性能的影响并不明显。另一方面，随着NXP的增加，如红色实现和虚线所示，CCM.1的临界喷射系数先增加后减小，而临界冷凝压力则逐渐下降；值得注意的是，与CM.1在最佳喷嘴距ONXP = 48.0 mm的临界性能相比，CCM.1在喷嘴距70.0 ~79.0 mm范围内（见红色阴影部分）可同时获得更佳的临界喷射系数和临界冷凝压力。
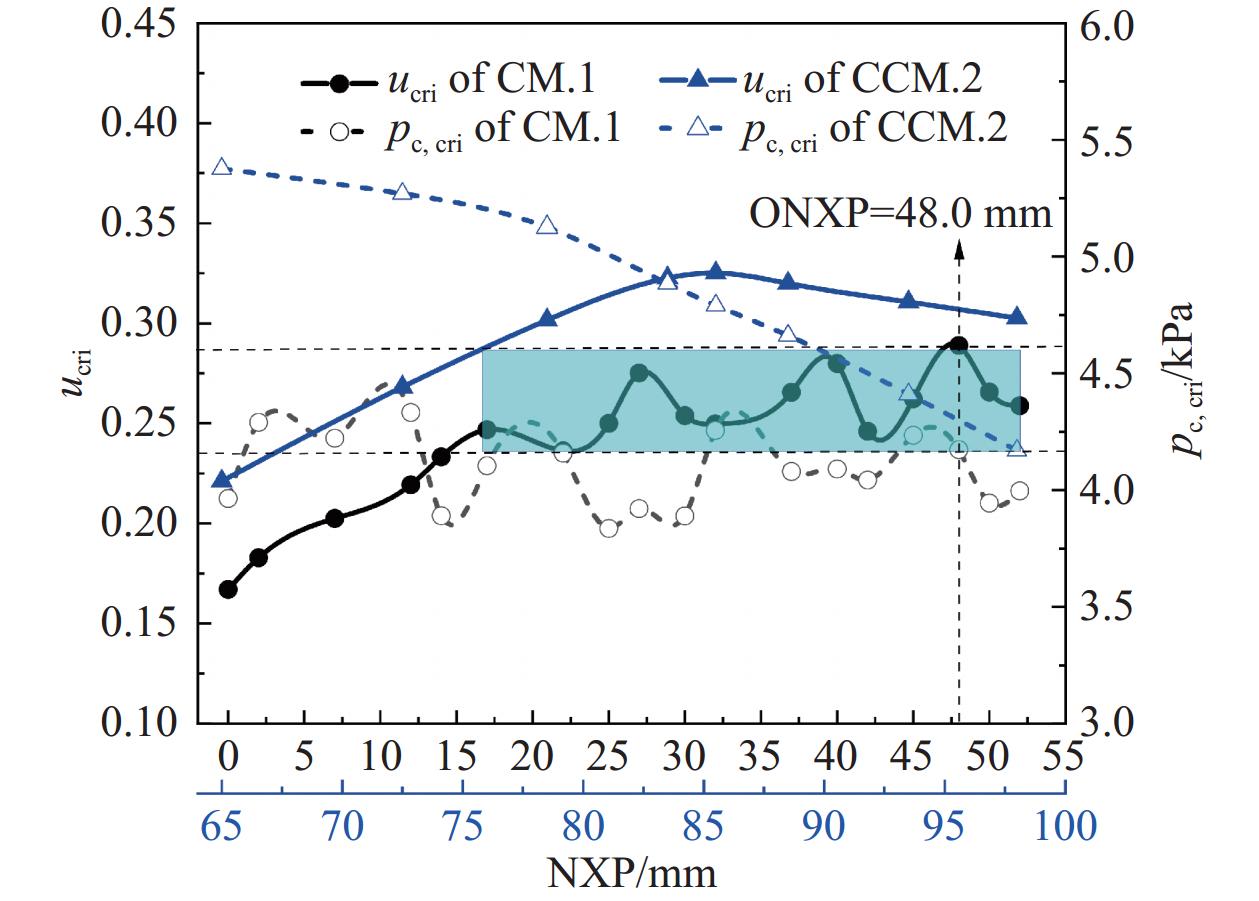
如图7所示，同样以最佳喷嘴距ONXP = 48.0 mm下的CM.1喷射器（Ar = 52.6不变）临界性能作为对比基准，当将锥−柱形混合室喷射器的截面比Ar降低为37.2，即采用CCM.2喷射器时在喷嘴距76.0~98.0 mm范围（见蓝色阴影部分）内均可同时获得更佳临界喷射系数和临界冷凝压力。显然，相比于采用同CM.1等截面比（Ar = 52.6）的CCM.1喷射器，采用CCM.2喷射器可以扩大锥−柱形混合室在临界喷射系数、临界背压均优于柱形混合室喷射器时的喷嘴距范围。
图6和图7的讨论结果首次表明：相对于柱形混合室喷射器的设计性能（在最佳喷嘴距处临界性能），锥−柱形混合室喷射器在一定喷嘴距范围内可实现临界喷射系数ucri和临界冷凝压力pc, cri的多目标优化，且适当地降低锥−柱形混合室的截面比更有利于喷射器的性能优化。然而，在可变几何结构情况下，为了进一步探究锥−柱形混合室喷射器相对于柱形混合室喷射器具有更好的机械性能，需要引入一个综合性能因素，即热力学完善度η，相对于临界喷射系数和临界冷凝压力，其优势在于其定义同时考虑到了ucri和pc, cri两者的影响。
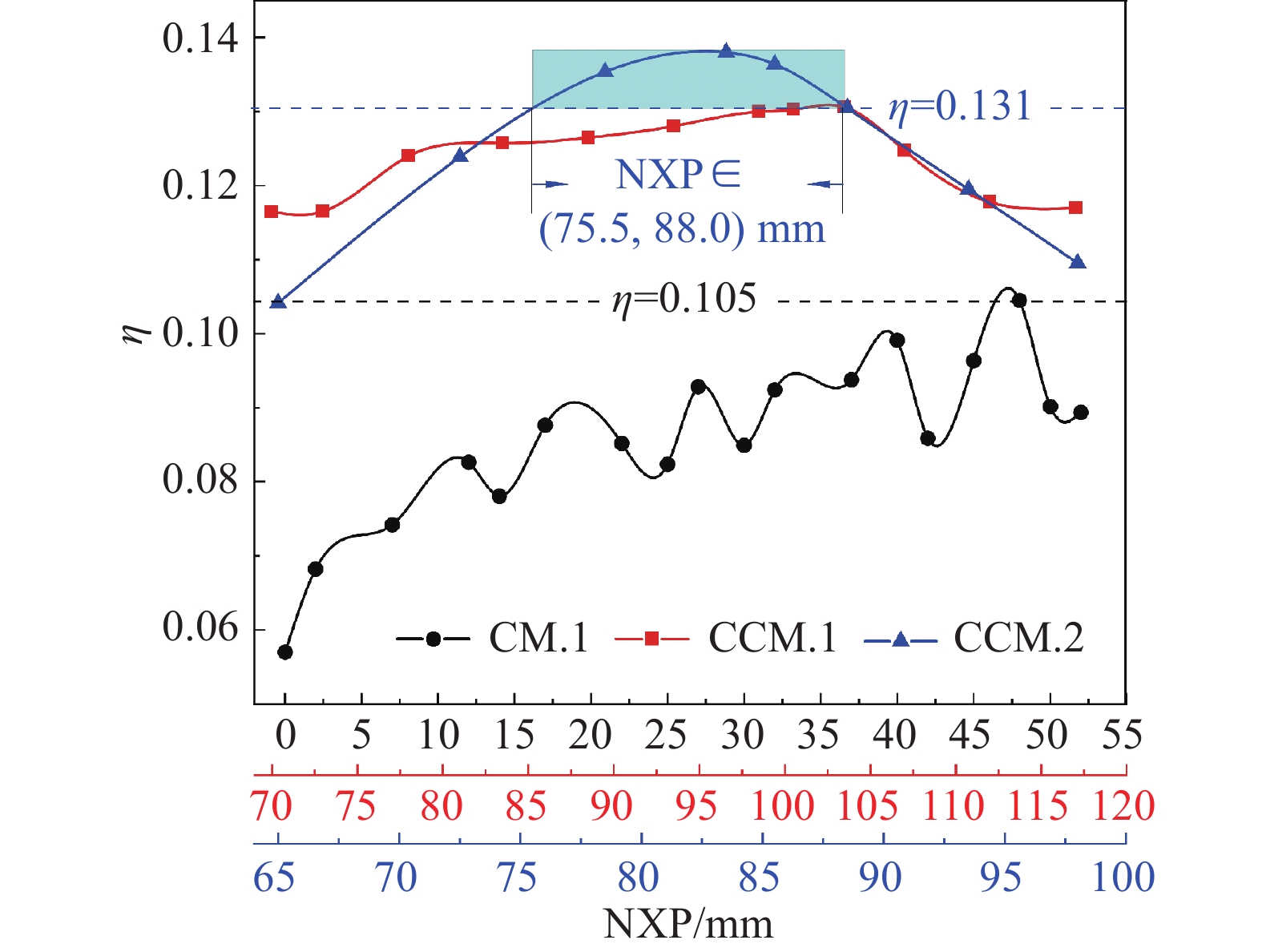
如图8所示，黑、红及蓝色实线分别为CM.1（Ar = 52.6）、CCM.1（Ar = 52.6）及CCM.2（Ar = 37.2）的热力学完善度η随喷嘴距NXP的变化情况：随着NXP的增加，CM.1喷射器的热力学完善度呈波动状态，并在最佳喷嘴距ONXP = 48.0 mm时达最大值0.105；而CCM.1和CCM.2喷射器的热力学完善度先增加后减小，并分别在喷嘴距为103.5 mm 和83.5 mm时达最大值0.131、0.138；在实验喷嘴距范围内，锥−柱形混合室喷射器CCM.1和CCM.2的热力学完善度均优于柱形混合室喷射器CM.1的其ONXP处的热力学完善度；降低锥−柱形混合室喷射器截面比，即采用CCM.2（Ar = 37.2）替代CCM.1（Ar = 52.6）将会在喷嘴距NXP = 75.5~88.0 mm范围内获得更佳的热力学完善度。
综上，等截面比下，与最佳喷嘴距的圆柱形混合室喷射器性能相比，锥−柱形混合室喷射器在合适的喷嘴距范围内具有更好的临界喷射系数和临界冷凝压力，减小锥−柱形混合室喷射器截面比，该喷嘴距范围扩大，但临界性能变化更急剧。此外，综合性能因素热力学完善度的分析结果显示：锥−柱形混合室喷射器比圆柱形混合室喷射器具备更佳的机械性能；且锥−柱形混合室喷射器热力学完善度存在一最佳值；通过恰当降低锥−柱形混合室喷射器截面比，可在一定喷嘴距范围内进一步提高锥−柱形混合室喷射器的机械性能。
-
为了进一步解释较最佳喷嘴距的圆柱形混合室喷射器，锥−柱形混合室喷射器在不同喷嘴距范围及截面比下存在临界喷射系数和临界背压均更优的现象，采用CFD进行分析，在临界模式下通过数值模拟得到喷射器内部流场变化和熵产率大小及分布, 对不同类型喷射器的综合性能差异深入探究。
-
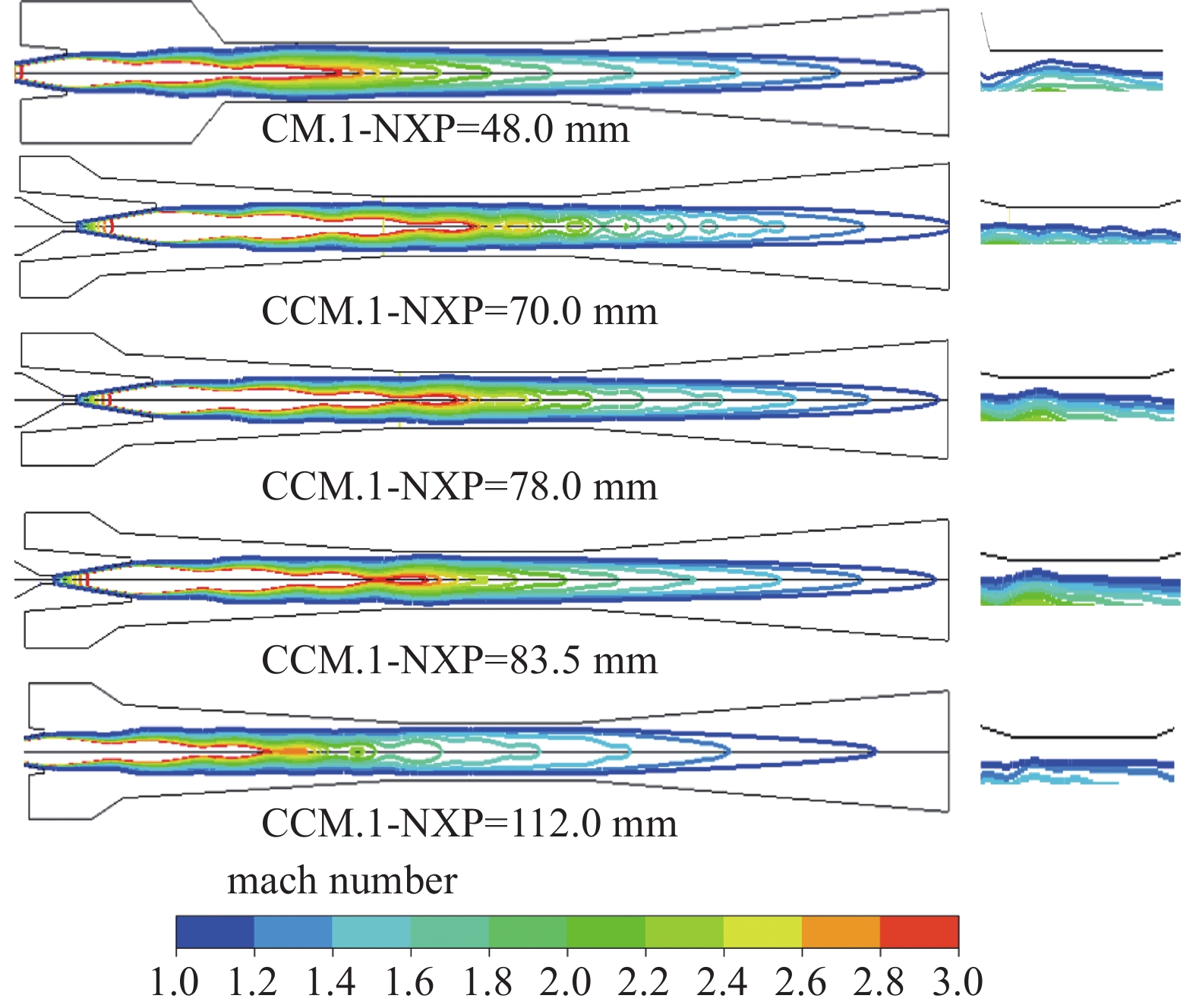
如图9和10所示，工作蒸气经喷嘴加速成为超音速流体后，在喷嘴出口压力作用下形成膨胀−压缩−膨胀（欠膨胀时）Y型激波链；或形成压缩−膨胀−压缩（过度膨胀时）Y型激波链。CM.1和CCM.1喷射器（等截面比Ar = 52.6）的激波链长度存在差异：首先，CM.1喷射器在最佳喷嘴距时，吸入室内两股蒸气之间较大的速度差导致剪切作用力强烈，混合蒸气进入混合室喉部前，由于空间急剧缩小，混合蒸气与吸入室内壁发生强烈的撞击，形成巨大涡流，大大增加混合蒸气的动量损失，这导致此时喷射器的临界冷凝压力较小。
另外，在轴向上，无论是CM.1 还是CCM.1，工作流体剪切二次流体形成的剪切传质混合层伴随出现呈波动状态的Y型激波链[37-38]，且从喷嘴出口开始受到混合室后端压力影响，导致该剪切传质混合层厚度亦存在波动，而剪切传质混合层厚度大小与喷射系数呈正相关作用[37]。对于柱形混合室喷射器而言，混合蒸气壅塞（双壅塞）往往发生在柱形混合室入口附近[24]，此时在柱形混合室入口对应的剪切传质混合层厚度决定了双壅塞喷射系数（临界喷射系数）。显然在轴向距离（即喷嘴距NXP）和剪切传质混合层厚度波动的双重因素下，柱形混合室喷射器的临界喷射系数随NXP的变化而产生了波动性，该解释也得到相关研究的佐证[39]。
此外，相比于CM.1，锥−柱形混合室喷射器CCM.1在喷嘴距70.0~78.0 mm时（此时临界喷射系数和临界冷凝压力均优于CM.1喷射器最临界性能），激波链长度明显更长，意味着混合蒸气实现较低的动量损失；激波链沿着混合室喉部到达扩压室，形成第二冲击波（见图9），第二冲击波属于将流体速度由超音速变为亚音速的压缩冲击波，导致喷射器具有更高的临界冷凝压力，这获得了有关报告[35, 40-41]的支持；Ariafar K等[42-43]证明剪切混合过程是提高喷射系数的关键，由图10的马赫数等值线图可知，与CM.1相比，CCM.1在喷嘴距70.0~78.0 mm时，混合室喉部内的二次蒸气速度达到音速（Ma = 1）时与喷射器内壁之间的有效流动横截面积更大（喉部空白区域），说明更多的二次蒸气通过混合室喉部，并伴随着激波链与工作蒸气进行剪切混合，提高了喷射器的引射性能，临界喷射系数更高；随着NXP的增加，CCM.1的有效流动横截面积逐渐增加，临界喷射系数增加，然而混合室内流体边界层分离更加严重，涡流增强，混合流动动量损失增加，导致临界背压降低，直接表现为更短的激波链长度（见图9）；增加NXP到一定值时，激波链长度小于CM.1喷射器，此时CCM.1喷射器的临界冷凝压力将不再大于CM.1喷射器（如NXP = 83.5或112.0 mm）。
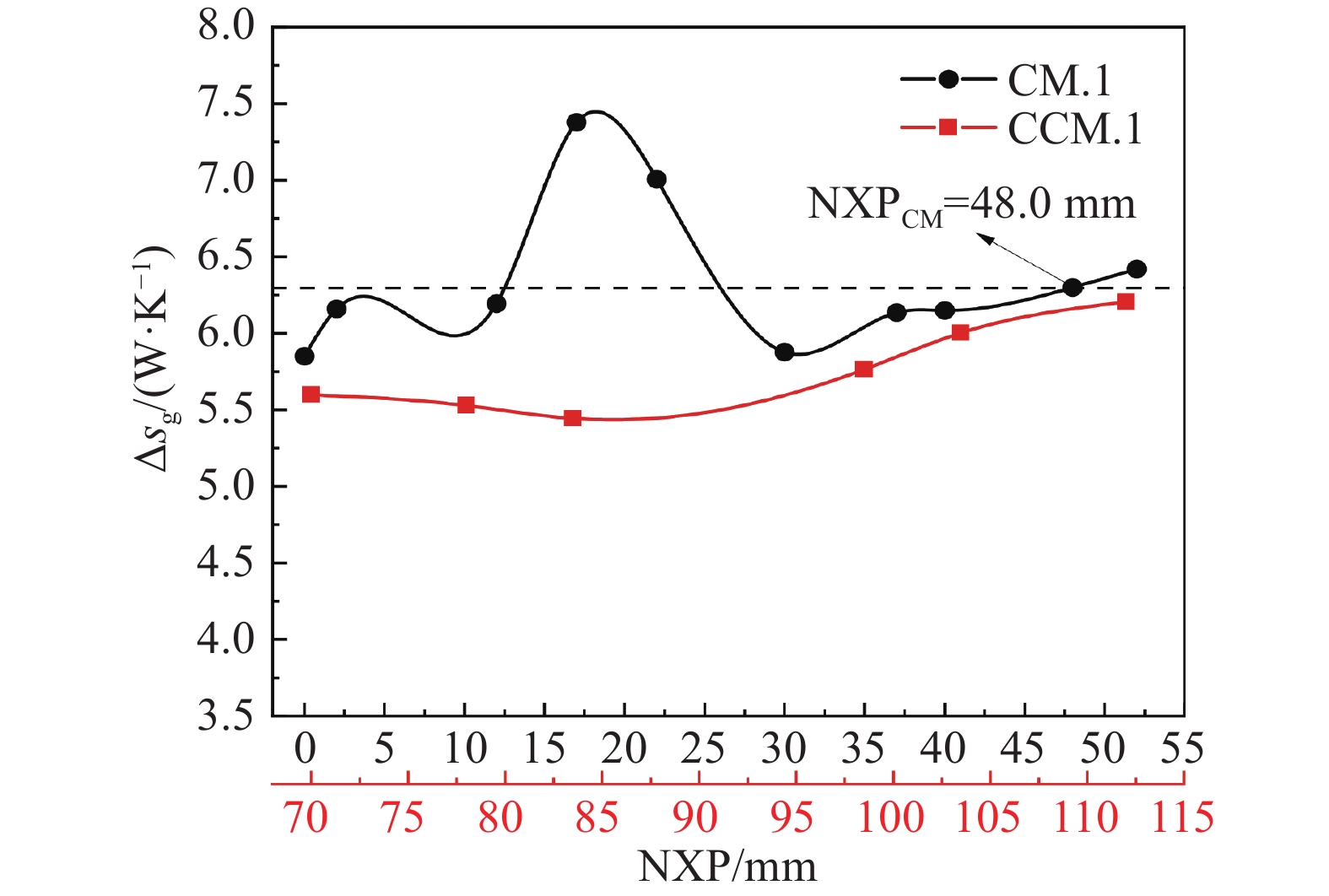
如图11所示，随着NXP的增加，CM.1喷射器熵产率呈较大波动，CCM.1喷射器熵产率先缓慢降低后逐渐增大，且均小于CM.1喷射器在其最佳喷嘴距处熵产率值，这是导致CM.1喷射器的热力学完善度更低的主要原因。
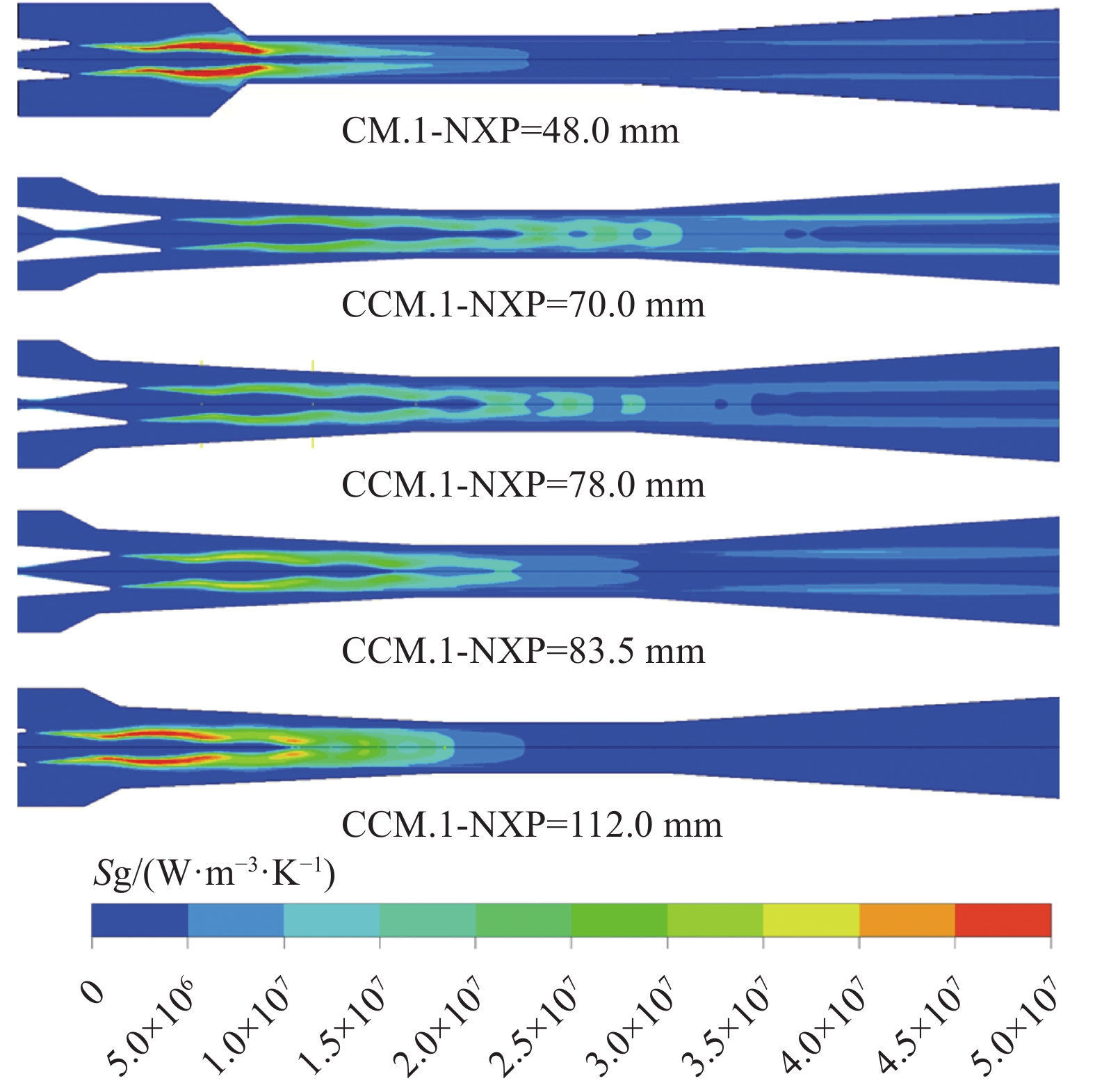
如图12所示，CM.1在最佳喷嘴距时，混合蒸气与吸入室壁的剧烈撞击导致该区域的不可逆损失急剧增加，较高的熵产率发生在吸入室及混合室喉部入口附近；CCM.1在喷嘴距为70.0 mm 时，第二冲击波到达扩压室，导致扩压室的熵产率较大，随着NXP的增加，第二冲击波逐渐向混合室移动，直至消失，激波链逐渐缩短，并集中在混合室收敛段，造成混合室熵产率不断增加，且分布在混合室收敛段，扩压室熵产率逐渐减小；CCM.1喷射器在喷嘴距为70.0~78.0 mm时，熵产率较低且主要发生在混合室和扩压室内部，该结果得到最新研究成果的印证[44]。
以上分析可知：等截面比下，与最佳喷嘴距处的圆柱形混合室喷射器临界情况相比，锥−柱形混合室喷射器在合适的喷嘴距范围内不仅能实现混合流较小的动量损失，还能增大二次蒸气在混合室喉部的有效流动横截面积，因此获得更好的临界喷射系数和临界冷凝压力；此外，与圆柱形混合室喷射器相比，锥−柱形混合室喷射器有效避免了流体混合阶段不可逆损失的急剧增加，从而获得更高的热力学完善度，即具备更佳的机械性能。
-
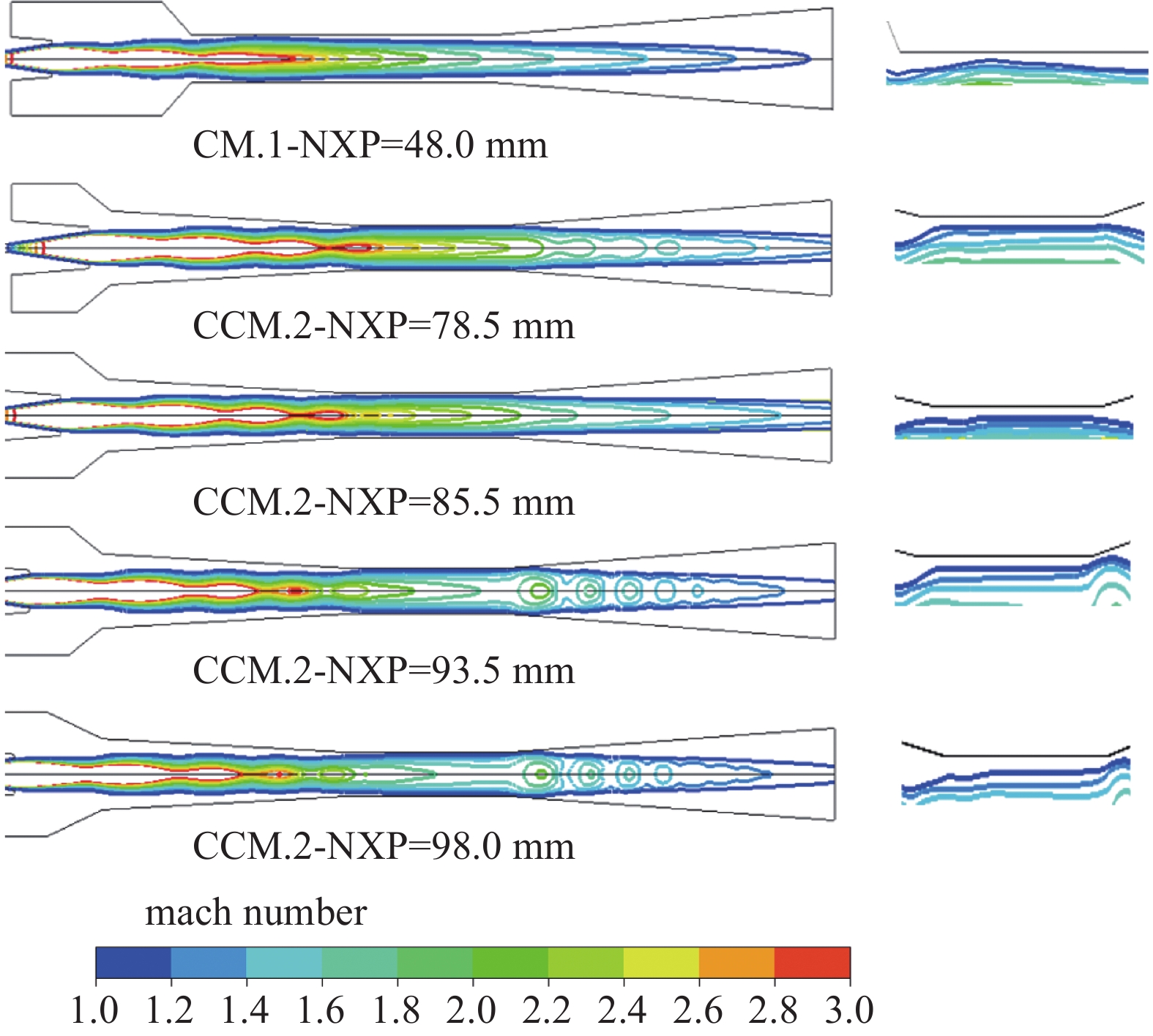
如图13所示，相比于CM.1在最佳喷嘴距处的情况，CCM.2在研究喷嘴距范围78.5~93.5 mm内（此时临界喷射系数和临界冷凝压力均更优）混合蒸气激波链长度更长，同样实现了较小的动量损失。
此外，由图14的马赫数等值线可知，CCM.2的二次蒸气在混合室喉部内的有效流动横截面积（喉部空白区域）比CM.1喷射器更大。值得注意的是，在CCM.2中，混合室喉部二次蒸气在相等有效横截面积的流动距离更长，说明伴随着激波链，工作蒸气和二次蒸气进行更稳定的剪切混合，促进两股蒸气之间的能量交换，进一步增强了喷射器对后端背压压缩效应的抵抗能力，使得CCM.2在较大的NXP范围内保持更高的临界喷射系数和临界冷凝压力。
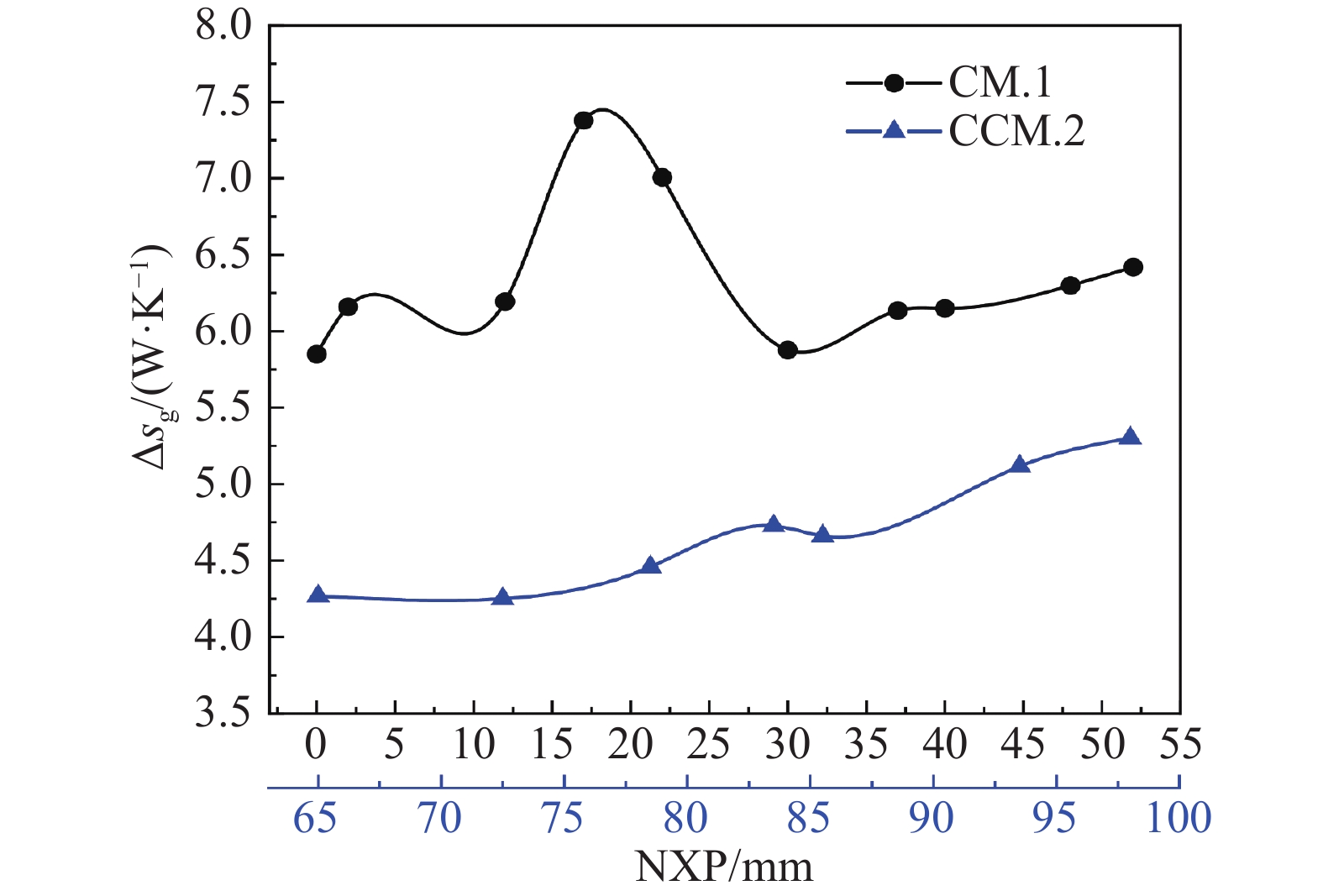
图14为CM.1和CCM.2的熵产率随NXP的变化情况：与CM.1（Ar = 52.6）相比，CCM.2（Ar = 37.2）呈现出更小的熵产率，说明喷射器内部不可逆损失得到更小化，提高了喷射器的热力学完善度。而图11与图15对比发现降低锥−柱形混合室截面比，即将CCM.2（Ar = 37.2）替换CCM.1（Ar = 52.6）时，熵产率更低，这便是适当降低截面比可提高锥−柱形混合室喷射器机械性能的热力学原因。
如图16可知：整体而言，与CM.1相比，CCM.2中熵产率强度明显更低；另外，随着NXP的增加，CCM.2中较高的熵产率向混合室收敛段集中，因而热力学完善度以更快的速率达到最高点；然而，随着NXP进一步增大，混合室收敛段的熵产率强度逐渐增大，这导致热力学完善度随之降低。
根据上述分析，在降低锥−柱形混合室喷射器截面比情况下，与圆柱形混合室喷射器在最佳喷嘴距的情况相比，锥−柱形混合室喷射器在合适的喷嘴距范围内同样可获得更佳临界喷射系数和临界冷凝压力的原因是：与柱形混合室相比，锥−柱形混合室内混合蒸气激波链长度更长，增强了喷射器对后端背压压缩的抵抗能力且可实现较小的动量损失；同时，锥−柱形混合室内二次蒸气在混合室喉部内的有效流动横截面积更大。此外，恰当较少截面比可降低锥−柱形混合室内混合蒸气的熵产率，从而进一步提高喷射器的热力学完善度。
-
本文通过实验与数值分析相结合的方法，研究等截面比和非等截面比情况下带圆柱形和锥−柱形混合室喷射器在不同喷嘴距的综合性能差异，得到结论主要包括：
（1）等截面比下，与最佳喷嘴距的圆柱形混合室喷射器临界性能相比，锥−柱形混合室喷射器在合适的喷嘴距范围内可同时获得更优的临界喷射系数和临界冷凝压力；减小锥−柱形混合室喷射器截面比，该喷嘴距范围扩大。上述现象原因是锥−柱形混合室减小混合流的动量损失和增大二次蒸气在混合室喉部的有效横截面积；降低锥−柱形混合室截面比后，锥−柱形混合室内混合蒸气激波链长度更长，进一步增强了喷射器对后端背压压缩的抵抗能力，同时还增加了二次蒸气在相等有效横截面积的流动距离。
（2）等截面比下，锥−柱形混合室喷射器的热力学完善度比圆柱形混合室喷射器的热力学完善度更高；降低锥−柱形混合室喷射器截面比，可进一步提高喷射器的热力学完善度。原因是锥−柱形混合室可有效避免流体在混合阶段不可逆损失的急剧增加，减小锥−柱形混合室截面比则进一步减小了喷射器熵产率。
（3）与圆柱形混合室喷射器相比，锥−柱形混合室喷射器可通过调整其喷嘴距或恰当地降低截面比，以提高喷射器的热力学完善度，实现喷射器临界性能的多目标优化。
基于喷嘴距可调的锥−柱形与圆柱形混合室喷射器性能对比分析
Comparative Analysis of the Performance for Nozzle Exit Position Adjustable Conical-Cylindrical and Cylindrical Mixing Chamber Ejectors
-
摘要: 合理选择混合室结构是提高蒸气喷射器系统性能的重要途径。在喷嘴距和截面比可调的情况下研究了锥−柱形与圆柱形混合室喷射器的临界性能差异，并通过引入热力学完善度和熵产率模型，对这两种喷射器进行全面对比。结果表明：与圆柱形混合室喷射器在最佳喷嘴距处的情况相比，在等截面比下，锥−柱形混合室喷射器在一个合适的喷嘴距范围可获得更佳的临界喷射系数和临界冷凝压力（即实现多目标优化），其原因是采用锥−柱形混合室可减小混合流的动量损失和增大二次蒸气在混合室内的有效流通截面积，而恰当地减小锥−柱形混合室截面比时，该喷嘴距范围扩大；此外，在实验喷嘴距范围内，锥−柱形混合室喷射器的热力学完善度更具优势；降低锥−柱形混合室截面比时，可在一定的喷嘴距范围内进一步提高锥−柱形混合室喷射器的热力学完善度优势，其热力学原因是喷射器内部熵产率进一步降低。研究结果为可变几何结构喷射器临界性能的多目标优化提供新的参考思路。Abstract: The rational choice of mixing chamber structure is important to improve the performance of vapor ejector systems. The critical performance differences between conical-cylindrical mixing chamber and cylindrical mixing chamber ejectors were investigated with a nozzle exit position (NXP) and area ratio (Ar) adjustable ejector, and a comprehensive comparison of the two types of ejectors was made by introducing thermodynamic perfection and entropy generation rate models. The results demonstrated that compared with the performance of the cylindrical mixing chamber ejector (CME) at the optimal nozzle exit position, the equal area ratio conical-cylindrical mixing chamber ejector (CCME) exists a NXP range where both the critical entrainment ratio and critical condensing pressure are larger (i.e., multi-objective optimization is achieved). The mechanism of this phenomenon is the use of CCM can reduce the momentum loss of the mixed flow and increase the effective flow cross-sectional area of the secondary vapor. The NXP range can be widened by appropriately reducing the Ar of the CCME. Besides, the thermodynamic perfection of the CCME is more advantageous in the range of the experimental NXP than CME. When reducing the Ar of the CCME, the thermodynamic perfection of the CCME can be further improved within a certain range of NXP, and the thermodynamic reason is that the entropy production rate inside the CCME is further reduced. The results provide a new idea for the multi-objective optimization of the critical performance for variable geometry ejectors.
-
-
图 1 喷射器。 （a）柱形混合室，（b）锥−柱形混合室
Figure 1. Structure of ejectors. (a) Cylindrical mixing chambers, (b) conical-cylindrical mixing chambers
图 3 实验装置。（a）实验现场，（b）喷嘴及混合-扩压室，（c）可调式喷射器，（d）喷射器主体，（e）螺纹结构
Figure 3. Diagram of experimental device. (a) Experimental site, (b) nozzle and Mixing-diffuser, (c) adjustable ejector, (d) ejector body, (e) screw thread structure
图 4 实验用主喷嘴和三个喷射器的几何尺寸
Figure 4. Geometry of the primary nozzle and the three experimental ejectors
图 8 三种喷射器的热力学完善度变化
Figure 8. Variation of thermodynamic perfection of the threeejectors with NXP
图 9 CM.1和CCM.1喷射器速度云图和涡流分布
Figure 9. Velocity cloud image and vortex distribution of CM.1 and CCM.1
图 11 CM.1和CCM.1喷射器的熵产率随喷嘴距的变化
Figure 11. Change of the entropy production rates for CM.1 and CCM.1 with NXP
图 12 CM.1和CCM.1熵产率分布
Figure 12. Distribution of the entropy production rates for CM.1 and CCM.1
图 13 CM.1和CCM.2速度云图和涡流分布
Figure 13. Velocity cloud image and vortex distribution of CM.1 and CCM.2
图 16 CM.1和CCM.2熵产率分布
Figure 16. Distribution of the entropy production rate for CM.1 and CCM.2
表 1 温度和压力测量传感器规格
Table 1. Specifications of measuring pressure and temperature transducers
传感器 测量参数 型号 精度 量程 压力传感器 发生器压力 MIK-P3000-C 0.075%FS 0~350 kPa （PABS） 蒸发器压力 MIK-P3000-C 0.075%FS 0~100 kPa （PABS） 排出压力 MIK-P3000-C 0.075%FS 0~100 kPa （PABS） 冷凝器压力 MIK-P3000-C 0.075%FS 0~100 kPa （PABS） 温度传感器 发生器温度 CWQ-315 PT100 0.25%FS 0~150℃ 蒸发器温度 CWQ-315 PT100 0.25%FS 0~100℃ 冷凝器温度 CWQ-315 PT100 0.25%FS 0~100℃ 
下载: 导出CSV
表 2 网格独立性检验
Table 2. Grid independence test
网格数 模拟值 实验值 误差% 40356 0.335 0.289 15.91 81612 0.330 0.289 14.18 139744 0.338 0.289 16.95 196532 0.335 0.289 15.91
下载: 导出CSV
表 3 实验和模拟结果的对比
Table 3. Comparison of experimental and simulation results
名称 NXP/mm 临界喷射系数 临界冷凝压力 实验 模拟 误差% 实验 模拟 误差% CM.1 27 0.275 0.230 −16.36 3.92 3.50 −10.71 40 0.280 0.241 −13.93 4.09 3.41 −16.63 48 0.289 0.333 15.22 4.17 3.30 −20.86 CCM.1 83.5 0.430 0.398 −7.44 4.07 3.25 −20.15 98.5 0.427 0.428 0.23 3.80 3.15 −17.11 112 0.396 0.395 −0.25 3.51 3.10 −11.68 CCM.2 78 0.302 0.316 4.64 5.12 4.70 −8.20 93.5 0.325 0.309 −4.92 4.41 4.40 −0.23 98.00 0.310 0.30 −2.58 4.17 4.15 −0.48
下载: 导出CSV
-
[1] Tashtoush B M, Al-Nimr M A, Khasawneh M A, et al. A comprehensive review of ejector design, performance, and applications[J]. Applied Energy,2019,240:138−172 doi: 10.1016/j.apenergy.2019.01.185 [2] Eames W I. A new prescription for the design of supersonic jet-pumps: the constant rate of momentum change method[J]. Applied Thermal Engineering,2002,22(2):121−131 doi: 10.1016/S1359-4311(01)00079-5 [3] Kitrattana B, Aphornratana S, Thongtip T. Investigation on improvement potential of steam ejector performance in refrigeration cycle via constant rate of momentum change design method[J]. Applied Thermal Engineering,2023,231:120953 doi: 10.1016/j.applthermaleng.2023.120953 [4] He S, Li Y, Wang R Z. Progress of mathematical modeling on ejectors[J]. Renewable and Sustainable Energy Reviews,2009,13(8):1760−1780 doi: 10.1016/j.rser.2008.09.032 [5] Sokolo E, Zinger H M. Ejector[M]. Beijing: science press, 1977: 280 [6] Keenan J H, Neumann E P, Lustwerk F. An investigation of ejector design byanalysis and experiment[J]. Journal of Applied Mechanics,1950,17:299−309 doi: 10.1115/1.4010131 [7] Yapıcı R, Ersoy H. Performance characteristics of the ejector refrigeration system based on the constant area ejector flow model[J]. Energy Conversion and Management,2005,46(18-19):3117−3135 doi: 10.1016/j.enconman.2005.01.010 [8] Petrenko V O, Huang B J, Shestopalov K O, et al. An advanced solar-assisted cascade ejector cooling/CO2 sub-critical mechanical compression refrigeration system[C]. The proceedings of the ISES Solar World Congress, 2011 [9] Shestopalov K O, Huang B J, Petrenko V O, et al. Investigation of an experimental ejector refrigeration machine operating with refrigerant R245fa at design and off-design working conditions. Part 1. Theoretical analysis[J]. International Journal of Refrigeration,2015,55:201−211 doi: 10.1016/j.ijrefrig.2015.01.016 [10] Shestopalov K O, Huang B J, Petrenko V O, et al. Investigation of an experimental ejector refrigeration machine operating with refrigerant R245fa at design and off-design working conditions. Part 2. Theoretical and experimental results[J]. International Journal of Refrigeration,2015,55:212−223 doi: 10.1016/j.ijrefrig.2015.02.004 [11] Del Valle J G, Jabardo J M S, Ruiz F C, et al. An experimental investigation of a R-134a ejector refrigeration system[J]. International Journal of Refrigeration,2014,46:105−113 doi: 10.1016/j.ijrefrig.2014.05.028 [12] 陈洪杰, 卢苇, 曹聪, 等. 圆柱形及圆锥形混合室气体喷射器的适用参数区探讨[J]. 化工学报,2013,64(6):2043−2049 (in Chinese) Chen H J, Lu W, Cao C, et al. Discussion on the applicable parameters of gas ejectors in cylindrical and Conical mixing chamber[J]. CIESC Journal,2013,64(6):2043−2049 [13] Tashtoush B, Alshare A, Al-Rifai S. Performance study of ejector cooling cycle at critical mode under superheated primary flow[J]. Energy Conversion and Management,2015,94:300−310 doi: 10.1016/j.enconman.2015.01.039 [14] Sierra-Pallares J, Valle J G D, Carrascal P G, et al. A computational study about the types of entropy generation in three different R134a ejector mixing chambers[J]. International Journal of Refrigeration,2016,63:199−213 doi: 10.1016/j.ijrefrig.2015.11.007 [15] 季建刚, 倪海, 黎立新, 等. 蒸汽喷射压缩器的变工况特性模拟与分析[J]. 化工学报,2008,59(3):557−561 (in Chinese) doi: 10.3321/j.issn:0438-1157.2008.03.004 Ji J G, Ni H, Li L X, et al. Simulation and analysis of steam jet compressor under variable operating conditions[J]. CIESC Journal,2008,59(3):557−561 doi: 10.3321/j.issn:0438-1157.2008.03.004 [16] 谭丽萍, 陈洪杰, 葛敬, 等. 喷嘴距及混合室喉部长度对喷射器性能综合影响研究[J]. 真空科学与技术学报,2024,44(2):156−166 (in Chinese) Tan L P, Chen H J, Ge J, et al. Numerical analysis of flow parameters and performance of steam ejector[J]. Chinese Journal Vacuum Science and Technology,2024,44(2):156−166 [17] 邵天, 杜亚威, 刘燕, 等. 蒸汽喷射器的三维数值模拟研究[J]. 真空科学与技术学报,2014,34(3):305−311 (in Chinese) Shao T, Du Y W, Liu Y, et al. Three-dimensional numerical simulation of steam ejector[J]. Chinese Journal Vacuum Science and Technology,2014,34(3):305−311 [18] Nguyen V V, Varga S, Soares J, et al. Applying a variable geometry ejector in a solar ejector refrigeration system[J]. International Journal of Refrigeration,2020,113:187−195 doi: 10.1016/j.ijrefrig.2020.01.018 [19] Wang L, Liu J, Zou T, et al. Auto-tuning ejector for refrigeration system[J]. Energy,2018,161(15):536−543 [20] Ge J, Chen H J, Jin Y, et al. Conical-cylindrical mixer ejector design model for predicting optimal nozzle exit position[J]. Energy,2023,283:129190 doi: 10.1016/j.energy.2023.129190 [21] Shahzamanian B, Varga S, Soares J, et al. Performance evaluation of a variable geometry ejector applied in a multi-effect thermal vapor compression desalination system[J]. Applied Thermal Engineering,2021,195:117177 doi: 10.1016/j.applthermaleng.2021.117177 [22] Zhang J, Zhai X, Li S. Numerical studies on the performance of ammonia ejectors used in ocean thermal energy conversion system[J]. Renewable Energy,2020,161:766−776 doi: 10.1016/j.renene.2020.07.025 [23] Ge J, Chen H J, Li J, et al. Experimental comparison of critical performance for variable geometry ejectors with different mixer structures[J]. Chemical Engineering Journal,2023,478:147487 doi: 10.1016/j.cej.2023.147487 [24] Chen H J, Zhu J H, Ge J, et al. A cylindrical mixing chamber ejector analysis model to predict the optimal nozzle exit position[J]. Energy,2020,208:118302 doi: 10.1016/j.energy.2020.118302 [25] Besagni G, Cristiani N, Croci L, et al. Computational fluid-dynamics modelling of supersonic ejectors: screening of modelling approaches, comprehensive validation and assessment of ejector component efficiencies[J]. Applied Thermal Engineering,2020,186:116431 [26] 秦汉时, 方凯跃, 高洪辉, 等. 基于正交试验的蒸汽喷射器喷嘴结构优化[J]. 真空科学与技术学报,2024,7(44):612−618 (in Chinese) Qin H S, Fang K Y, Gao H H, et al. Optimization of steam ejector nozzle structure based on orthogonal test[J]. Chinese Journal Vacuum Science and Technology,2024,7(44):612−618 [27] ANSYS Inc. Ansys-fluent 18.0 user's guide[M]. Canonsburg, PA: ANSYS Inc., 2018 [28] Herwig H, Kock F. Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problems[J]. Heat and Mass Transfer,2007,43(3):207−215 [29] Sciacovelli A, Verda V, Sciubba E. Entropy generation analysis as a design tool—A review[J]. Renewable and Sustainable Energy Reviews,2015,43:1167−1181 doi: 10.1016/j.rser.2014.11.104 [30] Kock F, Herwig H. Local entropy production in turbulent shear flows: a high-Reynolds number model with wall functions[J]. International Journal of Heat and Mass Transfer,2004,47:2205−2215 doi: 10.1016/j.ijheatmasstransfer.2003.11.025 [31] 张文辉, 李奇. 天然气引射器内部熵产分析[J]. 过程工程学报,2023,23(6):870−879 (in Chinese) Zhang W H, Li Q. Analysis of entropy generation in natural gas ejector[J]. The Chinese Journal of Process Engineering,2023,23(6):870−879 [32] Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal,1994,32(8):1598−1605 doi: 10.2514/3.12149 [33] Lamberts O, Chatelain P, Bartosiewicz Y. Numerical and experimental evidence of the Fabri-choking in a supersonic ejector[J]. International Journal of Heat and Fluid Flow,2018,69:194−209 doi: 10.1016/j.ijheatfluidflow.2018.01.002 [34] Bumrungthaichaichan E, Ruangtrakoon N, Thongtip T. Performance investigation for CRMC and CPM ejectors applied in refrigeration under equivalent ejector geometry by CFD simulation[J]. Energy Reports,2022,8:12598−12617 doi: 10.1016/j.egyr.2022.09.042 [35] Ruangtrakoon N, Thongtip T, Aphornratana S, et al. CFD simulation on the effect of primary nozzle geometries for a steam ejector in refrigeration cycle[J]. International Journal of Thermal Sciences,2013,63:133−145 doi: 10.1016/j.ijthermalsci.2012.07.009 [36] Bumrungthaichaichan E. How can the appropriate near-wall grid size for gas cyclone CFD simulation be estimated[J]. Powder Technology,2022,396:327−344 doi: 10.1016/j.powtec.2021.10.031 [37] Tang Y Z, Liu Z L, Li Y X, et al. Study on fundamental link between mixing efficiency and entrainment performance of a steam ejector[J]. Energy,2021,215:119128 doi: 10.1016/j.energy.2020.119128 [38] Kundu P K, Cohen I M, David D R. Fluid mechanics (sixth edition)[M]. San Diego: academic press, 2015 [39] Poirier M. Influence of operating conditions on the optimal nozzle exit position for vapor ejector[J]. Applied Thermal Engineering,2022,210:118377 doi: 10.1016/j.applthermaleng.2022.118377 [40] Wang K, Wang L, Jia L, et al. Optimization design of steam ejector primary nozzle for MED-TVC desalination system[J]. Desalination,2019,471:114070 doi: 10.1016/j.desal.2019.07.010 [41] Thongtip T, Aphornratana S. Development and performance of a heat driven R141b ejector air conditioner: Application in hot climate country[J]. Energy,2018,160:556−572 doi: 10.1016/j.energy.2018.07.043 [42] Ariafar K, Buttsworth D, Al-Doori G, et al. Effect of mixing on the performance of wet steam ejectors[J]. Energy,2015,93:2030−2041 doi: 10.1016/j.energy.2015.10.082 [43] Ariafar K, Buttsworth D, Al-Doori G, et al. Mixing layer effects on the entrainment ratio in steam ejectors through ideal gas computational simulations[J]. Energy,2016,95:380−392 doi: 10.1016/j.energy.2015.12.027 [44] Chen H, Ge J, Xu Z. A study on the evolution laws of entrainment performances using different mixer structures of ejectors[J]. Entropy,2024,26:891 doi: 10.3390/e26110891 -
图( 16) 表( 3)
计量
- 文章访问数: 27
- HTML全文浏览数: 27
- PDF下载数: 0
- 施引文献: 0