首页
登录
注册
-
泡沫金属多孔材料的很多应用都要用到其内部孔隙的表面，如用于换热器、散热器、催化反应器、高效电极基体、消音降噪装置、电化学过程和人工骨骼组织工程等[1-2]。此时产品比表面积的大小对其使用性能具有重要的作用，该项指标由此成为整个多孔部件的一个关键参量。此外，泡沫金属的比表面积对于其在吸附、过滤、分离等技术领域的应用也有很大的影响[3]。
获悉多孔材料的比表面积对研究多孔制品的表面活性、界面作用、表面吸附、过程催化、力学性能等都具有重要意义[4]。例如，在用作催化剂载体时，多孔制品较高的比表面积即有利于提高活性金属的负载量，有利于界面反应和传质扩散等[5]。再如，热交换器的散热效率取决于热传输面积、热传输系数和流阻特性等[6]。泡沫金属在比表面积大、导热性高和热传输性能佳等方面占有优势。
因其较大的表面积和优越的热动力性能，以及良好的流体透过性能，开口多孔材料非常适合于热控制的用途[7]。热传导与比表面积有着密切的关系，较大的体积比表面积将有利于热传输过程[8-9]。泡沫金属的比表面积在热对流和热辐射过程中发挥着重要的作用，而有效热导率则反映了其热传导能力。因此，精确地估算其比表面积和有效热导率，是研究泡沫金属热传输增强机制的重要前提[10]。
由于测量条件和材料取样等限制，往往可能遇到对多孔产品比表面积难以甚至无法进行实际测量的情况。因此，利用易知易测的指标来间接求算出产品的比表面积，就显示出良好的实践意义。前面作者提出了一个通过孔隙率和孔径来计算多孔材料比表面积的普适化公式[11-12]，本文即对该计算公式展开系列泡沫金属及相关多孔产品的实践应用和验证，研究涉及不同材质和不同结构的多孔结构产品。
-
从本文作者提出的多孔材料八面体结构模型出发，结合相应的数学处理，得到了关于多孔材料比表面积的模型表征计算公式[11-12]：
式中Sv为多孔体的体积比表面积，d和θ分别为多孔体的孔径和孔隙率，Ks为多孔体的材料常数或产品常数，n为表征孔隙结构形态的几何因子。其中方括号内的孔隙率“θ”参量应优先代入多孔体的开孔率，但在开孔率未知且闭孔率不大的情况下也可直接代入总孔率而进行近似计算；最后一项孔隙率“θ”参量则本身就是平时说的产品孔隙率，即总孔率。
本计算公式的提出，开创了采用孔隙率和孔径这两个基本参量，通过一般化数理关系表达而有效计算多孔材料比表面积的新途径。其中由本文作者当时提出的修正项“(1−θ)n”，更是本计算公式得以成功的关键[11-12]。此处表征孔隙几何因素的n，与多孔产品内部的具体结构方式有关，故亦为取决于材质种类和制备工艺的材料常数。
-
模型表征公式的普适性需要不同工艺方法制造的不同材质和不同结构多孔产品来验证。为了考察该计算公式的普适性，作者查阅了国内外其他研究者发表的相关研究工作，发现了多组关于泡沫金属比表面积的数据，可用于本模型表征公式的实践应用和验证。
-
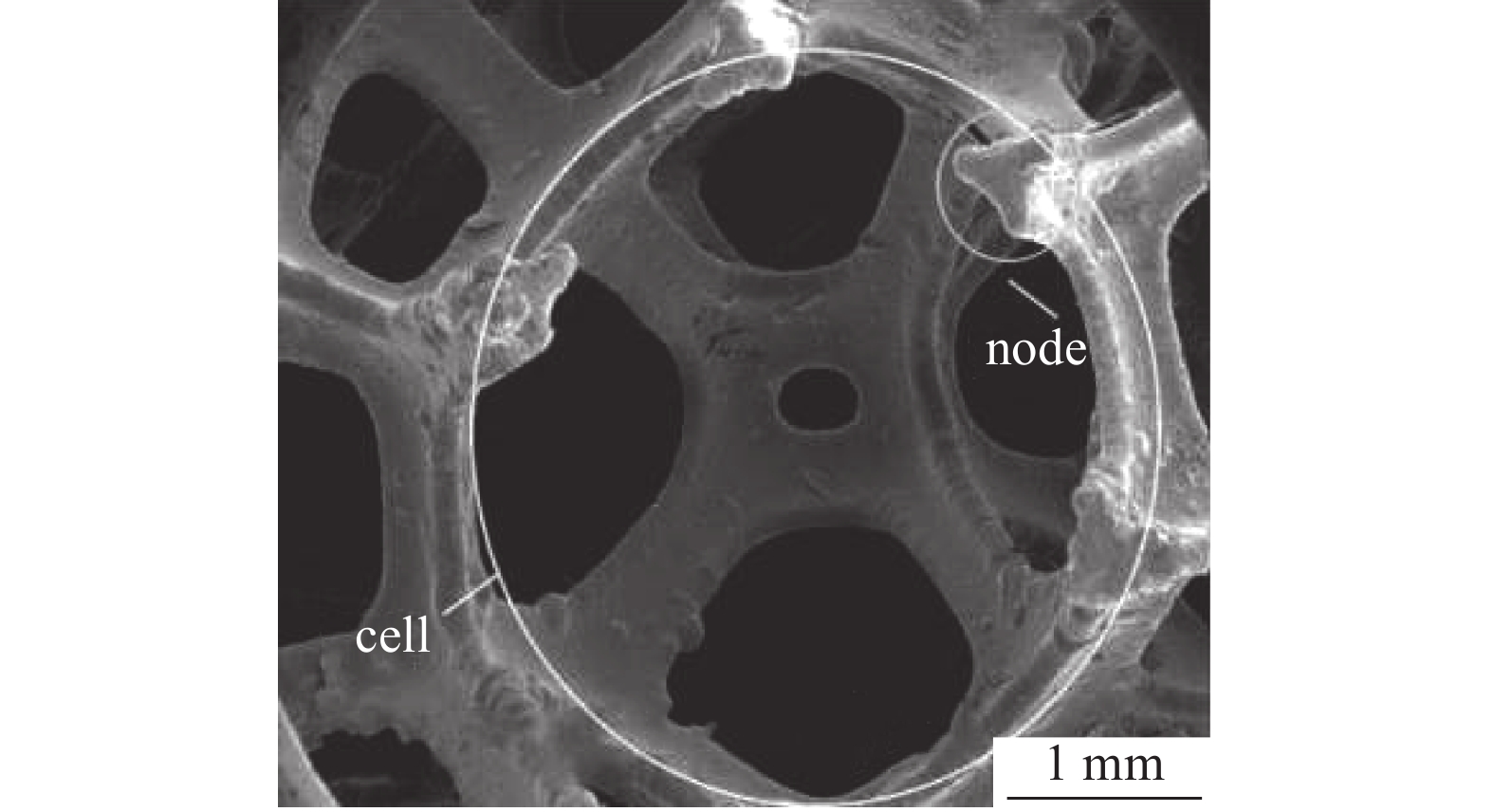
首先考察一种电沉积工艺制备的多孔Cu/Ni复合材料[3]：以聚氨酯泡沫为基体涂覆石墨导电胶，镀铜后镀镍，如此重复得到不同镀层厚度的样品；烧结并除去有机基体，即得网状Cu/Ni复合材料。产品的结构形态参见图1，总体上属于随机型孔隙结构的多孔产品。样品结构参数的测算结果见表1，每个数据点均由3个样品测量获得。
-
将测量计算得到的样品孔隙率θ、平均孔径d和比表面积Sv0值对式（1）进行拟合，求得Ks = 753.1和n = –0.2267，即有[3]：
根据上式计算该多孔产品的比表面积，所得计算值列于表2中。
由表2中比表面积的对应数据可看出，本多孔Cu/Ni复合材料的比表面积和本模型表征公式的计算结果有较高的吻合度。两者的相对偏差平均偏差小于1%，在0.6%左右。这说明本计算公式取得了很大成功。
-
本部分考察的是采用电沉积工艺制备的泡沫铜，高温烧结而成，呈近十四面体孔隙结构（图2）[13]。制品孔隙率在91.5% ~ 96.5%之间，孔径为1.1~2.4 mm。有关测算参量见表3。
-
将式（1）应用于该泡沫铜制品。数据拟合结果表明，公式的几何因子取n ≈ −0.515时，可获得最稳定的对应Ks值：对应的平均值为Ks ≈ 463.15。将n = −0.515和Ks = 463.15代入式（1），得
根据上式计算该多孔产品的比表面积，所得计算值列于表4中。
由表4中多孔产品比表面积的对应数据对照可以看出，本模型公式计算结果与源于文献的对应值取得了良好的一致性。计算值和源文献值的平均偏差小于2%，在1.2%左右。这又一次说明本模型公式取得成功，强化地证明了本模型公式对网状泡沫金属可以获得令人满意的实践计算效果。
从前期计算工作对电沉积工艺生产泡沫镍的实践成功[11-12]，到上一部分对多孔Cu/Ni复合材料的应用成功，再到本部分对本泡沫铜的应用成功，比较可靠地验证了本模型表征公式在网状泡沫金属产品市场的实用性。
-
本部分考察的是采用高压渗流法制备的泡沫铝[14]：将易燃球形载体做成预制块，通过高压作用在预制块中高速渗流ZL104铝合金熔体；冷却凝固后烧除黏结料和可燃载体，得到孔隙贯通的泡沫铝。制品总体上亦为随机型孔隙结构（见图3），孔隙率在73.0%~85.8%之间，孔径为2.66~2.85 mm。测算参量见表5。
-
将式（1）应用于该泡沫铝制品。数据拟合结果表明：公式的几何因子取n ≈ +0.4时，可获得非常稳定的对应Ks值，对平均值的相对波动只在−0.5% ~ +0.6%之间，对应的平均值为Ks ≈ 2.818 [11-12]。将n = +0.4和Ks = 2.818代入式（1），得
根据上式计算该多孔产品的比表面积，所得计算值列于表6中。
由表6中多孔产品比表面积的对应数据对照可以看出，本模型公式计算结果与源文献对应数据取得了很好的一致性。计算值和源文献值的平均偏差甚至小于0.5%，在0.35%左右。这再次说明本模型公式可以获得很好的实践效果，体现出对多孔材料比表面积计算的可靠性。
-
文献[6]研究了一种近十四面体孔隙结构的泡沫金属，其产品形态见图4，亦为三维网状结构。其考虑的孔隙率范围在95% ~ 98%之间，对应孔径范围为2.5~10.5 mm之间。该文献测算得出的结构参量见表7。
-
将式（1）应用于该泡沫铜制品。数据拟合结果表明，公式的几何因子取n ≈ 0时，可获得最稳定的对应Ks值：对应的平均值为Ks ≈ 148.29。将n = 0和Ks = 148.29代入式（1），得
根据上式计算该多孔产品的比表面积，所得计算值列于表8中。
由表8中多孔产品比表面积的对应数据对照可以看出，本模型公式计算结果与源于文献的对应值取得了良好的一致性。计算值和文献值的平均偏差小于2%，在1%左右。可见本模型公式的计算继续取得成功。
-
碳元素属于非金属元素，但石墨与金属一样具有良好的导电性，因此也将多孔石墨材料一并考察。研究表明，多孔体内部的孔隙结构对其物理性能和渗透性能有重要影响，其中比表面积是表征其孔隙结构的重要参量[15]。文献[15]对系列商用多孔石墨材料进行研究，通过压汞实验检测试样的孔隙结构参量（表9）。
-
由于式（1）计算的是多孔产品的体积比表面积，因此在应用式（1）之前，要将表9的质量比表面积进行换算。根据推演，得出如下换算关系：
式中Sv为多孔体的体积比表面积（cm2/cm3或m2/cm3），ρs为石墨骨架本身的体密度（g/cm3），θ为多孔体的孔隙率，Sm为多孔体的质量比表面积（cm2/g或m2/g）。
通过式（6）换算得到的对应体积比表面积列于表10，然后将式（1）应用于该多孔石墨过滤材料。数据拟合结果表明，公式的几何因子取n ≈ −0.4时，可获得最稳定的对应Ks值：对应的平均值为Ks ≈ 7.588。将n = −0.4和Ks = 7.588代入式（1），得
根据上式计算该多孔产品的比表面积，所得计算值一并列于表10中。
由表10中多孔产品比表面积的对应数据对照可以看出，本模型公式计算结果与源于文献的对应值取得了良好的一致性。计算值和源文献值的平均偏差小于5%，在2.8%左右。这说明本模型公式对非金属材质的多孔制品仍可获得良好的实践计算效果。
-
从式（1）的应用情况可以看到，本计算公式具有较强的适应性：它可很好地适用于随机型孔隙结构的多孔产品[3,11,12,14,15]，也可很好地适用于近十四面体孔隙结构的特类多孔产品[6,13]；既成功地适合了电沉积工艺制备的泡沫金属[3,11-13]，也很好地符合渗流铸造工艺所得泡沫金属[14]；既成功地应用于金属多孔材料[3,6,11-14]，也成功地应用于非金属多孔材料[15]。不同材质通过不同工艺制得的多孔产品，其孔棱/孔壁的形状特征、表面特点、连结方式及内部缺陷状态等都可能大不一样。但是，本公式将这些取决于材质种类和制备工艺的具体细观结构因素，成功地纳入一个材料常数（Ks）和一个结构因子（n），使得公式的适用范围面向不同工艺、不同材质和不同的具体结构，实践证明是可行的。可见，本公式可望成为计算多孔材料比表面积的普适性数理模型，期待着更广泛的实践应用。
另外，本模型关系式的适用范围，在理论上对孔径、孔隙率、开孔率等指标并无限制，这从其推导过程可清楚看出[11]。从本文考察的几种多孔产品计算情况来看，也证实了这一点。考察对象中既有孔隙率超过90%的高孔率产品[6,13]，也有孔隙率低于45%的较低孔率产品[15]，还有孔隙率介于70%-80%之间的中间孔率产品[3,14]；涉及的孔隙尺寸既有毫米级的宏孔产品[3,6,14]，也有微米级的微孔产品[13,15]。但考虑到多孔产品比表面积的实际检测，不同方法各有优缺点，对于所能检测的孔径等指标范围也都各自有一定限制[1]。因此，对于同一样品，不同检测方法可能对比表面积得出测试结果各异，本模型关系式可能会对应地呈现不同的计算偏差。但只要选用的检测方法能够尽量逼近真值，本模型关系式就可展示良好的效果。当然，本模型关系式基于开口网状多孔材料，不适于闭孔结构，即不适于开孔率远小于闭孔率的情况。但一般只有那些利用内部孔隙界面作用的多孔产品需要考虑比表面积指标，因此实际上不会遇到闭孔结构或开孔率过低的多孔产品需要这种计算。
-
对特定结构多孔材料的推演或对某一多孔产品测试结果的模拟和总结，得出的推演关系或经验关系都难以成为一般化的普适性计算公式。而本计算公式具有一般化的意义，且以上实践应用结果证明其对于泡沫金属及相关多孔产品具有良好的普适性。其中本文作者当时提出的修正项“(1−θ)n”，更是本计算公式得以成功的关键[11-12]，成就了本公式的计算效果。
本计算公式的初步推演始于作者提出的八面体模型[11]。诚然，也可换用其他一些结构形式的孔隙单元而进行类似的推演，如Gibson-Ashby模型的立方结构孔隙单元或Kelvin模型的十四面体结构孔隙单元等，按照本文作者的思路，得出类似的计算公式。但若没有本文作者提出的修正项[(1−θ)n]，则不能得出对多孔材料比表面积实现成功计算的一般化数理表征。因此，这个修正项是解决问题的灵魂。可以推断：仅仅通过更换孔隙结构模型的方式，用类似的方法进行重复性推演，得出相似的数理关系虽在具体表达上可能略有不同，但本质上没有区别，计算效果也最多不过是微小的变化。
-
（1）运用如下计算公式可较好地估算各类泡沫金属及相关多孔产品的比表面积：
式中Sv是多孔产品的比表面积，其单位为cm2/cm3或m2/cm3；d是多孔产品的孔径，其单位为μm或mm；θ是多孔产品的开孔率（%），当开孔率未知而闭孔率不大时可直接代入总孔率以进行近似计算；Ks为多孔产品的材料常数或产品常数，其单位随Sv和d两者的单位而定（实际应用时可不必写出）；n为表征多孔产品孔隙结构形态的几何因子。
（2）本模型关系公式既可实践应用于不同工艺方法制备的泡沫金属，也可实践应用于多孔石墨材料等非金属多孔产品；既可实践应用于随机型孔隙结构的多孔材料产品，也可实践应用于特定孔隙结构的多孔材料产品。这说明本计算公式体现了较强的计算功能，具备了普适性的特点。
八面体模型理论应用：泡沫金属的比表面积
Application of the Octahedral Model Theory to Evaluating the Specific Surface Area of Porous Metal Foams
-
摘要: 基于作者从自建八面体模型出发提出的多孔材料比表面积计算公式，对系列泡沫金属及相关多孔产品进行对应的实践研究。考察不同材质和不同结构的泡沫金属产品，对该计算公式展开系列的实践应用和验证。考察对象中既有孔隙率超过90%的高孔率产品，也有孔隙率低于45%的较低孔率产品，还有孔隙率介于70%-80%的中间孔率产品；涉及的孔隙尺寸既有毫米级的宏孔产品，也有微米级的微孔产品。结果显示，本多孔材料比表面积表征公式可较好地适应所有这些多孔产品的计算，其平均计算偏差均在3%以内，多为1%左右。这说明本表征关系较好地反映了泡沫金属及相关多孔产品比表面积与孔隙率和孔径两者的关系规律，具有良好的泡沫金属及相关多孔产品比表面积计算实践能力。Abstract: Based on the equation from the octahedron model to conveniently calculate the specific surface area of porous materials, the practical investigations are correspondingly carried out on a series of metal foam products. This paper investigates more metal foam products with different material species and various structures and develops a series of practical applications and verification of the present calculation formula. Among the investigated objects, there are highly porous products with porosity exceeding 90%, lowly porous products with porosity below 45%, and intermediately porous products with porosity between 70% and 80%. The pore sizes involved include both millimeter and micrometer scales. The research results show that the characterization formula of specific surface area can adapt well to the calculation of all these porous products, with the average calculation deviation within 3%, mostly around 1%. This indicates that this characterization formula well reflects the relationship between the specific surface area and the porosity and pore diameter for metal foams and the relevant porous product, and has a good practical ability to calculate the specific surface area of metal foams and the relevant porous product.
-
Key words:
- Porous material /
- Metal foam /
- Specific surface area /
- Calculation formula /
- Octahedron model .
-
-
样品编号 沉积层厚度δ /μm 平均孔径d /μm 孔隙率θ/% 比表面积Sv0/（cm2/cm3） 1 8.7 24.5 94.8 106.5 2 16.3 24.2 93.3 109.7 3 24.2 24.0 90.3 113.3 4 33.4 23.7 88.2 116.3 5 47.1 23.5 86.1 117.9 
下载: 导出CSV
表 2 多孔Cu/Ni复合材料的比表面积计算结果[3]
Table 2. Calculation results of specific surface area of the porous Cu/Ni composite material [3]
样品
编号Sv0 /（cm2/cm3）
源于表1Sv /（cm2/cm3）
源于式（2）计算Abs（ΔSv/Sv0）
/%1 106.5 105.8 0.66 2 109.7 110.2 0.46 3 113.3 114.2 0.79 4 116.3 116.3 0.00 5 117.9 116.3 1.38 平均 0.66 注：表中Sv为产品比表面积的模型公式计算值，ΔSv = Sv−Sv0，下同。
下载: 导出CSV
表 3 泡沫铜的有关实验检测参量[13]
Table 3. Experimental values of structural parameters of the copper foam samples [13]
样品编号 孔隙率θ /% 孔隙尺寸d /mm 比表面积Sv0 /（cm2/cm3） 1 91.5 1.256 269.070 2 92.26 1.150 306.287 3 92.74 0.755 456.080 4 94.57 0.930 404.430 5 96.23 0.656 591.030 6 96.35 2.385 165.747
下载: 导出CSV
表 4 泡沫铜的比表面积计算结果
Table 4. Calculation results of specific surface area of the copper foam
样品
编号Sv0/（cm2/cm3）
源于表3Sv /（cm2/cm3）
源于式（3）计算Abs（ΔSv/Sv0）
/%1 269.070 271.085 0.75 2 306.287 302.070 1.38 3 456.080 466.142 2.21 4 404.430 399.027 1.34 5 591.030 597.617 1.11 6 165.747 165.091 0.39 平均 1.19
下载: 导出CSV
样品编号 孔隙率θ/% 孔径d/mm 比表面积Sv0/（cm2/cm3） 1 73.0 2.66 15.7 2 76.6 2.68 14.7 3 78.6 2.73 13.8 4 82.0 2.76 12.5 5 85.8 2.85 10.7
下载: 导出CSV
样品
编号Sv0/（cm2/cm3）
源于表5Sv/（cm2/cm3）
源于式（4）计算Abs（ΔSv/Sv0）
/%1 15.7 15.66 0.25 2 14.7 14.69 0.07 3 13.8 13.85 0.36 4 12.5 12.56 0.48 5 10.7 10.64 0.56 平均 0.35
下载: 导出CSV
表 7 近十四面体孔隙结构泡沫金属的有关结构参量[6]
Table 7. Relevant structural parameters of the metal foam with roughly tetrakaidecahedral cells [6]
样品编号 孔隙率θ/% 孔隙尺寸d/mm 比表面积Sv0/（m2/m3） 1 95.0 10.16 255.34 2 96.5 10.16 225.36 3 98.0 10.16 182.19 4 95.0 5.08 505.22 5 96.5 5.08 440.84 6 98.0 5.08 352.53 7 95.0 2.54 1007.74 8 96.5 2.54 878.20 9 98.0 2.54 695.52
下载: 导出CSV
表 8 泡沫铜的比表面积计算结果
Table 8. Calculation results of specific surface area of the copper foam
样品
编号Sv0/（m2/dm3）
源于表7Sv/（m2/dm3）
源于式（5）计算Abs（ΔSv/Sv0）
/%1 255.34×10−3 253.39×10−3 0.76 2 225.36×10−3 221.97×10−3 1.50 3 182.19×10−3 177.22×10−3 2.73 4 505.22×10−3 506.78×10−3 0.31 5 440.84×10−3 443.95×10−3 0.70 6 352.53×10−3 354.44×10−3 0.54 7 1007.74×10−3 1013.56×10−3 0.58 8 878.20×10−3 887.90×10−3 1.10 9 695.52×10−3 708.89×10−3 1.92 平均 1.13
下载: 导出CSV
表 9 多孔石墨过滤材料的孔隙结构参量[15]
Table 9. Pore structure parameters of the porous graphite filter material [15]
样品编号 平均孔隙率θ/% 平均孔径d/μm 骨架密度ρs/（g/cm3） 质量比表面积Sm/（m2/g） 1 03.92 0.0299 2.4372 2.169 2 10.95 0.0622 1.9989 3.607 3 16.26 0.0855 1.9920 4.523 4 39.38 0.4041 1.9812 3.354
下载: 导出CSV
表 10 多孔石墨过滤材料的比表面积计算结果
Table 10. Calculation results of specific surface area of the porous graphite filter material
下载: 导出CSV
-
[1] Liu P S, Chen G F. Porous Materials: Processing and applications [M]. Boston: Elsevier Science, 2014 [2] 刘培生, 夏凤金, 程伟. 多孔材料性能模型研究2: 实验验证[J]. 材料工程,2019,47(7):35−49 (in Chinese) doi: 10.11868/j.issn.1001-4381.2018.001411 Liu P S, Xia F J, Cheng W. Study on property model for porous materials 2: experimental verification[J]. Journal of Materials Engineering,2019,47(7):35−49 doi: 10.11868/j.issn.1001-4381.2018.001411 [3] 杨碧莲, 李星吾, 阮莹, 等. 多孔Cu/Ni复合材料的电沉积法制备及其性能[J]. 稀有金属材料与工程,2019,48(10):3215−3220 (in Chinese) Yang B L, Li X W, Ruan Y, et al. Electrodeposition processing of porous Cu/Ni composites and their performance[J]. Rare Metal Materials and Engineering,2019,48(10):3215−3220 [4] 陈金妹, 谈萍, 王建永. 气体吸附法表征多孔材料的比表面积及孔结构[J]. 粉末冶金工业,2011,21(2):45−49 (in Chinese) doi: 10.3969/j.issn.1006-6543.2011.02.010 Chen J M, Tan P, Wang J Y. Characterization of pore structure and specific surface area based on gas adsorption applied for porous materials[J]. Powder Metallurgy Industry,2011,21(2):45−49 doi: 10.3969/j.issn.1006-6543.2011.02.010 [5] 韦良, 赵燕熹, 向勇, 等. 大孔径高比表面积介孔硅泡沫的制备和表征[J]. 武汉理工大学学报,2013,35(6):34−38 (in Chinese) doi: 10.3963/j.issn.1671-4431.2013.06.007 Wei L, Zhao Y X, Xiang Y, et al. Preparation and characterization of mesocellar silica foam with large pore size and high surface area[J]. Journal of Wuhan University of Technology,2013,35(6):34−38 doi: 10.3963/j.issn.1671-4431.2013.06.007 [6] Shen H M, Liu C, Yang L H, et al. Pore-scale numerical investigation on comprehensive heat transfer performance of homogeneous and graded metal foam heat sinks[J]. Thermal Science,2024,28(2B):1529−1544 [7] Baloyo J M. Open-cell porous metals for thermal management applications: fluid flow and heat transfer[J]. Materials Science and Technology,2017,33(3):265−276 doi: 10.1080/02670836.2016.1180795 [8] Zhu F, Hu X S, Wang X C, et al. Experimental and numerical investigation of the melting process of aluminum foam/paraffin composite with low porosity[J]. Numerical Heat Transfer, Part A: applications,2020,77(12):998−1013 doi: 10.1080/10407782.2020.1747289 [9] Jiang C P, Chen F L, Yan P, et al. Prediction of effective stagnant thermal conductivities of porous materials at high temperature by the generalized self-consistent method[J]. Philosophical Magazine,2012,92(16):2032−2047 doi: 10.1080/14786435.2012.661888 [10] Shen H M, Ye Q, Meng G X. The simplified analytical models for evaluating the heat transfer performance of high-porosity metal foams[J]. Int J Thermophys,2018,39:87−101 doi: 10.1007/s10765-018-2405-0 [11] 刘培生. 多孔金属比表面积的计算方法[J]. 材料研究学报,2009,23(4):415−420 (in Chinese) doi: 10.3321/j.issn:1005-3093.2009.04.015 Liu P S. Calculation method for the specific surface area of porous metals[J]. Chinese Journal of Materials Research,2009,23(4):415−420 doi: 10.3321/j.issn:1005-3093.2009.04.015 [12] Liu P S. A new method for calculating the specific surface area of porous metal foams[J]. Philosophical Magazine Letters,2010,90(6):447−453 doi: 10.1080/09500831003745571 [13] Chen J, Zhang X, Li C, et al. Calculation method of specific surface area of foam metal based on an ideal tetradecahedron model for lithium ion battery[J]. International Journal of Photoenergy,2020,1(1):Article ID 2478579. [14] 马立群, 何德坪. 新型泡沫铝的制备及其孔结构的控制[J]. 材料研究学报,1994,8(1):10−17 (in Chinese) Ma L Q, He D P. Fabrication and pore structure control of new type aluminium foams[J]. Chinese Journal of Materials Research,1994,8(1):10−17 [15] 王启立, 胡亚非, 何敏, 等. 石墨多孔介质孔隙度与比表面积的分形描述[J]. 煤炭学报,2010,35(10):1725−1729 (in Chinese) Wang Q L, Hu Y F, He M, et al. Fractal description of porosity and specific surface area for porous media of graphite[J]. Journal of China Coal Society,2010,35(10):1725−1729 -
图( 4) 表( 10)
计量
- 文章访问数: 45
- HTML全文浏览数: 45
- PDF下载数: 0
- 施引文献: 0