-
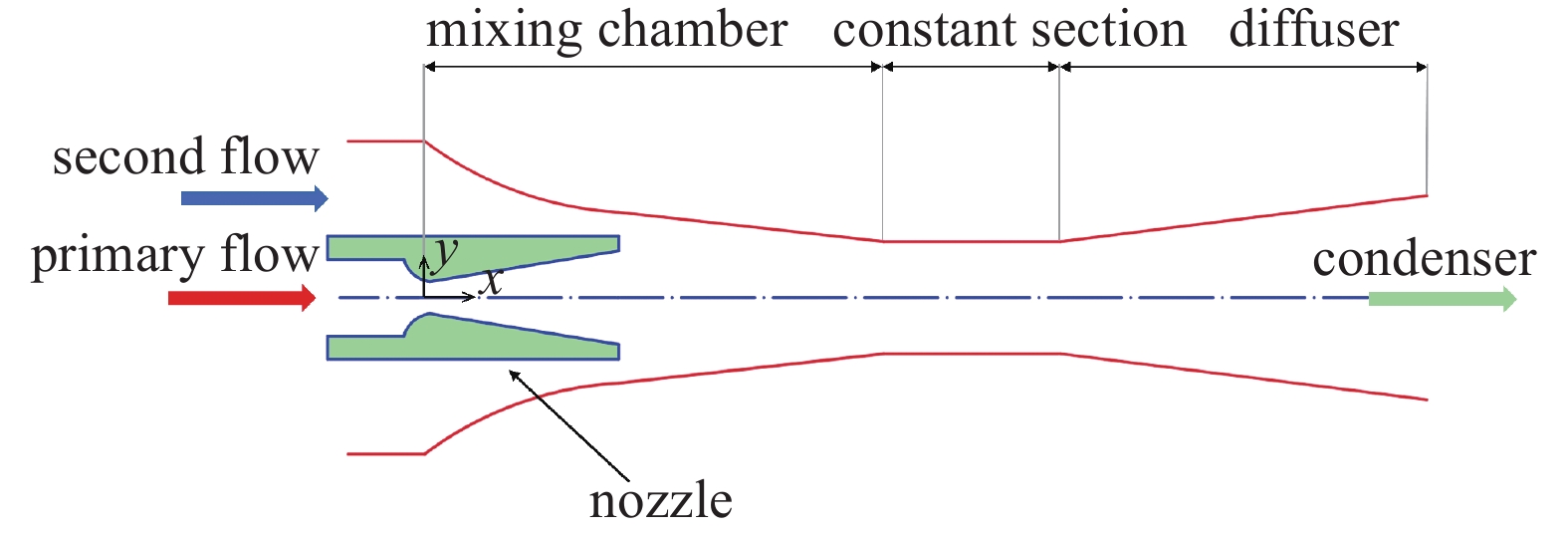
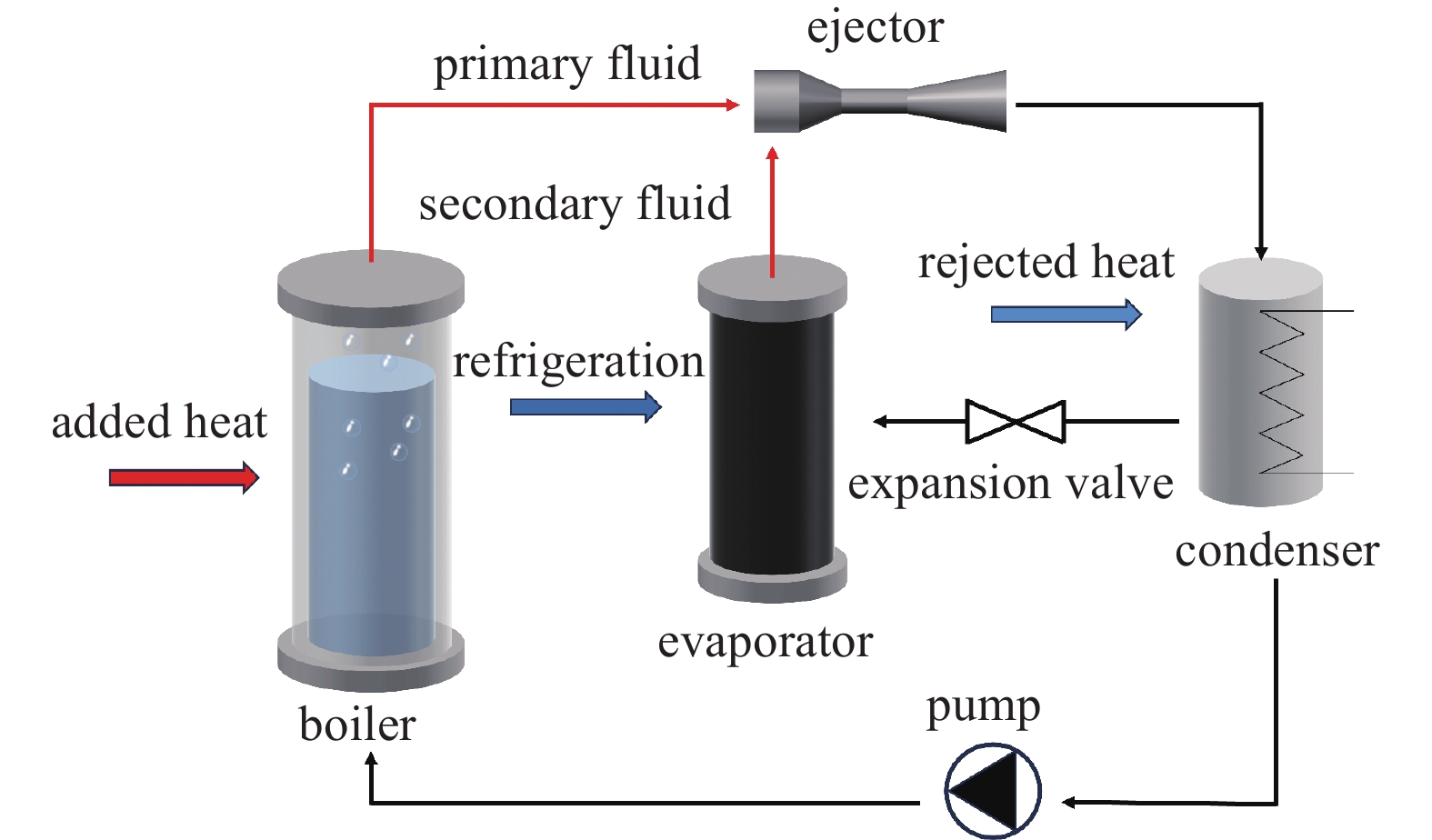
蒸汽喷射器制冷系统(ERS)作为一种以热力驱动的制冷方式,已成为传统电力制冷技术的有力替代方案。ERS具有较高的可靠性和较低的维护需求,由于其无活动部件的结构设计,使得运行更加稳定,从而在全生命周期内展现出良好的经济性和稳定性[1]。此外,ERS可充分利用低品位热源(如太阳能[2]以及工业废热[3]),能源成本优势尤为突出。更重要的是,ERS能够显著减少温室气体排放,这得益于其节能效果和对环境无害的水或者环保制冷剂的使用[4]。相关原理图如图1所示。这些优势使ERS在节能减排和可持续发展领域中具有广阔的应用前景。
喷射器作为ERS中的关键角色,系统的整体效率极大地依赖于喷射器的表现。喷射系数常用来表征蒸汽喷射器的性能,其定义为二次流与一次流质量流量的比值,表明一次流对二次流的夹带能力。多年来,学者们已经开展了许多工作来研究喷射器的几何形状对其性能的影响[5-10]。Chunnanond K等[7]认为主喷嘴的几何形状对喷射器的性能有很大影响,较小喉部直径的喷射器可以提高喷射器的制冷能力。Reis L B等[10]提出了贝塞尔曲线的参数化研究,并通过调整贝塞尔曲线控制点的坐标从而改变喷射器几何形状,提高了喷射器的效率。Zhang G等[11]提出了一种改进的冷凝模型来评估蒸汽喷射器的性能并采用多目标遗传算法对主喷嘴的几何形状进行优化,结果表明,喷射系数提高27.5%。在Ahmed F等[12]的研究中,应用了人工神经网络(ANN)来评估蒸汽喷射器的性能参数。通过使用三种优化算法对ANN模型进行训练,研究发现使用ADAM优化器的模型预测效果最为准确。上诉研究需要依托大量数据支持。基于计算复杂度与时间成本的考量,研究者开始采用伴随方法来解决这一问题。
本文基于喷射系数这一性能指标,采用CFD方法对喷射器进行仿真分析。通过伴随敏感性可视化方法获取蒸汽喷射器中的敏感性区域并得出具体结构参数。单因素分析为正交实验提供合理的结构取值范围,利用L9(34)正交表结合仿真分析对喷射器进行初步优化,随后采取伴随方法进行二次优化。
-
喷射器主要由主喷嘴、混合室、等面积段以及扩散段组成,其中主喷嘴由收缩段、喉管以及主喷嘴扩散段组成,如图2所示。低品位热能驱动锅炉产生的高温高压一次流体经由主喷嘴膨胀加速达到超音速,从而形成低压力区,因而二次流体被携带并进入混合室。在此,二次流体通过剪切作用与主射流进行快速混合,形成动量和能量的交换,混合导致的代价为一次流速度不断降低,而二次流流速增加,并在等面积段处两股流体完全混合。在等面积段下游处,高压区域致使流速经历剧烈的变化,从超音速转变为亚音速,伴随生成的激波引发压缩效应,最终在扩散段中实现压力的进一步提升[13-14]。
蒸汽喷射器的主要几何特征列于表1。由于两股气流的快速混合过程,通过壁面的传热被忽略。在喷射器的数值模拟中,Realizable k-ε和SST k-ω模型是两种常用的湍流模型,二者与实验数据表现出良好的一致性[15]。然而,在实际仿真过程中,采用SST k-ω模型时,模拟过程容易出现收敛性问题。鉴于这些考虑,本文选择使用Realizable k-ε模型,同时采用增强壁面函数,以确保模拟的稳定性。将一次流入口和二次流入口设置为压力入口,分别为270260 Pa和1228 Pa。一次流体饱和温度为130℃,二次流体饱和温度为10℃。模拟中采用的几何结构和操作条件取自Sriveerakul T等[16]的实验研究。
-
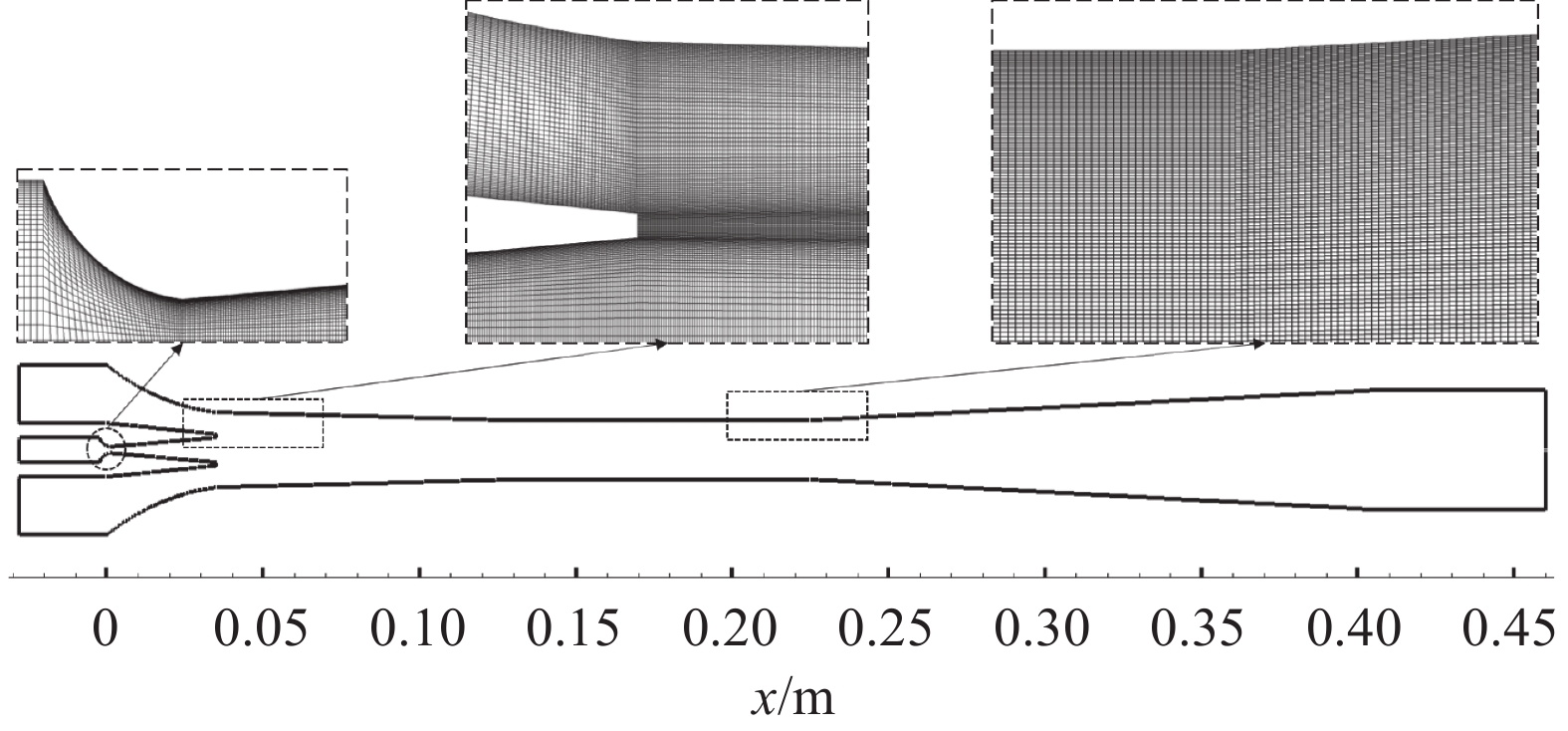
在蒸汽喷射器领域,常采用二维轴对称假设进行数值模拟分析。使用软件ANSYS ICEM软件创建模型计算域与网格,并采用四边形结构化网格,计算区域为喷射器全域,如图3所示。基于喷射器的基本原理,对一次流、二次流混合区域、边界层、结构过渡区域等有可能出现高压力、速度梯度的区域采用更为精密的网格来准确捕捉这些变化,图3中放大处即为主要网格加密区域。
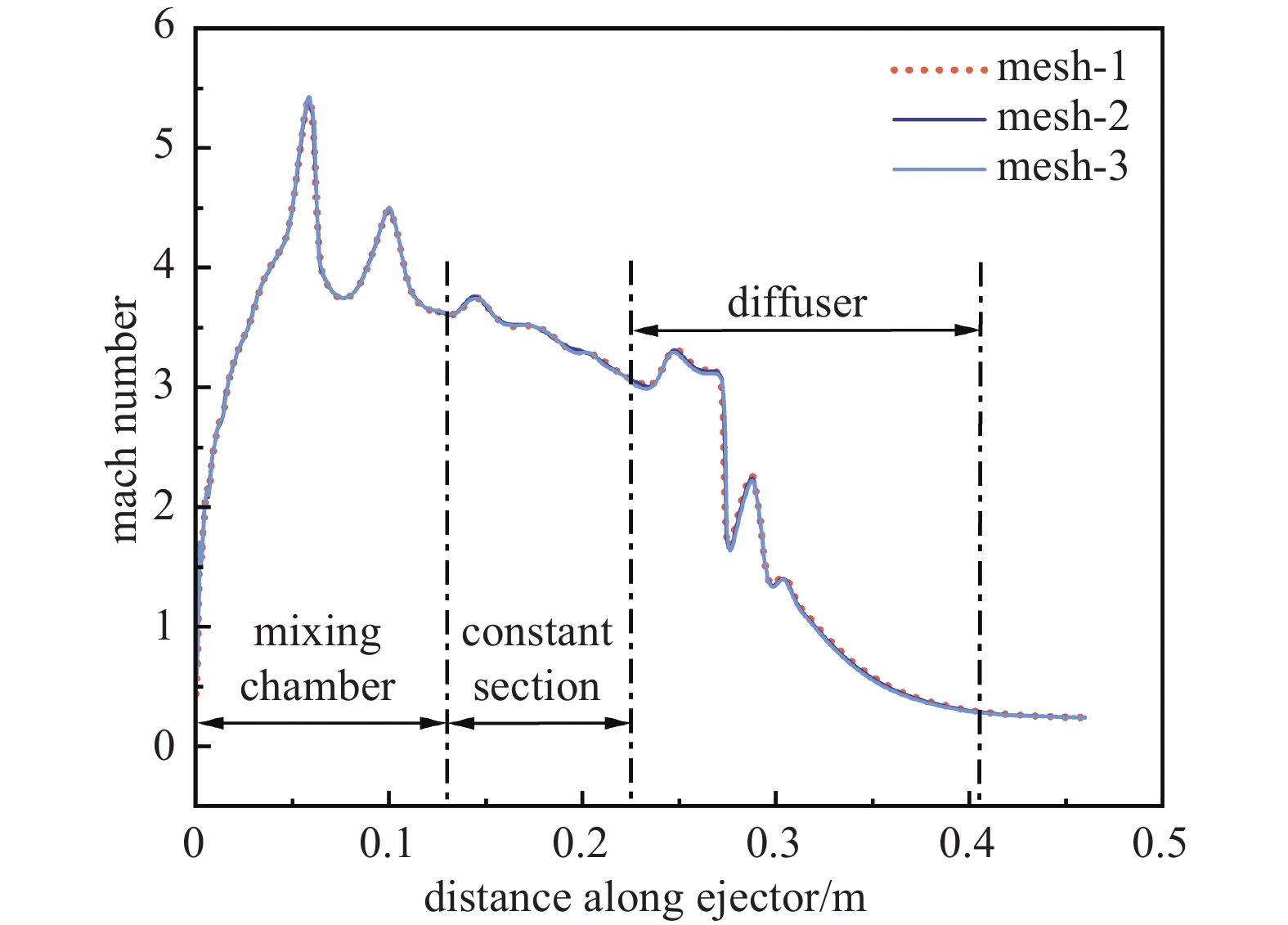
划分了三种网格,分别具有15 w、20 w、40 w个单元。图4为三种网格马赫数对比图,整体趋势十分一致。综合考虑计算精度与速度后,选择方案二的网格进行后续研究。
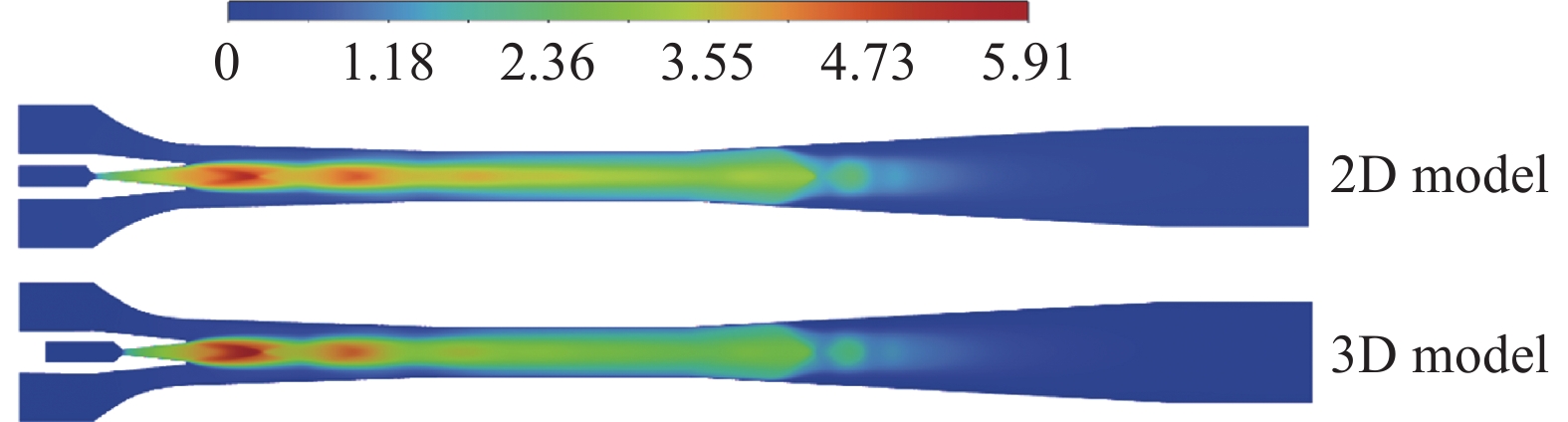
伴随方法不适用于二维轴对称领域,故本文将采用三维模型对喷射器进行伴随方法分析,因此分析比较二维三维模型的差异变得尤为重要。对于三维模型而言,网格数量较大,选择500 w网格数量的结构进行后续仿真分析。图5为二维三维马赫数沿轴对称对比图,可见二维与三维差异很小。由于三维模型网格数量庞大,故本文仅在使用伴随方法时考虑三维模型。
-
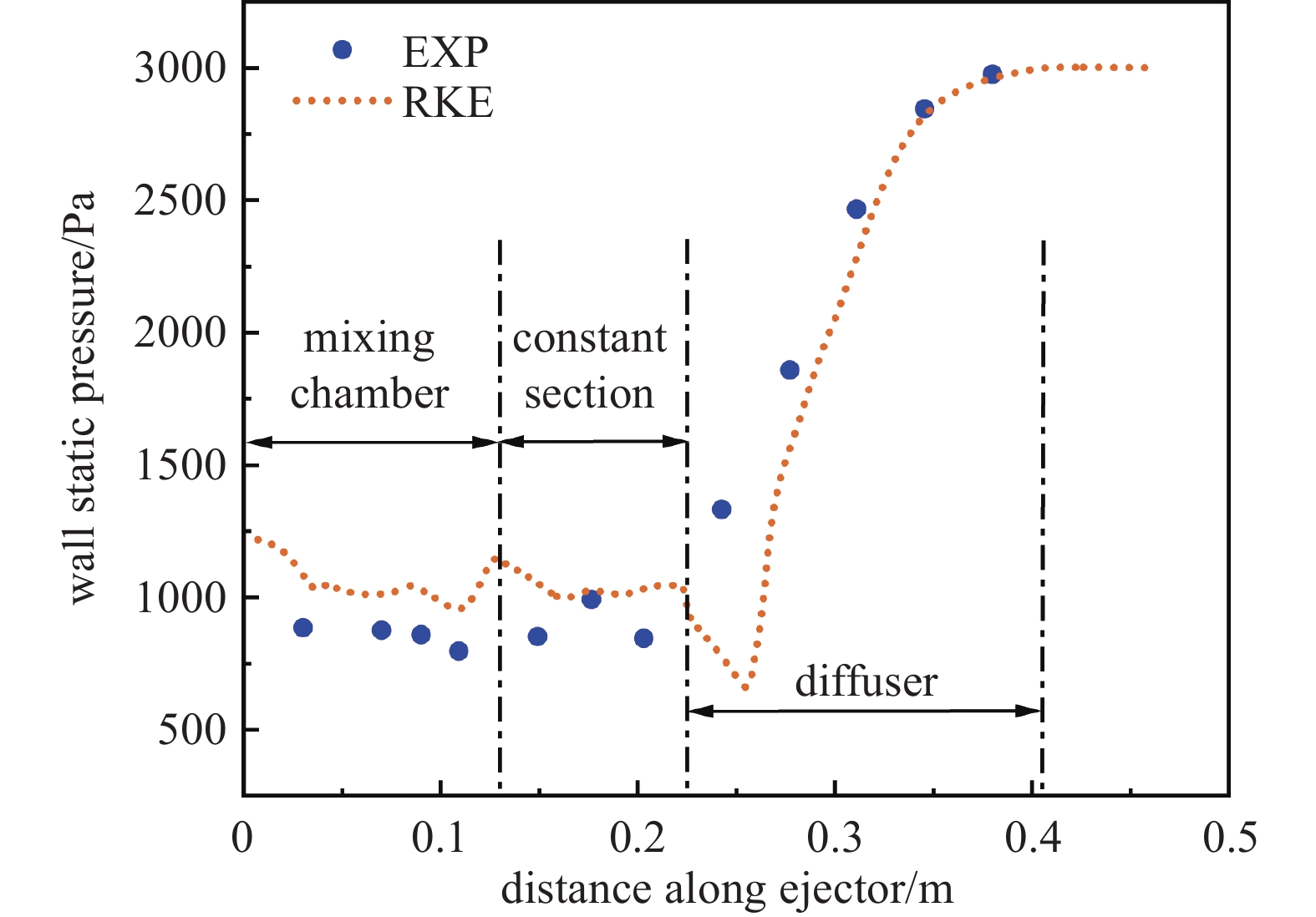
图6为实验与Realizable k-ε湍流模型仿真模拟的壁面静压分布图,本文中实验数据来源于Sriveerakul T等[16]的实验研究。由图中可得,在整个轴向范围内,仿真结果与实验数据的总体趋势基本一致,展现了仿真模型的可靠性。
-
伴随方法是一种用来计算单一输出变量相对于所有变量的导数的工具。伴随方法蒸汽喷射器内部的流动被认为是稳定可压缩的,由N-S方程、连续性方程和能量方程控制。本文将喷射系数作为优化目标,即目标函数:
在给定流场情况下,目标函数可以定义为喷射器的结构参数c与其所对应的流场变量q的函数[17]:
N–S方程其收敛情况下其数值残差为:
当设计变量网格节点位置发生改变时,目标函数同样会发生改变:
式中可以直接通过结构变化获得,故可通过以下步骤,利用
$\delta c$ 替换$\delta q$ 。控制方程残差的变分为[18]:定义拉格朗日乘数:
将公式(3)带入公式(6)中,可得:
对公式(6)进行求导,并联立公式(3)与公式(6)可得:
依据转自共轭原则,即:
公式(8)即可简化为:
通过求解该方程并评估目标函数对于结构参数变化的梯度。
-
利用伴随求解器对蒸汽喷射器进行敏感性分析。与流场计算相似,首先需要进行伴随计算。将收敛条件设置为所有方程的残差小于10−5。相较于传统的参数化方法,伴随方法提供了一种可视化方案来评估形状对于目标函数,即ER值的参数敏感性关系。
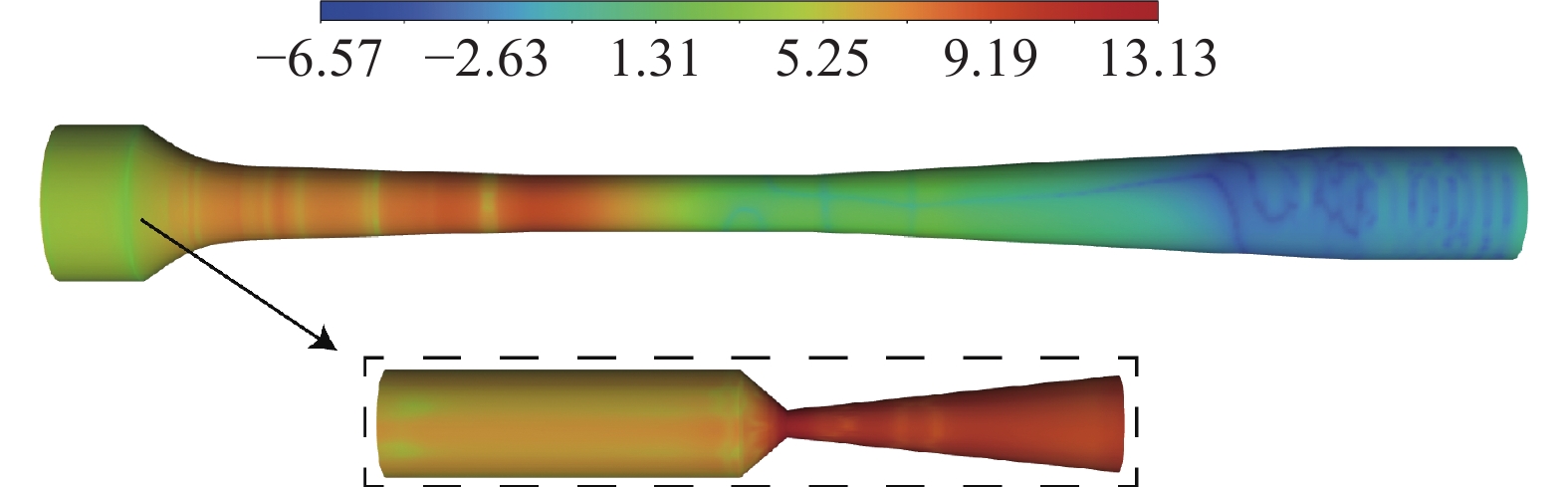
图7为蒸汽喷射器敏感性分析图。从图中可看出,主喷嘴区域的形状变化对于喷射系数而言十分敏感,其次为第一激波区域以及高压力、速度梯度区域。喷射器扩散段区域的形状改变量对喷射系数的影响微乎其微。故本文首先将对上诉区域中的重要参数进行单因素分析,通过追寻喷射系数变化原因。
-
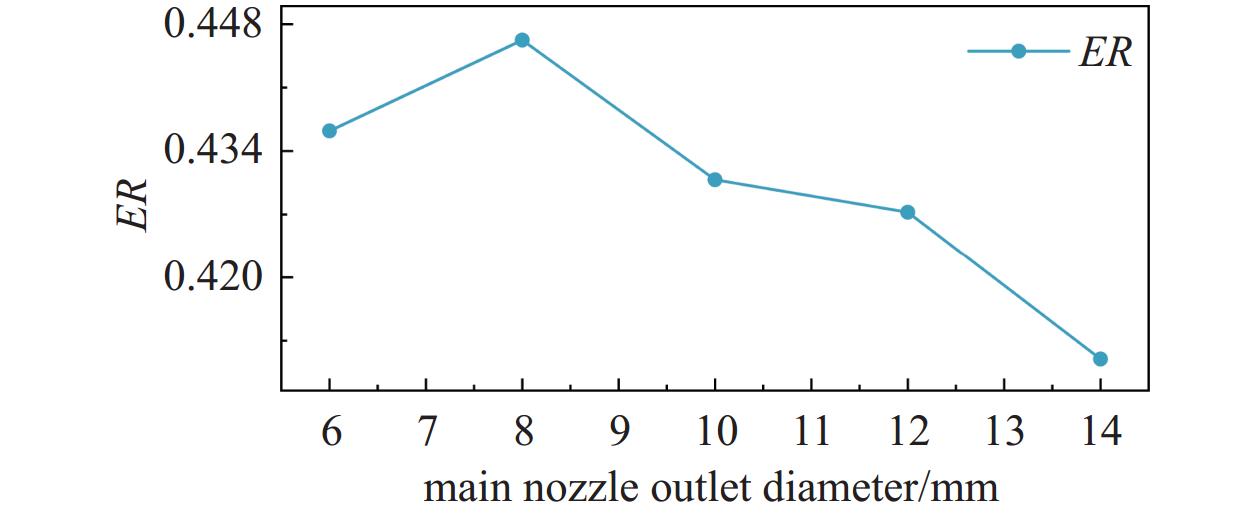
图8为喷射器性能受主喷嘴出口直径影响的可视化结果。直径的改变将导致主喷嘴出口速度发生明显改变。可见,随着直径的增加,喷射系数呈现出先上升后下降的趋势,表明存在一个优化点使得喷射系数达到峰值。
-
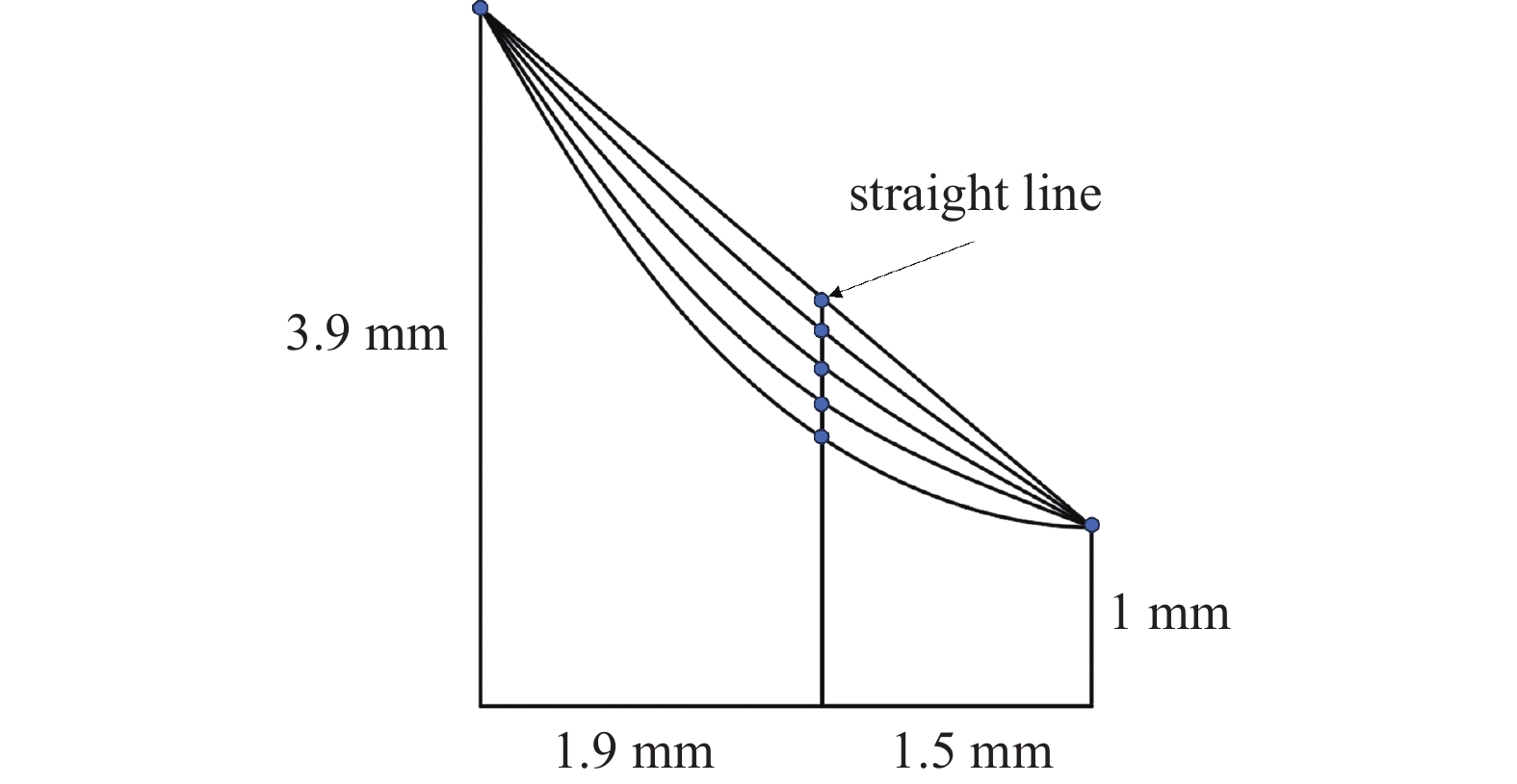
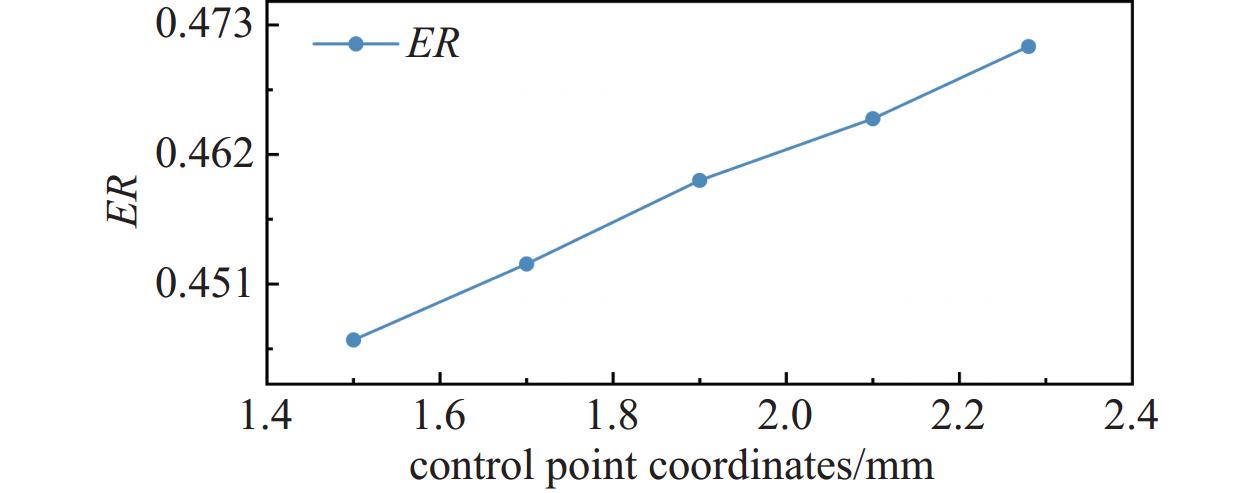
样条曲线广泛应用于建模、设计以及流体力学领域,样条曲线可以保证曲线的平滑过渡,以减少流动分离、降低阻力。图9为不同控制点位置下,喷射器主喷嘴收缩段形状曲线的示意图。随着控制点坐标的变化,最大曲率不断增加。
图10为主喷嘴收缩段形状曲线与喷射器性能的关系图,从图中可看出,随着曲率的不断减少,射流动量减弱,二次流阻流面积不断扩张,直至变为直线,喷射系数不断增加,意味着喷射器的引射能力不断加强。
-
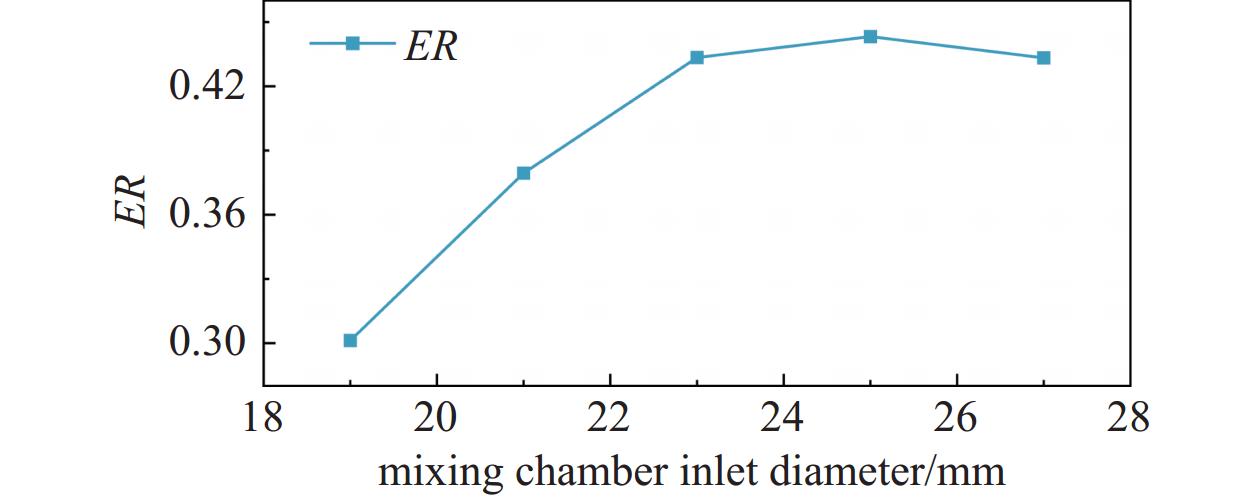
图11揭示了喷射系数随喷嘴出口直径的变化规律,由于固定了主喷嘴出口直径喉管直径,一次流质量流量未发生明显变化,喷射系数表现为先上升后下降,说明存在最优解使得喷射系数最大。降低入口直径将降低一次流与二次流的剪切混合和粘性作用,混合室内射流动量过大,压缩了二次流的流动面积,喷射器的夹带能力降低。
-
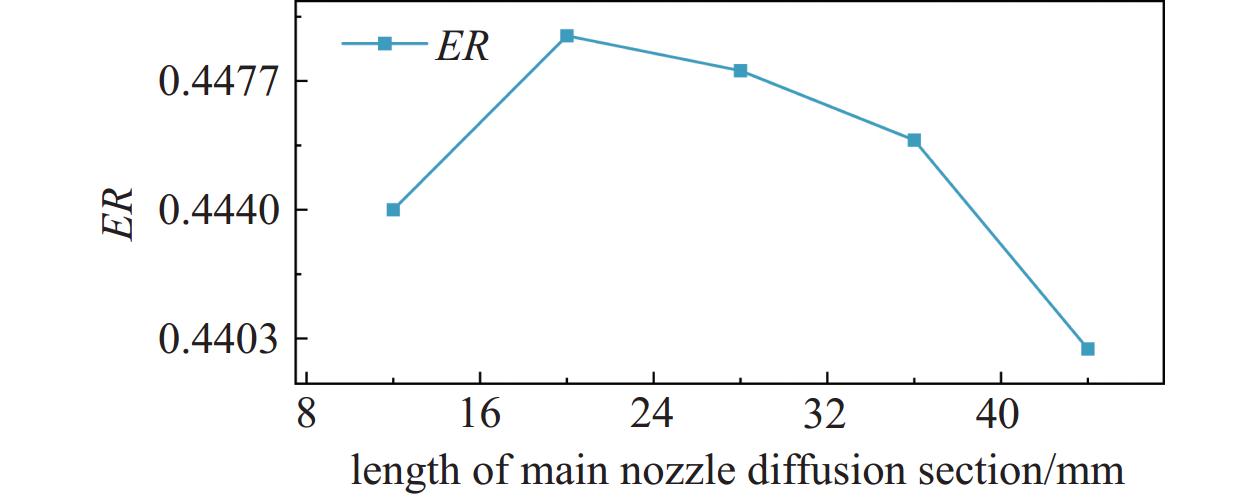
图12展示了喷射系数与主喷嘴扩散段长度之间的变化关系。随着扩散段长度的增加,喷射系数首先显著增加,表明扩散段的增加有助于改善喷射性能。然而,当扩散段长度超过某一临界值后,喷射系数开始减小,过长的扩散段可能导致喷射性能的下降。在优化喷嘴结构时,扩散段长度的选择需要权衡喷射性能与结构的整体性能效果,避免扩散段长度过长而导致对性能的反向影响。
-
单因素分析可量化单一特定因素对目标的影响,在描述参数独立影响方面具有优势,然而在揭示关键结构参数间的复杂交互作用时存在局限性。为克服局限性并更全面优化蒸汽结构,同时减少实验次数,本文采用正交实验方法。
将主喷嘴出口直径、混合室入口直径、控制点坐标以及扩散段长度这三个因数作为优化对象,以喷射系数作为优化对象,每个对象选取三个水平,共计采用九组试验,记作L9(34)。依据正交表中的各个结构,建立九组模型并进行仿真计算,以得出喷射系数值,如表2、3所示。
采用极差分析的方式,对结果进行显著性分析。依据R值判断,主喷嘴收缩段形状曲线对喷射器性能影响最大。同时ki值最大的水平即为该因素的最优水平,则依据ki可得最佳配置为:A1B2C3D3,然而由于部分因素的水平响应均值差异较小,可能导致最佳配置并非全局最优值。因此在原正交试验的基础上,采用控制变量法进行补充分析,仅调整单一因素的水平,并增加试验次数,重新进行仿真模拟,对喷射系数进行更精细的分析。最终,进一步优化后的参数组合为A1B3C3D3,相较于原型,优化后的ER值提高了7.6%。
-
依据前文中的优化分析,得出了最优的结构参数解,三维模型得出的ER值为0.469。依据敏感性分析结果,本文将专注于主喷嘴区域作为网格变形限制区域。在伴随方法中,通过多次流场与伴随计算逐步优化几何形状,以提高目标函数。这种反复调整和优化的过程被称为迭代,然而,迭代过程并非无限进行。终止条件包括多种情况,如达到预期的优化目标,网格变形异常导致流量下降过大或内部结构扭曲不符合实际情况。将优化目标设置为提高ER值,迭代以提高25%ER值作为目标,选择此目标的原因为避免过大的ER值致使临界背压值,即喷射器以最大能力工作时的最终压力过低。
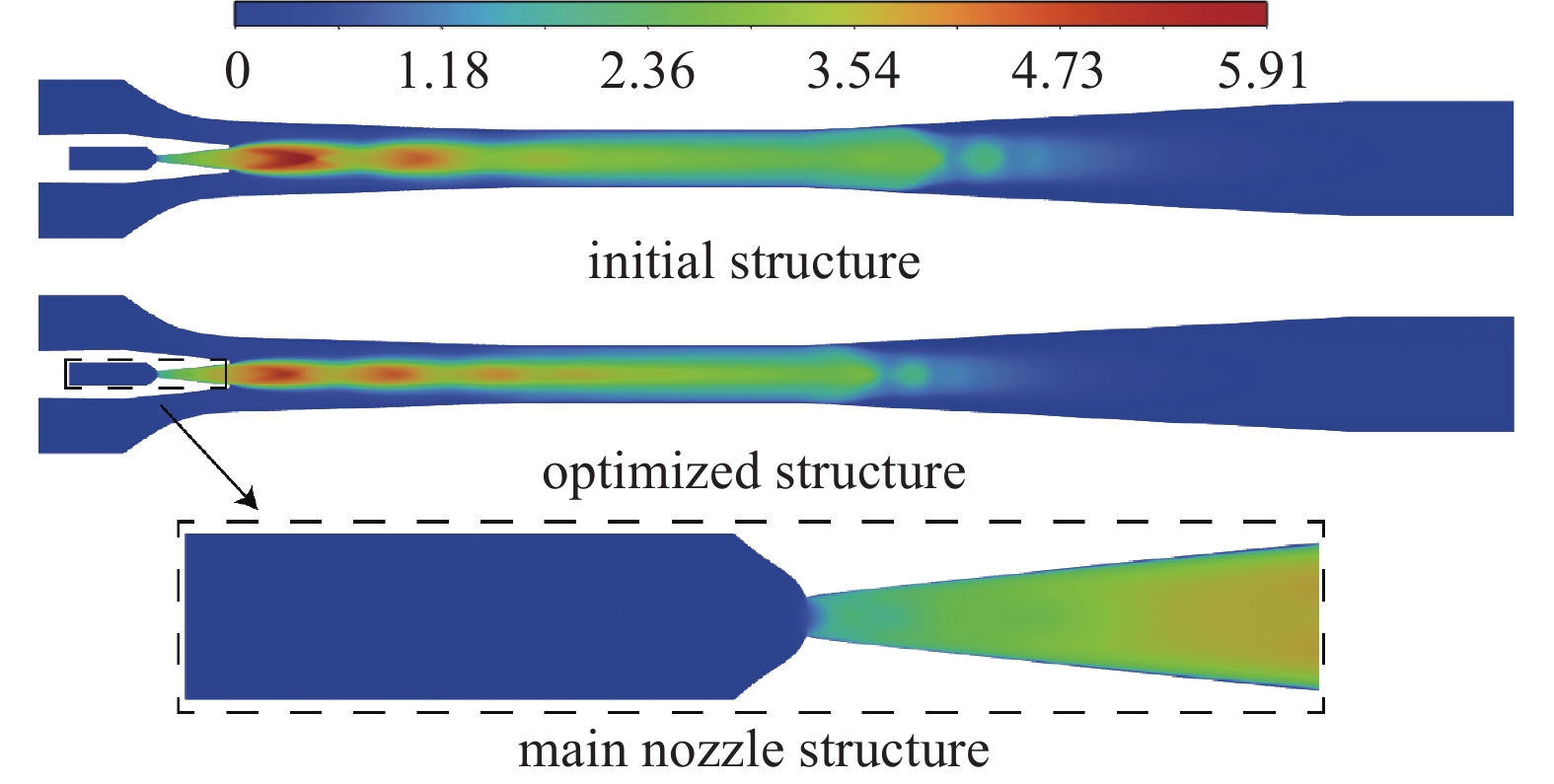
图13展示了结构优化前后的马赫数分布轮廓,并放大了主喷嘴区域以直观地对比其形状的变化,ER值增大至0.594,相较于初始结构,提高了26.7%。从图中可以清晰看出,主喷嘴的收缩段区域发生了显著的几何改变。优化后的收缩段区域呈现出外凸的特征,这一外凸部分由两部分构成:第一部分为较为陡峭的前段,锥形结构设计使流体在进入喷嘴扩张段之前可以得到快速加速的效果;第二部分为曲率半径较大的后段,可以实现更平滑的过渡,增强流动的均匀性和稳定性。这种外凸设计与传统的内凹式曲线有显著不同,内凹式设计通常侧重于通过更急剧的收缩来提升流速,但同时可能引发能量损失,而优化后的外凸形状通过合理的曲线分段过渡,既实现了初期流动的加速效果,又有效地降低了能量损失。这样的结构改进显著提升了喷嘴的性能,使得ER值达到了预期目标。
-
本研究的主要内容在于通过优化蒸汽喷射器的结构参数,提高喷射系数以适应实际的工业需求。本文得出的结论如下:
(1)伴随方法能够有效识别流场中的敏感区域,并通过可视化方式呈现,能够帮助快速识别对喷射性能影响最大的关键区域。
(2)建立L9(34)正交表,通过极差分析筛选出最优结构参数组合,使ER值提高了7.6%。
(3)经过伴随优化多次迭代后,主喷嘴收缩段线型呈现出分段式外凸曲线。相较于传统内凹或者锥形收缩段设计,分段式外凸曲线减缓了内凹设计可能带来的能量损失,改善了流动的稳定性,使得ER值进一步提高了26.7%。
基于伴随优化和正交实验的蒸汽喷射器结构优化
Optimization of Steam Ejector Structure Based on Adjoint Optimization and Orthogonal Experiment
-
摘要: 作为蒸汽喷射器制冷系统(ERS)中的核心组件,蒸汽喷射器的性能对整体系统的运行效果具有重要影响,其性能的优劣直接决定了制冷效率。将伴随方法应用于喷射器领域,建立了可视化方案对喷射器进行敏感性分析,筛选出关键结构参数;通过单因素分析方法确定关键结构参数的水平范围,建立L9(34) 正交表,得出最优结构参数组合;对最优结构参数组合的主喷嘴结构采用伴随优化方法进一步优化。研究表明:伴随方法能够在复杂的几何结构中快速识别出影响性能的关键区域;正交实验得到的最优结构参数组合使喷射系数(ER)值提升7.6%,伴随优化方法使ER值再次提高26.7%;主喷嘴收缩段采用分段式外凸曲线能够使流体在喷嘴区域实现更平滑的流体加速过程,减缓了能量损失,将显著提高喷射器的性能。Abstract: As the core component of the steam ejector refrigeration system (ERS), the performance of the steam ejector has a significant impact on the overall system's operation, directly determining the refrigeration efficiency. The adjoint method is applied to the ejector field, and a visualization scheme is established for sensitivity analysis to identify key structural parameters. The range of levels for the key parameters is determined through single-factor analysis, and an L9(34) orthogonal table is constructed to derive the optimal structural parameter combination. The adjoint optimization method is further applied to optimize the main nozzle structure of the optimal parameter combination. The study shows that the adjoint method can quickly identify key regions affecting performance in complex geometries. The optimal parameter combination obtained through orthogonal experiments improves the ejector's entrainment ratio (ER) by 7.6%, while the adjoint optimization method further increases the ER by 26.7%. The use of a segmented convex curve for the nozzle contraction section enables a smoother fluid acceleration process in the nozzle region, reducing energy loss and significantly enhancing the ejector's performance.
-
Key words:
- Ejector /
- Adjoint Optimization /
- Orthogonal Experiment /
- Nozzle /
- Computational Fluid Dynamics .
-

-
表 1 蒸汽喷射器的主要几何参数
Table 1. Main geometrical parameters of the steam ejector
几何形状 数值 喷嘴喉部直径 2 mm 喷嘴出口位置 35 mm 喷嘴扩散段长度 34 mm 喷嘴出口直径 8 mm 等面积段长度 95 mm 扩散段长度 180 mm 混合室长度 130 mm 表 2 正交水平表
Table 2. Orthogonal level list
A/mm B/mm C/mm D/mm Leve 1 7 23 1.9 16 Leve 2 8 24 2.09 20 Leve 3 9 25 2.28 24 表 3 正交表
Table 3. Orthogonal list
A B C D ER 1 1 1 1 1 0.447 2 1 2 2 2 0.47 3 1 3 3 3 0.48 4 2 1 2 3 0.456 5 2 2 3 1 0.475 6 2 3 1 2 0.454 7 3 1 3 2 0.458 8 3 2 1 3 0.45 9 3 3 2 1 0.457 k1 0.466 0.454 0.45 0.46 k2 0.462 0.465 0.462 0.461 k3 0.455 0.464 0.471 0.462 R 0.011 0.011 0.021 0.002 -
[1] Besagni G, Mereu R, Inzoli F. Ejector refrigeration: A comprehensive review[J]. Renewable and Sustainable Energy Reviews,2016,53:373−407 doi: 10.1016/j.rser.2015.08.059 [2] Ma X, Zhang W, Omer S A, et al. Experimental investigation of a novel steam ejector refrigerator suitable for solar energy applications[J]. Applied Thermal Engineering,2010,30(11-12):1320−1325 doi: 10.1016/j.applthermaleng.2010.02.011 [3] Ghaebi H, Parikhani T, Rostamzadeh H, et al. Proposal and assessment of a novel geothermal combined cooling and power cycle based on Kalina and ejector refrigeration cycles[J]. Applied Thermal Engineering,2018,130:767−781 doi: 10.1016/j.applthermaleng.2017.11.067 [4] Ruangtrakoon N, Aphornratana S, Sriveerakul T. Experimental studies of a steam jet refrigeration cycle: effect of the primary nozzle geometries to system performance[J]. Experimental thermal and fluid science,2011,35(4):676−683 doi: 10.1016/j.expthermflusci.2011.01.001 [5] Fu W, Li Y, Liu Z, et al. Numerical study for the influences of primary nozzle on steam ejector performance[J]. Applied Thermal Engineering,2016,106:1148−1156 doi: 10.1016/j.applthermaleng.2016.06.111 [6] Hu J, Shi J, Liang Y, et al. Numerical and experimental investigation on nozzle parameters for R410A ejector air conditioning system[J]. International journal of refrigeration,2014,40:338−346 doi: 10.1016/j.ijrefrig.2013.12.008 [7] Chunnanond K, Aphornratana S. An experimental investigation of a steam ejector refrigerator: the analysis of the pressure profile along the ejector[J]. Applied thermal engineering,2004,24(2-3):311−322 doi: 10.1016/j.applthermaleng.2003.07.003 [8] 张国玉, 王晓冬, 刘静雯. 喷嘴出口状态对水蒸汽喷射器流动行为及其性能的影响[J]. 真空科学与技术学报,2023,43(9):762−770 (in Chinese) Zhang G Y, Wang X D, Liu J W. Numerical investigation of the nozzle exit state and its effect on the performance of the steam ejector[J]. Chinese Journal Vacuum Science and Technology,2023,43(9):762−770 [9] Ruangtrakoon N, Thongtip T, Aphornratana S, et al. CFD simulation on the effect of primary nozzle geometries for a steam ejector in refrigeration cycle[J]. International Journal of Thermal Sciences,2013,63:133−145 doi: 10.1016/j.ijthermalsci.2012.07.009 [10] Reis L B, dos Santos Gioria R. Optimization of liquid jet ejector geometry and its impact on flow fields[J]. Applied Thermal Engineering,2021,194:117132 doi: 10.1016/j.applthermaleng.2021.117132 [11] Zhang G, Dykas S, Yang S, et al. Optimization of the primary nozzle based on a modified condensation model in a steam ejector[J]. Applied Thermal Engineering,2020,171:115090 doi: 10.1016/j.applthermaleng.2020.115090 [12] Ahmed F, Chen W. Investigation of steam ejector parameters under three optimization algorithm using ANN[J]. Applied Thermal Engineering,2023,225:120205 doi: 10.1016/j.applthermaleng.2023.120205 [13] Sriveerakul T, Aphornratana S, Chunnanond K. Performance prediction of steam ejector using computational fluid dynamics: Part 2. Flow structure of a steam ejector influenced by operating pressures and geometries[J]. International Journal of Thermal Sciences,2007,46(8):823−833 doi: 10.1016/j.ijthermalsci.2006.10.012 [14] Xiao J, Wu Q, Chen L, et al. Assessment of different CFD modeling and solving approaches for a supersonic steam ejector simulation[J]. Atmosphere,2022,13(1):144 doi: 10.3390/atmos13010144 [15] Han Y, Wang X, Sun H, et al. CFD simulation on the boundary layer separation in the steam ejector and its influence on the pumping performance[J]. Energy,2019,167:469−483 doi: 10.1016/j.energy.2018.10.195 [16] Sriveerakul T, Aphornratana S, Chunnanond K. Performance prediction of steam ejector using computational fluid dynamics: Part 1. Validation of the CFD results[J]. International Journal of Thermal Sciences,2007,46(8):812−822 doi: 10.1016/j.ijthermalsci.2006.10.014 [17] Czerwiński G, Wołoszyn J. Optimization of air cooling system using adjoint solver technique[J]. Energies,2021,14(13):3753 doi: 10.3390/en14133753 [18] Roth R, Ulbrich S. A discrete adjoint approach for the optimization of unsteady turbulent flows[J]. Flow, turbulence and combustion,2013,90:763−783 doi: 10.1007/s10494-012-9439-3 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: